Enhancing Electric Vehicle Charger Performance with Synchronous Boost and Model Predictive Control for Vehicle-to-Grid Integration

Abstract

This paper investigates optimizing the power exchange between electric vehicles (EVs) and the grid, with a specific focus on the DC-DC converters utilized in vehicle-to-grid (V2G) systems. It specifically explores using model predictive control (MPC) in synchronous boost converters to enhance efficiency and performance. Through experiments and simulations, this paper shows that replacing diodes with SIC MOSFETs in boost converters significantly improves efficiency, particularly in synchronous mode, by minimizing the deadtime of SIC MOSFETs during switching. Additionally, this study evaluates MPC’s effectiveness in controlling boost converters, highlighting its advantages over traditional control methods. Real-world validations further validate the robustness and applicability of MPC in V2G systems. This study utilizes TMS320F28379D, one of Texas Instruments’ leading digital signal processors, enabling the implementation of MPC with a high PWM frequency of up to 200 MHz. This processor features dual 32-bit CPUs and a 16-bit ADC, allowing for high-resolution readings from sensors. Leveraging digital signal processing technologies and advanced electronic circuits, this study advances the development of high-performance boost converters, achieving power outputs of up to 48 watts and output voltages of 24 volts. Electronic circuits (PCB boards) have been devised, implemented, and evaluated to showcase their significance in advancing efficient V2G integration.

1. Introduction

Electric vehicles (EVs) present a highly competitive and promising transportation alternative compared to internal combustion engine (ICE) vehicles, primarily due to their contributions to carbon neutrality and resource efficiency [1]. They bring forth a multitude of benefits, including reduced greenhouse gas emissions and access to preferential parking. Among these advantages, electric vehicle manufacturers and proponents are emphasizing the potential of vehicle-to-grid (V2G) charging. This innovative approach allows an EV’s battery to supply power to utilities. V2G charging offers advantages not only to EV owners but also strengthens the electrical grid while providing financial incentives. There are two charging alternatives: OFF-board and On-board [2]. Bidirectional on-board converters are essential for electric vehicles (EVs) to operate in V2X mode [3,4]. In V2G mode, a collaborative effort between a front-end AC-DC converter and a back-end DC-DC converter enables the transfer of energy from an EV’s battery back to the grid. To ensure successful V2G operation, the DC-link voltage must exceed the peak voltage of the grid. It is important to note that the battery voltage typically remains lower than the DC-link voltage. Therefore, a DC-DC step-up converter is necessary [5]. Within the context of V2G functionality, the DC-DC converter operates in boost mode, also known as discharging mode, as shown in Figure 1. The DC-DC boost converter is a widely used for connecting the PV array to the DC link [6,7]. Boost converters commonly employ a PI controller in conjunction with pulse width modulation (PWM) for control [8]. When constructing the control loop for power electronic converters, it is advisable to consider the average model, which may introduce offset errors and is not well-suited for linear controllers [9]. Recently, model predictive control (MPC) has gained significant attention for its application in power converters, benefiting from advancements in control theory and the maturation of digital signal processing technologies [10,11]. In summary, the MPC algorithm assimilates the system’s states to predict subsequent states, iteratively updating predictions with each computation cycle. Unlike traditional PID control, MPC achieves the optimal control sequence by minimizing the cost function [12]. Nevertheless, the conventional finite control set (FCS) MPC algorithm results in a variable switching frequency, which is undesirable due to the potential generation of high acoustic noises and harmonics. Therefore, both the PID controller and MPC have been simulated and realized. This paper introduces a system that employs a battery that discharges the battery into a resistor load to compare different algorithms. To improve the system, a synchronous boost configuration was implemented. To enhance the system further, a DSP board, specifically the F28379D DSP launchpad, was utilized. This DSP board features dual CPUs, each operating at a speed of 100 MHz, and 16 ADC pins with high-resolution capabilities at 12/16 bits. The proposed converter was initially simulated on MATLAB-Simulink 2023a, and output voltage results for both PID and MPC algorithms were obtained. Subsequently, the converter was implemented on the DSP board, and output voltage measurements were conducted using the board’s ADC.

To ensure precision, a gain was employed to align the real value with the reference voltage, thereby maintaining output voltage equality. This article is structured into specific sections: Section 2 provides an overview of the detailed DC-DC converter model, while Section 3 focuses on the PID algorithm. Section 4 further explores the proposed model predictive algorithm. Section 5 introduces the Hardware in the Loop (HIL) concept, with a more detailed discussion in Section 6. The results from simulations and experiments are detailed in Section 7, and this paper wraps up with Section 8.

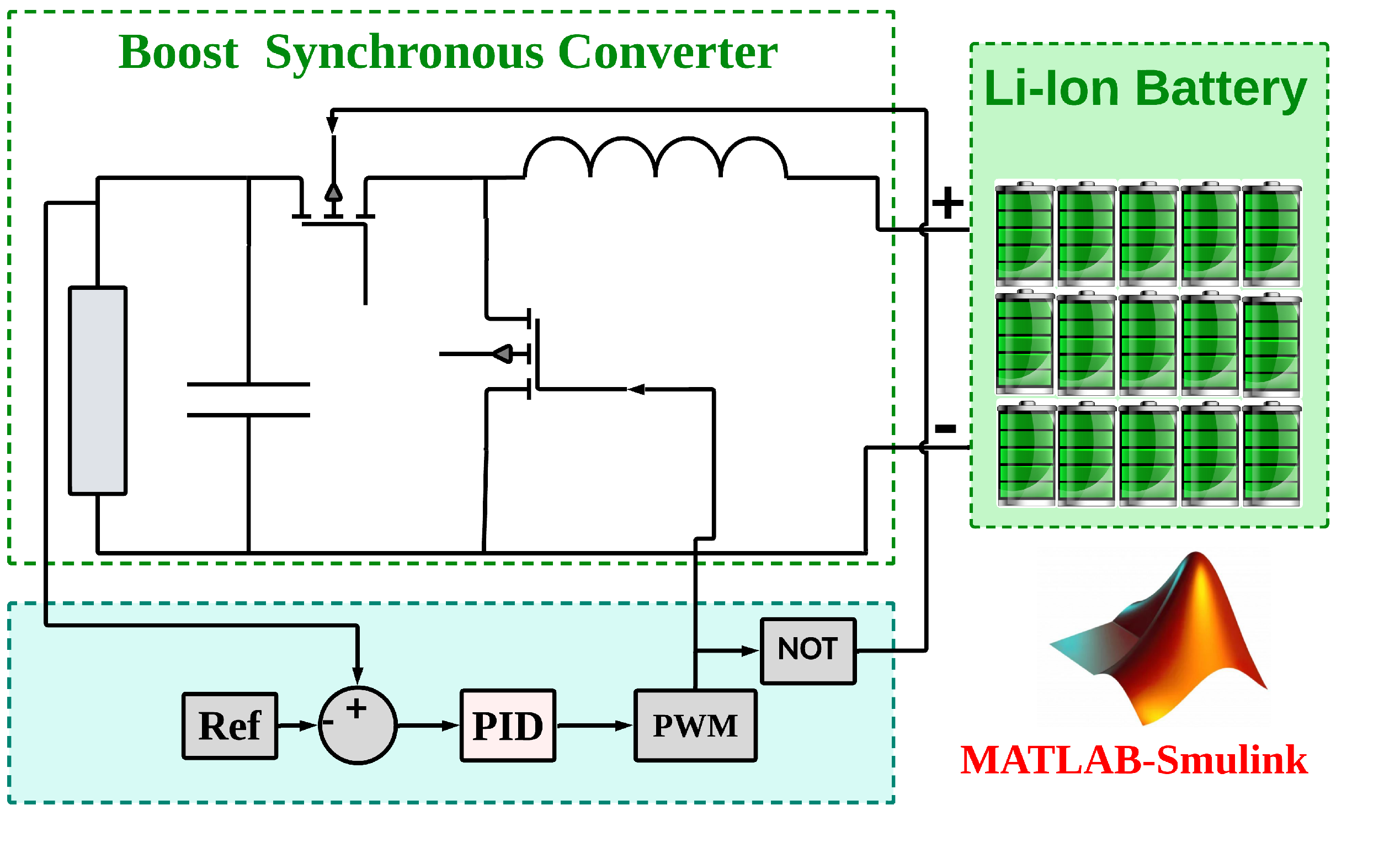
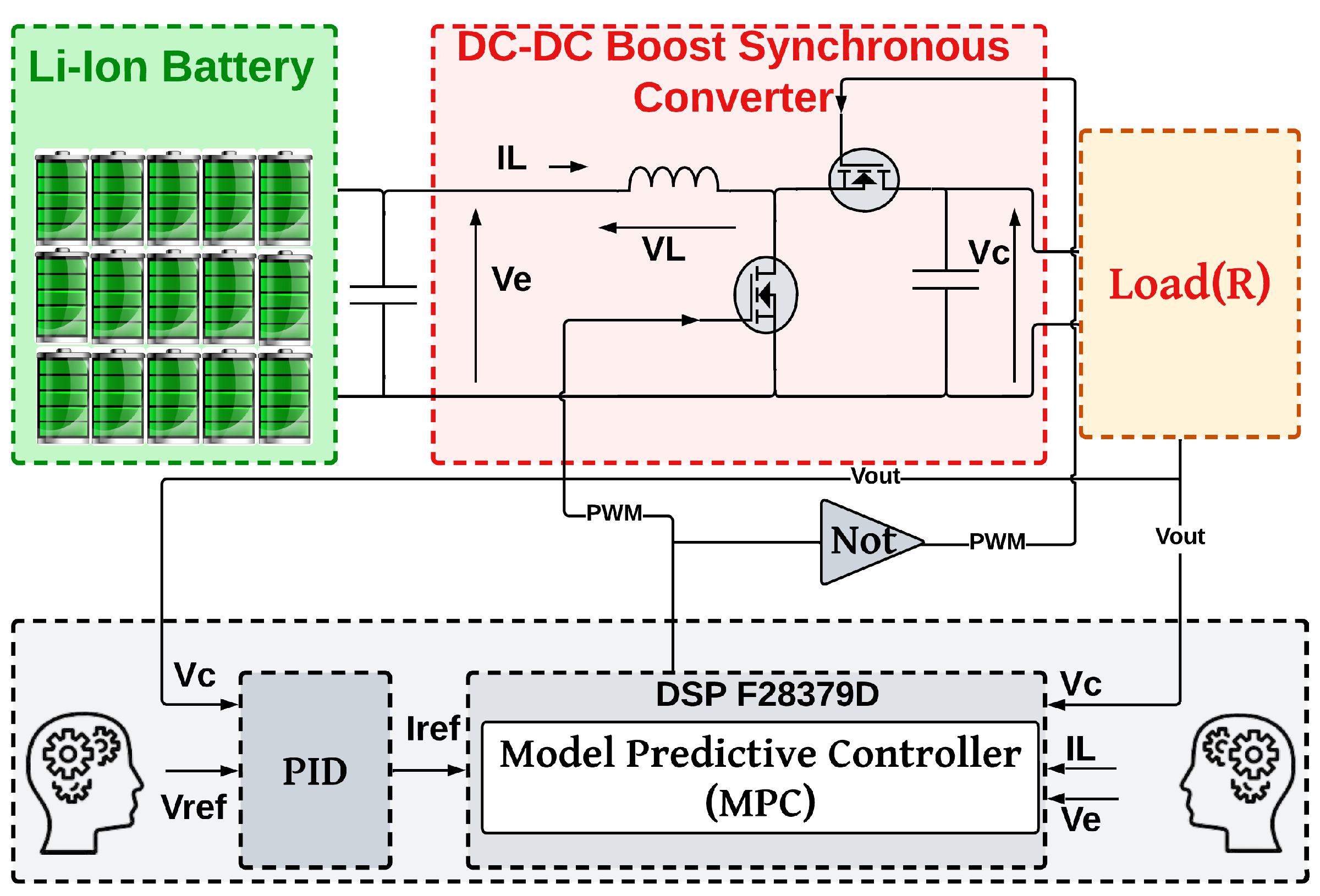
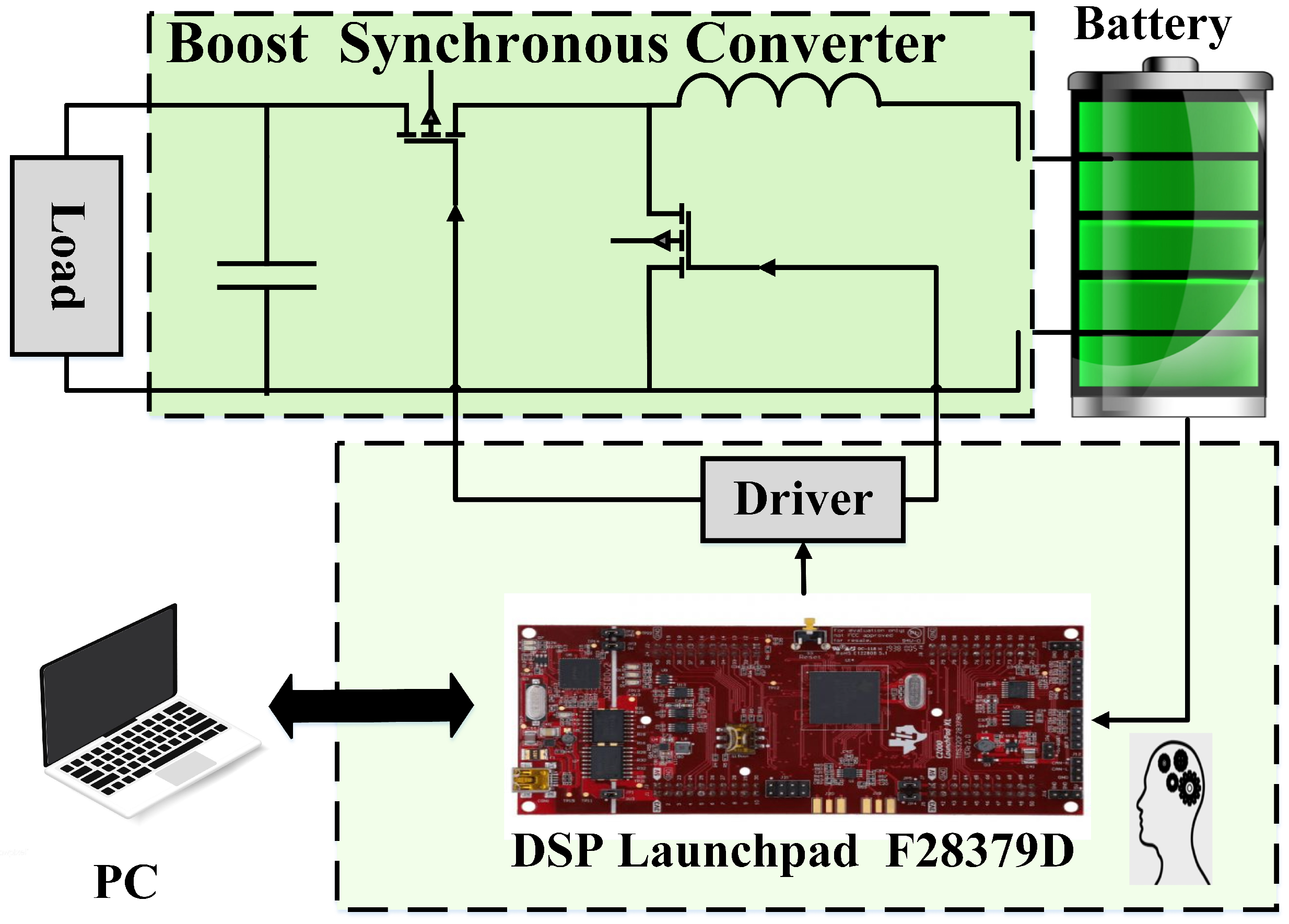
2. DC-DC Boost Converter

A traditional DC-DC Boost converter comprises fundamental components: a boost inductor, two semiconductor devices (a diode and a transistor), and an output capacitor connected in parallel with the load, as illustrated in Figure 2.

The output voltage of a boost synchronous converter, often recognized as an up-converter, exceeds the input voltage. A basic DC source, such as a battery, can function as the input for a boost synchronous converter, or alternatively, it can be sourced through a rectifier directly from an AC source, like a solar panel. The fundamental principle behind the Boost converter lies in the inductor’s inherent resistance to abrupt changes in current, attributed to fluctuations in the magnetic field. Boost synchronous converters are recognized to operate in two distinct modes. Switching action is achieved using MOSFETs or IGBTs. Due to its superior processing speed when compared to IGBTs, MOSFETs are favored for low-voltage applications. Transistors switching period is given by

Mode 1:

$$T_{ON}=D·T_r$$

(1)

Mode 2:

$$T_{Off}=(1-D)·T_r$$

(2)

The inductor voltage: Mode 1:

$$L\frac{di}{dt}=V_e$$

(3)

Mode 2:

$$L\frac{di}{dt}=V_s-V_e$$

(4)

Putting Equation (1) into Equation (2) of mode 1 and mode 2: Mode 1:

$$L\frac{▵i}{D·T_r}=V_e$$

(5)

Mode 2:

$$L\frac{▵i}{(1-D)·T_r}=V_s-V_e$$

(6)

Ripple current $▵i$: Mode 1:

$$▵i_{On}=\frac{V_{e}D{T}_r}{L}$$

(7)

Mode 2:

$$▵i_{Off}=\frac{(V_s-V_e)(1-D)T_r}{L}$$

(8)

Since the ripple current Equation (1) is equal to Equation (2):

$$▵i_{On}=▵i_{Off}$$

$$V_e·D=V_s-V_e-D(V_s-V_e)$$

$$V_e=V_s-D{V}_s$$

$$\frac{V_s}{V_e}=\frac{1}{1-D}$$

(9)

where $V_e$ is the input voltage, $V_s$ output voltage, $T_r$ switching period, D is the duty cycle, and $▵i$ is the ripple current.

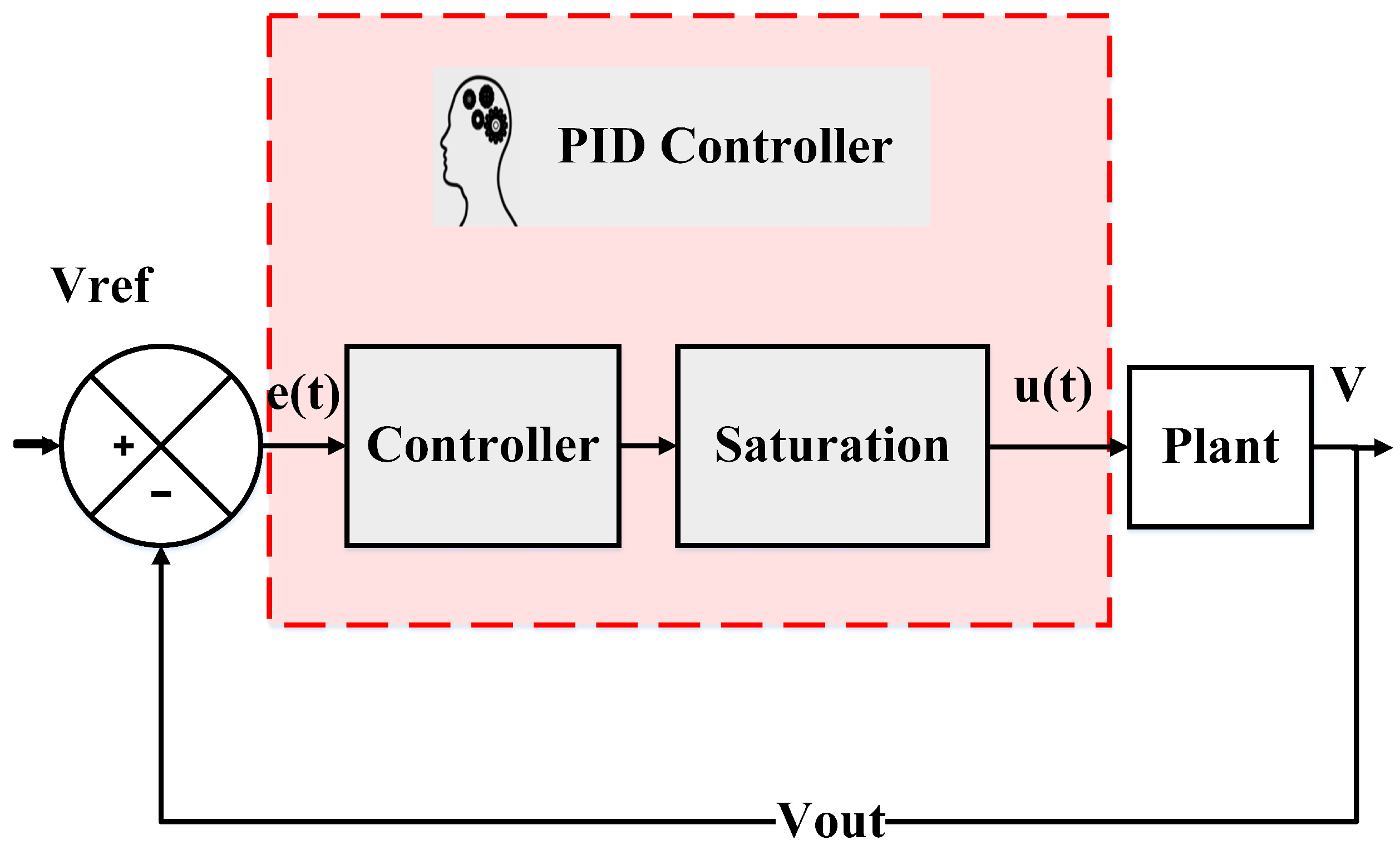
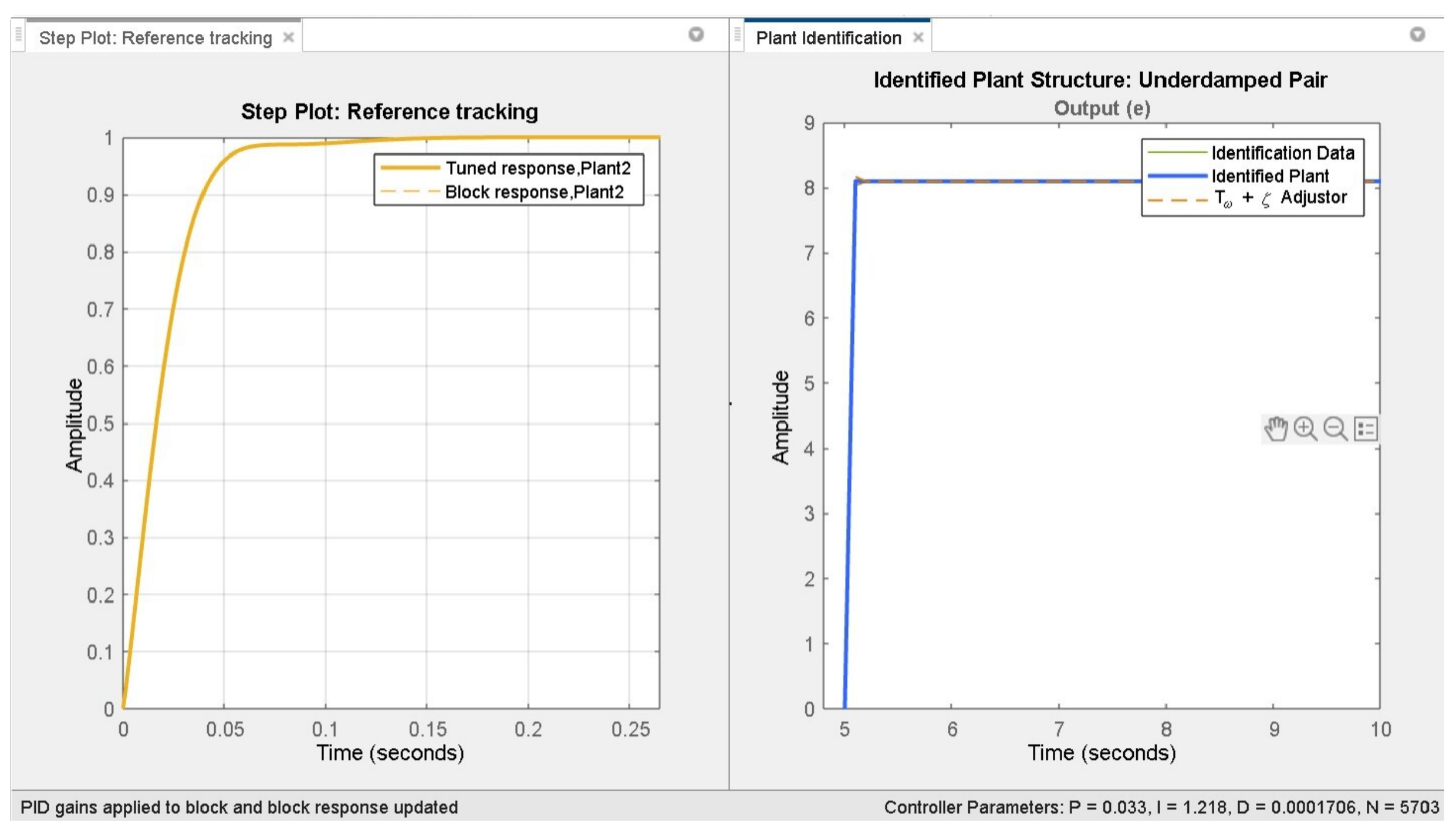
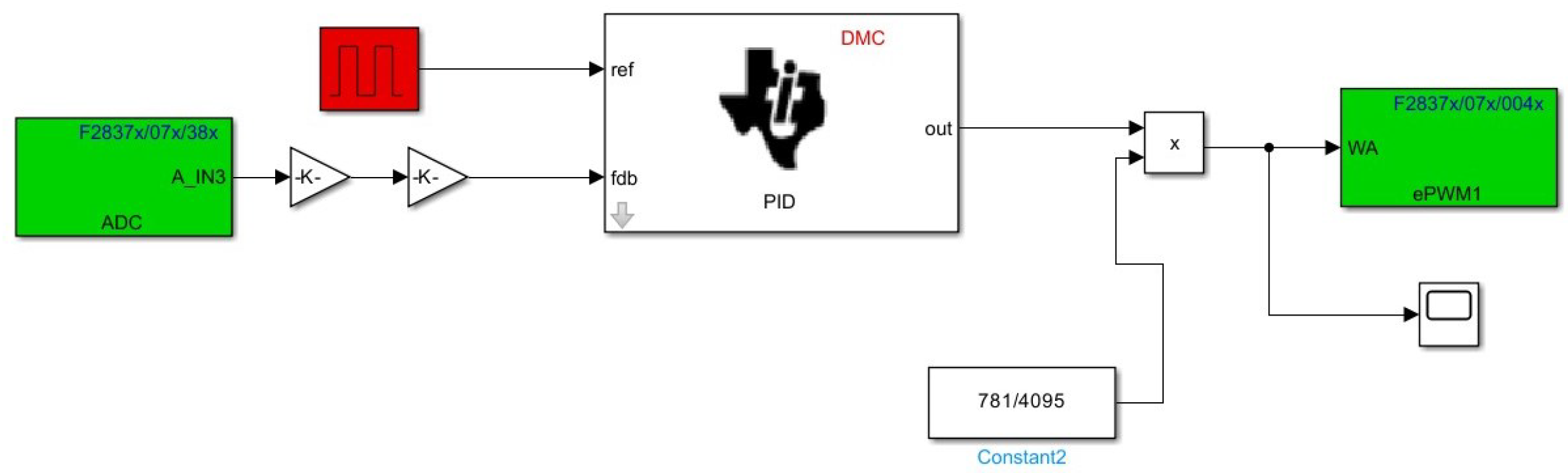
3. PID Controller

Various control methods have been suggested to ensure both stability and rapid transient response, including the fuzzy logic controller, artificial neural network (ANN), PID controller, and PI controller. Additionally, several optimization techniques, such as genetic algorithm, particle swarm optimization, and bacterial foraging optimization, have been put forth [13,14,15,16]. Among the most straightforward and extensively employed controllers for many years, we find the PID controller. The acronym PID corresponds to proportional (P), integral (I), and derivative (D) controllers. The diagram depicted in Figure 3 illustrates the standard block diagram of a PID controller.

The subject of investigation is the system being examined, representing the plant, which is appropriately stimulated to achieve comprehensive closed-loop control with efficacy. A PID controller can be articulated as follows:

$$H_S=K_P+\frac{K_I}{S}+K_{D}S$$

(10)

where $K_P$ is proportional gain, $K_I$ is integral gain, and $K_D$ is derivative gain. The signal e(t), depicted in Figure 3, symbolizes the tracking error derived from the disparity between the input reference signal, denoted as $V_{DC}$, and the actual output signal $V_{Ref}$. This tracking error is directed to the PID controller, which computes the signal’s derivative and integral. The resultant output of the PID controller, labeled as u(t), and applied to the system, is computed by adding the proportional gain ($K_P$) multiplied by the magnitude of the error signal, the integral gain ($K_I$) multiplied by the integral of the error signal, and the derivative gain ($K_D$) multiplied by the derivative of the error signal.

The depicted system, presented in Figure 4, showcases the essential function of the PID controller, which plays a key role in ensuring that the output voltage aligns with the reference voltage. The PID tuning used in MATLAB-Simulink was illustrated in Figure 5 and Figure 6. These figures demonstrate the values of the coefficients of the PID controller based on tuning. The system is visually depicted in Figure 1 through a MATLAB-Simulink simulation. For the initial attempt, we developed a DC-DC converter integrated with a lithium–ion battery. The PID controller coefficients were determined through tuning, a process demonstrated in Figure 7. The goal of the design is to track the reference signal from a Simulink step block. The PID tuner offers a rapid and versatile method to tune single-loop PID controller blocks within Simulink. Using this tool, users can adjust PID controller settings to ensure a strong design with the desired response time. The typical workflow for utilizing the PID tuner includes the following:

(1)

Initiating the PID tuner, which automatically derives a linear plant model from the Simulink model and crafts an initial controller design.

(2)

Adjusting the controller within the PID tuner by modifying design parameters across two design modes. The tuner then calculates PID settings that effectively stabilize the system.

(3)

Transferring the tuned controller parameters to the PID controller block and evaluating the controller’s performance within Simulink.

Figure 5 displays the PID controller parameters prior to identification, with values such as a proportional setting of 0.005427, an integral setting close to 2.263, and a derivative setting at 0.0003017. After PID tuning, as illustrated in Figure 6, we refined these values for enhanced system performance and robustness. Specifically, the integral setting was adjusted to 1.218, and the proportional setting now stands at approximately 0.033.

4. Model Predictive Controller (MPC)

Model predictive control (MPC) operates by optimizing a cost function while considering system limitations, utilizing forecasts of upcoming system performance within a set time frame. Due to the stability concerns associated with a single prediction horizon in MPC, numerous prior studies have employed multiple prediction steps [17,18,19]. However, this approach necessitates a considerable demand for the sampling process and involves complex computations. In [15], an MPC algorithm with a one-prediction horizon is introduced for the boost converter. This algorithm aims to address non-minimum phase issues by incorporating input-state linearization. The main phases of MPC include forecasting, fine-tuning, and executing control measures, which are reiterated with every control cycle. Figure 8 illustrates the circuit diagram of the DC-DC boost synchronous converter, while Figure 9 shows the simulation of synchronouns converter with MPC under MATLAB-Simulink. In this representation, $S_1$ corresponds to the first switch, $S_2$ represents the second switch, $iL$ stands for the inductor, and $V_C$ symbolizes the output capacitor. Disregarding the series resistance, voltage for the subsequent sampling instance can be formulated as follows:

$$S\to 1\to V_L=L\frac{d{i}_L\left(t\right)}{dt}=(V_e-i_L{R}_L)S$$

(11)

$$S\to 0\to V_L=L\frac{d{i}_L\left(t\right)}{dt}=(V_e-i_L{R}_L-V_c)(1-S)$$

(12)

$$\frac{d{i}_L\left(t\right)}{dt}=\frac{1}{L}\left[(V_e-i_L{R}_L-V_c)(1-S)\right]$$

(13)

$V_C$ is equal to $V_s$, where $Ve$ signifies the input voltage and $V_s$ signifies the output voltage.

Deriving from the operational principle, we can deduce the subsequent state-space equation for the converter:

$$\left[\begin{array}{c}\frac{d{i}_L}{dt}\\ \frac{d{V}_C}{dt}\end{array}\right]=\left[\begin{array}{cc}0& \frac{S-1}{L}\\ \frac{1-S}{L}& \frac{-1}{RC}\end{array}\right]\left[\begin{array}{cc}0& \frac{S-1}{L}\\ \frac{1-S}{L}& \frac{-1}{RC}\end{array}\right]\left[\begin{array}{c}{i}_L\\ V_C\end{array}\right]+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]V_e$$

In this context, S represents the switching signal. When the switch is activated, it takes on a value of 1; otherwise, it remains at 0. Assuming a sufficiently high sampling frequency, the state variables in Equation (1) can be discretized using the conventional forward Euler approximation method. This transformation is expressed as follows:

$$\left\{\begin{array}{c}\frac{d{i}_L}{dt}=\frac{i_L(t+1)-i_L\left(t\right)}{T_S}\hfill \\ \frac{d{V}_C}{dt}=\frac{V_C(t+1)-V_C\left(t\right)}{T_S}\hfill \end{array}\right.$$

Here, $T_s$ denotes the switching cycle. By incorporating Equation (2), the anticipated inductor current and projected capacitor voltage for the subsequent sampling instance can be formulated as follows:

$$i_L(t+1)=i_L\left(t\right)+\frac{1}{L}[V_f-(1-t)·V_C\left(t\right)]·T_S$$

(14)

$$g={(i_L(t+1)-i_L\left(t\right))}^2$$

(15)

In summary, MPC presents significant benefits in the converter system, making it a compelling control approach for various applications. Leveraging the foresight of MPC and tackling the unique obstacles in power electronics allows engineers to craft sophisticated, resilient, and effective control strategies for a wide range of uses. MPC demonstrates faster convergence to the set point during steady state operations, with reduced offsets in comparison to the PID controller. In summary, the MPC controller showcases superior performance over the PID controller. MPC stands as an advanced control technique employed to regulate processes while adhering to specified constraints. Widely adopted across various industries, including power electronics, MPC operates based on dynamic models of the process, typically linear empirical models derived from system identification. A distinctive advantage of MPC lies in its capability to optimize the current time slot while also considering subsequent time intervals. Unlike the linear–quadratic regulator (LQR), which operates on a singular optimization, MPC continuously re-optimizes, ensuring real-time adaptability. Furthermore, MPC possesses foresight, enabling it to forecast future occurrences and adjust control actions proactively—a feature absent in PID controllers. Although predominantly digital, there is ongoing research exploring the integration of specialized analog circuitry to enhance MPC’s response time, despite its inherent complexity compared to PID control. This paper shows the performance of the PID controller in terms of stability and predictive capacity for this converter model.

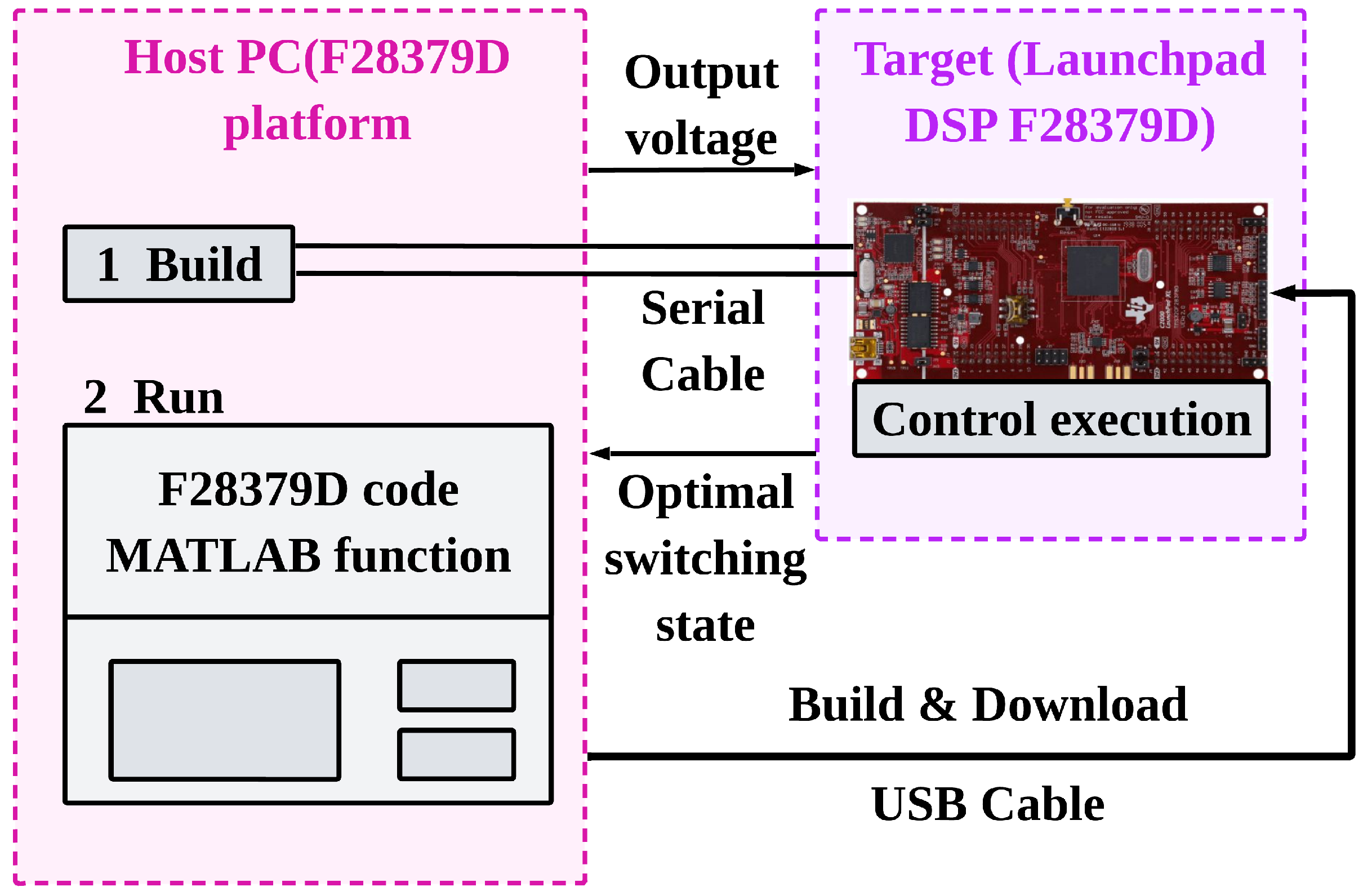
5. Hardware in the Loop

HIL simulation replicates real-time situations, mirroring the timing of an actual process in both input and output signals. This simulation type requires collaboration between a host-PC and the specific system. Usually conducted in controlled laboratory settings, HIL testing offers a reliable and secure platform for evaluating prototype controllers under diverse conditions and workloads. In contrast to purely numerical simulations, HIL simulations prioritize authenticity by considering elements like noise, disturbances, and real-world challenges that may be overlooked in idealized conditions, potentially leading to significant oversights. The advantages of HIL simulations include minimized risks, accelerated development cycles, and heightened suitability for high-stakes and critical applications.

The main goal of HIL simulation is to assess a hardware device using a simulator before it is implemented in real-world operations. It is crucial to test each component of the system separately to verify its proper functioning. For example, evaluating a controller’s performance in simulated scenarios before incorporating it into the real-world process can be extremely advantageous. Moreover, HIL testing provides a safe environment for assessment without the potential risks of equipment damage or compromising safety. In our research, we utilized HIL simulation to verify and validate the proposed MPC for the DC converter. Figure 10 illustrates the main elements and signal routes of the HIL simulation related to our suggested system. In the typical HIL simulation configuration, the proposed MPC runs on the DSP launchpad F28379D, while the boost converter is simulated on the host-PC. The HIL simulation requires interaction between the host-PC and the F29379D board, which is achieved through a serial connection. Consequently, the host-PC sends the output voltage Vc and the current iL to the F28379D launchpad. Upon receiving these signals, the proposed MPC determines the best switching state for the subsequent moment.

6. Implementation of DC-DC

Within our experimental arrangement, the established conversion process involves a battery as the power source, supplying energy to a DC load through a boost converter. This converter is under the control of both PID and MPC controllers, aimed at maintaining the desired voltage level. The system’s schematic representation is depicted in Figure 11. Figure 12 showcases the developed PCB board. As depicted in this figure, the SMD type driver, Irf2110, is utilized. This driver enables both MOSFETs to switch simultaneously, leveraging a bootstrap capacitor that ensures that the high-side switch activates when the low side is off. Additionally, two capacitors—one for input and another for output—are incorporated into this PCB board to effectively filter the input voltage.

The primary methodology for measurement employed in this experimental setup revolves around the acquisition of both the current, denoted as I, generated by the battery, and the voltage, represented as V, across its terminals. These specific variables, I and V, are procured through the utilization of current and voltage sensors connected to the inputs of the onboard analog-to-digital converter with a 12-bit resolution. This converter is integrated into the DSP LAUNCHXL-F28379D board, which features dual CPUs, each operating at a frequency of 100 MHz. Additionally, the board encompasses 16 ADC pins, capable of high-resolution data conversion, reaching up to 16 bits. Programmed to function as an acquisition instrument, the DSP board consistently transmits the acquired numeric values (I, V) in real time to a computer via an RS232/USB serial converter. The visual representation of the constructed prototype, used for validating the developed MPC algorithm, is illustrated in Figure 13 below.

With respect to the computational aspect, a program was developed using the Matlab-Simulink framework. This program is meticulously crafted to acquire the pertinent data (I, V), which subsequently serve as inputs for our MPC and PID algorithms. These algorithms are responsible for determining the optimal duty cycle for the DSP (F28379D), thereby enabling the generation of an enhanced pulse width modulation (ePWM) signal. This PWM signal is then directed to a driver, which in turn amplifies the current control of the MOSFET transistor situated within the Boost converter.

7. Results and Discussion

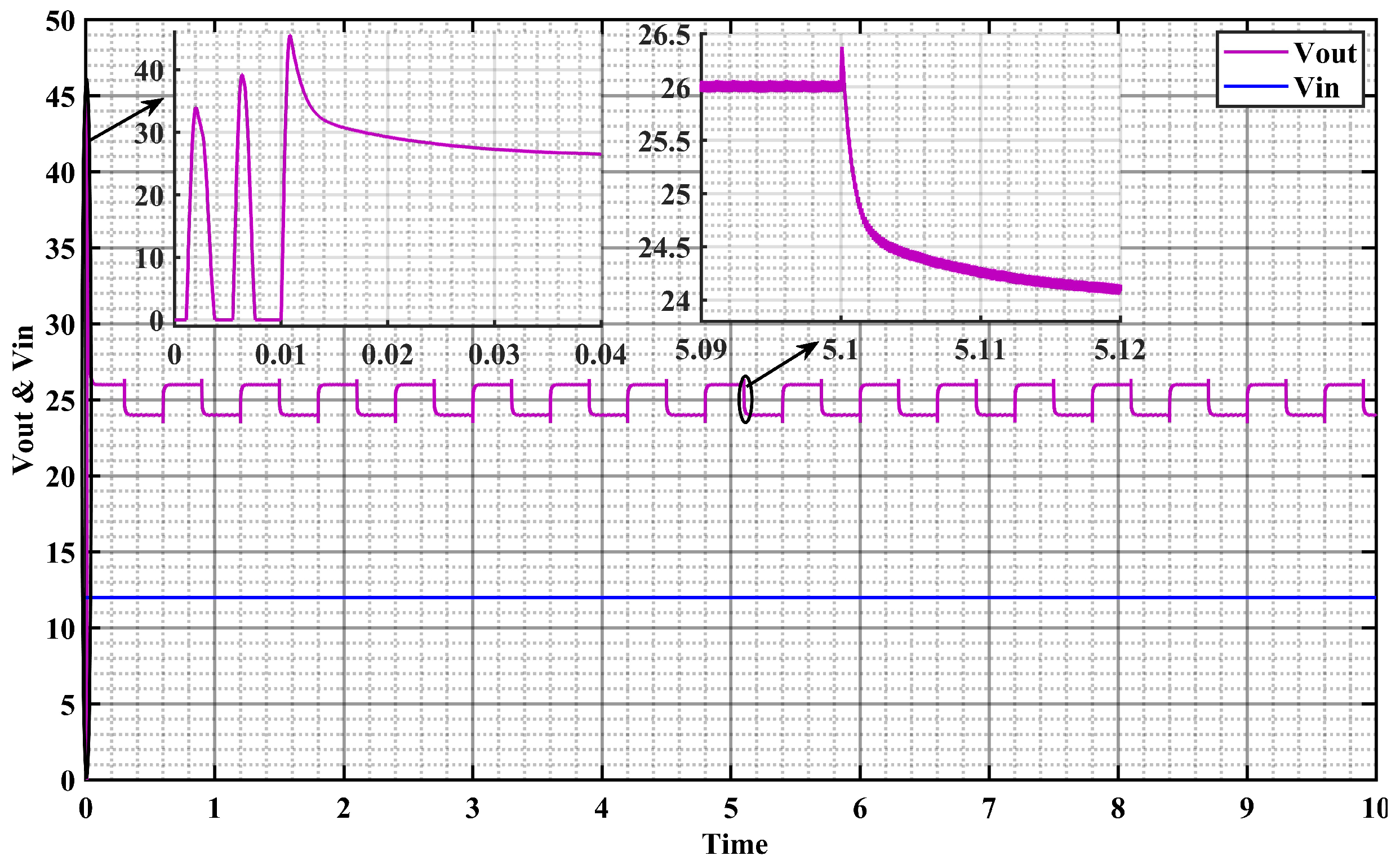
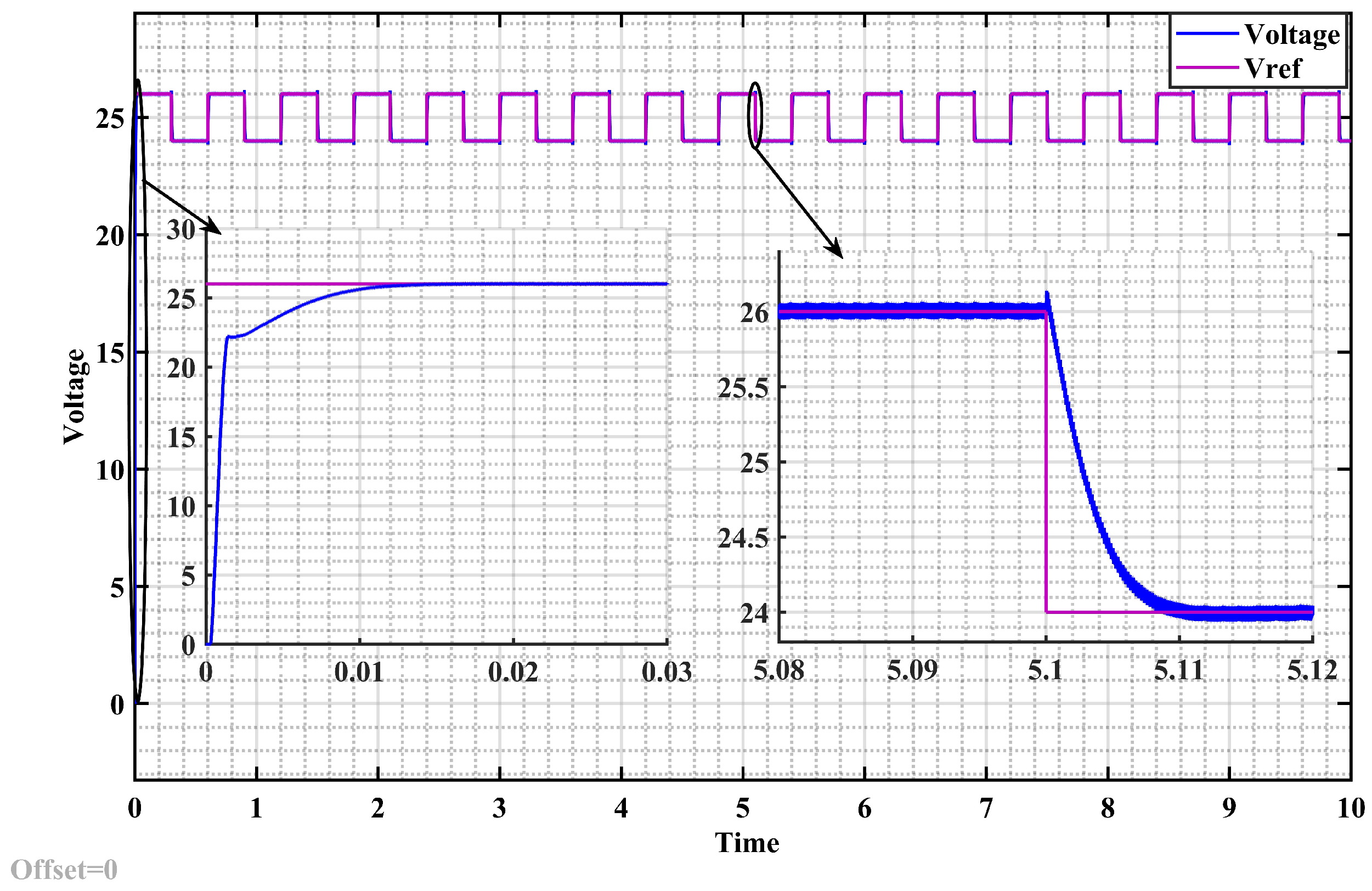
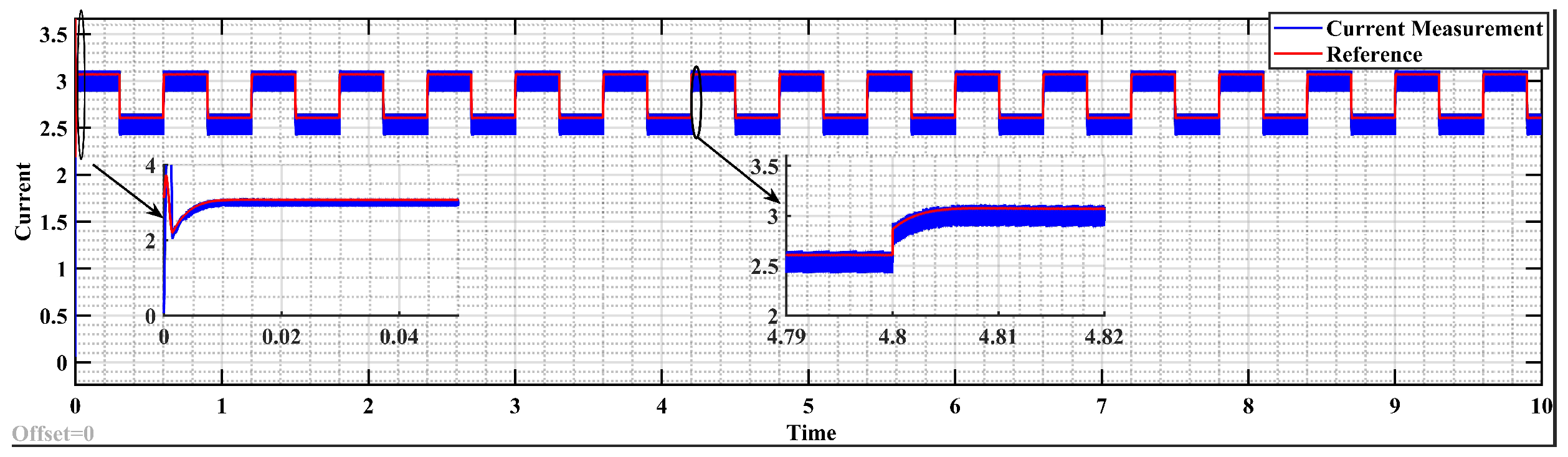
7.1. Results of Simulation

Figure 14 illustrates the real-world system tested with both PID and MPC controllers. In this setup, the battery serves as the primary power source for the system, while a DSP board is employed to control its operations.

Furthermore,

Table 1. System parameters.

Parameter	Value
$V_{out}$	24 V
Capacitor C	47 µF
Inductor L	2.5 mH
Sampling time $T_s$	34 µs

serves as a comprehensive reference, detailing the specific parameters employed during the simulation of the boost converter in simulation mode. These parameters encompass various aspects of the converter’s configuration, including input voltage levels, inductance values, capacitance values, and switching frequencies. By providing a detailed breakdown of these parameters,

Table 2. PI parameters.

Parameters	Values
$K_P$	0.334
$K_I$	1.2

offers valuable insights into the simulation setup and helps contextualize the findings presented in the accompanying figures.

Concerning the acquisition, retention, and processing of the I and V measurements, the block diagrams in Figure 15 and Figure 16 visually depict the structural framework of the program we have developed within the Matlab-Simulink environment. This program efficiently facilitates the real-time visualization of various attributes.

Transitioning to Figure 17, the graphical representation depicts the intricate relationship between the output voltage and the input voltage of the system. Notably, the output voltage exhibits a pronounced overshoot of more than 47 volts, indicating a transient instability in the voltage response. This overshoot suggests that the system’s voltage regulation mechanisms may be inadequately tuned or that there are inherent limitations within the PID controller-driven system that impede its ability to maintain a consistent voltage output. Such fluctuations in voltage can lead to operational inefficiencies and potentially compromise the reliability of the system in real-world applications.

Moving to Figure 18, the graph depicts the output voltage in relation to the reference signal. Notably, the voltage profile exhibits a striking absence of overshoot, in marked contrast to the behavior observed with the PID controller. This absence of overshoot in the output voltage signifies enhanced stability and precision in voltage regulation, crucial for maintaining reliable energy delivery. Moreover, the output voltage precisely tracks the reference signal, showcasing the effectiveness of the MPC controller in accurately following desired setpoints. This precise tracking capability is essential for ensuring optimal energy transfer and utilization, contributing to the overall efficiency and effectiveness of the system.

In Figure 19, the plotted graph vividly captures the fluctuation of the inductor current over time, revealing a distinctive initial overshoot that peaks at 18A during the system’s initialization phase. This initial surge in current signifies the transient response of the system as it adjusts to the applied input conditions. However, as the system progresses toward stability, this overshoot gradually diminishes, eventually reaching a level below +4.5A. This reduction in overshoot reflects the system’s ability to settle into a steady-state condition, where the current variations become more controlled and predictable.

In Figure 20, the visual representation of the inductor current showcases a distinct absence of overshoot, underscoring the system’s stability and efficiency under the control of the MPC algorithm. This absence of overshoot in the inductor current highlights the optimized energy transfer dynamics within the system, indicative of the precise control afforded by MPC. Additionally, the system’s operation with the MPC controller demonstrates an impressive combination of speed and robustness, indicating its capability to swiftly adapt to changing conditions while maintaining stable energy flows.

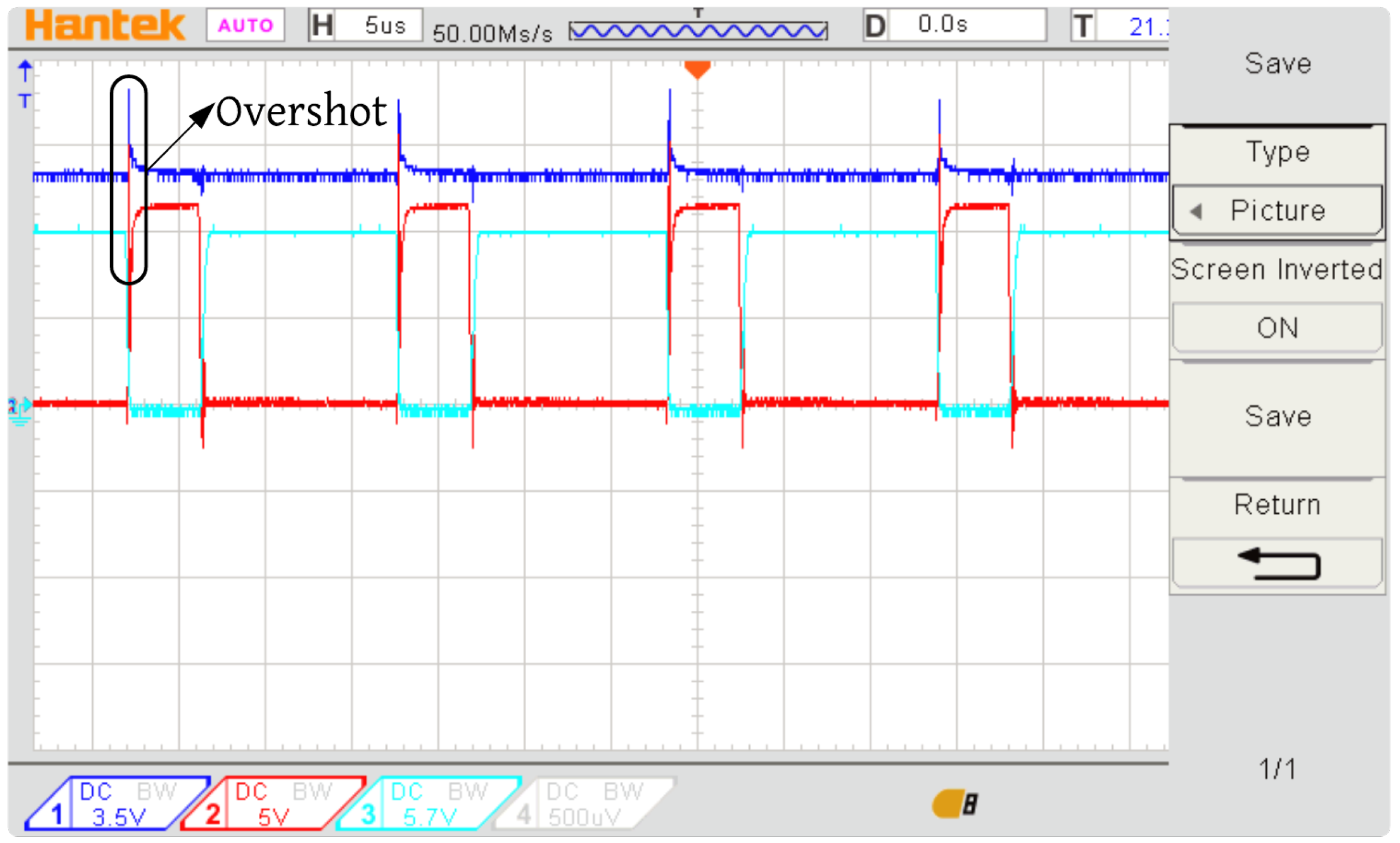
7.2. Experimental Results

Figure 21 provides a graphical representation of the output voltage at a reference value of 12 volts, offering valuable insights into the system’s performance under various control conditions. Initially, the PID controller effectively tracks the reference voltage, maintaining alignment with the desired setpoint. However, alterations in the state of the two MOSFETs lead to an unexpected overshoot of 15 volts, momentarily disrupting the stability of the system. Although transient, this overshoot indicates a deviation from the desired voltage level, emphasizing the importance of precise control mechanisms in managing energy transfer dynamics. Additionally, Figure 21 highlights the deadtime of the two MOSFETs, a critical parameter influencing the switching behavior and overall efficiency of the system. The graph demonstrates that the deadtime, approximately 100 ns in duration, is carefully generated by the DSP (digital signal processor) board through specific configurations. This deadtime interval plays a crucial role in preventing cross-conduction and ensuring smooth transitions during the switching process, thereby optimizing energy transfer and minimizing losses.

In addition to the experimental findings shown in Figure 21,

Table 3. System parameters.

Parameter	Value
$V_{out}$	24 V
Capacitor C	470 µF
Inductor L	5 mH
$F_s$	50 KHz
Input DC	12 V
Sampling time $T_s$	34 µs

provides a comprehensive overview of the parameters used during the experimental mode simulation of the boost converter. These parameters cover various aspects of the converter’s operation, including input voltage levels, inductance values, capacitance values, and deadtime configurations, offering valuable insights into the experimental setup and helping contextualize the observed performance trends. By carefully controlling these parameters, researchers can fine-tune the operation of the boost converter to optimize energy efficiency and reliability in real-world applications.

Figure 22 provides a comprehensive view of both the output voltage and the PWM signals controlling the two MOSFETs when the boost synchronous is regulated by the MPC controller. This detailed visualization offers invaluable insights into the dynamic behavior of the system under MPC control, revealing the intricate interplay between control signals and output responses.

The outcomes in Figure 22 serve as compelling visual evidence of the effectiveness of the MPC controller in regulating boost synchronous. Notably, the output voltage profile demonstrates impeccable stability and precision, closely tracking the reference signal with remarkable accuracy. This precise alignment between the output voltage and the desired setpoint underscores the superior performance and control capabilities facilitated by the MPC algorithm. By orchestrating the switching of the MOSFETs in response to real-time system dynamics, the MPC controller ensures optimal energy transfer and utilization, ultimately enhancing the efficiency and reliability of the boost converter system.

Furthermore, the accompanying PWM signals of the two MOSFETs provide additional insights into the control strategy implemented by the MPC controller. These signals, meticulously modulated to regulate the switching of the MOSFETs, demonstrate the sophisticated control mechanisms employed to maintain synchrony and stability within the boost converter system. The synchronized operation of the MOSFETs orchestrated by the MPC controller is crucial for achieving consistent and precise output voltage regulation, essential for meeting the demands of diverse energy applications.

Overall, the outcomes in

Table 4. Comparison the performances of the MPC and PID controllers.

Technique	Response Time	Overshot
$MPC$	$R_T$= 0.01 s	D = 0 V
$PID$	$R_T$= 0.5 s	D = 3.45 V

underscore the pivotal role of MPC-based control strategies in optimizing energy transfer dynamics and enhancing the performance of boost converter systems. By leveraging advanced control algorithms and precise modulation techniques, MPC enables the seamless integration of renewable energies and facilitates the transition toward a more sustainable and resilient energy future.

8. Conclusions

The findings of this research are significant for improving efficiency, reliability, and performance optimization within V2G systems, thereby fostering sustainable energy integration and promoting the adoption of electric vehicles (EVs). DC-DC converters have been both simulated and implemented for V2G integration, with the findings organized as follows:

• Model predictive control (MPC) addresses challenges in DC-DC boost converters by considering system dynamics and constraints in real time.
• Experimental validation of synchronous boost converters and MPC involves hardware-in-the-loop simulations, benchtop testing, and field trials.
• Transitioning from diodes to MOSFETs in boost converters enhances efficiency by minimizing conduction losses, but may introduce challenges like increased switching losses.
• The TMS320F28379D digital signal processor enables real-time control of boost converters with high PWM frequencies and precise sensor readings.
• MPC outperforms PID control in simulation and experimental settings by providing improved transient response, reduced overshoot by $90\%$, and enhanced disturbance rejection.
• Boost converter simulation parameters are determined based on component datasheets and system requirements, with validation against real-world measurements.
• The overshot in output voltage with PID control may result from inherent limitations like integral windup and slow response, which MPC effectively mitigates.