Optimization Operation Strategy for Shared Energy Storage and Regional Integrated Energy Systems Based on Multi-Level Game

Abstract

Regional Integrated Energy Systems (RIESs) and Shared Energy Storage Systems (SESSs) have significant advantages in improving energy utilization efficiency. However, establishing a coordinated optimization strategy between RIESs and SESSs is an urgent problem to be solved. This paper constructs an operational framework for RIESs considering the participation of SESSs. It analyzes the game relationships between various entities based on the dual role of energy storage stations as both energy consumers and suppliers, and it establishes optimization models for each stakeholder. Finally, the improved Differential Evolution Algorithm (JADE) combined with the Gurobi solver is employed on the MATLAB 2021a platform to solve the cases, verifying that the proposed strategy can enhance the investment willingness of energy storage developers, balance the interests among the Integrated Energy Operator (IEO), Energy Storage Operator (ESO) and the user, and improve the overall economic efficiency of RIESs.

1. Introduction

Against the backdrop of the “Dual Carbon” goals, improving the current energy supply structure and promoting sustainable economic development have become mainstream trends [1]. The development of clean energy and the enhancement of the overall energy utilization efficiency are essential aspects of this trend [2]. This places higher demands on the stability and flexibility of electricity dispatch. In this context, the Regional Integrated Energy System (RIES) has garnered widespread attention due to its features of multi-energy coupling and reliable energy supply [3,4].

In the design and evaluation of the RIES, it is crucial to allocate energy storage systems appropriately in order to ensure the sustainability of the energy supply, as well as the economic efficiency and reliability of the RIES. By the end of 2023, China had completed the construction and operation of new energy storage projects, with a cumulative installed capacity of 3.139 GW/6.687 GWh. However, the current independent construction of energy storage systems involves a large capital investment and a long payback period, which limits the development of energy storage systems [5,6]. The new generation of Shared Energy Storage Systems (SESSs) that have emerged in the context of the energy internet provide an effective solution to these issues [7,8]. A SESS integrates independently dispersed energy storage resources on the source, grid, and load sides for unified collaborative scheduling, which improves the utilization rate of energy storage resources and the reliability of energy supply and use in RIES. Reference [9] applies a community energy storage system, taking into account the flexible resources on the demand side, such as heating, ventilation, and air conditioning systems, and proposes a coordinated optimization strategy that satisfies user comfort while reducing energy consumption costs. Reference [10] applies a combination of long- and short-term storage to an RIES, reducing the load forecasting errors through rolling optimization of long-term energy balance models and short-term power balance models, fully utilizing energy storage resources, and meeting the autonomous operation requirements of multi-energy microgrids. Reference [11] constructs a mechanism considering energy interaction between multiple IESs in neighboring regions, using shared storage to balance the energy flow and reduce the overall operating costs of the system. However, the above studies did not consider the energy storage system as an independent stakeholder, did not consider multi-party conflicts of interest, and the interests of energy storage investors were not guaranteed, which is not conducive to the promotion and construction of energy storage systems. To address these issues, references [12,13] establish a multi-party energy interaction mechanism based on a carbon trading incentive mechanism considering the system’s low-carbon characteristics, solving the multi-party interest conflict in the RIES while reducing environmental pollution. References [14,15] analyze various operation modes of shared energy storage systems and propose a model for leasing energy storage capacity, focusing on the scientific configuration of energy storage system parameters, which is more in line with the actual operation of RIESs and better leverages the flexibility of energy storage systems to regulate loads.

Game theory is one of the standard tools for analyzing the economics of complex sequential strategy models. By using game theory, the cooperation and competition among multiple stakeholders in RIESs can be clarified, and the enthusiasm of each stakeholder to participate in energy transactions can be fully utilized [16,17,18]. References [19,20] consider the multiple uncertainties caused by the emergence of large-scale producer–consumer clusters. Reference [20] utilizes a non-cooperative game based on stochastic dynamic programming to develop a universal framework for both day-ahead and real-time electricity markets, significantly reducing the operational costs of microgrids and the charging costs of electric vehicles. Reference [21] examines the interests among multiple stakeholders in RIESs with shared energy storage, constructs a “one-leader-multiple-follower” game model, and develops a dynamic pricing mechanism for electric and thermal energy, achieving a win–win situation for all involved parties. Reference [22] establishes a game model based on Stackelberg game theory, with the distributed energy storage system as the leader and the load side as the follower, considering both the economic benefits and the load-side energy satisfaction index. Reference [23], considering the competitive and cooperative relationships among various stakeholders, constructs both a cooperative game model and a non-cooperative game model to achieve optimal energy distribution. However, these studies are all based on the traditional master–slave game structure of the participating subjects in the game analysis, the Energy Storage Operator (ESO) is fixed in the conditions of the leader or follower, which does not take into account the duality of the participating subjects as both the follower and the leader, as well as the simultaneous master–slave relationship and competitive relationship that exists between the two subjects under the circumstance, and the lack of mobilization of the subjects to participate in the optimization of the enthusiasm.

Aiming at the above problems, this paper proposes an optimal operation strategy for SESSs and RIESs based on a multi-level game. The strategy analyzes the master–slave relationship between the two when the ESO chooses to charge from the Integrated Energy Operator (IEO) and the competitive relationship between the two when meeting the load demand on the user side, and it integrates the user-side electric demand response and electric heat production. A multilevel master–slave game model is constructed with the IEO as the head leader, the ESO as the secondary leader, and the user as the follower. The model can stimulate the enthusiasm of each subject to participate in the coordinated operation, thus enhancing the overall economic efficiency of RIESs. In order to solve the model, the adaptive differential evolution algorithm with external archiving (JADE) combined with the Gurobi solver is used, and the results of the case analysis verify the effectiveness of the optimized operation strategy proposed in this paper.

2. Structure and Operation Mode of the RIES

The RIES architecture proposed in this paper consists of three entities: the IEO, the ESO, and the user. The energy coupling relationships are illustrated in Figure 1.

The IEO serves as an intermediary between the external grid, the user, and the ESO within the RIES, being capable of bidirectional energy transmission. The IEO is equipped with a micro gas turbine, which purchases gas from the external gas network for power generation. Simultaneously, it generates waste heat that enters a waste heat boiler and provides thermal energy to the user side through a heat exchange device.

The SESS is configured on the ESO side, and its deployment reduces the load volatility of the RIES while also increasing the diversity of energy choices for the user. The SESS chooses to charge from the IEO side and then provides discharge services to the user side. The ESO adjusts its charging and discharging operations based on price signals and user energy demands, setting reasonable selling prices and selecting appropriate time periods to enhance its own revenue.

The user side includes both electrical and thermal loads, equipped with photovoltaic power generation units and electric heating devices. The user can optimize their internal operating status and flexibly choose various energy sources to meet their energy needs based on their own interests and load requirements. For electrical loads, when the self-generated electricity meets the demand, the surplus electricity can be sold to the external grid; when the self-generated electricity is insufficient to meet the demand, the user can choose to purchase electricity from the IEO or ESO based on the time-of-use electricity prices. For thermal loads, in addition to the heat exchange units provided by the IEO, the thermal loads can also be satisfied by the user-side electric heating devices.

3. Game Relationships among Stakeholders

In the RIES, different entities have their own interests and conflicts, leading to a situation of mutual game theory. The IEO formulates a set of strategies for the daily electricity and heat selling prices. The ESO formulates charging and discharging strategies and selling prices for the user based on the IEO’s pricing strategy, considering its own profit and the SESS capacity, and it adjusts the charging and discharging strategies and selling prices reasonably. Upon receiving the selling price strategies for energy from the IEO and ESO, the user side adjusts the electricity and heat load for each time period in real time based on the price signals and energy demand, plans the energy purchasing strategy, and uploads the strategy to the IEO and ESO.

When the selling energy price from the IEO is high, the ESO will adjust the selling energy price to increase profit, and the user side will prioritize cheaper energy sources for purchase. If the user side purchases a large amount of energy, the IEO and ESO will re-formulate the selling energy price strategy, and the ESO will adjust the charging and discharging strategies accordingly.

Due to the sequential decision-making process of the three parties, the entire process can be viewed as a multi-level game model with the IEO as the head leader, the ESO and user as followers, and the ESO as the secondary leader of the user in the RIES.

The IEO, the ESO and the user objective functions are $F_{\mathrm{IEO}}$, $F_{\mathrm{ESO}}$ and $F_{\mathrm{user}}$, respectively, all of which are optimized to maximize the operational benefits, as shown in the game relationship diagram in Figure 2.

4. Decision-Making Model of Each Stakeholder

4.1. Subsection Operation Model of the IEO

The IEO is responsible for integrating and coordinating various energy resources, such as electricity, natural gas, and thermal energy. Additionally, as the head leader within the RIES, the IEO aims to maximize its operational efficiency by employing dynamic time-of-use electricity pricing and heating prices as decision variables. The optimization objective of the IEO is to maximize its operational benefits, and its objective function is defined as follows:

$$\max F_{\mathrm{IEO}}={\displaystyle \sum _{t=1}^T}(C_{\mathrm{ESO},\mathrm{sell}}^t+C_{\mathrm{user},\mathrm{sell}}^t-C_{\mathrm{grid}}^t-C_{\mathrm{mt}}^t)$$

(1)

In the formula, divide one day into T time slots, where t represents the t-th time slot. In the t-th time slot, $C_{\mathrm{ESO},\mathrm{sell}}^t$ and $C_{\mathrm{user},\mathrm{sell}}^t$, respectively, represent the revenue for the IEO after selling energy to the ESO and the user, $C_{\mathrm{grid}}^t$ represents the interaction cost between the IEO and the grid (IEO acquiring/selling electricity, with $C_{\mathrm{grid}}^t$ being positive/negative), and $C_{\mathrm{mt}}^t$ represents the gas cost used by IEO. The expressions for the above are as follows:

$$C_{\mathrm{grid}}^t=[\max (L_{\mathrm{u}}^t+P_{\mathrm{char}}^t-P_{\mathrm{mt},\mathrm{e}}^t,0)p_{\mathrm{e},\mathrm{s}}^t+\min (L_{\mathrm{u}}^t+P_{\mathrm{chr}}^t-P_{\mathrm{mt},\mathrm{e}}^t,0)p_{\mathrm{e},\mathrm{b}}^t]\mathsf{\Delta }t$$

(2)

$$C_{\mathrm{ESO},\mathrm{sell}}^t=p_{\mathrm{e},\mathrm{s}}^t{P}_{\mathrm{chr}}^t\mathsf{\Delta }t$$

(3)

$$C_{\mathrm{user},\mathrm{sell}}^t=(L_{\mathrm{h}}^t{p}_{\mathrm{h},\mathrm{s}}^t+L_{\mathrm{e}}^t{p}_{\mathrm{e},\mathrm{s}}^t)\mathsf{\Delta }t$$

(4)

In the formula, $P_{\mathrm{chr}}^t$, $L_{\mathrm{h}}^t$, $L_{\mathrm{e}}^t$ represent the electric power purchased by the ESO from the IEO and the electric and thermal power purchased by the user from the IEO during the t-th time slot; and $p_{\mathrm{e},\mathrm{s}}^t$, $p_{\mathrm{h},\mathrm{s}}^t$ represent the selling prices of electricity and heat by the IEO.

The IEO is equipped with a micro gas turbine, responsible for providing electricity and heat, with its main fuel being natural gas. The relationship between its operating cost and electric-thermal output during the t-th time slot can be expressed as:

$$C_{\mathrm{mt}}^t=({\lambda }_{\mathrm{gas}}\frac{P_{\mathrm{mt},\mathrm{e}}^t}{{\mathrm{H}}_{\mathrm{gas}}{\eta }_{\mathrm{mt},\mathrm{e}}})\mathsf{\Delta }t$$

(5)

$$P_{\mathrm{mt},\mathrm{h}}^t=\frac{1-{\eta }_{\mathrm{mt},\mathrm{e}}-{\eta }_{\mathrm{mt},\mathrm{loss}}}{{\eta }_{\mathrm{mt},\mathrm{e}}}{\eta }_{\mathrm{mt},\mathrm{h}}{P}_{\mathrm{mt},\mathrm{e}}^t$$

(6)

In the formula, ${\lambda }_{\mathrm{gas}}$ is the unit price of natural gas; $P_{\mathrm{mt},\mathrm{e}}^t$, $P_{\mathrm{mt},\mathrm{h}}^t$ are the electric and thermal power outputs during the t-th time slot; ${\mathrm{H}}_{\mathrm{gas}}$ is the low calorific value of gas; and ${\eta }_{\mathrm{mt},\mathrm{e}}$, ${\eta }_{\mathrm{mt},\mathrm{h}}$, ${\eta }_{\mathrm{mt},\mathrm{loss}}$ are, respectively, the power generation efficiency, heating coefficient, and heat dissipation loss rate of the micro gas turbine.

When the IEO interacts with the external grid for energy exchange, it needs to adhere to the power constraints of the grid to ensure that the energy purchased or sold does not exceed the carrying capacity of the interconnection lines, thereby maintaining the stable operation of the grid. At this point, the following constraints should be met:

$$\{\begin{array}{r}\begin{array}{c}0⩽P_{\mathrm{eg},\mathrm{s}}^t⩽{\zeta }_{\mathrm{eg},\mathrm{s}}^t{P}_{\mathrm{eg},\mathrm{s}}^{\max }\\ 0⩽P_{\mathrm{eg},\mathrm{b}}^t⩽{\zeta }_{\mathrm{eg},\mathrm{b}}^t{P}_{\mathrm{eg},\mathrm{b}}^{\max }\end{array}\\ {\zeta }_{\mathrm{eg},\mathrm{b}}^t+{\zeta }_{\mathrm{eg},\mathrm{s}}^t⩽1\end{array}$$

(7)

In the equation, $P_{\mathrm{eg},\mathrm{s}}^t$/$P_{\mathrm{eg},\mathrm{b}}^t$ represent the selling/purchasing electric power from the grid to the IEO; $P_{\mathrm{eg},\mathrm{b}}^{\max }$/$P_{\mathrm{eg},\mathrm{s}}^{\max }$ represent the maximum selling/purchasing electric power from the grid to the IEO; and ${\zeta }_{\mathrm{eg},\mathrm{s}}^t$ and ${\zeta }_{\mathrm{eg},\mathrm{b}}^t$ are Boolean variables, indicating the flag for selling/purchasing electric power from the grid to the IEO, meaning that only one action of selling/purchasing electricity can be conducted at a time

Additionally, in order to ensure the interests of various stakeholders, the energy purchase/sale prices of the IEO need to satisfy the following constraints:

$$p_{\mathrm{eg},\mathrm{b}}^t<p_{\mathrm{e},\mathrm{s}}^t<p_{\mathrm{eg},\mathrm{s}}^t$$

(8)

$$p_{\mathrm{h},\min }^t<p_{\mathrm{h},\mathrm{s}}^t<p_{\mathrm{h},\max }^t$$

(9)

$${\displaystyle \sum }_{i=1}^T{p}_{\mathrm{e},s}^t⩽T\overline{p_{\mathrm{e}}^t}$$

(10)

$${\displaystyle \sum }_{i=1}^T{p}_{\mathrm{h},s}^t⩽T\overline{p_{\mathrm{h}}^t}$$

(11)

In the equations, $p_{\mathrm{eg},\mathrm{b}}^t$, $p_{\mathrm{eg},\mathrm{s}}^t$ represent the purchasing and selling electricity prices from the grid during the t-th time slot of the day; $p_{\mathrm{h},\min }^t$, $p_{\mathrm{h},\max }^t$ represent the upper and lower limits of the selling price of heat specified by the IEO; and $\overline{p_{\mathrm{e}}^t}$, $\overline{p_{\mathrm{h}}^t}$ represent the average selling electricity and heat prices.

4.2. Operation Model of the ESO

The ESO references the selling energy prices of the IEO and the energy consumption situation on the user side, reasonably formulating its electricity price strategy and charging/discharging plans to maximize its total revenue while meeting the energy needs of the user. The objective function can be expressed as:

$$\max F_{\mathrm{ESO}}={\displaystyle \sum }_{t=1}^T(C_{\mathrm{ESO},\mathrm{dis}}^t-C_{\mathrm{ESO},\mathrm{sell}}^t-C_{\mathrm{ESO},\mathrm{op}}^t)$$

(12)

$$C_{\mathrm{ESO},\mathrm{dis}}^t={\displaystyle \sum _{t=1}^T}{p}_{\mathrm{dis}}^t{P}_{\mathrm{dis}}^t\mathsf{\Delta }t$$

(13)

$$C_{\mathrm{ESO},\mathrm{op}}^t=k_c{C}_{\mathrm{ESO},\mathrm{sell}}^t$$

(14)

In the equation, $P_{\mathrm{chr}}^t$, $P_{\mathrm{dis}}^t$ represent the charging and discharging power of the ESO in the t-th time slot; $p_{\mathrm{dis}}^t$ represents the price at which the ESO sells electricity in the t-th time slot; and $k_c$ represents the operational and maintenance costs of the ESO.

In order to ensure the ESO’s healthy participation in market competition, the following constraints are imposed on its selling electricity prices:

$$0.8p_{\mathrm{e},\mathrm{s}}^t\le p_{\mathrm{dis}}^t\le 1.4p_{\mathrm{e},\mathrm{s}}^t$$

(15)

In order to ensure that the shared energy storage system can continuously provide services in consecutive time slots within the same period and across different periods, that is, to maintain energy continuity and ensure the conservation of charging and discharging power within a single period, the following conditions must be satisfied:

$$E_{\mathrm{eso}}^t=E_{\mathrm{eso}}^{t-1}(1-{\eta }_{\mathrm{o}})+(P_{\mathrm{chr}}^t{\eta }^{+}-\frac{P_{\mathrm{dis}}^t}{{\eta }^{-}})\mathsf{\Delta }t$$

(16)

$${\displaystyle \sum }_{t=1}^T{P}_{\mathrm{chr}}^t{\eta }^{+}-{\displaystyle \sum }_{t=1}^T\frac{P_{\mathrm{dis}}^t}{{\eta }^{-}}=0$$

(17)

In the equation, ${\eta }_{\mathrm{o}}$, ${\eta }^{+}$, ${\eta }^{-}$ represent the energy self-loss rate when the ESO is operating, the efficiency when the ESO is charging, and the efficiency when the ESO is discharging, respectively.

At any given moment, the charging or discharging power is subject to the ESO’s allowed maximum power limit, while the total charging or discharging power in any time period is subject to the ESO’s allowed maximum capacity limit. These constraints should be satisfied as follows:

$$\{\begin{array}{c}\mid \frac{E_{\mathrm{eso}}^{t+1}-E_{\mathrm{eso}}^t}{\mathsf{\Delta }t}\mid \le {\zeta }_{\mathrm{chr}}^t{P}_{\mathrm{chr}}^{\max }\\ \begin{array}{l}\mid \frac{E_{\mathrm{eso}}^{t+1}-E_{\mathrm{eso}}^t}{\mathsf{\Delta }t}\mid \le {\zeta }_{\mathrm{dis}}^t{P}_{\mathrm{dis}}^{\max }\\ {\zeta }_{\mathrm{chr}}^t+{\zeta }_{\mathrm{dis}}^t\le 1\end{array}\end{array}$$

(18)

In the equation, $P_{\mathrm{chr}}^{\max }$, $P_{\mathrm{dis}}^{\max }$ represent the allowed maximum charging and discharging power by the ESO, while ${\zeta }_{\mathrm{chr}}^t$, ${\zeta }_{\mathrm{dis}}^t$ are Boolean variables representing the charging/discharging state of the energy storage device at the t-th time slot, restricting the energy storage device to perform only one charging or discharging action at a time.

In order to ensure the stability and lifespan of the shared energy storage system, the constraints on the total number of charging and discharging cycles and its maximum capacity within one period for the ESO are as follows:

$${\displaystyle \sum _{t=1}^T}({\zeta }_{\mathrm{chr}}^t+{\zeta }_{\mathrm{dis}}^t)\le {\chi }^{\max }$$

(19)

$$E_{\mathrm{eso}}^{\min }\le E_{\mathrm{eso}}^t\le E_{\mathrm{eso}}^{\max }$$

(20)

In the equation, ${\chi }^{\max }$ represents the maximum number of charging and discharging cycles allowed by the ESO within period the t-th time slot, while $E_{\mathrm{eso}}^{\min }$, $E_{\mathrm{eso}}^{\max }$, respectively, represent the minimum and maximum values of the capacity specified for the SESS.

4.3. Operation Model of the User

The user side adjusts the energy load based on its energy demand, selects energy sources reasonably, and considers the user load satisfaction index, aiming to maximize the operational efficiency of the user side. The objective function is:

$$\max F_{\mathrm{user}}={\displaystyle \sum }_{t=1}^T(U_{\mathrm{user}}^t-C_{\mathrm{user}}^t-C_{\mathrm{q}}^t)$$

(21)

In the equation, $U_{\mathrm{user}}^t$ represents the electricity utility function; $C_{\mathrm{user}}^t$ represents the total cost of purchasing and selling electricity and heat by the user side; and $C_{\mathrm{q}}^t$ represents the penalty cost for reducing the heat load and the decrease in user load satisfaction due to the interrupted heat load.

The above equations can be further expressed as:

$$U_{\mathrm{user}}^t=\left(a{L_{\mathrm{u}}^t}^2+b{L}_{\mathrm{u}}^t\right)\mathsf{\Delta }t$$

(22)

$$C_{\mathrm{user}}^t=(p_{\mathrm{h},\mathrm{s}}^t{L}_{\mathrm{h}}^t+p_{\mathrm{e},\mathrm{s}}^t(L_{\mathrm{e}}^t+L_{\mathrm{eh}}^t)+p_{\mathrm{dis}}^t{L}_{\mathrm{e},\mathrm{dis}}^t-p_{\mathrm{l},\mathrm{s}}^t{L}_{\mathrm{l},s}^t)\mathsf{\Delta }t$$

(23)

$$C_{\mathrm{q}}^t=\beta ({L_{\mathrm{w},\mathrm{h}}^t}^2)\mathsf{\Delta }t$$

(24)

$$L_{\mathrm{u}}^t=L_{\mathrm{e}}^t+L_{\mathrm{e},\mathrm{dis}}^t-L_{\mathrm{pv}}^t$$

(25)

In the equations, $L_{\mathrm{u}}^t$, $L_{\mathrm{e},\mathrm{dis}}^t$, $L_{\mathrm{eh}}^t$, $L_{\mathrm{l},s}^t$, $L_{\mathrm{w},\mathrm{h}}^t$ and $L_{\mathrm{pv}}^t$ represent the net electrical load after adjusting the energy consumption load, the electrical energy obtained by the user side from the ESO, the electrical energy consumed by the user side’s electric heating equipment for heat production, the electrical energy sold by the user side to the external grid, the actual heat load reduction on the user side, and the forecasted output of photovoltaic equipment, respectively, within the t-th time slot. $a$ and $b$ represent the parameters of the quadratic function characterizing the electricity utility function; $p_{\mathrm{l},\mathrm{s}}^t$ represents the selling electricity price to the external grid by the user side in the t-th time slot; and $\beta$ represents the penalty coefficient for reducing and interrupting the heat load.

The user-side electricity load can be divided into two parts: the rigid electricity load with high reliability requirements and the interruptible flexible electricity load. In this paper, the former is not adjusted, while the flexible electricity load is moved to periods with lower electricity prices based on the price signals received by the user side, aiming to reduce electricity costs. Meanwhile, the user-side heat load can be partially reduced to lower electricity costs. The constraints for shifting and reducing the load on the user side should be satisfied as follows:

$$L_{\mathrm{u}}^t=L_{\mathrm{e},\mathrm{g}}^t+L_{\mathrm{e},\mathrm{s}}^t+L_{\mathrm{eh}}^t$$

(26)

$$L_{\mathrm{u},\mathrm{h}}^t=L_{\mathrm{v},\mathrm{h}}^t-L_{\mathrm{w},\mathrm{h}}^t$$

(27)

$$L_{\mathrm{e},\mathrm{s},\min }^t\le L_{\mathrm{e},\mathrm{s}}^t\le L_{\mathrm{e},\mathrm{s},\max }^t$$

(28)

$$0\le L_{\mathrm{w},\mathrm{h}}^t\le L_{\mathrm{w},\mathrm{h},\max }^t$$

(29)

$${\displaystyle \sum }_t^T{L}_{\mathrm{e},\mathrm{s}}^t\mathsf{\Delta }t=0$$

(30)

In the equations, $L_{\mathrm{e},\mathrm{g}}^t$, $L_{\mathrm{e},\mathrm{s}}^t$ represent the rigid electricity load and the flexible electricity load; $L_{\mathrm{v},\mathrm{h}}^t$ represents the heat load before adjustment; and $L_{\mathrm{e},\mathrm{s},\min }^t$/$L_{\mathrm{e},\mathrm{s},\max }^t$ and $L_{\mathrm{w},\mathrm{h},\max }^t$ represent the minimum/maximum values for shifting the flexible electricity load and the maximum reduction amount for the heat load.

The electric heating equipment on the user side in this paper can meet all forms of the user’s heat demand. The user can consider selecting the source of heat energy based on price signals to maximize the benefits for the user side. The constraints for the operation of the electric heating equipment are as follows:

$$L_{\mathrm{e},\mathrm{h}}^t={\eta }_{\mathrm{h}}^l{L}_{\mathrm{eh}}^t$$

(31)

$$0\le L_{\mathrm{e},\mathrm{h}}^t\le L_{\mathrm{e},\mathrm{h},\max }^t$$

(32)

In the equations, $L_{\mathrm{e},\mathrm{h}}^t$ and $L_{\mathrm{e},\mathrm{h},\max }^t$ represent the heat generated by the electric heating equipment and the upper limit of heat generation in the t-th time slot of the day; and ${\eta }_{\mathrm{h}}^l$ represents the conversion efficiency of the user-side electric heating equipment.

For the methods of obtaining heat energy on the user side, the following options are provided:

$$L_{\mathrm{u},\mathrm{h}}^t=\{\begin{array}{l}{\zeta }_{\mathrm{h}}{L}_{\mathrm{w},\mathrm{h}}^t+(1-{\zeta }_{\mathrm{h}})L_{\mathrm{e},\mathrm{h}}^t\hspace{1em}\hspace{1em}(L_{\mathrm{u},\mathrm{h}}^t\le L_{\mathrm{w},\mathrm{h},\max }^t)\\ {\zeta }_{\mathrm{h}}{L}_{\mathrm{w},\mathrm{h},\max }^t+L_{\mathrm{e},\mathrm{h}}^t\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(L_{\mathrm{u},\mathrm{h}}^t>L_{\mathrm{w},\mathrm{h},\max }^t)\end{array}$$

(33)

$${\zeta }_{\mathrm{h}}=\{\begin{array}{cc}0& (\frac{p_{\mathrm{e},\mathrm{s}}^t}{{\eta }_{\mathrm{h}}^l}\le p_{\mathrm{h},\mathrm{s}}^t)\\ 1& (\frac{p_{\mathrm{e},\mathrm{s}}^t}{{\eta }_{\mathrm{h}}^l}>p_{\mathrm{h},\mathrm{s}}^t)\end{array}$$

(34)

5. Decision-Making Model of Each Stakeholder

The multi-level leader–follower game model is solved using the adaptive differential evolution algorithm with external archiving (JADE) combined with the Gurobi solver on the MATLAB 2021a platform.

In the JADE algorithm, the crossover and scaling factors of the IEO are dynamically maintained based on the historical performance of the objective function in each iteration. The strategy is as follows: if the current individual performs better than its neighbors in the previous generation, then the original crossover and scaling factors remain unchanged; if the current individual performs worse in the previous generation, an exponential transformation is adopted to gradually adjust the values of the crossover and scaling factors. This allows the better-performing individuals to pass on their factors to the offspring, increasing the efficiency of the offspring search, thus finding the global optimum faster. This makes the JADE algorithm suitable for solving high-dimensional nonlinear optimization problems such as maximizing the total revenue of the IEO. The steps and flowchart of the game solution are shown in Figure 3.

The specific implementation process of the multi-level leader–follower game is as follows:

(1)

Initialize the parameters of the IEO, the ESO, and the user side, set the initial population number in the JADE algorithm to 40, with mutation probability and crossover probability of 10% and 80%; $K=0$, $K_{\max }=120$.

(2)

The leader IEO will transmit the pricing strategies of the initial electricity and heat prices generated to the followers, the ESO and the user.

(3)

The ESO responds first, formulating the charging strategy to transmit to the IEO while also determining the selling price to transmit to the user side.

(4)

The user side accepts the selling price strategies from the IEO and ESO, optimizes its energy consumption structure to maximize its benefits, formulates its energy purchase strategy, and reports it to the IEO and ESO.

(5)

Based on the genetic crossover selection and mutation, priority is given to ensuring the highest overall system efficiency. Subsequently, the IEO ensures the maximization of its own operational efficiency, guiding the ESO and the user in dynamic optimization, updating the ESO’s charging strategy and the user side’s energy purchasing strategy. Where $F_{IEO}^{k^{*}}$ is the maximum value of the objective function of the IEO in the previous iteration process.

(6)

Repeat steps (3) to (5) until the selling price strategy of the IEO, the charging strategy and selling price strategy of the ESO, and the energy purchasing strategy of the user side reach a game equilibrium solution or the maximum number of iterations is reached, then output the optimization results.

6. Case Study Analysis

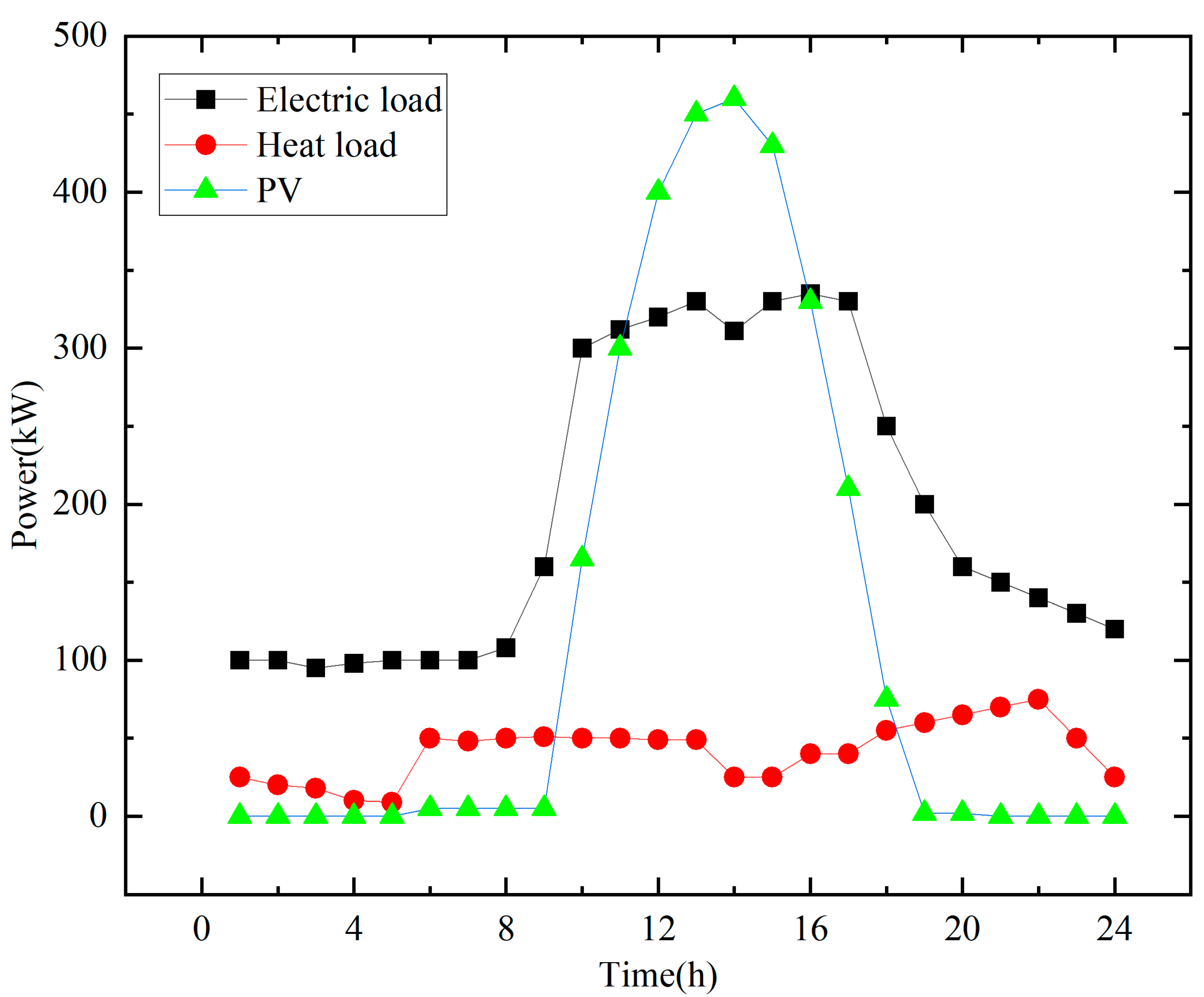
The actual example described in this paper is a community model including the IEO and ESO supplying energy to several residential buildings. It is assumed that a day can be divided into T = 24 time periods, with each residence equipped with electric heating equipment and solar power generation devices on the roof. The IEO side is equipped with a micro gas turbine. The electricity and heat energy demand of the user side, as well as the photovoltaic output within one cycle, are shown in Figure 4.

6.1. Analysis of the Economic Results of RIES Operation

Using the operational strategies described in this paper, after each party reaches a game equilibrium, the electricity selling price curves of the IEO and ESO are as shown in Figure 5a, where the overall trends of the IEO’s and ESO’s electricity selling prices follow the same fluctuations as the grid’s electricity selling prices.

During the off-peak hours of the grid’s time-of-use electricity prices from 0:00~6:00 and 22:00~24:00, the ESO’s selling price is generally higher than the IEO’s, averaging 9.5% higher. This is because the ESO cannot perform charging and discharging activities simultaneously, so it should choose to charge during the periods when the IEO’s electricity selling prices are relatively low throughout the entire cycle. At these times, setting a high selling price by the ESO can encourage the user to purchase electricity from the IEO. On the other hand, this is also due to the efficiency losses during charging and discharging, making the IEO’s selling cost higher than the ESO’s. During the peak hours of the grid’s time-of-use electricity prices from 9:00~14:00 and 17:00~22:00, the ESO’s selling price is generally 19.1% lower compared to the IEO’s, making the user more inclined to obtain electricity from the ESO. During the normal hours of the grid’s time-of-use electricity prices from 6:00~9:00 and 14:00~17:00, the ESO’s selling price is generally 9.2% higher than IEO’s, at which times the user is more inclined to obtain electricity from the IEO.

From Figure 6, it can be observed that the SESS charges during 87.5% of the off-peak periods of the electricity price (0:00~5:00 and 22:00~24:00) and discharges during 80% of the peak periods (9:00~11:00, 12:00~14:00 and 17:00~22:00). The ESO follows the principle of “charge low, discharge high”, but it does not charge to the full capacity during charging, nor does it discharge in every peak period. This is because, in the game process, this charging and discharging mode effectively reduces the decrease in the IEO’s profits caused by the addition of the ESO, and it also reduces the user side’s electricity purchase costs during peak price periods. During the flat-rate electricity price periods (6:00~9:00 and 14:00~17:00), the capacity of the SESS remains unchanged. This ensures that the energy storage equipment reduces the number of charge and discharge cycles, reduces the operating costs, and extends its service life.

Figure 7 shows the supply–demand balance of the user-side electricity load after the game optimization. The flexible electricity load has been shifted from the continuous high-price period of 9:00~18:00 to the two continuous periods of 0:00~9:00 and 18:00~24:00, which has improved the user’s benefits while achieving the goal of “peak shaving and valley filling”. However, the period 18:00~22:00, which receives the transferred flexible electricity load, belongs to the high-price period. This is mainly due to three reasons. Firstly, this method of electricity load transfer ensures that electricity loads with long continuous operation times can also participate in the transfer, increasing the proportion of flexible electricity load in the total load and making the adjustment more flexible. Secondly, there is a proportional limit to the flexible electricity load that can be absorbed in each unit time period of the entire cycle. Finally, the micro gas turbine used by the IEO in this paper operates according to a heat-to-electricity strategy, and the electricity generated by the micro gas turbine can be thermally absorbed by the transferrable flexible electricity load.

The IEO’s thermal energy selling price curve is shown in Figure 5b, combined with the supply–demand balance of the user’s thermal load after game optimization shown in Figure 8. During the periods of low or relatively low electricity prices from 0:00~8:00 and 23:00~24:00, electric heating is used as the source of thermal energy supply, effectively reducing the user’s heating costs. During the period of higher electricity prices from 9:00~22:00, the user tends to use the IEO as the source of thermal energy supply. During some time periods, the thermal energy supply of the user side comes from both electric heating and the IEO. This is because, on the one hand, thermal energy regulation has inertia, and on the other hand, for example, the thermal load surges during the period of 19:00~22:00, thus a combined heating supply mode is adopted. The optimized user thermal load is reduced throughout the entire cycle. Observing the IEO’s thermal selling price curve, it can be seen that the selling price of thermal energy is lower during 0:00~9:00 and 22:00~24:00, which coincides with the use of the IEO as the source of thermal energy during 8:00~9:00 and 22:00~23:00. In other time periods, even if the selling price of thermal energy is high, it still maintains a price advantage as electricity prices increase. Therefore, there is not much fluctuation in prices, and the user also tends to use the IEO as the source of thermal energy.

6.2. Analysis of the Economic Results of RIES Operation

To illustrate the effectiveness of the multi-level game optimization scheduling proposed in this paper in terms of economy and system stability, the following three scenarios are set for comparative analysis:

• Scenario 1: The economic operation strategy proposed in this paper, where the IEO’s electricity and heat selling prices, as well as the ESO’s electricity selling prices, are all non-fixed values.
• Scenario 2: The IEO’s electricity and heat selling prices are non-fixed values, while the ESO’s electricity selling prices are fixed.
• Scenario 3: The IEO’s electricity and heat selling prices are non-fixed values, with no ESO participation in the system operation.

Table 1. Revenues of various entities and overall revenues in different scenarios.

	Revenue (CNY)	IEO	ESO	User	RIES
Scenario
1		628.01	382.51	5705.11	6715.63
2		543.54	207.85	5874.52	6625.91
3		676.70	0.00	5552.30	6229.00

reflects the returns of each subject and the overall returns of RIES under different scenarios, Comparing the revenues of each entity in Scenario 1 and Scenario 3, it can be observed that in Scenario 1 compared to Scenario 3, where the ESO did not participate in the energy system operation, the user-side revenue increased by CNY 152.81, a 2.8% increase. The ESO’s participation in the system operation resulted in an increase of CNY 382.51 in revenue. The overall revenue of the RIES increased by CNY 486.63, a 7.8% increase. It is evident that the ESO’s participation in the RIES’s operation reduces the load fluctuation of the RIES, improves the overall economic efficiency, and enhances the overall performance of the energy system. However, the IEO’s revenue decreased by CNY 48.69, a 7.2% reduction. This decrease is attributed to the competitive relationship between the IEO and the ESO in supplying energy to the user side. After optimization, the total energy consumption on the user side remains constant, leading to a decrease in the IEO’s revenue.

To verify the impact of the ESO’s electricity price strategy on the economic efficiency of the system after the ESO participates in the energy system operation, a comparison of the revenues of each entity in Scenario 1 and Scenario 2 was conducted. Relative to Scenario 2, in Scenario 1, the IEO’s revenue increased by CNY 84.47, a 15.5% increase; the ESO’s revenue increased by CNY 174.66, an 84.03% increase; the user revenue decreased by CNY 169.41, a 2.9% reduction; and the overall system revenue increased by CNY 89.72, a 1.4% increase. It is evident that the non-fixed electricity price strategy of the ESO led to an overall increase in revenue. At the same time, the ESO’s revenue increased significantly, enhancing the enthusiasm for the ESO’s participation in the investment.

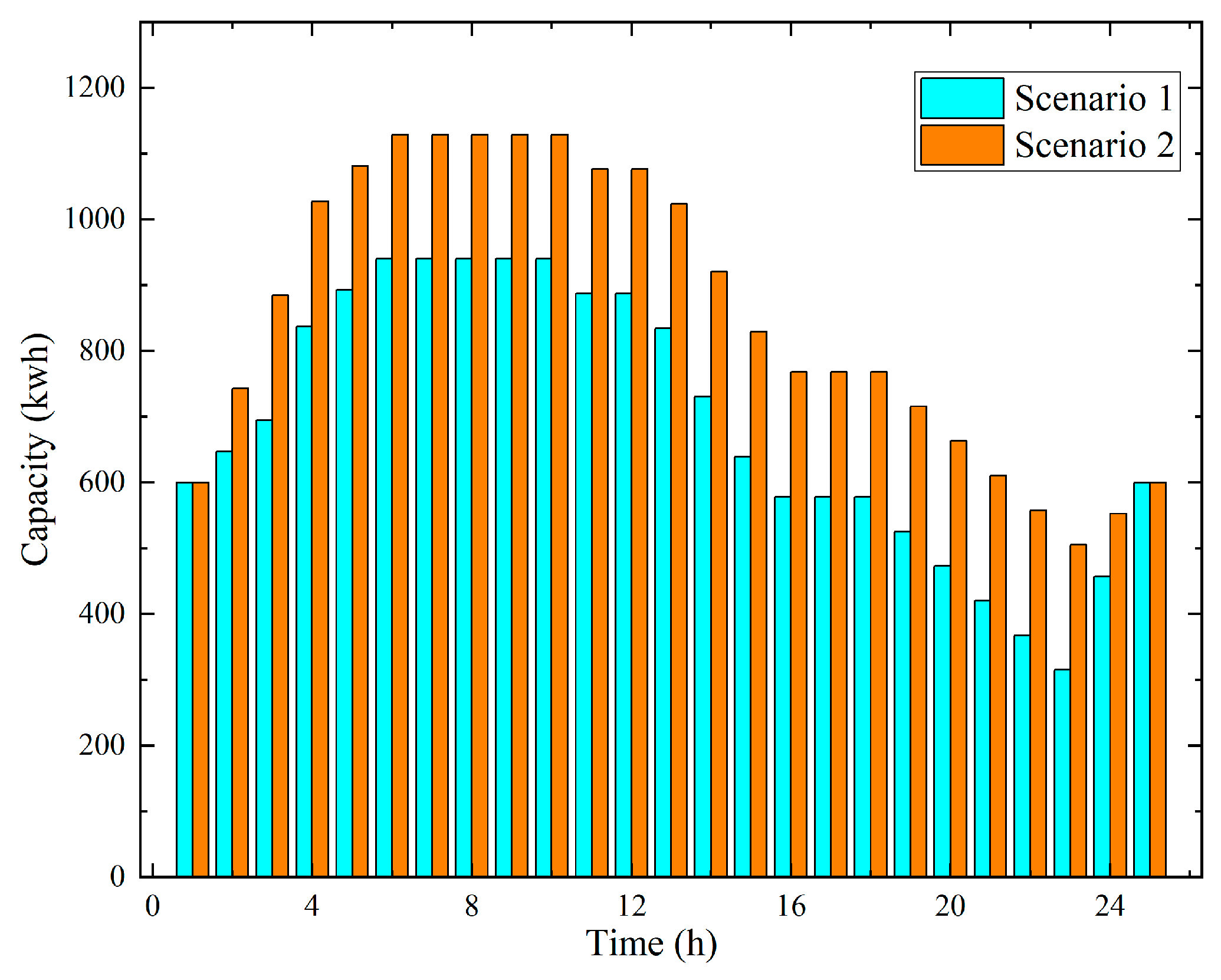
The graph in Figure 9 shows the capacity variation of the ESO’s energy storage system in Scenarios 1 and 2 during different time periods within one cycle. It can be seen that the charging and discharging periods of the ESO are almost the same in both scenarios. However, in Scenario 2, where the ESO’s selling price is fixed, the ESO cannot adjust its price appropriately during peak periods of the IEO’s electricity price and the user’s energy demand to increase its revenue, thus not fully utilizing the flexibility of the ESO. Additionally, due to the lower ESO electricity price in this scenario, the user is more inclined to choose the ESO as their energy source, leading to higher user-side profits in Scenario 2 compared to Scenario 1, but further reducing the ESO’s benefits.

The graph in Figure 10 shows the user-side electricity load curve for the entire cycle under the three scenarios. It can be seen that in all three scenarios, compared to the original scenario, the electricity load achieves the goal of “peak shaving and valley filling”, resulting in a smoother load curve. With the participation of the ESO in the energy system operation, the entire load curve becomes smoother, reducing the peak and valley loads and improving the overall system stability. However, compared to Scenario 1, in Scenario 2, the ESO’s selling price is generally lower during the 9:00~16:00 period, leading the user side to prefer electric heating to meet the heating demand, resulting in a higher electricity load in Scenario 2 compared to Scenario 1.

7. Conclusions

(1) Existing studies mostly utilize the leader–follower mode of master–slave game models, where each entity in the model can only choose to be a leader or a follower. This paper considers the dual role of the ESO as a buyer/seller of energy, constructing a multi-level game model that fully exploits the tripartite flexibility of source–load–storage, achieving multi-entity and multi-level coordinated optimization scheduling.

(2) With the development of shared energy storage services and the increasing variety of user-side energy-consuming devices, this paper considers the coupling of the IEO-side electricity and heat, as well as the participation of the user-side electric heating devices. It also takes into account the competitive relationship between the IEO and ESO in energy supply, making the constructed model more comprehensive and better suited to the actual operational scenarios of energy systems.

(3) Compared to centralized algorithms, the method of using the heuristic JADE algorithm combined with the Gurobi solver for model solving achieves the distributed solving of the model, better safeguarding the data privacy of the IEO, the ESO, and the user.

(4) The comparison of three scenarios validates that the energy system economic operation strategy proposed in this paper, based on multi-level games with shared energy storage, can maximize the overall benefits of the system, achieving mutually beneficial cooperation between the IEO, the ESO, and the user.

The optimization operating strategy for the RIES presented in this paper is designed based on a scenario where all the stakeholders provide complete information. However, in actual trading markets, it cannot be guaranteed that all the parties involved in the game are absolutely rational, and the phenomenon of incomplete information is inevitable, leading to unreliable operating strategies. Therefore, how to achieve the optimal resource allocation strategy in scenarios of incomplete information merits attention.