Abstract
Non-technical losses (NTL) have been a growing problem over the years, causing significant financial losses for electric utilities. Among the methods for detecting this type of loss, those based on Artificial Intelligence (AI) have been the most popular. Many works use the electricity consumption profile as an input for AI models, which may not be sufficient to develop a model that achieves a high detection rate for various types of energy fraud that may occur. In this paper, using actual electricity consumption data, additional statistical and temporal features based on these data are used to improve the detection rate of various types of NTL. Furthermore, a model that combines both the electricity consumption data and these features is developed, achieving a better detection rate for all types of fraud considered.
1. Introduction
The electric power system is made up of generating facilities, high-voltage transmission lines and medium- and low-voltage distribution networks. Not all the energy produced is delivered completely to the end user, which means that electrical losses occur during all stages of the process. These losses are divided into technical losses (TLs) and non-technical losses (NTLs), and the distribution sector has the highest value of them in the entire system [1].
NTLs, also known as commercial losses, are units of energy that are delivered and consumed but are not billed by the electric power utility. There are four ways to account for an NTL [2], namely:
- Fraud: When a consumer attempts to deceive an electric power utility. This is usually carried out by tampering with energy meters, making them register a lower electricity energy consumption than actually consumed;
- Bypass: The bypass is a clandestine connection made directly from the power grid to the load, without passing through the energy meter;
- Bribery: Bribing power utility employees is another common practice. Corruption can come from both the consumer and the employee;
- Non-payment: The consumer ignores the energy bill and does not pay. It can also happen when a residential consumer no longer lives there, when a commercial consumer’s company goes bankrupt, or even due to a malfunction of a meter that does not record electricity consumption.
NTL is a global problem that affects underdeveloped, developing and even fully developed countries. According to the Northeast Group LLC report [3], USD 96 billion is lost annually across the planet. In the United States of America, in 2009, the annual loss of power utilities was estimated at approximately USD 6 billion [4]. BC Hydro, one of Canada’s largest power utilities, reported that in 2011, the annual loss due to electricity fraud was approximately CA$100 million [5]. In underdeveloped and developing countries, the situation tends to worsen. The main emerging countries record annual losses of USD 58.7 billion [6]. In Brazil, in 2022, NTLs represented 14.6% of all losses in the low-voltage power system. In relation to the entire Brazilian system (low, medium and high voltage), NTLs represented 6.3% of the total loss [7]. In some Latin American countries, financial losses caused by NTL are, to some extent, shared between electricity companies and users (including those who have not committed any type of fraud) [8].
Power Quality (PQ) can be negatively affected by clandestine illegal connections, as the amount of power that will flow through the system is different from what is expected. In this case, disturbances such as voltage fluctuations, overvoltages, undervoltages and harmonics, among other problems, may occur [9]. This can result in fire-risk hazards and even cause widespread blackouts.
With the advent of smart grids (SG), advanced metering infrastructure (AMI) devices were developed to facilitate communication between the energy meter and the power company. However, this two-way flow of communication inevitably leads to problems related to cyber security, such as data leakage and theft/alteration of consumer electricity data [10,11,12]. In other words, the AMI can be hacked and reprogrammed with the intention of committing fraud related to electricity theft [13].
In addition to the traditional tampering that was used to commit fraud, new methods of energy theft have been developed to attack AMI, which can cause even more loss of revenue for the power company.
Therefore, due to the large financial losses caused, reduction in PQ and also due to new methods of electricity theft through AMI, it is necessary to develop new techniques or systems to detect energy theft to further prevent the growth of NTL. One can take advantage of the large amount of data that is transmitted and stored in the SG to create Machine Learning (ML) and Deep Learning (DL) models that can efficiently detect when and what type of energy fraud is being committed. The contributions of this work are as follows:
- Application of DL models to classify whether a consumer is honest or has committed some type of fraud;
- Use of statistical and temporal features as additional inputs to improve the model’s classification performance;
- Combination of two DL architectures to develop a more robust model to detect NTL.
The remainder of the paper is organized as follows. Section 2 contains work related to NTL detection. Section 3 presents the detailed methodology regarding DL architectures, the dataset preprocessing step, the equations used to generate different cases of energy theft and the models developed to detect them. In Section 4, the results are presented. Section 5 concludes the paper and presents some suggestions for future work to continue the research.
2. Related Work
Initial attempts to detect NTL relied on field inspections by power company employees, which were human-resource-intensive, required high operating costs [14] and were also considered ineffective [15,16].
Based on that, new methods have been developed to improve NTL detection, and are usually divided into three categories [17]:
- Theoretical analysis: Demographic and socioeconomic factors can provide the energy company with information about locations where an NTL may occur more frequently;
- Hardware-based method: It is related to the infrastructure and design of specific measurement devices. For example, integrated circuits (ICs) were installed to detect tampering in energy meters [18] and an additional current transformer (CT) was added to achieve the same result [19]. The disadvantage of this approach is the high costs related to the manufacture, installation and maintenance of these new devices;
- Non-hardware based method: The most widely used method for detecting NTL [17]. Deviations in energy consumption and other electrical quantities, such as voltage and current, occur in an NTL scenario. Using data collected from consumers, a data-oriented/ML method (supervised or unsupervised learning) or a network-oriented method (state estimation or load flow) can be developed to detect whether they are committing any type of fraud.
A labeled dataset with historical energy consumption data from consumers from different cities was used to train a Support Vector Machine (SVM) to classify abnormal or fraudulent activity [15]. The trained SVM had a 60% hit rate, much higher than the 3% rate that the energy company previously had using manual inspections.
In [20], data from commercial and industrial consumers were used to train an Optimum-Path Forest classifier (OPF). Instead of using energy consumption (kWh), other electrical quantities were used, such as reactive energy consumption (kVArh), power factor (PF), installed power (), among others. The Harmony Search (HS) algorithm was used to extract important features and reduce the dimensionality of the problem, improving the accuracy of the classifier. HS also provided superior results when compared to another traditional feature extraction technique, Principal Component Analysis (PCA).
It is not customary to have a labeled dataset that indicates whether a consumer has committed fraud. Based on this and using AMI data, ref. [11] proposed six equations that generate malicious samples based on data from honest users. For each consumer, a multiclass SVM is trained using historical data and the data generated by these equations. An energy theft detector is presented that compares the total energy consumption of a neighborhood measured by a transformer meter with the total energy reported by smart meters. If an NTL is detected, consumers in that area are flagged as suspicious, and based on new samples from each of these costumers, the classifier decides whether any of them are committing fraud or not.
Zanetti et al. [21] proposed two new equations to generate malicious samples in addition to those proposed by [11] and used a similar approach that also requires data from meters of the low-voltage grid (LVG) transformer. It uses a “detector” that compares the reports from the LVG meter and the residential smart meters. Then, a state machine approach that defines three states in the grid, normal (), suspicious () or abnormal (), is used to identify users with abnormal consumption patterns.
Using a real labeled dataset that contains time series with daily measurements, Zheng et al. [22] developed a neural network made up of two distinct parts. The first is called the wide network, which consists of fully connected layers that aim to capture global features of 1-D data (time series of electrical energy consumption), and another Deep Convolutional Neural Network (CNN) that identifies the non-periodicity of energy theft and the periodicity of a regular consumer based on 2-D data (the 1-D data are transformed into weekly measurements). Finally, the output of both networks is combined into a sigmoid activation function to classify whether a consumer has committed fraud or not. To improve the model’s performance, some preprocessing steps were taken, such as linear interpolation to impute missing values and the empirical rule, with two standard deviations of the mean value to detect outliers in the dataset.
A new equation to model energy theft is proposed in [23]. It considers that an attack increases linearly over time; that is, energy consumption decreases linearly rather than decreasing abruptly. Then, based on some equations from [11] and this new proposed equation, a hybrid model that uses voltage sensitivity analysis, power system optimization and Support Vector Machines (SVM) is used to perform the detection of NTLs.
It is well known that labeled energy theft datasets have more samples of honest users than fraudulent ones. Therefore, these datasets are considered unbalanced and can cause potential learning problems for ML algorithms [24]. Using the same dataset as [22], the authors of [25] used a VGG-16 architecture (consisting of multiple convolution and pooling layers) to extract features and employed an XGBoost (Decision Tree-based algorithm) to carry out the final classification. The XGBoost hyperparameters were optimized using a firefly optimization algorithm. To address the problem of an unbalanced dataset, the Adasyn method was used to oversample the minority class.
An ensemble consisting of several boosting and bagging methods was built to detect energy theft [26]. The idea behind the ensemble is to train several models and combine each of the outputs into a single one that has better predictive performance than each of the individual models. Using the same equations as [11], malicious samples were generated, but instead of creating a multiclass problem, it was framed as a binary classification problem. The performance of the models was tested with undersampling (near miss) and oversampling (SMOTE) techniques, with the latter showing slightly better results.
All malicious samples generated by the equations from previous works [11,21,23] and additional equations were used in [27] to create a more diverse case of energy theft. A multiclass classification problem was framed and several ML algorithms were used to solve it. These models were compared with each other to verify their global and class classification performance. Other tests were carried out in which parameters of the equations that generated the malicious samples (such as intensity and duration of attacks) were modified to verify the models’ behavior. All these results can be used as a basis for future work in the NTL detection field.
A comprehensive review study of non-hardware-based methods was carried out in [28]. Data-oriented/ML methods are the most used approach to detect NTL, and they generally use electrical quantities as features, such as voltage, demand and mainly electricity consumption. These works employ traditional ML algorithms, like SVM, Artificial Neural Networks (ANN), Decision Tree (DT) or Bayesian Classifiers.
Based on that, this work employs two DL architectures, Multi-Layer Perceptron (MLP) and Long Short-Term Memory (LSTM) to solve the NTL detection problem. To improve the model performance, in addition to the user energy consumption, statistical (mean and variance) and temporal features (X and Y coordinates of the centroid of the energy consumption time series) are used as additional inputs. Finally, a model consisting of the two aforementioned networks is defined to work in parallel with the static features (statistical and temporal) and the time series of energy consumption.
3. Materials and Methods
3.1. Deep Learning Architectures
DL models are widely used to solve problems in the most diverse areas of science. They are mathematical models trained on data to solve basically two types of problems: regression or classification. Since the MLP and the LSTM models are well-known models used to solve these types of problems, they were chosen to solve the NTL detection problem.
3.1.1. MLP
MLP is a deep feedforward artificial neural network (without feedback connections) consisting of input, hidden, and output layers that process data in a unidirectional flow with the goal of approximating a function (learning a pattern) [29]. It defines a function where is the input vector and is the weight vector that the network learns. The backpropagation algorithm is used to train these types of networks [30].
3.1.2. LSTM
Unlike the MLP, the LSTM network is a bidirectional network (containing feedback connections), where the output of some nodes influences the input of this same node in future steps. Like any Recurrent Neural Network (RNN), LSTM specializes in sequential data processing and solves the problem of vanishing or exploding gradients that the former exhibits [29]. This is carried out by adding a gate mechanism to control the flow of information and gradient updates. In Figure 1, an LSTM cell is presented with its respective gates, input value, hidden and cell states, x, h and C, respectively, and t is the timestep. The sigmoid activation function in the green block represents the forget gate, which decides which information is useful to the model (a value of 0 means that nothing is useful and everything should be discarded, while a value of 1 means everything is useful). The two red blocks represent the input gate that computes the values that will be updated and stored in the LSTM cell through the combination of the sigmoid and hyperbolic tangent activation functions. After this, the LSTM cell is updated from state to . Finally, the yellow blocks represent the output gate that uses the updated cell state through a hyperbolic tangent function to decide which information will be provided as output in the current time step and will be used as the hidden state in the next time step.
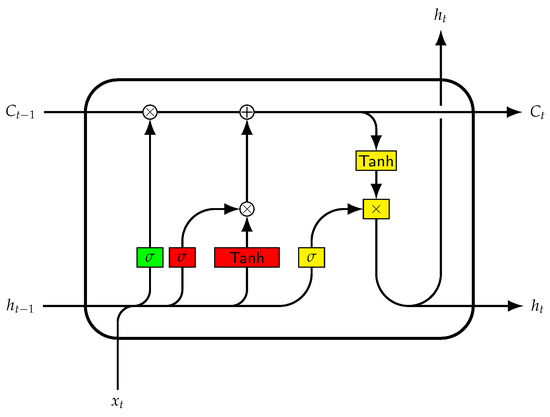
Figure 1.
LSTM cell.
3.2. Dataset
The dataset used in this work was created by the Commission for Energy Regulation (CER) in Ireland and is provided by the Irish Social Science Data Archive (ISSDA) on request [31]. It contains data on electricity consumption of more than 6400 users at half-hour intervals (48 reports per day), collected over 535 days between 2009 and 2010.
Data from 650 randomly chosen consumers were used. Some preprocessing steps were required due to missing or incompatible data to ensure that consistent data are used to train the developed models.
- If a half-hourly measurement is not available, the entire day is discarded (missing data case);
- If there is incompatible data, for example, in a single day, a consumer has more than 48 half-hourly measurements, the entire day is also discarded (a possible case of an error in data storage);
- During certain days, some users reported 0 energy consumption. In these cases, if a user has zero energy consumption for more than 1/4 of the day, that entire day is ignored (in case of a possible meter failure).
After that, the half-hourly measurements are resampled to hourly, with the aim of reducing the number of model inputs.
Consider . Each univariate energy consumption time series has the following format , and a matrix of dimensions M can be created with the time series of all consumers:
with measurements per series.
3.3. Energy Theft Attack Models
The data provided by ISSDA is assumed to be from honest consumers, as they have agreed to participate in the smart meter installation process. Based on this, equations are needed to model the consumption behavior of fraudulent users. In this work, the same eleven equations used in [27] are used, with some modifications to generate more practical cases of energy theft, as they cover a large number of possibilities for these types of NTL. Let , , be the eleven possibilities of fraud/attack, as follows.
- Attack 1: Each time series is multiplied by a random value , between 0.1 and 0.9 that reduces energy consumption:
- Attack 2: Each smart meter reports 0 while the attack occurs (complete bypass). and represent the start and end times of the attack, respectively. In this work, unless otherwise indicated, all attacks that occur during a period start randomly between 08:00:00 and 16:00:00 and the last 4 h, that is, :
- Attack 3: This attack is similar to Attack 1, but instead of multiplying the whole time series by a random value, the measurements in the time series at each time t are multiplied by a different random value, , between 0.1 and 0.9:
- Attack 4: Similar to Attack 2, but instead of completely bypassing the meter, a partial bypass occurs:
- Attack 5: Actual consumption is replaced by the product between average consumption and different random values:
- Attack 6: A cut-off point, , is selected. A measurement in a time series is replaced by the cut-off point if it is greater than it. The selected point is a random value between 120% and 130% of the average energy consumption, i.e., :
- Attack 7: A cut-off point, , is selected. The maximum value between 0 and the difference between energy consumption and the cut-off point is considered:
- Attack 8: Unlike other attacks, this one does not simulate a sudden drop in energy consumption, but rather the drop occurs linearly over time until the maximum attack intensity. This gradual decay is controlled by the rate of variation in the attack intensity, that is, the slope s:where , and .
- Attack 9: Each energy consumption time series is replaced by its average value:
- Attack 10: The energy consumption pattern reverses over time. Attacks of this type occur in situations where the price of energy is different throughout the day. For example, a user who consumes more electricity and has a higher energy tariff at the end of the day, when reversing their pattern, will have a reduced energy bill:
- Attack 11: Another attack that aims to take advantage of different energy rates throughout the day. Consumption is reduced only at a certain interval (peak hours, when the tariff is high) and redistributed throughout the day (when the tariff is lower). This way, the customer’s total consumption remains the same throughout the day:Here is the reduction factor, and for this specific attack, the start time, , happens randomly between 18:00:00 and 20:00:00 and ends randomly at any given time after it has started. Therefore, is the number of hours during the day and is the number of hours during which the attack occurs. is amount of energy that was reduced in the process.
The same number of samples are generated for each attack and all are equal to the number of samples from honest users. Each attack is assigned an integer label to create the output vector . Finally, the dataset , , which consists of input/output pairs, can be created to train/test the DL models, where represents the samples of honest users, and are the samples of each type of attack.
3.4. Features for NTL Detection
Some attacks are more difficult to detect than others. This is because a consumer who commits fraud in which they steal a small amount of electricity may be misclassified as an inherently low-consumption consumer [21,27].
Based on this information, attacks that are difficult to detect are types 1, 3 and 4 when fraud is committed using high values of , and , respectively. Therefore, additional features can be used to improve the detection performance of a model, especially in the case of these attacks.
In this work, for a single time series, , the following features were used as additional input to the models:
- Mean: Most attacks reduce energy consumption, so it is reasonable to assume that the energy consumption value of a fraudulent user is lower than that of an honest user. Therefore, the average value can add valuable information for fraud detection and is calculated as follows:As shown in Figure 2, the mean value of a user who commits type 1 fraud is lower than their real consumption, which could help improve the detection of this type of attack.
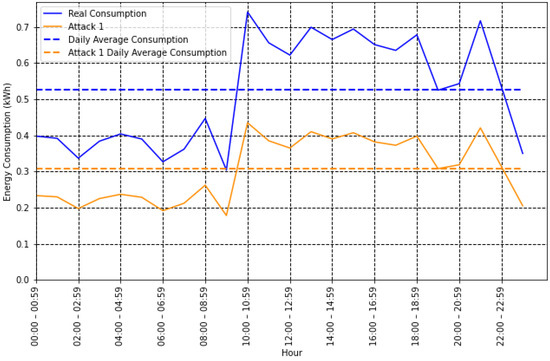 Figure 2. Honest and type 1 attack with average value.However, for a type 10 attack, where fraud is committed by reversing the energy consumption pattern, the average value does not change, as shown in Figure 3. Therefore, additional features are needed to improve the classification process.
Figure 2. Honest and type 1 attack with average value.However, for a type 10 attack, where fraud is committed by reversing the energy consumption pattern, the average value does not change, as shown in Figure 3. Therefore, additional features are needed to improve the classification process.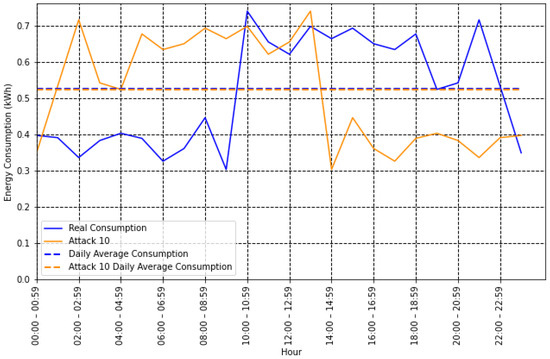 Figure 3. Honest and type 10 attack with average value.
Figure 3. Honest and type 10 attack with average value. - Variance: Indicates how far the set of measurements is spread from the average value. Similarly to the average value, the variance of a user who commits fraud will be smaller than the variance of an honest user.
- Centroid (center of mass): Contains information about the time and value of energy consumption. It can potentially help detect an NTL because some attacks tend to occur at specific times of the day, reducing energy consumption only during that interval. The centroid coordinates and can be determined as follows [32]:In Figure 4, the centroids for type 10 attacks are illustrated. The coordinate is essential in this case to help differentiate the honest user from the fraudulent one.
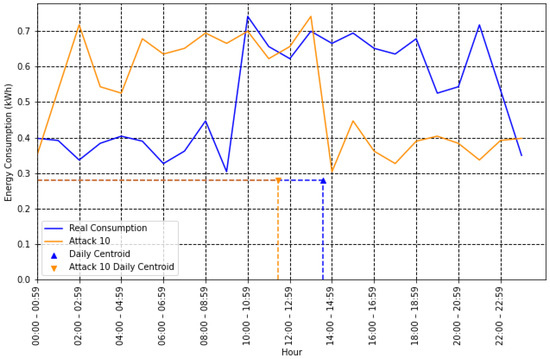 Figure 4. Honest and type 10 attack with centroid coordinates.
Figure 4. Honest and type 10 attack with centroid coordinates.
3.5. Developed Models
Several models have been developed to perform NTL detection. Some models use only the time series itself as input, while others use combinations of time series, statistical (average value and variance of the time series) and/or temporal features (centroid coordinates of the time series). The idea behind using these features is to aggregate information that can help detect NTL. As LSTM networks have been widely used in all types of sequence recognition problems, such as time series forecasting and classification [29,33], a final model is proposed that contains two modules—one module that contains an MLP that processes only statistical and temporal features and the other an LSTM that processes the time series itself. Their outputs are concatenated and serve as input to another MLP that indicates whether the user committed fraud or not.
In addition to different inputs, some models are trained with specific classes (easy or hard-to-detect classes) to show that additional features are needed to achieve higher classification performance. An honest user is labeled as class 0. MLP-M1 and MLP-M2 models take energy consumption time series as input and are only easy (class 2, 5, 6, 7, 8, 9, 10 and 11) and hard-to-detect frauds (class 1, 3 and 4), respectively. Models M3 to M8 use the 12 classes (classes 0 to 11) as output. MLP-M3 takes time series as input. MLP-M4 uses the time series as input and its daily average value. MLP-M5 uses the same input as MLP-M4 plus the daily variance of the time series. MLP-M6 uses the same input as MLP-M5 plus centroid X and Y coordinates of the time series. LSTM-M7 only uses the time series as input. M8 is the proposed parallel LSTM-MLP network. The MLP processes and learns information related to statistical and temporal features (4 inputs related to the average value, variance and both centroid coordinates), while the LSTM receives as input the energy consumption time series (24 inputs). Their outputs are concatenated and passed to another MLP to perform the final classification through a softmax activation function. Figure 5 illustrates this proposed model.
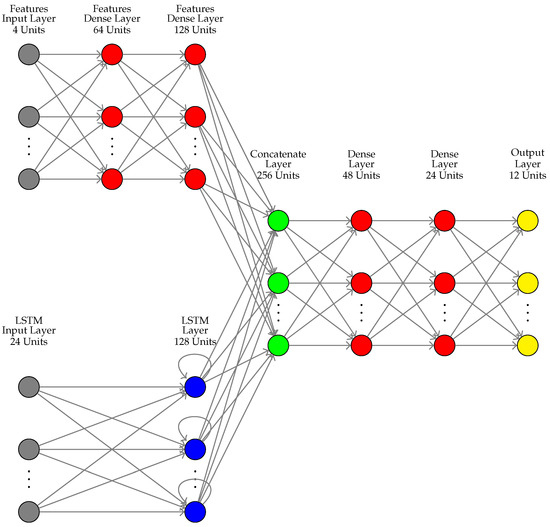
Figure 5.
M8-Parallel LSTM-MLP network.
A summary of all 8 models developed in this work is given in Table 1 with their respective number of input and output nodes.

Table 1.
Summary of developed models.
All of these models were developed in Python using the Keras library. A training/validation/test split of 0.6/0.2/0.2 was defined. The number of training epochs was set at 300. To avoid overfitting, the early stopping method was used with 50 epochs to monitor the validation loss. The batch size was set to 512.
The MLP-M1 to MLP-M6 models feature MLP networks with 2 hidden layers, as shown in Table 2 with the corresponding number of units. Adam optimizer, ReLU activation for hidden layers, and Softmax activation for the output layer were employed.

Table 2.
MLP models hidden layers.
The LSTM-M7 model contains a single LSTM layer with 128 units that is followed by an MLP with 2 hidden layers with 48 and 24 units, respectively. The M8 model also uses 2 hidden layers for each MLP and a single layer for the LSTM. The hyperbolic tangent and sigmoid activation functions are used in the LSTM layer. The number of units for each layer is presented in Figure 5.
3.6. Classification Metrics
The NTL detection problem is multiclass; therefore, common metrics to evaluate the performance of the model to solve this type of problem are , and -.
is the ratio between the True Positive () and the sum of and the False Positive (). It indicates, of all cases predicted as positive, how many were actually positive. In other words, a high precision value indicates that the model has a low rate of False Positives, meaning that when it predicts a positive class, it is likely to be correct.
is the ratio between and the sum of and the False Negative (TN). It indicates, of all actual positive cases, how many were correctly predicted by the model. A high recall value indicates that the model effectively identifies most positive instances, minimizing the number of False Negatives.
- is the harmonic mean between and . It is useful when there is a need to balance those two metrics in a classification task, such as the NTL detection problem, where classifying an honest user as fraudulent or vice versa has different implications and costs.
4. Results and Discussion
Table 3 presents the average of the three classification metrics for all classes used in the MLP-M1 and MLP-M2 models. When only the easy-to-detect classes are present (MLP-M1), the energy consumption time series as input is sufficient to achieve an - value of 0.909. Also, when only the hard-to-detect classes are present (MLP-M2), the model performance becomes significantly worse.

Table 3.
Classification metrics for MLP-M1 and MLP-M2 models.
But in practice, all types of fraud can occur and must be considered. The MLP-M3 model achieves 0.723 -. To improve NTL detection, statistical and temporal features were used, and the results for each of these models can be seen in Table 4. It can be seen that there is a slight improvement for all metrics with each new feature added (MLP-M4, MLP-M5 and MLP-M6), and that the centroid coordinates provide the best overall improvement with an - value of 0.779 (MLP-M6).

Table 4.
Classification metrics for MLP models with all classes.
However, better classification results are necessary, as it is extremely important that a dishonest consumer is not classified as honest, causing financial losses for the company. Another more serious situation would be classifying an honest consumer as dishonest, which creates legal, ethical, and reputational problems for the electric power company.
For this, two networks containing LSTM layers were trained. Their result can be observed in Table 5, which shows a significant increase in relation to the MLP-M6 model.

Table 5.
Classification metrics for LSTM-M7 and M8 models.
M8 achieved an overall 13.61% improvement in detection performance over the MLP-M6 model and demonstrated better performance compared to working exclusively with an LSTM network in the M7 model, indicating the effectiveness of combining two networks that work in parallel and can better learn the time series pattern and the features extracted from them.
Figure 6 illustrates the classification metrics by class for the M8 model. It can be seen that this model achieves an almost perfect - for some classes.
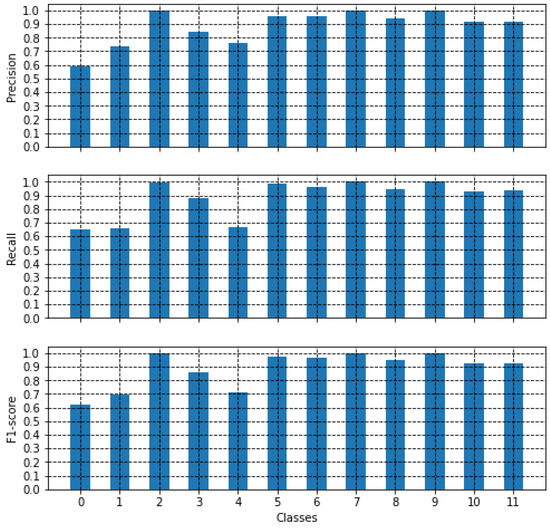
Figure 6.
Precision, Recall and F1-score for each class of M8 model.
Figure 7 shows the Receiver Operating Characteristic (ROC) curve, with the Area Under the Curve (AUC) for each class. Only honest users and type 1, 3 and 4 attacks do not achieve the perfect AUC score. This is because the patterns of this type of fraud are quite similar to each other. All other attacks have an AUC equal to 1, showing how effective the M8 model is in separating these classes.
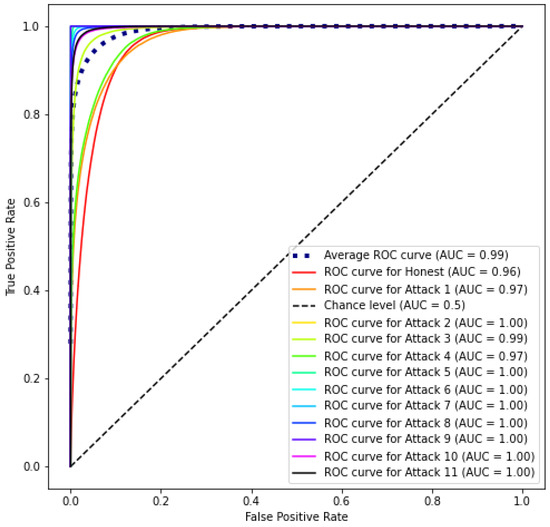
Figure 7.
ROC–AUC curve of the M8 model.
For a more intuitive assessment of the performance of the proposed model, Figure 8 includes a confusion matrix for each class. The model effectively detects most types of energy fraud, achieving a detection rate greater than 92.7% for all easily detectable frauds. Furthermore, it has a high detection rate of 88.41% for a challenging fraud type (type 3). However, for the remaining challenging classes (classes 1 and 4), the model presents an overall detection rate of around 66%.
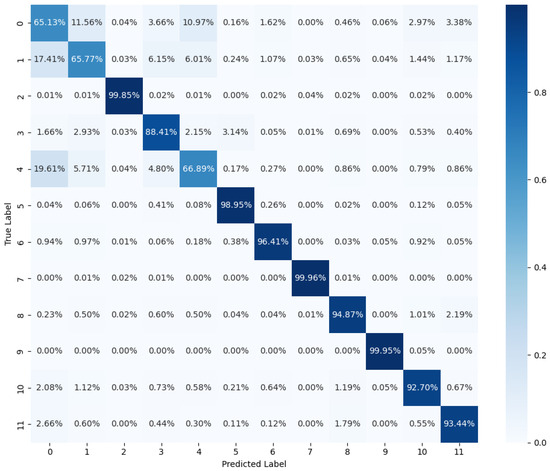
Figure 8.
Confusion matrix of M8 model.
The M8 model showed better performance compared to previous works. In [23], the proposed model achieved an AUC score of 0.99 similar to M8, but in that work, only four types of attacks were simulated, and all were easy-to-detect frauds. The best developed model in [27] achieved an average - of 0.75, which is 17.3% lower than M8.
It is worth noting that all models developed in this work are scalable, as they can process and test energy fraud from a single customer instantly or from thousands of customers in a few minutes.
Finally, from a business and social point of view, fraud detection, in addition to improving the financial health of companies, is a factor of social justice due to the fact that a high number of fraudulent users will represent an increase in tariffs for honest consumers or cause financial difficulties for electricity companies.
5. Conclusions
The NTL problem is widespread and causes billions of dollars in losses annually across the world. Because on-site inspections are an expensive and ineffective way to detect this type of loss, data-oriented methods have recently been employed to improve detection. In this work, statistical and temporal features extracted from energy consumption time series were used as additional input for a parallel LSTM-MLP network that was developed to detect NTL, improving the detection rate for all types of fraud that can occur in smart metering devices. Based on the results, there is still room for improvement, especially in increasing the detection of classes considered difficult to detect. For future work, other types of DL methods can be used, such as a 1-D Convolutional Neural Network (Conv1D) that works with one-dimensional data or the combination of this Conv1D and an LSTM. Methods that were developed specifically for time series classification can also be employed. More features, such as statistical, temporal or even domain frequency (like Fourier coefficients), can be added to better classify whether a user has committed fraud or not. Also, a feature importance algorithm could be used to provide more information on the features that are really useful, increasing the interpretability of the developed models. In addition, different hyperparameter optimization techniques can be employed to try to further improve the performance of the proposed model.
Author Contributions
Conceptualization, M.A.S., A.A.F. and R.R.B.d.A.; methodology, M.A.S., H.T.V.G., A.A.F. and R.R.B.d.A.; software, M.A.S., H.T.V.G. and R.M.d.L.N.; validation, O.N.N., M.M.d.S.L. and G.L.T.; formal analysis, A.A.F. and R.R.B.d.A.; investigation, M.A.S. and H.T.V.G.; resources, O.N.N., M.M.d.S.L., G.L.T. and R.R.B.d.A.; data curation, M.A.S., H.T.V.G. and R.M.d.L.N.; writing—original draft preparation, M.A.S.; writing—review and editing, M.A.S., H.T.V.G., R.M.d.L.N., O.N.N., M.M.d.S.L. and G.L.T.; visualization, M.A.S. and H.T.V.G.; supervision, A.A.F. and R.R.B.d.A.; project administration, R.R.B.d.A.; funding acquisition, R.R.B.d.A. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financed by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior-Brasil (CAPES)-Finance Code 001. Implemented at Federal University of Pernambuco (UFPE), nº 23076.051696/2023-96, through the PROPG nº 09/2023 announcement.
Data Availability Statement
Data were obtained from the Commission for Energy Regulation and are available at https://www.ucd.ie/issda/data/commissionforenergyregulationcer/ (accessed on 12 August 2022), with the permission of the Irish Social Science Data Archive.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Navani, J.; Sharma, N.; Sapra, S. Technical and Non-Technical Losses in Power System and Its Economic Consequence in Indian Economy. Int. J. Electron. Comput. Sci. Eng. 2012, 1, 757–761. [Google Scholar]
- Smith, T.B. Electricity theft: A comparative analysis. Energy Policy 2004, 32, 2067–2076. [Google Scholar] [CrossRef]
- Northeast Group LLC. Electricity Theft and Non-Technical Losses: Global Markets, Solutions and Vendors. Available online: http://www.northeast-group.com/ (accessed on 20 September 2023).
- McDaniel, P.; McLaughlin, S. Security and Privacy Challenges in the Smart Grid. IEEE Secur. Priv. Mag. 2009, 7, 75–77. [Google Scholar] [CrossRef]
- BC Hydro. Smart Metering & Infrastructure Program Business Case. Available online: https://app.bchydro.com/content/dam/BCHydro/customer-portal/documents/projects/smart-metering/smi-program-business-case.pdf (accessed on 20 September 2023).
- de Souza Savian, F.; Mairesse Siluk, J.C.; Bisognin Garlet, T.; Moraes do Nascimento, F.; Renes Pinheiro, J. Non-technical losses in electricity distribution: A bibliometric analysis. IEEE Lat. Am. Trans. 2021, 19, 359–368. [Google Scholar] [CrossRef]
- ANEEL. Perdas de Energia Elétrica na Distribuição. Available online: https://portalrelatorios.aneel.gov.br/luznatarifa/perdasenergias (accessed on 20 September 2023).
- de Oliveira Ventura, L.; Melo, J.D.; Padilha-Feltrin, A.; Fernández-Gutiérrez, J.P.; Sánchez Zuleta, C.C.; Piedrahita Escobar, C.C. A new way for comparing solutions to non-technical electricity losses in South America. Util. Policy 2020, 67, 101113. [Google Scholar] [CrossRef]
- Olaoluwa, O.G. Electricity Theft and Power Quality in Nigeria. Int. J. Eng. Res. Technol. 2017, 6, 1180–1184. [Google Scholar]
- Wang, W.; Lu, Z. Cyber security in the Smart Grid: Survey and challenges. Comput. Netw. 2013, 57, 1344–1371. [Google Scholar] [CrossRef]
- Jokar, P.; Arianpoo, N.; Leung, V.C.M. Electricity Theft Detection in AMI using customers’ consumption patterns. IEEE Trans. Smart Grid 2016, 7, 216–226. [Google Scholar] [CrossRef]
- Mrabet, Z.E.; Kaabouch, N.; Ghazi, H.E.; Ghazi, H.E. Cyber-security in smart grid: Survey and challenges. Comput. Electr. Eng. 2018, 67, 469–482. [Google Scholar] [CrossRef]
- Morgoev, I.D.; Dzgoev, A.E.; Kuzina, A.V. Algorithm for Operational Detection of Abnormally Low Electricity Consumption in Distribution. In Proceedings of the Advances in Automation V, Sochi, Russia, 10–16 September 2023; Radionov, A.A., Gasiyarov, V.R., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 37–49. [Google Scholar]
- Nizar, A.H.; Dong, Z.Y.; Jalaluddin, M.; Raffles, M.J. Load Profiling Method in Detecting non-Technical Loss Activities in a Power Utility. In Proceedings of the 2006 IEEE International Power and Energy Conference, Putra Jaya, Malaysia, 28–29 November 2006; pp. 82–87. [Google Scholar] [CrossRef]
- Nagi, J.; Yap, K.S.; Tiong, S.K.; Ahmed, S.K.; Mohamad, M. Nontechnical Loss Detection for Metered Customers in Power Utility Using Support Vector Machines. IEEE Trans. Power Deliv. 2010, 25, 1162–1171. [Google Scholar] [CrossRef]
- Saeed, M.S.; Mustafa, M.W.; Hamadneh, N.N.; Alshammari, N.A.; Sheikh, U.U.; Jumani, T.A.; Khalid, S.B.A.; Khan, I. Detection of Non-Technical Losses in Power Utilities—A Comprehensive Systematic Review. Energies 2020, 13, 4727. [Google Scholar] [CrossRef]
- Viegas, J.L.; Esteves, P.R.; Melício, R.; Mendes, V.; Vieira, S.M. Solutions for detection of non-technical losses in the electricity grid: A review. Renew. Sustain. Energy Rev. 2017, 80, 1256–1268. [Google Scholar] [CrossRef]
- Ngamchuen, S.; Pirak, C. Smart anti-tampering algorithm design for single phase smart meter applied to AMI systems. In Proceedings of the 2013 10th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Krabi, Thailand, 15–17 May 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Dey, H.S.; ul Mamun, M.; Shahadat, M.; Ahamed, A.; Ahamed, S.U.; Arefin, K.S. Design and Implementation of a Novel Protection Device to Prevent Tampering and Electricity Theft in Commercial Energy Meters. J. Comput. Inf. Technol. 2010, 1, 88–94. [Google Scholar]
- Ramos, C.C.; Souza, A.N.; Chiachia, G.; Falcão, A.X.; Papa, J.P. A novel algorithm for feature selection using Harmony Search and its application for non-technical losses detection. Comput. Electr. Eng. 2011, 37, 886–894. [Google Scholar] [CrossRef]
- Zanetti, M.; Jamhour, E.; Pellenz, M.; Penna, M.; Zambenedetti, V.; Chueiri, I. A Tunable Fraud Detection System for Advanced Metering Infrastructure Using Short-Lived Patterns. IEEE Trans. Smart Grid 2019, 10, 830–840. [Google Scholar] [CrossRef]
- Zheng, Z.; Yang, Y.; Niu, X.; Dai, H.N.; Zhou, Y. Wide and Deep Convolutional Neural Networks for Electricity-Theft Detection to Secure Smart Grids. IEEE Trans. Ind. Inform. 2018, 14, 1606–1615. [Google Scholar] [CrossRef]
- Messinis, G.M.; Rigas, A.E.; Hatziargyriou, N.D. A Hybrid Method for Non-Technical Loss Detection in Smart Distribution Grids. IEEE Trans. Smart Grid 2019, 10, 6080–6091. [Google Scholar] [CrossRef]
- Domingues, I.; Amorim, J.P.; Abreu, P.H.; Duarte, H.; Santos, J. Evaluation of Oversampling Data Balancing Techniques in the Context of Ordinal Classification. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Khan, Z.A.; Adil, M.; Javaid, N.; Saqib, M.N.; Shafiq, M.; Choi, J.G. Electricity Theft Detection Using Supervised Learning Techniques on Smart Meter Data. Sustainability 2020, 12, 8023. [Google Scholar] [CrossRef]
- Gunturi, S.K.; Sarkar, D. Ensemble machine learning models for the detection of energy theft. Electr. Power Syst. Res. 2021, 192, 106904. [Google Scholar] [CrossRef]
- Chuwa, M.G.; Wang, F. A review of non-technical loss attack models and detection methods in the smart grid. Electr. Power Syst. Res. 2021, 199, 107415. [Google Scholar] [CrossRef]
- Guarda, F.G.K.; Hammerschmitt, B.K.; Capeletti, M.B.; Neto, N.K.; dos Santos, L.L.C.; Prade, L.R.; Abaide, A. Non-Hardware-Based Non-Technical Losses Detection Methods: A Review. Energies 2023, 16, 2054. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 23 July 2018).
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Pearson Education: Hoboken, NJ, USA, 2011. [Google Scholar]
- Commission for Energy Regulation. The Smart Metering Electricity Customer Behaviour Trials. Available online: https://www.ucd.ie/issda/data/commissionforenergyregulationcer/ (accessed on 16 October 2022).
- Strang, G.; Herman, E. Calculus Volume 1; OpenStax: Houston, TX, USA, 2016. [Google Scholar]
- Pham, T. Time–frequency time–space LSTM for robust classification of physiological signals. Sci. Rep. 2021, 11, 6936. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).