Operational Analysis of an Axial and Solid Double-Pole Configuration in a Permanent Magnet Flux-Switching Generator
Abstract
1. Introduction
2. Doubly Salient Permanent Magnet (DSPM) Machine and Methodology of Study Overview
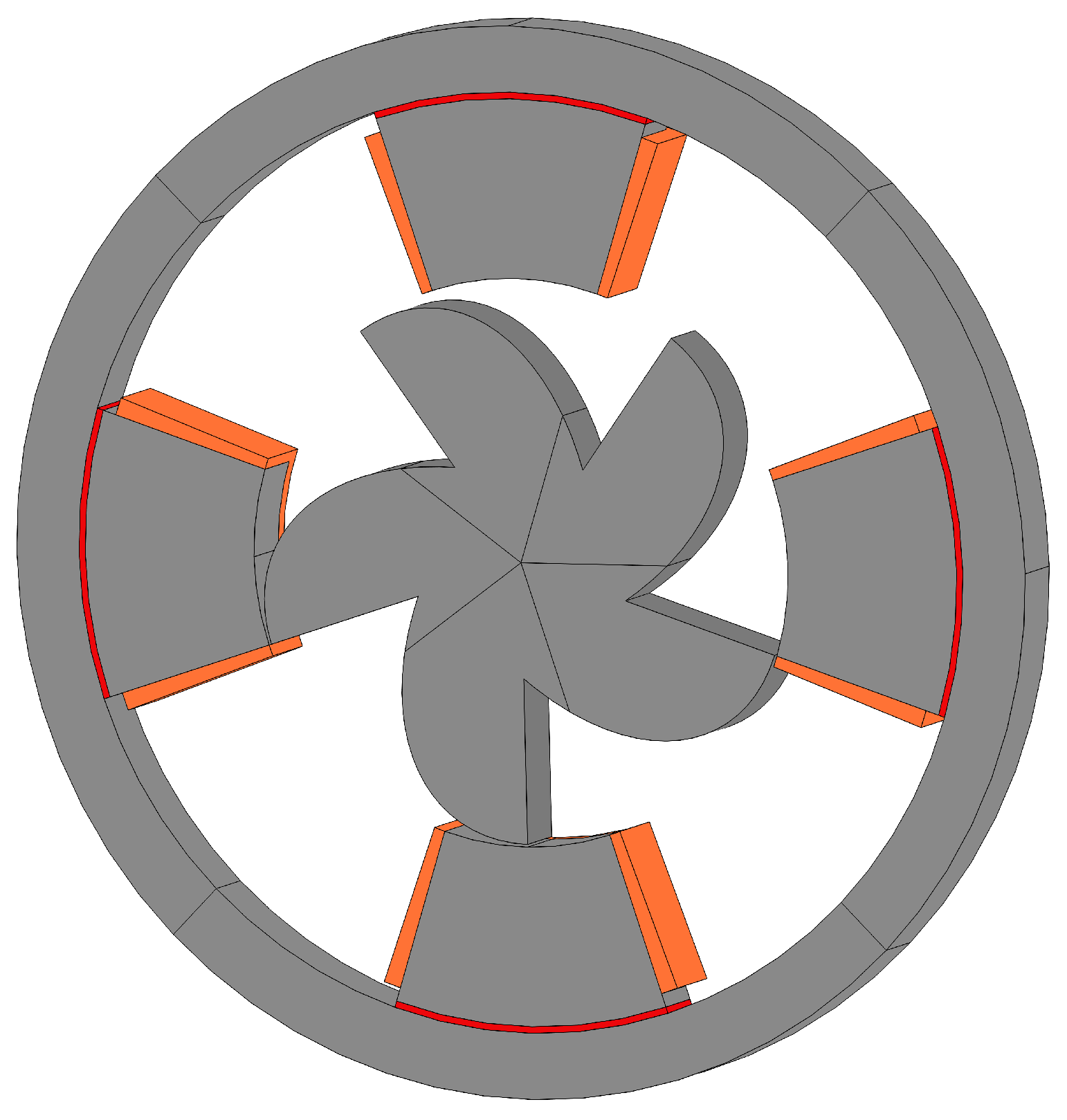
2.1. Geometry
2.2. Materials
2.3. Generator Specifications
2.4. FEM Study of DSPM S4R5 Machine
2.4.1. Magnetic Flux and Torque Calculation
Magnetic Flux Calculation
Electromagnetic Torque Calculation: Arkkio’s Method
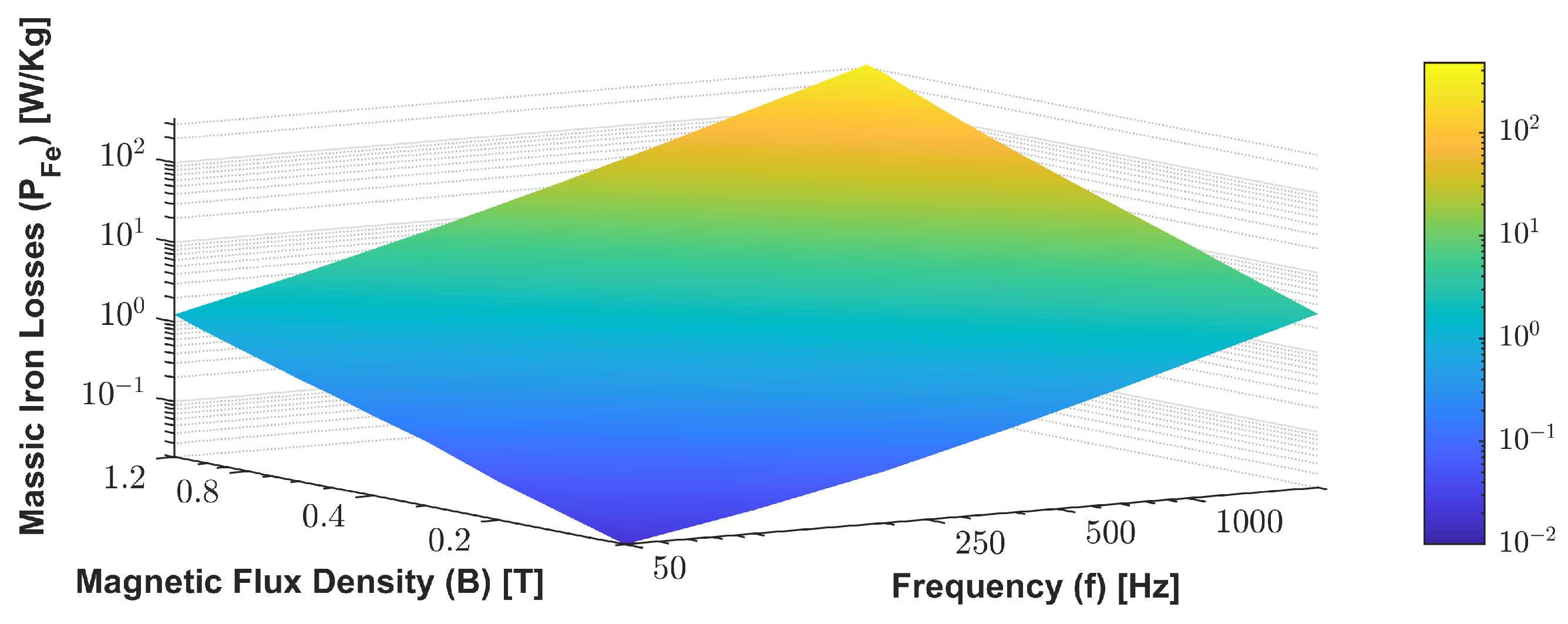
2.4.2. Iron Losses Determination
Modeling of Iron Losses
Iron Losses’ Data Map
Determination of Iron Losses
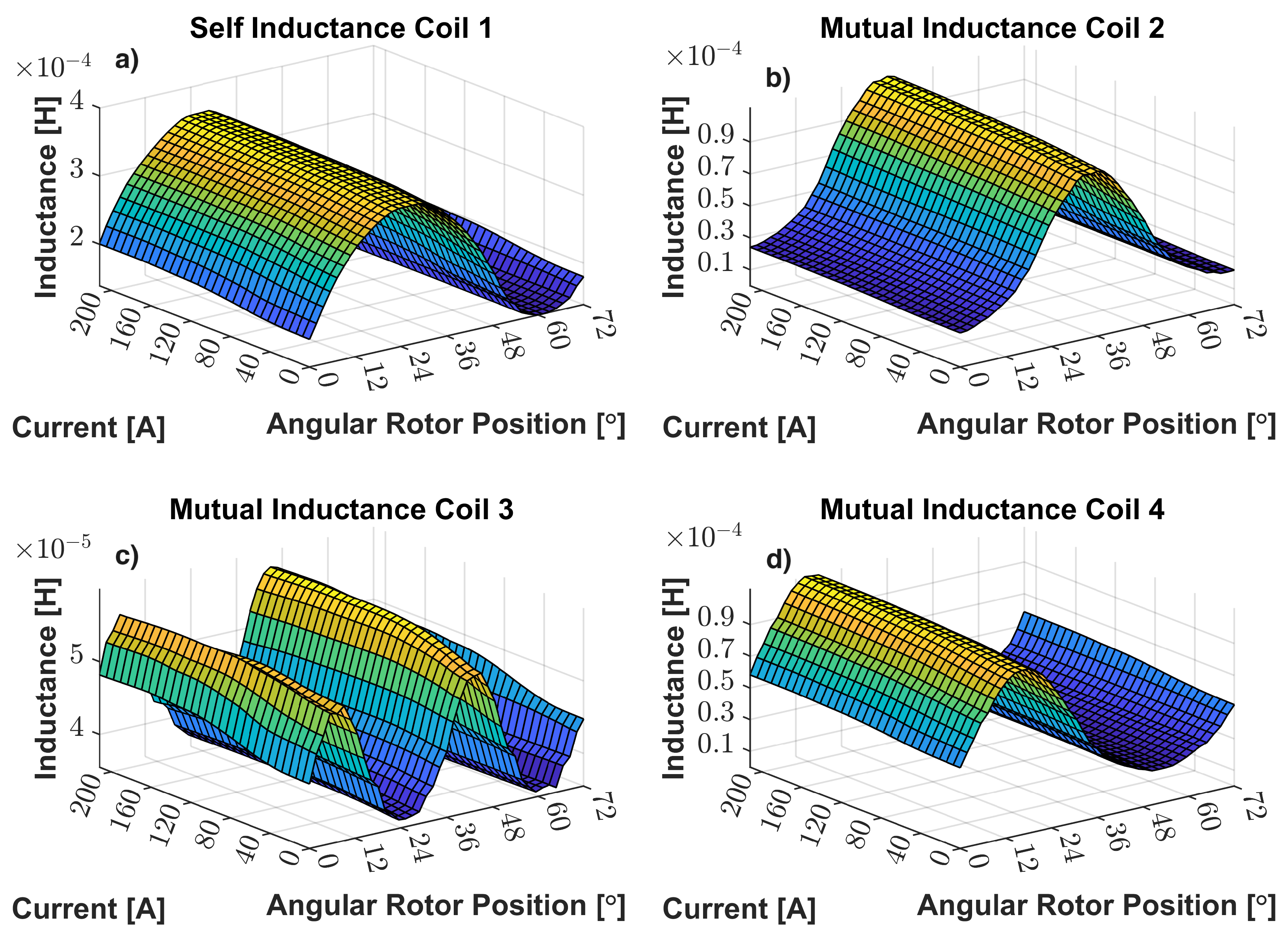
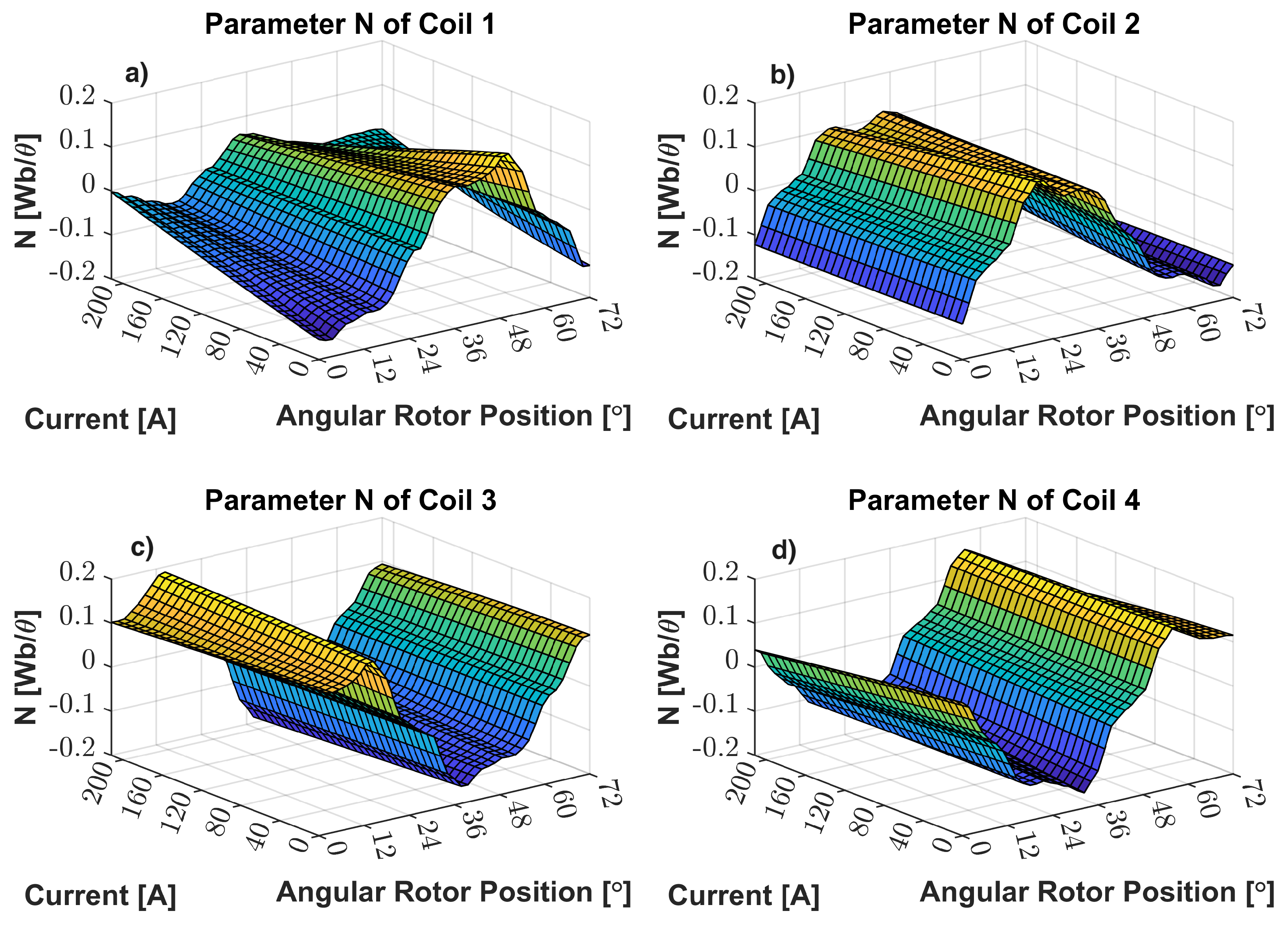
2.4.3. Electrical Equivalent Circuit Study
2.5. Geometry Optimization
2.5.1. Optimization Objectives
2.5.2. Design Variables
2.5.3. Constraints
2.5.4. Optimization Program: Genetic Algorithm
3. Results
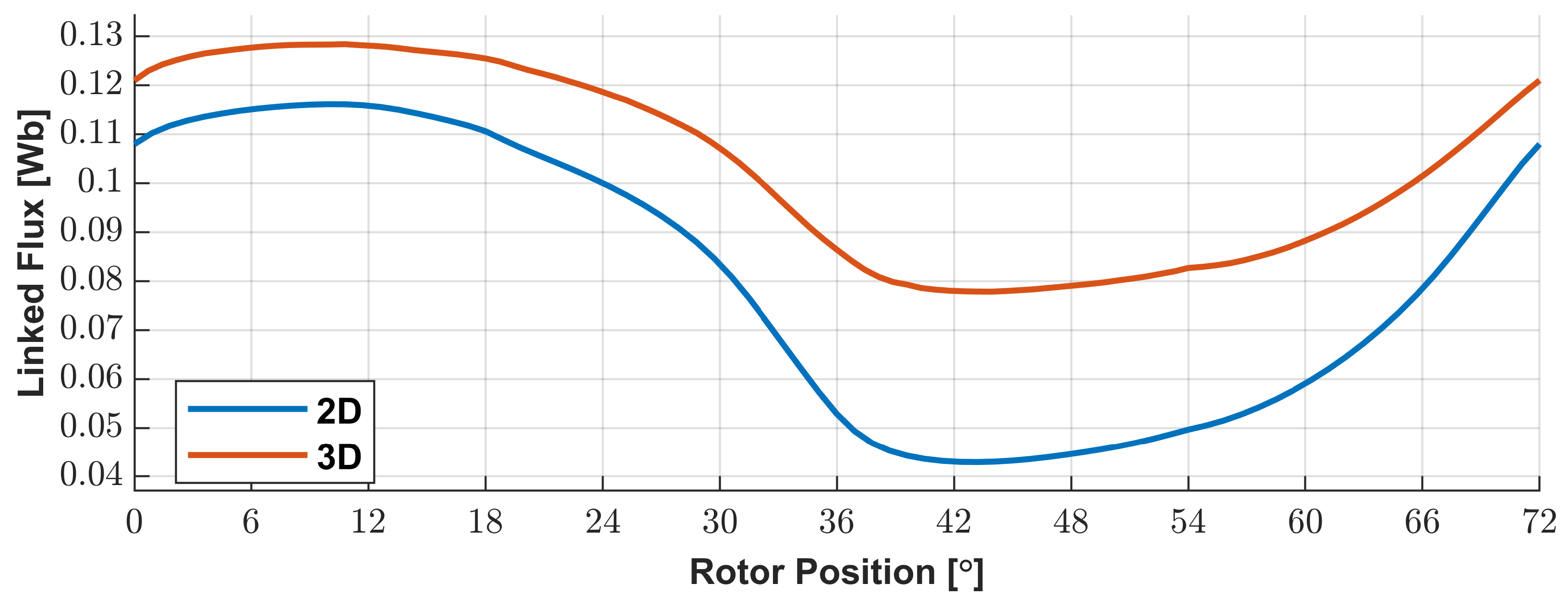
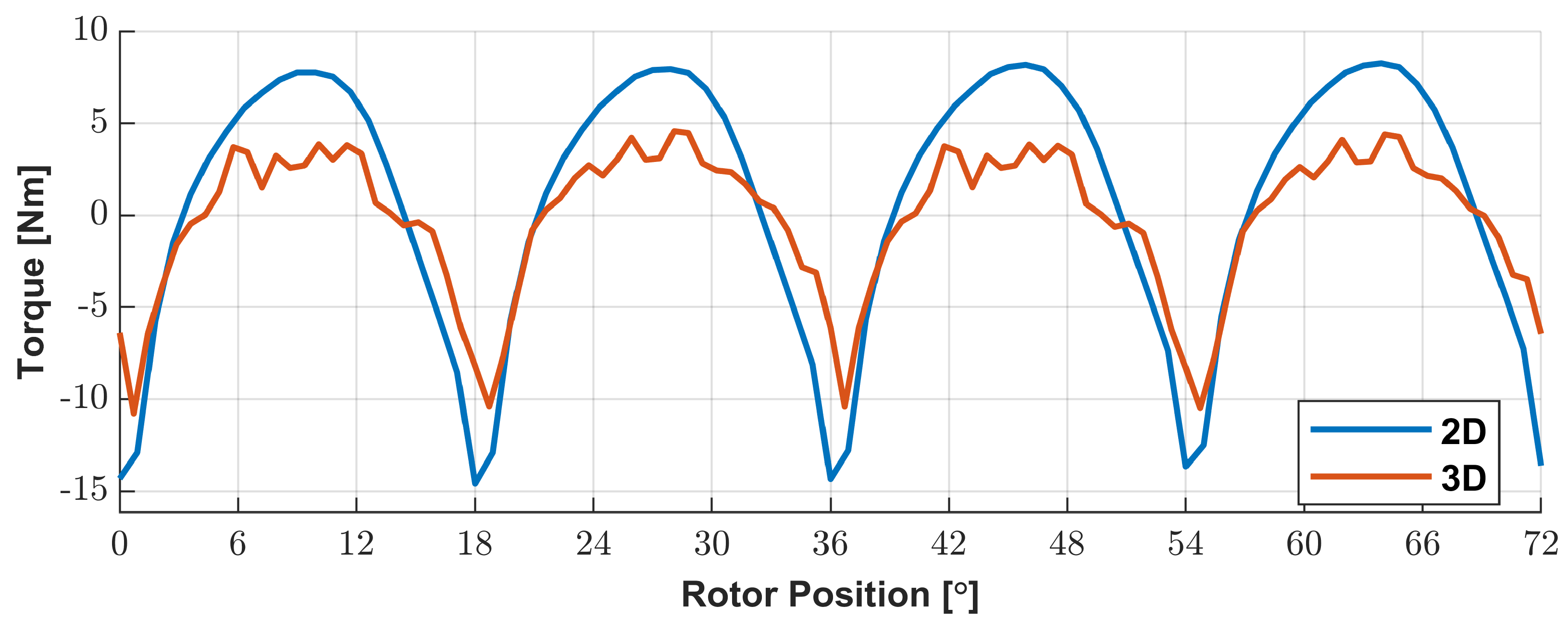
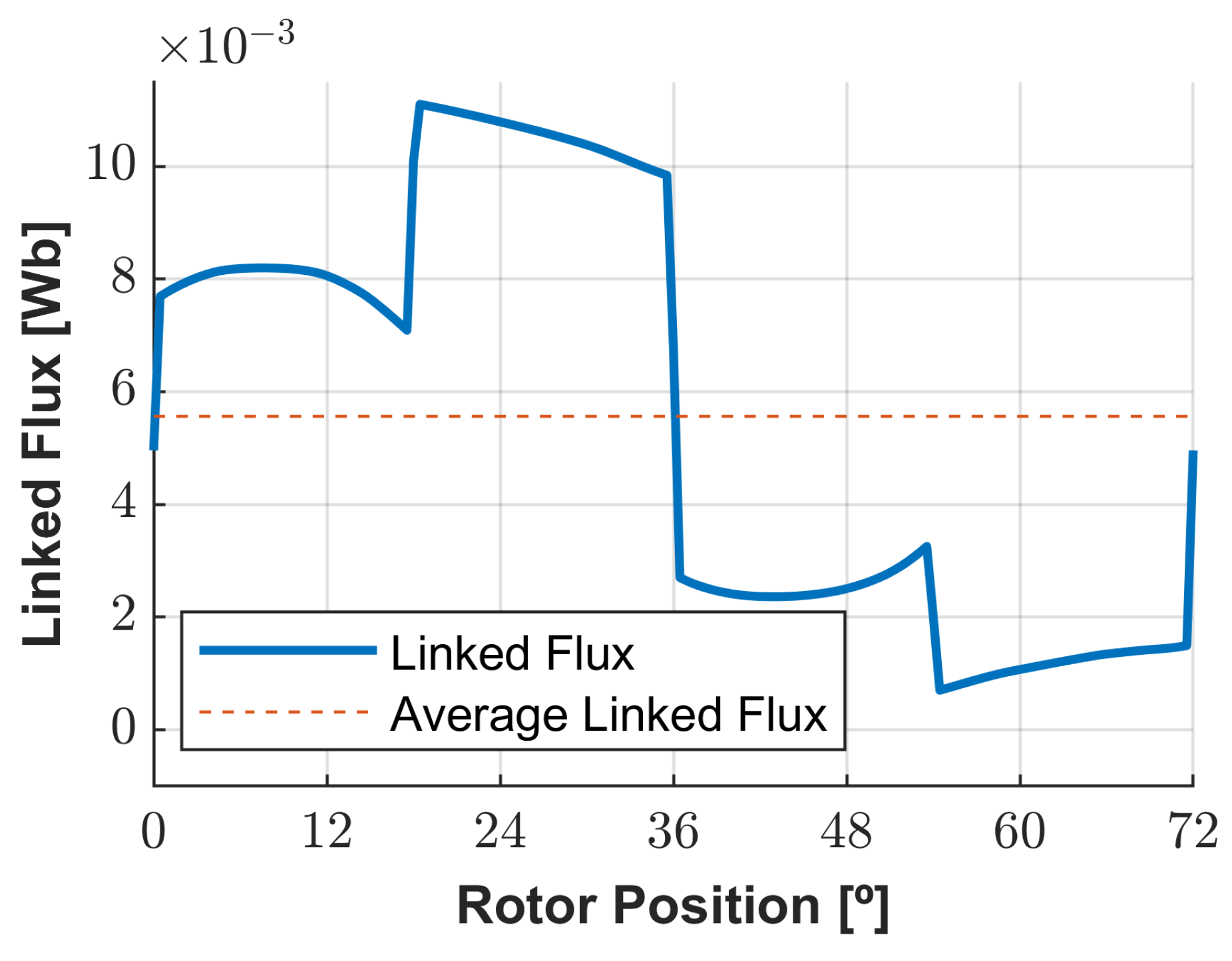
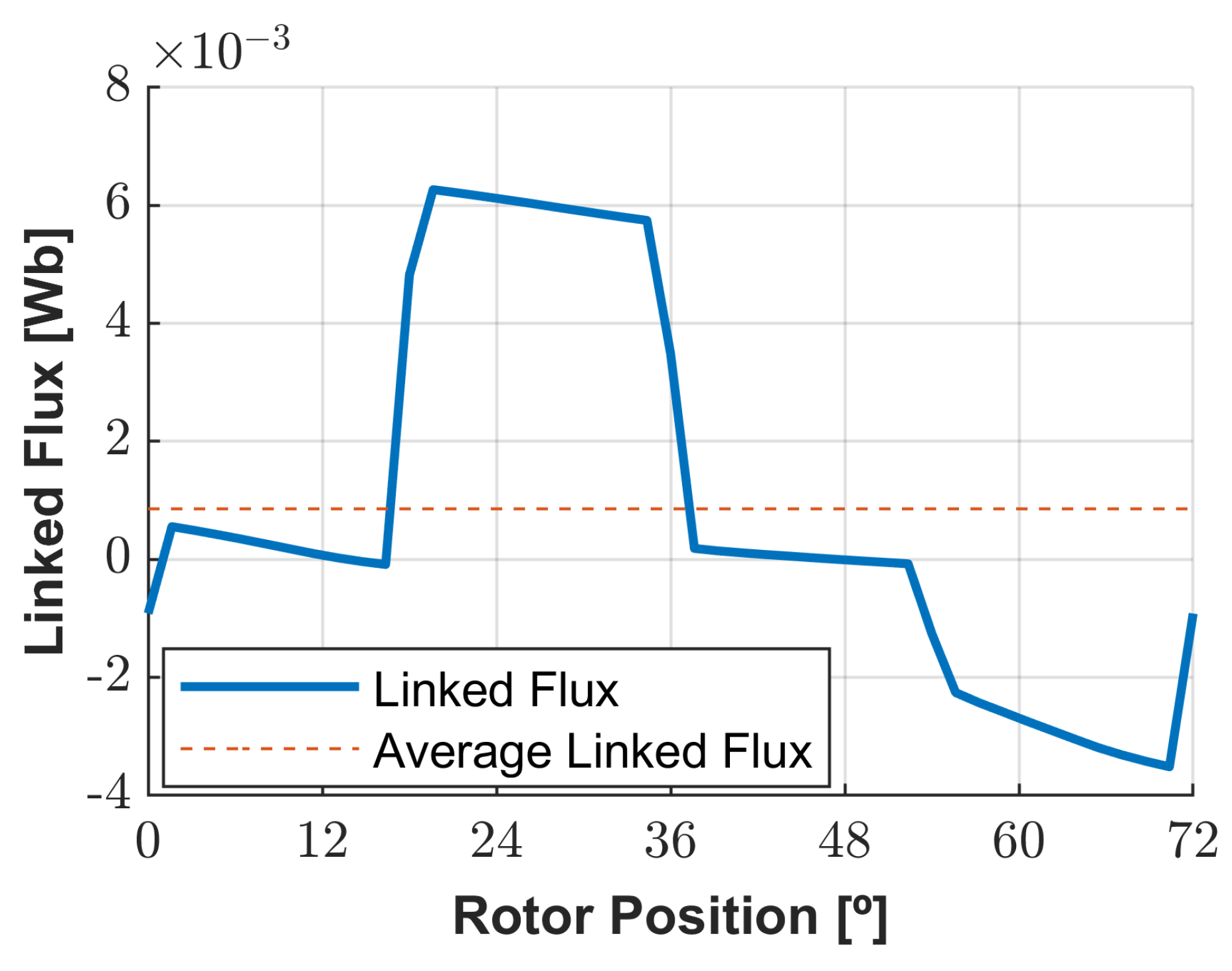
3.1. Comparison of Flux and Torque Calculations Based on 2D and 3D Geometries at No Load and Lumped Parameters Study
3.2. Iron Loss Calculations at No Load
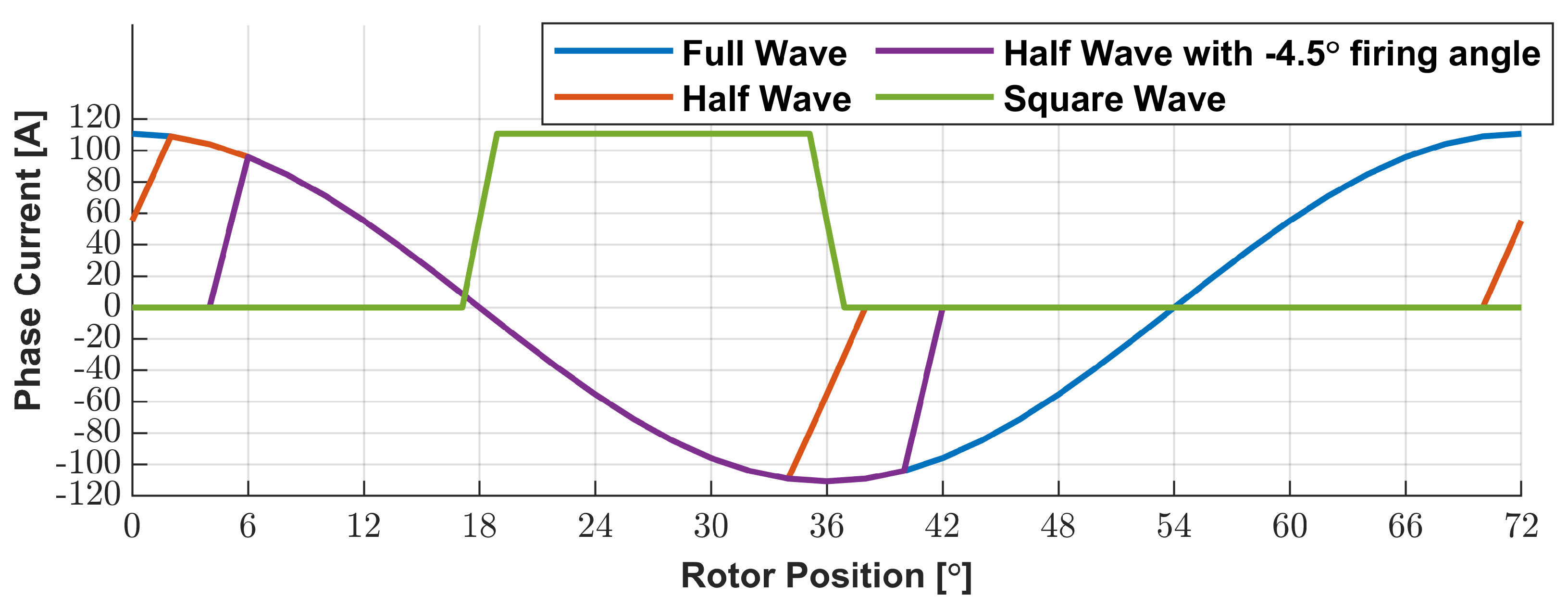
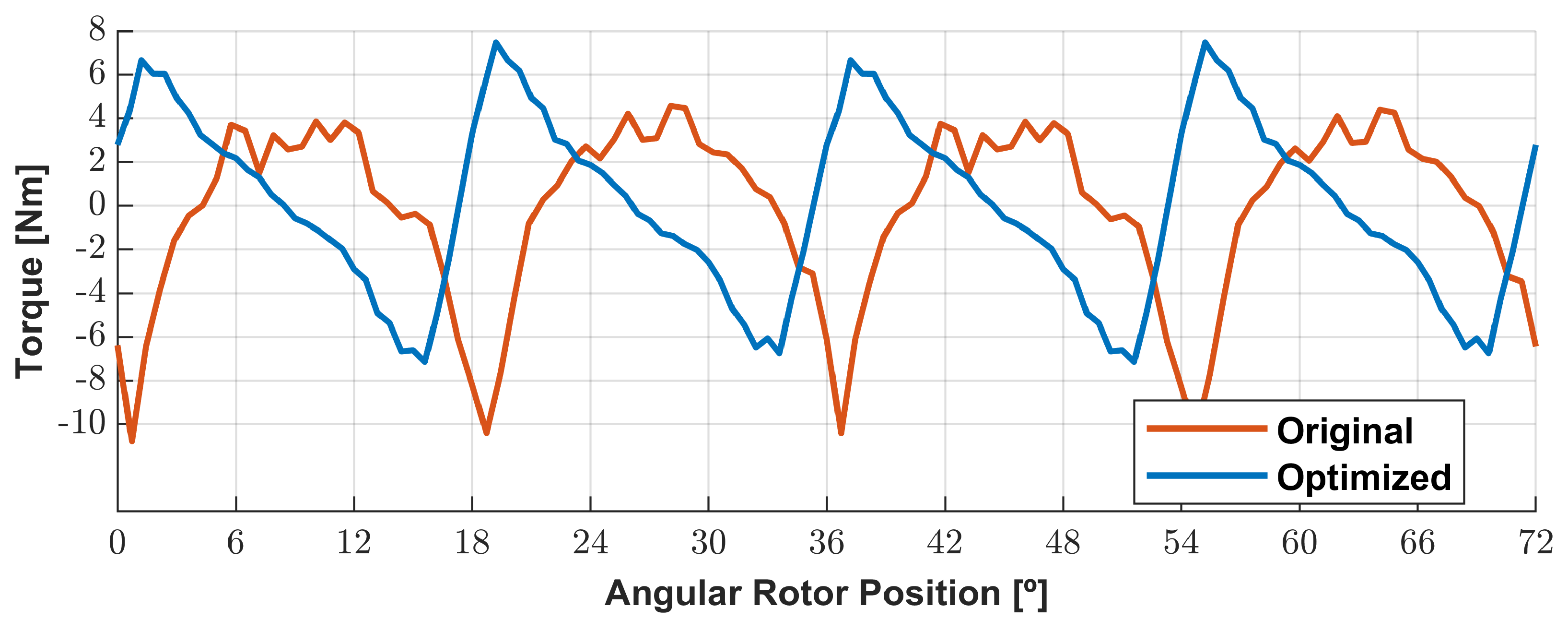
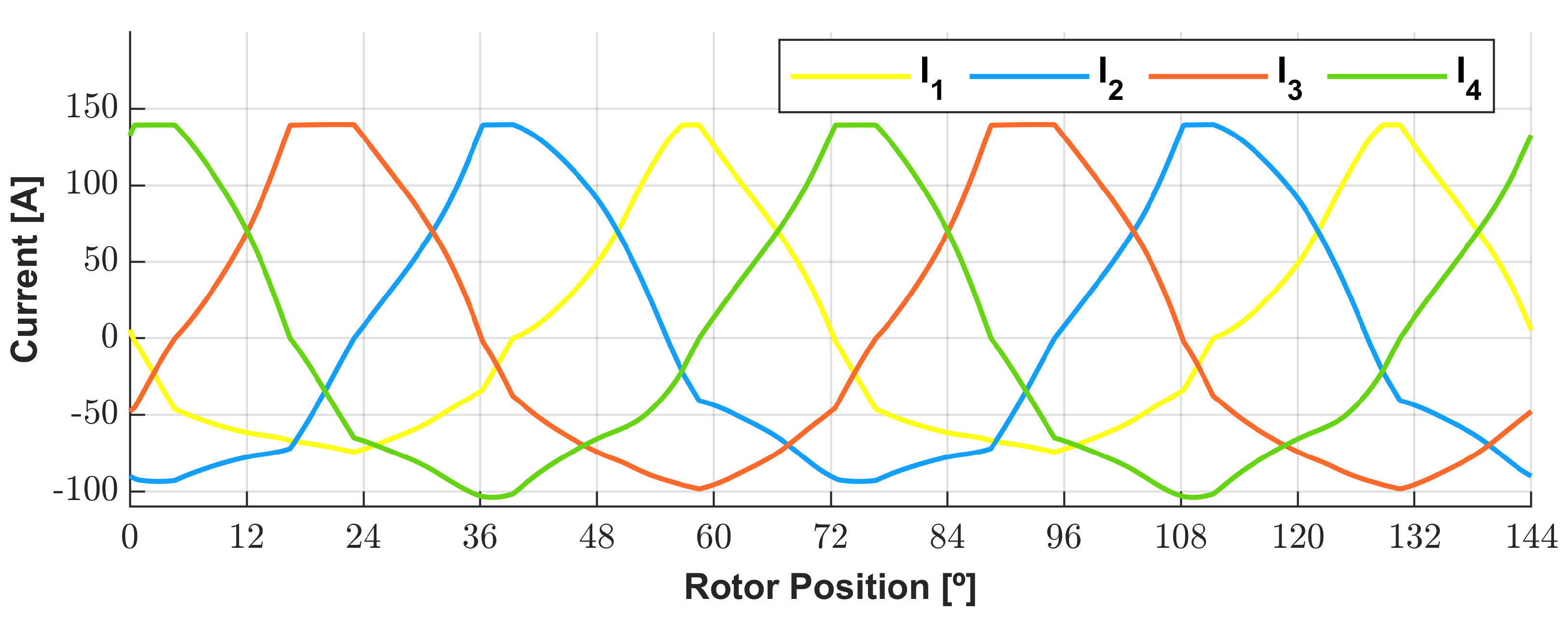
3.3. Phase Current Shape Study
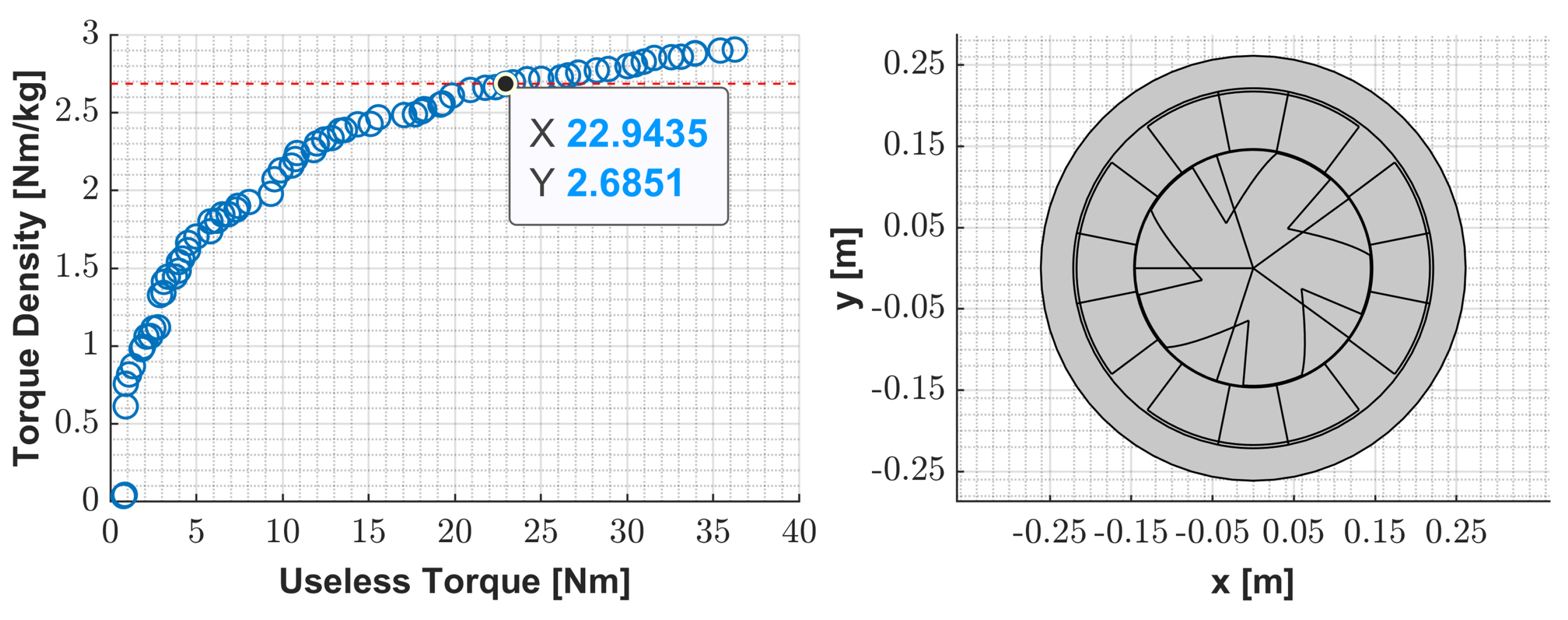
3.4. Optimization of the DSPM S4R5 Machine Results
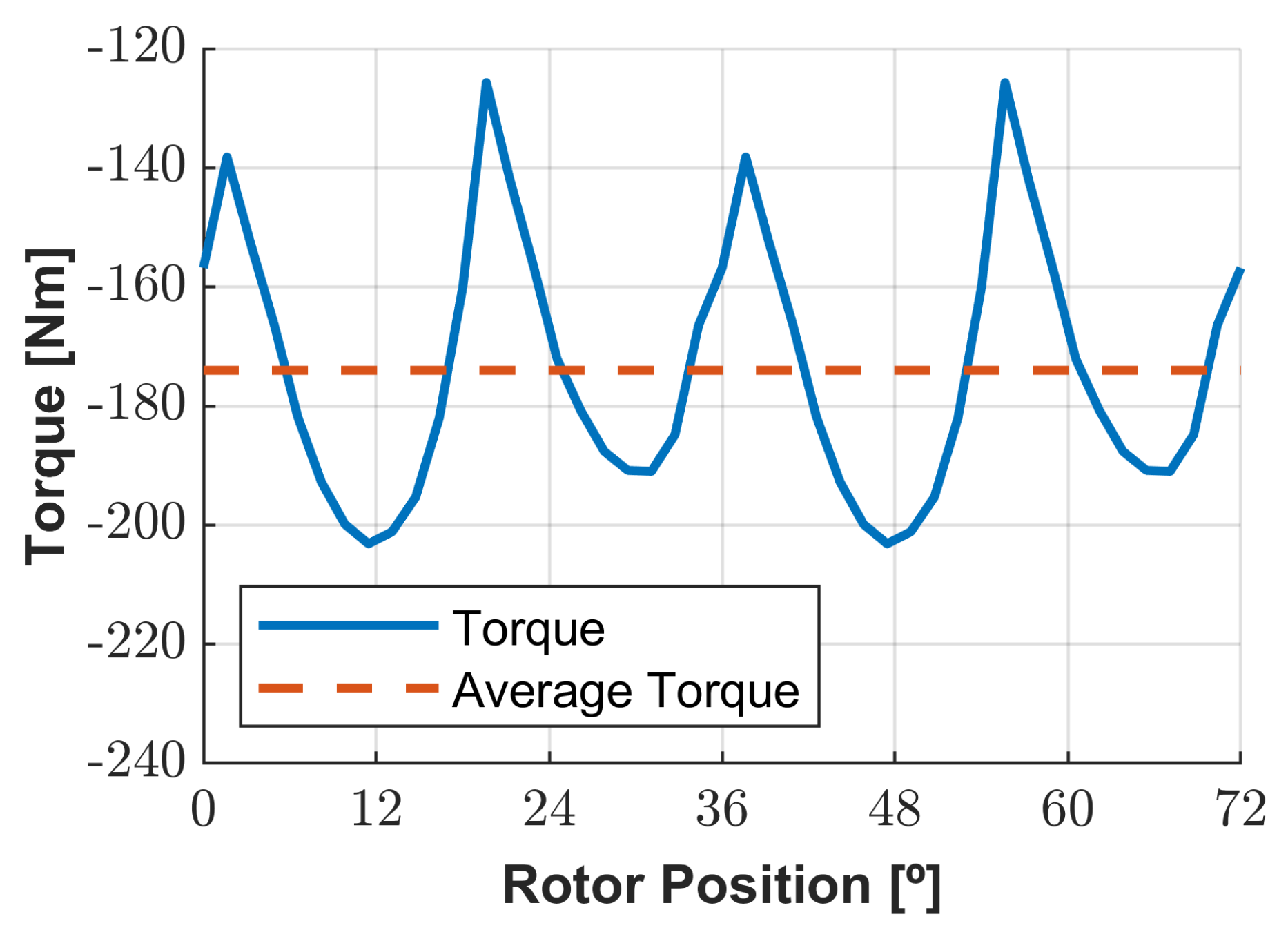
3.5. Comparison of Initial and Optimized Geometries at No Load and Lumped Parameters Study
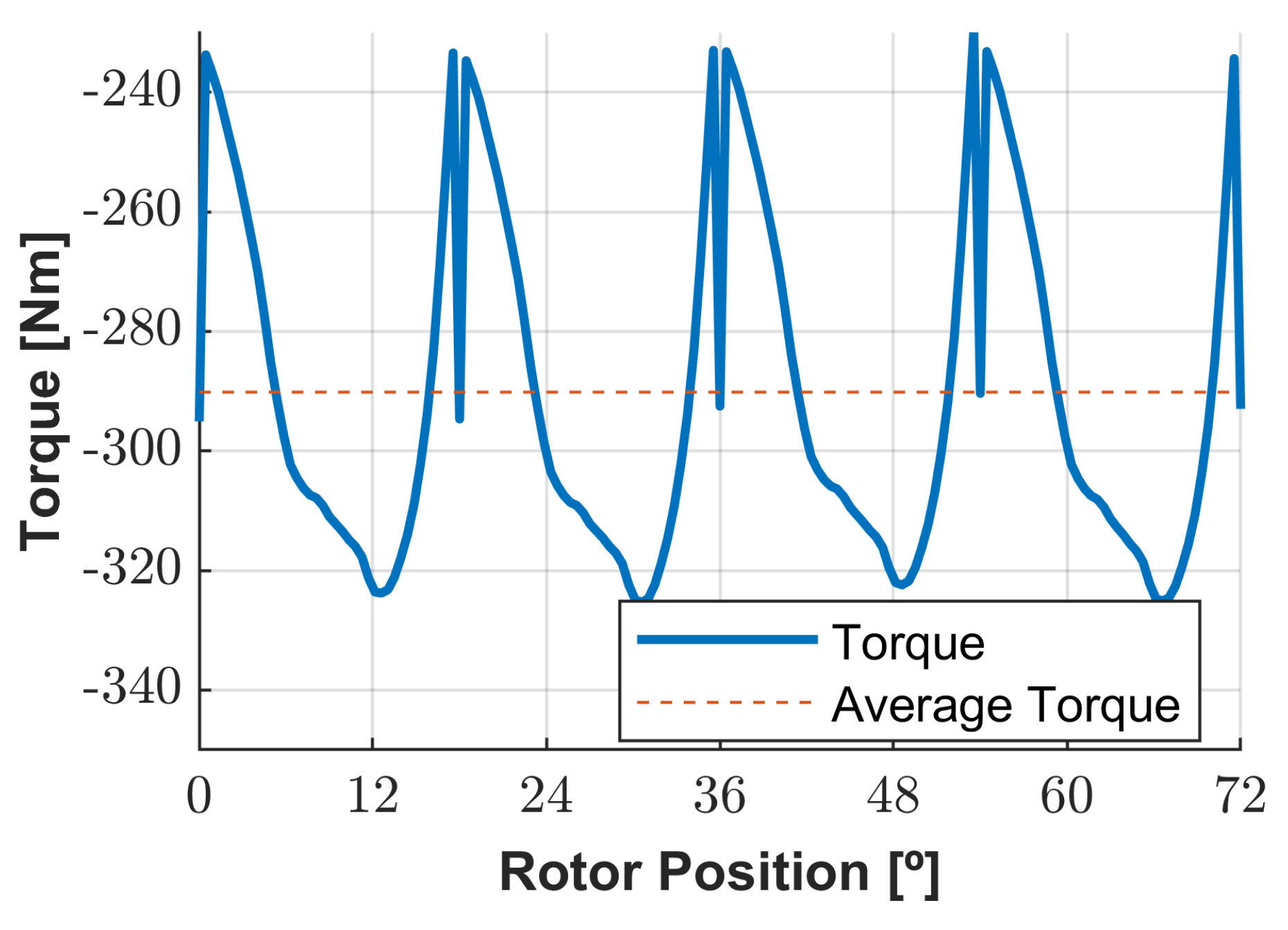
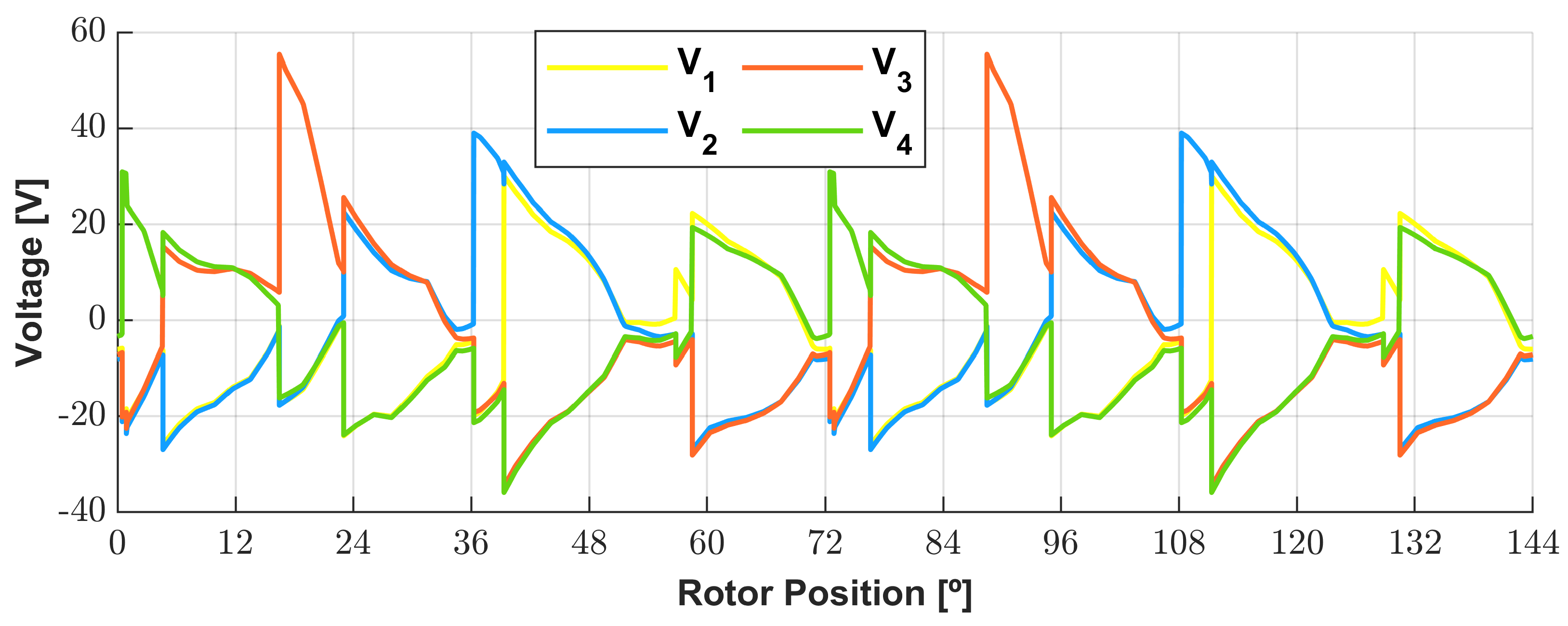
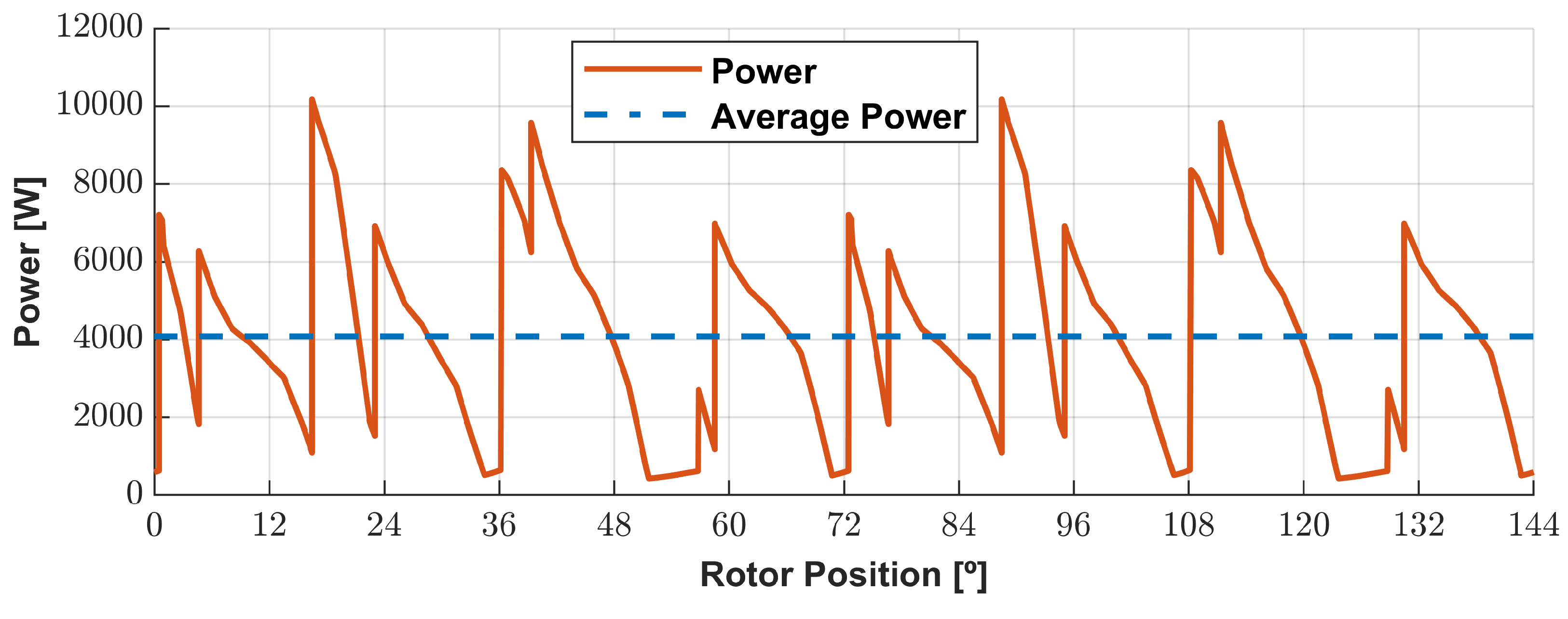
3.6. Loading Analysis of the Optimized Geometry
3.6.1. Aircraft Equivalent Electrical System
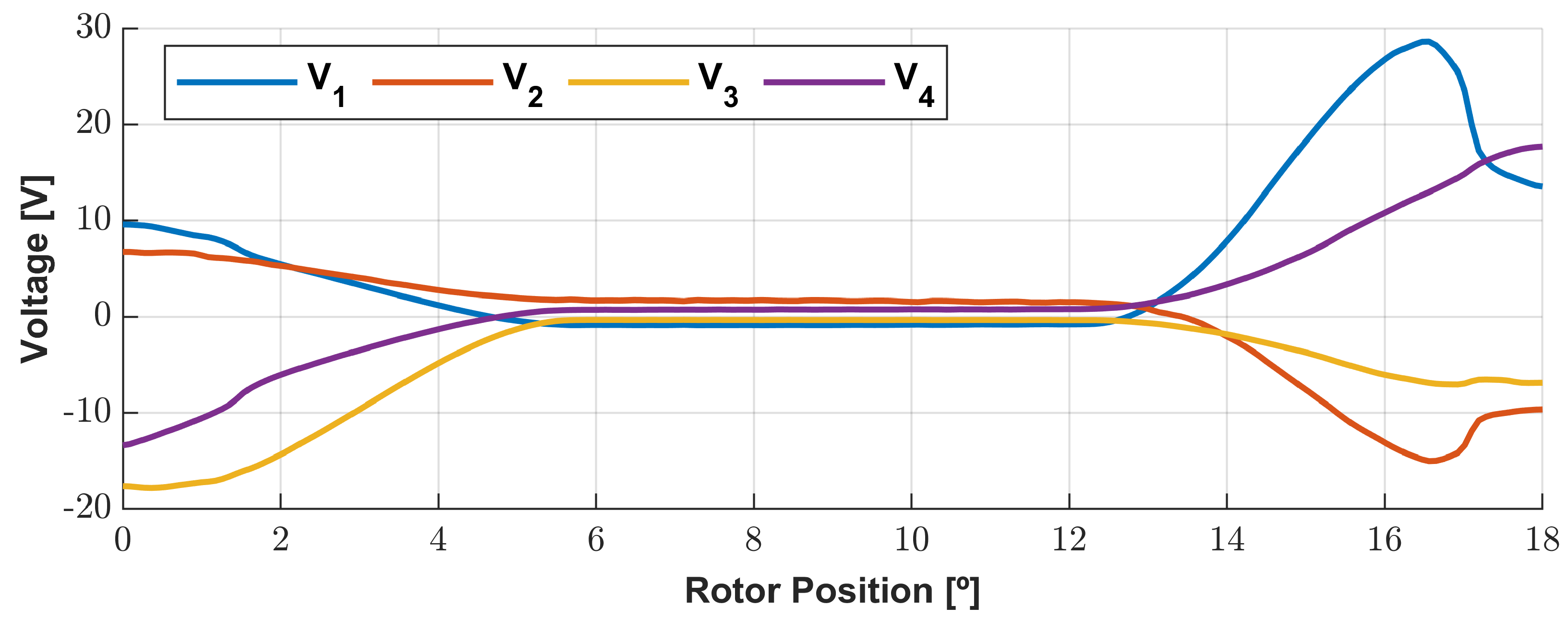
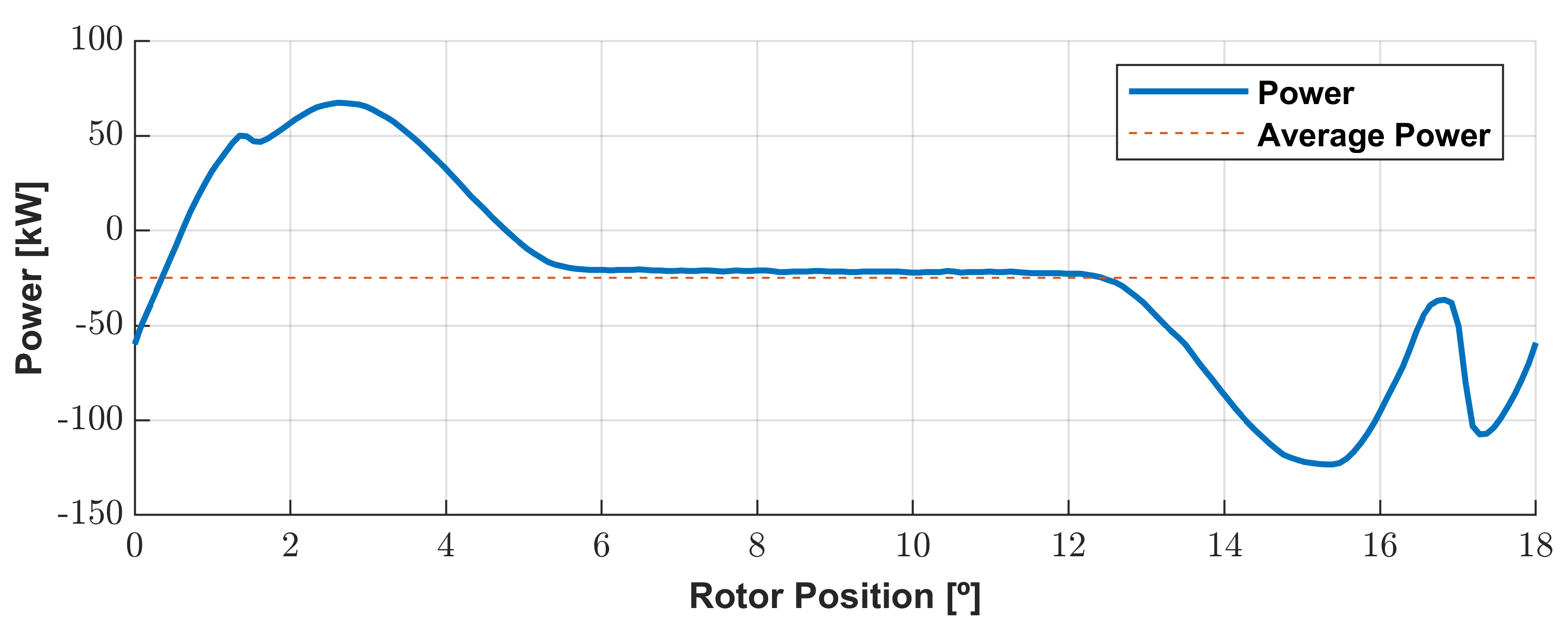
3.6.2. Electrical Response of the Generator with Non-Commanded AC/DC Converter
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Madonna, V.; Giangrande, P.; Galea, M. Electrical power generation in aircraft: Review, challenges, and opportunities. IEEE Trans. Transp. Electrif. 2018, 4, 646–659. [Google Scholar] [CrossRef]
- Cavagnino, A.; Li, Z.; Tenconi, A.; Vaschetto, S. Integrated generator for more electric engine: Design and testing of a scaled-size prototype. IEEE Trans. Ind. Appl. 2013, 49, 2034–2043. [Google Scholar] [CrossRef]
- Rucker, J.E.; Kirtley, J.L.; McCoy, T.J. Design and analysis of a permanent magnet generator for naval applications. In Proceedings of the IEEE Electric Ship Technologies Symposium, Philadelphia, PA, USA, 27 July 2005; pp. 451–458. [Google Scholar]
- Farahani, E.F.; Baker, N.J.; Mahmouditabar, F. An Innovative H-Type Flux Switching Permanent Magnet Linear Generator for Thrust Force Enhancement. Energies 2023, 16, 5976. [Google Scholar] [CrossRef]
- Fernández, D.; Martinez, M.; Reigosa, D.; Guerrero, J.M.; Alvarez, C.M.S.; Briz, F. Permanent magnets aging in variable flux permanent magnet synchronous machines. IEEE Trans. Ind. Appl. 2020, 56, 2462–2471. [Google Scholar] [CrossRef]
- Haavisto, M.; Tuominen, S.; Kankaanpää, H.; Paju, M. Time dependence of demagnetization and flux losses occurring in sintered Nd-Fe-B permanent magnets. IEEE Trans. Magn. 2010, 46, 3582–3584. [Google Scholar] [CrossRef]
- Wheeler, P.; Bozhko, S. The more electric aircraft: Technology and challenges. IEEE Electrif. Mag. 2014, 2, 6–12. [Google Scholar] [CrossRef]
- Lando, J.L. Fixed Frequency Electrical Generation System and Corresponding Control Procedure. U.S. Patent 7,064,455, 20 June 2006. [Google Scholar]
- Esteves, A.N.F. Design and Optimization of an Axial and Solid Double-Inner-Rotor Configuration in PM Flux Switching Generators. Master’s Thesis, Instituto Superior Técnico, Lisboa, Portugal, 2021. [Google Scholar]
- Reimers, D. Bezier Curves. 2011. Available online: https://ctan.math.utah.edu/ctan/tex-archive/macros/latex/contrib/lapdf/bezinfo.pdf (accessed on 27 February 2024).
- Silva, J.L.D. Analyses of Solutions for the Attenuation of Cogging Torque in Flux Switching Electrical Generators with Permanent Magnets in the Stator. Master’s Thesis, Instituto Superior Técnico, Lisboa, Portugal, 2016. [Google Scholar]
- Di Tommaso, A.O.; Genduso, F.; Miceli, R.; Nevoloso, C. Fast procedure for the calculation of maximum slot filling factors in electrical machines. In Proceedings of the 2017 Twelfth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 11–13 April 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Arkkio, A. Analysis of Induction Motors Based on the Numerical Solution of the Magnetic Field and Circuit Equations. Ph.D. Thesis, Helsinki University of Technology, Espoo, Finland, 1987. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Gibbs, M.S.; Maier, H.R.; Dandy, G.C.; Nixon, J.B. Minimum number of generations required for convergence of genetic algorithms. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 565–572. [Google Scholar]
- Peixoto, I.S.; da Silva, F.F.; Fernandes, J.F.; Vaschetto, S.; Branco, P.C. A Distributed Equivalent-Permeability Model for the 3D Design Optimization of Bulk Superconducting Electromechanical Systems. IEEE Trans. Appl. Supercond. 2023, 33. [Google Scholar] [CrossRef]
- Barbie, E.; Rabinovici, R.; Kuperman, A. Analytic formulation and optimization of weighted total harmonic distortion in single-phase staircase modulated multilevel inverters. Energy 2020, 199, 117470. [Google Scholar] [CrossRef]
- Chen, H.; Tang, T.; Han, J.; Ait-Ahmed, N.; Machmoum, M.; Zaïm, M.E.H. Current waveforms analysis of toothed pole Doubly Salient Permanent Magnet (DSPM) machine for marine tidal current applications. Int. J. Electr. Power Energy Syst. 2019, 106, 242–253. [Google Scholar] [CrossRef]
- Hua, W.; Cheng, M. A new model of vector-controlled doubly-salient permanent magnet motor with skewed rotor. In Proceedings of the 2008 International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008; pp. 3026–3031. [Google Scholar]
- Bi, Y.; Fu, W.; Niu, S.; Huang, J. Comparative Analysis of Consequent-Pole Flux-Switching Machines with Different Permanent Magnet Arrangements for Outer-Rotor In-Wheel Direct-Drive Applications. Energies 2023, 16, 6650. [Google Scholar] [CrossRef]

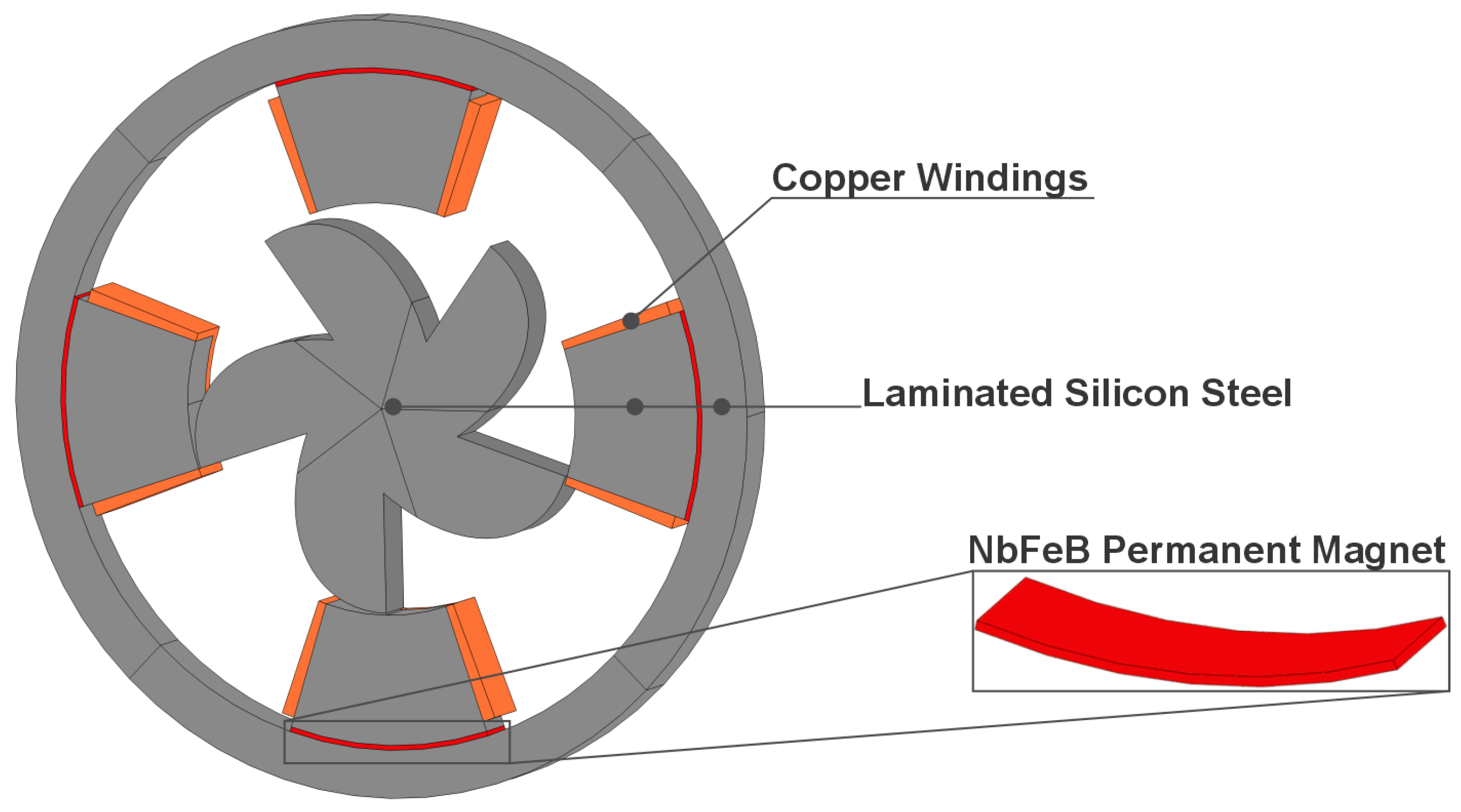
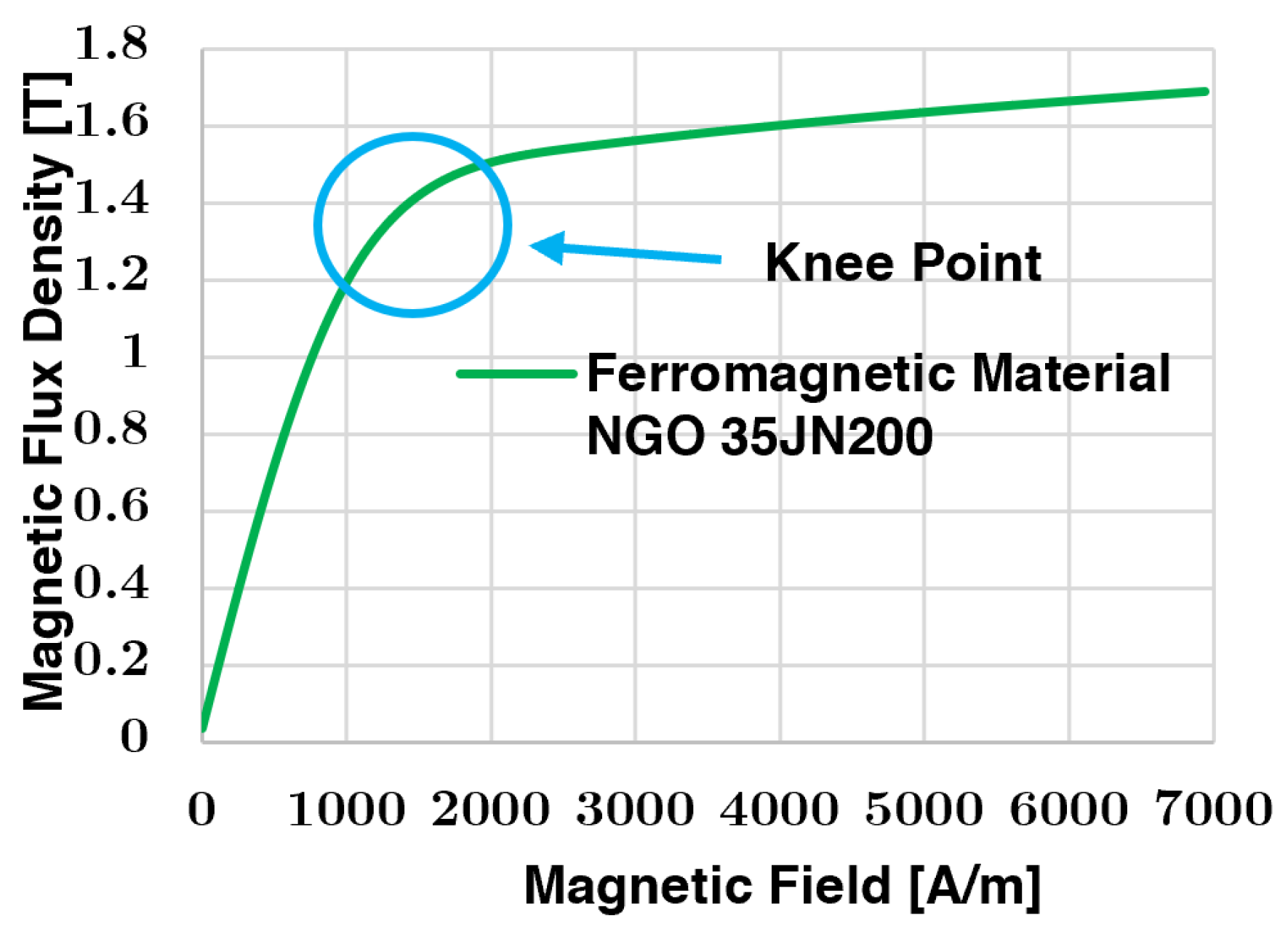

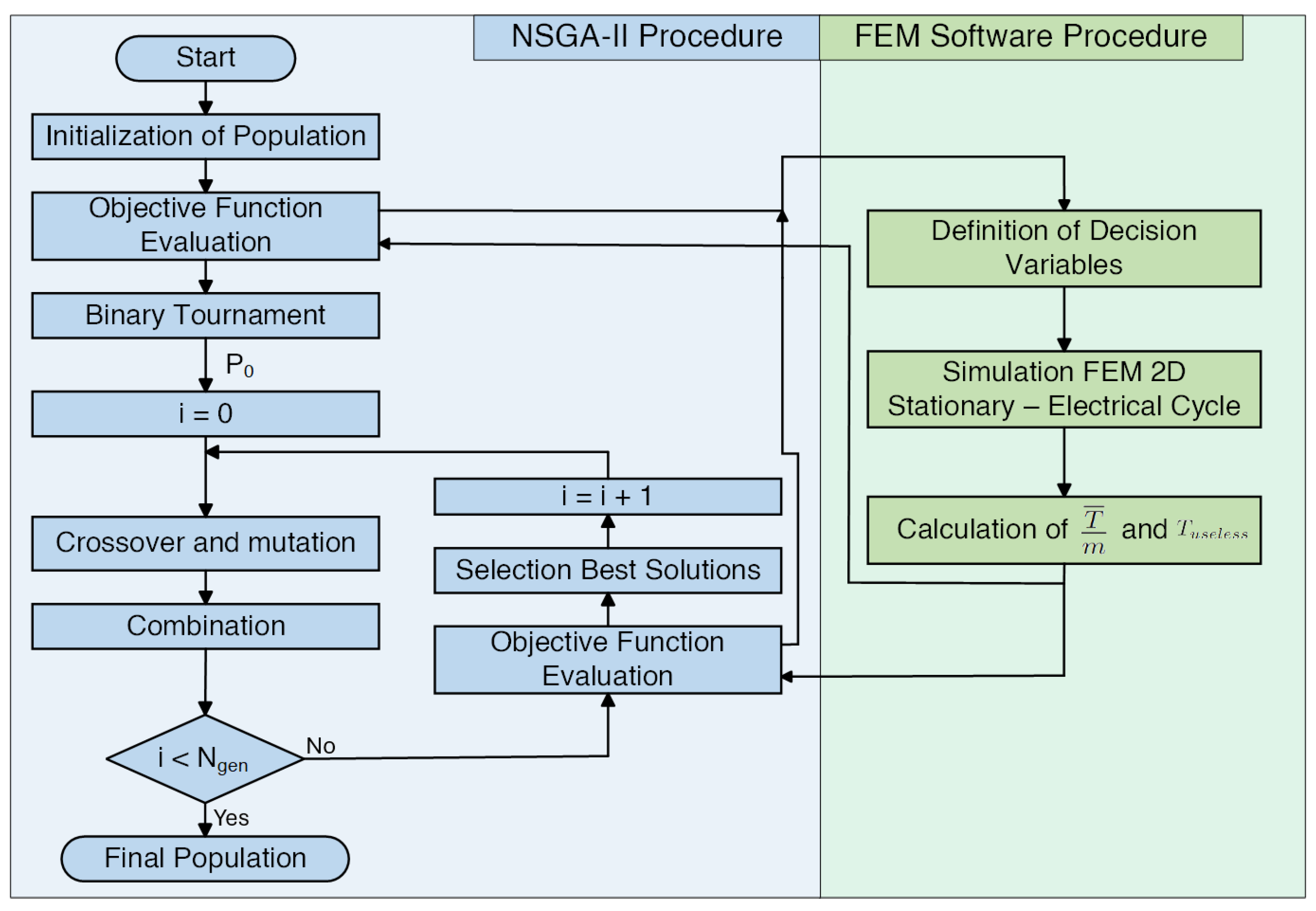

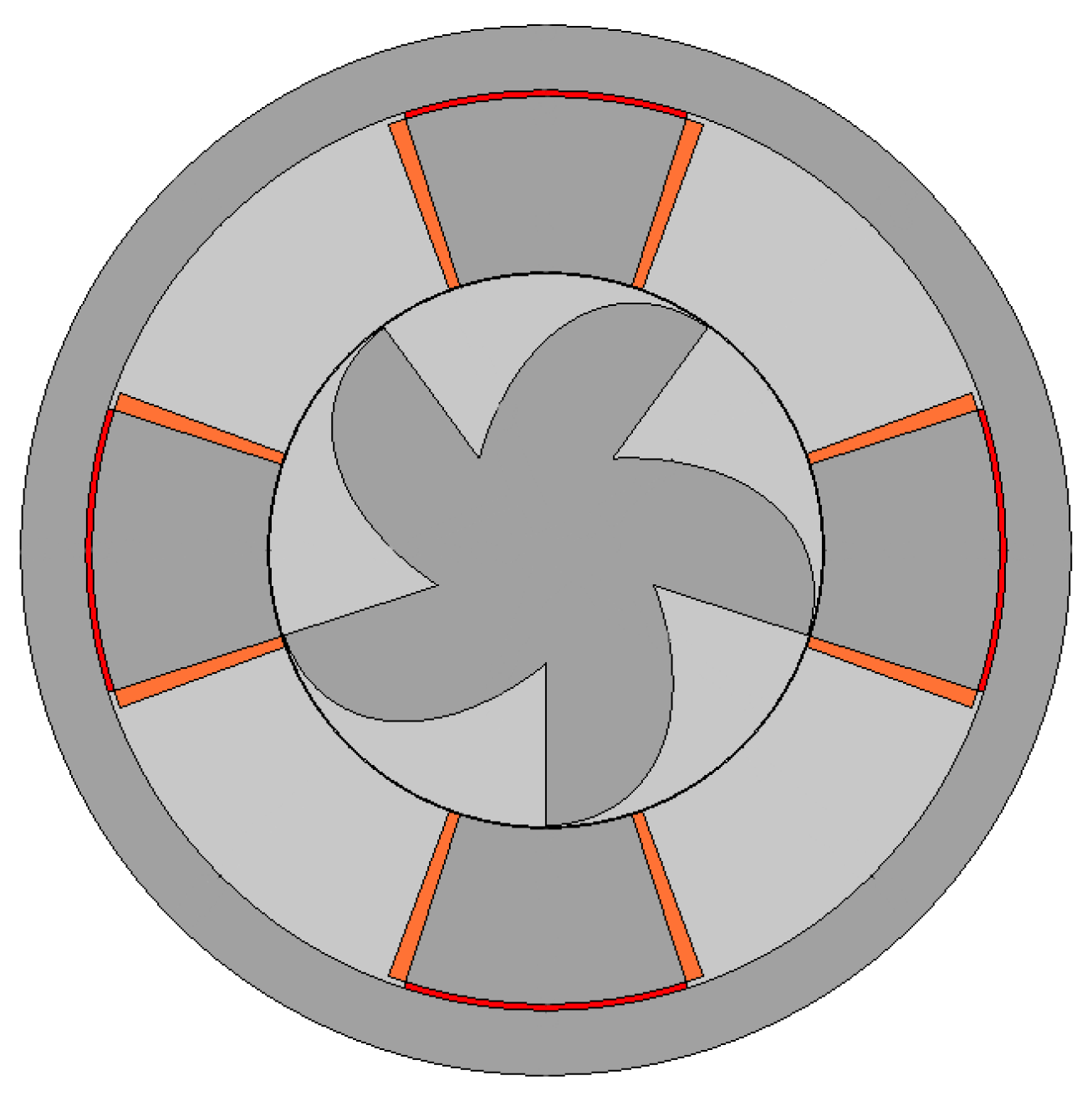



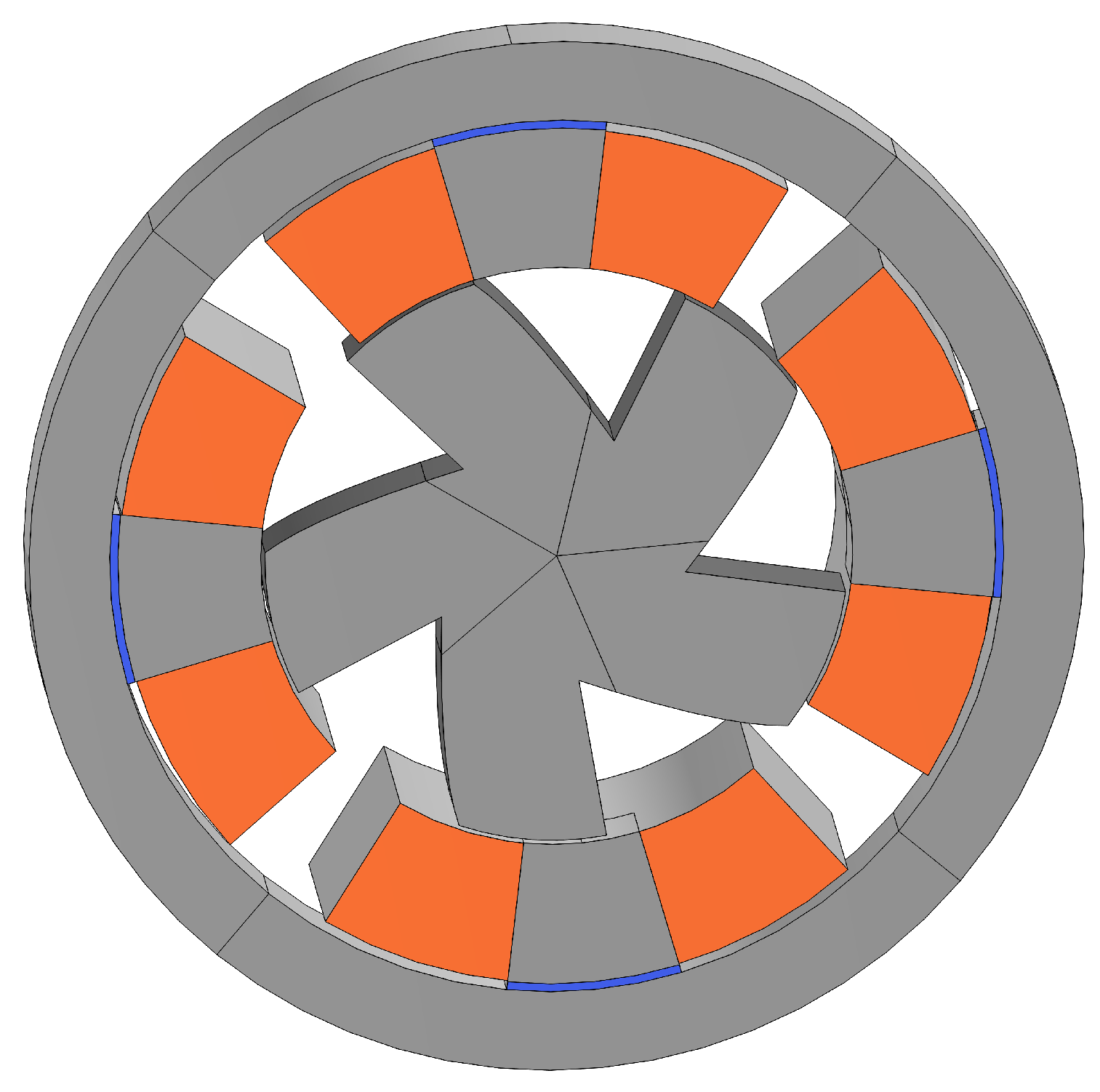

| Parameter | Description | Dimension |
|---|---|---|
| External radius of ring stator | 324 [mm] | |
| Internal radius of ring stator | 284 [mm] | |
| External radius of rotor | 170 [mm] | |
| Internal radius of rotor | 70 [mm] | |
| Depth of stator poles | 112.4 [mm] | |
| Depth of rotor poles | 100 [mm] | |
| Depth of PMs | 4 [mm] | |
| g | Airgap distance | 1.6 [mm] |
| Rotor pole angle | 36° | |
| Stator pole angle | 36° | |
| Rotor pole pitch | ||
| Stator pole pitch | ||
| Winding length | 100 [mm] | |
| Winding aperture angle | 0.04 [rad] | |
| DSPM total length | 80 [mm] |
| Design Variable | Lower and Upper Limits |
|---|---|
| 240–290 [mm] | |
| 135–155 [mm] | |
| 70–90 [mm] | |
| 50–110 [mm] | |
| 4–50 [mm] | |
| g | 1.95–2.2 [mm] |
| 0.05–0.45 [rad] | |
| 55–70 [mm] | |
| 0.25–0.65 [rad] | |
| 0.5–0.8 [rad] | |
| 170–220 [mm] | |
| −0.1–0.1 [rad] | |
| 0.2–0.6 | |
| 0.2–0.7 | |
| 0.4–1 |
| Current Waveform | [Nm] | [Nm] | |
|---|---|---|---|
| Cosine wave | |||
| Half-cosine | |||
| Half-cosine with firing angle | |||
| Square wave |
| Parameter | Dimension |
|---|---|
| [mm] | |
| [mm] | |
| [mm] | |
| [mm] | |
| 4 [mm] | |
| g | [mm] |
| [rad] | |
| [mm] | |
| [rad] | |
| [rad] | |
| [mm] | |
| [rad] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neto, M.G.; da Silva, F.F.; Branco, P.J.d.C. Operational Analysis of an Axial and Solid Double-Pole Configuration in a Permanent Magnet Flux-Switching Generator. Energies 2024, 17, 1698. https://doi.org/10.3390/en17071698
Neto MG, da Silva FF, Branco PJdC. Operational Analysis of an Axial and Solid Double-Pole Configuration in a Permanent Magnet Flux-Switching Generator. Energies. 2024; 17(7):1698. https://doi.org/10.3390/en17071698
Chicago/Turabian StyleNeto, Manuel Garcia, Francisco Ferreira da Silva, and Paulo José da Costa Branco. 2024. "Operational Analysis of an Axial and Solid Double-Pole Configuration in a Permanent Magnet Flux-Switching Generator" Energies 17, no. 7: 1698. https://doi.org/10.3390/en17071698
APA StyleNeto, M. G., da Silva, F. F., & Branco, P. J. d. C. (2024). Operational Analysis of an Axial and Solid Double-Pole Configuration in a Permanent Magnet Flux-Switching Generator. Energies, 17(7), 1698. https://doi.org/10.3390/en17071698









