Abstract
Interconnected microchannels (IMCs) in flow boiling have the advantages of optimized heat transfer performance, energy savings and high efficiency, compact size, and strong customizability. They provide new solutions for thermal management and heat transfer at the microscale and have broad application prospects. To further investigate the effect of microchannels with different numbers of transverse sections on the flow boiling heat transfer, we performed numerical simulations on a rectangular microchannel (RMC) and IMCs with 3, 5, and 7 transverse microchannels at high and low mass flux. It was found that fluid experiences similar bubble and slug flow in different numbers of IMCs and the RMC at low mass flux. At a heat flux of q = 90 W/cm2, the downstream regions of the IMCs produce vapor films that span the channels, obstructing the cross-section and weakening the flow exchange between the channels, which lead the heat transfer performance factor of IMC-3, reaching 148.43%, 110.04%, and 116.92% of the RMC, IMC-5, and IMC-7. Under high-quality flux, as the heat flux increases, the heat transfer coefficient increases and the pressure drop decreases due to the existence of lateral microchannels introduced in the interconnected microchannels. Whether at high or low mass flux, structural reasons pertaining to the RMC can easily lead to the accumulation of bubbles and the occurrence of slugs, and the flow boiling instability increases with the increase of heat flux, which leads to a pressure drop and heat transfer performance generally lower than that of IMCs under the same conditions. At q = 120 W/cm2, IMC-7 showed the best heat transfer enhancement. Its heat transfer performance factor was 129.37%, 120.594% and 107.98% of the RMC, IMC-3, and IMC-5, respectively. This article provides theoretical support for the design of interconnected microchannels in thermal management.
1. Introduction
Microelectronic devices have become pervasive in sectors such as aerospace, biochemistry, nuclear technology, and various other industries. As the power density of these electronic devices has steadily risen, recent data suggests that the peak heat flux of densely integrated microelectronic components has surpassed 1000 W/cm2 [1,2,3]. However, traditional single-phase heat exchange methods such as air cooling and water cooling have shortcomings such as large volume and small heat transfer capacity and can no longer meet the problem of high heat flow heat dissipation. The heat dissipation problem of electronic equipment has become an urgent problem to be solved [4]. Flow boiling within microchannel heat sinks is often considered an efficient cooling technique, such as for cooling high-performance computing devices like ASICs (Application Specific Integrated Circuits). Furthermore, the flow boiling heat transfer mechanism enables microchannel heat sinks to exhibit a more uniform temperature distribution along the flow direction. Therefore, the flow boiling characteristics within microchannels have attracted significant attention from many researchers [5,6]. Parallel microchannels, with their large heat transfer area, can efficiently achieve cooling [7], thereby addressing issues related to localized temperature increases [8,9]. Numerous studies have focused on modifying the cross-sectional shape of parallel microchannels to enhance their heat transfer capabilities, including rectangular sections [10,11,12], triangular sections [13], and trapezoidal sections [14,15].
Despite the advantages of parallel microchannels mentioned above, there are still many challenges. M. Özdemir et al. [16] identified flow boiling instability as a common issue in parallel microchannel heat exchangers, where severe flow boiling instability can affect system performance and may lead to system failure. Chen et al. [17] and Huang et al. [18] found in their studies on flow boiling in parallel microchannels that the agglomeration of bubbles, leading to channel blockages, made the flow unstable and caused significant pressure drop oscillations. Fang et al. [19] and S. Singh et al. [20] used numerical simulations and experimental studies, respectively, to research flow boiling in microchannels. In their studies, both teams discovered that the aggregation of bubbles leading to slug formation caused local dry-out phenomena. D. Bogojevic et al. [21] observed local dry-out in silicon-based microchannel boiling, caused by the rapid evaporation of thin liquid films in annular flow, accompanied by reverse vapor flow at the inlet. Qu et al. [22] also discovered the phenomenon of the reverse vapor flow in parallel microchannels. The flow instabilities caused by uneven flow distribution, identified by numerous scholars in parallel microchannels, led to pressure drop oscillations, premature local dry-out, and flow reversal. These issues can significantly reduce the reliability of microchannel heat sinks.
To address this issue, interconnected microchannels with cross-linked regions are considered a good choice. Jiang et al. [23] were the pioneers in introducing the idea of interconnected microchannels. Their experimental model featured transverse grooves integrated within parallel microchannels. Owing to these transverse grooves, there is an enhancement in fluid transfer and mixing, which in turn fosters a more homogeneous temperature distribution across non-uniformly heated surfaces. Interconnected microchannels have been employed to facilitate lateral fluid movement and mixing during single-phase convection processes. Following this, Gan et al. [24], Xia et al. [25], and Chimres et al. [26] undertook both experimental and numerical studies focusing on the benefits of re-establishing thermal boundary layers within the cross-section of these interconnected microchannels. The amplification in single-phase heat transfer efficacy through these channels has been consistently demonstrated in their findings. Deng et al. [27] executed a flow boiling experimental investigation on interconnected microchannels featuring eight transverse channels. To gauge the temperatures, five thermocouples were systematically positioned at the base of the microchannels along the flow trajectory. Their findings revealed that these interconnected microchannels exhibited a more consistent temperature distribution, and there was a notable enhancement in the flow boiling heat transfer. Chen et al. [28] embarked on an examination of flow boiling heat transfer within interconnected microchannels integrated with micro-connected slots. Their observations revealed that these specific slots facilitate fluid amalgamation, resulting in a homogenized flow distribution within the interconnected microchannels. Notably, both the enhanced HTC and CHF exhibited improvements across all the experimental conditions. Deng et al. [29] introduced and innovated upon pin-fin interconnected recessed microchannels tailored for microchannel cooling mechanisms. Their research highlighted that these interconnected microchannels not only afford optimal regions for bubble nucleation and transit but also mitigate the bubble confinement effect within the channel. Compared with parallel microchannels, pin-fin interconnected microchannels can increase heat transfer up to nearly three times in water tests. Ma et al. [30] designed three different sizes of fully interconnected microchannels and experimentally investigated the effect of the flow boiling characteristics of HFE-7100 in a microchannel heat sink. The results showed that the flow boiling of the interconnected microchannels was more stable and the heat transfer coefficient and critical heat flow density were increased by 5.5 and 1.82 times, respectively, compared with those of the plain wall microchannels. Zhang et al. [31] conducted a comparative test between interconnected microchannels and traditional rectangular microchannels. They observed through high-speed cameras that both IMCs and the RMC were dominated by nucleate boiling mode, and IMCs could dissipate higher heat fluxes than the RMC, also exhibiting better stability and a higher critical heat flux.
Two-phase heat transfer, flow instability, and pressure drops in interconnected microchannels have been assessed across varying heat and mass fluxes. Direct comparative analyses examining flow boiling performance between interconnected channels and parallel channels are infrequent in the literature. In the current study, the flow and heat transfer characteristics in multiple interconnected regions within microchannels were thoroughly investigated. The effects of different numbers of interconnected channels on heat transfer characteristics were compared, while interconnected microchannels with different numbers of transversal microchannels were compared with rectangular microchannels to explore the potential for enhanced flow boiling.
2. Numerical Model
2.1. Physical Model
In the current investigation, an initial design incorporated a model featuring three parallel microchannels, each spaced longitudinally by 0.7 mm and having dimensions W × H × L=2.4 mm × 1 mm × 10 mm, as depicted in Figure 1a. Subsequently, three transverse microchannels, oriented perpendicular to the flow direction, were introduced. The flow direction was partitioned into four equidistant cross-sectional regions, yielding interconnected microchannels, illustrated in Figure 1b. Figure 1c,d showcase configurations with six and eight evenly spaced cross-sections in the flow direction, respectively. Both longitudinal and transverse microchannels maintain uniform geometric profiles, as elucidated in Figure 1. The channels possess a width (Wch) of 0.4 mm, a height (Hch) of 0.5 mm, and the fins have a width (Wfin) of 0.3 mm. Relevant geometric parameters are tabulated in Table 1.
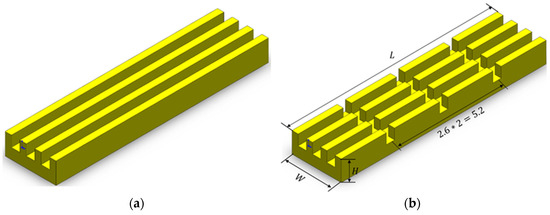
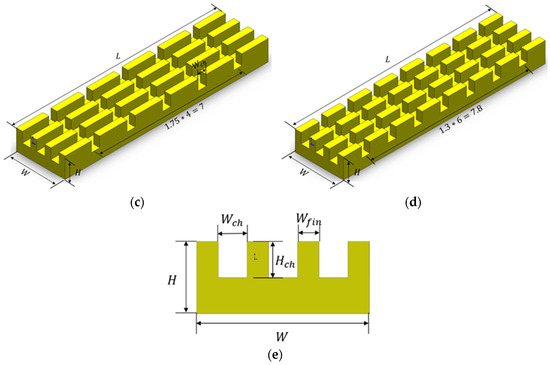
Figure 1.
The geometry of the channel: (a) RMC; (b) IMC-3; (c) IMC-5; (d) IMC-7; (e) cross-section of microchannels.

Table 1.
Geometrical dimensions.
2.2. Numerical Method
Within this investigation, flow boiling within microchannels was simulated using computational fluid dynamics (CFDs) software. The boundary between the two fluid phases was defined employing the volume of fluid (VOF) methodology. The computational framework is constructed based on the following fundamental assumptions.
- (1)
- The heat flux only acts on the bottom surface of the microchannel.
- (2)
- The working fluid is water, the flow state is laminar flow, the inlet temperature and velocity are evenly distributed, there is no slip on the wall, and there is no jump in temperature.
- (3)
- Ignore radiation heat transfer.
- (4)
- Neglect the effect of microchannel wall roughness.
- (5)
- The thermophysical properties of a fluid are defined using piecewise linear functions with respect to temperature.
2.2.1. Governing Equations
The volume of fluid (VOF) model [32], as implemented by ANSYS Fluent 15.0, is designed to simulate the boundary between immiscible fluids. This technique monitors the interface by considering the volume fraction of the involved fluids. The liquid phase is defined as , which represents the ratio of the volume of the liquid in a certain unit to the volume of the entire unit. For vapor–liquid two-phase flow, the volume fraction of vapor is . The cumulative volume fractions of both phases equate to 1.
Continuity Equation (Mass Conservation) [33]:
where and are the densities of liquid phase and vapor phase, is the velocity vector, respectively. and are the mass sources for liquid phase and vapor phase, respectively.
The density is articulated as follows:
Energy equation [33]:
where E represents the total energy, encompassing both internal and kinetic energies, T denotes the temperature, k signifies the thermal conductivity, and corresponds to the volumetric heat source. Total energy is articulated as follows:
Momentum equation [33]:
where is the viscosity, is the gravity and is the surface tension.
At the interface of a droplet or bubble, molecular forces give rise to surface tension, which is integral to flow behaviors at the microscale. Within the volume of fluid (VOF) framework, the continuous surface force model [34] (CSF model) typically characterizes surface tension. Its representation in the momentum equation [35] is articulated as
where is the surface tension coefficient and is the curvature of the interface.
Utilizing an amalgamation of the VOF and Lee models [35], the phenomena of evaporation and condensation at the liquid–vapor interface can be delineated as
where and are the mass transfer rates due to evaporation and condensation, respectively. can be understood as the relaxation factor, which can be articulated as [36,37]
R denotes the ideal gas constant, M represents the molar mass of water, is characterized through the accommodation coefficient in conjunction with the vapor’s intrinsic properties, and L signifies the latent heat.
2.2.2. Initial and Boundary Conditions
The initial inlet mass fluxes are 100 kg·m−2·s−1 and 200 kg·m−2·s−1, respectively; the initial inlet fluid temperature is 353.15 K, the initial vapor phase volume fraction is 0, and the operating pressure is 1 atmosphere. The velocity boundary condition is adopted at the inlet, the pressure boundary condition is adopted at the outlet, and the wall boundary condition is set to fixed and no-slip. At the bottom of the microchannel is the heated surface, which is subject to a constant and uniform heat flux with a variation range of 50~120 W/cm2, where λ is the thermal conductivity of copper. All other surfaces are kept adiabatic.
2.2.3. Numerical Solver Options
Numerical analysis is conducted using the commercial finite volume method-based solver ANSYS Fluent. The volume of fluid (VOF) method is employed to simulate two-phase flow boiling in parallel channels. The control equations in their partial differential form are solved using a control-volume based collocated grid approach. The laminar viscosity model is selected to represent low Reynolds number flow conditions. To ascertain computational convergence and expedite the convergence trajectory, the SIMPLE algorithm is implemented for coupling the pressure and velocity fields. PRESTO (Pressure Staggering Option) is used for the discretization of the pressure terms. Unsteady terms are solved using a first-order implicit scheme, with a smaller time step (5 × 10−6 s) employed. This time step is chosen to avoid numerical instability and achieve convergence of the numerical code. The geometric reconstruction scheme uses a piecewise linear method to represent the interface between fluids and takes into account the calculation of volume fractions. The QUICK scheme is used for the discretization of momentum and energy equations. The solution is considered converged once the residuals of the continuity and momentum equations reach 10−6, and the residual of the energy equation reaches 10−8.
In the numerical study presented here, the microchannel’s structure is founded on copper as the constitutive material. The operative fluid coursing through the microchannel is water, encapsulating both its liquid and gaseous states. For the precision of the numerical predictions, the thermophysical characteristics of water are set as a piecewise linear function of temperature. Gravitational acceleration is oriented counter to the Z-axis direction, exhibiting a magnitude of 9.8 m/s2.
2.3. Data Reduction
The heat transfer coefficient can be articulated as [38]
where Ab is the heating area, At is the total heat transfer area, Tw is the wall average temperature, Tf [38] is the water average temperature, and Tin and Tout are the inlet and outlet temperatures.
The pressure drop is determined by [38]
Pin and Pout represent the average pressure of channel inlet and the average pressure of channel outlet.
To represent the average heat transfer coefficient per unit pressure drop, this research presents the heat transfer performance factor, denoted as J, formulated as follows [39]:
2.4. Validation of Grid Independence and Model
For grid independence verification, five distinct grid configurations were employed for the computational model presented in this study. Using the computational outcomes from IMC-7, characterized by a bottom wall heat flux of 70 W/cm2 and an inlet velocity of 0.2 m/s as a representative case, the wall’s average temperature served as the benchmark criterion, as illustrated in Figure 2. Examination of Figure 2 reveals that, as the grid count escalates, the rate of change in the wall’s average temperature tends to stabilize. A subsequent analysis determined that the relative discrepancy between Tw acquired from the fourth grid configuration and Tw from the finest grid was a mere 0.0662%. Consequently, the fourth grid configuration was selected, comprising a total of 860,000 grid cells.
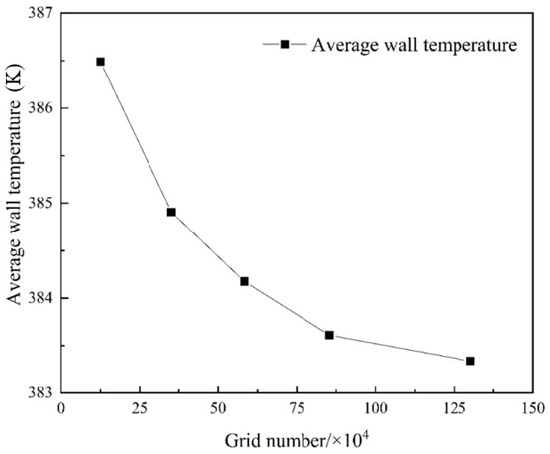
Figure 2.
Wall temperature for grid independence test.
In order to verify the accuracy of the numerical simulation, the Nusselt number and Reynolds number curves obtained by Deng et al. [40] in the experiment (channel width of 0.64 mm, depth of 1 mm, and length of 45 mm) were used to verify the simulation results. The numerical simulation was carried out in a single rectangular straight microchannel at q = 267 kW/m2 and Tin = 33 °C. As delineated in Figure 3, the correlation between the average Nusselt number (Nu) and Reynolds number (Re) for the standard rectangular microchannel specimen is presented. The observed trajectory, wherein Nu ascends in tandem with Re, aligns coherently with the predictions from Deng’s correlation. The experimental data resonates closely with Deng’s correlation, manifesting a deviation contained within 3.5%. The simulated Nusselt number at low Reynolds numbers is lower than the experimental value. This deviation can be attributed to the enhanced wall heat transfer with rough wall surfaces. However, in simulation work, the wall is considered a smooth surface. Thus, we think the selected simulation model is suitable for investigating the flow boiling characteristics in the heat sinks.
Figure 3.
Comparison of the average Nusselt number simulation and experimental results in rectangular microchannels [40].
3. Results and Discussion
3.1. Flow and Heat Transfer Process through Microchannels at Low Mass Flux
3.1.1. The Effect of Heat Flux on Bubble Nucleation at Low Inlet Mass Flux
Flow and heat transfer was calculated in three types of interconnected microchannels and a rectangular microchannel at low mass flux. The low mass flux at the inlet of microchannels is 100 kg·m−2·s−1. The bottom surface of microchannels is a heating surface, with a heat flux ranging from 50 W/cm2 to 90 W/cm2. The fluid in microchannels undergoes a process of bubble generation, growth, and detachment from the wall. The distribution of bubbles in interconnected and rectangular microchannels during a steady state is shown in Figure 4, Figure 5, Figure 6 and Figure 7 under different heat fluxes. The flow in interconnected microchannels and the rectangular microchannel are all in the early stage of bubble flow, when heat flux is less than 50 W/cm2. There are a number of tiny bubbles in the microchannels at this stage, which can easily detach from the wall to enter the mainstream of the fluid. The bubble flow in the microchannels is listed when the heat flux is 50 W/cm2, as shown in Figure 4a, Figure 5a, Figure 6a and Figure 7a. With the increase in the number of transversal microchannels, there is a slight rise in the quantity of bubbles. These bubbles primarily exist in isolation, with the fewest bubbles observed in the RMC.
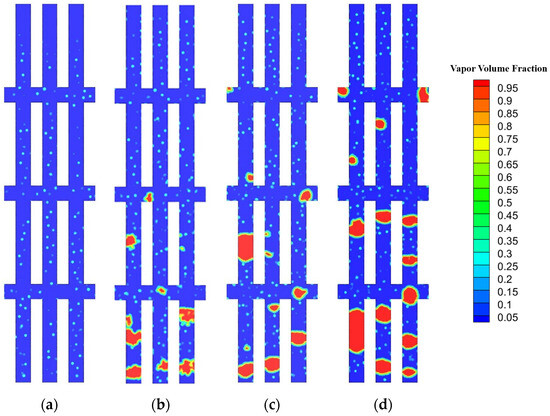
Figure 4.
Two-phase flow pattern of IMC-3 at mass flux 100 kg·m−2·s−1 at heat flux: (a) q = 50 W/cm2; (b) q = 70 W/cm2; (c) q = 80 W/cm2; (d) q = 90 W/cm2.
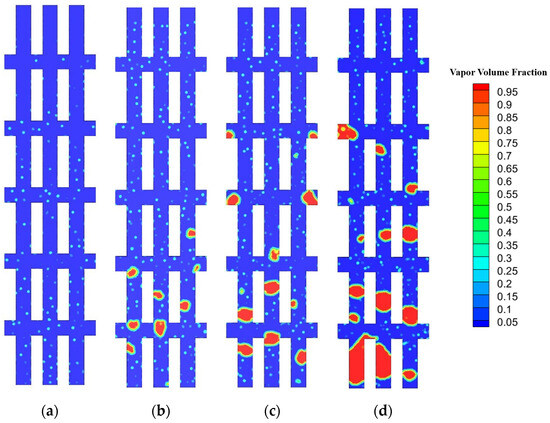
Figure 5.
Two-phase flow pattern of IMC-5 at mass flux 100 kg·m−2·s−1 at heat flux: (a) q = 50 W/cm2; (b) q = 70 W/cm2; (c) q = 80 W/cm2; (d) q = 90 W/cm2.
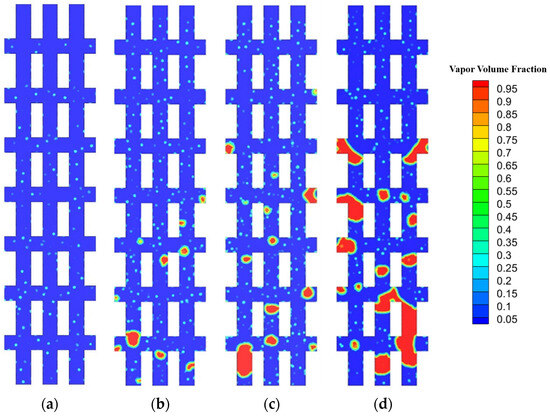
Figure 6.
Two-phase flow pattern of IMC-7 at mass flux 100 kg·m−2·s−1 at heat flux: (a) q = 50 W/cm2; (b) q = 70 W/cm2; (c) q = 80 W/cm2; (d) q = 90 W/cm2.
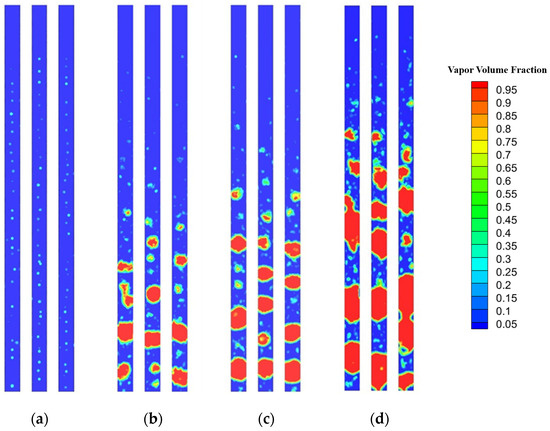
Figure 7.
Two-phase flow pattern of RMC at mass flux 100 kg·m−2·s−1 at heat flux: (a) q = 50 W/cm2; (b) q = 70 W/cm2; (c) q = 80 W/cm2; (d) q = 90 W/cm2.
When the heat flux of the bottom increases to 70 W/cm2, the flow in the microchannel reaches the late stage of bubbly flow. This transition is marked by a significant increase in the number of larger bubbles within the channel. Some bubbles grow on the wall and detach after becoming large, while other smaller bubbles detach from the wall and merge with each other in the mainstream to form larger bubbles. The rates of bubble generation and detachment from the channel walls significantly surpass those observed at a heat flux of 50 W/cm². The growth and detachment of bubbles also causes fluctuations in the surrounding liquid, which intensifies the surging of bubbles. As depicted in Figure 4b, Figure 5b, Figure 6b and Figure 7b, the RMC demonstrates the most significant fluctuations compared to the other three channels.
When the heat flux on the bottom of the microchannel increases to 70 W/cm2, the flow in the RMC has progressed to the early stage of slug flow, while in other IMCs it is still bubble flow, with only individual bubble sizes reaching the channel width. A large number of bubbles are generated, detaching from the wall and entering the mainstream, where they continue to grow or merge into larger bubbles. The frequency of bubble detachment from the wall exceeds that observed under the previous two heat flux conditions. At a heat flux of 80 W/cm2, the flow within the microchannel is primarily bubbly flow, with slug flow secondary. As observed in Figure 4c, Figure 5c, Figure 6c and Figure 7c, the RMC has a higher number of slugs, while the number of slugs in IMC-3, IMC-5, and IMC-7 are similar. The emergence of slug flow blocks the channel, which not only inhibits the formation of new bubbles on the surface near the slugs, but also reduces the bubble detachment frequency. Furthermore, it exacerbates flow fluctuations, leading to unstable flow patterns. When the heat flux is 90 W/cm², the flow in the channel has progressed to the late stages of slug flow. More bubbles grow on the wall, leading to more frequent bubble coalescence, and the formed slugs tend to merge with the upstream and downstream slugs, resulting in longer slugs. Figure 7d shows a number of slugs in the RMC. Propelled by the mainstream, these slugs gradually elongate, resulting in the longest slug among all channels in the RMC. In an IMC, shorter slugs are observed in the mainstream of the channel. However, within the interconnected regions, some bubbles grow on the cross-section, forming blocky or film-like structures that obstruct the cross-section and weaken the flow exchange between channels. These phenomena can be observed in Figure 4d and Figure 6d.
Figure 8 presents the computed vapor volume fraction within the flow microchannels. At a heat flux of 50 W/cm2, the vapor volume fraction is at its minimum, a consequence of the flow being in the nascent phase of the bubble flow regime. In comparison to the interconnected microchannel, the RMC registers the lowest vapor volume. Among the IMCs, the variance in vapor volume is not significant. When the heat flux increases to 60 W/cm2, the vapor volume fraction increases approximately three times compared to the value at 50 W/cm2. This substantial increment stems from the flow’s progression into the advanced phases of the bubbly flow regime upon being subjected to a heat flux of 60 W/cm2. At low heat fluxes, IMCs have a larger heat transfer area, and transversal microchannels provide stable nucleation sites, resulting in greater vapor volume fractions than with the RMCs. IMC-7 has seven transversal microchannels to maximize its heat transfer area and thus the largest vapor volume fraction. At a heat flux of 70 W/cm2, the flow in the RMC transitions to the initial slug flow stage. The vapor volume fraction increased by 121.2% compared with at 60 W/cm2, which can be attributed to the formation of slug in the channel. After increasing the heat flux, boiling becomes intense. Since there are no interconnected areas in the RMC, the detached bubbles are more likely to merge to form large bubbles or slugs. This causes the steam volume fraction in the RMC to rise rapidly at this stage. The interconnected areas in the IMC provide more space for the bubbles to move around, making it less likely for the bubbles to aggregate, so IMCs remain in bubble flow. Although the vapor volume fraction in the IMCs increases, it is not as obvious as the increase in the RMC. Upon reaching a heat flux level of 90 W/cm2, the vapor volume fraction exhibits a modest rise relative to the values observed at 80 W/cm2. This is attributed to intensified bubble blockages and the presence of more pronounced slugs. These factors further inhibit bubble expansion, indicating that the flow has ventured into the terminal phase of the slug flow regime.
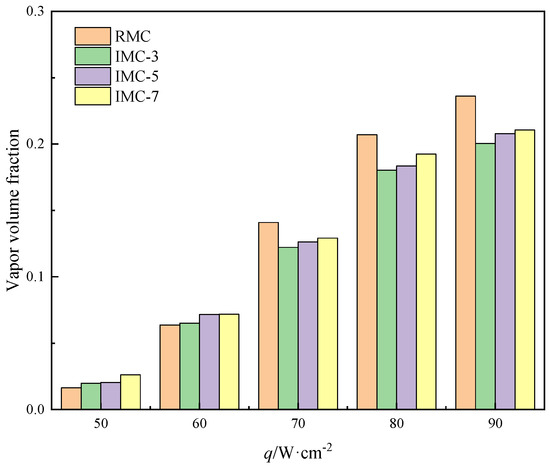
Figure 8.
Vapor volume fraction under various heat fluxes at a mass flux of 100 kg·m−2·s−1.
3.1.2. The Effect of Heat Flux on Flow Resistance at Low Mass Flux
Flow resistance is expressed by pressure drops at the inlet and outlet of the flow channel. The pressure drop at the inlet and outlet of the four microchannels changes with the heat flux, as shown in Figure 9. The pressure drop in the four channels has little difference as the heat flux is less than 50 W/cm2. All channels are in the initial stage of bubbly flow, with the primary resistance due to flow friction. The number of bubbles generated during this period is too small to impact the flow, hence the resistance difference in IMC-3, IMC-5, IMC-7, and the RMC is minimal. When the heat flux reaches 60 W/cm2, the flow pattern transitions from the early to the late stage of bubbly flow, leading to an increase in flow resistance within the microchannel compared to the heat flux at 50 W/cm2. At this stage, the expansion of bubbles, detachment from the wall, merging of bubbles, and so on, have a significant impact on flow resistance. As show in Figure 8 and Figure 9, the flow resistance correlates with the volume of vapor, increasing as the vapor volume augments. The transverse microchannels enhance fluid mixing, and there is a correlation between their number and the resistance, with the latter increasing as the number of cross-sections augments. When the heat flux reaches 70 W/cm2, the pressure drop change is greater than that under the first two heat fluxes. The resistance is not only from the flow resistance, but also from the bubble movement. When the flow is in the early stages of slug flow, the flow pattern changes from the inlet bubble flow to the outlet slug flow; the flow involves squeezing, merging, and slugging between bubbles, and the flow state in the channel changes greatly. Slug flow in the RMC is the most severe, as shown in Figure 7, because the RMC restricts the expansion and movement of bubbles; bubbles can only expand upstream and downstream, leading to longer slug flow and flow fluctuations. Thus, the RMC has the largest pressure drop. When the heat flux is 90 W/cm2, the resistance in all channels increases a lot. The flow at the heat flux has developed to the end of slug flow. The collision and coalescence between bubbles become more frequent than with the previous heat flux, and slugs are also merged into longer slugs. Some cross-sections are filled with vapor plug, making the flow pattern more unstable. It can be seen from Figure 4d, Figure 5d, Figure 6d and Figure 7d that the RMC has the most slugs, and its resistance is also the highest. Slugs also exist in IMC-3, IMC-5, and IMC-7, and the resistance in the flow channel also increases. Blockages occurred at the downstream interconnections in the channels, with the phenomenon being more severe in IMC-7, where even large vapor films spanning across adjacent channels appeared.
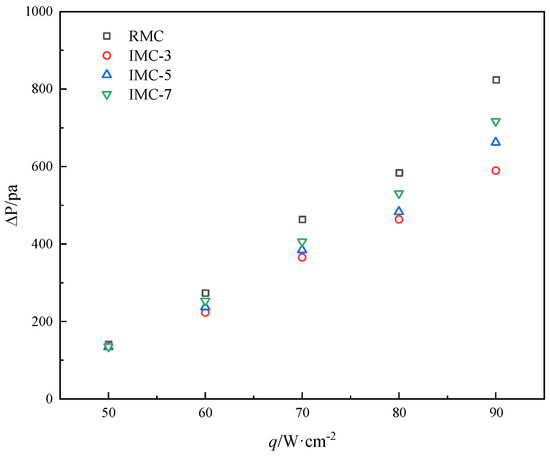
Figure 9.
Two-phase pressure drop for four microchannels as a function of base heat flux at a mass flux of 100 kg·m−2·s−1.
3.1.3. The Effect of Heat Flux on Heat Transfer at Low Inlet Mass Flux
HTC at low inlet mass flux was calculated, as shown in Figure 10. In the heat flux range of 50 to 90 W/cm2, the fluid exhibits a bubble flow pattern. Bubbles readily detach from the wall and integrate into the primary flow stream.
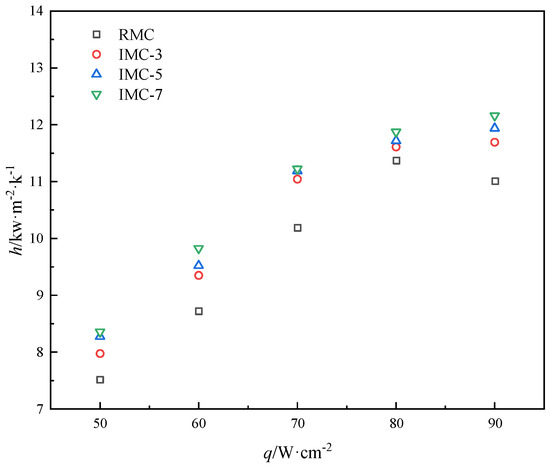
Figure 10.
Two-phase heat transfer coefficient for four microchannels as a function of base heat flux at a mass flux of 100 kg·m−2·s−1.
As the heat flux escalates, the number of bubbles proliferates, resulting in a concomitant swift rise in HTC. The transection in microchannels with IMC increases nucleation sites, promotes bubble nucleation, and transection in microchannels can enhance fluid mixing in adjacent channels. A review of Figure 10 indicates that HTC in the IMC surpasses that of the RMC. Further, there is a sequential escalation in HTC across IMC-3, IMC-5, and IMC-7 configurations. When heat flux is greater than 80 W/cm2, the fluid is in slug flow. At this stage, the length of the vapor plug increases, which inhibits the bubble from leaving the wall, but the mixing of fluid in adjacent channels at transections improves flow to a certain extent. Thus the heat transfer coefficient in IMCS is higher than in the RMC. However, when heat flux increases to 90 W/cm2, slug blocking and vapor film are also formed at the interconnection transections, and the mixing of fluids in adjacent channels is also weakened. HTC does not increase rapidly with heat flux, and its growth rate is slower than that of low heat flux. There are more slugs in the RMC, which greatly reduces the frequency of bubble detachment. The existence of the slug also reduces the effective flow area of the liquid phase and increases the contact area between the channel wall and the steam, making the heat transfer effect worse.
3.1.4. The Heat Transfer Factor at Low Mass Flux
Figure 11 delineates the trend of the J-factor across four distinct microchannels as a function of heat flux. The heat transfer performance factor signifies the heat transfer coefficient per unit of pressure drop. A higher J-factor means a higher heat transfer coefficient per unit pressure drop in the channel. A perusal of Figure 11 underscores a declining trend of the heat transfer performance factor as heat flux increases. At lower heat flux, IMC-7 has the highest heat transfer coefficient because more interconnected areas provide sufficient nucleation sites and a larger heat transfer surface area. At the same time, the vapor volume fraction in the channel is small, and the bubbles have little impact on the flow resistance, so the pressure drops in the four channels are almost the same. Thus the J-factor in IMC-7 is the largest. However, as heat flux amplifies, this beneficial disparity diminishes. On the contrary, under high heat flux conditions, IMC-3 becomes the channel with the highest J-factor, mainly due to its smaller pressure drop than other channels. The pressure drop of IMC-7 is significantly enhanced by the presence of a vapor film, resulting in a lower J-factor than that of IMC-3 and IMC-5. When heat flux is at 90 W/cm2, the presence of more vapor plugs in the RMC reduces bubble detachment and increases the vapor–solid contact surface, which not only results in a lower heat transfer coefficient but also a higher pressure drop. And the J-factor for IMC-3 exhibits an elevation of 148.43%, 110.04%, and 116.92% when compared to the RMC, IMC-5, and IMC-7, respectively.
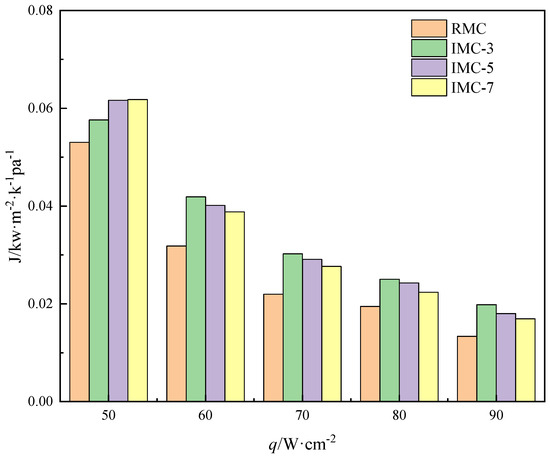
Figure 11.
The J-factor for four microchannels as a function of base heat flux at a mass flux of 100 kg·m−2·s−1.
3.2. Flow and Heat Transfer Process through Microchannels at High Mass Flux
3.2.1. The Effect of Heat Flux on Bubble Nucleation at High Inlet Mass Flux
Flow and heat transfer were calculated in microchannels at high mass flux. The high mass flux at the inlet of the microchannels is 200 kg·m−2·s−1. In this study, the heat flux ranges from 50 W/cm2 to 120 W/cm2. Figure 12, Figure 13, Figure 14 and Figure 15 depict the two-phase flow patterns of IMC-3, IMC-5, IMC-7, and the RMC at some heat flux. When the heat flux is less than 50 W/cm2, subcooled fluid enters the microchannel, and its temperature is below the saturation temperature. As it flows through the channel and comes into contact with the heated wall of the microchannel, its temperature will gradually rise. In this stage, even though the fluid’s temperature is increasing, no bubbles have formed yet. Even if a portion of the fluid is heated to the saturation temperature near the outlet, only tiny bubbles are generated on the wall, which can be approximately regarded as single-phase liquid flow; the number of bubbles is less than that at the same heat flux and mass flux of 100 kg·m−2·s−1. There is little difference in the number of bubbles generated in the RMC, IMC-3, IMC-5, and IMC-7. The flow within the RMC, IMC-3, IMC-5, and IMC-7 is at the initial stage of bubbly flow, which resembles the same stage when the heat flux is 50 W/cm² and the mass flux is 100 kg·m−2·s−1. The number of bubbles in all four channels is minimal, and bubbles are able to detach from the wall quickly. The quantity of bubbles is greatest in IMC-7, given that it has the largest heat transfer area. When the heat flux escalates to 80 W/cm², the flow pattern within the RMC, IMC-3, IMC-5, and IMC-7 progresses to the intermediate stage of bubbly flow. The volume of the bubbles further expands, with some larger volume bubbles forming on the wall and detaching into the mainstream liquid. It is observed that the most quantity of bubbles is in the RMC, and the instability of flow is most pronounced among the four channels. The number of bubbles in the IMC-3, IMC-5, and IMC-7 channels exhibits minimal differences. When heat flux increases to 90 W/cm2, as seen in Figure 12, Figure 13 and Figure 14 the flow in IMC-3, IMC-5, and IMC-7 are in the initial stage of slug flow, which is similar to flow observed when the heat flux is 70 W/cm2 and the mass flux is 100 kg·m−2·s−1. Slugs occur downstream of the flow channel close to the outlet, but they do not fully block the cross-section. Conversely, Figure 15 shows that the flow in the RMC is in the late stage of bubble boiling, with a profusion of bubbles and absence of slugs. Instability is most pronounced in the RMC. When the heat flux reaches 120 W/cm2, the flows in the RMC, IMC-3, and IMC-5 have entered the middle or late stages of slug flow. Bubbles collide violently to form elongated slugs, leading to blockages in the microchannels. The blockage is most severe in the RMC, followed by IMC-3 and IMC-5. However, the flow in IMC-7 is just transitioning into the initial stage of slug flow, with only a limited number of slugs in the channel. The rate of flow pattern change is the fastest in the RMC, followed by IMC-3, IMC-5, and IMC-7. The slowest change is observed in IMC-7, potentially due to its superior internal dredging performance.

Figure 12.
Two-phase flow pattern of IMC-3 at mass flux 200 kg·m−2·s−1 at heat flux: (a) q = 50 W/cm2; (b) q = 70 W/cm2; (c) q = 80 W/cm2; (d) q = 90 W/cm2; (e) q = 120 W/cm2.
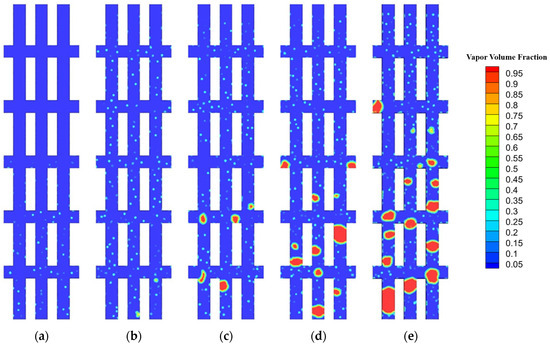
Figure 13.
Two-phase flow pattern of IMC-5 at mass flux 200 kg·m−2·s−1 at heat flux: (a) q = 50 W/cm2; (b) q = 70 W/cm2; (c) q = 80 W/cm2; (d) q = 90 W/cm2; (e) q = 120 W/cm2.
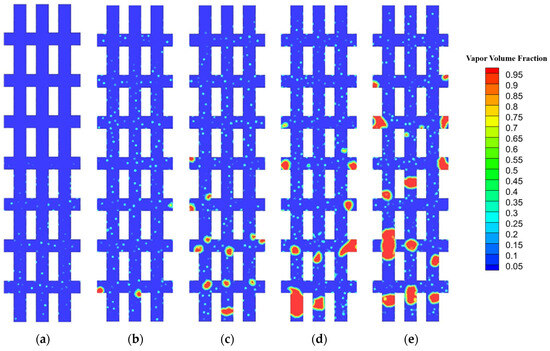
Figure 14.
Two-phase flow pattern of IMC-7 at mass flux 200 kg·m−2·s−1 at heat flux: (a) q = 50 W/cm2; (b) q = 70 W/cm2; (c) q = 80 W/cm2; (d) q = 90 W/cm2; (e) q = 120 W/cm2.
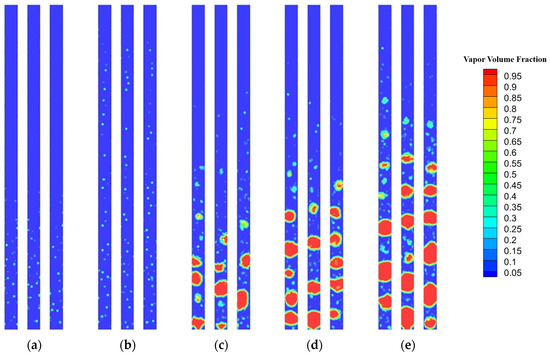
Figure 15.
Two-phase flow pattern of RMC at mass flux 200 kg·m−2·s−1 at heat flux: (a) q = 50 W/cm2; (b) q = 70 W/cm2; (c) q = 80 W/cm2; (d) q = 90 W/cm2; (e) q = 120 W/cm2.
Figure 16 show the vapour volume fraction in the microchannel at a mass flux of 200 kg·m−2·s−1. When the heat flux is lower than 70 W/cm2, the flow in the channel is a bubble flow or even approximates a single-phase flow, and the vapor volume fraction is small. As mentioned in Section 3.1.1, the addition of lateral microchannels in interconnected microchannels can provide stable nucleation points and increase the heat transfer area. More interconnection channels are conducive to generate more bubbles under low heat flux, so the vapor volume fraction of IMC is higher than that of the RMC. At a heat flux of 50 W/cm2, compared with IMC-7, which has the largest vapor volume fraction, the RMC has a vapor volume fraction of 164.96% of IMC-7. When the heat flux further increases, the boiling in the channel becomes more intense. Due to the existence of interconnected areas in the IMC, the bubbles do not easily converge, so the vapor volume fraction of the IMC does not increase significantly. The bubbles in the RMC easily merge to form large bubbles and slugs during the flow process, causing the vapor volume fraction in the channel to change significantly. At a heat flux of 80 W/cm2, compared with IMC-7, which has the largest vapor volume fraction, the vapor volume fraction of IMC-7 is only 117.98% of the RMC, and the gap between the two is smaller than when the heat flux is 50 W/cm2. When the heat flux reaches 100 W/cm2, the limitations of the RMC structure make it easier for bubbles to merge, resulting in slugs blocking the channel, causing the vapor volume fraction to rise faster. The vapor volume fraction at this time is already similar to that of IMC. When the heat flux reaches 120 W/cm2, the vapor volume fraction in the RMC has exceeded IMC. Compared with IMC-7, which has the smallest gas volume fraction, the RMC is 103.74% of IMC-7.
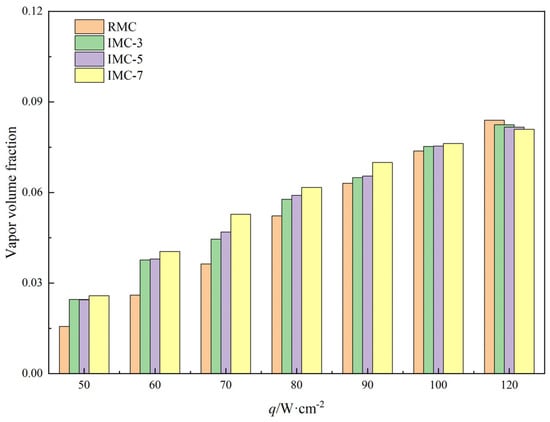
Figure 16.
Vapor volume fraction of different heat fluxes at a mass flux of 200 kg·m−2·s−1.
3.2.2. The Effect of Heat Flux on Flow Resistance at High Mass Flux
Figure 17 illustrates the variations of two-phase flow pressure drop in relation to the heat flux, under a mass flux of 200 kg·m−2·s−1. The trend of pressure drops at a mass flux of 200 kg·m−2·s−1 is similar to that at a mass flux of 100 kg·m−2·s−1. As mentioned above, when heat flux is lower than 50 W/cm2, the fluid can be approximately regarded as single-phase flow; its resistance is determined by the friction of the flow. The flow resistance in the IMC exceeds that in the RMC due to its interconnected channels that provide a larger heat transfer area. As demonstrated in Figure 17, the pressure drop within the RMC is the smallest. The fewer interconnected areas for fluid flow within an IMC, the smaller the heat transfer area, the lower the flow resistance, and therefore the corresponding lower pressure drop. Once the heat flux exceeds 70 W/cm2, the fluid is in bubble flow, where the resistance is caused by flow resistance and vapor–liquid friction. The friction between bubbles and liquid in bubble flow cannot be ignored, and as the heat flux increases, the friction between bubbles and the liquid increases, leading to an increase in the two-phase pressure drop. This is also the characteristic of internal resistance in bubble flow. At 90 W/cm2, it can be seen in Figure 12, Figure 13, Figure 14 and Figure 15 that the RMC is in the initial stage of slug flow, while IMC-3, IMC-5, and IMC-7 are in the later stage of bubble flow; the diameter of bubble does not reach the same width as the channel, and there is less slug in the channel. When the heat flux is 120 W/cm2, the RMC has entered the later stage of slug flow, with a lower bubble detachment frequency. Bubbles merge with each other to form slugs, and the formed slugs are further elongated, with the most severe blockage occurring in the RMC. IMC has fewer plugs in the channel due to the presence of interconnecting regions. And the more interconnection regions, the less the bubble confinement, resulting in less mergers between bubbles. As the number of interconnected channels increases, the number and length of plugs decrease, and the two-phase instability decreases accordingly; so IMC-7 has the smallest pressure drop. As shown in Figure 17, the flow resistance in the RMC is significantly higher than that in IMC-3, and IMC-5, and IMC-7.
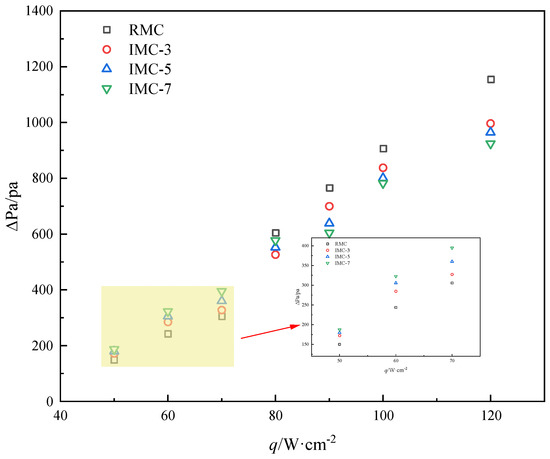
Figure 17.
Two-phase pressure drops for four microchannels as a function of base heat flux at a mass flux of 200 kg·m−2·s−1.
3.2.3. The Effect of Heat Flux on Heat Transfer at High Inlet Mass Flux
The variation of the heat transfer coefficient with heat flux in four different microchannels when the mass flux is 200 kg·m−2·s−1 is shown in Figure 18. The heat transfer coefficient increases with heat flux between 50 W/cm2 and 100 W/cm2. When the heat flux is greater than 100 W/cm2, the HTC of the RMC decreases as the heat flux increases. When the heat flux is 50 W/cm2, the fluid is in bubble flow under this heat flux, and the HTC has little difference. The heat transfer coefficient of the fluid in the RMC is smaller in four channels; a possible reason is that the heat transfer area of the RMC is smaller than that of the IMCs, and there is no interconnected area that can provide stable nucleation sites for the vapor core. In the interconnecting channels, the greater the number of transverse microchannels, the larger the heat transfer area and the more stable nucleation sites, thus IMC-7 has a better HTC. When the high heat flux is greater than 90 W/cm2, the HTC of IMC-7 is the largest, followed by IMC-5, IMC-3, and the RMC. The fluid in the RMC is in the early stage of slug flow, while IMC-7, IMC-5, and IMC-3 are in the late stage of bubble flow. The interconnected regions in IMC provide more space for bubble movement, reducing the constraint on bubbles. More interconnected regions mean less bubble restriction. Moreover, the sharp right-angle edges at the intersections can divide passing bubbles into smaller ones, leading to a certain reduction in slug formation inside the channels. Thus, IMC-7 has the largest HTC. An increased mass flux causes the liquid to flow across the heated surface faster than a low mass flux, which helps to carry away the generated vapor bubbles more quickly. Faster bubble detachment increases the contact opportunities between new liquid and the heated surface, promoting the generation of more bubbles. This continuous bubble generation and detachment process enhances heat transfer, so high-quality flow is achieved under the same heat flux. The amount has a better heat transfer coefficient. There are many factors that affect heat transfer, including bubble quantity, bubble volume, flow pattern, number of cross-sectional areas, and pressure drop in the flow channel. The flow resistance in the RMC channel has always been the highest, while in interconnected microchannels, the heat transfer area and flow pattern have a comprehensive impact on heat transfer under high-quality flow conditions.
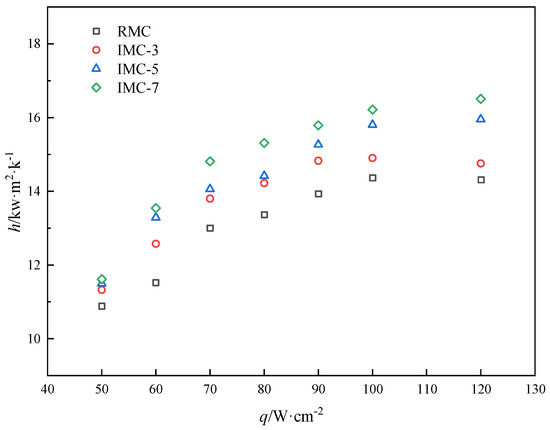
Figure 18.
Two-phase heat transfer coefficient for four microchannels as a function of base heat flux at a mass flux of 200 kg·m−2·s−1.
3.2.4. The Heat Transfer Performance Factor at Low Mass Flux
Figure 19 delineates the trend of the J-factor across four distinct microchannels as a function of heat flux at a mass flux of 200 kg·m−2·s−1. An inspection of Figure 19 reveals that the J-factor for the channels tends to decline as the heat flux increases. When the heat flux increases, the RMC is prone to bubbles blocking the channel, resulting in an increase in pressure drop and a smaller J-factor. In contrast, IMC takes advantage of the larger flow space of interconnected channels, which reduces bubble merging and reduces the occurrence of slugs. It improves the heat transfer coefficient while having a smaller pressure drop than the RMC. Therefore, the J-factor of IMC is larger than the RMC. Specifically, at a heat flux of 120 W/cm2, the J-factor for IMC-7 stands at 144.032% relative to the RMC, 120.594% when compared to IMC-3, and 107.98% in relation to IMC-5. This shows that under high heat flux, more interconnected areas in IMC-7 can effectively reduce the accumulation of bubbles and reduce the occurrence of slugs while maintaining a high heat transfer coefficient and a small pressure drop. The large number of slugs that appear in the RMC cause the surface heat transfer to deteriorate and increase the channel pressure drop, thus it has the smallest J-factor.
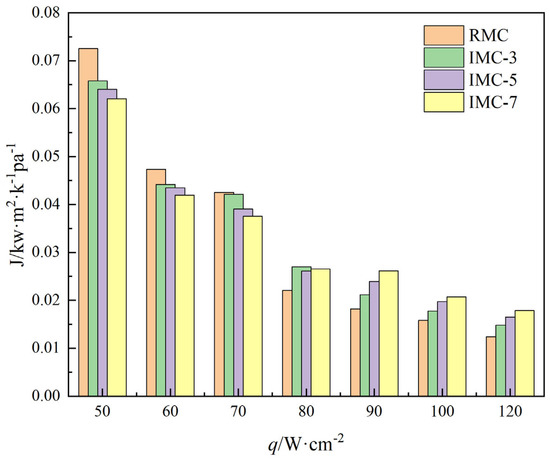
Figure 19.
The J-factor for four microchannels as a function of base heat flux at a mass flux of 200 kg·m−2·s−1.
4. Conclusions
Numerical simulations were conducted on the flow and heat transfer characteristics of interconnected microchannels (IMC-3, IMC-5, IMC-7) with varying cross-sectional designs and rectangular microchannels (RMCs). These simulations were performed under both high and low mass flux conditions with a heat flux range spanning 50 W/cm2 to 120 W/cm2. Key parameters such as the two-phase flow pattern, heat transfer coefficient (HTC), and pressure drop within the channel were examined. Based on the analysis, the subsequent conclusions were derived:
- (1)
- At low mass flux and the same heat flux, the flow patterns of IMCs and the RMC are basically the same. At high mass flux, when heat flux is relatively smaller, the flow pattern of interconnected microchannels and rectangular microchannels is basically the same. With the increase of heat flux, more interconnected regions have a better dredging effect, which can maintain bubble flow at a large range of heat flux. The vapor volume fraction of the RMC increases faster than that of IMCs under both mass fluxes. The reason is that the movement of bubbles is restricted in the RMC channel, causing bubbles to merge frequently to form larger slugs.
- (2)
- Under high mass flux, flow friction resistance is the primary contributor to pressure drop during the initial stage of bubbly flow. At low heat flux, the heat transfer area in IMCs is larger than that in the RMC, so the pressure drop in IMCs is larger than that in the RMC. However, at high heat fluxes, the instability of the two-phase flow is the main factor in the pressure drop, and the large number of slugs present in the RMC makes the vapor-liquid friction significant, resulting in the highest pressure drop. In IMCs, channels with more interconnection regions have smaller pressure drops due to less restriction of bubbles, resulting in fewer segment plugs. At low mass flux, the pressure drop remains highest in the RMC, whereas in IMCs, the greater the number of interconnected channels, the higher the pressure drop.
- (3)
- The HTC in IMCs increases with the increase in the number of transections, both at low mass flux and high mass flux. At low heat flux, IMCs have a larger heat transfer area and stable nucleation sites, which can generate more bubbles and rapidly detach from the wall, thus having a larger HTC than the RMC. While at high heat fluxes, IMCs have the presence of interconnected regions leading to smaller plugs and larger solid–liquid contact areas, and therefore have a higher HTC than RMCs.
- (4)
- At lower mass fluxes, with an increase in the heat flux, the J-factor of IMC-7 gradually diminishes. However, at higher heat fluxes, the J-factor of IMC-3 is notably better. For instance, at a heat flux of q = 90 W/cm2, the heat transfer performance factor of IMC-3 reaches 148.43%, 110.04%, and 116.92% of the RMC, IMC-5, and IMC-7. On the other hand, under higher mass fluxes and at q = 120 W/cm2, IMC-7 exhibits the best enhanced heat transfer performance. Its heat transfer performance factor is 129.37%, 120.594%, and 107.98% of the RMC, IMC-3, and IMC-5 respectively.
Author Contributions
Conceptualization, Y.L. and Z.C.; methodology, Y.L.; software, Y.L.; validation, Y.L., Z.C. and C.H.; data curation, Y.L.; writing—original draft preparation, Y.L.; writing—review and editing, Y.L.; visualization, Y.L. and Y.S.; supervision, Y.L., Z.C. and H.X.; funding acquisition, Z.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Hebei Provincial Natural Science Foundation, grant number E2021202125.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the value of further research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tuckerman, D.B.; Pease, R.F.W. High-performance heat sinking for VLSI. IEEE Electron Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Mudawar, I. Two-phase microchannel heat sinks theory, applications, and limitations. ASME J. Electr. Packag. 2011, 133, 041002. [Google Scholar] [CrossRef]
- Markal, B.; Aydin, O.; Avci, M. Effect of aspect ratio on saturated flow boiling in microchannels. Int. J. Heat Mass Transf. 2016, 93, 130–143. [Google Scholar] [CrossRef]
- Yang, S.; Li, J.; Cao, B.; Wu, Z.; Sheng, K. Investigation of Z-type manifold microchannel cooling for ultra-high heat flux dissipation in power electronic devices. Int. J. Heat Mass Transf. 2024, 218, 124792. [Google Scholar] [CrossRef]
- Cheng, P.; Wang, G.; Quan, X. Recent Work on Boiling and Condensation in Microchannels. J. Heat Transfer-Trans. ASME 2009, 131, 043211. [Google Scholar] [CrossRef]
- Kandlikar, S.G. History, Advances, and Challenges in Liquid Flow and Flow Boiling Heat Transfer in Microchannels: A Critical Review. J. Heat Transf. 2012, 134, 034001. [Google Scholar] [CrossRef]
- Bertsch, S.S.; Groll, E.A.; Garimella, S.V. Refrigerant flow boiling heat transfer in parallel microchannels as a function of local vapor quality. Int. J. Heat Mass Transf. 2008, 51, 4775–4787. [Google Scholar] [CrossRef]
- Guo, K.; Li, H.; Feng, Y.; Zhao, J.; Wang, T. Numerical Investigation on Single Bubble and Multiple Bubbles Growth and Heat Transfer During Flow Boiling in A Microchannel Using the VOSET Method. Microgravity Sci. Technol. 2019, 31, 381–393. [Google Scholar] [CrossRef]
- Xia, G.; Cheng, Y.; Cheng, L.; Li, Y. Heat Transfer Characteristics and Flow Visualization during Flow Boiling of Acetone in Semi-Open Multi-Microchannels. Heat Transf. Eng. 2018, 40, 1349–1362. [Google Scholar] [CrossRef]
- Gawali, D.B.S.; Swami, V.B.; Thakre, S.D. Theoretical and Experimental Investigation of Heat Transfer Characteristics through a Rectangular Microchannel Heat Sink. Int. J. Innov. Res. Sci. Eng. Technol. 2014, 3, 15631–15640. [Google Scholar] [CrossRef]
- Lv, Y.; Xia, G.; Cheng, L.; Ma, D. Experimental investigation into unstable two phase flow phenomena during flow boiling in multi-microchannels. Int. J. Therm. Sci. 2021, 166, 106985. [Google Scholar] [CrossRef]
- Jain, S.; Jayaramu, P.; Gedupudi, S. Modeling of pressure drop and heat transfer for flow boiling in a mini/micro-channel of rectangular cross-section. Int. J. Heat Mass Transf. 2019, 140, 1029–1054. [Google Scholar] [CrossRef]
- Hetsroni, G.; Mosyak, A.; Pogrebnyak, E.; Segal, Z. Periodic boiling in parallel micro-channels at low vapor quality. Int. J. Multiph. Flow 2006, 32, 1141–1159. [Google Scholar] [CrossRef]
- Chung, J.N.; Na, Y.W. A Numerical Simulation of Two-Phase Flow Instabilities in a Trapezoidal Microchannel. Front. Heat Mass Transf. 2018, 11, 1–14. [Google Scholar] [CrossRef]
- Wang, G.; Cheng, P.; Bergles, A.E. Effects of inlet/outlet configurations on flow boiling instability in parallel microchannels. Int. J. Heat Mass Transf. 2008, 51, 2267–2281. [Google Scholar] [CrossRef]
- Özdemir, M. A Review of Single-Phase and Two-Phase Pressure Drop Characteristics and Flow Boiling Instabilities in Microchannels. J. Therm. Eng. 2018, 4, 2451–2463. [Google Scholar] [CrossRef]
- Chen, S.; Chen, X.; Luo, G.; Zhu, K.; Chen, L.; Hou, Y. Flow boiling instability of liquid nitrogen in horizontal mini channels. Appl. Therm. Eng. 2018, 144, 812–824. [Google Scholar] [CrossRef]
- Huang, H.; Pan, L.-M.; Yan, R.-G. Flow characteristics and instability analysis of pressure drop in parallel multiple microchannels. Appl. Therm. Eng. 2018, 142, 184–193. [Google Scholar] [CrossRef]
- Fang, C.; David, M.; Rogacs, A.; Goodson, K. Volume of Fluid Simulation of Boiling Two-Phase Flow in a Vapor-Venting Microchannel. Front. Heat Mass Transf. 2010, 1, 1–11. [Google Scholar] [CrossRef]
- Duryodhan, V.S.; Singh, S.; Agrawal, A. Boiling flow through diverging microchannel. Sadhana 2013, 38, 1067–1082. [Google Scholar] [CrossRef][Green Version]
- Bogojevic, D.; Sefiane, K.; Walton, A.; Lin, H.; Cummins, G. Two-phase flow instabilities in a silicon microchannels heat sink. Int. J. Heat Fluid Flow 2009, 30, 854–867. [Google Scholar] [CrossRef]
- Qu, W.; Mudawar, I. Transport Phenomena in Two-Phase Micro-Channel Heat Sinks. J. Electron. Packag. 2004, 126, 213–224. [Google Scholar] [CrossRef]
- Jiang, L.; Koo, J.-M.; Wang, E.; Bari, A.; Cho, E.S.; Ong, W.; Prasher, R.S.; Maveety, J.; Kim, M.S.; Kenny, T.W.; et al. Cross-Linked Microchannels for VLSI Hotspot Cooling. ASME Int. Mech. Eng. Congr. Expo. 2002, 36428, 13–17. [Google Scholar]
- Xu, J.; Gan, Y.; Zhang, D.; Li, X. Microscale heat transfer enhancement using thermal boundary layer redeveloping concept. Int. J. Heat Mass Transf. 2005, 48, 1662–1674. [Google Scholar] [CrossRef]
- Chai, L.; Xia, G.; Zhou, M.; Li, J.; Qi, J. Optimum thermal design of interrupted microchannel heat sink with rectangular ribs in the transverse microchambers. Appl. Therm. Eng. 2013, 51, 880–889. [Google Scholar] [CrossRef]
- Chingulpitak, S.; Chimres, N.; Nilpueng, K.; Wongwises, S. Experimental and numerical investigations of heat transfer and flow characteristics of cross-cut heat sinks. Int. J. Heat Mass Transf. 2016, 102, 142–153. [Google Scholar] [CrossRef]
- Deng, D.; Xie, Y.; Huang, Q.; Wan, W. On the flow boiling enhancement in interconnected reentrant microchannels. Int. J. Heat Mass Transf. 2017, 108, 453–467. [Google Scholar] [CrossRef]
- Cheng, X.; Wu, H. Enhanced flow boiling performance in high-aspect-ratio groove-wall microchannels. Int. J. Heat Mass Transf. 2021, 164, 120468. [Google Scholar] [CrossRef]
- Deng, D.; Chen, L.; Wan, W.; Fu, T.; Huang, X. Flow boiling performance in pin fin-interconnected reentrant microchannels heat sink in different operational conditions. Appl. Therm. Eng. 2019, 150, 1260–1272. [Google Scholar] [CrossRef]
- Ma, J.; Li, W.; Tang, D.; Li, C. Effects of micro-slots in fully interconnected microchannels on flow boiling heat transfer. Appl. Therm. Eng. 2023, 231, 120703. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, Y.; Yuan, W.; Zeng, J.; Xie, Y. A comparative study of flow boiling performance in the interconnected microchannel net and rectangular microchannels. Int. J. Heat Mass Transf. 2016, 98, 814–823. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Mulbah, C.; Kang, C.; Mao, N.; Zhang, W.; Shaikh, A.R.; Teng, S. A review of VOF methods for simulating bubble dynamics. Prog. Nucl. Energy 2022, 154, 104478. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Lee, W.H. A pressure iteration scheme for two-phase flow modeling. In Multiphase Transport Fundamentals, Reactor Safety, Applications; Hemisphere Publishing: Washington, DC, USA, 1980; pp. 407–432. [Google Scholar]
- Hertz, H. On the evaporation of liquids, especially mercury, in vacuo. Ann. Phys. 1882, 17, 177. [Google Scholar] [CrossRef]
- Knudsen, M. Maximum rate of vaporization of mercury. Ann. Phys. 1915, 47, 697. [Google Scholar] [CrossRef]
- Qiu, J.; Zhou, J.; Zhao, Q.; Qin, H.; Chen, X. Numerical investigation of flow boiling characteristics in cobweb-shaped microchannel heat sink. Case Stud. Therm. Eng. 2021, 28, 101677. [Google Scholar] [CrossRef]
- Qi, D.; He, J.; Xu, Y.; Lin, M.; Wang, Q. Effect of rib diameter on flow boiling heat transfer with staggered rib arrays in a heat sink. Energy 2022, 239, 122323. [Google Scholar] [CrossRef]
- Deng, D.; Wan, W.; Tang, Y.; Shao, H.; Huang, Y. Experimental and numerical study of thermal enhancement in reentrant copper microchannels. Int. J. Heat Mass Transf. 2015, 91, 656–670. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).