Using Deep Learning to Detect Anomalies in On-Load Tap Changer Based on Vibro-Acoustic Signal Features
Abstract
1. Introduction
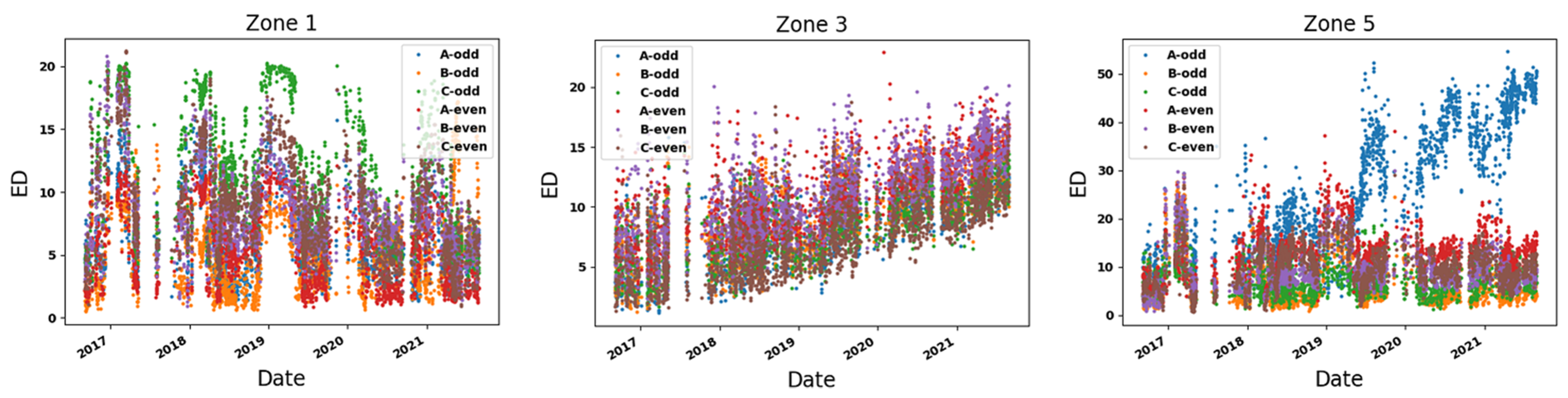
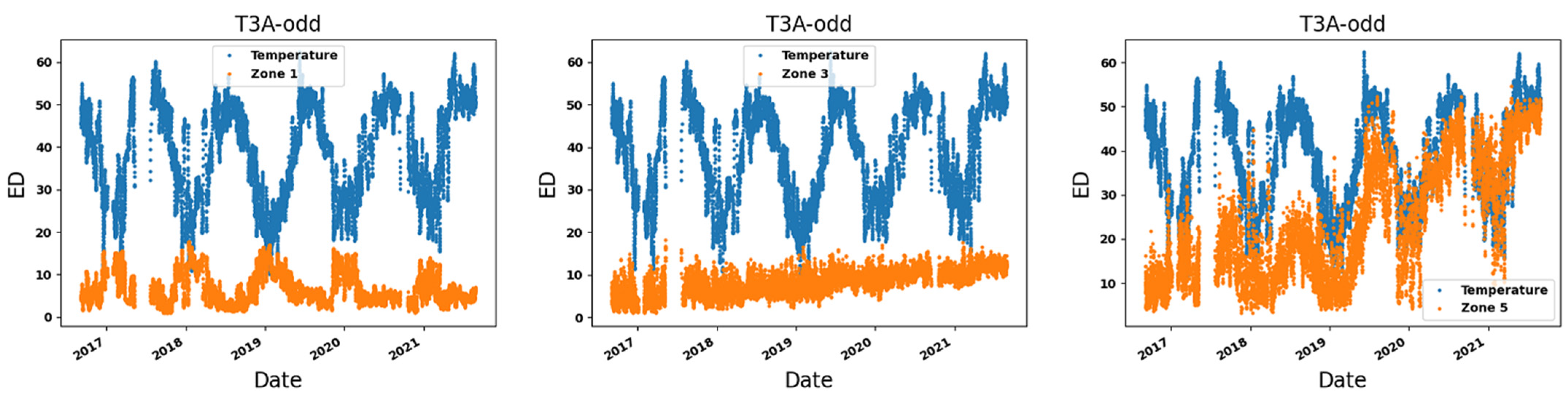
2. Data Collection, Pre-Processing, and Feature Extraction
3. The Underlying Concept
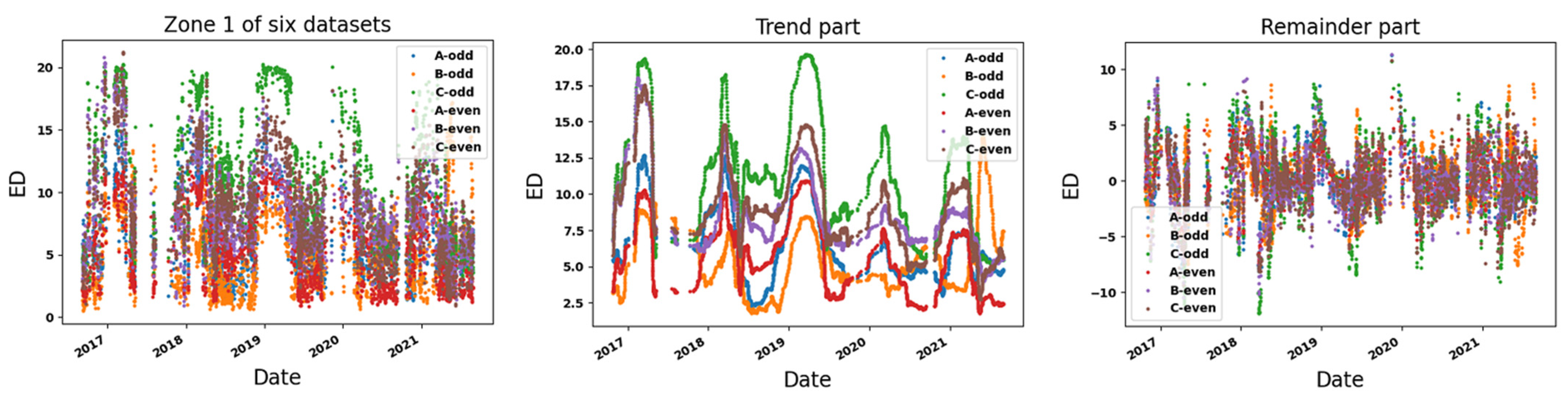
3.1. Time Series Decomposition
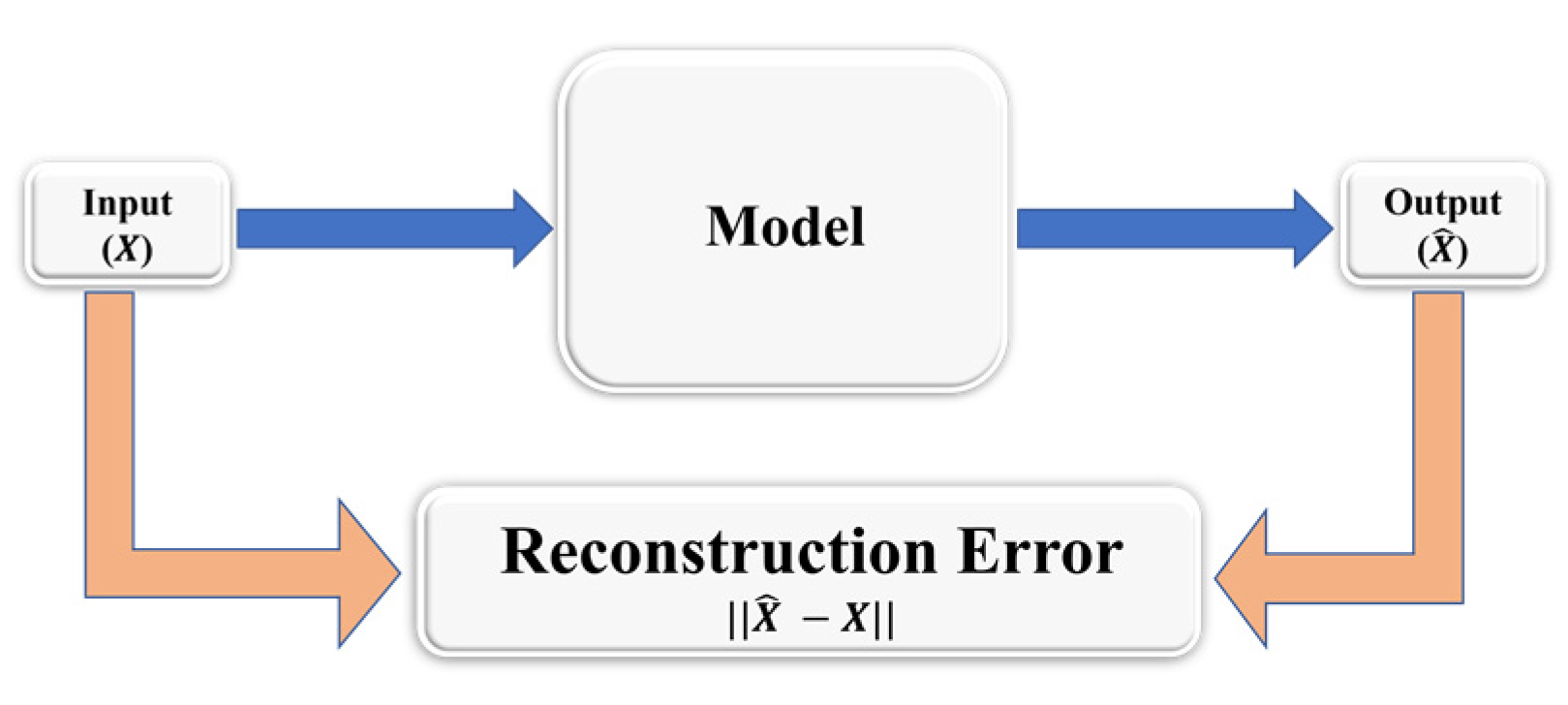
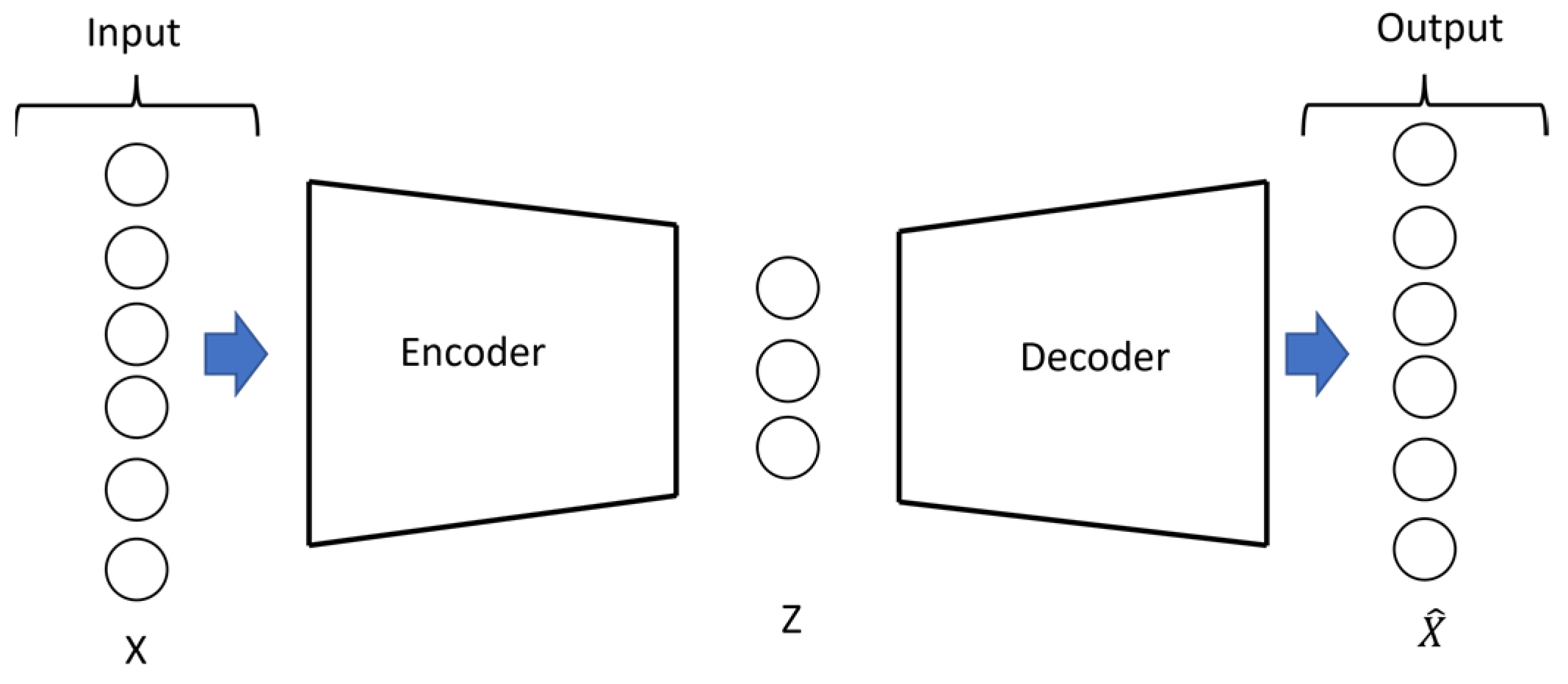
3.2. Deep Autoencoder-Based Anomaly Detection
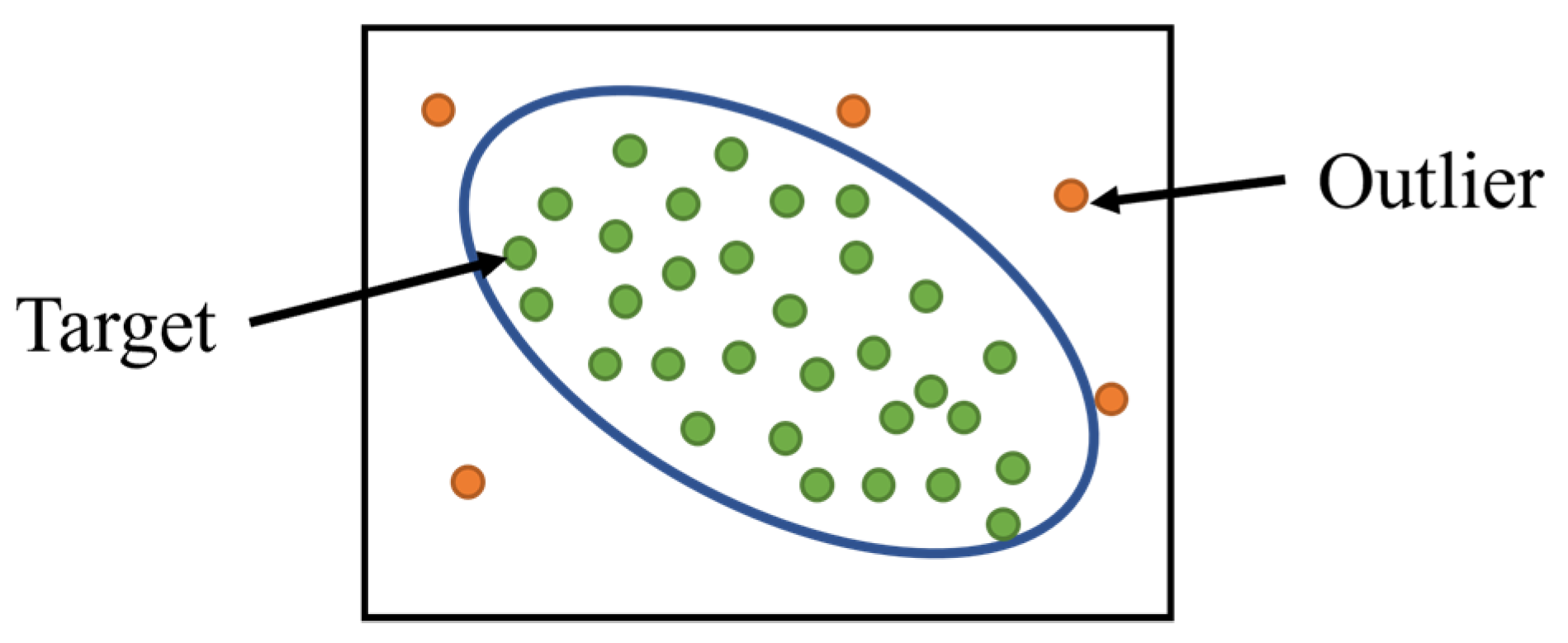
3.3. One-Class Classification
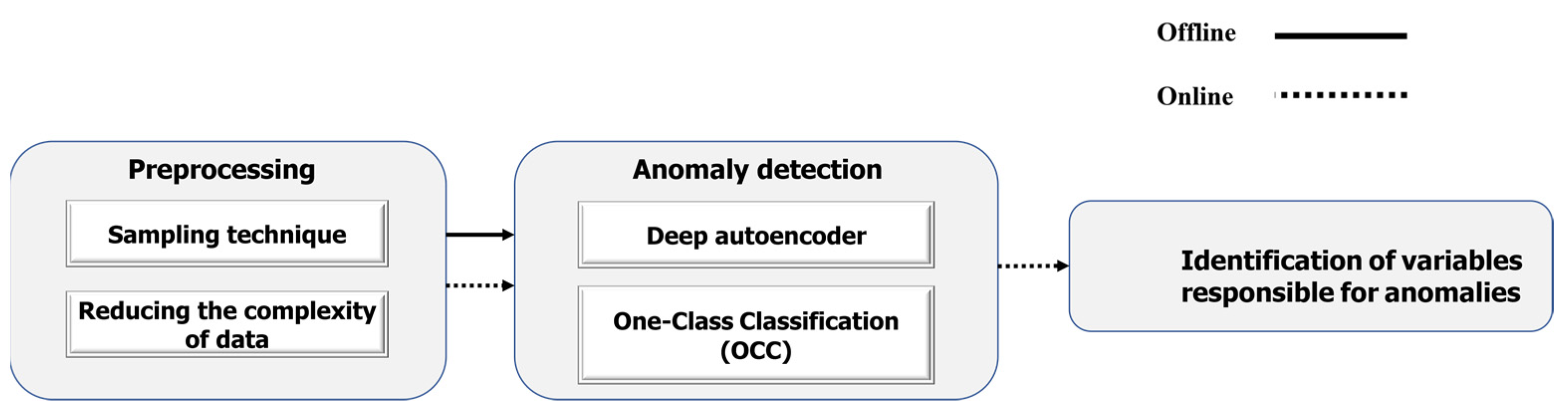
4. Methodology
4.1. Preprocessing
4.1.1. Sampling Method
4.1.2. Reducing the Complexity of Data
4.2. Anomaly Detection
4.2.1. Preprocessing
- Standardization: z-score function, presented in Equation (3), is used to standardize the time series data [41].
- Sliding window: A time series can be subdivided into several parts of the same size using the sliding window technique. In this technique, there are two indicators, including window size (W) and step size (s), which indicate the length of the window and the amount of stride in subsequent windows, respectively. In this work, a sliding window with s = 1, which causes the creation of overlapping windows, is applied to achieve a short time series (parts).
4.2.2. Offline Sector
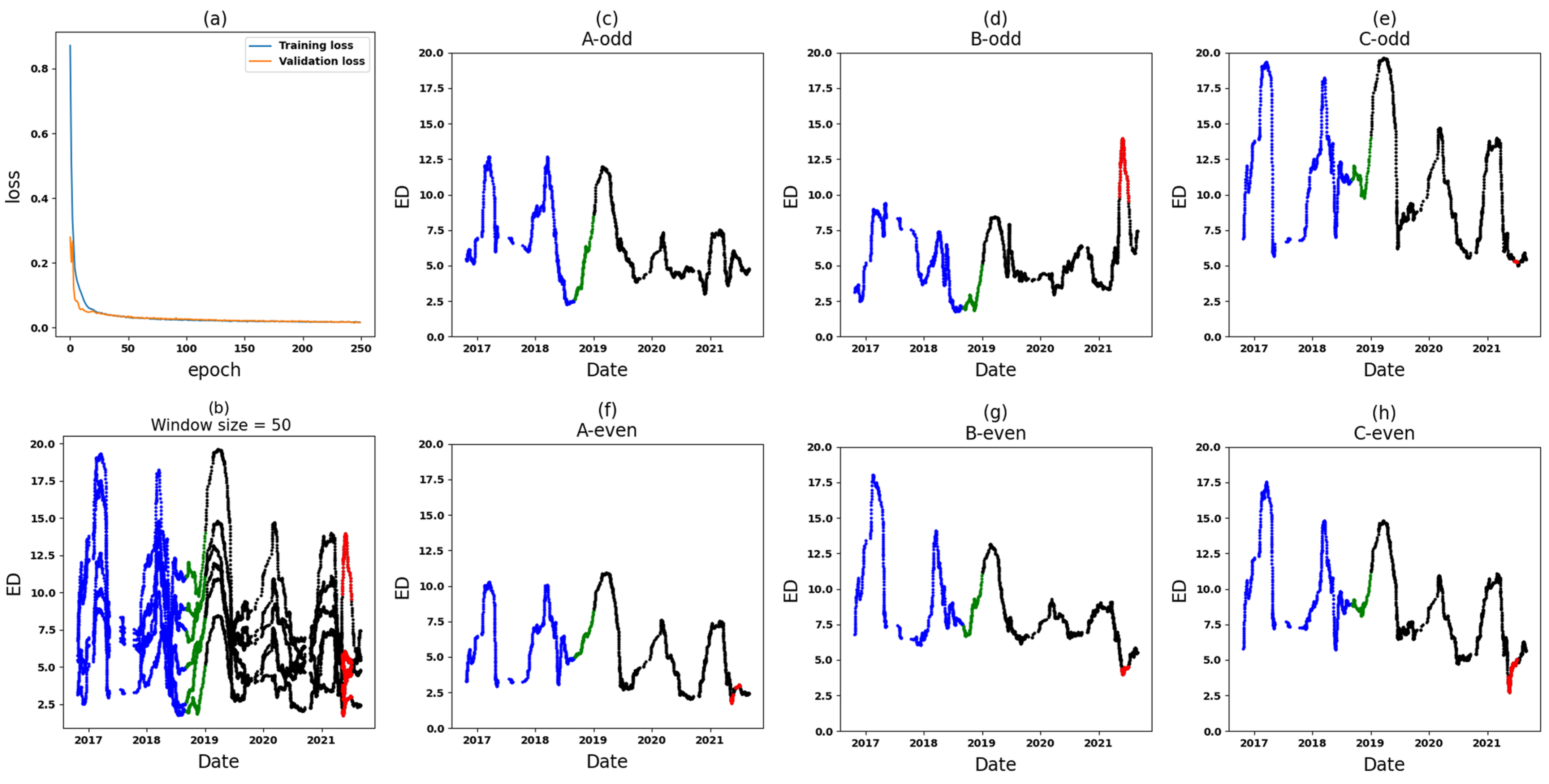
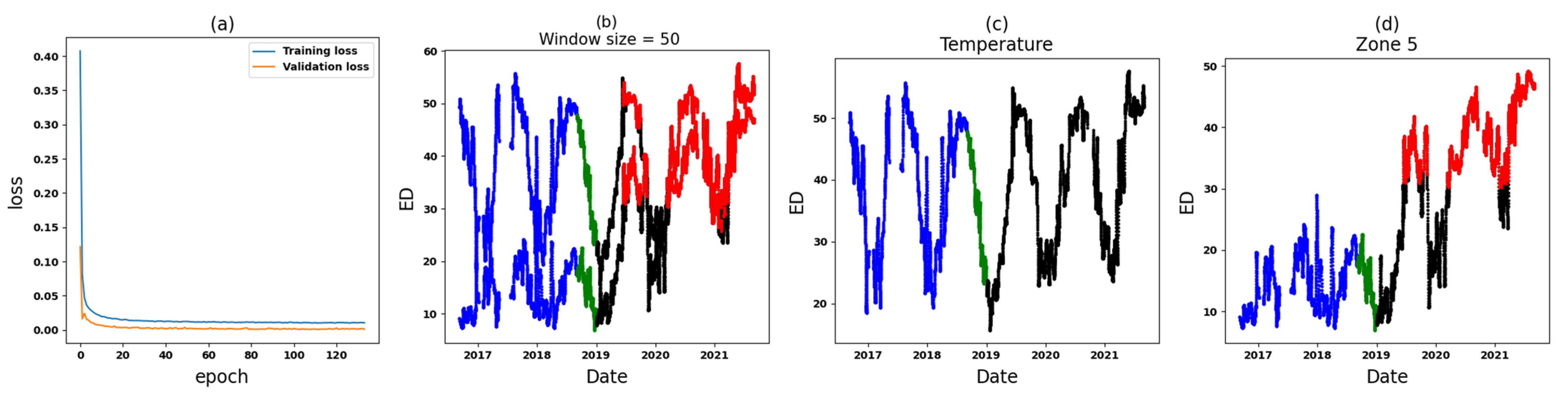
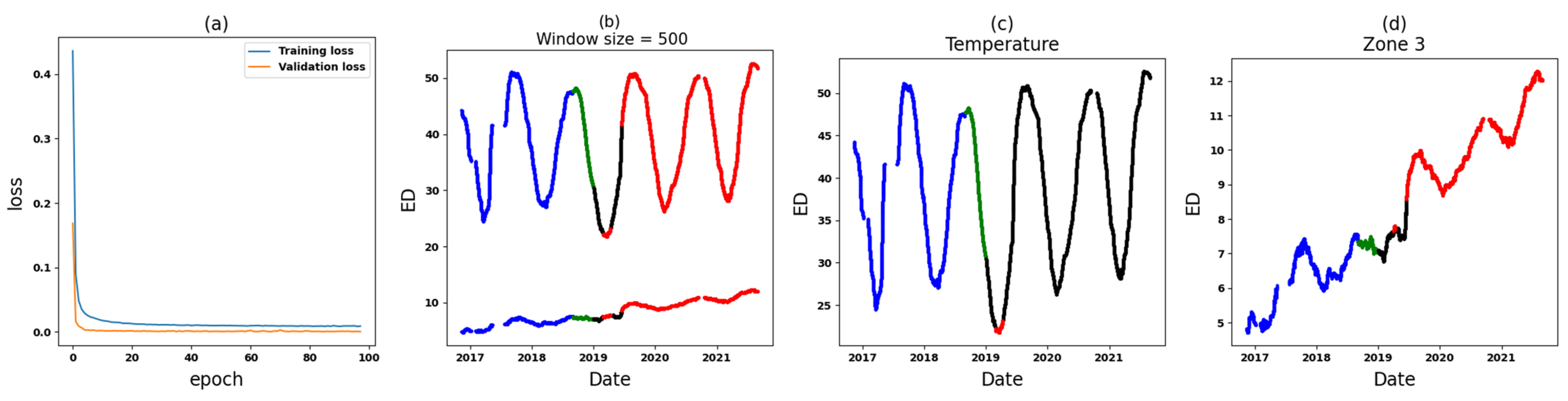
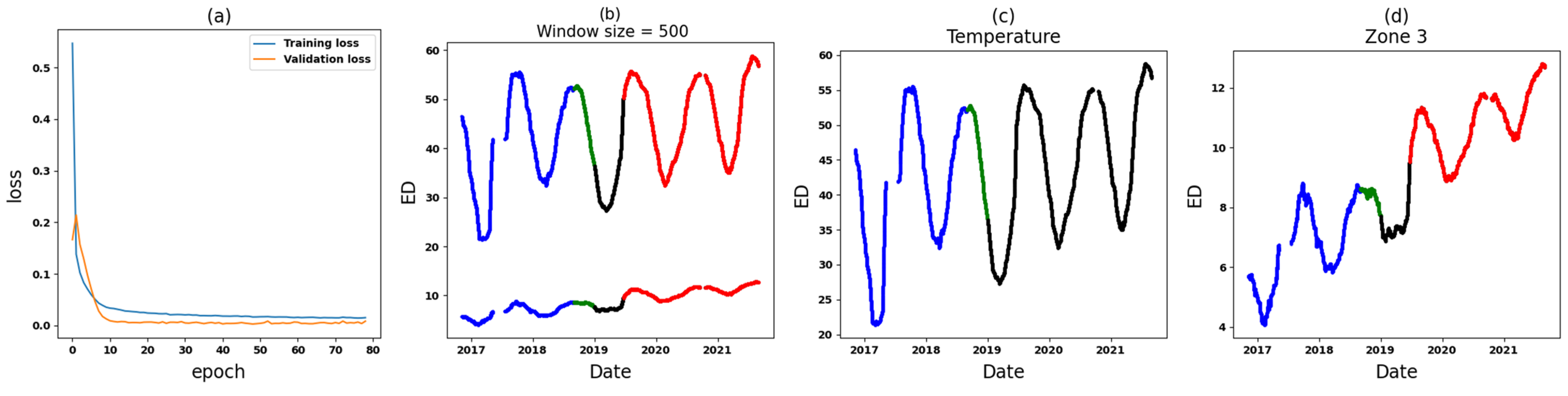
- Training the model: A convolutional autoencoder is used as a model to detect anomalies. In this model, the encoder and decoder use two layers. It is important to note that the model is trained using a set that contains normal data. Additionally, a validation set containing normal data is utilized to prevent overfitting and to determine when to halt the training process.
- Reconstruction errors are computed between the original (X) and reconstructed () data. MSE is then used to compute the reconstruction error.
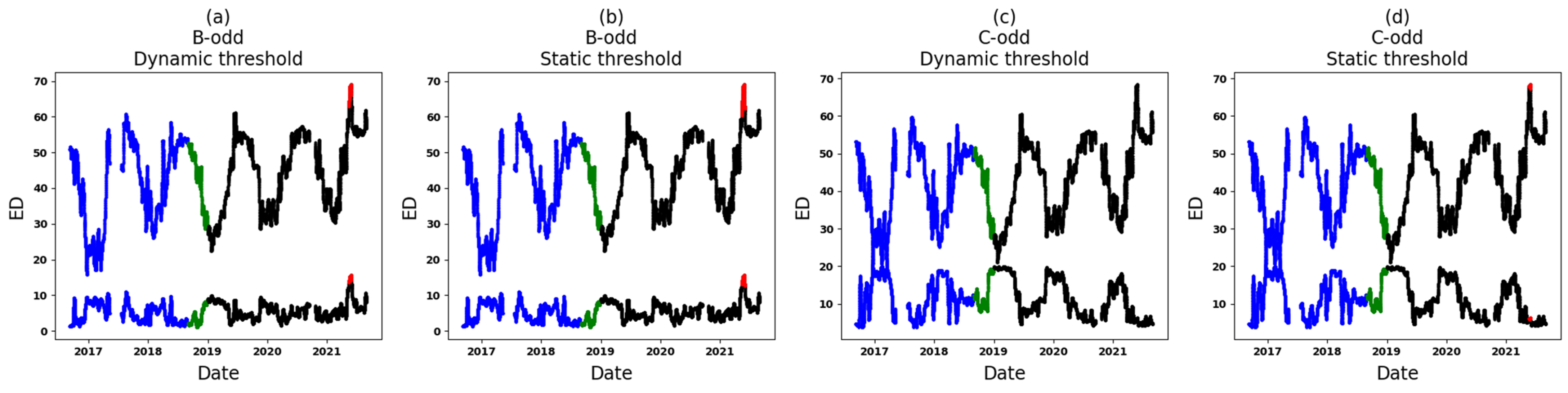
- The Application of One-Class Classification (extracting anomaly scores based on KDE and selecting a static threshold): During this stage, the KDE method is utilized and tailored to the reconstruction errors of the training set. Following this, the log-likelihood of every instance in both the training and validation sets is calculated. This reconstruction log-likelihood is used as the anomaly score in the anomaly detection model. As such, a high score indicates that the input is suitably reconstructed. The threshold is determined by considering the minimum anomaly score found within both the training and validation sets. It should be noted that the threshold is rounded down to the nearest whole number. This means that values such as 2.1 and 2.7 would be rounded down to 2.
4.2.3. Online Sector
4.3. Identification of Variables at the Origin of Anomalies
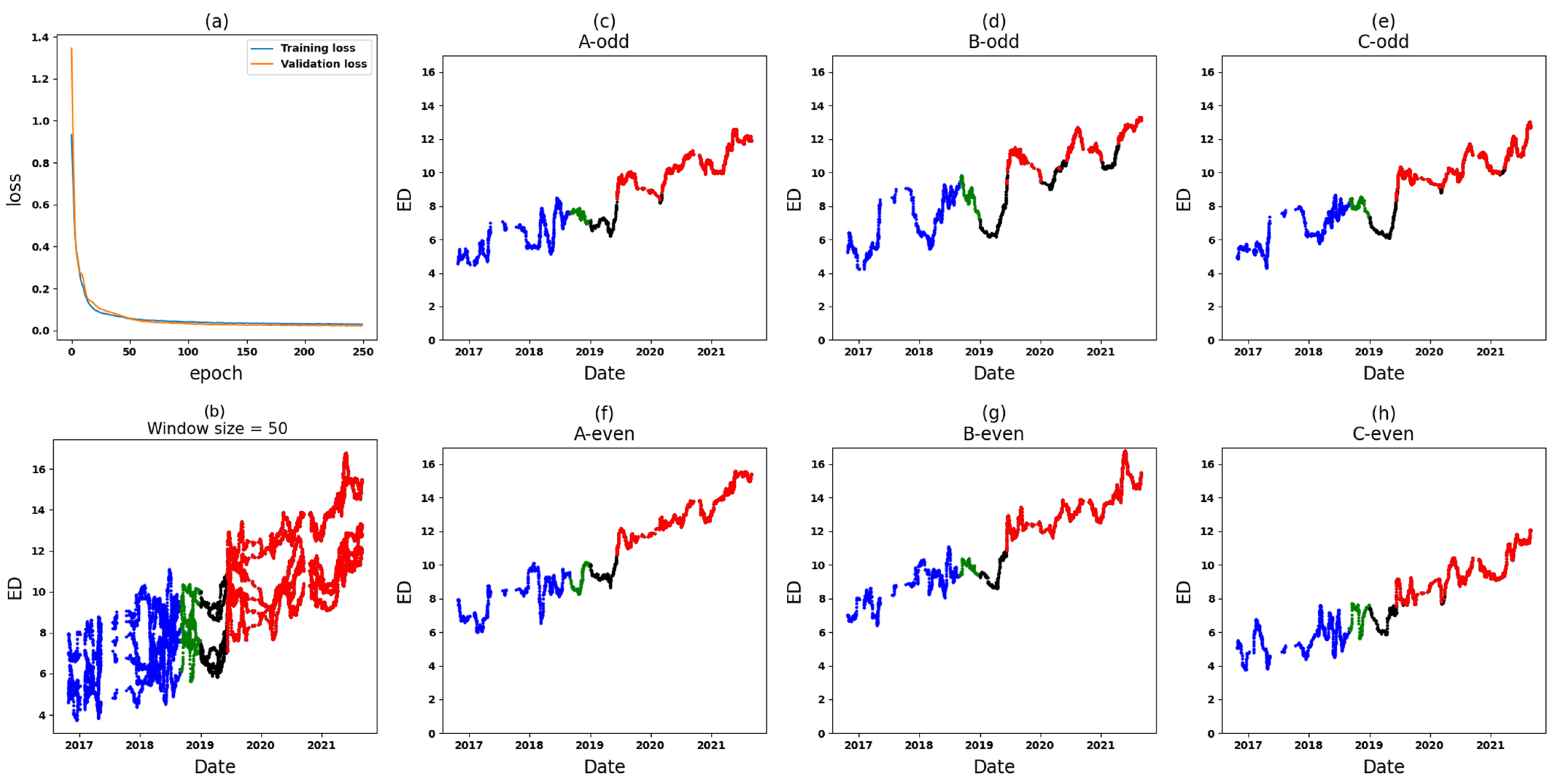
5. Results
5.1. Comparative Analysis
5.2. Individual Analysis of Each Dataset
6. Discussion
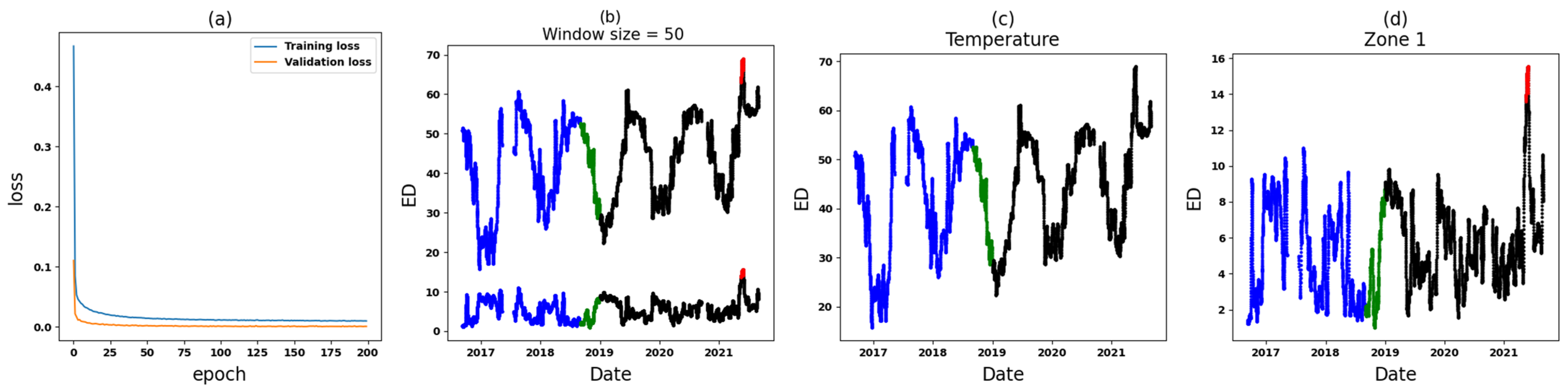
- Zone 1: In the comparative analysis, anomalies are identified in a specific segment of the test set (see Figure 13). Following this, Zone 1 of T3A-odd and Zone 1 of T3B-odd are individually scrutinized. Based on the outcomes of the individual analyses, anomalies attributed to sudden variations are found specifically in T3B-odd (see Figure 16). These anomalies continue for around 14 days, after which there are no further anomalies. Consequently, it can be inferred that there might not be a significant cause for concern or an important alarm.
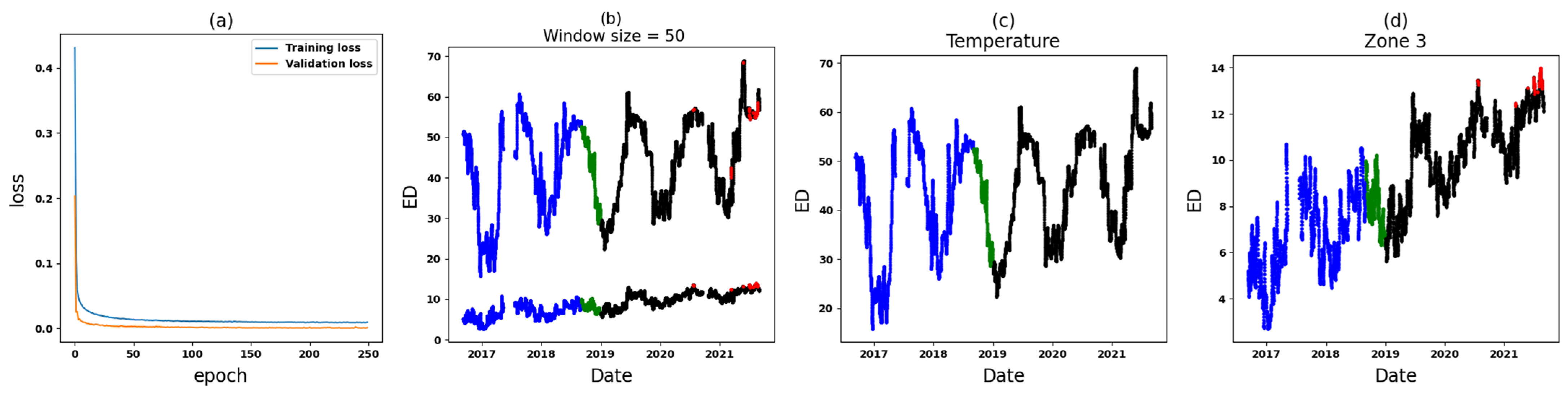
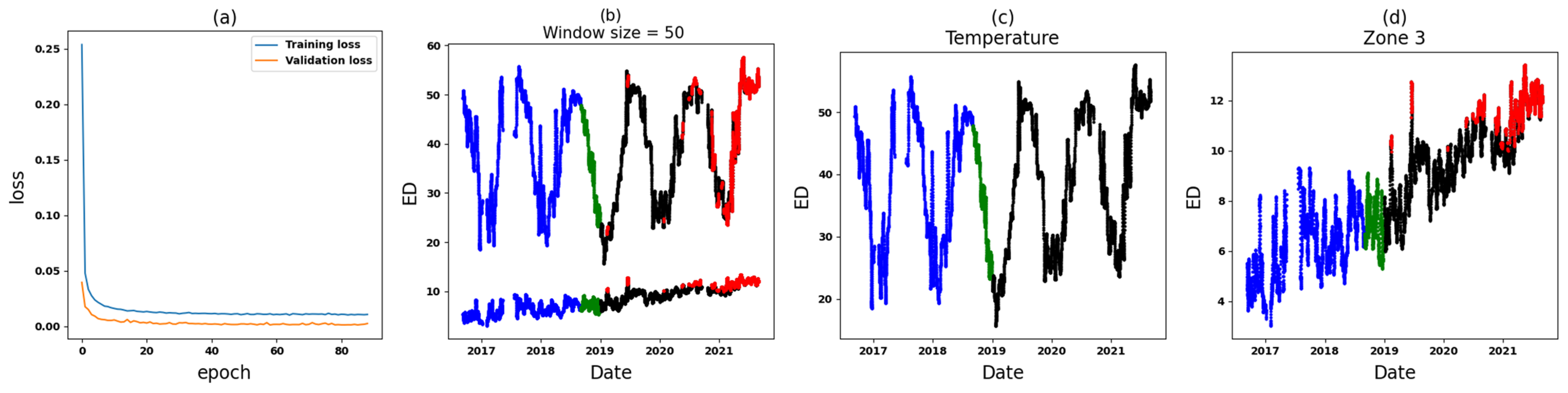
- Zone 3: In the comparative analysis, anomalies are observed spanning from 9 June 2019, until the end of September 2021 (see Figure 14). Notably, a crucial observation within this timeframe is that all input variables (Zone 3 in six datasets) are implicated as the cause of these anomalies, causing significant concern. To further understand the circumstances within this zone, Figure 17 and Figure 18 depict the results for Zone 3 of the T3B-odd and T3A-odd datasets, respectively, based on sudden variation. Additionally, Figure 20 and Figure 22 illustrate the results for Zone 3 of the T3A-odd and T3B-odd datasets, respectively, based on long-term changes. Upon examination of these figures, while some anomalies are identified based on sudden variations, it is evident that long-term changes are prevalent in this area. Consequently, the presence of persistent long-term changes raises an important alarm within this particular zone.
- Zone 5: In the comparative analysis, anomalies were consistently observed since 9 June 2019. Primarily, these anomalies are attributed to T3A-odd (refer to Figure 15). Upon conducting individual analyses of Zone 5 within both T3A-odd and T3B-odd datasets, continuous anomalies are detected solely in Zone 5 of dataset T3A-odd, indicating occurrences associated with both sudden variations and long-term changes. Notably, no anomalies were found in Zone 5 of the T3B-odd dataset. Consequently, these findings strongly suggest that significant alterations occurred specifically within Zone 5 of the T3A-odd dataset (see Figure 19 and Figure 21).
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rao, U.M.; Fofana, I.; Bétié, A.; Senoussaoui, M.; Brahami, M.; Briosso, E. Condition monitoring of in-service oil-filled transformers: Case studies and experience. IEEE Electr. Insul. Mag. 2019, 35, 33–42. [Google Scholar] [CrossRef]
- Wang, M.; Vandermaar, A.J.; Srivastava, K.D. Review of condition assessment of power transformers in service. IEEE Electr. Insul. Mag. 2002, 18, 12–25. [Google Scholar] [CrossRef]
- Ismail, F.B.; Mazwan, M.; Al-Faiz, H.; Marsadek, M.; Hasini, H.; Al-Bazi, A.; Yang Ghazali, Y.Z. An Offline and Online Approach to the OLTC Condition Monitoring: A Review. Energies 2022, 15, 6435. [Google Scholar] [CrossRef]
- Li, H.; Dou, L.; Li, S.; Kang, Y.; Yang, X.; Dong, H. Abnormal State Detection of OLTC Based on Improved Fuzzy C-means Clustering. Chin. J. Electr. Eng. 2023, 9, 129–141. [Google Scholar] [CrossRef]
- Duan, J.; Zhao, Q.; Zhu, L.; Zhang, J.; Hong, J. Time-dependent system reliability analysis for mechanical on-load tap-changer with multiple failure modes. Appl. Math. Model. 2024, 125, 164–186. [Google Scholar] [CrossRef]
- Yan, Y.; Qian, Y.; Ma, H.; Hu, C. Research on imbalanced data fault diagnosis of on-load tap changers based on IGWO-WELM. Math. Biosci. Eng. 2023, 20, 4877–4895. [Google Scholar] [CrossRef] [PubMed]
- Feizifar, B.; Müller, Z.; Fandi, G.; Usta, O. A Collective Condition Monitoring Algorithm for On-Load Tap-Changers. In Proceedings of the International Conference on Environment and Electrical Engineering and Industrial and Commercial Power Systems Europe, Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar]
- Liu, Z.; Xia, X.; Ji, S.; Shi, Y.; Zhang, F.; Fu, Y.; Jiang, Z. Fault diagnosis of OLTC based on time-frequency image analysis of vibration signal. In Proceedings of the Condition Monitoring and Diagnosis, Perth, WA, Australia, 23–26 September 2018; pp. 1–6. [Google Scholar]
- Zhang, C.; Ren, W.; Chen, Y.; Yang, X.; Jiang, D. Experimental investigation on electrical and mechanical vibration responses of diverter switches within OLTCs. Electr. Eng. 2023, 106, 407–417. [Google Scholar] [CrossRef]
- Seo, J.; Ma, H.; Saha, T.K. On Savitzky–Golay filtering for online condition monitoring of transformer on-load tap changer. IEEE Trans. Power Deliv. 2017, 33, 1689–1698. [Google Scholar] [CrossRef]
- Rivas, E.; Burgos, J.C.; Garcia-Prada, J.C. Condition assessment of power OLTC by vibration analysis using wavelet transform. IEEE Trans. Power Deliv. 2009, 24, 687–694. [Google Scholar] [CrossRef]
- Kang, P.; Birtwhistle, D. Characterisation of vibration sigsnals using continuous wavelet transform for condition assessment of on-load tap-changers. Mech. Syst. Signal Process. 2003, 17, 561–577. [Google Scholar] [CrossRef]
- Rivas, E.; Burgos, J.C.; García-Prada, J.C. Vibration analysis using envelope wavelet for detecting faults in the OLTC tap selector. IEEE Trans. Power Deliv. 2010, 25, 1629–1636. [Google Scholar] [CrossRef]
- Kang, P.; Birtwhistle, D. Condition assessment of power transformer on-load tap-changers using wavelet analysis. IEEE Trans. Power Deliv. 2001, 16, 394–400. [Google Scholar] [CrossRef]
- Seo, J.; Ma, H.; Saha, T.K. Vibration measurement and signal processing for condition assessment of OLTC of transformer. In Proceedings of the IEEE PES Asia-Pacific Power and Energy Engineering Conference, Brisbane, QLD, Australia, 15–18 November 2015; pp. 1–5. [Google Scholar]
- Seo, J.; Ma, H.; Saha, T.K. Analysis of vibration signal for power transformer on-load tap changer (OLTC) condition monitoring. In Proceedings of the IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Huang, W.; Peng, C.; Jin, L.; Liu, J.; Cai, Y. Fault Diagnosis of On-load Tap-changer Based on Vibration Signal. OP Conf. Ser. Mater. Sci. Eng. 2019, 605, 012005. [Google Scholar] [CrossRef]
- Duan, X.; Zhao, T.; Li, T.; Liu, J.; Zou, L.; Zhang, L. Method for diagnosis of on--load tap changer based on wavelet theory and support vector machine. J. Eng. 2017, 2017, 2193–2197. [Google Scholar] [CrossRef]
- Dabaghi-Zarandi, F.; Behjat, V.; Gauvin, M.; Picher, P.; Ezzaidi, H.; Fofana, I. Power Transformers OLTC Condition Monitoring Based on Feature Extraction from Vibro-Acoustic Signals: Main Peaks and Euclidean Distance. Sensors 2023, 23, 7020. [Google Scholar] [CrossRef]
- Gauvin, M.; Picher, P.; Riendeau, S.; Léonard, F.; Rajotte, C. Field Experience with Tapchanger and Bushing Monitoring; CIGRE SC A: Kyoto, Japan, 2011. [Google Scholar]
- Picher, P.; Riendeau, S.; Gauvin, M.; Léonard, F.; Dupont, L.; Goulet, J.; Rajotte, C. New Technologies for Monitoring Transformer Tap-Changers and Bushings and Their Integration into a Modern IT Infrastructure; CIGRE: Paris, France, 2012. [Google Scholar]
- Abeywickrama, N.; Kouzmine, O.; Kornhuber, S.; Picher, P. Application of novel algorithms for continuous bushing and OLTC monitoring for increasing newtwork reliability. In Proceedings of the International Council on Large Electric systems (CIGRE), Paris, France, 24–29 August 2014; pp. 24–29. [Google Scholar]
- Li, Y.-L.; Jiang, J.-R. Anomaly detection for non-stationary and non-periodic univariate time series. In Proceedings of the IEEE Eurasia Conference on IOT, Communication and Engineering, Yunlin, Taiwan, 23–25 October 2020; pp. 177–179. [Google Scholar]
- Cheng, L.; Dong, G.; Ren, L.; Yang, R.; Liu, B.; Rong, Y.; Li, D. Anomaly detection and analysis based on deep autoencoder for the storage tank liquid level of oil depot. J. Phys. Conf. Ser. 2022, 2224, 012013. [Google Scholar] [CrossRef]
- Li, G.; Jung, J.J. Deep learning for anomaly detection in multivariate time series: Approaches, applications, and challenges. Inf. Fusion 2023, 91, 93–102. [Google Scholar] [CrossRef]
- Li, T.; Comer, M.L.; Delp, E.J.; Desai, S.R.; Mathieson, J.L.; Foster, R.H.; Chan, M.W. Anomaly scoring for prediction-based anomaly detection in time series. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–7. [Google Scholar]
- Chen, N.; Tu, H.; Duan, X.; Hu, L.; Guo, C. Semisupervised anomaly detection of multivariate time series based on a variational autoencoder. Appl. Intell. 2023, 53, 6074–6098. [Google Scholar] [CrossRef]
- Li, S.; Dou, L.; Li, H.; Li, Z.; Kang, Y. An Electromechanical Jointed Approach for Contact Pair Fault Diagnosis of Oil-Immersed On-Load Tap Changer. Electronics 2023, 12, 3573. [Google Scholar] [CrossRef]
- Cichoń, A.; Włodarz, M. OLTC Fault detection Based on Acoustic Emission and Supported by Machine Learning. Energies 2023, 17, 220. [Google Scholar] [CrossRef]
- Dokumentov, A.; Hyndman, R.J. STR: A seasonal-trend decomposition procedure based on regression. Monash Econom. Bus. Stat. Work. Pap. 2015, 13, 2015-13. [Google Scholar]
- Mishra, A.; Sriharsha, R.; Zhong, S. OnlineSTL: Scaling time series decomposition by 100x. arXiv 2021, arXiv:2107.09110. [Google Scholar] [CrossRef]
- Provotar, O.I.; Linder, Y.M.; Veres, M.M. Unsupervised anomaly detection in time series using lstm-based autoencoders. In Proceedings of the IEEE International Conference on Advanced Trends in Information Theory, Kyiv, Ukraine, 18–20 December 2019; pp. 513–517. [Google Scholar]
- Kim, S.; Jo, W.; Shon, T. APAD: Autoencoder-based payload anomaly detection for industrial IoE. Appl. Soft Comput. 2020, 88, 106017. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Tran, K.P.; Thomassey, S.; Hamad, M. Forecasting and Anomaly Detection approaches using LSTM and LSTM Autoencoder techniques with the applications in supply chain management. Int. J. Inf. Manag. 2021, 57, 102282. [Google Scholar] [CrossRef]
- An, J.; Cho, S. Variational autoencoder based anomaly detection using reconstruction probability. Spec. Lect. IE 2015, 2, 1–18. [Google Scholar]
- Gamboa, J.C.B. Deep learning for time-series analysis. arXiv 2017, arXiv:1701.01887. [Google Scholar]
- Perera, P.; Oza, P.; Patel, V.M. One-class classification: A survey. arXiv 2021, arXiv:2101.03064. [Google Scholar]
- Cao, V.L.; Nicolau, M.; McDermott, J. One-class classification for anomaly detection with kernel density estimation and genetic programming. In Proceedings of the Genetic Programming, Porto, Portugal, 30 March–1 April 2016; pp. 3–18. [Google Scholar]
- Zhu, F.; Ye, N.; Yu, W.; Xu, S.; Li, G. Boundary detection and sample reduction for one-class support vector machines. Neurocomputing 2014, 123, 166–173. [Google Scholar] [CrossRef]
- Lang, C.I.; Sun, F.-K.; Lawler, B.; Dillon, J.; Al Dujaili, A.; Ruth, J.; Cardillo, P.; Alfred, P.; Bowers, A.; Mckiernan, A. One Class Process Anomaly Detection Using Kernel Density Estimation Methods. IEEE Trans. Semicond. Manuf. 2022, 35, 457–469. [Google Scholar] [CrossRef]
- Chen, H.; Liu, H.; Chu, X.; Liu, Q.; Xue, D. Anomaly detection and critical SCADA parameters identification for wind turbines based on LSTM-AE neural network. Renew. Energy 2021, 172, 829–840. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dabaghi-Zarandi, F.; Behjat, V.; Gauvin, M.; Picher, P.; Ezzaidi, H.; Fofana, I. Using Deep Learning to Detect Anomalies in On-Load Tap Changer Based on Vibro-Acoustic Signal Features. Energies 2024, 17, 1665. https://doi.org/10.3390/en17071665
Dabaghi-Zarandi F, Behjat V, Gauvin M, Picher P, Ezzaidi H, Fofana I. Using Deep Learning to Detect Anomalies in On-Load Tap Changer Based on Vibro-Acoustic Signal Features. Energies. 2024; 17(7):1665. https://doi.org/10.3390/en17071665
Chicago/Turabian StyleDabaghi-Zarandi, Fataneh, Vahid Behjat, Michel Gauvin, Patrick Picher, Hassan Ezzaidi, and Issouf Fofana. 2024. "Using Deep Learning to Detect Anomalies in On-Load Tap Changer Based on Vibro-Acoustic Signal Features" Energies 17, no. 7: 1665. https://doi.org/10.3390/en17071665
APA StyleDabaghi-Zarandi, F., Behjat, V., Gauvin, M., Picher, P., Ezzaidi, H., & Fofana, I. (2024). Using Deep Learning to Detect Anomalies in On-Load Tap Changer Based on Vibro-Acoustic Signal Features. Energies, 17(7), 1665. https://doi.org/10.3390/en17071665







