Preventive-Security-Constrained Optimal Power Flow Model Considering IPFC Control Modes
Abstract
1. Introduction
- (1)
- A PSCOPF model considering IPFC control modes is established to fully utilize IPFC control potential, improving the economy and security of the system. IPFC control modes affect power flow distribution after contingencies and control characteristics under different control modes are analyzed, which are then employed as constraints of the optimization model. Economy and security margin are taken as the multi-objective function in the optimization, and the preventive-security-constrained technique is involved in realizing the optimal selection of IPFC control modes and control parameters in advance.
- (2)
- The corresponding method to solve the proposed model is deduced. Iterative schemes of converter output voltages and equivalent injected power for different IPFC control modes are derived respectively, and the power and voltages required in the proposed model can then be obtained. The calculated power and voltages in the objective function and constraints are further used to obtain the optimal result of the proposed model.
- (3)
- Advantages of the proposed model are proved in the case study through comparison with the original system, with the conventional model, and with optimization not considering IPFC control modes. Numerical results show that the optimal solution of the proposed model can decrease operation costs, improve voltage stability, and eliminate the risk of overload.
2. PSCOPF Model Considering IPFC Control Modes
2.1. Objective Function
- (1)
- Economy Function
- (2)
- Security Function
2.2. Constraints
- (1)
- Equality Constraints
- (2)
- Inequality Constraints
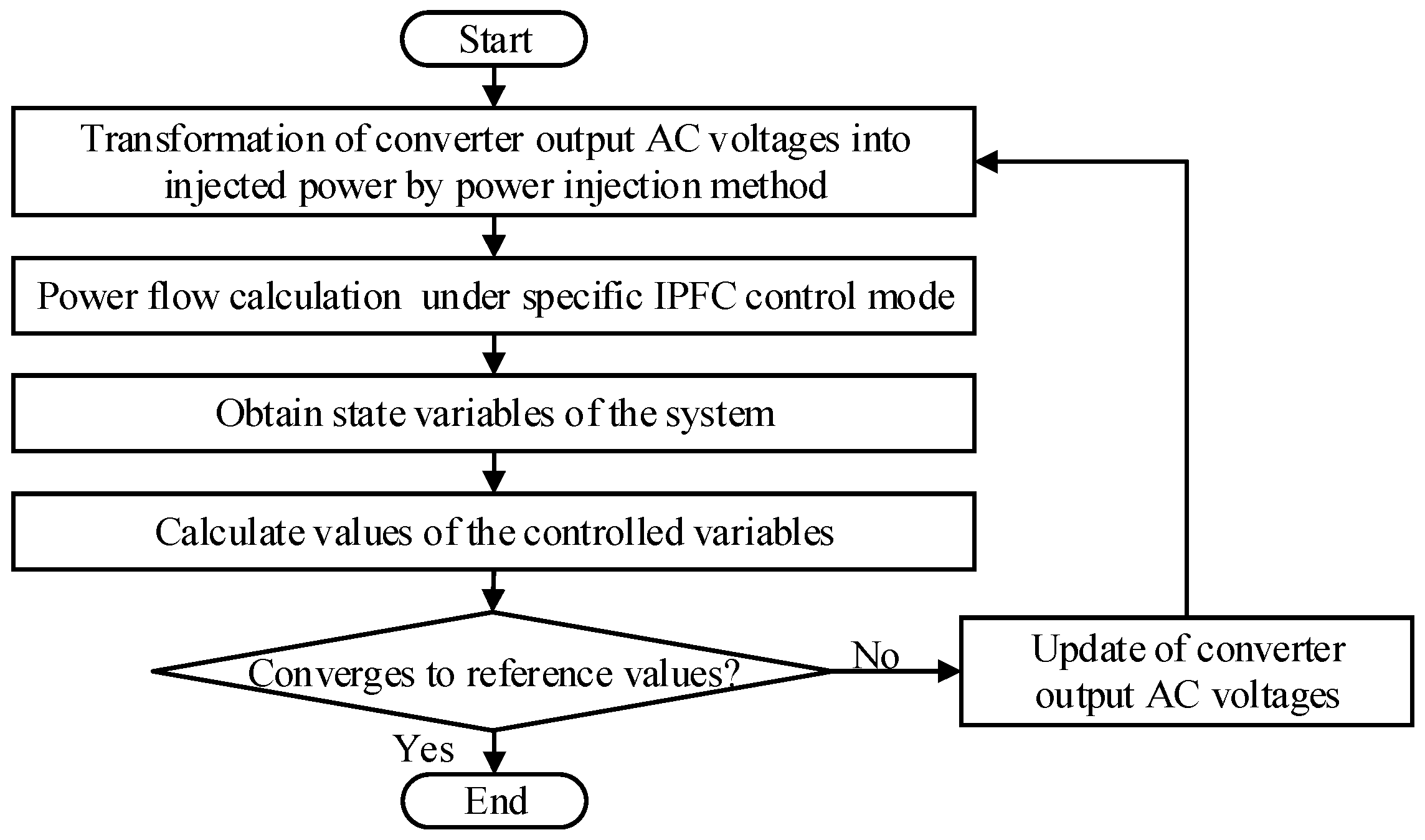
3. Solution Method for the PSCOPF Model Considering IPFC Control Modes
3.1. Framework of the Solution Method
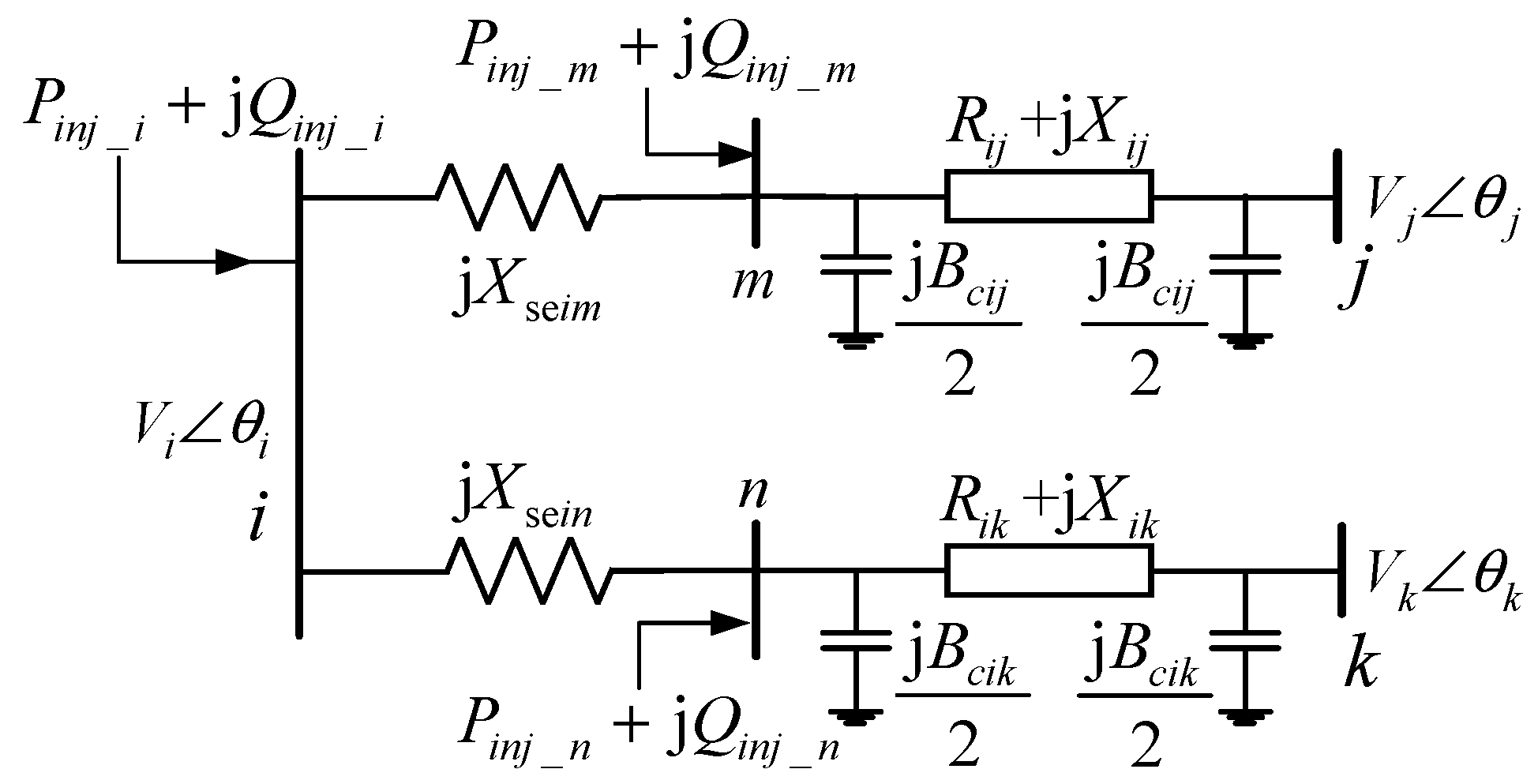
3.2. Power Flow Calculation in the PSCOPF Model Solution Process
- (1)
- Iterative Updates of Series Output Voltages for the Master Converter
- (2)
- Iterative Updates of Series Output Voltages for the Slave Converter
4. Case Studies
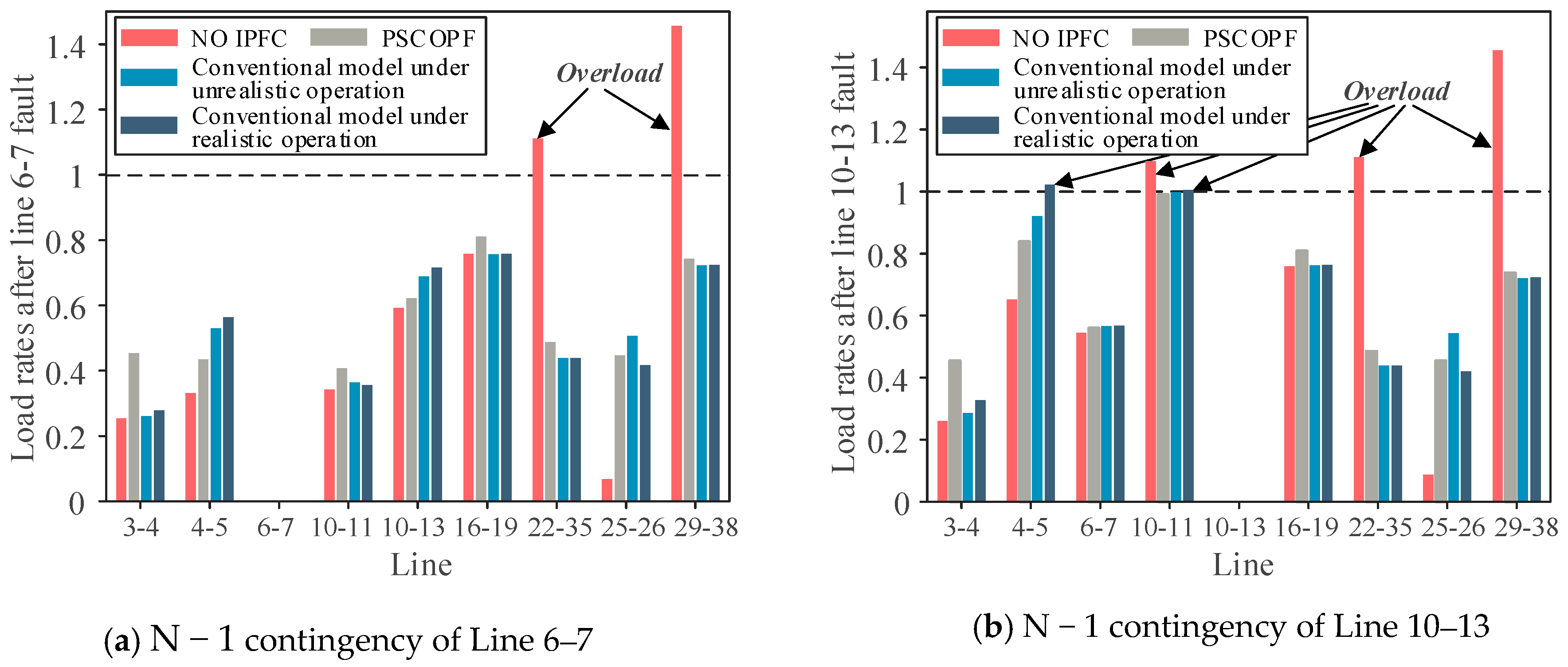
4.1. Optimization Results of the PSCOPF Model Considering IPFC Control Modes
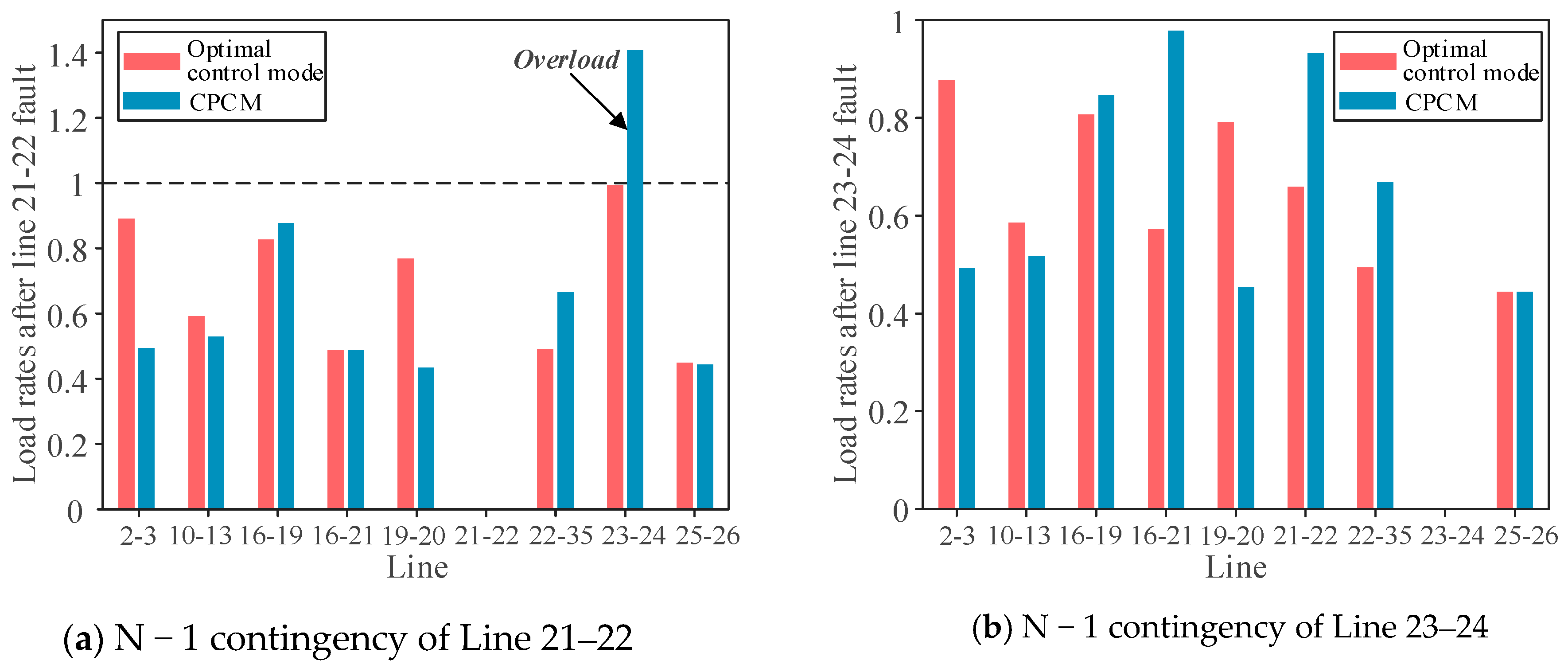
4.2. Comparison with a Fixed IPFC Control Mode
5. Future Research
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bavafa, F.; Niknam, T.; Azizipanah-Abarghooee, R.; Terzija, V. A New Biobjective Probabilistic Risk-Based Wind-Thermal Unit Commitment Using Heuristic Techniques. IEEE Trans. Ind. Inform. 2017, 13, 115–124. [Google Scholar] [CrossRef]
- Claeys, S.; Deconinck, G.; Geth, F. Voltage-dependent Load Models in Unbalanced Optimal Power Flow Using Power Cones. IEEE Trans. Smart Grid 2021, 12, 2890–2902. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, J. ATC Determination with FACTS Devices Using PTDFs Approach for Multi-transactions in Competitive Electricity Markets. Int. J. Electr. Power Energy Syst. 2013, 44, 308–317. [Google Scholar] [CrossRef]
- Jiang, S.; Gole, A.M.; Annakkage, U.D.; Jacobson, D.A. Damping Performance Analysis of IPFC and UPFC Controllers Using Validated Small-signal Models. IEEE Trans. Power Deliv. 2011, 26, 446–454. [Google Scholar] [CrossRef]
- Azbe, V.; Mihalic, R. The Control Strategy for an IPFC Based on the Energy Function. IEEE Trans. Power Syst. 2008, 3, 1662–1669. [Google Scholar] [CrossRef]
- Eremia, M.; Liu, C.C.; Edris, A.A. Interline Power Flow Controller (IPFC). In Advanced Solutions in Power Systems: HVDC, FACTS, and Artificial Intelligence; John Wiley & Sons: Hoboken, NJ, USA, 2016; pp. 638–640. [Google Scholar]
- Moghadasi, S.; Kazemi, A.; Firuzabad, M.F.; Edris, A. Composite System Reliability Assessment Incorporating an Interline Power-flow Controller. IEEE Trans. Power Deliv. 2008, 23, 1191–1199. [Google Scholar] [CrossRef]
- Jiang, X.; Chow, J.H.; Edris, A.; Fardanesh, B.; Uzunovic, E. Transfer Path Stability Enhancement by Voltage-sourced Converter-based FACTS Controllers. IEEE Trans. Power Deliv. 2010, 25, 1019–1025. [Google Scholar] [CrossRef]
- Mishra, A.; Kumar, G.V.N. Congestion Management of Power System with Interline Power Flow Controller Using Disparity Line Utilization Factor and Multi-objective Differential Evolution. CSEE J. Power Energy Syst. 2015, 1, 76–85. [Google Scholar] [CrossRef]
- Soofi, A.F.; Manshadi, S.D.; Liu, G.; Dai, R. A SOCP Relaxation for Cycle Constraints in the Optimal Power Flow Problem. IEEE Trans. Smart Grid 2021, 12, 1663–1673. [Google Scholar] [CrossRef]
- Vijay, K.Y.N.; Sivanagaraju, S.; Suresh, C.V. Analyzing the Effect of Dynamic Loads on Economic Dispatch in the Presence of Interline Power Flow Controller Using Modified BAT Algorithm. J. Electr. Syst. Inf. Technol. 2016, 3, 45–67. [Google Scholar] [CrossRef]
- Rostami, M.; Lotfifard, S. Optimal Remedial Actions in Power Systems Considering Wind Farm Grid Codes and UPFC. IEEE Trans. Ind. Inform. 2020, 16, 7264–7274. [Google Scholar] [CrossRef]
- Gong, L.; Wang, C.H.; Zhang, C.X.; Fu, Y. High-Performance Computing Based Fully Parallel Security-Constrained Unit Commitment with Dispatchable Transmission Network. IEEE Trans. Power Syst. 2019, 34, 931–941. [Google Scholar] [CrossRef]
- Yan, M.; Shahidehpour, M.; Paaso, A.; Zhang, L.; Alabdulwahab, A.; Abusorrah, A. A Convex Three-Stage SCOPF Approach to Power System Flexibility with Unified Power Flow Controllers. IEEE Trans. Power Syst. 2021, 36, 1947–1960. [Google Scholar] [CrossRef]
- Dawn, S.; Kumar, T.P.; Kumar, G.A.; Panda, R. An Approach for System Risk Assessment and Mitigation by Optimal Operation of Wind Farm and FACTS Devices in a Centralized Competitive Power Market. IEEE Trans. Sustain. Energy 2019, 10, 1054–1065. [Google Scholar] [CrossRef]
- Liu, B.; Yang, Q.; Zhang, H.; Wu, H. An Interior-point Solver for AC Optimal Power Flow Considering Variable Impedance-based FACTS Devices. IEEE Access 2021, 9, 154460–154470. [Google Scholar] [CrossRef]
- Wang, L.; Li, H.; Wu, C. Stability Analysis of an Integrated Offshore Wind and Seashore Wave Farm Fed to a Power Grid Using a Unified Power Flow Controller. IEEE Trans. Power Syst. 2013, 28, 2211–2221. [Google Scholar] [CrossRef]
- Park, B.; DeMarco, C.L. Advanced Modeling of DERs and UPFC Devices with Sparse Tableau Formulation for ACOPF. Electr. Power Syst. Res. 2019, 174, 105870. [Google Scholar] [CrossRef]
- Hussein, M.E.; Rabea, F.; Kamel, S.; Oda, E.S. Effective Modeling of OUPFC Into Newton-Raphson Power Flow Considering Multi-Control Modes and Operating Constraints. IEEE Access 2021, 9, 129394–129406. [Google Scholar] [CrossRef]
- Bhowmick, S.; Das, B.; Kumar, N. An Advanced IPFC Model to Reuse Newton Power Flow Codes. IEEE Trans. Power Syst. 2009, 24, 525–532. [Google Scholar] [CrossRef]
- Ding, T.; Bo, R.; Li, F.; Sun, H. Optimal Power Flow with the Consideration of Flexible Transmission Line Impedance. IEEE Trans. Power Syst. 2016, 31, 1655–1656. [Google Scholar] [CrossRef]
- Galvani, S.; Hagh, M.T.; Sharifian, M.B.B.; Mohammadi-Ivatloo, B. Multiobjective Predictability-Based Optimal Placement and Parameters Setting of UPFC in Wind Power Included Power Systems. IEEE Trans. Ind. Inform. 2019, 15, 878–888. [Google Scholar] [CrossRef]
- Singh, P.; Senroy, N.; Tiwari, R. Guaranteed Convergence Embedded System for SSSC and IPFC. IEEE Trans. Power Syst. 2021, 36, 2725–2728. [Google Scholar] [CrossRef]
- Naveen Kumar, G.; Surya Kalavathi, M. Cat Swarm Optimization for Optimal Placement of Multiple UPFC’s in Voltage Stability Enhancement Under Contingency. Int. J. Electr. Power Energy Syst. 2014, 57, 97–104. [Google Scholar] [CrossRef]
- Hou, Q.C.; Zhang, N.; Kirschen, D.S.; Du, E.; Cheng, Y.H.; Kang, C.Q. Sparse Oblique Decision Tree for Power System Security Rules Extraction and Embedding. IEEE Trans. Power Syst. 2021, 36, 1605–1615. [Google Scholar] [CrossRef]
- Padullaparti, H.V.; Nguyen, Q.H.; Santoso, S. Optimal Placement and Dispatch of LV-SVCs to Improve Distribution Circuit Performance. IEEE Trans. Power Syst. 2019, 34, 2892–2900. [Google Scholar] [CrossRef]
- Mhanna, S.; Mancarella, P. An Exact Sequential Linear Programming Algorithm for the Optimal Power Flow Problem. IEEE Trans. Power Syst. 2022, 37, 666–679. [Google Scholar] [CrossRef]
- Thomas, J.J.; Grijalva, S. Flexible Security-constrained Optimal Power Flow. IEEE Trans. Power Syst. 2015, 30, 1195–1202. [Google Scholar] [CrossRef]
- Wu, X.; Wang, R.; Wang, Y.; Wang, L. A Novel UPFC Model and its Convexification for Security-Constrained Economic Dispatch. IEEE Trans. Power Syst. 2022, 37, 4202–4213. [Google Scholar] [CrossRef]
- Arroyo, J.M.; Fernandez, F.J. Application of a Genetic Algorithm to N-k Power System Security Assessment. Int. J. Electr. Power Energy Syst. 2013, 49, 114–121. [Google Scholar] [CrossRef]
- Kessel, P.; Glavitsch, H. Estimating the Voltage Stability of a Power System. IEEE Trans. Power Deliv. 1986, 1, 346–354. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Lin, F.; Li, W.; Wang, L.Y.; Zhao, J. Incorporating Generator Equivalent Model into Voltage Stability Analysis. IEEE Trans. Power Syst. 2013, 28, 4857–4866. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Chen, C. A Novel Power Injection Model of IPFC for Power Flow Analysis Inclusive of Practical Constraints. IEEE Trans. Power Syst. 2006, 21, 1550–1556. [Google Scholar] [CrossRef]
- Wu, X.; Zhou, Z.Y.; Liu, G.; Qi, W.C.; Xie, Z.J. Preventive Security-constrained Optimal Power Flow Considering UPFC Control Modes. Energies 2017, 10, 1199. [Google Scholar] [CrossRef]
- Engelbrecht, A.P. Particle Swarm Optimization. In Computational Intelligence: An Introduction; John Wiley & Sons: Chichester, UK, 2007; pp. 289–314. [Google Scholar]
- Athay, T.; Podmore, R.; Virmani, S. A Practical Method for the Direct Analysis of Transient Stability. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 573–584. [Google Scholar]


| Parameters | PSCOPF Model | Conventional Model under Unrealistic Operation | Conventional Model under Realistic Operation | System without IPFC |
|---|---|---|---|---|
| Objective function value | 7.6793 × 104 | 7.7404 × 104 | 1.8264 × 107 | 3.4553 × 108 |
| Economy function reflecting operation cost | 4.7546 × 104 | 4.6786 × 104 | 4.8213 × 104 | 4.5613 × 104 |
| Security function about voltage stability index | 1.4624 | 1.5309 | 1.6770 | 1.5155 |
| Number of average overloaded lines (N − 1) | 0 | 0 | 0.1818 | 3.4545 |
| Parameters | PSCOPF Model Considering IPFC Control Modes | PSCOPF Model with a Fixed IPFC Control Mode |
|---|---|---|
| Objective function value | 7.6793 × 104 | 9.1656 × 106 |
| Control mode and corresponding control target | ICCM, Zref = −0.03462 + j 0.01887p.u. | CPCM, Pmjref = 2.0745p.u., Qmjref = 1.3372p.u. |
| Control target of the slave converter | Pnkref = 0.7843p.u. | Pnkref = 2.0975p.u. |
| Economy function reflecting operation cost | 4.7546 × 104 | 4.5192 × 104 |
| Voltage stability index of the security function | 1.4624 | 1.4765 |
| Number of average overloaded lines (N − 1) | 0 | 0.0909 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, H.; Hu, C.; Wu, X. Preventive-Security-Constrained Optimal Power Flow Model Considering IPFC Control Modes. Energies 2024, 17, 1660. https://doi.org/10.3390/en17071660
Cai H, Hu C, Wu X. Preventive-Security-Constrained Optimal Power Flow Model Considering IPFC Control Modes. Energies. 2024; 17(7):1660. https://doi.org/10.3390/en17071660
Chicago/Turabian StyleCai, Hui, Chunke Hu, and Xi Wu. 2024. "Preventive-Security-Constrained Optimal Power Flow Model Considering IPFC Control Modes" Energies 17, no. 7: 1660. https://doi.org/10.3390/en17071660
APA StyleCai, H., Hu, C., & Wu, X. (2024). Preventive-Security-Constrained Optimal Power Flow Model Considering IPFC Control Modes. Energies, 17(7), 1660. https://doi.org/10.3390/en17071660







