1. Introduction
Nowadays, the high levels of greenhouse gas emissions resulting in global warming are regarded as one of the major issues worldwide [
1]. Green hydrogen, produced through water electrolysis using renewable energy sources (RESs), has gained significant attention in recent years as a promising solution to address global energy and climate challenges. Its potential applications span across various sectors, including transportation, power generation, and industrial processes, making it a versatile and attractive energy carrier [
2]. However, despite the considerable progress made in the development of green hydrogen production technologies, its large-scale deployment still faces several barriers, primarily due to the intermittent nature of RESs and the high costs associated with electrolysis processes.
Among all RESs, the most used are photovoltaic (PV) and wind power generation, which mainly depend on weather conditions [
3]. Thus, the availability of electricity from RESs is uncertain, affecting both the economy and the safety of water electrolysis. On the one hand, a hydrogen production plant cannot work when the input power is unavailable, which will reduce the operating hours of the plant and increase total production costs [
4]. On the other hand, the direct use of fluctuating power from RESs will cause several problems such as crossover gas and electrolyzer degradation, challenging the normal operation of electrolysis [
5]. Therefore, it is necessary to overcome these issues related to the intermittent nature of RESs.
Water electrolysis is an electrochemical process that splits water into hydrogen and oxygen. Regarding water electrolysis technologies for hydrogen production, currently, there are three main methods available or under development: alkaline electrolysis, proton exchange membrane (PEM) electrolysis, and solid oxide electrolysis cells (SOECs). In this paper, we only focus on the first two as SOECs have not yet been commercialized, although individual companies are now aiming to bring them to market [
6]. Alkaline electrolysis is the most mature and commercial technology with over 100 years of history. It is highly durable, and already available at large scale, with relatively low capital cost [
7]. However, this conventional technology is not designed to be operated with fluctuating power sources, and it shows a very poor performance when the power supply is switched off [
5]. PEM electrolysis is relatively resistant to fluctuating power due to its fast response and flexible operation, which allows it to provide a service with a larger load range than alkaline electrolysis, especially in the low load range, and to take advantage of dynamic electricity prices [
8]. Moreover, PEM electrolysis shows less performance degradation when power interruption occurs [
5]. Thus, it is beneficial in operations with intermittent power sources like RESs. However, the high cost of precious metal electrode catalysts and the shorter lifetime of PEM electrolyzers hinder the wide deployment of this technology [
9].
Theoretically, the influence of RES power fluctuations on electrolyzers should be considered when modeling to avoid security risks. However, the existing literature usually ignores this issue to simplify the model [
7], or just advocates for PEM technology by highlighting the limits of alkaline technology without a specific techno-economic analysis [
10], leading to misestimation of the actual benefits brought by alkaline electrolysis [
11]. The authors in [
12] adopt the engineering model of an alkaline electrolyzer in a green hydrogen production system without any constraints for the uncertain input power. Few authors explicitly model the impacts of fluctuating power supply. In [
13], the limitation of alkaline technology is modeled as ramp-up constraints during the start-up period by setting the needed time for electrolyzers to be operational. However, the influence of uncertain power input on electrolyzers is ignored. In [
14], the authors compared the cost of an off-grid hydrogen production plant when using alkaline and PEM electrolyzers. The differences between alkaline and PEM technologies are considered but only in terms of economics, ignoring environmental and safety factors. In [
15], the low dynamic load range restriction is modeled for alkaline technology. The authors analyzed both the economic and environmental impacts of complementing green hydrogen production with grid electricity in an average pricing scheme. Therefore, how to model the fluctuations’ influences on electrolyzers is still a challenge.
Moreover, electricity pricing schemes are diverse according to the electricity market and the employed model. In the wholesale market, electricity prices are available 24 h ahead (“day-ahead prices”) and 1 h ahead (“real-time prices”). Some papers omit dynamic prices to facilitate calculation. For example, the authors in [
15] use the average electricity price to calculate hydrogen production cost, simplifying the optimization problem. Generally, a hydrogen production plant can reduce its operating cost by extending production capacity during periods of cheap electricity. In [
16], GAMS optimization is used based on day-ahead electricity prices to compare the electricity cost with different operation times only for PEM electrolysis. In [
17], yearly historical data are utilized to determine the electricity price at which the levelized cost becomes minimal. The authors in [
18] consider both flat-rate pricing schemes and real-time pricing schemes for grid-connected hydrogen production.
The levelized cost of hydrogen (LCOH) is usually used to analyze the economic performance of hydrogen production. The LCOH is a measure of the average net present cost of hydrogen production for a plant over its lifetime [
15]. It is used to account for all the capital and operating costs of producing hydrogen and to compare different methods on a consistent basis.
This paper aims to analyze the techno-economic benefits of complementing green hydrogen production with grid electricity. An evaluation model for LCOH is proposed, including the CO2 penalty, under a wholesale electricity market. The proposed model allows the hydrogen production plant to perform the following:
Determine the bidding process in the grid electricity market to reduce the LCOH.
Improve hydrogen productivity without significantly increasing CO2 emission levels.
Ensure the load of the electrolyzers meets the requirements of safe operation.
Different capital expenditures (CAPEX) and different operating expenses (OPEX) are evaluated in the proposed model. And the features of alkaline and PEM electrolysis are also considered in our analysis. Moreover, an optimal operation strategy is developed to solve this nonlinear evaluation model. It can calculate the optimal amount of grid electricity required in each time step to cover the intermittency of RESs.
The main contributions of this paper compared with the existing literature are as follows:
An evaluation model for LCOH is proposed, including CO2 emission costs in a wholesale electricity market. It considers both the economic and environmental impacts of grid-connected systems and can take advantage of dynamic electricity prices.
The influences of RES fluctuations on alkaline and PEM electrolyzers are considered. A minimum load restriction is required to avoid explosion due to high crossover gas concentrations.
A novel operation strategy for hydrogen production plants is developed to determine optimal bidding in the grid electricity market to minimize the LCOH. It can simplify the above optimization problem and solve it without any complex algorithms.
Some recent research also focuses on grid-connected hydrogen production systems. In [
19], the authors aimed to smooth the wind farms’ output fluctuation to produce hydrogen constantly with the grid-connected system, but they ignored the characteristics of electrolyzers. The evaluation model for the LCOH with CO
2 emissions and a low load range restriction is applied in [
15] as well. However, it calculates the LCOH with the average electricity price, ignoring the advantages brought by dynamic electricity prices. The wholesale electricity market is considered in [
17,
18]. However, in [
17], it only focuses on transforming grid electricity into hydrogen, excluding RESs. The CO
2 penalty is not discussed in [
18], and it requires the prediction of hydrogen production demand and assumes that hydrogen plants do not produce more than the forecasted demand. To the best of the authors’ knowledge, an evaluation model for the LCOH in the wholesale electricity market, considering CO
2 emission costs and the influences of RES fluctuations on electrolyzers, has not yet been discussed in any literature.
The remainder of this paper is organized as follows:
Section 2 introduces the off-grid system and grid-connected system for producing hydrogen by electrolysis.
Section 3 presents the LCOH model employed and the optimal operation strategy to minimize the LCOH for hydrogen production plants. A case study in the Kyushu area is performed to illustrate hydrogen production with alkaline and PEM electrolyzers. The simulation results are shown in
Section 4 to evaluate the performance of the proposed LCOH model. Finally, conclusions are drawn in
Section 5.
2. Hydrogen Production by Water Electrolysis
Green hydrogen production by water electrolysis requires 100% RES electricity, which can be achieved with an off-grid production plant, as shown in
Figure 1. The power supply is usually wind power or solar power. However, directly using RES electricity may cause some problems. For RES electricity, since the RESs are not always available, the plant may work only during certain hours in a day, reducing the operation hours. In this case, the CAPEX is relatively high, usually not at a competitive cost. Moreover, for alkaline electrolyzers, the fluctuating power input may lead to crossover gas and performance degradation [
5]. Water electrolysis can produce not only H
2 but also O
2. Crossover gas is a mix of H
2 and O
2, which can easily explode. From [
20], we know that crossover gas reaches relatively high concentrations in an alkaline electrolyzer when power generation is relatively low, sometimes even more than 1% in the experimental simulations, which is dangerous. Therefore, to keep the crossover gas concentration under control, it is necessary to set a minimum load restriction for alkaline electrolyzers. As for PEM electrolyzers, since they are able to operate with fluctuating power, there are no minimum load requirements for PEM electrolyzers. The electrolyzer must stop operating when the power falls below the operating range. During shutdown, RESs cannot be utilized, leading to a reduction in overall energy efficiency.
One potential solution is using grid electricity to complement the power supply to the electrolyzer. This situation is presented in
Figure 2. In this case, the electrolyzer will use RES electricity whenever it is available and grid electricity when necessary. Although the electricity cost and emission cost of grid electricity are higher than that of RES electricity, this method can extend the operating hours of the electrolyzer, reaching a higher capacity factor and higher hydrogen production. Thus, the electrolyzer in this system is more productive than the only-RES case, reducing the CAPEX. Moreover, this method can also avoid crossover gas and slow electrolyzer degradation.
Figure 3 describes an example of an alkaline electrolyzer working in the above two systems. Consider an off-grid photovoltaic hydrogen production plant that operates in the daytime when solar energy is available. Because of the minimum load restriction, part of the RES electricity cannot be utilized. When connecting to the grid, it is possible to use the RES electricity below the operating range and increase hydrogen production by injecting grid electricity, which will significantly influence reduction of the CAPEX per unit (“unitary CAPEX”). However, the average electricity cost and emission cost will increase due to the grid electricity used. There exists a trade-off between the unitary CAPEX and average electricity cost and emission cost.
3. Model
In this paper, we perform the optimization in a wholesale electricity market, which is closer to the real situation in Japan. The proposed model is general, so it can be applicable in other wholesale markets globally. However, it is important to note that some countries set fixed charge rates for electricity, in which case our research may not be suitable.
3.1. Optimization Model of the LCOH
The objective function of the optimal
LCOH can be defined as follows:
where
is the
LCOH,
is the average electricity cost,
stands for the unitary CAPEX,
represents the OPEX excluding the electricity cost per unit (“unitary OPEX”), and
means the average emission cost.
For the electricity cost, it includes the basic electricity cost,
and
, and the wheeling charge cost,
. Here, we assume that only grid electricity requires a wheeling charge since the green hydrogen production plants are usually in the same place as the
RES. Then, the average electricity cost
is as follows:
where
where
and
are the total electricity cost of
RESs and grid power,
is the total wheeling charge cost, and
means hydrogen production. When the time period
T = 1 year,
will be the annual hydrogen production,
.
and
stand for electricity used from
RESs and the grid in time-step
t.
and
represent
RES and grid electricity prices in time-step
t.
is the wheeling charge price.
is the efficiency of hydrogen production.
To ensure the total load within the operating range, the above equations are subject to the following constraint:
where
means the total electricity used in time-step
t, and
and
represent the minimum and maximum load for the electrolyzers. For an alkaline electrolyzer, the minimum load restriction here is set to be 10% of the capacity [
6]. In the case of a PEM electrolyzer, the minimum load is set as zero.
The unitary
CAPEX can be calculated as the quotient between the annualized
CAPEX,
and the annual production of hydrogen,
, as follows:
The unitary
OPEX can be obtained as follows:
where
is the fixed cost, such as the maintenance cost and employee salaries, and
is the variable cost depending on total hydrogen production volume, for example, the water consumption cost.
We assumed that there is no CO
2 emission related to RES electricity. Thus, the average emission cost can be calculated as follows:
where
is the emission factor, which presents the CO
2 emission related to the grid electricity used, and
is the CO
2 tax.
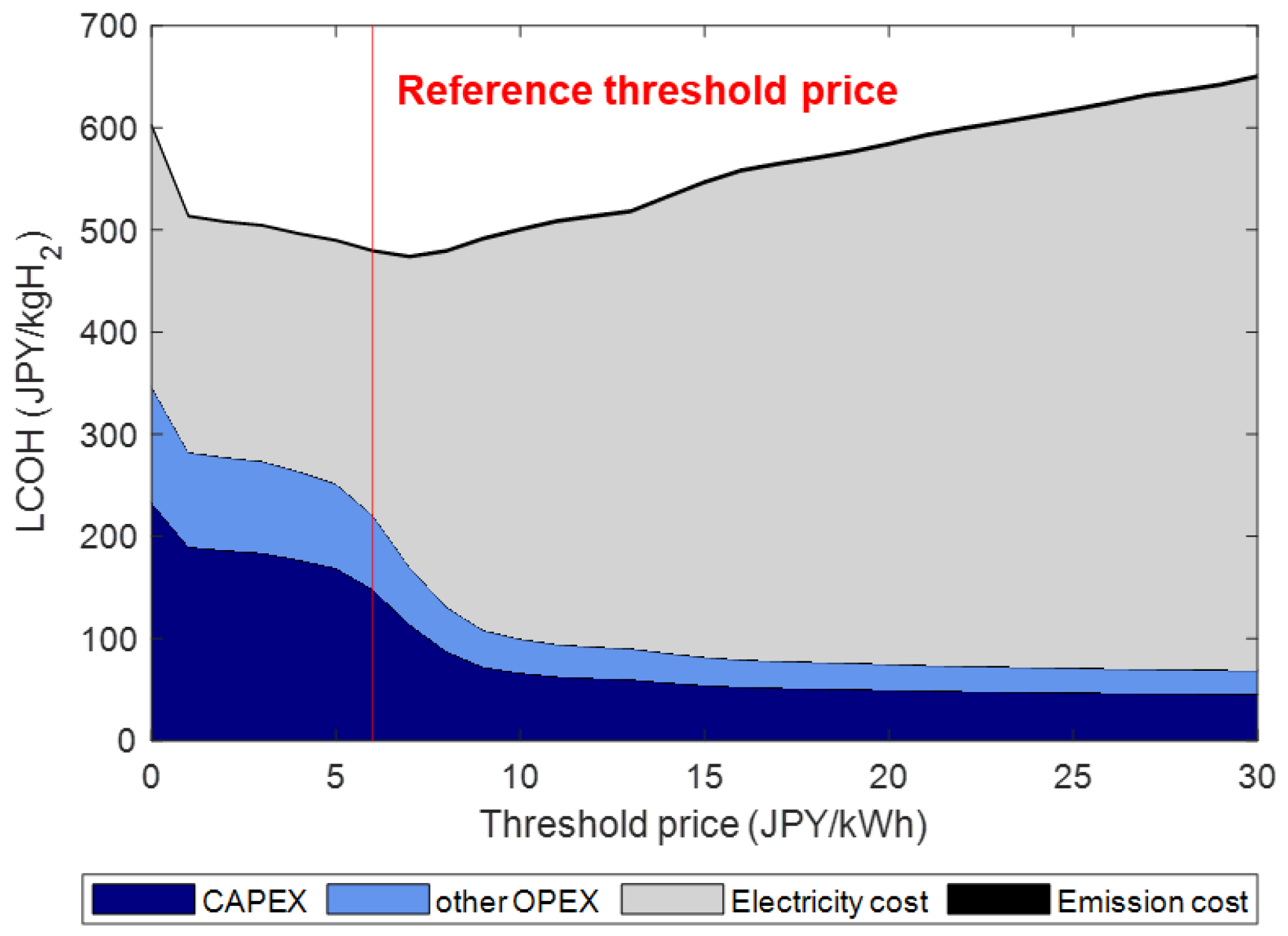
Finally, the LCOH can be obtained by adding the result of (2), (8), (9), and (10). Here, we suppose that hydrogen production will use RES electricity whenever it is available, and grid electricity when necessary. To minimize the LCOH means to find an optimal operation strategy for the variable, . However, regarding the evaluation models, the , which can be calculated by and , is in the denominator of the equations. Thus, this optimization problem is nonlinear, which is hard to solve directly. Another limitation is that the electricity spot price cannot be available one year in advance. One simplified but reasonable strategy is to find the threshold price (TP) according to historical data to estimate whether the current electricity price is relatively high or low. This strategy only uses historical data and solves the nonlinear problem by determining alone. Although it may not obtain the global optimum of the original model due to the simplification, the solution still shows a high performance in a practical situation without any complex algorithms. The specific process of the operation strategy will be introduced in the next section.
3.2. Operation Strategy in the Wholesale Market
In this section, an operation strategy is proposed to determine the electricity bidding process for a hydrogen production plant to minimize the LCOH in the wholesale electricity market.
The details of the subsequent steps in determining the operation strategy of the water electrolysis plants are illustrated in
Figure 4. In this paper, the time-step is set as 30 min, and the period
T = 1 year. We can determine the threshold price by analyzing historical data. Firstly, we calculate the LCOH at different initial threshold prices using last year’s electricity prices. Then, we plot a graph of the LCOH against the threshold price, and the threshold price is obtained by identifying the point on the figure with the lowest LCOH value. The threshold price is determined in a one-year version, considering the grid price fluctuations throughout the whole year. Next, by comparing the current grid electricity price with the threshold price, the operation state of an electrolyzer is determined from two scenarios. If
, the electrolyzer is set as the maximum load to produce more hydrogen. Otherwise (
), hydrogen production will return to the required minimum load. In this case, grid electricity is only used to make up the difference from the minimum load. So, if
, there is no need to consume additional power from the grid. Thus,
can be calculated as follows:
where
TP means the threshold price.
Finally, the LCOH can be calculated with . The procedure is applied for every time-step within the period. Moreover, the proposed method is capable of estimating negative electricity pricing by using the threshold price, although it does not yet exist in the current Japan electricity market.
This research allows variable H2 production rates, but in some cases, a fixed H2 production rate for downstream applications is required. That is to say, the load of electrolyzers should remain stable. In such situations, grid electricity can still complement the input power when RES electricity is insufficient. Conversely, when RES power exceeds the demand, the excess power can be integrated into the grid or stored in batteries.
5. Conclusions
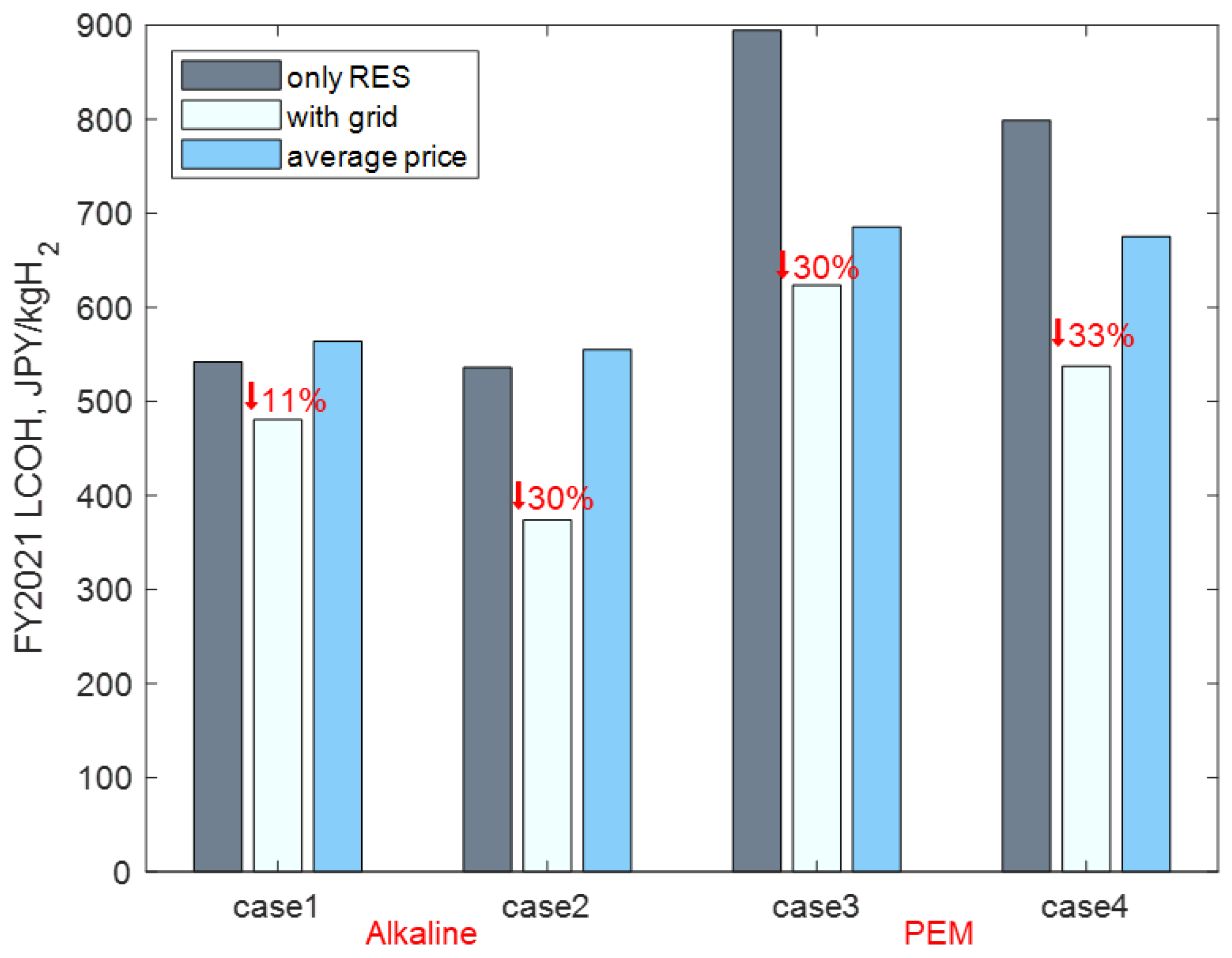
The objective of this paper is to analyze the techno-economic benefits of complementing green hydrogen production with grid electricity. A model is proposed to evaluate the LCOH, including CO2 emissions, to minimize the LCOH in the wholesale electricity market. The proposed model considers the influence of power fluctuations from RESs on water electrolysis, especially the minimum load restriction of alkaline electrolyzers to avoid crossover gas. Moreover, an optimal operation strategy is developed to solve the above nonlinear optimization problem. By injecting grid electricity, the LCOH decreases by 11% to 33%, compared to using an only-RES supply. Hydrogen productivity increases by 86% to 140%, while CO2 emission levels are maintained within an acceptable range. In addition, electrolyzer efficiency and the CAPEX have larger impact magnitudes on the LCOH, while the impact of the CO2 tax is relatively small compared to other factors.
Regarding future work, our main objective is to enhance the algorithm and achieve better results. The threshold price used in this paper is based on historical data. Although it is a simple approach, it may not lead to the lowest LCOH. Therefore, to estimate the threshold price more accurately, it is necessary to include the prediction of electricity prices. By forecasting electricity prices, the threshold price can be calculated using recent and future data, resulting in a more precise outcome. In addition, in the off-grid system scenario, akaline electrolyzers are not suitable for real conditions, as they cannot frequently start and stop, leading to safety issues. Therefore, the inclusion of a battery may be necessary in this case. Moreover, to study the entire hydrogen supply chain, it may be useful to include some elements such as the compression, storage, and distribution of hydrogen to demand locations. The inclusion of these elements may alter some of the results obtained here.