Distributed Optimization of Islanded Microgrids Integrating Multi-Type VSG Frequency Regulation and Integrated Economic Dispatch

Abstract

The question of how to simultaneously perform frequency regulation and integrated economic scheduling for microgrids with low-inertia islanding operation under communication constraints is a difficult problem that needs to be solved for many current applications. To this end, this paper establishes a microgrid scheduling control model containing a virtual synchronous generator (VSG) with multiple types of power sources and proposes a distributed optimization algorithm that integrates frequency regulation and comprehensive economic scheduling to simultaneously realize frequency regulation and economic scheduling in a microgrid. Firstly, a distributed economic dispatch problem is proposed based on a comprehensive consideration of the costs and benefits of various types of power VSGs, as well as the overall inertia and standby capacity requirements of the microgrid, which minimizes the integrated costs incurred by the participation of each type of VSG in the frequency regulation and improves the stable operation of the microgrid in terms of frequency under perturbation. Then, the optimal scheduling problem is solved by reconstructing the optimization problem based on considering the dynamic characteristics of microgrid inverters and using event-triggered communication to sense and compensate for the supply-demand imbalance online. The proposed method can avoid inter-layer coordination across time scales, improve the inertia, frequency regulation capability, and economy of the system, and enhance its robustness to short-term communication failures. Finally, simulation results are used to verify the effectiveness of the method.

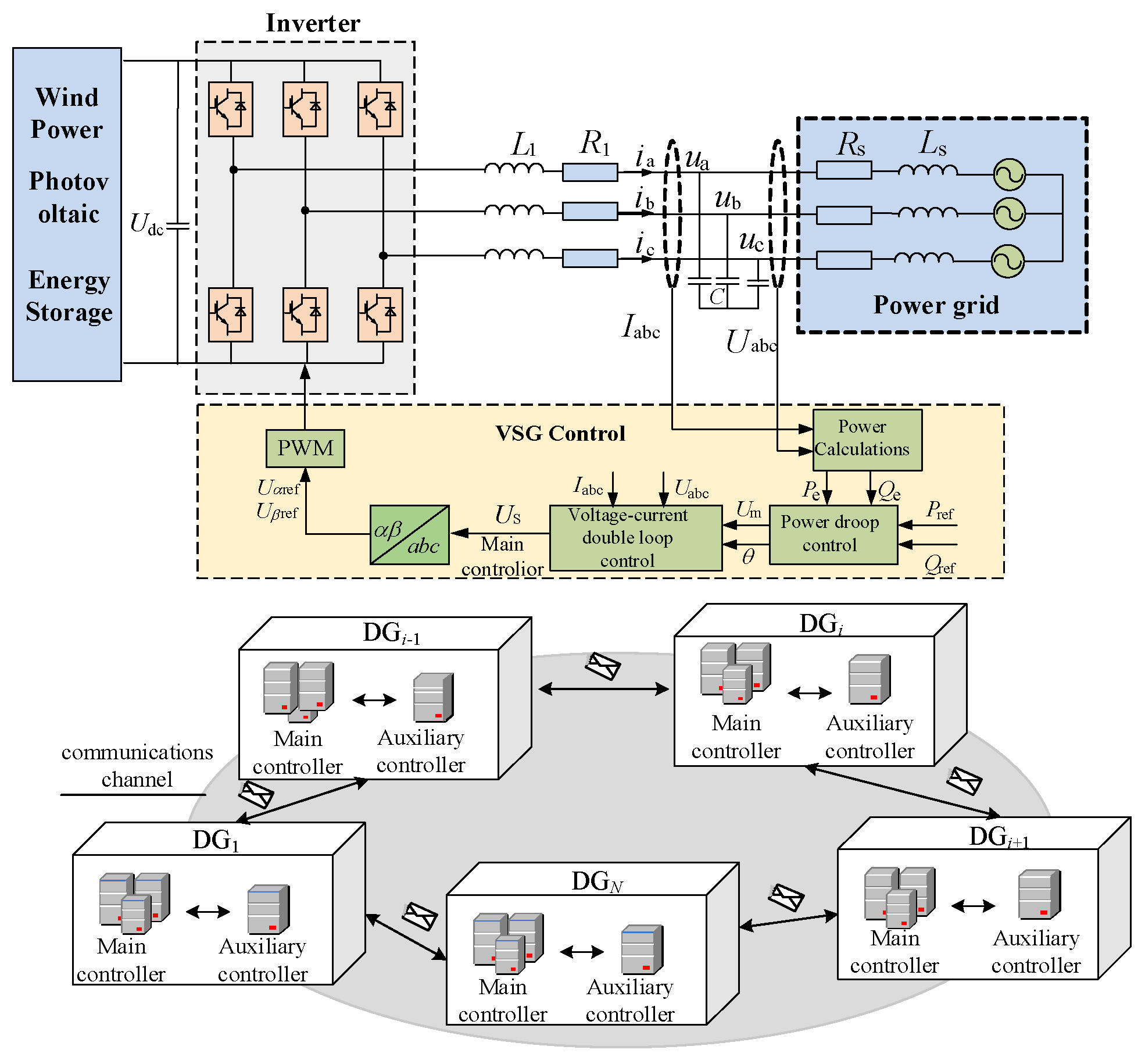
1. Introduction

In recent years, due to the gradual increase of the proportion of new energy, microgrids are often in planned or unplanned islanding operation modes, wherein their inertia level and communication capability are seriously lower than normal, frequency regulation and economic dispatch problems are prominent, dispatch control difficulty increases, and improper dispatch strategies may also cause certain economic losses. Virtual synchronous machine (VSG) technology is widely used because it can reduce the difficulty of microgrid frequency regulation and provide inertia support [1,2]. At present, the interaction and coordinated control of multiple types of VSGs (wind/photovoltaic/energy storage VSGs) in microgrids improves the dynamic response of the frequency of islanded microgrids; however, how best to simultaneously consider the frequency regulation (FR) capability of multiple types of VSGs as well as the comprehensive economic benefits in the scheduling and control model of islanded microgrids is a key issue to be solved.

Many studies have focused on microgrid islanding as well as energy scheduling for microgrids, and literature [3] improved distribution network resilience by advancing static islanding for single or multiple time sections. Literature [4] investigated the microgrid recovery steps and their control algorithms used after extreme disasters that lead to widespread power outages. However, the above studies only focus on a single microgrid or a single generation unit in a microgrid, and none of them consider the frequency regulation (FR) capability and economy of the microgrid. Distributed approaches using neighborhood communication and encouraging cooperation can centrally optimize the allocation of multiple microgrid resources while retaining the performance advantages of centralized approaches. Considering that an Inverter-Based Microgrid (IBMG) can seamlessly integrate wind and PV output power to maintain the frequency and voltage stability of the grid, it can achieve coordinated and optimized scheduling of multiple resources between and within multiple microgrids [5]. This means the technology has more significant economic benefits and frequency regulation abilities; as such, it has been widely promoted and applied in practical applications. Frequency regulation (FR) and integrated economic dispatch (IED), which need to be considered during the operation of microgrids, are handled by secondary and tertiary controls operating on different time scales, respectively [6]. For frequency regulation, literature [7,8] constructed a microgrid frequency stability-constrained optimal dispatch model containing wind/light/diesel/storage multi-type VSGs, and proposed a coordinated control strategy containing virtual synchronous generators, which increased the overall inertia and standby capacity level of the microgrid and improved the dynamic response of the microgrid frequency, but it did not take into account the variability in the operating cost and efficiency of the units involved in frequency regulation. To optimize the economics of microgrids in the frequency regulation process, literature [9,10] proposes an improved sag control method based on marginal cost and a secondary frequency regulation method based on virtual synchronous machine technology and taking into account the participation of loads, which maximizes the comprehensive benefits of the whole network, but the system lacks inertia and the frequency regulation fluctuates greatly. In summary, analysis shows that frequency regulation (FR) and economic dispatch (ED) are handled by secondary and tertiary controls operating on different time scales, respectively. ED (or, more precisely, energy management), in general, seeks to solve optimization problems involving cost behavior, supply-demand balance, system efficiency and reliability, and physical constraints of controllable devices. An important factor to consider in the construction and operation of new energy microgrids is that their operation processes are prone to intermittency and stochasticity, in which case coordination between layers can reduce the timeliness and effectiveness of control and optimization. With the increasing integration of renewable and sustainable energy sources in microgrids, prediction errors of these sources may reduce the economic efficiency of microgrids due to the time scale gap between economic dispatch at large time scales and frequency restoration control at small time scales. Conventional microgrids with multi-timescale optimal scheduling are unable to balance FR and IDE, a high percentage of new energy microgrids operating in islands are more susceptible to intermittency and stochasticity, and coordination between layers as well as communication failures can reduce the timeliness and effectiveness of control and optimization. Therefore, if FR and IDE can be considered while avoiding the separation of time scales, system performance is bound to be improved [11].

Traditional methods using hierarchical optimization may result in each layer focusing only on its own optimization objective while ignoring the optimization of the overall system. This may cause each layer to fall into a local optimal solution, thus failing to achieve the global optimal solution. To address this problem, the introduction of distributed control considers IED in combination with FR, which enables each node to obtain more comprehensive information by enhancing information sharing and collaboration among nodes to avoid the occurrence of locally optimal solutions. Literature [12] used a distributed average proportional integral (DAPI) algorithm to transfer consistent signals and locally measured frequencies to neighboring nodes, but it only achieves proportional power sharing, which cannot be customized for participants with different generation costs. Literature [13,14,15] established many optimization-based control methods based on Secondary Frequency Control (SFC) and Load Frequency Control which can be adapted to the integration of new energy VSG grids by satisfying the supply-demand balance and various inequality constraints. However, in the recent literature [16,17,18], the updating of decision variables is limited to quadratic objective functions, which may not apply to some more complex cases. Usually, the key to optimization-based control methods is the a priori information about the generation and total net power flow [19], and once the information accuracy is not up to the expectation, its control effectiveness will be lost to some extent. Literature [20] proposed a distributed gradient-based algorithm to solve the distributed economic dispatch problem (DEDP), but it requires a coordinating agent to compute the intermediate terms needed to accelerate convergence. Literature [21] proposed a feedback-based projected gradient algorithm to solve the frequency and economic problems of microgrids, but it is less robust to distributed communication faults and only considers the incremental cost of photovoltaic (PV) power generation, which cannot be applied to more complex microgrid topologies as well as communication scenarios. Literature [22] proposes a fully distributed framework consisting of two coordinated modules, where one module computes the optimal generation reference and the other one tracks the received reference. One of the main drawbacks of the above approach is that as the system size grows, either the auxiliary control module or the cluster leader election process leads to increased communication costs and implementation difficulties. On the contrary, monitoring the overall power mismatch based entirely on local frequency feedback and execution individually by distributed generators can reduce the communication burden and line resistance losses with better applicability and economy.

Based on the above analysis, this paper proposes a distributed optimization algorithm integrating frequency regulation (FR) and integrated economic dispatch (IED) for a high-percentage new energy islanded microgrid to regulate the frequency to a nominal value while dynamically optimizing the comprehensive benefits of the microgrid. The main contributions are as follows: (1) Under the constraints of inertia support and standby compensation capacity of various new energy VSGs, comprehensive cost modeling is carried out, taking into account the cost of each power source and the benefit of load VSGs. This modeling is able to make full use of the significant frequency regulation characteristics of VSGs for islanded microgrids and, at the same time, take into account the local economy, which solves the limitations of the traditional frequency regulation and control means in the optimization process. (2) Optimization of output power distribution among DGs using DEDP equations to guarantee frequency tuning while taking into account economic efficiency to meet specific power loads at the lowest cost. (3) The power mismatch estimation is carried out by using an event-triggered, mechanism-based projection gradient algorithm (PGA) for power mismatch estimation, while realizing accurate active power sharing and frequency regulation, which enhances the robustness of the system to short-term communication failures and reduces the communication burden.

2. System Architecture and Analysis

2.1. Microgrid Scheduling Architecture with Multi-Type VSG Participation

As the core of the whole scheduling architecture, the microgrid control center is responsible for the energy management of the system [22]. It realizes the optimal scheduling of all controllable resources in the system by combining with the local control in the lower IBMG structure, i.e., under the constraints of meeting the system inertia, standby demand, power balance, and the comprehensive economic benefits of various types of power VSGs and load VSGs, the power benchmark value of the multiple types of resources with each unit output, VSG and conventional unit, power mismatch, etc., and is optimized in a coordinated manner through the coordinated consideration of the operating characteristics of multiple types of resources. Under the constraints of system inertia, power demand, power balance, and the comprehensive economic efficiency of multiple types of resources and load VSGs, the coordinated consideration of the operating characteristics of multiple types of resources and load power demand is used to coordinate and optimize the power reference value of multiple types of VSGs with the output of each unit, the state of loading, the standby reserve of VSGs and conventional units, and power mismatch at each operating point. Under active impact disturbance, multi-type VSGs can autonomously provide flexible and controllable inertia support and primary frequency regulation (FR) service to the system and dynamically regulate the imbalance of power in the network.

The optimal scheduling architecture of a microgrid with the participation of multiple types of VSGs is shown in Figure 1:

2.2. Multi-Agent IBMG Model

The IBMG topology and control method based on VSG control is shown in Figure 2, and all types of distributed generation (DG) in the scheduling architecture are in this topology.

Although distributed optimization can take into account both frequency regulation and economic dispatch, each node only has access to local information in a distributed environment, and the lack of global information may result in failure to obtain the overall optimal solution. Multi-agent theory (MAT) provides a framework for distributed decision-making that allows multiple agents to make decisions based on local information and emphasizes information exchange and coordination among agents, allowing them to solve distributed optimization problems based on cooperation to achieve the global objective. With the help of multi-agent theory [23], each DG is assigned an agent (including a primary controller and a secondary controller) to manage the generation behavior of locally connected new energy sources. Peer-to-peer communication is used to disseminate the necessary information to all the required agents, where the agents can only access the local information but are allowed to share the information with neighboring agents through the communication network.

In Figure 2, a three-phase full-bridge inverter is used in the main circuit; the DC side is connected to a new energy generation system, such as wind/photovoltaic/energy storage; its DC voltage is $U_{dc}$; L₁ is the filter inductor and C is the filter capacitor, which forms an LC filter for filtering; R₁ is the resistor; and the grid side is represented by an infinite system composed of the line inductance Ls, the line resistor Rs, and the AC voltage source. In the secondary controller, local frequency feedback and neighboring information about the incremental cost are used to generate setpoints for the primary controller containing three control loops (voltage, current, and sag control loops).

The injected power at inverter i is:

$$\begin{array}{c}{P}_{e,i}=V_i^2{\displaystyle \sum _{j\in {\mathcal{S}}_i}}{G}_{ij}-{\displaystyle \sum _{j\in {\mathcal{S}}_i}}{V}_i{V}_j\left|Y_{ij}\right|\cos \left({\theta }_{ij}-{\varphi }_{ij}\right)\\ Q_{e,i}=-V_i^2{\displaystyle \sum _{j\in {\mathcal{S}}_i}}{B}_{ij}-{\displaystyle \sum _{j\in {\mathcal{S}}_j}}{V}_i{V}_j\left|Y_{ij}\right|\sin \left({\theta }_{ij}-{\varphi }_{ij}\right)\end{array}$$

(1)

where $V_i$ is the voltage amplitude of DG_i; $G_{ij}$ and $B_{ij}$ denote the conductance and conductance of ij line, respectively; $Y_{ij}=G_{ij}+j{B}_{ij}$; ${\theta }_{ij}={\theta }_i-{\theta }_j$ is the phase angle difference between inverters i and j; ${\varphi }_{ij}=\arctan \left(B_{ij}/G_{ij}\right)$; and $S_i$ is the physically connected inverter group of inverter i.

The active and reactive power outputs of the DG are suppressed by an LC filter that filters out the high-frequency components associated with the voltage and current controllers from the instantaneous active power output $P_i$ and reactive power output $Q_i$ of the inverter:

$$\begin{array}{c}{\tau }_{P,i}{\dot{P}}_i^e=-P_i^e+P_i,\\ {\tau }_{Q,i}{\dot{Q}}_i^e=-Q_i^e+Q_i,\end{array}$$

(2)

where $P_i^e$ and $Q_i^e$ are the measured active/reactive power output of inverter i, and ${\tau }_{P,i}$ and ${\tau }_{Q,i}$ are the time constants of the filter.

2.3. Analysis of VSG-Based Models

One of the problems posed by the transition from conventional to renewable power sources is that islanded microgrids cannot rely on generator inertia to provide as much spinning reserve as conventional power systems. In this regard, VSG technology can be handled effectively. VSG is a technology that simulates a stationary power electronic device to operate as a rotating motor by embedding the mathematical model of a synchronous generator into the control algorithm of an inverter and making it have the functions of damping the rapid fluctuation of voltage and frequency, automatic power distribution, and synchronous grid operation by simulating the synchronous generator’s primary frequency and voltage regulation. According to the synchronous generator rotor equations of motion and electromagnetic equations, the VSG active-frequency first-order dynamic equations are obtained as shown below:

$$\{\begin{array}{l}J{\omega }_{\mathrm{n}}\frac{\mathrm{d}{\omega }_{\mathrm{m}}}{\mathrm{d}t}=P_{\mathrm{M}}-P_{\mathrm{eVSG}}-D_{\mathrm{p}}\left({\omega }_{\mathrm{m}}-{\omega }_{\mathrm{n}}\right)\hfill \\ \hspace{1em}\hspace{1em}\frac{\mathrm{d}{\theta }_{\mathrm{m}}}{\mathrm{d}t}={\omega }_{\mathrm{m}}\hfill \end{array}$$

(3)

where J is the virtual rotational inertia of the VSG; ${\omega }_{\mathrm{n}}$ and ${\omega }_{\mathrm{m}}$ are the rated angular velocity and rotor angular velocity of the VSG; $P_{\mathrm{M}}$ and $P_{\mathrm{eVSG}}$ are the virtual mechanical power and the output electrical power of the VSG, respectively; $D_{\mathrm{p}}$ is the virtual damping coefficient; and ${\theta }_{\mathrm{m}}$ is the rotor angle of the VSG. The phase angle and voltage amplitude of the VSG control are shown below:

$$\begin{array}{l}{\omega }_i^{\mathrm{VSG}}={\omega }^n-k_{P,i}\left(P_i^m-P_i^d\right)\\ V_i^{\mathrm{VSG}}=V_i^n-k_{Q,i}\left(Q_i^m-Q_i^d+q_i\right)\end{array}$$

(4)

where ${\omega }^n$ is the nominal frequency; $k_{P,i}$ and $k_{Q,i}$ are the controller gains for frequency droop and voltage droop determined by the frequency/voltage limitation and the maximum allowable active/reactive power output; $P_i^d$ and $Q_i^d$ denote the setpoints of the active and reactive power outputs, respectively, which are traditionally supplied by the secondary controllers; $V_i^n$ is the nominal voltage magnitude; and $q_i=k_{q,i}{V}_i$ is the variable introduced for better sharing of the reactive power in the presence of resistive losses.

According to the power balance relationship in the literature [24], the active/reactive power output delivered to the local loads and the grid can be expressed as:

$$\begin{array}{l}{P}_{z,i}=P_{l,i}+P_{e,i}+P_{\mathrm{M},i}-P_{g,i}-P_{\mathrm{eVSG},i}\\ \hspace{0.17em}{Q}_i=Q_{l,i}+Q_{e,i}\end{array}$$

(5)

where $P_{l,i}$ and $Q_{l,i}$ are the active and reactive loads aggregated at the inverter i, respectively, and $P_{g,i}$ is the output power of the conventional genset connected to the inverter i.

Combining Equations (2)–(5) yields an overall model for DGi:

$${\dot{\theta }}_i={\omega }_i$$

(6)

$$\begin{array}{c}{\tau }_{P,i}{\dot{\omega }}_i^{\mathrm{VSG}}=-k_{P,i}(P_{l,i}+P_{e,i}+P_{\mathrm{M},i}-P_{g,i}-\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{P}_{\mathrm{eVSG},i}-P_i^d)-\left({\omega }_i^{\mathrm{VSG}}-{\omega }^n\right)\end{array}$$

(7)

$$\begin{array}{l}{\tau }_{Q,i}{\dot{V}}_i^{\mathrm{VSG}}=-k_{Q,i}\left(Q_{l,i}+Q_{e,i}-Q_i^d+q_i\right)-\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\left(V_i^{\mathrm{VSG}}-V_i^n\right)\end{array}$$

(8)

3. Integrated Management of FR and IED

In this section, the control objective of integrating IEDs and FRs is proposed based on fully taking into account the frequency regulation (FR) characteristics of VSGs, and the distributed integrated economic dispatch problem is transformed into an optimal control problem. The output power allocation among DGs and the frequency regulation (FR) capability under disturbances are optimized to meet the specific power load demand at the lowest integrated cost.

3.1. Frequency Recovery Conditions Considering VSG Inertia and Standby Requirements

When the microgrid is perturbed, the inertia characteristic of the DG effectively slows down the rate of frequency change, while the standby capacity facilitates the recovery of frequency when it goes out of control by providing additional power support. When a frequency change is detected at the inverter side, the VSG can autonomously adjust its output power in response to the microgrid frequency change, utilizing the inertial link and primary frequency regulation (FR) to respond to its change, absorbing/releasing the unbalanced power, and providing short-lived support to the microgrid frequency, which reduces the amount of the microgrid’s unbalanced power and frequency deviation.

3.1.1. Inertia and Standby Constraints

Considering the differences in inertia between different types of power sources, the transient support power of various types of VSGs is shown below.

Wind power VSGs can absorb/release rotor kinetic energy according to the real-time frequency rate of change to provide inertial support for the microgrid:

$$\mathsf{\Delta }{P}_{\mathrm{Wind}}^{\mathrm{VSG}}=-2H_{\mathrm{Wind}}^{\mathrm{VSG}}\cdot \frac{P_{\mathrm{Wind}}^{\max }}{f_0}\cdot \frac{\mathrm{d}f}{\mathrm{d}t}$$

(9)

where $\mathsf{\Delta }{P}_{\mathrm{Wind}}^{\mathrm{VSG}}$ is the inertia support power of the wind power VSG during frequency change; $H_{\mathrm{Wind}}^{\mathrm{VSG}}$ is the equivalent inertia time constant; $P_{\mathrm{Wind}}^{\max }$ is the rated capacity of the wind power VSG; and $f_0$ and $f$ are the reference frequency and real-time frequency of the microgrid, respectively.

Unlike wind VSGs, PV arrays do not contain mechanical rotating parts and are usually operated in maximum power mode with an equivalent inertia of 0. Therefore, PV VSGs need to be equipped with an additional energy storage unit to provide inertial support to the microgrid and to simulate the primary frequency regulation (FR) function of a synchronous generator. The inverter controls the energy storage unit of the PV VSG to provide transient power support to the microgrid according to the frequency change:

$$\mathsf{\Delta }{P}_{\mathrm{PV}}^{\mathrm{VSG}}=-\left(2H_{\mathrm{PV}}^{\mathrm{VSG}}\cdot \frac{\mathrm{d}f}{\mathrm{d}t}+\frac{1}{{\delta }_v}\cdot \mathsf{\Delta }f\right)\frac{P_{\mathrm{PV}}^{\max }}{f_0}$$

(10)

where $\mathsf{\Delta }{P}_{\mathrm{PV}}^{\mathrm{VSG}}$ is the transient support power of the VSG; $H_{\mathrm{PV}}^{\mathrm{VSG}}$ is the virtual inertia time constant of the VSG; ${\delta }_v$ is the modulation coefficient of the VSG; and $P_{\mathrm{PV}}^{\max }$ is the rated power of the VSG energy storage unit.

An energy storage VSG can actively participate in microgrid optimization scheduling due to its bidirectional power flow characteristics, and also provide fast power support under power disturbance accidents, which improves the anti-risk and anti-disturbance capability of the microgrid. The energy storage VSG inertia time constant can be characterized as:

$$H_{\mathrm{ES}}^{\mathrm{VSG}}=\frac{Q_{\mathrm{ES},t}}{\left|Q_{\mathrm{ES}}^{\max }\right|\cdot S_0}{C}_{\mathrm{ES}}^{\max }$$

(11)

where $Q_{\mathrm{ES},t}$ and $Q_{\mathrm{ES}}^{\max }$ are the residual power and rated capacity of the energy storage at time t; $S_0$ is the unit base power; and $C_{\mathrm{ES}}^{\max }$ is the maximum charge/discharge multiplier of the energy storage.

The transient support power of the storage VSG during frequency fluctuation is:

$$\mathsf{\Delta }{P}_{\mathrm{ES}}^{\mathrm{VSG}}=-\left(2H_{\mathrm{ES}}^{\mathrm{VSG}}\cdot \frac{\mathrm{d}f}{\mathrm{d}t}+\frac{1}{{\delta }_s}\cdot \mathsf{\Delta }f\right)\frac{P_{\mathrm{ES}}^{\max }}{f_0}$$

(12)

where ${\delta }_s$ and $P_{\mathrm{ES}}^{\max }$ are the energy storage VSG modulation factor and power rating, respectively.

Considering the overall inertia of each type of VSG in the microgrid, the following constraints can be obtained:

$$\begin{array}{c}{E}_{\mathrm{sys},t}^{\min }={\displaystyle \sum _{i=1}^{N_i}}{H}_G{P}_{g,t}^{\max }+{\displaystyle \sum _{\mathrm{W}=1}^{N_{\mathrm{W}}}}{H}_{\mathrm{Wind}}^{\mathrm{VSG}}{P}_{\mathrm{Wind},t}^{\mathrm{av}}+\\ {\displaystyle \sum _{\mathrm{V}=1}^{N_{\mathrm{V}}}}{H}_{\mathrm{PV},t}^{\mathrm{VSG}}{P}_{\mathrm{PV}}^{\max }+{\displaystyle \sum _{\mathrm{S}=1}^{N_{\mathrm{S}}}}{H}_{\mathrm{ES},t}^{\mathrm{VSG}}{P}_{\mathrm{ES}}^{\max }\ge \frac{\mid -\mathsf{\Delta }{P}_{\mathrm{loss}}|f_0}{2R_{\mathrm{oCoF}}^{\mathrm{ex}}}\end{array}$$

(13)

where $E_{\mathrm{sys}}$ is the total rotational kinetic energy of the microgrid; $H_G$ and $P_{g,t}^{\max }$ are the inertia time constant and rated capacity of the conventional units; $P_{\mathrm{Wind},t}^{\mathrm{av}}$ is the predicted maximum power of the wind power in period t; $\mathsf{\Delta }{P}_{\mathrm{loss}}$ is the active loss under the microgrid’s perturbation; $R_{\mathrm{oCoF}}^{\mathrm{ex}}$ is the set threshold of the maximum frequency rate of change; and the subscripts i, W, V, and S, and $N_i$, $N_w$, $N_v$, and $N_s$ denote the total number of conventional synchronous units, wind turbine VSGs, photovoltaic VSGs, and energy storage VSGs in the microgrid, respectively.

The overall total standby capacity of the microgrid and its demand constraints are shown in the following equation:

$$R_t^{\mathsf{\Sigma }}=\sum _{i=1}^{N_i}{R}_{i,t}^{\mathrm{G}}+\sum _{\mathrm{W}=1}^{N_{\mathrm{W}}}{R}_{\mathrm{W},t}^{\mathrm{VSG}}+\sum _{\mathrm{V}=1}^{N_{\mathrm{V}}}{R}_{\mathrm{V},t}^{\mathrm{VSG}}+\sum _{\mathrm{S}=1}^{N_{\mathrm{S}}}{R}_{\mathrm{S},t}^{\mathrm{VSG}}$$

(14)

$$R_t^{\mathsf{\Sigma }}\ge \max \left\{\mathsf{\Delta }{P}_{\mathrm{loss}}^{\max },{\xi }_{\mathrm{load}},{\sigma }_{\mathrm{load}}\right\}$$

(15)

where $R_{i,t}^{\mathrm{G}}$, $R_{\mathrm{W},t}^{\mathrm{VSG}}$, $R_{\mathrm{V},t}^{\mathrm{VSG}}$, and $R_{\mathrm{S},t}^{\mathrm{VSG}}$ are the standby capacities provided by conventional units, wind VSGs, PV VSGs, and energy storage VSGs in period t, respectively; $\mathsf{\Delta }{P}_{\mathrm{loss}}^{\max }$ is the imbalance power under the maximum N − 1 fault of the microgrid; ${\xi }_{\mathrm{load}}$ is the reliability coefficient; and ${\sigma }_{\mathrm{load}}$ is the standard deviation of the equivalent load error. The specific calculation process can be referred to in the literature [8], and will not be repeated in this paper.

The microgrid frequency will be stabilized at the synchronous frequency ${\omega }^{\mathrm{sync}}$, but it cannot be restored to the nominal value by only the main control. Summing Equation (7) and calling equation ${\displaystyle \sum _{i=1}^N}{P}_{e,i}=\mathsf{\Delta }{P}_{\mathrm{loss}}$ obtains the following:

$${\omega }^{\mathrm{sync}}={\omega }^n+\frac{{\displaystyle \sum _{i=1}^N}\left(P_i^d+P_{g,i}-P_{l,i}\right)+E_{\mathrm{sys}}-\mathsf{\Delta }{P}_{\mathrm{loss}}}{{\displaystyle \sum _{i=1}^N}\left(1/k_{P,i}\right)}$$

(16)

If the power injection between DGs is relatively small compared to the line capacity, a sufficient condition for frequency restoration can be derived as shown below:

$$\begin{array}{c}{\displaystyle \sum _{i=1}^N}{P}_i^{\min }+{\displaystyle \sum _{i=1}^N}{P}_{g,i}+E_{\mathrm{sys},t}^{\min }\le {\displaystyle \sum _{i=1}^N}{P}_{l,i}+\mathsf{\Delta }{P}_{\mathrm{loss}}\le \\ {\displaystyle \sum _{i=1}^N}{P}_i^{\max }+{\displaystyle \sum _{i=1}^N}{P}_{g,i}+E_{\mathrm{sys},t}^{\max }\end{array}$$

(17)

where $P_i^{\max }$ and $P_i^{\min }$ are the maximum and minimum power limits of $P_i^d$, and $E_{\mathrm{sys},t}^{\max }$ and $E_{\mathrm{sys},t}^{\min }$ are the maximum and minimum values of the transient support power of the microgrid VSGs. The microgrid system will be synchronized to the nominal frequency when, and only when, ${\displaystyle \sum _{i=1}^N}{P}_i^d+{\displaystyle \sum _{i=1}^N}{P}_{g,i}+E_{\mathrm{sys}}={\displaystyle \sum _{i=1}^N}{P}_{l,i}+\mathsf{\Delta }{P}_{loss}$

Therefore, the overall power balance can be chosen as the global equality constraint and the integrated management of FR and IED can be achieved by solving a well-constructed optimization problem.

3.1.2. System Power Constraints

Based on the inertia constraints, spare capacity constraints, and global active constraints expressed in Equation (17) in Section 3.1, various types of basic constraints in the microgrid’s islanded operation state can be listed as follows:

$$P_i^{\min }\le P_{i,t}^{\mathrm{G}}+R_{i,t}^{\mathrm{G}}\le P_i^{\max }$$

(18)

$$-R{D}_i^{\max }\le P_{i,t}^{\mathrm{G}}-P_{i,t-1}^{\mathrm{G}}\le R{U}_i^{\max }$$

(19)

$$P_{\mathrm{Wind},t}^{\mathrm{VSG}}=(1-\beta )P_{\mathrm{Wind},t}^{\mathrm{av}},P_{\mathrm{Wind},t}^{\mathrm{av}}\ge 0.2P_{\mathrm{Wind}}^{\max }$$

(20)

$$P_{\mathrm{PV},t}^{\mathrm{VSG}}=P_{\mathrm{PV},t}^{\mathrm{av}}$$

(21)

$$-P_{\mathrm{ES}}^{\max }\le P_{\mathrm{ES},t}^{\mathrm{VSG}}\le P_{\mathrm{ES}}^{\max }$$

(22)

$$Q_{\mathrm{ES},t}=Q_{\mathrm{ES},t-1}-\mathsf{\Delta }T\cdot P_{\mathrm{ES},t}^{\mathrm{VSG}}\cdot {\eta }_{\mathrm{ES}}$$

(23)

$$S_{\mathrm{OC}-\mathrm{ES},t}=Q_{\mathrm{ES},t}\cdot {\left|Q_{\mathrm{ES}}^{\max }\right|}^{-1}$$

(24)

$$S_{\mathrm{OC}-\mathrm{ES}}^{\min }\le S_{\mathrm{OC}-\mathrm{ES},t}\le S_{\mathrm{OC}-\mathrm{ES}}^{\max }$$

(25)

$$R_{\mathrm{oCoF}-t,n}=-\frac{\mathsf{\Delta }{P}_{t,n}^{\mathrm{fault}}{f}_0}{2E_{\mathrm{sys},t,n}}$$

(26)

$$\mathsf{\Delta }{f}_{t,n}=\mathsf{\Delta }{f}_{t,n-1}+R_{\mathrm{oCoF}-t,n}\cdot \mathsf{\Delta }n$$

(27)

$$\{\begin{array}{l}\left|\mathsf{\Delta }{f}_{t,n}\right|\le \mathsf{\Delta }{f}^{\mathrm{ex}}\hfill \\ \left|R_{\mathrm{oCoF}-t,n}\right|\le R_{\mathrm{oCoF}}^{\mathrm{ex}}\hfill \end{array}$$

(28)

where Equations (18) and (19) are the maximum/minimum technical output constraints of the conventional unit and the climbing rate constraints of the unit in the adjacent scheduling period; Equations (20) and (21) are the steady-state output constraints of the wind VSG and the photovoltaic VSG, respectively; Equations (22)–(25) are the output constraints and the charge state constraints of the storage VSG; and Equations (26)–(28) are the frequency stabilization constraints under disturbances. Within these equations, $R{D}_i^{\max }$ and $R{U}_i^{\max }$ are the maximum downward/upward creep rates of the conventional unit i; $S_{\mathrm{OC}-\mathrm{ES},t}$, $S_{\mathrm{OC}-\mathrm{ES}}^{\min }$ and $S_{\mathrm{OC}-\mathrm{ES}}^{\max }$ are the storage VSG battery charge states and their upper and lower bounds; $\mathsf{\Delta }T$ is the interval between neighboring scheduling periods; $\mathsf{\Delta }{P}_{t,n}^{\mathrm{fault}}$ is the battery charging/discharging efficiency; $\mathsf{\Delta }{P}_{t,n}^{\mathrm{fault}}$ is the amount of real-time active imbalance in the system; and $R_{\mathrm{oCoF}-t,n}$ and $E_{\mathrm{sys},t,n}$ are the frequency rate of change corresponding to the nth step moment and the total kinetic energy, respectively, after the active perturbation in period t.

The frequency regulation capability of the islanding mode is insufficient, and it is necessary to limit the maximum grid-connected power of any power source in the network and leave some space for load cutting, i.e.:

$$P_t^{\mathrm{limit}}\le \frac{2E_{\mathrm{sys},t,n}{R}_{\mathrm{oCoF}}^{\mathrm{ex}}}{f_0}$$

(29)

where $P_t^{\mathrm{limit}}$ is the maximum amount of active shock that the microgrid can withstand.

The conventional unit output constraints, as well as the overall power balance constraints within the microgrid, are as follows:

$$P_i^{\min }\le P_{i,t}^{\mathrm{G}}+R_{i,t}^{\mathrm{G}}\le \min \left\{P_i^{\max },P_t^{\mathrm{limit}}\right\}$$

(30)

$$\begin{array}{c}\sum _{i=1}^{N_{\mathrm{i}}}{P}_{i,t}^{\mathrm{G}}+\sum _{\mathrm{W}=1}^{N_{\mathrm{W}}}{P}_{\mathrm{Wind},t}^{\mathrm{VSG}}+\sum _{\mathrm{V}=1}^{N_{\mathrm{V}}}{P}_{\mathrm{PV},t}^{\mathrm{VSG}}+\sum _{\mathrm{S}=1}^{N_{\mathrm{S}}}{P}_{\mathrm{ES},t}^{\mathrm{VSG}}+\\ \sum _{i\in VS{G}_{\mathrm{L}}}L\left(P_i\right)=\sum _{d=1}^{N_{\mathrm{d}}}\left(P_{d,t}-P_{d,t}^{\mathrm{cut}}\right)\end{array}$$

(31)

where $P_{d,t}$ is the power demand of load d at period t; and $P_{d,t}^{\mathrm{cut}}$ is the load shedding amount.

3.2. Cost Modeling with Integrated Benefits

Due to the lack of dispatchability and the absence of flexible storage devices for conventional new energy generation, a microgrid has to be operated in a relatively conservative manner and also needs to consider the additional opportunity cost due to the change of DG operation mode, which cannot alleviate the FR and IED burdens of microgrid operators. However, the multi-type VSG complementary system used in this paper, which is equipped with energy storage devices, improves the overall dispatchability of the system while avoiding the above problems and can improve the overall efficiency when load VSGs are involved in frequency regulation (FR).

The operating costs of various types of VSG power sources, as well as conventional units in microgrids, are mostly composed of battery maintenance and replacement costs, synchronized unit standby costs, external grid power purchase costs, load-shedding penalty costs, fuel costs, and pollution control costs. Quoting the quadratic form fitted in the literature [9], the following equation can be obtained:

$$f\left(P_i\right)={\alpha }_i{P}_i^2+{\beta }_i{P}_i+{\gamma }_i+c_R{R}_{t,i}^{\mathsf{\Sigma }}\hspace{1em}i\in VS{G}_G$$

(32)

where $f\left(P_i\right)$ is the cost function of the i-th VSG power supply; $\alpha$, $\beta$, $\gamma$ are the corresponding cost fitting coefficients reflecting the operating costs of VSG power supplies with different output powers (for example, when the distributed power source is an internal combustion engine or a fuel cell, the cost coefficient is mainly determined by the cost of fuel, and when it is a renewable energy source and an energy storage system, the cost coefficient is mainly determined by the maintenance and replacement cost of the storage, the efficiency of the converter, and so on); $c_R$ is the cost coefficient of the VSG standby capacity; and $VS{G}_G$ is the set of all VSG power supplies.

Load VSGs can bring electricity consumption benefits to the microgrid, and the greater the load utilization, the higher the benefits, and vice versa for lower benefits. Based on the literature [10] its mathematical model can be developed as follows:

$$L\left(P_i\right)=\{\begin{array}{l}{\lambda }_i{P}_i-{\eta }_i{P}_i^2 P_i\le {\lambda }_i/2{\eta }_i\hfill \\ {\lambda }_i^2/4{\eta }_i P_i\ge {\lambda }_i/2{\eta }_i\hfill \end{array}i\in VS{G}_{\mathrm{L}}$$

(33)

where $L\left(P_i\right)$ is the power usage benefit function of the i-th load VSG; $\lambda$ and $\eta$ are the benefit coefficients of the corresponding loads; $VS{G}_L$ is the set of load VSGs.

According to Equations (32) and (33), the objective function of microgrid comprehensive benefit optimization can be obtained as:

$$\begin{array}{l} \min \sum _{i\in VS{G}_{\mathrm{G}}}f\left(P_i\right)-\sum _{i\in VS{G}_{\mathrm{L}}}L\left(P_i\right)\\ \forall i\in {\mathrm{VSG}}_{\mathrm{G}}\cup {\mathrm{VSG}}_{\mathrm{L}}:P_i^{\min }\le P_i\le P_i^{\max }\end{array}$$

(34)

where $P_i^{\max }$ and $P_i^{\min }$ are the upper and lower power limits of the power source VSG and load VSG.

The traditional frequency regulation process allocates power according to the capacity of each unit without considering the differences in the operating costs and efficiency of the units involved in frequency regulation, which is not conducive to the economic operation of the microgrid. In this paper, while realizing the rapid recovery of microgrid frequency, the comprehensive benefit of the whole network is maximized.

3.3. DEDP Equation

To coordinate the time scale difference between the economic dispatch on a large time scale and the frequency restoration control on a small time scale, this method optimizes the output power allocation among DGs by using the DEDP equation, and takes into account the economic benefits while guaranteeing the frequency adjustment to satisfy the specific power loads mentioned in the literature [20] at the lowest cost. Based on the frequency, power constraints, and comprehensive economic benefits, the model in Section 2.1 of this paper is established to comprehensively take into account the frequency adjustment and the economic benefits of the objective function, which is shown as follows:

$$\min Z(P_i)=\sum _{i=1}^N[f\left(P_i\right)-L(P_i)]$$

(35a)

$$\mathrm{s}.\mathrm{t}. \sum _{i=1}^N\left(P_{l,i}-E_{\mathrm{sys}}-P_{g,i}-P_i^d\right)+\mathsf{\Delta }{P}_{\mathrm{loss}}=0$$

(35b)

$$P_i^{\min }\le P_i\le P_i^{\max }\hspace{1em}\forall i\in {\mathrm{VSG}}_{\mathrm{G}}\cup {\mathrm{VSG}}_{\mathrm{L}}$$

(35c)

The local feasibility constraints (LFCs) in Equation (35c) need to be explicitly dealt with during the allocation because they mainly affect the solution to which the optimization algorithm eventually converges. LFCs are usually dealt with by including a logarithmic barrier function or a linear quadratic function in the objective function. These penalty terms can eliminate the LFCs and convexify the objective function of the linear programming problem, but constraint conflicts cannot be completely avoided during the convergence process if the decision variables are not properly initialized.

In this paper, we utilize the projection operation $P_{\mathsf{\Omega }}(x):{ℝ}^N\to \mathsf{\Omega }$ to transform $P_i$ into the feasible domain given by (35b), where the projection of x onto the closed convex set $\mathsf{\Omega }$ is defined by $P_{\mathsf{\Omega }}(x)=\arg \underset{y\in \mathsf{\Omega }}{\min }||x-y||$ in literature [16]. When combined with the gradient approach, this perfectly eliminates constraint conflicts, regardless of how $P_i$ is initialized; moreover, it allows seamless operation between different loading levels, weather conditions, and grid configurations without any reinitialization process, thus unlocking the scalability potential of the microgrid.

Due to the introduction of projection operations, the constructed objective function is strongly convex, and the features can be inferred in the projection domain as follows:

$$\nabla Z(x)-\nabla Z(y),x-y\ge m{\rho }_i\left|\right|x-y|{|}^2$$

(36)

where $m$ is an adjustable positive coefficient; ${\rho }_i$ is introduced as an integrated cost coefficient and expressed as a normalized ratio; $x,y\in {\mathsf{\Omega }}_i$, and ${\mathsf{\Omega }}_i=\left\{P_i\mid P_i^{\min }\le P_i\le P_i^{\max }\right\}$.

Thus, DEDP is a convex optimization problem that combines the objective function being convex, the LFC being convex, and the equational constraint function being affine.

The Lagrangian function of Equation (35) is given by the following equation:

$$\begin{array}{l}L=\mu [{\displaystyle \sum _{i=1}^N}\left(P_{l,i}-E_{\mathrm{sys}}-P_{g,i}-P_i^d\right)+\mathsf{\Delta }{P}_{\mathrm{loss}}]+\\ \hspace{1em}\hspace{0.17em}\hspace{0.17em}{\displaystyle \sum _{i=1}^N}Z\left(P_i\right)\end{array}$$

(37)

where $\mu$ is the dyadic variable associated with the equation constraints in Equation (35b). According to the KKT condition in literature [19], the necessary conditions for $P_i$ to be a minimum are as follows:

$$\mu ={\left(1-\frac{\partial \mathsf{\Delta }{P}_{\mathrm{loss}}}{\partial P_i}\right)}^{-1}\nabla Z\left(P_i\right)$$

(38)

$$\sum _{i=1}^N{P}_i=\sum _{i=1}^N\left(P_{l,i}-P_{g,i}-E_{\mathrm{sys}}\right)+\mathsf{\Delta }{P}_{\mathrm{loss}}$$

(39)

Since Equation (38) contains differential terms reflecting complex dynamics, the analytical solution may be computationally difficult to handle, and, in this paper, we take a generalized solution with the aid of the graph theory of Section 2.2, i.e., letting $\left(\partial \mathsf{\Delta }{P}_{\mathrm{loss}}\right)/\left(\partial P_i\right)=0$, even though the resulting result may be slightly different from the ideal scheduling:

$$\{\begin{array}{l}\nabla f\left(P_i^{*}\right)={\mu }^{*}=1_N{\mu }_0\\ 1_N^{\mathrm{T}}\left(P_l-E_{\mathrm{sys}}-P_g-P^{*}\right)+\mathsf{\Delta }{P}_{\mathrm{loss}}=0\end{array}$$

(40)

where $\left(P_i^{*},{\mu }^{*}\right)$ describes the original dyadic optimal pair of the original problem; and ${\mu }_0$ is an agreement on the incremental cost (IC) that all agents do not deviate from each other.

4. Projected Gradient (PGA) Algorithm Based on Event-Triggered Communication

Due to the strong intermittency and randomness of new energy units’ output, isolated island microgrids with a high proportion of wind and photovoltaic power require precise energy management and control strategies during operation to ensure the stability of system operation. Considering that the distance between the units on the island is often far, the communication cost between different units and between the units and the dispatch center is high and it is difficult for conventional algorithms to perform active power sharing and frequency regulation of the system in the absence of sufficient real-time data. Based on the above problems, this paper proposes a projected gradient (PGA) algorithm based on an event-triggered mechanism, which only needs to share a small amount of data to sense an overall active power mismatch and automatically compensate for it, which greatly reduces the communication cost while ensuring the stability of the system.

Distributed new energy sources do not have direct access to inverter measurements and dispatchable power information, and Equation (35b) has limitations and implementation difficulties. The event-triggered, communication-based approach can provide an alternative to it, which can locally sense the overall active power mismatch without knowing $P_{l,i}$, $P_{g,i}$ or $\mathsf{\Delta }{P}_{\mathrm{loss}}$ and automatically compensate for the power loss without additional sensors, and can be directly applied to microgrids with unknown line parameters.

In this paper, an event-triggered mechanism for communication via asynchronous unidirectional information transfer is used so that the only information that needs to be shared among the agents of the system is the latest incremental cost (IC) information, thus avoiding unnecessary data transmission and utilizing the limited channel capacity.

The only information shared between neighboring DGs is the latest information about ${\mu }_i$, denoted by ${\mu }_i^{*}$, which will remain unchanged until the next event triggering agent i. The ${\mu }_i^{*}$ is the relative measurement error. To simplify the notation, this is denoted with ${\mu }_i^{*}(t):={\mu }_i\left(t_i^l\right)$, $t\in \left[t_i^l,t_i^{l+1}\right)$, and $e_i={\mu }_i^{*}-{\mu }_i$ as the relative measurement error. An event is triggered only when the following time-dependent thresholds are satisfied:

$$\begin{array}{c}{T}_i(t):=d_i{e}_i^2-\frac{1}{4}{\displaystyle \sum _{j\in {\mathcal{N}}_i}}{\left({\mu }_i^{*}-{\mu }_j^{*}\right)}^2\ge \\ c_1\exp \left(-c_2\left(t-t_i^l\right)\right)\end{array}$$

(41)

where $c_1$, $c_2$, and >0 are the adjustment coefficients used to achieve the desired communication reduction effect, and a trade-off between convergence speed and communication volume is required.

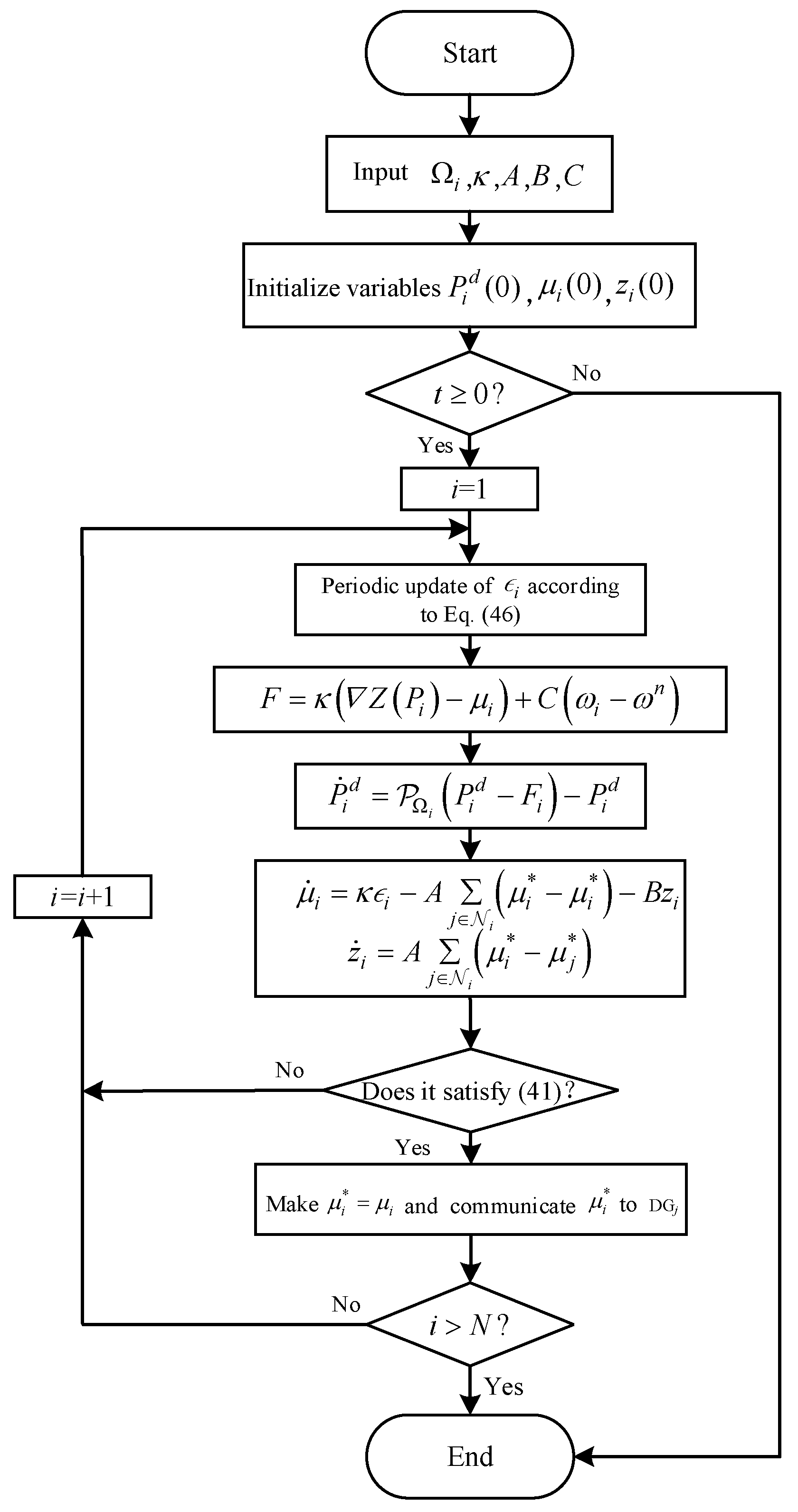
In traditional distributed scheduling control, coordinating two distributed control loops, i.e., the reference computation loop and the reference tracking loop, requires costly information exchanges for four state variables. To reduce the communication burden, distributed secondary control based on event-triggered communication is often used. Distributed active power controllers and distributed frequency controllers advocate sharing information about dyadic variables, auxiliary variables, and local frequency measurements among neighbors. However, in the implemented consensus protocols, there is no auxiliary variable that ensures the consistency of the dual variables, which will result in the energy not being truly balanced. Therefore, an organic combination of the above methods, a projected gradient (PGA) algorithm with event-triggered communication is shown in Figure 3, for which the selection and setting of parameters can be found in the literature [25] and will not be repeated here.

The specific formula of the PGA algorithm in Figure 3 is shown below:

$${\dot{P}}^d=P_{\mathsf{\Omega }}\left(P^d-F\right)-P^d$$

(42)

$$\dot{\mu }=\kappa ϵ-Aℒ{\mu }^{\ast }-Bz$$

(43)

$$\dot{z}=Aℒ{\mu }^{\ast }$$

(44)

$$F=\kappa \left(\nabla Z\left(P\right)-\mu \right)+C\left(\omega -1_N{\omega }^n\right)$$

(45)

$$ϵ={\tau }_P{k}_P^{-1}\dot{\omega }+k_P^{-1}\left(\omega -1_N{\omega }^n\right)$$

(46)

where $P^d=col\left(P_i^d\right)$; $\mu =col\left({\mu }_i\right)$; $z=col\left(z_i\right)$; $\omega =\mathrm{col}({\omega }_i)$; $ϵ=\mathrm{col}({ϵ}_i)$ $\nabla Z(P)=\mathrm{col}(\nabla Z(P_i))$; ${\mu }^{\ast }=col\left({\mu }_i^{\ast }\right)$; ${\tau }_P=diag\left({\tau }_{P_i}\right)$; $k_P=diag\left(k_{P_i}\right)$.

As shown in (42)–(46), this paper manages IEDs and FRs in an integrated manner, eliminates redundant distributed frequency controllers, and accomplishes a more complete economic scheduling while realizing frequency regulation [26,27]. The PGA algorithm is utilized to address the shortcomings of the conventional approach by maintaining the steady state consistency of the dyadic variables by keeping the auxiliary variables, and only the latest information about the dyadic variables needs to be sent to the neighboring DGs in the communication part, which will reduce the required communication to a relatively minimal level.

5. Simulation Verification

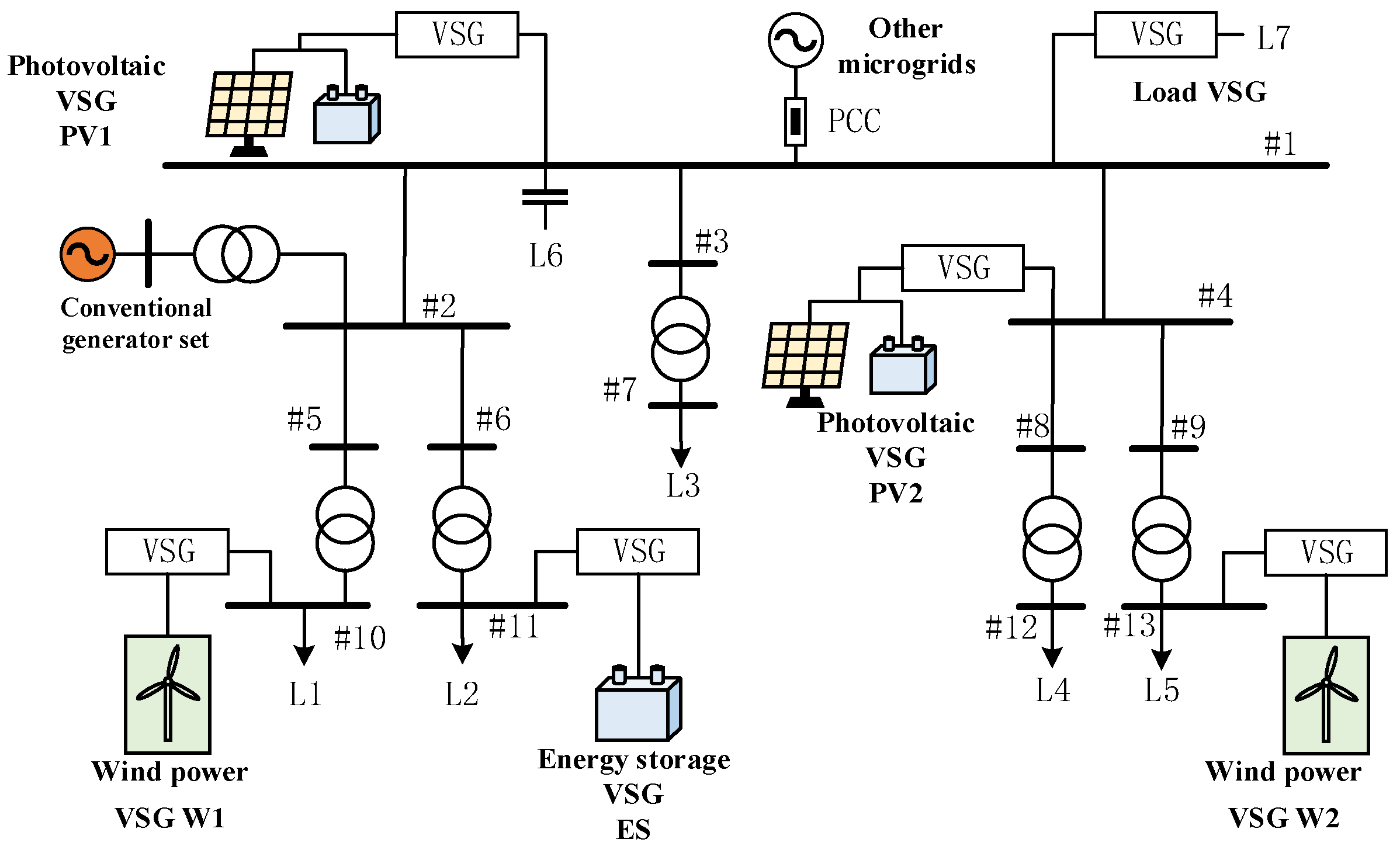
Firstly, the MATLAB/Simulink-based VSG microgrid model is constructed based on the reference IEEE13 node, whose structure is shown in Figure 4, and each type of VSG power source (W1 and 2 denote wind power VSGs; PV1 and 2 denote photovoltaic VSGs; and ES denotes energy storage VSGs) is connected by a ring communication network as shown in Figure 5, and each DG can obtain information through the communication network from each DG can access the required information from its neighboring DGs through the communication network, and L1–L7 denote the loads (refer to the load data of the traditional 13 nodes) [28,29]. The effectiveness of the integrated IED and FR method in this paper is verified based on the simulation results. Then, based on MATLAB R2021a software, the Gurobi solver is invoked to solve the traditional optimization method and compared with the results obtained from the PGA optimization method based on the DEDP equations in this paper, to verify the validity of the model in this paper as well as the adaptability of the frequency and economy.

The main parameters of various distributed VSG power sources and microgrid systems are shown in

Table 1. Main parameters of microgrid system.

Parameter Name	Value
rated voltage/V	380
Rated frequency/Hz	50
filter capacitor/µF	150
Filter Inductors/mH	5
$R_{oCoF}^{ex}$/(Hz/s)	1
$\mathsf{\Delta }{f}^{ex}$/Hz	0.8

,

Table 2. Power and load VSG parameters.

Parameter Name	Conventional Units	W1	W2	PV1	PV2	ES
Rated active/kW	70	60	60	50	50	55
energy storage capacity/(kW·h)	-	-	-	75	75	75
inertial time constant (ITC)/s	5.0	8.0	8.0	1~3	1~3	1~3
adjustment factor/%	4.5	4.0	5.0	2.0	2.0	3.0
virtual reactance/mH	-	4.0	4.0	4.0	4.0	4.0
Active power inertia	-	10.0	10.0	10.0	10.0	10.0
damping factor	-	50.0	50.0	50.0	50.0	50.0
$\eta$/(Yuan/(kW2·h))	0.35	0.35	0.35	0.35	0.35	0.35
$\lambda$/(Yuan/(kW·h))	7.0	7.0	7.0	7.0	7.0	7.0

and

Table 3. Cost/benefit coefficient PGA coefficient [30,31].

Parameter Name	Conventional Units	W1	W2	PV1	PV2	ES
$c_R$/(Yuan/(kW·h))	0.66	0.56	0.56	0.32	0.32	0.45
$\alpha$/(Yuan/(kW2·h))	0.12	0.105	0.105	0.084	0.084	0.12
$\beta$/(Yuan/(kW·h))	1.3	1.4	1.4	0.7	0.7	0.98
$\gamma$/(Yuan/h)	0.105	0.35	0.35	0.01	0.01	0.35
$k_{P,i}$	4.4 × 10−5	4.6 × 10−5	5.4 × 10−5	4.1 × 10−5	4.1 × 10−5	5.8 × 10−5
${\tau }_{P,i}$	0.016	0.016	0.016	0.016	0.016	0.016
${\rho }_i$	1.4	1.7	1.0	0.5	0.8	1.9

.

According to the algorithm of this paper $\kappa$ = 1.9, A = 5, B = 2, C = 30 and m = 2.2 are chosen.

5.1. Integrated FR with IED Dispatch Control

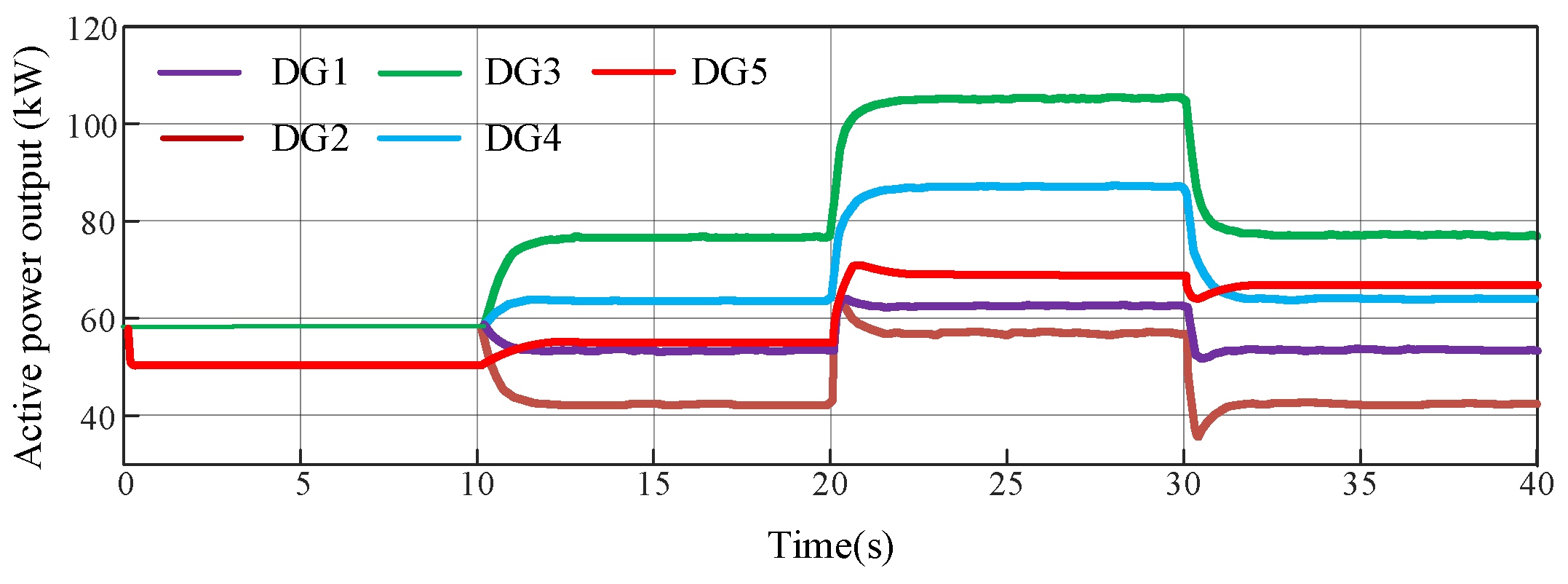
To verify the frequency regulation capability (disturbance resistance) of a microgrid integrated FR with IED scheduling and its economy, in this section, perturbations are added to the active power load and weather conditions at 0.2 s and 0.4 s, respectively, in which the amount of active power perturbation $\mathsf{\Delta }{P}_{\mathrm{loss}}$ is 20 kW and the amount of reduction of the wind power output due to the weather change is 15 kW. The active power output of each type of VSG power supply is shown in Figure 5. 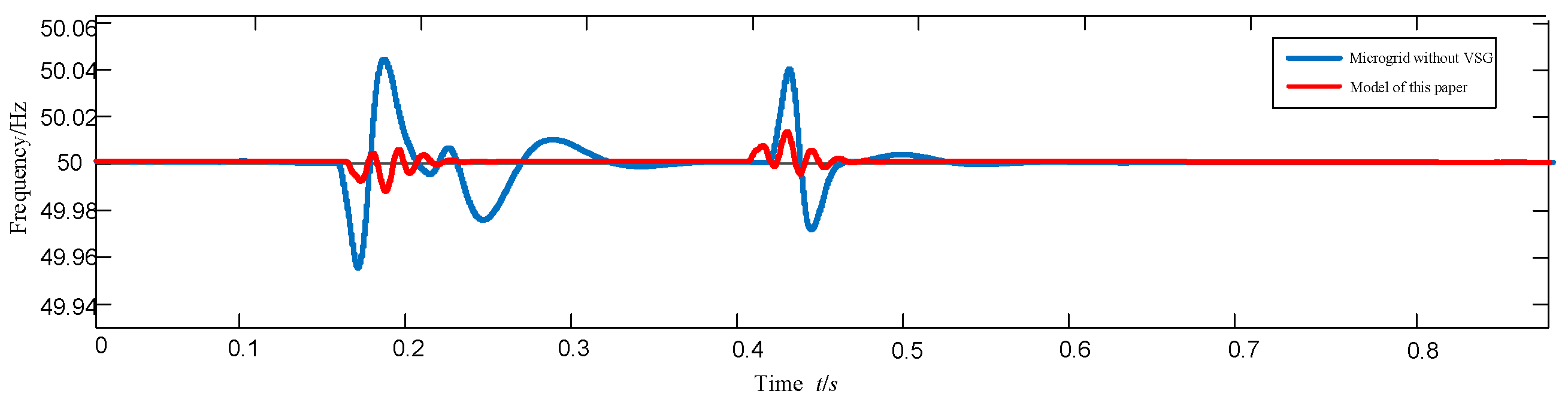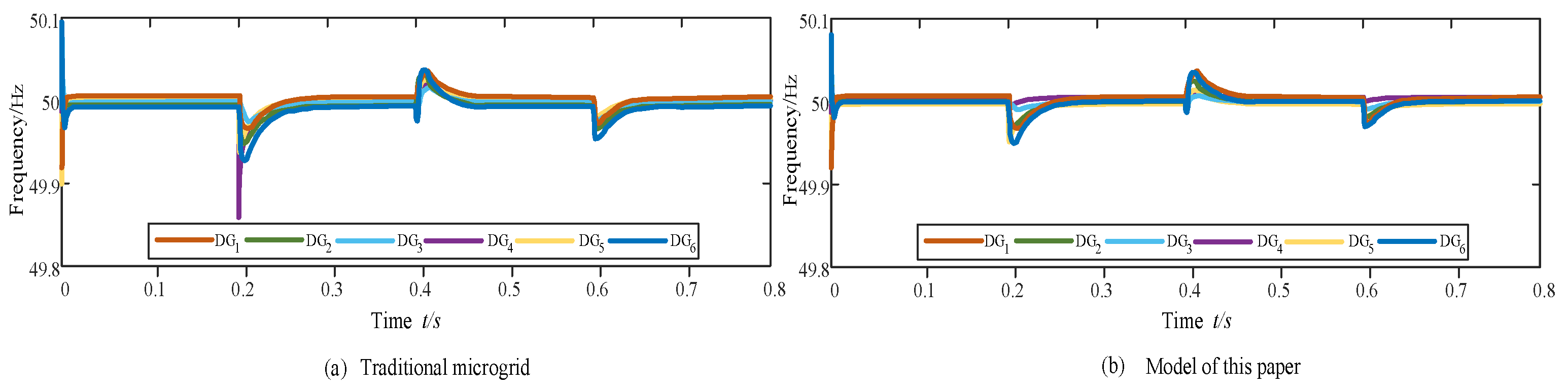From the frequency change curve at the PCC shown in Figure 6, it can be seen that the traditional microgrid scheduling control strategy without VSG has a large frequency fluctuation at the PCC after the disturbance at the other microgrid side, and it takes 0.25 s to recover to the rated value, whereas the model of the multi-type VSG power supply and the scheduling method adopted in this paper can make the frequency fluctuation at the PCC smaller and the recovery speed quicker. According to the frequency change curves of various types of VSG power sources shown in Figure 7a,b, it can be seen that the frequency fluctuation of traditional distributed power sources without VSG can reach 0.15 Hz after a disturbance, with the risk of going off-grid and having poor disturbance resistance; while in this paper, after fully taking into account the role of the inertial support of VSGs, the frequency fluctuations of various types of DGs are controlled to be less than 0.8 Hz and the microgrid’s frequency regulation (FR) capability and stability are significantly improved.

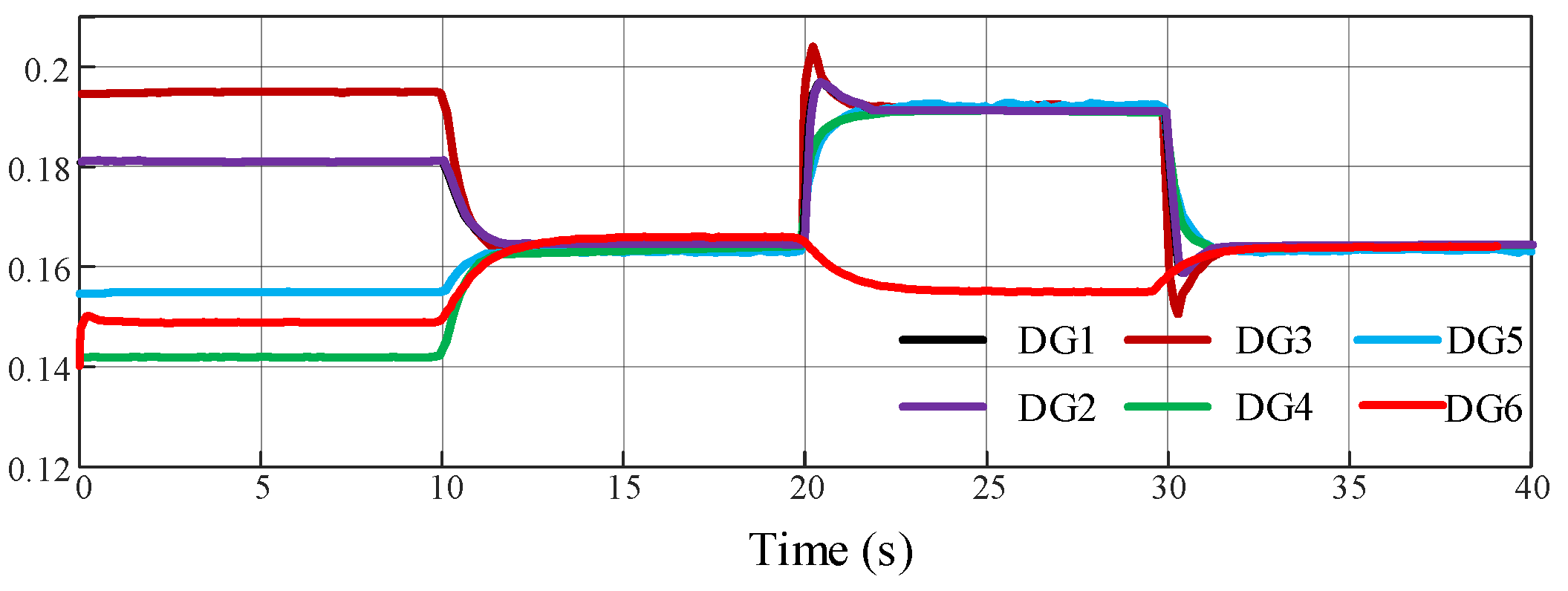
The incremental cost $\mu$ variation curves for each DG under the scheduling approach in this paper are shown in Figure 8.

From the above figure, it can be seen that an arbitrarily initialized $1_N^{\mathrm{T}}z(0)=0$ can be automatically projected between its LFCs subject to $P_i^d$ and constraint violations can be avoided completely throughout the process. By utilizing the local communication network, the active power setpoints of the DGs are optimally adjusted. Therefore, when global optimal dispatch is achieved, the active power setpoint of each DG may be different and may vary with load disturbances and weather conditions. Optimal scheduling is achieved when the frequency is adjusted to the nominal value, which means that FR and IED are done simultaneously.

5.2. Validation of PGA Algorithm

This section compares the moment-by-moment performance of the proposed algorithm with he DAPI algorithm and a traditional distributed gradient algorithm under active load variation over time. The PGA algorithm is based on event-triggered communication and the other two algorithms are based on periodic communication with an interval of 0.1 s. The dynamic frequency tuning and optimization process of the different scheduling algorithms is simulated for a time period t = 100 s.

Figure 9 and Figure 10 represent the system frequency change under time-varying load $P_l$ change and the overall comprehensive economic efficiency change of the system, respectively. From Figure 9, it can be seen that the system frequency stability is significantly better than the other two algorithms under the joint regulation of VSG control and PGA algorithm, which is because the PGA algorithm can locally and quickly sense the overall active mismatch of the system feedback and coordinate the DGs to utilize the VSG for transient frequency support after the frequency change, which avoids the separation of the time scales, while the distributed gradient algorithm is unable to effectively control frequency and the DAPI algorithm is limited to proportional power sharing and cannot provide an optimal solution. In terms of comprehensive economic benefits, the scheduling results of the three methods are shown in Figure 10, and the comprehensive economic cost of the PGA algorithm is significantly lower than that of the DAPI algorithm because it takes into account the load VSG benefits in the optimization and makes use of the frequency feedback control; since the distributed gradient algorithm also adopts the neighbor communication and event triggering mechanism for the power allocation, its communication resources and comprehensive cost are comparable to that of the PGA algorithm, but the PGA algorithm, which considers various types of power VSG control methods, is superior to the distributed gradient algorithm in terms of frequency regulation capability, so the PGA algorithm is the overall optimal solution.

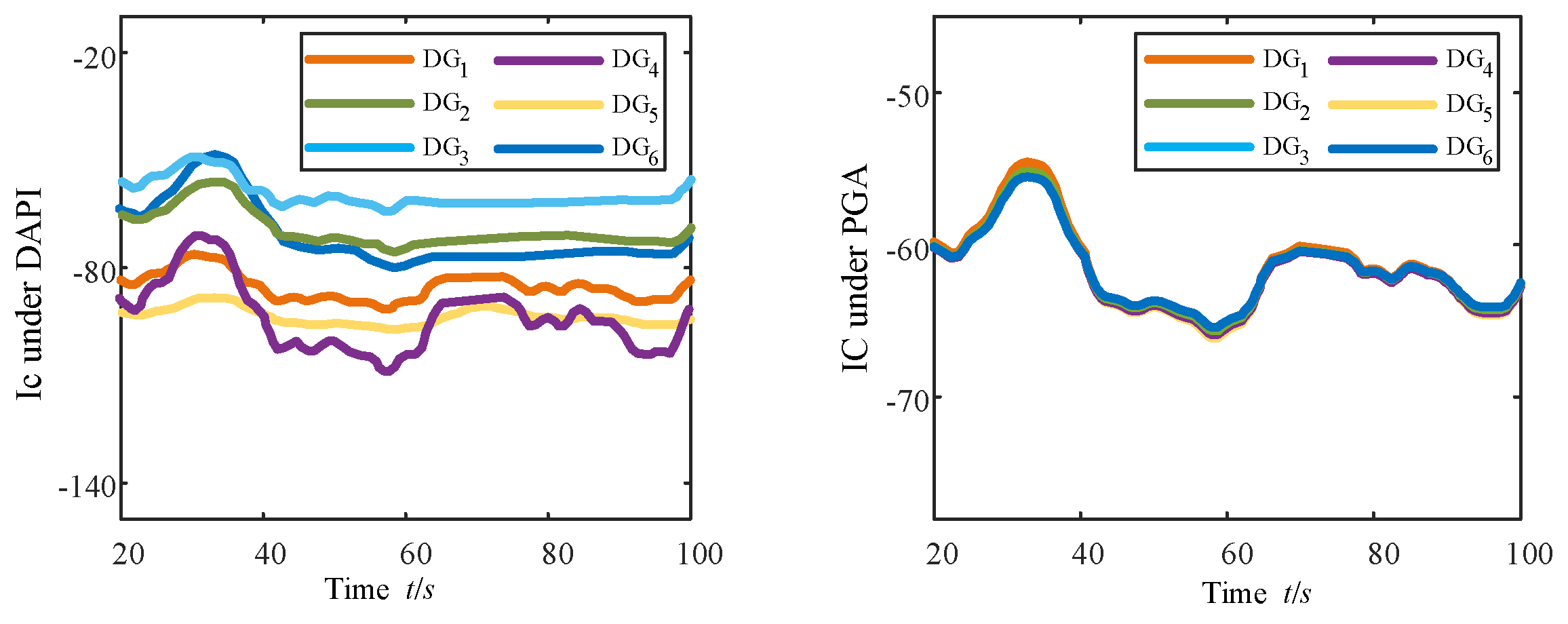
Figure 11 represents the ICs under the DAPI algorithm and the PGA algorithm. It can be seen from the figure that the time-triggered communication mechanism adopted by the PGA algorithm can solve the fairness problem that cannot be solved by the DAPI algorithm, i.e., each DG agent adopting the PGA algorithm possesses the same ICs, which implies that, despite the high degree of heterogeneity of the power generation conditions/preferences of the various types of DGs, the sharing of active power is strictly guaranteed to facilitate scheduling fairness as well as communication consistency.

6. Conclusions

In this paper, a distributed optimization algorithm integrating frequency regulation (FR) and integrated economic dispatch (IED) is proposed for an islanded microgrid with a high percentage of new energy generation which dynamically minimizes the integrated economic costs of the system, taking into account the inertia and capacity constraints of various types of VSG power sources, and, at the same time, estimates the power mismatch using a distributed algorithm based on event-triggered communication and regulates the frequency to a nominal value. Finally, the closed-loop stability is rigorously established and asymptotically converges to the optimal solution under reasonable operating assumptions to realize the global optimal dispatch of the microgrid. The main conclusions are as follows:

(1)

In this paper, an integrated microgrid dispatch model containing multiple types of VSG power sources is constructed which makes full use of the inertia and standby capacity of VSGs for frequency regulation, improves the effect of frequency regulation (FR) while effectively relieving the frequency regulation (FR) pressure of conventional units, realizes the synergistic complementarity of multiple frequency regulation (FR) resources, and strengthens the system’s disturbance-resistant capability and economy.

(2)

In this paper, a feedback-based projected gradient (PGA) algorithm with event-triggered communication is proposed for the scheduling control of integrated FR and IED. Unlike traditional feed-forward methods, the algorithm estimates power mismatch by taking into account the dynamic characteristics of IBMGs, does not require inter-unit negotiation, and avoids separation of multiple time scales.

This paper does not address the impact of multiple types of VSG power sources on frequency regulation and economic dispatch, and fails to consider the impact of different communication topologies on the microgrid control strategy. The integrated economic dispatch of multiple types of VSG power sources under different communication topologies will be further discussed in subsequent research.