Abstract
PV power generation is developing fast in both centralized and distributed forms under the background of constructing a new power system with high penetration of renewable sources. However, the control performance and stability of the PV system is seriously affected by the interaction between PV internal control loops and the external power grid. The impact of the PV system on the reliability, stability, and power quality of power systems has restricted them to further participate in power supplies with a large capacity. Traditional control methods have become ineffective at dealing with these problems as the PV system becomes increasingly complex and nonlinear. Intelligent control as a more advanced technology has been integrated into the PV system to improve system control performance and stability. However, intelligent control for the PV system is still in the early stages due to the extensive calculation and intricate implementation of intelligent algorithms. Further investigations should be carried out to effectively combine intelligent control with the PV system to constitute an intelligent PV power system with multiple functions, high stability, and high-performance. This paper provides a systematic classification and detailed introduction of various intelligent optimization methods in a PV inverter system based on the traditional structure and typical control. The future trends and research topics are given to provide a reference for the intelligent optimization control in the PV system.
1. Introduction
Photovoltaic power generation as one kind of important renewable energy has begun transitioning from an alternative power source to the main energy source in recent years [1]. During this process, centralized and distributed PV systems have become the two main energy streams [2]. The new power systems consist of a high percentage of renewable energy and a large percentage of power electronics, causing many new issues related to system control [3].
An important technique to address the issue of stability and reliability of PV systems is optimizing converters’ control. Power converters’ control is intricate and affects the overall stability of the system because of the interactions between different control loops inside the converter, parallel converters, and the power grid [4,5]. For a grid-connected PV system, inverters are the crucial part required to convert dc power from solar arrays to ac power transported into the power grid. The control performance and stability of inverters severely affect the PV system, and lots of works have explored how to analyze and improve PV inverters’ control stability [6].
In general, PV inverters’ control can be typically divided into constant power control, constant voltage and frequency control, droop control, etc. [7]. Of these, constant power control is primarily utilized in grid-connected inverters to control the active and reactive power generated by the PV system [8]. Frequency and voltage control is usually adopted in grid-forming inverters for the PV system to support system voltage and frequency [9]. Droop control generally refers to inverters’ active-frequency and reactive-voltage droop control. If the droop curves are properly designed, the inverters can adaptively adjust their output active and reactive power to finally work on an optimal parallel condition. In addition, PV inverters with droop control can be controlled as virtual synchronous generators when the inertial coefficient is constructed inside [10]. In these control modes, the specific classic controllers mainly include a proportional-integral (PI) controller, a proportional resonance (PR) controller, a repetitive (RP) controller, etc. [11]. In a PV system, the PI controller is mostly used for the dc voltage control and the ac current and voltage control on the d-q reference frame. The PR controller is usually utilized in tracking ac signals such as an inverter current in a α-β reference frame [12]. The RP controller is also used to track ac signals, but with higher harmonic rejection ability and lower stability, as it introduces resonators at harmonic frequency points compared with the PR controller [13,14].
Although conventional control techniques are straightforward and reliable, it is always hard for them to deal with the complicated coupling and interaction problems in PV inverter systems [15]. Control system optimization based on artificial intelligence is an effective way to improve the performance of PV inverters, allowing them to handle complicated control issues such as nonlinear dynamic interaction and multiple time-scale coupling [16]. Fuzzy control, as one of the most popular intelligent methods, has been widely utilized in the control of PV inverter systems, such as fuzzy PID control [17], repetitive-fuzzy control [18], fuzzy PR and PI control [19], and fuzzy PCI (proportional complex integral) with PR control [20]. The biggest advantage of fuzzy control is that it can realize self-tuning of parameters to allow real-time adjustment of the controller according to system operation status [21]. Fuzzy PCI and fuzzy PR have been employed in conjunction with standard PI and PR control, respectively, to improve the dynamic response and robustness of the system while eradicating the steady-state error. Other AI methods such as expert systems (ES), artificial neural networks (ANN or NNW), genetic algorithms (GA), and adaptive neuro-fuzzy algorithms (ANFIS) have also been applied to PV inverter system optimization [22]. However, these intelligent algorithms are usually computation-burdened and difficult to implement in real time, especially for fast control tasks.
With the rapid development of processors, intelligent technology has become part of all aspects of our lives, in addition to PV systems [23]. Intelligent PV plants will be an important part of the next generation of intelligent power grids with the application of big data, cloud computing, etc. [24]. Although various intelligent technologies have been used in a PV inverter system, the intelligence of the whole system is still at a rather low level. The intelligent methods are mainly utilized together with the traditional controllers to improve the system control speed and reliability. More work has to be carried out for further high-level utilization of intelligent control in PV systems and for the construction of highly stable, reliable, and multifunctional PV systems.
This paper reviews the intelligent optimal control of a PV inverter system to provide a reference for existing technologies and future development directions. Firstly, a brief overview of a grid-connected PV system and the conventional control strategies are given in Section 2 and Section 3, respectively. Section 4 concludes the state-of-the-art and development trends of intelligent optimization control in PV systems. Section 5 prospects future research directions based on this review. 6 concludes this paper.
2. Grid-connected PV Inverter System
A simplified PV system is presented in Figure 1. The system consists of a PV array, loads, transformers, dc/dc converters, and dc/ac inverters. The grid-connected PV system can convert the dc power output from the PV array into ac power for delivery to the power grid [25].
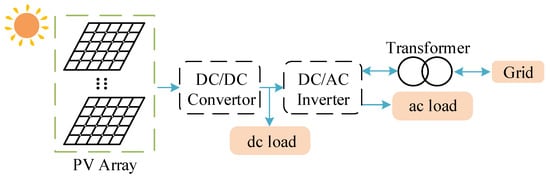
Figure 1.
Diagram of grid-connected PV system.
Inverters play an important role in grid-connected PV systems. The dc side voltage of the inverter is generally provided by a pre-stage boost converter with a constant output voltage Vdc. Based on the dc voltage, the inverter converts dc power into ac and connects with the public grid via an LCL filter [26], as shown in Figure 2.
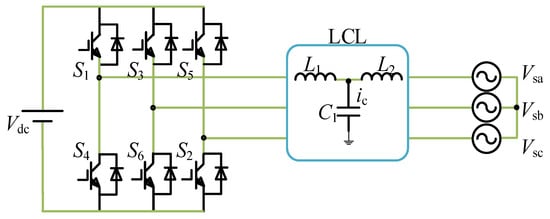
Figure 2.
Main circuit topology of grid-connected inverter.
3. Typical Control of Grid-Connected PV Inverters
The control performance of PV inverters determines the system’s stability and reliability. Conventional control is the foundation for intelligent optimization of grid-connected PV systems. Therefore, a brief overview of these typical controls should be given to lay the theoretical foundation of further contents. This section reviews the PQ control, constant voltage and frequency control, and traditional droop control in a grid-connected PV inverter system.
3.1. P-Q Control
The main purpose of PQ control is to make the PV system output constant active and reactive power [27], as shown in Figure 3. The PV output active and reactive power stays constant when the frequency and voltage vary within a limited range [28,29]. The active power output by the inverter is stabilized at the reference value Pref when system frequency fluctuates in the range fmin < f < fmax. Similarly, the reactive power output by the inverter is maintained at the reference value Qref when the system bus voltage varies in Vmin < V < Vmax.
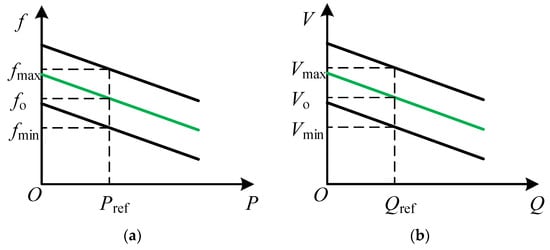
Figure 3.
PQ control schematic diagram. (a) Constant P; (b) constant Q.
According to the coordinate transformation, the PQ control can be implemented in the αβ reference frame and dq reference frame, as illustrated in Figure 4 and Figure 5, respectively. As shown in Figure 4, the grid-side current iabc and voltage ugabc at PCC (common connection point) are used to calculate the output active power P and reactive power Q. The output power is then compared to the power reference Pref and Qref to produce the active and reactive current reference [30]. In the PV system, the outer PQ control is usually modified as dc voltage control, as shown in Figure 5. The current reference in the q axis determines the PV output reactive power [31]. The current reference in the d axis is generated via dc voltage control to adjust the PV output active power in order to maintain the dc link power balance and stabilize dc voltage [32].
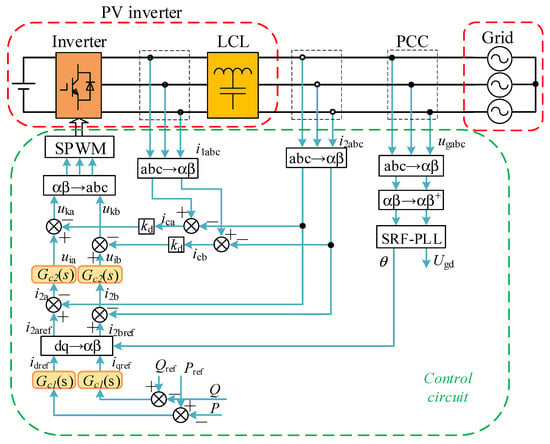
Figure 4.
PQ Control in αβ reference frame.
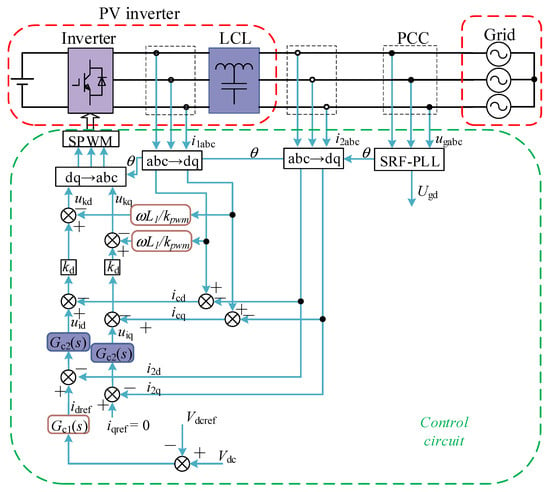
Figure 5.
PQ Control in dq reference frame.
The PQ control aims to control the PV output power, thus improving the system output capacity [33]. In the PQ control mode, energy storage devices are necessary to maintain the power balance on the dc bus to guarantee dc voltage stability [34].
3.2. Constant Voltage and Frequency (V/F) Control
The PQ control allows for active and reactive power regulation of the PV system, but it does not ensure system output voltage and frequency. V/F control can be used to maintain the voltage and frequency of the PV system in off-grid or weak-grid circumstances [35].
The block diagram for the three-phase grid-connected inverter’s V/F control is shown in Figure 6. In V/F control, the inverter output voltage is directly controlled [36]. The internal current loop is typically set up within the voltage control to increase the dynamic performance for quick regulation of the system’s output voltage and frequency [37].
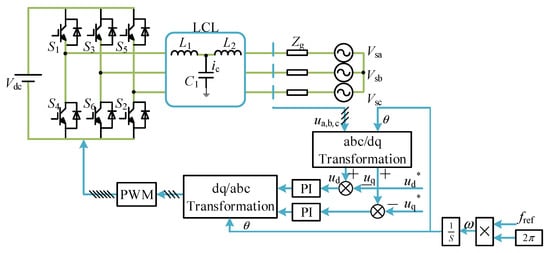
Figure 6.
V/F control of inverters.
Inverter V/F control is used for PV islanding operation and weak grid situations to support system voltage and frequency. When employing a master–slave control strategy, the V/F control needs to support the voltage and frequency of the entire network [38]. Generally, inverters can be converted from grid-connected mode to islanding mode when the public grid is rather weak or when the power quality is insufficient to fulfill the demands of the load [39]. The smooth transition from PQ control to V/F control is the core of this conversion [40], but achieving effective real-time detection of the grid state and timely control of the inverters is challenging [41]. In addition, the stability issues that occur during the switching process need to be further explored. Advanced technologies such as feature extraction, big data, and intelligent decision-making should be utilized for system better control [42].
3.3. Droop Control
Droop control is implemented in PV inverters by simulating the droop characteristics of the synchronous generator in a conventional power system [43,44]. Figure 7 shows the droop curves, by which the system can regulate and distribute the active power via P/f droop and the reactive power via Q/V droop. Taking the P/f droop as an example, as the load increases, the operating point shifts from point A to point B from the droop curves. Figure 7a shows that system frequency declines and more power is output for loads [45].
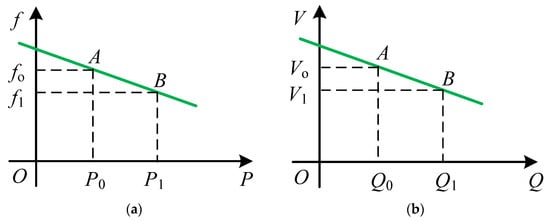
Figure 7.
Droop control curves. (a): P-f control; (b): Q-V control.
The grid-connected inverter system with droop control is shown in Figure 8 [46]. The amplitude and frequency of inverter output voltage are derived using the droop curves illustrated in Figure 8. The closed-loop voltage and current control are used to improve the system’s dynamic performance [47]. In general, droop control works as the first stage of system power and frequency regulation. It cannot realize zero error control because of the constant droop curve [48]. Therefore, implementing secondary control by redesigning the droop curve to change its equilibrium points is necessary [49]. For instance, in the P/f droop curve, the system frequency reduces when output power rises. Only if the output power is the rated reference power can the frequency be stabilized at the reference point. Therefore, the power reference should be controlled to adapt for the rated frequency point by secondary control.
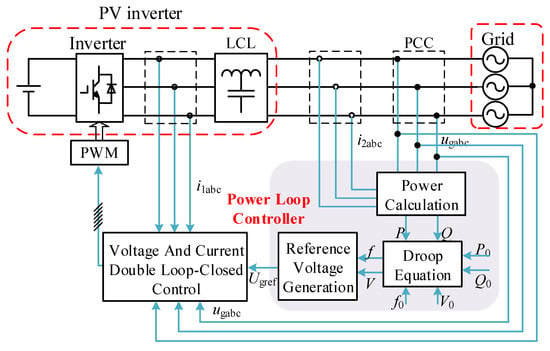
Figure 8.
Droop control in grid-connected inverter system.
By designing different slopes of droop curves for parallel inverters, the active power demanded by load can be distributed according to the capacity of different generation units [50,51]. However, the line impedance between parallel inverters affects the distribution of active and reactive power [52]. The system’s frequency and voltage are influenced by both active power and reactive power, which seriously affect the performance of traditional droop control [53]. Optimizing droop control with intelligent algorithms for system better control performance is an important research topic.
4. Intelligent Optimization Control of PV System
Intelligent control such as fuzzy logic control (FLC), expert system control (ES), artificial neural networks (ANN), and adaptive neuro-fuzzy inference system (ANFIS) offer significant advantages for dealing with highly nonlinear objects and uncertain mathematical models [54]. These methods can be utilized in the PV system to improve the system stability and reliability. In particular, as the PV plant grows large and the power grid becomes complex, it becomes difficult to accurately model and control the nonlinear and multi-coupled PV inverter system [55]. By combining conventional control with intelligent methods, the dynamic and static characteristics of the PV system can be improved without the complex derivation of system-accurate mathematical models.
4.1. Fuzzy Optimization Control
Among various intelligent control methods, fuzzy logic control (FLC) is relatively mature and is very suitable for objects whose dynamic characteristics are not easy to obtain [56]. FLC is less sensitive to parameters and load variations and outperforms conventional controllers in terms of response time, stability time, and robustness [57]. FLC generally does not require insight into the detailed structure and parameters of the system, nor does it require a mathematical model to describe the system precisely [58]. The control logic can be constructed using a fuzzy language and a suitable membership function, and when well designed, FLC often outperforms other more complex controllers.
The application of FLC cooperated with PI control in a PV inverter system is given in Figure 9, where r(t) is the reference value (the current reference in the d-q frame or the dc voltage reference) and y(t) is the actual value. The error between the reference and the actual value is e(t), with its change rate expressed as de/dt. FLC mainly consists of three parts, i.e., fuzzification, fuzzy interference, and defuzzification. The results output by FLC are ΔKp and ΔKi, which are used to adjust PI controller parameters Kp and Ki.
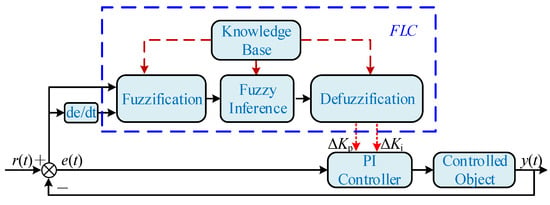
Figure 9.
Block diagram of fuzzy PI control.
The detailed implementation of FLC optimization in PV inverter systems can be roughly divided into 3 steps [59]. Step 1: Design a conventional linear digital controller. Step 2: Convert this controller into a fuzzy logic implementation. Step 3: Implement the fuzzy logic using the heuristic knowledge of the system and trial-and-error methods to improve the controller’s performance.
FLC can also combine with PR controller to generate fuzzy PR for control optimization of ac components such as current and voltage in a α-β frame [60]. Fuzzy PI and PR enhance the inverter’s ability to resist unexpected disturbance and realize self-adaptation compared with conventional PI and PR controllers. It has been demonstrated that FLC has a superior performance to traditional controllers when it comes to lowering system voltage and current overshoot and improving system dynamic performance [61]. However, the membership function and fuzzy rules have a significant impact on system control accuracy and are in need of further investigation [62]. Furthermore, complicated grid conditions such as large grid impedance and reactive power compensation have not been taken into account. In fact, as the scale of the PV system increases, the performance of FLC is severely affected by complex grid conditions. In particular, when there are no static operating points, if and how FLC can improve system stability needs to be further studied.
FLC can be employed directly within the current and voltage control without being combined with traditional controllers, but directly substituting PI and PR controllers [63,64] introduced FLC into the synchronous control part to improve the synchronization stability of inverters. The implementation is shown in Figure 10. A hybrid scheme is formed by combining fuzzy control with conventional PI control in phase-locked loop. The difference is that this FLC is not designed to regulate PI parameters but works as an independent controller to control the system directly. The delayed signal cancellation (DSC) is a pre-filter that extracts the positive sequence components of the grid voltage [65]. Dip detection enables the single-input fuzzy logic controller (SFLC) in time by monitoring grid voltage dips. The hybrid logic controller (HLC2) enables logic switching between DSC and SFLC. This control scheme can prevent the synchronization instability under voltage dips and significantly increases the inverter synchronization speed. However, the internal mechanism of how fuzzy control increases synchronization stability and the efficiency for complex systems has to be further analyzed and proved.
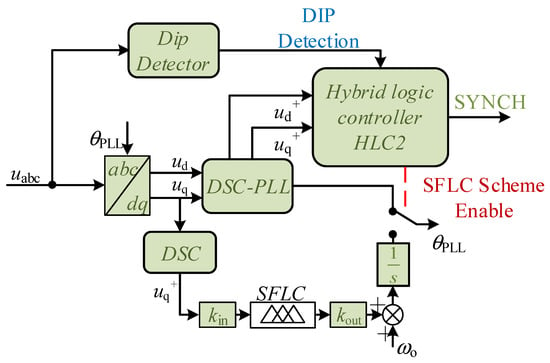
Figure 10.
Diagram of hybrid-scheme controller.
In summary, FLC can improve the dynamic and static performance and is therefore widely used in many control loops of the PV inverter system. In particular, for some nonlinear and complex coupling situations, fuzzy control can avoid the difficulties of system modeling and facilitate control optimization. However, the performance of fuzzy control is strongly influenced by the fuzzy logic and the membership function, and the design process requires a high level of experience; therefore, the design guidelines should be further investigated for PV inverter systems, especially with regard to the complex grid-connected situation.
4.2. Expert System Optimization Control
Expert system usually refers to a class of computerized intelligent program systems with expertise and experience [66]. The current development of expert system design is relatively mature, however, its application in PV inverter system is still in its infancy [67]. The fundamental structure of an expert system is illustrated in Figure 11.
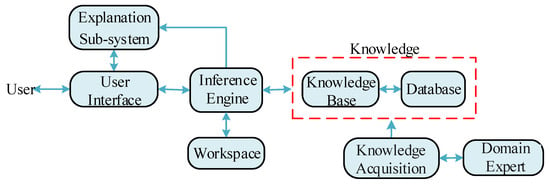
Figure 11.
Block diagram of basic expert system control.
Expert systems try to control the system using the knowledge of domain experts [68]. Knowledge engineers translate domain specialists’ knowledge into expert systems [69]. Knowledge can be divided into two categories: the knowledge base (i.e., the information that supports expert knowledge) and data base (i.e., information that is supported by data, facts, and statements) [67]. The knowledge base consists of a set of generative rules [70]. The inference engine attempts to validate the rules using either forward-linking or backward-linking methods.
Expert PID control is a typical application of expert systems in PV inverters optimization control. Similar to fuzzy PI, expert PID control in PV inverters takes advantage of experts’ experience to modify PID parameters [71]. Because of the introduction of expert experience, inverter systems with expert PID generally have better stability and more dynamic performance [72]. However, as the controller parameters are adjusted according to expert experience, the knowledge and inference process plays an important role in system design.
4.3. ANN Optimization Control
Compared to fuzzy control and expert control, ANN control can approximate any nonlinear continuous function with arbitrary accuracy and is highly adaptable to complex conditions with self-learning capability for multi-objective control [73,74,75,76]. In addition, ANN distributes and stores information in the neurons within the neural network, which is highly robust and fault tolerant [77]. The characteristics of ANN, such as its self-learning, self-organizing and self-adaptive capabilities, can help to handle uncertain or unknown systems [78].
Figure 12 shows the control of the PV inverters with ANN, in which the internal current control loop is realized by a neural network. The current reference is generated by an external power loop, and the ANN controller adjusts the actual feedback current to follow the reference current.
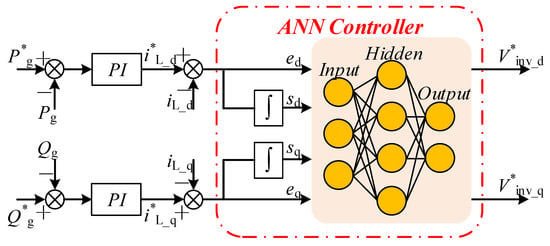
Figure 12.
The neural-network-based PQ control of PV inverters.
The ANN has four layers in terms of network structure: one input layer, two hidden layers, and one output layer [79]. The input layer contains four inputs, two of which include the error vector edq(k), and the other two include the integration of the error sdq(k), which are respectively defined as:
The output layer is v∗inv_dq(k). The ratio of the inverter output voltage vinv_dq to the ANN output voltage v∗inv_dq is the pulse width modulation (PWM) gain, noted as kPWM, then vinv_dq is:
where A(edq(k), sdq(k), ω) denotes the mathematical model of the neural network and w is the neural network weight vector.
The utilization of ANNs in a PV inverter system can solve the difficulties of designing controller parameters for the complex coupled nonlinear system [80,81]. On the other hand, training an ANN demands a large amount of data and is time consuming [82]. The challenge of designing a neural network is determining how to maximize the parameters that need to be sought in the network, assuming that the number of layers and the number of neurons in each layer have been established [83]. It has been suggested that the gradient descent optimization (GDO) approach can be used to train the MLP (multilayer perceptron) controller (MLPC) [84]. On this foundation, ANN can be utilized much more profitably and can be more resilient than sliding mode controllers [85].
Fuzzy logic and neural networks are two common intelligent control techniques that have their own drawbacks in practice. Fuzzy neural networks combining the benefits of fuzzy control and neural network are one of the hottest areas of intelligent control research [86].
4.4. Adaptive Neuro-Fuzzy Algorithm Optimization
Using fuzzy control principles and combining the advantages of both FLC and ANN, the neuro-fuzzy controller has many advantages, such as the learning capabilities of neural networks, parallel knowledge/data processing capabilities, and human fuzzy logic reasoning capabilities [87,88,89,90]. The ANFIS (adaptive neural network fuzzy inference system) is a fuzzy inference system based on the Takagi–Sugeno model [91]. The fundamental fuzzy control processes (i.e., fuzzification, fuzzy inference, and defuzzification) are implemented by neural networks [92]. The learning mechanism of neural networks can extract rules from input and output sample data to create an adaptive neuro-fuzzy controller [93]. The system can develop toward self-adaptation, self-organization, and self-learning by self-adjusting the fuzzy inference control rules using offline training and online learning algorithms.
4.4.1. Adaptive Neuro-Fuzzy Optimization for PV Inverter with PQ Control
By combining ANFIS with traditional PID controller the adaptive fuzzy neural PID control can be implemented in a PV inverter system to address the issues of system instability and long response times [94,95]. The ANFIS-based PID control in the PV inverter system is given in Figure 13. The membership function and rule base of the fuzzy controller is determined by ANFIS using ANN, and the PID control parameters are modified online [96]. The external loop controls the voltages of the dc bus and the point of common coupling (PCC) to generate the current reference on the d-q axis, which are denoted, respectively, as I∗d, I∗q. By managing the grid-connected current, the internal control loop regulates the system power. There are four ANFISPIDs (ANFIS-based PID controls) in the inner and outer control loops whose outputs are the PID parameters and inputs are the error and error change rate of control objects such as the dc voltage, PCC voltage, and active and reactive currents:
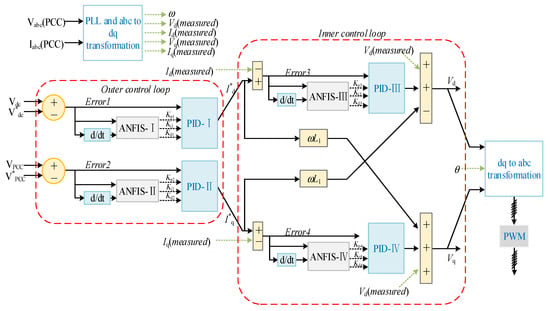
Figure 13.
PID control of grid-connected inverter based on ANFIS.
ANFIS controls the PV system without an accurate system model. Combined with conventional PID, ANFIS allows for faster online parameters modification and greater generalization capability [97]. However, the ANFIS-derived membership function is not compatible with multiple control problems in complex conditions, such as control conflicts within the grid-connected inverter, large line distribution impedance, phase sequence asymmetry, and transient instability, etc.
A new adaptive neuro-fuzzy control method has been proposed in [98]. The main objective is to simultaneously achieve smooth bi-directional currents control and nonlinear unbalanced load compensation. However, in practice, any time a new unit is added, the system must re-learn each unit’s state information, which severely restricts its practical application.
4.4.2. Adaptive Neuro-Fuzzy Optimization for a PV Inverter with Droop Control
As previously indicated, ANFIS generates input/output mapping using membership functions (MFs) and appropriate input/output (I/O) mappings based on fuzzy if–then rules. The settings of MF can be altered through learning. During this process, the fuzzy rules are modified by appropriate neural network training without any knowledge of membership functions and rules [99]. The configuration of the membership function depends on their parameters, which are automatically selected by ANFIS, and the appropriate I/O data are used to build the FIS. Compared with conventional droop control, the FIS has two inputs: active power (P) and reactive power (Q), and the output is either the frequency (f) or the voltage (V). A typical structure for PV inverters based on ANFIS is shown in Figure 14, Among them, the symbol “&” represents the sum of the input signal, and the symbol “N” represents the ratio of the triggering intensity of the i-th node to the sum of all rule triggering intensities.
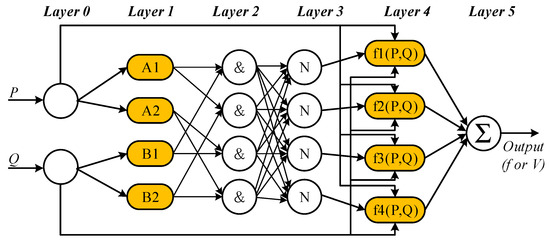
Figure 14.
Droop control of inverter based on ANFIS.
This is a model-free droop control which can eliminate the dependence of conventional droop control on line parameters. It has been proved that the system with ANFIS has a more ideal dynamic performance and higher reliability with regard to sharp changes in active and reactive power [100]. From the control point of view, the essence of ANFIS is a type of nonlinear system control. Theoretically, ANFIS can be implemented under nonlinear working conditions and any nonlinear mapping with arbitrary accuracy. However, due to the huge amount of computation of the neural network, the contradiction between the calculation time and the control accuracy of ANFIS under various operating conditions needs to be resolved.
Summarizing the above discussion, Table 1 shows the advantages and disadvantages of the different control methods. Most traditional control methods are simple in design but struggle to cope with complex nonlinear coupling systems. Intelligent control methods have great robustness and adaptability to different systems. However, intelligent control methods rely heavily on training data and practical experience.

Table 1.
Comparison of different control methods.
5. Research Prospects
As a result of the development of cloud computing, big data, and other advanced technologies, artificial intelligence is now widely used in all walks of life. Low-carbon and intelligence are the mainstream characteristics of modern power systems. Power electronics combined with intelligent control help PV systems to be observable, controllable, and adjustable. However, the degree of intelligence of PV systems is still at a low level. The potential of intelligent control to improve PV system power quality and stability has yet to be explored. Based on our review, this paper presents the following research prospects.
The function of PV inverters can be further improved by intelligent optimization. Grid-connected PV inverters can be controlled in grid-following and grid-forming mode. Traditionally, PV inverters work in grid-following mode to output the maximum amount of power by controlling the output current. However, grid-forming inverters can support system voltage and frequency and play an important role in weak power grids. Inverters with two operation modes are attracting more attention. Determining how to adaptively switch two control modes and improve system stability according to the grid conditions using intelligent optimization needs further investigation.
The intelligent optimization should be deployed in a way that affects the system’s overall performance and makes the PV system an intelligent unit. Current optimization mostly concentrates on improving the performance of a certain control loop. Further study is required to determine how to coordinate and optimize the system to solve the interaction problems between different control loops and improve the system’s global control performance. A centralized or upper intelligent controller deserves more attention.
More intelligent algorithms should be introduced and modified to improve PV systems’ intelligence and hybrid control. Combining these systems with traditional and intelligent methods will be a good choice in future research. Even for intelligent controllers with many benefits in dealing with complex and nonlinear system control problems, their performance is largely reliant on the design process. The design of fuzzy rules and membership functions in fuzzy control has yet to be further explored to improve the system’s response speed and accuracy. Data processing techniques such as real-time data gathering and feature extraction pose challenges for ANN and other related control methods that require a lot of data support. The cooperation of intelligent control and traditional control will be an important research topic for a long time. The shortcomings of intelligent control, such as that it is time consuming and hard to implement in real time can be solved with the help of traditional control. On the other hand, intelligent control can be utilized to make up for the problems of traditional control, such as difficulties in system modeling and adaptive regulation of controller parameters.
Deeper and more comprehensive intelligent control should be investigated with regard to an intelligent PV system. Although the performance of the PV system has been improved by intelligent optimization, there is still a long way to go before we can achieve a fully intelligent PV system. Many aspects of PV systems should be taken into consideration, including (but not limited to) the intelligent control of power converters, the intelligent operation and protection control system, and the intelligent sensing and detection technologies. Furthermore, the intelligent distributed PV system with the demand response, user-side intelligent housekeepers, and optimal power flow will contribute significantly to PV system promotion and application.
6. Conclusions
A centralized and distributed PV system is an important part of a renewable power system. Intelligent control of PV systems helps to constitute the smart grid and energy internet. However, the current research on intelligent PV systems is still in its infancy. In this paper, the research on typical control and intelligent optimization of PV inverter systems is reviewed. Future development and research topics are discussed and summarized. The combination of intelligent methods and traditional control is a good choice for improving these systems’ performance. Multi-layer and multi-aspect intelligent control can be investigated to improve the intelligence and control of PV systems. The research in this paper can provide a reference for the intelligent development and stability control of PV systems.
Author Contributions
Conceptualization, Q.Z. and M.M.; methodology, Z.Z. and Q.Z.; software, S.W. and Q.Z.; validation, M.M., Z.Z. and Q.Z.; formal analysis, Q.Z. and S.S.; investigation, Q.Z. and Z.Z.; resources, D.M. and Q.H.; data curation, S.W. and M.M.; writing—original draft preparation, Z.Z.; writing—review and editing, Q.Z.; visualization, M.M.; supervision, Q.Z. and M.M.; project administration, Q.Z.; funding acquisition, Q.Z. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Colleges and Universities of Anhui Province, grant number 2022AH050326, and the National Natural Science Foundation of China, grant number 52107177.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
Author Zhaorong Zhai was employed by the company Suixi Power Supply Company, State Grid Anhui Electric Power Co., Ltd. Author Shijing Wang was employed by the company State Grid Anhui Wuhu Power Supply Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Li, Z.; Zhang, R.; Sun, H.; Zhang, W.; Mei, C. Review on key technologies of hydrogen generation, storage and transportation based on mul-ti-energy complementary renewable energy. Trans. China Electrotech. Soc. 2021, 36, 446–462. [Google Scholar]
- Chen, W.; Ai, X. Influence of grid-connected photovoltaic system on power network. Electr. Power Autom. Equip. 2013, 33, 26–32+39. [Google Scholar]
- Zhou, X.; Chen, S.; Lu, Z.; Huang, Y.; Ma, S.; Zhao, Q. Technology features of the new generation power system in China. Chin. Soc. Elec. Eng. 2018, 38, 1893–1904. [Google Scholar]
- Xie, X.; He, J.; Mao, H.; Li, H. New issues and classification of power system stability with high shares of renewables and power electronics. Chin. Soc. Elec. Eng. 2021, 41, 461–475. [Google Scholar]
- Zhang, Q.; Mao, M.; Ke, G.; Zhou, L.; Xie, B. Stability problems of photovoltaic (PV) inverter in weak grid: A review. IET Power Electron. 2020, 13, 2165–2174. [Google Scholar] [CrossRef]
- Zheng, K.; Zhou, L.; Zhang, Q.; Xie, B.; Li, H. Stability analysis and parameter optimization design of photovoltaic grid-connected inverter under digital control. Trans. China Electrotech. Soc. 2018, 33, 1802–1813. [Google Scholar]
- Zhang, X.; Li, M.; Guo, Z.; Wang, J.; Han, F.; Fu, X. Review and perspectives on control strategies for renewable energy grid-connected inverters. J. Glob. Energy Interconnect. 2021, 4, 506–515. [Google Scholar]
- Weckx, S.; Gonzalez, C.; Driesen, J. Combined central and local active and reactive power control of PV inverters. IEEE Trans. Sustain. Energy 2014, 5, 776–784. [Google Scholar] [CrossRef]
- Tang, X.; Hu, X.; Li, N.; Deng, W.; Zhang, G. A novel frequency and voltage control method for islanded microgrid based on multienergy storages. IEEE Trans. Smart Grid 2014, 7, 410–419. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, H.; Wan, T.; Shi, D.; Lyu, L.; Cai, G. An integrated control algorithm of power distribution for islanded microgrid based on improved virtual synchronous generator. IET Renew. Power Gener. 2021, 15, 2674–2685. [Google Scholar] [CrossRef]
- Mao, P.; Zhang, M.; Zhu, Y.; Zhang, W. A novel current controller in photovoltaic grid-connected inverter. J. Chin. Inst. Eng. 2021, 44, 277–292. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, L.; Li, H.; Zheng, C.; Xie, B. Oscillation analysis and suppression of large-scale grid-connected photovoltaic system considering SVG equipment. Chin. Soc. Elec. Eng. 2019, 39, 2636–2644. [Google Scholar]
- Ye, J.; Liu, L.; Xu, J.; Shen, A. Frequency adaptive proportional-repetitive control for grid-connected inverters. IEEE Trans. Ind. Electron. 2020, 68, 7965–7974. [Google Scholar] [CrossRef]
- Jiang, F.; Zheng, L.; Song, J. Repetitive-based dual closed-loop control approach for grid-connected inverters with LCL filters. Chin. Soc. Elec. Eng. 2017, 37, 2944–2954. [Google Scholar]
- Wang, Y.; Wang, X.; Blaabjerg, F.; Chen, Z. Harmonic instability assessment using state-space modeling and participation analysis in inverter-fed power systems. IEEE Trans. Ind. Electron. 2016, 64, 806–816. [Google Scholar] [CrossRef]
- Xiang, X.; Luo, A.; Li, Y. Intelligent control method of power supply for tundish electromagnetic induction heating system. J. Mod. Power Syst. Clean Energy 2020, 8, 1188–1195. [Google Scholar] [CrossRef]
- Kluska, J.; Zabinski, T. PID-like adaptive fuzzy controller design based on absolute stability criterion. IEEE Trans. Fuzzy Syst. 2019, 28, 523–533. [Google Scholar] [CrossRef]
- Wang, Y. Research on Inverter Based on Repetitive and Fuzzy Control. Master’s Thesis, Tianjin University, Tianjin, China, 2020. [Google Scholar]
- Li, H.; Yang, X.; Wang, Y. Research on grid-connected three-phase inverter based on fuzzy PR control and PI control. Electric. Drive 2016, 46, 55–59. [Google Scholar]
- Yang, X.; Guo, K.; Yang, F.; Xue, B.; Wang, T. A control strategy of grid-connected inverter with three-phase LC filter based on fuzzy PCI and PR control. J. Electr. Power Sci. Technol. 2020, 35, 20–26. [Google Scholar]
- Liang, L. The application of fuzzy PID controller in coupled-tank liquid-level control system. In Proceedings of the 2011 International Conference on Electronics, Communications and Control (ICECC), Ningbo, China, 9–11 September 2011. [Google Scholar]
- Bose, B.K. Artificial intelligence applications in renewable energy systems and smart grid–some novel applications. In Power Electronics in Renewable Energy Systems and Smart Grid: Technology and Applications, 12th ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2019; pp. 625–675. [Google Scholar]
- Azeroual, M.; Boujoudar, Y.; Iysaouy, L.E.; Aljarbouh, A.; Fayaz, M.; Qureshi, M.S.; Rabbi, F.; Markhi, H.E. Energy management and control system for microgrid based wind-PV-battery using multi-agent systems. Wind. Eng. 2022, 46, 1247–1263. [Google Scholar] [CrossRef]
- Mohbey, K.K.; Kumar, S. The impact of big data in predictive analytics towards technological development in cloud computing. Int. J. Eng. Syst. Model. Simul. 2022, 13, 61. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, L.; Mao, M.; Xie, B.; Zheng, C. Power quality and stability analysis of large-scale grid-connected photovoltaic system consid-ering non-linear effects. IET Power Electron. 2018, 11, 1739–1747. [Google Scholar] [CrossRef]
- Ibrahim, N.F.; Mahmoud, M.M.; Al Thaiban, A.M.; Barnawi, A.B.; Elbarbary, Z.S.; Omar, A.I.; Abdelfattah, H. Operation of grid-connected PV System with ANN-based MPPT and an otimized LCL filter using GRG algorithm for enhanced power quality. IEEE Access 2023, 11, 106859–106876. [Google Scholar] [CrossRef]
- Yang, D.; Wang, X.; Liu, F.; Xin, K.; Liu, Y.; Blaabjerg, F. Adaptive reactive power control of PV power plants for improved power transfer capability under ultra-weak grid conditions. IEEE Trans. Smart Grid 2017, 10, 1269–1279. [Google Scholar] [CrossRef]
- Nayak, P.; Patel, T.; Munda, N.; Mallick, R.K. Optimal PQ control of solar photovoltaic based microgrids with battery storage. In Proceedings of the 2019 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 22–23 March 2019. [Google Scholar]
- Haider, S.; Li, G.; Wang, K. A dual control strategy for power sharing improvement in islanded mode of AC microgrid. Prot. Control. Mod. Power Syst. 2018, 3, 10. [Google Scholar] [CrossRef]
- Jiang, X.; Zhou, Y.; Ming, W.; Yang, P.; Wu, J. An overview of soft open points in electricity distribution networks. IEEE Trans. Smart Grid 2022, 13, 1899–1910. [Google Scholar] [CrossRef]
- Das, A.; Batzelis, E.I.; Anand, S.; Sahoo, S.R. Network-agnostic adaptive PQ adjustment control for grid voltage regulation in PV systems. IEEE Trans. Ind. Appl. 2022, 58, 5792–5804. [Google Scholar] [CrossRef]
- Yi, G. Micro-grid constant power control strategy analysis under grid voltage imbalance. Trans. China Electrotech. Soc. 2015, 30, 377–387. [Google Scholar]
- Poonahela, I.; Bayhan, S.; Abu-Rub, H.; Begovic, M.M.; Shadmand, M.B. An effective finite control set-model predictive control method for grid integrated solar PV. IEEE Access 2021, 9, 144481–144492. [Google Scholar] [CrossRef]
- Bai, W.; Abedi, M.R.; Lee, K.Y. Distributed generation system control strategies with PV and fuel cell in microgrid operation. Control. Eng. Pr. 2016, 53, 184–193. [Google Scholar] [CrossRef]
- Khan, R.; Islam, N.; Das, S.K.; Muyeen, S.M.; Moyeen, S.I.; Ali, M.F.; Tasneem, Z.; Islam, M.R.; Saha, D.K.; Badal, M.F.R.; et al. Energy sustainability–survey on technology and control of microgrid, smart grid and virtual power plant. IEEE Access 2021, 9, 104663–104694. [Google Scholar] [CrossRef]
- Wang, Y.; Kuang, Y.; Xu, Q. A current-limiting scheme for voltage-controlled inverter using instantaneous current to generate virtual impedance. IEEE J. Emerg. Sel. Top. Circuits Syst. 2023, 13, 524–535. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, H.; Zhu, Z. Improved VSG control strategy based on the combined power generation system with hydrogen fuel cells and super capacitors. Energy Rep. 2021, 7, 6820–6832. [Google Scholar] [CrossRef]
- Li, Y.; He, L.; Liu, F.; Li, C.; Cao, Y.; Shahidehpour, M. Flexible voltage control strategy considering distributed energy storages for DC distribution network. IEEE Trans. Smart Grid 2017, 10, 163–172. [Google Scholar] [CrossRef]
- Pannala, S.; Patari, N.; Srivastava, A.K.; Padhy, N.P. Effective control and management scheme for isolated and grid connected DC microgrid. IEEE Trans. Ind. Appl. 2020, 56, 6767–6780. [Google Scholar] [CrossRef]
- Yang, L.; Song, G.; Wenhui, S.; Guoqing, H.; ZhengPing, W. Integrated control strategy for smooth switching of the PV and battery-storage micro-grid based on operation state tracking. J. Eng. 2019, 2019, 1062–1067. [Google Scholar] [CrossRef]
- Fard, A.Y.; Shadmand, M.B. Multitimescale three-tiered voltage control framework for dispersed smart inverters at the grid edge. IEEE Trans. Ind. Appl. 2020, 57, 824–834. [Google Scholar] [CrossRef]
- Ahsan, F.; Dana, N.H.; Sarker, S.K.; Li, L.; Muyeen, S.M.; Ali, F.; Tasneem, Z.; Hasan, M.; Abhi, S.H.; Islam, R.; et al. Data-driven next-generation smart grid towards sustainable energy evolution: Techniques and technology review. Prot. Control. Mod. Power Syst. 2023, 8, 1–42. [Google Scholar] [CrossRef]
- Meng, X.; Liu, J.; Liu, Z. A Generalized droop control for grid-supporting inverter based on comparison between traditional droop control and virtual synchronous generator control. IEEE Trans. Power Electron. 2018, 34, 5416–5438. [Google Scholar] [CrossRef]
- Peng, J.C.H.; Raman, G.; Soon, J.L.; Hatziargyriou, N.D. Droop-controlled inverters as educational control design project. IEEE Trans. Power Syst. 2021, 37, 1623–1633. [Google Scholar] [CrossRef]
- Wang, Z.; Yi, H.; Zhuo, F.; Lv, N.; Ma, Z.; Wang, F.; Zhou, W.; Liang, J.; Fan, H. Active power control of voltage-controlled photovoltaic inverter in supporting islanded microgrid without other energy sources. J. Emerg. Sel. Top. Power Electron. 2021, 10, 424–435. [Google Scholar] [CrossRef]
- Pogaku, N.; Prodanovic, M.; Green, T.C. Modeling, analysis and testing of autonomous operation of an inverter-based microgrid. IEEE Trans. Power Electron. 2007, 22, 613–625. [Google Scholar] [CrossRef]
- Mousavi, S.Y.M.; Jalilian, A.; Savaghebi, M.; Guerrero, J.M. Autonomous control of current- and voltage-controlled dg interface inverters for reactive power sharing and harmonics compensation in islanded microgrids. IEEE Trans. Power Electron. 2018, 33, 9375–9386. [Google Scholar] [CrossRef]
- Li, Z.; Chan, K.W.; Hu, J.; Guerrero, J.M. Adaptive droop control using adaptive virtual impedance for microgrids with variable pv outputs and load demands. IEEE Trans. Ind. Electron. 2020, 68, 9630–9640. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Khazaei, J. Unified distributed control of battery storage with various primary control in power systems. IEEE Trans. Sustain. Energy 2021, 12, 2332–2341. [Google Scholar] [CrossRef]
- Siano, P.; De Marco, G.; Rolan, A.; Loia, V. A survey and evaluation of the potentials of distributed ledger technology for peer-to-peer transactive energy exchanges in local energy markets. IEEE Syst. J. 2019, 13, 3454–3466. [Google Scholar] [CrossRef]
- Obaid, Z.A.; Cipcigan, L.M.; Abrahim, L.; Muhssin, M.T. Muhssin Frequency control of future power systems: Reviewing and evaluating challenges and new control methods. J. Mod. Power Syst. Clean Energy 2019, 7, 9–25. [Google Scholar] [CrossRef]
- Cao, W.; Han, M.; Zhang, X.; Guan, Y.; Guerrero, J.M.; Vasquez, J.C. An integrated synchronization and control strategy for parallel-operated inverters based on V–I droop characteristics. IEEE Trans. Power Electron. 2021, 37, 5373–5384. [Google Scholar] [CrossRef]
- Fan, B.; Li, Q.; Wang, W.; Yao, G.; Ma, H.; Zeng, X.-J.; Guerrero, J.M. A Novel droop control strategy of reactive power sharing based on adaptive virtual impedance in microgrids. IEEE Trans. Ind. Electron. 2021, 69, 11335–11347. [Google Scholar] [CrossRef]
- Mohammadi, E.; Alizadeh, M.; Asgarimoghaddam, M.; Wang, X.; Simoes, M.G. A review on application of artificial intelligence techniques in microgrids. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 878–890. [Google Scholar] [CrossRef]
- Li, W.; Li, B.; Gao, H.; Peng, C.; Zhang, W.; Li, Y.; Ji, X. Survey and practice on architecture and deployment method of digital twin system for intelligent substation. In Proceedings of the 2023 7th International Symposium on Computer Science and Intelligent Control (ISCSIC), Nanjing, China, 27–29 October 2023. [Google Scholar]
- Wei, Z.-X.; Doctor, F.; Liu, Y.-X.; Fan, S.-Z.; Shieh, J.-S. An optimized type-2 self-organizing fuzzy logic controller applied in anesthesia for propofol dosing to regulate BIS. IEEE Trans. Fuzzy Syst. 2020, 28, 1062–1072. [Google Scholar] [CrossRef]
- Ali, M.; Kotb, H.; AboRas, M.K.; Abbasy, H.N. Frequency regulation of hybrid multi-area power system using wild horse optimizer based new combined Fuzzy Fractional-Order PI and TID controllers. Alex. Eng. J. 2022, 61, 12187–12210. [Google Scholar] [CrossRef]
- Yap, K.Y.; Sarimuthu, C.R.; Lim, J.M.-Y. Artificial intelligence based MPPT techniques for solar power system: A review. J. Mod. Power Syst. Cle. 2020, 8, 1043–1059. [Google Scholar]
- Zhang, Q.; Zhai, Z.; Sun, S.; Liu, X.; Qian, J.; Liu, S.; Fang, W. Fuzzy optimization for improving transient synchronization stability of VSCs in se-ries-compensated system. IEEE Trans. Ind. Appl. 2024, 60, 3578–3587. [Google Scholar] [CrossRef]
- Zhen, H.; Liu, G.; Ma, X.; Xu, D.; Zhang, W.; Yan, C.; Wang, L. An energy storage test power supply based on fuzzy quasi proportional resonance control. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nanjing, China, 27–29 May 2022. [Google Scholar]
- Zaky, M.S.; Metwaly, M.K. A performance investigation of a four-switch three-phase inverter-fed IM drives at low speeds using fuzzy logic and PI controllers. IEEE Trans. Power Electron. 2016, 32, 3741–3753. [Google Scholar] [CrossRef]
- Duţu, L.C.; Mauris, G.; Bolon, P. A fast and accurate rule-base generation method for mamdani fuzzy systems. IEEE Trans. Fuzzy Syst. 2018, 26, 715–733. [Google Scholar] [CrossRef]
- Mahmoud, M.M.; Salama, H.S.; Aly, M.M.; Abdel-Rahim, A.-M.M. Design and implementation of FLC system for fault ride-through capability enhancement in PMSG-wind systems. Wind. Eng. 2020, 45, 1361–1373. [Google Scholar] [CrossRef]
- Hamed, H.A.; Abdou, A.F.; Bayoumi, E.H.E.; El-Kholy, E.E. A fast recovery technique for grid-connected converters after short dips using a hybrid structure PLL. IEEE Trans. Ind. Electron. 2017, 65, 3056–3068. [Google Scholar] [CrossRef]
- Gulipalli, S.C.; Gude, S.; Peng, S.C.; Chu, C.C. Multiple delayed signal cancellation filter-based enhanced frequency-locked loop under adverse grid conditions. IEEE Trans. Ind. Appl. 2022, 58, 6612–6628. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, Y. Study on artificial intelligence: The state of the art and future prospects. J. Ind. Inf. Integr. 2021, 23, 100224. [Google Scholar] [CrossRef]
- Bose, B. Expert system, fuzzy logic, and neural network applications in power electronics and motion control. Proc. IEEE 1994, 82, 1303–1323. [Google Scholar] [CrossRef]
- Ding, F. Neural Network Expert Systems; Science Press: Beijing, China, 2006. [Google Scholar]
- Kasabov, N. Foundations of Neural Networks, Fuzzy Systems, and Knowledge Engineering; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Kumar, S.L. Knowledge-based expert system in manufacturing planning: State-of-the-art review. Int. J. Prod. Res. 2018, 57, 4766–4790. [Google Scholar] [CrossRef]
- Dequan, S.; Guili, G.; Zhiwei, G.; Peng, X. Application of expert fuzzy PID method for temperature control of heating furnace. Procedia Engi-Neering 2012, 29, 257–261. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, G. Optimal predictive control method of PWM rectifiers based on artificial intelligence. Mob. Inf. Syst. 2021, 2021, 3688228. [Google Scholar] [CrossRef]
- Yao, Z.; Yao, J.; Sun, W. Adaptive RISE control of hydraulic systems with multilayer neural-networks. IEEE Trans. Ind. Electron. 2018, 66, 8638–8647. [Google Scholar] [CrossRef]
- Ma, Y.; Zhu, G.; Li, Z. Error-driven-based nonlinear feedback recursive design for adaptive NN trajectory tracking control of surface ships with input saturation. IEEE Intell. Transp. Syst. Mag. 2019, 11, 17–28. [Google Scholar] [CrossRef]
- Hou, S.; Fei, J.; Chen, C.; Chu, Y. Finite-time adaptive fuzzy-neural-network control of active power filter. IEEE Trans. Power Electron. 2019, 34, 10298–10313. [Google Scholar] [CrossRef]
- Yi, J.; Li, J. Distributed containment control with prescribed accuracy for nonstrict-feedback switched nonlinear multiagent systems. IEEE Syst. J. 2023, 17, 5671–5682. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Umar, A.M.; Linus, O.U.; Arshad, H.; Kazaure, A.A.; Gana, U.; Kiru, M.U. Comprehensive review of artificial neural network applications to pattern recognition. IEEE Access 2019, 7, 158820–158846. [Google Scholar] [CrossRef]
- Gheibi, O.; Weyns, D.; Quin, F. Applying machine learning in self-adaptive systems: A systematic literature review. ACM Trans. Auton. Adapt. Syst. 2020, 15, 1–37. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M. Neural Network Design; PWS Publishing Co.: Boston, MA, USA, 1997. [Google Scholar]
- Mahmud, N.; Zahedi, A.; Mahmud, A. A Cooperative operation of novel PV inverter control scheme and storage energy management system based on ANFIS for voltage regulation of grid-tied PV system. IEEE Trans. Ind. Inform. 2017, 13, 2657–2668. [Google Scholar] [CrossRef]
- Mehrasa, M.; Babaie, M.; Sharifzadeh, M.; Al-Haddad, K. An input–output feedback linearization control method synthesized by artificial neural network for grid-tied packed E-cell inverter. IEEE Trans. Ind. Appl. 2021, 57, 3131–3142. [Google Scholar] [CrossRef]
- Lu, R.; Hong, S.H.; Yu, M. Demand response for home energy management using reinforcement learning and artificial neural network. IEEE Trans. Smart Grid 2019, 10, 6629–6639. [Google Scholar] [CrossRef]
- Wen, Y.W.; Peng, S.H.; Ting, C.K. Two-stage evolutionary neural architecture search for transfer learning. IEEE Trans. Evolut. Comput. 2021, 25, 928–940. [Google Scholar] [CrossRef]
- Kaymanesh, A.; Babaie, M.; Chandra, A.; Al-Haddad, K. PEC Inverter for Intelligent electric spring applications using ANN-based con-troller. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 704–714. [Google Scholar] [CrossRef]
- Akpolat, A.N.; Dursun, E.; Kuzucuoğlu, A.E. AI-aided control of a power converter in wind energy conversion system. In Proceedings of the 2020 Innovations in Intelligent Systems and Applications Conference (ASYU), Istanbul, Turkey, 15–17 October 2020. [Google Scholar]
- Babaie, M.; Sharifzadeh, M.; Al-Haddad, K. Three-phase grid-connected NPC inverter based on a robust artificial neural network controller. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020. [Google Scholar]
- Won, Y.J. Comparative study of artificial neural network (ANN), adaptive neuro-fuzzy inference system (ANFIS) and multiple linear regression (MLR) for modeling of Cu (II) adsorption from aqueous solution using biochar derived from rambutan (Nephelium lappaceum) peel. Environ. Monit. Assess 2020, 192, 439. [Google Scholar]
- de Moura, J.P.; Neto, J.V.d.F.; Rego, P.H.M. A neuro-fuzzy model for online optimal tuning of PID controllers in industrial system applications to the mining sector. IEEE Trans. Fuzzy Syst. 2019, 28, 1864–1877. [Google Scholar] [CrossRef]
- Hou, S.; Chu, Y.; Fei, J. Robust intelligent control for a class of power-electronic converters using neuro-fuzzy learning mechanism. IEEE Trans. Power Electron. 2021, 36, 9441–9452. [Google Scholar] [CrossRef]
- Xue, G.; Chang, Q.; Wang, J.; Zhang, K.; Pal, N.R. An adaptive neuro-fuzzy system with integrated feature selection and rule extraction for high-dimensional classification problems. IEEE Trans. Fuzzy Syst. 2022, 31, 2167–2181. [Google Scholar] [CrossRef]
- Vargas, O.S.; Aldaco, S.E.D.L.; Alquicira, J.A.; Vela-Valdés, L.G.; Núñez, A.R.L. Adaptive network-based fuzzy inference system (ANFIS) applied to inverters: A survey. IEEE Trans. Power Electron. 2023, 39, 869–884. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Padmanaban, S.; Holm-Nielsen, J.B.; Blaabjerg, F.; Bhaskar, M.S. An experimental estimation of hybrid ANFIS–PSO-based MPPT for PV grid integration under fluctuating sun irradiance. IEEE Syst. J. 2020, 14, 1218–1229. [Google Scholar] [CrossRef]
- Pratama, M.; Pedrycz, W.; Webb, G.I. An incremental construction of deep neuro fuzzy system for continual learning of non-stationary data streams. IEEE Trans. Fuzzy Syst. 2019, 28, 1315–1328. [Google Scholar] [CrossRef]
- Altin, N.; Sefa, I. Simulation of neuro-fuzzy controlled grid interactive inverter. In Proceedings of the 2011 XXIII International Symposium on Information, Communication and Automation Technologies (ICAT), Bosnia and Herzegovina, Balkans, 27–29 October 2011. [Google Scholar]
- Yin, H.; Yi, W.; Wu, J.; Wang, K.; Guan, J. Adaptive fuzzy neural network PID algorithm for BLDCM speed control system. Mathematics 2021, 10, 118. [Google Scholar] [CrossRef]
- Kumar, P.; Arya, S.R.; Mistry, K.D.; Yadav, S. A self-tuning ANFIS DC link and ANN-LM controller based DVR for power quality enhancement. CPSS Trans. Power Electron. Appl. 2023, 8, 424–436. [Google Scholar] [CrossRef]
- Mlakic, D.; Baghaee, H.R.; Nikolovski, S. A Novel ANFIS-Based Islanding Detection for Inverter-Interfaced Microgrids. IEEE Trans. Smart Grid 2018, 10, 4411–4424. [Google Scholar] [CrossRef]
- Jang, J.-S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Yu, W.; Li, X. Fuzzy identification using fuzzy neural networks with stable learning algorithms. IEEE Trans. Fuzzy Syst. 2004, 12, 411–420. [Google Scholar] [CrossRef]
- Mateu, T.H.A. Real-time selective harmonic minimization in cascaded multilevel inverters with varying DC sources. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 4302–4306. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).