Abstract
A reasonable inflating strategy must be developed for filling an onboard hydrogen storage tank with hydrogen gas. The inflow hydrogen temperature has always been a constant value in filling cases. However, in our opinion, the optimal inflow hydrogen temperature is not supposed to be a fixed value but a value that constantly changes and adjusts with filling time, i.e., the inflow hydrogen temperature is a function of the filling time. How to determine this functional relationship is a critical problem to be addressed. Herein, an approach is introduced. A dual-zone model is presented to research the thermal effect during the process of charging hydrogen storage tanks. Based on the numerical results of the dual-zone model, the charging process was divided into three stages, allowing us to obtain data for 1331 filling cases. Then, a back propagation (BP) neural network model was built to analyze the data, and the implicit relationship between the inflow hydrogen temperatures and maximum hydrogen temperature pressure could be deduced. With this implicit relationship, the critical values of the inflow hydrogen temperatures can be obtained from the critical situation. Suppose the inflow hydrogen temperatures in a practical case are higher than the critical values. In that case, the highest hydrogen temperature in the tank will exceed the limited safety value of 358 K. In contrast, if the inflow hydrogen temperatures are lower than the critical values, then more energy will be needed to precool the inlet hydrogen temperature. Thus, theoretically, the critical inflow hydrogen temperatures should be at their optimal values.
1. Introduction
With the gradual depletion of fossil fuels, the environmental and energy crises are becoming increasingly severe. Hydrogen energy has emerged as an ideal alternative energy in recent decades. The preparation, purification, storage, delivery, and use of hydrogen are essential for developing and utilizing hydrogen energy. Hydrogen storage is vital in keeping the hydrogen energy system reliable and efficient and ensuring system safety. There are three main methods for storing hydrogen: metal hydrogen storage, liquefied hydrogen storage, and gaseous hydrogen storage. Gaseous hydrogen storage in high-pressure tanks is the method predominantly used for automotive applications. However, when hydrogen is to be filled into a tank in a fuel cell vehicle at a refueling station, the temperature and pressure inside the tank will rise rapidly. For safety reasons, an inflation protocol has been proposed that the highest hydrogen temperature inside the tank should not exceed 358 K, and the hydrogen pressure must be lower than 125% of the rated working pressure of the tank.
Controlling the hydrogen in the tank within the temperature and pressure constraints while minimizing the charging time is challenging but some research on this topic [1,2,3] can be found.
An analysis of heat transfer during the charging process of a type IV tank was carried out [1], in which the effects of the initial temperature, inlet nozzle diameter, and filling time on hydrogen temperature were investigated. A three-cascade storage system was introduced for refueling stations [2], and it was found that a storage system with three buffers could save about 34% more energy than one with a single buffer. A simulation of a hydrogen filling station for electric vehicles with fuel cells was designed and conducted [3]. The conclusions of these studies are very meaningful. However, their main focus is on the impact of the type and construction of hydrogen storage tank, as well as the final thermal effect of the hydrogen storage systems, and there is little literature dedicated to the study of inflow hydrogen temperature.
In addition, some numerical models have been built to research and optimize the thermodynamic effects on the hydrogen tank during the fast-filling process [4,5,6,7,8,9,10,11]. A hydrogen fueling station thermodynamic model was introduced to simulate the hydrogen temperature, hydrogen pressure, and mass flow rate at any position during the charging process [4]. A two-dimensional numerical model was developed to predict the active pressurization process and the fluid’s thermal stratification in an aerospace fuel storage tank [5]. A three-dimensional computational fluid dynamics simulation model was proposed to study the fast-filling problem in the type III onboard hydrogen tank [6]. A computational fluid dynamic model was built where the effects of station parameters on the storage density of the tank were carried out [7]. A two-dimensional axisymmetric model of a type III hydrogen tank for a bus was built to investigate the temperature evolution during the fast-filling process [8]. Refueling protocols for heavy-duty fuel cell vehicles were optimized, and a refueling strategy was presented for a type III tank with a normal working pressure of 35 Mpa [9]. The precooling process of a cryogenic compressed hydrogen storage tank was simulated using the ANSYS Fluent Software Version 2020R1 [10]. An investigation into filling a horizontal hydrogen tank designed for light-duty vehicles was conducted using multi-physics numerical simulations [11].
Based on the established mathematical physics model, research has also been widely carried out on the related parameters [3,12]. A hydrogen filling station for electric vehicles with fuel cells was designed and simulated, in which the hydrogen temperature, pressure, and mass flow rate were investigated [3]. The effects of mass flow rate, hydrogen temperature, and initial wall temperature on the state of charge were studied [12]. In addition, there some special ways to improve the inflation process were suggested. An innovative solution to slow gas-to-wall heat transfer was presented by introducing a porous infill into gas tanks [13]. Even though these studies provide inspiration for parameter research, in their cases, the parameters are all set at constant values. There is rarely a case which a parameter changes with filling time.
According to the literature, when determining the precooling temperature, the value is always set at a constant value during the whole charge process, as shown in Figure 1a. However, from our perspective, there will be an optimal inflow hydrogen temperature for a specific charge case, as shown in Figure 1b. The optimal inflow hydrogen temperature is supposed to be a function filling time. However, determining this functional relationship is a critical problem to be addressed.

Figure 1.
Different methods to deal with inflow hydrogen temperature.
To solve this problem, a relevant mathematical–physical model has been established to research the thermal effect of the hydrogen tank. Initially, we want to derive an analytical solution for inflow hydrogen temperature through the mathematical–physical model. However, obtaining the explicit expression of the inflowing hydrogen’s temperature is undoubtedly tricky.
An innovative method is proposed in this article to reveal the functional relationship. The idea is as follows.
Firstly, the charge process is discretized.
Here, an example is given in which the charging process is discretized into three stages, as shown in Figure 1c. Each stage has its own an inflow hydrogen temperature. There are many values of , and ; thus, it is hard to determine which set of values is the best for our needs. Herein, the critical state is taken into consideration. A set of critical values exist which correspond to the critical state when the highest hydrogen temperature inside the tank reaches 358 K and the hydrogen pressure reaches 125% of the rated working pressure of the tank. Suppose that the inflow hydrogen temperatures in the practical cases exceed the critical values. In that case, the highest hydrogen temperature and pressure in the tank will exceed the limited values. In contrast, the inflow hydrogen temperatures increase more slowly than the critical values; thus, more energy will be needed to precool the inlet hydrogen temperature. The critical values are supposed to be the theoretical optimal values.
Further, if the charging process is discretized into more stages, such as five stages (Figure 1d), ten stages (Figure 1e), or even N stages where step size approaches 0, then set of critical inflow hydrogen temperature values is the ultimate result that we need.
Secondly, the critical inflow hydrogen temperature values are determined.
In previous parameter research, how to determine the highest hydrogen temperature and pressure based on given charge parameters is always shown, i.e., . Now, it is necessary to determine the charge parameter values in reverse based on the highest hydrogen temperature and pressure, i.e., . From the perspective of mathematics, it is equivalent to solving the inverse function of the previous mathematical–physical model. Similarly, it is difficult to obtain the inverse function.
It is challenging to unveil the quantitative relationship between parameters through experimental methods in the process of parameter research, especially when dealing with multiple gradient parameters. However, this is precisely where the AI method excels. AI methods can train and verify large amounts of data to establish the relationship between input and output, as demonstrated in numerous studies [14,15,16,17]. Therefore, it can assist us in studying the mathematical relationship between multiple sets of inflow hydrogen temperatures and the highest hydrogen temperature, as well as the final hydrogen pressure.
We can use the BP neural network model to train the group data . Thus, we can obtain the mapping relationship between and . By giving the critical condition where the hydrogen temperature is 358 K and the hydrogen pressure is 87.5 MPa, the set of critical inflow hydrogen temperature values can be obtained. The groups of data can be calculated based on the numerical solution of the mathematic–physical model.
The fundamental novelty of our work is that we present a method to obtain the variable values of the inflow hydrogen temperature, which not only keeps the hydrogen storage tank safe, but also saves energy during the charge process.
2. Mathematical Formulation and Numerical Solution
A lumped parameter model that treats the tank as a whole was developed to investigate the thermal effect of the compressed hydrogen storage tank. In the lumped parameter model, the compressed hydrogen tank, shown in Figure 2, is divided into two zones. One is the gas zone, and the other is the wall zone. Both zones take into account mass conservation and energy conservation equations.

Figure 2.
Heat and mass transfer diagram of compressed hydrogen storage tank.
For the gas zone, the mass conservation equation can be written as:
where is the mass flow rate, is the hydrogen mass, is the filling time.
The energy conservation equation can be written as follows:
where is the internal surface area of the tank, is the wall temperature, and is the temperature of the hydrogen. is the constant-pressure specific heat, is inflowing hydrogen’s temperature, and is the constant-volume specific heat.
is the heat transfer coefficient between the hydrogen and the tank. In addition, it has been proved that the heat transfer coefficient between the hydrogen and the tank is a crucial factor affecting the thermal effects of hydrogen storage tanks, and some work has been carried out to modify this parameter [18]. is supposed to be an expression of parameters such as the Reynolds number, the dynamic viscosity of hydrogen, the hydrogen’s density, and so on, it can be written as follows:
where
is the thermal conductivity of the hydrogen, is the Reynolds number, is the internal diameters of the tank, , is the correction factor, = 0.21, is the dynamic viscosity of the hydrogen, and is the internal diameter of the injector, . and can can be obtained through the NIST.
For the wall zone, the energy conservation equation can be written as follows:
where is the mass of the tank wall, is the external surface area of the tank, is the heat transfer coefficient between the tank and the ambient fluid, and is the temperature of the ambient fluid; is the specific heat of the tank wall.
In the model, the wall shell and inner wall are considered as a whole; thus, the heat capacity of the tank’s walls can be considered as the weighted average of the tank wall shell and inner wall, i.e.,
The hydrogen pressure can be calculated using an equation of state (EOS) based on the computed temperature and hydrogen mass. The EOS for an ideal gas can be written as:
where is the universal gas constant, is the tank volume, is the molar mass of hydrogen, and is the hydrogen’s pressure. The behavior of hydrogen under practical operating conditions may deviate from the ideal gas; hence, applying the ideal gas’ EOS may cause errors; thus, the EOS for real gas is utilized instead. By introducing a compressibility factor Z, the EOS for real gas can be modified as follows:
The compressibility factor can be obtained by looking up the standard reference data provided by the US National Institute of Standards and Technology (NIST) [19].
NIST has published a dataset (REFPROP software Version 9.0) of fluid thermodynamic and transport properties. The compressibility factor for hydrogen gas can be obtained from the software. Additionally, REFPROP is highly compatible with MATLAB/Simulink Version R2022a. After importing the dataset into MATLAB/Simulink, the compressibility factor at the initial moment can be obtained by referencing tables in the dataset based on the initial hydrogen temperature and pressure. Subsequently, the hydrogen’s temperature and pressure can be iteratively calculated using the MATLAB/Simulink model, allowing for the retrieval of a new compressibility factor based on the calculated hydrogen temperature and pressure.
It is worth mentioning that other EOS can also be utilized as long as the hydrogen pressure can be calculated correctly.
3. Numerical Solution
A numerical model has been established using MATLAB/Simulink simulation platform software, as shown in Figure 3. The EOS for real gas is utilized in the numerical model. Here, two charging conditions are taken into consideration: one uses the variable mass flow rate, and the other uses the constant mass flow rate. The constant mass flow rate is the average value of the variable mass flow rate.

Figure 3.
Numerical model based on MATLAB/Simulink.
In addition, during the actual charge process, a safety check should be conducted on the airtightness of the hydrogen refueling gun after it is connected to the hydrogen storage tank. The charge process only commences once the check is confirmed. Thus, it should be noted that a buffer time is present during which the mass flow rate is set to zero.
The numerical solution for hydrogen temperature and pressure can be calculated using the MATLAB/Simulink model. However, when solving with the Simulink model, any changes in the conditions or parameters involved in the calculation require manual modification of the corresponding module’s configuration. In the subsequent optimization process, numerous datasets are needed for calculation and analysis; necessitating the manual adjustment of parameters or condition values for each calculation, which can be somewhat troublesome. To simplify this calculation process, the corresponding numerical calculation process is implemented using the Python programming language and Scipy.
Scipy, written in Python, solves the same equations as the MATLAB/Simulink approach. To obtain numerical solutions, Scipy and other prerequisites must be imported into the integrated development environment (IDE) using Python. Then, Equations (1), (2), (5) and (8) need to be rewritten in the programming language’s format. After rewriting these derivative functions and algebraic equations, the step size and range of the independent variable also need to be specified. Running the Python program allows us to obtain the corresponding numerical method.
4. Results and Discussion
A Type IV tank with a volume of 29 L is taken into consideration [20]. The physical parameters of the tank are shown in Table 1.

Table 1.
Values of the tank’s physical parameters.
The specific refueling parameters are shown in Table 2.

Table 2.
The refueling parameters values of the tank.
The initial hydrogen mass can be calculated with the use of the EOS for real gas, .
Two kinds of mass flow rates are utilized in our model, as shown in Figure 4.

Figure 4.
Two kinds of mass flow rate.
The WebPlotDigitizer software (version: 4.6; settings: averaging window algorithm, ∆X = 5 Px, and ∆Y = 5 Px) was employed to automatically extract the data points’ values from Figure 2b in Ref. [20]. These values can be plotted alongside our simulation data, as depicted in Figure 5.
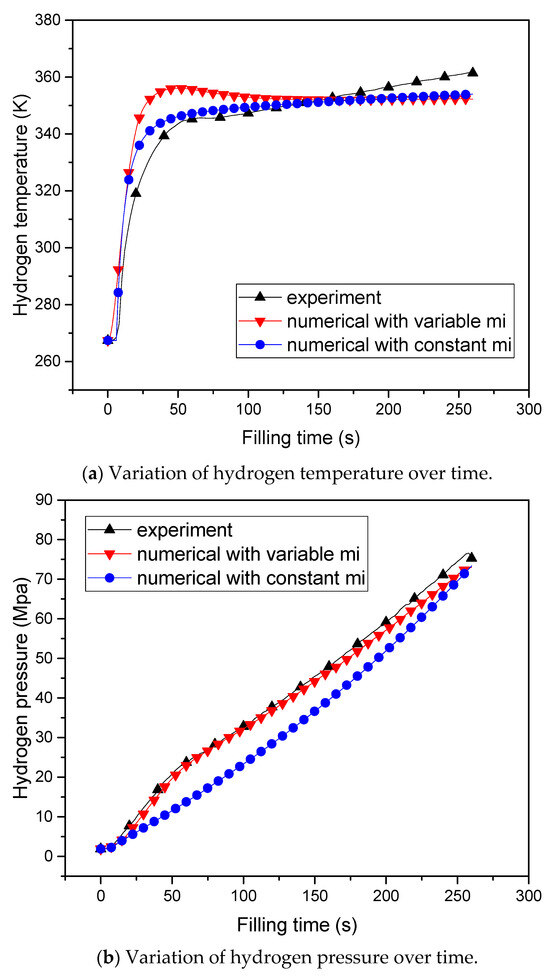
Figure 5.
The numerical results of the hydrogen storage tank.
4.1. Numerical Result Based on MATLAB/Simulink
Based on the given conditions and parameters, the thermal effects of the hydrogen storage tank can be calculated. The numerical results are illustrated in Figure 5. Figure 5a depicts the variation in hydrogen temperature over time. The comparison chart reveals that, when utilizing a constant mass flow rate, the simulated hydrogen temperature closely aligns with the experimental data.
Figure 5b shows the variation in hydrogen pressure over time. There is a certain error at the end of the curve of hydrogen pressure. When calculating the highest hydrogen pressure, the numerical result with the variable mass flow rate was 72.98 MPa, while the numerical result with the constant mass flow rate was 73.37 MPa, and the experimental result was 75.29 MPa.
The error may arise because the constant-pressure specific heat and the constant-volume specific heat are both set as fixed values during the charging process, whereas in the actual inflation process, they tend to vary slightly with charge time.
4.2. Numerical Result Based on Python/Scipy
The MATLAB/Simulink model confirms the applicability of the mathematical–physical model. But now, a large amount of data are required, which will be utilized to train and validate the BP neural network model. To obtain the data, the charging process is also divided into three stages; each stage has its own inflow hydrogen temperature (, , ). The inflow hydrogen temperature is a value taken from a set, and then in return, the set elements take values from 248 K to 298 K in steps of 5 K. There are 11 elements in the set, and according to the arrangement and combination relationship, 11 × 11 × 11 = 1331 charge strategies are presented. A numerical model based on Python/Scipy can simultaneously solve and save the results of these 1331 cases, namely the highest hydrogen temperature and pressure for each case can be obtained.
From a mathematical perspective, it is indeed necessary to divide the charging process into smaller segments. This approach yields values of the inflow hydrogen temperatures that align more closely with a curve, resulting in more accurate outcomes. However, considering a higher number of stages would demand a larger dataset (three stages require 113 = 1331 cases, while N stages require 11N cases), exponentially increasing the computational workload and time needed for AI training and validation. The results would also become more challenging to converge, although this has little impact on the overall trend of the final results. Moreover, in practical hydrogen tank filling scenarios, a large hydrogen storage tank typically serves as the gas source. Introducing more stages would require additional gas source tanks with varying inflow hydrogen temperatures, adding complexity to the system. To streamline the calculation, we have chosen to consider only three stages.
Partial numerical results based on Python/Scipy are shown in Table 3.

Table 3.
Partial numerical results based on Python/Scipy.
The BP neural network model is a forward propagation error backpropagation model of information, comprising three parts: an input layer, a hidden layer, and an output layer. This model elucidates the implicit relationship between the input and output layers through the training and validation of the data. For the physical problems we aim to solve, the data from 1331 examples serve as the requisite input. The objective is to uncover the implicit relationship among the three inflow hydrogen temperatures, the highest hydrogen temperature, and the final hydrogen pressure. Here, 95% of the data are allocated for training purposes. while the remaining 5% are reserved for validation and analysis.
Based on MATLAB, a corresponding BP neural network model can be established, as shown in Figure 6, where the inflow hydrogen temperature values of three stages are used as input layers, and the highest hydrogen temperature and highest hydrogen pressure are used as output layers. We selected the sigmoid function as the activation function, and set the default number of neurons in the hidden layer to 6. On this basis, the results shown in Figure 7 were obtained.
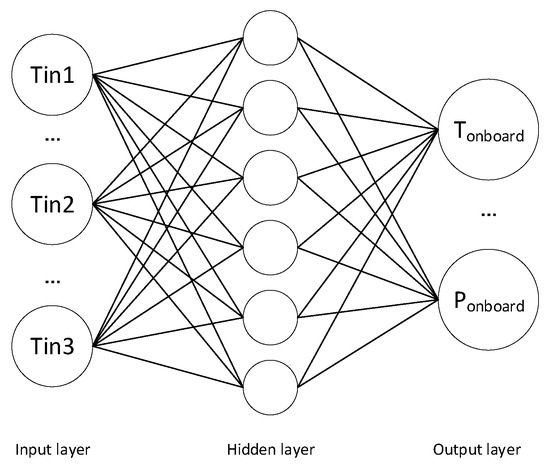
Figure 6.
Basic framework of BP neural network model.
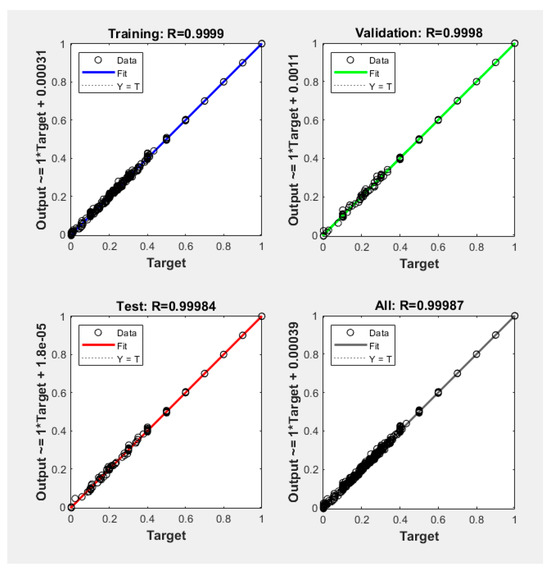
Figure 7.
Regression coefficients of the BP neural network model.
In the BP neural network model, 95% of the cases (i.e., 1264 cases) are utilized for training the model. The remaining cases are utilized to validate the model. The regression coefficients of the BP neural network model are close to one, which means that the BP neural network model is close to the numerical solution of the present model.
Although the BP neural network model has yielded favorable results, to mitigate the impact of result randomness, we have employed another AI method for comparison—the Decision Tree Regression Algorithm. By establishing a corresponding AI model in Matlab/Simulink, utilizing the same 1331 types of data, and employing identical training and validation set scales, the results presented in Figure 8 were obtained. The regression coefficients of the Decision Tree Regression Algorithm are also close to one, affirming the capability of obtaining a well-defined mapping relationship between inflow hydrogen temperatures, the highest hydrogen temperature, and final hydrogen pressure.
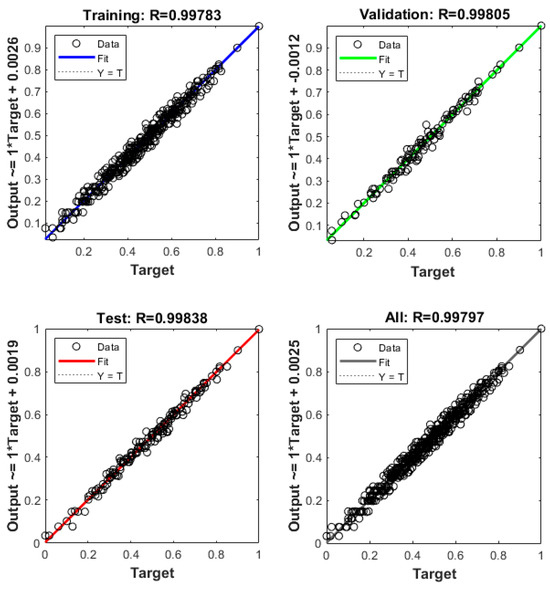
Figure 8.
Regression coefficients of the Decision Tree Regression Algorithm.
It turns out that the mapping relationship between the inflow hydrogen temperatures and the highest hydrogen temperature and pressure can be obtained based on a BP neural network model. With the mapping relationship, given a critical state where the highest hydrogen temperature is 358 K, the highest hydrogen pressure is not taken into consideration since the maximum hydrogen pressure makes it challenging to reach the critical value in practice; thus, three inflow hydrogen temperatures at each stage can be obtained, which are shown in Table 4. The three critical inflow hydrogen temperatures are 298.00 K, 282.71 Kand 276.40 K, respectively.

Table 4.
Prediction of three inflow hydrogen temperatures under critical state based on BP neural network model.
By substituting the optimal inflow hydrogen temperatures predicted by the BP neural network model into the numerical model for thermal effect analysis, the highest hydrogen temperature and final hydrogen pressure can be calculated, respectively. The highest hydrogen temperature is 355 K, which is only 3 K away from the safety temperature threshold of 358 K, while the final hydrogen pressure inside the tank is 70.9 MPa, which does not exceed the safety limit for hydrogen pressure.
5. Conclusions
A new charge strategy has been proposed in which the inflow hydrogen temperature is supposed to change and adjust to the filling time. Our primary objective was to determine the variable inflow hydrogen temperature, which posed a critical challenge in our work. To address this, we propose a method for seeking the variable inflow hydrogen temperature.
A mathematical–physical model was built to obtain the numerical solutions of the hydrogen temperature, hydrogen pressure, and wall temperature, and it has been proved that the model agrees well with experimental results. We further established a numerical model based on Python/Scipy software Version 1.10.1 to calculate 1331 cases. Then, a three-layer BP neural network model was established, and trained on the data from the 1331 cases, which allowed us to obtain the implicit relationship between the inflow hydrogen temperatures and the highest hydrogen temperature and pressure.
The implicit relationship can help to determine the optimal inflow hydrogen temperature values and develop a corresponding refueling strategy. Considering the critical situation where the highest hydrogen temperature is 358 K, the inflow hydrogen temperatures in the subsequent stages can be forecast.
Under the premise of achieving the same filling quality and ensuring safety, the required precooling energy is minimized when using the critical inflow hydrogen temperatures.
Furthermore, scenarios in which the charging process is divided into more stages can be considered. Additionally, more optimization analyses are necessary due to concerns about the randomness and contingency of the results obtained from the BP neural network model. The results for the three inflow hydrogen temperatures should be optimized to be more continuous, so that the average value is more likely to be higher. Generally, temperature and pressure are set at fixed values but they are supposed to vary slightly with the charging process. These results will be considered in the next step of our work.
Author Contributions
Conceptualization, P.-C.S.; methodology, X.W.; software, X.W. and C.H.; validation, D.L.; formal analysis, D.L.; investigation, X.W. and C.H.; resources, P.-C.S.; data curation, S.D.; writing—original draft preparation, X.W. and C.H.; writing—review and editing, S.D. and P.-C.S.; visualization, S.D.; supervision, C.H.; project administration, D.L. and S.D.; funding acquisition, P.-C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the National Key R&D Program of China (2021YFB2601603), the National Natural Science Foundation of China (52176191, 51476120), the Natural Science Foundation of Hubei Province of China (2021CFB071), the 111 Project (B17034), and the Innovative Research Team Development Program of the Ministry of Education of China (IRT_17R83).
Data Availability Statement
The data are contained within the article.
Conflicts of Interest
Authors Xu Wang, Chun Hui and Dongwei Liu were employed by the company China Automotive Technology & Research Center Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Couteau, A.; Eggenschwiler, P.D.; Jenny, P. Heat transfer analysis of high-pressure hydrogen tank fillings. Int. J. Hydrogen Energy 2022, 47, 23060–23069. [Google Scholar] [CrossRef]
- Xiao, L.; Chen, J.; Wu, Y.; Zhang, W.; Ye, J.; Shao, S.; Xie, J. Effects of pressure levels in three-cascade storage system on the overall energy consumption in the hydrogen refueling station. Int. J. Hydrogen Energy 2021, 46, 31334–31345. [Google Scholar] [CrossRef]
- Keerthana, S.; Vuddanti, S.; Salkuti, S.R. Design and Simulation of Hydrogen Filling Station for Fuel Cell Electric Vehicle Charging Applications. Recent Adv. Power Syst. 2022, 812, 381–396. [Google Scholar]
- Kuroki, T.; Nagasawa, K.; Peters, M.; Leighton, D.; Kurtz, J.; Sakoda, N.; Monde, M.; Takata, Y. Thermodynamic modeling of hydrogen fueling process from high-pressure storage tank to vehicle tank. Int. J. Hydrogen Energy 2021, 46, 22004–22017. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, Y.; Liu, Y.; Li, Y. Effect of gas injection mass flow rates on the thermal behavior in a cryogenic fuel storage tank. Int. J. Hydrogen Energy 2022, 47, 14703–14713. [Google Scholar] [CrossRef]
- Wu, X.; Liu, J.; Shao, J.; Deng, G. Fast filling strategy of type III on-board hydrogen tank based on time-delayed method. Int. J. Hydrogen Energy 2021, 46, 29288–29296. [Google Scholar] [CrossRef]
- Sapre, S.; Vyas, M.; Pareek, K. Impact of refueling parameters on storage density of compressed hydrogen storage tank. Int. J. Hydrogen Energy 2021, 46, 16685–16692. [Google Scholar] [CrossRef]
- Zhao, B.; Wei, H.; Peng, X.; Feng, J.; Jia, X. Experimental and Numerical Research on Temperature Evolution during the Fast-Filling Process of a Type III Hydrogen Tank. Energies 2022, 15, 3811. [Google Scholar] [CrossRef]
- Xu, Z.; Dong, W.; Yang, K.; Zhao, Y.; He, G. Development of efficient hydrogen refueling station by process optimization and control. Int. J. Hydrogen Energy 2022, 47, 23721–23730. [Google Scholar] [CrossRef]
- He, M.; Jia, Q.M.; Lv, C.; Wu, J.H.; Zhang, Y.; Zhu, W.P.; Zhang, M.M.; Gong, L.H. Analysis of the factors influencing the precooling process of cryogenic compressed hydrogen storage tank. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1240, 012030. [Google Scholar] [CrossRef]
- Gonin, R.; Horgue, P.; Guibert, R.; Fabre, D.; Bourguet, R.; Ammouri, F.; Vyazmina, E. A computational fluid dynamic study of the filling of a gaseous hydrogen tank under two contrasted scenarios. Int. J. Hydrogen Energy 2022, 47, 23278–23292. [Google Scholar] [CrossRef]
- Oh, S.J.; Yoon, J.H.; Jeon, K.S.; Choi, J. A study on the thermal characteristics of hydrogen storage vessel related to condition of charging. J. Mech. Sci. Technol. 2022, 36, 1579–1586. [Google Scholar] [CrossRef]
- Li, H.; Lyu, Z.; Liu, Y.; Han, M.; Li, H. The effects of infill on hydrogen tank temperature distribution during fast fill. Int. J. Hydrogen Energy 2021, 46, 10396–10410. [Google Scholar] [CrossRef]
- Ye, F.; Ma, S.; Tong, L.; Xiao, J.; Bénard, P.; Chahine, R. Artificial neural network based optimization for hydrogen purification performance of pressure swing adsorptio. Int. J. Hydrogen Energy 2019, 44, 5334–5344. [Google Scholar] [CrossRef]
- Thankachan, T.; Prakash, K.S.; Pleass, C.D.; Rammasamy, D.; Prabakaran, B.; Jothi, S. Artificial neural network to predict the degraded mechanical properties of metallic materials due to the presence of hydrogen. Int. J. Hydrogen Energy 2017, 42, 28612–28621. [Google Scholar] [CrossRef]
- Bicer, Y.; Dincer, I.; Aydin, M. Maximizing performance of fuel cell using artificial neural network approach for smart grid applications. Energy 2016, 116, 1205–1217. [Google Scholar] [CrossRef]
- Ghaedi, M.; Ghaedi, A.M.; Abdi, F.; Roosta, M.; Sahraei, R.; Daneshfar, A. Principal component analysis-artificial neural network and genetic algorithm optimization for removal of reactive orange 12 by copper sulfide nanoparticles-activated carbon. J. Ind. Eng. Chem. 2014, 20, 787–795. [Google Scholar] [CrossRef]
- Bourgeois, T.; Ammouri, F.; Weber, M.; Knapik, C. Evaluating the temperature inside a tank during a filling with highly-pressurized gas. Int. J. Hydrogen Energy 2015, 40, 11748–11755. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology (NIST). Reference Fluid Thermodynamic and Transport Properties Database (REFPROP) Version 9.0. Available online: https://www.nist.gov/srd/refprop (accessed on 1 November 2010).
- de Miguel, N.; Cebolla, R.O.; Acosta, B.; Moretto, P.; Harskamp, F.; Bonato, C. Compressed hydrogen tanks for on-board application: Thermal behaviour during cycling. Int. J. Hydrogen Energy 2015, 40, 6449–6458. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).