Optimization Control Strategy for Transition Season Blinds Balancing Daylighting, Thermal Discomfort, and Energy Efficiency

Abstract

Natural lighting in office buildings is often affected by excessive solar heat gain and discomfort glare, and the transitional seasons are no exception. Therefore, addressing the issue of natural lighting in buildings has always been a challenge in developing shading control strategies. This study designed a model-based calculation method for shading blind control indicators. The method combines existing physical models for sky conditions, solar radiation, heat transfer, thermal comfort, glare, and illuminance calculations and incorporates modifications and additions. Additionally, an equivalent energy-saving model for shading was established. A shading blind control strategy balancing indoor light and the thermal environment with energy savings during transitional seasons was proposed. In transitional seasons, this method can eliminate 100% of glare, reduce discomfort illuminance duration by 81.3% and heat discomfort duration by 87.5% and save 81.3% of lighting energy consumption when air conditioning is used. By comparing the simulation results of an office building in Xi’an with the results obtained from this calculation method, the absolute error percentage was found to be 6.83%, verifying the reliability of the calculation method. Finally, the proposed control strategy was compared with common methods such as no blinds, end-angle control, and fixed-angle control to evaluate its performance in terms of daylighting, thermal comfort, and energy savings. The results showed that the control strategy proposed in this study has significant advantages with respect to various performance indicators.

1. Introduction

1.1. The Importance of Natural Lighting and the Selection of Shading Devices

Natural light plays a significant role in architectural design, impacting the visual and thermal comfort of indoor occupants and positively affecting human health. Adequate natural light helps regulate the body’s circadian rhythm, promotes metabolism, and regulates daily routines [1]. In turn, this can enhance the efficiency of indoor occupants. To control the level of daylight indoors, buildings often use shading devices to make optimal use of natural light and improve the indoor lighting environment. However, the process of introducing natural light into a building’s interior can often have a certain impact on the indoor thermal environment. For example, in summer, ensuring adequate daylight indoors by introducing natural light often increases the indoor heat load. During transitional seasons or winter, only considering indoor heat gain can lead to glare issues [2]. As outdoor meteorological conditions change, the impact of natural light on indoor lighting and thermal environments also varies. Therefore, studying the coupled effect of natural light on the optical and thermal environments of buildings and balancing indoor daylight levels and heat gain by controlling shading devices are essential requirements for human-cantered, low-carbon fine control of buildings. Considering the need for coupled control of indoor lighting and thermal environments, electric shading blinds were chosen as the shading devices investigated in this study. Compared to common shading panels or curtains, electric shading blinds can achieve more precise control, thereby improving the indoor lighting and thermal environment more effectively to meet the needs of low-carbon buildings.

1.2. Current Status of Common Shading Control Indicators

In recent years, many scholars have started to research the control of shading devices. Initially, the purpose of studying shading devices was solely to make optimal use of natural light to improve the indoor lighting environment. Scholars point out that in daylighting design for office buildings, there is a focus on providing adequate illuminance to ensure visual comfort while avoiding glare [3]. Due to considerations of comfort and productivity, Chinese building lighting design standards indicate that for daylighting through building side windows, the lowest value of the daylight factor should be used as the standard. Glare is typically caused by excessively high brightness levels or high brightness contrasts in a scene. Scholars often use glare equations involving the absolute and relative glare factors [4], the Daylight Glare Index (DGI) [5,6,7], and the Daylight Glare Probability (DGP) [8,9] to assess the likelihood of discomfort glare. With the increase in building energy consumption, awareness of building energy efficiency has become more prevalent. Some scholars have studied the impact of blind control on the cooling and heating loads during hot summers and cold winters [10,11,12]. Therefore, proper shading control can not only improve the indoor lighting environment but also effectively save energy consumption for indoor lighting and air conditioning in buildings, making energy conservation an important goal of shading control.

1.3. Access to Shading Control Indicators

Accurate shading control indicators are essential for improving indoor lighting conditions and saving energy. In previous studies, experimental measurements and simulation software were commonly used to obtain these indicators. For experimental measurements, for example, illuminance sensors were installed on the ceiling, and the glare situation at the most unfavourable glare point in the work area was calculated using a physical model [13]. In another study, solar radiation sensors were installed on the roof, and illuminance meters were placed in the work area to collect illuminance data [14]. High-dynamic-range (HDR) cameras and digital single-lens reflex (DSLR) cameras were placed in the direction of human eye lines and work surfaces to capture luminance images [15,16], and a fisheye lens camera was used to capture sky images [17]. Indoor illuminance and glare data were obtained through data processing based on these setups. These studies have accurately obtained indoor illuminance and glare data through experimental measurements. However, single-sensor detection cannot meet the requirements of multi-point control, and the data processing for images obtained using HDR cameras is complex. Additionally, setting up a sensor system is complex and costly. Currently, there is a lack of research on obtaining data on changes in indoor lighting and air conditioning energy consumption under shading control through experimental measurements.

With respect to obtaining energy consumption data through simulation software, some researchers have simplified the process. For instance, a scholar conducted simulations using EnergyPlus (Version 8.7) software on a three-story office building in the central region during the summer months (June to August) to obtain indoor lighting and air conditioning energy consumption data [18]. Another study involved combined shading simulations of overcast days in Shenyang and Chengdu with Radiance and EnergyPlus software, obtaining indoor daylighting and energy consumption indicators. The combined software simulation was more efficient and yielded more reliable and accurate results compared to single software simulations [19]. Additionally, scholars used Rhinoceros (Version 7.0) and Grasshopper (Version 7.0) software to simulate a library in Indonesia to obtain indoor illuminance and glare conditions [20]. These studies demonstrate that using simulation software can provide the illuminance, glare, and energy consumption indicators required for shading control and can also facilitate simulations over extended periods and under different weather conditions. However, most existing research has focused on clear or overcast sky conditions, while actual skies are more dynamic, which presents certain limitations in practical applications [21]. There is still a lack of research on cloudy sky conditions.

1.4. Current Research Status of Shading Control Strategies

In the research on architectural shading control strategies, various methods and techniques have been proposed to solve the problems of glare, light harvesting, and energy saving; for example, the early cut-off angle control strategy blocks excessive direct light in winter and summer by adjusting the angle of shading [22,23,24], which effectively reduces glare but, at the same time, lowers the indoor illuminance level. As a result, scholars further developed daylight redirection control strategies, which redistribute light to different locations in the room by adjusting the angle of shading [25,26], resulting in more uniform indoor lighting. However, there is still a risk of glare in high-direct-light situations. In addition, some studies have proposed an analytical model based on the sun’s position and the geometry of blinds and windows, which enhances the daylight level in the room by controlling the height of the blinds and the angle of the blinds but cannot completely avoid the occurrence of glare [23]. These open-loop control strategies are relatively simple and therefore widely used. However, in order to further improve the shading performance, some scholars proposed a winter and summer shading control strategy for architectural lighting components in the Netherlands, where the control system adjusts the blind angle and height according to the sky ratio and the clarity index for the current sky condition; this strategy was found to achieve better results in terms of avoiding glare and satisfying the lighting index [27]. Meanwhile, a study developed a model-based control (MBC) algorithm to effectively evaluate glare by using direct sunlight, scattered light, and transmitted illuminance as model inputs in winter [28]. However, this study required the measurement of multiple model input parameters. Therefore, scholars developed a blind control method that does not involve the measurement of photometric values, using sky images as an actuator to control automatic shading devices, which can control blinds in real time but is unreliable under partly cloudy skies and under certain circumstances [22].

With the concept of energy conservation taking hold, scholars have begun to incorporate indoor lighting and air conditioning energy consumption into the control metrics for shading in order to achieve energy savings. Some studies have considered factors such as heat loss, solar gain, and daylighting to develop control strategies applicable in winter and summer that are able to reduce cooling energy and ensure appropriate levels of daylighting [29]. Also, some adaptive light and dark treatments and daylighting systems (Shape Variable Mashrabiya-SVM) have been developed to avoid direct light in winter while converting it into diffuse light to improve indoor daylighting performance and save some lighting energy [30]. Some studies have also explored dynamic shading control strategies with constant and variable set points to improve indoor lighting and reduce indoor heat gain at the same time [31]. Meanwhile, some scholars have used EnergyPlus simulation experiments to obtain building indoor energy consumption and daylighting data [32] and developed simulation-based, data-driven automated shading control strategies to predict planar illuminance and glare via machine learning algorithms [14,29]. Significant improvements in the indoor light environment and reductions in lighting energy consumption of up to 80% have been achieved. However, most current studies focus on shading control in winter and summer, with a lack of simulation studies covering long time scales [33]. Moreover, by testing buildings that are not cooled and heated during the transitional seasons (spring and autumn), scholars have found that overcooling and overheating often occur as well, especially on cloudy and clear, cloudless days [34]; however, there is a lack of research on shading control during the transitional seasons.

1.5. Purpose and Contribution of the Study

Many current simulation studies mainly develop control strategies based on fully clear and fully cloudy sky states, while there are relatively few studies on cloudy sky types. Meanwhile, experimental studies have problems such as complicated sensor system arrangement, difficulty in determining the number and locations of sensors, and high cost. On the other hand, building shading control mainly focuses on the indoor light environment, and a few studies have taken into account the parameters of the light and heat environment. The control strategies that take into account light and heat are all for winter and summer, and there are very few studies on the control of blinds for indoor light and heat coupling in transitional seasons such as spring and autumn.

Therefore, this study proposes a set of shading control parameter calculation methods based on outdoor solar parameters and indoor and outdoor temperatures and obtains indoor illuminance, glare value, thermal comfort, and energy consumption parameters through model calculation. At the same time, this study also proposes a shading blind control strategy for transitional seasons that balances the indoor light and heat environment and saves energy. In order to create a comfortable indoor light and thermal environment while maximising the use of natural lighting to reduce energy consumption. Taking an office building in Xi’an as an example, the indoor illuminance, glare value, and thermal comfort are selected as constraints to optimise the blind blade angle, and their performance in terms of lighting, thermal comfort, and energy saving is evaluated in comparison with the common blindless, cut-off angle control, and fixed-angle control methods.

The main objective of this study is to design a set of blind control methods that balance light and heat environments and energy saving in the transition seasons. The combination of light environment comfort, thermal comfort, and energy saving as the shading control objective in the transition seasons provides a low-cost, efficient, and simple method of obtaining shading control indexes for future research on shading blind control. It also provides an efficient and practical shading control strategy for future green intelligent buildings. In future development, we can build an automatic shading control system to realise this control strategy in full-size office buildings, and we can also adjust the shading control strategy by combining the users’ personal preferences for the comfort of the light and heat environment so as to better satisfy the users’ practical needs.

The structure of this study is as outlines as follows. Section 2, Section 3 and Section 4 are shown in Figure 1, Section 2 completes the calculation of the blind control indexes through the modified combination of physical calculation models, Section 3 optimises the control of the blind blade angle using the dataset obtained from the physical model calculations, and Section 4 verifies the accuracy and reliability of the proposed calculation method through simulation experiments, as well as comparing the optimised control strategy proposed in this study with other control strategies. Finally, the conclusions and contributions of this study are presented in Section 5.

2. Materials and Methods

2.1. Simulation Setup

The simulation room is located in Xi’an, China, an office on the third floor of an office building with south-facing windows. A model of a private office space with south-facing windows in Xi’an was created in SketchUp (Version 2017) and EnergyPlus (Version 9.2.0) as shown in Figure 2, with office dimensions of 8 m × 5 m × 3.4 m. The room is mainly lit by the south-facing windows, which are located in the centre of the south wall, with a length of 3 m and a width of 2 m. The bottom of the window is 0.8 m from the floor, and the reference point of the working surface is located in the middle of the window, with a height of 0.8 m and a distance of 1.5 m from the window. The height of the line of sight of the human eye is 1.2 m, parallel to the window. In addition, the exterior of the window was equipped with a system of blinds of equal size to shade the sun. The specific design parameters of the model are shown in

Table 1. Model parameters.

Office Space Parameters	Value	Unit	Note
Wall U value	0.54	W/m²·K	Fixed
Window-to-wall ratio (WWR)	0.15	-	Fixed
Floor reflectivity	0.2	-	Fixed
Wall reflectivity	0.6	-	Fixed
Ceiling reflectance	0.8	-	Fixed
Window parameters
SHGC	0.42	W/m²·K	Fixed
Window U value	5.14	-	Fixed
Visible light transmittance	0.85	-	Fixed
Visible light reflectance	0.05	-	Fixed
Blind parameters
Blade width	0.05	m	Fixed
Blade gap	0.05	m	Fixed
Leaf reflectance	0.7	-	Fixed
Leaf absorption rate	0.3	-	Fixed

. The above parameters were used as the basis for calculating the shading control parameters, and the building was used from 06:00 to 18:00 h. These detailed parameterisations helped to ensure the accuracy and reliability of the experiments.

The solar radiation data and outdoor temperature data used in the simulation experiments were taken from the typical meteorological year data files of Xi’an provided by EnergyPlus, and the time-by-time heat gain and the parameters of the photothermal environment were simulated for a transitional season without the operation of cooling and heating equipment and indoor windows without blinds.

2.2. Shading Control Index Calculation Model

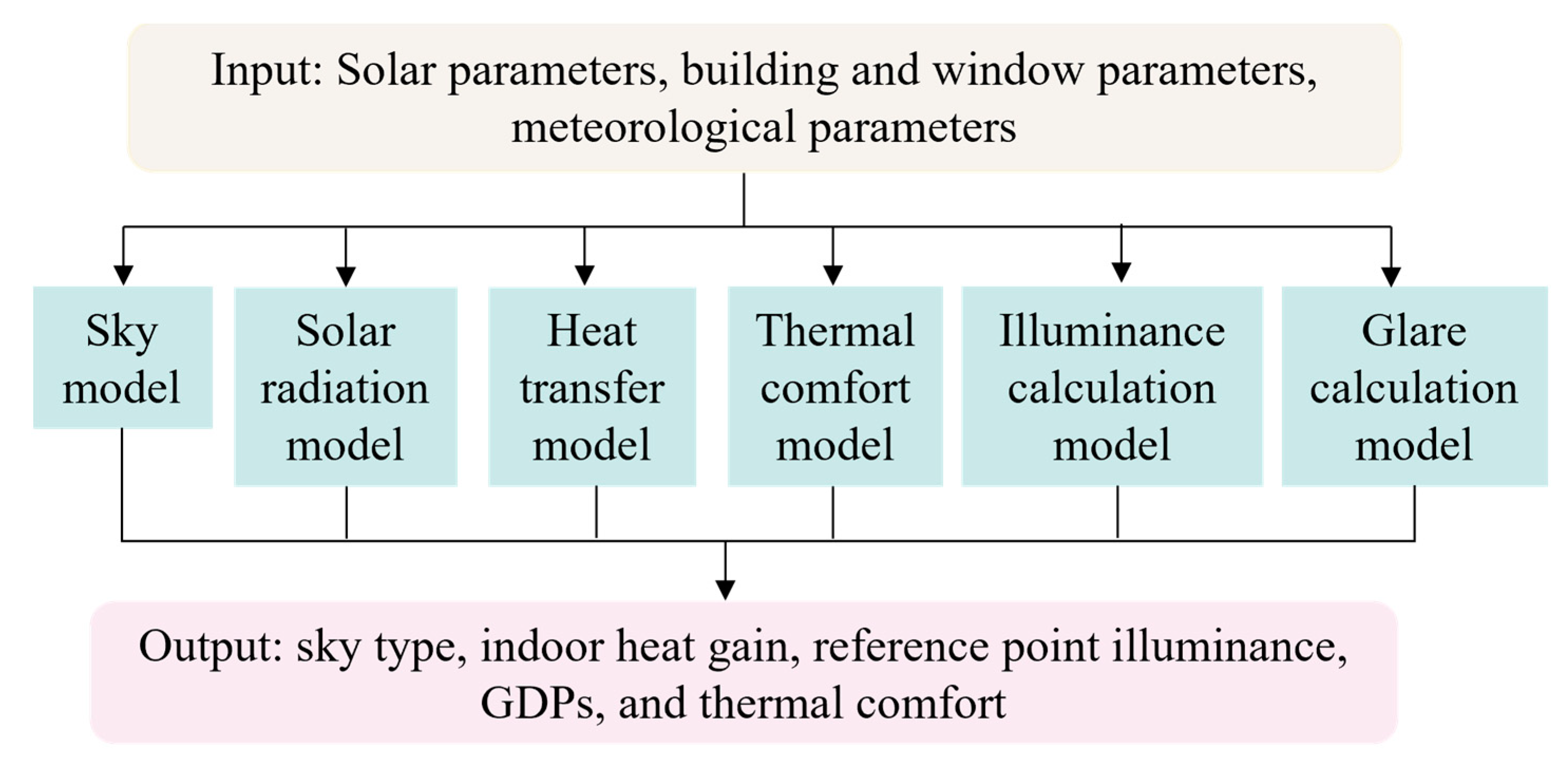
In view of the problems associated with arranging sensor detection and simulation software simulations, this study extended and modified some of the models by combining classical physical calculation models (sky model, solar radiation model, heat transfer model, thermal comfort model, illuminance calculation model, and glare probability model) (direct transmittance calculation model for the solar radiation model, heat gain calculation model, and thermal comfort model with blinds) (heat gain calculation model and indoor temperature calculation model when blinds are used in the thermal comfort model), and an equivalent energy-saving shading model was also established. By optimising the combination of these models, a set of calculation methods for the control parameters of shading blinds was established, and the indicators to be measured were calculated. The calculation principle is shown in Figure 3, which includes the following five main indicators: sky type, indoor heat gain, reference point illuminance, glare probability, and thermal comfort. The improved and established physical calculation models are described in the following.

2.2.1. Optical Models

Some experts, such as the authors of [35,36] classify the sky into the following three types: clear, cloudy, and cloudy. According to [37], these three sky types can be classified by sky ratio, diffuse radiation coefficient, clear sky index, etc. It was found that the reliability of these three methods is high. In view of the available data on diffuse radiation in the horizontal plane and the total radiation data in the horizontal plane, this paper chooses the diffuse radiation coefficient method to classify the sky, and the classification table is shown in

Table 2. Classification table for the state of the sky.

${\mathit{K}}_{\mathit{d}}$ Range	Sky Type
$K_d$ < 0.33	Sunny
$0.33<K_d$ < 0.8	Cloudy
0.8 < $K_d$	Overcast

.

The calculation formula is as follows:

$$K_d=\frac{I_d}{I_G}$$

(1)

where $K_d$ is the coefficient of diffuse radiation, $I_d$ is the amount of diffuse radiation (W/m²) in the horizontal plane, and $I_G$ is the total radiation (W/m²) in the horizontal plane.

There are three main components of heat gain entering the room through the external window system, as follows: the component generated by solar radiation, the thermal radiation component of the external window system, and the convective heat transfer component with the outside world. The solar radiation entering the room consists of direct solar radiation and scattered solar radiation [38].

When direct sunlight strikes the blind area of an exterior window, a portion of the direct light enters the interior directly through the gaps in the blinds. As shown in Figure 4, the ratio of the direct-entry portion to the total incident light can be considered the direct solar transmittance at that moment; the ratio of unobstructed space to total space between the blinds can be calculated by the following formula:

$${\tau }_D^d=1-\frac{n_1}{n}=1-\frac{m·sin(\delta -\theta )}{(n·sin(90°-\delta ))}$$

(2)

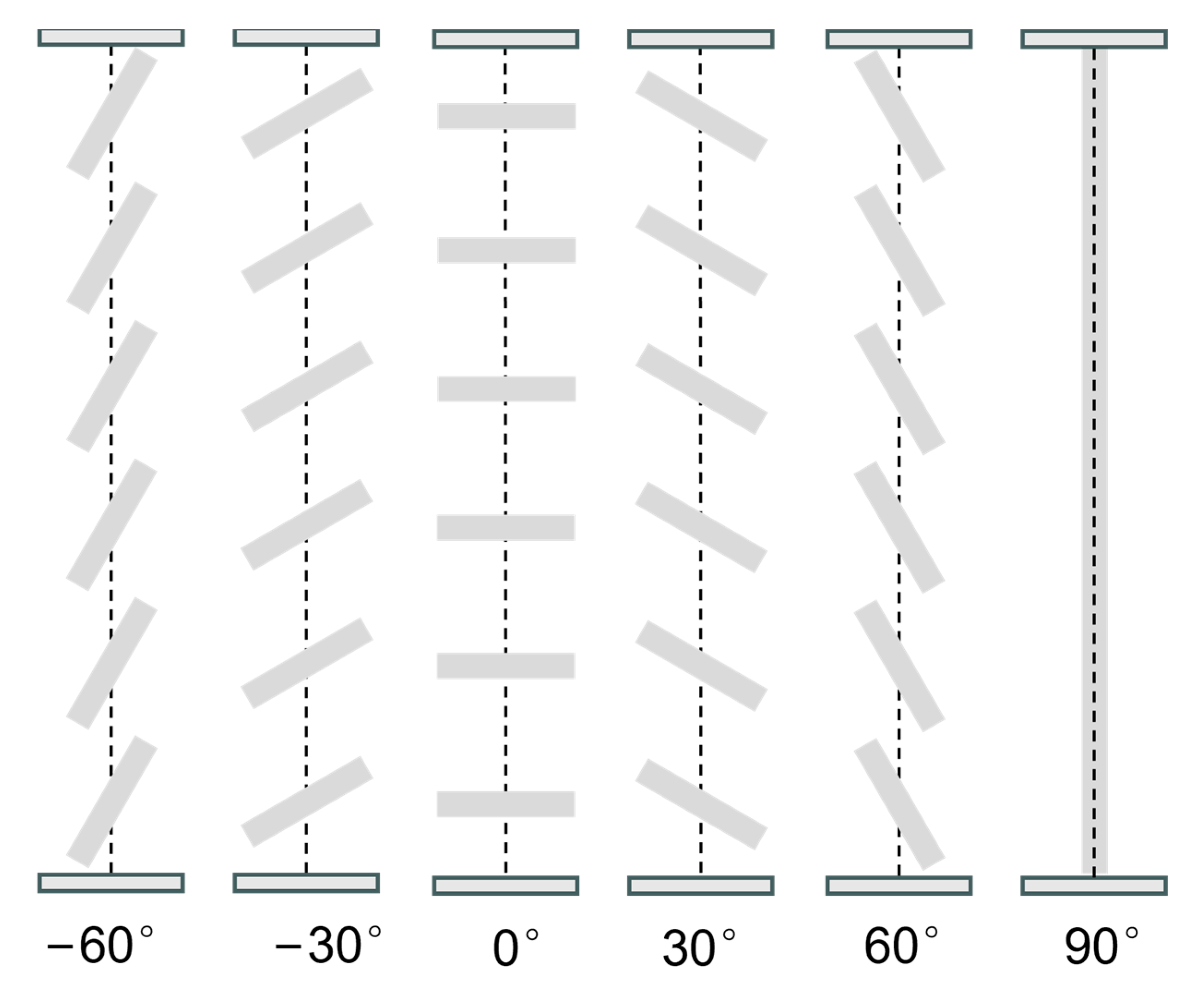
where $\delta$ is the solar altitude angle (rad); $\theta$ is the blind angle (rad); $n$ and $m$ are the blind blade gap and width, respectively (m); and $n_1$ indicates no direct light entering into the region (m). In this study, the same slits and widths of blind blades were selected as the research objects. The specific blind angle model is illustrated in Figure 5. Expanding upon the above, the calculation model for solar direct transmittance is extended from 0° to 90° to −90° to 90°, as presented in the following formula:

$$\left\{\begin{array}{l}-90°\le \theta \le 0°\left\{\begin{array}{l}0°\le \delta \le \frac{90°+\theta }{2},{\tau }_D^{\mathrm{b}}=1+\sin \theta -\tan \delta \cos \theta \\ \frac{90°+\theta }{2}\le \delta ,{\tau }_D^b=0\end{array}\right.\\ 0°<\theta \le 90°\left\{\begin{array}{l}0\le \delta \le \theta ,{\tau }_D^b=1-\sin \theta +\tan \delta \cos \theta \\ \theta \le \delta \le \frac{90°+\theta }{2},{\tau }_D^b=1+\sin \theta -\tan \delta \cos \theta \\ \frac{90°+\theta }{2}\le \delta ,{\tau }_D^b=0\end{array}\right.\end{array}\right.$$

(3)

The direct transmission of direct solar radiation through blinds is calculated as follows:

$$I_D^d=I_D·{\tau }_D^d$$

(4)

where $I_D$ is the direct solar radiation. Direct solar radiation incident on a blind blade is reflected between the blades, considering only secondary reflections [39]. The part that enters the window surface is the direct solar diffuse transmission radiation, and the calculation of the direct solar diffuse transmission coefficient is completed by using the model for calculation of the transmission coefficient of direct solar diffuse radiation proposed by Pfrommer.

The diffuse radiation entering through the blinds can be calculated according to the diffuse radiation calculation model used in [40,41]. The error of this method can be controlled within 3%.

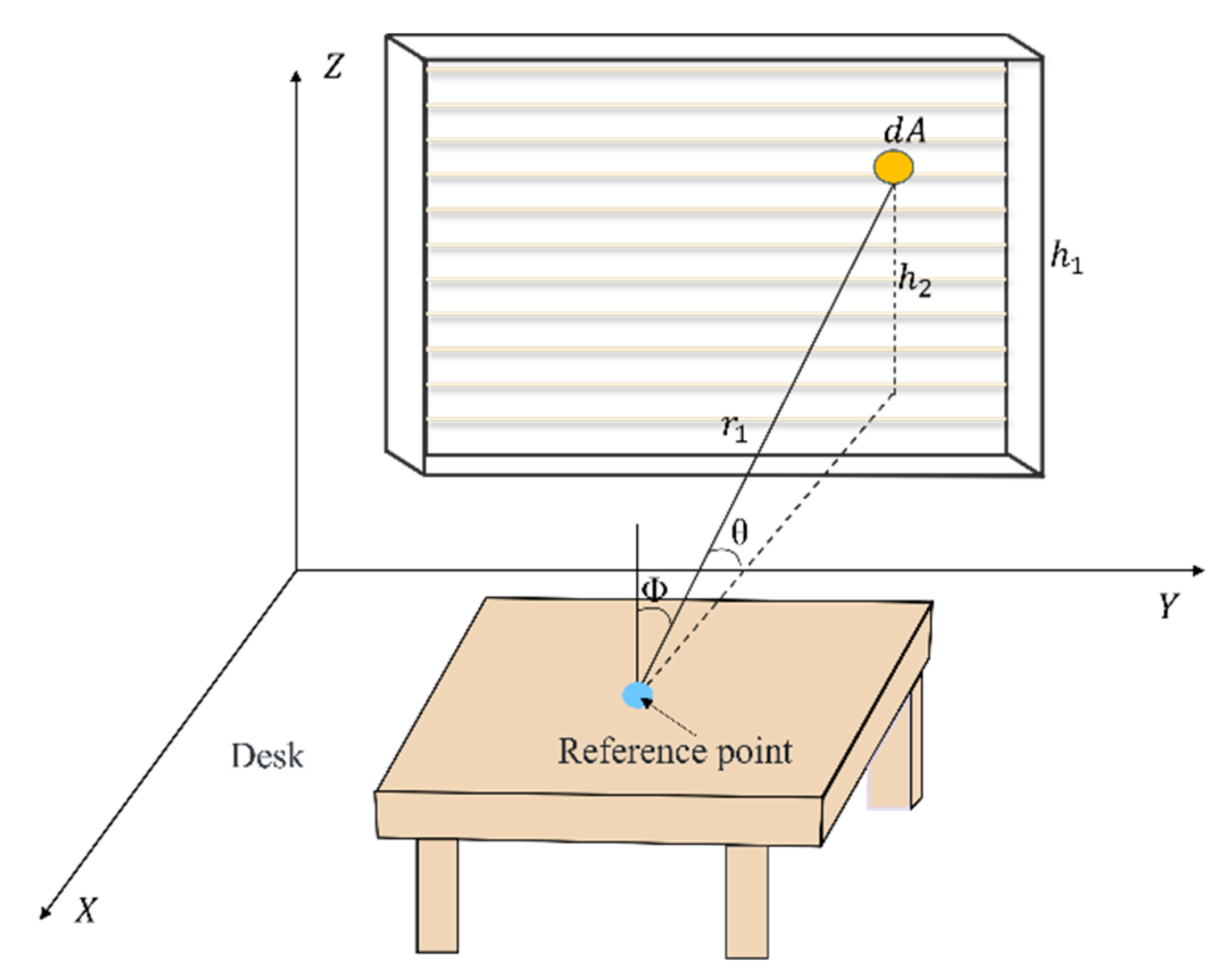
Figure 6 shows that after the sun passes through the external window system, part of it is filtered by the blinds and windows, and the remaining part passes through the external window system into the interior, where the location of the sun in the sky (dA) contributes to the illuminance at a point on the horizontal plane [27]. The solar illuminance contributed by the window to a point inside the room can be determined by the following equation:

$$E_i={\displaystyle {\int }_{{\varphi }_L}^{{\varphi }_R}{\displaystyle {\int }_{{\theta }_{\min }}^{{\theta }_{\max }}L{\tau }_w}}{\tau }_b\sin \varphi \cos \varphi d\theta d\varphi$$

(5)

where $L$ is the brightness of the outdoor sky; ${\tau }_b$ is the solar radiation transmittance of the external blind shading device; ${\tau }_w$ is the solar radiation transmittance of the window glass; ${\varphi }_R$ and ${\varphi }_L$ are reference points in the lower-left and lower-right corners of the window, respectively, that form a straight line parallel to the XZ plane (rad); and ${\theta }_{\max }$ and ${\theta }_{\min }$ are reference points in the lower-left and lower-right corners of the window forming a straight line parallel to the XY plane (rad).

The commonly used metrics for the measurement of discomfort glare in human eyes are DGP and DGI. DGI is applicable to the metric of indoor lighting glare, and DGP is applicable to the metric of daylight glare. The calculation of DGP is more complicated, time-consuming, and labour-intensive because simplified daylight glare probability (DGP) was developed based on this, and discomfort glare is considered to occur when DGP > 0.35, which is closely related to the vertical illuminance of the human eye [42], the calculation formula of which is as follows:

$$\mathrm{DGPs}=6.22\times {10}^{-5}\times E_v+0.184$$

(6)

2.2.2. Thermal Model

The heat transfer process of an external window system with or without blinds is shown in Figure 7, and the energy-saving effect of the external window system on the building consists of two parts, which are the radiant part and the heat transfer part [43]. $\mathsf{\Delta }{Q}_s$ is solar radiation entering the room through the window (kW·h) to be reduced and can be calculated on the basis of the solar transmittance of the external window system using the following formula:

$$\mathsf{\Delta }{Q}_s=\frac{A·({\tau }_w-{\tau }_s)·(I_D+I_d)·H}{1000}$$

(7)

$${\tau }_s={\tau }_b·{\tau }_w$$

(8)

where $A$ is the area of the external window (m²), ${\tau }_s$ is the equivalent solar transmittance of the window shading system, ${\tau }_b$ is the solar transmittance of the external blind shading device, ${\tau }_w$ is the solar transmittance of the window glass, and $H$ is the time. $\mathsf{\Delta }{Q}_t$ is the amount of heat transfer (heat convection and heat radiation) reduced by the application of blind devices (kW·h), calculated as follows:

$$\mathsf{\Delta }{Q}_t=\frac{A·(K_w-K_s)·(T_{out}-T_{in})·H}{1000}$$

(9)

where $K_s$ is the combined heat transfer coefficient of the external window system with shading, $K_w$ is the equivalent heat transfer coefficient of the window glass, $T_{out}$ is the outdoor temperature, and $T_{in}$ is the indoor temperature.

In research on human thermal comfort, most of scholars’ studies have centred around summer and winter in different climate zones, seldom investigating transition seasons. Yang Liu et al. conducted a study on human thermal comfort using an adaptive model in Xi’an and found that a heat-neutral temperature provides a better human thermal comfort sensation; they also established a climate-adaptive model for the Xi’an region [44], the formula of which is as follows:

$${\mathrm{T}}_n=0.3322{\mathrm{T}}_{out}+14.26$$

(10)

where ${\mathrm{T}}_n$ is the indoor thermal neutral temperature. Based on the theoretical basis of a passive solar room, in this study, we established a model for calculating the average indoor temperature after using blinds, the formula of which is as follows:

$$T_{\mathrm{j}}=T_i+\frac{\mathsf{\Delta }Q}{k_{NLC}+24\times 3.6\times A_0\times U_{gl}}$$

(11)

where $\mathsf{\Delta }Q$ represents the use of blinds before and after the change in indoor heat gain (kW·h), $T_i$ represents the use of blinds before the average room temperature is reached (°C), $T_{\mathrm{j}}$ represents the use of blinds after the average room temperature is reached (°C), $k_{NLC}$ represents the room’s net load coefficient, and $A_0{U}_{gl}$ represents the area of the enclosure and the heat transfer coefficient of the product.

2.2.3. Shading Equivalent Energy Efficiency Model

In office buildings, when indoor illuminance does not satisfy people’s work needs, they usually choose to open lighting equipment to obtain the appropriate illuminance; an indoor illuminance range of 300 Lux to 3000 Lux has been proposed as an acceptable level [45]. Therefore, the use of shading equipment to control the illuminance value within an acceptable range for indoor work can contribute lighting energy savings. The lighting energy savings achieved by the use of blinds are calculated as follows:

$$\mathsf{\Delta }{E}_L=(H_{\mathrm{n}}-H_s)\times P$$

(12)

where $H_{\mathrm{n}}$ represents the use of blinds to achieve acceptable indoor illuminance within a given range of time (h), $H_s$ represents the use of blinds to achieve acceptable indoor illuminance within a given time range (h), and $P$ represents the power used by indoor lighting fixtures (W).

By dividing the blind angles from −90° to 90° into 36 parts at 5° intervals, based on the above physical model, the datasets of illuminance value, glare value, heat gain, thermal comfort, and energy consumption of the indoor reference points under these 36 different blind angles were calculated. The results provide a data reference for the control of blinds later.

3. Control Strategy for Shading Blinds

In building interior lighting, it is desirable to make full use of natural light instead of artificial lighting in order to achieve energy savings; however, the introduction of too much natural light poses a risk of glare in the room and may result in too much solar radiation entering the room, increasing the amount of heat gain in the room and, thus, leading to an increase in the room temperature, which can affect the thermal comfort of the room. In office buildings, the problem of discomfort glare is unacceptable to the occupants of the room. Therefore, the elimination of indoor discomfort glare is the primary objective of shading control. A positive correlation has been found between the probability of glare and vertical human eye illuminance. Eliminating indoor discomfort glare may result in surface illuminance not being able to meet the requirements of indoor work so that lighting energy savings cannot be realised; it may also reduce the solar radiation entering the room, which reduces the indoor heat gain, lowering the indoor temperature and affecting the thermal comfort of the room.

Based on the above contradiction between indoor glare, illuminance, thermal comfort, and energy consumption in shading control, this study proposes a set of transitional season blind control strategies that balance lighting, thermal discomfort, and energy savings. Considering people’s aversion to discomfort glare and the fact that the presence of glare seriously affects the work of indoor occupants, the primary goal of this strategy is to eliminate discomfort glare indoors. Since the natural light level in a room not only affects the visual comfort of indoor personnel but also affects the energy consumption of indoor lighting, when natural lighting can meet the demand of indoor illumination, the energy consumption of artificial lighting can be eliminated so as to achieve the goal of energy savings. Compared to indoor thermal comfort, although indoor temperature is usually more comfortable in transition seasons, there are also a few times when thermal discomfort occurs, so this strategy adopts appropriate indoor illuminance as the second control objective and indoor thermal comfort as the secondary control objective. The strategy can be used to effectively control the indoor temperature and save energy consumption under the premise of ensuring indoor illuminance and glare comfort. The specific control process is shown in Figure 8 below.

3.1. Unoccupied Indoors

During transition seasons, when changes in the thermal environment inside the room do not occur instantaneously, adjusting the angle of the blinds can effectively control the heat gain into the room when indoor staff are temporarily away. If the indoor temperature is below the neutral thermal temperature, the heat gain into the room can be increased by adjusting the blind angle. This brings the indoor temperature closer to the neutral thermal temperature and provides a more comfortable thermal environment. Conversely, if the room temperature is above the neutral thermal temperature, the heat gain into the room can be reduced by adjusting the blind angle to ensure that the room temperature meets human thermal comfort requirements as much as possible when the staff return again.

3.2. Occupied Indoors

3.2.1. Sunny or Cloudy

The outdoor sky type can be categorised as sunny, cloudy, or overcast based on the real-time calculation of the outdoor scattered radiation coefficient. Studies have shown that under sunny or cloudy skies during transition seasons, the interior may be affected by direct light, leading to problems with glare. Due to the different orientations of building windows, there may be direct light entering the interior at different moments. Therefore, in the presence of direct light, the blind angle is first adjusted to meet the glare requirements at the indoor work point based on the obtained dataset. Once the indoor glare meets the criterion of DGP < 0.35, the blind angle is adjusted to ensure that the indoor work surface illuminance is within the range of 300 < E < 3000, within the range of blind angles that satisfy the glare requirement. Ultimately, within the range of blind angles that satisfy both requirements, the blind angle is adjusted to maximise indoor thermal comfort and bring the indoor temperature close to the thermo-neutral temperature. If it is not possible to adjust the blind angle so that the indoor working surface meets the demand, then the maximum improvement in indoor thermal comfort is achieved within the range of blind angles that prevent glare.

3.2.2. Overcast Sky

It was found that in the case of natural daylighting, the presence of direct light on sunny days with high solar radiation creates a risk of glare inside the room; therefore, glare is virtually non-existent on cloudy days during transitional seasons. Therefore, under cloudy sky types, natural lighting is not considered an indicator of glare. Therefore, a balance between meeting indoor illuminance needs and thermal comfort needs will need to be found. The control strategy adjusts the blind angle to the range where natural lighting meets the work surface illuminance requirements, within which the blind angle is adjusted to maximise indoor thermal comfort; if natural lighting does not meet the work surface illuminance requirements, the blinds are simply adjusted to the angle that maximises indoor thermal comfort.

4. Results and Discussion

4.1. Verification of Calculation Accuracy

In order to verify the excellent performance of the louvre angle optimisation control strategy designed in this study, this chapter first validates the accuracy of the proposed calculation method. The indoor heat gain was selected as the validation index for the accuracy of the calculation by comparing the results of the simulation software and the results of the calculation method proposed in this study, taking the fully cloudy day of 31 March and the sunny day of 12 May as examples. The mean relative error ($MAPE)$ and coefficient of determination ($R^2$), which are commonly used in similar studies, were chosen to evaluate the accuracy of the calculation method; the smaller the value of $MAPE$ and the closer the value of the coefficient of determination to 1, the more accurate the results of the calculation. The calculation formulas are as follows:

$$MAPE=\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{x_i-y_i}{x_i}}\times 100\%$$

(13)

$$R^2=1-\frac{{\displaystyle \sum _{i=1}^n{(x_i-y_i)}^2}}{{\displaystyle \sum _{i=1}^n{(x_i-\overline{x_i})}^2}}$$

(14)

where $x_i$ is the calculated value at the moment $i$, $y_i$ is the simulated value at moment $i$, and $n$ is the number of samples.

Table 3. Statistical table of absolute errors in simulated and calculated room heat gains.

	31 March		12 May
Time	Simulated Heat Gain (W)	Calculated Heat Gain (W)	Simulated Heat Gain (W)	Calculated Heat Gain (W)
6:00	−98.62	−91.66	−234.23	−253.93
7:00	−57.71	−60.42	−269.01	−292.5
8:00	−44.71	−49.37	−243.94	−259.49
9:00	312.91	291.73	−128.15	−134.5
10:00	583.82	571.6	231.93	214.36
11:00	947.09	953.8	668.5	702
12:00	1305.85	1369.11	1212.62	1247.7
13:00	1539.93	1695.81	1644.78	1727.4
14:00	1596.9	1653.24	1946.43	2059.42
15:00	1259.85	1295.36	2161.43	2207.63
16:00	889.25	903.55	1867.32	1997.02
17:00	572.1	601.89	916.72	961.68
18:00	402.15	428.46	578.91	628.3

shows the results of the time-by-time simulations and calculations for the two days.

A comparison of the simulation results with the calculation results is shown in

Table 4. Evaluation indicator results.

Date	MAPE	R2
31 March	5.1%	0.9918
12 May	5.9%	0.9891

below. On 31 March, the mean average relative error (MAPE) was only 5.1%, and the coefficient of determination (R²) was 0.9918, which was almost 1. On 12 May, the mean average relative error (MAPE) was 5.9%, and the coefficient of determination (R²) was 0.9891. However, for the commonly used models for indoor heat gain calculation, the acceptable range of mean relative error is usually within 10%. From these data, it can be seen that the accuracy of the calculation method proposed in this study is better.

4.2. Validation of Control Strategy Performance

In order to verify the excellent performance of the blind angle optimisation control strategy proposed in this study, we compared its effectiveness with that of several control strategies in terms of anti-glare, improvement of the quality of indoor light, improvement of thermal comfort, and energy savings in an indoor environment, namely blind cut-off angle control and fixed-angle blind control (using 45°, which is the most commonly used fixed blind angle), which are widely used without blinds and with blinds, respectively.

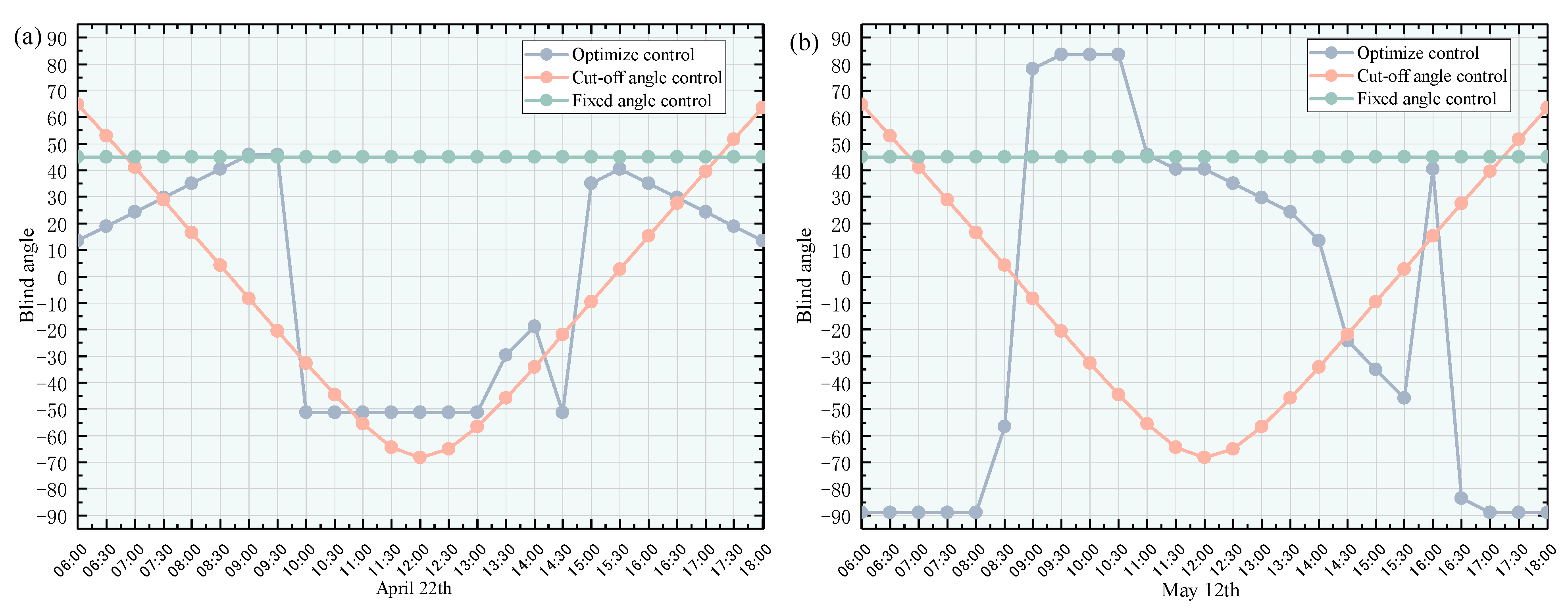
Figure 9 shows the variation of blind blade angle under the optimised control, cut-off angle control and fixed-angle control as proposed in this study on a fully cloudy day (22 April) and a fully sunny day (22 May). Under cut-off angle control, the variation of blind blade angle is basically the same during these two days. This is due to the fact that the cut-off angle is affected by the solar altitude angle, and the variation of the solar altitude angle was also basically the same on these two days, resulting in consistent blind angle variation under cut-off angle control. For fixed-angle control, the blade angle was fixed at a constant 45°. In contrast, under the optimised control strategy proposed in this study, the blind blade angle change is not necessarily regular. As shown in Figure 9a, from 6:00 a.m. to 10:00 a.m., the indoor temperature is lower than the heat centre temperature, and the solar radiation outside is weak. In order to meet the indoor illuminance demand, the external window system is required to provide more solar radiation transmittance to introduce more natural light and increase the indoor heat gain so that the indoor temperature approaches the thermo-neutral temperature. Therefore, as the solar altitude angle increases, the blind angle also increases to ensure greater solar transmittance. Between 10:00 and 2:00 p.m., as the outdoor solar radiation increases, natural light is sufficient to meet the indoor illuminance demand. In order to further improve indoor thermal comfort, the blind angle needs to be adjusted to increase the indoor heat gain so that the indoor temperature approaches the neutral thermal temperature. After 15:00, the outdoor solar radiation gradually decreases, and the sun’s altitude angle decreases, so in order to meet the indoor illuminance demand, the blind angle is also reduced. The trends from 6:00 a.m. to 10:00 a.m. and after 15:00 a.m. are basically symmetrical. As shown in Figure 9b, from 6:00 a.m. to 8:00 a.m., because the indoor temperature is higher than the thermo-neutral temperature and the outdoor solar radiation is higher than the thermo-neutral temperature, natural light cannot meet the indoor illuminance demand, so the blinds are in the closed in order to reduce the solar radiation entering into the room so as to improve indoor thermal comfort. After 8:00 a.m., the solar radiation gradually increases, and natural light is able to meet the indoor illuminance demand, but to avoid glare, between 9:00 and 11:00, the blinds are basically closed. In other time periods, the blind angle can meet the requirements of glare within a certain range. Adjusting the blind angle within the range makes the indoor illumination meet the requirements on the one hand and causes the indoor temperature to approach the thermo-neutral temperature on the other hand so as to achieve equilibrium. Therefore, the change of blind angle does not have a fixed law.

4.2.1. Glare

Figure 10 demonstrates the variation of the probability of glare at the indoor reference point throughout the day on 12 May for the following four approaches: no blinds, the optimised control method proposed in this study, cut-off angle control, and fixed-angle control. In the case of no blinds, the risk of glare exists from 8:30 to 17:00, with the probability of glare reaching its maximum at 11:00. With cut-off angle control, glare occurs from 8:30 to 10:30 and from 14:30 to 15:30, with a glare duration of 3 h. Under fixed-angle control, glare is present from 9:30 to 12:30, with a glare duration of 5 h. In contrast, under the optimised control strategy proposed in this study, discomfort glare is successfully avoided throughout the day. The optimised control strategy proposed in this study reduces the occurrence of discomfort glare by 100% compared to the other three cases.

4.2.2. Daylighting

Figure 11 shows the variation of illuminance at the reference point of the indoor work surface for the whole days of 22 April and 12 May under four scenarios, with the ideal indoor illuminance values ranging from 300 to 3000 lux. As shown in Figure 11a, the work surface illuminance is unsatisfactory for 7 h during the whole day when there are no blinds. With cut-off angle control, the unsatisfactory work surface illuminance hours are reduced to 6 h; with fixed-angle control, they are reduced to 5 h; and when using optimised control, the unsatisfactory illuminance time point is exactly the same as with cut-off angle control.

As shown in Figure 11b, the trend of indoor work surface illuminance without blinds increases, then decreases, and the duration of an unsatisfied work surface illuminance requirement reaches 8 h in a whole day. In the case of cut-off angle control, the length of time during the whole day that does not meet the working surface illuminance requirement is reduced to 3 h; in the case of fixed-angle control, the length of the length of time during the whole day that does not meet the working surface illuminance requirement is reduced to 1.5 h; and in the case of optimised control, the length of time during the whole day that does not meet the requirement is reduce to only 1 h.

In comparison, on 22 April, the optimised control strategy reduces the number of hours of unsatisfactory illumination by 1 h compared to cut-off angle control and reduces the number of hours of unsatisfactory illumination in the room by 28.6% compared to no blinds. On 12 May, the optimised control strategy reduces unsatisfactory illuminance by 2 h compared to cut-off angle control, by 0.5 h compared to fixed-angle control, and by 81.3% compared to no blinds.

4.2.3. Thermal Comfort

Figure 12 shows the variation of indoor temperature without blinds, indoor thermally neutral temperature, and indoor temperature with blinds for all three control methods throughout the day on 22 April and 12 May. Since the human body is more sensitive to temperature and is able to perceive a 1 °C temperature difference, a range of 1° above and below the thermo-neutral temperature was used as the thermal comfort temperature.

On 22 April, the indoor temperature was within the thermal comfort temperature range for all three scenarios, namely no blinds, cut-off angle control, and fixed-angle control. This shows that the effect of these four methods on the indoor temperature is not significant, which may be due to the fact that on this day, the solar radiation was low, and therefore, control of the blinds had very little effect on the indoor temperature. The optimised control strategy brings the indoor temperature closer to the thermo-neutral temperature compared to the other three methods.

On the 12th of May, when there were no blinds, the indoor temperature was not within the thermally comfortable temperature range during the three hours from 15:30 to 18:00. When cut-off and fixed-angle control strategies were used, the indoor temperature was not within the thermal comfort temperature range for 2.5 h between 16:00 and 18:00, while when control was optimised, the indoor temperature was not within the thermal comfort temperature range for only 0.5 h.

Compared with the other three cases, on 12 April, the indoor temperature was within the thermal comfort temperature range for all four control methods. However, the indoor temperature was closer to the thermally neutral temperature under the optimised control method. On 12 May, optimised control reduced the number of hours of thermal discomfort by 2 h compared to cut-off and fixed-angle control; compared to no blinds, optimised control reduced the number of hours of not being within the thermal comfort temperature range by 2.5 h, reducing the number of hours of not being within the thermal comfort temperature range by 87.5%.

4.2.4. Lighting Energy Consumption

When natural lighting can meet the illumination requirements for indoor work, the use of indoor lighting fixtures can be reduced, achieving savings in lighting energy consumption. From the data in Figure 11, it can be seen that on 22 April, the control strategy proposed in this study reduces the duration of unsatisfied illuminance requirements by 2 h compared with the case with no blinds, which is equivalent to reducing the use of lighting fixtures by 2 h, saving 28.6% of lighting energy consumption; compared with cut-off angle control, it reduces the duration of unsatisfied illuminance requirements by 0.5 h and saves 9.1% of lighting energy; and the energy saving-effect is the same as with the fixed-angle control. On 12 May, the control strategy proposed in this study saves 81.3% of the lighting energy consumption compared with the case without blinds, 50% of lighting energy consumption compared with cut-off angle control and 25% of lighting energy consumption compared with fixed-angle control. It can be seen that the optimised control strategy can make more effective use of natural lighting and reduce lighting energy consumption.

4.2.5. Adaptation Analysis

In order to prove the adaptability of this control strategy in other regions, this study also analysed the adaptability of the blind control strategy for transition seasons in different climate zones, selecting Xi’an (cold region), Lhasa (cold region), Changsha (hot summer and cold winter region), Kunming (mild region), and Shantou (hot summer and warm winter region) as representatives. The results confirm the effectiveness of the blind control strategy for transition seasons proposed in the present study in terms of improving the indoor thermal and light environments, as well as energy savings, in each climate zone. The results are shown in

Table 5. Control effects by climate region.

Climatic Region	Representative City	Reduced Glare Hours (%)	Reduced Hours of Discomfort Illumination (%)	Reduction Hours of Thermal Discomfort (%)	Energy Savings (%)
Cold region	Xi’an	100%	81.3%	87.5%	81.3%
Bitterly cold region	Lhasa	100%	53.8%	23%	53.8%
Hot summer, cold winter region	Changsha	100%	61.5%	69.2%	61.5%
Moderate region	Kunming	100%	76.9%	30.7%	76.9%
Hot summer, warm winter region	Shantou	100%	84.6%	7.6%	84.6%

below.

Figure 5 shows that the blind control strategy for transition seasons proposed in this study is adaptable to different climate zones. The strategy shows the best control effect in cold regions. In addition, in terms of improving the indoor light environment and energy savings, good results were achieved in mild regions and hot summer and warm winter regions, whereas in terms of improving indoor thermal comfort, the effect in hot summer and cold winter regions also showed good results; however, the effect in hot summer and warm winter regions was not satisfactory.

5. Conclusions

In this study, a set of model-based control index calculation methods for shading blinds was designed. Indoor reference point illuminance, glare probability, heat gain, thermal comfort, and energy savings before and after the use of blinds were calculated, and a dataset of 36 different blind angles was obtained. On this basis, a control strategy for shading blinds in transitional seasons that balances the indoor light and heat environment and energy savings is proposed. The strategy first screens blind angles that satisfy indoor glare requirements, then screens blind angles that satisfy indoor illuminance requirements and finally determines the blind angles that can maximise indoor thermal comfort.

For the above strategy, a simulation experiment was conducted in EnergyPlus simulation software for a south-facing private office in Xi’an, Shaanxi Province, China. The blind control strategy proposed in this study was compared with no-blind, traditional cut-off angle control, and fixed-angle control strategies. The daylighting performance, thermal comfort, and energy savings of each approach were compared; the results are summarised as follows.

Compared to the other three strategies, the control strategy proposed in this study significantly reduced the indoor DGP values. Discomfort glare was reduced by 100% and completely eliminated.

The proposed strategy reduces the number of hours unsatisfactory indoor illuminance for human eye comfort by 81.3% compared to no blinds under relatively sunny weather conditions, as well reducing the hours of thermal discomfort by 87.5% and saving 81.3% of lighting energy consumption.

Compared to cut-off angle and fixed-angle control, the strategy proposed in this study reduces unsatisfactory illuminance hours by 50% while reducing thermal discomfort hours by 80% of and saving 50% of lighting energy.

Analysis of the obtained results shows that the optimised blind control strategy for transitional seasons proposed in this study performs significantly better than cut-off angle control and fixed-angle control. The strategy is able to completely eliminate uncomfortable indoor glare and significantly improve the indoor light and heat environment, which is of great significance in office premises. This not only improves the comfort and productivity of indoor workers but also saves lighting energy. The strategy is particularly suitable for private office buildings that do not require cooling or heating equipment during transition seasons and has great potential to improve the indoor thermal and lighting environment and save energy, especially on sunny days during transition seasons.

However, due to time contstraints and practical limitations of experimental conditions, we were not able to conduct an experimental study in a full-size office workplace. Although the designed calculation method can replace sensor system detection and software simulation methods to obtain the control indexes of shading blinds, there are some limitations, and the results calculated by the physical model may be biased and not as accurate as the results obtained by sensor detection and software simulation. Another limitation is that, considering that daylighting has a certain impact on indoor lighting energy consumption, the real needs of users in different environments will increase the difficulty of future studies. The optimised control strategy for shading blinds proposed in this study takes the comfort of the indoor light environment as the first control objective and the comfort of the indoor thermal environment as the second control objective, without taking into account the real needs of users in different environments. Some users may pay more attention to indoor thermal comfort, and different control sequences may affect the final control performance of the strategy. Accurately determining users’ real needs in different environments and controlling sun-shading blinds in real time according to users’ needs may be the next steps to study.