Abstract
This work is aimed at investigating the capabilities and limits of the mid-fidelity numerical solver DUST for the evaluation of wind turbines aerodynamic performance. In particular, this study was conducted by analysing the benchmarks NREL-5 and Phase VI wind turbines, widely investigated in the literature via experimental and numerical activities. The work was started by simulating a simpler configuration of the NREL-5 turbine to progressively integrate complexities such as shaft tilt, cone effects and yawed inflow conditions, offering a detailed portrayal of their collective impact on turbine performance. A particular focus was then given to the evaluation of aerodynamic responses from the tower and nacelle, as well as aerodynamic behavior in yawed inflow condition, crucial for optimizing farm layouts. In the second phase, the work was focused on the NREL Phase VI turbine due to the availability of experimental data on this benchmark case. A comparison of DUST simulation results with both experimental data and high-fidelity CFD tools shows the robustness and adaptability of this mid-fidelity solver for these applications, thus opening a new scenario for the use of such mid-fidelity tools for the preliminary design of novel wind turbine configurations or complex environments as wind farms, characterised by robust interactional aerodynamics.
1. Introduction
In recent years, the challenge of developing sustainable ways to produce energy has caused the amount of interest in wind energy to rapidly increase. This challenge has been accompanied by an evolution in the methods used to evaluate the aerodynamic performance of wind turbines, representing a key factor for the development of more effective solutions in this field. These methods vary widely in complexity and fidelity, each serving different needs within the industry. To evaluate the aerodynamic performance of wind turbines, previous research studies were mainly directed at experiments considering both wind tunnels [1] or wind field measurements. Although the aerodynamics of wind turbines are extremely complicated, accurate measurements are still essential in the field of wind energy research even if they require a substantial economical effort. Nevertheless, numerical methods have been shown to be a valid and cheaper alternative to accurately calculate wind turbine aerodynamic performance. Indeed, numerical methods offer a different degree of fidelity based on their mathematical formulation and the computational effort required.
Starting from lower order numerical methods widely used for the study of wind turbines, blade element momentum (BEM) theory [2] represents a two-dimensional method suitable to provide a fast estimation of aerodynamic forces on rotating blades. However, the BEM method does not consider span-wise flow features on the blade and cannot capture the fine details related to boundary layer modelling. Moreover, this method relies on empirical functions to reproduce dynamic stall effects or blade tip loss due to compressibility [3]. Thus, the BEM method, while computationally efficient, is limited in accuracy, particularly for the simulations of complex flow conditions characterised by interactional aerodynamics or when stall phenomena occurs. On the other hand, Computational Fluid Dynamics (CFD) methods based on solving Navier-Stokes equations provide more comprehensive and accurate results in wind turbines applications, thanks to an effective modelling of blade boundary layers and of a physical representation of their wakes [4]. In particular, a great effort was spent on the use of high-fidelity commercial CFD software for wind turbine system applications, as shown for example by the works by Rezaeiha et al. [5,6]. Moreover, several works in the literature use uncertainty quantification methods in order to evaluate error propagation in high-fidelity CFD numerical simulations, as shown for example in [7,8]. The trade-off for the increasing accuracy is a significant increase in computational resources and time, making CFD less practical for early-stage design and more suited for final validation and detailed analysis of wind turbine applications.
Mid-fidelity numerical methods, widely investigated in recent years particularly for rotary wing applications, strike a balance between computational efficiency and accuracy. These methods, mainly based on the Vortex Particle Method (VPM) for wake modelling [9,10], showed to be promising to provide a more accurate representation of both aerodynamic loads and interactional flow physics of wind turbines at comparatively lower computational costs with respect to high-fidelity CFD. Thus, these tools can be considered quite interesting to be used for the preliminary design phase of wind turbine configurations or complex environments as wind farms, characterised by robust interactional aerodynamics. Indeed, several mid-fidelity aerodynamic codes were developed in recent years to support the design process of rotary wing applications. Just to cite few examples, DLR developed UPM [11], an unsteady panel and free-wake code originally intended for aeroacoustic simulations of helicopters but recently applied on arbitrary complex configurations as compound rotorcraft [12]. Moreover, GENeral Unsteady Vortex Particle (GENUVP) software, based on a panel method coupled with a VPM solver, was developed at the National Technical University of Athens (NTUA) for both aerodynamic and aeroacoustic simulations of rotary wing applications, from helicopters to wind turbines [13].
Starting from a collaboration with Airbus, Politecnico di Milano developed the mid-fidelity aerodynamic solver DUST implementing a robust formulation of different aerodynamic elements from lifting lines to surface panels. This numerical solver, based on the use of VPM for wake modelling, was thoroughly validated against experiments and high-fidelity CFD over several rotorcraft configurations with increasing complexity [14,15,16,17] and now represents one of the most mature mid-fidelity solvers widely used both in academics and industry, particularly for the preliminary design of multi-rotors architectures in aeronautics. Thus, the present work aims to provide a thorough validation of the DUST solver for a different challenge, i.e., the aerodynamic characterisation of wind turbines. The validation of DUST within this work will consist of a meticulous comparison of aerodynamic load and response predictions with those from high-fidelity CFD codes and experimental standards. With this aim, two benchmark test cases widely investigated in wind energy field were selected.
The first benchmark is the NREL (National Renewable Energy Laboratory) offshore 5 MW baseline wind turbine (NREL-5 ). It was developed as a theoretical framework for validating turbine models [18] and was extensively validated using the NREL BEM model FAST [19]. Indeed, due to the fact that all details of the geometry and airfoil properties of the turbine are publicly available, this three-blade turbine, in an upwind, horizontal axis configuration, was widely investigated in the literature. URANS simulations of the NREL-5 were performed in [20,21,22]. Then, particular interest was given to the study of wake prediction, as shown in [23,24,25]. This wind turbine reference was also used as a good benchmark to validate Fluid Structure Interaction tool chains, as shown in [26,27,28,29,30].
The second benchmark used in this work is represented by NREL Unsteady Aerodynamics Experiment Phase VI (‘NREL Phase VI’), performed on a 20 kW, 10 m diameter, two-bladed rotor wind turbine in the NASA Ames Research Center wind tunnel [1]. The main purpose of the tests was to acquire measurements on the aerodynamic and structural response of a horizontal axis wind turbine. Many researchers have performed simulations of the NREL Phase VI experiment for validation of their solvers. Sorensen et al. [31] and Langer Moller et al. [32] used a RANS simulation to predict loading and force coefficients, while in Hsu et al. [33], fluid-structure interaction simulations were performed with stabilized multiscale methods on this test case.
The specific goals of the present work were therefore to corroborate the accuracy of DUST against high-fidelity simulations for the NREL-5 wind turbine, with a particular emphasis on the impact of principal wind turbine parameters such as rotor shaft tilt, rotor cone angle, yawed inflow and blade-tower interaction. Moreover, DUST simulations were also performed for the NREL Phase VI small wind turbine to confirm the code’s robustness by comparison with experimental data, focusing on the code’s ability to accurately forecast performance metrics particularly focused on high yawed conditions. Generally, this research aims to establish the foundation for the broader application of mid-fidelity codes in wind energy, particularly during iterative design and analysis phases requiring a proper balance between computational swiftness and accuracy.
2. DUST Software
The mid-fidelity open-source software DUST www.dust.polimi.it (accessed on 1 March 2024) has been developed by Politecnico di Milano since 2017 for the simulation of the interactional aerodynamics of rotorcraft and unconventional aircraft configurations [34]. The code is released under the open-source MIT license. The capabilities of the code have been extended in recent years and DUST has been also coupled to the open-source multibody solver MBDyn [35], also developed at Politecnico di Milano, enabling the performance of aeroelastic analysis of complete rotorcraft configurations. The mathematical formulation of DUST relies on an integral boundary element formulation of the aerodynamic problem and VPM of the wakes. This choice naturally fits the Helmholtz decomposition of the velocity field from a mathematical point of view and avoids the numerical instabilities occurring with connected models of the wake. A model can be composed of several components, connected to user-defined reference frames, whose position and motion can be defined in a hierarchical way. Different aerodynamic elements allow for different levels of fidelity in the model, ranging from lifting line elements to zero-thickness lifting surfaces and surface panels for thick solid bodies.
Since the VPM is a grid-free Lagrangian approach that models the free vorticity of wakes, a DUST model needs only surface meshes eliminating the need for a volume mesh of the flow surrounding the object being studied. This approach enables a robust representation of the interacting wakes generated by lifting surfaces and bodies, as is typically seen in rotary-wing vehicle applications. A DUST model can be made up of multiple components that use different aerodynamic elements, offering varying levels of accuracy in the model ranging from lifting line elements [36,37] to vortex lattices and surface panels [38].
The lifting line (LL) element used in DUST is a one-dimensional model that represents thin, slender lifting bodies. The element considers the sectional aerodynamic coefficients of lift, drag, and pitching moment calculated on the base on the local angle of attack, the local Reynolds number and the local Mach number. By taking into account the airfoil’s camber and thickness, as well as the effects of viscosity and compressibility, the model is able to accurately calculate aerodynamic loads. However, since the problem is stated in explicit form, numerical instability may occur during aerodynamic or aeroelastic analysis.
The vortex lattice (VL) method offers a discrete representation of the average surface of thin lifting bodies by modeling them as a sheet of vortex rings with an intensity of . This is equivalent to a piecewise-uniform surface doublet distribution. While the VL method accounts for compressibility effects by applying a Prandtl-Glauert correction to the loads, it cannot capture the non-linear behavior of aerodynamic loads. To ensure numerical stability, the VL element utilizes a fully implicit numerical scheme. The non-linear vortex lattice element (NL-VL) has been implemented in order combine a surface discretisation with the capability of LL to use an aerodynamic database to introduce viscous corrections. This hybrid element formulated according to an implicit method allows for a higher robustness in terms of accuracy and numerical stability. Further details about the formulations of this quite novel element can be found in [39].
The surface panels (SP) are formulated as a Morino-like problem [38] in implicit form. This allows the SP element to accurately describe the real shape of the component by applying non-penetration boundary conditions in the physical position. However, the SP element is not able to capture the non-linear effects on aerodynamic loads.
The reader is referred to [34] for a complete mathematical formulation of the code.
3. Numerical Models
3.1. NREL-5 MW Configuration
The first test case considered is the NREL-5 offshore wind turbine. It is a three-bladed horizontal axis utility scale turbine with a rotor diameter D = 126 developed by Jonkman et al. [18]. This is a widely used test case for aerodynamics and aeroelasticity research as all details of the turbine geometry and of the operating conditions are public, which is not the case for large-scale commercial turbines. The NREL-5 machine is a purely theoretical wind turbine and therefore no experimental data is available to validate simulations. However, the extensive simulations conducted on this test case lend substantial credibility to its applicability for this study. A summary of the turbine’s essential features is presented in Table 1 and illustrated in Figure 1.

Table 1.
Summary of the NREL-5 MW wind turbine properties.
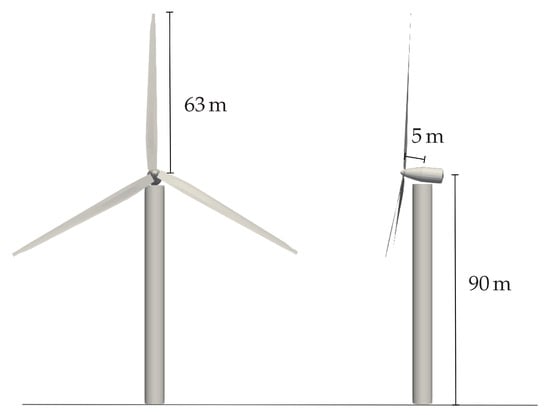
Figure 1.
Main geometrical quantities of the NREL-5 MW wind turbine.
The blade includes two non-lifting cylindrical segments and a combination of five DU airfoils and one NACA airfoil distributed over 18 spanwise sections. Specifications regarding the airfoil positioning, chord lengths and angles of twist used to build the DUST numerical model are detailed in Table 2.

Table 2.
Summary of the main properties of the NREL-5 MW wind turbine blade.
The hub of the NREL-5 wind turbine is positioned 5 upwind from the tower’s centerline and elevated 90 above the ground in an undeflected state. This configuration aligns with the vertical distance from the tower top to the hub height, set at . Consequently, the yaw bearing’s elevation above ground or mean sea level (MSL) is established at .
The wind turbine configuration and parameters used in DUST simulations for the NREL-5 wind turbine are listed in Table 3. A total of four rotor configurations are explored, each addressing different aspects of rotor and wind turbine performance. Configurations C1, C3, and C4 are assessed under direct rated inflow conditions, whereas configuration C2 is evaluated with a yaw inflow angle up to 30°. Finally, to investigate the blade tower interaction, a full wind turbine configuration was considered, dealing with C4 case rotor modelling.

Table 3.
Simulation parameters of the NREL-5 wind turbine.
Thus, the DUST numerical model of this wind turbine includes blades, tower, hub and nacelle. The tower and the nacelle surface are modelled using surface panels (SP), specifically 2700 elements for the tower and 600 elements for the nacelle. Two different models of the blades are built using both lifting lines (LL) and non-linear vortex lattices (NL-VL). Both aerodynamic elements require input tables containing the aerodynamic coefficients of two-dimensional airfoils to introduce the viscous corrections on the load obtained with the potential solution. The airloads tables are obtained by XFoil [40] simulations performed before the stall region, i.e., for a range of angle of attack between and 15°. Airfoil aerodynamic coefficients in the angle of attack range between and 180° are obtained through the Viterna method [41]. The selection of the time-step discretisation of the simulations over the rotor revolution and of the spatial spanwise discretisation of the blades was dictated by the will to balance computational efficiency with the fidelity of load pattern capture, thus serving the dual aims of computational economy and detailed aerodynamic characterization. Indeed, one of the main goals of the activity is to evaluate DUST proficiency in capturing the fundamental aerodynamic phenomena pertinent to wind turbine simulations and to ensure that the tool remains computationally economical. Indeed, the scope of the present work is to show the capability of the tool to be used for the preliminary design of novel wind turbine concepts or multiple rotors configurations as wind farms. As a matter of fact, the requirement of this work was to perform all the simulations using a commercial laptop. With this aim, the validity of the choice of parameters was verified by comparison with high-fidelity CFD results by Dose [26] for the C1 configuration. Figure 2 shows DUST simulations results of the NREL-5 wind turbine obtained with a discretisation of 75 elements along the span-wise direction and 72 time-steps per revolution for a total duration of the simulation of 50 , corresponding to about 10 rotor revolutions. In particular, DUST simulations results are reported for both LL and NL-VL elements with the same span-wise discretisation but different chord-wise elements for the latter method. A convergence of integral loads can be observed for DUST simulations after 30 s corresponding to almost eight revolutions. A good correlation in terms of aerodynamic power between CFD and DUST results, considering both LL and NL-VL elements, is obtained. A reasonably good agreement was found in terms of aerodynamic thrust, particularly considering NL-VL elements, while LL elements seem to slightly under-predict the CFD thrust output. In particular, the sensitivity analysis to chord-wise discretisation shown in Figure 2 leads to the choice of five elements for all the simulations performed on the NREL-5 wind turbine in this work. Generally, the good accuracy observed with respect to CFD for the calculation of integral loads confirms the suitability of the time and spatial discretisation selected for DUST simulations of this wind turbine.
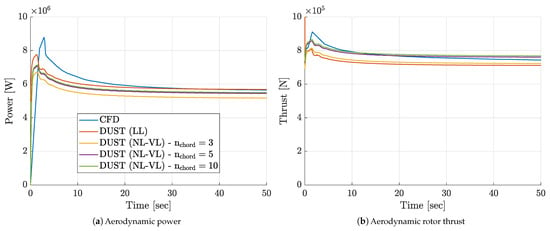
Figure 2.
Comparison of the aerodynamic power and thrust computed by DUST and CFD by Dose et al. [26] for the NREL-5 wind turbine in C1 configuration; .
Figure 3 shows the mesh of the complete DUST numerical model of the NREL-5 wind turbine.

Figure 3.
Mesh of the NREL-5 wind turbine built for DUST simulations (blades modelled with NLVL with ).
3.2. NREL Phase VI Configuration
The second test case considered is the NREL Unsteady Aerodynamics Experiment (UAE) Phase VI wind turbine [1] tested at NASA Ames wind tunnel. A summary of the turbine’s essential features is presented in Table 4.

Table 4.
Summary of the NREL Phase VI wind turbine properties.
The rotor blades use the NREL S809 airfoil and the relative specifications regarding the chord and twist distributions are detailed in Table 5.

Table 5.
Summary of the main properties of the NREL Phase VI wind turbine blade.
The hub of the NREL Phase VI wind turbine is positioned upwind from the tower’s centerline and elevated above the ground in an undeflected state. The base and tip diameter of the tower are and , respectively. The model of the NREL Phase VI wind turbine is shown in Figure 4. The DUST numerical model includes the rotor and the tower-nacelle assembly in order to be consistent for the comparison with experimental results. The tower and the nacelle are modelled by surface panels using 2700 and 600 elements, respectively. For the present test case, the DUST numerical models of the blades are built using NL-VL elements only. Following the same approach considered for the previous wind turbine, the selection of the number of time-steps and span-wise elements discretisation was validated by comparison with experimental results, now available for this wind turbine. DUST simulation results obtained by discretising each blade with 50 elements along the span-wise direction and varying the chord-wise elements distribution are compared in Figure 5 with experimental thrust and torque measured in [1] and CFD data [32]. The representation of wind turbine loads evaluated by DUST, plotted as function of the number of revolutions, highlights the bumps related to the passage of two blades in front of the pylon and shows a converged behaviour after almost four rotor revolutions. The DUST numerical model presents reasonable accuracy with experimental data for thrust and slightly underestimates the torque, showing a weak sensitivity with respect to chord-wise element discretisation. Thus, as performed for the previous wind turbine, a discretisation of five chord elements was considered as a good trade-off and therefore was used for all the simulations performed on this wind turbine in this work.
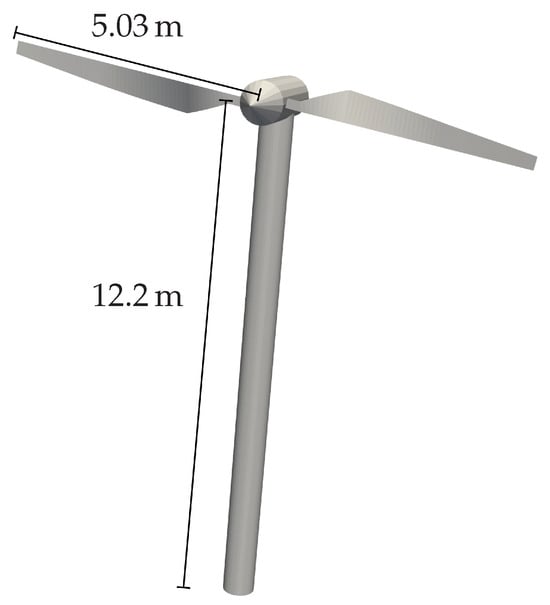
Figure 4.
NREL Phase VI model.
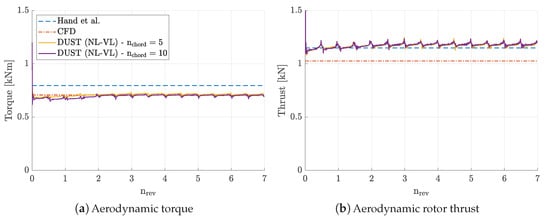
Figure 5.
Comparison of the aerodynamic power and thrust computed by DUST, CFD by [32] and experimental results from [1] NREL Phase VI wind turbine; .
The wind turbine configuration and parameters used in DUST simulations for the NREL Phase VI wind turbine are listed in Table 6. In particular, the simulations consider the full model with blade pitch at 3° windward and different yaw angles.

Table 6.
Simulations parameters of the NREL Phase VI wind turbine.
4. Results and Discussion
4.1. NREL-5 MW Wind Turbine
The first step of the validation process involves simulating the simplest configuration of the wind turbine C1 at rated conditions, not taking into account neither the shaft tilt angle nor blade cone angle . DUST results are compared to the ones obtained with high-fidelity numerical simulation conducted by Dose et al. [26] using the RANS approach and by Leng et al. [28].
Figure 6 shows the comparison of the normal and tangential sectional forces acting along the normalised spanwise coordinate of the blade computed by the DUST NL-VL model and high-fidelity CFD simulation by Dose et al. [26]. The normal force density comparison illustrated in Figure 6a exhibits a close alignment between DUST and high-fidelity CFD data along almost the majority of the blade span. However, near the blade tip, DUST slightly underestimated the normal force. This behaviour is expected as wing tips are characterized by a more complex flow regime where three-dimensional phenomena and tip vortices generation typically leads to significant viscous effects and separated flow regions, which cannot be accurately captured by the DUST mid-fidelity approach. Tangential force density comparison depicted in Figure 6b shows an underestimation of DUST computation before the first 30% of blade span and a slight overestimation in the central spanwise region. The high-fidelity CFD model, however, shows a more pronounced decrease in tangential force towards the blade tip with respect to the DUST results. Generally speaking, the behaviour of the sectional force comparison confirms the capability of DUST to competently reproduce the general force distribution along the blade span.
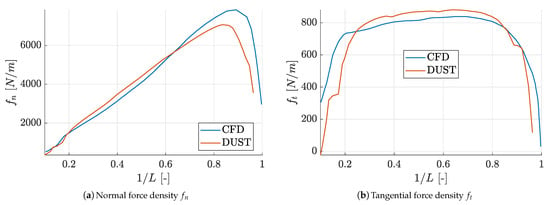
Figure 6.
Blade sectional force comparison computed by DUST (NL-VL) and CFD by Dose et al. [26] for the NREL-5 wind turbine in C1 configuration; .
The performance of a wind turbine is significantly affected by the wind turbine wake. Therefore, a crucial step for DUST validation is the ability to correctly capture the wake development and its main features in terms of velocity field. Then, the deficit of the axial velocity in the wake calculated by DUST is compared with the high-fidelity simulation by [42], considering four streamwise positions located at different distances x downstream from the rotor plane. The comparison of velocity profiles is shown in Figure 7 as function of z, representing the distance from the shaft axis parallel to the rotor plane.
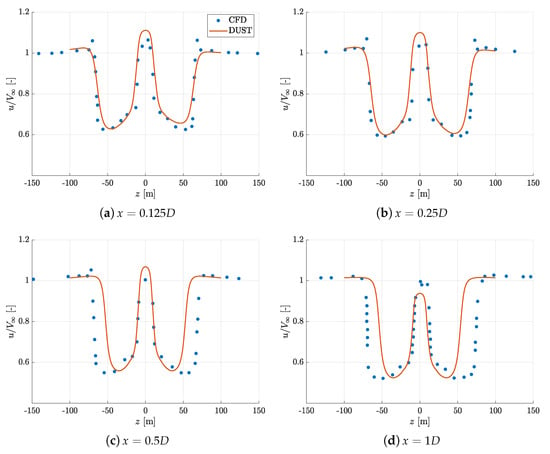
Figure 7.
Comparison of the axial velocity distributions at different downstream locations computed by DUST and CFD by Fan et al. [42] for the NREL-5 wind turbine in C1 configuration; .
A reasonably good agreement was found between axial velocity profiles in the wake of the wind turbine, particularly near to the rotor disk, i.e., and . Some discrepancies were found at higher distances where CFD results show a slightly larger extension of the wake, probably due to numerical diffusion. Generally, Figure 8 illustrates the wake structure computed by DUST shown as an iso-surface of the vortex Q-criterion. Readers are referred to results reported in [42] to appreciate the capability of DUST to capture the behaviour of the wake structure computed by CFD.
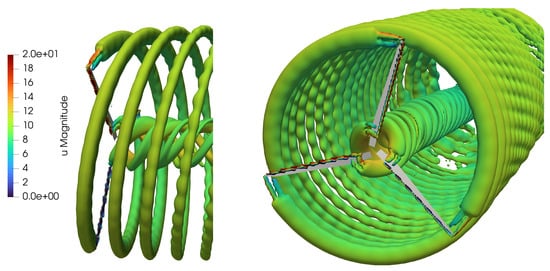
Figure 8.
Instantaneous iso-surface for the vortex criterion Q coloured by the velocity magnitude calculated by DUST for the NREL-5 wind turbine in C1 configuration; .
The influence of blade cone angle and shaft tilt angle on the aerodynamic performance under rated inflow conditions is now explored by comparing results obtained with DUST and high-fidelity CFD by Dose et al. [26] over C1, C3 and C4 cases. Generally, the sensitivity of integral loads to cone and tilt angles variations is minimal. Indeed, by adding a blade cone angle, a slight increase in the rotor power is observed. On the other hand, introducing a shaft tilt slightly reduces rotor power and thrust. In particular, the integral power and thrust on the rotor are compared in Table 7. Both DUST models provide values quite similar to high-fidelity CFD findings. A difference below 2% is found for power evaluation with both LL and NL-VL elements, while thrust evaluation obtained by DUST with NL-VL is in quite good agreement with CFD. An underestimation of rotor thrust of about 8% is found for the LL DUST model with respect to CFD.

Table 7.
Comparison of integral rotor power and thrust computed by DUST and high-fidelity CFD by Dose et al. [26]; .
Case C4 enabled us to provide an insight into the effects of varying freestream velocity, thanks to high-fidelity CFD results from Sørensen and Johansen [20], Lin et al. [21], Wu and Nguyen [22]. Figure 9 compares the computed power and thrust as function of wind speeds. Generally, both DUST models capture the behaviour of power and thrust curves evaluated by CFD, thus confirming the capability to correctly model the effects of wind inflow on rotor performance. In particular, the LL element model tends to slightly overestimate power production below the rated wind speed, while the NL-VL element model slightly overestimates rotor power above the rated speed. Now considering thrust evaluation, the LL element model tends to underestimate CFD high-fidelity data along the entire velocity spectrum, while a comparatively better agreement is obtained with the NL-VL element model.
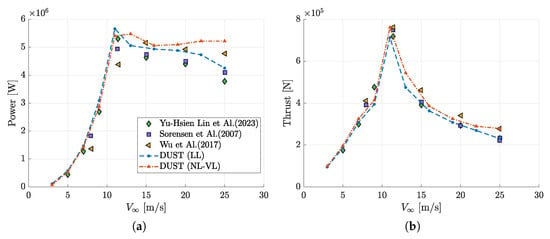
Figure 9.
Comparison of integral rotor power (a) and thrust (b) computed by DUST and high-fidelity CFD by Sørensen and Johansen [20], Lin et al. [21], Wu and Nguyen [22] as function of inflow wind speeds for the NREL-5 wind turbine in C4 configuration.
Different yawed configurations are then investigated. At first, a yaw angle is considered to assess the integral and the sectional parameters with respect to high-fidelity CFD simulation by Dose et al. [26]. Then, other two yaw angles configurations are considered, namely , and , respectively, to be compared with the LES study by yaw [24]. Table 8 compares the integral rotor power and thrust computed for C2 configuration with where errors in terms of power and thrust with respect to CFD by Dose et al. [26] are below 10% for the LL model and below 5% for the NL-VL model. Compared to the axial flow condition case, power and thrust outputs decrease in accordance to CFD evaluation by Dose et al. [26]. Results by Dose et al. [26] are based on the blade resolving CFD method, so dynamic stall effects occurring particularly in yawed conditions are implicitly included. On the other hand, no dynamic stall models are considered in DUST formulation.

Table 8.
Comparison of integral rotor power and thrust computed by DUST and high-fidelity CFD by Dose et al. [26] for configuration C2 with 30° yaw; .
In order to quantify the local effect on blades subjected to yawed inflow, sectional normal and tangential forces are compared at three different spanwise coordinates in Figure 10 as a function of blade azimuthal angle in the last computed revolution. DUST tends to calculate higher normal and tangential force densities up to 60% of the span coordinate, while a slightly lower normal force density is found near the blade tip compared to the high-fidelity CFD results. Nevertheless, generally the global behaviour of the sectional forces acting on blades are captured by DUST representation also in yawed condition.
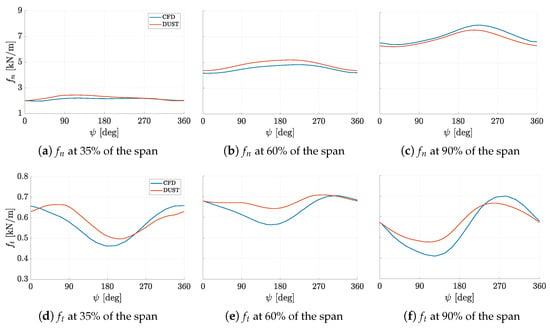
Figure 10.
Blade sectional force comparison computed by DUST (NL-VL) and CFD by Dose et al. [26] for the NREL-5 wind turbine in configuration C2 at with 30° yaw. At , the tracked blade points vertically up.
Another important feature to better understand the capability to capture the wind turbine wake behaviour for yawed configuration is the study of the evolution of the wake center-lines and the associated skew angles. The wake center-lines are imaginary lines that run through the middle of the wake, marking the trajectory of the region with the highest velocity deficit caused by the wind turbine and representing the path that the wake follows downstream of the turbine. This line can be calculated as the integral of the velocity deficit on a wake section perpendicular to the flow direction divided by the area of that section [43]. This method gives an average value that accounts for the different velocities across the entire wake area, providing a singular measure of the wake’s strength. The skew angles, instead, give a more quantitative analysis of the wake center trajectories. Skew angle is the angular measure between the position vector extending from the rotor disk midpoint and the normal vector to the rotor disc, as shown in Figure 11 and defined in Equation (1). Figure 12 shows the skew angles behaviour calculated by DUST compared with LES results by Kim and Lee [25], for yawed conditions ranging from to . The comparison shows how DUST is capable to correctly evaluate the wake center line evolution and the corresponding skew angles that change with respect to yaw angle and show a peak around .
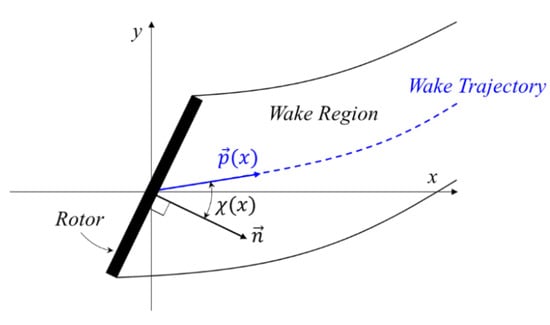
Figure 11.
Skew angle () representation, from [25].
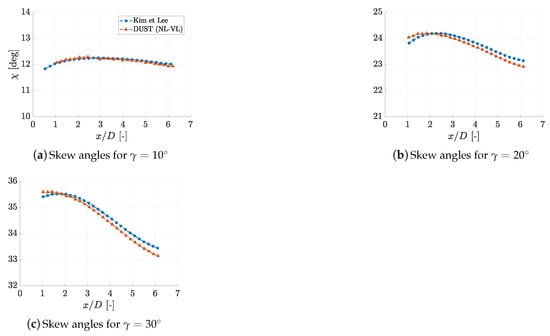
Figure 12.
Comparison of the skew angles for with the results obtained by Kim and Lee [25]; .
A more general evaluation of DUST capabilities to capture wind turbine wake is provided by the visualization of the flow fields. Figure 13 and Figure 14 show the contours of the averaged and instantaneous streamwise velocity computed by DUST (NL-VL) at different yaw angles. This flow field representation highlights the capability of DUST to evaluate the evolution and deflection of the wakes occurring at yawed conditions, as well as the highly unsteady behaviour of the flow fields in these conditions. If compared with LES results by Kim and Lee [25], the global behaviour of the flow field is captured but the speed of deformation of the sectional shape of the wakes computed by DUST is higher. Indeed, the coherence of the wake shape is lost at a lower distance from the rotor disk with respect to LES computation by Kim and Lee [25], as shown by the contours of the averaged streamwise velocity on transversal planes shown in Figure 15.
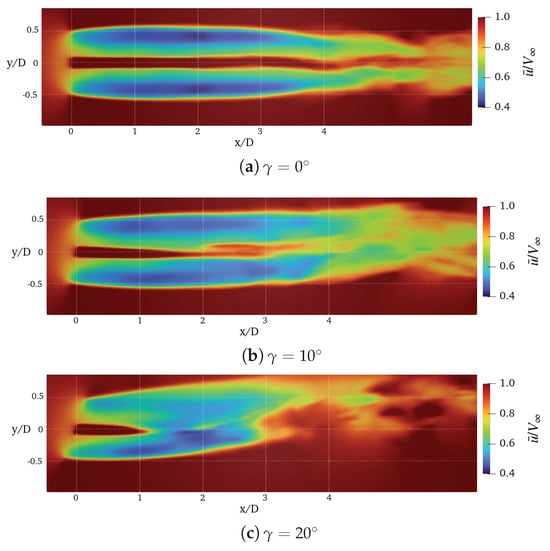
Figure 13.
Contours of the averaged streamwise velocity, , computed by DUST (NL-VL) on longitudinal planes for the NREL-5 wind turbine at with different yaw angles.
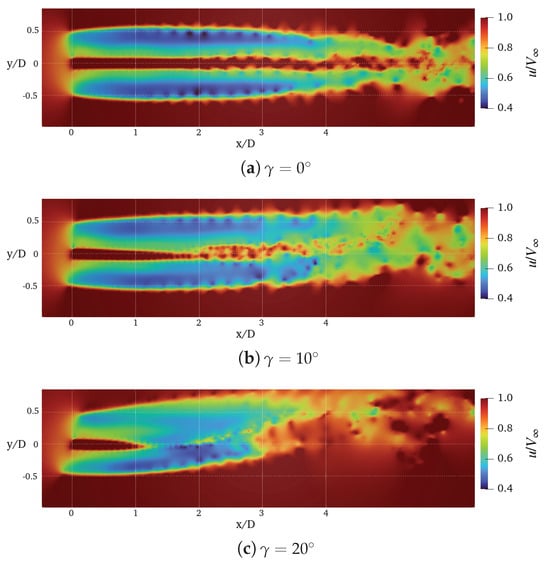
Figure 14.
Contours of the instantaneous streamwise velocity, , computed by DUST (NL-VL) on longitudinal planes for the NREL-5 wind turbine at with different yaw angles.
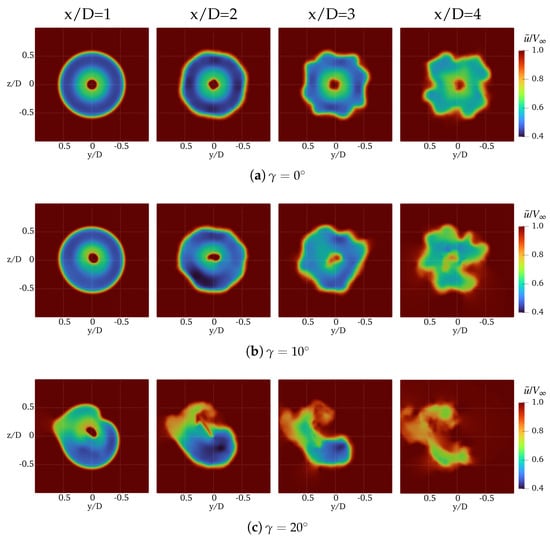
Figure 15.
Contours of the averaged streamwise velocity, , computed by DUST (NL-VL) on transversal planes for the NREL-5 wind turbine at with different yaw angles.
The final configuration considered deals with the complete case equipped with tower and nacelle for C4 rotor condition. Figure 16 illustrates a visualisation of the wake structure computed by DUST for the complete wind turbine shown as an iso-surface of the vortex Q-criterion.
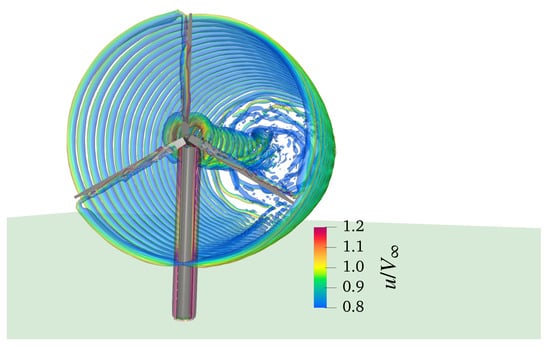
Figure 16.
Instantaneous flow field computed by DUST for the full turbine configuration: iso-surface of Q-criterion colored by adimensional free-stream velocity.
As performed before, DUST simulation results using both LL and NL-VL models are compared with the high-fidelity CFD calculation by Yu and Kwon [30] and Lin et al. [21]. The results in terms of integral loads comparison are presented in Table 9 for a single rotor and a full wind turbine.

Table 9.
Comparison of integral rotor power and thrust computed by DUST and high-fidelity CFD at by Lin et al. [21] for configuration C4.
The introduction of nacelle and tower provides a reduction of the rotor performance for both power and thrust. This behaviour is captured by DUST simulations, thus showing the capability to reproduce interactional effects between rotor wake and tower, as performed by CFD. In particular, the NL-VL model shows integral values in quite good agreement with high-fidelity CFD [21] as evaluated differences are below than 5% for both power and thrust.
4.2. NREL Phase VI
The second part of the validation deals with the NREL Phase VI wind turbine and was focused in particular on the analysis of highly yawed conditions for 7 m/s freestream velocity. Firstly, an overview of rotor thrust and torque computed by DUST at zero yaw is given in Table 10 and compared with experiments by Hand et al. [1] and high-fidelity CFD data by Länger-Möller et al. [32].

Table 10.
Rotor loads comparison for a full NREL Phase VI wind turbine at 7 m/s and zero yaw with high-fidelity CFD results from [32] and experimental results from [1].
A good agreement of the integral load values are found for DUST simulations for the complete wind turbine model, as thrust is near to the mean experimental value, while torque is slightly underestimated similarly to CFD. A detailed insight on loads behaviour is provided by the time history of the single blade aerodynamic torque evaluated on the last computed revolution, compared with experiments and CFD [33] in Figure 17. Results distinctly illustrate the capability of DUST to reproduce time evolution of the blade torque observed by experiments and particularly the bump occurring as a blade passes in front of the tower around the azimuthal angle of .
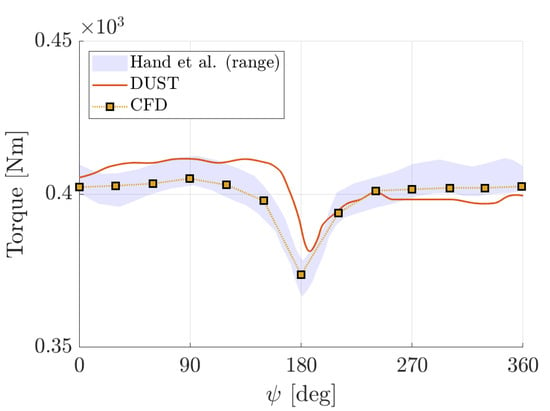
Figure 17.
Comparison of the time history of the single blade aerodynamic torque over a full revolution compared with high-fidelity results from [33] and experimental results from [1] at . The standard deviation of the experimental load is reported as a banded region.
Now, the attention is focused on the evaluation of loads for yawed conditions. Thus, blade sectional normal and tangential force are compared in Figure 18 and Figure 19, respectively, for different yaw angles. In particular, DUST results are compared with NREL measurements [1] and with numerical results obtained by RANS simulations [44] and by a non-linear vortex lattice method (NVLM) described in [45].
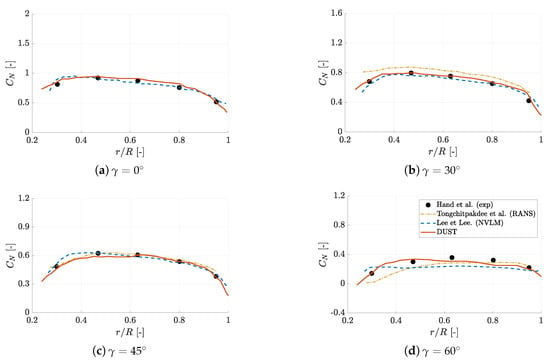
Figure 18.
Averaged normal force coefficient densities for different yaw angles compared with the NREL measurement data [1] and numerical results using RANS [44] and non-linear vortex lattice method (NVLM) [45].
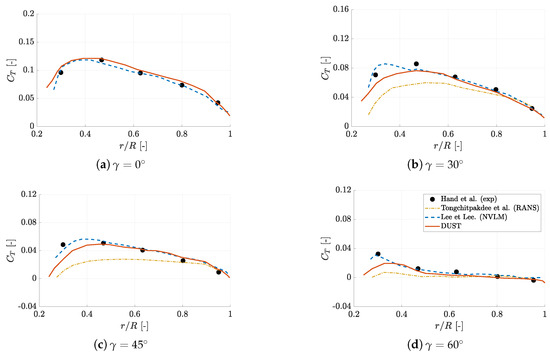
Figure 19.
Averaged tangential force coefficient densities for different yaw angles compared with the NREL measurement data [1] and numerical results using RANS [44] and non-linear vortex lattice method (NVLM) [45].
The trends of the normal sectional forces computed by DUST resemble the experimental data for the considered yawed angles, just showing a slight downward offset with respect to the mean experimental values at , similarly to that found by both the RANS and NVLM approach used as a comparison. Concerning tangential force density, a reasonably good agreement with experiments and NVLM approach results [44] is obtained particularly at . Some discrepancies are observed at higher yaw angles in the inner blade region, where also the RANS approach shows larger error with respect to experiments. On the other hand, a quite good agreement with both experimental and numerical data is also found for higher yaw angles in the outer half region of the blade. Generally, the sectional load values obtained by DUST resemble an accuracy comparable with the similar NVLM method used in [45] and somewhat higher than the one obtained by high-fidelity CFD, thus further confirming the promising capability of the DUST mid-fidelity approach for the evaluation of wind turbine aerodynamic performance also under deeply yawed conditions.
Finally, a representation of the wind turbine wakes under the different considered yawed conditions is shown in Figure 20 by means of iso-surfaces of Q-criterion coloured by non-dimensional axial velocity component contours. To impose the yaw rotation, the entire turbine was rotated as performed during the wind tunnel tests, assuming the was flow always directed from left to right. This comparison shows the capability of DUST to evaluate the coherent vortical structure of the wind turbine wake as well as their deflection related to the different yawed conditions.
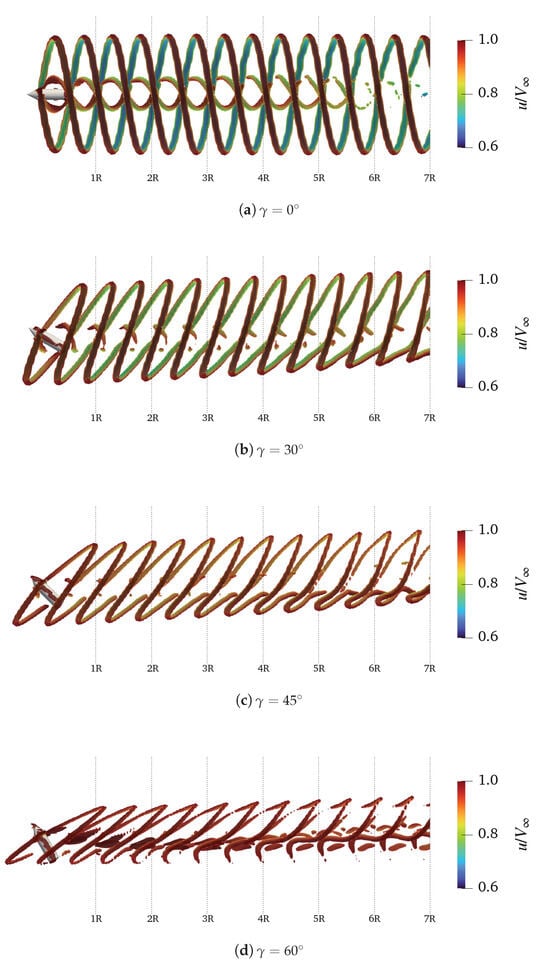
Figure 20.
Comparison of the iso-surfaces of Q-criterion coloured by non-dimensional axial velocity component contours for the NREL Phase VI wind turbine at 7 m/s at different yaw.
5. Conclusions
The present activity was aimed to validate the mid-fidelity numerical solver DUST for the evaluation of wind turbine aerodynamics. This study involved the numerical modelling of two wind turbines widely investigated in the literature for numerical tool validation purposes. A thorough comparison of DUST simulations results with both experimental and high-fidelity CFD data showed the limits and capabilities of the mid-fidelity solver to reproduce loads and flow field characteristics in different operating conditions including high yaw angles.
In particular, the study of the NREL-5 wind turbine indicates that DUST is capable to provide a reasonably good degree of accuracy with respect to high-fidelity CFD for the computation on integral loads, showing errors always below 10%. In particular, the non-linear vortex lattice method implemented in DUST showed higher fidelity with respect to the lifting line method, particularly at higher inflow speeds. A similar accuracy in terms of integral loads is found in yawed conditions even if the local comparison of force density along blade span indicates some appreciable discrepancies with respect to CFD, particularly for the tangential component. Concerning the reproduction of the wind turbine wake, DUST shows a global good evaluation of wake evolution and trajectory also under yawed conditions. Nevertheless, quantitative comparison shows a better representation of the near field, while higher discrepancies are found further from the rotor disk where deformation of the sectional shape of the wake is higher with respect to LES representation, particularly under yawed conditions.
Thanks to the availability of experimental results, the study of the NREL Phase VI wind turbine provides a reasonably strong evaluation of the capabilities of DUST, particularly focused on the analysis of loads under yawed conditions. The integral loads computed with DUST are in reasonably good agreement with both experimental and CFD data. A more detailed insight on the blade force densities along the span showed a general agreement between DUST and numerical approaches characterised by different degrees of fidelity, particularly for the normal force component. Higher discrepancies with experiments are found for the tangential components, particularly on the inner region of the blade.
Generally, the outcomes of the present work encourage the use of thee DUST mid-fidelity approach for the preliminary aerodynamic design of wind turbine configurations requiring a huge number of simulations that could be performed with a somewhat lower computational cost with respect to high-fidelity CFD. In particular, the capability of this VPM-based solver to reproduce interactional flow physics mechanisms of rotary wing machines opens a new scenario for the use of mid-fidelity solvers in the design phase of wind farms.
Author Contributions
Conceptualization, A.S. and A.Z.; methodology, A.S. and A.Z.; software, A.S. and A.F.; validation, A.S., A.F. and A.Z.; formal analysis, A.S. and A.F.; investigation, A.S. and A.F.; resources, A.S. and A.Z.; data curation, A.S. and A.F.; writing—original draft preparation, A.S. and A.F.; writing—review and editing, A.S. and A.Z.; visualization, A.S. and A.F.; supervision, A.S. and A.Z.; project administration, A.Z.; funding acquisition, A.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data would be available on request to authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| x | Streamwise coordinate |
| y | Transverse coordinate |
| z | Vertical coordinate normal to ground |
| u | Axial velocity component |
| Freestream velocity | |
| Lifting line | |
| Non-linear vortex lattice | |
| R | Rotor radius |
| D | Rotor diameter |
| P | Aerodynamic power |
| T | Aerodynamic thrust |
| Power coefficient | |
| Thrust coefficient | |
| Normal force density | |
| Tangential force density | |
| Normalized span | |
| Normal force density coefficient | |
| Tangential force density | |
| Rotor speed | |
| Pitch angle | |
| Shaft tilt angle | |
| Rotor cone angle | |
| Azimuth angle | |
| Twist angle | |
| Yaw angle | |
| Skew angle |
References
- Hand, M.M.; Simms, D.A.; Fingersh, L.J.; Jager, D.W.; Cotrell, J.R.; Schreck, S.; Larwood, S.M. Unsteady Aerodynamics Experiment Phase VI: Wind Tunnel Test Configurations and Available Data Campaigns; National Renewable Energy Laboratory: Golden, CO, USA, 2001. [CrossRef]
- Glauert, H. Airplane Propellers. In Aerodynamic Theory: A General Review of Progress Under a Grant of the Guggenheim Fund for the Promotion of Aeronautics; Springer: Berlin/Heidelberg, Germany, 1935; pp. 169–360. [Google Scholar] [CrossRef]
- Hansen, M.; Sørensen, J.; Voutsinas, S.; Sørensen, N.; Madsen, H. State of the art in wind turbine aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 2006, 42, 285–330. [Google Scholar] [CrossRef]
- Alesbe, I.; Abdel-Maksoud, M.; Aljabair, S. Investigation of the Unsteady Flow Behaviour on a Wind Turbine Using a BEM and a RANSE Method. J. Renew. Energy 2016, 2016, 6059741. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Micallef, D. CFD simulation of two tandem floating offshore wind turbines in surge motion. J. Phys. Conf. Ser. 2020, 1618, 052066. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Kalkman, I.; Blocken, B. CFD simulation of a vertical axis wind turbine operating at a moderate tip speed ratio: Guidelines for minimum domain size and azimuthal increment. Renew. Energy 2017, 107, 373–385. [Google Scholar] [CrossRef]
- Cravero, C.; De Domenico, D.; Marsano, D. Uncertainty Quantification Analysis of Exhaust Gas Plume in a Crosswind. Energies 2023, 16, 3549. [Google Scholar] [CrossRef]
- Xia, L.; Zou, Z.J.; Wang, Z.H.; Zou, L.; Gao, H. Surrogate model based uncertainty quantification of CFD simulations of the viscous flow around a ship advancing in shallow water. Ocean. Eng. 2021, 234, 109206. [Google Scholar] [CrossRef]
- Cottet, G.H.; Koumoutsakos, P.D. Vortex Methods: Theory and Practice; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Winckelmans, G.S. Topics in Vortex Methods for the Computation of Three-and Two-Dimensional Incompressible Unsteady Flows. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1989. [Google Scholar]
- Yin, J.; Ahmed, S. Helicopter Main-Rotor/Tail-Rotor Interaction. J. Am. Helicopter Soc. 2000, 4, 293–302. [Google Scholar] [CrossRef]
- Wentrup, M.; Yin, J.; Kunze, P.; Streit, T.; Wendisch, J.; Schwarz, T.; Pinacho, J.; Kicker, K.; Fukari, R. An overview of DLR compound rotorcraft aerodynamics and aeroacoustics activities within the CleanSky2 NACOR Project. In Proceedings of the 74th AHS Annual Forum & Technology Display, Phoenix, AZ, USA, 14–17 May 2018. [Google Scholar]
- Opoku, D.; Triantos, D.; Nitzsche, F.; Voutsinas, S. Rotorcraft Aerodynamic and Aeroacoustic Modelling using Vortex Particle Methods. In Proceedings of the Proceedings of the 23rd International Congress of Aeronautical Sciences, ICAS, Toronto, ON, Canada, 8–13 September 2002. [Google Scholar]
- Montagnani, D.; Tugnoli, M.; Fonte, F.; Zanotti, A.; Droandi, G.; Syal, M. Mid-Fidelity Analysis of Unsteady Interactional Aerodynamics of Complex VTOL Configurations. In Proceedings of the 45th European Rotorcraft Forum, Warsaw, Poland, 17–19 September 2019. [Google Scholar]
- Zanotti, A.; Algarotti, D. Aerodynamic interaction between tandem overlapping propellers in eVTOL airplane mode flight condition. Aerosp. Sci. Technol. 2022, 124, 107518. [Google Scholar] [CrossRef]
- Droandi, G.; Syal, M.; Bower, G. Analysis of the Interactional Aerodynamics of the Vahana eVTOL Using a Medium Fidelity Open Source Tool. In Proceedings of the VFS Aeromechanics for Advanced Vertical Flight Technical Meeting, AHS International, San Jose, CA, USA, 21–23 January 2020. [Google Scholar]
- Piccinini, R. Rotor-Rotor Aerodynamic Interactions for eVTOL Aircraft Configurations. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2020. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; US Department of Energy (US): Oak Ridge, TN, USA, 2009. [CrossRef]
- Jonkman, J.M.; Buhl, M.L., Jr. FAST User’s Guide—Updated August 2005; US Department of Energy (US): Oak Ridge, TN, USA, 2005. [CrossRef]
- Sørensen, N.; Johansen, J. UPWIND, Aerodynamics and aeroelasticity Rotor aerodynamics in atmospheric shear flow. In Proceedings of the European Wind Energy Conference & Exhibition, EWEC 2007, Milan, Italy, 7–10 May 2007. [Google Scholar]
- Lin, Y.H.; Chen, H.K.; Wu, K.Y. Prediction of aerodynamic performance of NREL offshore 5-MW baseline wind turbine considering power loss at varying wind speeds. Wind Energy 2023, 26, 493–515. [Google Scholar] [CrossRef]
- Wu, C.H.K.; Nguyen, V.T. Aerodynamic simulations of offshore floating wind turbine in platform-induced pitching motion. Wind Energy 2017, 20, 835–858. [Google Scholar] [CrossRef]
- Rahimi, H.; Hartvelt, M.; Peinke, J.; Schepers, J.G. Investigation of the current yaw engineering models for simulation of wind turbines in BEM and comparison with CFD and experiment. J. Phys. Conf. Ser. 2016, 753, 022016. [Google Scholar] [CrossRef]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Aerodynamics of Horizontal Axis Wind Turbines. In Wind Energy Handbook; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; Chapter 3; pp. 39–136. [Google Scholar] [CrossRef]
- Kim, H.; Lee, S. Large Eddy Simulation of Yawed Wind Turbine Wake Deformation. Energies 2022, 15, 6125. [Google Scholar] [CrossRef]
- Dose, B.; Rahimi, H.; Herráez, I.; Stoevesandt, B.; Peinke, J. Fluid-structure coupled computations of the NREL 5MW wind turbine by means of CFD. Renew. Energy 2018, 129, 591–605. [Google Scholar] [CrossRef]
- Hsu, M.C.; Bazilevs, Y. Fluid—Structure Interaction Modeling of Wind Turbines: Simulating the Full Machine. Comput. Mech. 2012, 50, 821–833. [Google Scholar] [CrossRef]
- Leng, J.; Gao, Z.; Wu, M.C.; Guo, T.; Li, Y. A fluid-structure interaction model for large wind turbines based on flexible multibody dynamics and actuator line method. J. Fluids Struct. 2023, 118, 103857. [Google Scholar] [CrossRef]
- Imiela, M.; Wienke, F. Towards Multidisciplinary Wind Turbine Design using High-Fidelity Methods. In Proceedings of the 33rd Wind Energy Symposium, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Yu, D.O.; Kwon, O.J. Predicting wind turbine blade loads and aeroelastic response using a coupled CFD–CSD method. Renew. Energy 2014, 70, 184–196. [Google Scholar] [CrossRef]
- Sørensen, N.N.; Michelsen, J.A.; Schreck, S. Navier–Stokes predictions of the NREL phase VI rotor in the NASA Ames 80 ft × 120 ft wind tunnel. Wind Energy 2002, 5, 151–169. [Google Scholar] [CrossRef]
- Länger-Möller, A.; Löwe, J.; Kessler, R. Investigation of the NREL phase VI experiment with the incompressible CFD solver THETA. Wind Energy 2017, 20, 1529–1549. [Google Scholar] [CrossRef]
- Hsu, M.C.; Akkerman, I.; Bazilevs, Y. Finite element simulation of wind turbine aerodynamics: Validation study using NREL Phase VI experiment. Wind Energy 2014, 17, 461–481. [Google Scholar] [CrossRef]
- Tugnoli, M.; Montagnani, D.; Syal, M.; Droandi, G.; Zanotti, A. Mid-fidelity approach to aerodynamic simulations of unconventional VTOL aircraft configurations. Aerosp. Sci. Technol. 2021, 115, 106804. [Google Scholar] [CrossRef]
- Savino, A.; Cocco, A.; Zanotti, A.; Tugnoli, M.; Masarati, P.; Muscarello, V. Coupling mid-fidelity aerodynamics and multibody dynamics for the aeroelastic analysis of rotary-wing vehicles. Energies 2021, 14, 6979. [Google Scholar] [CrossRef]
- Gallay, S.; Laurendeau, E. Nonlinear generalized lifting-line coupling algorithms for pre/poststall flows. AIAA J. 2015, 53, 1784–1792. [Google Scholar] [CrossRef]
- Piszkin, S.T.; Levinsky, E. Nonlinear Lifting Line Theory for Predicting Stalling Instabilities on Wings of Moderate Aspect Ratio; AD-A027 645; General Dynamics San Diego Ca Convair Div; U.S. Department of Commerce National Technical Information Service: Alexandria, VA, USA, 1976.
- Morino, L.; Kuot, C.C. Subsonic potential aerodynamics for complex configurations: A general theory. AIAA J. 1974, 12, 191–197. [Google Scholar] [CrossRef]
- Cocco, A.; Colli, A.; Savino, A.; Masarati, P.; Zanotti, A. A non-linear unsteady vortex lattice method for aeroelastic rotor loads evaluation. In Proceedings of the 48th European Rotorcraft Forum (ERF 2022), Winterthur, Switzerland, 6–8 September 2022; pp. 1–8. [Google Scholar]
- Drela, M. XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils. In Low Reynolds Number Aerodynamics; Mueller, T.J., Ed.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–12. [Google Scholar]
- Viterna, L.A.; Corrigan, R.D. Fixed Pitch Rotor Performance of Large Horizontal Axis Wind Turbines; NASA Lewis Research Center: Cleveland, OH, USA, 1982.
- Fan, Z.; Li, S.; Gao, Z.; Zhang, L.; Zheng, X.; Zhu, W.; Shen, W.; Sjholm, M.; Mikkelsen, T.K.; Wang, T.; et al. On the importance of wind turbine wake boundary to wind energy and environmental impact. Energy Convers. Manag. 2023, 277, 116664. [Google Scholar] [CrossRef]
- Bastankhah, M.; Porté-Agel, F. Wind tunnel study of the wind turbine interaction with a boundary-layer flow: Upwind region, turbine performance, and wake region. Phys. Fluids 2017, 29, 065105. [Google Scholar] [CrossRef]
- Tongchitpakdee, C.; Benjanirat, S.; Sankar, L.N. Numerical simulation of the aerodynamics of horizontal axis wind turbines under yawed flow conditions. J. Sol. Energy Eng. 2005, 127, 464–474. [Google Scholar] [CrossRef]
- Lee, H.; Lee, D.J. Wake impact on aerodynamic characteristics of horizontal axis wind turbine under yawed flow conditions. Renew. Energy 2019, 136, 383–392. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).