Investigation on Transition Characteristics of a Modified RAE5243 Airfoil
Abstract
1. Introduction
2. Experimental Setup
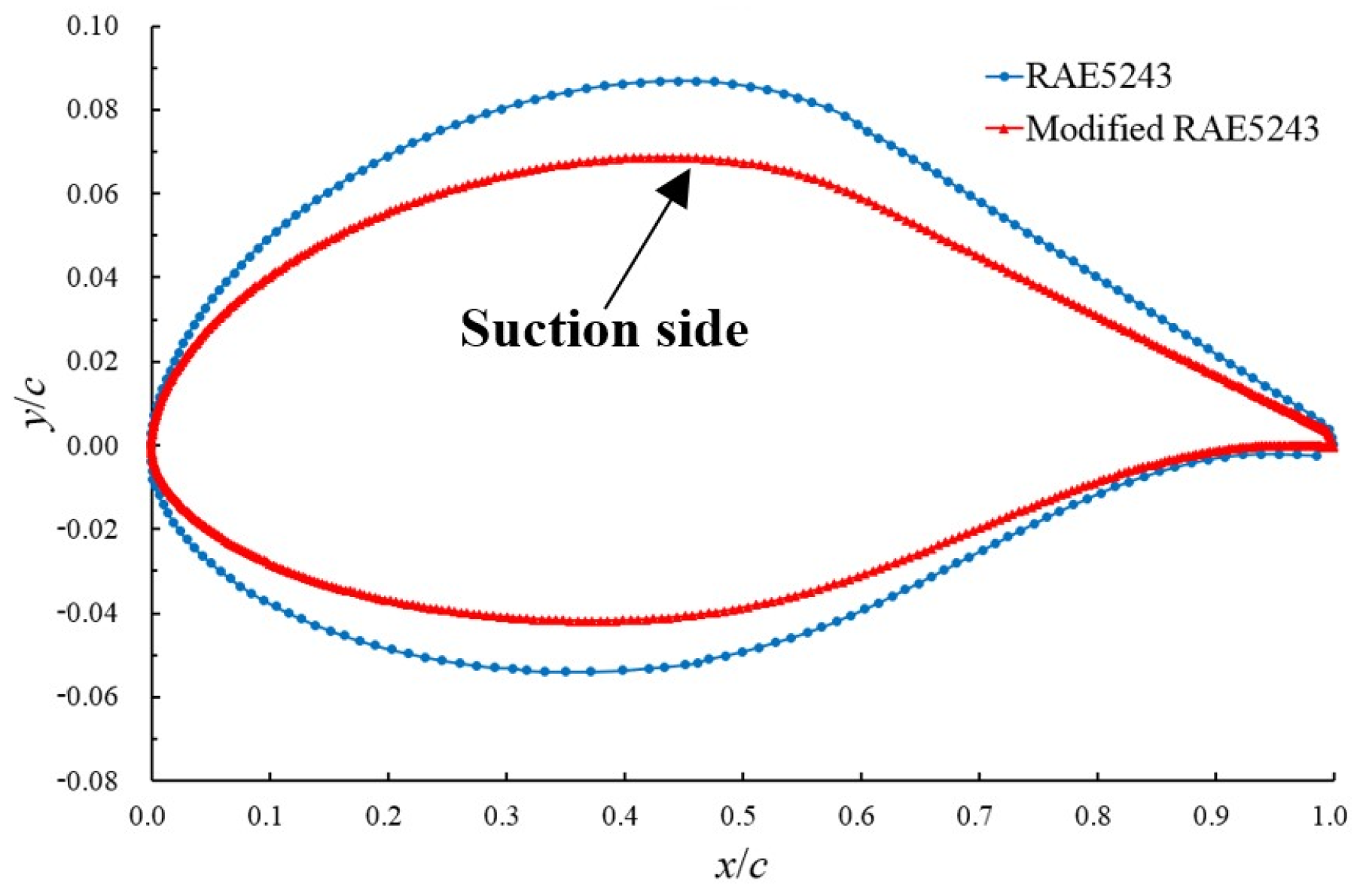
2.1. Test Model
2.2. Infrared Measurement System
2.3. Wind Tunnel
2.4. Work Frame
3. Preparation
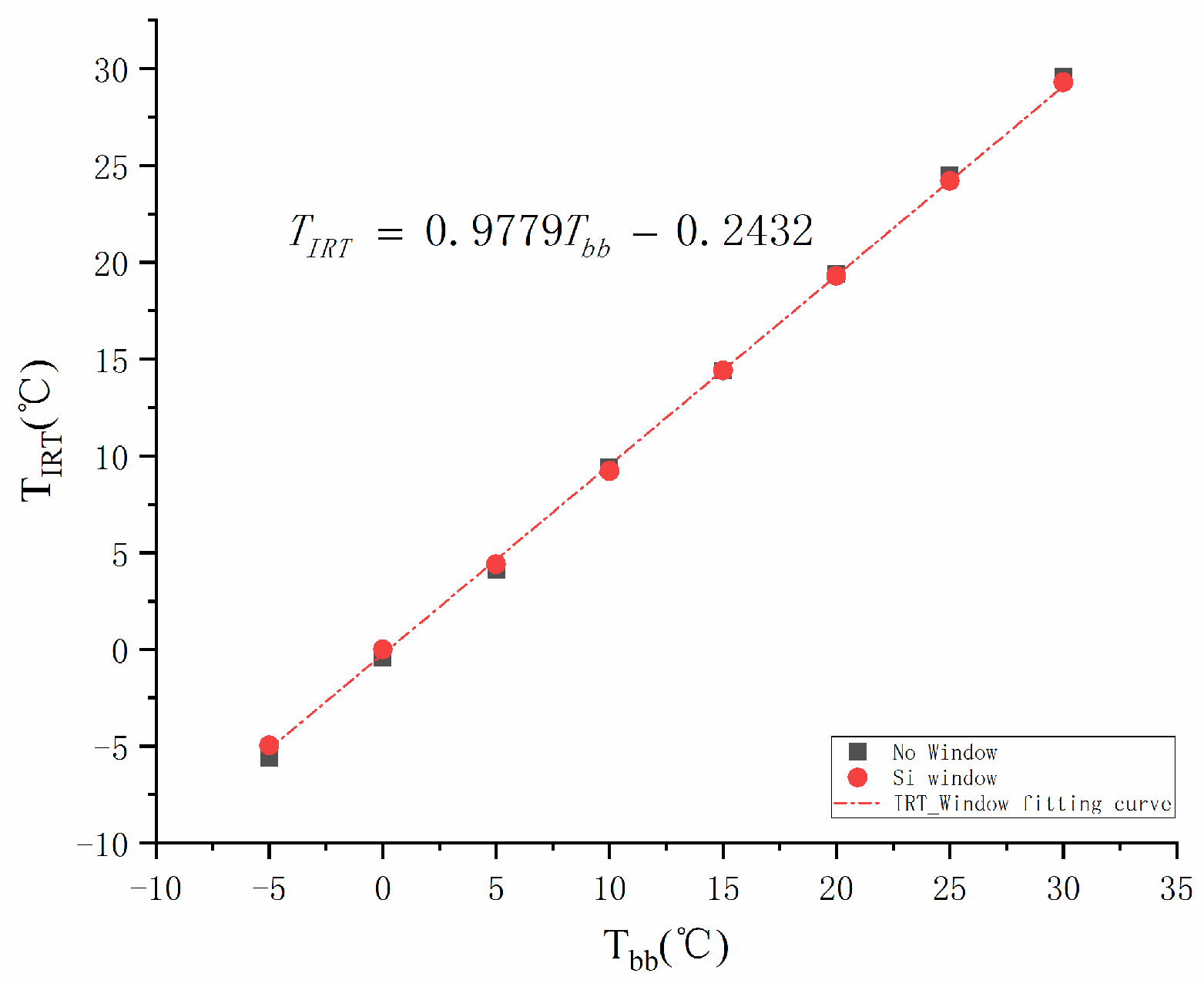
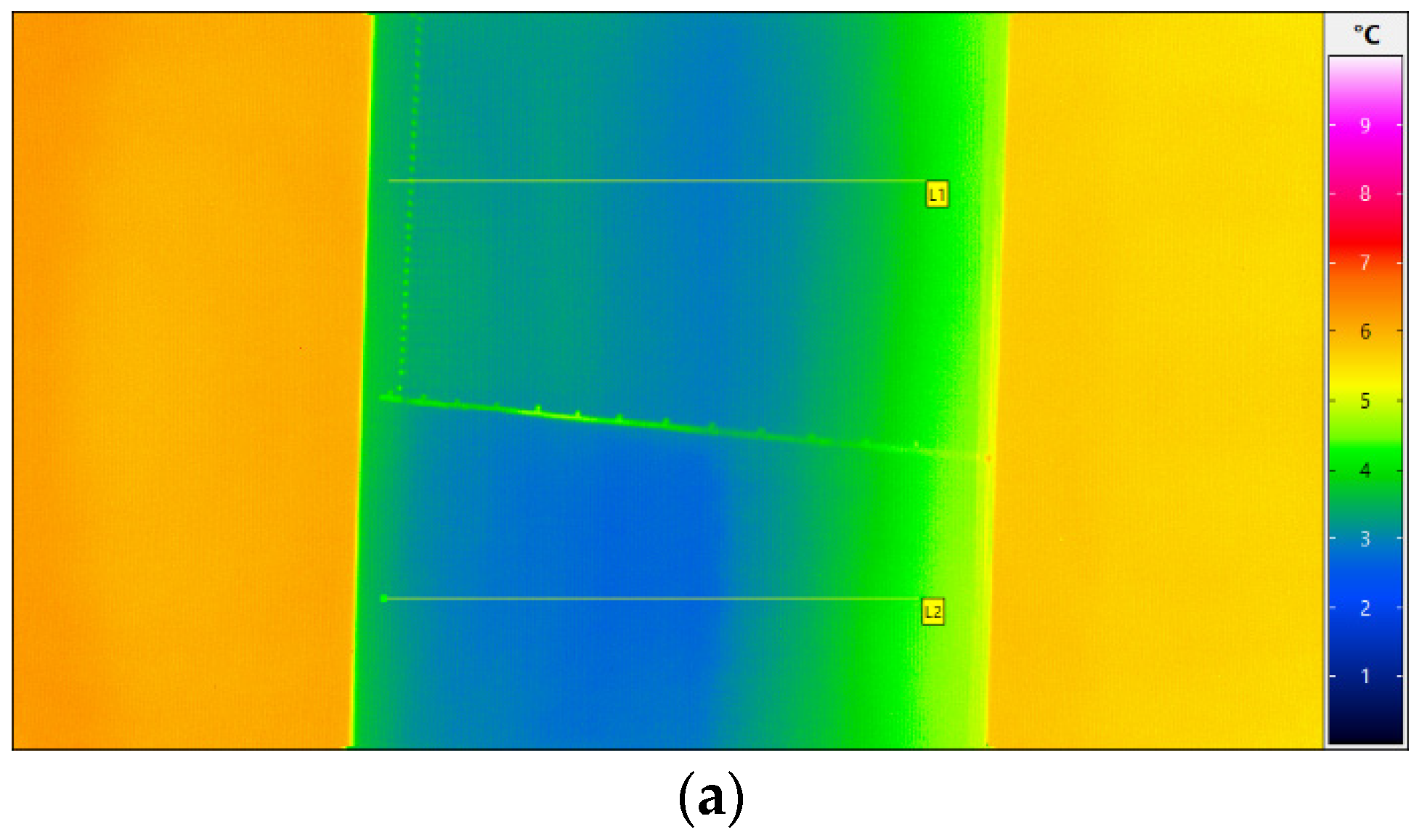
3.1. Calibration of the Infrared Thermal Imager
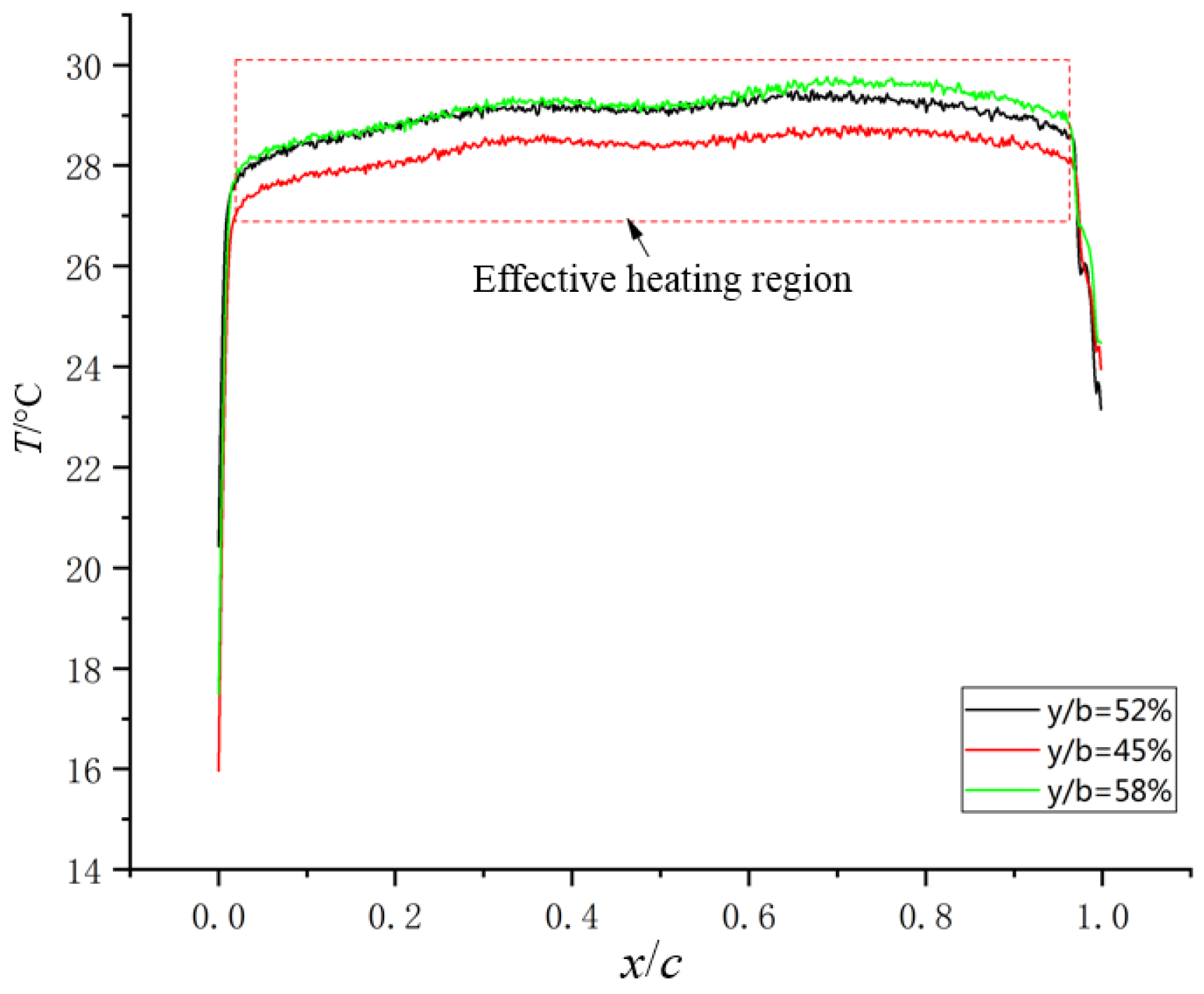
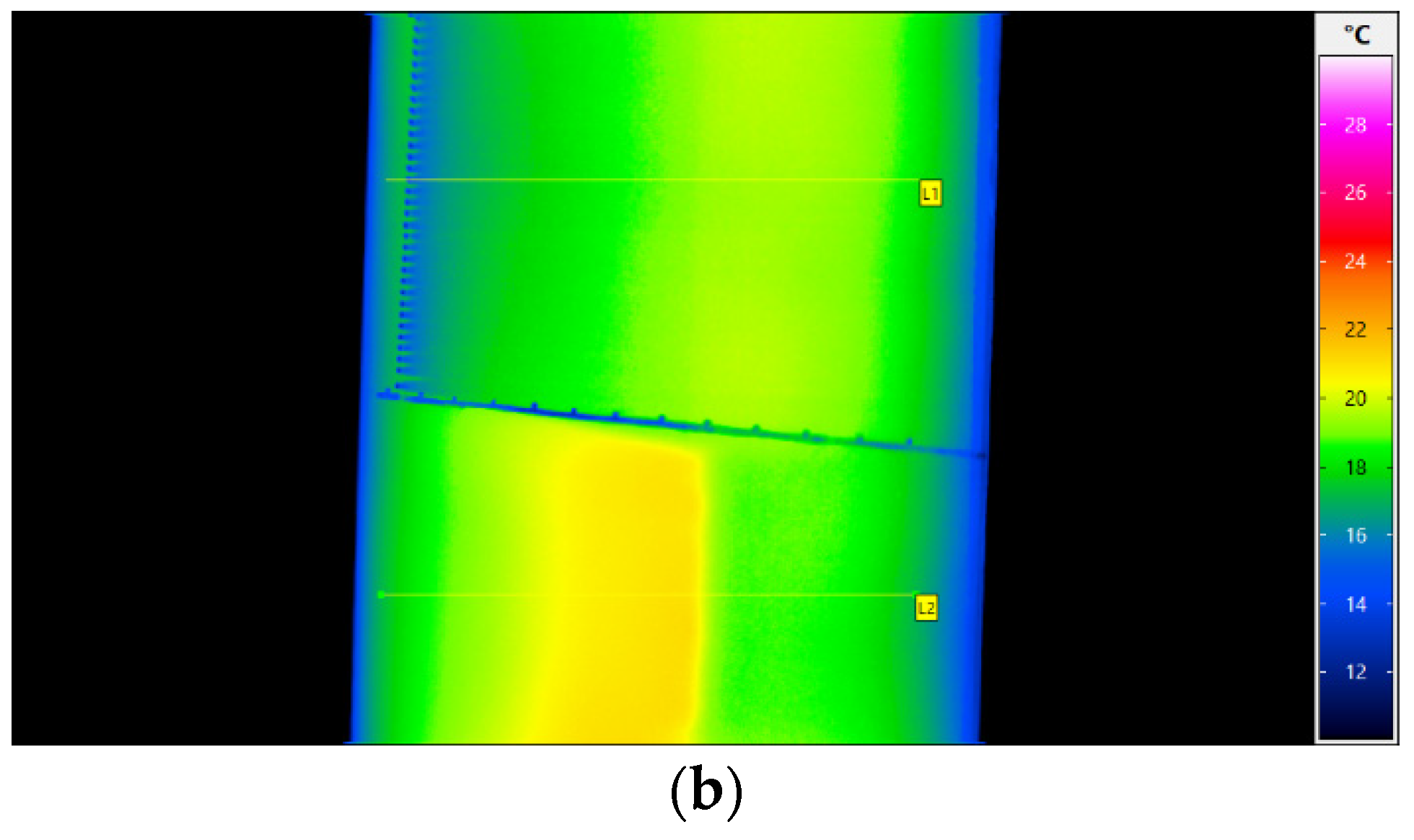
3.2. Heating Uniformity
4. Results and Discussion
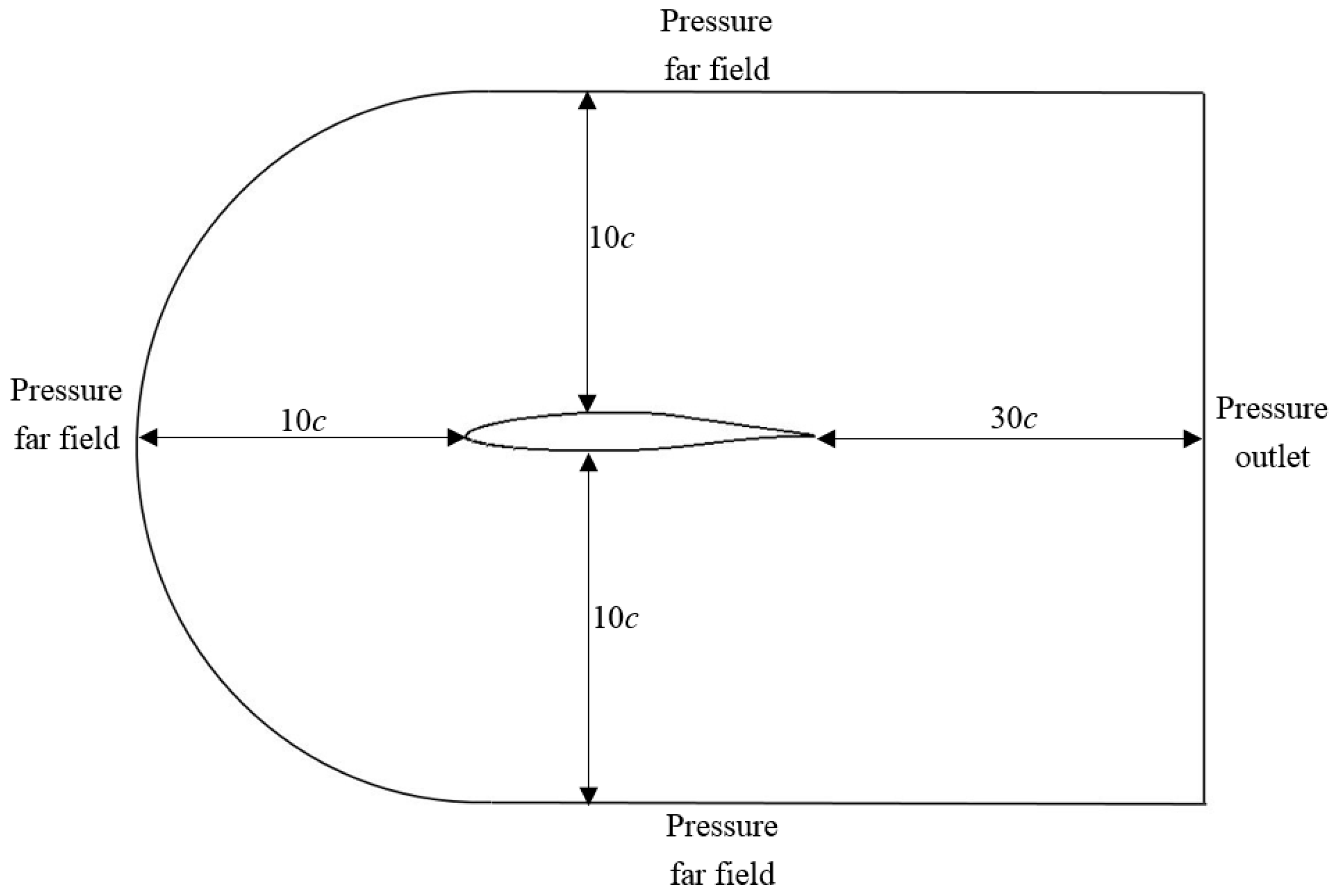
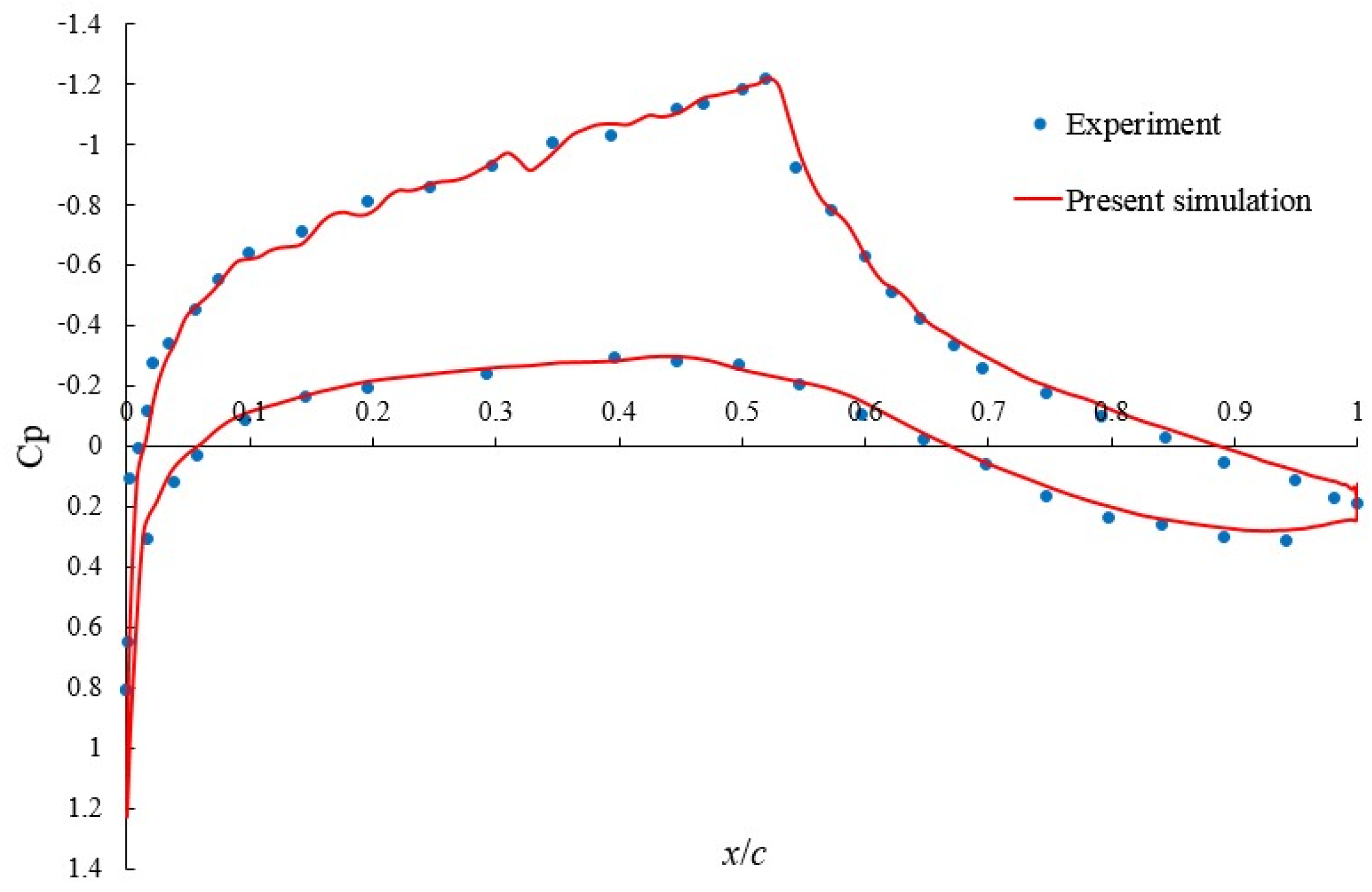
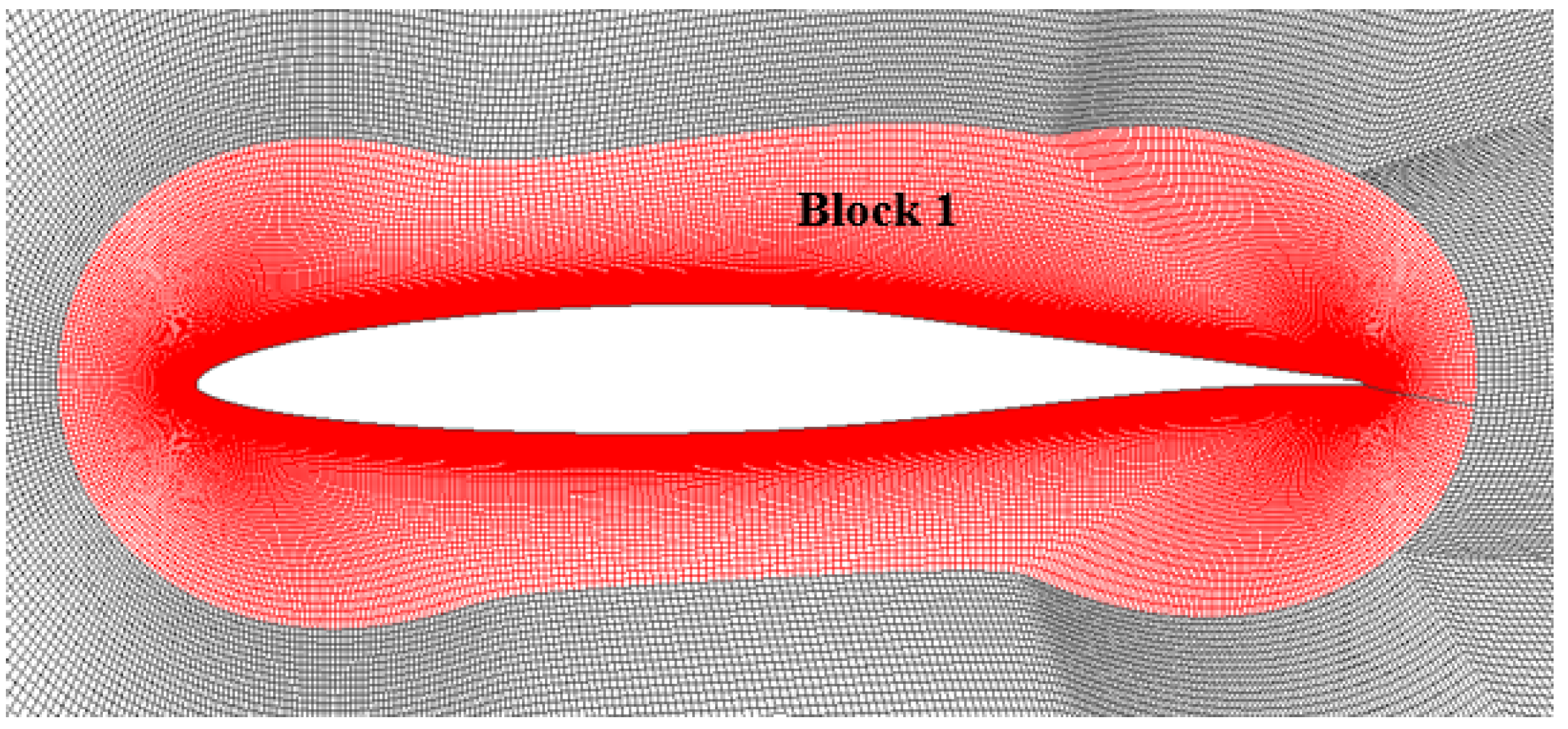
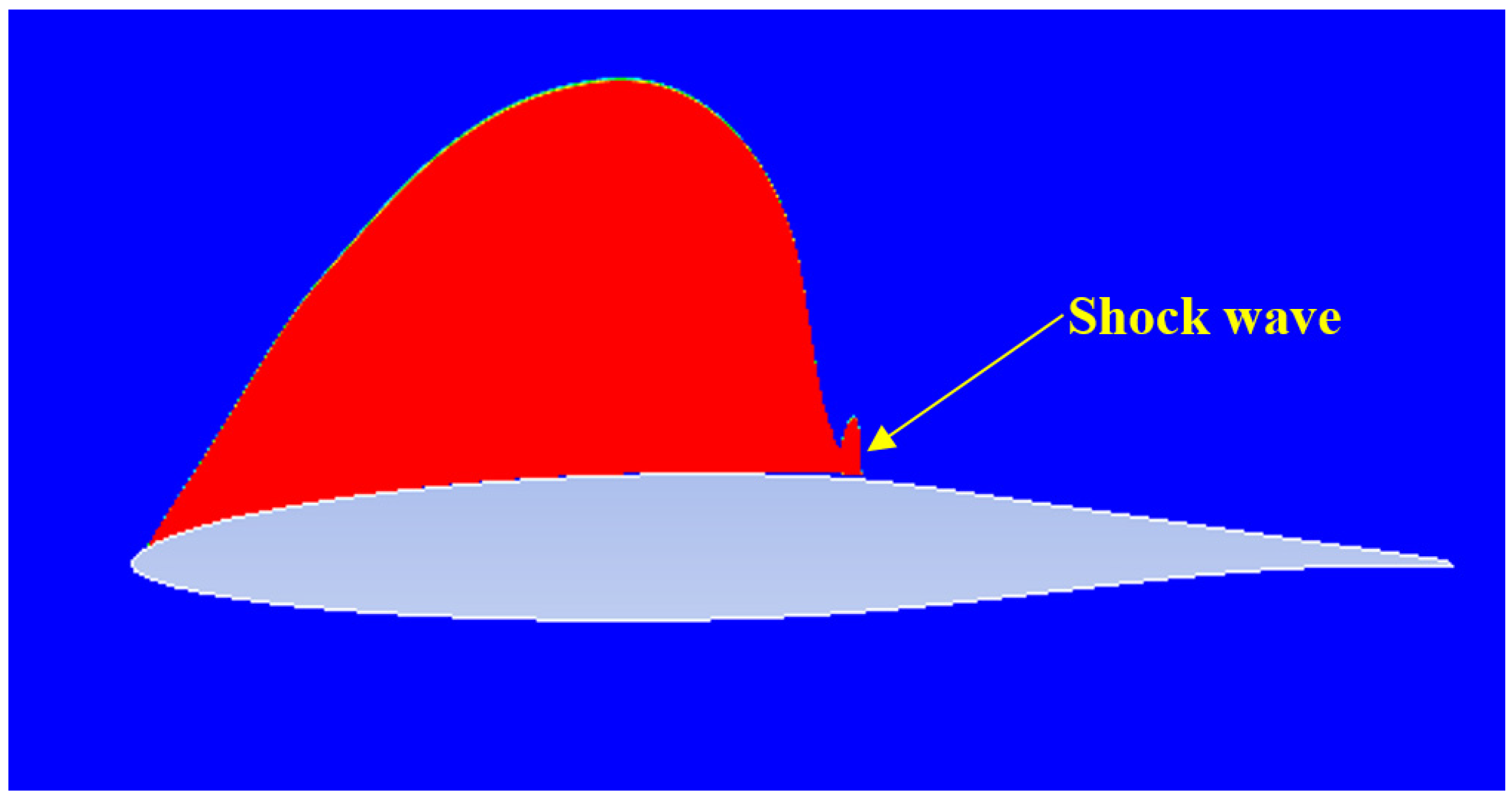
4.1. Simulation Method
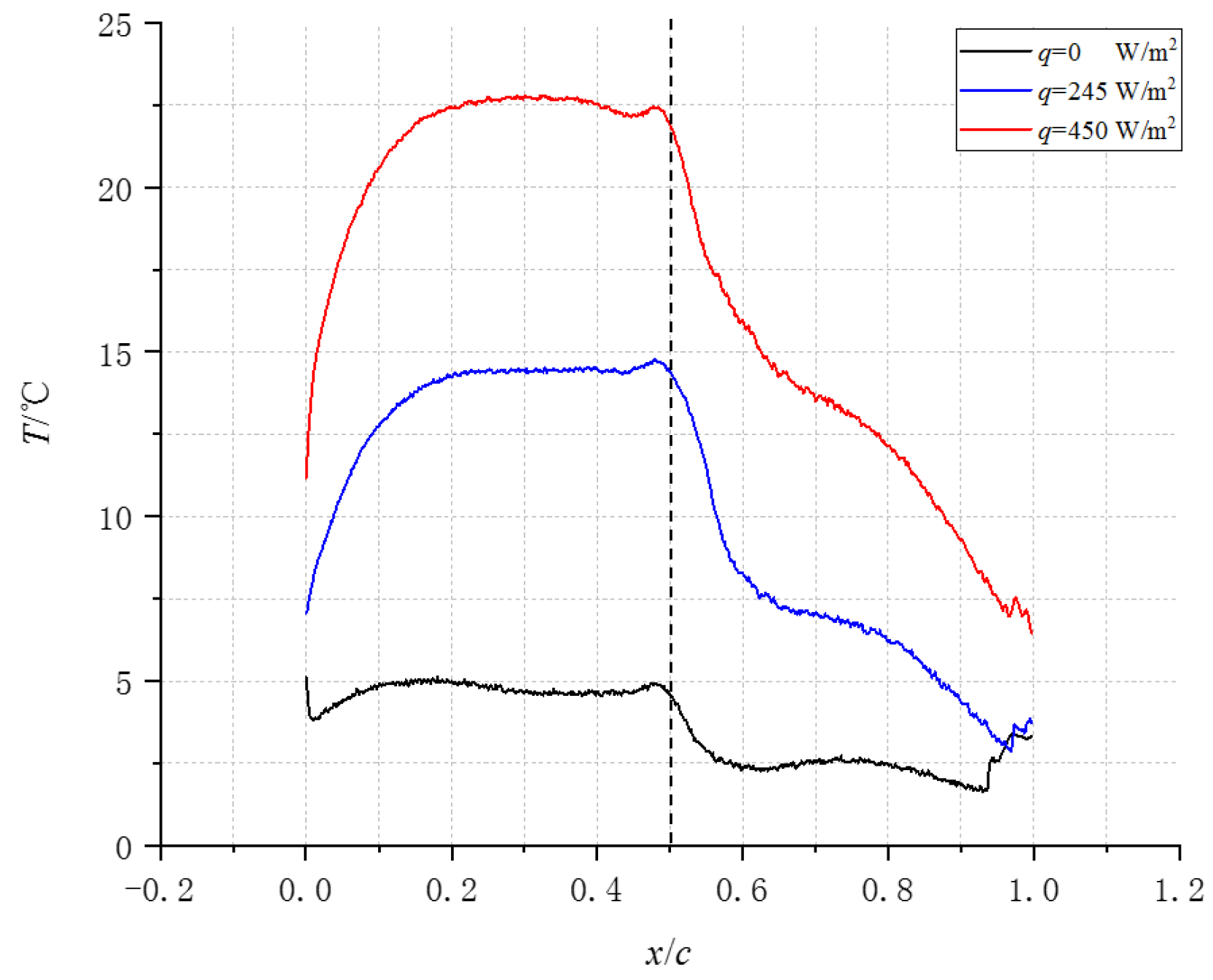
4.2. Results and Analysis
- a.
- Impact of the heating power
- b.
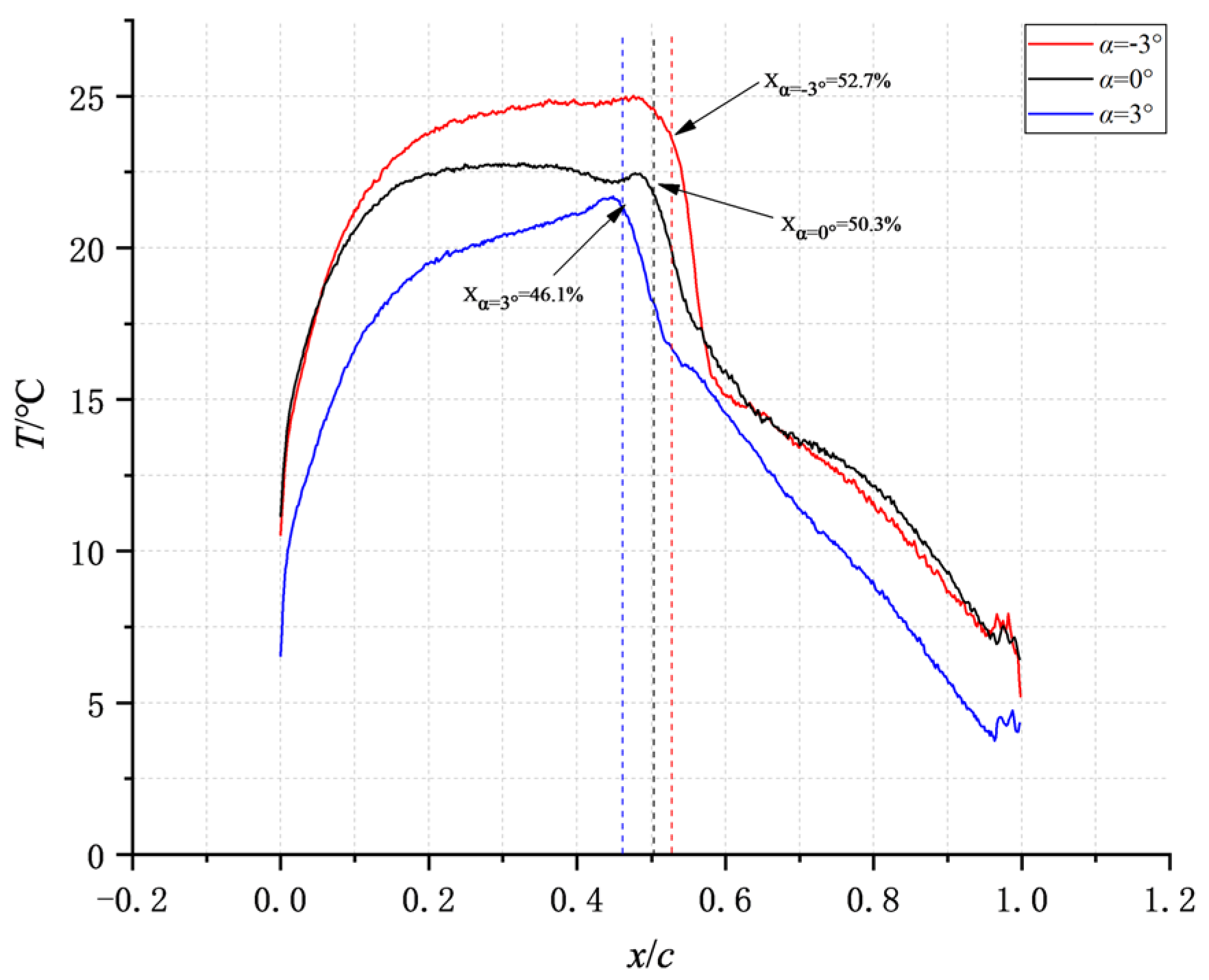
- Effect of AOA
- c.
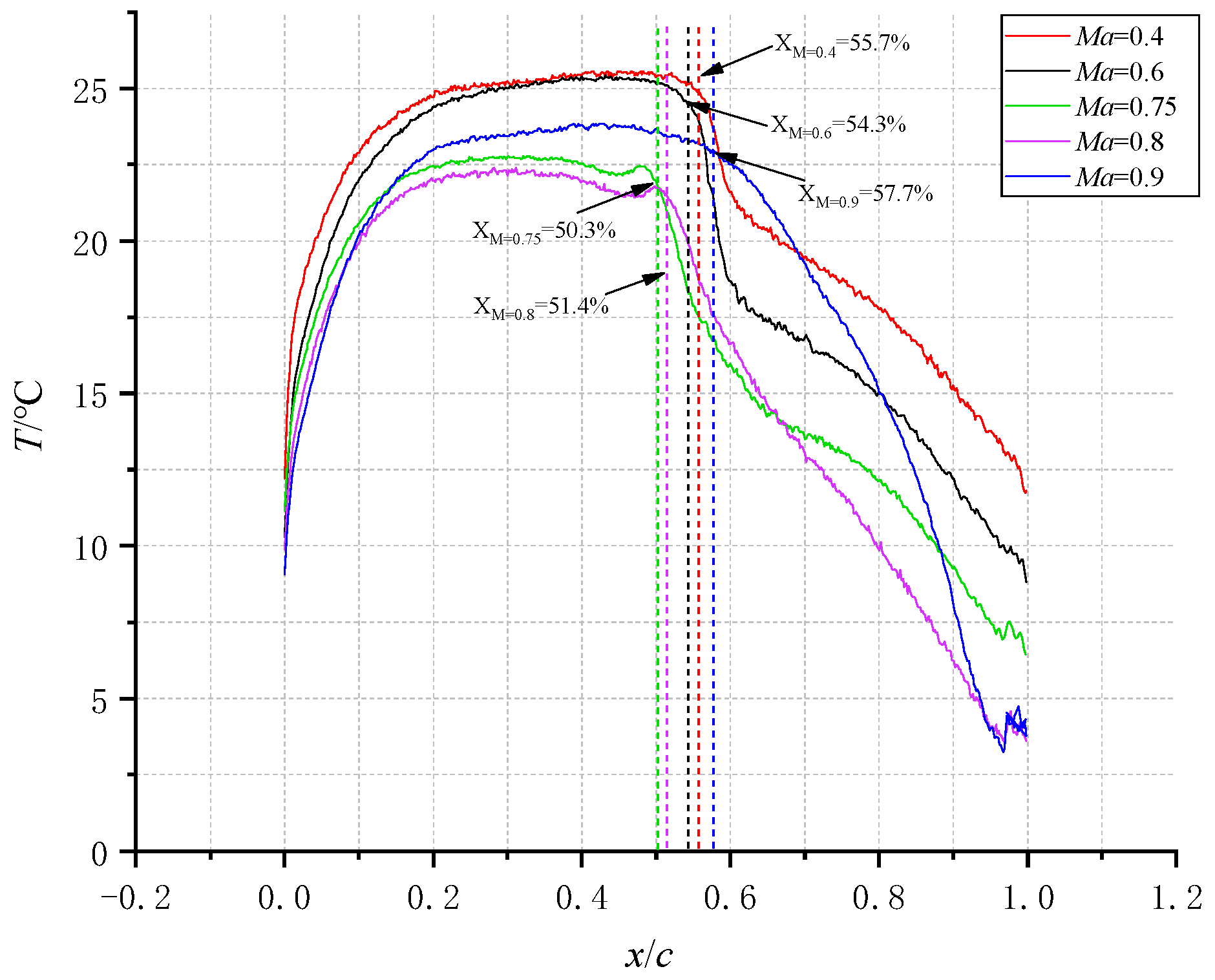
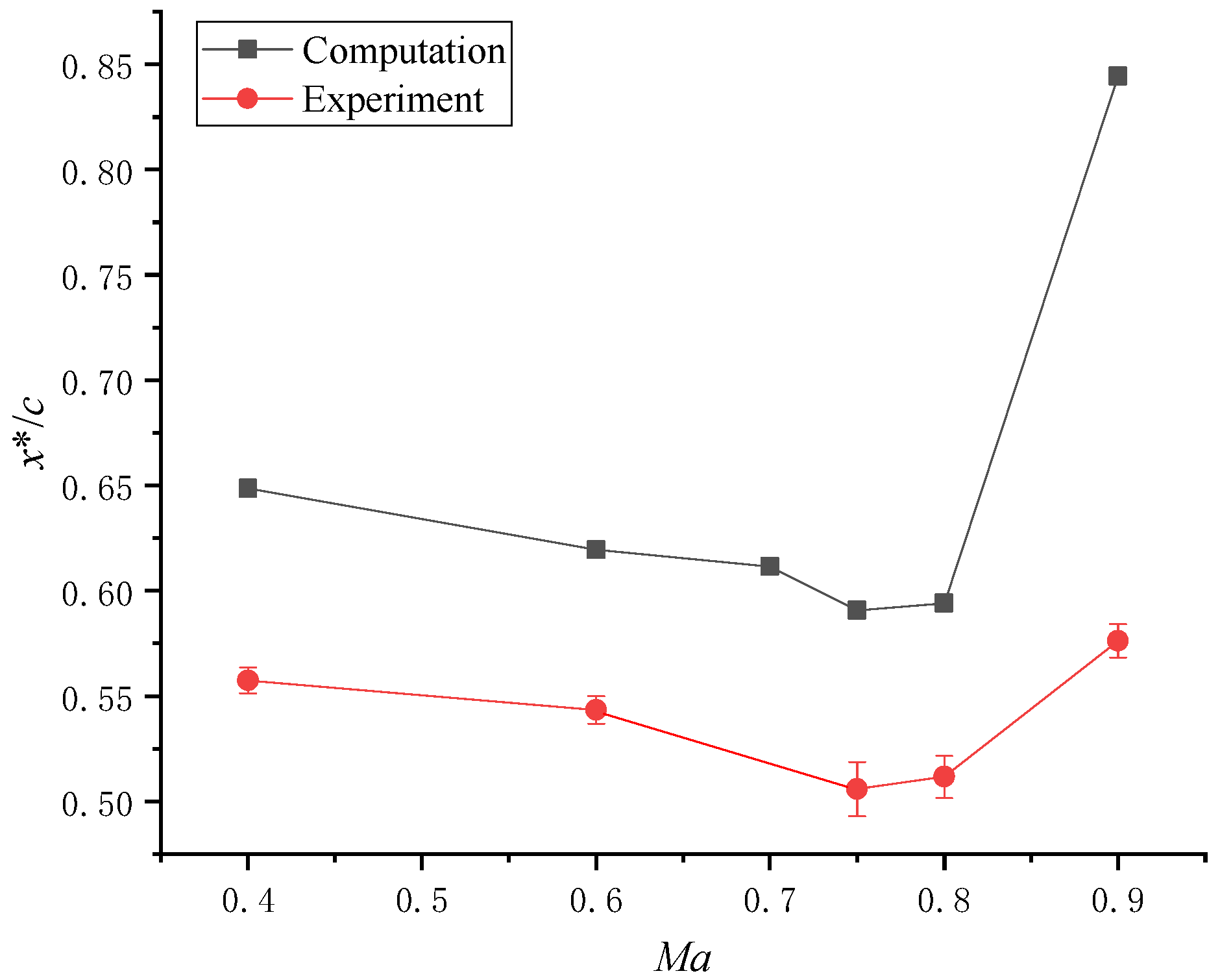
- Effect of Mach number
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schrauf, G. Status and perspectives of laminar flow. Aeronaut. J. 2005, 109, 639–644. [Google Scholar] [CrossRef]
- Thibert, J.J.; Reneaux, J.; Schmitt, R.V. ONERA Activities on Drag Reduction. ICAS-90-3.6.1. 1990. Available online: https://www.icas.org/ICAS_ARCHIVE/ICAS1990/ICAS-90-3.6.1.pdf (accessed on 21 February 2023).
- Lai, G.J.; Li, Z.D.; Zhang, Y.Z. Research on natural laminar airfoil wind tunnel test at high Reynolds number. Aeronaut. Sci. Technol. 2017, 28, 12–15. [Google Scholar]
- Streit, T.; Horstmann, K.H.; Schrauf, G.; Hein, S.; Fey, Y.; Egami, A.; Perraud, J.; El Din, I.S.; Cella, U.; Quest, J. Complementary numerical and experimental data analysis of the ETW TELFONA Pathfinder wing transition tests. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. [Google Scholar]
- Vermeersch, O.; Yoshida, K.; Ueda, Y.; Arnal, D. Natural laminar flow wing for supersonic conditions: Wind tunnel experiments, flight test and stability computations. Prog. Aerosp. Sci. 2015, 79, 64–91. [Google Scholar] [CrossRef]
- Collifer, F.S. An Overview of Recent Subsonic Laminar Flow Control Flight Experiments. AIAA-1993-2987. 1993. Available online: https://arc.aiaa.org/doi/10.2514/6.1993-2987 (accessed on 23 February 2023).
- Zhu, Z.Q.; Wu, Z.C.; Chen, Y.C.; Vicente, J.; Valero, E. Advanced Technology of Aerodynamic Design for Commercial Aircraft; Shanghai Jiaotong University Press: Shanghai, China, 2013. [Google Scholar]
- Fujino, M.; Yoshizaki, Y.; Kawamura, Y. Natural-laminar-flow airfoil development for a lightweight business jet. J. Aircr. 2003, 40, 609–615. [Google Scholar] [CrossRef]
- Fujino, M. Design and development of the Honda jet. J. Aircr. 2005, 42, 755–764. [Google Scholar] [CrossRef]
- Hiroaki, I.; Yoshine, U.; Naoko, T. Natural laminar flow wing design for a low-boom supersonic aircraft. In Proceedings of the AIAA SciTech Forum, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Owens, L.R.; Beeler, G.B.; King, R.A.; Chou, A.; Balakumar, P.; Banks, D. Supersonic traveling crossflow wave characteristics in ground and flight tests. In Proceedings of the AIAA SciTech Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Wang, F.; Eriqitai, W.Q.; Schulein, E. Experimental investigation of HLFC mechanism on swept wing. J. Aerosp. Power 2010, 25, 918–924. [Google Scholar]
- Sugiura, H.; Yoshida, K.; Tokugawa, N.; Takagi, S.; Nishizawa, A. Transition measurements on the natural laminar flow wing at Mach 2. J. Aircr. 2002, 39, 996–1002. [Google Scholar] [CrossRef]
- Costantini, M.; Henne, U.; Risius, S.; Klein, C. A robust method for reliable transition detection in temperature-sensitive paint data. Aerosp. Sci. Technol. 2021, 113, 106702. [Google Scholar] [CrossRef]
- Fujisawa, N.; Aoyama, A.; Kosaka, S. Measurement of shear-stress distribution over a surface by liquid-crystal coating. Meas. Sci. Technol. 2003, 14, 1655–1661. [Google Scholar] [CrossRef]
- Arshia, T.; Massoud, T.; Mehran, M.; Hamidreza, E.; Mehdi, S. An experimental study on boundary layer transition detection over a pitching supercritical airfoil using hot-film sensors. Int. J. Heat. Fluid. Flow. 2020, 86, 108743. [Google Scholar]
- Driver, D.M.; Drake, A. Skin friction measurements using oil film interferometry in the 11’ transonic wind tunnel. AIAA J. 2008, 46, 2401–2407. [Google Scholar] [CrossRef]
- Vavra, A.J.; Solomon, W.D., Jr.; Drake, A. Comparison of boundary layer transition measurement techniques on a laminar flow wing. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Garbeff, T.J., II; Baerny, J.K. Recent advancements in the infrared flow visualization system for the NASA Ames unitary plan wind tunnels. In Proceedings of the AIAA SciTech Form, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Geng, Z.H.; He, X.Z.; Wang, X.N.; Yang, Z. Non-intrusive test technique investigation of transition measurement with infrared image in low speed wind tunnel. J. Exp. Fluid. Mech. 2010, 24, 77–82. [Google Scholar]
- Klein, C.; Henne, U.; Yorita, D.; Ondruss, V.; Beifuss, O.; Hensch, A.-K.; Quest, J. Application of carbon nanotubes and temperature-sensitive paint for the detection of boundary layer transition under cryogenic conditions. In Proceedings of the AIAA SciTech Form, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Goodman, K.Z.; Lipford, W.E.; Watkins, A.N. Boundary-layer detection at cryogenic conditions using temperature sensitive paint coupled with a carbon nanotube heating layer. Sensors 2016, 16, 2062. [Google Scholar] [CrossRef] [PubMed]
- Langtry, R.B.; Menter, F.R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Fulker, J.L.; Simmons, M.J. An experimental investigation of passive shock/boundary-layer control on an aerofoil. In EUROSHOCK-Drag Reduction by Passive Shock Control; Notes on Numerical Fluid Mechanics; Stanewsky, E., Delery, J., Fulker, J., Geissler, W., Eds.; Friedr. Vieweg and Sohn Verlagsgesellschaft mbH: Braunschweig/Wiesbaden, Germany, 1997. [Google Scholar]
- Huang, Y.; Qian, F.X.; Yu, K.L.; He, B.H.; Chang, L.X.; Lin, X.D. Experimental investigation on boundary-layer artificial transition based on transition trip disk. J. Exp. Fluid. Mech. 2006, 20, 59–62. [Google Scholar]









| 30% Span Section | 70% Span Section | |||||
|---|---|---|---|---|---|---|
| No. | 1 | 2 | 3 | 4 | 5 | 6 |
| T/°C | 30.1 ± 0.2 | 29.3 ± 0.2 | 29.5 ± 0.2 | 28.0 ± 0.2 | 27.0 ± 0.2 | 28.7 ± 0.2 |
| Ma | 0.4 | 06 | 0.7 | 0.75 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|
| P∞/Pa | 89,560 | 79,180 | 75,700 | 72,300 | 72,160 | 67,995 |
| T∞/K | 291 | 280 | 273 | 270 | 266 | 258 |
| Block 1 | CL | CD | x*up/c | x*down/c | |
|---|---|---|---|---|---|
| Grid-1 | 328 × 131 | 0.338197 | 0.006702 | 0.614394 | 0.619396 |
| Grid-2 | 494 × 131 | 0.316018 | 0.006556 | 0.630063 | 0.627264 |
| Grid-3 | 660 × 131 | 0.302512 | 0.006454 | 0.627642 | 0.631153 |
| Grid-4 | 727 × 131 | 0.299501 | 0.006433 | 0.629443 | 0.632857 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Wang, H.; Zhang, Z.; Liu, X.; Qian, F. Investigation on Transition Characteristics of a Modified RAE5243 Airfoil. Energies 2024, 17, 1489. https://doi.org/10.3390/en17061489
Liu Z, Wang H, Zhang Z, Liu X, Qian F. Investigation on Transition Characteristics of a Modified RAE5243 Airfoil. Energies. 2024; 17(6):1489. https://doi.org/10.3390/en17061489
Chicago/Turabian StyleLiu, Zhiyong, Hongbiao Wang, Zhao Zhang, Xiang Liu, and Fengxue Qian. 2024. "Investigation on Transition Characteristics of a Modified RAE5243 Airfoil" Energies 17, no. 6: 1489. https://doi.org/10.3390/en17061489
APA StyleLiu, Z., Wang, H., Zhang, Z., Liu, X., & Qian, F. (2024). Investigation on Transition Characteristics of a Modified RAE5243 Airfoil. Energies, 17(6), 1489. https://doi.org/10.3390/en17061489





