Determining Fast Battery Charging Profiles Using an Equivalent Circuit Model and a Direct Optimal Control Approach
Abstract
1. Introduction
2. Literature Review
2.1. Optimised Charging Methods
2.2. Fast Charging as an Optimal Control Problem
2.3. Battery Models
- Electrochemical modelling of the inner battery cell behaviour;
- Electric equivalent network or abstract modelling (also called an equivalent circuit model), where the battery is modelled as an electric circuit of passive electronic components.
2.3.1. Electrochemical Models
2.3.2. Equivalent Circuit Models
3. Battery’s Fast-Charging Problem Statement
3.1. The CC-CV Algorithm
| Algorithm 1 CC-CV cycle |
|
1: procedure CC-CV () 2: while and ) do 3: CC charge at end while 4: while ( and ) do 5: CV constant at 6: Decrease end while end of procedure |
3.2. The Battery Model
3.3. Mathematical Representation of the Equivalent Circuit Model
4. Battery’s Fast-Charging Problem Formulation
4.1. Case 1: Two-Phase Optimal Control Problem with Configurable Switching Time
4.2. Case 2: Two-Phase Optimal Control Problem with Two Path Constraints
4.3. Case 3: Two-Phase Optimal Control Problem with Two Path Constraints and Parameterisation of the Endpoint Cost
5. Results and Discussion
5.1. Characteristics of the Battery Cell
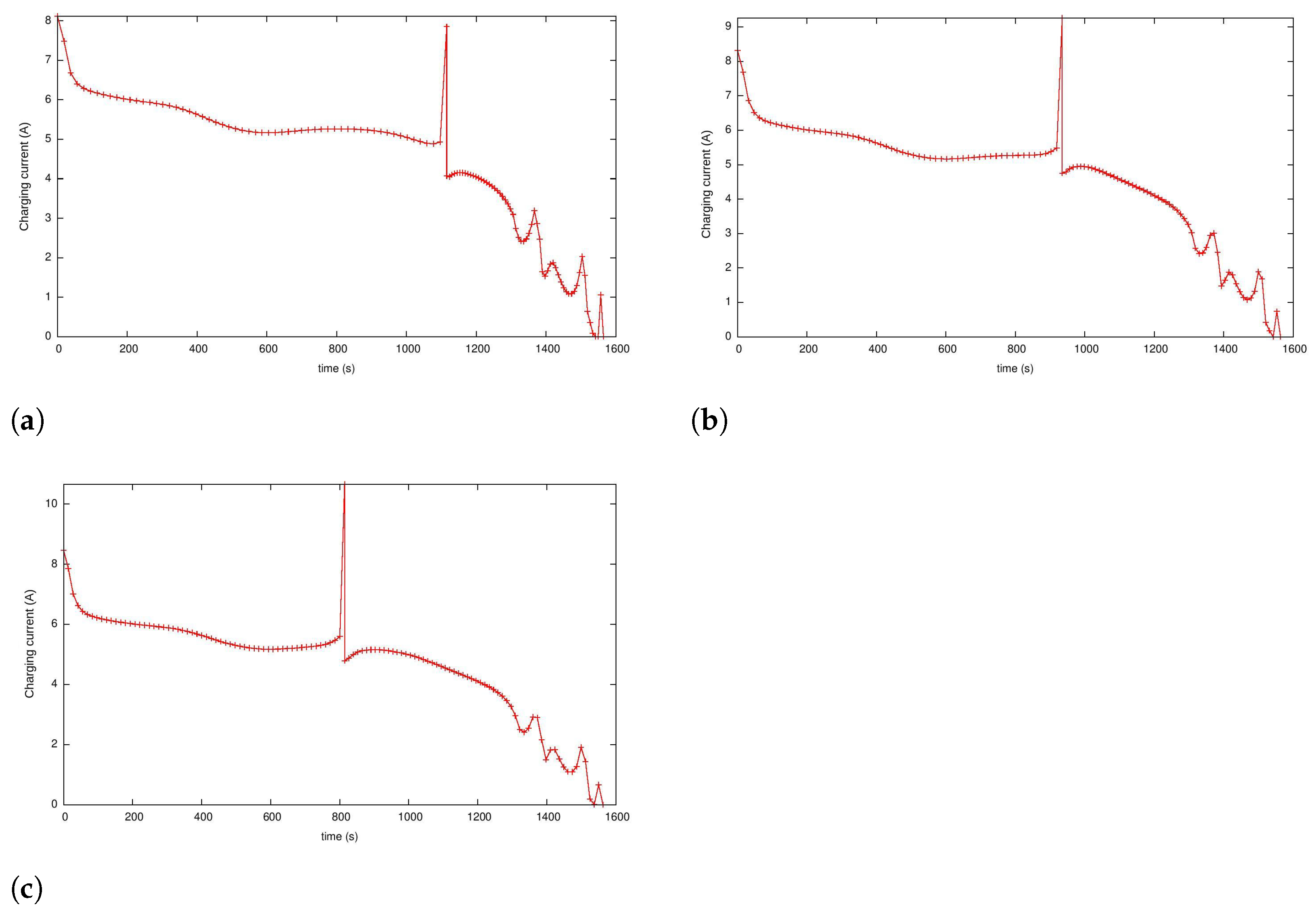
5.2. Case 1: Two-Phase Minimum Time Charging
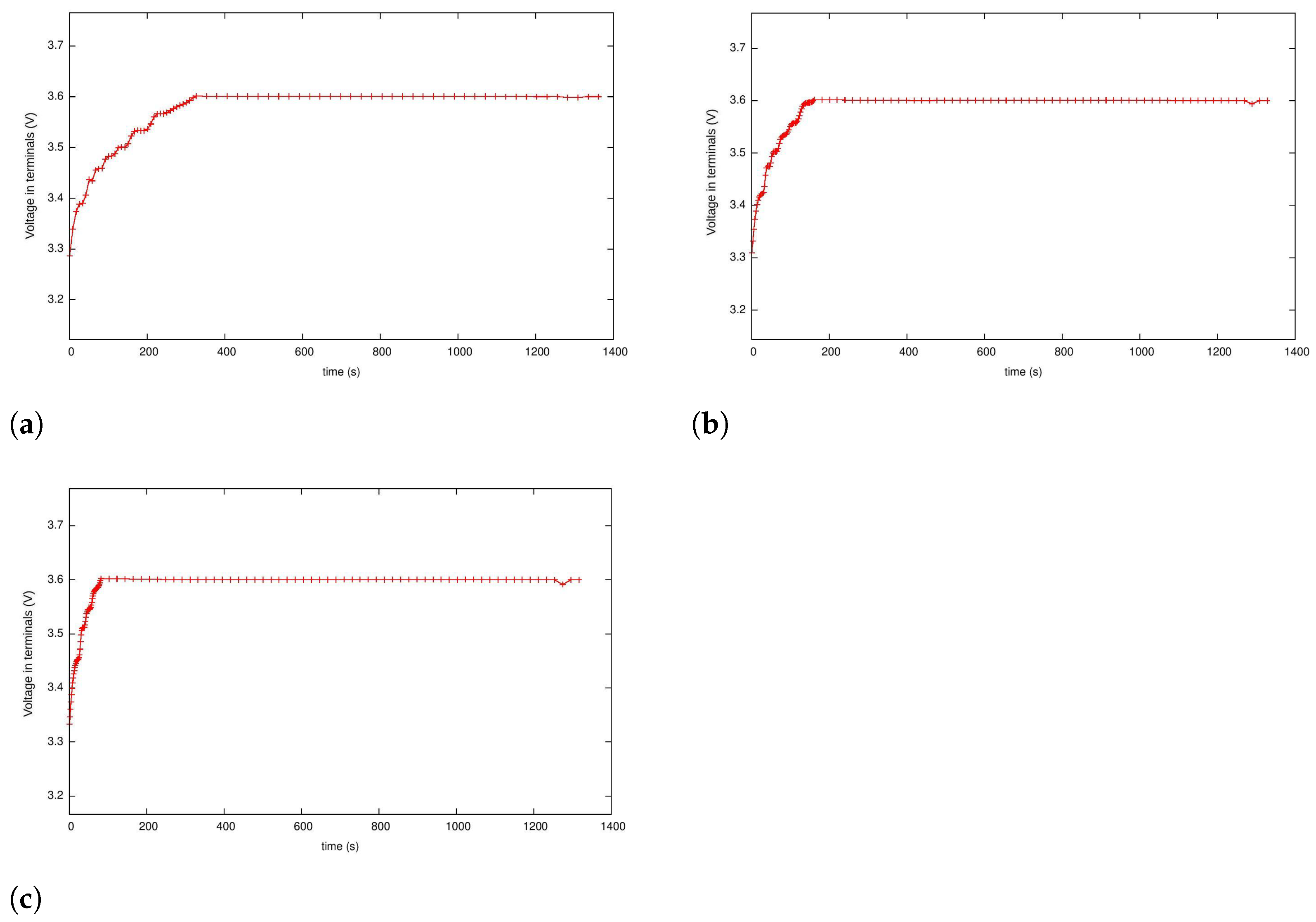
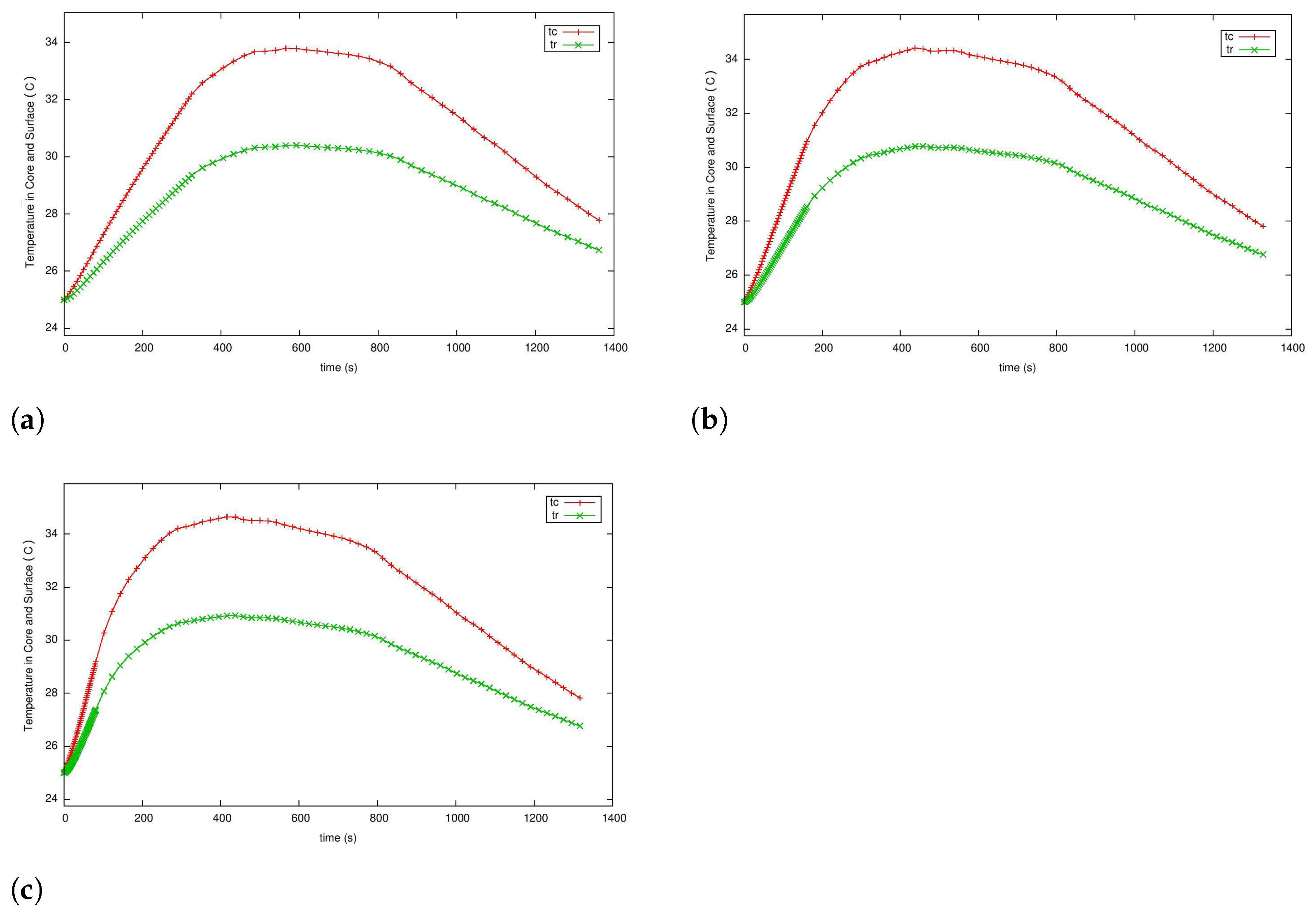
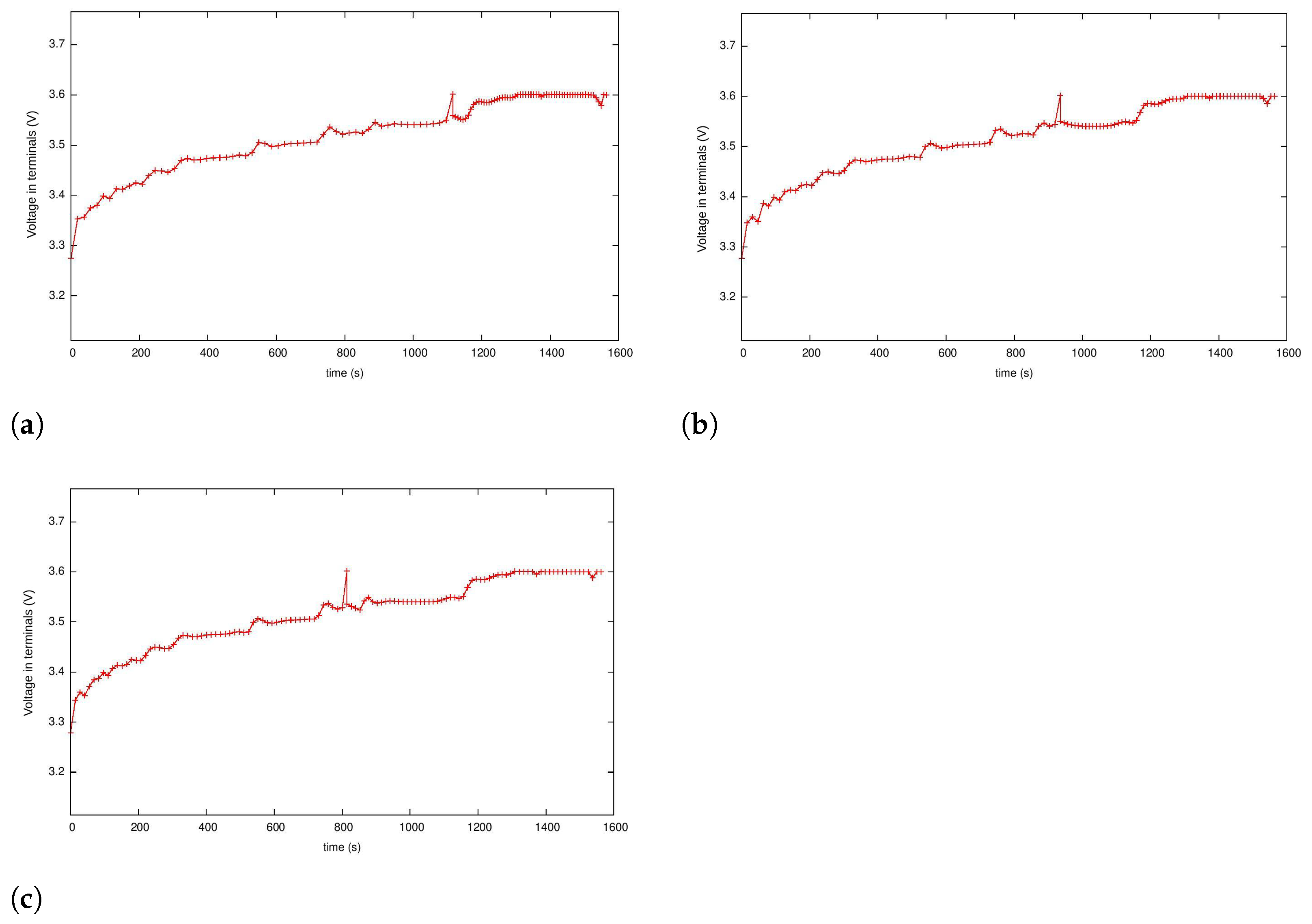
5.3. Case 2: Fast Charging as a Two-Phase Optimal Control Problem with Temperature and Terminal Voltage Path Constraints
5.4. Case 2a: Fast Charging without Temperature Path Constraint
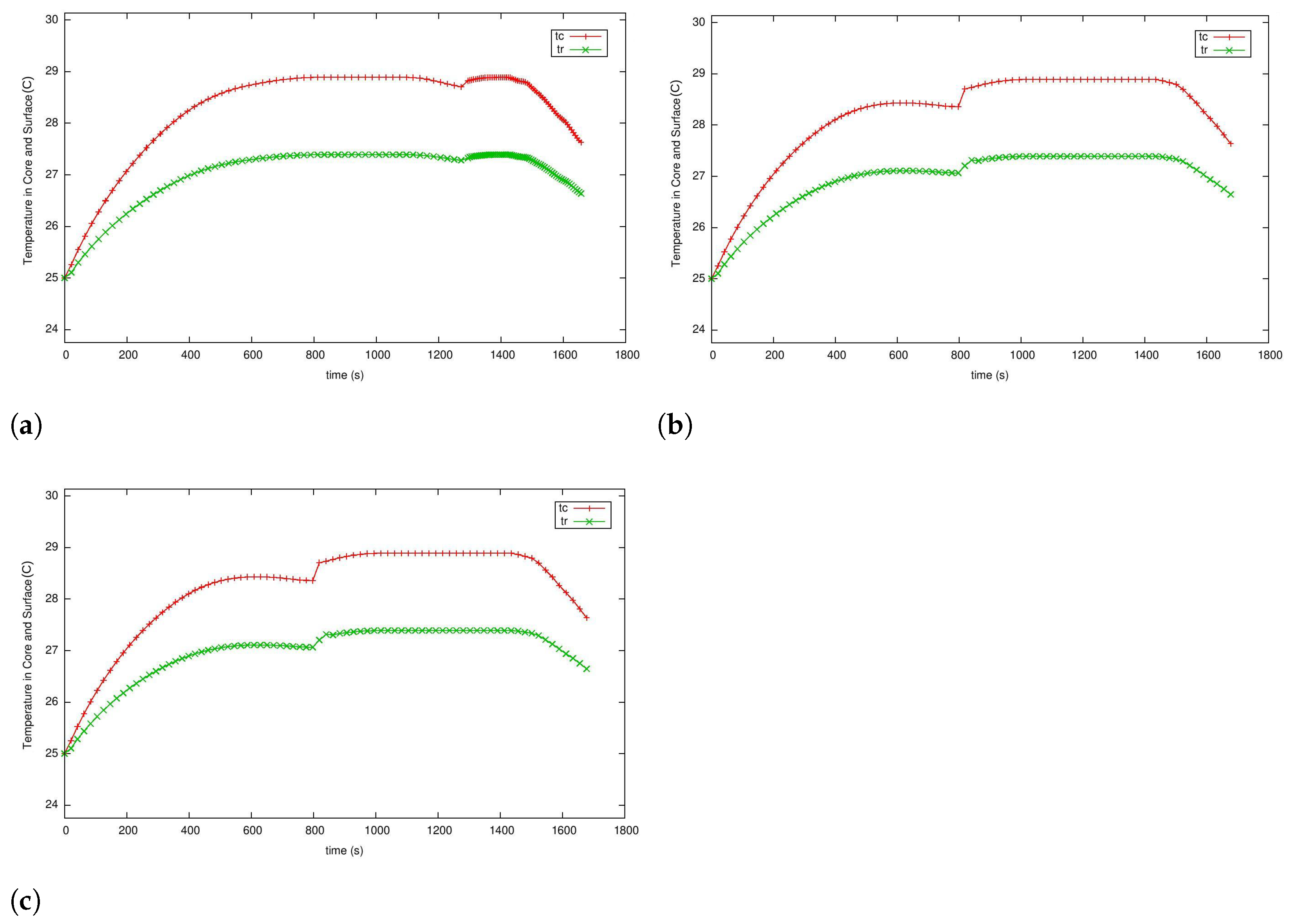
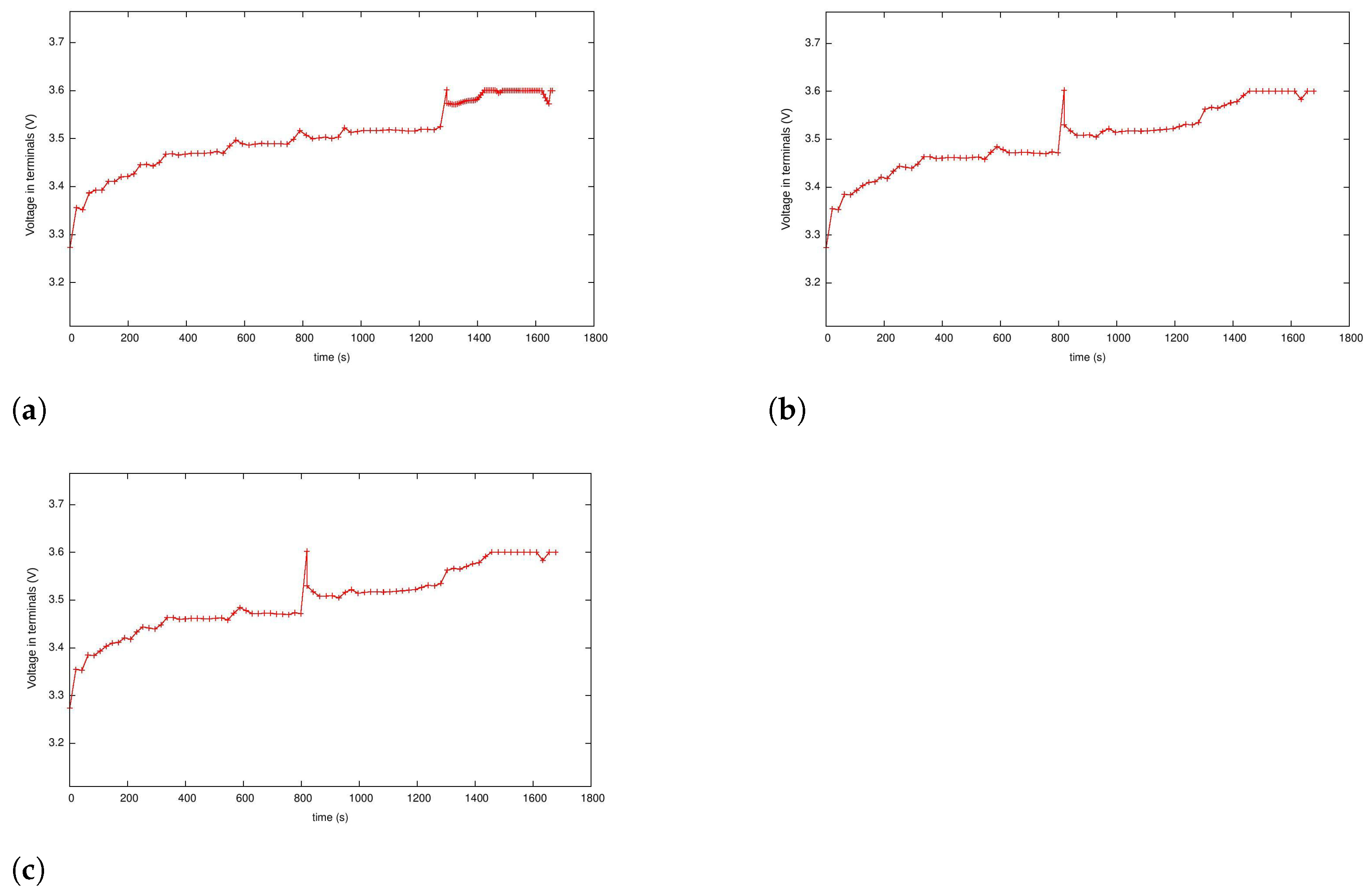
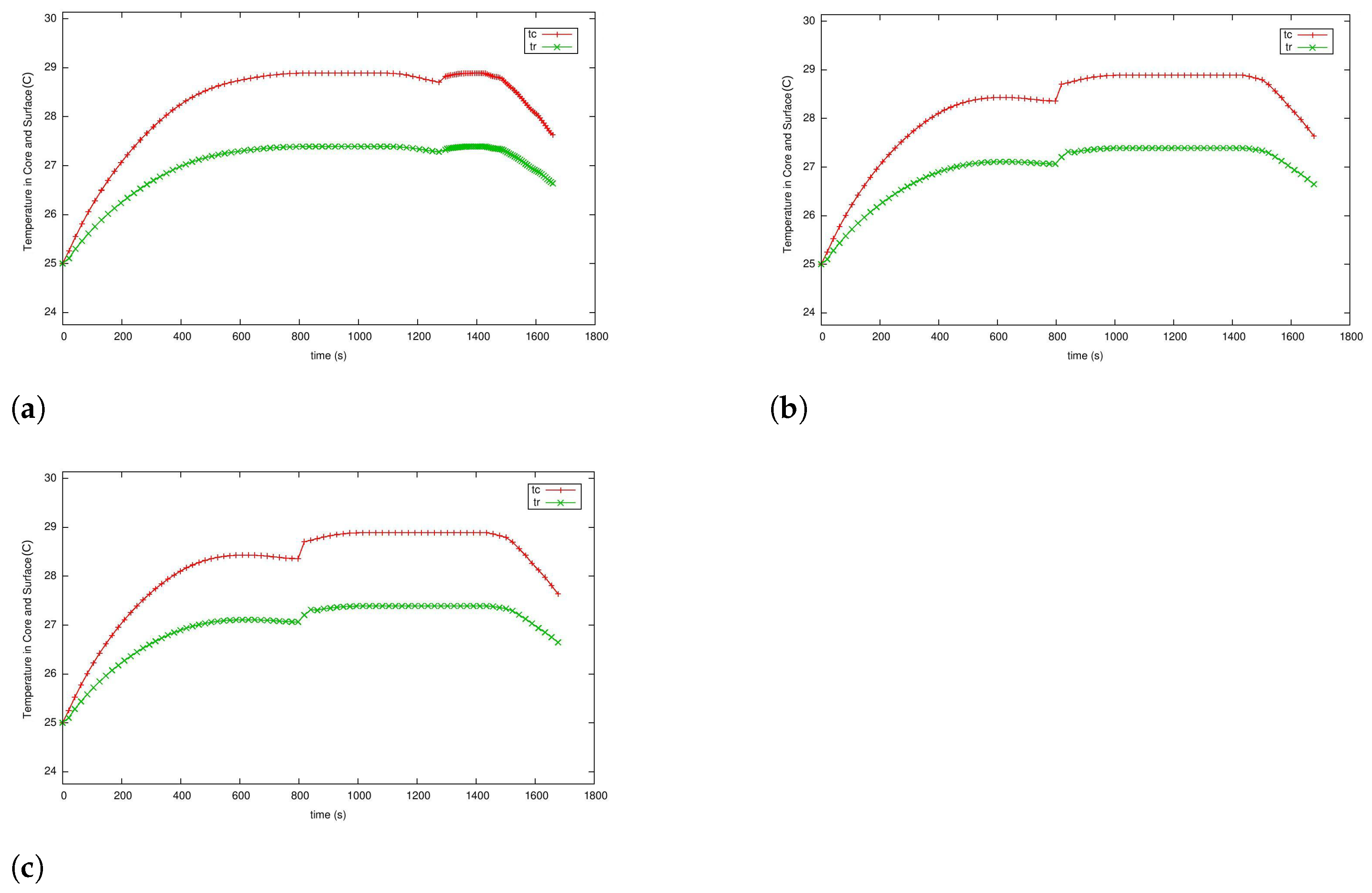
5.4.1. Case 2b: Fast Charging with the Temperature Path Constraint
Results and Discussion
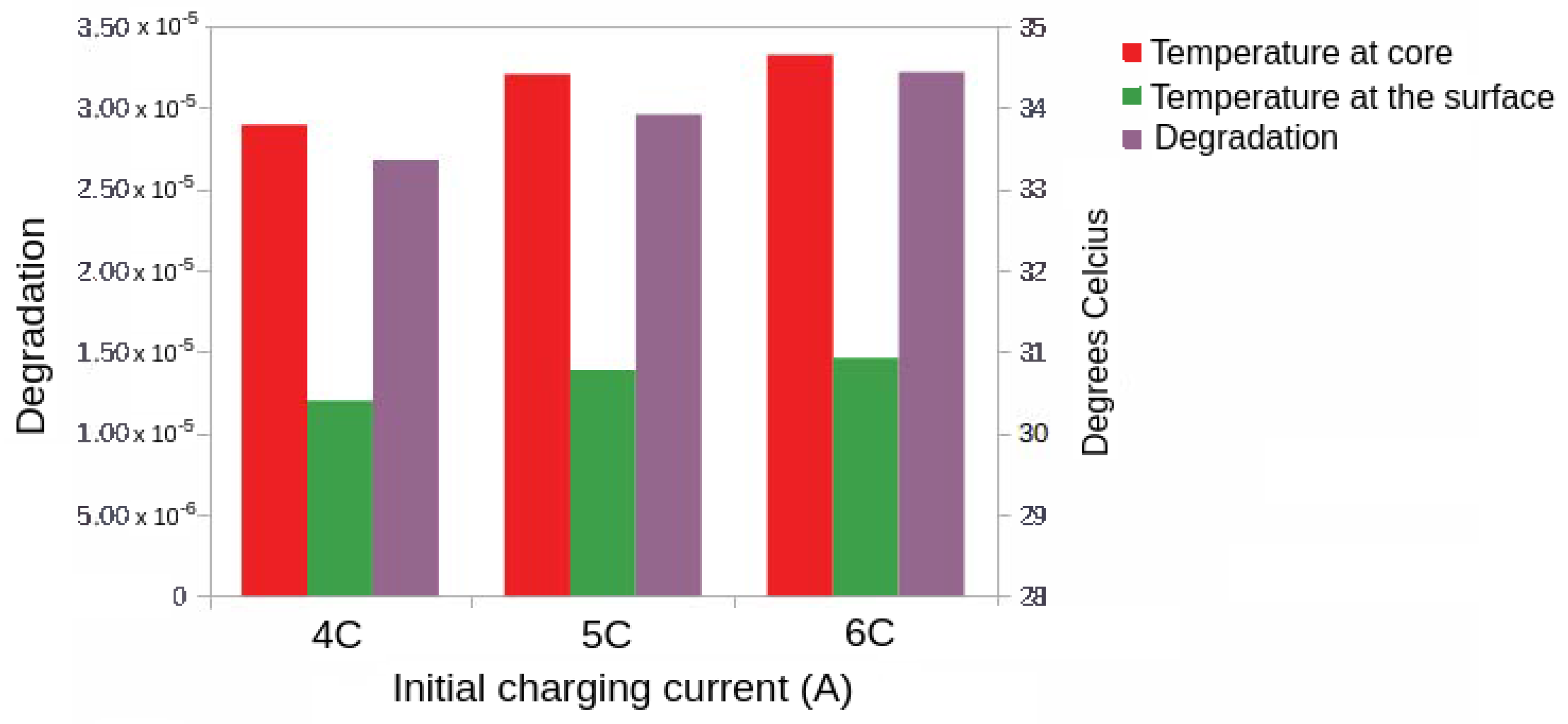
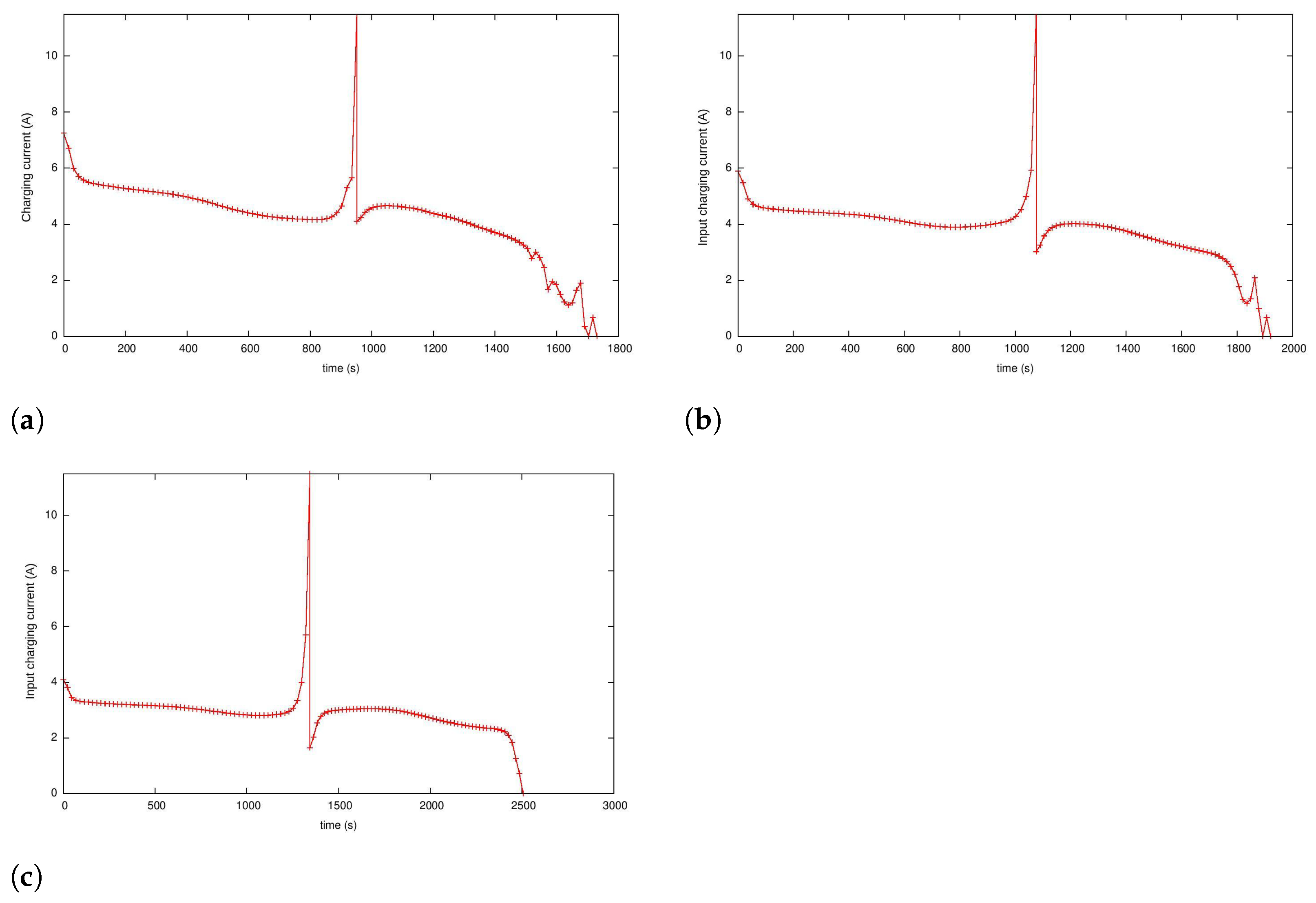
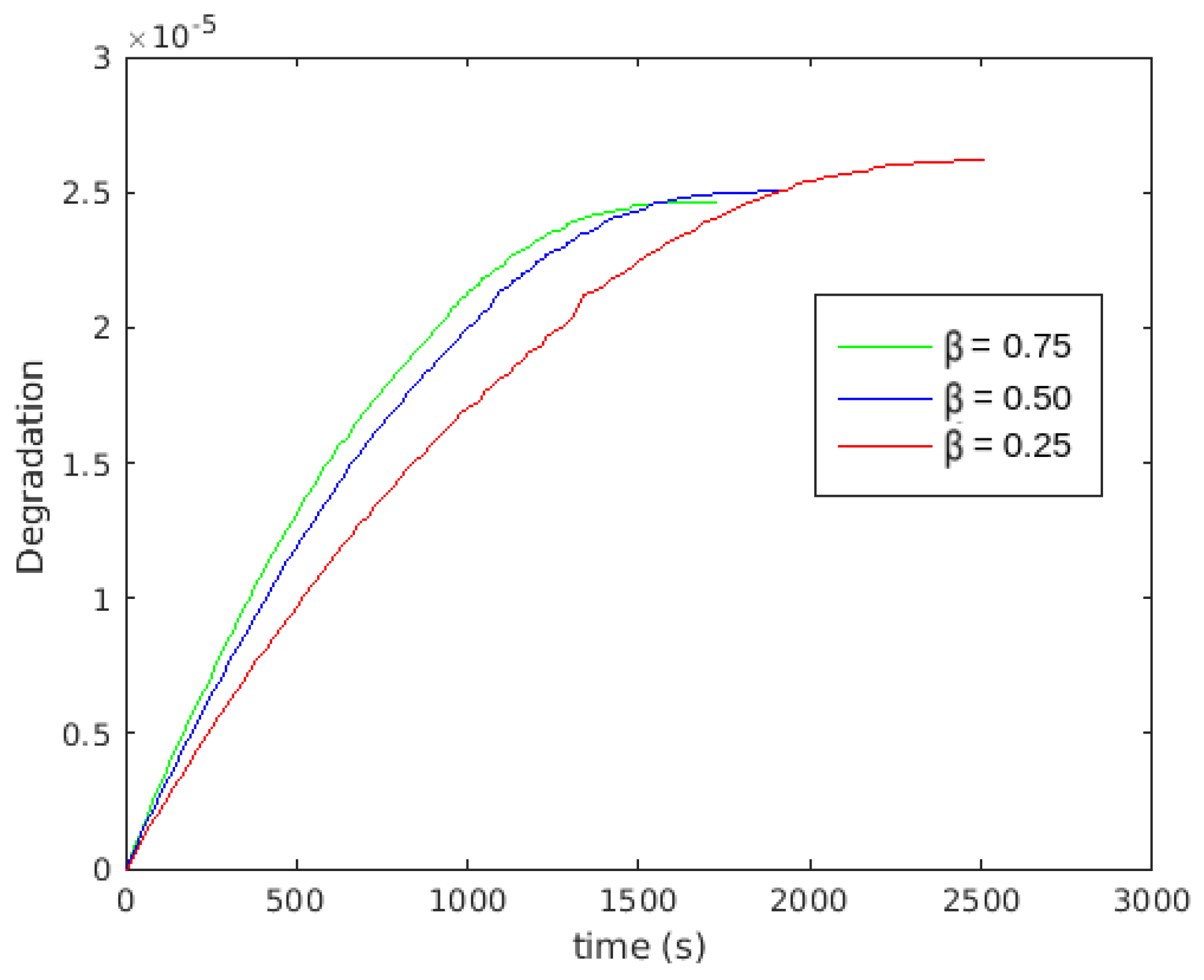
5.4.2. Case 3: Fast Charging Considering Degradation in the Endpoint Cost
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, C.L.; Wang, S.C.; Liu, Y.H.; Tsai, M.C. An Optimum Fast Charging Pattern Search for Li-Ion Batteries Using Particle Swarm Optimization. In Proceedings of the 6th International Conference on Soft Computing and Intelligent Systems, and the 13th International Symposium on Advanced Intelligence Systems, SCIS-ISIS 2012, Kobe, Japan, 20–24 November 2012. [Google Scholar]
- Yang, X.; Zhang, G.; Ge, S.; Wang, C.Y. Fast charging of lithium-ion batteries at all temperatures. Proc. Natl. Acad. Sci. USA 2018, 115, 7266–7271. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion batter management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- CESafety. FoI Data Reveals Extent of Electric Vehicle Battery Fires in UK. Available online: https://www.fsmatters.com/FoI-data-reveals-extent-of-EV-fires-in-UK (accessed on 11 November 2022).
- O’Kane, S.E.; Ai, W.; Madabattula, G.; Alonso-Alvarez, D.; Timms, R.; Sulzer, V.; Edge, J.S.; Wu, B.; Offer, G.J.; Marinescu, M. Lithium-ion battery degradation: How to model it. Phys. Chem. Chem. Phys. 2022, 24, 7909–7922. [Google Scholar] [CrossRef] [PubMed]
- Ramadass, P.; Haran, B.; Gomadam, P.; White, R.; Popov, B. Development of First Principles Capacity Fade Model for Li-Ion Cells. J. Electrochem. Soc. 2004, 151, A196. [Google Scholar] [CrossRef]
- Keil, P.; Jossen, A. Charging protocols for lithium-ion batteries and their impact on cycle life—An experimental study with different 18650 high-power cells. J. Energy Storage 2016, 6, 125–141. [Google Scholar] [CrossRef]
- Abdel-Monem, M.; Trad, K.; Omar, N.; Hegazy, O.; Van den Bossche, P.; Van Mierlo, J. Influence analysis of static and dynamic fast-charging current profiles on ageing performance of commercial lithium-ion batteries. Energy 2017, 120, 179–191. [Google Scholar] [CrossRef]
- Juhlin, O. Modeling of Battery Degradation in Electrified Vehicles. Master’s Thesis, Linköping University, Linköping, Sweden, 2016. [Google Scholar]
- Lei, S.; Zeng, Z.; Cheng, S.; Xie, J. Fast-charging of lithium-ion batteries: A review of electrolyte design aspects. Battery Energy 2023, 2, 20230018. [Google Scholar] [CrossRef]
- Weiss, M.; Ruess, R.; Kasnatscheew, J.; Levartovsky, Y.; Levy, N.; Minnmann, P.; Stolz, L.; Waldmann, T.; Wohlfahrt-Mehrens, M.; Aurbach, D.; et al. Fast Charging of Lithium-Ion Batteries: A Review of Materials Aspects. Adv. Energy Mater. 2021, 11, 2101126. [Google Scholar] [CrossRef]
- Gao, Y.; Rojas, T.; Wang, K.; Liu, S.; Daiwei Wang, T.C.; Wang, H.; Ngo, A.T.; Wang, D. Low-temperature and high-rate-charging lithium metal batteries enabled by an electrochemically active monolayer-regulated interface. Nat. Energy 2020, 5, 534–542. [Google Scholar] [CrossRef]
- Li, L.; Zhang, D.; Deng, J.; Gou, Y.; Fang, J.; Cui, H.; Zhao, Y.; Cao, M. Carbon-based materials for fast charging lithium-ion batteries. Carbon 2021, 183, 721–734. [Google Scholar] [CrossRef]
- Reniers, J.M.; Mulder, G.; Ober-Blöbaum, S.; Howey, D.A. Improving optimal control of grid-connected lithium-ion batteries through more accurate battery and degradation modelling. J. Power Sources 2018, 379, 91–102. [Google Scholar] [CrossRef]
- Cordis. Advanced Materials for Batteries: Research Results. Available online: https://cordis.europa.eu/project/id/608931/reporting (accessed on 5 November 2022).
- Schimpe, M.; von Kuepach, M.E.; Naumann, M.; Hesse, H.C.; Smith, K.; Jossen, A. Comprehensive Modeling of Temperature-Dependent Degradation Mechanisms in Lithium Iron Phosphate Batteries. J. Electrochem. Soc. 2018, 165, A181–A193. [Google Scholar] [CrossRef]
- Xu, M.; Wang, R.; Zhao, P.; Wang, X. Fast charging optimization for lithium-ion batteries based on dynamic programming algorithm and electrochemical-thermal-capacity fade coupled model. J. Power Sources 2019, 438, 227015. [Google Scholar] [CrossRef]
- Ramadass, P.; Haran, B.; White, R.; Popov, B.N. Capacity fade of Sony 18650 cells cycled at elevated temperatures: Part II. Capacity fade analysis. J. Power Sources 2002, 112, 614–620. [Google Scholar] [CrossRef]
- Yin, P.; Wang, N.; Shang, Y.; Gu, P.; Duan, B.; Zhang, C. Study on the Effect of High Temperature and High-Current Rate on Fast Charging of Lithium-ion Batteries. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 5841–5846. [Google Scholar]
- Moon, J.S.; Lee, J.H.; Ha, I.Y.; Lee, T.K.; Won, C.Y. An Efficient Battery Charging Algorithm based on State-of-Charge Estimation for Electric Vehicle. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011. [Google Scholar]
- Abdollahi, A.; Han, X.; Avvari, G.; Raghunathan, N.; Balasingam, B.; Pattipati, K.; Bar-Shalom, Y. Optimal battery charging, Part I: Minimizing time-to-charge, energy loss, and temperature rise for OCV-resistance battery model. J. Power Sources 2016, 303, 388–398. [Google Scholar] [CrossRef]
- Kannan, D. An Introduction to Fast Charging and Pulse Charging. Available online: https://medium.com/batterybits/an-introduction-to-fast-charging-and-pulse-charging-21cd21a599ae (accessed on 18 November 2022).
- Wu, Y.; Long, X.; Lu, J.; Wu, Y.; Zhou, R.; Liu, L. Effect of temperature on the high-rate pulse charging of lithium-ion batteries. J. Electroanal. Chem. 2022, 922, 116773. [Google Scholar] [CrossRef]
- Notten, P.; het Veld, J.O.; van Beek, J. Boostcharging Li-ion batteries: A challenging new charging concept. J. Power Sources 2005, 145, 89–94. [Google Scholar] [CrossRef]
- Wu, C.; Liu, Y.; Zhou, T.; Cao, S.A. Multistage Current Charging Method for Energy Storage Device of Microgrid Considering Energy Consumption and Capacity of Lithium Battery. Energies 2022, 15, 4526. [Google Scholar] [CrossRef]
- Cho, I.H.; Lee, P.Y.; Kim, J.H. Analysis of the Effect of the Variable Charging Current Control Method on Cycle Life of Li-ion Batteries. Energies 2019, 12, 3023. [Google Scholar] [CrossRef]
- Liu, Y.H.; Luo, Y.F. Search for an Optimal Rapid-Charging Pattern for Li-Ion Batteries Using the Taguchi Approach. IEEE Ind. Electron. 2010, 57, 3963–3971. [Google Scholar] [CrossRef]
- Cheng, M.W.; Wang, S.M.; Lee, Y.S.; Hsiao, S.H. Fuzzy controlled fast charging system for lithium-ion batteries. In Proceedings of the 2009 International Conference on PEDS, Taipei, Taiwan, 2–5 November 2009; pp. 1498–1503. [Google Scholar]
- Velho, R.; Calado, M.; Pombo, J.; Fermeiro, J.; Mariano, S. New Charging Algorithm for Li-Ion Battery Packs Based on Artificial Neural Networks. Batteries 2022, 8, 89–94. [Google Scholar]
- Liu, C.; Liu, L. Optimizing Battery Design for Fast Charge through a Genetic Algorithm Based Multi-Objective Optimization Framework. ECS Trans. 2017, 77, 257–267. [Google Scholar] [CrossRef]
- Jain, S.; Simon, D. Genetic Algorithm Based Charge Optimization of Lithium-Ion Batteries in Small Satellites. In Proceedings of the 19th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 8–11 August 2005. [Google Scholar]
- Shepherd, C. Design of Primary and Secondary Cells—Part 2. An Equation Describing Battery Discharge. J. Electrochem. Soc. 1965, 112, 657–664. [Google Scholar] [CrossRef]
- Lee, S.; Kim, Y.; Siegel, J.B.; Stefanopoulou, A.G. Optimal control for fast acquisition of equilibrium voltage for Li-ion batteries. J. Energy Storage 2021, 40, 102814. [Google Scholar] [CrossRef]
- Perez, H.E.; Hu, X.; Dey, S.; Moura, S.J. Optimal Charging of Li-Ion Batteries with Coupled Electro-Thermal-Aging Dynamics. IEEE Trans. Veh. Technol. 2017, 66, 7761–7770. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- García-Heras, J.; Soler, M.; Sáez, F.J. A Comparison of Optimal Control Methods for Minimum Fuel Cruise at Constant Altitude and Course with Fixed Arrival Time. Procedia Eng. 2014, 80, 231–244, 3rd International Symposium on Aircraft Airworthiness (ISAA 2013). [Google Scholar] [CrossRef]
- Betts, J.T. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010. [Google Scholar]
- Morad, M. Mathematical Modeling of Lithium-Ion Batteries and Improving Mathematics Learning Experience for Engineering Students. Master’s Thesis, University of Kansas, Kansas City, KS, USA, 2017. [Google Scholar]
- Adachi, M.; Kuhn, Y.; Horstmann, B.; Osborne, M.A.; Howey, D.A. Bayesian Model Selection of Lithium-Ion Battery Models via Bayesian Quadrature. IFAC-PapersOnLine 2023, 56, 10521–10526. [Google Scholar] [CrossRef]
- Liu, J. Computationally Efficient Online Model-Based Control and Estimation for Lithium-Ion Batteries. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2017. [Google Scholar]
- Doyle, C.; Fuller, T.F.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Doyle, C.; Newman, J. The use of mathematical modeling in the design of lithium/polymer battery systems. Electrochim. Acta 1995, 40, 2191–2196. [Google Scholar] [CrossRef]
- Doyle, C. Design and Simulation of Lithium Rechargeable Batteries. Ph.D. Thesis, University of California, Berkley, CA, USA, 1995. [Google Scholar]
- Rao, L.; Newman, J. Heat-Generation Rate and General Energy Balance for Insertion Battery Systems. J. Electrochem. Soc. 1997, 144, 2697. [Google Scholar] [CrossRef]
- Wu, J.; Ihsan-Ul-Haq, M.; Chen, Y.; Kim, J.K. Understanding solid electrolyte interphases: Advanced characterization techniques and theoretical simulations. Nano Energy 2021, 89, 106489. [Google Scholar] [CrossRef]
- Mohtat, P.; Pannala, S.; Sulzer, V.; Siegel, J.B.; Stefanopoulou, A.G. An Algorithmic Safety VEST for Li-ion Batteries During Fast Charging. IFAC-PapersOnLine 2021, 54, 522–527. [Google Scholar] [CrossRef]
- Haruta, M.; Okubo, T.; Masuo, Y.; Yoshida, S.; Tomita, A.; Takenaka, T.; Doi, T.; Inaba, M. Temperature effects on SEI formation and cyclability of Si nanoflake powder anode in the presence of SEI-forming additives. Electrochim. Acta 2017, 224, 186–193. [Google Scholar] [CrossRef]
- Dong, H.; Wang, J.; Wang, P.; Ding, H.; Song, R.; Zhang, N.S.; Zhao, D.N.; Zhang, L.J.; Li, S.Y. Effect of temperature on formation and evolution of solid electrolyte interphase on SiGraphite@C anodes. J. Energy Chem. 2022, 64, 190–200. [Google Scholar] [CrossRef]
- Świerczynski, M.; Stroe, D.I.; Stan, A.I.; Teodorescu, R.; Sauer, D.U. Selection and Performance-Degradation Modeling of LiMO2/Li4Ti5O12 and LiFePO4/C Battery Cells as Suitable Energy Storage Systems for Grid Integration with Wind Power Plants: An Example for the Primary Frequency Regulation Service. IEEE Trans. Sustain. Energy 2014, 5, 90–101. [Google Scholar] [CrossRef]
- Shabani, M.; Dahlquist, E.; Wallin, F.; Yan, J. Techno-economic impacts of battery performance models and control strategies on optimal design of a grid-connected PV system. Energy Convers. Manag. 2021, 245, 114617. [Google Scholar] [CrossRef]
- Appleton, S.; Fotouhi, A. A Model-Based Battery Charging Optimization Framework for Proper Trade-offs Between Time and Degradation. J. Automot. Innov. 2023, 6, 204–219. [Google Scholar] [CrossRef]
- Li, Y.; Yang, J.; Liu, W.; Wang, L.; Liao, C. Linear parameter-varying modeling and identification of lithium-ion battery for control-oriented applications. J. Power Sources 2021, 507, 230304. [Google Scholar] [CrossRef]
- Ning, B.; Cao, B.; Wang, B.; Zou, Z. Adaptive sliding mode observers for lithium-ion battery state estimation based on parameters identified online. Energy 2018, 153, 732–742. [Google Scholar] [CrossRef]
- Turker; Gunes; Erden. Equivalent Circuit Based Neural Network Model of Microstrip Discontinuities. In Proceedings of the 2006 IEEE 14th Signal Processing and Communications Applications, Antalya, Turkey, 16–19 April 2006; pp. 1–4. [Google Scholar]
- Cui, Z.; Hu, W.; Zhang, G.; Zhang, Z.; Chen, Z. An extended Kalman filter based SOC estimation method for Li-ion battery. Energy Rep. 2022, 8, 81–87. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, X.; Fang, Y.; Yin, Y. On SOC estimation of lithium-ion battery packs based EKF. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013; pp. 7668–7673. [Google Scholar]
- Zhang, C.; Guo, Y.; Wang, C.; Li, S.; Curnick, O.; Amietszajew, T.; Bhagat, R. A new design of experiment method for model parametrisation of lithium ion battery. J. Energy Storage 2022, 50, 104301. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, X.; Wei, M. Adaptive Kalman filter based state of charge estimation algorithm for lithium-ion battery. Chin. Phys. B 2022, 24, 81–87. [Google Scholar] [CrossRef]
- Moura, S.J.; Argomedo, F.B.; Klein, R.; Mirtabatabaei, A.; Krstic, M. Battery State Estimation for a Single Particle Model With Electrolyte Dynamics. IEEE Trans. Control Syst. Technol. 2017, 25, 453–468. [Google Scholar] [CrossRef]
- Amir, S.; Gulzar, M.; Tarar, M.O.; Naqvi, I.H.; Zaffar, N.A.; Pecht, M.G. Dynamic Equivalent Circuit Model to Estimate State-of-Health of Lithium-Ion Batteries. IEEE Access 2022, 10, 18279–18288. [Google Scholar] [CrossRef]
- Valle, B.; Wentz, C.T.; Sarpeshkar, R. An Ultra-compact and Efficient Li-ion Battery Charger Circuit for Biomedical Applications. In Proceedings of the International Symposium on Circuits and Systems (ISCAS) 2010, Paris, France, 30 May–2 June 2010; pp. 1224–1227. [Google Scholar]
- Buchmann, I. Batteries in a Portable World; Cadex Electronics, Inc.: Richmond, BC, Canada, 2001. [Google Scholar]
- Rodrigues, M.T.F.; Shkrob, I.A.; Colclasure, A.M.; Abraham, D.P. Fast Charging of Li-Ion Cells: Part IV. Temperature Effects and “Safe Lines” to Avoid Lithium Plating. J. Electrochem. Soc. 2020, 167, 130508. [Google Scholar] [CrossRef]
- Pistoia, G. Lithium-Ion Batteries Advances and Applications; Chapter 14: Satellite Lithium-Ion Batteries; Elsevier Science and Technology: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Grandjean, T.R.B.; McGordon, A.; Jennings, P.A. Structural Identifiability of Equivalent Circuit Models for Li-Ion Batteries. Energies 2017, 10, 90. [Google Scholar] [CrossRef]
- Fairweather, A.; Foster, M.; Stone, D. Modelling of VRLA batteries over operational temperature range using Pseudo Random Binary Sequences. J. Power Sources 2012, 207, 56–59. [Google Scholar] [CrossRef]
- Samad, N.A.; Wang, B.; Siegel, J.B.; Stefanopoulou, A.G. Parameterization of Battery Electrothermal Models Coupled With Finite Element Flow Models for Cooling. J. Dyn. Syst. Meas. Control 2017, 139, 071003. [Google Scholar] [CrossRef]
- Tran, M.K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
- Choi, E.; Chang, S. A Temperature-Dependent State of Charge Estimation Method Including Hysteresis for Lithium-Ion Batteries in Hybrid Electric Vehicles. IEEE Access 2020, 8, 129857–129868. [Google Scholar] [CrossRef]
- Chin, C.S.; Gao, Z.; Chiew, J.H.K.; Zhang, C. Nonlinear Temperature-Dependent State Model of Cylindrical LiFePO4 Battery for Open-Circuit Voltage, Terminal Voltage and State-of-Charge Estimation with Extended Kalman Filter. Energies 2018, 11, 2467. [Google Scholar] [CrossRef]
- Nejad, S.; Gladwin, D.; Stone, D. A systematic review of lumped-parameter equivalent circuit models for real-time estimation of lithium-ion battery states. J. Power Sources 2016, 316, 183–196. [Google Scholar] [CrossRef]
- Ding, Y.; Castanier, M.; Perez, H.; Sigel, J.; Lin, X. Parameterization and Validation of an Integrated Electro-Thermal LFP Battery Model. In Proceedings of the ASME 2012 5th Annual Dynamic Systems and Control Conference Joint with the JSME 2012 11th Motion and Vibration Conference (DSCC2012-MOVIC2012), Fort Lauderdale, FL, USA, 17–19 October 2012; American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 386–391. [Google Scholar]
- Dodd, N.; Preece, F.J.W.; Williams, G.T. Chapter 2–Electrical system analysis. In Electrical Systems and Equipment, 3rd ed.; Littler, D., Ed.; British Electricity International: Pergamon, Turkey; Oxford, UK, 1992; pp. 84–192. [Google Scholar]
- Becerra, V.M. PSOPT Optimal Control Software. Available online: https://www.psopt.net/ (accessed on 28 November 2022).
- Lin, X.; Perez, H.E.; Siegel, J.B.; Stefanopoulou, A.G.; Li, Y.; Anderson, R.D.; Ding, Y.; Castanier, M.P. Online Parametrization of Lumped Thermal Dynamics in Cylindrical Lithium Ion Batteries for Core Temperature Estimation and Health Monitoring. IEEE Trans. Contrib. Syst. Techol. 2013, 21, 183–196. [Google Scholar]
- Xiong, R.; Yu, Q.; Wang, L.Y. Open circuit voltage and state of charge online estimation for lithium ion batteries. Energy Procedia 2017, 142, 1902–1907. [Google Scholar] [CrossRef]
- Betts, J. Survey of Numerical Methods for Trajectory Optimization. J. Guid. Control Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Rao, A. A Survey of Numerical Methods for Optimal Control. Adv. Astronaut. Sci. 2010, 135, 497–528. [Google Scholar]
- Becerra, V.M. Solving complex optimal control problems at no cost with PSOPT. In Proceedings of the 2010 IEEE International Symposium on Computer-Aided Control System Design, Yokohama, Japan, 8–10 September 2010; pp. 1391–1396. [Google Scholar]
- Betts, J.T.; Biehn, N.; Campbell, S.L. Convergence of Nonconvergent IRK discretisations of Optimal Control Problems with State Inequality Constraints. Siam J. Sci. Comput. 2002, 23, 1981–2007. [Google Scholar] [CrossRef]
- LithiumWerks. 26650 Lithium Ion Power Cell, 2019. Available online: https://power-wings.com/wp/wp-content/uploads/2020/08/26650-Power-Cell.pdf (accessed on 25 February 2024).



| Temperature Range | Type of Damage |
|---|---|
| <0 °C | Lithium plating due to non-uniformities in the cell caused by manufacturing defects. |
| 0–55 °C | No damage to the battery. |
| 55–160 °C | Higher heat dissipation. SEI film starts to decompose. Lithium reacts in the electrolyte. breaks down and produces . |
| 160–300 °C | Electrolyte starts decomposing. Releases flammable gasses. Fire and thermal runaway |
| Voltage Range | Type of Damage |
|---|---|
| ≤2.2 V 1 | In the charge phase, the precipitate is metallic Cu, which can ultimately cause a short circuit between the electrodes. |
| 2.2–4.2 V | No damage to the battery. |
| ≥4.2 V 2 | Risk of lithium metal plating. |
| Parameter | Value/Units | Description |
|---|---|---|
| Interpolated value a, | Internal resistance of the lithium–ion battery | |
| Interpolated value a, | Cell’s no-load self-discharge | |
| Interpolated value a, | Charge-transfer resistance | |
| Interpolated value a, F | Bulk charge storage of the cell | |
| Interpolated value a, F | Electrodes’ double-layer effect | |
| 3.09 | Resistance to convective cooling | |
| 1.94 | Thermal resistance | |
| 4.5 | Heat capacity of the cell container | |
| 62.7 | Heat capacity inside the battery | |
| C | 2.3 A-h | Nominal capacity of A123 ANR26650M1 |
| R | 8.314 | Universal gas constant |
| Interpolated value a | Open circuit voltage | |
| V | Voltage at the battery terminals | |
| 278.15 K | Ambient temperature | |
| - | State of charge | |
| V | Double layer capacitance & charge transfer voltage (V) | |
| V | Diffusion process modelling voltage | |
| K | Temperature at the core | |
| K | Temperature at the surface | |
| - | State of health | |
| u | A | Input current |
| Case | Sub-Case | Description |
|---|---|---|
| 1 | Minimum time. CC-CV emulation. | |
| 2 | Minimum time and energy losses with temperature path constraint. | |
| 2.a | Temperature path constraint above protection. | |
| 2.b | Temperature path constraint. | |
| 3 | Minimum time and energy loss with endpoint cost parameterisation. |
| Battery Parameter | Value | Variable |
|---|---|---|
| Nominal capacity @25 °C | 2.3 Ah | C |
| Recommended charge current | 3 A | I |
| Max continuous charge current | 10 A | |
| Recommended charge voltage | 3.6 V | |
| Cut-off current | Taper to 125 mA | |
| Temperature range | 0 °C to 55 °C | 1 |
| Life cycle at 1C/1C, 100% DOD | >4000 cycles |
| (A) | Final State of Charge (%) | Optimal Cost | (s) | (s) | Degradation |
|---|---|---|---|---|---|
| 4C | 99 | 1361.80 | 325.72 | 1361.80 | 2.68 |
| 5C | 99 | 1328.00 | 160.78 | 1328.00 | 2.96 |
| 6C | 99 | 1316.36 | 81.31 | 1316.36 | 3.22 |
| (A) | Optimal Cost | Endpoint Cost | Running Cost | (s) | (s) 1 | Degradation |
|---|---|---|---|---|---|---|
| 4C | 2777.67 | 1564.60 | 1213.68 | 1153.40 | 1564.60 | 2.44 |
| 5C | 2777.08 | 1563.80 | 1213.27 | 934.90 | 1563.80 | 2.44 |
| 6C | 2777.68 | 1677.50 | 1214.78 | 814.18 | 1562.89 | 2.44 |
| (A) | Optimal Cost | Endpoint Cost | Running Cost | (s) | (s) 1 | Degradation |
|---|---|---|---|---|---|---|
| 4C | 2791.11 | 1656.94 | 1134.17 | 1294.12 | 1656.94 | 2.45 |
| 5C | 2797.56 | 1677.53 | 1120.03 | 818.80 | 1677.53 | 2.46 |
| 6C | 2797.55 | 1677.50 | 1120.05 | 818.79 | 1677.50 | 2.46 |
| Endpoint Cost | Running Cost | (s) | (s) | Degradation | |
|---|---|---|---|---|---|
| 0.25 | 626.41 | 753.63 | 2505.66 | 1344.23 | |
| 0.50 | 960.51 | 963.21 | 1921.02 | 1075.91 | |
| 0.75 | 1297.63 | 1076.82 | 1730.18 | 951.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Saenz, J.; Becerra, V. Determining Fast Battery Charging Profiles Using an Equivalent Circuit Model and a Direct Optimal Control Approach. Energies 2024, 17, 1470. https://doi.org/10.3390/en17061470
Gonzalez-Saenz J, Becerra V. Determining Fast Battery Charging Profiles Using an Equivalent Circuit Model and a Direct Optimal Control Approach. Energies. 2024; 17(6):1470. https://doi.org/10.3390/en17061470
Chicago/Turabian StyleGonzalez-Saenz, Julio, and Victor Becerra. 2024. "Determining Fast Battery Charging Profiles Using an Equivalent Circuit Model and a Direct Optimal Control Approach" Energies 17, no. 6: 1470. https://doi.org/10.3390/en17061470
APA StyleGonzalez-Saenz, J., & Becerra, V. (2024). Determining Fast Battery Charging Profiles Using an Equivalent Circuit Model and a Direct Optimal Control Approach. Energies, 17(6), 1470. https://doi.org/10.3390/en17061470







