A Non-Iterative Coordinated Scheduling Method for a AC-DC Hybrid Distribution Network Based on a Projection of the Feasible Region of Tie Line Transmission Power
Abstract
1. Introduction
- (1)
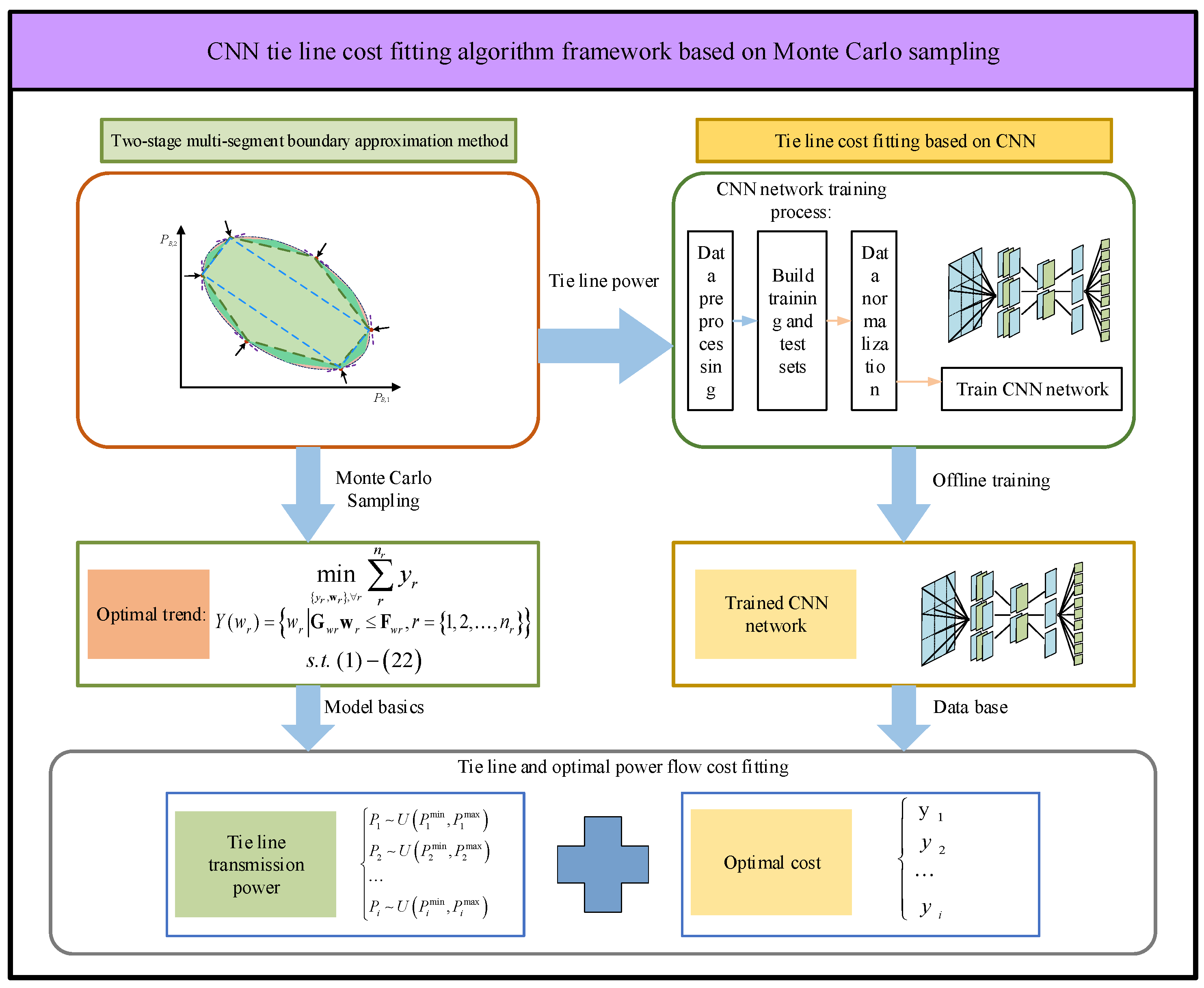
- A two-stage multi-segment boundary approximation method (TSM) is proposed to describe the accurate feasible region of tie line power in an AC/DC hybrid distribution network. In the first stage of the TSM method, the linear constraints of the AC/DC hybrid distribution network are iteratively solved to obtain an approximate feasible region. In the second stage, the approximate feasible region of the first stage is modified by nonlinear constraints, and finally, the high-precision approximation of the real feasible region is obtained. Examples demonstrate how the suggested method’s accuracy and speed are significantly better than those of previous approaches.
- (2)
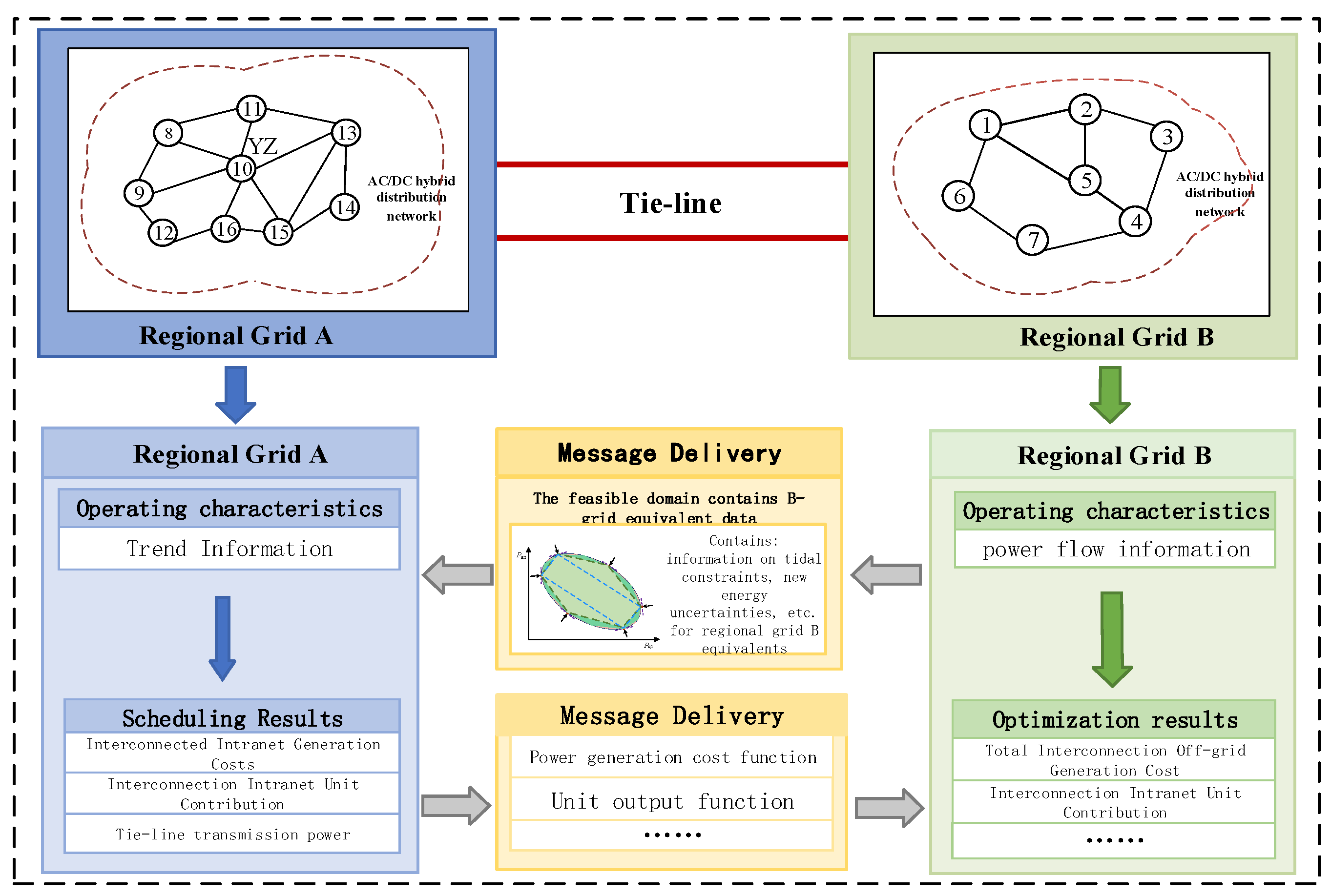
- A non-iterative coordinated optimization method based on feasible region projection is proposed. Aiming at the problem that the feasible region of tie line transmission power cannot retain cost information, a convolutional neural network (CNN) cost function fitting method is proposed. Through Monte Carlo sampling, the functional relationship between tie line transmission power and operating cost is obtained. Under the premise of protecting information privacy, alternating iteration is avoided, and high-precision coordinated operation of the AC/DC hybrid distribution network system is realized.
2. Materials and Methods
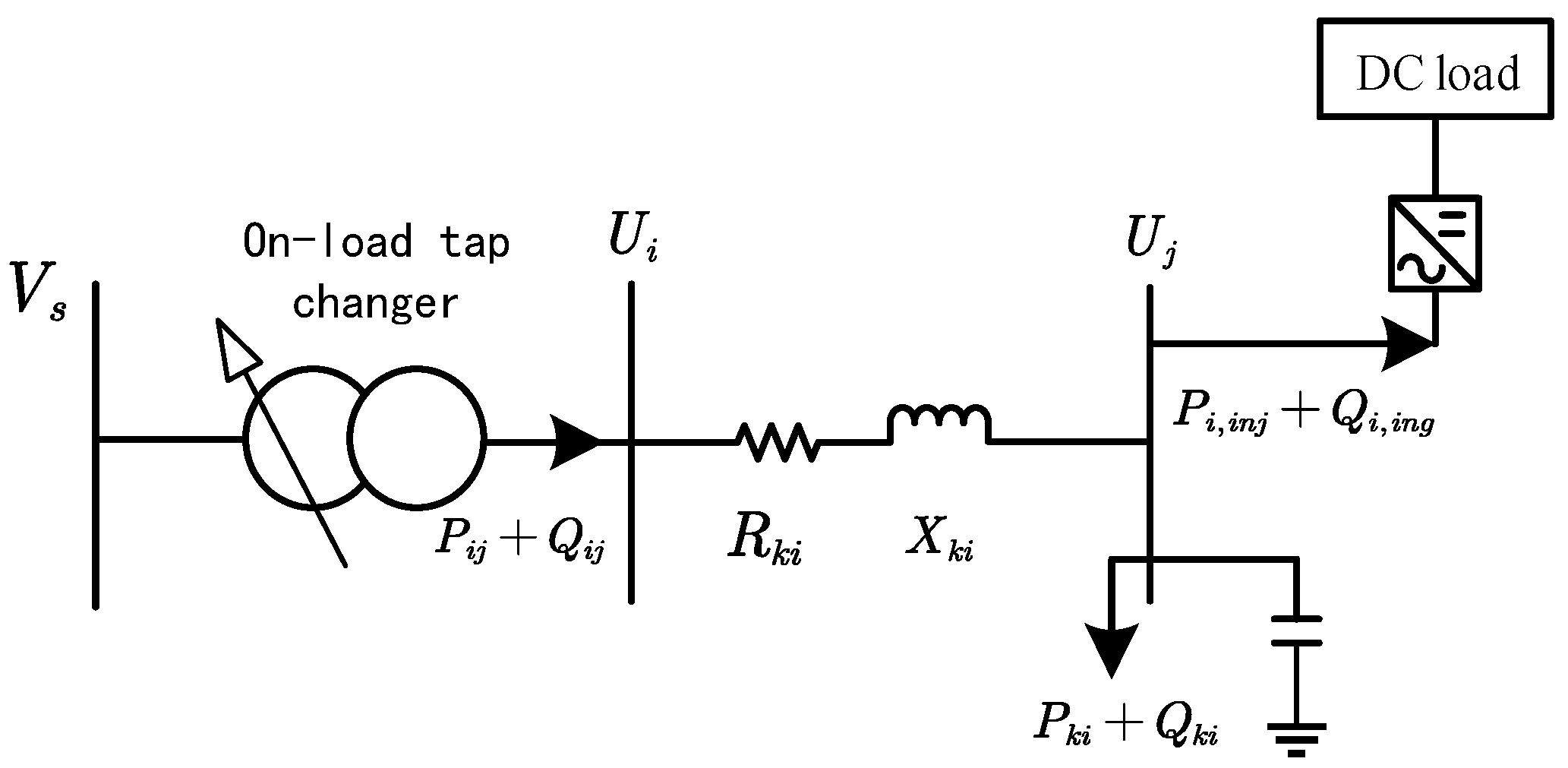
2.1. AC Network Modeling
2.1.1. AC Power Flow Equation
2.1.2. AC Distribution Network Security Constraints
2.2. DC Network Modeling
2.2.1. DC Power Flow Equation
2.2.2. DC Distribution Network Security Constraints
2.3. Converter Mathematical Model
3. Method of Characterization of the Feasible Region of the Tie Line
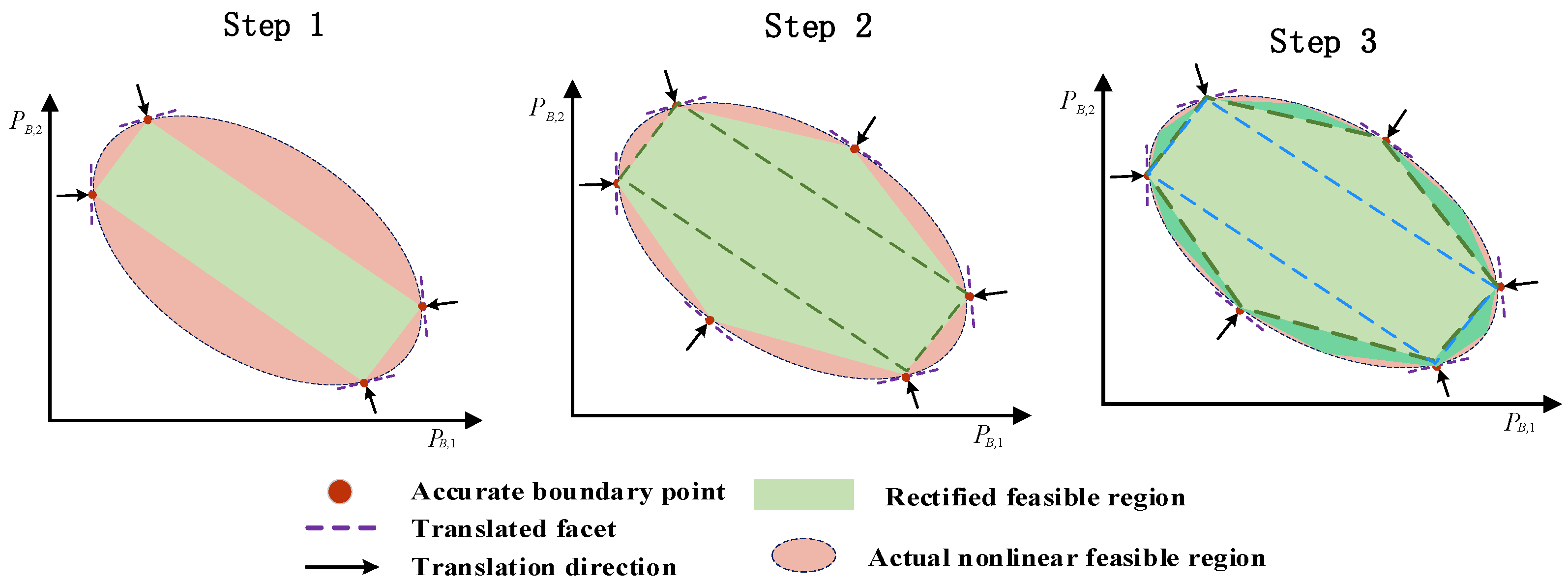
3.1. Search Process of Multi-Segment Boundary Approximation Method
- (1)
- Initialization of Boundary Points
- (2)
- Iteratively updating the approximation polytope
- (3)
- Accuracy Judgement of Multipoint Approximation
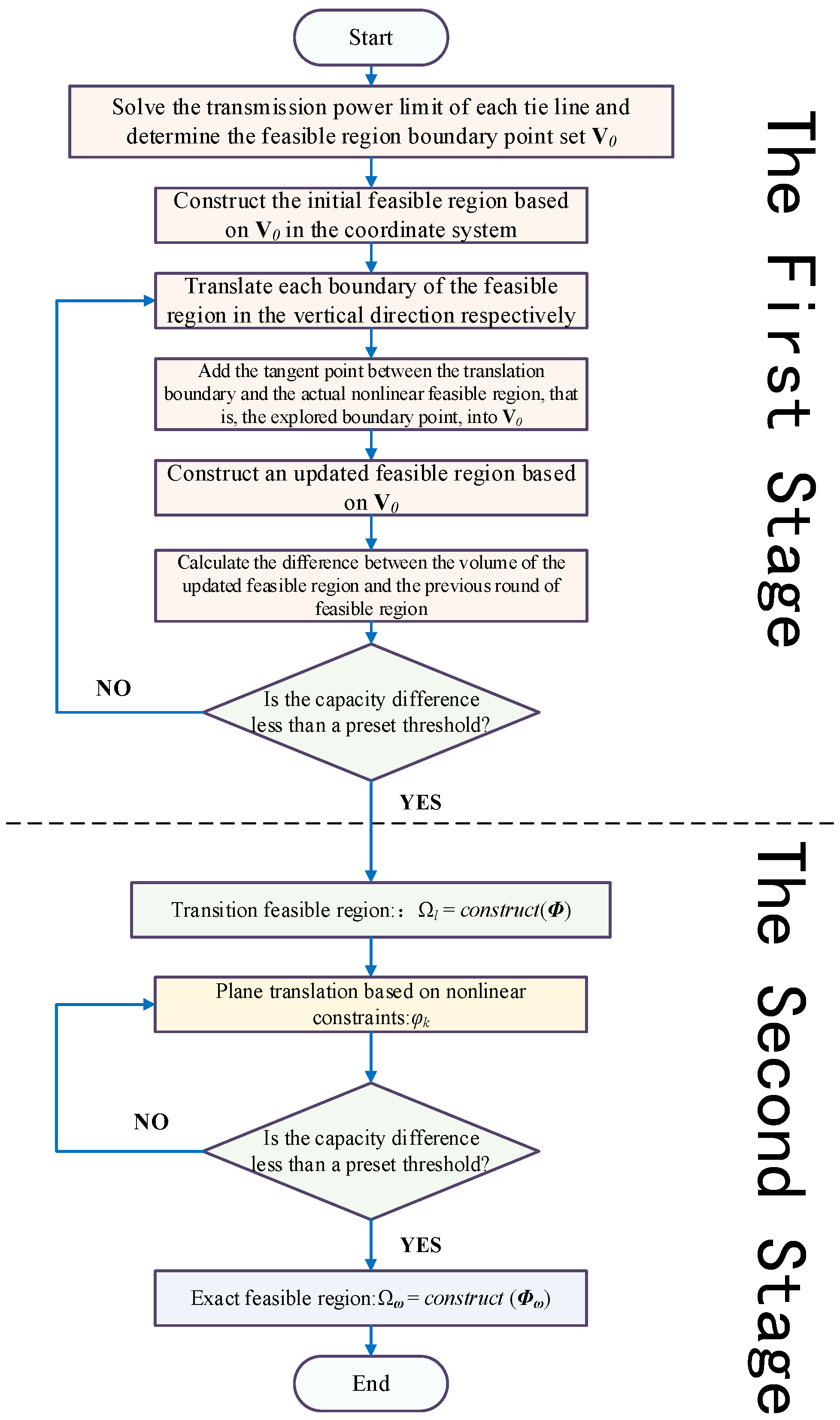
3.2. Two-Stage Multi-Segment Boundary Approximation Method (TSM)
| Algorithm 1: Two-stage multi-segment (TSM) |
 |
- (1)
- First-stage fast approximation. In the first stage, linearized grid constraints are used to quickly and iteratively search for boundary points of the feasible region. This can greatly improve computational efficiency and quickly obtain a rough approximation of the feasible region. The hybrid grid linear model is as follows:
- (i)
- AC linearized branch power flow model
- (ii)
- DC linearized branch power flow model
- (iii)
- VSC linearized model
- (2)
- The second stage of precise correction. The rough feasible region obtained in the first stage may have certain errors. The second stage uses precise nonlinear grid constraints to correct the boundary points obtained in the first stage and modify inaccurate boundary points. Finally, a high-precision feasible region approximation is obtained. Two-stage collaborative work not only ensures accuracy, but also greatly improves the convergence speed.
4. Artificial Intelligence-Based Scheduling Framework for Interconnected Systems
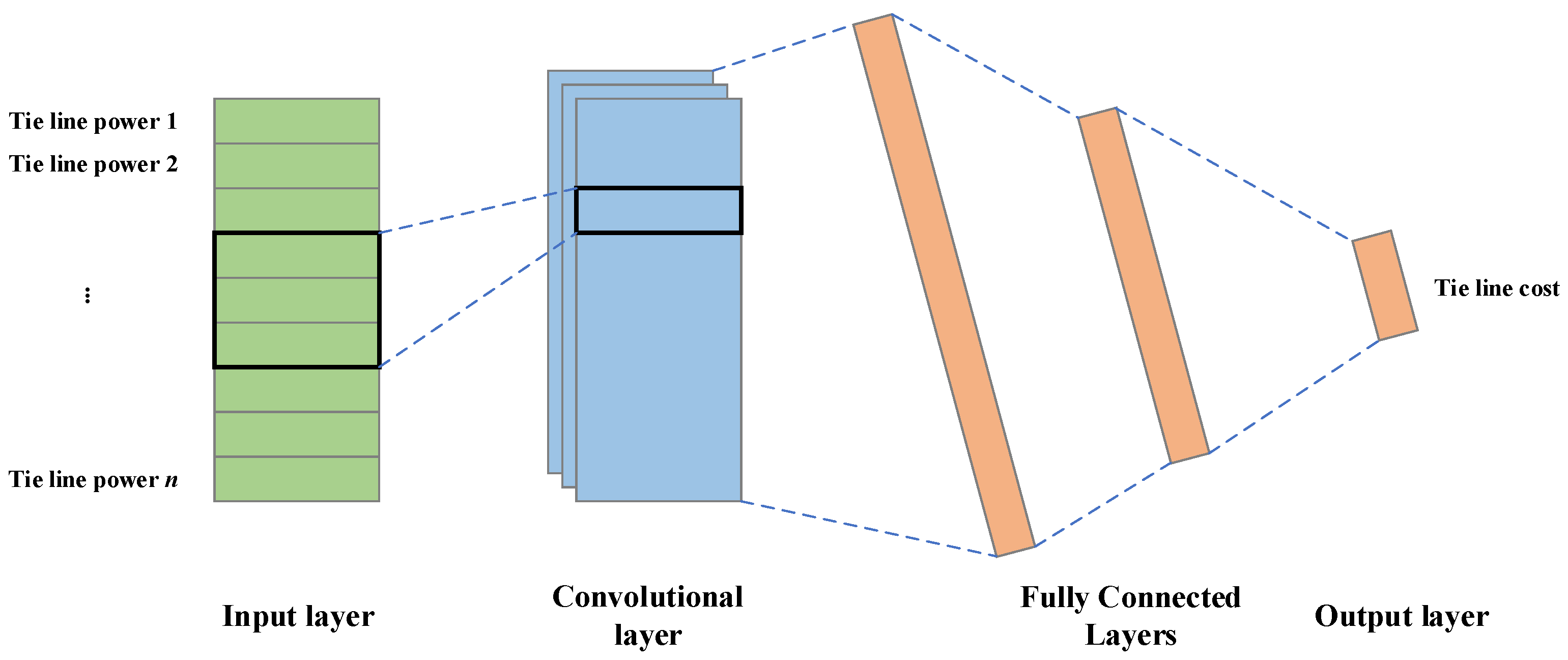
4.1. Convolutional Neural Network Model
4.2. Cost Fitting of Feasible Region of Tie Line in AC/DC Hybrid Power Grid Based on Convolutional Neural Network (CNN)
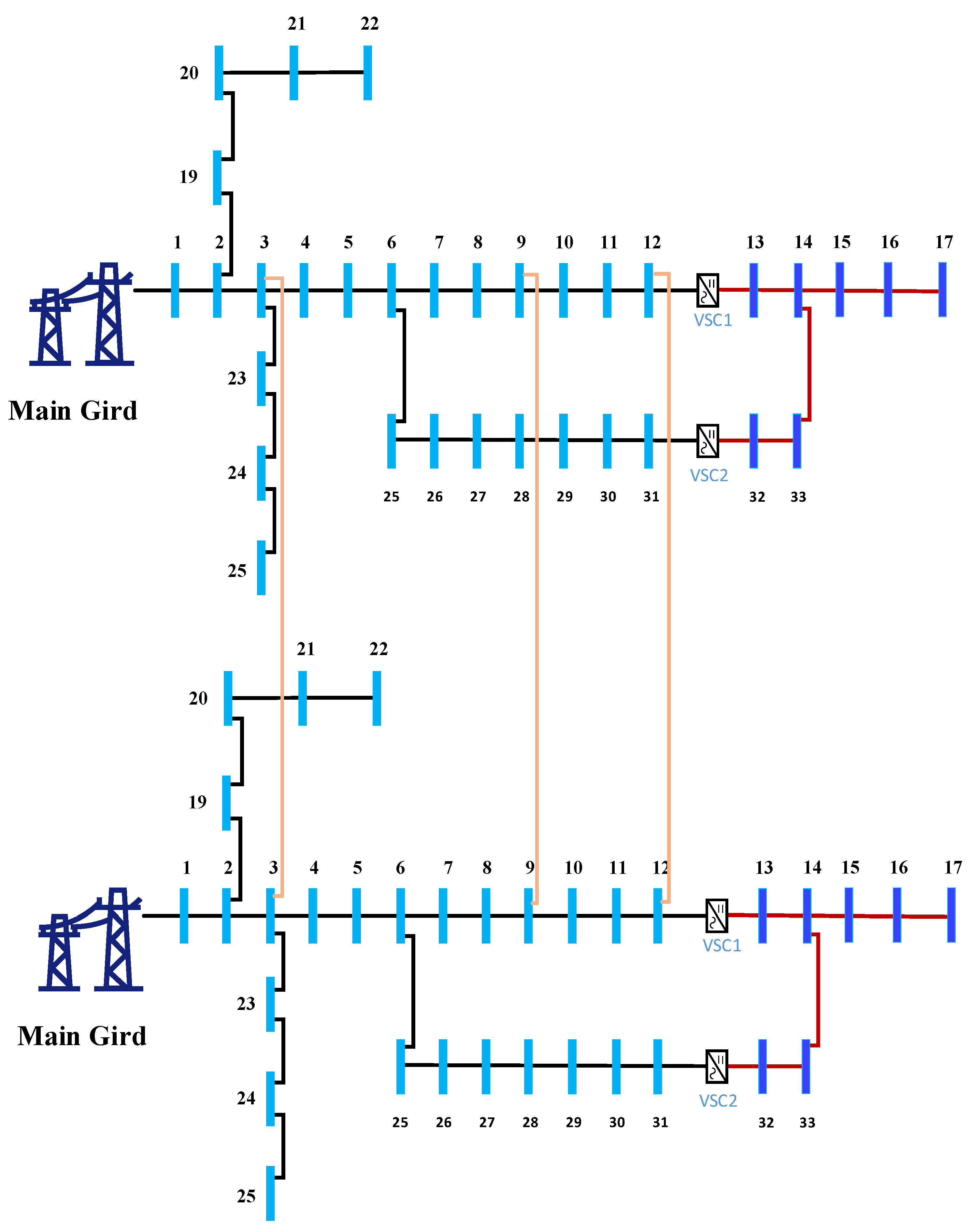
5. Case Studies
5.1. Simulation Setup and Comparison Methods
5.2. CNN-Based Cost Function Fitting
5.3. A Paradigm for Dispatching Interconnected Systems That Take into Account the Practical Range of AC/DC Hybrid Power Grid Transmission
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, H.; Zhou, M.; Zhang, S.; Zhang, L.; Li, G.; Sun, Y. Exploiting the Operational Flexibility of Wind Integrated Hybrid AC/DC Power Systems. IEEE Trans. Power Syst. 2020, 36, 818–826. [Google Scholar] [CrossRef]
- Xiao, H.; Pei, W.; Deng, W.; Ma, T.; Zhang, S.; Kong, L. Enhancing risk control ability of distribution network for improved renewable energy integration through flexible DC interconnection. Appl. Energy 2021, 284, 116387. [Google Scholar] [CrossRef]
- Sarangi, S.; Sahu, B.K.; Rout, P.K. Distributed generation hybrid AC/DC microgrid protection: A critical review on issues, strategies, and future directions. Int. J. Energy Res. 2020, 44, 3347–3364. [Google Scholar] [CrossRef]
- Ertugrul, N.; Abbott, D. DC is the Future [Point of View]. Proc. IEEE 2020, 108, 615–624. [Google Scholar] [CrossRef]
- Zhao, J.; Wu, Z.; Long, H.; Sun, H.; Wu, X.; Chan, C.; Shahidehpour, M. Optimal Operation Control Strategies for Active Distribution Networks under Multiple States: A Systematic Review. J. Mod. Power Syst. Clean Energy 2023. Available online: https://ieeexplore.ieee.org/abstract/document/10355075 (accessed on 6 February 2024).
- Dong, Y.; Shan, X.; Yan, Y.; Leng, X.; Wang, Y. Architecture, Key Technologies and Applications of Load Dispatching in China Power Grid. J. Mod. Power Syst. Clean Energy 2022, 10, 316–327. [Google Scholar] [CrossRef]
- Biskas, P.; Bakirtzis, A.; Macheras, N.; Pasialis, N. A Decentralized Implementation of DC Optimal Power Flow on a Network of Computers. IEEE Trans. Power Syst. 2005, 20, 25–33. [Google Scholar] [CrossRef]
- Gil-González, W.; Montoya, O.D.; Grisales-Noreña, L.F.; Cruz-Peragón, F.; Alcalá, G. Economic dispatch of renewable generators and BESS in DC microgrids using second-order cone optimization. Energies 2020, 13, 1703. [Google Scholar] [CrossRef]
- Kalakova, A.; Nunna, H.S.V.S.K.; Jamwal, P.K.; Doolla, S. A Novel Genetic Algorithm Based Dynamic Economic Dispatch With Short-Term Load Forecasting. IEEE Trans. Ind. Appl. 2021, 57, 2972–2982. [Google Scholar] [CrossRef]
- Ellahi, M.; Abbas, G. A Hybrid Metaheuristic Approach for the Solution of Renewables-Incorporated Economic Dispatch Problems. IEEE Access 2020, 8, 127608–127621. [Google Scholar] [CrossRef]
- Liu, Y.; Ćetenović, D.; Li, H.; Gryazina, E.; Terzija, V. An optimized multi-objective reactive power dispatch strategy based on improved genetic algorithm for wind power integrated systems. Int. J. Electr. Power Energy Syst. 2022, 136, 107764. [Google Scholar] [CrossRef]
- Dey, B.; Bhattacharyya, B.; Márquez, F.P.G. A hybrid optimization-based approach to solve environment constrained economic dispatch problem on microgrid system. J. Clean. Prod. 2021, 307, 127196. [Google Scholar] [CrossRef]
- Wang, J.; Peng, Y. Distributed optimal dispatching of multi-entity distribution network with demand response and edge computing. IEEE Access 2020, 8, 141923–141931. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Q.; Liu, Z.; Wu, X. A Distributed Black-Start Optimization Method for Global Transmission and Distribution Network. IEEE Trans. Power Syst. 2021, 36, 4471–4481. [Google Scholar] [CrossRef]
- Li, X.; Zeng, Y.; Lu, Z. Decomposition and coordination calculation of economic dispatch for active distribution network with multi-microgrids. Int. J. Electr. Power Energy Syst. 2022, 135, 107617. [Google Scholar] [CrossRef]
- Hou, J.; Zhai, Q.; Zhou, Y.; Guan, X. A Fast Solution Method for Large-Scale Unit Commitment Based on Lagrangian Relaxation and Dynamic Programming. IEEE Trans. Power Syst. 2023, 39, 3130–3140. [Google Scholar] [CrossRef]
- Qader, M.R. Power management in a hydrothermal system considering maintenance using Lagrangian relaxation and augmented Lagrangian methods. Alex. Eng. J. 2022, 61, 8177–8188. [Google Scholar] [CrossRef]
- Maneesha, A.; Swarup, K.S. A survey on applications of Alternating Direction Method of Multipliers in smart power grids. Renew. Sustain. Energy Rev. 2021, 152, 111687. [Google Scholar] [CrossRef]
- Lu, X.; Yin, H.; Xia, S.; Zhang, D.; Shahidehpour, M.; Zhang, X.; Ding, T. A Real-Time Alternating Direction Method of Multipliers Algorithm for Nonconvex Optimal Power Flow Problem. IEEE Trans. Ind. Appl. 2020, 57, 70–82. [Google Scholar] [CrossRef]
- Sun, S.; Fu, J.; Wei, L.; Li, A. Multi-objective optimal dispatching for a grid-connected micro-grid considering wind power forecasting probability. IEEE Access 2020, 8, 46981–46997. [Google Scholar] [CrossRef]
- Sun, S.; Wang, C.; Wang, Y.; Zhu, X.; Lu, H. Multi-objective optimization dispatching of a micro-grid considering uncertainty in wind power forecasting. Energy Rep. 2022, 8, 2859–2874. [Google Scholar] [CrossRef]
- Shang, Y.; Liu, M.; Shao, Z.; Jian, L. Internet of smart charging points with photovoltaic Integration: A high-efficiency scheme enabling optimal dispatching between electric vehicles and power grids. Appl. Energy 2020, 278, 115640. [Google Scholar] [CrossRef]
- Tang, K.; Dong, S.; Ma, X.; Lv, L.; Song, Y. Chance-Constrained Optimal Power Flow of Integrated Transmission and Distribution Networks With Limited Information Interaction. IEEE Trans. Smart Grid 2020, 12, 821–833. [Google Scholar] [CrossRef]
- Lin, W.; Jin, X.; Jia, H.; Mu, Y.; Xu, T.; Xu, X.; Yu, X. Decentralized optimal scheduling for integrated community energy system via consensus-based alternating direction method of multipliers. Appl. Energy 2021, 302, 117448. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Z.; Guo, C.; Wang, J.; Ding, Y. Fully Distributed Robust Reserve Scheduling for Coupled Transmission and Distribution Systems. IEEE Trans. Power Syst. 2020, 36, 169–182. [Google Scholar] [CrossRef]
- Zhou, H.; Erol-Kantarci, M.; Liu, Y.; Poor, H.V. A Survey on Model-Based, Heuristic, and Machine Learning Optimization Approaches in RIS-Aided Wireless Networks. IEEE Commun. Surv. Tutor. 2023. [Google Scholar] [CrossRef]
- Wang, F.; Xuan, Z.; Zhen, Z.; Li, K.; Wang, T.; Shi, M. A day-ahead PV power forecasting method based on LSTM-RNN model and time correlation modification under partial daily pattern prediction framework. Energy Convers. Manag. 2020, 212, 112766. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, J.; Dai, W.; Wang, C.; Jian, J.; Shi, B.; Wu, T. A feasible region evaluation method of renewable energy accommodation capacity. Energy Rep. 2021, 7, 1513–1520. [Google Scholar] [CrossRef]
- Yang, G.; Xu, M.; Wang, W.; Lei, S. Coordinated Dispatch Optimization between the Main Grid and Virtual Power Plants Based on Multi-Parametric Quadratic Programming. Energies 2023, 16, 5593. [Google Scholar] [CrossRef]
- Lin, W.; Yang, Z.; Yu, J.; Jin, L.; Li, W. Tie-Line Power Transmission Region in a Hybrid Grid: Fast Characterization and Expansion Strategy. IEEE Trans. Power Syst. 2019, 35, 2222–2231. [Google Scholar] [CrossRef]
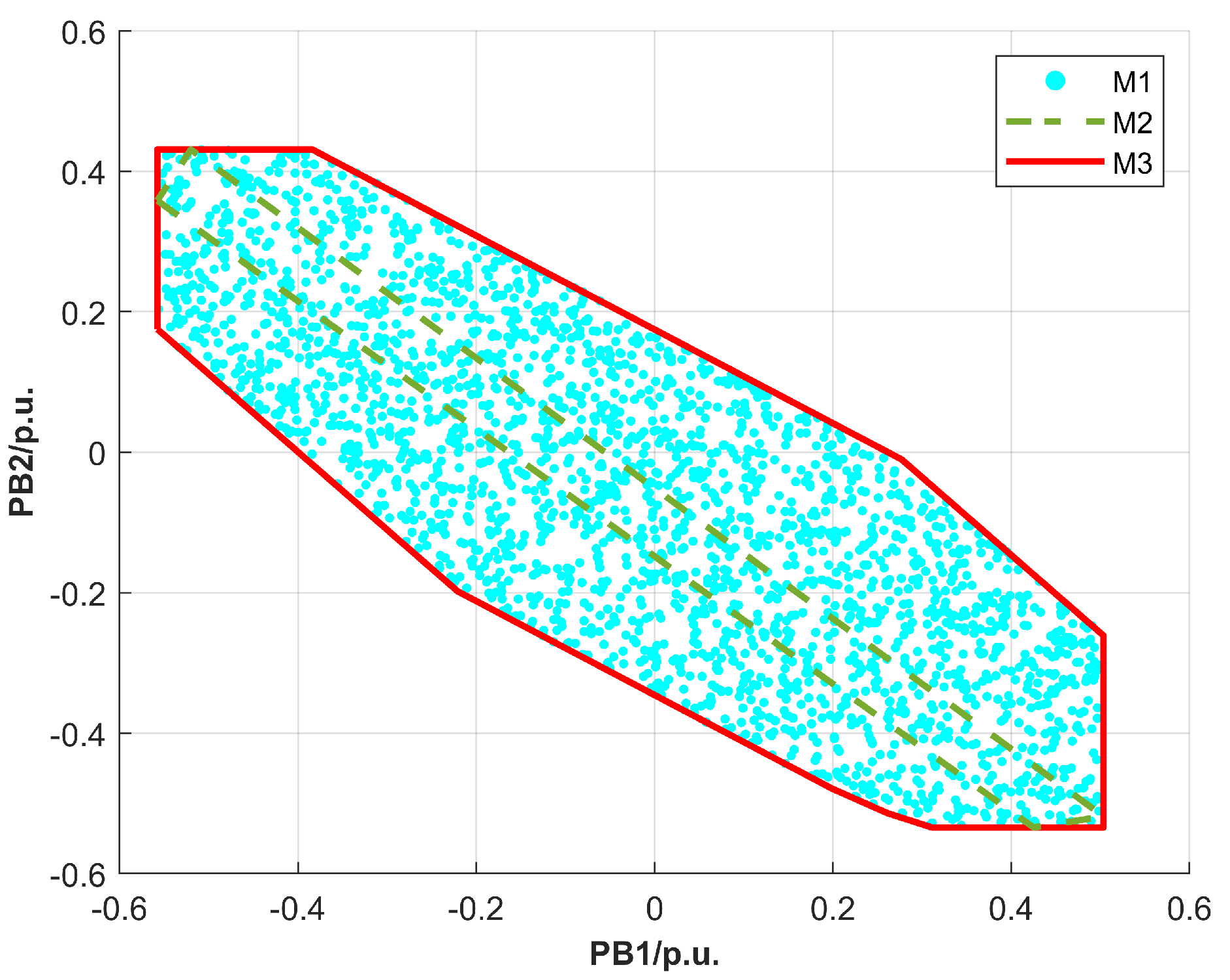
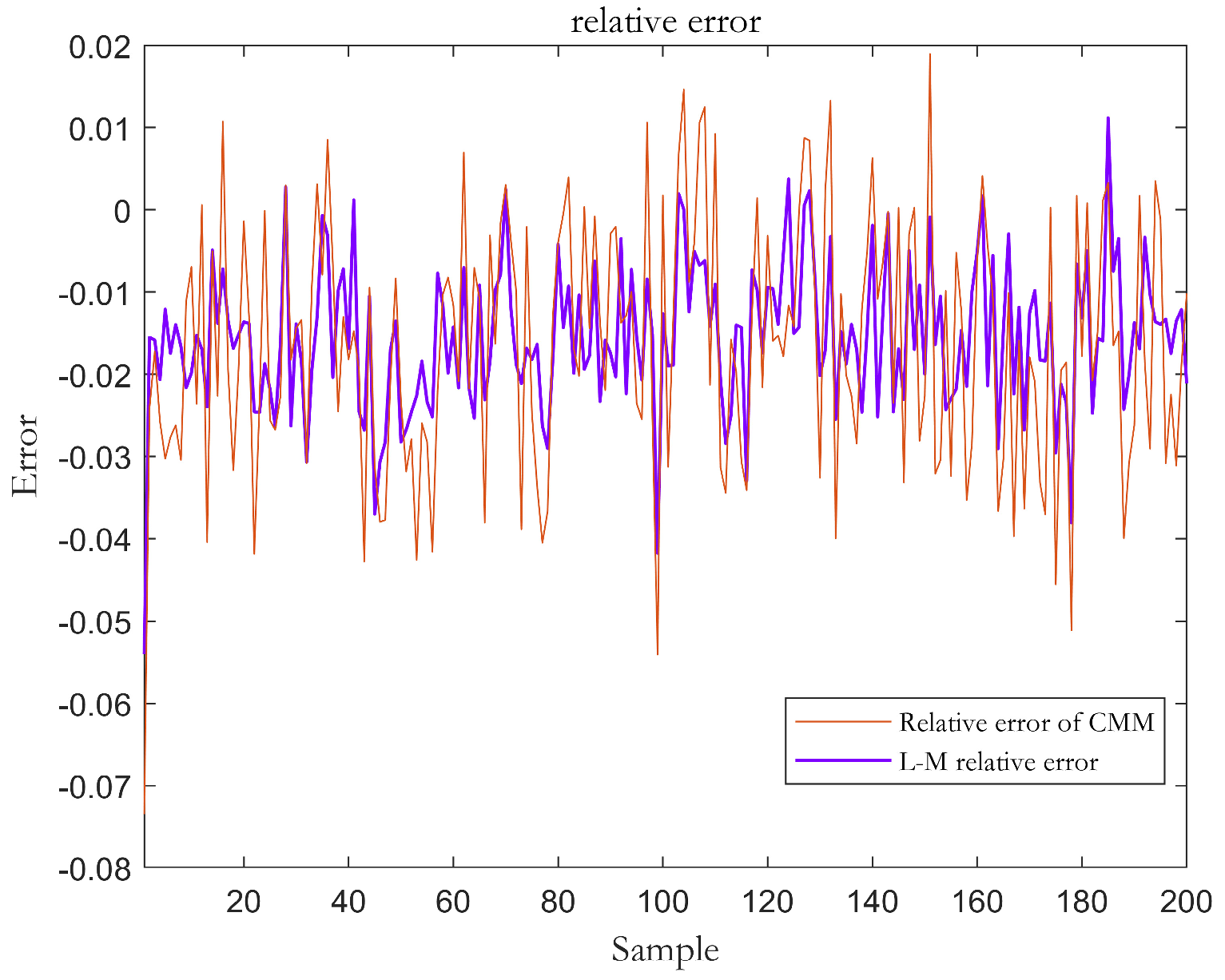
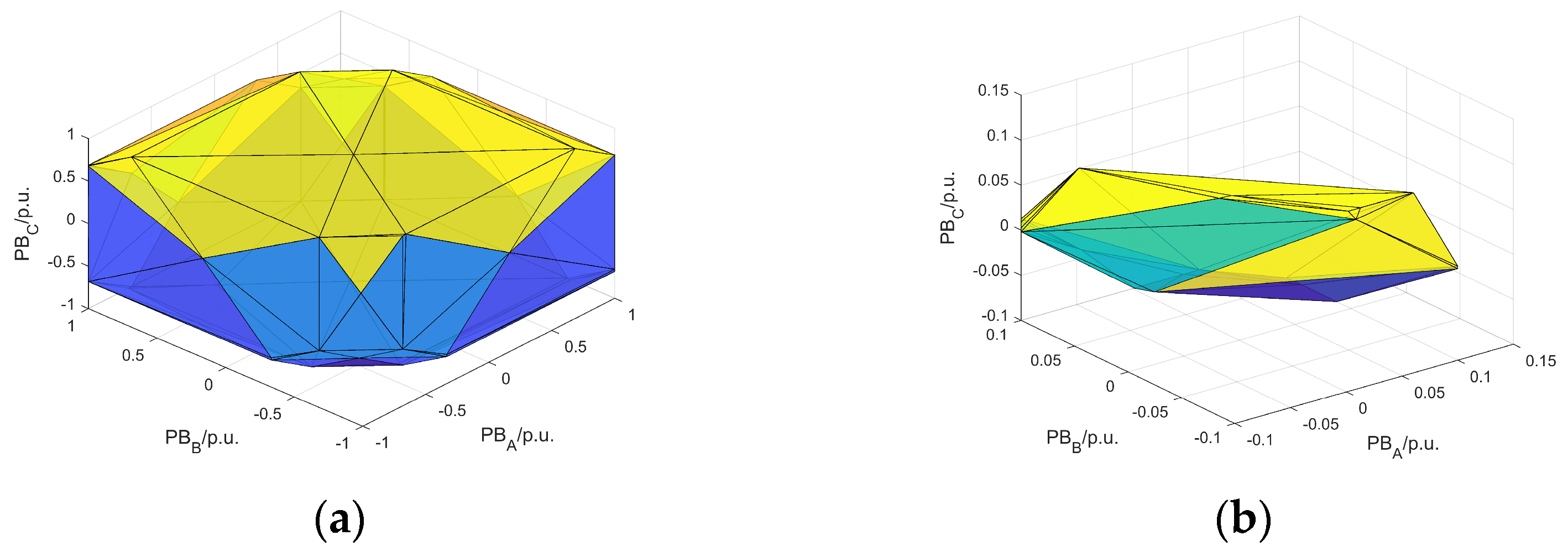
| Method | CR | ER | Time (s) | Volume (MW2) |
|---|---|---|---|---|
| M0 | - | - | 87,165.3 | 0.5382 |
| M1 | 18.21% | 0% | 2.44 | 0.0979 |
| M2 | 99.86% | 0.01% | 4.63 | 0.5375 |
| Number of Layers | Type | Structure and Parameters |
|---|---|---|
| First layer | Input layer | Enter the tie line power, and the number of input parameters is 6 |
| Second layer | Conv layer | 16 convolution kernels, convolution sum size 3 × 1 |
| Batchnorm layer | Batch normalization | |
| ReLU layer | The kernel in the network layer uses L2 regularization | |
| Maxpool layer | Pool size 2 × 1, stride 2 | |
| Third floor | Conv layer | 32 convolution kernels, convolution sum size 3 × 1 |
| Batchnorm layer | Batch normalization | |
| ReLU layer | The kernel in the network layer uses L2 regularization | |
| Maxpool layer | Pool size 2 × 1, stride 2 | |
| Fourth floor | Conv layer | 64 convolution kernels, convolution sum size 3 × 1 |
| Batchnorm layer | Batch normalization | |
| ReLU layer | The kernel in the network layer uses L2 regularization | |
| Maxpool layer | Pool size 2 × 1, stride 2 | |
| Fifth floor | FullyConnected layer | 128 neurons fully connected layer |
| Sixth floor | FullyConnected layer | 9 neuron fully connected layers |
| Seventh floor | Output layer | Output fitting results |
| Number of layers | Type | Structure and parameters |
| Method | RMSE | MAPE | R2 |
|---|---|---|---|
| M0 | 1.2584 | 0.0142 | 0.8173 |
| M1 | 0.9129 | 0.0090 | 0.9649 |
| Scheduling Solution Method | Tie Line Transmission Power (p.u.) | ||
|---|---|---|---|
| PB1 | PB2 | PB3 | |
| M0 | 0.712 | 0.062 | 0.124 |
| M1 | 0.694 | 0.058 | 0.153 |
| M2 | 0.709 | 0.058 | 0.104 |
| M3 | 0.710 | 0.065 | 0.125 |
| Scheduling Solution Method | Area 1 | Area 2 | Total Time | Total Generation Cost | ||
|---|---|---|---|---|---|---|
| Cost | Time | Cost | Time | |||
| ($) | (s) | ($) | (s) | (s) | ($) | |
| M0 | 1.05 × 104 | - | 2.52 × 104 | - | 3.0741 | 2.3178 × 104 |
| M1 | 1.15 × 104 | 71.353 | 2.58 × 104 | 18.253 | 86.605 | 2.5225 × 104 |
| M2 | 1.13 × 104 | 62.534 | 2.48 × 104 | 15.302 | 77.832 | 2.4835 × 104 |
| M3 | 1.03 × 104 | 22.357 | 2.48 × 104 | 10.724 | 33.081 | 2.3182 × 104 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, W.; Gao, Y.; Goh, H.H.; Jian, J.; Zeng, Z.; Liu, Y. A Non-Iterative Coordinated Scheduling Method for a AC-DC Hybrid Distribution Network Based on a Projection of the Feasible Region of Tie Line Transmission Power. Energies 2024, 17, 1462. https://doi.org/10.3390/en17061462
Dai W, Gao Y, Goh HH, Jian J, Zeng Z, Liu Y. A Non-Iterative Coordinated Scheduling Method for a AC-DC Hybrid Distribution Network Based on a Projection of the Feasible Region of Tie Line Transmission Power. Energies. 2024; 17(6):1462. https://doi.org/10.3390/en17061462
Chicago/Turabian StyleDai, Wei, Yang Gao, Hui Hwang Goh, Jiangyi Jian, Zhihong Zeng, and Yuelin Liu. 2024. "A Non-Iterative Coordinated Scheduling Method for a AC-DC Hybrid Distribution Network Based on a Projection of the Feasible Region of Tie Line Transmission Power" Energies 17, no. 6: 1462. https://doi.org/10.3390/en17061462
APA StyleDai, W., Gao, Y., Goh, H. H., Jian, J., Zeng, Z., & Liu, Y. (2024). A Non-Iterative Coordinated Scheduling Method for a AC-DC Hybrid Distribution Network Based on a Projection of the Feasible Region of Tie Line Transmission Power. Energies, 17(6), 1462. https://doi.org/10.3390/en17061462





