Optimal Operation of Residential Battery Energy Storage Systems under COVID-19 Load Changes
Abstract
1. Introduction
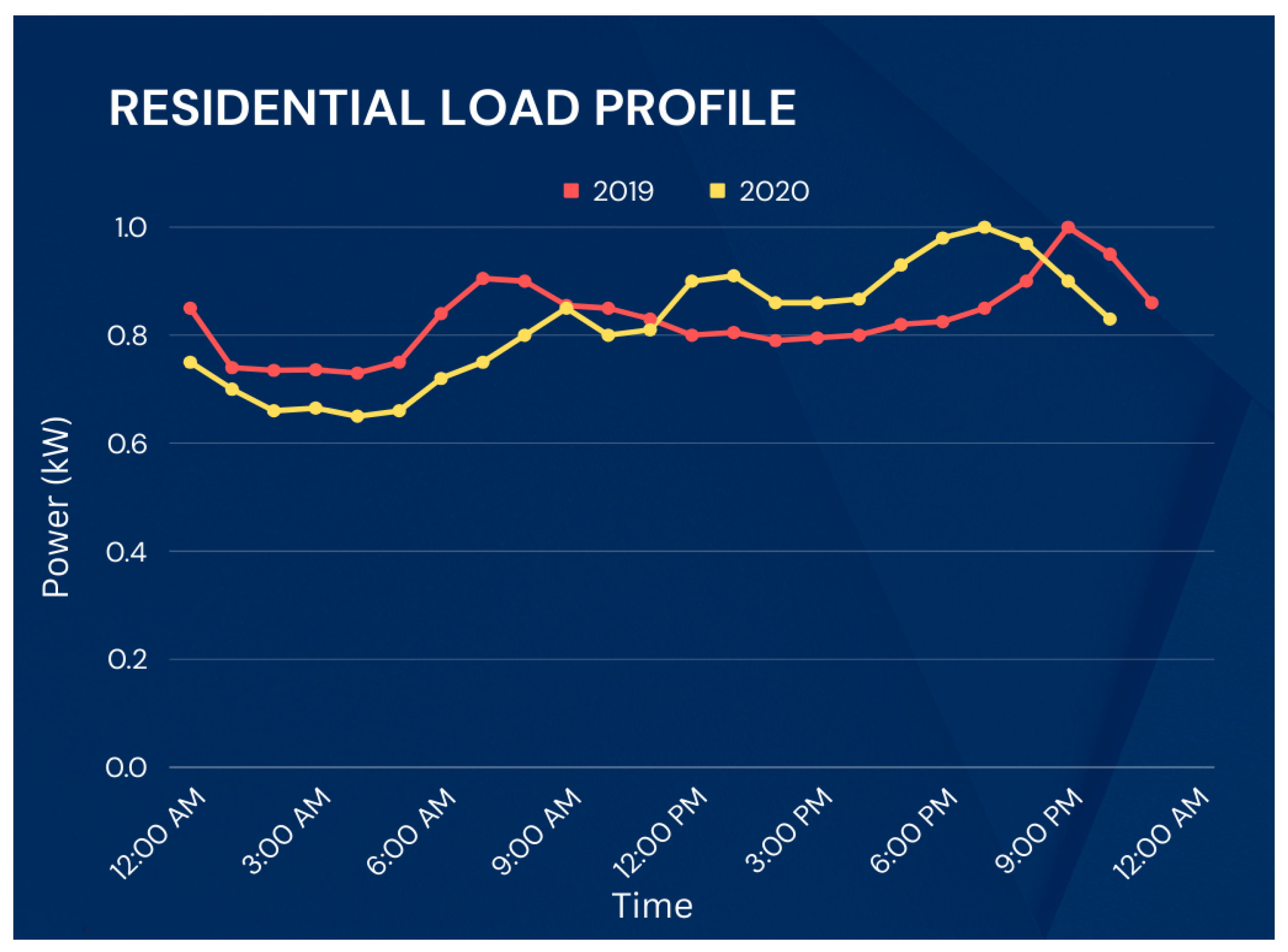
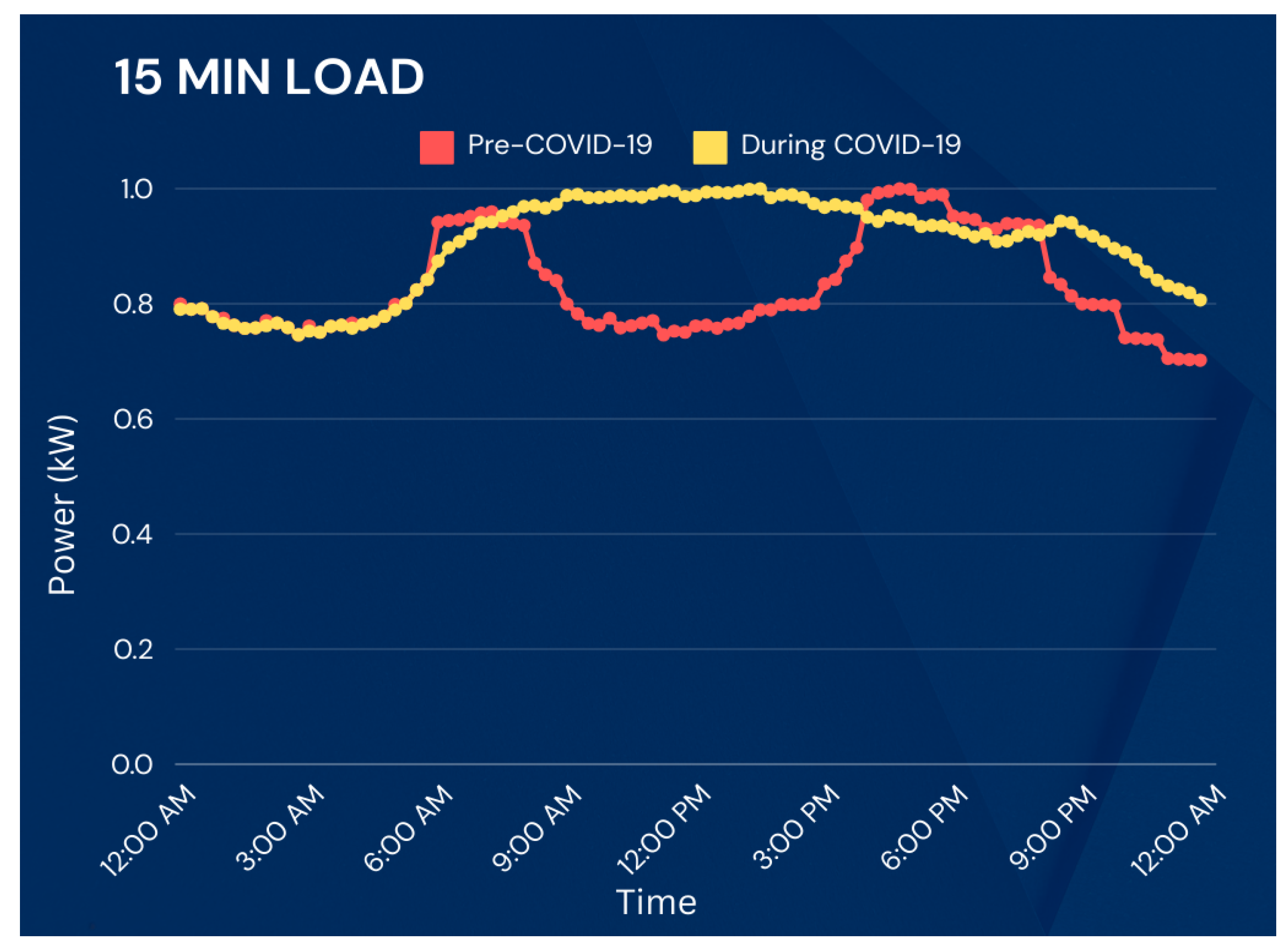
- The consideration of loads during and after COVID-19.
- Cost optimization from a utility perspective.
- A study of a real-life model using supervisory control and data acquisition (SCADA) real-time data.
- The use of a BESS without solar.
2. Literature Review
2.1. Load Changes
2.2. Cost Optimization
3. Methods and Algorithm
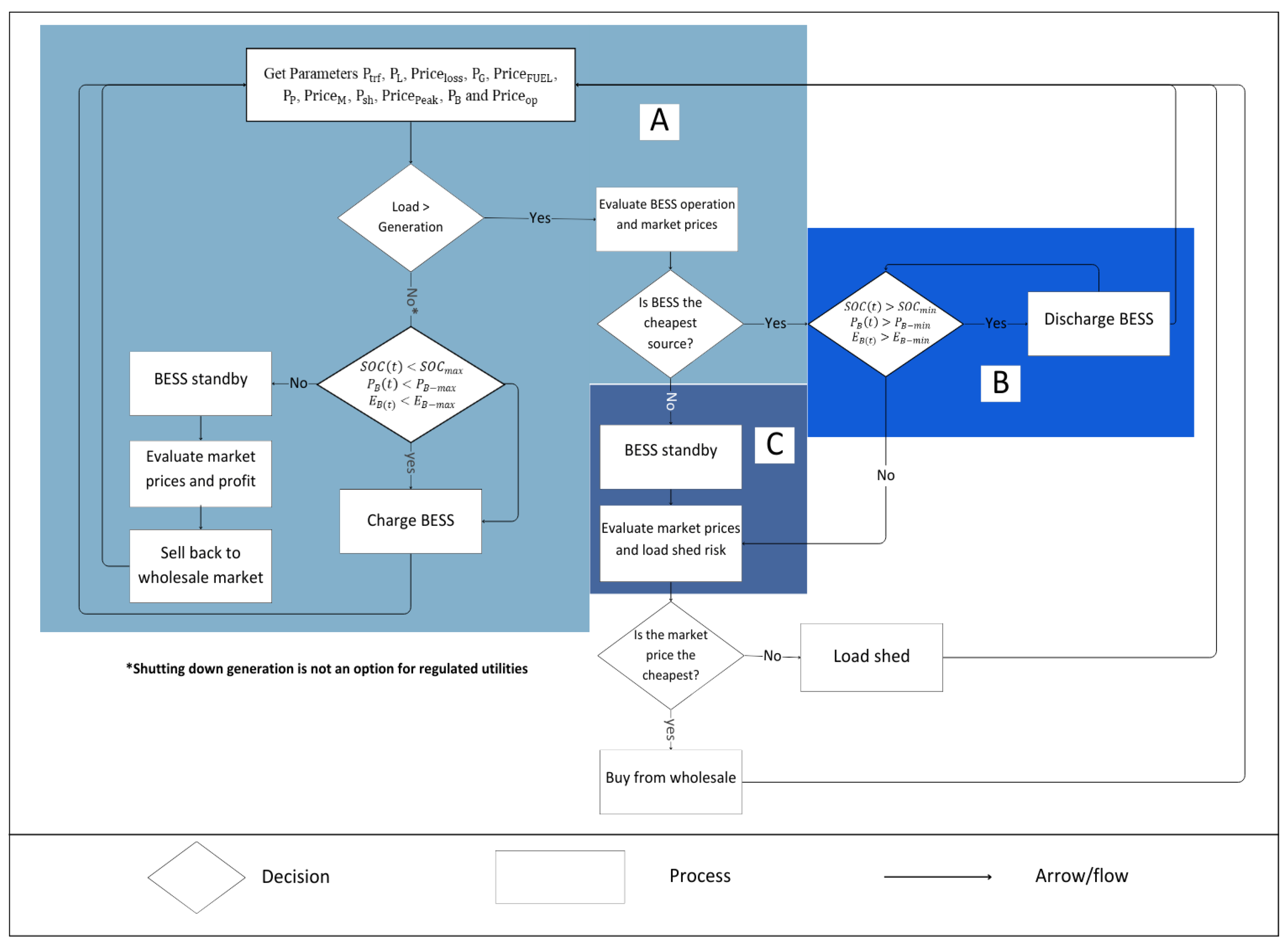
3.1. Method Overview
3.2. Objective Function
- is the cost of the distribution losses;
- is the cost of running utility-owned generation;
- is the cost of the power purchased from the wholesale energy market;
- is the cost of generation at peak times;
- is the battery operation cost;
- is the battery capacity—state of charge;
- and are the weights assigned based on their relative importance.
- is the power purchased from the wholesale market;
- is the market prices;
- is the generated power;
- is the generation fuel prices;
- is the peak loads;
- is the peak prices;
- is the transformer losses;
- is the line losses;
- is the losses cost;
- is the BESS power;
- is the BESS operation cost;
- is the BESS capacity—depth of discharge;
- As shown in Figure 3, the inputs to the optimization problem are time-variant transformer power losses, line losses, generation outputs, generation–fuel curves, power purchased from the wholesale market, power generated during the peak time, and new load profiles that reflect the COVID-19 load changes gathered from a SCADA real-time system, in addition to wholesale market prices and peak prices that are collected from the wholesale market. All the inputs are collected every 15 mins and every hour.
- The outputs are the power purchased from the wholesale market, the power purchased during peak hours, and the battery output power. The optimization problem is a linear constrained problem that is solved using a MILP algorithm.
- The electricity prices comprise four main components: (1) wholesale market cost , (2) generation fuel cost , (3) losses cost , and (4) BESS operation cost .
- The cost function will not consider the cost of transmission losses because they are almost negligible compared with the distribution losses.
3.3. Objective Function Constraints
- Load balance: Maintaining the load balance is crucial to ensure the optimal performance and availability of a system.where
- is the total load demand;
- is the total system losses;
- is the total system generation;
- is the total BESS power.
- Battery constraints: Battery constraints are added to ensure that batteries operate within their normal limits.where
- is the minimum BESS output power;
- is the maximum BESS output power;
- is the minimum BESS capacity;
- is the maximum BESS capacity;
- is the BESS capacity at time = t.
- State of charge and depth of discharge: To extend the lifetime of the battery, it is essential that it not be fully charged or discharged at any time. For this reason, the SOC and DoD are considered to be between 20% and 80%.where
- is the minimum state of charge;
- is the maximum state of charge;
- is the state of charge at time = t;
- is the minimum depth of discharge;
- is the maximum depth of discharge;
- is the depth of discharge at time = t.
- Charging rate: To avoid any thermal safety hazards, batteries need to charge and discharge according to their charge rate.where
- is the discharge rate;
- is the BESS-rated discharge rate;
- is the charge rate;
- is the BESS-rated charge rate.
3.4. Summary of Proposed Approach
- The value of the power purchased from the wholesale market,
- The value of the power purchased during peak hours,
- The battery output power,
- The battery mode of operation (charge, discharge, or standby); it is based on the sign of the battery output power , a negative value being discharge while a positive value is charge and zero is standby.
4. Case Study
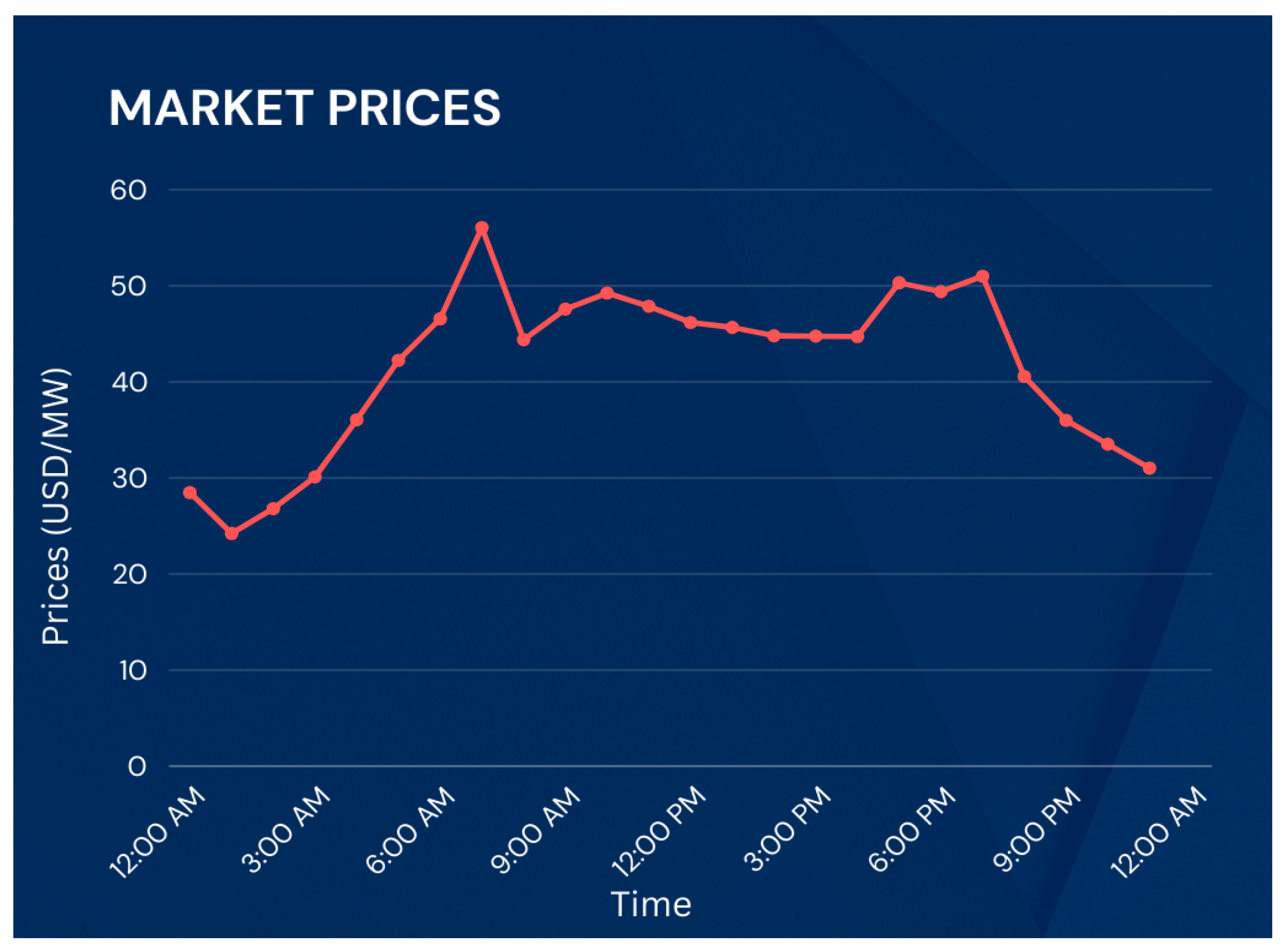
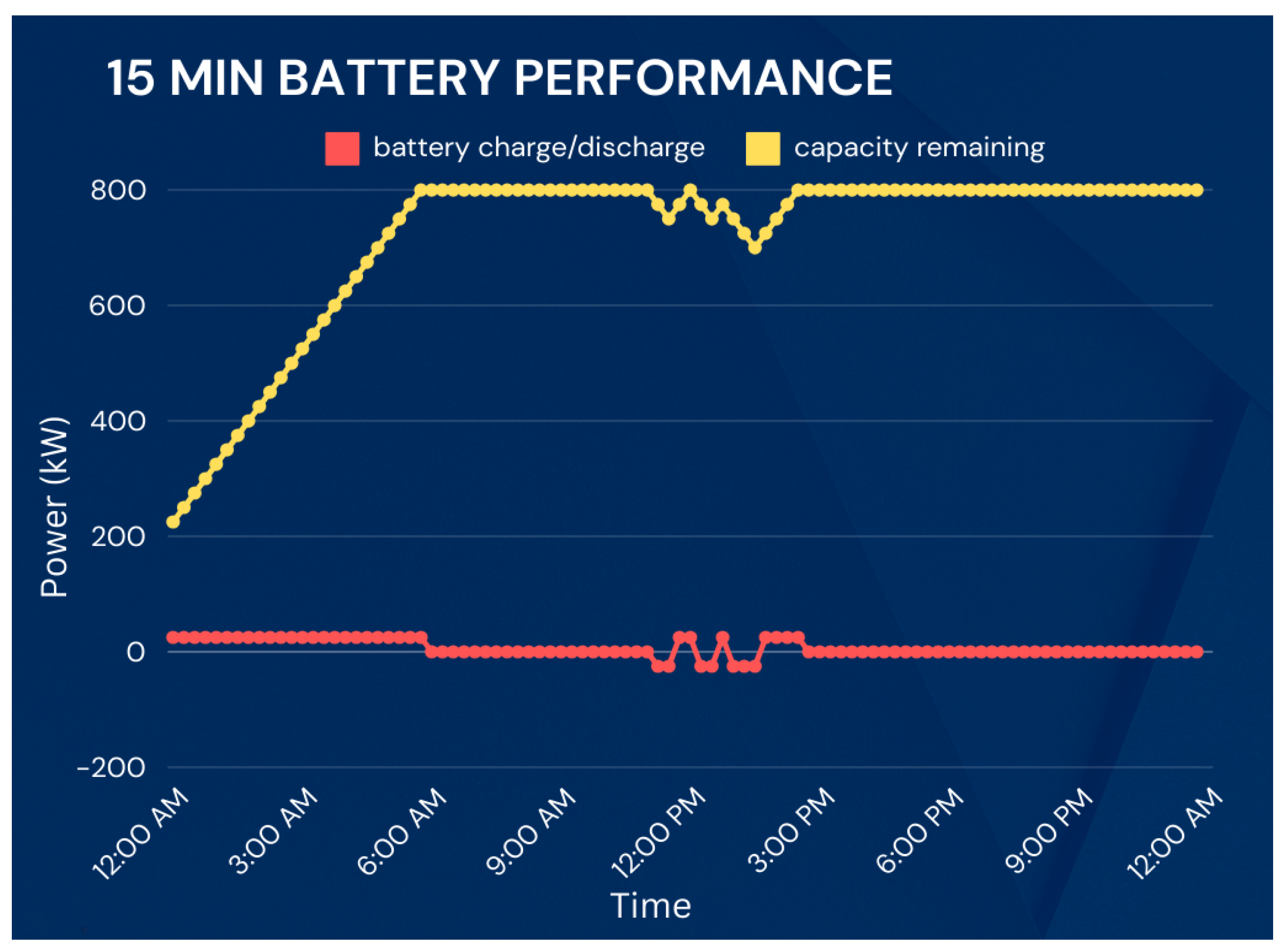
4.1. Case Study 1: DTE Energy 315-Bus System, 15 minutes Intervals
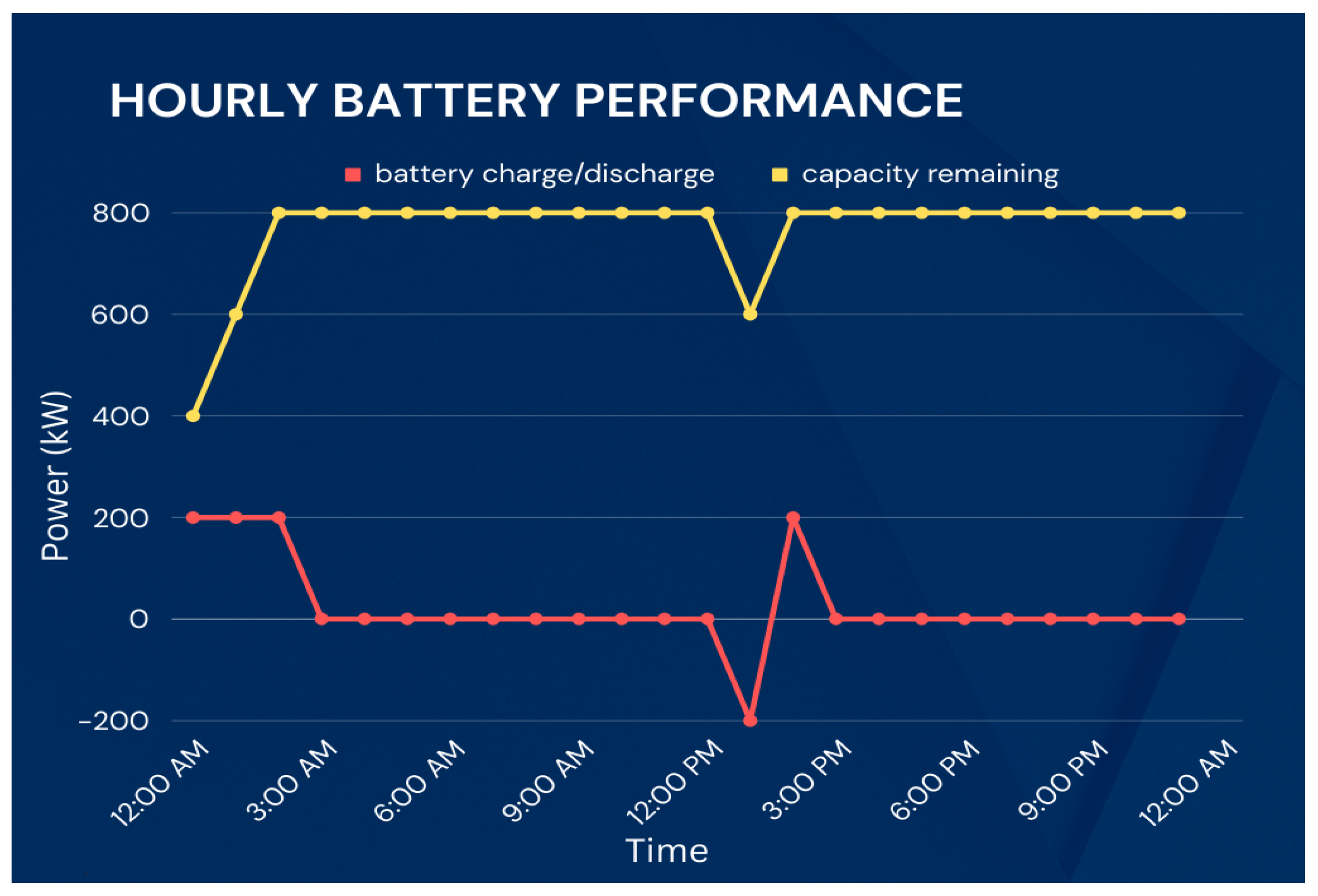
4.2. Case Study 2: DTE Energy 315-Bus System, 1 h Intervals
4.3. Case Study 3: DTE Energy 315-Bus System, without BESS
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, P.; Fan, Y.; Klemeš, J. Impacts of COVID-19 on Energy Demand and Consumption: Challenges, Lessons and Emerging Opportunities. Appl. Energy 2021, 285, 116441. [Google Scholar] [CrossRef] [PubMed]
- Karami, H.; Sanjari, M.; Hosseinian, S.H.; Gharehpetian, G.B. An Optimal Dispatch Algorithm for Managing Residential Distributed Energy Resources. IEEE Trans. Smart Grid 2014, 5, 2360–2367. [Google Scholar] [CrossRef]
- Vahidinasab, V. Optimal distributed energy resources planning in a competitive electricity market: Multiobjective optimization and probabilistic design. Renew. Energy 2014, 66, 354–363. [Google Scholar] [CrossRef]
- Olivieri, Z.; McConky, K. Optimization of Residential Battery Energy Storage System Scheduling for Cost and Emissions Reductions. Energy Build. 2020, 210, 109787. [Google Scholar] [CrossRef]
- Symeonidou, M.M.; Zioga, C.; Papadopoulos, A.M. Life cycle cost optimization analysis of battery storage system for residential photovoltaic panels. J. Clean. Prod. 2021, 309, 127234. [Google Scholar] [CrossRef]
- Roldán-Blay, C.; Escrivá, G.; Roldán-Porta, C.; Alvarez, C. An optimisation algorithm for distributed energy resources management in micro-scale energy hubs. Energy 2017, 132, 126–135. [Google Scholar] [CrossRef]
- Tooryan, F.; Hassanzadehfard, H.; Collins, E.; Jin, S.; Ramezani, B. Optimization and energy management of distributed energy resources for a hybrid residential microgrid. J. Energy Storage 2020, 30, 101556. [Google Scholar] [CrossRef]
- Elkhattam, W.; Hegazy, Y.; Salama, M. An Integrated Distributed Generation Optimization Model for Distribution System Planning. IEEE Trans. Power Syst. 2005, 20, 1158–1165. [Google Scholar] [CrossRef]
- Koller, M.; Borsche, T.; Ulbig, A.; Andersson, G. Defining a degradation cost function for optimal control of a battery energy storage system. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Setlhaolo, D.; Xia, X. Optimal scheduling of household appliances with a battery storage system and coordination. Energy Build. 2015, 94, 61–70. [Google Scholar] [CrossRef]
- Gallo, P.; Guerrero, J.M.; Musca, R.; Riva Sanseverino, E.; Vasquez Quintero, J.C.; Zizzo, G. Effects of COVID-19 pandemic on the Italian power system and possible countermeasures. Electr. Power Syst. Res. 2021, 201, 107514. [Google Scholar] [CrossRef]
- Leadbetter, J.; Swan, L. Battery storage system for residential electricity peak demand shaving. Energy Build. 2012, 55, 685–692. [Google Scholar] [CrossRef]
- Qarnain, S.S.; Muthuvel, S.; Bathrinath, S. Review on government action plans to reduce energy consumption in buildings amid COVID-19 pandemic outbreak. Mater. Today Proc. 2021, 45, 1264–1268. [Google Scholar] [CrossRef]
- Bahmanyar, A.; Estebsari, A.; Ernst, D. The impact of different COVID-19 containment measures on electricity consumption in Europe. Energy Res. Soc. Sci. 2020, 68, 101683. [Google Scholar] [CrossRef] [PubMed]
- Krarti, M.; Aldubyan, M. Review analysis of COVID-19 impact on electricity demand for residential buildings. Renew. Sustain. Energy Rev. 2021, 143, 110888. [Google Scholar] [CrossRef]
- Madurai Elavarasan, R.; Shafiullah, G.; Raju, K.; Mudgal, V.; Arif, M.; Jamal, T.; Subramanian, S.; Balaguru, V.; Reddy, S.; Subramaniam, U. COVID-19: Impact Analysis and Recommendations for Power Sector Operation. Appl. Energy 2020, 279, 115739. [Google Scholar] [CrossRef]
- Abdeen, A.; Kharvari, F.; Gunay, B. The Impact of the COVID-19 on households’ hourly electricity consumption in Canada. Energy Build. 2021, 250, 111280. [Google Scholar] [CrossRef]
- Mishra, P.; Latif, A.; Emmanuel, M.; Shi, Y.; McKenna, K.; Smith, K.; Nagarajan, A. Analysis of degradation in residential battery energy storage systems for rate-based use-cases. Appl. Energy 2020, 264, 114632. [Google Scholar] [CrossRef]
- Kleissl, J.; Nottrott, A.; Washom, B. Energy dispatch schedule optimization and cost benefit analysis for grid-connected, photovoltaic-battery storage systems. Renew. Energy 2013, 55, 230–240. [Google Scholar] [CrossRef]
- Basak, P.; Chowdhury, S.; Dey, S.; Chowdhury, S. A literature review on integration of distributed energy resources in the perspective of control, protection and stability of microgrid. Renew. Sustain. Energy Rev. 2012, 16, 5545–5556. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhao, J.; Song, Y.; Luo, F.; Meng, K.; Qiu, J.; Hill, D. Optimal Operation of Battery Energy Storage System Considering Distribution System Uncertainty. IEEE Trans. Sustain. Energy 2018, 9, 1051–1060. [Google Scholar] [CrossRef]
- Li, L.; Mu, H.; Li, N.; Li, M. Economic and environmental optimization for distributed energy resource systems coupled with district energy networks. Energy 2016, 109, 947–960. [Google Scholar] [CrossRef]
- Wang, T.; O’Neill, D.; Kamath, H. Dynamic Control and Optimization of Distributed Energy Resources in a Microgrid. IEEE Trans. Smart Grid 2014, 6, 2884–2894. [Google Scholar] [CrossRef]
- Comello, S.; Reichelstein, S. The emergence of cost effective battery storage. Nat. Commun. 2019, 10, 2038. [Google Scholar] [CrossRef] [PubMed]
- Barzkar, A.; Hosseini, S. A novel peak load shaving algorithm via real-time battery scheduling for residential distributed energy storage systems. Int. J. Energy Res. 2018, 42, 2400–2416. [Google Scholar] [CrossRef]
- Kashem, M.; Le, A.; Negnevitsky, M.; Ledwich, G. Distributed generation for minimization of power losses in distribution systems. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 8. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, Y.; Dong, Z. Probability-Weighted Robust Optimization for Distributed Generation Planning in Microgrids. IEEE Trans. Power Syst. 2018, 33, 7042–7051. [Google Scholar] [CrossRef]
- Atwa, Y.; El-Saadany, E.; Salama, M.; Seethapathy, R. Optimal Renewable Resources Mix for Distribution System Energy Loss Minimization. IEEE Trans. Power Syst. 2010, 25, 360–370. [Google Scholar] [CrossRef]
- Chouhan, S.; Tiwari, D.; Inan, H.; Solanki, S.; Feliachi, A. DER optimization to determine optimum BESS charge/discharge schedule using Linear Programming. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Rahimi, A.; Zarghami, M.; Vaziri, M.; Vadhva, S. A simple and effective approach for peak load shaving using battery storage systems. In Proceedings of the North American Power Symposium (NAPS), Manhattan, KS, USA, 22–24 September 2013; pp. 1–5. [Google Scholar]
- Hung, D.; Nadarajah, M.; Bansal, R. Analytical Strategies for Renewable Distributed Generation Integration Considering Energy Loss Minimization. Appl. Energy 2013, 105, 75–85. [Google Scholar] [CrossRef]
- Abdmouleh, Z.; Gastli, A.; Ben-Brahim, L.; Haouari, M.; Al-Emadi, N. Review of optimization techniques applied for the integration of distributed generation from renewable energy sources. Renew. Energy 2017, 113, 266–280. [Google Scholar] [CrossRef]
- Borges, C.; Djalma, F. Impact of distributed generation allocation and sizing on reliability, losses and voltage profile. In Proceedings of the 2003 IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003; Volume 2, p. 5. [Google Scholar] [CrossRef]
- Aman, M.; Jasmon, G.; Mokhlis, H.; Abu Bakar, A.H. Optimal placement and sizing of a DG based on a new power stability index and line losses. Int. J. Electr. Power Energy Syst. 2012, 43, 1296–1304. [Google Scholar] [CrossRef]
- Ren, H.; Zhou, W.; Nakagami, K.; Gao, W.; Wu, Q. Multi-objective optimization for the operation of distributed energy systems considering economic and environmental aspects. Appl. Energy 2010, 87, 3642–3651. [Google Scholar] [CrossRef]
- Omu, A.; Choudhary, R.; Boies, A. Distributed energy resource system optimisation using mixed integer linear programming. Energy Policy 2013, 61, 249–266. [Google Scholar] [CrossRef]
- Di Somma, M.; Yan, B.; Bianco, N.; Graditi, G.; Luh, P.; Mongibello, L.; Naso, V. Operation optimization of a distributed energy system considering energy costs and exergy efficiency. Energy Convers. Manag. 2015, 103, 739–751. [Google Scholar] [CrossRef]
- Hannan, M.A.; Wali, S.; Ker, P.J.; Abd Rahman, M.; Mansor, M.; Ramachandaramurthy, V.K.; Muttaqi, K.; Mahlia, T.M.I.; Dong, Z. Battery energy-storage system: A review of technologies, optimization objectives, constraints, approaches, and outstanding issues. J. Energy Storage 2021, 42, 103023. [Google Scholar] [CrossRef]
- Di Somma, M.; Yan, B.; Bianco, N.; Graditi, G.; Luh, P.; Mongibello, L. Multi-objective design optimization of distributed energy systems through cost and exergy assessments. Appl. Energy 2017, 204, 1299–1316. [Google Scholar] [CrossRef]
- Ahmadi, B.; Ceylan, O.; Ozdemir, A. A multi-objective optimization evaluation framework for integration of distributed energy resources. J. Energy Storage 2021, 41, 103005. [Google Scholar] [CrossRef]
- Jayasekera, N.; Masoum, M.; Wolfs, P. Optimal Operation of Distributed Energy Storage Systems to Improve Distribution Network Load and Generation Hosting Capability. IEEE Trans. Sustain. Energy 2015, 7, 250–261. [Google Scholar] [CrossRef]
- Arcos-Vargas, A.; Lugo-Laguna, D.; Núñez, F. Residential Peak Electricity Management. A storage and control systems application taking advantages of smart meters. Int. J. Electr. Power Energy Syst. 2018, 102, 110–121. [Google Scholar] [CrossRef]
- Nizami, M.; Hossain, M.; Mahmud, K.; Ravishankar, J. Energy Cost Optimization and DER Scheduling for Unified Energy Management System of Residential Neighborhood. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC / I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Bhamidi, L.; Sivasubramani, S. Multi-objective home energy management with battery energy storage systems. Sustain. Cities Soc. 2019, 47, 101458. [Google Scholar] [CrossRef]
- Delfino, F.; Ferro, G.; Parodi, L.; Robba, M.; Rossi, M.; Caliano, M.; Di Somma, M.; Graditi, G. A multi-objective Energy Management System for microgrids: Minimization of costs, exergy in input, and emissions. In Proceedings of the 2021 International Conference on Smart Energy Systems and Technologies (SEST), Vaasa, Finland, 6–8 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- MISO. Available online: https://www.misoenergy.org/markets-and-operations/real-time--market-data/market-reports/ (accessed on 22 November 2022).



| Ref. | Year | Focused Topics | Research Gaps | Optimization Method | DER Composition |
|---|---|---|---|---|---|
| [35] | 2010 | To minimize energy cost and environmental impact, considering electricity buyback, carbon tax, and fuel-switching biogas. | Research is not specific to BESS specifically; it studies DERs in general. DER operation cost and pay back period were not considered. | multi-objective linear programming (MOLP) | PV, fuel cell |
| [36] | 2013 | Find the optimal unit size, location, and distribution network structure while minimizing annual investment and operating cost. In addition to analyzing the economic and environmental impacts of DERs compared to traditional generation. | Very minimal constraints were considered in the algorithm and the paper is focused on multiple DERs not limited to BESS. | MILP | solar thermal, PV, heat pumps, wind turbines (WTs) |
| [37] | 2015 | To minimize a weighted sum of the total energy cost and total primary exergy input. | Losses were not considered. | MILP with Pareto frontiers | biomass boiler, solar thermal plant, Combined Cooling Heating and Power (CCHP), reversible heat pump, thermal BESS |
| [39] | 2017 | To determine the types, numbers, and sizes of energy devices to reduce annual cost and increase the overall exergy efficiency combining heat and PV using MOLP. | Considered all DERs the same. This research did not consider different DERs’ constraints. | MOLP | PV |
| [41] | 2015 | To minimize distribution system loss and battery cycle loss. BESS is investigated for three main services options: (1) voltage regulation; (2) loss reduction; and (3) peak reduction. | Rates of charge and discharge were not considered, which could cause a safety hazard. | MOLP | PV, BESS |
| [42] | 2018 | To minimize customer bill and battery degradation cost. | BESS constraints were not included as part of the study and focused on customer’s benefits. | not identified | thermal storage, compressed air, chemical batteries |
| [21] | 2018 | To minimize the customer’s energy cost while reducing aggregated demand peaks by optimally scheduling residential storage units. | Losses were not taken into consideration. | MOLP | PV, BESS, Electric Vehicle (EV) |
| [43] | 2018 | To minimize the real-time energy gap and battery operation cost where power loss reduction is implied using particle swarm optimization. | For constraints, only BESS power and SOC were considered. | non-linear mixed- integer programming | WT, PV, BESS |
| [44] | 2019 | To minimize total energy bill and total system peak load demand using mixed- integer linear programming, which is then converted to a linear combination by weighted sum. | Losses were not considered as part of the objective function. | MOLP | BESS, time-shiftable residential appliances |
| [29] | 2016 | To minimize total energy cost by making sure that at each hour the cheapest available generation is dispatched to meet system load using linear programming. | System losses were not included in the study. | MILP | BESS, PV |
| [7] | 2020 | To minimize the total cost of DERs, reduce environmental emission, and increase penetration level using particle swarm optimization. | Multiple DERs were considered in the study. System losses were not included. | particle swarm optimization | WT, PV, BESS |
| [4] | 2020 | Reduce the CO2 emission, increase the penetration of RES, and minimize the total cost of the MG. | Losses were not included as part of the study. | MOLP | BESS, PV |
| [40] | 2021 | A new formulation for optimal allocation and sizing of DERs and energy storage systems (ESSs) to improve voltage profile and minimize annual costs using a multi-objective multiverse optimization method (MOMVO). | Very limited ESS constraints also considering distributed generation in the study. | multi-objective multiverse optimization method | WT PV, BESS |
| [45] | 2021 | To minimize the cost and emissions and maximize the overall exergy efficiency of the system. | Minimal constraints were considered in the study. | MOLP | BESS, PV |
| [38] | 2021 | To provide a comprehensive review of BESS concerning optimal sizing, system constraints, and various optimization models and their advantages and weakness. | Research review included very basic BESS constraints, such as capacity and state of charge. | MOLP | PV, WT, BESS |
| Device | Count |
|---|---|
| Circuit breaker | 1 |
| Cable | 40 |
| Fuse | 28 |
| Overhead by phase | 579 |
| Recloser | 1 |
| Regulator by phase | 5 |
| Capacitor | 2 |
| Load | 272 |
| Transformers | 273 |
| BESS | 100 |
| Bus | 315 |
| Specification | Quality |
|---|---|
| Usable capacity | 27 kWh |
| Depth of discharge | 100% |
| Efficiency | 81.6% |
| Continuous power | 10 kW |
| Chemistry | Lithium iron phosphate |
| Without BESS | With BESS | |
|---|---|---|
| Losses | 21% | 8% |
| Total losses cost | USD767 | USD290 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hijazi, Z.; Hong, J. Optimal Operation of Residential Battery Energy Storage Systems under COVID-19 Load Changes. Energies 2024, 17, 1420. https://doi.org/10.3390/en17061420
Hijazi Z, Hong J. Optimal Operation of Residential Battery Energy Storage Systems under COVID-19 Load Changes. Energies. 2024; 17(6):1420. https://doi.org/10.3390/en17061420
Chicago/Turabian StyleHijazi, Zahraa, and Junho Hong. 2024. "Optimal Operation of Residential Battery Energy Storage Systems under COVID-19 Load Changes" Energies 17, no. 6: 1420. https://doi.org/10.3390/en17061420
APA StyleHijazi, Z., & Hong, J. (2024). Optimal Operation of Residential Battery Energy Storage Systems under COVID-19 Load Changes. Energies, 17(6), 1420. https://doi.org/10.3390/en17061420







