Numerical Simulation Study on the Influence of Cracks in a Full-Size Core on the Resistivity Measurement Response
Abstract
1. Introduction
2. Methods and Principles
2.1. Fundamentals of Finite Element Theory
2.2. The Basic Equation of a Stable Current Field
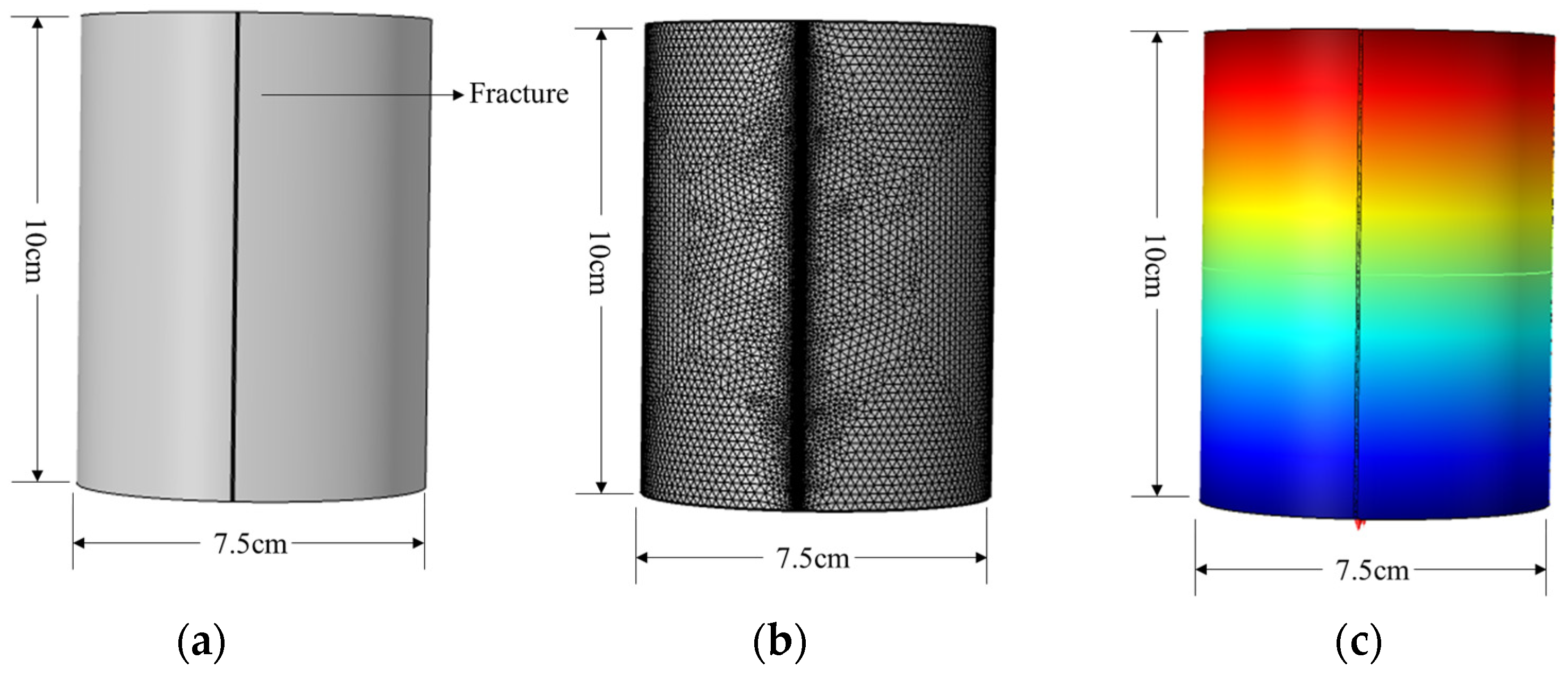
2.3. Simulation Principle and Model Construction of Core Resistivity Response
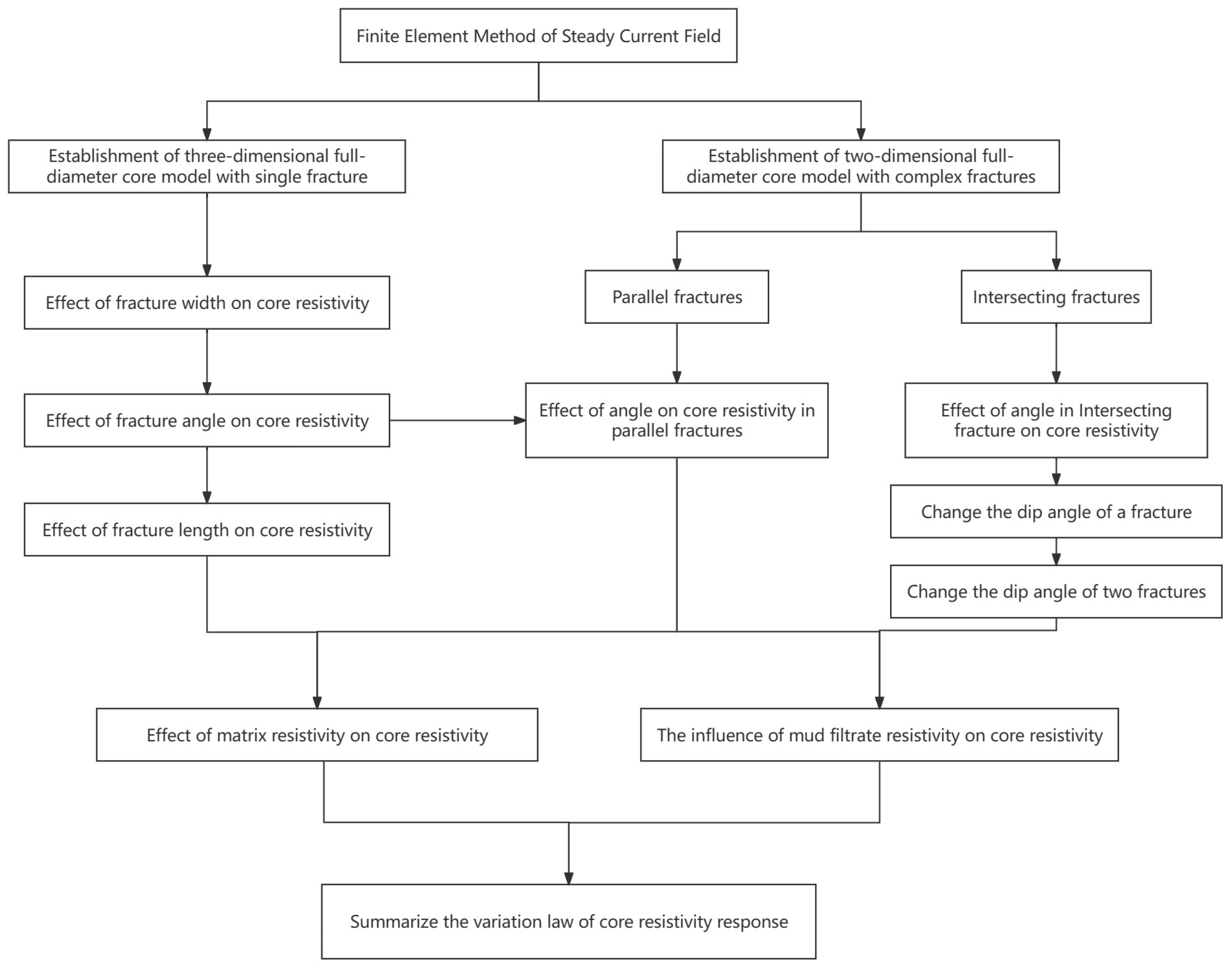
3. Results
3.1. The Resistivity Response Mechanism of a Single-Fracture Model
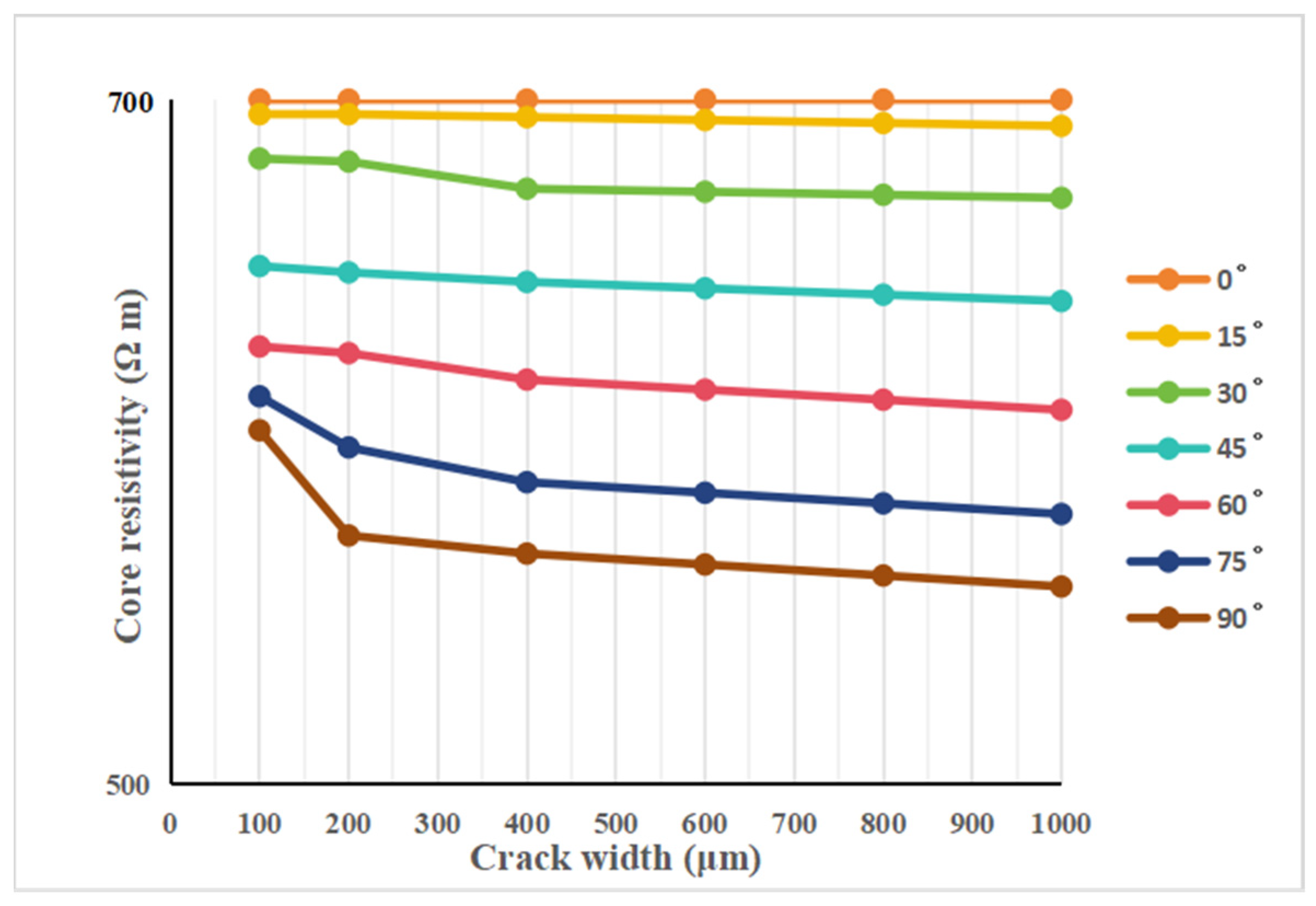
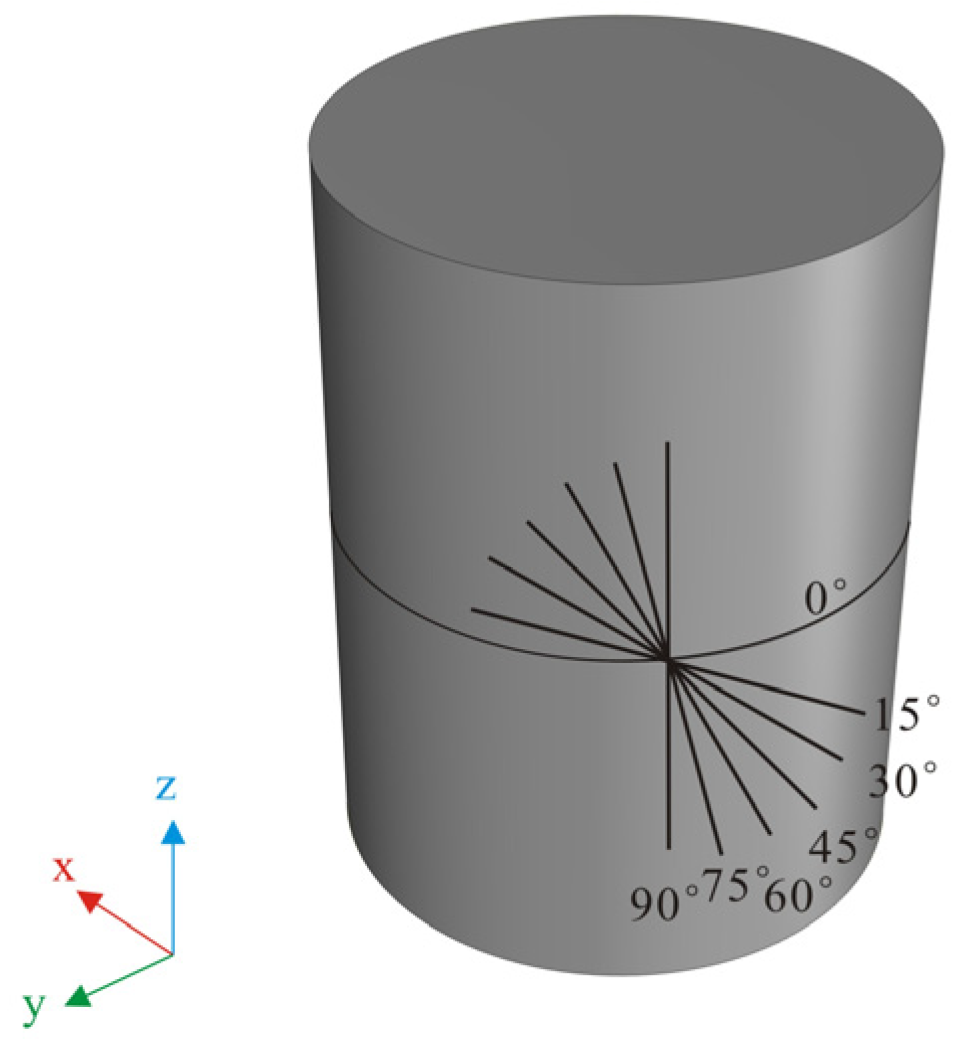
3.1.1. Core Resistivity Response Characteristics of Different Fracture Widths and Angles
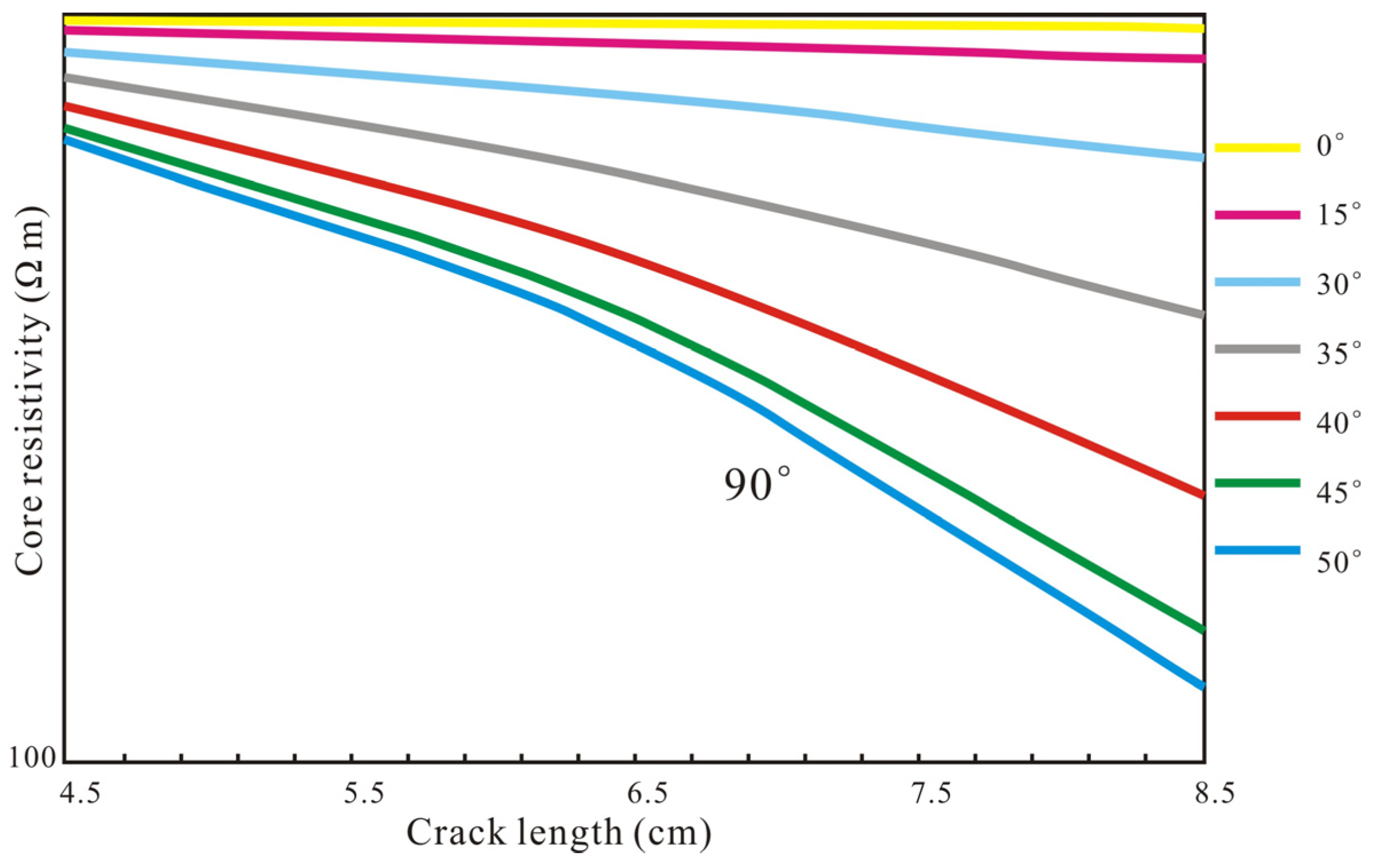
3.1.2. Core Resistivity Response Characteristics of Fracture Length
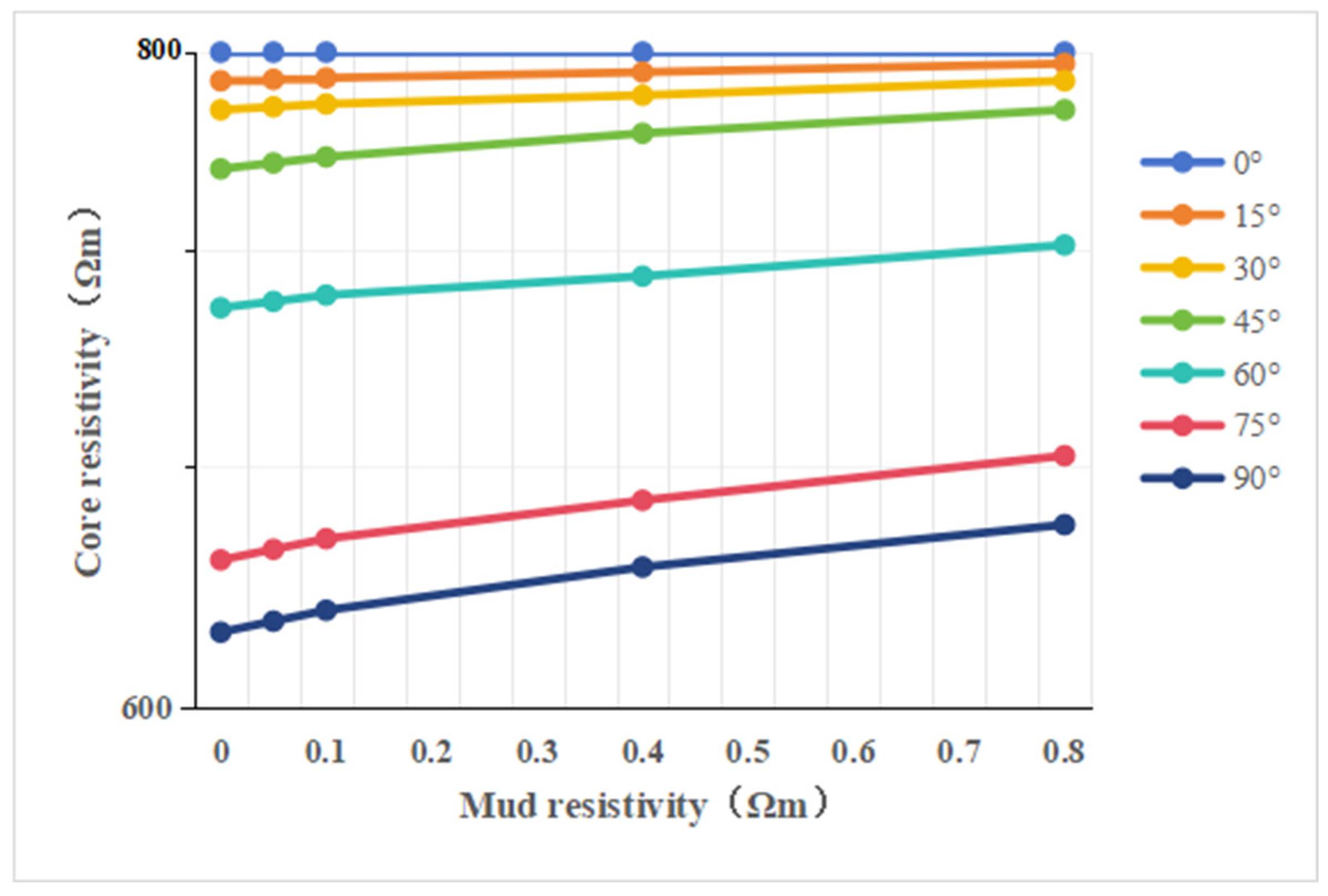
3.1.3. Core Resistivity Response Characteristics of Mud Resistivity
3.2. Resistivity Response Mechanism of Complex Fracture Model
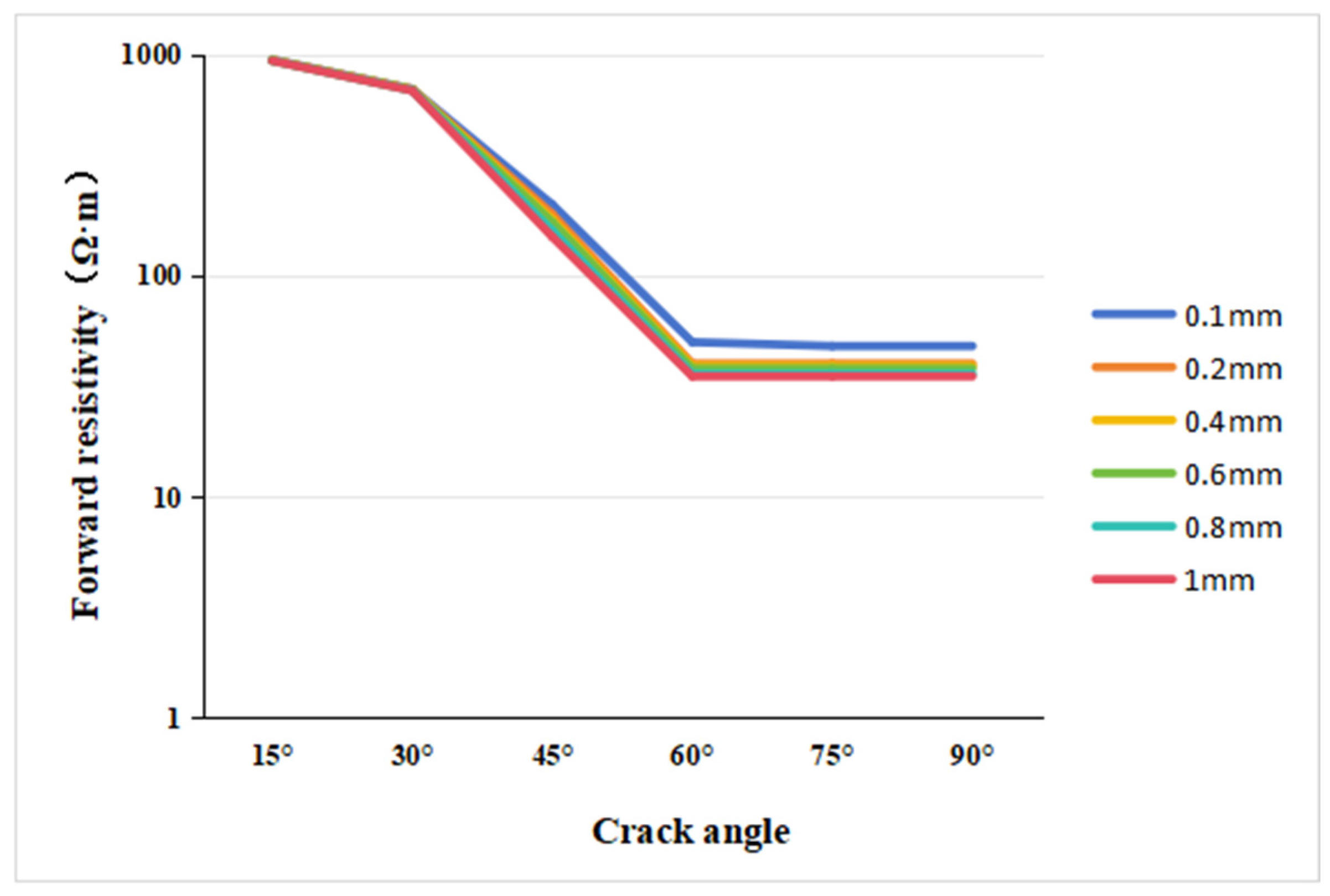
3.2.1. Core Resistivity Response Characteristics of Parallel Fractures
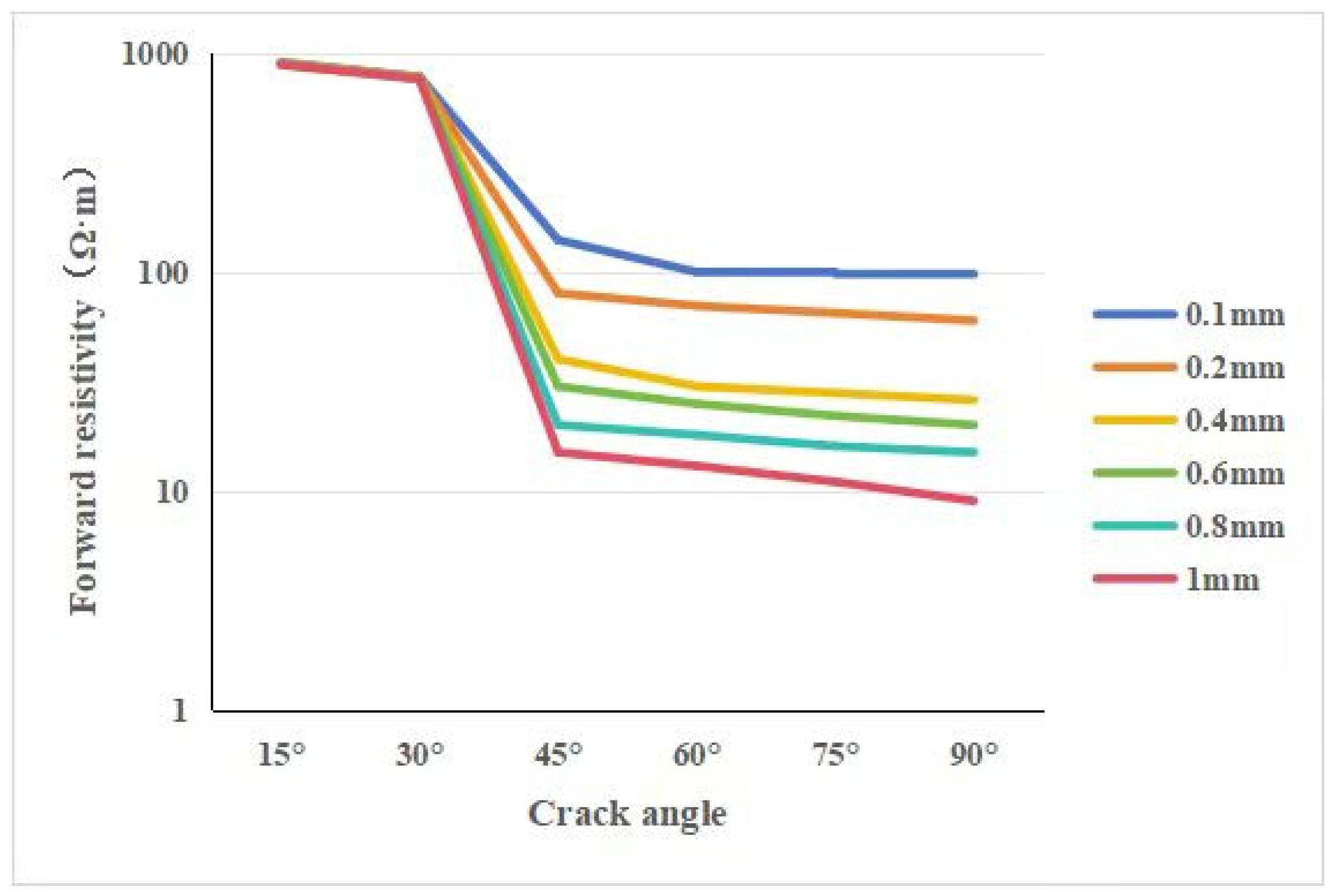
3.2.2. Core Resistivity Response Characteristics of Intersecting Fractures
4. Discussion
4.1. The Difference between Core Resistivity and Logging Resistivity
4.2. The Core Resistivity Response of The Cross Fracture Is Affected by the Background Value of the Matrix and the Resistivity of the Mud
4.3. The Contribution of This Study and the Limitations of the Research
5. Recommendations
- For fractured reservoirs, especially igneous reservoirs, imaging logging is necessary because when the fractures are crossed and irregular, using the resistivity method to determine the fracture occurrence is unreliable, and there are multiple solutions. At this time, imaging logging can be used to solve the fracture parameters finely, which provides more reliable data support for the subsequent calculation of permeability and saturation.
- The discussion part of Reference [6] reveals the influence of the invasion phenomenon on resistivity measurement, and the fractured reservoir is more obviously affected by the invasion. In order to ensure the reliability of resistivity logging response value, the interval between drilling time and logging time should be shortened as much as possible.
- The calculation of permeability can be corrected by referring to the angle of fracture, and the permeability model can be corrected according to the actual working area and the research results of this study, which can improve the reliability of reservoir evaluation.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, M.W.; Collett, T.S. Gas hydrate saturations estimated from fractured reservoir at Site NGHP-01-10, Krishna-Godavari Basin, India. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Lai, J.; Wang, G. Fractal analysis of tight gas sandstones using high-pressure mercury intrusion techniques. J. Nat. Gas Sci. Eng. 2015, 24, 185–196. [Google Scholar] [CrossRef]
- Li, P.; Zheng, M.; Bi, H.; Wu, S.; Wang, X. Pore throat structure and fractal characteristics of tight oil sandstone: A case study in the Ordos Basin, China. J. Pet. Sci. Eng. 2017, 149, 665–674. [Google Scholar] [CrossRef]
- Cai, J.; Wei, W.; Hu, X.; Wood, D.A. Electrical conductivity models in saturated porous media: A review. Earth-Sci. Rev. 2017, 171, 419–433. [Google Scholar] [CrossRef]
- Wang, G.; Carr, T.R. Organic-rich Marcellus Shale lithofacies modeling and distribution pattern analysis in the Appalachian Basin. AAPG Bull. 2013, 97, 2173–2205. [Google Scholar] [CrossRef]
- Zhao, Q.; Guo, J.; Zhang, Z. A method for judging the effectiveness of complex tight gas reservoirs based on geophysical logging data and using the L block of the Ordos Basin as a case study. Processes 2023, 11, 2195. [Google Scholar] [CrossRef]
- Li, M.; Zhang, C. An Improved Method to Accurately Estimate TOC of Shale Reservoirs and Coal-Measures. Energies 2023, 16, 2905. [Google Scholar] [CrossRef]
- Chu, H.; Liao, X.; Chen, Z.; Zhao, X.; Liu, W.; Zou, J. Pressure transient analysis in fractured reservoirs with poorly connected fractures. J. Nat. Gas Sci. Eng. 2019, 67, 30–42. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, J.; Yang, G.; Tao, S.; Ni, C.; Zhang, B.; He, X.; Lin, J.; Huang, D.; Liu, M.; et al. New research progress of Jurassic tight oil in central Sichuan Basin, SW China. Pet. Explor. Dev. Online 2016, 43, 954–964. [Google Scholar] [CrossRef]
- Khoshbakht, F.; Azizzadeh, M.; Memarian, H.; Nourozi, G.H.; Moallemi, S.A. Comparison of electrical image log with core in a fractured carbonate reservoir. J. Pet. Sci. Eng. 2012, 86, 289–296. [Google Scholar] [CrossRef]
- Aghli, G.; Moussavi-Harami, R.; Tokhmechi, B. Integration of sonic and resistivity conventional logs for identification of fracture parameters in the carbonate reservoirs (A case study, Carbonate Asmari Formation, Zagros Basin, SW Iran). J. Pet. Sci. Eng. 2020, 186, 106728. [Google Scholar] [CrossRef]
- Luthi, S.M.; Souhaite, P. Fracture apertures from electrical borehole scans. Geophysics 1990, 55, 821–833. [Google Scholar] [CrossRef]
- Wang, D. Study on Interpretation Method of Micro-Resistivity Imaging Logging in Fractured Reservoir. Ph.D. Thesis, China University of Petroleum, Beijing, China, 2001. [Google Scholar]
- Ke, S.; Sun, G. On quantitative evaluation of fractures by STAR Imager II. Well Logging Technol. 2002, 26, 101–103. [Google Scholar]
- Chen, A. Numerical simulation and analysis of microresistivity imaging tool. Nat. Gas Ind. 2006, 26, 83–85. [Google Scholar]
- Cao, Y. The Numerical Stimulation and Experimental Verification of Electrical Imaging Logging in Fractured Formations. Master’s Thesis, Yangtze University, Jingzhou, China, 2014. [Google Scholar]
- Ponziani, M.; Slob, E.; Luthi, S.; Bloemenkamp, R.; Nir, I.L. Experimental validation of fracture aperture determination from borehole electric microresistivity measurements. Geophysics 2015, 80, 175–181. [Google Scholar] [CrossRef]
- Ammar, A.I. Development of numerical model for simulating resistivity and hydroelectric properties of fractured rock aquifers. J. Appl. Geophys. 2021, 189, 104319. [Google Scholar] [CrossRef]
- Epov, M.I.; Moskaev, I.A.; Nechaev, O.V.; Glinskikh, V.N. Effect of Tilted Uniaxial Electrical Anisotropy Parameters on Signals of Electric and Electromagnetic Logging Soundings according to Results of Numerical Simulation. Russ. Geol. Geophys. 2023, 64, 735–742. [Google Scholar] [CrossRef]
- He, J.; Liu, T.; Wen, L.; He, T.; Li, M.; Li, J.; Wang, L.; Yao, X. Numerical simulation analysis of difference from a radial resistivity testing method for cylindrical cores and a conventional testing method. Mathematics 2022, 10, 2885. [Google Scholar] [CrossRef]
- Tan, M.; Wang, P.; Li, J.; Liu, Q.; Yang, Q. Numerical simulation and fracture evaluation method of dual laterolog in organic shale. J. Appl. Geophys. 2014, 100, 1–13. [Google Scholar] [CrossRef]
- Deng, S.; Li, L.; Li, Z.; He, X.; Fan, Y. Numerical simulation of high-resolution azimuthal resistivity laterolog response in fractured reservoirs. Pet. Sci. 2015, 12, 252–263. [Google Scholar] [CrossRef][Green Version]
- Liu, D.; Ma, Z.; Xing, X.; Li, H.; Guo, Z. Numerical simulation of LWD resistivity response of carbonate formation using self-adaptive hp-FEM. Appl. Geophys. 2013, 10, 97–108. [Google Scholar] [CrossRef]
- Kang, Z.; Li, X.; Ni, W.; Li, F.; Hao, X. Using logging while drilling resistivity imaging data to quantitatively evaluate fracture aperture based on numerical simulation. J. Geophys. Eng. 2021, 18, 317–327. [Google Scholar] [CrossRef]
- Zhao, J.; Sun, J.; Liu, X.; Chen, H.; Cui, L. Numerical simulation of the electrical properties of fractured rock based on digital rock technology. J. Geophys. Eng. 2013, 10, 055009. [Google Scholar] [CrossRef]
- Wang, N.; Li, K.; Sun, J.; Wang, D.; He, X.; Xiang, Z.; Liu, H.; Wang, P. Research on dual lateral log simulation of shale bedding fractures under different influencing conditions. Front. Energy Res. 2023, 11, 1249985. [Google Scholar] [CrossRef]
- Kim, J.; Hong, C.; Kim, J.; Chong, S. Theoretical and Numerical Study on Electrical Resistivity Measurement of Cylindrical Rock Core Samples Using Perimeter Electrodes. Energies 2021, 14, 4382. [Google Scholar] [CrossRef]
- Aghli, G.; Moussavi-Harami, R.; Mohammadian, R. Reservoir heterogeneity and fracture parameter determination using electrical image logs and petrophysical data (a case study, carbonate Asmari Formation, Zagros Basin, SW Iran). Pet. Sci. 2020, 17, 51–69. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre-and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Zhao, X.; Lee, Y.Y.; Liew, K.M. Free vibration analysis of functionally graded plates using the element-free kp-Ritz method. J. Sound Vib. 2009, 319, 918–939. [Google Scholar] [CrossRef]
- Beirão da Veiga, L.; Brezzi, F.; Marini, L.D.; Russo, A. Virtual element method for general second-order elliptic problems on polygonal meshes. Math. Models Methods Appl. Sci. 2016, 26, 729–750. [Google Scholar] [CrossRef]
- Hao, R.; Lu, Z.; Ding, H.; Chen, L. A nonlinear vibration isolator supported on a flexible plate: Analysis and experiment. Nonlinear Dyn. 2022, 108, 941–958. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, Z.; Xiao, H.; Zhang, C.; Zhu, L.; Wang, C. Quantitative interpretation of coal industrial components using a gray system and geophysical logging data: A case study from the Qinshui Basin, China. Front. Earth Sci. 2023, 10, 1031218. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, C.; Zhang, C.; Zhou, X.; Zhang, Z.; Nie, X.; Liu, W.; Zhu, B. Challenges and prospects of digital core-reconstruction research. Geofluids 2019, 2019, 7814180. [Google Scholar] [CrossRef]






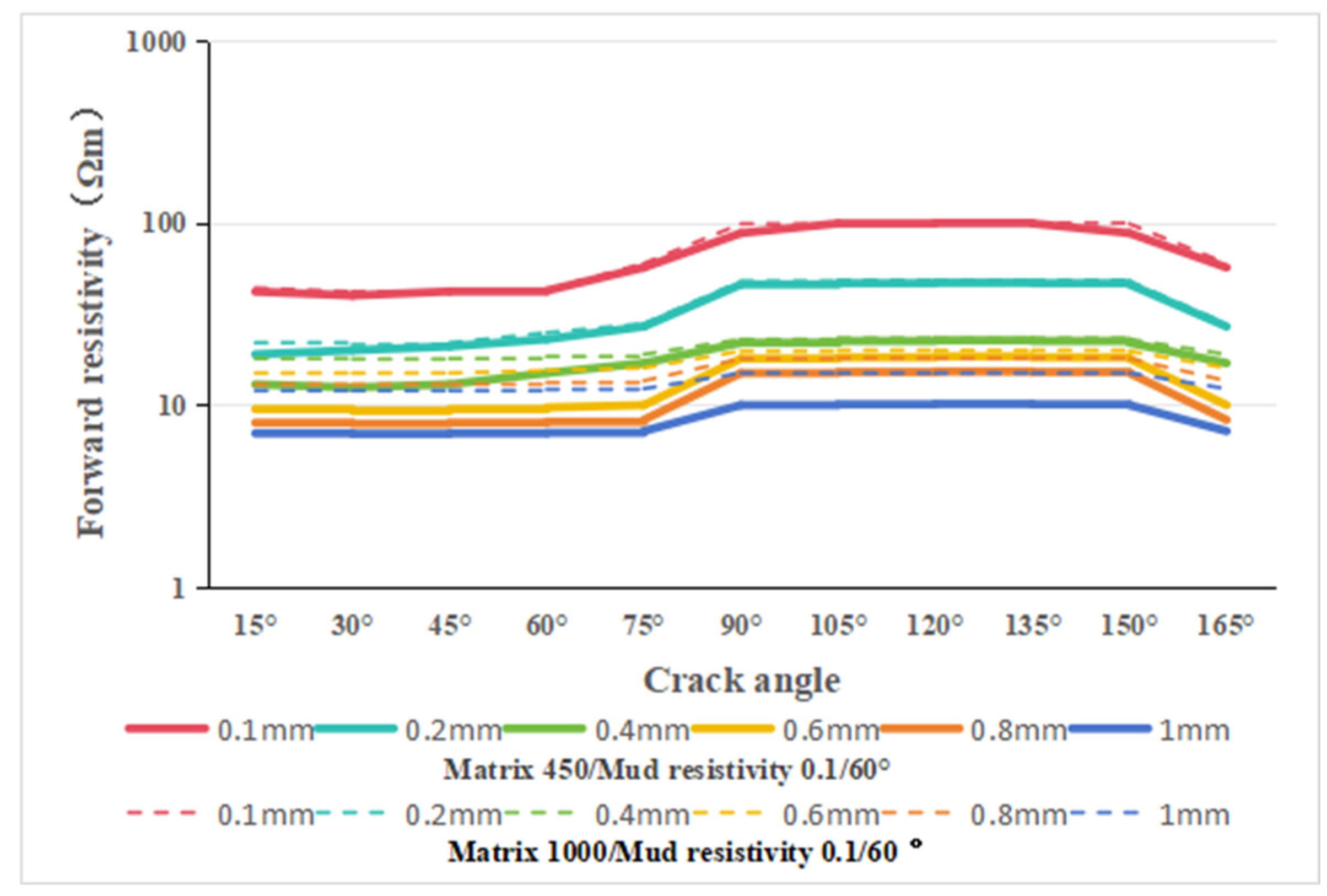
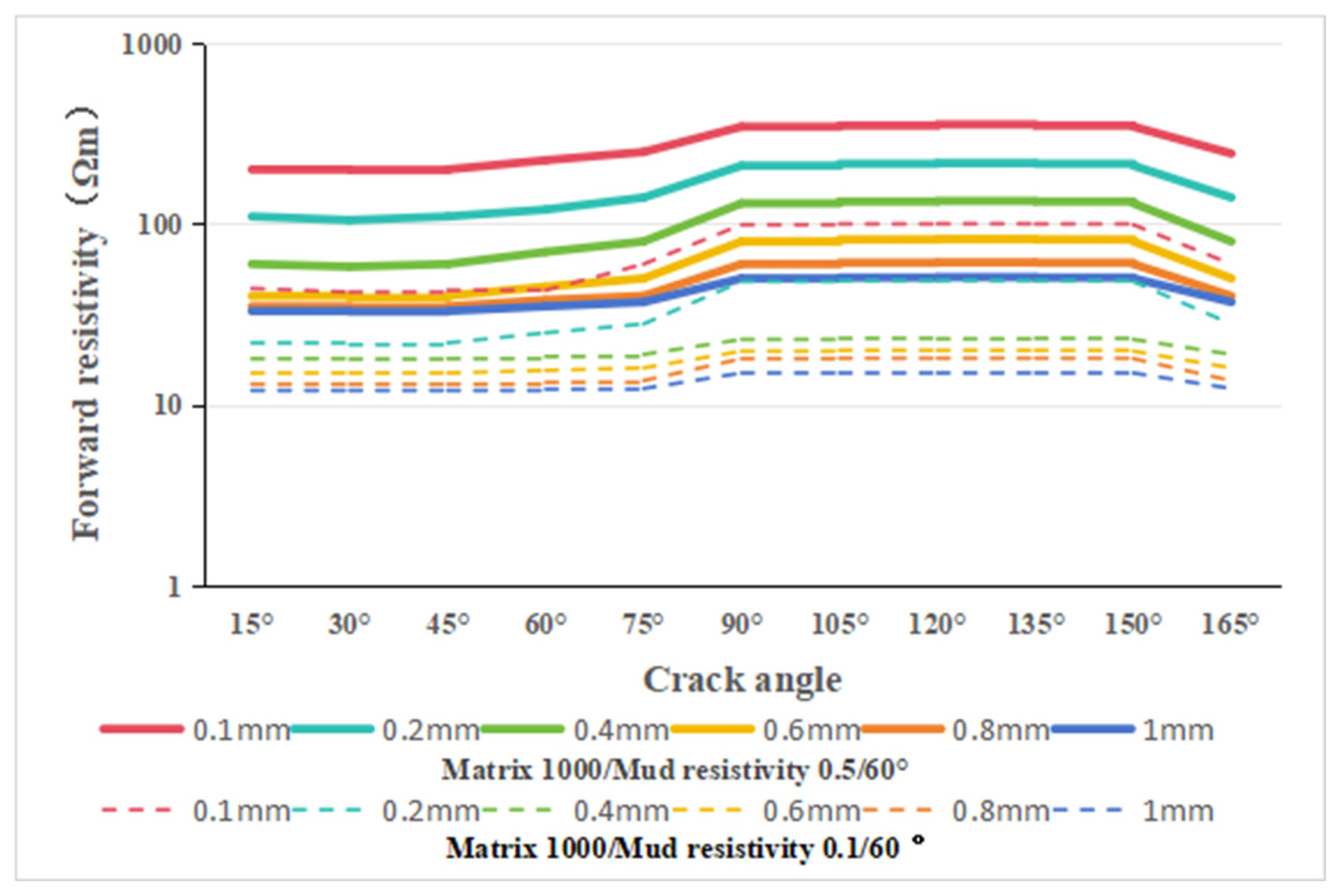
| Coefficient | ||||
|---|---|---|---|---|
| 100 | 0.001 | 100,000 | 1,250,000 | 0.08 |
| 100 | 0.1 | 1000 | 12,500 | 0.08 |
| 100 | 10 | 10 | 125 | 0.08 |
| 100 | 1000 | 0.1 | 1.25 | 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, H.; Zhang, Z.; Guo, J.; Fang, S.; Wang, C. Numerical Simulation Study on the Influence of Cracks in a Full-Size Core on the Resistivity Measurement Response. Energies 2024, 17, 1386. https://doi.org/10.3390/en17061386
Zheng H, Zhang Z, Guo J, Fang S, Wang C. Numerical Simulation Study on the Influence of Cracks in a Full-Size Core on the Resistivity Measurement Response. Energies. 2024; 17(6):1386. https://doi.org/10.3390/en17061386
Chicago/Turabian StyleZheng, Hanwen, Zhansong Zhang, Jianhong Guo, Sinan Fang, and Can Wang. 2024. "Numerical Simulation Study on the Influence of Cracks in a Full-Size Core on the Resistivity Measurement Response" Energies 17, no. 6: 1386. https://doi.org/10.3390/en17061386
APA StyleZheng, H., Zhang, Z., Guo, J., Fang, S., & Wang, C. (2024). Numerical Simulation Study on the Influence of Cracks in a Full-Size Core on the Resistivity Measurement Response. Energies, 17(6), 1386. https://doi.org/10.3390/en17061386






