Abstract
Fractured rock mass is extensively distributed in Karst topography regions, and its geological environment is different from that of the quaternary strata. In this study, the influences on geological environment induced by the construction and operation of a large-scale borehole group of ground source heat pumps are analyzed by a thermo-hydro-mechanical (THM) coupling numerical model. It was found that groundwater is redirected as the boreholes can function as channels to the surface, and the flow velocity in the upstream of borehole group is higher than those downstream. This change in groundwater flow enhances heat transfer in the upstream boreholes but may disturb the original groundwater system and impact the local geological environment. Heat accumulation is more likely to occur downstream. The geo-stress concentration appears in the borehole area, mainly due to exaction and increasing with the depth. On the fracture plane, tensile stress and maximum shear stress simultaneously occur on the upstream of boreholes, inducing the possibility of fracturing or the expansion of existing fractures. There is a slight uplift displacement on the surface after the construction of boreholes. The correlations of the above THM phenomena are discussed and analyzed. From the modeling results, it is suggested that the consolidation of backfills can minimize the environmental disturbances in terms of groundwater redirection, thermal accumulation, occurrence of tensile stress, and possible fracturing. This study provides support for the assessment of impacts on geological environments resulting from shallow geothermal development and layout optimization of ground heat exchangers in engineering practices.
1. Introduction
A vertical closed-loop ground source heat pump (GSHP) is the most used technology to recover shallow geothermal energy, which is a promising and green energy to decarbonize the cooling and heating sector in buildings [1]. In such a GSHP system, the ground is utilized as a heat sink, and a large number of heat exchange boreholes are constructed in which the U-pipes are accommodated to exchange heat with the geological formation. The boreholes usually are 120–150 m deep with a diameter ranging from 100 to 200 mm and are placed in a group with a spacing of 5 m to each other. The borehole can be backfilled with grout or drilling debris.
The karstic landscape, mainly composed of carbonate rock mass, is highly fractured and cavernous. The hydrogeological conditions are very complex, and fractures and caves usually function as main water storage and conduct bodies. The vertical runoff zone for groundwater is within a certain depth near the surface (usually 2–10 m) and is also called the epikarst zone; it is unsaturated and describes where the karst development is mainly vertical and extremely uneven, including sinkholes, karst windows, vertical shaft, etc. The surface karstic water in the epikarst zone is of strong hydraulic connection as the atmospheric precipitation is the major source, having strong seasonal fluctuation. Below the epikarst zone is the saturation karst zone, which is usually within a depth of 100 m. The groundwater is circulated and alternated intensely, dominated by horizontal karstification development. In deeper stratum, the hydrodynamic conditions and karstification gradually weaken [2].
Since the boreholes are located in the epikarst zone and saturation zone, and they commonly penetrate the rock matrix and fractures, the construction and operation of borehole groups might have an impact on the geological environment of the region. Molson et al. [3] have concluded that local temperature anomalies in the subsurface might result from the extraction or release of heat to the formation, further altering the chemical, physical, and microbiological characteristics of aquifers. Other studies have pointed out that the temperature field around the borehole heat exchanger is likely to spread to the downstream direction of groundwater, and the heat migration direction is consistent with the groundwater seepage direction [4,5,6]. It is observed that the higher the seepage velocity of groundwater is, the lower the temperature in the boreholes is, and the more difficult it is for heat to accumulate [7]. However, the groundwater flow also makes the heat distribution in the borehole group extremely uneven, and heat accumulation is more obvious in the downstream section of the group [8,9]. In contrast, the degree of heat accumulation is significantly reduced in the upstream of seepage flow, where the thermal interference is weaker. It can be assumed that in areas with more developed karst fractures, the abundant groundwater flow would drag the heat inside the rock, and soil migrates along with it [10]. Therefore, an appropriate optimal placement of a borehole group can be adopted to improve the overall heat transfer capacity of ground heat exchangers [11,12].
Some large-scale projects need a large number of boreholes to meet the load requirement, with up to more than 1000 boreholes in some project cases. The installation of a borehole group may alter the hydrogeological conditions of the penetrated aquifer and other connected ones [13,14]. Inappropriate drilling and grouting might cause pollution to groundwater, and the pollutants may contaminate other clean water sources connected to the aquifer [15,16,17]. Thus, it is advised to consider natural backfill materials if possible and to use mature backfilling techniques. In addition, the borehole group should be arranged along the seepage direction to minimize its interference in the water flow and water head difference between upstream and downstream. Studies have shown [18] that the heat exchange capacity of crisscrossed borehole arrangements is improved compared with the aligned arrangement, and the groundwater flow is also less disturbed.
Based on investigations of some cases of environmental hazards, Fleuchaus and Blum [19] found that leakage through the annual space in borehole grouting caused the connection of aquifers and further resulted in damages, including land subsidence and ground uplifts. Based on a literature review, field investigations, and temperature measurements, Zhu et al. have analyzed the thermal pollution and groundwater contamination risks induced by GSHP systems [20]. It was found that disturbances to ground temperature will cause variations in water evaporation, dissolved oxygen, chemical reaction concentration of microbes, and the growth of plants. Their research also pointed out that the interface between the grouting material and a U-pipe can function as a preferred flow path for groundwater, bringing in potential risks of subsidence and contamination.
In some cases, antifreeze is added into the circulated heat carrier to allow the U-bend loop heat exchange system to work below 0 °C. Through experiments and numerical simulation, Anbergen et al. [21] have found that there are alternate thermal stresses due to heat loading and effective tangential stress induced by the frozen pore water pressure. Such a freeze–thaw cycle could cause possible crack development and failure of the grouting material in boreholes, further leading to an increase in the hydraulic conductivity of grout and connections between different aquifers.
Allan and Philappacopoulus [22] have also pointed out that because the grout and pipe have significantly different coefficients of thermal expansion, the conductor pipe can contract from the grout at low temperatures. Poor bonding between the grout and the borehole or poor bonding between the grout and the heat conductor pipe can form a conductive pathway for contaminant transport.
In summary, the installation and operation of the borehole groups may cause changes to the groundwater field, and these changes will in turn influence the heat transfer of the ground heat exchangers. Most previous studies about the environmental impact of borehole heat exchange systems focus on the connection of different aquifers through boreholes, disturbance on ground surface, contamination by grouting material, and thermal pollution to the ground. Also, most research is based on the quaternary strata, and there is little about the karstic environment.
It must be noted that the impacts on the geological environment occur not only in terms of groundwater field. The drilling and backfilling of boreholes will change the ground stress of the rock formation, and such changes will in turn affect the subsurface water storage and water-conducting spaces. In addition, periodic heat extraction and release will exert thermal stress on the rock mass. It is obvious that the impact of shallow geothermal energy development on environmental geology is a complex thermo-hydro-mechanical (THM) coupling process. The current research mostly focuses on the impact of the backfill process on groundwater quality and the impact of borehole groups on water flow and water head. But more in-depth research is still needed on the THM interaction mechanism between borehole groups and rock mass, and its impact to the geological environment.
The THM coupling process reflects the physical behavior of porous media under the complex conditions of multiphysical fields [23]. THM coupling analysis has a wide range of applications in the field of geo-engineering. Chen [24] has analyzed the coupling of temperature, seepage, and stress to evaluate the stability of a dam. Zhu et al. [25] have established a THM coupling simulation in order to clarify the release of seismic fault stress, taking into account the influence of maximum horizontal principal stress direction and fault dip angle. The development and operation of enhanced geothermal systems (EGSs) involve the THM coupling problem of fractured rock mass. Analysis of the spatiotemporal evolution of the seepage, temperature, and stress fields in the model is significantly interesting to researchers [26,27,28]. In addition, THM coupling analysis of energy piles and surrounding soils shows that the stress field displays visible changes under the cyclic loading of heating and cooling [29,30,31]. Similarly, the spatiotemporal evolution patterns of the groundwater, temperature, and geo-stress fields in the fractured rock mass that result from the installation and operation of boreholes in GSHP systems are particularly important in assessing the environmental impacts associated with shallow geothermal development.
This study is based on the karstic environment, where fractured carbonate rock mass extensively exists. It utilizes numerical simulation to study the THM coupling influence mechanism of borehole groups on the geological environment, identifying the changes in ground temperature, groundwater, and geo-stress fields. The research result provides a reference for assessing environmental impact, as well as practical guidance for minimizing environmental disturbances and optimizing the layout of borehole groups.
2. THM Coupling Equations
2.1. Assumptions
The backfill material in boreholes and the rock mass are both porous media materials, and following assumptions are made in the simulation:
Ⅰ. The groundwater flow in fractured rock mass follows Darcy’s law;
Ⅱ. The backfill material in boreholes and the rock mass are elastic materials, and the fractures can be simplified as the fracture medium. The boreholes are backfilled with original drilling debris (carbonate rock) since they are environmentally friendly and their heat conductivity is high. Due to the effect of incomplete consolidation during backfilling, the actual porosity of backfill material is higher than that of surrounding rock mass;
Ⅲ. The fractured rock mass is a dual media, consisting of fractures and matrix with low porosity [2];
Ⅳ. There are both convective and conductive heat transfers in the rock mass, and radioactive transfer can be neglected; and
Ⅴ. The water flows by forced convection.
2.2. Equations
Water flow in pores is presented by Darcy’s Law:
where u is the Darcy flow rate, m/s; k is the permeability of porous medium, m2; μ is the fluid dynamic viscosity, Pa∙s; p is the pore pressure, Pa; ρ is the fluid density, kg/m3; g is the gravitational acceleration, m/s2; D is elevation, m; S is rock matrix water storage coefficient, 1/Pa; t is time, s; and Q is seepage source term, s−1;
Water flow in fractures is controlled by the modification of Darcy’s Law:
where Sf is the fracture water storage coefficient, 1/Pa; kf is the fracture permeability, m2; df is the fracture aperture, m; Qf is the flow velocity between a fracture plane and rock matrix, m/s, and ; n is the normal direction of a fracture plane; ef is fracture volume strain; and ▽τ is the derivative along the tangential direction of a fracture.
The seepage velocity of pore water is very slow compared to that in fractures, so the heat convection by pore water is neglected and only the thermal conduction is considered in a rock matrix:
where ρs is the density of the rock matrix, kg/m3; λs is the thermal conductivity of the rock matrix, W/(m∙K); w is the heat source, W/m3; cs is the specific heat capacity of the rock matrix, J/(kg∙K); and Ts is the block temperature, K.
The temperature field in fracture water flow is presented as follows:
where the first term on the left side is the convection effect of fracture water on the temperature field; cf is the specific heat capacity of water, J/(kg∙K); λf is the thermal conductivity of water, W/(m∙K); uf is the fracture water velocity, m/s; Tf is the fracture water temperature, K; and Wf is the heat absorbed by the fracture water from the bedrock, W/m3.
The energy equation of the incompressible fluid flowing in the U-pipe is as follows:
where A is the cross-sectional area of U-pipe, m2; ud is the fluid velocity in U-pipe, m/s; fD is the Darcy friction coefficient; dh is the average hydraulic diameter, m; Qwall is external heat transfer on pipe wall, W/m; and Q0 is general heat source, W/m.
The heat transfer between the U-pipe and the surrounding environment is as follows:
where (hZ)eff is the effective value of the pipe heat transfer coefficient h (W/(m2∙K)) multiplied by the pipe wall perimeter Z, m; and TEXT is the outer wall temperature on pipe, K.
The stress balance equation and displacement field equation in the rock matrix are as follows:
where αBpi is the water pressure effect; βTTs,i is the temperature stress effect; σij is the stress tensor, Pa; Fi is the body force, Pa; μs is the shear modulus, also known as the second parameter of Lamé; L is the Lamé first parameter; u is displacement, m; E is elastic modulus, Pa; ν is Poisson’s ratio; p is water pressure, Pa; αB is Biot coupling coefficient, ≤1; βT is thermal expansion factor; αT is thermal expansion coefficient, 1/K; and Ts is rock temperature, K.
3. Model Validation
A comparison of analytical and numerical solutions can be used to ensure the accuracy of a THM coupling simulation. This validation approach is widely used in EGS research [32,33]. Figure 1a shows a schematic diagram of a 100 m × 100 m × 100 m three-dimensional single-fracture rock mass, where df is the fracture aperture. Water flows from the left to the right on the fracture plane, which is located at z = 50 m. In the model, the water flows into the rock mass at 0.01 m/s to extract heat. If the thermal conductivity of the rock matrix along the x-axis is zero, the three-dimensional single-fracture model can be simplified to a two-dimensional model, as shown in Figure 1b [34,35]. Sun et al. [32] have provided an analytical solution for the two-dimensional single-fracture model (Equation (11)).
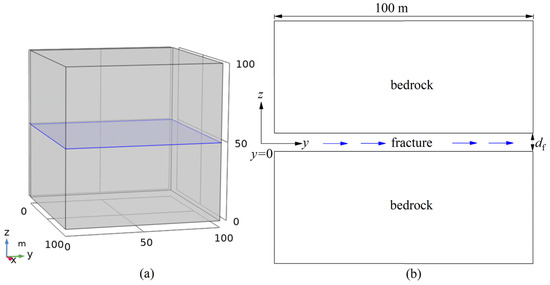
Figure 1.
Schematic diagram of heat flow coupling in a single fracture. (a) is the 3D single-crack heat flow mode; and (b) is the simplified 2D single-crack heat-flow coupling model.
The water temperature can be calculated according to Equation (11):
where Tf is the temperature of fracture water flow, K; λ is the thermal conductivity, W/(m∙K); and ρ is the density, kg/m3. In the table below, s and f represent rock mass and fractures, erfc is the complementary error function, and U is the unit step function.
The two rock matrixes separated by the fractures are assumed to be anisotropic and impermeable. The parameters used in the analytical solution and the two-dimensional numerical model are shown in Table 1 [34]. The simulation duration is 100 days (d), and the analytical solution and the numerical solution are compared in Figure 2.

Table 1.
Parameters used in model validation.
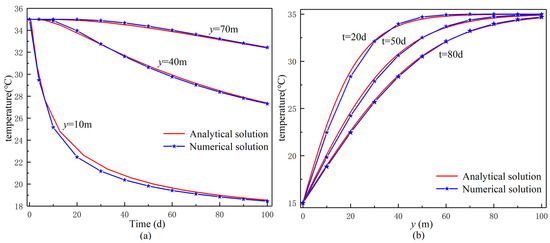
Figure 2.
Comparison of analytic and numerical solutions. (a) is the variation of temperature at three point with time; and (b) is the variation of fracture surface temperature at different times.
Figure 2a shows the temperature variation with time at three different positions (y = 10 m, y = 40 m, y = 70 m) in the fracture. Figure 2b is the temperature curve in the fracture at different times (t = 20 d, t = 50 d, t = 80 d). It can be seen that the analytical and numerical solutions are generally consistent, and the error may be caused by discretization. This verification ensures the accuracy and reliability of the coupling model used in this paper.
4. Establishment of Numerical Model
4.1. Geometric Model
According to the general vertical pattern of karstic environments [2], a representative geometric rock mass model with two horizontal fractures was assumed and established. Figure 3a,b shows the models before and after the construction of the borehole group, respectively.
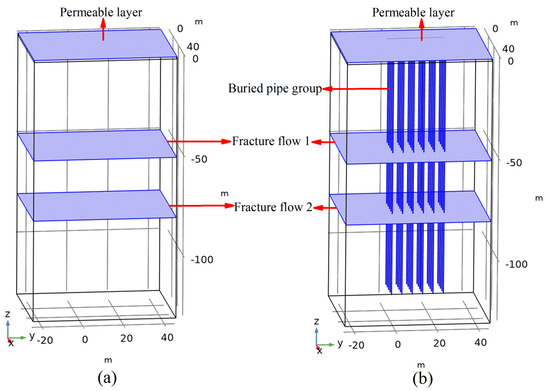
Figure 3.
Geometry model. (a) is the without buried pipe; and (b) is the with a buried pipe group.
As shown in Figure 3, the depths of simulated rock mass and the boreholes are 130 m and 120 m, respectively; the length and width of the model are 70 m and 60 m, respectively; and there are 30 boreholes, with a hole spacing of 5 m and a diameter of 180 mm. The borehole spacing was set according to the value suggested by ASHARE [36]. Polyethylene U-pipes with an inner diameter of 26 mm are installed in boreholes. The heat carrier (water) flow velocity in the pipes is 0.7 m/s, and the water inlet temperature is 308.15 kelvin (K). Since the depth of the rock mass is 130 m, the temperature value is assumed to be 291.15 K. Horizontal fracture water flow 1 (Z = −50 m) and horizontal fracture water flow 2 (Z = −80 m) exits in the rock mass, and the apertures of both fractures are 5 mm. The arrangement of the borehole group is shown in Figure 4.
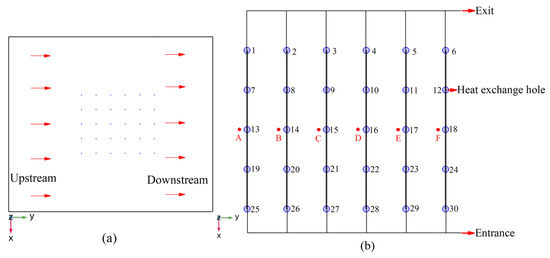
Figure 4.
Top view of the layout of a borehole group. (a) is the layout of heat exchange holes; and (b) is the enlarged view of heat exchange holes (the read dots are 0.2 m away form the hole).
Figure 3b shows the geometric model of the borehole group when the top surface is open. This means that there is a 1 m thick permeable layer that is close to the ground surface, such as grassland in reality. In order to compare to the original stratum, the model without a borehole group was introduced, as shown in Figure 3a, and the distribution of the seepage field and stress field of both cases were compared. The parameters of the two cases are the same.
The model parameters are listed in Table 2. Some of the other parameters are the same as in the model validation part already listed in Table 1. The parameters were assumed according to common conditions in karstic environments.

Table 2.
Model parameters.
4.2. Meshing
A free tetrahedral mesh is used to customize the cell size in boreholes (Figure 5). For the fracture flow, a free triangular mesh is used to ensure that it is easier to connect with the interface of boreholes. The mesh in the rock mass at the junction with a borehole is refined using free tetrahedral mesh.
Figure 5.
Schematic diagram of mesh division. (a) is the overall; and (b) is the interface between the heat exchange hole and the fracture surface; and (c) is the enlarged view of the heat exchange hole.
4.3. Initial and Boundary Conditions
Since this study was conducted to investigate the environmental impact of a GSHP system in extreme heat imbalance conditions, the simulation only considers the cooling period of a summer of 4 months, when the borehole group only induces heat into the subsurface.
(1) Groundwater field: Jiang et al. [37] have measured the groundwater flow velocity and flow direction in a geological exploration borehole in the Zigui karst area in central China, and they found that the average groundwater flow velocity in fractures ranged between 268.67 and 2733.48 μm/s. Since the modeled formation is at a shallow depth in this study, and the fracture apertures are expected to be wider compared with deeper fractures, the flow velocity at the inlets of the two horizontal fractures is set at 1000 μm/s. The groundwater in the pores of the rock mass is assumed to be in a nearly stagnant state according to the dual model. When the top surface is assumed to be an open boundary of the permeable layer, there is mass exchange through the surface. The other sides of the model are saturated and assumed to be without mass flow except on the interfaces with facture planes.
(2) Temperature field: the initial temperature of the rock mass, the borehole, the U-pipes, and the water flow inside are all set to 291.15 K, a normal ground temperature in the karstic region in central and south China as the background. The inlet water temperature of the U-pipe is 308.15 K. The top and bottom of the model are open to heat exchange.
(3) Stress field: all four sides of the model are subjected to normal constraints, with fixed constraints at the bottom and free boundaries at the top. Stresses in the X, Y, and Z directions caused by gravity are applied to the model.
5. Simulation Results
5.1. Groundwater Field
(1) Water velocity
Figure 6a shows that when there is no borehole, the flow velocity in the rock mass is low. The streamlines demonstrate that the fracture water tends to seep to the surface.
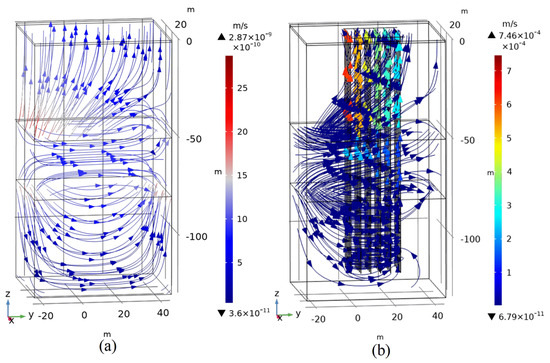
Figure 6.
Groundwater field with or without the borehole group. (a) is the without buried pipe group; and (b) is the with the buried pipe group.
Figure 6b shows that when there is a borehole group, the streamlines near the fracture plane are denser, and the seepage velocity in the rock matrix is low. The seepage velocity in the boreholes is higher, especially in those near the upstream of the fracture flow. Above fracture plane 1, the seepage velocity is the highest while it gradually decreases near the downstream. Because of mass balance, the higher velocity in upstream holes leads to lower flow velocity in downstream boreholes.
In Figure 6b, streamlines pointing to the top indicate that there is seepage to the ground surface. Because the permeability and porosity of the backfill material in boreholes are higher than those of matrix rock, which are lower, the streamlines are more concentrated in the borehole region, and the groundwater on the fracture plane tends to flow into the boreholes.
(2) Pore pressure and flow velocity on fracture planes
It can be seen from Figure 7a,b that when there is no borehole, the fracture plane pore pressure is evenly distributed along the X direction and decreases with a certain gradient along the Y direction; when there is a borehole group, the pore pressure near the upstream is greater and its gradient increases significantly in the upstream area of the borehole.
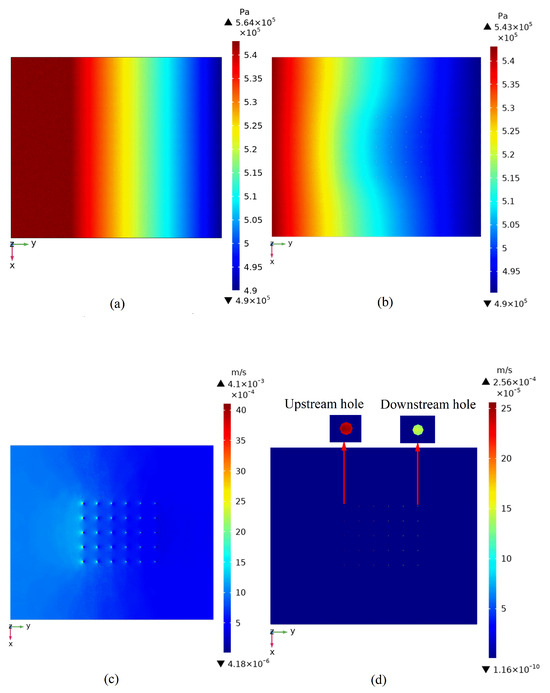
Figure 7.
Pore pressure and flow velocity distribution at different cross-sections. (a) is the pore presure of fracture 1 (without buried pipe group); (b) is the pore presure of fracture 1 (with a buried pipe group); (c) is the flow velocity of fracture 1 (with a buried pipe group); and (d) is the flow velocity of non-fracture surface at Z= −65 (enlarged view of heat exchange holes).
Figure 7c shows the flow velocity distribution on fracture plane 1 penetrated by the borehole group. The seepage velocity is higher near the upstream boreholes (left in the figure), and the velocity reduces in the downstream area.
Figure 7d shows the flow velocity distribution on a non-fracture plane (Z = −65 m). Because the porosity and permeability of the rock matrix are low, the flow velocity in this section is low and even. In addition, according to the enlarged view of water seepage velocity in the two boreholes at the top of the figure, the seepage velocity in the upstream boreholes is obviously higher than that in the downstream boreholes, which is relatively low.
In order to quantitatively analyze the flow velocity distribution on the fracture plane along the flow direction, three intercept lines perpendicular to the flow direction on the fracture plane were taken for analysis. The line Y = −10 m is at the upstream of the fracture flow; Y = 35 m is at the downstream of the fracture flow; and Y = 0 m passes through the first row of borehole, as shown in Figure 8a.
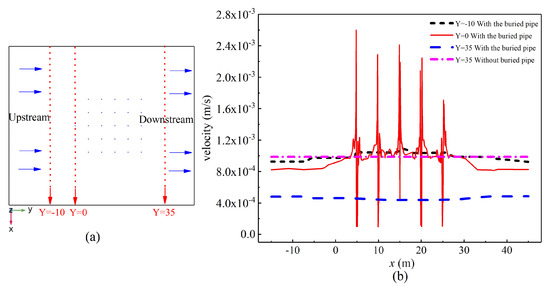
Figure 8.
Velocity distribution of the cross-section, and the cross-section on fracture plane 1 (Z = −50 m). (a) is the cross-section distribution; and (b) is the velocity distribution on the cross-section.
Figure 8b exhibits the velocity distribution of the intercept lines with or without boreholes. The velocity on Y = 0 m passing the boreholes varies more extensively and strongly, and both the maximum and minimum values appear around the boreholes. The flow velocity on the intercept lines that do not pass the borehole is relatively stable. Additionally, the flow velocity in the boreholes near the upstream (Y = −10 m) is higher than that of the downstream boreholes (Y = 35 m).
The flow velocity on Y = 35 m was selected to compare its values with and without boreholes. When there are boreholes, the average velocity is significantly lower than that without a buried pipe, which is close to that of the fracture entrance, and is higher than twice that of the values with boreholes. As depicted before, the fracture water tends to flow through the boreholes that act as conduits, and results in a lower velocity downstream.
(3) Flow velocity in boreholes
As shown in Figure 9, the seepage velocity is the highest in the borehole sections above fracture plane 1 close to the upstream, and the velocity gradually decreases as it approaches the downstream. Between fracture planes 1 and 2, the overall seepage velocity value is lower. The seepage velocity in the boreholes below fracture plane 2 is the lowest. This is because the ground surface is set as an open boundary in the model while its bottom is a closed boundary; hence, the upstream fracture water is more likely to flow to the surface.
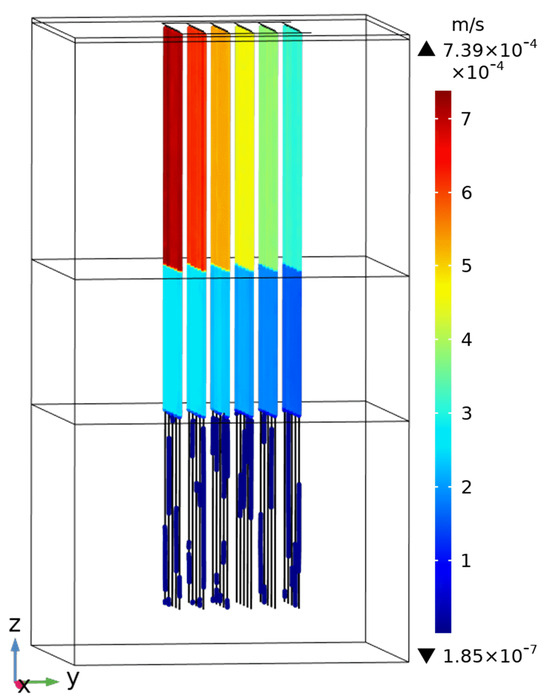
Figure 9.
Flow velocity distribution in the borehole.
5.2. Temperature Field
(1) Temperature field in the rock mass
Figure 10a,b shows the temperature distribution in the rock mass after the heat pump system operates for 60 days and 120 days, respectively. Heat accumulation can be observed in the area of the boreholes, and the maximal temperature appears at the surface.
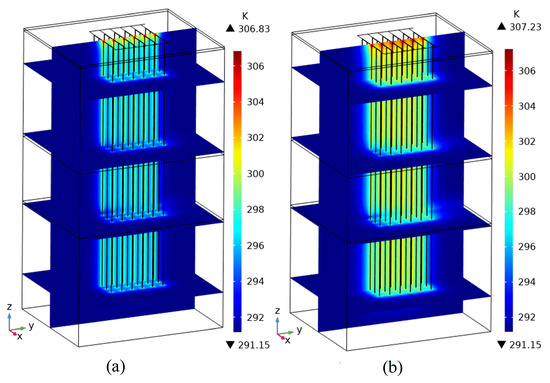
Figure 10.
Distribution of temperature field in the body. (a) is the operation for 60 days; and (b) is the operation for 120 days.
(2) Temperature field in fractures
After 120 days of operation, the temperature field of fracture plane 1 and fracture plane 2 are shown in Figure 11a,b. Due to the convective heat transfer at the fracture flow, the temperature field displays an occurrence of stretching. Also, there is obviously less heat accumulation around the upstream boreholes, which is beneficial to heat exchange. From Figure 11b, it is known that heat is more likely to accumulate downstream.
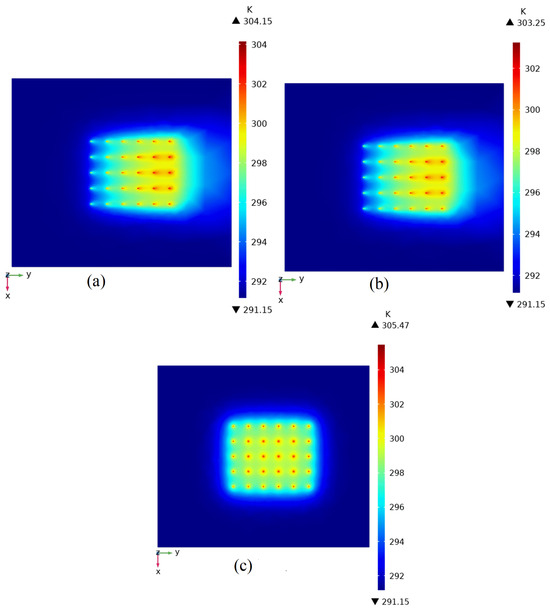
Figure 11.
Temperature distribution of different depths after 120 days of operation. (a) Fracture plane 1 at the depth of Z = −50 m; (b) fracture plane 2 at the depth of Z = −85 m; (c) no fracture at the depth of Z = −65 m.
To compare, Figure 11c shows the relatively even temperature distribution at the depth of Z = −65 m, where there is no fracture water flow and the heat transfer is almost conductive.
To conclude, the temperature field in the fracture flow areas tends to extend along with the flow direction, and the temperature field outside the fracture flow is relatively even. This occurs because the seepage velocity in the porous medium is very low compared to that of fracture water, and there is little convection and heat from the boreholes, which is finally transferred to the rock mass around mainly by conduction.
The temperature field distribution of the fracture plane was further analyzed by taking intercept lines of the fracture plane 1 (Z = −50 m), as shown in Figure 12a. Lines Y = 0 m and Y = 25 m are perpendicular to the flow direction, and lines X = 12.5 m and X = 15 m are along the flow direction. Among these lines, lines Y = 0 m, Y = 25 m, and X = 15 m pass through the boreholes.
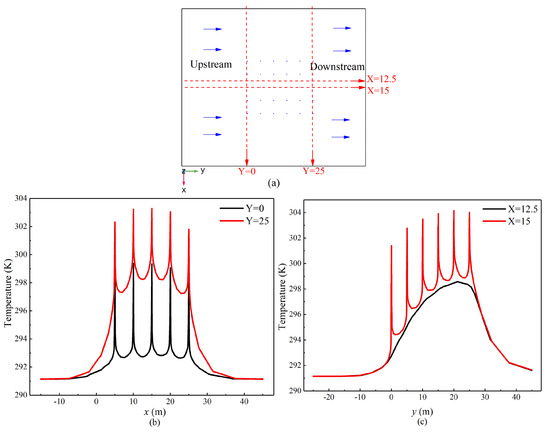
Figure 12.
Temperature distribution of fracture plane 1 (Z = −50 m) after 120 days of operation. (a) is the crack surface section (Z=−50); (b) is the vertical to seepage direction; and (c) is the parallel to flow direction.
As shown in Figure 12b, after the GSHP operates for 120 days, the temperature of the borehole area located at the upstream (Y = 0 m) is lower than that of the downstream (Y = 25 m) due to the higher flow rate upstream and, hence, the stronger convective heat transfer effect. The upstream boreholes intercept and redirect part of the fracture water that should flow downstream, resulting in higher temperature and weaker convective heat transfer at the downstream.
Figure 12b shows the temperature change on X = 15 m and X = 12.5 m parallel to the seepage direction, indicating the same trend in which the closer to the downstream, the higher the temperature.
The temperature change in the six points on fracture plane 1 along the time were selected and shown in Figure 13. All the points are located just before the borehole wall (as shown in Figure 4b). It can be seen from the figure that the temperature around the hole gradually increases with time as heat is continually injected by the U-pipes. Overall, the temperature increase and heat accumulation of the downstream points are more obvious.
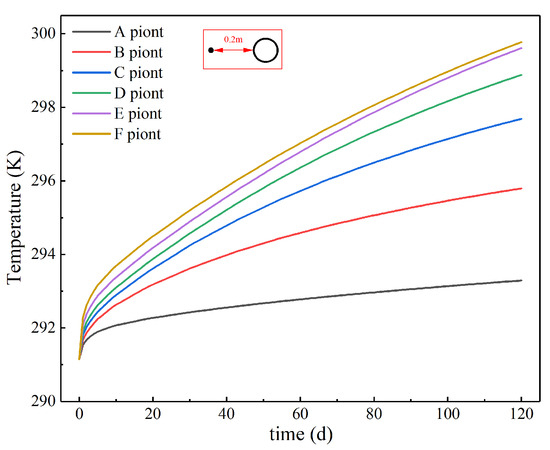
Figure 13.
Temperature distribution at the intercept points on fracture plane 1 (Z = −50 m).
5.3. Maximum Principal Stress Distribution
(1) Maximum principal stress in the rock mass
Figure 14 shows that the stress concentration in the borehole group is obvious. The maximum principal stress is between −1.05 × 106 and 9.49 × 105 Pa. In the model, the tensile stress is labeled as positive and the compressive stress is labeled as negative. As the depth increases, the stress concentration becomes more significant. After the construction of the borehole group, excavation stress appears in the surrounding rock, leading to a stress concentration around the boreholes. In addition, heat accumulation also results in thermal stress in the borehole group region.
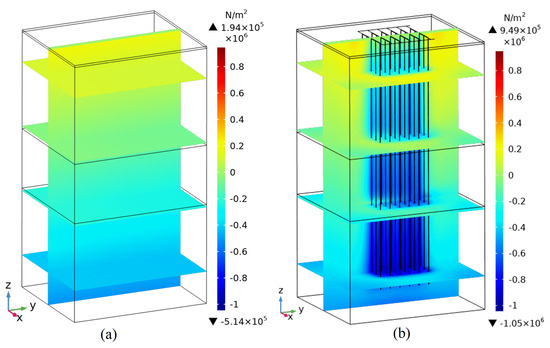
Figure 14.
Distribution of the maximum principal stress in the rock mass with or without a borehole group. (a) is the without buried pipe group; and (b) is the with the buried pipe group.
(2) Principal stress distribution at different depths
It can be seen from Figure 15a that when there is no borehole, the maximum principal stress range of fracture plane 1 is −4.67 × 104~−8.67 × 104 Pa, indicating that the fracture plane is only affected by compressive stress and that the stress distribution is relatively even.
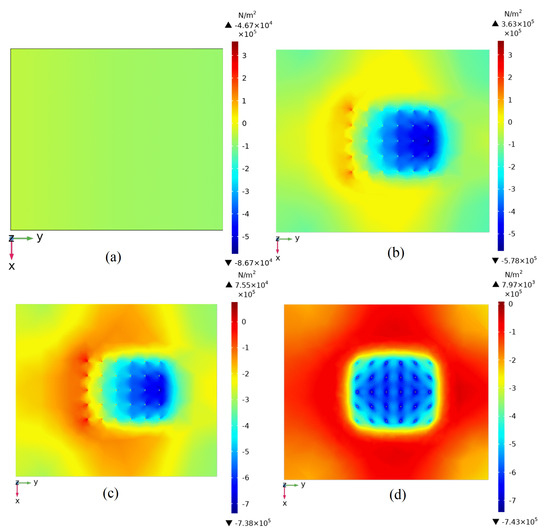
Figure 15.
Principal stress distribution of different sections. (a) is the Z=−50 fracture plane 1 (without buried pipe group); and (b) is the Z=−50 fracture plane 1(with buried pipe group); and (c) is the Z=−80 fracture plane 2 (with buried pipe group); and (d) is the Z=−65 non-fracture surface (with buried pipe group).
After 120 days of operation, the THM coupling effect becomes stronger. From Figure 15b,c, it can be seen that the ranges of the maximum principal stress on fracture plane 1 and fracture plane 2 are 3.63 × 105~−5.78 × 105 Pa and 7.55 × 104~−7.38 × 105 Pa, respectively, indicating that there exists both tensile stress and compressive stress on the fracture plane. The upstream region of the borehole group is subjected to tensile stress, and the compressive stress is mainly concentrated downstream.
The distribution of maximum principal stress on non-fracture planes is shown in Figure 15d. The area with the borehole group shows more concentrated compressive stress, and tensile stress exists in a few areas outside of the borehole group.
5.4. Maximum Shear Stress Distribution
(1) Distribution of maximum shear stress in rock mass
As shown in Figure 16a,b, the maximum shear stress gradually increases with the depth. After 120 days of operation, the maximum shear stress value increases from 7.94 × 105 Pa to 1.39 × 106 Pa.
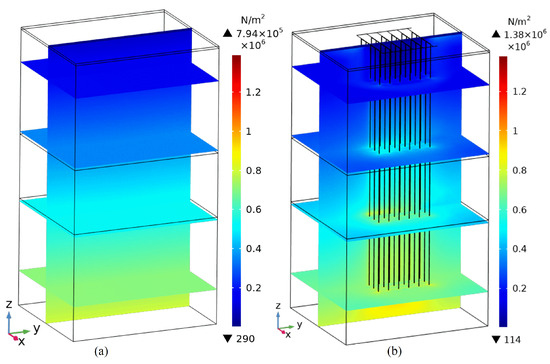
Figure 16.
Distribution of maximum shear stress in the rock mass with or without borehole groups. (a) is the without buried pipe group; and (b) is the with the buried pipe group.
Figure 16b shows the maximum shear stress distribution in the rock mass after 120 days of operation. As the depth increases, the maximum shear stress concentration in the area of borehole group is more visible.
(2) Maximum shear stress distribution of different depths
The maximum shear stress distributions at different depths are shown in Figure 17a–d. When there is no borehole, the maximum shear stress on fracture plane 1 ranges from 3.54 × 105 Pa to 3.59 × 105 Pa, and it is evenly distributed.
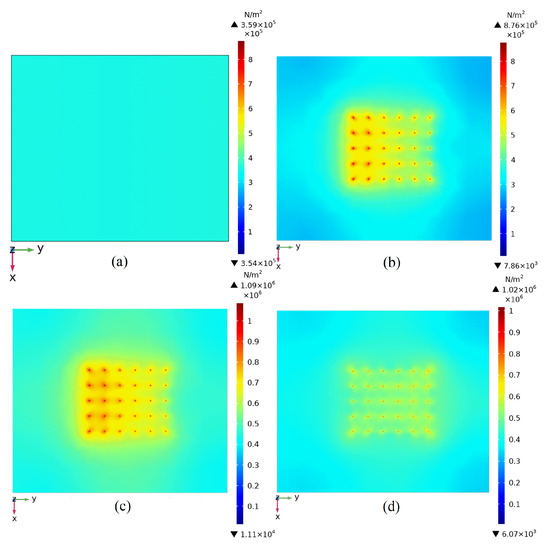
Figure 17.
Maximum shear stress distribution of different sections. (a) is the Z=−50 fracture plane 1 (without buried pipe group); and (b) is the Z=−50 fracture plane 1(with buried pipe group); and (c) is the Z=−80 fracture plane 2 (with buried pipe group); and (d) is the Z=−65 non-fracture surface (with buried pipe group).
The maximum shear stress distributions on fracture plane 1 and fracture plane 2 after operation of 120 days is shown in Figure 17b,c, and the stress ranges are 7.86 × 103~8.76 × 105 Pa and 1.11 × 104~1.09 × 106 Pa, respectively. The figure shows that the stress around the boreholes is more concentrated, and the stress concentration around the boreholes upstream is significantly greater than that around the downstream boreholes.
Figure 17d shows the maximum shear stress distribution on the non-fracture plane (Z = −65 m), where stress is concentrated around the boreholes but the distribution is relatively even.
5.5. Displacement in the Rock Mass
Figure 18 shows the displacement of the Z component (vertical direction) after 120 days of operation, and the maximum value is 0.184 cm. After the installation of boreholes, the groundwater field is disturbed and the pore pressure is redistributed. The displacement is caused by the joint impacts of thermal stress, pore pressure, and excavation stress.
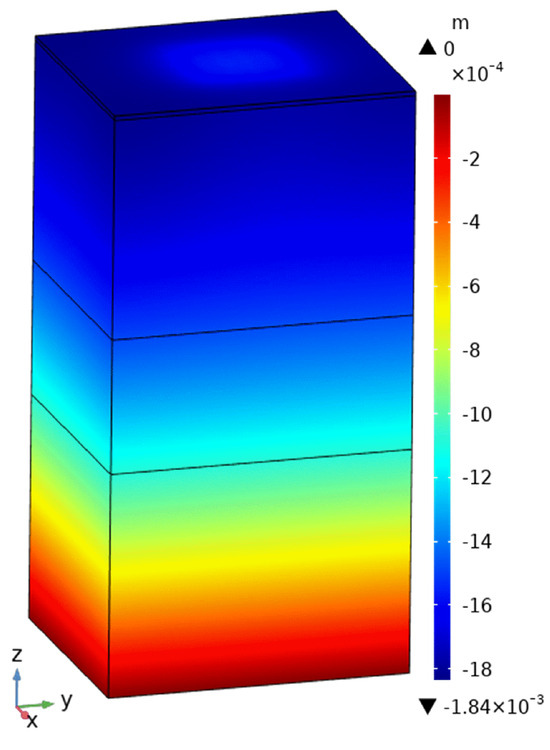
Figure 18.
Displacement field, Z component (with borehole group).
Figure 19 exhibits the change in the displacement field at point A on the surface (Figure 4b). The displacement of point A increases with the operating time of the heat pump, but the value is still very small.
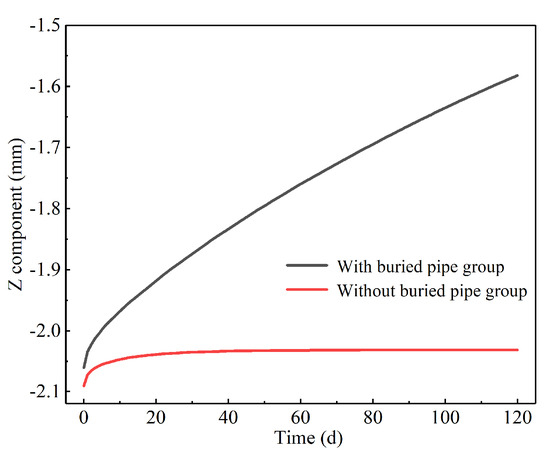
Figure 19.
Variation curve of displacement field at point A on XOY plane (Z = 0 m).
6. Discussion
After the construction of a borehole group in fractured rocks, the THM coupling effect has a certain impact on the geological environment in the project site.
According to the modeling results of groundwater flow field, the boreholes may function as water-conducting channels, transferring fracture water to the surface. This is because the permeability and porosity of the backfill material in the boreholes are higher than that of the rock matrix. In addition, the installation of the borehole group changes the pore pressure and flow velocity distribution on the fracture plane, and the fracture water flow velocity is higher in the upstream (Figure 7), so the convective heat transfer is enhanced in the upstream area [1]. Deng et al. [38] have found that fractures, especially those of wide aperture, would dominant the energy flow through the rock mass, playing a key role in influencing the energy transfer and replenishment processes. As the groundwater is redirected from fractures to boreholes, less water flow is available for the downstream area, resulting in a heat accumulation risk.
The temperature field is shown in Figure 10. The water flow in the boreholes is capable of adsorbing heat, which is converted into fluid kinetic energy and further pushes the fracture water flow upwards along the boreholes. From Figure 11 and Figure 12, it can be seen that on the fracture plane the heat migrates along flow direction and accumulates downstream. However, the entire rock mass, including the area of the borehole group, has a limited temperature increase (less than 16 K in Figure 10), so the thermal stress is slight.
The stress distribution is exhibited in Figure 14b. The excavation stress and thermal stress around the boreholes together lead to a stress concentration. It should be kept in mind that, as discussed in the last paragraph, the thermal stress is slight and the excavation stress is the dominating component. The compressive stress might result in a decrease in permeability and a low seepage velocity in the borehole area, which further leads to a large amount of fracture water flowing through the boreholes.
Comparing the stress fields on the fracture planes and the non-fracture planes, it can be seen that the fracture water flow has an obvious influence on the stress field. Because the seepage velocity in the pores upstream of the borehole group increases significantly (Figure 7), the effective stress on the upstream fracture planes decreases, and even tensile principal stress appears (Figure 15). According to Figure 17, the maximum shear stress also occurs upstream of the boreholes on the fracture plane, so there exists possibilities of secondary fracturing or activation of the existing fractures. New fractures would further enhance convective heat transfer but might also result in a loss of backfill materials from the boreholes.
Most previous research has assumed that the boreholes were placed in soils, and that the original permeability of grout is lower than that of the surrounding soil. Long-term thermal-thaw cycles result in debonding between grout and the borehole surface as well as grout cracking due to the formation of connecting channels of aquifers and pathways for contaminants. In this study, it is assumed that the boreholes are backfilled with drilling debris which has a higher porosity and permeability than those of the rock matrix due to incomplete consolidation. Since the temperature increase in the borehole area is small from the modeling result, variation in the permeability of boreholes due to thermal cycles was not considered. Sensitivity analyses of the uncertainty of backfill consolidation and consequent variation in permeability was not performed in this study due to the lack of experimental data. Another uncertainty is the variety of the fracture net. The form of a fracture net can be random and various, and the modeling work was essentially performed on primary fractures, which are major water storage and conduct bodies. The influence of secondary fractures is worth including and investigating in future research.
From the modeling results and the discussion above, it is known that the redirection of groundwater flow into the boreholes has the most obvious impact on the geological environment, since it would further impact the distribution of ground temperature, pore pressure, and effective stress in a rock mass. Therefore, in engineering practice, assurance of the consolidation of backfill material to increase its permeability is an effective approach to minimizing subsurface disturbances and environmental impact. The environmental disturbances can be significantly reduced if the permeability of a borehole is close to that of the rock mass.
Based on the modeling results and limitations in the assumptions of this study, future research works in the following areas are suggested. The first is the advanced measurement and digital twin modeling of the complex fracture net. The second is the correlation between the consolidation and permeability of backfill material, as well as its dynamical mechanical–transport coupling behaviors under the seasonal fluctuation in hydrogeological conditions. The third is the gathering of field measurements of ground temperature, groundwater flows, and subsurface displacement and stress, which are missed in current actual GSHP projects. The suggested research would provide more accurate input, support more reliable validation and optimization of the modeling and, hence, improve the prediction of geological environment impacts.
7. Conclusions
In this paper, the THM coupling impact of shallow geothermal borehole groups in fractured rock mass on the geological environment was studied by simulations of subsurface temperature, groundwater flow, and stress fields. The main conclusions are as follows:
(1) Due to the higher permeability of unconsolidated backfills, the boreholes might function as water conduits and some of the fracture water may flow to the surface through them. This change in groundwater flow enhances heat transfer in the upstream boreholes but may disturb the original groundwater system and impact the local geological environment. Since most ground source heat pump projects are located in urban areas, the redirected groundwater flow to the surface could result in further damages to the surface facility. Changes in the fracture water direction simultaneously decrease the pore pressure downstream, which is mainly manifested by the phenomenon in which the pore pressure gradient on fracture planes becomes larger.
(2) The fracture water flow brings a strong convective transfer effect, making the temperature field have a tendency to extend along with the seepage direction. In the non-fracture area heat transfer depends on conduction, and the heat is evenly distributed around the boreholes. Therefore, the existence of the fracture plane is more likely to improve the performance of borehole heat exchangers, especially the upstream ones.
Borehole layout should be optimized according to the disturbance of the groundwater flow. Designers are suggested to calculate the heat exchange rate of U-pipes both upstream and downstream based on different expected flow rates, respectively. Cooling load should be distributed between upstream and downstream boreholes based on their different heat transfer rates. Overall, more boreholes should be located in upstream areas and undertake more cooling load.
(3) The maximum principal stress is concentrated in the borehole group area, and the stress concentration becomes more obvious as the depth increases. The maximum shear stress is concentrated around each borehole, and it is more obvious in upstream areas. On the non-fracture planes, maximum shear stress is also concentrated around the boreholes but is more evenly distributed than that on the fracture planes. Therefore, in practice, more attention should be paid to the stress concentration around the boreholes near the fracture plane, especially to the possibility of secondary fracturing or the activation of existing fractures in the upstream area.
(4) There is a slight uplift displacement in the borehole group area, which results from the joint effects of thermal stress, redistribution of pore press, and excavation stress.
(5) The impact of a borehole group on the geological environment of a fractured rock mass is a complex THM coupling process. In general, the influence due to the redirection of groundwater from fractures to boreholes is obvious, as it not only changes the pattern of groundwater, but also alters ground temperature, pore pressure, and effective stress in a rock mass, leading to possible fracturing risks. In practice, it is suggested that consolidating backfill materials could minimize the aforementioned environmental disturbances.
Author Contributions
Conceptualization, Y.R. and P.P.; methodology, X.T.; software, L.T.; formal analysis, D.L. and B.Y.; writing—original draft preparation, B.Y.; writing—review and editing, D.L.; supervision, Y.R. and J.P.; project administration, P.P.; funding acquisition, Y.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Research Program of the Bureau of Geology and Mineral Exploration and Development Guizhou Province, China, Grant Number 2021[14], and the Science and Technology Support Program of Guizhou Province, China, Grant Number [2022]232. And The APC was funded by the Science and Technology Research Program of the Bureau of Geology and Mineral Exploration and Development Guizhou Province, China, Grant Number 2021[14].
Data Availability Statement
All data, models, and code generated or used during the study appear in the article.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. The authors in front of Guizhou Shallow Geothermal Energy Development Co., Ltd. have no conflict of interest.
Nomenclature
| u | Darcy flow rate (m/s) | A | cross-sectional area of U-pipe (m2) |
| k | permeability of the porous medium (m2) | ud | fluid velocity in the pipe (m/s) |
| μ | dynamic viscosity of the fluid (Pa∙s) | fD | Darcy friction coefficient |
| p | pore pressure (Pa) | dh | average hydraulic diameter (m) |
| ρ | fluid density (kg/m3) | Qwall | external heat transfer of the pipe wall (W/m) |
| g | gravitational acceleration (m/s2) | Q0 | general heat source (W/m) |
| D | elevation (m) | h | effective value of the pipe heat transfer coefficient (W/(m2∙K)) |
| S | rock matrix water storage coefficient (1/Pa) | Z | pipe wall perimeter (m) |
| t | time (s) | TEXT | pipe outer wall temperature (K) |
| Q | seepage source term (s−1) | αBpi | water pressure effect |
| Sf | fracture water storage coefficient (1/Pa) | βTTs,i | temperature stress effect |
| kf | fracture permeability (m2) | σij | stress tensor (Pa) |
| df | fracture aperture (m) | Fi | body force (Pa) |
| Qf | flow exchange between the fracture plane and the rock matrix (W) | μs | shear modulus, also known as the second parameter of Lame |
| n | direction of the fracture plane | λ | Lame’s first parameter |
| ef | fracture plane volume strain | ui,jjuj,ji | displacement (m) |
| ▽τ | derivative along the tangential direction of the fracture | E | elastic modulus (Pa) |
| ρs | density of the rock matrix (kg/m3) | ν | Poisson’s ratio |
| λs | thermal conductivity of the rock matrix (W/(m∙K)) | αB | Biot coupling coefficient |
| w | heat source (W/m3) | βT | thermal expansion factor |
| cs | specific heat capacity of the rock matrix (J/(kg∙K)) | αT | thermal expansion coefficient (1/K) |
| Ts | block temperature (K) | Ts | rock temperature (K) |
| cf | specific heat capacity of water (J/(kg∙K)) | T0 | bedrock initial temperature (°C) |
| λf | thermal conductivity of water (W/(m∙K)) | Tin | fracture water initial temperature (°C) |
| uf | fracture water velocity (m/s) | ϕh | borehole porosity |
| Tf | fracture water temperature (K) | ϕr | rock mass porosity |
| Wf | heat absorbed by the fracture plane water from the bedrock (W/m3) | Φf | porosity of fractures 1 and 2 |
References
- Deng, F.; Pei, P.; Li, W.; Wang, L.; Ren, Y. Study on design and calculation method of borehole heat exchangers based on seasonal patterns of groundwater. Renew. Energy 2024, 220, 119711. [Google Scholar] [CrossRef]
- Wang, M. Groundwater and Geological Environment in Karst Area of Guizhou Province; Geological Publishing House: Beijing, China, 2015; ISBN 9787116094093. [Google Scholar]
- Molson, J.W.; Frind, E.O.; Palmer, C.D. Thermal energy storage in an unconfined aquifer 2. Model development, validation and application. Water Resour. Res. 1992, 28, 2857–2867. [Google Scholar] [CrossRef]
- Yoshioka, M.; Takakura, S.; Uchida, Y. Estimation of groundwater flow from temperature monitoring in a borehole heat exchanger during a thermal response test. Hydrogeol. J. 2017, 26, 853–867. [Google Scholar] [CrossRef]
- Dehkordi, S.; Schincariol, R. Effect of thermal-hydrogeological and borehole heat exchanger properties on performance and impact of vertical closed-loop geothermal heat pump systems. Hydrogeol. J. 2014, 22, 89–203. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Yuan, X.; Niu, X.; Liu, J. Investigation of the influence of groundwater seepage on the heat transfer characteristics of a ground source heat pump system with a 9-well group. Build. Simul. 2019, 12, 857–868. [Google Scholar] [CrossRef]
- Wang, Y. Three-Dimensional simulation and Experimental Study on U-Vertical Buried Pipes with Groundwater Runoff Variation. Urban Geol. 2018, 13, 41–50. [Google Scholar]
- Capozza, A.; Carli, M.D.; Zarrella, A. Investigations on the influence of aquifers on the ground temperature in ground-source heat pump operation. Appl. Energy 2013, 107, 350–363. [Google Scholar] [CrossRef]
- Samson, M.; Dallaire, J.; Gosselin, L. Influence of groundwater flow on cost minimization of ground coupled heat pump systems. Geothermics 2018, 73, 100–110. [Google Scholar] [CrossRef]
- Zeng, Z.; Xu, Y.; Lv, H.; Fan, L.; Mo, H.; Qin, H. Experimental study on ground source heat pump air conditioning system in karst area. J. Guangxi Univ. (Nat. Sci. Ed.) 2017, 42, 260–267. [Google Scholar]
- Zhu, D.; Diao, N.; Yu, M. Ground Heat Exchanger with Multi-boreholes Simplified Heat Transfer Research based on the Seepage Model. Build. Energy Environ. 2016, 35, 21–24+84. [Google Scholar]
- Li, Y.; Mao, J.; Geng, S.; Zhang, H.; Han, X. Analyis and Optimization of Multi-boreholes based on moving finite line source model. Acta Energiae Solaris Sin. 2015, 36, 1287–1293. [Google Scholar]
- Bonte, M.; Stuyfzand, P.J.; Hulsmann, A.; Beelen, P.V. Underground Thermal Energy Storage: Environmental Risks and Policy Developments in the Netherlands and European Union. Ecol. Soc. 2011, 16, 22. [Google Scholar] [CrossRef]
- Saner, D.; Juraske, R.M.; Kübert, B.P.; Hellweg, S.; Bayer, P. Is it only CO2 that matters A life cycle perspective on shallow geothermal systems. Renew. Sustain. Energy Rev. 2010, 14, 1798–1813. [Google Scholar] [CrossRef]
- Butscher, C.; Huggenberger, P.; Auckenthaler, A.; Bänninger, D. Risikoorientierte Bewilligung von ErdwrmesondenRisk-oriented approval of borehole heat exchangers. Grundwasser 2011, 16, 13–24. [Google Scholar] [CrossRef]
- Klotzbücher, T.; Kappler, A.; Straub, K.L.; Haderlein, S.B. Biodegradability and groundwater pollutant potential of organic anti-freeze liquids used in borehole heat exchangers. Geothermics 2007, 36, 348–361. [Google Scholar] [CrossRef]
- Hähnlein, S.; Bayer, P.; Ferguson, G.; Blum, P. Sustainability and policy for the thermal use of shallow geothermal energy. Energy Policy 2013, 59, 914–925. [Google Scholar] [CrossRef]
- Yang, G.; Ge, M. Research on group arrangement method of ground heat exchanger under coupled thermal conduction and groundwater seepage conditions. Renew. Energy 2014, 32, 1182–1187. [Google Scholar]
- Fleuchaus, P.; Blum, P. Damage event analysis of vertical ground source heat pump systems in Germany. Geotherm. Energy 2017, 5, 5–10. [Google Scholar] [CrossRef]
- Zhu, K.; Fang, L.; Diao, N.; Fang, Z. Potential underground environmental risk caused by GSHP systems. Procedia Eng. 2017, 205, 1477–1483. [Google Scholar] [CrossRef]
- Anbergen, H.; Frank, J.; Mueller, L.; Sass, I. Freeze-Thaw-Cycles on Borehole Heat Exchanger Grouts: Impact on the Hydraulic Properties. Geotech. Test J. 2014, 37, 639–651. [Google Scholar] [CrossRef]
- Allan, M.L.; Philippacopoulos, A.J. Ground water protection issues with geothermal heat pumps. Geotherm. Resour. Counc. Trans. 1999, 23, 101–105. [Google Scholar]
- Sun, P.; Yang, D.; Chen, Y. Introduction to Coupling Models for Multiphysics and Numerical Simulations; China Science and Technology Press: Beijing, China, 2007; ISBN 9787504646347. [Google Scholar]
- Chen, Y.; Lei, B.; Li, X.; Yang, C. Flow-Numerical Simulation of the Stability of A solid Tailing Coupling. Ind. Saf. Environ. Prot. 2020, 46, 4–6+12. [Google Scholar]
- Zhu, C.; Shan, X.; Zhang, G.; Liu, Q.; Jiao, Z. Three-dimensional thermo-hydro-mechanical coupled modeling of thermal anomalies before the 2008 Wenchuan earthquake. Geosci. J. 2020, 24, 689–699. [Google Scholar] [CrossRef]
- Bai, B. Research on Hydrodynamic Parameters in Rock Reservoir and Optimization of Geothermal System; China University of Petroleum (East China): Qingdao, China, 2018. [Google Scholar]
- Fan, Z. Study on In-Situ Stress of Tight Reservoir under Multi-Field Coupling; China University of Petroleum (East China): Qingdao, China, 2017. [Google Scholar]
- Xin, Y. Numerical Investigation of EGS with Coupling Method Based Fractal Characteristics of Fracture System; China University of Petroleum (East China): Qingdao, China, 2019. [Google Scholar]
- Salciarin, D.; Ronchi, F.; Claudio, R.; Tamagnini, C. Thermo-hydro-mechanical response of a large piled raft equipped with energy piles: A parametric study. Acta Geotech. 2017, 12, 703–728. [Google Scholar] [CrossRef]
- Laloui, L.; Nuth, M.; Vulliet, L. Experimental and numerical investigations of the behaviour of a heat exchanger pile. Int. J. Numer. Anal. Methods Geomech. 2010, 30, 763–781. [Google Scholar] [CrossRef]
- Donna, A.D.; Laloui, L. Numerical analysis of the geotechnical behaviour of energy piles. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 861–888. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, X.; Xu, Y.; Yao, J.; Wang, H.; Lv, S.; Sun, Z.; Huang, Y.; Cai, M.; Huang, X. Numerical simulation of the heat extraction in EGS with thermal-hydraulic-mechanical coupling method based on discrete fractures model. Energy 2017, 120, 20–33. [Google Scholar] [CrossRef]
- Qin, F. Heat Transfer Process and Optimization of Enhanced Geothermal System (EGS) Based on Heat Flow-Solid Coupling Analysis; Kunming University of Science and Technology: Kunming, China, 2020. [Google Scholar]
- Yao, C.; Shao, Y.; Yang, J.; Huang, F.; He, C.; Jiang, Q.; Zhou, C. Effects of fracture density, roughness, and percolation of fracture network on heat-flow coupling in hot rock masses with embedded three-dimensional fracture network. Geothermics 2020, 87, 101846. [Google Scholar] [CrossRef]
- Dan, Z. Numerical Simulation Study of the Wellbore Heat Transfer and the Thermal-Hydraulic Coupling in Random Fracture Reservoirs; Northeast Petroleum University: Daqing, China, 2021. [Google Scholar]
- Kavanaugh, S.; Rafferty, K. Geothermal Heating and Cooling: Design of Ground-Source Heat Pump Systems; ASHRAE: Peachtree Corners, GA, USA, 2014. [Google Scholar]
- Jiang, W.; Zhou, H.; Li, Y.; Liu, W.; Gong, C.; Ge, X. Permeability Measurement of Karst Fractured Media Based on Groundwater Velocity and Direction Within a Borehole. Saf. Environ. Eng. 2018, 25, 1–7+18. [Google Scholar]
- Deng, F.; Pei, P.; Ren, Y.; Luo, T.; Chen, Y. Investigation and evaluation methods of shallow geothermal energy considering the influences of fracture water flow. Geotherm. Energy 2023, 11, 25. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).