Tackling Uncertainty: Forecasting the Energy Consumption and Demand of an Electric Arc Furnace with Limited Knowledge on Process Parameters
Abstract
1. Introduction
1.1. The EAF Process
1.2. Forecast Modelling
1.3. Energy Forecast Modelling of EAFs
1.4. Research Needs
- Is a neural network approach suitable for forecasting the energy demand in a temporally resolved manner to monitor the contracted grid connection capacity of an EAF?
- How can optimized electricity procurement be supported by a statistic–stochastic energy consumption forecast model based on non-perfect knowledge?
- How accurate and robust are the forecast results qualitatively and quantitatively?
2. Materials and Methods
2.1. Machine Learning: LSTM Neural Networks for Intra-Hour Forecast
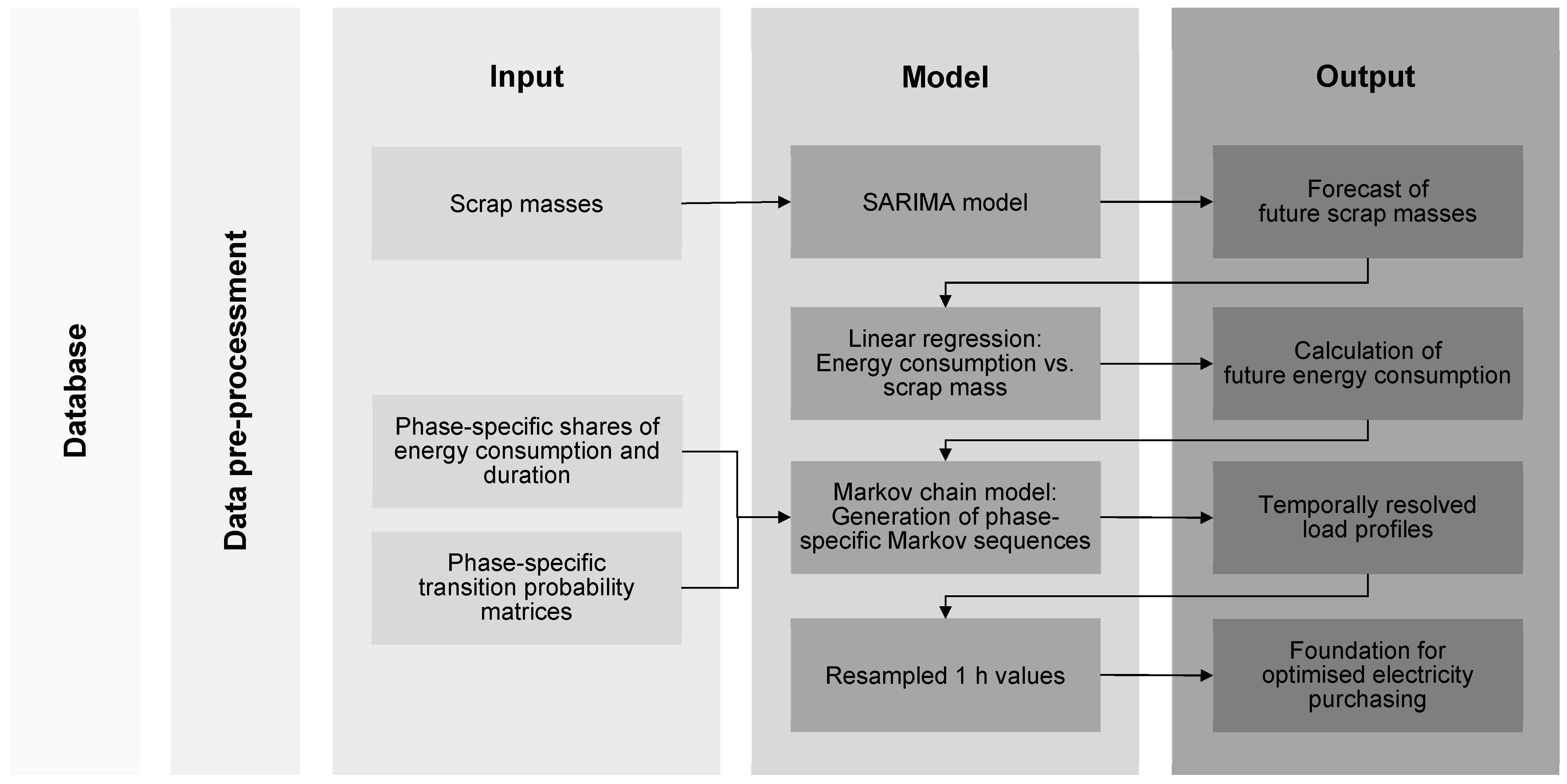
2.2. Statistic–Stochastic Model: SARIMA and Markov Chains for Day-Ahead Forecast
3. Results and Discussion
3.1. Intra-Hour Forecast
3.1.1. O-LSTM NN
3.1.2. M-LSTM NN
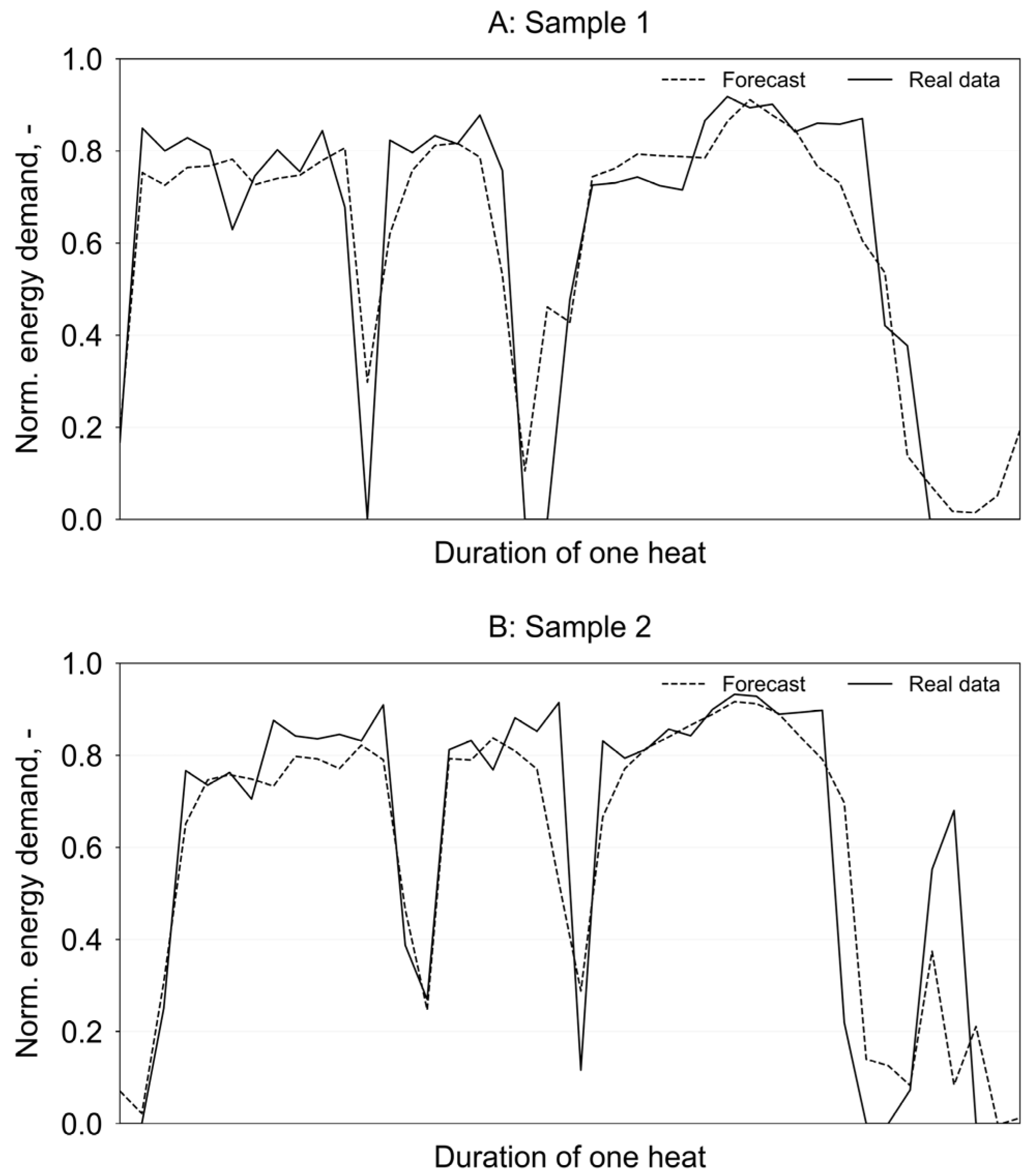
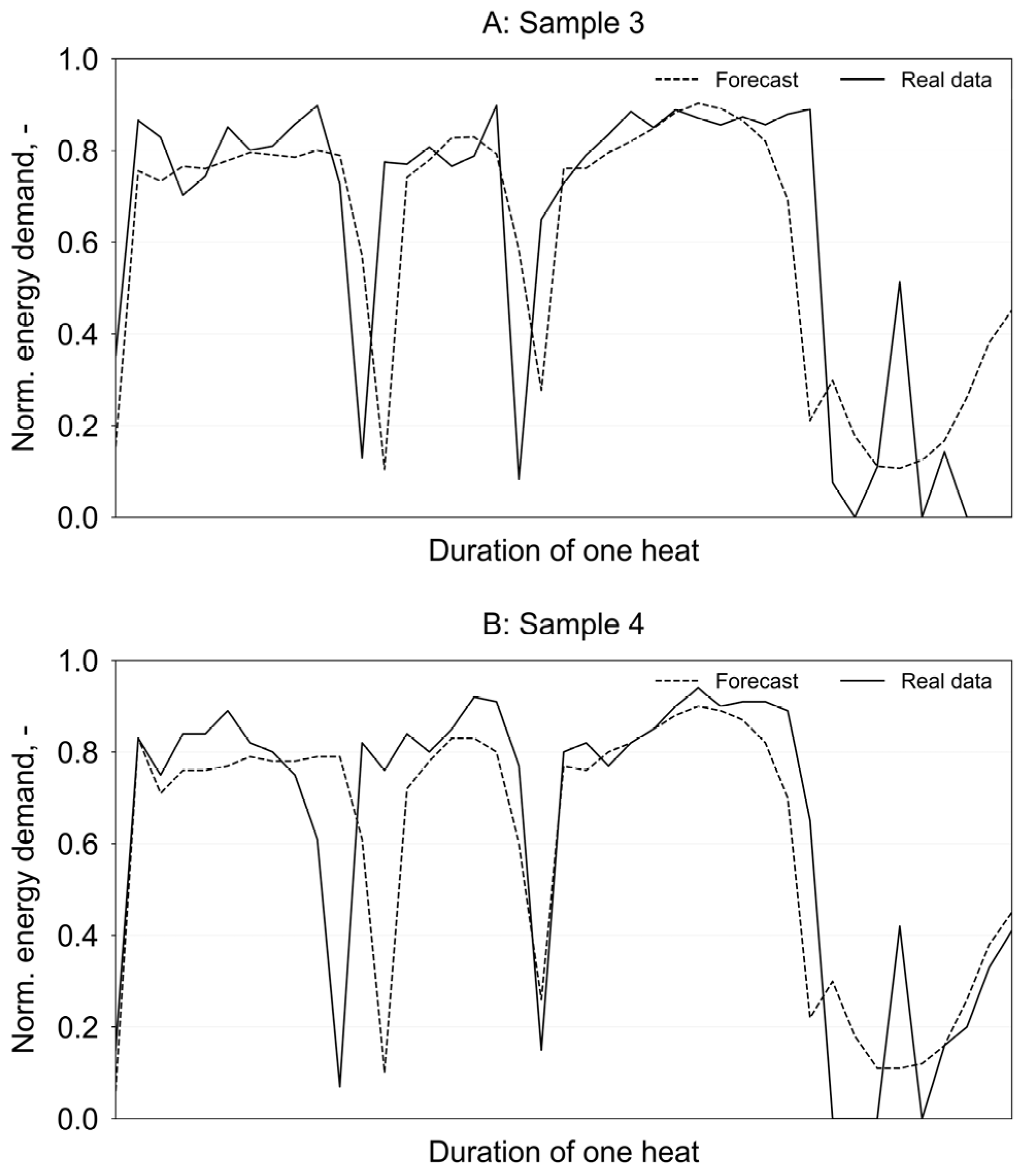
3.2. Day-Ahead Forecast
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Greening, L.A.; Boyd, G.; Roop, J.M. Modeling of industrial energy consumption: An introduction and context. Energy Econ. 2007, 29, 599–608. [Google Scholar] [CrossRef]
- Paulus, M.; Borggrefe, F. The potential of demand-side management in energy-intensive industries for electricity markets in Germany. Appl. Energy 2011, 88, 432–441. [Google Scholar] [CrossRef]
- International Energy Agency. Iron and Steel Technology Roadmap: Towards More Sustainable Steelmaking; International Energy Agency: Paris, France, 2021. [Google Scholar]
- Fan, Z.; Friedmann, S.J. Low-carbon production of iron and steel: Technology options, economic assessment, and policy. Joule 2021, 5, 829–862. [Google Scholar] [CrossRef]
- Marchiori, F.; Belloni, A.; Benini, M.; Cateni, S.; Colla, V.; Ebel, A.; Lupinelli, M.; Nastasi, G.; Neuer, M.; Pietrosanti, C.; et al. Integrated Dynamic Energy Management for Steel Production. Energy Procedia 2017, 105, 2772–2777. [Google Scholar] [CrossRef]
- Chen, C.; Liu, Y.; Kumar, M.; Qin, J.; Ren, Y. Energy consumption modelling using deep learning embedded semi-supervised learning. Comput. Ind. Eng. 2019, 135, 757–765. [Google Scholar] [CrossRef]
- Carlsson, L.S.; Samuelsson, P.B.; Jönsson, P.G. Modeling the Effect of Scrap on the Electrical Energy Consumption of an Electric Arc Furnace. Processes 2020, 8, 1044. [Google Scholar] [CrossRef]
- European Ferrous Recovery and Recycling Federation. EU-27 Steel Scrap Specification; European Ferrous Recovery and Recycling Federation: Brussels, Belgium, 2007. [Google Scholar]
- Carlsson, L.S.; Samuelsson, P.B.; Jönsson, P.G. Predicting the Electrical Energy Consumption of Electric Arc Furnaces Using Statistical Modeling. Metals 2019, 9, 959. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Wang, Y.; Weron, R.; Yang, D.; Zareipour, H. Energy Forecasting: A Review and Outlook. IEEE Open J. Power Energy 2020, 7, 376–388. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V.; Semenoglou, A.-A.; Mulder, G.; Nikolopoulos, K. Statistical, machine learning and deep learning forecasting methods: Comparisons and ways forward. J. Oper. Res. Soc. 2022, 74, 840–859. [Google Scholar] [CrossRef]
- Barker, J. Machine learning in M4: What makes a good unstructured model? Int. J. Forecast. 2020, 36, 150–155. [Google Scholar] [CrossRef]
- Çamdalı, Ü.; Tunç, M. Modelling of electric energy consumption in the AC electric arc furnace. Int. J. Energy Res. 2002, 26, 935–947. [Google Scholar] [CrossRef]
- Logar, V.; Dovžan, D.; Škrjanc, I. Mathematical Modeling and Experimental Validation of an Electric Arc Furnace. ISIJ Int. 2011, 51, 382–391. [Google Scholar] [CrossRef]
- Zhou, D.; Gao, F.; Guan, X.; Chen, Z.; Li, S.; Lu, Q. Daily electricity consumption forecast for a steel corporation based on NNLS with feature selection. In Proceedings of the 2004 International Conference on Power System Technology, 2004. PowerCon 2004, Singapore, 21–24 November 2004; pp. 1292–1297. [Google Scholar] [CrossRef]
- Andonovski, G.; Tomažič, S. Comparison of data-based models for prediction and optimization of energy consumption in electric arc furnace (EAF). IFAC-PapersOnLine 2022, 55, 373–378. [Google Scholar] [CrossRef]
- Kovačič, M.; Stopar, K.; Vertnik, R.; Šarler, B. Comprehensive Electric Arc Furnace Electric Energy Consumption Modeling: A Pilot Study. Energies 2019, 12, 2142. [Google Scholar] [CrossRef]
- Carlsson, L.; Samuelsson, P.; Jönsson, P. Using Interpretable Machine Learning to Predict the Electrical Energy Consumption of an Electric Arc Furnace. Stahl Eisen 2019, 139, 24–29. [Google Scholar]
- Dock, J.; Janz, D.; Weiss, J.; Marschnig, A.; Kienberger, T. Time- and component-resolved energy system model of an electric steel mill. Clean. Eng. Technol. 2021, 4, 100223. [Google Scholar] [CrossRef]
- Baumann, S.; Gnisia, M.; Feifel, P.; Klingauf, U. Identifikation und Behandlung von Ausreißern in Flugbetriebsdaten für Machine Learning Modelle. In Proceedings of the Deutscher Luft- und Raumfahrtkongress 2018, Friedrichshafen, Germany, 6 September 2018. [Google Scholar]
- Visplore—Software for Visual Time Series Analysis, Visplore (v2023 a (1.5.2)); Visplore GmbH: Vienna, Austria, 2020.
- Butt, F.M.; Hussain, L.; Mahmood, A.; Lone, K.J. Artificial Intelligence based accurately load forecasting system to forecast short and medium-term load demands. Math. Biosci. Eng. 2020, 18, 400–425. [Google Scholar] [CrossRef] [PubMed]
- Staudemeyer, R.C.; Morris, E.R. Understanding LSTM—A Tutorial into Long Short-Term Memory Recurrent Neural Networks. arXiv 2019, arXiv:1909.09586v1. [Google Scholar]
- Elgeldawi, E.; Sayed, A.; Galal, A.R.; Zaki, A.M. Hyperparameter Tuning for Machine Learning Algorithms Used for Arabic Sentiment Analysis. Informatics 2021, 8, 79. [Google Scholar] [CrossRef]
- Carlsson, L.S.; Samuelsson, P.B.; Jönsson, P.G. Interpretable Machine Learning—Tools to Interpret the Predictions of a Machine Learning Model Predicting the Electrical Energy Consumption of an Electric Arc Furnace. Steel Res. Int. 2020, 91, 2000053. [Google Scholar] [CrossRef]
- Taieb, S.B.; Sorjamaa, A.; Bontempi, G. Multiple-output modeling for multi-step-ahead time series forecasting. Neurocomputing 2010, 73, 1950–1957. [Google Scholar] [CrossRef]
- Fang, T.; Lahdelma, R. Evaluation of a multiple linear regression model and SARIMA model in forecasting heat demand for district heating system. Appl. Energy 2016, 179, 544–552. [Google Scholar] [CrossRef]
- Andoh, P.Y.; Sekyere, C.K.K.; Mensah, L.D.; Dzebre, D.E.K. Forecasting Electricity Demand in Ghana with the SARIMA Model. J. Appl. Eng. Technol. Sci. 2021, 3, 1–9. [Google Scholar] [CrossRef]
- Musbah, H.; El-Hawary, M. SARIMA Model Forecasting of Short-Term Electrical Load Data Augmented by Fast Fourier Transform Seasonality Detection. In Proceedings of the 2019 IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019. [Google Scholar]
- Hu, W.; Tong, S.; Mengersen, K.; Connell, D. Weather variability and the incidence of cryptosporidiosis: Comparison of time series poisson regression and SARIMA models. Ann. Epidemiol. 2007, 17, 679–688. [Google Scholar] [CrossRef] [PubMed]
- Esfahani, M.T.; Vahidi, B. A New Stochastic Model of Electric Arc Furnace Based on Hidden Markov Model: A Study of Its Effects on the Power System. IEEE Trans. Power Deliv. 2012, 27, 1893–1901. [Google Scholar] [CrossRef]
- Chen, F.; Sastry, V.V.; Venkata, S.S.; Athreya, K.B. A Robust Markov-Like Mode for Three Phase Arc Furnaces. Caribb. Colloq. Power Qual. 2003, 2003, 1–6. [Google Scholar]
- Stewart, W. Probability, Markov Chains, Queues, and Simulation: The Mathematical Basis of Performance Modeling; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Austrian Power Grid AG. Ausgleichsenergiepreise. Available online: https://markttransparenz.apg.at/markt/Markttransparenz/Netzregelung/Ausgleichsenergiepreise (accessed on 4 November 2023).
- Austrian Power Grid AG. Day-Ahead Preise. Available online: https://markttransparenz.apg.at/markt/Markttransparenz/Uebertragung/EXAA-Spotmarkt (accessed on 4 November 2023).
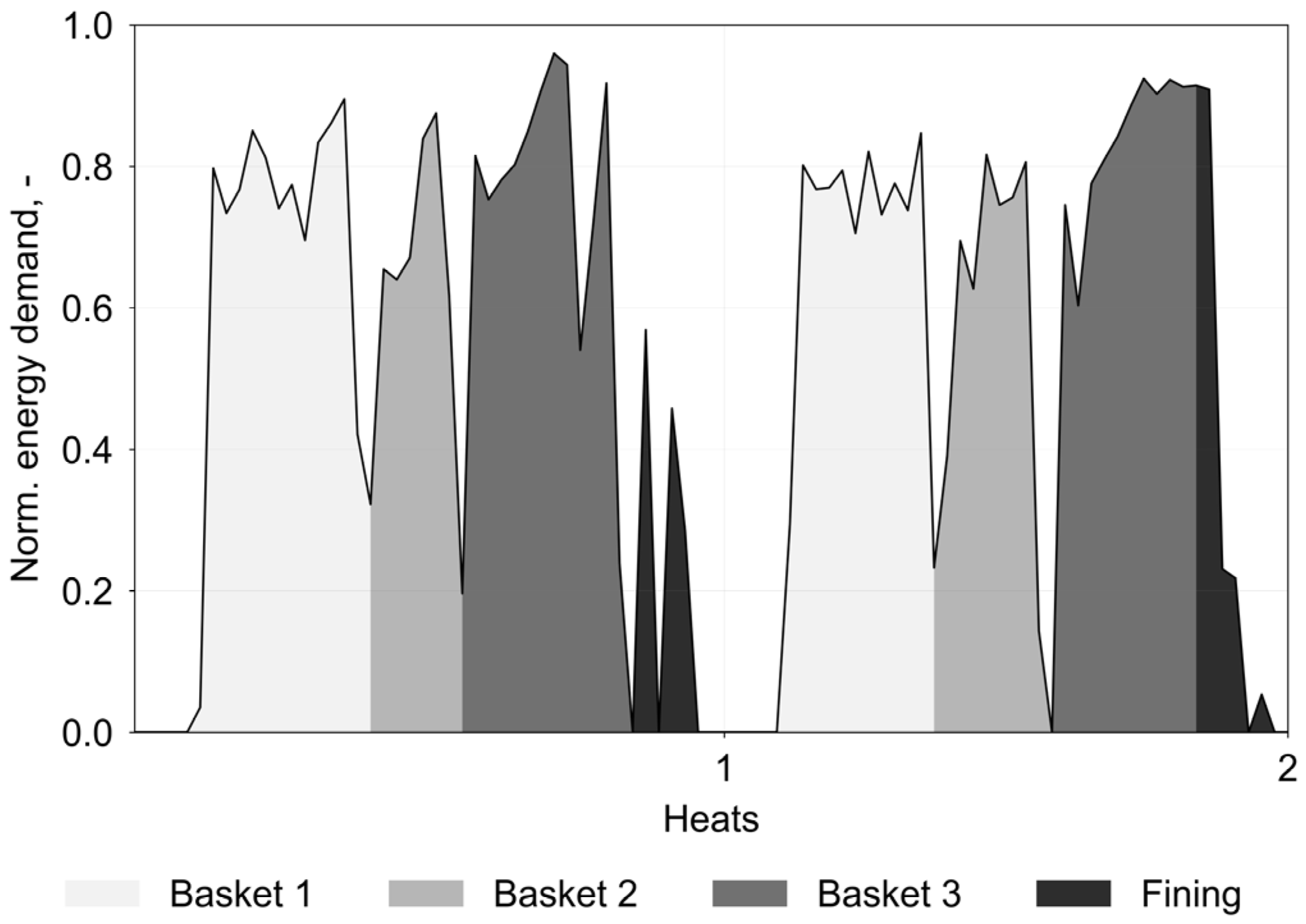





| Scrap Mass [%] | Duration [%] | Heat-Based Energy Consumption [%] | |
|---|---|---|---|
| Preparation | - | 5.2 | 0.2 |
| Basket 1 | 47.4 | 29.0 | 31.6 |
| Basket 2 | 24.1 | 16.2 | 19.6 |
| Basket 3 | 28.5 | 18.2 | 25.7 |
| Fining | - | 25.2 | 20.8 |
| Tapping | - | 6.2 | 2.1 |
| Category | Specification | Dimensions | Density | Steriles | Aimed Analytical Contents (Residuals) in % | ||
|---|---|---|---|---|---|---|---|
| Cu | Sn | Cr, Ni, Mo | |||||
| Old Scrap | E1 | Thickness < 6 mm <1.5 × 0.5 × 0.5 m | ≥0.5 | <1.5% | ≤0.400 | ≤0.020 | Σ ≤ 0.300 |
| Old Scrap | E3 | Thickness ≥ 6 mm <1.5 × 0.5 × 0.5 m | ≥0.6 | ≤1% | ≤0.250 | ≤0.010 | Σ ≤ 0.250 |
| New Scrap | E8 | Thickness < 3 mm <1.5 × 0.5 × 0.5 m | ≥0.4 | <0.3% | Σ ≤ 0.300 | Σ ≤ 0.300 | Σ ≤ 0.300 |
| Shredded | E40 | n.d. | >0.9 | <0.4% | Σ ≤ 0.250 | Σ ≤ 0.020 | n.d. |
| High Residual Scrap | EHRM | max. 1.5 × 0.5 × 0.5 m | ≥0.6 | <0.7% | ≤0.400 | ≤0.030 | Σ ≤ 1.0 |
| Approach | Target Variable, Unit | Error Measure for … |
|---|---|---|
| O-LSTM NN | Energy Demand, MW | 15 min |
| M-LSTM NN | Energy Demand, MW | 15 min |
| Statistic–stochastic model | ||
- SARIMA | Scrap mass, t | Hours (heats) |
- Markov | Energy Consumption, MWh | One hour |
| rRMSE, % | MAPE, % | |||||||
|---|---|---|---|---|---|---|---|---|
| 0′–15′ | 15′–30′ | 30′–45′ | 45′–60′ | 0′–15′ | 15′–30′ | 30′–45′ | 45′–60′ | |
| Sample 1 | 3.71 | 1.02 | 3.42 | 11.97 | 11.75 | 0.95 | 2.94 | 7.66 |
| Sample 2 | 1.30 | 8.44 | 6.16 | 41.43 | 1.64 | 7.55 | 5.40 | 41.59 |
| Sample 3 | 7.97 | 0.73 | 6.50 | - | 5.87 | 0.60 | 15.90 | - |
| Sample 4 | 10.00 | 14.83 | 2.05 | 2.76 | 7.33 | 14.36 | 2.09 | 17.71 |
| Sample 5 | 30.38 | 16.29 | 0.17 | 3.22 | 25.06 | 25.13 | 0.18 | 2.55 |
| Mean | 10.67 | 8.26 | 3.66 | 11.88 | 10.33 | 9.72 | 5.30 | 17.38 |
| rRMSE, % | MAPE, % | |||||||
|---|---|---|---|---|---|---|---|---|
| 0′–15′ | 15′–30′ | 30′–45′ | 45′–60′ | 0′–15′ | 15′–30′ | 30′–45′ | 45′–60′ | |
| Sample 1 | 18.71 | 3.35 | 15.39 | 50.63 | 60.11 | 3.13 | 13.30 | 32.40 |
| Sample 2 | 41.87 | 12.94 | 8.04 | 46.49 | 53.84 | 11.48 | 7.19 | 46.30 |
| Sample 3 | 10.00 | 0.44 | 5.81 | - | 7.46 | 0.37 | 14.22 | - |
| Sample 4 | 11.67 | 4.51 | 4.45 | 17.49 | 8.59 | 4.41 | 4.35 | 13.64 |
| Sample 5 | 25.75 | 41.01 | 9.23 | 38.67 | 21.33 | 63.35 | 7.23 | 30.01 |
| Mean | 21.60 | 12.45 | 8.58 | 38.32 | 30.27 | 16.55 | 9.26 | 30.59 |
| rRMSE, % | MAPE, % | |||||||
|---|---|---|---|---|---|---|---|---|
| 10 Heats | 20 Heats | 30 Heats | 60 Heats | 10 Heats | 20 Heats | 30 Heats | 60 Heats | |
| (App. 7 h) | (App. 14 h) | (App. 21 h) | (36(+) h) | (App. 7 h) | (App. 14 h) | (App. 21 h) | (36(+) h) | |
| Sample 1 | 3.12 | 3.44 | 3.44 | 3.98 | 2.13 | 2.72 | 2.95 | 3.36 |
| Sample 2 | 4.52 | 4.73 | 4.20 | 4.09 | 2.64 | 4.33 | 2.84 | 3.47 |
| Sample 3 | 3.88 | 3.76 | 3.66 | 3.77 | 2.03 | 2.89 | 3.10 | 2.94 |
| Sample 4 | 2.80 | 3.55 | 3.77 | 3.45 | 1.63 | 2.77 | 2.53 | 2.80 |
| Sample 5 | 2.15 | 2.15 | 3.23 | 3.23 | 2.52 | 1.66 | 3.02 | 2.47 |
| Mean | 3.29 | 3.53 | 3.66 | 3.70 | 2.19 | 2.87 | 2.89 | 3.01 |
| rRMSE, % | MAPE, % | |||||||
|---|---|---|---|---|---|---|---|---|
| 10 Heats | 20 Heats | 30 Heats | 60 Heats | 10 Heats | 20 Heats | 30 Heats | 60 Heats | |
| (App. 7 h) | (App. 14 h) | (App. 21 h) | (36(+) h) | (App. 7 h) | (App. 14 h) | (App. 21 h) | (36(+) h) | |
| Sample 1 | 16.07 | 14.13 | 25.99 | 23.96 | 10.65 | 8.88 | 17.17 | 15.26 |
| Sample 2 | 22.67 | 23.44 | 24.75 | 23.26 | 13.26 | 14.48 | 15.17 | 17.93 |
| Sample 3 | 15.40 | 22.23 | 21.04 | 23.44 | 10.47 | 16.16 | 14.20 | 15.08 |
| Sample 4 | 15.57 | 19.99 | 27.05 | 25.36 | 10.41 | 13.45 | 23.66 | 21.30 |
| Sample 5 | 21.83 | 20.68 | 19.80 | 18.02 | 15.83 | 13.57 | 11.73 | 10.44 |
| Mean | 18.31 | 20.09 | 23.73 | 22.81 | 12.12 | 13.31 | 16.39 | 16.00 |
| Standard Load Profile | Forecast Model | |||
|---|---|---|---|---|
| MWh to Be Balanced, % | Cost Savings, % | MWh to Be Balanced, % | Cost Savings, % | |
| Sample 1 | 8.42 | 1.48 | 3.33 | 0.61 |
| Sample 2 | 15.60 | −3.39 | 1.23 | −0.17 |
| Sample 3 | 16.06 | −3.82 | −0.95 | −0.66 |
| Sample 4 | 14.20 | −2.60 | 2.83 | 0.52 |
| Sample 5 | 6.31 | −0.47 | −2.71 | 0.75 |
| Mean | 12.12 | −1.76 | 2.21 | 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zawodnik, V.; Schwaiger, F.C.; Sorger, C.; Kienberger, T. Tackling Uncertainty: Forecasting the Energy Consumption and Demand of an Electric Arc Furnace with Limited Knowledge on Process Parameters. Energies 2024, 17, 1326. https://doi.org/10.3390/en17061326
Zawodnik V, Schwaiger FC, Sorger C, Kienberger T. Tackling Uncertainty: Forecasting the Energy Consumption and Demand of an Electric Arc Furnace with Limited Knowledge on Process Parameters. Energies. 2024; 17(6):1326. https://doi.org/10.3390/en17061326
Chicago/Turabian StyleZawodnik, Vanessa, Florian Christian Schwaiger, Christoph Sorger, and Thomas Kienberger. 2024. "Tackling Uncertainty: Forecasting the Energy Consumption and Demand of an Electric Arc Furnace with Limited Knowledge on Process Parameters" Energies 17, no. 6: 1326. https://doi.org/10.3390/en17061326
APA StyleZawodnik, V., Schwaiger, F. C., Sorger, C., & Kienberger, T. (2024). Tackling Uncertainty: Forecasting the Energy Consumption and Demand of an Electric Arc Furnace with Limited Knowledge on Process Parameters. Energies, 17(6), 1326. https://doi.org/10.3390/en17061326







