Research on Adaptive Cycle Engine Mode Transition Control Method

Abstract

Mode transition is an important dynamic process of an adaptive cycle engine (ACE). In order to obtain a smooth mode transition process, the closed-loop controller is designed based on the strong robust augmented linear quadric regulator (ALQR) method, and with the objective of minimizing the thrust fluctuation in the process of mode transition, an open-loop geometrical mechanism control schedules optimization method based on Bézier curves is proposed, so that the closed-loop control and the open-loop control can work in coordination. The simulation results at the subsonic cruise operating point and supersonic cruise operating point show that based on the optimized open-loop geometrical mechanism control schedules and the designed closed-loop ALQR control system, the ACE achieves fast and smooth geometrical mechanisms and engine output transition during the mode transition process with a maximum thrust fluctuation of 2.58%, which is much smaller than that of the traditional linear variation geometric mechanisms with a maximum 4.64% thrust fluctuation, which verifies the effectiveness of the proposed control method.

1. Introduction

As a novel variable cycle engine (VCE), an adaptive cycle engine (ACE) has the advantages of high specific thrust at supersonic cruise, low specific fuel consumption and high thrust-to-weight ratio at subsonic cruise [1,2,3]. So, it has attracted wide attention [4,5]. Its high performance is due to the ability of ACE to switch between triple-bypass and double-bypass modes, thus enabling it to operate in a thermal cycle that is more compatible with the flight state. Switching between the two modes is one of the key technologies of the ACE, and it is crucial to design an optimal mode switching control law to ensure the ACE operates safely, smoothly and quickly during the mode transition process [6,7].

Most of the research on ACE is about steady state modeling, characterization and performance optimization [8,9], etc. The research on mode transition control has been reported less [10]. The simple linear interpolation between the two modes is often used for geometric mechanism adjustment during the mode transition process, which is not able to ensure the performance of the engine during the transition state [11]. GE researched the mode transition process of the YF120 engine, but the control law design method was kept strictly confidential [12,13,14,15]. Grönstedt [16] of Sweden conducted an optimization study on the transition performance of a selective bleed VCE, and the guide vane angles of the three compression components, the adjustable areas of the three nozzles and the fuel flow were optimized by using the SQP algorithm to ensure a safe and smooth transition. Wang Hao [17] et al. proposed a mode transition method with stepwise thrust change, and optimized the mode transition control law by using a differential evolutionary algorithm. However, no validation tests have been conducted for the robustness and adaptability of the control law. Yangjing Wang [18] et al. determined the control variables corresponding to the starting and ending points of mode transition based on the sequential quadratic programming method, and the control variables are changed linearly to the ending point within 2.5 s. Chen Shangxi [19] adopted a simple linear variation control law for open-loop control geometric during the mode transition of VCE and a normal and stable transition process is achieved. Zhu Baibin [20] presented a mode transition control method combining of high-pressure speed controlled by fuel flow in closed-loop and other control variables adjusted in open-loop. However, the regulation schedule curves of the open-loop control variable s were given. Compared with the above method where the mode transition and geometric mechanisms adjustment are carried out simultaneously, Zheng Junchao [21] et al. proposed that the mode transition point should be set to where the low pressure rotor speed and the thrust are the same under the two modes, and the geometric mechanisms (except the mode selection valve) are kept unchanged during mode transition through pre-adjusting the geometric mechanism linearly to the mode transition point, achieving a smooth mode transition process.

It can be seen that most of the mode conversion methods reported currently use linear change geometric mechanism control laws. Although this control method can achieve the normal and stable mode transition of VCE, the output parameters of the engine are prone to fluctuate greatly during the mode conversion process, which affects the safe operation of the engine. As a strongly nonlinear system, the nonlinear control law may be more suitable for VCE mode transition process. To achieve optimal mode transition control schedules of the geometric mechanism, in this paper, the particle swarm optimization (PSO) was adopted to optimize the trajectories of the open-loop geometric mechanism constructed by Bézier curves to ensure the cooperation of the open-loop and the closed-loop geometric mechanisms. To ensure the robustness of the control system in the switching process, the augmented linear quadratic regulator (ALQR) method was adopted to design the closed-loop controller. The trajectories of the open-loop geometric mechanisms were optimized in the outer loop to ensure a smooth and safe mode transition process.

The remainder of this paper is organized as follows. Section 2 briefly introduces the principle of the mode transition process; Section 3 presents the ALQR control method used in the closed-loop control; Section 4 gives the structure of the proposed geometric mechanism optimization system; in Section 5, simulation and analysis are reported to verify the feasibility and effectiveness of the proposed method; Section 6 presents a summary.

2. Introduction of the Mode Transition Process

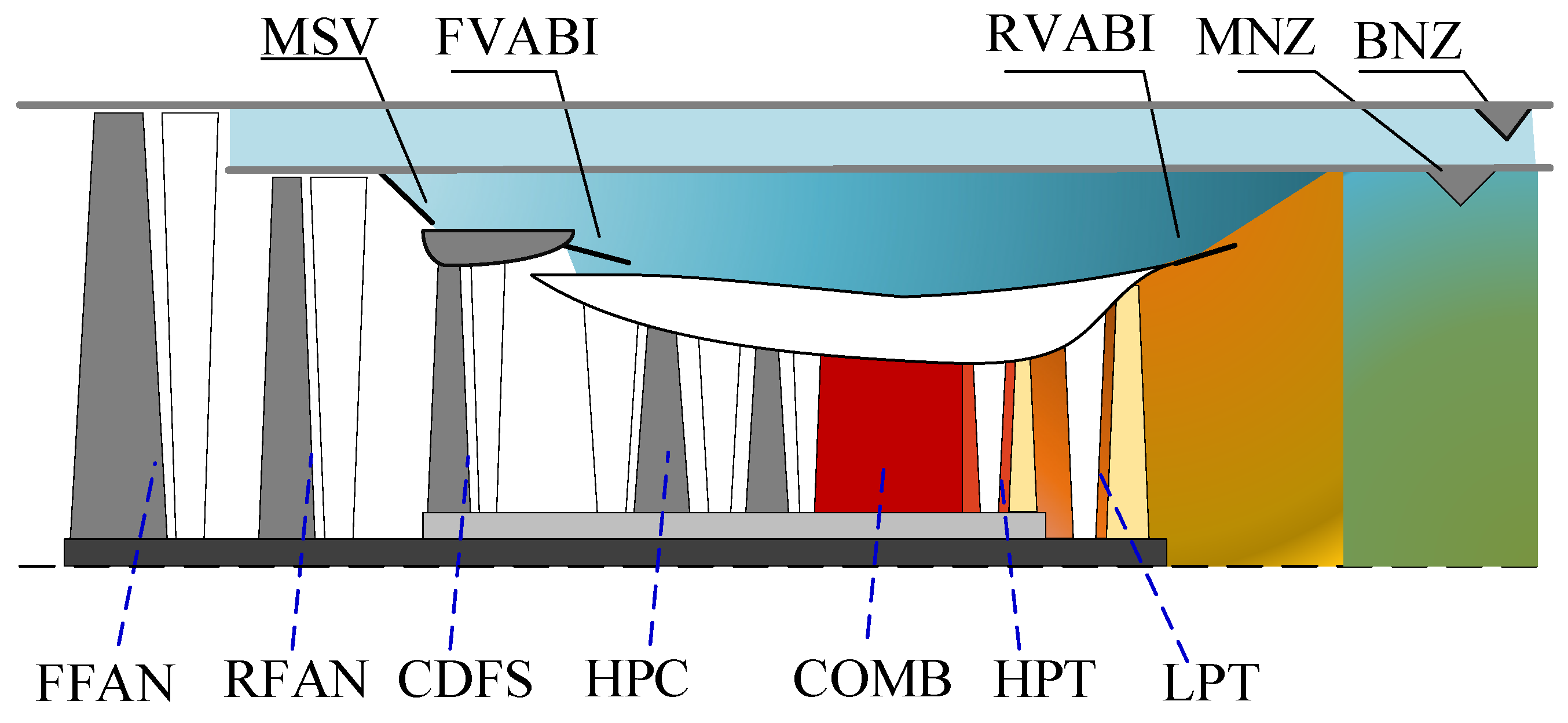
The structure of the ACE studied in this paper is shown in Figure 1. The core-driven-fan stage (CDFS) and high-pressure compressor (HPC) are driven by the high-pressure turbine (HPT). The front fan (FFAN) and the rare fan (RFAN) are driven by the low-pressure turbine (LPT). The mode selection valve (MSV) controls the open and closed states of the second bypass [22,23,24]. When the MSV is closed (MSV = 0), the ACE will operate at the double bypass mode. Otherwise, the ACE operates at the triple bypass mode (MSV = 1). The mode transition refers to the process whereby the MSV of ACE changes between 0 and 1.

There are 10 variable geometrics in the ACE researched, including the MSV, front and rare variable-area bypass injector (F/R VABI), variable stator vanes (VSV) of RFAN, CDFS and HPC, variable area guiders (VAG) of HPT and LPT, the third bypass nozzle area (BNZ) and the main nozzle (MNZ). The VSVs of RFAN and the VAG of HPT are scheduled according to the corrected speed of the LP and HP rotors to ensure the stable working of ACE. The schedules of the other variable geometrics are not determined during the mode transition process. Therefore, it is necessary to research their coordination working method to ensure the mode transition process is smooth and safe.

3. Closed-Loop Controller Design

The researched ACE adopts the double-variable closed-loop control method. The LP rotor speed N_L and the engine thrust F are kept constant through the regulation of the main fuel W_fm and the main nozzle area A₈. Considering that ALQR has the characteristics of a simple structure and strong robustness, and has a good research basis in aero engines [25,26,27], the ALQR method was adopted to design the controller of the ACE.

The modeling principles and methods of aircraft engines have become relatively mature, as detailed in reference [28]. The nonlinear mathematical model of ACE in the text is expressed as follows:

$$\{\begin{array}{l}\dot{\mathit{x}}=f(\mathit{x},\mathit{u})\\ \mathit{y}=h(\mathit{x},\mathit{u})\end{array}$$

(1)

Linearize Equation (1) at the equilibrium point (where the low-pressure speed is 100%) and obtain the state variable model as follows:

$$\{\begin{array}{l}\Delta \dot{\mathit{x}}=\mathit{A}\Delta \mathit{x}+\mathit{B}\Delta \mathit{u}\\ \Delta \mathit{y}=\mathit{C}\Delta \mathit{x}+\mathit{D}\Delta \mathit{u}\end{array}$$

(2)

where Δx = [ΔN_L, ΔN_H]^T, Δu = [ΔW_fm, ΔA₈]^T, Δy = [ΔN_L, ΔF]^T are the state, control and output vectors of the ACE, Δ indicates that the variables are small relative deviations from the equilibrium operating point (the magnitude of deviation in this paper is 1%) [28], N_H is the HP rotor speed. A, B, C, D are system matrixes of appropriate dimensions.

Taking into account the dynamics of the actuators (i.e., geometric mechanism), the controlled object is the series connection of the actuator and the engine, and described as:

$$\{\begin{array}{l}\Delta {\dot{\mathit{x}}}_{\mathsf{p}}={\mathit{A}}_{\mathsf{p}}\Delta {\mathit{x}}_{\mathsf{p}}+{\mathit{B}}_{\mathsf{p}}\Delta {\mathit{u}}_{\mathsf{r}}\\ \Delta \mathit{y}={\mathit{C}}_{\mathsf{p}}\Delta {\mathit{x}}_{\mathsf{p}}+{\mathit{D}}_{\mathsf{p}}\Delta {\mathit{u}}_{\mathsf{r}}\end{array}$$

(3)

where $\Delta {\mathit{x}}_{\mathsf{p}}={[\Delta N_{\mathsf{L}} \Delta N_{\mathsf{H}} \Delta W_{\mathsf{f}\mathsf{m}} \Delta A_8]}^{\mathsf{T}}$, $\Delta {\mathit{u}}_{\mathrm{r}}={[\Delta W_{\mathrm{fmr}} \Delta A_{8\mathrm{r}}]}^{\mathsf{T}}$ are the commands of the actuators.

$${\mathit{A}}_{\mathsf{p}}=\left[\begin{array}{l}\mathit{A} \mathit{B}\\ \mathsf{0} {\mathit{A}}_{\mathsf{a}}\end{array}\right],{\mathit{B}}_{\mathsf{p}}=\left[\begin{array}{l} \mathsf{0}\\ {\mathit{B}}_{\mathsf{a}}\end{array}\right],{\mathit{C}}_{\mathsf{p}}=\left[\mathit{C} \mathit{D}\right],{\mathit{D}}_{\mathsf{p}}=\mathsf{0}$$

(4)

where Aa, Ba are the system matrixes of the actuators.

To achieve the robust step signal tracking ability, the tracking errors are augmented into the state vector, so the model is changed into

$$\Delta \dot{\overline{\mathit{x}}}=\overline{\mathit{A}}\Delta \overline{\mathit{x}}+\overline{\mathit{B}}\Delta \overline{\mathit{u}}$$

(5)

where $\Delta \overline{\mathit{x}}={[\Delta {\dot{\mathit{x}}}_{\mathrm{P}}^T {\mathit{e}}^T ]}^T$, e = [N_Lr F_r]^T − [N_L F]^T is the tracking error vector, N_Lr, F_r are the commands of N_L, F. $\overline{\mathit{A}}=\left[\begin{array}{l} {\mathit{A}}_{\mathsf{p}} \mathsf{0}\\ -{\mathit{C}}_{\mathsf{p}} \mathsf{0}\end{array}\right],\overline{\mathit{B}}=\left[\begin{array}{l} {\mathit{B}}_{\mathsf{p}}\\ -{\mathit{D}}_{\mathsf{p}}\end{array}\right],\Delta \overline{\mathit{u}}=\Delta {\dot{\mathit{u}}}_{\mathsf{r}}$.

The ALQR controller for Equation (5) is

$$\begin{gathered} \Delta \overline{\mathit{u}}=\overline{\mathit{K}}\Delta \overline{\mathit{x}}=\left[\begin{array}{cc}{\mathit{K}}_{\dot{\mathit{x}}}& {\mathit{K}}_{\mathsf{e}}\end{array}\right]\left[\begin{array}{c}{\dot{\mathit{x}}}_{\mathsf{p}}\\ \mathit{e}\end{array}\right]={\mathit{K}}_{\dot{\mathit{x}}}{\dot{\mathit{x}}}_{\mathsf{p}}+{\mathit{K}}_{\mathsf{e}}\mathit{e} \\ \Delta {\mathit{u}}_{\mathsf{r}}={\displaystyle {\int }_0^t\overline{\mathit{u}}(\tau )d\tau }={\mathit{K}}_{\dot{\mathit{x}}}{\mathit{x}}_{\mathsf{p}}+{\mathit{K}}_{\mathsf{e}}{\displaystyle {\int }_0^t\mathit{e}}(\tau )d\tau \end{gathered}$$

(6)

where $\overline{\mathit{K}}=-{\mathit{R}}^{-\mathsf{1}}{\overline{\mathit{B}}}^{\mathsf{T}}\mathit{P}$, P is the solution of the following Riccati equation.

$${\overline{\mathit{A}}}^{\mathsf{T}}\mathit{P}+\mathit{P}\overline{\mathit{A}}-\mathit{P}\overline{\mathit{B}}{\mathit{R}}^{-1}{\overline{\mathit{B}}}^{\mathsf{T}}\mathit{P}+\mathit{Q}=\mathsf{0}$$

(7)

where $\mathit{Q}\ge \mathsf{0}$, $\mathit{R}\ge \mathsf{0}$ are the weighted matrixes of the following functional equation.

$$\underset{\mathit{Q},\mathit{R}}{\min J}={\displaystyle {\int }_0^{\infty } (\Delta {\overline{\mathit{x}}}^{\mathsf{T}}\mathit{Q}\Delta \overline{\mathit{x}}+\Delta {\overline{\mathit{u}}}^{\mathsf{T}}\mathit{R}\Delta \overline{\mathit{u}})dt}$$

(8)

So, the property of the controller is determined by the weighted matrixes Q and R. To obtain the optimal controller, the PSO is adopted to optimize the parameters of Q and R. As a swarm-based algorithm, PSO searches the best solution thought the experiences of its own and the colony’s. The performance indicators of the optimization process are as follows:

$$\underset{Q,R}{\min J}={\displaystyle {\int }_{\tau =0}^{t1}{\left[{\mathit{y}}_{\mathsf{r}1}\left(\tau \right)-N_{\mathsf{L}}\left(\tau \right)\right]}^2+{\left[{\mathit{y}}_{\mathsf{r}2}\left(\tau \right)-F\left(\tau \right)\right]}^2}d\tau$$

(9)

where [y_1r y_2r]^T = [N_Lr F_r]^T, [y₁ y₂]^T = [N_L F]^T.

To simplify the optimization process and ensure the positiveness of the weighted matrixes, Q∈$\mathfrak{R}$^6×6, R∈$\mathfrak{R}$^2×2 are set to diagonal matrixes. Therefore, the dimension of the optimization is 8 and the optimal controller matrix $\overline{\mathit{K}}$ can be obtained after optimization. The fuel flow and the nozzle area can be determined by the closed-loop control.

4. Open-Loop Geometrics Scheduling Optimization

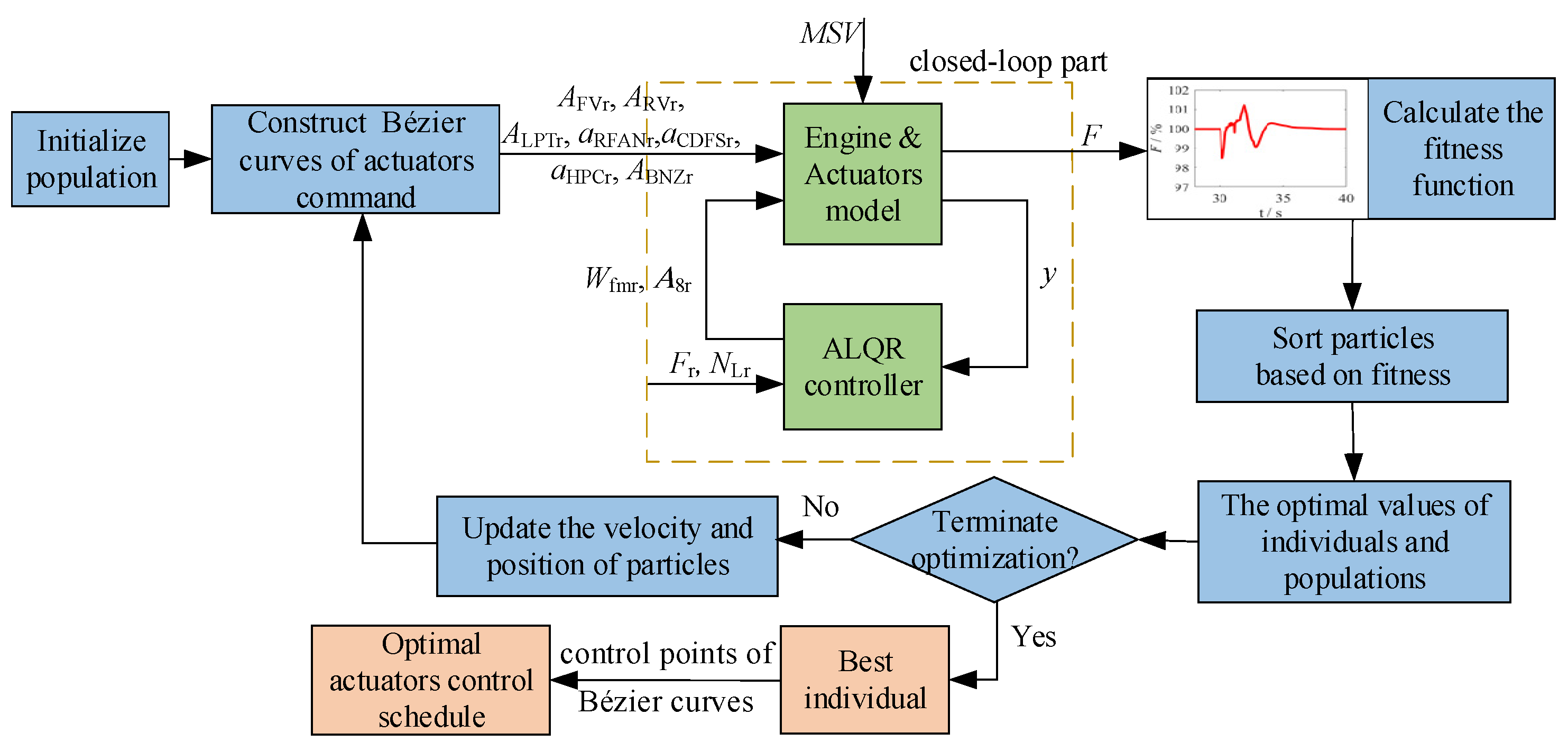
During the ACE mode transition process, in addition to the area of MNZ, VSVs of RFAN and VAG of HPT (the area of MNZ is the closed-loop control variable, and the VSVs of RFAN and VAG of HPT remain unchanged), the input trajectories of the other seven geometric mechanisms need to be determined. During the mode transition process, the MSV varies linearly between 0 and 1. In order to achieve the coordination between open-loop and closed-loop geometries, the inner loop adopts an ALQR steady-state controller, and the outer loop adopts PSO to optimizes the regulation schedules of the undetermined open-loop geometries according to the Bézier curve constructed [29]. The process of optimization is shown in Figure 2, where A_FVr, A_RVr, A_LPTr and A_BNZr represent the command of FVBI area, RVBI area, LPT VAG area and BNZ area; α_RFANr, α_CDFSr and α_LPTr represent the angle commands of RFAN’s VSV, CDFS’s VSV and HPC’s VSV, respectively.

A_FVr, A_RVr, A_LPTr, A_BNZr are the area commands of the FABI, RVABI, LPT VAG, BNZ, respectively. α_RFANr, α_CDFSr, α_HPCr are the angle commands of the VSV of FFAN, CDFS, HPC, respectively. They are scheduled based on the Bézier curves optimized by the PSO.

Bézier curves are mathematical curves applied to two-dimensional graphics applications. A Bézier curve equation B_z(t) containing np + 1 control points P_i (i = 0, 1, …, n_p) can be expressed as a linear combination of Bernstein polynomials of order n.

$${\mathit{B}}_{\mathsf{z}}(\mathcal{\kappa })={\displaystyle \sum _{i=0}^{n_{\mathsf{p}}}({\mathit{C}}_{n_{\mathsf{p}}}^i{\mathit{P}}_i{(1-\mathcal{\kappa })}^{n_{\mathsf{p}}-i}{\mathcal{\kappa }}^i)},\mathcal{\kappa }\in [0,1]$$

(10)

where $\mathcal{\kappa }$ is the scaling parameter. When it is changed from 0 to 1, the point on the Bessel curve moves from the starting point to the end point ${\mathit{C}}_{n_{\mathsf{p}}}^i=\frac{n_{\mathsf{p}}!}{(n_{\mathsf{p}} - i)!i!}$.

Each geometric mechanism adopts five control points, and the mode transition time is set to 2 s; then, the time instants corresponding to the five control points are [0 s, 0.5 s, 1 s, 1.5 s, 2 s]. For seven open-loop control geometrics, seven Bézier curves are constructed, so there are 35 control points that need to be optimized. The position vector X and the velocity vector V of the ith particle can be denoted as X_i = [X_i1, X_i2, …, X_i35], V_i = [V_i1, V_i2, …, V_i35]. The optimal position searched so far by the ith particle is p_best,i and the optimal position searched by the swarm is g_best. So, the velocity and position of the particles are updated as follows:

$$\{\begin{array}{l}{\mathit{V}}_i^{g+1}=\omega {\mathit{V}}_i^g+c_1{r}_1(p_{\mathrm{best},i}-{\mathit{X}}_i^g) +c_2{r}_2(g_{\mathrm{best}}-{\mathit{X}}_i^g)\\ {\mathit{X}}_i^{g+1}={\mathit{X}}_i^g+{\mathit{V}}_i^g\end{array}$$

(11)

where g represents current iteration. $\omega$ is an inertia factor, c₁, c₂ are non-negative acceleration factors, r₁, r₂ are random numbers between 0 and 1.

The target of the closed-loop control is to maintain F constant during the mode transition process. Therefore, the particles are evaluated by the maximum offset of thrust to the command during the mode transition process.

$$\underset{{\mathit{X}}_i}{\min \Delta F}=\max \{\left|F_{\mathsf{r}}-F_{\max }\right|,\left|F_{\mathsf{r}}-F_{\min }\right|\}$$

(12)

where F_max, F_min are the maximum and minimum thrust during the state transition process.

Each particle forms seven Bézier curves that generates the commands of the seven geometric mechanisms (i.e., actuators) during the mode transition process, and the particles are evaluated by Equation (12) that are determined by the cooperating of the open-loop geometric mechanisms and the closed-loop geometric mechanisms (determined by the ALQR). When the optimization satisfied the terminate condition, the best individual was output and formed optimal actuator control schedules of the open-loop geometric mechanisms.

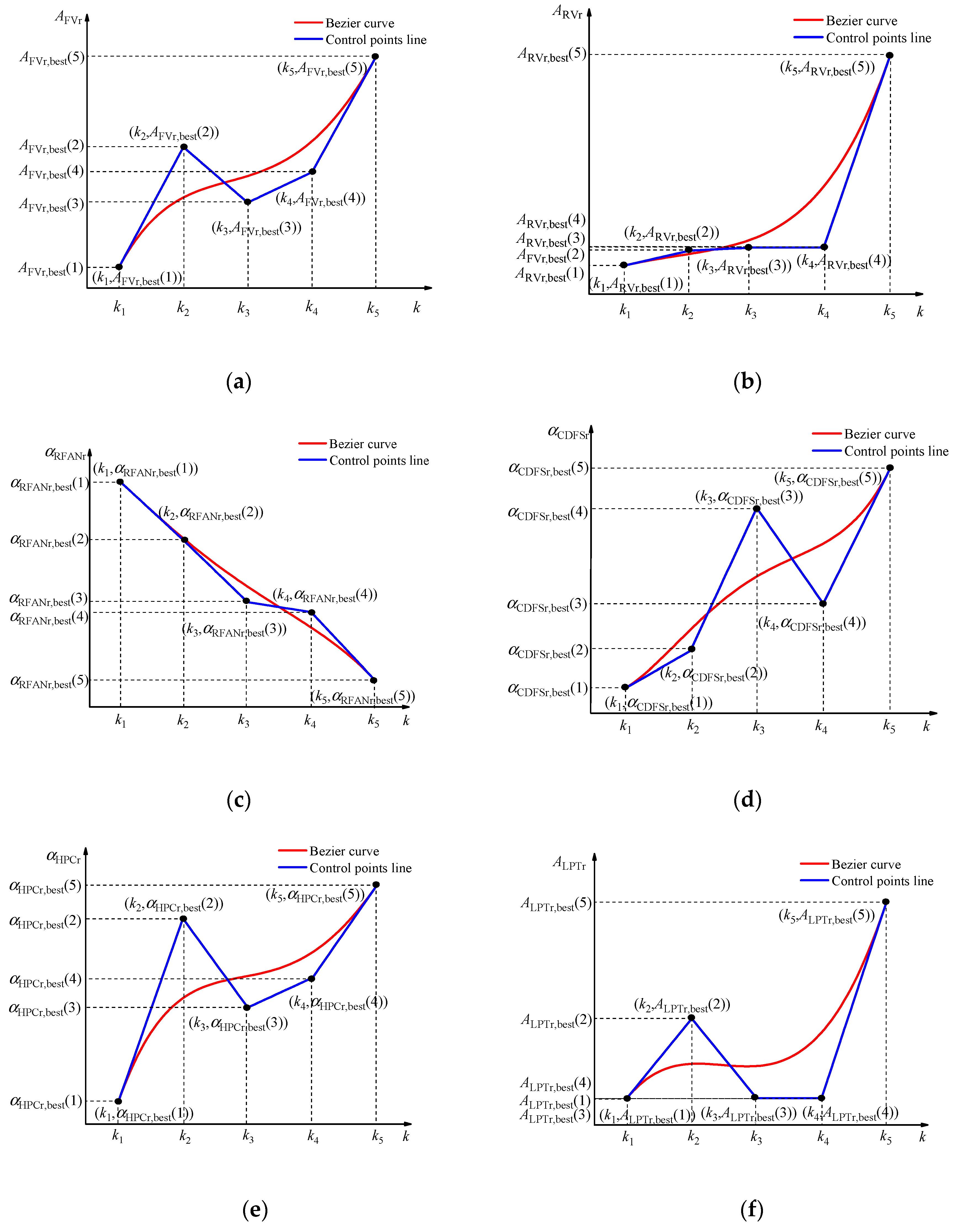
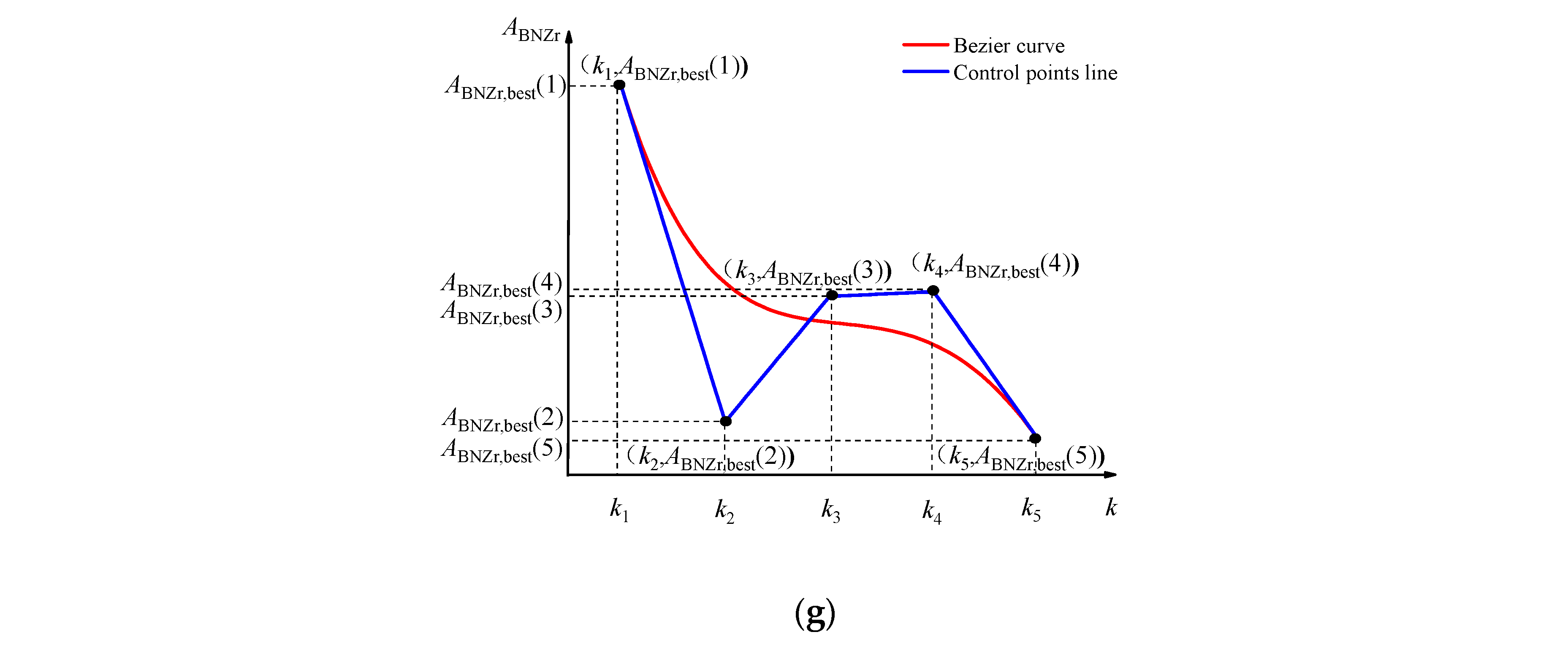
Taking the switching from three-bypass mode to two-bypass mode at the subsonic cruise operating point (H = 10 km, Ma = 0.9) as an example, the Bézier curve of each mechanism obtained is shown in Figure 3, where “Bézier curve” represents the Bézier curve calculated by the optimal control points, and “Control points line” represents the variation of the optimal control points. The optimization of the Bézier curve is starting from the equilibrium point of the three-bypass operation mode, and ending point at the equilibrium point of the double-bypass operation mode.

From Figure 3, it can be seen that the control schedules of the seven geometric mechanisms show an irregular smooth transition with the increase of the scaling factor κ. When κ changes linearly from 0 to 1, the time t changes linearly from 0 to 2 s, which allows the commands of the open-loop geometrical mechanisms to be varied over time during the mode transition process.

5. Validation

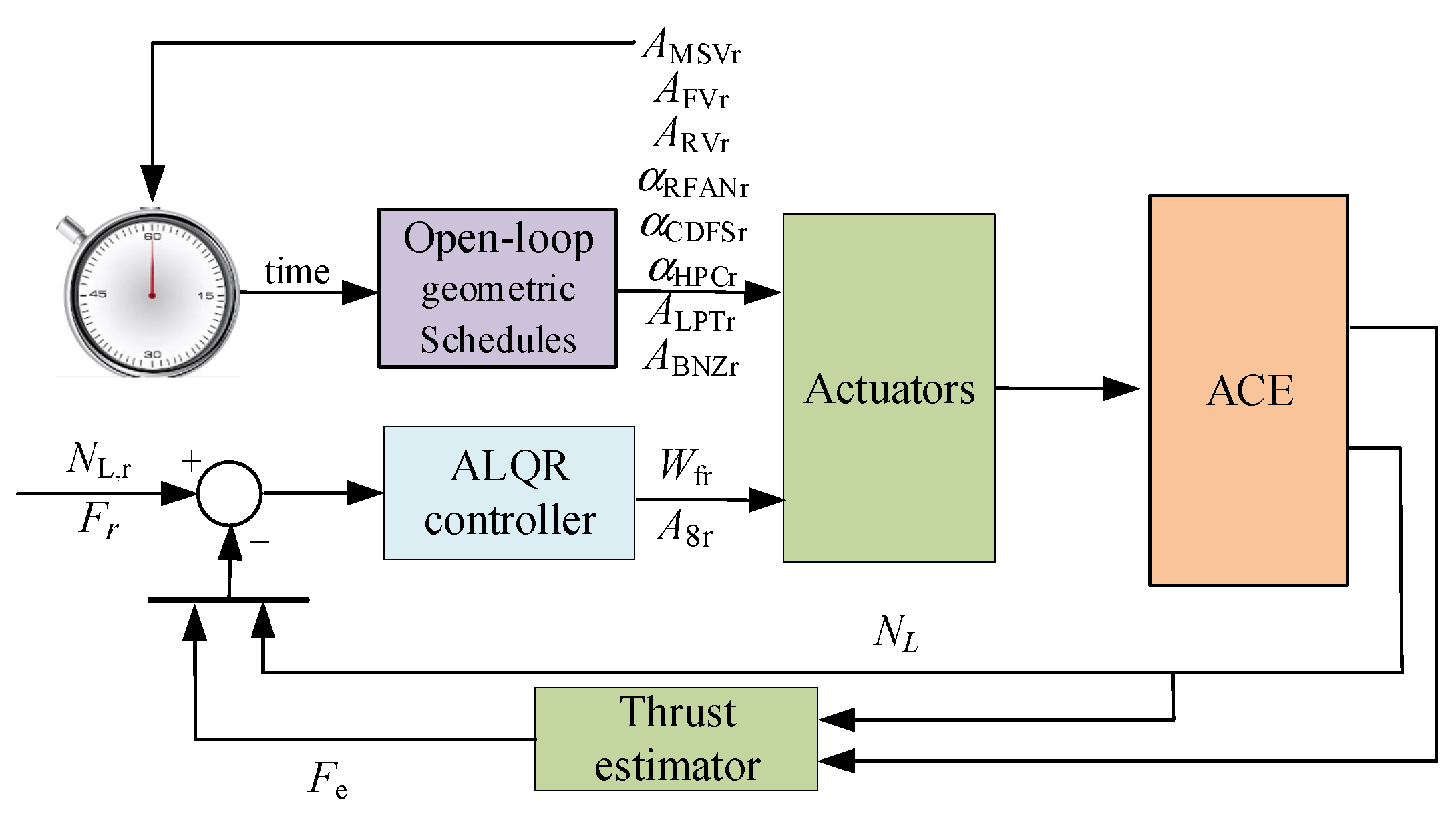
In order to verify the effectiveness, robustness and adaptability of the mode transition control, the transitions between double and triple-bypass mode are carried out in two typical flight conditions, subsonic cruise and supersonic cruise. In addition, the influence of Bézier curves orders on mode transition control are researched. Based on the open-loop geometric commands optimized under different conditions, a joint simulation verification of the open-loop and closed-loop regulation is carried out, and the structure of the control system verified in the simulation is shown in Figure 4. At this point, the optimization results of ALQR controller parameters ${\mathit{K}}_{\dot{\mathit{x}}}$ and ${\mathit{K}}_{\mathsf{e}}$ are:

$$\begin{array}{l}{\mathit{K}}_{\dot{\mathit{x}}}=\left[\begin{array}{l} -10.9122 -25.2422 -15.5508 -0.0681\\ -100.1029 -64.9813 -1.4131 -10.3695\end{array}\right]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\mathit{K}}_{\mathsf{e}}=\left[\begin{array}{l}-5.2087 87.7928\\ 200.9401 47.2531\end{array}\right]\end{array}$$

(13)

When a mode transition starts, the MSV area command changes with time and triggers the time counter for the mode transition; then, the seven geometry mechanism commands optimized by PSO are scheduled according to the time variation. The feedback thrust Fe is estimated by the thrust estimator of the neural network which is not introduced and the estimation error is not taken into account in this paper.

5.1. Validation of Mode Transition Control Effectiveness

(1)

Result at the subsonic cruise point

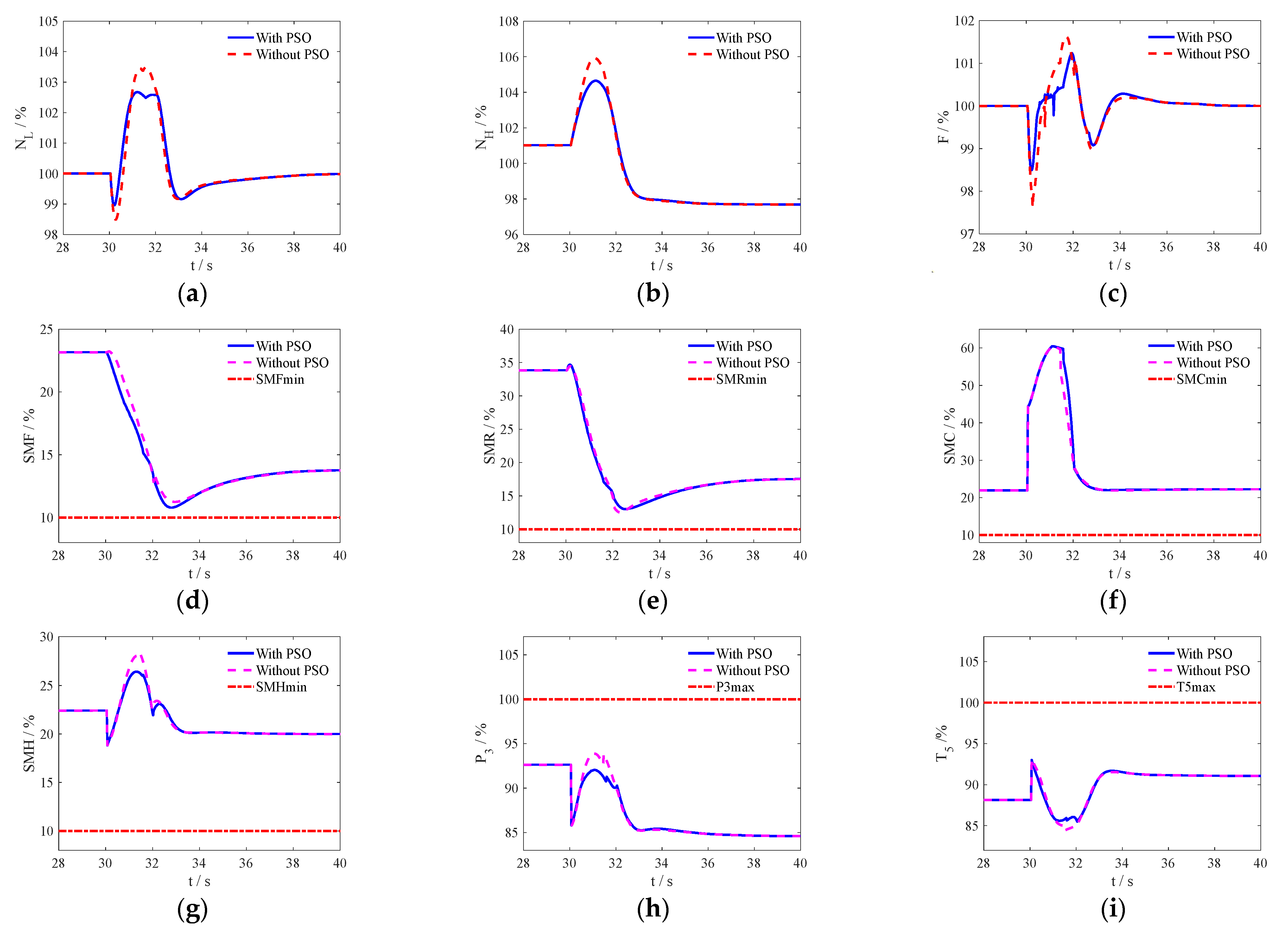
In this simulation, the ACE is switched from triple-bypass mode to double-bypass mode at the subsonic cruise operating point (H = 10 km, Ma = 0.9). The optimized actuator commands and engine responses are shown in Figure 5 and Figure 6, where “with PSO” denotes the optimization results obtained from the PSO, and “without PSO” is the result obtained from the conventional linear variation geometry mechanism. In Figure 6, SMF, SMR, SMC, SMH are the surge margin of FFAN, RFAN, CDFS, HPC. respectively, and P₃ and T₅ are the output pressure and temperature of HPC and LPT, respectively. The subscript “min” and “max” represent the minimum and maximum limitation of the corresponding variables.

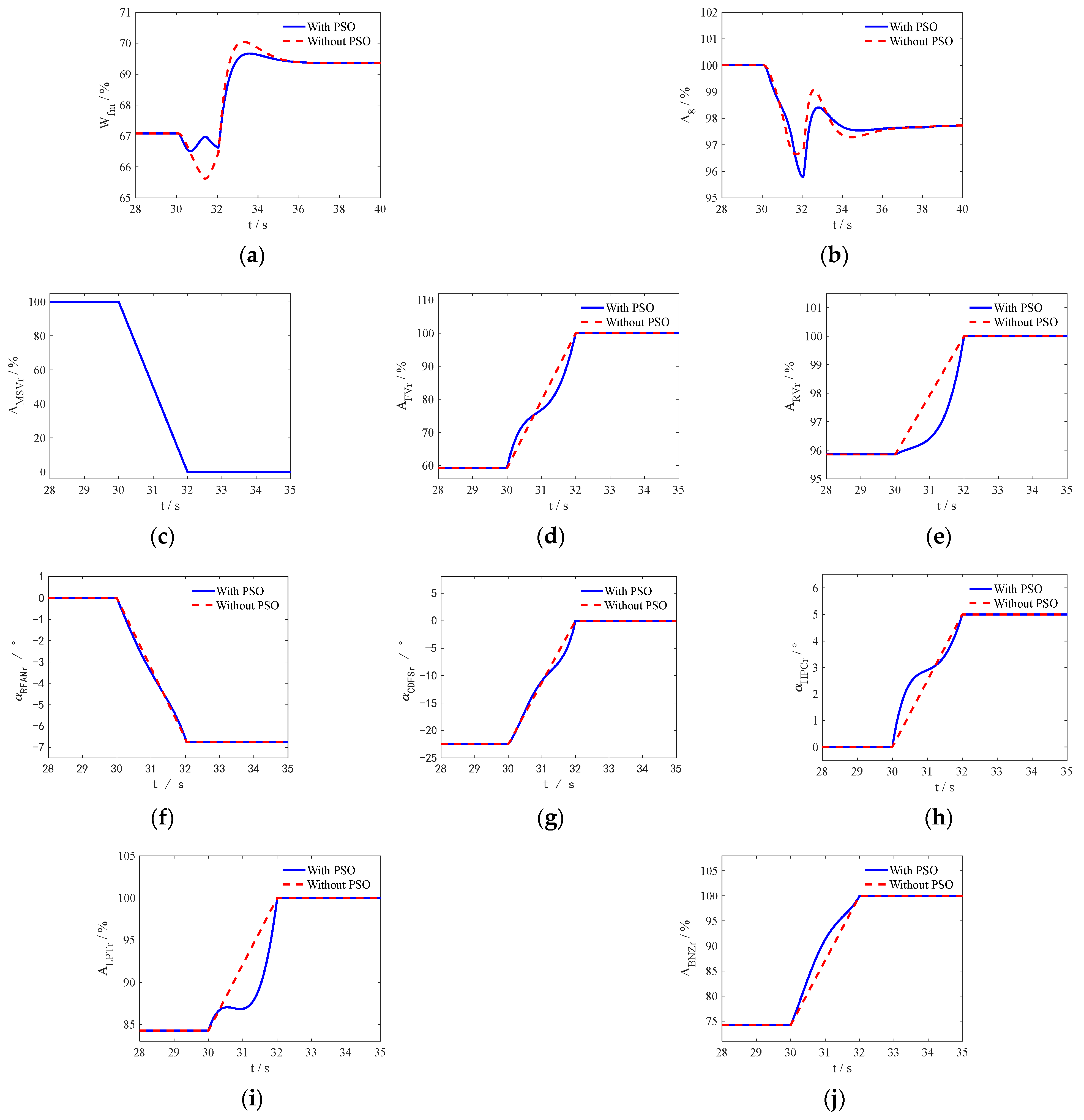
As Figure 5 shows, the transition from triple-bypass to double-bypass mode starts at 30 s. Figure 5a,b show the variation curves of the closed-loop control varaibles, where the fuel flow W_fm increases and the area of MNZ A₈ decreases. Figure 5c shows that the MSV area linearly changes from its maximum value to 0 within 2 s. From Figure 5d–j, it can be seen that other geometric mechanisms of PSO exhibit nonlinear changes simultaneously. Except for the closed-loop control of the MNZ region A₈ being closed to a smaller size, the area and guide vane angle of other open-loop geometric mechanisms have increased to allow for more flow during the MSV closing process. The fuel flow W_fmr is increased by 3.42% to maintain constant thrust in the dual-bypass mode, which also demonstrates that the triple-bypass mode has higher economy at subsonic cruise condition.

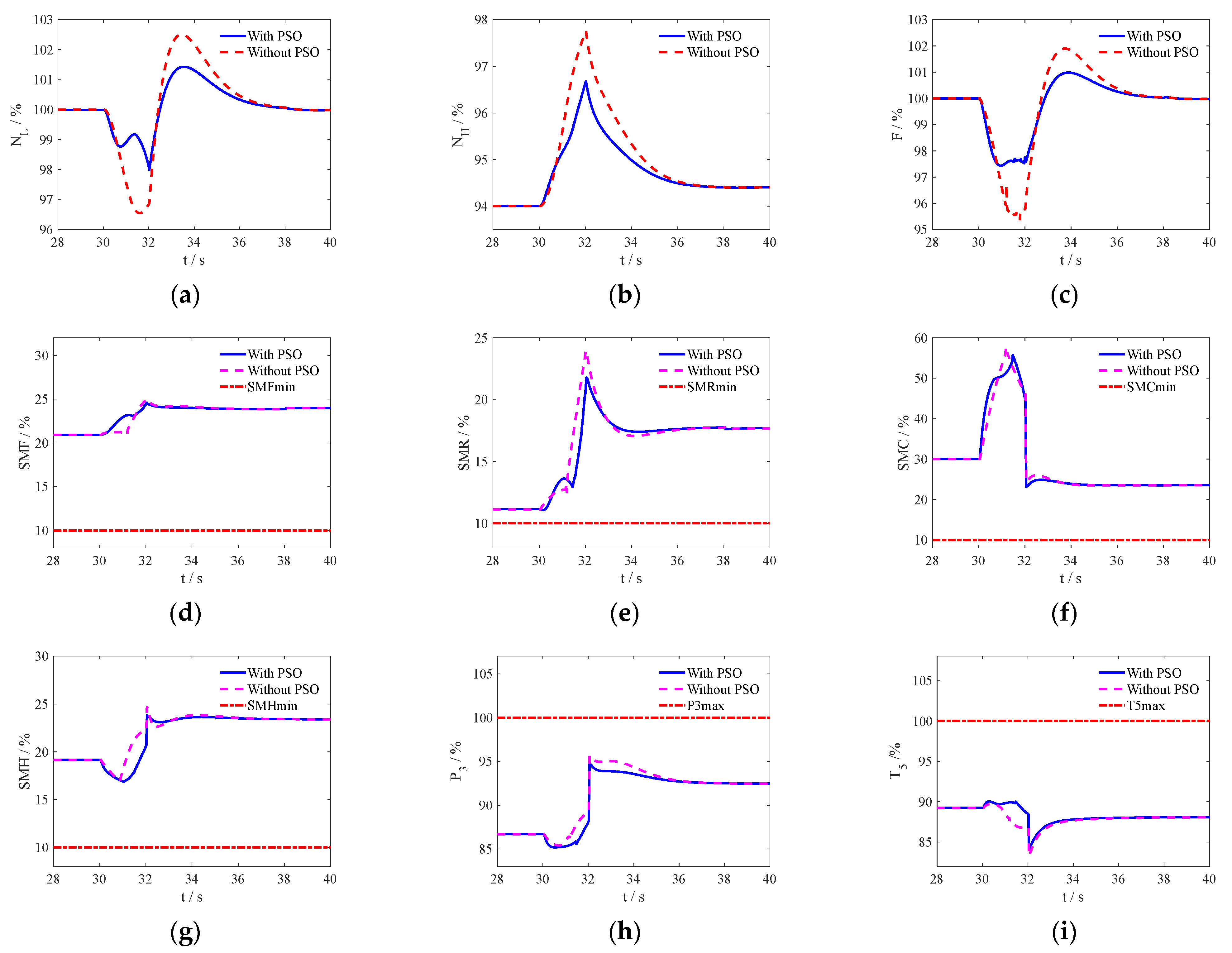
As Figure 6 shows, it can be concluded from Figure 6d–i that regardless of whether PSO optimization is present or not, the engine output is far from the constraint boundary. From Figure 6a–c, during the transition process, the fluctuations in closed-loop thrust F and LP rotor speed N_L are 2.58% and 2%, respectively. In the absence of linear changes in PSO, these numbers are 4.64% and 3.45%, respectively. In addition, the fluctuation of the HP rotor speed N_H under PSO is 2.28%, which is significantly smaller than the response of 3.35% without PSO. The results show that compared with traditional linear change methods, the mode transition control method can achieve a smooth, safe and fast transition from triple-bypass mode to double-bypass mode, and the control system with the optimized geometric mechanism control schedule achieves smaller thrust and rotor speed response fluctuations during the state transition process; the effectiveness of the control method proposed in this article has been verified.

(2)

Result at the supersonic cruise point

In this simulation, the ACE is switched from double-bypass mode to triple-bypass mode at the subsonic cruise operating point (H = 10 km, Ma = 1.2), and the optimized actuator commands and engine responses are compared with that of the traditional linear variation actuator commands as shown in Figure 7 and Figure 8.

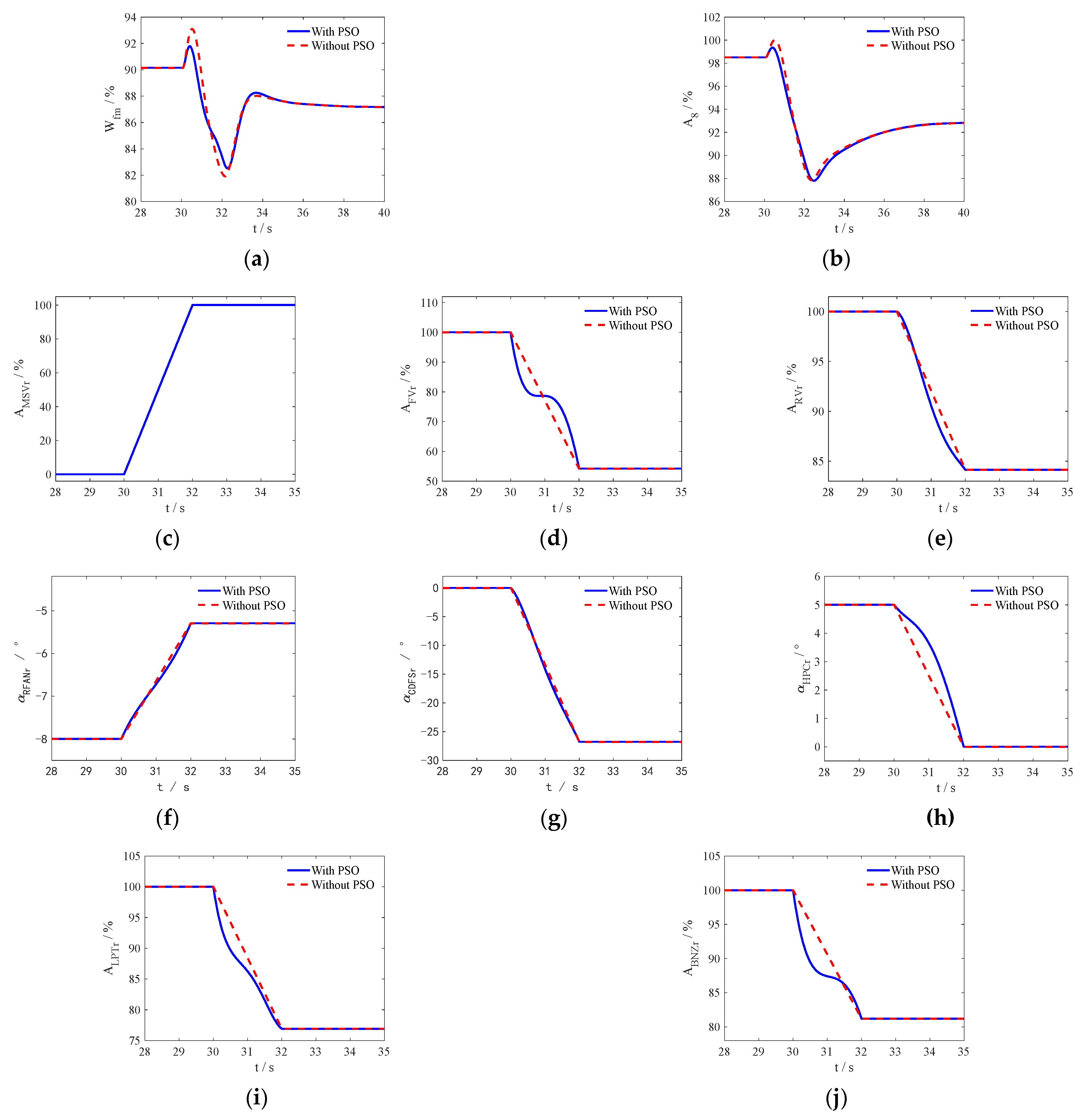
As Figure 7 shows, the transition from double-bypass to triple-bypass mode starts at 30 s. As shown in Figure 7a,b, the closed-loop control variables W_fmr and A_8r have both decreased. Figure 7c shows that the MSV area linearly changes from 0 to 100% within 2 s. Figure 7d–j show that during the mode transition process, the other geometric mechanisms optimized by PSO exhibit nonlinear changes, Except for α_RFANr is increased during the mode transition, the command for areas and guide vane angles of other geometric mechanisms are reduced to match the increased flow rate of the second bypass during the MSV opening process. The fuel flow W_fm decreased by 3.32%, which also proves that the dual-bypass mode has higher fuel efficiency under supersonic cruise conditions.

Figure 8d–i indicate that regardless of whether the PSO method is used or not, the engine outputs are far from the constraint boundary. Figure 8a–c show that during the transition process, the fluctuations in closed-loop thrust F and LP rotor speed N_L are 1.5% and 2.67%, respectively. In the absence of linear changes in PSO, these numbers are 2.4% and 3.5%, respectively. In addition, the fluctuation of HP rotor speed N_H under PSO conditions is 3.4%, which is significantly smaller than the response of 4.7% under no PSO conditions. The results show that the mode transition control method can realize smoothly, safely and quickly switching from the double-bypass mode to the triple-bypass mode, and the control system with optimized geometrical mechanisms control schedules achieves much smaller response fluctuation magnitudes of thrust and rotor speeds during the mode transition process compared with the traditional linear variation methods, which proves the effectiveness of the control method proposed in this paper.

5.2. Validation of Mode Transition Control Robustness and Adaptability

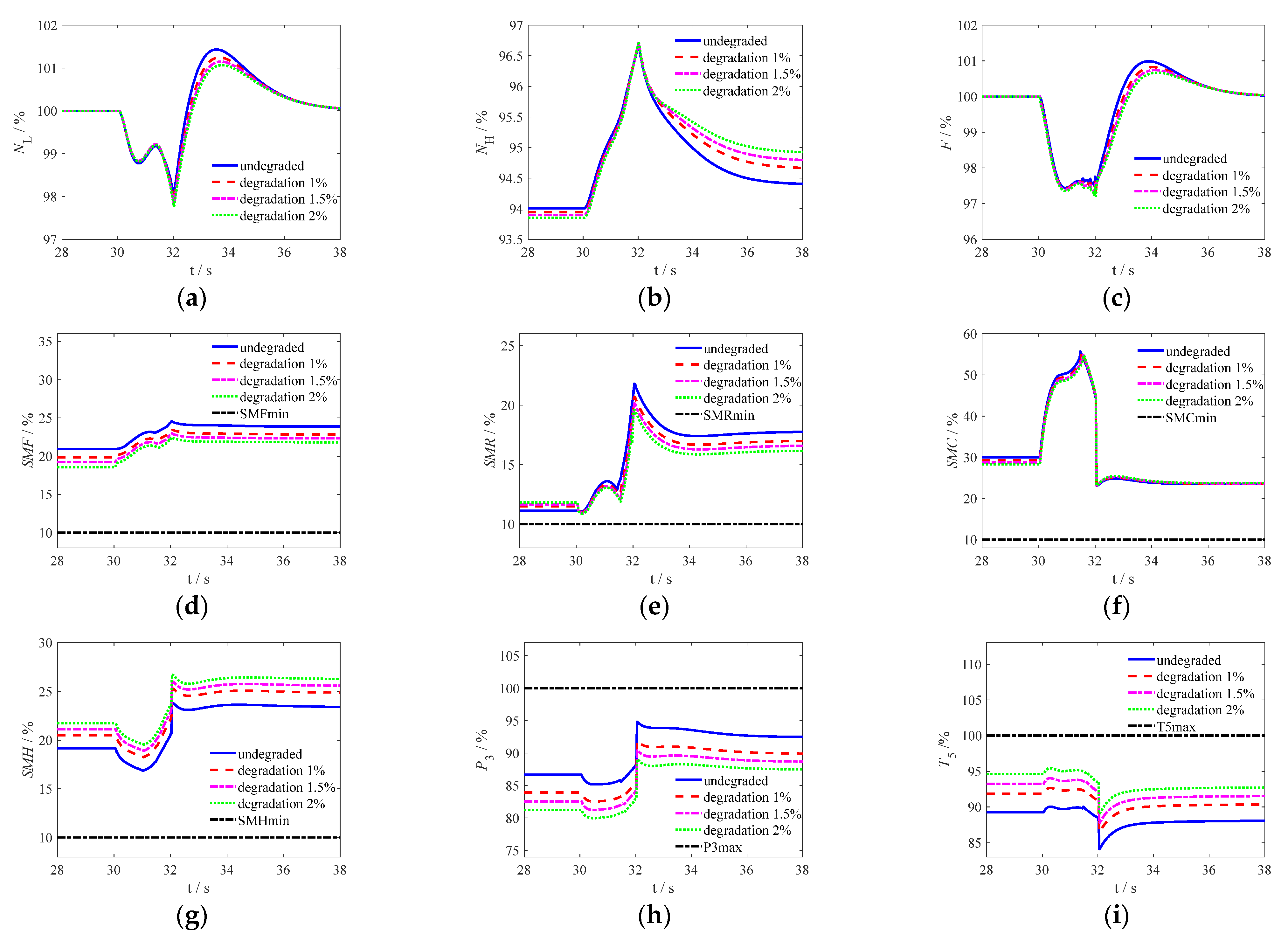
To verify the robustness and adaptability of mode transition control, the individual differences of the engine were simulated by varying degrees of engine degradation. Taking the subsonic cruise control operating point as an example, under different performance degradation conditions of ACE, the open-loop geometric mechanism schedule optimized under rated conditions are used under different degradation conditions to verify the effectiveness of the control method.

Taking the subsonic cruise point as an example, the performance degradation of the six major components of ACE, namely FFAN, RFAN, CDFS, HPC, HPT and LPT, occur simultaneously. The simultaneous degradation of 1%, 1.5%, 2% are simulated and compared with the rated engine. The responses are shown in Figure 9, where “undegraded”, “degradation 1%”, “degradation 1.5%” and “degradation 2%” respectively represent the rated and different degradation engine, and the subscripts “min” and “max” represent the minimum and maximum limits of the corresponding variables.

It can be seen from Figure 9d–i that under various degradation conditions, the output of the engine is far away from the constraint boundary. From Figure 9a–c, the fluctuations of LP rotor speed N_L, HP rotor speed N_H and closed-loop thrust F during the mode transition process are shown in

Table 1. The fluctuation magnitude of ACE output under different degradation conditions.

Degradation Magnitude/(%)	Fluctuation Magnitude/(%)
	NL	NH	F
0	2.007	2.281	2.561
1	2.118	2.044	2.654
1.5	2.186	1.921	2.657
2	2.243	1.807	2.804

. In the table, the fluctuation represents the maximum absolute deviation of each output parameter from its final steady-state value during the mode conversion process.

According to Table 1, it can be seen that under different performance degradation conditions of ACE, there is not much difference in the fluctuation magnitude of the output parameters of ACE. When degraded by 2%, the fluctuation of thrust is maximum, but it is still smaller than the traditional linear variation geometric mechanisms control method under rated conditions. Therefore, the results indicate that the control method for ACE mode conversion has good robustness and adaptability.

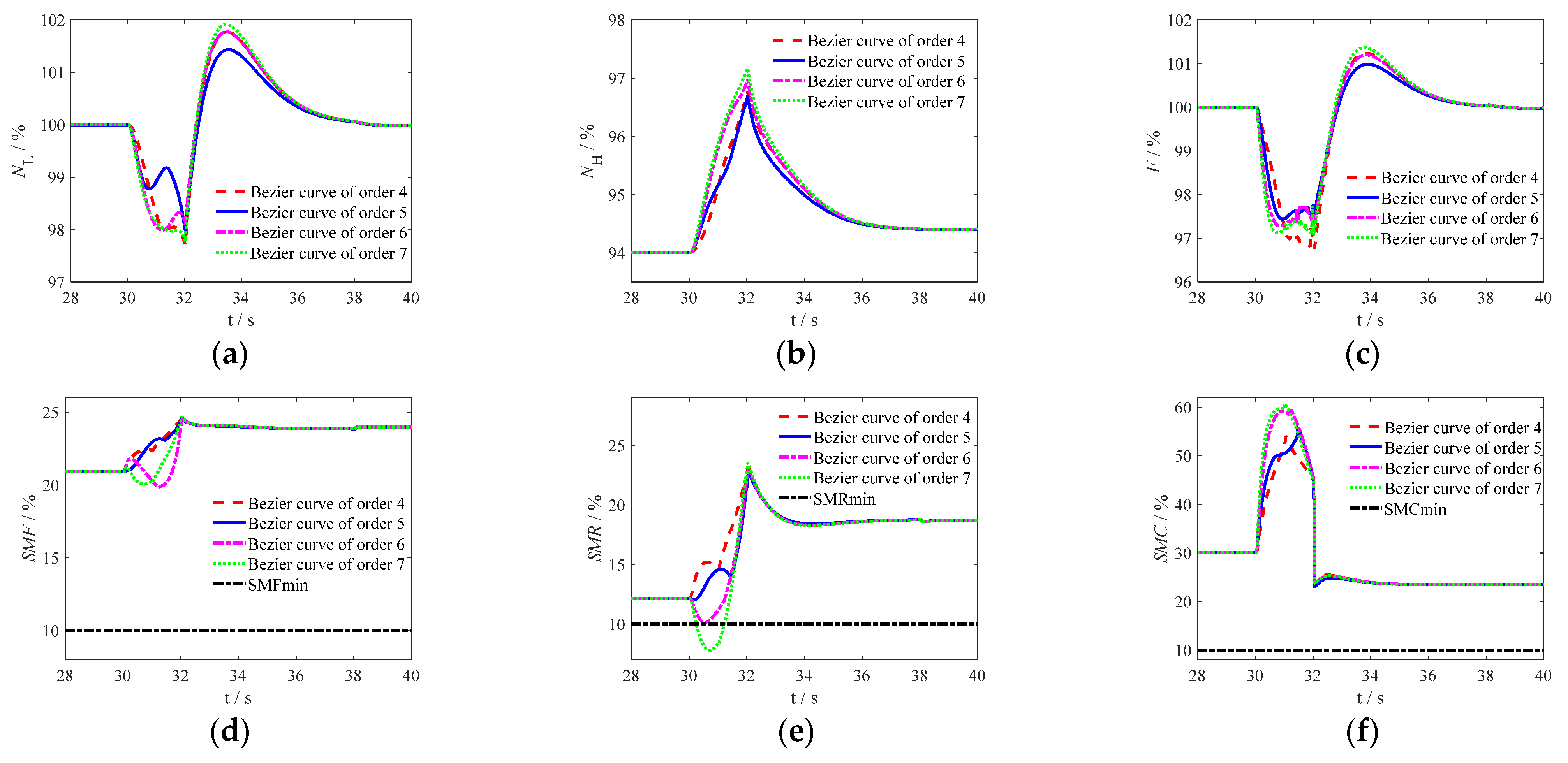
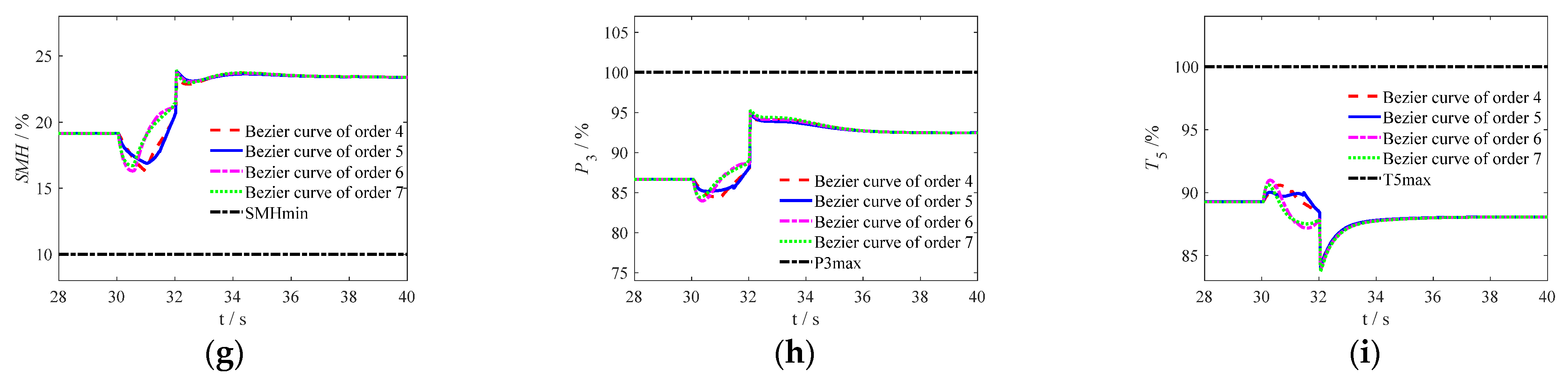
5.3. Influence of the of Bézier Curve’s Order on ACE Mode Transition

In order to compare the influence of Bézier curves of order on ACE mode conversion, the regulation schedules of open-loop geometric mechanisms constructed by Bézier curves of fourth order, fifth order, sixth order and seventh order are optimized (the computational complexity of Bézier curves increases by order with the increase of the number of control points, so the maximum order of Bézier curves selected in this paper is seven) Using the structure shown in Figure 2. Taking the subsonic operating point as an example, the optimal results of different Bézier curves were used for ACE mode transition control, and the output parameters of ACE were obtained as shown in Figure 10. Among them, “Bézier curve of order 4”, “Bézier curve of order 5”, “Bézier curve of order 6”, and “Bézier curve of order 7” respectively results obtained from different order Bézier curves respectively.

As shown in Figure 10, from Figure 10a–c, the fluctuations of the low-pressure rotor speed N_L, high-pressure rotor speed N_H and thrust F of ACE are listed in

Table 2. The fluctuation magnitude of ACE output for Bézier curves of different orders.

The Order of the Bézier Curve	Fluctuation Magnitude/(%)
	NL	NH	F
4	2.293	2.365	3.233
5	2.007	2.281	2.561
6	2.007	2.569	2.721
7	2.218	2.758	2.924

to detail the influence of the Bézier curve’s orders.

According to Figure 10d–i and Table 2, the SMR at the seventh order Bézier curve optimization condition over the lower limit, so the optimization result is not acceptable. The output parameters of the engine are far from the constraint boundary under all other conditions. As the order of the Bézier curve increases, the fluctuation of ACE closed-loop output shows a trend of first decreasing and then increasing. When the order of the Bézier curve is five, the fluctuation of the ACE output is minimized, which can meet the requirements of ACE mode conversion. Moreover, the order of the fifth order Bézier curve is suitable to make the calculation simpler and reduce the burden of calculation. Therefore, it is reasonable to use a fifth order Bézier curve to construct the control schedule of the open-loop geometric mechanism in mode transition process of ACE.

6. Conclusions

In this paper, the research on mode transition control is carried out for ACE. The ALQR controller is designed to maintain thrust and LP rotor speed constant through the regulation of W_fm and A₈, and based on this closed-loop control, the PSO algorithm is used to optimize the model transition control schedules of other open-loop geometric mechanisms, so as to make the change of the open-loop geometric mechanisms match with the demand of closed-loop control.

The use of Bézier curves to construct the transition state control schedule of the open-loop geometrical mechanism is a feasible method to achieve a smooth transition of the geometrical mechanism, and it is easy to optimize the geometrical structure change curves through optimizing the control points of the Bézier curves. The control system with the optimized geometrical mechanism schedules shows advantages to that of the traditional linear variation scheduling method in rotor speeds and thrust fluctuation magnitudes during the mode transition process. In addition, it was verified that the ACE mode transition control method proposed in the article has good robustness and adaptability.

Comparing the simulation results of mode transition under two flight conditions, it can also be concluded that the ACE at subsonic cruise and supersonic cruise points exhibits different economic characteristics under different operating modes. Therefore, the next step will be to study the optimal mode transition working point, in order to fully utilize the economic performance of ACE throughout the entire flight envelope.