Abstract
Underground hydrogen storage in geological structures is considered appropriate for storing large amounts of hydrogen. Using the geological Konary structure in the deep saline aquifers, an analysis of the influence of depth on hydrogen storage was carried out. Hydrogen injection and withdrawal modeling was performed using TOUGH2 software, assuming different structure depths. Changes in the relevant parameters for the operation of an underground hydrogen storage facility, including the amount of H2 injected in the initial filling period, cushion gas, working gas, and average amount of extracted water, are presented. The results showed that increasing the depth to approximately 1500 m positively affects hydrogen storage (flow rate of injected hydrogen, total capacity, and working gas). Below this depth, the trend was reversed. The cushion gas-to-working gas ratio did not significantly change with increasing depth. Its magnitude depends on the length of the initial hydrogen filling period. An increase in the depth of hydrogen storage is associated with a greater amount of extracted water. Increasing the duration of the initial hydrogen filling period will reduce the water production but increase the cushion gas volume.
1. Introduction
Green hydrogen is perceived as the successor to fossil fuels. It is considered crucial for the global effort toward climate neutrality [1,2] in the decarbonization of energy and industry [3,4,5]. Hydrogen could soon play a significant role as an energy carrier in the transportation, chemical, and metallurgical industries, as well as the aviation and maritime sectors [6,7,8].
Most hydrogen production comes from fossil fuels (i.e., non-renewable hydrogen, also known as grey hydrogen), but this gas can also be produced by electrolyzing water from renewable sources (i.e., renewable hydrogen, also known as green hydrogen) [5,9,10]. Energy production from renewable sources (such as solar and wind) is strictly dependent on weather conditions. This causes the production and supply of renewable energy (RES) to be intermittent. As a result, it is crucial to store surplus energy produced during periods of increased supply to compensate for any shortfalls during periods of increased demand [11,12,13]. Green hydrogen storage [5,14,15] will improve the efficiency of renewable energy production, balance energy supply and demand, and contribute to energy security [15,16,17].
1.1. State of the Art
The lack of adequate hydrogen storage systems for various applications is a significant barrier to the development of the hydrogen economy [18]. Hydrogen storage technologies are based on physical and chemical methods. The physical methods include storage in vessels, storage in gas networks, and underground storage. The chemical (material) methods are based on physisorption and chemisorption processes. Both groups of methods are at different stages of technological development. The physical methods are easier to implement and much more common, but they have some limitations. The material methods, which are assumed to be almost free of disadvantages, are not yet sufficiently developed for their widespread use. Nevertheless, they are being intensively researched and developed. Large-scale hydrogen storage requires a very high capacity due to its low volumetric energy density. Underground hydrogen storage (UHS) in suitable geological structures, such as deep aquifers, depleted hydrocarbon deposits, and salt caverns, can fulfill these requirements [19,20,21,22,23,24].
The growing interest in hydrogen storage (UHS) in deep aquifers stems from their large storage capacities. Aquifers are of particular interest among geological structures being considered for underground hydrogen storage due to their wide distribution in sedimentary basins and large capacities compared with other underground hydrogen storage options. However, the geological understanding of aquifer structures is relatively poor. Therefore, a lot of research is needed. The growth of interest in aquifer hydrogen storage is evidenced in the publication of review papers on various aspects of this technology [21,25,26,27,28,29,30,31,32,33,34]. Attention should also be paid to articles that present barriers to implementing UHS on an industrial scale [31,35,36]. Chico Sambo et al. showcased underground hydrogen storage facilities that are currently operational and in development worldwide [37].
The technical aspects of UHS in deep aquifers are of interest to both researchers and practitioners. In terms of the modeling results of hydrogen storage at different depths presented in this paper, these technical aspects include the feasibility of seasonal hydrogen storage, case studies of hydrogen storage and cyclic gas withdrawal, the determination of fracture pressure and capillary pressure, the flow rate weighted average, the evaluation of the effect of the storage depth on the total capacity, the working gas and cushion gas amount, and the volume of produced reservoir water [38,39].
The operation of underground gas storage facilities is influenced by fracturing and capillary pressure parameters. These pressures should be considered for underground hydrogen storage safety at the initial design stage of the injection process. Sainz-Garcia et al. [40] propose adopting minimum capillary pressure values for safety reasons when considering hydrogen storage. The method proposed by Iglauer [41] for estimating the values of the wetting angle between the hydrogen, rock, and water and the surface tension between water and H2 for different reservoir depth levels allows the capillary pressure of the overburden to be more precisely estimated. Luboń and Tarkowski [42,43] outlined the use of capillary pressure analysis to simulate hydrogen storage in deep aquifers. The modeling was performed considering the results of Sainz-Garcia et al. [40] and Pan et al. [44]. The authors assumed low capillary pressure values in their considerations. An analysis of the effects of the fracture and capillary pressures and the injection well location on the dynamic storage capacity of CO2 and H2 was presented in [43].
Another important aspect addressed in the literature is the impact of the preconditioning stage of an underground hydrogen storage facility on its operational efficiency, which also translates into the safety and economics of the process. Okoroafor et al. [45] analyzed hydrogen injection, storage, and withdrawal scenarios using storage simulations and presented the key parameters for ensuring optimal hydrogen storage and offtake. Pfeiffer and Bauer [46] and Ershadnia et al. [47] indicated that hydrogen withdrawal is effective if a low-density and -viscosity cushion gas is used and if the amount of extracted water and shut-in period between injection and production stages are minimized.
The results of Wang et al. [48] on H2 transport in porous media show that UHS in depleted gas reservoirs with irreducible water saturation has fewer risks of hydrogen trapping during the extraction process. Understanding the flow of hydrogen in rocks as a function of pore size is crucial for its safe underground storage. This issue also plays a key role in assessing the capacity and performance of underground hydrogen storage [49,50]. A computer simulation of hydrogen injection in the Suliszewo structure [42] showed that underground hydrogen storage in a deep aquifer can be realized with reasonable hydrogen recovery parameters.
UHS requires the use of a cushion gas, which maintains a sufficient pressure during the underground storage and affects the efficiency of the injection and withdrawal of the hydrogen [51]. The ratio of the cushion gas to the working gas reflects the hydrogen storage efficiency [52]. The cushion gas is a significant cost of UHS, as mentioned by Paterson [53], when considering the use of other gases. Mahdi Kanaani et al. [54] indicated that the effect of the cushion gas in depleted oil reservoirs is more important in the initial stage of hydrogen storage. Mahdi et al. [55] discussed the underground hydrogen storage efficiency in a heterogeneous sandstone reservoir, highlighting the role of the cap rock, the effect of hydrogen injection rates on hydrogen recovery rates, and the potential for hydrogen leakage from underground storage.
Feldmann et al. [56] showed that the hydrodynamic behavior of H2 and its interaction with reservoir fluids is an important aspect in the initial and later cyclic storage operations in depleted gas reservoirs. Heinemann et al. [51] emphasized that the volume of the cushion gas directly affects the injection and withdrawal efficiency of the working gas in saline aquifers. Pfeiffer et al. [57,58] presented modeling results for the initial filling stage of an underground storage facility with hydrogen and nitrogen (cushion gas), as well as for the hydrogen discontinuous injection and withdrawal. The suitability of simulation models for estimating storage characteristics, such as well flow rate and pressure changes, was confirmed by Pfeiffer and Bauer [46]. Sainz-Garcia et al.’s numerical modeling results for seasonal hydrogen storage produced from RES [40] showed that seasonal hydrogen storage can be carried out with rational hydrogen recovery rates.
According to Iglauer [41], the depth at which the largest total hydrogen storage capacity is found is approximately 1100 m. Computer simulations of the hydrogen storage in the Suliszewo structure carried out by Luboń and Tarkowski [39] found that the volume of the cushion gas and the total storage capacity increased as the first filling period of the storage facility with hydrogen increased. The working capacity increases with depth, achieving maximum values at a depth of 1195 m, after which it stabilizes and then decreases with depth below 1395 m. In addition, the proportion of the cushion gas and the total storage capacity increases as the first hydrogen storage filling period increases.
1.2. Objectives
The depth of a reservoir is a factor that influences the suitability of a geological structure for underground hydrogen storage, as it is linked to the pressure and temperature conditions at a given depth. There are a few examples of publications in this area. An earlier study [39] on the Suliszewo structure for hydrogen storage showed that the total storage capacity for this gas increases with depth, achieving maximum values at approximately 1195 m, after which it decreases. The authors investigated whether this trend was confirmed in the case of another geological structure in the deep aquifer.
These studies used hydrogen injection modeling to show how the relevant parameters (the hydrogen amount injected during the initial injection period, the ratio of the cushion gas to the working gas, the average amount of extracted water, and the H2 storage capacity) change as a function of the depth of the geological structure in the deep aquifer. This study modeled hydrogen injection into the Konary anticlinal geological structure selected for underground hydrogen storage. Seven cases of hydrogen storage with different reservoir top depths (483 m, 683 m, 883 m, 1083 m, 1283 m, 1483 m, and 1683 m below sea level (bsl)) were analyzed. The hydrogen storage capacity was estimated for these variants. A geological model of the actual depth of the structure’s roof (683 m bsl) was built based on existing geological and reservoir data. For the other depths considered, identical petrophysical rock parameters were assumed in the modeling, and the pressure and temperature were assumed to be at levels corresponding to the respective depths.
This article assessed the technical aspects of underground hydrogen storage. This subject is important, as it allows us to assess the impact of the depth on the storage capacity and, thus, on the volume of the working gas and cushion gas needed for underground storage. The presented results should be of interest to researchers involved in modeling hydrogen injection in porous structures.
2. Materials and Methods
2.1. Geological Model of the Konary Structure
A geological model of the Konary structure was built as part of earlier study [38], in which the Lower Jurassic reservoir—the Komorowo Formation—was adopted as the storage formation. The data used to create the geological model are presented in detail by Luboń and Tarkowski [38] and Luboń [59,60]. Two deep wells within the Konary structure were modeled: Konary IG-1 and Byczyna 1. Based on the analysis of geophysical data on Byczyna 1 [61], the storage formation was subdivided into ten layers, where the determined values of porosity, permeability, and rock density were allocated (Figure 1). The kriging method was used for interpolation.
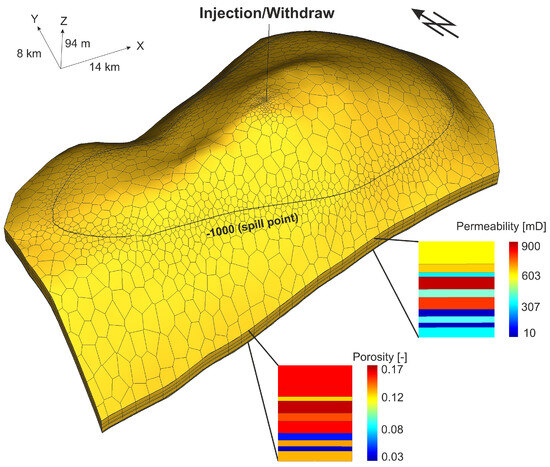
Figure 1.
Model of the Konary structure with vertical permeability and porosity profile.
2.2. Modeling Assumptions
The modeling presented in this paper used the Konary structure model presented in the authors’ earlier work and Section 2.1. The methodology of this work included the following steps.
The construction of 7 models for different depths (483 m, 683 m, 883 m, 1083 m, 1283 m, 1483 m, and 1683 m bsl) of the reservoir formation, assuming the same reservoir parameters, with the pressure and temperature derived from the reservoir conditions:
- The determination of the fracture and capillary pressure of the caprock for the 7 different depths;
- The simulation of hydrogen injection and recovery for the 7 models in 3 scenarios: 2-, 3-, and 4-year periods;
- Modeling the initial filling to determine flow rate, total storage capacity, working gas, cushion gas, and CG/WG ratio;
- Performing 30 cyclic storage operations (with 6 months of withdrawal and 6 months of injection) to verify the storage operation under the assumptions made and determine the amount of water withdrawn during hydrogen storage operation.
Seven models were constructed for different depths. Based on the geological model of the structure made for the actual depth of the reservoir horizon (683 m bsl), 6 variants of the Konary structure were constructed at different depths of the reservoir horizon and with different pressure and temperature parameters. The petrophysical parameters of the reservoir horizon were identical for all models. The models were performed for the following depth variants: +200 (483 m bsl); 0, i.e., the true depth (683 m bsl); −200 (883 m bsl); −400 (1083 m bsl); −600 (1283 m bsl); −800 (1483 m bsl); and −1000 (1683 m bsl) (Table 1).

Table 1.
Reservoir pressures, fracturing pressures, and capillary pressures for analyzed variants.
The fracture pressure and capillary pressure of the overburden was calculated as follows. The fracture pressure, the capillary pressure of the overburden, and the total capillary and initial pressure were calculated for the 7 model variants (Table 1). The scheme to calculate the fracture pressure was presented in the articles by Luboń and Tarkowski [38,39] and was the same as that in previous analyses of hydrogen storage simulations [42,43] and CO2 injection simulations [59,60]. The capillary pressure value of the overburden was calculated using the methodology to evaluate these properties in CO2 storage processes [43,59,60,62], but with the corresponding surface tension and wetting angle values for hydrogen [38,39,41]. The minimum pressure values were included in the considerations for hydrogen storage safety.
Simulation of hydrogen injection and withdrawal for the 7 scenarios considered: Simulations of hydrogen injection were performed in the Transportation of Unsaturated Groundwater and Heat 2 (TOUGH2) PetraSim software (version 5.4) in the EOS5 equation of state [63]. The number of computing cells in the PetraSim software TOUGH2 for each of the 6 variants of the model was approximately 20,000. The assumption was made that the injection and subsequent withdrawal would be carried out through a single well at the structure top. Initial filling: In this work, three periods were used for the initial filling of the Konary structure: four, three, and two years of hydrogen injections. Hydrogen was injected with flow rates chosen according to the permissible pressures via trial and error so the pressure prevailing in the upper part of the storage (i.e., in the top part of the reservoir and at the top of the structure) did not exceed the total of the initial pressure and the capillary pressure of caprock. The flow rate could be increased when the pressure dropped by 0.1 MPa, assuming that the pressure due to injection does not exceed the sum of the caprock capillary pressure and the initial pressure. These steps were repeated until the end of the injection simulations lasting 2, 3, or 4 years. Thus, the variable flow rate of hydrogen was determined for the injection periods of four, three, and two years. The simulation was carried out in this way due to a limitation of the software used, whereby we could only set the flow rate of the fluid to be injected but could not set the limit pressure. Therefore, we met the condition of not exceeding the allowable pressures by adjusting the flow rate. The total capacity of hydrogen injected in the initial filling stage was calculated as the product of the determined flow rate and its occurrence time. A weighted average of the hydrogen flow rate was then determined. The calculation assigned a weight based on the timing of a particular flow rate, and the total of these weights equaled 1.
Cyclic (30-year) storage operation: The calculated time-weighted average hydrogen flow rate was employed during the six-month period of hydrogen withdrawal, and the working gas volume was thus calculated. This value of the working gas was used for 30 cycles of UHS operation, during which this amount of hydrogen was injected and withdrawn at 6-month intervals. Brine was also extracted during each hydrogen injection and withdrawal cycle. During the six-month hydrogen withdrawal period, the cushion gas capacity is the variance between the total capacity and the working gas.
3. Results
The simulations of the operation of the storage facility located in the Konary structure were carried out for seven depth variants of the reservoir horizon with three initial filling periods of 2, 3, and 4 years. The flow rate, total capacity, cushion gas, working gas, and amount of extracted water were determined for these scenarios (Table 2).

Table 2.
Flow rate, total capacity, working gas, cushion gas, and amount of extracted water for the analyzed depths and lengths of the initial injection period into the Konary structure.
The flow rate parameter (the weighted average of the hydrogen injection periods in the initial filling period) varied between 0.93 and 1.54 kg/s, depending on the depth variant. This indicates that a higher flow rate can be used as the depth increases up to 1483 m. However, at a depth of more than 1683 m, the flow rate decreased to 1.44 kg/s. The possibility of using a higher flow rate with increasing depth (up to 1483 m bsl) means that more hydrogen can be stored with increasing depth, thus increasing the total capacity. For the shortest initial filling period (2 years), this capacity increased from 57,830 Mg at the shallowest depth below sea level to 98,182 Mg at a depth of 1483 m (Table 2 and Figure 2). Increasing the depth to 1683 m resulted in a decrease in the total capacity to 90,711 Mg. For the 3-year initial filling period, the total capacity ranged from 88,441 Mg at the shallowest depth considered to 148,323 Mg at a depth of 1483 m. However, for the longest initial filling period (4 years), the total capacity at the shallowest depth was 118,129 Mg, and at the greatest depth considered, it was 181,048 Mg, with a maximum total capacity of 191,941 Mg at a depth of 1483 m.
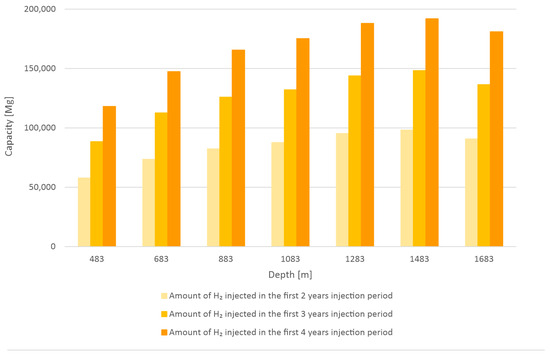
Figure 2.
Amount of H2 injected in the three analyzed injection periods for seven considered depths.
Similar trends were observed in the working gas volume results, which also increased with increasing depth up to 1483 m (Table 2 and Figure 3). Since a single value of the weighted average flow rate was calculated for all initial filling periods for each of the depths considered, the working gas volume did not vary according to the initial filling period. Its value ranged from 14,655 Mg at the shallowest depth to 24,358 Mg at a depth of 1438 m. The working gas volume decreased to 22,679 Mg at a depth of 1683 m.
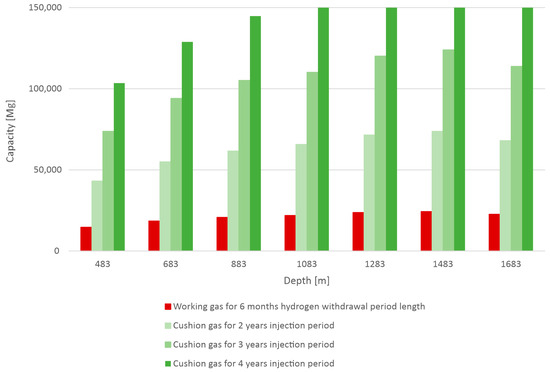
Figure 3.
Amount of H2 as a working gas and cushion gas in the three analyzed injection periods for seven considered depths.
The gas cushion volume also increased with increasing depth up to 1483 m (Table 2 and Figure 3). For the shortest initial filling period, it ranged from 43,176 Mg at the shallowest depth of 483 m bsl to 73,824 Mg at a depth of 1483 m bsl. For the 3-year initial filling period, it was 73,786 Mg at the shallowest depth and 113,789 Mg at the greatest depth. In contrast, for the longest four-year initial filling period, the gas cushion was 103,375 Mg at the shallowest depth and 158,369 Mg at the greatest depth.
A certain amount of water was extracted during the 6-month hydrogen recovery cycle (the quantity of water extracted throughout the withdrawal cycle) (Table 2 and Figure 4). This quantity increased with a decreasing initial filling period and increasing storage depth. For the shortest initial filling period of 2 years, the amount of water extracted at the shallowest depth of 483 m was 10,195 Mg, while the amount was 35,218 Mg at the greatest depth of 1683 m. For the longest initial filling period equal to 4 years, the amount of exploited water was equal to 4246 Mg at the shallowest depth, while the amount was 13,078 Mg at the greatest depth.
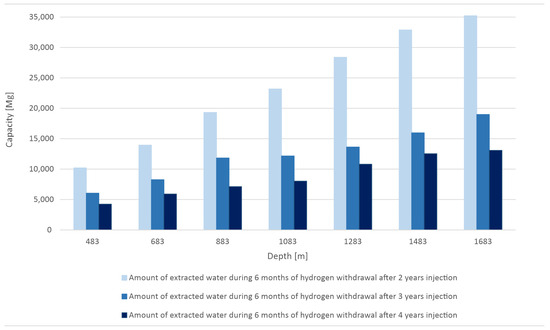
Figure 4.
Amount of water extracted during H2 withdrawal in the three analyzed injection periods for seven considered depths.
4. Discussion
The purpose of modeling the hydrogen injection into the deep aquifer was to show how important parameters for the storage facility’s operation, such as the amount of H2 injected during the initial filling period, the cushion gas, the working gas, and the average amount of extracted water, changed as a function of the depth of the structure. Analyses were performed for the geological Konary structure. The simulations were carried out for seven different depths of the potential hydrogen storage (483 m, 683 m, 883 m, 1083 m, 1283 m, 1483 m, and 1683 m bsl). The analysis assumed identical petrophysical parameters between the rocks and considered the pressure and temperature variations related to depth. The modeling of the storage’s cyclic operation was carried out for 2, 3, and 4 years of hydrogen initial filling. The starting point for the modeling was the determination of the fracture pressure and capillary pressure of the caprock, as presented in the authors’ previous work [38,39]. The flow rate adopted in this paper during the initial filling period was selected so the pressure increase in the storage formation (because of the hydrogen injection) did not exceed the pressure, causing the fracturing and capillary pressure of the caprock. These assumptions and the simulations allowed us to obtain new, insightful results related to those in the literature.
In the case of the Konary structure, an increasing flow rate was possible as the depth increased to 1483 m. The flow rate magnitude decreased with further increases in the depth.
Our analyses for different depths (483–1683 m) determined that the total hydrogen storage capacity and the amount of working gas increase with depth. The Konary structure allows for the storage of the maximum amount of hydrogen at a depth of 1483 m (approximately 1500 m). The hydrogen storage capacity of the analyzed reservoir horizon is lower below and above this depth. A similar analysis carried out for the Suliszewo structure [39] showed that the optimal depth for hydrogen storage was 1395 m (approximately 1400 m). In a similar study by Iglauer [41], the highest storage capacity was found at a depth of approximately 1100 m. In the cases of the Konary and the Suliszewo structures, the displacement of this limit to the 1400–1500 m depth interval is most likely due to the specific geological conditions of each structure. This indicates that establishing the ideal storage depth necessitates a customized approach for each structure analyzed for hydrogen storage. Heinemann et al. [51] highlighted the advantages of placing hydrogen storage at increased depths.
The large amount of cushion gas required for hydrogen storage was noted by Pfeiffer and Bauer [46]. Heinemann et al. [51,52] emphasized that the cushion gas quantity influences the working gas’s injection and withdrawal efficiency. In our case, the amount of cushion gas significantly increased with the extension of the initial filling period and the depth of the hydrogen storage foundation up to 1483 m, where the maximum amount was recorded. The volume of the gas cushion decreased at greater depths.
The cushion gas-to-working gas (CG/WG) ratio was calculated based on the determined amounts of cushion gas and working gas. The CG/WG ratio did not significantly vary with depth (Table 2 and Figure 5).
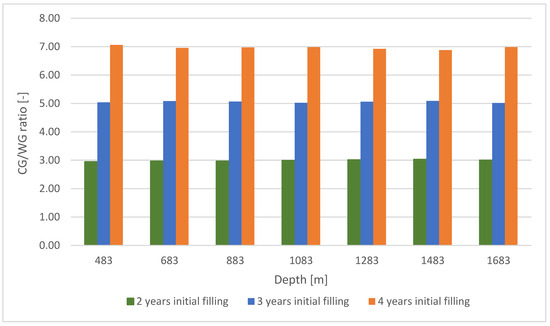
Figure 5.
Cushion gas-to-working gas (CG/WG) ratio calculated based on data in Table 2.
The results of studies on various factors influencing the CG/WG ratio presented by Heinemann et al. [51,52] indicate that the ratio decreases with increasing depth. This discrepancy could be explained by the adoption of different modeling assumptions for the injection and cyclic operation of the hydrogen storage. The results presented in this paper also indicate that the CG/WG ratio depends on the length of the initial filling period. The longer the initial filling period, the higher the CG/WG ratio, assuming the same working gas volume. It ranged from 2.9–3.03 for a two-year initial filling period, 5.02–5.09 for a three-year initial filling period, to 6.92–7.06 for the longest four-year initial filling period.
The quantity of water extracted decreases as the duration of the initial filling period for hydrogen recovery increases, amount of cushion gas, and CG/WG ratio increase. These relationships confirm the results obtained by Heinemann et al. [51] and Lysyy et al. [64]. It was also found that the volume of extracted water rises in correlation with the depth of hydrogen storage, which hinders the recovery of the injected hydrogen. This problem was also reported in other articles [21,65]. Excessive water production can occur in aquifer hydrogen storage along with hydrogen extraction. Various methods are used to reduce the amount of water extracted, such as maintaining a constant well pressure to control water extraction [66], using an appropriate production well configuration [40], and using a cushion gas [51]. Moreover, the hydrogen migration in the storage formation can be controlled by modifying the filtration parameters. Injecting aqueous foam above the gas–saline interface can reduce brine coning in the production wells [67]. Raising the water–gas interface may be an important factor in reducing H2 storage (when a buffer gas is not used). Hydrogen withdrawal operations should be completed before coning leads to the production of large volumes of water [68].
Hydrogen storage simulations allow the most accurate storage capacity estimates to be obtained and the analysis of various factors that can affect the entire storage process. Many researchers have already performed such simulations under different assumptions. It is believed that depleted hydrocarbon reservoirs are best suited for hydrogen storage. Nevertheless, Delshad et al. compared depleted hydrocarbon reservoirs with deep saline aquifers [69] and showed that both are suitable for storing and extracting large quantities of hydrogen. However, each location must be optimized in terms of the number and location of injection and extraction wells, as well as the operational design, including the cost of proper site classification. Mahdi et al. [55] developed a three-dimensional model of a heterogeneous reservoir, like the framework of this article, and used it to analyze the effect of overburden and the hydrogen flow rate on the performance of underground hydrogen storage. The results showed that both rock overburden and the injection rate significantly impact hydrogen leakage and the amount of trapped and recovered hydrogen. Jadhawar and Saeed’s simulation results [70] showed that aquifer permeability heterogeneity significantly affects the H2 recovery efficiency, where a more homogeneous rock improves H2 productivity. Bo et al. [71] found that the geological structure, i.e., the heterogeneity of the facies and reservoir formation dip, affects the flow regime of the injected and recovered hydrogen. Similar studies were conducted by Pan et al. [72] and Wang et al. [48], centering on the impact of relative permeability hysteresis, wettability, and the withdrawal rate of H2 on the performance of underground hydrogen storage (UHS) in saline aquifers. Chai et al. [73] used modeling to analyze the intricate interactions between hydrogen and rock or fluid in an aquifer reservoir. The results of their numerical simulations provide a better understanding of the hydrogen storage process in an aquifer (e.g., H2 accumulation in the upper part of the aquifer and multiple cycles are beneficial to increase hydrogen extraction from cushion gases, and N2 has a higher efficiency than CO2). However, apart from the authors’ previous work [39] and Iglauer’s theoretical considerations [41], no analysis of the effect of depth on hydrogen storage capacity is available in the literature.
5. Conclusions
Hydrogen injection into a deep aquifer at different depths was modeled to show the changes in the relevant parameters for the operation of an underground hydrogen storage facility, including the amount of H2 injected in the initial filling period, cushion gas, working gas, and average amount of extracted water.
Increasing the depth of the storage foundation to 1483 m had a positive effect on parameters such as the flow rate of the amount of injected hydrogen, working gas, and total capacity. Below this depth, the trend was reversed. In the case of the Konary structure, a depth of approximately 1500 m was considered the most favorable for hydrogen storage based on the analyzed parameters.
The cushion gas-to-working gas (CG/WG) ratio did not significantly change with increasing depth. Its magnitude depended on the length of the initial hydrogen filling period.
An increase in the depth of the hydrogen storage foundation is associated with a greater amount of operating water. Increasing the duration of the initial hydrogen filling period will reduce the water production but increase the gas cushion volume.
Author Contributions
Conceptualization, K.L. and R.T.; methodology, K.L.; software, K.L.; validation, R.T. and B.U.-M.; formal analysis, K.L.; investigation, K.L.; resources, R.T. and B.U.-M.; data curation, K.L., R.T. and B.U.-M.; writing—original draft, K.L., R.T. and B.U.-M.; writing—review and editing, R.T. and B.U.-M.; visualization, K.L.; supervision, R.T.; funding acquisition, B.U.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the “Excellent Science” program of the Ministry of Education and Science of the Republic of Poland (grant no. DNK/SP/547981/2022).
Data Availability Statement
Data are contained within the article.
Acknowledgments
This work was supported by the Mineral and Energy Economy Research Institute of the Polish Academy of Sciences (research subvention).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hassan, Q.; Sameen, A.Z.; Salman, H.M.; Jaszczur, M.; Al-Jiboory, A.K. Hydrogen energy future: Advancements in storage technologies and implications for sustainability. J. Energy Storage 2023, 72, 108404. [Google Scholar] [CrossRef]
- Kumar, S.; Jufar, S.R.; Kumar, S.; Foroozesh, J.; Kumari, S.; Bera, A. Underground hydrogen storage and its roadmap and feasibility in India toward Net-Zero target for global decarbonization. Fuel 2023, 350, 128849. [Google Scholar] [CrossRef]
- COM/2020/301. Available online: https://eur-lex.europa.eu/legal-content/PL/TXT/?uri=CELEX:52020DC0301 (accessed on 30 December 2020).
- Abdin, Z.; Zafaranloo, A.; Rafiee, A.; Mérida, W.; Lipiński, W.; Khalilpour, K.R. Hydrogen as an energy vector. Renew. Sustain. Energy Rev. 2020, 120, 109620. [Google Scholar] [CrossRef]
- Noussan, M.; Raimondi, P.P.; Scita, R.; Hafner, M. The role of green and blue hydrogen in the energy transition—A technological and geopolitical perspective. Sustainability 2021, 13, 298. [Google Scholar] [CrossRef]
- OECD. The Future of Hydrogen. Seizing Today’s Opportunities. 2019. Available online: https://read.oecd-ilibrary.org/energy/the-future-of-hydrogen_1e0514c4-en#page1 (accessed on 3 March 2024).
- Arenillas, I.A.; Ortega, M.F.; Torrent, J.G.; Moya, B.L. Hydrogen as an Energy Vector: Present and Future. In Sustaining Tomorrow via Innovative Engineering; World Scientific: Singapore, 2021; pp. 83–129. [Google Scholar]
- Ghorbani, B.; Zendehboudi, S.; Saady, N.M.C.; Dusseault, M.B. Hydrogen storage in North America: Status, prospects, and challenges. J. Environ. Chem. Eng. 2023, 11, 109957. [Google Scholar] [CrossRef]
- Olabi, A.G.; Bahri, A.S.; Abdelghafar, A.A.; Baroutaji, A.; Sayed, E.T.; Alami, A.H.; Rezk, H.; Abdelkareem, M.A. Large-vscale hydrogen production and storage technologies: Current status and future directions. Int. J. Hydrogen Energy 2021, 46, 23498–23528. [Google Scholar] [CrossRef]
- Yang, M.; Hunger, R.; Berrettoni, S.; Sprecher, B.; Wang, B. A review of hydrogen storage and transport technologies. Clean Energy 2023, 7, 190–216. [Google Scholar] [CrossRef]
- Lebrouhi, B.E.; Djoupo, J.J.; Lamrani, B.; Benabdelaziz, K.; Kousksou, T. Global hydrogen development—A technological and geopolitical overview. Int. J. Hydrogen Energy 2022, 47, 7016–7048. [Google Scholar] [CrossRef]
- Abdalla, A.M.; Hossain, S.; Nisfindy, O.B.; Azad, A.T.; Dawood, M.; Azad, A.K. Hydrogen production, storage, transportation and key challenges with applications: A review. Energy Convers. Manag. 2018, 165, 602–627. [Google Scholar] [CrossRef]
- El-Shafie, M.; Kambara, S.; Hayakawa, Y. Hydrogen Production Technologies Overview. J. Power Energy Eng. 2019, 7, 107–154. [Google Scholar] [CrossRef]
- Sgobbi, A.; Nijs, W.; De Miglio, R.; Chiodi, A.; Gargiulo, M.; Thiel, C. How far away is hydrogen? Its role in the medium and long-term decarbonisation of the European energy system. Int. J. Hydrogen Energy 2016, 41, 19–35. [Google Scholar] [CrossRef]
- Schultz, R.A.; Heinemann, N.; Horváth, B.; Wickens, J.; Miocic, J.M.; Babarinde, O.O.; Cao, W.; Capuano, P.; Dewers, T.A.; Dusseault, M.; et al. An overview of underground energy-related product storage and sequestration. Geol. Soc. Lond. Spec. Publ. 2023, 528, 15–35. [Google Scholar] [CrossRef]
- Maggio, G.; Nicita, A.; Squadrito, G. How the hydrogen production from RES could change energy and fuel markets: A review of recent literature. Int. J. Hydrogen Energy 2019, 44, 11371–11384. [Google Scholar] [CrossRef]
- Matos, C.R.; Carneiro, J.F.; Silva, P.P. Overview of Large-Scale Underground Energy Storage Technologies for Integration of Renewable Energies and Criteria for Reservoir Identification. J. Energy Storage 2019, 21, 241–258. [Google Scholar] [CrossRef]
- Amirthan, T.; Perera, M.S.A. The role of storage systems in hydrogen economy: A review. J. Nat. Gas Sci. Eng. 2022, 108, 104843. [Google Scholar] [CrossRef]
- Tarkowski, R.; Lankof, L.; Luboń, K.; Michalski, J. Hydrogen storage capacity of salt caverns and deep aquifers versus demand for hydrogen storage: A case study of Poland. Appl. Energy 2024, 355, 122268. [Google Scholar] [CrossRef]
- Tarkowski, R. Perspectives of using the geological subsurface for hydrogen storage in Poland. Int. J. Hydrogen Energy 2017, 42, 347–355. [Google Scholar] [CrossRef]
- Zivar, D.; Kumar, S.; Foroozesh, J. Underground hydrogen storage: A comprehensive review. Int. J. Hydrogen Energy 2021, 46, 23436–23462. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, Y.; Chen, C. Numerical simulation of the impact of different cushion gases on underground hydrogen storage in aquifers based on an experimentally-benchmarked equation-of-state. Int. J. Hydrogen Energy 2024, 50, 495–511. [Google Scholar] [CrossRef]
- Xue, W.; Wang, Y.; Chen, Z.; Liu, H. An integrated model with stable numerical methods for fractured underground gas storage. J. Clean. Prod. 2023, 393, 136268. [Google Scholar] [CrossRef]
- Lankof, L.; Tarkowski, R. Assessment of the potential for underground hydrogen storage in bedded salt formation. Int. J. Hydrogen Energy 2020, 45, 19479–19492. [Google Scholar] [CrossRef]
- Tarkowski, R. Underground hydrogen storage: Characteristics and prospects. Renew. Sustain. Energy Rev. 2019, 105, 86–94. [Google Scholar] [CrossRef]
- Thiyagarajan, S.R.; Emadi, H.; Hussain, A.; Patange, P.; Watson, M. A comprehensive review of the mechanisms and efficiency of underground hydrogen storage. J. Energy Storage 2022, 51, 104490. [Google Scholar] [CrossRef]
- Muhammed, N.S.; Haq, B.; Al Shehri, D.; Al-Ahmed, A.; Rahman, M.M.; Zaman, E. A review on underground hydrogen storage: Insight into geological sites, influencing factors and future outlook. Energy Rep. 2022, 8, 461–499. [Google Scholar] [CrossRef]
- Navaid, H.B.; Emadi, H.; Watson, M.; Herd, B.L. A comprehensive literature review on the challenges associated with underground hydrogen storage. Int. J. Hydrogen Energy 2022, 48, 10603–10635. [Google Scholar] [CrossRef]
- Muhammed, N.S.; Haq, B.; Abdullah, D.; Shehri, A.; Al-Ahmed, A.; Rahman, M.M.; Zaman, E.; Iglauer, S. Hydrogen storage in depleted gas reservoirs: A comprehensive review. Fuel 2022, 337, 127032. [Google Scholar] [CrossRef]
- Miocic, J.M.; Heinemann, N.; Alcalde, J.; Edlmann, K.; Schultz, R.A. Enabling secure subsurface storage in future energy systems: An introduction. Geol. Soc. Lond. Spec. Publ. 2023, 528, SP528-2023. [Google Scholar] [CrossRef]
- Hematpur, H.; Abdollahi, R.; Rostami, S.; Haghighi, M.; Blunt, M.J. Review of underground hydrogen storage: Concepts and challenges. Adv. Geo-Energy Res. 2023, 7, 111–131. [Google Scholar] [CrossRef]
- Aslannezhad, M.; Ali, M.; Kalantariasl, A.; Sayyafzadeh, M.; You, Z.; Iglauer, S.; Keshavarz, A. A review of hydrogen/rock/brine interaction: Implications for Hydrogen Geo-storage. Prog. Energy Combust. Sci. 2023, 95, 101066. [Google Scholar] [CrossRef]
- Pan, B.; Yin, X.; Ju, Y.; Iglauer, S. Underground hydrogen storage: Influencing parameters and future outlook. Adv. Colloid Interface Sci. 2021, 294, 102473. [Google Scholar] [CrossRef]
- Aftab, A.; Hassanpouryouzband, A.; Xie, Q.; Machuca, L.L.; Sarmadivaleh, M. Toward a Fundamental Understanding of Geological Hydrogen Storage. Ind. Eng. Chem. Res. 2022, 61, 3233–3253. [Google Scholar] [CrossRef]
- Tarkowski, R.; Uliasz-Misiak, B. Towards underground hydrogen storage: A review of barriers. Renew. Sustain. Energy Rev. 2022, 162, 112451. [Google Scholar] [CrossRef]
- Raza, A.; Arif, M.; Glatz, G.; Mahmoud, M.; Al Kobaisi, M.; Alafnan, S.; Iglauer, S. A holistic overview of underground hydrogen storage: Influencing factors, current understanding, and outlook. Fuel 2022, 330, 125636. [Google Scholar] [CrossRef]
- Sambo, C.; Dudun, A.; Samuel, S.A.; Esenenjor, P.; Muhammed, N.S.; Haq, B. A review on worldwide underground hydrogen storage operating and potential fields. Int. J. Hydrogen Energy 2022, 47, 22840–22880. [Google Scholar] [CrossRef]
- Luboń, K.T.; Tarkowski, R. Numerical simulation of hydrogen storage in the Konary deep saline aquifer trap. Gospod. Surowcami Miner. Miner. Resour. Manag. 2023, 39, 103–124. [Google Scholar] [CrossRef]
- Luboń, K.; Tarkowski, R. The influence of the first filling period length and reservoir level depth on the operation of underground hydrogen storage in a deep aquifer. Int. J. Hydrogen Energy 2023, 48, 1024–1042. [Google Scholar] [CrossRef]
- Sainz-Garcia, A.; Abarca, E.; Rubi, V.; Grandia, F. Assessment of feasible strategies for seasonal underground hydrogen storage in a saline aquifer. Int. J. Hydrogen Energy 2017, 42, 16657–16666. [Google Scholar] [CrossRef]
- Iglauer, S. Optimum geological storage depths for structural H2 geo-storage. J. Pet. Sci. Eng. 2022, 212, 109498. [Google Scholar] [CrossRef]
- Luboń, K.; Tarkowski, R. Numerical simulation of hydrogen injection and withdrawal to and from a deep aquifer in NW Poland. Int. J. Hydrogen Energy 2020, 45, 2068–2083. [Google Scholar] [CrossRef]
- Luboń, K.; Tarkowski, R. Influence of capillary threshold pressure and injection well location on the dynamic CO2 and H2 storage capacity for the deep geological structure. Int. J. Hydrogen Energy 2021, 46, 30048–30060. [Google Scholar] [CrossRef]
- Pan, B.; Yin, X.; Iglauer, S. Rock-fluid interfacial tension at subsurface conditions: Implications for H2, CO2 and natural gas geo-storage. Int. J. Hydrogen Energy 2021, 46, 25578–25585. [Google Scholar] [CrossRef]
- Okoroafor, E.R.; Saltzer, S.D.; Kovscek, A.R. Toward underground hydrogen storage in porous media: Reservoir engineering insights. Int. J. Hydrogen Energy 2022, 47, 33781–33802. [Google Scholar] [CrossRef]
- Pfeiffer, W.T.; Bauer, S. Comparing simulations of hydrogen storage in a sandstone formation using heterogeneous and homogenous flow property models. Pet. Geosci. 2019, 25, 325–336. [Google Scholar] [CrossRef]
- Ershadnia, R.; Singh, M.; Mahmoodpour, S.; Meyal, A.; Moeini, F.; Hosseini, S.A.; Sturmer, D.M.; Rasoulzadeh, M.; Dai, Z.; Soltanian, M.R. Impact of geological and operational conditions on underground hydrogen storage. Int. J. Hydrogen Energy 2023, 48, 1450–1471. [Google Scholar] [CrossRef]
- Wang, H.; Xin, Y.; Kou, Z.; Qu, Y.; Wang, L.; Ning, Y.; Ren, D. Numerical study of the efficiency of underground hydrogen storage in deep saline aquifers, rock springs uplift, Wyoming. J. Clean. Prod. 2023, 421, 138484. [Google Scholar] [CrossRef]
- Hashemi, L.; Blunt, M.; Hajibeygi, H. Pore-scale modelling and sensitivity analyses of hydrogen-brine multiphase flow in geological porous media. Sci. Rep. 2021, 11, 8348. [Google Scholar] [CrossRef] [PubMed]
- Hashemi, L.; Glerum, W.; Farajzadeh, R.; Hajibeygi, H. Contact angle measurement for hydrogen/brine/sandstone system using captive-bubble method relevant for underground hydrogen storage. Adv. Water Resour. 2021, 154, 103964. [Google Scholar] [CrossRef]
- Heinemann, N.; Scafidi, J.; Pickup, G.; Thaysen, E.M.; Hassanpouryouzband, A.; Wilkinson, M.; Satterley, A.K.; Booth, M.G.; Edlmann, K.; Haszeldine, R.S. Hydrogen storage in saline aquifers: The role of cushion gas for injection and production. Int. J. Hydrogen Energy 2021, 46, 39284–39296. [Google Scholar] [CrossRef]
- Heinemann, N.; Wilkinson, M.; Adie, K.; Edlmann, K.; Thaysen, E.M.; Hassanpouryouzband, A.; Haszeldine, R.S. Cushion Gas in Hydrogen Storage—A Costly CAPEX or a Valuable Resource for Energy Crises? Hydrogen 2022, 3, 550–563. [Google Scholar] [CrossRef]
- Paterson, L. The implications of fingering in underground hydrogen storage. Int. J. Hydrogen Energy 1983, 8, 53–59. [Google Scholar] [CrossRef]
- Kanaani, M.; Sedaee, B.; Asadian-Pakfar, M. Role of Cushion Gas on Underground Hydrogen Storage in Depleted Oil Reservoirs. J. Energy Storage 2022, 45, 103783. [Google Scholar] [CrossRef]
- Mahdi, D.S.; Al-Khdheeawi, E.A.; Yuan, Y.; Zhang, Y.; Iglauer, S. Hydrogen underground storage efficiency in a heterogeneous sandstone reservoir. Adv. Geo-Energy Res. 2021, 5, 437–443. [Google Scholar] [CrossRef]
- Feldmann, F.; Hagemann, B.; Ganzer, L.; Panfilov, M. Numerical simulation of hydrodynamic and gas mixing processes in underground hydrogen storages. Environ. Earth Sci. 2016, 75, 1165. [Google Scholar] [CrossRef]
- Pfeiffer, W.T.; al Hagrey, S.A.; Köhn, D.; Rabbel, W.; Bauer, S. Porous media hydrogen storage at a synthetic, heterogeneous field site: Numerical simulation of storage operation and geophysical monitoring. Environ. Earth Sci. 2016, 75, 1177. [Google Scholar] [CrossRef]
- Pfeiffer, W.T.; Beyer, C.; Bauer, S. Hydrogen storage in a heterogeneous sandstone formation: Dimensioning and induced hydraulic effects. Pet. Geosci. 2017, 23, 315–326. [Google Scholar] [CrossRef]
- Luboń, K. CO2 storage capacity of a deep aquifer depending on the injection well location and cap rock capillary pressure. Gospod. Surowcami Miner. Miner. Resour. Manag. 2020, 36, 173–196. [Google Scholar] [CrossRef]
- Luboń, K. Influence of Injection Well Location on CO2 Geological Storage Efficiency. Energies 2022, 14, 8604. [Google Scholar] [CrossRef]
- Central Geological Database of the Polish Geological Institute. Available online: https://baza.pgi.gov.pl/en (accessed on 3 March 2024).
- Cavanagh, A.; Wildgust, N. Pressurisation and Brine Displacement Issues for Deep Saline Formation CO2 Storage. Energy Procedia 2011, 4, 4814–4821. [Google Scholar] [CrossRef]
- Pruess, K.; Oldenburg, C.; Moridis, G. TOUGH2 User’s Guide, Version 2. In Lawrence Berkley National Laboratory LBNL-43134; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1999; pp. 1–197. [Google Scholar]
- Lysyy, M.; Fernø, M.; Ersland, G. Seasonal hydrogen storage in a depleted oil and gas field. Int. J. Hydrogen Energy 2021, 49, 25160–25174. [Google Scholar] [CrossRef]
- Pfeiffer, W.T.; Bauer, S. Subsurface Porous Media Hydrogen Storage—Scenario Development and Simulation. Energy Procedia 2015, 76, 565–572. [Google Scholar] [CrossRef]
- Ernesto, J.; Fuentes, Q.; Santos, D.M.F. Technical and Economic Viability of Underground Hydrogen Storage. Hydrogen 2023, 4, 975–1000. [Google Scholar] [CrossRef]
- Persoff, P.; Pruess, K.; Benson, S.M.; Wu, Y.S.; Radke, C.J.; Witherspoon, P.A.; Shikari, Y.A. Aqueous Foams for Control of Gas Migration and Water Coning in Aquifer Gas Storage. Energy Sources 1990, 12, 479–497. [Google Scholar] [CrossRef]
- Hanson, A.G.; Kutchko, B.; Lackey, G.; Gulliver, D.; Strazisar, B.R.; Tinker, K.A.; Wright, R.; Haeri, F.; Huerta, N.; Baek, S.; et al. Subsurface Hydrogen and Natural Gas Storage: State of Knowledge and Research Recommendations Report DOE/NETL-2022/3236; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 2022.
- Delshad, M.; Alhotan, M.; Fernandes, B.R.B.; Umurzakov, Y.; Sepehrnoori, K. Pros and Cons of Saline Aquifers against Depleted Hydrocarbon Reservoirs for Hydrogen Energy Storage. In Proceedings of the Proceedings—SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–5 October 2022; p. SPE-210351-MS. [Google Scholar]
- Jadhawar, P.; Saeed, M. Mechanistic evaluation of the reservoir engineering performance for the underground hydrogen storage in a deep North Sea aquifer. Int. J. Hydrogen Energy 2024, 50, 558–574. [Google Scholar] [CrossRef]
- Bo, Z.; Hörning, S.; Underschultz, J.R.; Garnett, A.; Hurter, S. Effects of geological heterogeneity on gas mixing during underground hydrogen storage (UHS) in braided-fluvial reservoirs. Fuel 2024, 357, 129949. [Google Scholar] [CrossRef]
- Pan, B.; Liu, K.; Ren, B.; Zhang, M.; Ju, Y.; Gu, J.; Zhang, X.; Clarkson, C.R.; Edlmann, K.; Zhu, W.; et al. Impacts of relative permeability hysteresis, wettability, and injection/withdrawal schemes on underground hydrogen storage in saline aquifers. Fuel 2023, 333, 126516. [Google Scholar] [CrossRef]
- Chai, M.; Chen, Z.; Nourozieh, H.; Yang, M. Numerical simulation of large-scale seasonal hydrogen storage in an anticline aquifer: A case study capturing hydrogen interactions and cushion gas injection. Appl. Energy 2023, 334, 120655. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).