The Ability of Convergent–Divergent Diffusers for Wind Turbines to Exploit Yawed Flows on Moderate-to-High-Slope Hills

Abstract

Small-to-medium-sized wind turbines operate with wind speeds that are often modest, and it is therefore essential to exploit all possible means to concentrate the wind and thus increase the power extracted. The advantage that can be achieved by positioning the turbine on hilly reliefs, which act as natural diffusers, is well known, and some recent studies can be found on the effects of the characteristics of hilly terrain on the turbine performance. The literature shows numerous investigations on the behavior of ducted wind turbines, i.e., equipped with a diffuser. But so far, there is a lack of studies on the flow acceleration effects achievable by combining natural relief and a diffuser together. In this study, we analyze the performance of a 50 kW ducted turbine positioned on the top of hills of various shapes and slopes, with the aim of identifying the geometric characteristics of the diffuser most suitable for maximizing power extraction. The results show that a symmetrical convergent–divergent diffuser is well suited to exploit winds skewed by the slope of the hill, and therefore characterized by significant vertical velocity components. Due to its important convergent section, the diffuser is able to convey and realign the flow in the direction of the turbine axis. However, the thrust on the diffuser and therefore on the entire system increases dramatically, as does the turbulence released downwind.

1. Introduction

The need to harness all the different renewable energy sources distributed across a territory renews interest in wind turbines of any size. Furthermore, in the case of groups of users isolated from the electricity grid, as in the case of small islands, the exploitation of wind energy is still the best choice. However, small-to-medium-sized wind turbines are penalized twice: firstly, they have lower Reynolds numbers (Re) than larger turbines due to the size of the blades; secondly, and more importantly, they work within the boundary layer at rather low altitudes, for which the flow does not have high speeds due to the effect of the proximity of obstacles to the ground (shrubs, roughness of the ground). It is therefore desirable to adopt methods to concentrate the flow, thus increasing the flow rate processed by the turbine and therefore the power output. There are at least three ways to intensify wind speed. One consists in placing the turbine on smooth, rounded hills [1], with flat and free terrain at least in the prevailing wind direction; the acceleration occurs at the crest, but hills with sharp crests or stepped profiles followed by plateaus are considered not favorable due to the risk of flow separation and to the release of a wake with low flow speed and high turbulence. The second way concerns exclusively micro-turbines for built environments, and consists in placing the turbine on appropriately shaped roofs (the best being vaulted and double-sloped ones, [2]) or where the flow is channeled as for instance occurring between two adjacent buildings [3]. The third way is to place the turbine in the throat of a diffuser. Yet, it has to be noted that the latter possibility is absolutely unsuitable for large turbines, since the diffuser itself is subjected to a thrust in the direction of the flow, which would increase dramatically in the case of gusty winds and during storms. Moreover, the mass of the diffuser complicates the yaw adjustment operations, unless a flanged diffuser is used (which makes the system self-yawing), not to mention the weight of the diffuser on the turbine support tower. However, for moderate-sized turbines, the diffuser is a low-cost solution for increasing the power of a wind turbine in low-speed winds. Several experimental studies [4,5,6,7,8,9,10,11,12,13] demonstrate the effectiveness of diffusers in increasing the power generated by the turbine; the best performance is reached if a brim is adopted [5,7,13] due to the viscous interactions at the diffuser exit section between the flow passing inside and the flow passing outside the diffuser, with an increase in power output by a factor of 2÷5 compared with a bare turbine [7]. Moreover, using a diffuser, it is also possible to reduce the aerodynamic noise since the vortices released at the tips of the turbine blade are greatly attenuated by their interactions with the boundary layer taking place at the diffuser walls [7]. Another reason that could make the use of the diffuser even more attractive is the good performance in yawed winds (i.e., which arrive on the rotor misaligned with respect to the axis) demonstrated by diffusers equipped with at least some converging section [8,14,15,16,17]: this is interesting especially for turbines located on hilly reliefs, where the slope adds vertical components to the wind speed.

Unfortunately, studies on the combination of the accelerating effects on the flow of hills and diffusers are lacking in the literature, since the studies on the effects of hilly terrain are without turbines, or with bare turbines. For instance, among the first, there are the experimental wind tunnel investigations [18,19,20]: study [18] is an analysis of the flow characteristics and speed-up on low and smoothed hills of different shapes and aspect ratios (i.e., half-length to the height of the relief); study [19] is focused on the flow separation behavior occurring in two-dimensional hills with trapezoidal profiles, characterized by different slopes; in [20], the flow acceleration characteristics and the turbulence generation over sharp-edged escarpments with different slopes are assessed. The investigations with turbines in the atmospheric boundary layer can be performed with a scaled model in a wind tunnel [21] or by means of full-scale CFD, of which the most accurate are based on the Large Eddy Simulation method [22,23,24] or on the Delayed Detached Eddy Simulation [25]; in some cases, a simplified two-dimensional shape of hills is assumed [22,23], and otherwise, the complex topography of a real terrain is reproduced [21,24,25,26]. Considering the actual topography can be important because it influences wind intensity and direction and the intensity of turbulence, in [26], it is proved how even relatively very low reliefs, located upstream of the escarpment on which the turbines are positioned, can significantly influence the characteristics of the wind reaching the rotors. These analyses with turbines are focused not only on power production and turbine loads but also on the development and energy recovery of the turbine’s wake, since this is a practical aspect of fundamental importance for choosing the optimal layout of a wind farm.

It would therefore be extremely interesting and useful from a practical point of view to analyze the performance of convergent–divergent diffusers in realistic hilly contexts, to understand whether beneficial synergistic effects can arise.

Yet, what are affordable and reliable methods for this kind of challenging investigation? Experimental campaigns are expensive and only affordable for scaled small turbines operating under simplified conditions, often far from the real environment. On the other hand, 3D CFD investigations including the blades in the calculation grid would need huge computational resources and time, making them prohibitive to run many simulations of a turbine operating in transient (i.e., time-marching) conditions, especially in the case of large 3D domains replicating the terrain geometry. To drastically reduce calculation time, in recent years, some lower-fidelity CFD approaches have been developed, which can be called hybrid BEM-CFD models, where BEM stands for Blade-Element/Momentum theory. The idea underlying these methods is to mimic the presence of the turbine by introducing source terms into the momentum balance equation for only the region of the grid (i.e., the “turbine disk”) swept by the rotation of the blades, while, throughout the rest of the domain, the flow field is solved using the traditional URANS equations. In this way, the turbine disk does not require a fine grid as it is not necessary to resolve the boundary layer that in reality would develop on the blade walls since the blades are not physically included. The complexity and accuracy of hybrid methods can be very high, as in the case of the Actuator Line (AL), which, however, still requires unacceptable calculation times when applied to the simulation of numerous cases with large computational domains. At the minimum level of complexity and calculation time requirement, we find the Actuator Disc (AD), an approach widely adopted, for instance, to simulate wind farms even with coarse grids; yet, this latter approach is not able to incorporate any geometric characteristics of the turbine. In the middle between AL and AD there is the Virtual Blade Model (VBM), which is an implementation of BEM theory [27] within the CFD software ANSYS Fluent. This model, originally developed by Zori and Rajagopalan for helicopter rotors as far back as 1995 [28], was applied, several years later, to both hydrokinetic turbines [29,30,31,32] and wind turbines [33,34,35,36], providing results that achieved good correspondence with experimental data regarding not only the power extracted but also the behavior of the wake released downstream of the rotor [32,33].

In this study, we adopt VBM to predict the performance of a 50 kW turbine working in realistic full-scale natural environments characterized by hilly reliefs of different profiles: some smooth, and others steep or sharp. Our objective is to analyze the behavior of two diffusers, possessing very different shapes of the converging section, to understand if and how much it is possible to further increase the power extracted, especially in the most unfavorable conditions for the bare turbine, which are those of flows arriving misaligned at the rotor since they are distorted by the slope of the hill.

2. Methodology

2.1. The Turbine Virtual Model, VBM

In our work, the turbine blades are not physically represented in the calculation grid, and in fact, their action is mimicked according to the hybrid BEM-CFD Virtual Blade Model (VBM) approach, which was implemented in Fluent by Zori and Rajagopalan [28] via a “User-Defined Function” (UDF). VBM simulates the effects of blade rotation by introducing source terms into the momentum transport equation; these source terms act within a flow-permeable disk (the “rotor disk” in the following), whose area is equal to the area swept by the blades. These source terms are forces per unit volume in the x, y, and z directions calculated using the classical Blade-Element theory, so that the fluid within the disk is affected by the same forces it would be subjected to if blades were present. The domain swept by the blades, i.e., the rotor disk, is visible in yellow in Figure 1; it is divided into small cells in the radial direction from the hub to the tip of the blade and in the azimuthal direction, θ.

The outputs are the thrust and the torque (and therefore the power) of the turbine, calculated by integrating, respectively, the values of the axial and tangential components of the force on all the cells of the rotor disk. The required inputs are the lift and drag coefficients of the airfoil, tabulated as a function of the angle of attack, AoA, and the Reynolds number, Re; the turbine radius, R; the number of blades, Nb; the distribution of the blade chord, c, and of the twist angle, β, along the blade dimensionless radial direction, ξ; the turbine angular speed, Ω. Before reporting the fundamental equations of VBM, let us define the relative velocity of the flow, W, as the vector composition of the wind absolute speed incoming to the blade and the tangential speed of the blade due to the turbine rotation. On the basis of the values of AoA and Re calculated by the CFD solver, the lift and drag coefficients are interpolated from the tabulated coefficients set in input; then, the lift and drag forces for the unit span, $f_{L,D}$, are calculated as a function of the local values of c and W by means of the following relation [27]:

$$f_{L,D}=C_{L,D}\left(AoA,Re\right)·c\left(\xi \right)·\rho ·W^2/2$$

where $C_{L,D}$ is the lift or drag coefficient per unit span and $\rho$ is the air density. Then, for each cell belonging to the rotor disk, the lift and drag forces, $F_{L,D cell}$, are averaged during one complete revolution:

$$F_{L,D cell}=N_b·f_{L,D}·dr·r·d\theta /\left(2·\pi ·r\right)$$

where r is the local radius, and dr and dθ are the radial and azimuthal width of the cell. At this point, the momentum source terms, ${\overrightarrow{S}}_{cell}$, are calculated as volume forces:

$${\overrightarrow{S}}_{cell}=-{\overrightarrow{F}}_{cell}/V_{cell}$$

where $V_{cell}$ is the cell volume, and the arrow above the variables has been used in order to indicate the usual compact vector notation, i.e., replacing (including all of them) the three equations in x, y, and z. In the rotor disk, the flow is loaded with these forces and the process is repeated until convergence is achieved, that is, until such a reduction in momentum so as to generate a slowdown of the absolute flow consistent with the value of W that was used to calculate the force coefficients; throughout the remaining domain, the calculation is performed using the standard 3D URANS. The VBM allows us to vary the blade pitch angle as occurring during a load control operation, and moreover, it incorporates a tip loss formulation to estimate the torque lost due to the vortices released at the blade tips.

We chose a 50 kW turbine as it is an attractive size for several energy applications, and is still small enough to be used with a diffuser. The diameter is 16.16 m, and the hub height is 27 m. The rotor geometry is the same of the NREL Phase-VI, a two-bladed wind turbine based on the S809 airfoil and frequently adopted as a benchmark case due to a wide availability of published experimental data. However, since the diameter of the original Phase-VI is just 10 m, we needed to scale the geometry. The C_L,D data sets are taken from [37], and furthermore, we used the XFoil software to extend the values of the C_L,D coefficients to Re greater than those to which the experimental data of the literature refer. The distributions of the blade chord and twist are taken from [38] and scaled to our turbine size; the pitch angle of the blades is regulated at 3°, as in the experimental tests.

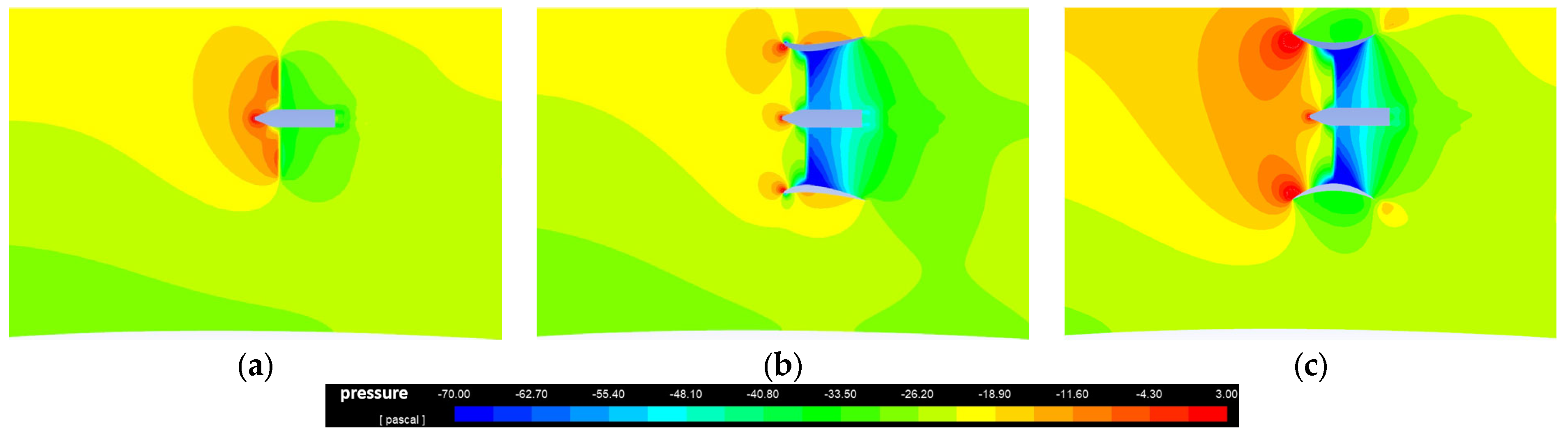
2.2. Geometry of the Two Diffusers

This study is focused on analyzing the effects of the shape of the diffuser when the recipient turbine is placed on hilly terrain. Two diffusers are taken into consideration, both equipped with a converging section. As shown in Figure 2, they have in common the overall length, L, the maximum thickness, the diameters of the throat and exit, and therefore the aspect ratio, AR, defined as the ratio between the exit and the throat areas; in this study, AR = 1.53. The sectional profile of the first diffuser is an NACA8308 airfoil (with the usual meaning of 4-digit NACAXXXX airfoils), which means that the length of the converging section corresponds to 30% of the chord; the airfoil chord is rotated 12° to obtain the desired AR. The second diffuser is symmetrical, and then the converging section is 50% of L; its sectional profile is defined by two parabolas, with formulas shown in Figure 2.

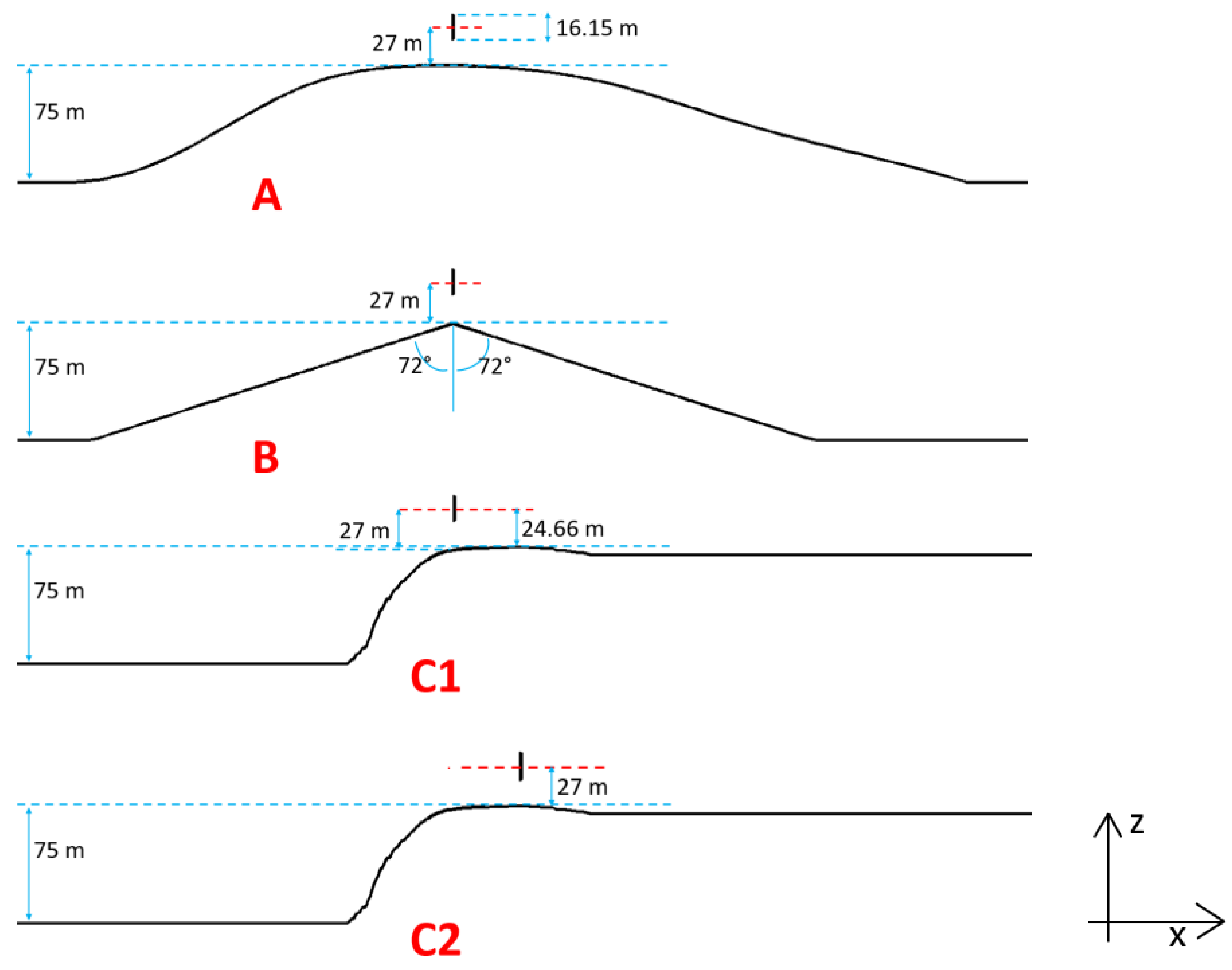
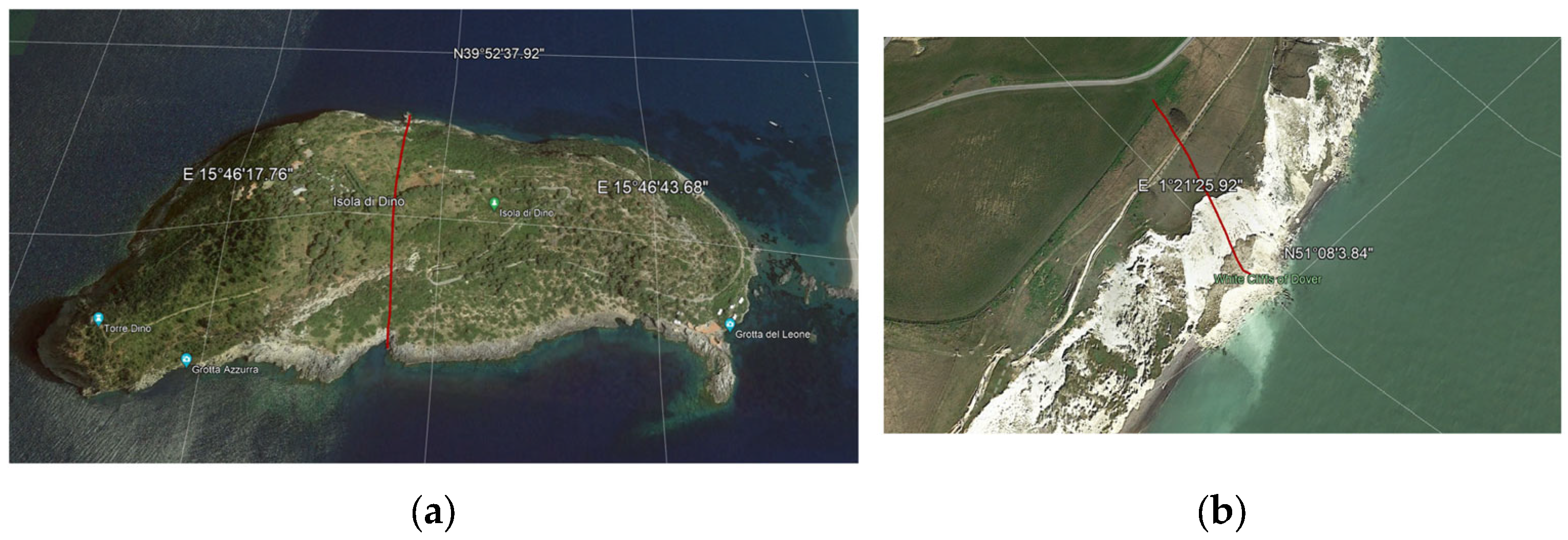
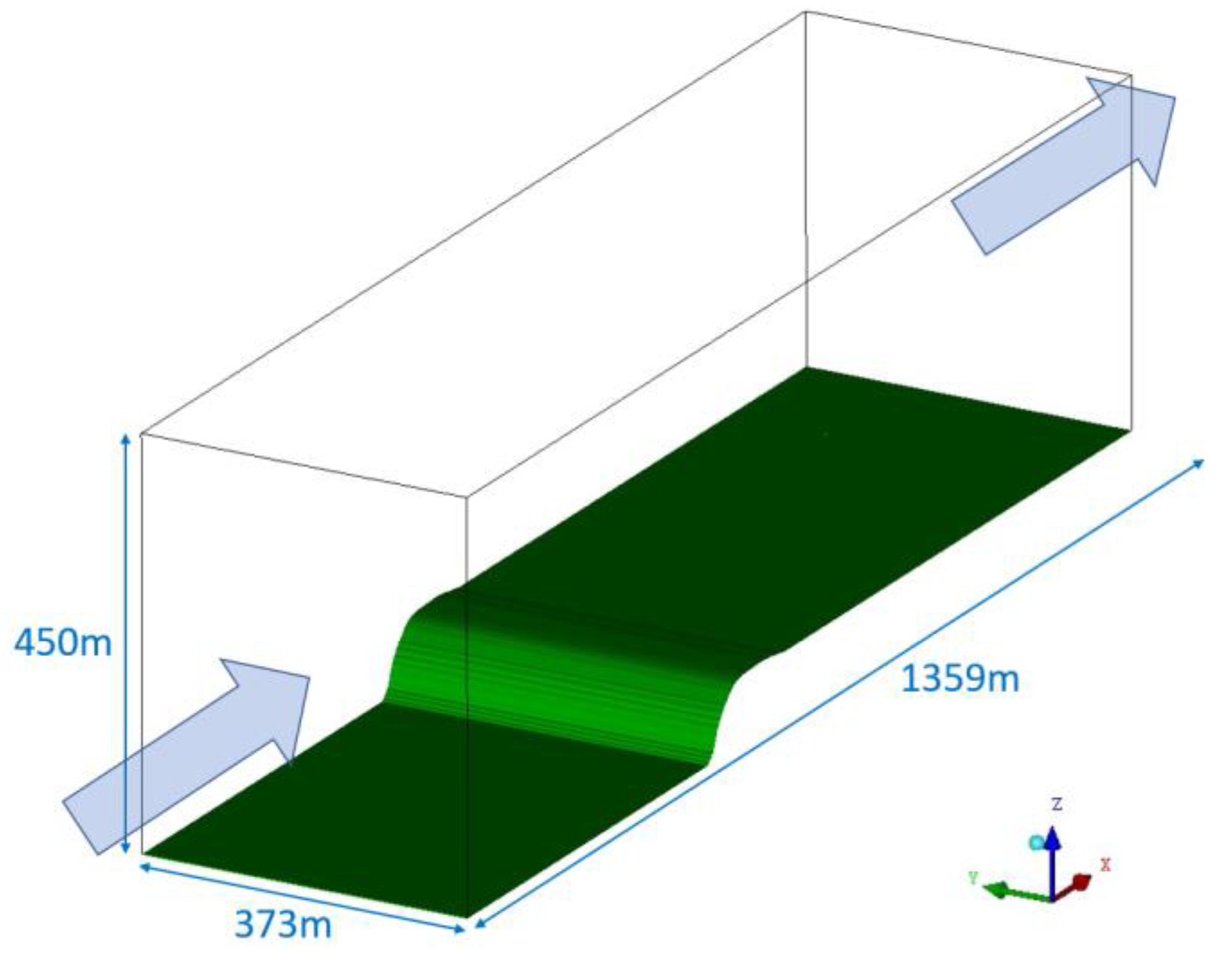
2.3. Characteristics of the Hilly Reliefs

We chose four hilly profiles (actually three, since for one of the profiles only the position of the turbine changes) that are representative of terrains that can occur in reality. Figure 3 shows the xz profiles, which are assumed to be parallel to the prevailing wind direction (coming from the left): A and C1 are characterized by almost horizontal flow, while B and C2 imply important vertical velocities of the flow. For all, the maximum height is 75 m. Their characteristics are summarized below.

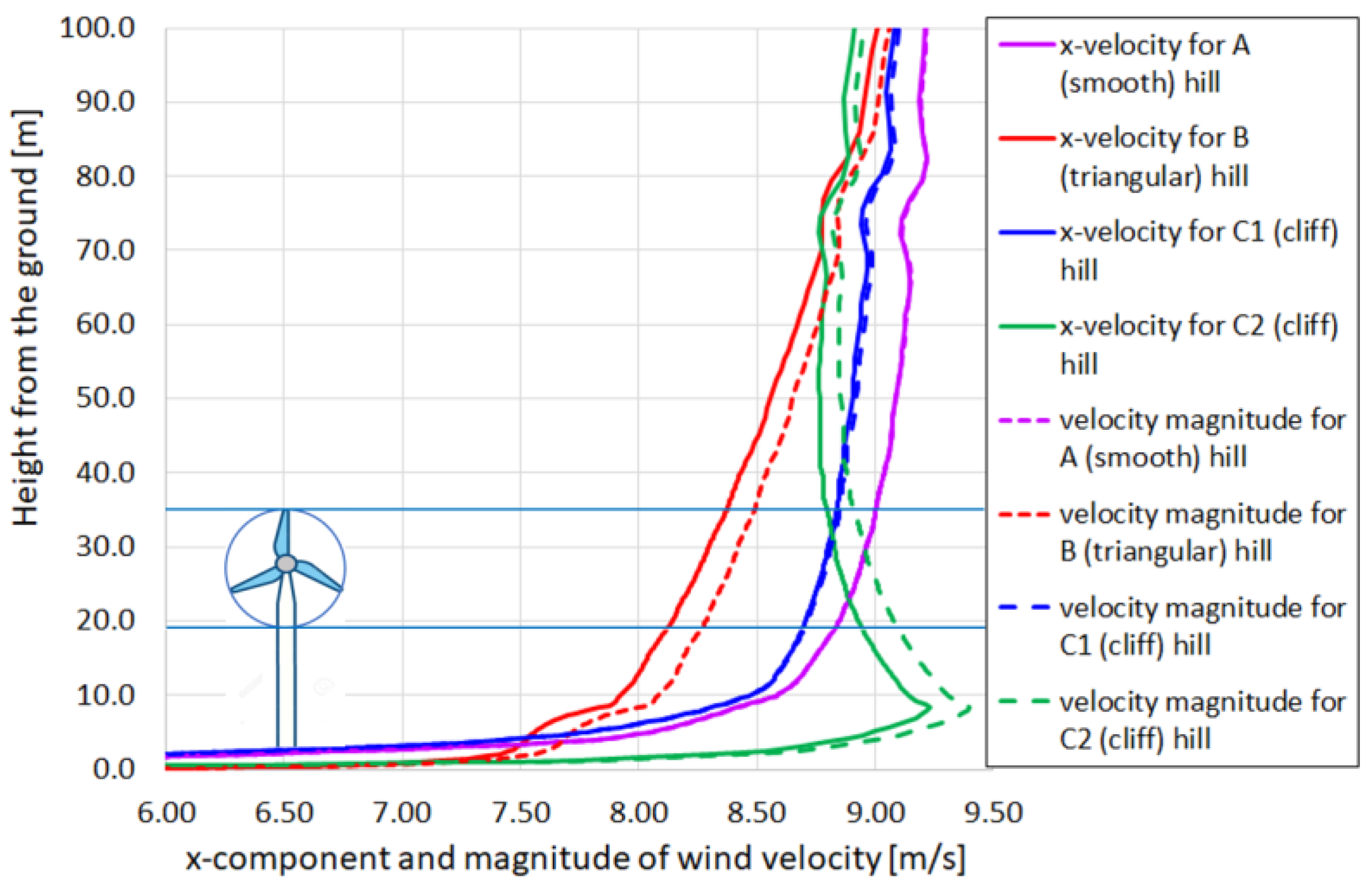
• A-hill. It is the typical recommended hill for wind turbine installation; its profile is well rounded with a smoothed ridge, and it is able to concentrate the wind gradually, avoiding increased turbulence in the turbine area, and without flow separation;
• B-hill. The shape is triangular, with a slope of 18° compared to the horizontal plane. Flow separation from the hilltop and a large turbulent wake released downstream of the hill are expected. For these reasons, the position of the turbine should be chosen with caution (assumed to be on the top in this study);
• C1-hill. It is a cliff-type relief but, unlike a stepped profile, it has a rounded ridge. The turbine is moved upstream from the plateau, above the ridge (2.34 m lower than the maximum height of the hill), where significant vertical velocities of the flow are expected;
• C2-hill. It is the same relief of C1, the difference being that the turbine is simulated on the plateau, at the maximum height of the hill. The literature advises to be careful, as flow separation could occur above the plateau.

The profiles for A and C1/C2 are drawn by means of the “Show Elevation Profile” of the Google Earth Pro tools, and are those, respectively, of the island of Dino (Italy) and the Cliff of Dover (UK). The path of Dino Island starts at 39°52′24.58″ N 15°46′19.49″ E and moves north–south, whereas for the Cliffs of Dover, it starts at 51°08′04.32″ N 1°21′26.20″ E and moves in a north–south direction. These paths are shown in red in Figure 4.

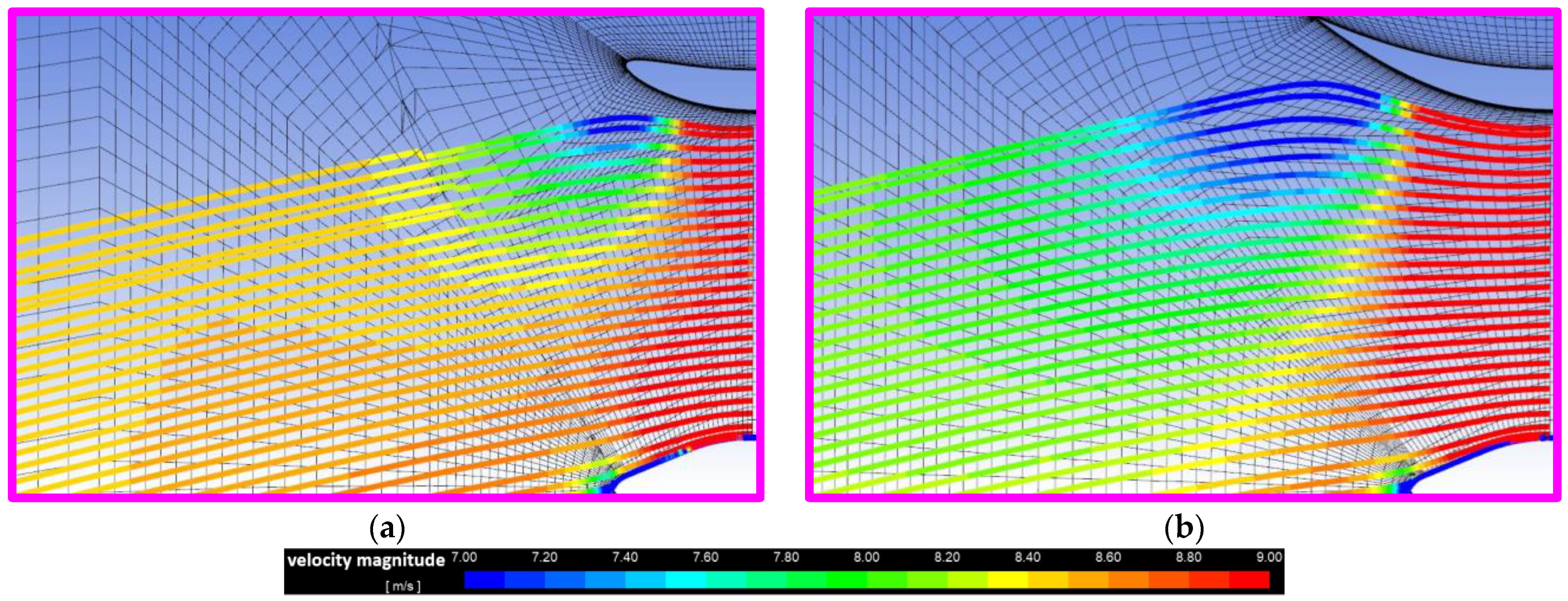
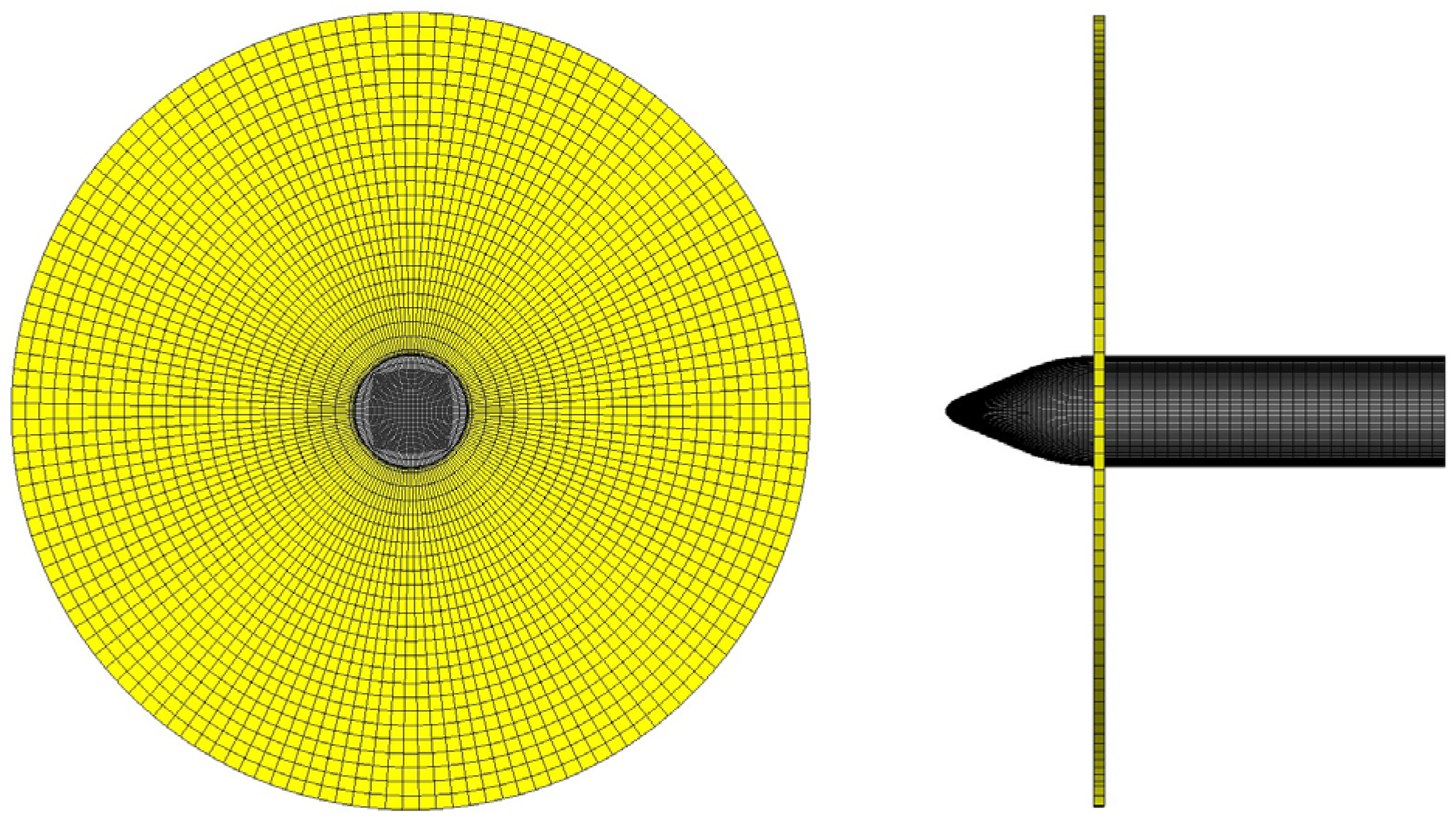
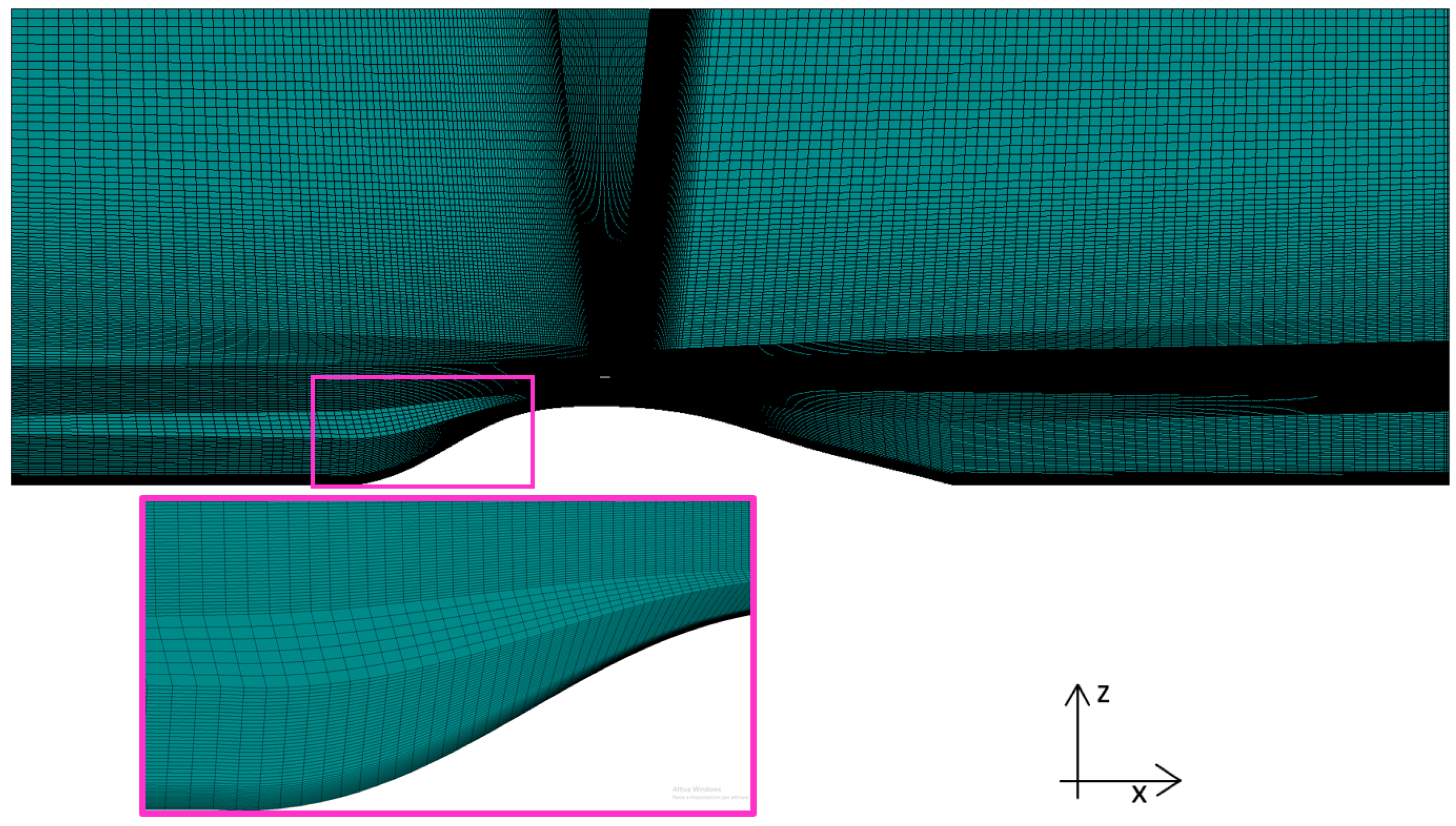
2.4. Domain Dimensions and Grids

For all the reliefs, the 3D surface of the hill is simplified along the y direction, and in fact, it is obtained by the simple translation of the xz profiles shown in Figure 3. Thus, the height is uniform in the y direction. This assumption appears sufficiently realistic in the case of the Cliffs of Dover and even in the case of Dino Island since, as can be observed in Figure 4a, its shape is rather regular and elongated in one of the directions (our y-axis). Figure 5 shows the calculation domain shape (the bottom corresponds to the cases C1/C2), together, the dimensions and the wind direction. Boundary conditions are the velocity inlet for the domain inlet; pressure outlet for the exit; wall with a roughness of 0.4 m for the terrain; symmetry for the lateral sides and for the top. ANSYS-ICEM has been used to obtain multi-block structured 3-D grids (i.e., made up of hexahedral cells only), with the addition of O-grids to thicken the distribution of cells in the areas of greatest interest, and at the same time to improve their quality. In proximity of the diffuser surfaces, and also of the turbine hub, refinements with exponential-law node distribution are set to obtain y+ < 1.0. Figure 6 depicts a xz scan-plane of the domain in the turbine region, with details of the grid refinements at the diffuser and hub walls.

Figure 7 shows the xz scan-plane of the complete domain, from the inlet to the outlet. The dark regions are due to very small cells. In structured grids, the need for small cells in the areas of interest (in our case, the area above the hill, where the turbine is located) implies the propagation of narrow cells up to the ends of the domain, and this is a major limitation, especially when the turbine is simulated in a huge space compared to its scale, because it increases the number of cells in the domain and therefore the calculation times. The only way to limit the total number of cells is to generate relatively large cells in the areas where the details of the flow field are not important (at a considerable distance from the turbine); for this reason, the grid in Figure 7 appears very coarse going toward the boundaries of the domain (with the exception of the terrain). As a result, the grids we used have a total number of cells between 7.3 M and 8.5 M.

2.5. Solver Setup

All the simulations are unsteady (i.e., time-marching), and performed by means of the ANSYS-Fluent 19.2 v code. The Realizable k-ε model with enhanced wall treatment is used for the turbulence closure. The velocity–pressure coupling is based on SIMPLEC (Semi-Implicit Method for Pressure-Linked Equations—Consistent), a modified form of the SIMPLE algorithm, commonly used in computational fluid dynamics to solve the Navier–Stokes equations. The following spatial discretization schemes are adopted: Least Squares Cell-Based (LSCB) for the gradient, and second order for the momentum, pressure, turbulent kinetic energy, and specific dissipation rate. The temporal discretization is treated with the bounded second-order implicit method. The convergence criterion is set with residuals of 5 × 10⁻⁵ for all the transport equations. The time-step size is 0.15 s for the preliminary phase performed for each hill relief without the turbine, while a value in seconds corresponding to 40° of blade rotation is set for simulations with the turbine in operation. These and other settings are summarized in

Table 1. Setup of simulations.

Setup of Simulations
Turbulence closure	Realizable k-ε
Velocity–pressure coupling	SIMPLEC
Spatial discretization	LSCB for gradient Second order for other variables
Temporal discretization	Second order implicit
Time step	0.15 s preliminary phase (turbine off), 40° of blade revolution (turbine on)
Convergence criterion	Residuals of 5 × 10−5
Turbine characteristics	Diameter of 16.16 m 2 blades Airfoil S809 Chord and twist distribution from [38] Pitch of 3°
Inlet velocity	$\left\{\begin{array}{c}U\left(z\right)=U\left(z_{ref}\right)·{(z⁄z_{ref})}^{\alpha }\\ z_{ref}=102 \mathrm{m}\\ U\left(z_{ref}\right)=\frac{7m}{s}\\ \alpha =0.2\end{array}\right.$

.

To conclude this section on the methodology, it must be specified that in a previous article [32], one of the authors of this work, together with N. Lombardi and colleagues from Strathclyde University, validated the overall numerical model by comparing axial thrust and power with the experimental data [39] available for a turbine in a laboratory scale working in a tow tank. Although the experimental turbine had a different geometry from ours (different airfoil and distributions of chord and twist angle), since the type and quality of the grid, as well as solution methods and convergence criteria, were the same as those adopted in the present work, the validation task was not repeated here. The reader can find details of the preliminary sensitivity analyses regarding the grid fineness, time-step size, and number of simulated turbine revolutions in Lombardi’s Master’s thesis [40].

3. Results

At the domain inlet, Hellman’s law for the wind velocity as a function of z is set:

$$\mathit{U}\left(\mathit{z}\right)=\mathit{U}\left({\mathit{z}}_{\mathit{r}\mathit{e}\mathit{f}}\right)·{(\mathit{z}⁄{\mathit{z}}_{\mathit{r}\mathit{e}\mathit{f}})}^{\mathit{\alpha }}$$

where z_ref is a reference height, U(z_ref) is the velocity at the reference height, α is an exponent dependent on the soil characteristics; we set z_ref = 102 m, which is the total height (i.e., including the hill) of the turbine hub, and U(z_ref) = 7 m/s; α = 0.2. Due to the very large size of the computational domains (the total number of cells is ~ 7.5 million), the time required for the simulations is quite long, even with the 100 HPC processors of the supercomputer (with unlimited RAM memory) that were used. In order to reduce calculation times, the flow fields without a turbine were obtained for each type of hill. The number of simulated seconds for this preliminarily phase should be sufficient to create a stable flow field, with a fully developed wake released from the hills; in this study, the time taken by the wind to sweep the domain twice, from the entrance to the exit, was chosen. Afterwards, these flow fields were used to initialize the simulations with the turbine in operation.

The streamlines for the three hills, without the presence of either the turbine or the diffuser, can be seen in Figure 8 on a vertical plane covering the entire length of the domain; the colormap is referred to the x-velocity. The flow appears to be accelerated above the top of all three reliefs, although to a lesser extent in the case of the triangular hill, which is also the only case in which the flow abruptly separates from the top, generating a large wake with vortex zones recirculating; for the cliff, no separation occurs even above the plateau (C1). Significant vertical wind speeds are observed where the turbine will be placed (see again the turbine locations in Figure 3) in cases B and C2. To quantify the wind speed, and therefore the kinetic power available in the z-range of interest for the turbine, it is useful to look at the diagram in Figure 9, which shows vertical profiles of the x-velocity and the velocity magnitude obtained (still without turbine/diffuser) exactly at the x-coordinate where the turbine will be placed. By focusing on the x-velocity curves, it can be seen that the highest average velocity (on the turbine diameter) is for A-hill, followed at a very short distance by C2, then by C1 and finally, with a greater gap, by B. But, examining the velocity magnitude curves, C2 allows a somewhat greater average velocity than A.

Before analyzing the cases with the turbine in operation, let us check that the diffusers are free from a flow separation/stall. Figure 10 shows the streamlines (departing from the diffuser throat) for the most critical diffuser, as it has a shorter divergent section, i.e., the symmetrical one; the turbine is working. The streamline features prove that the flow does not separate from the internal walls of the diffuser, and furthermore, very high values of the velocity magnitude are noted near the walls, which indicate that the flow inside the boundary layer is well energized. For this to happen, it is recommended to leave an annular gap of a certain thickness (we set 2.5% of the turbine radius) between the rotor disk and the diffuser throat wall, where a high momentum jet can be established [17,41,42,43].

Figure 11 depicts the streamlines approaching the turbine vertical diameter for the bare turbine (left column), the NACA-ducted turbine (central column), and the symmetric-ducted turbine (right column), obtained with the best angular velocity, which was 6.914 rad/s for all the hills; in other words, these streamlines represent the flow processed by the turbine.

Looking at the colors, it should not be surprising that the wind gradually slows as it advances toward the rotor disk, since the presence of the turbine is an obstacle that offers resistance to the incoming flow, consistent with the increase in the streamtube cross-section visible for all simulated cases. By analyzing and comparing the cases depicted, at least three important aspects are worth highlighting. The first is that the diffuser generally increases the flow rate, and therefore the power extracted, since the section of the streamtube appears to be wider for cases of a ducted turbine compared to cases of a bare turbine; in fact, once an upstream section is fixed (for example, the left side of the various figures), the greater the width of the streamtube cross-section, the greater the flow rate that reaches the turbine, and it is evident that in the figures of the central and right columns, the streamtube is wider than in the corresponding figures (i.e., for the same type of hill) in the left column. The second important aspect is that in the cases of a bare turbine, the flow approaches the rotor with the slope dictated by the particular morphology of the hilly relief: horizontal and therefore axial, in cases A and C1, and yawed in cases B and C2; it must be remembered that when the flow arrives as skewed, the flow rate that generates power is geometrically reduced, since only the “frontal” area (perpendicular to the flow) of the rotor serves this purpose. From this point of view, cases B and C2 are certainly penalized if the turbine is bare, but they are not, and this is the third and fundamental aspect to underline, if a diffuser is used. As can be seen in Figure 11e,f,k,l, as well as mentioned in some literature [8,14,15,16,17], the converging part of the diffuser seems to be able to collect the incoming skewed flow and redirect it toward the disk in the axial direction, with this also exploiting the energy content of the vertical components of wind speed. For the first time, we show that, as can be seen in greater detail in Figure 12 (which allows us to compare the behavior of the NACA diffuser and the symmetric one for C2), this beneficial effect is all the more relevant as the converging section is extended.

The power extracted for all the examined cases is shown in Figure 13 as a function of the turbine angular speed. The graph also shows the powers predicted with a simple axisymmetric domain (very large, to avoid any confinement effect) in conditions of a uniform inlet velocity of 7 m/s; since in the case of asymmetry the wind speed on the turbine disk is not accelerated by the presence of the hills, the optimal angular speed is obviously lower. It can be observed that positioning the bare turbine on hilly reliefs allows for approximately doubling the power compared to the case of an unconfined domain subject to uniform wind, and that the powers obtained for the bare turbines are similar for the cases A, C1, and C2, while for case B, the power is significantly lower, and this is consistent with the behavior of the x-velocity in the disk region already seen in Figure 9. It is also seen that a further very large power gain can be achieved by using the two diffusers; however, the exact amount of the benefit achievable depends on the type of diffuser and the type of hill.

To quantify the advantages of the diffuser, it is convenient to analyze the dimensionless powers on the basis of the power of the bare turbine in the axisymmetric domain (Figure 14a) and, above all, on the basis of the bare turbine on a given hill (Figure 14b). It is easy to argue that in all simulated cases, the most effective diffuser in concentrating the wind is the symmetrical one; in cases of horizontal wind (hills A and C1), both diffusers give power gains similar to those obtained in the axisymmetric domain (which were 73% for NACA diffuser, and 85% for symmetric diffuser); in cases of yawed wind (hills B and C2), the power increases achieved by the ducted turbines are even higher, i.e., +92% (hill B) and +89% (hill C2) with the NACA diffuser, and +112% (hill B) and +105% (C2-hill) with the symmetrical diffuser. This last result is very important as it establishes that the diffusers equipped with a converging section enable the turbine to also exploit the energy content of the vertical components of wind speed, which often occur above the ridges in real environments.

The main disadvantage deriving from the diffuser may be the axial force (thrust) on it, which will act on the turbine tower and the foundations in terms of increasing the bending moment. The diffuser thrust depends both on the flow accelerating effect (to which it is directly related [44]) and on the frontal area (i.e., normal to the flow) of the diffuser walls. Figure 15 depicts the pressure distribution on the vertical plane passing through the turbine axis for the A-hill for the bare and ducted turbines; it can be deduced that the loads due to pressure are significant, especially for the symmetrical diffuser due to its large frontal area, which amplifies the resistance offered to the wind.

To quantify the forces acting on the diffusers in comparison to the thrust acting on the turbine disk, Figure 16 shows (a) the forces in x and z directions predicted for the diffuser walls and (limited to the thrust) for the rotor disk, and (b) the x-forces normalized by the thrust of the bare turbine located on the same hill. It is interesting to observe that in the cases of winds with vertical components (B and C2), attention should be paid to the z-forces as they can be even more relevant than the x-forces (this is what happens for NACA diffuser); the diffuser thrust is about over half of the turbine thrust in the case of the NACA diffuser, while it can even almost reach the turbine thrust in the case of the symmetric diffuser.

Finally, the increase in turbulence released by the diffuser should also be carefully evaluated, which could be significant especially for the symmetrical diffuser [17] and especially in the case of skewed winds, as can be seen in Figure 17, which shows the turbulent kinetic energy on the vertical plane through the turbine axis for the ducted turbine on the A-hill and on the B-hill. The wakes generated by the turbine shaft (center of each figure) and the diffuser walls are visible. It is interesting to note that the symmetric diffuser always produces a thick wake, even in the case of horizontal flow (A-hill) for which, on the contrary, the NACA diffuser does not produce a significant wake. The presence of very thick wakes could be problematic in the case of installations of multiple turbines close together; furthermore, the aerodynamic noise implied by the wake of the diffuser should also be evaluated (at least in the case of skewed winds). However, it should be noted that with the low-order CFD method adopted in the current study, it is not possible to make a direct comparison with the turbulence in the wake generated by the turbine since the VBM model (without physical blades) greatly underestimates the turbulence in the turbine wake. This is the reason why the turbulence linked to the wake of the turbine is not visible in Figure 17, while in reality it is well known that it is relevant.

4. Conclusions

The behavior of two diffusers with similar overall dimensions (length, frontal area) but different shapes especially about the converging section was analyzed for a full-scale turbine positioned on various hilly terrains, representative of reliefs found in natural environments. The hills have the same height but different slopes and shapes, so in some cases, the flow at their top is horizontal, and in other cases, it has vertical velocity components, the energy content of which cannot be harnessed by bare turbines.

The effect of wind augmentation generated by the hill alone is such that it allows approximately a doubling of the power extracted compared to the case of an unconfined environment in uniform wind, but the optimal position of the turbine should be carefully identified (see the different performances of C1 and C2).

A further increase in the flow rate processed by the turbine is obtained by adopting the diffuser, which in the cases of horizontal winds allows an increase in power, compared to the bare turbine on the same hill, very similar to the increase predicted in an unconfined environment (73% for NACA diffuser, 85% for symmetrical diffuser).

The power gain given by the diffuser is even higher (~90% for NACA, ~110% for the symmetrical one) in the cases of wind made yawed by the slope of the hill, since the converging section of the diffuser acts for realigning and conveying the flow in the direction of the turbine axis, and this effect is all the more marked the wider the converging section.

However, for design purposes, it is necessary to carefully evaluate the additional horizontal and vertical loads of the wind on the diffuser, and thus on the entire system, which exceed half (almost reaching close to, in some cases) the thrust on the turbine.