Integrated Demand Response for Micro-Energy Grid Accounting for Dispatchable Loads
Abstract
1. Introduction
2. Micro-Energy Grid Energy Supply Structure and Modelling
2.1. Energy Supply Structure of Micro-Energy Grid
2.2. Modelling of Energy Plant Operation
2.2.1. Gas Turbine
2.2.2. Waste Heat Boiler
2.2.3. Heat Exchanger
2.2.4. Electric Boiler
2.2.5. Electric Refrigeration Air Conditioner
2.2.6. Absorption Chiller
2.2.7. Battery Energy Storage System
2.2.8. Ice Storage Air Conditioning
2.2.9. Phase Change Heat Storage
2.3. Dispatchable Load Model
2.3.1. Curtailable Loads
2.3.2. Transferable Load
2.3.3. Convertible Load
3. Integrated Demand Response Strategies for Micro-Energy Grids Accounting for Dispatchable Loads
3.1. Objective Function
3.2. Constraints
3.3. Model Solving
4. Case Analysis
4.1. Case Overview
4.2. Price-Based Comprehensive Demand Response Results
4.3. Incentivized Comprehensive Demand Response Results
5. Conclusions
- (1)
- The price-based comprehensive demand response strategy of micro-energy grid proposed in this paper can optimize the energy consumption structure of a micro-energy grid under the guidance of time-of-use electricity price, reduce operating costs, and ensure the consumption of new energy. For the power grid, the peak-to-valley difference can be reduced to achieve a win–win situation.
- (2)
- The incentive-based comprehensive demand response strategy of the micro-energy grid proposed in this paper enables the micro-energy grid to minimize its own costs while responding to the peak regulation demand of the upper level and obtain the peak shaving subsidy to further reduce its own operating cost. The proposed strategy fully excavates the demand response potential of the micro-energy grid through dispatchable load; the complementarity of electricity, heat, and cold realizes the comprehensive coordination and optimization of source–grid–load–storage, provides greater peak regulation capacity, and obtains greater benefits when participating in the incentive-based comprehensive demand response. Thus, it provides theoretical reference and support for the majority of multi-energy users to participate in the comprehensive demand response.
- (3)
- The method proposed in this paper can estimate whether the investment cost can be recovered by the micro-energy grid during the life cycle of the phase change heat accumulator and ice-cold storage device; additionally, it can provide a reference for the energy storage planning of the micro-energy grid. For the case of the micro-energy grid in this example, compared with the case of only electrochemical energy storage, the economic benefit and lower net cost of the micro-energy grid participating in the comprehensive demand response with the configuration of ice storage device are greater.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Acronyms | |
| AC | air conditioner |
| BESS | Battery energy storage system |
| DR | demand response |
| EB | Electric boiler |
| IDR | integrated demand response |
| GT | gas turbine |
| HE | heat exchanger |
| IES | integrated energy system |
| ISAC | ice storage air conditioner |
| PCHS | Phase change heat storage |
| PV | photovoltaic |
| WHB | waste heat boiler |
| Variables | |
| PGT | output of the gas turbine |
| HM_WHB | output medium-grade heat power of the waste heat boiler |
| HL_WHB | output low-grade heat power of the waste heat boiler |
| HM_HE | input medium-grade heat power of the heat exchanger |
| HL_HE | output low-grade heat power of the heat exchanger |
| HL_EB | output low-grade heat power of electric boiler |
| HC_AC | cold power output of electric refrigeration air conditioner |
| HC_AB | cold power output of the absorption chiller |
| SBS | amount of power stored in the battery storage |
| PBS,c | charging power of the battery |
| PBS,d | discharging power of the battery |
| HC_IS | cold power provided by the ice storage air conditioner |
| STK | ice storage volume in the ice storage tank |
| PTK | electric power consumed by the ice making in the ice storage tank |
| SHS | amount of heat stored in the heat storage |
| HL_HS,c | heat storage of the heat storage |
| HL_HS,d | exothermic power of the heat storage |
| Lcut | power of the curtailable load |
| Lshift | power of the shifter load |
| Lc | power of the cold load |
| U | Start stop status |
| Parameter | |
| H | efficiency |
| Pmax/Pmin | maximum/minimum power generation |
| rmax | maximum climbing rate |
| cse | Start–stop cost of the gas turbine |
| com | operation and maintenance costs |
| Hmax/Hmin | maximum/minimum heat power |
| Smax/Smin | maximum/minimum volume |
| σ | self-consumption rate |
| SOCmax/SOCmin | maximum/minimum battery running SOC |
References
- Xue, Y.; Yu, X. Beyond smart grid cyber physical social system in energy future. Proc. IEEE 2017, 105, 2290. [Google Scholar] [CrossRef]
- Yong, L.; Yao, Z.; Yi, T.; Cao, Y.; Bu, F. Optimal stochastic operation of integrated low carbon electric power, natural gas and heat delivery system. IEEE Trans. Sustain. Energy 2018, 9, 273–283. [Google Scholar]
- Chen, X.; Wang, C.; Wu, Q.; Dong, X.; Yang, M.; He, S.; Liang, J. Optimal operation of integrated energy system considering dynamic heat-gas characteristics and uncertain wind power. Energy 2020, 198, 117270. [Google Scholar] [CrossRef]
- Jia, H.J.; Wang, D.X. Research on Some Key Problems Related to Integrated Energy Systems. Autom. Electr. Power Syst. 2015, 39, 198–207. [Google Scholar]
- Wang, J. Planning and Optimal Operation of Regional Integrated Energy System. Master’s Thesis, Southeast University, Nanjing, China, 2017. [Google Scholar]
- Lv, J.W.; Zhang, S.X.; Cheng, H.Z. A review of regional integrated energy system planning research considering interconnection and interaction. Proc. CSEE 2021, 41, 4001–4021. [Google Scholar]
- Xu, Z.; Sun, H.B.; Guo, Q.L. Review and Prospect of Integrated Demand Response. Proc. CSEE 2018, 38, 7194–7205+7446. [Google Scholar]
- Palensky, P.; Dietrich, D. Demand side management: Demand response, intelligent energy systems, and smart loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Tian, S.; Wang, B.; Zhang, J. Key technologies for demand response under smart grid conditions. Proc. CSEE 2014, 34, 3576–3589. [Google Scholar]
- Sheikhi, A.; Bahrami, S.; Ranjbar, A.M. An autonomous demand response program for electricity and natural gas networks in smart energy hubs. Energy 2015, 89, 490–499. [Google Scholar] [CrossRef]
- Sun, Y.J.; Wang, Y.; Wang, B.B. Multi-time scale decision method for source-load interaction considering demand response uncertainty. Autom. Electr. Power Syst. 2018, 42, 106–113, 159. (In Chinese) [Google Scholar]
- Ding, Y.R.; Chen, H.K.; Wu, J. Multi-objective optimal dispatch of electricity-gas-heat integrated energy system considering comprehensive energy efficiency. Autom. Electr. Power Syst. 2021, 45, 64–73. (In Chinese) [Google Scholar]
- Wei, J.D.; Zhang, Y.; Wang, J.X. Decentralized demand management based on alternating direction method of multipliers algorithm for industrial park with CHP units and thermal storage. J. Mod. Power Syst. Clean Energy 2022, 10, 120–130. [Google Scholar] [CrossRef]
- Xu, H.; Dong, S.F.; He, Z.X. Electro-thermal comprehensive demand response based on multi-energy complementarity. Power Syst. Technol. 2019, 43, 480–487. [Google Scholar] [CrossRef]
- Zhang, D.; Zhu, H.; Zhang, H. Multi-objective optimization for smart integrated energy system considering demand responses and dynamic prices. IEEE Trans. Smart Grid 2022, 13, 1100–1112. [Google Scholar] [CrossRef]
- Tian, S.M.; Luan, W.P.; Zhang, D.X. Energy Internet Technology Form and Key Technologies. Proc. CSEE 2015, 35, 3482–3494. [Google Scholar]
- Yang, H.H.; Shi, B.W.; Huang, W.T. Optimal Scheduling Method for Micro Energy Grids Based on Integrated Demand Response. Electr. Power Constr. 2021, 42, 11–19. [Google Scholar]
- Zhu, L.; Niu, P.Y.; Tang, L.J. Robust optimization operation of micro-energy network considering the uncertainty of direct load control. Power Syst. Technol. 2020, 44, 1400–1413. [Google Scholar]
- Huang, C.; Zhang, H.; Song, Y.; Wang, L.; Ahmad, T.; Luo, X. Demand response for industrial micro-grid considering photovoltaic power uncertainty and battery operational cost. IEEE Trans. Smart Grid 2021, 12, 3043–3055. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Y.; Tang, W. Generic modelling and optimal day-ahead dispatch of micro-energy system considering the price-based integrated demand response. Energy 2019, 176, 171–183. [Google Scholar] [CrossRef]
- Chen, J.; Qi, B.; Rong, Z.; Peng, K.; Zhao, Y.; Zhang, X. Multi-energy coordinated microgrid scheduling with integrated demand response for flexibility improvement. Energy 2021, 217, 119387. [Google Scholar] [CrossRef]
- Sheikhahmadi, P.; Bahramara, S.; Mazza, A.; Chicco, G.; Shafie-Khah, M.; Catalão, J.P.S. Multi-Microgrids Operation with Interruptible Loads in Local Energy and Reserve Markets. IEEE Syst. J. 2023, 17, 1292–1303. [Google Scholar] [CrossRef]
- Bahramara, S.; Mazza, A.; Chicco, G.; Shafie-Khah, M.; Catalão, J.P. Comprehensive review on the decision-making frameworks referring to the distribution network operation problem in the presence of distributed energy resources and microgrids. Int. J. Elect. Power Energy Syst. 2020, 115, 105466. [Google Scholar] [CrossRef]
- Sun, C.H.; Wang, L.J.; Xu, H.L. User interaction load modelling and its application to microgrid day-ahead economic dispatch. Power Syst. Technol. 2016, 40, 2009–2016. [Google Scholar]
- Hosseini, S.M.; Carli, R.; Parisio, A.; Dotoli, M. Robust Decentralized Charge Control of Electric Vehicles under Uncertainty on Inelastic Demand and Energy Pricing. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; pp. 1834–1839. [Google Scholar] [CrossRef]
- Xu, Y.; Peng, S.; Liao, Q.; Yang, Z.; Liu, D.C.; Zou, H. Two-stage short-term optimal dispatch of MEP considering CAUR and HTTD. Electr. Power Autom. Equip. 2017, 37, 152–163. [Google Scholar]
- Ma, T.F.; Wu, J.; Hao, L.L. Energy Flow Modeling and Optimal Operation Analysis of Micro Energy Grid Based on Energy Hub. Power Syst. Technol. 2018, 42, 179–186. [Google Scholar] [CrossRef]


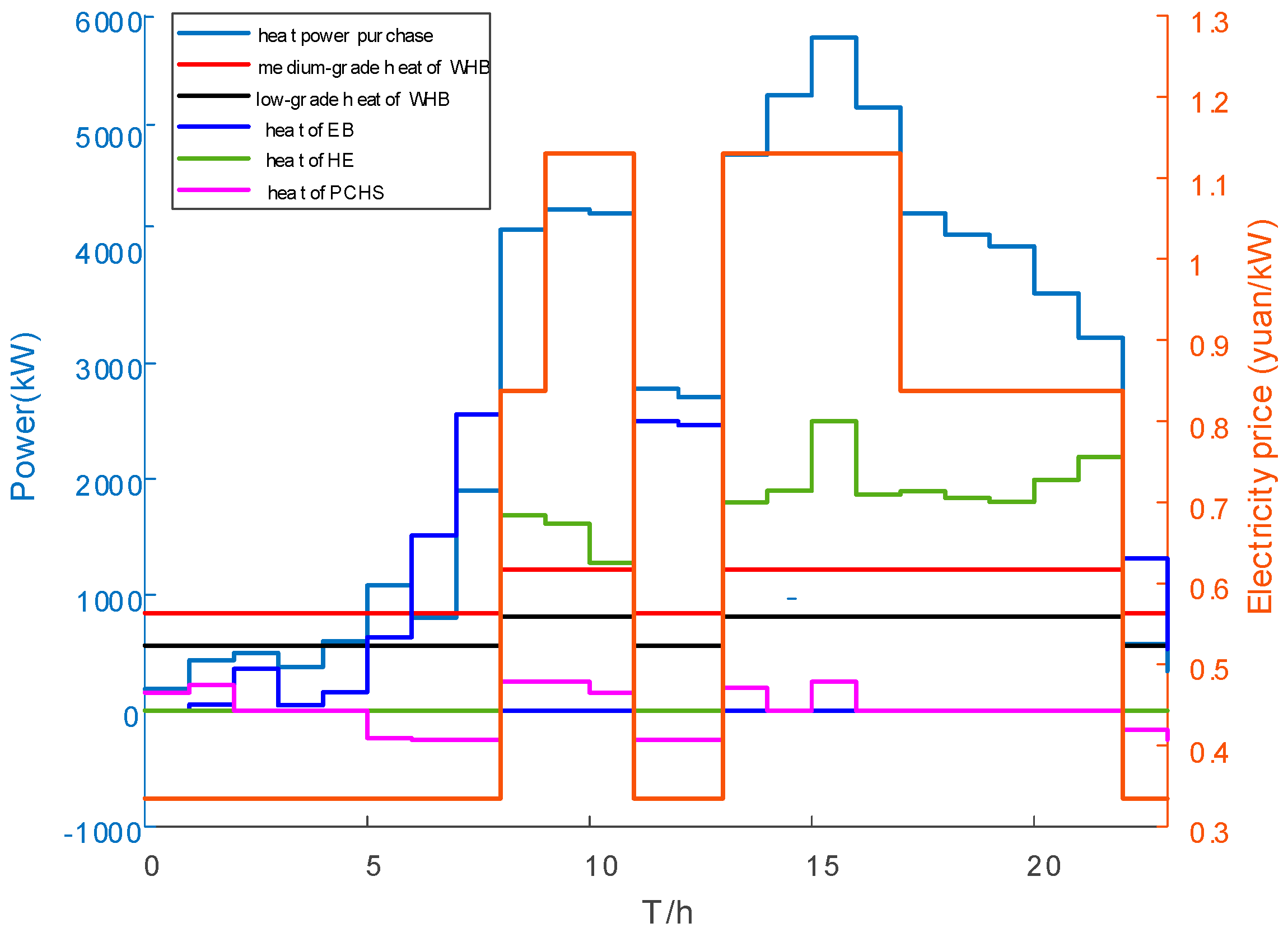
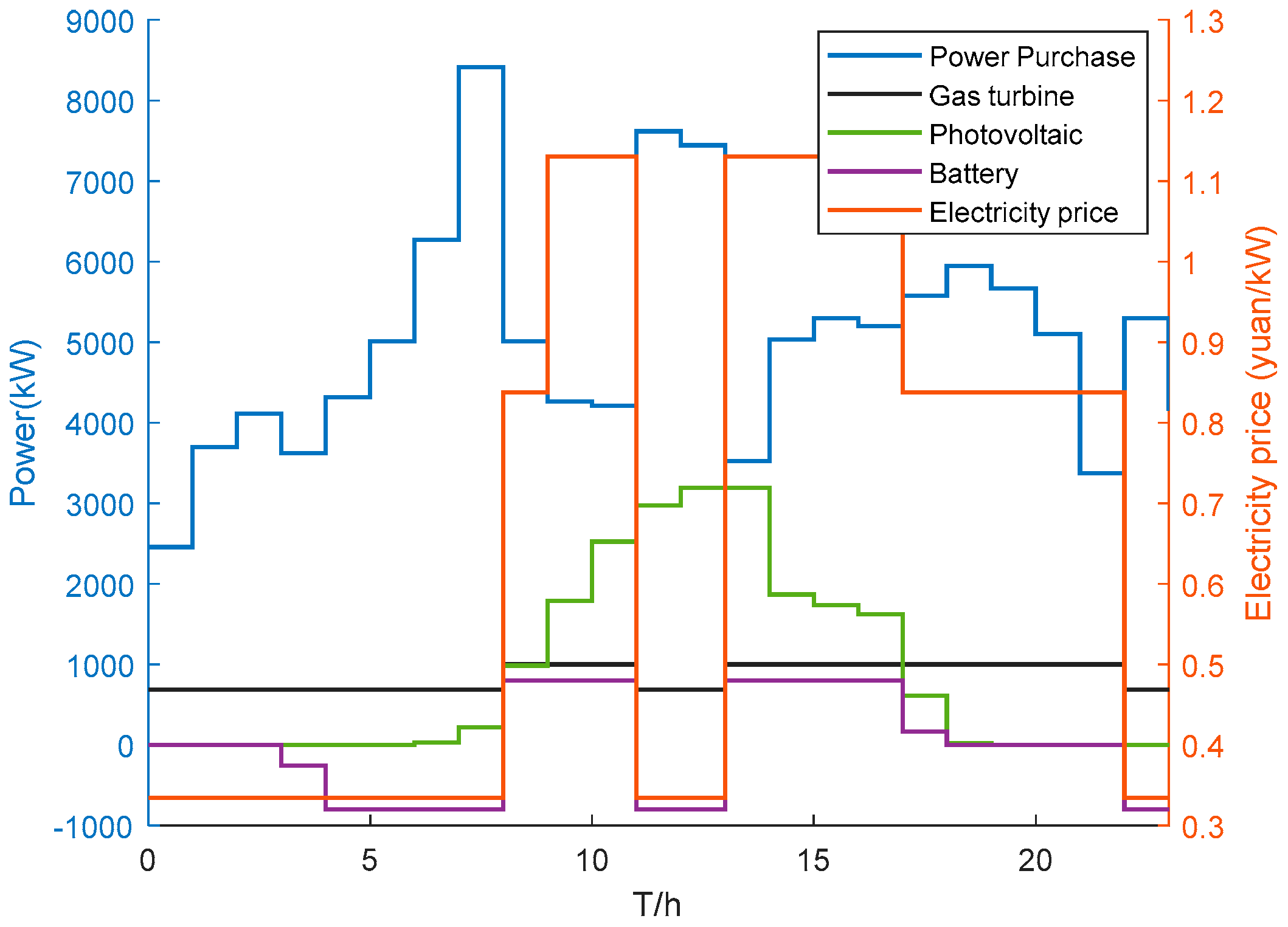
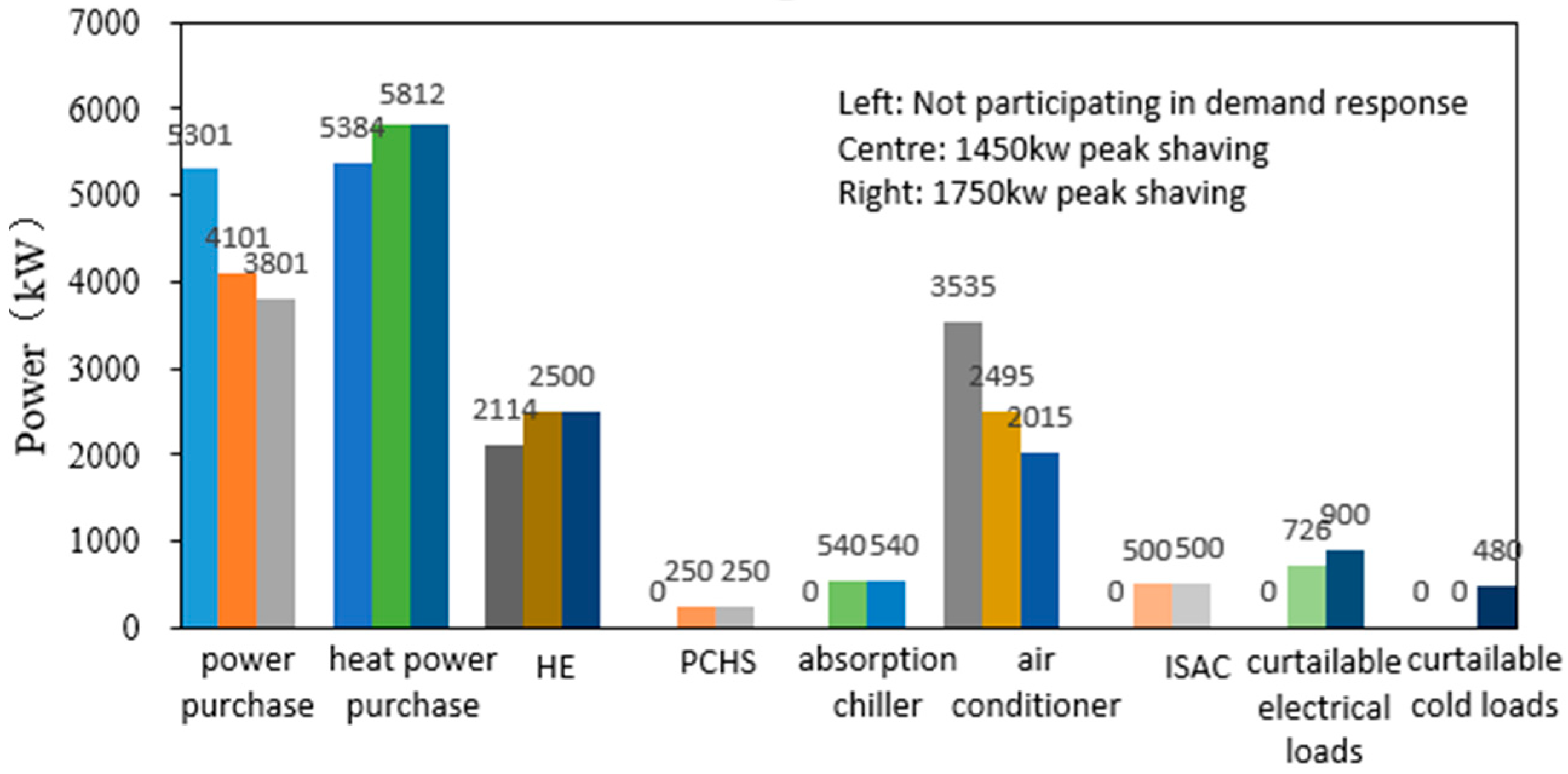
| Equipment | Parameter | Parameter Value | Equipment | Parameter | Parameter Value |
|---|---|---|---|---|---|
| Gas turbine | ηGT.e | 0.33 | Absorption chillers | ηAB | 0.85 |
| (kW). | 1000 | 850 | |||
| (kW) | 50 | Electric refrigeration and air conditioning | ηAC | 3.8 | |
| (kW/min) | 60 | (kW) | 1500 | ||
| cse (yuan) | 150 | com (CNY/kW) | 0.006 | ||
| com (yuan/kW) | 0.057 | Ice storage air conditioner | σTK | 0.001 | |
| Waste heat boilers | ηM_WHB | 0.6 | |||
| ηL_WHB | 0.4 | ηFRG | 3.5 | ||
| (kW) | 1500 | ηTK,c | 3.0 | ||
| (kW). | 1000 | ηTK,d | 0.85 | ||
| com (yuan/kW) | 0.020 | 100 | |||
| Heat exchanger | ηHE | 0.9 | 920 | ||
| 2500 | 500 | ||||
| com | 0.0003 | 500 | |||
| Phase change heat storage | ηEB | 0.8 | com (yuan/kW) | 0.008 | |
| (kW) | 3000 | Battery energy storage | (kWh) | 8000 | |
| com (yuan/kW). | 0.02 | 0.8 | |||
| ηHS,c/ηHS,d | 0.98 | ηBS,c/ηBS,d | 0.95 | ||
| σHS | 0.02 | σBS | 0.0025 | ||
| 100 | SOCmin | 0.1 | |||
| 800 | SOCmax | 0.9 | |||
| / | 250 | (kW) | 800 | ||
| com (yuan/kW). | 0.01 | com (CNY/kW). | 0.03 |
| The Type of Dispatchable Loads | Type of Energy | The Size of the Dispatchable Loads | Price Parameters |
|---|---|---|---|
| Curtailable loads | Electricity | 900 kW | a = 6.1 × 10−4 b = 2.23 |
| Curtailable loads | Cold | 500 kW | a = 3.5 × 10−5 b = 8.16 |
| Transferable load | Electricity | 450 kW 15:00–18:00 | c =1.38 |
| Shifter load | Medium-grade heat | 200 kW 15:00–16:00 | c =4.64 |
| Peak-To-Valley Hours | Time | Electricity Price (yuan/kWh) |
|---|---|---|
| Trough | 0:00–8:00 | 0.3343 |
| 11:00–13:00 | ||
| 22:00–24:00 | ||
| Peak | 8:00–9:00 | 0.8373 |
| 17:00–22:00 | ||
| Peak | 9:00–11:00 | 1.1303 |
| 13:00–17:00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wu, H.; Zhu, M.; Dong, M.; Dong, S. Integrated Demand Response for Micro-Energy Grid Accounting for Dispatchable Loads. Energies 2024, 17, 1255. https://doi.org/10.3390/en17051255
Zhang X, Wu H, Zhu M, Dong M, Dong S. Integrated Demand Response for Micro-Energy Grid Accounting for Dispatchable Loads. Energies. 2024; 17(5):1255. https://doi.org/10.3390/en17051255
Chicago/Turabian StyleZhang, Xianglong, Hanxin Wu, Mengting Zhu, Mengwei Dong, and Shufeng Dong. 2024. "Integrated Demand Response for Micro-Energy Grid Accounting for Dispatchable Loads" Energies 17, no. 5: 1255. https://doi.org/10.3390/en17051255
APA StyleZhang, X., Wu, H., Zhu, M., Dong, M., & Dong, S. (2024). Integrated Demand Response for Micro-Energy Grid Accounting for Dispatchable Loads. Energies, 17(5), 1255. https://doi.org/10.3390/en17051255





