Advanced Mud Displacement Modeling for Slim Hole Cementing Operations
Abstract
1. Introduction
2. Cement Displacement Analysis under the Uniform Wellbore Assumption
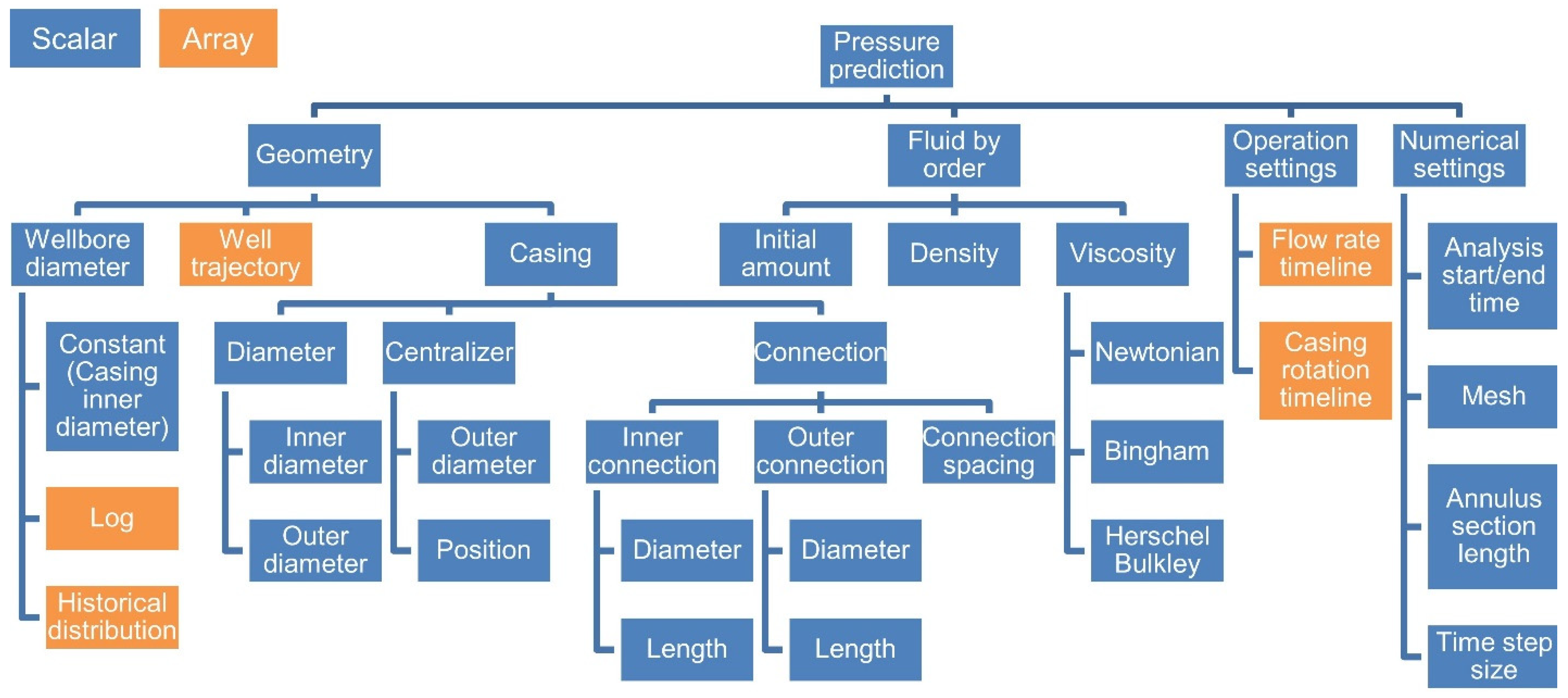
2.1. Problem Statement and Model Partitioning
2.2. 3D Modeling of Yield-Power-Law Fluid in Casing and Annulus
2.3. Casing Connections Modeling
2.4. Model Validation
2.5. Result Integration and Entire Displacement Analysis Process
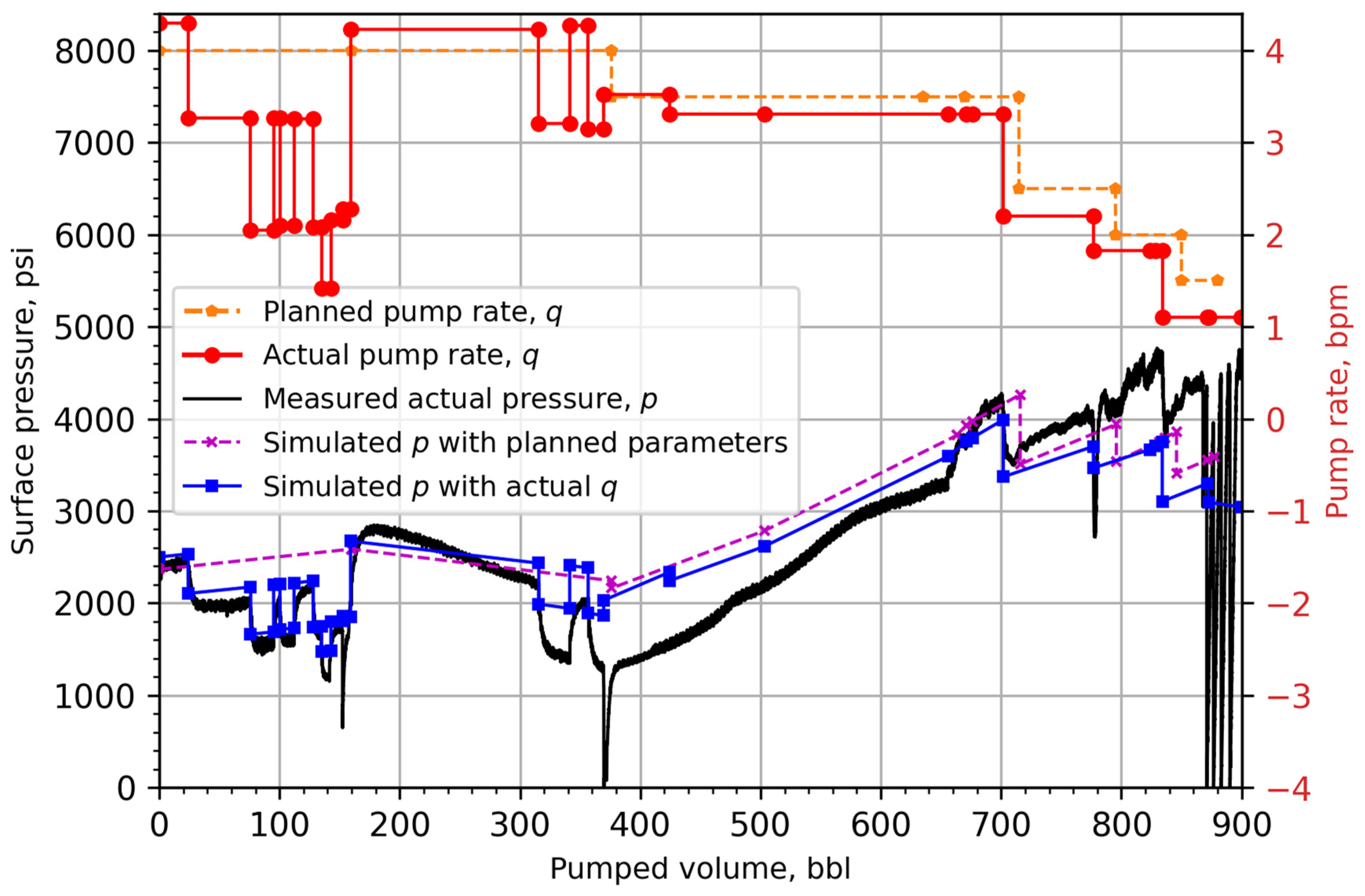
3. Field Case Study
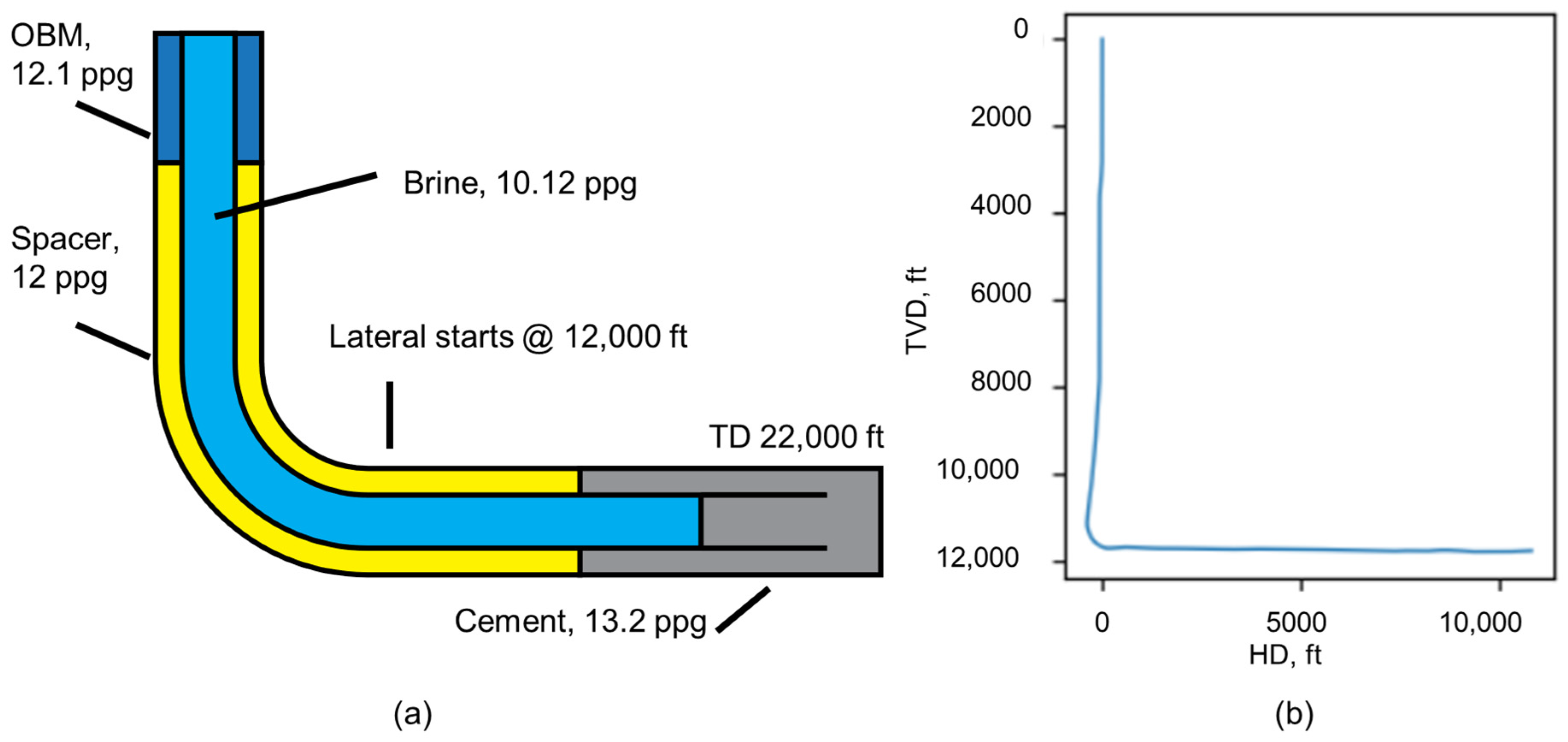
3.1. Case Introduction
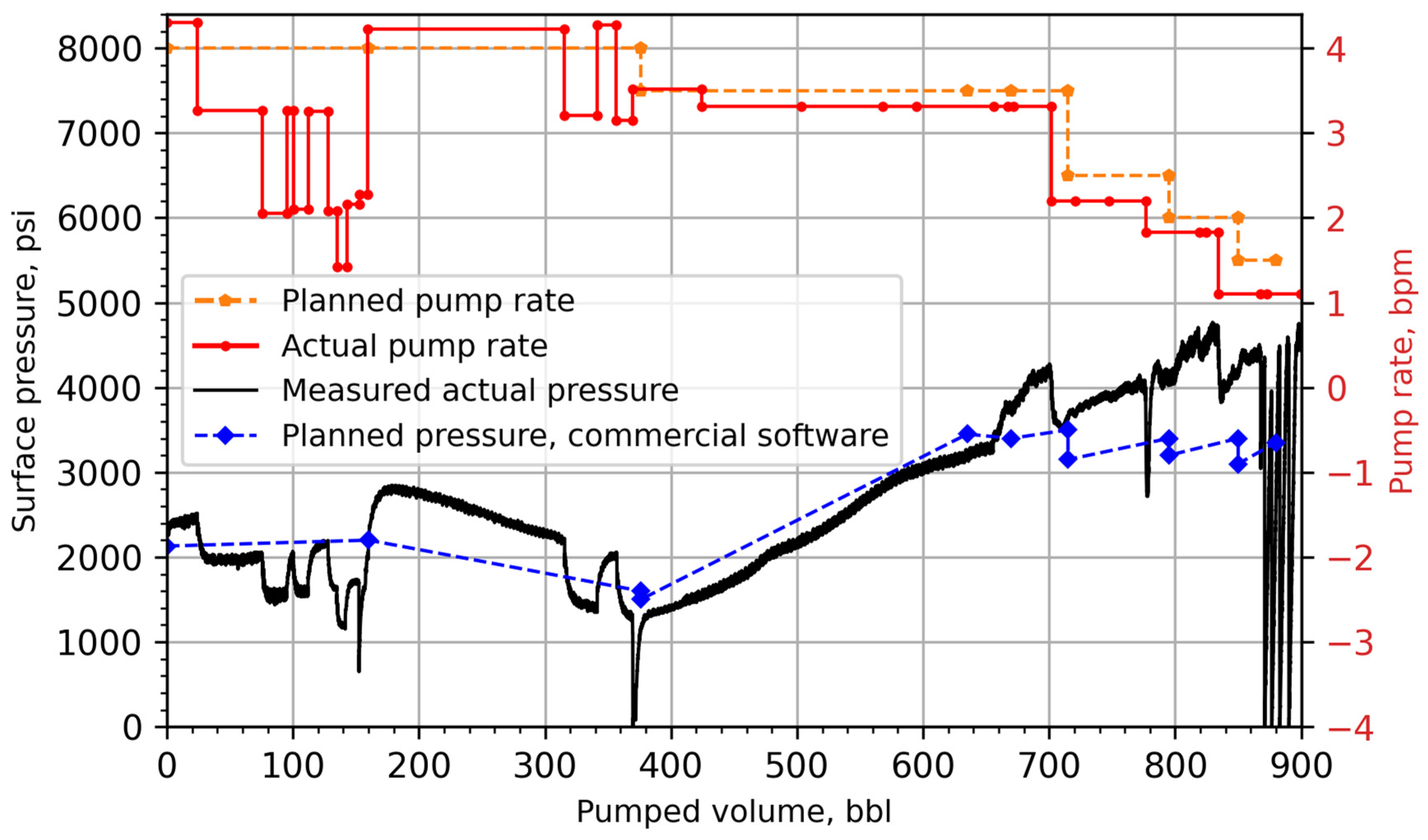
3.2. Factors Influencing Surface Pressure
3.3. Simulation Results
4. Conclusions
- The model was validated with a slim-hole cementing field case study for an unconventional shale well. It showed a marked improvement in predicting the trend and absolute peak value of the surface pressure with an acceptable precision (showing only 0.3–5.4% error), particularly when compared to the results of a commercial software model used in the field (showing 18.2% error).
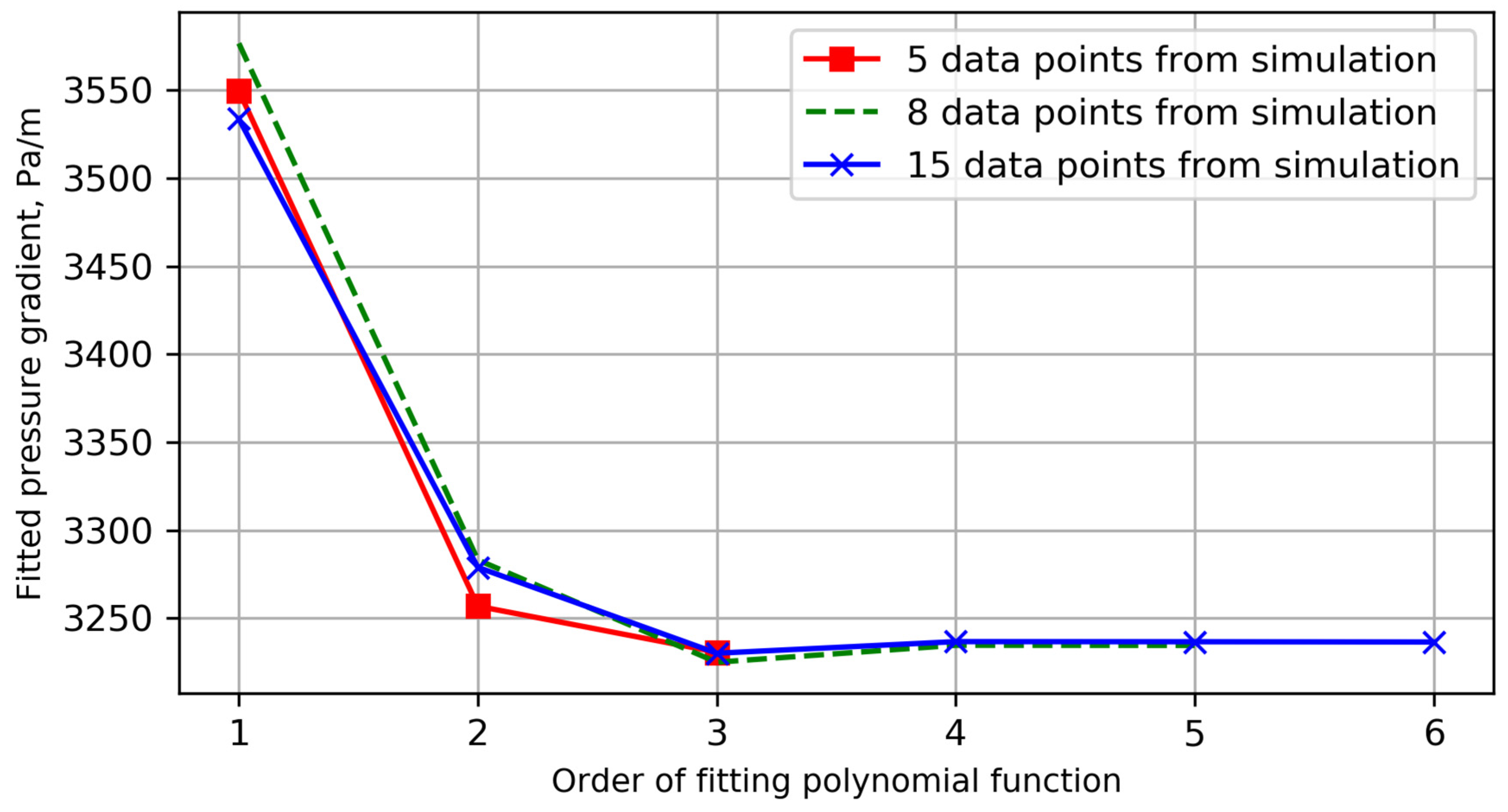
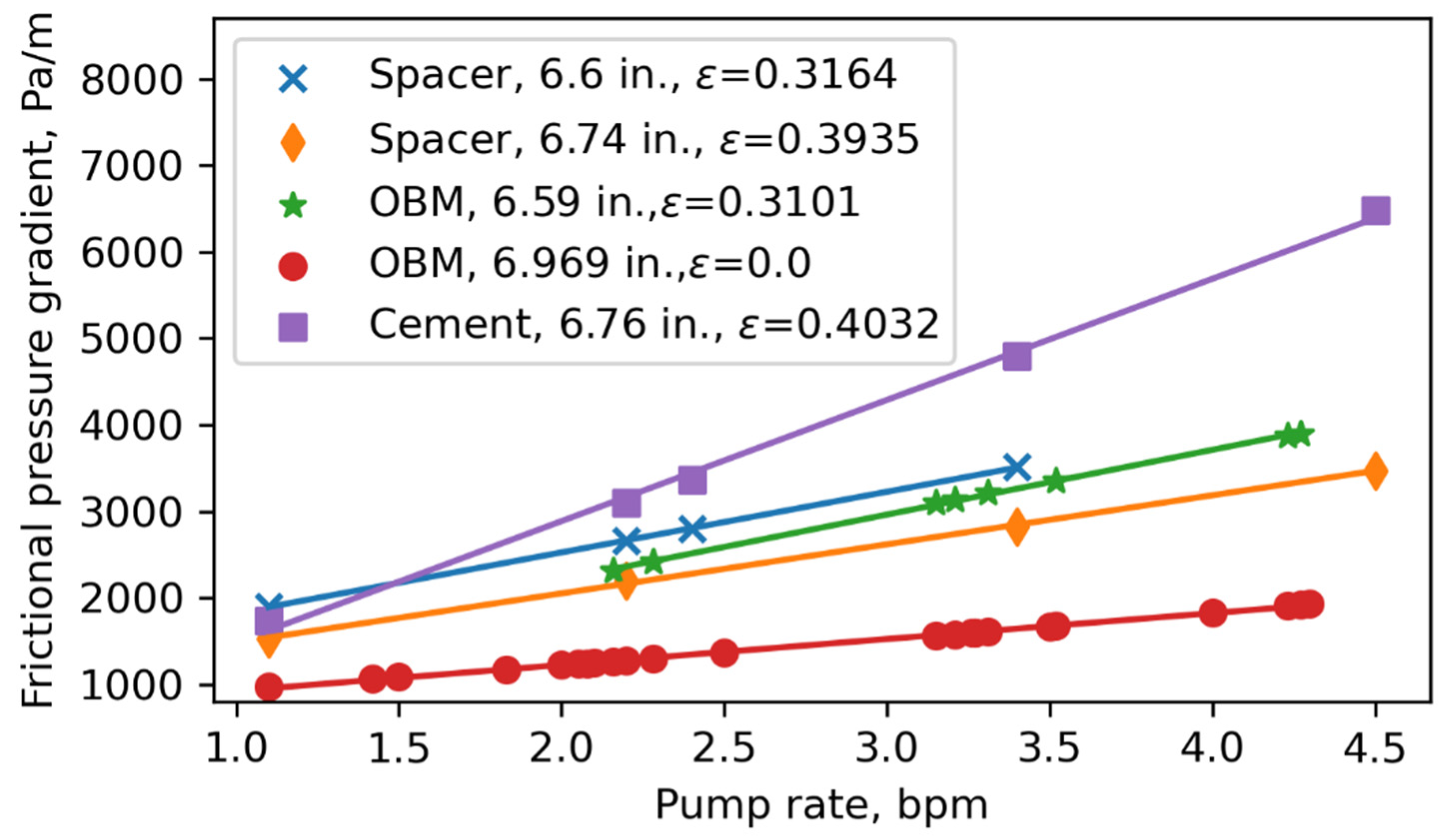
- A linear relationship between the flow rate and the frictional pressure gradient was used to calculate the frictional pressure gradient based on the data of the same fluid in the same well section at different flow rates. This linear interpolation method decreased the required number of simulation cases from 140 to 42, i.e., a 70% reduction with an associated reduction in simulation time.
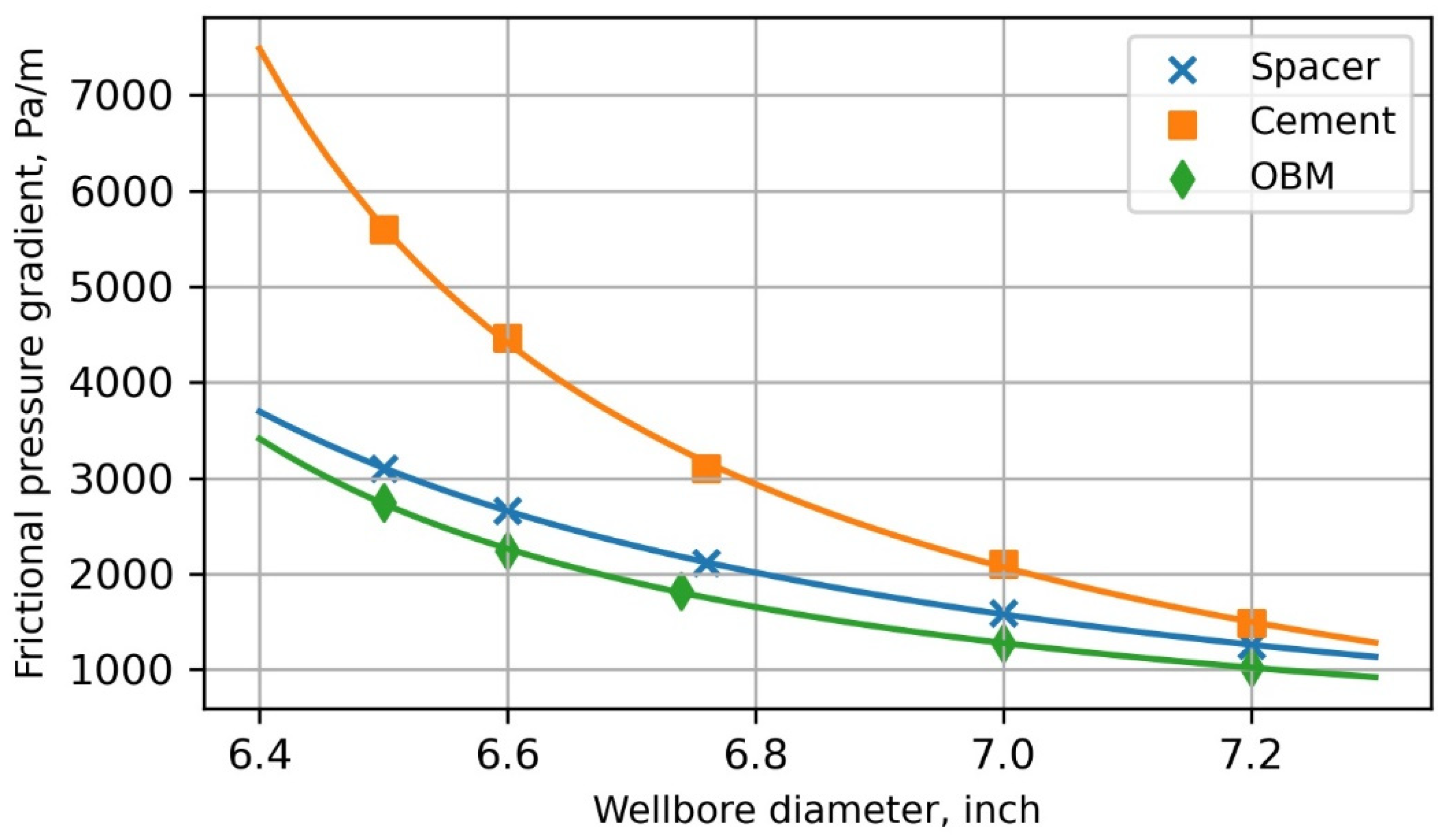
- Accurate casing and wellbore geometry estimation and fluid viscosity measurement were found to be of pivotal importance to obtaining correct pressure values. An average wellbore diameter was adopted to model the pressure gradient in each well section, noting that an analysis that explicitly considered the wellbore diameter distribution offered only a marginal improvement in accuracy.
5. Guidance for Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| BHA | Bottom hole assembly |
| BHCT | Bottom hole circulating temperature |
| BHST | Bottom hole static temperature |
| CDE | Cement displacement efficiency |
| Annular eccentricity | |
| HD | Horizontal displacement |
| KOP | Kick-off point |
| MAPE | Mean absolute percentage error |
| MLE | Maximum likelihood estimation |
| MPC | Managed pressure cementing |
| NPT | Non-productive time |
| OBM | Oil-based mud |
| Probability density function | |
| SBP | Surface back pressure |
| SSE | Sum squared error |
| TD | Total depth |
| TVD | True vertical depth |
| VOF | Volume of fluid |
Appendix A. 3D Modeling of Two-Phase Flow in the Annulus
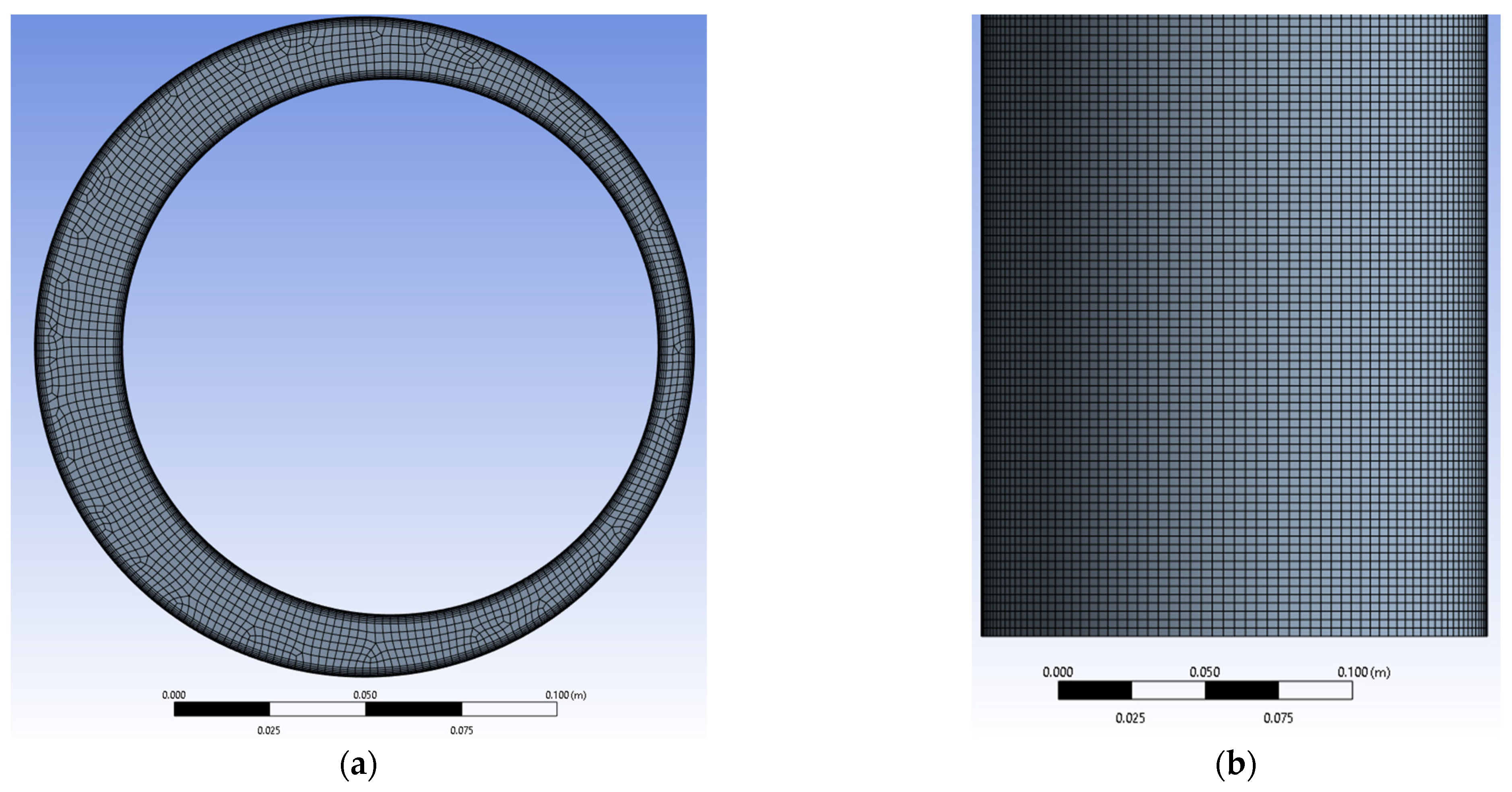
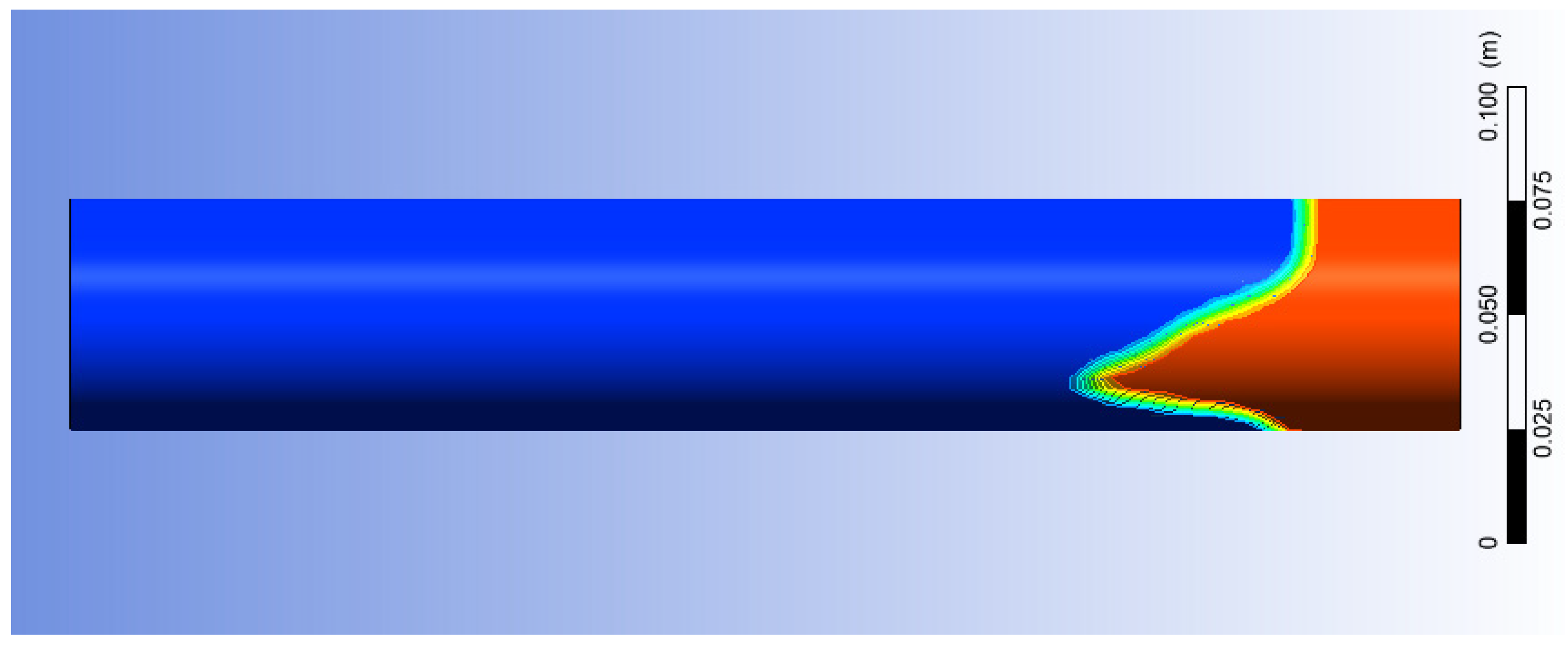

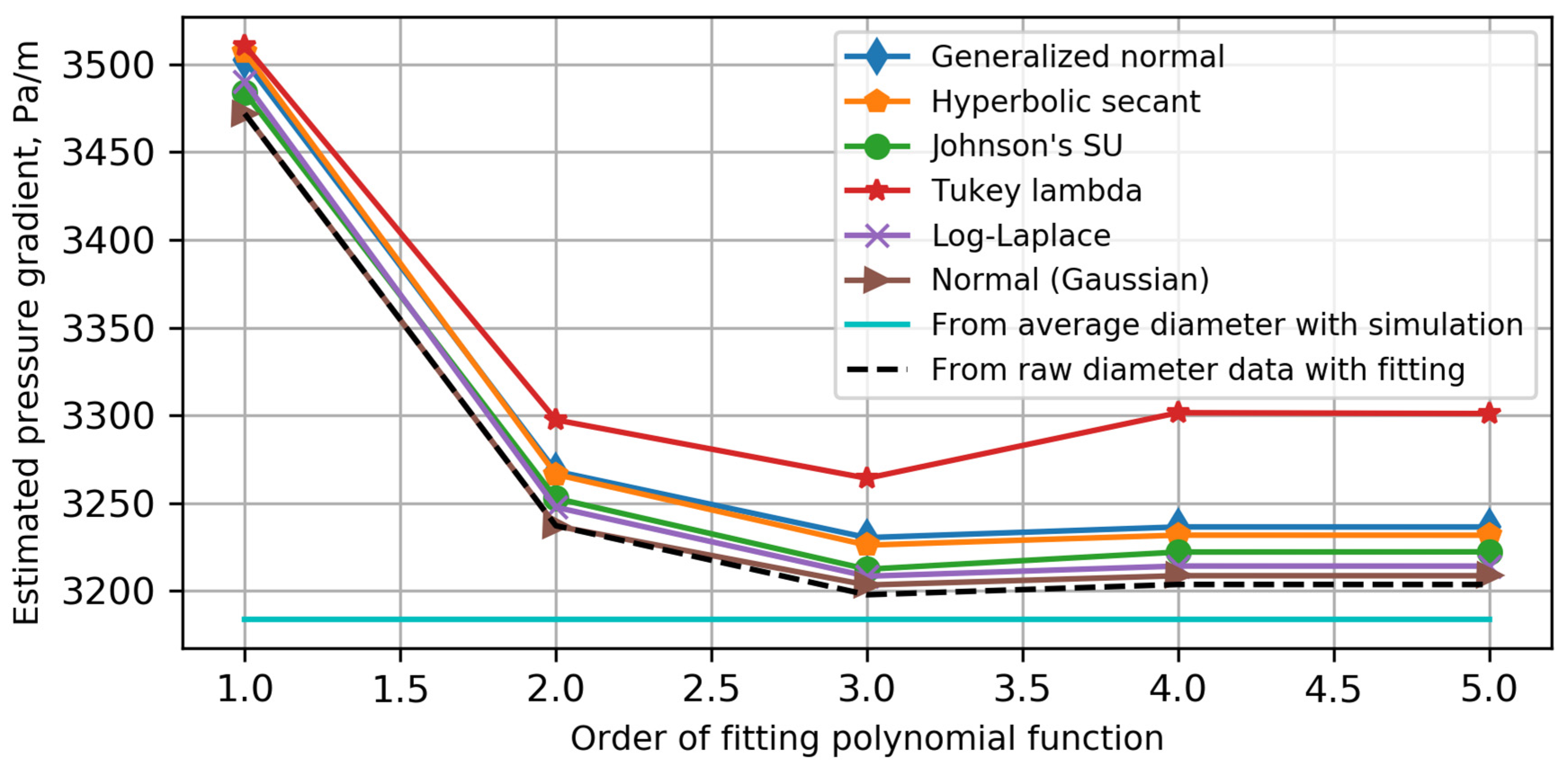
Appendix B. Wellbore Diameter Analysis and Data Fitting
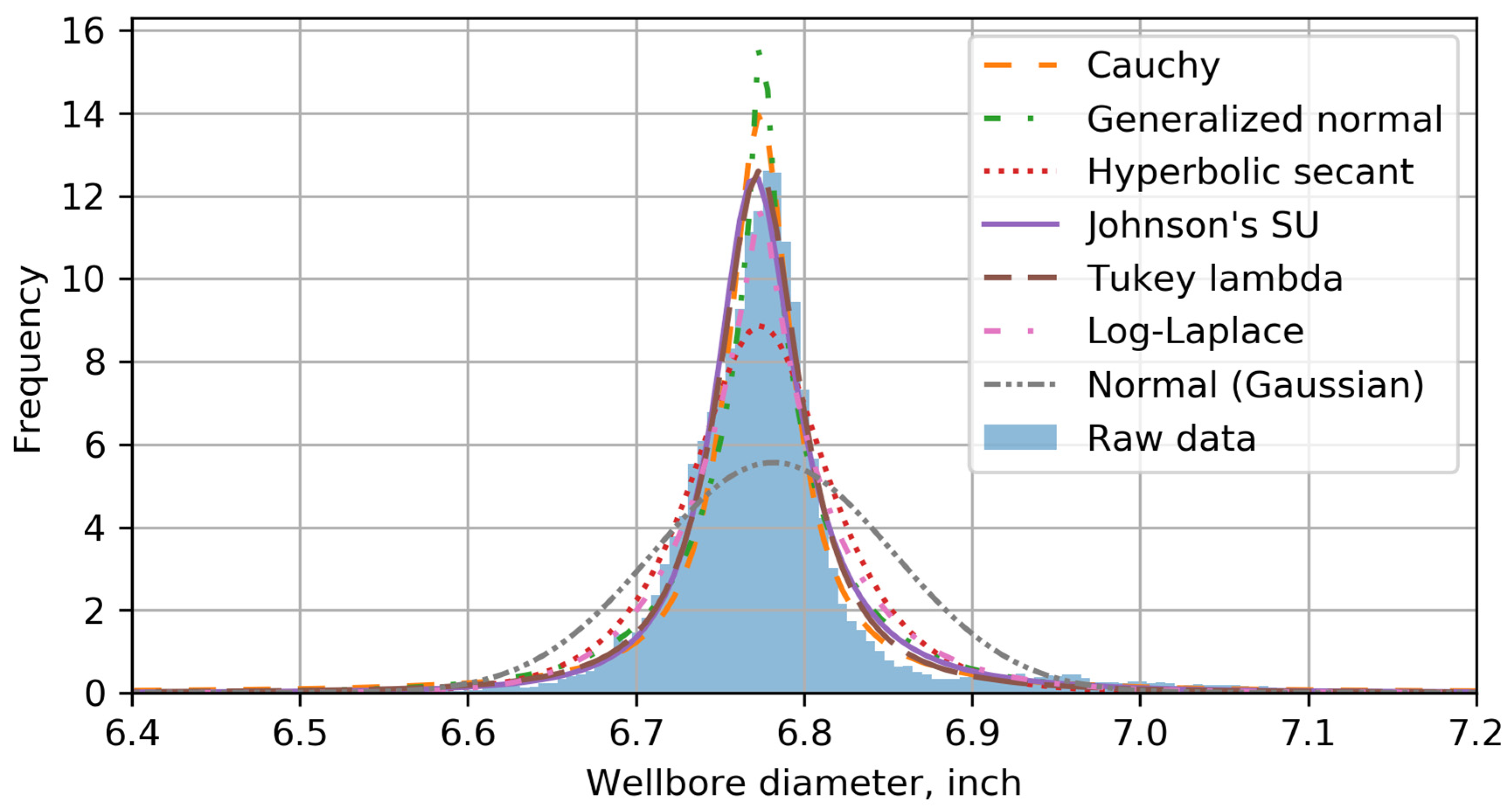
| Distribution Name | Number of Parameters | SSE | MAPE | |
|---|---|---|---|---|
| Cauchy | 2 | 41.3 | 806 | |
| Generalized normal | 3 | 57.6 | 136 | |
| Hyperbolic secant | 2 | 89.3 | 80.8 | |
| Johnson’s SU | 4 | 35.3 | 139 | |
| Tukey lambda | 3 | Tukey lambda is defined by the quantile function when location = 0 and scale = 1: | 21.1 | 276 |
| Log-Laplace | 2 | 43.9 | 75.0 | |
| Normal (Gaussian) | 2 | 356 | 120 |
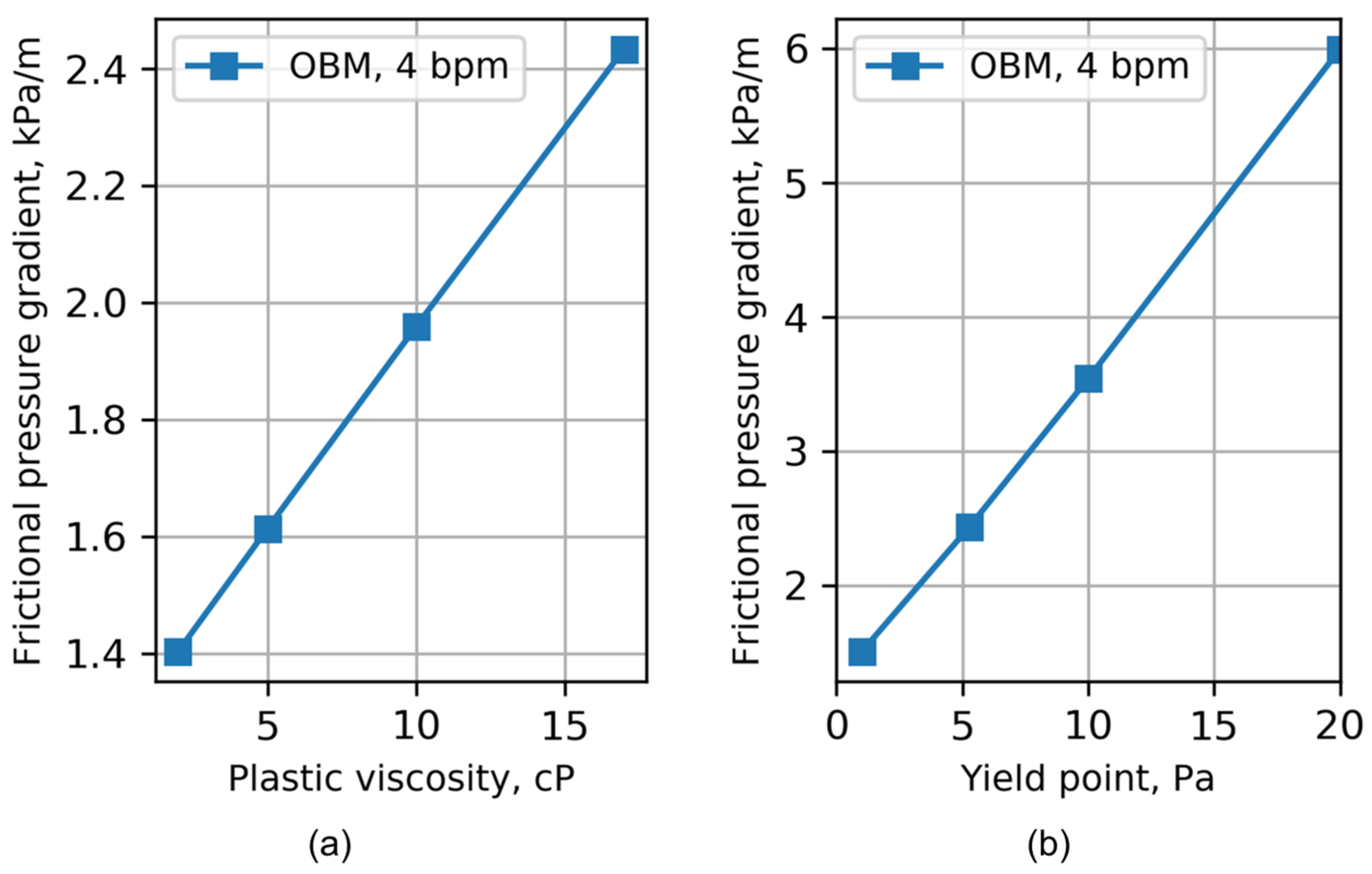
Appendix C. Annular Pressure Gradient Fitting and Interpolation

References
- Nelson, E.B.; Guillot, D. (Eds.) Well Cementing, 2nd ed.; Schlumberger: Sugarland, TX, USA, 2006. [Google Scholar]
- Enayatpour, S.; van Oort, E. Advanced modeling of cement displacement complexities. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, The Hague, The Netherlands, 14–16 March 2017. [Google Scholar] [CrossRef]
- Foroushan, H.K.; Bjørnar, L.; Jan, D.Y.; Arild, S. Cement Placement: An Overview of Fluid Displacement Techniques and Modelling. Energies 2021, 14, 573. [Google Scholar] [CrossRef]
- Zheng, D.; Miska, Z.; Ozbayoglu, E.; Zhang, Y. The Influence of Elliptical-Geometry Wellbore on Zonal Isolation. In Proceedings of the 56th U.S. Rock Mechanics/Geomechanics Symposium, Santa Fe, NM, USA, 26–29 June 2022. [Google Scholar] [CrossRef]
- McLean, R.H.; Manry, C.W.; Whitaker, W.W. Displacement mechanics in primary cementing. J. Pet. Technol. 1967, 19, 251–260. [Google Scholar] [CrossRef]
- Beirute, R.M.; Flumerfelt, R.W. Mechanics of the displacement process of drilling muds by cement slurries using an accurate rheological model. In Proceedings of the SPE Annual Fall Technical Conference and Exhibition, Denver, CO, USA, 9–12 October 1977. [Google Scholar] [CrossRef]
- Sun, J.; Li, Z.; Luo, P.; Huang, S. Numerical modeling of motion of displacement interface in eccentric annulus during primary cementing. Energy Sci. Eng. 2020, 8, 1579–1591. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, Z.; Zhao, Y.; Xue, Y.; Wang, C.; Xiong, C.; Chen, S. Theoretical and Experimental Study on Cementing Displacement Interface for Highly Deviated Wells. Energies 2023, 16, 733. [Google Scholar] [CrossRef]
- Savery, M.; Darbe, R.; Chin, W. Modeling fluid interfaces during cementing using a 3D mud displacement simulator. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2007. [Google Scholar] [CrossRef]
- Pks, S.; Yerubandi, K.B. Slim-Well Completions: A 3D Numerical Approach for Displacement to Design Effective Cementing Fluids. In Proceedings of the Trinidad and Tobago Energy Resources Conference, Port of Spain, Trinidad, 27–30 June 2010. [Google Scholar] [CrossRef]
- Chiney, A.; Yerubandi, K.B. 3D Displacement Simulator Realistically Predicts Free Fall during Cementing. In Proceedings of the SPE/IADC Middle East Drilling Technology Conference & Exhibition, Dubai, United Arab Emirates, 7–9 October 2013. [Google Scholar] [CrossRef]
- Chen, Z.; Chaudhary, S.; Shine, J. Intermixing of cementing fluids: Understanding mud displacement and cement placement. In Proceedings of the IADC/SPE Drilling Conference and Exhibition, Fort Worth, TX, USA, 4–6 March 2014. [Google Scholar] [CrossRef]
- Gao, H.; Ai, Z.; Zhang, J.; Zhou, B.; Chen, F.; Wang, W.; Liu, Z.; Deng, Q.; Shi, Y.; Wang, Z. Numerical Simulation of Improving Cementing Displacement Efficiency under Narrow Safety Density Window. In Proceedings of the SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition, Bali, Indonesia, 29–31 October 2019. [Google Scholar] [CrossRef]
- Bu, Y.; Tian, L.; Li, Z.; Zhang, R.; Wang, C.; Yang, X. Effect of casing rotation on displacement efficiency of cement slurry in highly deviated wells. J. Nat. Gas Sci. Eng. 2018, 52, 317–324. [Google Scholar] [CrossRef]
- Tardy, P.M.J.; Bittleston, S.H. A model for annular displacements of wellbore completion fluids involving casing movement. J. Pet. Sci. Eng. 2015, 126, 105–123. [Google Scholar] [CrossRef]
- Tardy, P.M.; Flamant, N.C.; Lac, E.; Parry, A.; Sutama, C.S.; Almagro, S.P. New generation 3D simulator predicts realistic mud displacement in highly deviated and horizontal wells. In Proceedings of the SPE/IADC Drilling Conference and Exhibition (p. D021S011R004), The Hague, The Netherlands, 14–16 March 2017; SPE: Kuala Lumpur, Malaysia, 2017. [Google Scholar] [CrossRef]
- Bogaerts, M.; Cardozo, J.; Flamant, N.; Giam, D.; Villar, V.; Lehr, J. Novel 3D Fluid Displacement Simulations Improve Cement Job Design and Planning in the Gulf of Mexico. In Proceedings of the SPE Annual Technical Conference and Exhibition, Calgary, AB, Canada, 30 September–2 October 2019. [Google Scholar] [CrossRef]
- Tardy, P.M. A 3D model for annular displacements of wellbore completion fluids with casing movement. J. Pet. Sci. Eng. 2018, 162, 114–136. [Google Scholar] [CrossRef]
- Foroushan, H.K.; Ozbayoglu, E.M.; Gomes, P.J.; Yu, M. Mud/cement displacement in vertical eccentric annuli. SPE Drill. Complet. 2020, 35, 297–316. [Google Scholar] [CrossRef]
- Maleki, A.; Frigaard, I. Primary cementing of oil and gas wells in turbulent and mixed regimes. J. Eng. Math. 2017, 107, 201–230. [Google Scholar] [CrossRef]
- Jung, H.; Frigaard, I.A. Evaluation of common cementing practices affecting primary cementing quality. J. Pet. Sci. Eng. 2022, 208, 109622. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, Z.; Zhou, Y.; Sheng, M.; Wu, B. Characteristic of Spiral Displacement Process in Primary Cementing of Vertical Well Washout. SPE J. 2023, 28, 509–521. [Google Scholar] [CrossRef]
- Li, X.; Novotny, R.J. Study on cement displacement by lattice-Boltzmann method. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. [Google Scholar] [CrossRef]
- Grasinger, M.; Li, Z.; Vuotto, A.; Brigham, J.; Iannacchione, A.; Vandenbossche, J. Simulation of cement slurry flow to assess the potential for voids and channels in wellbore cementing processes. In Proceedings of the SPE Eastern Regional Meeting, Morgantown, WV, USA, 13–15 October 2015. [Google Scholar] [CrossRef]
- Dixon, J.C. The Shock Absorber Handbook; John Wiley & Sons: Chichester, UK, 2008. [Google Scholar]
- Chilton, R.A.; Stainsby, R. Pressure loss equations for laminar and turbulent non-Newtonian pipe flow. J. Hydraul. Eng. 1998, 124, 522–529. [Google Scholar] [CrossRef]
- Wang, N.; Cheng, Z.; Lu, Y.; Jiang, W.; Zhou, J.; He, B.; Ren, G. A multibody dynamics model of contact between the drillstring and the wellbore and the rock penetration process. Adv. Mech. Eng. 2015, 7, 35–51. [Google Scholar] [CrossRef]
- Amani, M.; Al-Jubouri, M.; Shadravan, A. Comparative study of using oil-based mud versus water-based mud in HPHT fields. Adv. Pet. Explor. Dev. 2012, 4, 18–27. [Google Scholar] [CrossRef]
- Vajargah, A.K.; van Oort, E. Determination of drilling fluid rheology under downhole conditions by using real-time distributed pressure data. J. Nat. Gas Sci. Eng. 2015, 24, 400–411. [Google Scholar] [CrossRef]
- Khaled, M.S.; Wang, N.; Ashok, P.; van Oort, E. Downhole heat management for drilling shallow and ultra-deep high enthalpy geothermal wells. Geothermics 2023, 107, 102604. [Google Scholar] [CrossRef]
- Khaled, M.S.; Wang, N.; Ashok, P.; Chen, D.; van Oort, E. Strategies for Prevention of Downhole Tool Failure Caused by High Bottomhole Temperature in Geothermal and High-Pressure/High-Temperature Oil and Gas Wells. SPE Drill. Complet. 2023, 38, 243–260. [Google Scholar] [CrossRef]
- Fakoya, M.F.; Ahmed, R.M. A generalized model for apparent viscosity of oil-based muds. J. Pet. Sci. Eng. 2018, 165, 777–785. [Google Scholar] [CrossRef]



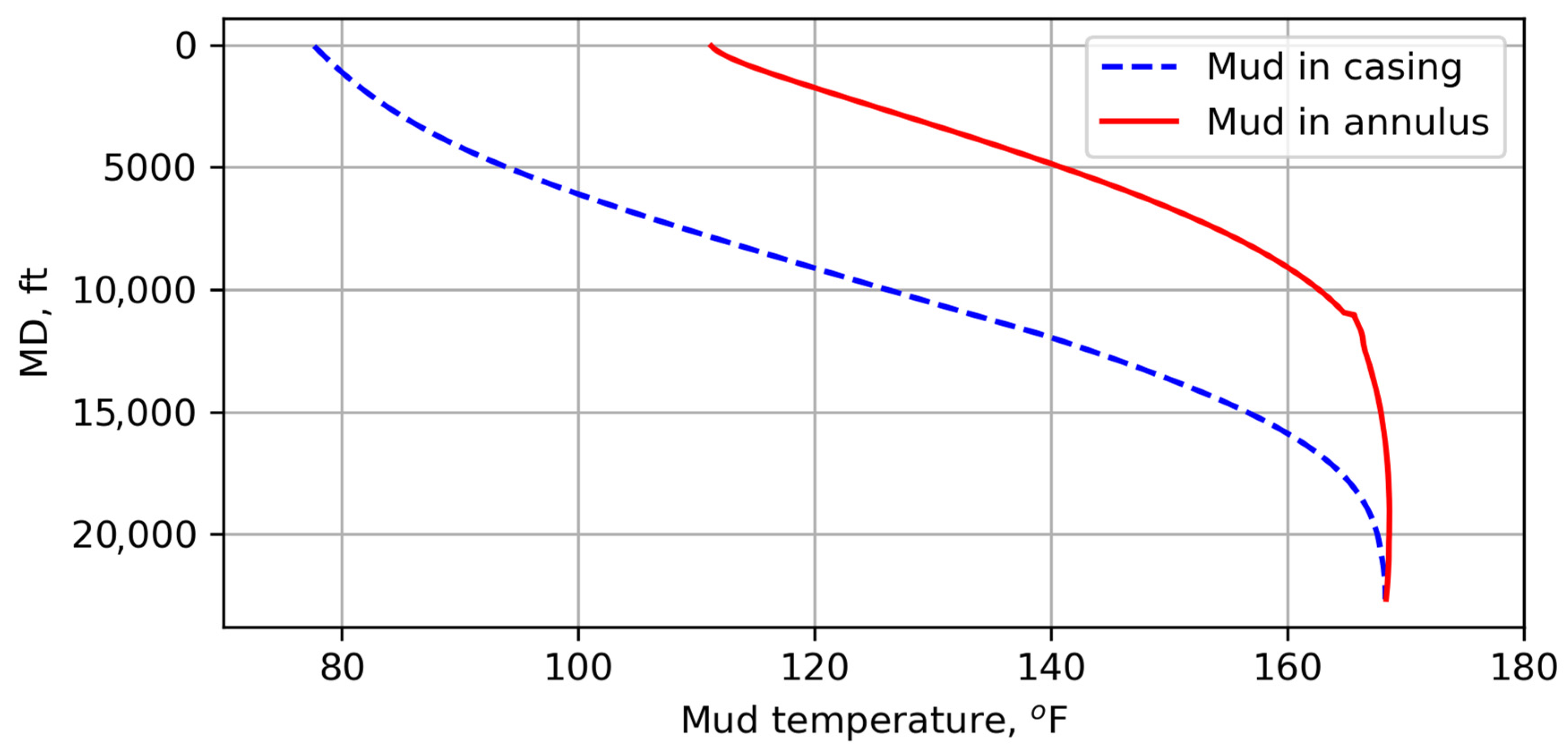

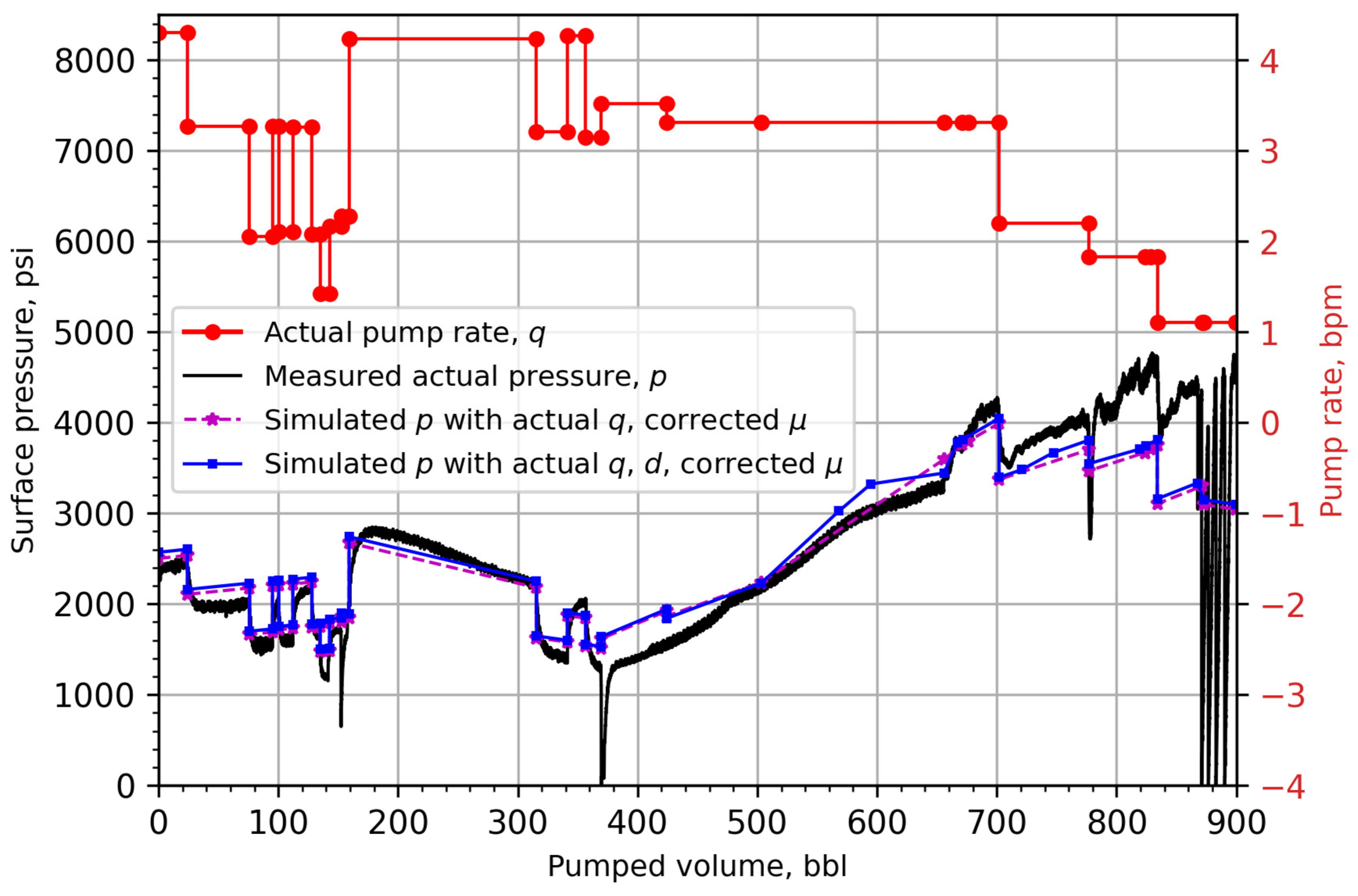
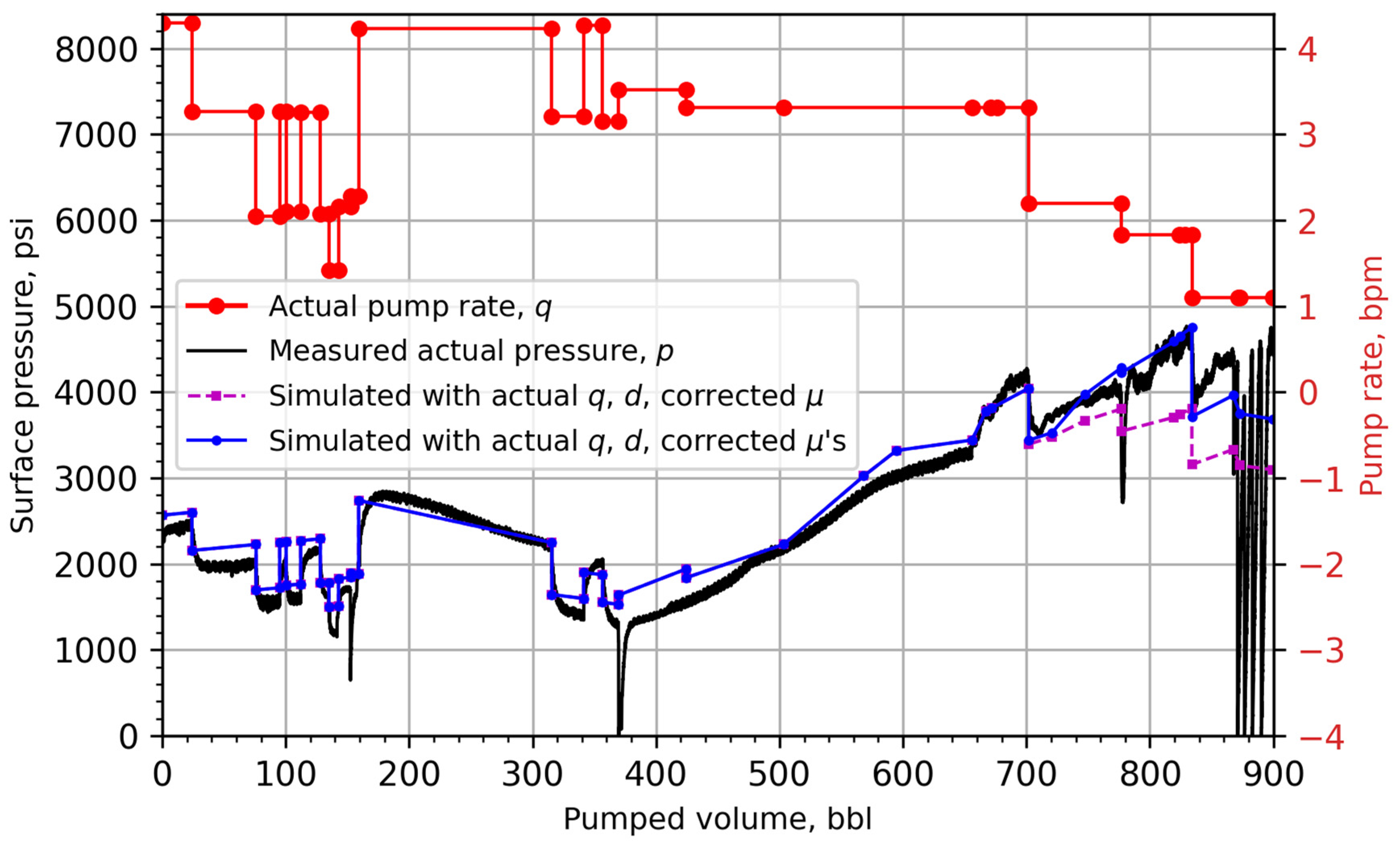
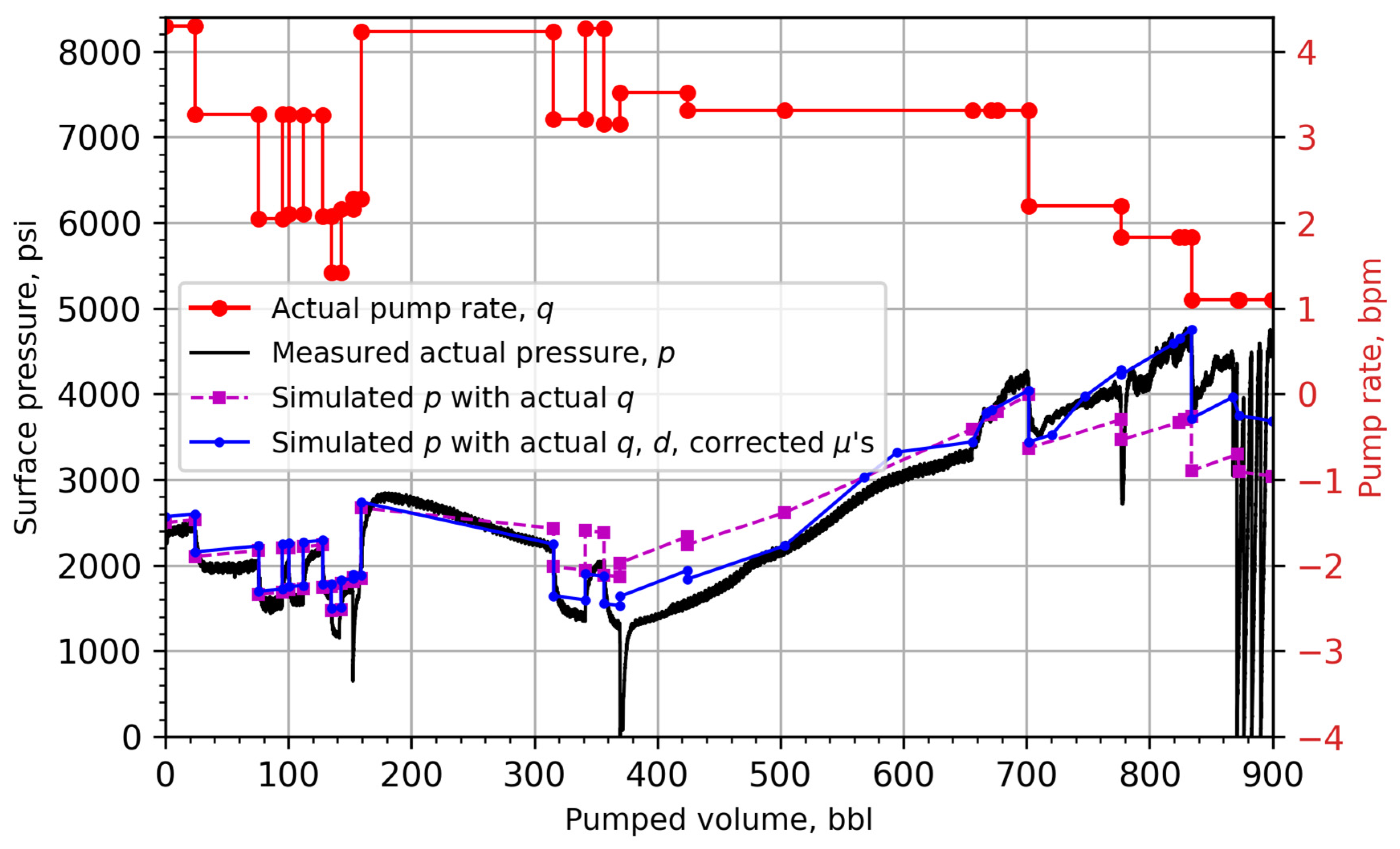

| Paper | Model | Simplification of Conservation Equations | Application |
|---|---|---|---|
| [9,10,11] | 3D finite difference. | Ignored the axial and azimuthal velocities as well as the azimuthal pressure gradient in the tangential momentum equation. | Velocity profile of the annular two-phase flow. Free fall of cement in the pipe. |
| [12] | Not reported. | Not reported. | Intermixing of mud and cement. |
| [2,13,14] | 3D finite volume. | None. | Pressure gradient and cement displacement efficiency in a section in the annulus. |
| [15,16,17,20,21] | (2+1)D finite volume. | Narrow gap assumption. Averaged the fluid volume fraction and velocity along the radial direction. | Pressure gradient and cement displacement efficiency in a section in the annulus. Pressure in the annulus during cement placement. |
| [18] | 3D finite volume. | Narrow gap assumption with radial variation of averaged fluid volume fraction and velocity. | Pressure gradient and cement displacement efficiency in a section in the annulus. |
| [19] | 3D semi-analytical. Sequential solution. | Narrow gap assumption. Assumed flow pattern at the widest and narrowest parts of the annulus. | Pressure gradient and cement displacement efficiency in a section in the annulus. |
| [22] | 3D finite volume. | None. | Pressure field and cement displacement near the centralizer. |
| [23,24] | 2D Lattice–Boltzmann. | Fluids are treated as particles moving and colliding. | Velocity profile of the annular two-phase flow. |
| Fluid | Density, ppg | Density, kg/m3 | (Plastic Viscosity, PV), cP | , Pa | Measurement Temperature, °F |
|---|---|---|---|---|---|
| OBM | 12.1 | 1450 | 17 | 5.27 | 150 |
| Spacer | 12.0 | 1438 | 16.3 | 7.56 | 168 |
| Cement | 13.2 | 1582 | 60.7 | 4.42 | 168 |
| Brine | 10.1 | 1213 | 1.0 | 0.96 | 120 |
| Temperature, °F | Plastic Viscosity, cP | Yield Point, Pa |
|---|---|---|
| 150 | 29.9 | 12.9 |
| 160 | 25.7 | 12.3 |
| 168 | 22.2 | 11.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, N.; Lamb, C.; Ashok, P.; van Oort, E.; Granier, G.; Gobert, T. Advanced Mud Displacement Modeling for Slim Hole Cementing Operations. Energies 2024, 17, 1226. https://doi.org/10.3390/en17051226
Wang N, Lamb C, Ashok P, van Oort E, Granier G, Gobert T. Advanced Mud Displacement Modeling for Slim Hole Cementing Operations. Energies. 2024; 17(5):1226. https://doi.org/10.3390/en17051226
Chicago/Turabian StyleWang, Ningyu, Christopher Lamb, Pradeepkumar Ashok, Eric van Oort, Garrett Granier, and Tatiana Gobert. 2024. "Advanced Mud Displacement Modeling for Slim Hole Cementing Operations" Energies 17, no. 5: 1226. https://doi.org/10.3390/en17051226
APA StyleWang, N., Lamb, C., Ashok, P., van Oort, E., Granier, G., & Gobert, T. (2024). Advanced Mud Displacement Modeling for Slim Hole Cementing Operations. Energies, 17(5), 1226. https://doi.org/10.3390/en17051226






