Measurement of Carbon Total Factor Productivity in the Context of Carbon–Electricity Market Collaboration: An Application of Biennial Luenberger Productivity Index
Abstract
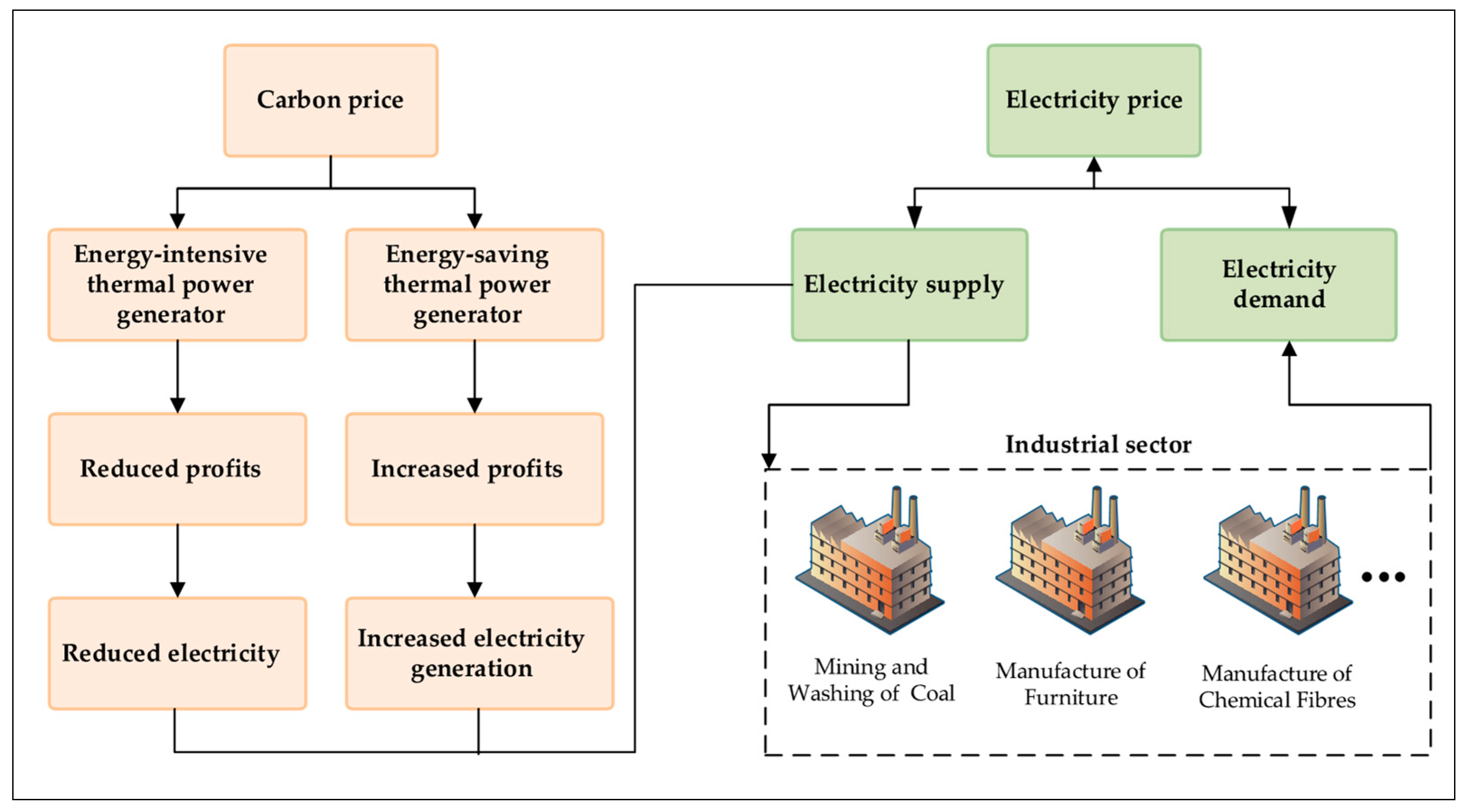
1. Introduction
2. Methodology and Data
2.1. BNDDF
2.2. Measurement of CTFP and PGI
2.3. Variables and Resources
3. Empirical Analysis and Discussion
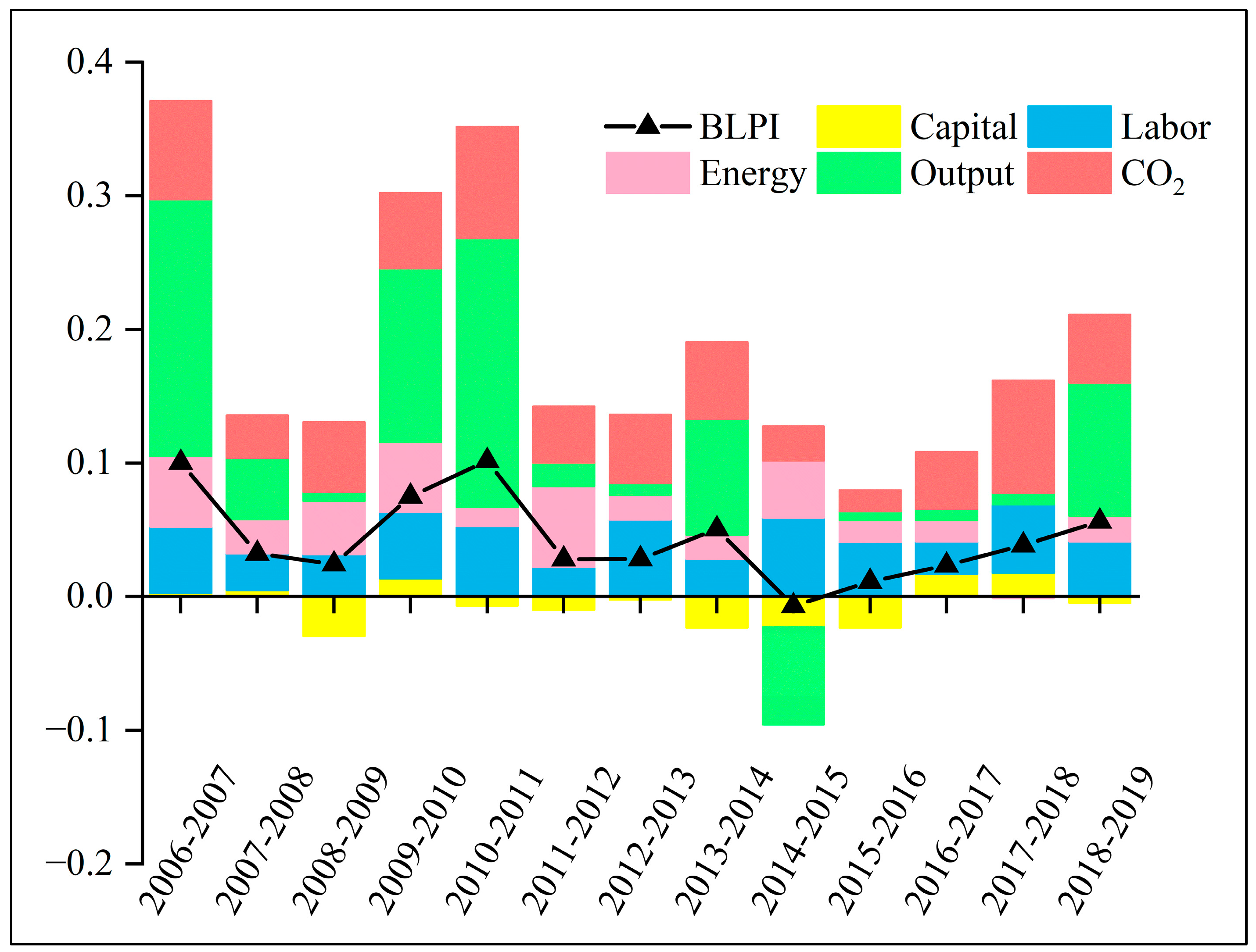
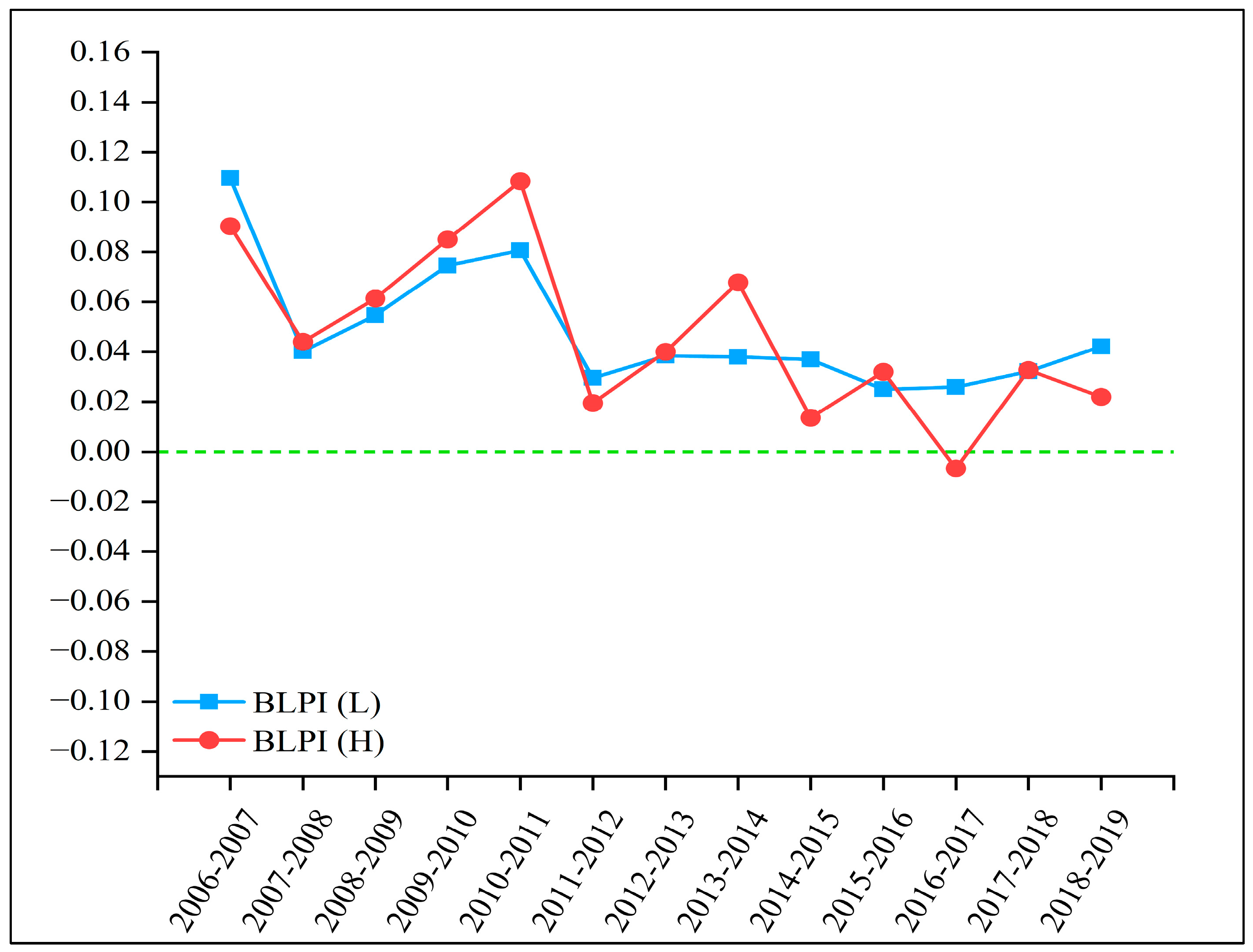
3.1. Trend Analysis of CTFP in China’s Industrial Sector
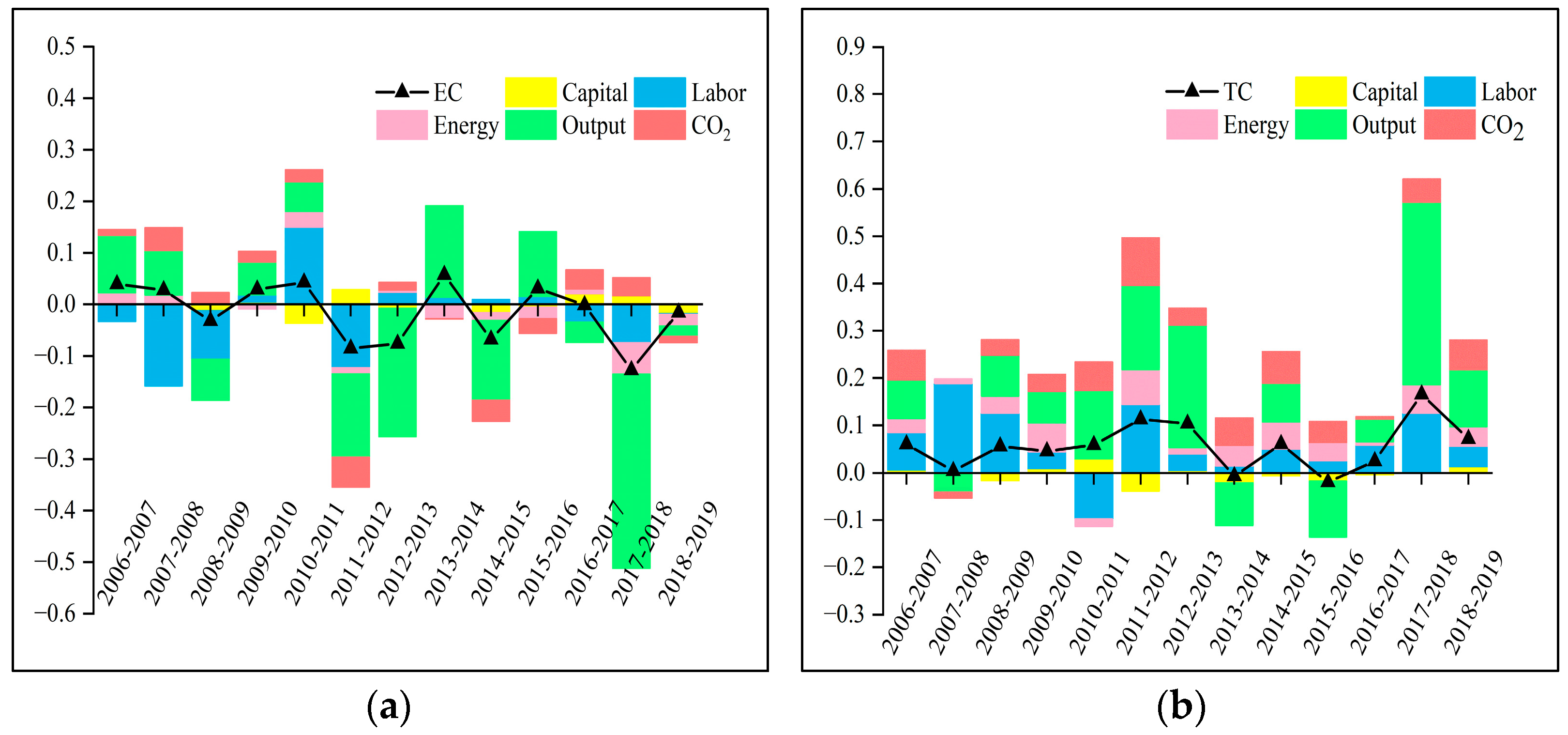
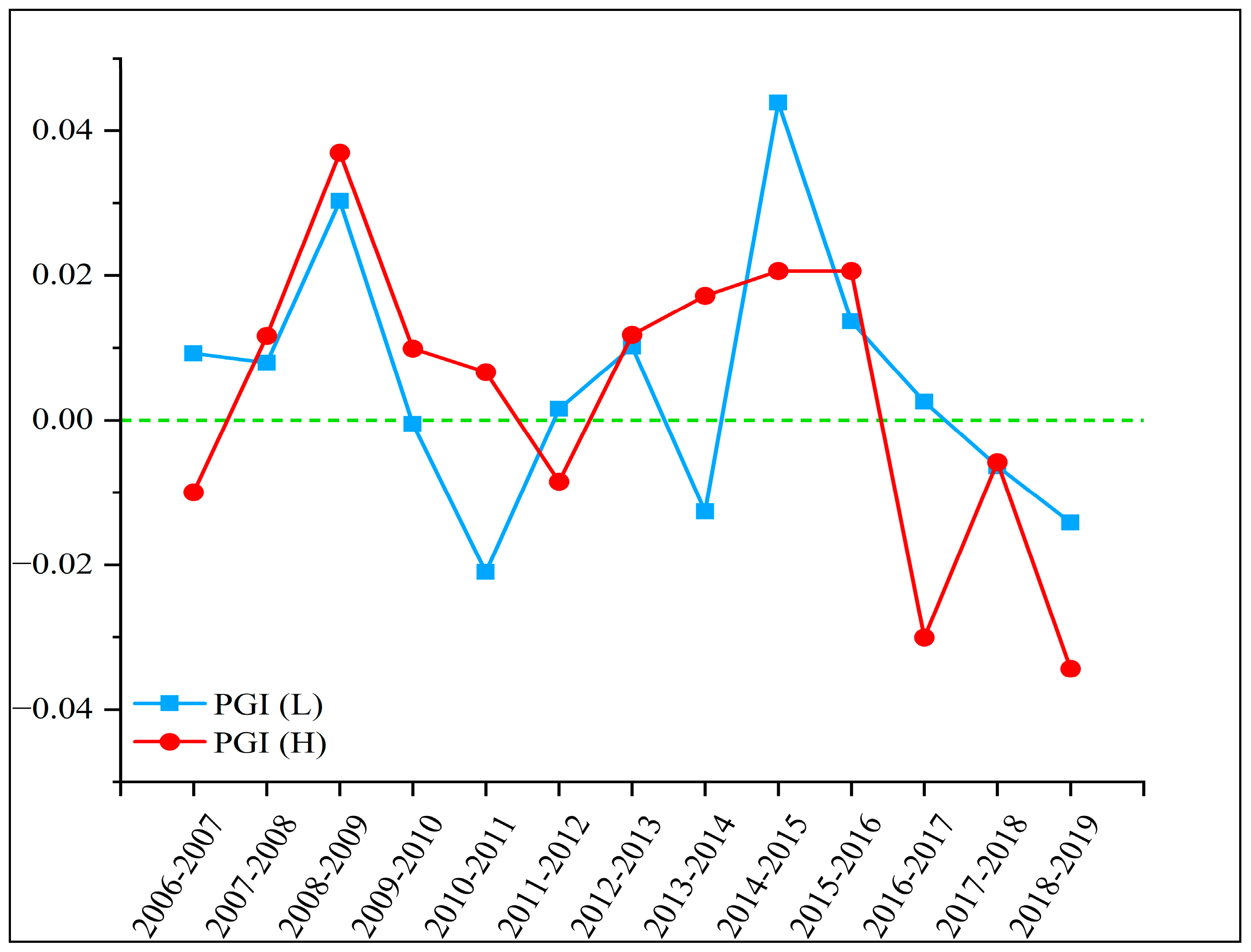
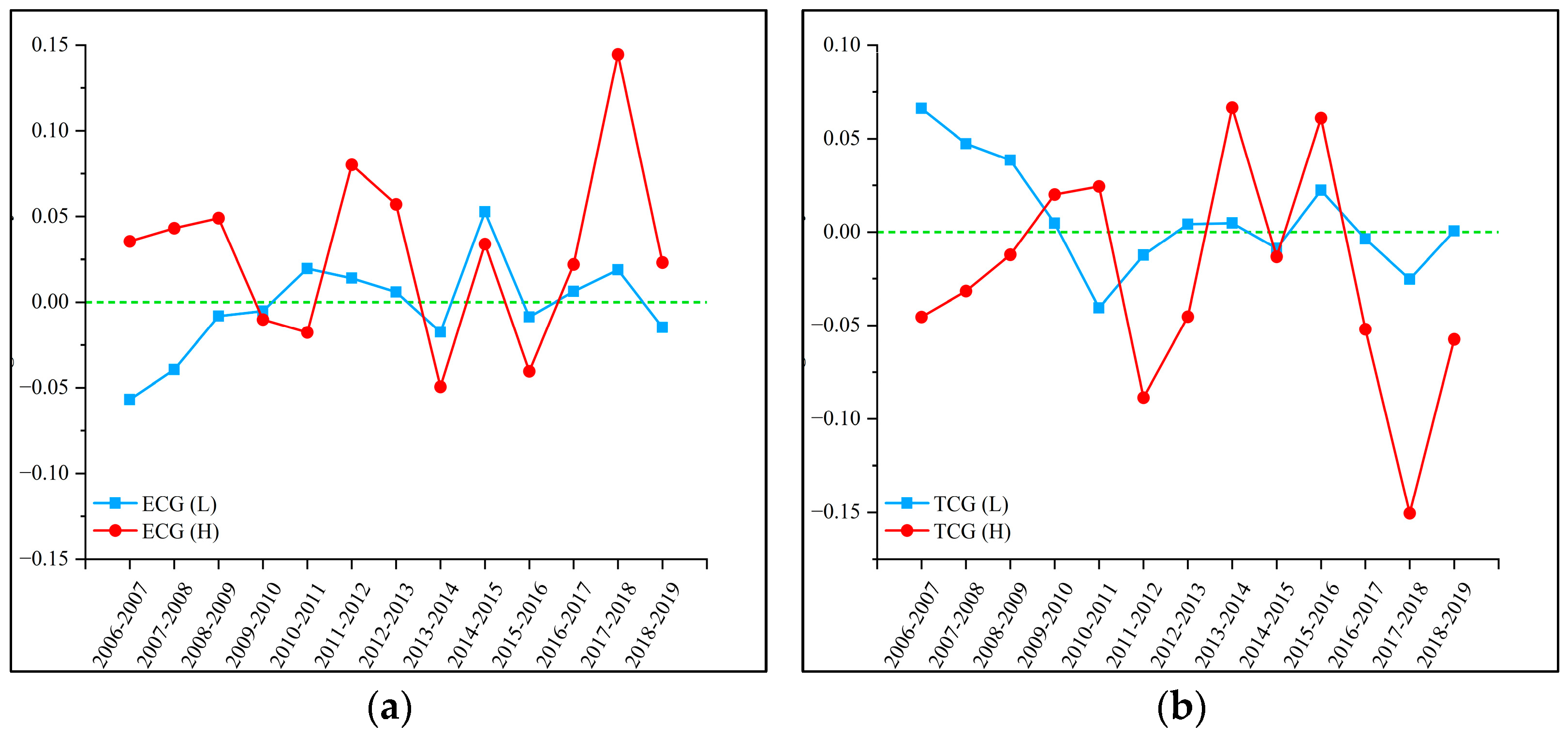
3.2. Trend Analysis of CTFP in the Sector Frontier
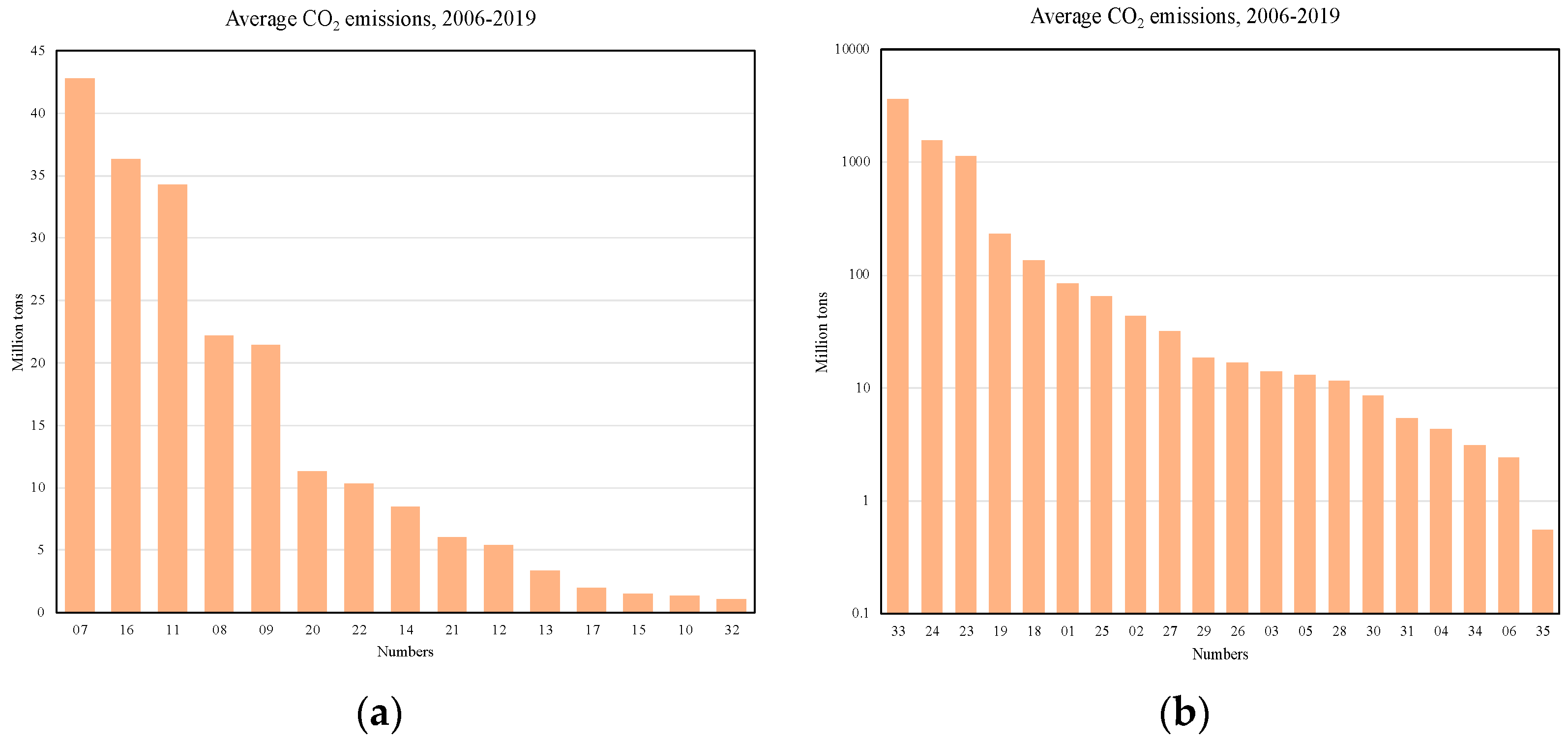
3.3. Trend Analysis of CTFP in Each Sub-Sector
3.4. Influencing Factors of CTFP in China’s Industrial Sector
- CTFP of China’s industrial sector showed an increasing trend from 2006 to 2019, which was attributed to TC.
- There were certain differences between the two sectors in terms of change in CTFP. The change in LIS was more stable, while the fluctuations in HIS were larger.
- At the sub-sector level, only three sub-sectors showed a decline in CTFP during the sample period. Processing of petroleum, coking and processing of nuclear fuel, production and supply of water, and production and supply of gas showed faster CTFP growth.
- R&D investment and R&D personnel had a positive impact on the CTFP, while energy structure was not conducive to the improvement of CTFP.
4. Conclusions and Policy Implications
4.1. Conclusions
4.2. Policy Implications
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LIS | Light industry sector |
| HIS | Heavy industry sector |
| CTFP | Carbon total factor productivity |
| BLPI | Biennial Luenberger productivity index |
| EC | Efficiency change |
| TC | Technology change |
| PGI | Productivity gap index |
| TCG | Technology change gap |
| ECG | Efficiency change gap |
Appendix A
| No. | Sub-Sectors | Types |
|---|---|---|
| 01 | Mining and Washing of Coal | H |
| 02 | Extraction of Petroleum and Natural Gas | H |
| 03 | Mining and Processing of Ferrous Metal Ores | H |
| 04 | Mining and Processing of Non-Ferrous Metal Ores | H |
| 05 | Mining and Processing of Non-metal Ores | H |
| 06 | Mining of Other Ores | H |
| 07 | Processing of Food from Agricultural Products | L |
| 08 | Manufacture of Foods | L |
| 09 | Manufacture of Liquor, Beverages, and Refined Tea | L |
| 10 | Manufacture of Tobacco | L |
| 11 | Manufacture of Textile | L |
| 12 | Manufacture of Textile, Wearing Apparel, and Accessories | L |
| 13 | Manufacture of Leather, Fur, Feather, and Related Products and Footwear | L |
| 14 | Processing of Timber, Manufacture of Wood, Bamboo, Rattan, Palm, and Straw Products | L |
| 15 | Manufacture of Furniture | L |
| 16 | Manufacture of Paper and Paper Products | L |
| 17 | Printing and Reproduction of Recording Media | L |
| 18 | Processing of Petroleum, Coking and Processing of Nuclear Fuel | H |
| 19 | Manufacture of Raw Chemical Materials and Chemical Products | H |
| 20 | Manufacture of Medicines | L |
| 21 | Manufacture of Chemical Fibers | L |
| 22 | Manufacture of Rubber and Plastics Products | L |
| 23 | Manufacture of Non-Metallic Mineral Products | H |
| 24 | Smelting and Pressing of Ferrous Metals | H |
| 25 | Smelting and Pressing of Non-Ferrous Metals | H |
| 26 | Manufacture of Metal Products | H |
| 27 | Manufacture of General Purpose Machinery | H |
| 28 | Manufacture of Special Purpose Machinery | H |
| 29 | Manufacture of Transport Equipment | H |
| 30 | Manufacture of Electrical Machinery and Apparatus | H |
| 31 | Manufacture of Computers, Communication, and Other Electronic Equipment | H |
| 32 | Manufacture of Measuring Instruments and Machinery | L |
| 33 | Production and Supply of Electric Power and Heat Power | H |
| 34 | Production and Supply of Gas | H |
| 35 | Production and Supply of Water | H |
| Sub-Sectors | EC | Capital | Labor | Energy | Output | CO2 |
|---|---|---|---|---|---|---|
| 01 | −0.059 | 0.000 | −0.020 | 0.000 | −0.169 | −0.002 |
| 02 | −0.081 | −0.019 | 0.000 | −0.009 | −0.216 | −0.018 |
| 03 | −0.076 | 0.000 | 0.001 | 0.004 | −0.228 | 0.000 |
| 04 | −0.103 | 0.000 | −0.008 | 0.002 | −0.317 | 0.010 |
| 05 | −0.005 | 0.000 | −0.029 | −0.002 | −0.004 | −0.001 |
| 06 | 0.042 | 0.000 | 0.000 | 0.077 | 0.027 | 0.073 |
| 07 | −0.009 | 0.000 | −0.052 | −0.009 | −0.009 | 0.000 |
| 08 | −0.010 | 0.000 | −0.052 | −0.003 | −0.010 | −0.002 |
| 09 | −0.012 | 0.000 | −0.044 | −0.004 | −0.015 | −0.003 |
| 10 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 11 | −0.006 | 0.000 | −0.038 | −0.011 | −0.004 | 0.002 |
| 12 | 0.003 | 0.000 | −0.014 | −0.015 | −0.009 | 0.027 |
| 13 | −0.030 | 0.000 | −0.070 | −0.045 | −0.007 | −0.045 |
| 14 | 0.011 | 0.000 | −0.039 | −0.007 | 0.038 | 0.012 |
| 15 | 0.002 | 0.000 | −0.026 | −0.036 | −0.005 | 0.033 |
| 16 | −0.015 | 0.000 | −0.038 | −0.005 | −0.027 | −0.004 |
| 17 | 0.006 | 0.008 | −0.059 | −0.026 | 0.053 | −0.011 |
| 18 | −0.041 | −0.029 | 0.000 | −0.075 | −0.011 | −0.076 |
| 19 | −0.036 | 0.000 | −0.011 | −0.003 | −0.099 | −0.005 |
| 20 | 0.003 | 0.000 | −0.046 | −0.010 | 0.001 | 0.028 |
| 21 | −0.023 | 0.000 | −0.024 | −0.011 | −0.032 | −0.025 |
| 22 | 0.003 | 0.000 | −0.049 | −0.011 | −0.009 | 0.037 |
| 23 | 0.003 | 0.000 | −0.044 | −0.001 | 0.026 | −0.001 |
| 24 | −0.016 | −0.010 | 0.013 | −0.002 | −0.046 | −0.002 |
| 25 | −0.023 | 0.000 | 0.024 | −0.003 | −0.068 | −0.009 |
| 26 | −0.014 | 0.000 | −0.032 | −0.005 | −0.023 | −0.007 |
| 27 | −0.011 | 0.000 | −0.038 | −0.007 | −0.026 | 0.007 |
| 28 | 0.002 | 0.000 | −0.042 | 0.001 | −0.014 | 0.033 |
| 29 | 0.000 | 0.015 | −0.045 | 0.003 | −0.044 | 0.053 |
| 30 | 0.022 | 0.002 | 0.026 | 0.023 | 0.000 | 0.050 |
| 31 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 32 | 0.003 | −0.015 | −0.032 | −0.022 | 0.000 | 0.031 |
| 33 | −0.021 | −0.009 | 0.000 | −0.006 | −0.057 | −0.001 |
| 34 | −0.013 | −0.002 | −0.022 | −0.006 | −0.035 | 0.005 |
| 35 | 0.016 | 0.003 | 0.015 | 0.001 | 0.042 | 0.000 |
| Sub-Sectors | TC | Capital | Labor | Energy | Output | CO2 |
|---|---|---|---|---|---|---|
| 01 | 0.037 | 0.000 | 0.081 | 0.015 | 0.055 | 0.023 |
| 02 | 0.114 | −0.024 | 0.000 | 0.001 | 0.332 | 0.016 |
| 03 | 0.039 | 0.000 | 0.094 | 0.015 | 0.061 | 0.021 |
| 04 | 0.044 | 0.000 | 0.085 | 0.017 | 0.050 | 0.047 |
| 05 | 0.021 | 0.000 | 0.063 | 0.010 | 0.030 | 0.010 |
| 06 | 0.039 | −0.015 | 0.146 | 0.000 | 0.083 | −0.009 |
| 07 | 0.026 | 0.000 | 0.062 | 0.013 | 0.038 | 0.016 |
| 08 | 0.029 | 0.000 | 0.074 | 0.028 | 0.031 | 0.022 |
| 09 | 0.039 | 0.000 | 0.069 | 0.034 | 0.057 | 0.026 |
| 10 | 0.077 | 0.050 | 0.078 | 0.084 | 0.000 | 0.159 |
| 11 | 0.027 | 0.000 | 0.058 | 0.014 | 0.028 | 0.028 |
| 12 | 0.041 | −0.003 | 0.156 | 0.088 | 0.058 | −0.015 |
| 13 | 0.088 | 0.003 | 0.138 | 0.085 | 0.001 | 0.187 |
| 14 | 0.026 | 0.000 | 0.055 | 0.019 | 0.022 | 0.033 |
| 15 | 0.035 | −0.025 | 0.108 | 0.066 | 0.053 | 0.002 |
| 16 | 0.045 | 0.000 | 0.071 | 0.015 | 0.084 | 0.022 |
| 17 | 0.047 | −0.025 | 0.126 | 0.017 | 0.118 | −0.016 |
| 18 | 0.273 | 0.180 | 0.000 | 0.534 | 0.039 | 0.542 |
| 19 | 0.043 | −0.002 | 0.074 | 0.005 | 0.092 | 0.012 |
| 20 | 0.048 | 0.000 | 0.065 | 0.017 | 0.075 | 0.040 |
| 21 | 0.054 | 0.000 | 0.062 | 0.014 | 0.078 | 0.060 |
| 22 | 0.043 | 0.000 | 0.064 | 0.017 | 0.029 | 0.072 |
| 23 | 0.028 | 0.000 | 0.078 | 0.006 | 0.054 | 0.002 |
| 24 | 0.062 | −0.049 | 0.002 | 0.000 | 0.199 | 0.002 |
| 25 | 0.040 | −0.008 | 0.032 | 0.004 | 0.091 | 0.019 |
| 26 | 0.032 | 0.000 | 0.051 | 0.006 | 0.054 | 0.023 |
| 27 | 0.029 | 0.000 | 0.061 | 0.015 | 0.045 | 0.016 |
| 28 | 0.044 | −0.018 | 0.068 | 0.031 | 0.048 | 0.056 |
| 29 | 0.050 | −0.161 | 0.003 | −0.089 | 0.263 | −0.031 |
| 30 | 0.049 | 0.026 | 0.076 | 0.073 | 0.000 | 0.088 |
| 31 | 0.030 | 0.039 | 0.057 | 0.041 | 0.000 | 0.046 |
| 32 | 0.038 | 0.018 | 0.078 | 0.060 | 0.000 | 0.063 |
| 33 | 0.072 | −0.014 | 0.000 | 0.001 | 0.221 | 0.001 |
| 34 | 0.057 | −0.003 | 0.063 | 0.035 | 0.092 | 0.046 |
| 35 | 0.176 | −0.033 | −0.013 | −0.016 | 0.550 | 0.000 |
References
- Zhou, H.; Hui, X.; Li, D.; Hu, D.; Chen, X.; He, X.; Gao, L.; Huang, H.; Lee, C.; Mu, X. Metal–organic framework-surface-enhanced infrared absorption platform enables simultaneous on-chip sensing of greenhouse gases. Adv. Sci. 2020, 7, 2001173. [Google Scholar] [CrossRef]
- Xu, X.; Cui, X.; Zhang, Y.; Chen, X.; Li, W. Carbon neutrality and green technology innovation efficiency in Chinese textile industry. J. Clean. Prod. 2023, 395, 136453. [Google Scholar] [CrossRef]
- Li, K.; Yan, Y.; Zhang, X. Carbon-abatement policies, investment preferences, and directed technological change: Evidence from China. Technol. Forecast. Soc. Social. Change 2021, 172, 121015. [Google Scholar] [CrossRef]
- Xu, L.; Fan, M.; Yang, L.; Shao, S. Heterogeneous green innovations and carbon emission performance: Evidence at China’s city level. Energy Econ. 2021, 99, 105269. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, Y. How does carbon emission price stimulate enterprises’ total factor productivity? Insights from China’s emission trading scheme pilots. Energy Econ. 2022, 109, 105990. [Google Scholar] [CrossRef]
- Song, Y.; Liu, T.; Ye, B.; Li, Y. Linking carbon market and electricity market for promoting the grid parity of photovoltaic electricity in China. Energy 2020, 211, 118924. [Google Scholar] [CrossRef]
- Fang, P.; Wan, L.; Fang, W. The Choice of Cooperative Governance Mechanism in Open Innovation Projects under the Synergy of the Electricity–Carbon Market. Energies 2023, 16, 6110. [Google Scholar] [CrossRef]
- Deng, J.; Zheng, Y.; Zhang, Y.; Liu, C.; Pan, H. Dynamic Spillovers between Carbon Price and Power Sector Returns in China: A Network-Based Analysis before and after Launching National Carbon Emissions Trading Market. Energies 2023, 16, 5578. [Google Scholar] [CrossRef]
- Wang, H.R.; Feng, T.T.; Zhong, C. Effectiveness of CO2 cost pass-through to electricity prices under “electricity-carbon” market coupling in China. Energy 2023, 266, 126387. [Google Scholar] [CrossRef]
- Wang, J.; Hu, M.; Rodrigues, J.F. The evolution and driving forces of industrial aggregate energy intensity in China: An extended decomposition analysis. Appl. Energy 2018, 228, 2195–2206. [Google Scholar] [CrossRef]
- Ouyang, X.; Fang, X.; Cao, Y.; Sun, C. Factors behind CO2 emission reduction in Chinese heavy industries: Do environmental regulations matter? Energy Policy 2020, 145, 111765. [Google Scholar] [CrossRef]
- Xu, B.; Xu, R. Assessing the carbon intensity of the heavy industry in China: Using a nonparametric econometric model. Environ. Impact Assess. Rev. 2023, 98, 106925. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, L.; Shuai, C.; Bian, J.; Zhu, M.; Tan, Y.; Ye, G. How is the environmental efficiency in the process of dramatic economic development in the Chinese cities? Ecol. Indic. 2019, 98, 349–362. [Google Scholar] [CrossRef]
- Mo, J.; Tu, Q.; Wang, J. Carbon pricing and enterprise productivity-The role of price stabilization mechanism. Energy Econ. 2023, 120, 106631. [Google Scholar] [CrossRef]
- Xiao, J.; Li, G.; Zhu, B.; Xie, L.; Hu, Y.; Huang, J. Evaluating the impact of carbon emissions trading scheme on Chinese firms’ total factor productivity. J. Clean. Prod. 2021, 306, 127104. [Google Scholar] [CrossRef]
- Yasmeen, R.; Zhang, X.; Tao, R.; Shah, W.U.H. The impact of green technology, environmental tax and natural resources on energy efficiency and productivity: Perspective of OECD Rule of Law. Energy Rep. 2023, 9, 1308–1319. [Google Scholar] [CrossRef]
- Shah, W.U.H.; Hao, G.; Yan, H.; Zhu, N.; Yasmeen, R.; Dincă, G. Role of renewable, non-renewable energy consumption and carbon emission in energy efficiency and productivity change: Evidence from G20 economies. Geosci. Front. 2023, 101631. [Google Scholar] [CrossRef]
- Zhu, Q.; Liu, C.; Li, X.; Zhou, D. The total factor carbon emission productivity in China’s industrial Sectors: An analysis based on the global Malmquist-Luenberger index. Sustain. Energy Technol. Assess. 2023, 56, 103094. [Google Scholar] [CrossRef]
- Malmquist, S. Index numbers and indifference surfaces. Trab. Estadística 1953, 4, 209–242. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Norris, M.; Zhang, Z. Productivity growth, technical progress, and efficiency change in industrialized countries. Am. Econ. Rev. 1994, 66–83. Available online: https://www.jstor.org/stable/2117971 (accessed on 1 July 2023).
- Xue, X.; Shen, Q.; Wang, Y.; Lu, J. Measuring the productivity of the construction industry in China by using DEA-based Malmquist productivity indices. J. Constr. Eng. Manag. 2008, 134, 64–71. [Google Scholar] [CrossRef]
- Lin, M.I.; Lee, Y.D.; Ho, T.N. Applying integrated DEA/AHP to evaluate the economic performance of local governments in China. Eur. J. Oper. Res. 2011, 209, 129–140. [Google Scholar] [CrossRef]
- Sun, W.; Li, Y.; Wang, D.; Fan, J. The efficiencies and their changes of China’s resources-based cities employing DEA and Malmquist index models. J. Geogr. Sci. 2012, 22, 509–520. [Google Scholar] [CrossRef]
- Wu, A.H.; Cao, Y.Y.; Liu, B. Energy efficiency evaluation for regions in China: An application of DEA and Malmquist indices. Energy Effic. 2014, 7, 429–439. [Google Scholar] [CrossRef]
- Li, H.; Wu, L. Analysis of financial support efficiency for China’s wind power industry. Energy Sources Part. B Econ. Plan. Policy 2016, 11, 1035–1041. [Google Scholar] [CrossRef]
- Liu, W.; Zhan, J.; Wang, C.; Li, S.; Zhang, F. Environmentally sensitive productivity growth of industrial sectors in the Pearl River Delta. Resour. Conserv. Recycl. 2018, 139, 50–63. [Google Scholar] [CrossRef]
- Wang, K.L.; Pang, S.Q.; Ding, L.L.; Miao, Z. Combining the biennial Malmquist–Luenberger index and panel quantile regression to analyze the green total factor productivity of the industrial sector in China. Sci. Total Environ. 2020, 739, 140280. [Google Scholar] [CrossRef]
- Chung, Y.H.; Färe, R.; Grosskopf, S. Productivity and undesirable outputs: A directional distance function approach. J. Environ. Manag. 1997, 51, 229–240. [Google Scholar] [CrossRef]
- He, F.; Zhang, Q.; Lei, J.; Fu, W.; Xu, X. Energy efficiency and productivity change of China’s iron and steel industry: Accounting for undesirable outputs. Energy Policy 2013, 54, 204–213. [Google Scholar] [CrossRef]
- Fu, Y.; He, C.; Luo, L. Does the low-carbon city policy make a difference? Empirical evidence of the pilot scheme in China with DEA and PSM-DID. Ecol. Indic. 2021, 122, 107238. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, X.; Wang, B.; Liu, X. Energy saving, GHG abatement and industrial growth in OECD countries: A green productivity approach. Energy 2020, 194, 116833. [Google Scholar] [CrossRef]
- Oh, D.H. A global Malmquist-Luenberger productivity index. J. Product. Anal. 2010, 34, 183–197. [Google Scholar] [CrossRef]
- Zhang, W.; Cheng, J.; Liu, X.; Zhu, Z. Heterogeneous industrial agglomeration, its coordinated development and total factor energy efficiency. Environ. Dev. Sustain. 2023, 25, 5511–5537. [Google Scholar] [CrossRef]
- Li, S.; Zhu, X.; Zhang, T. Optimum combination of heterogeneous environmental policy instruments and market for green transformation: Empirical evidence from China’s metal sector. Energy Econ. 2023, 123, 106735. [Google Scholar] [CrossRef]
- Fujii, H.; Managi, S.; Matousek, R. Indian bank efficiency and productivity changes with undesirable outputs: A disaggregated approach. J. Bank. Financ. 2014, 38, 41–50. [Google Scholar] [CrossRef]
- Zhou, T.; Huang, X.; Zhang, N. The effect of innovation pilot on carbon total factor productivity: Quasi-experimental evidence from China. Energy Econ. 2023, 125, 106895. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Pasurka, C.A., Jr. Environmental production functions and environmental directional distance functions. Energy 2007, 32, 1055–1066. [Google Scholar] [CrossRef]
- Pastor, J.T.; Asmild, M.; Lovell, C.K. The biennial Malmquist productivity change index. Socio-Econ. Plan. Sci. 2011, 45, 10–15. [Google Scholar] [CrossRef]
- Chambers, R.G.; Chung, Y.; Färe, R. Benefit and distance functions. J. Econ. Theory 1996, 70, 407–419. [Google Scholar] [CrossRef]
- Li, J.; Lin, B. Ecological total-factor energy efficiency of China’s heavy and light industries: Which performs better? Renew. Sustain. Energy Rev. 2017, 72, 83–94. [Google Scholar] [CrossRef]
- Kang, Y.Q.; Xie, B.C.; Wang, J.; Wang, Y.N. Environmental assessment and investment strategy for China’s manufacturing industry: A non-radial DEA based analysis. J. Clean. Prod. 2018, 175, 501–511. [Google Scholar] [CrossRef]
- Cui, H.; Wang, H.; Zhao, Q. Which factors stimulate industrial green total factor productivity growth rate in China? An industrial aspect. Greenh. Gases Sci. Technol. 2019, 9, 505–518. [Google Scholar] [CrossRef]
- Jiang, H.; Jiang, P.; Wang, D.; Wu, J. Can smart city construction facilitate green total factor productivity? A quasi-natural experiment based on China’s pilot smart city. Sustain. Cities Soc. 2021, 69, 102809. [Google Scholar] [CrossRef]
- Ding, T.; Li, H.; Tan, R.; Zhao, X. How does geopolitical risk affect carbon emissions?: An empirical study from the perspective of mineral resources extraction in OECD countries. Resour. Policy 2023, 85, 103983. [Google Scholar] [CrossRef]

| Index | Unit | Type | N | Mean | Std. Dev | Min | Max |
|---|---|---|---|---|---|---|---|
| K | CNY 100 million | L | 210 | 2454.816 | 1845.578 | 348.673 | 9316.616 |
| H | 280 | 8541.125 | 11,322.272 | 0.732 | 75,400.112 | ||
| L | 10,000 persons | L | 210 | 200.496 | 144.832 | 16.2 | 652.06 |
| H | 280 | 281.481 | 231.826 | 0.08 | 911.69 | ||
| E | 10,000 tons of SCE | L | 210 | 1878.886 | 1836.089 | 143.278 | 7487 |
| H | 280 | 11,407.257 | 15,962.733 | 126.51 | 69,342 | ||
| Y | CNY 100 million | L | 210 | 11,785.032 | 10,005.177 | 1460.379 | 58,969.151 |
| H | 280 | 24,709.962 | 21,792.325 | 3.79 | 87,384.372 | ||
| C | Million tons | L | 210 | 13.862 | 14.856 | 0.287 | 52.388 |
| H | 280 | 349.276 | 865.838 | 0.007 | 4641.959 |
| Sub-Sectors | BLPI | Capital | Labor | Energy | Output | CO2 |
|---|---|---|---|---|---|---|
| 01 | −0.023 | 0.000 | 0.062 | 0.016 | −0.114 | 0.020 |
| 02 | 0.032 | −0.043 | 0.000 | −0.009 | 0.116 | −0.002 |
| 03 | −0.036 | 0.000 | 0.095 | 0.020 | −0.167 | 0.020 |
| 04 | −0.059 | 0.000 | 0.077 | 0.019 | −0.267 | 0.057 |
| 05 | 0.016 | 0.000 | 0.034 | 0.008 | 0.026 | 0.009 |
| 06 | 0.081 | −0.015 | 0.146 | 0.077 | 0.110 | 0.064 |
| 07 | 0.017 | 0.000 | 0.010 | 0.004 | 0.029 | 0.016 |
| 08 | 0.019 | 0.000 | 0.021 | 0.025 | 0.021 | 0.020 |
| 09 | 0.028 | 0.000 | 0.024 | 0.029 | 0.042 | 0.023 |
| 10 | 0.077 | 0.050 | 0.078 | 0.084 | 0.000 | 0.159 |
| 11 | 0.021 | 0.000 | 0.019 | 0.002 | 0.024 | 0.030 |
| 12 | 0.044 | −0.003 | 0.142 | 0.073 | 0.049 | 0.012 |
| 13 | 0.058 | 0.003 | 0.068 | 0.040 | −0.005 | 0.141 |
| 14 | 0.038 | 0.000 | 0.016 | 0.011 | 0.060 | 0.045 |
| 15 | 0.037 | −0.025 | 0.081 | 0.029 | 0.048 | 0.035 |
| 16 | 0.030 | 0.000 | 0.033 | 0.010 | 0.057 | 0.018 |
| 17 | 0.052 | −0.017 | 0.067 | −0.008 | 0.170 | −0.027 |
| 18 | 0.233 | 0.151 | 0.000 | 0.459 | 0.028 | 0.466 |
| 19 | 0.007 | −0.002 | 0.063 | 0.002 | −0.007 | 0.007 |
| 20 | 0.051 | 0.000 | 0.019 | 0.007 | 0.076 | 0.068 |
| 21 | 0.032 | 0.000 | 0.038 | 0.004 | 0.046 | 0.035 |
| 22 | 0.045 | 0.000 | 0.015 | 0.006 | 0.021 | 0.109 |
| 23 | 0.031 | 0.000 | 0.034 | 0.004 | 0.079 | 0.001 |
| 24 | 0.045 | −0.059 | 0.015 | −0.002 | 0.152 | 0.000 |
| 25 | 0.017 | −0.008 | 0.056 | 0.000 | 0.023 | 0.010 |
| 26 | 0.018 | 0.000 | 0.019 | 0.001 | 0.031 | 0.016 |
| 27 | 0.018 | 0.000 | 0.023 | 0.008 | 0.020 | 0.023 |
| 28 | 0.045 | −0.018 | 0.025 | 0.032 | 0.034 | 0.089 |
| 29 | 0.050 | −0.146 | −0.042 | −0.086 | 0.219 | 0.022 |
| 30 | 0.071 | 0.028 | 0.101 | 0.095 | 0.000 | 0.137 |
| 31 | 0.030 | 0.039 | 0.057 | 0.041 | 0.000 | 0.046 |
| 32 | 0.041 | 0.002 | 0.046 | 0.038 | 0.000 | 0.094 |
| 33 | 0.051 | −0.023 | 0.000 | −0.006 | 0.163 | 0.000 |
| 34 | 0.109 | −0.061 | −0.008 | −0.006 | 0.319 | 0.032 |
| 35 | 0.193 | −0.029 | 0.002 | −0.015 | 0.592 | 0.000 |
| Factors | Measurement Methods | Unit |
|---|---|---|
| Scale | The number of industrial enterprises above designated size | 1 enterprise |
| R&D investment | The proportion of R&D expenditure in industrial output | % |
| R&D personnel | The number of R&D personnel | 1 personnel |
| ES | The proportion of coal consumption in total energy consumption | % |
| Variables | (1) | (2) | (3) |
|---|---|---|---|
| CTFP | EC | TC | |
| Ln (Scale) | 0.0076 (0.20) | −0.1245 ** (−1.99) | −0.0072 (−0.11) |
| R&D investment | 0.0851 ** (2.42) | −0.0511 (−1.39) | 0.1360 *** (3.62) |
| Ln (R&D personnel) | 0.1024 *** (4.66) | 0.1106 ** (2.54) | 0.2551 *** (5.75) |
| ES | −0.0891 *** (−7.69) | −0.0021 (−0.11) | −0.0515 ** (−2.40) |
| Constant | −5.5562 (−1.65) | 1.5177 *** (2.68) | −0.6770 (−1.17) |
| Year FE | Yes | Yes | Yes |
| Sub-sector FE | Yes | Yes | Yes |
| R2 | 0.4356 | 0.2637 | 0.3848 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Li, H.; Song, Z.; Shi, W.; Sheng, W. Measurement of Carbon Total Factor Productivity in the Context of Carbon–Electricity Market Collaboration: An Application of Biennial Luenberger Productivity Index. Energies 2024, 17, 1219. https://doi.org/10.3390/en17051219
Zhang L, Li H, Song Z, Shi W, Sheng W. Measurement of Carbon Total Factor Productivity in the Context of Carbon–Electricity Market Collaboration: An Application of Biennial Luenberger Productivity Index. Energies. 2024; 17(5):1219. https://doi.org/10.3390/en17051219
Chicago/Turabian StyleZhang, Li, Hao Li, Zhumeng Song, Wei Shi, and Wenxiang Sheng. 2024. "Measurement of Carbon Total Factor Productivity in the Context of Carbon–Electricity Market Collaboration: An Application of Biennial Luenberger Productivity Index" Energies 17, no. 5: 1219. https://doi.org/10.3390/en17051219
APA StyleZhang, L., Li, H., Song, Z., Shi, W., & Sheng, W. (2024). Measurement of Carbon Total Factor Productivity in the Context of Carbon–Electricity Market Collaboration: An Application of Biennial Luenberger Productivity Index. Energies, 17(5), 1219. https://doi.org/10.3390/en17051219





