Analysis and Suppression of Harmonic Resonance in Photovoltaic Grid-Connected Systems
Abstract
1. Introduction
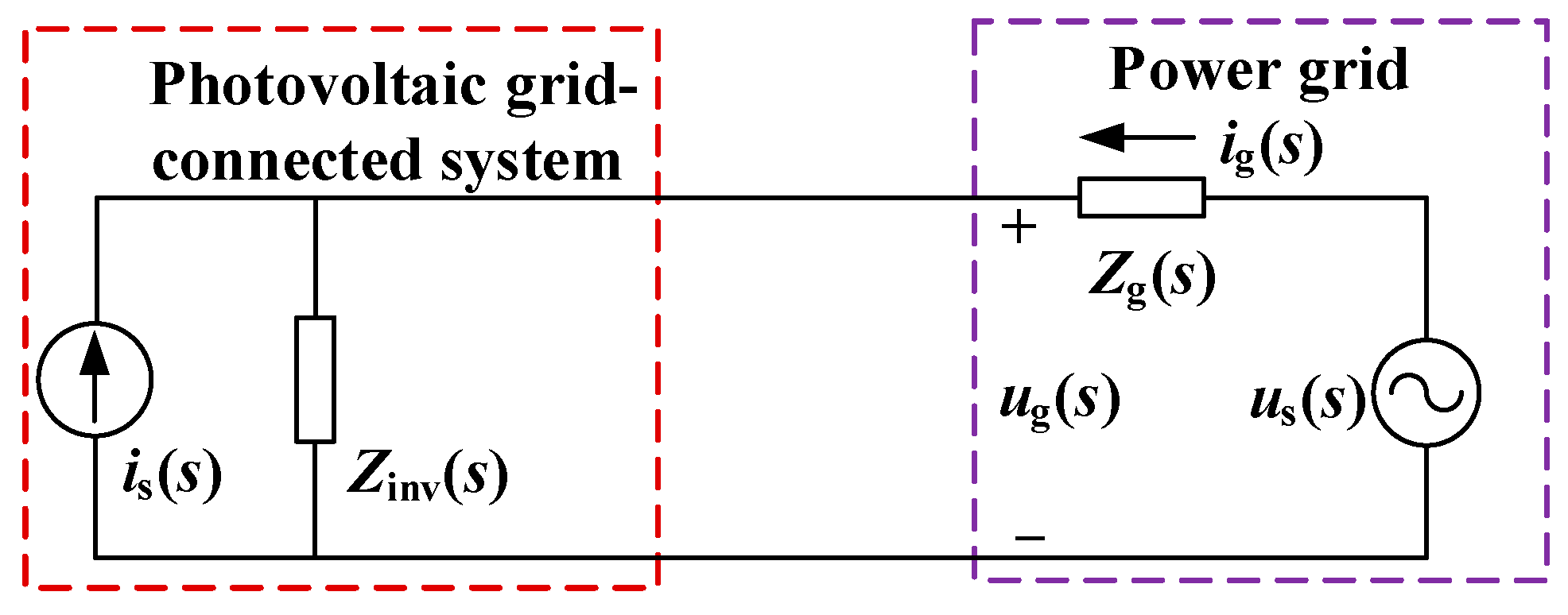
2. Modeling of Positive and Negative Sequence Impedance in Photovoltaic Grid-Connected Systems
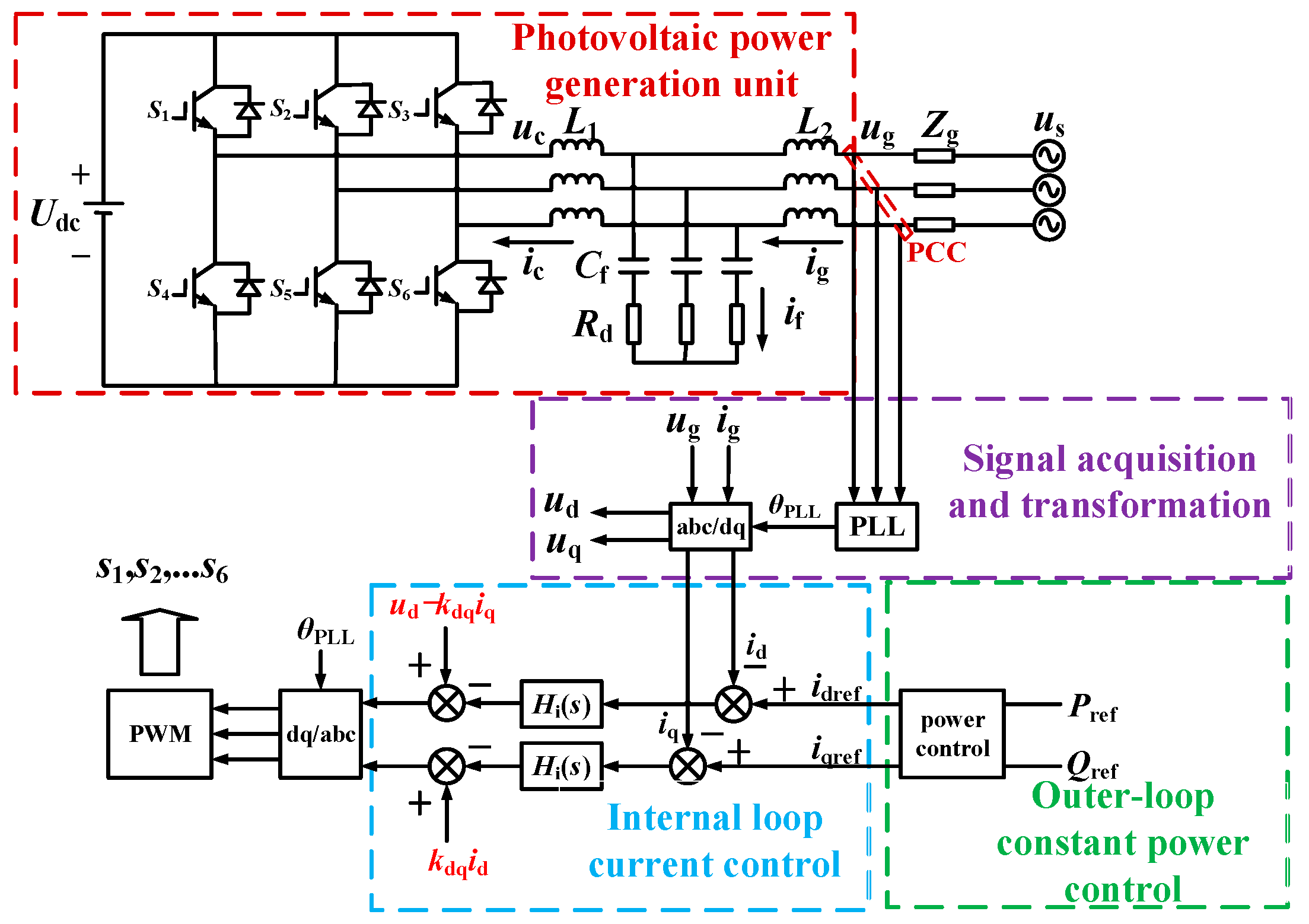
2.1. Photovoltaic Grid-Connected System Structure
2.2. Modular Impedance Modeling
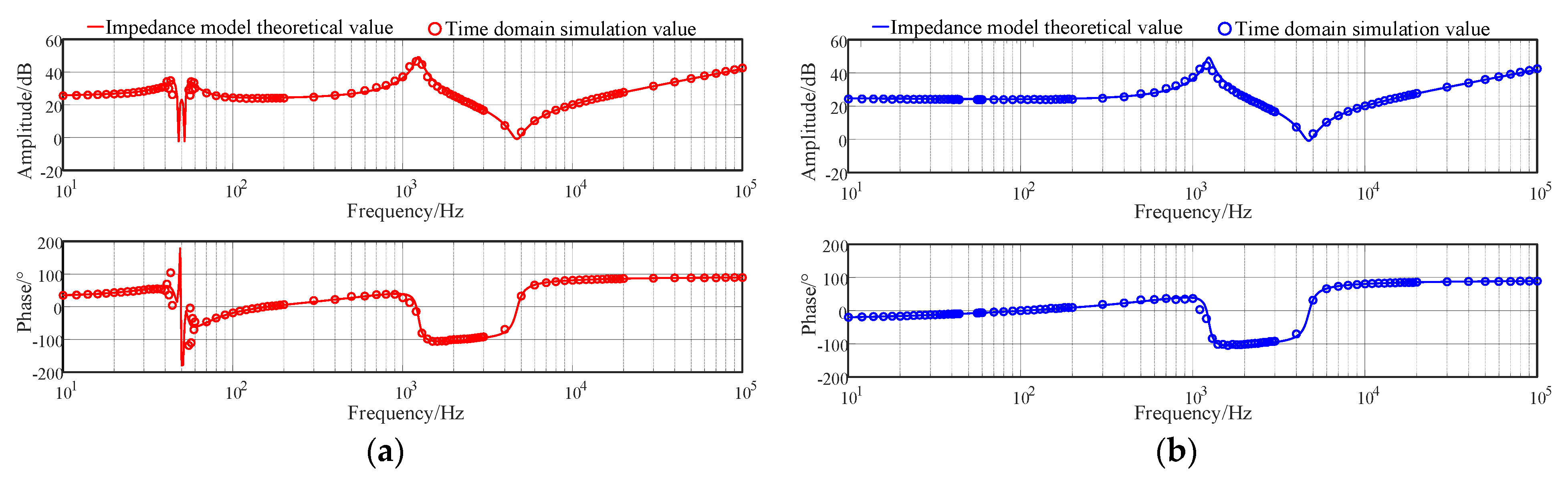
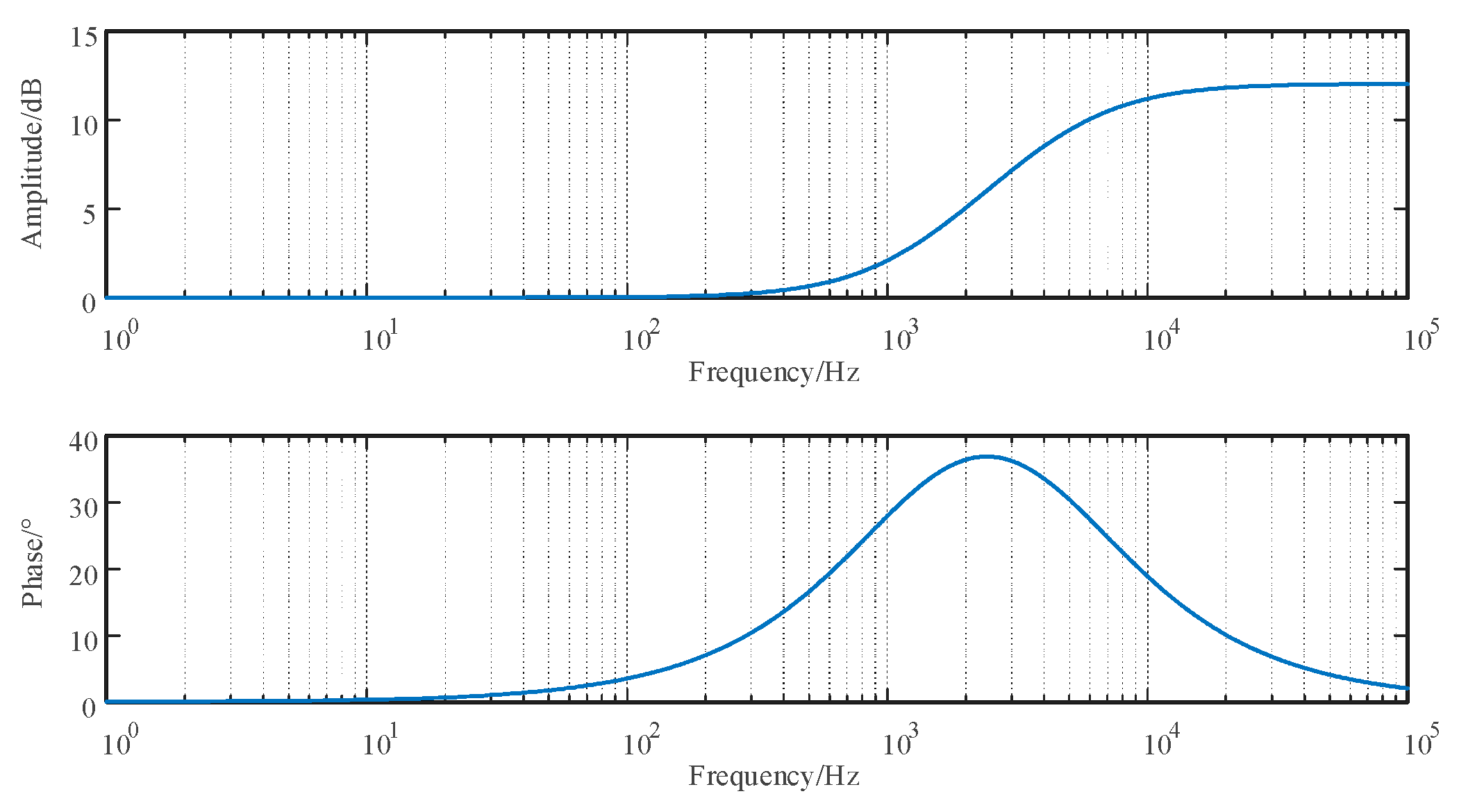
2.3. Frequency Sweeping Verification of Photovoltaic Series Impedance Model
3. Resonance Stability Analysis of Photovoltaic Grid-Connected Systems
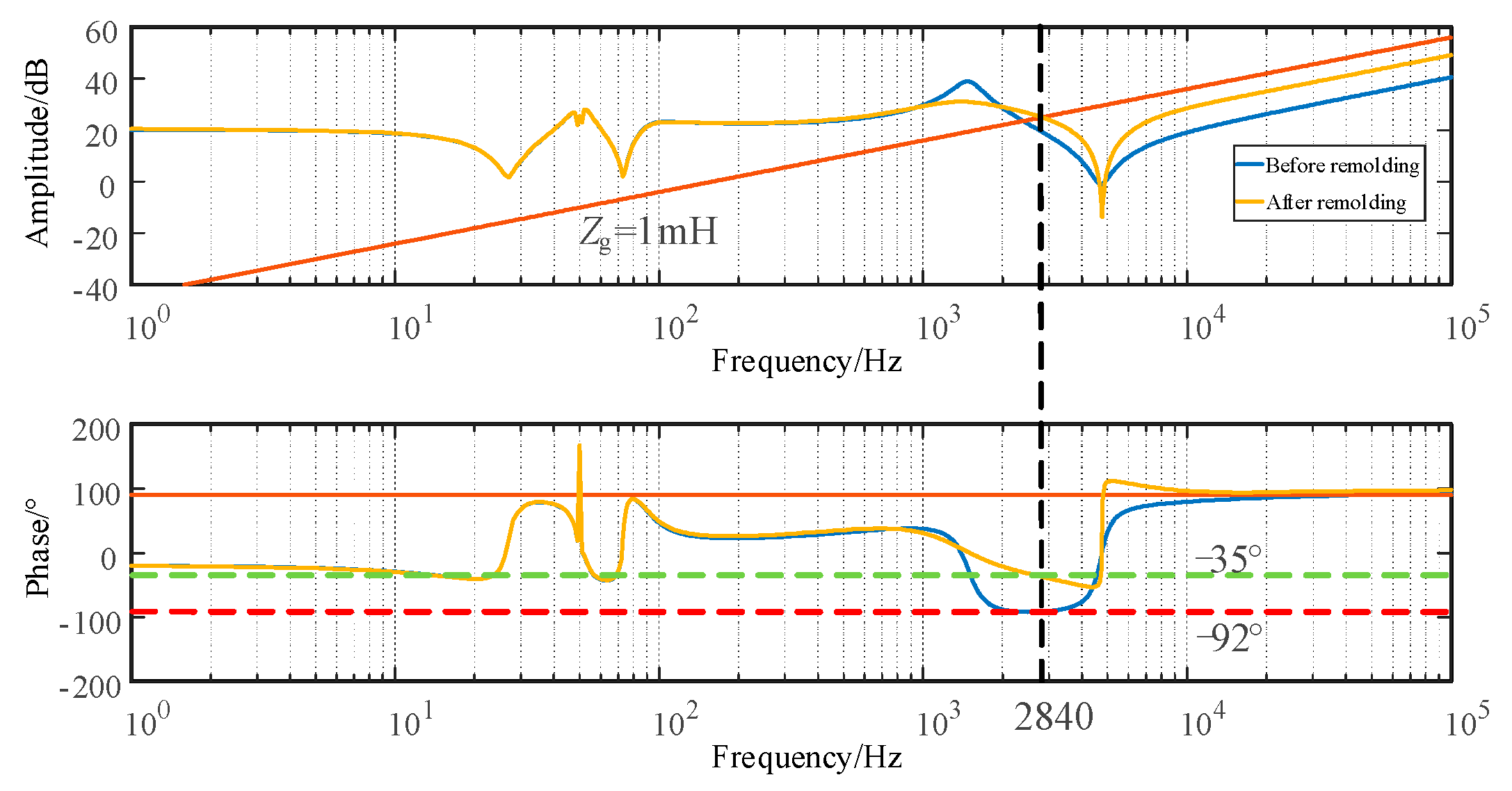
3.1. Resonance Stability Analysis
3.2. Analysis of the Impact of Parameter Variations on System Impedance Characteristics and Harmonic Resonance Characteristics
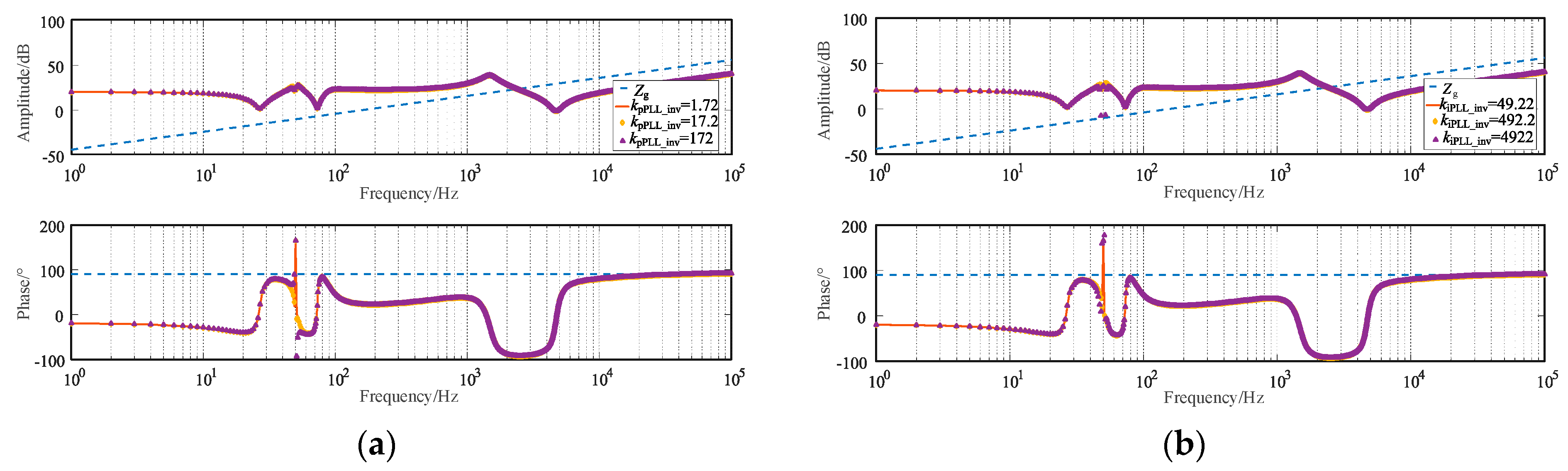
3.2.1. Analysis of the Influence of the Phase-Locked Loop (PLL) Proportional Integral Coefficient Change in the Photovoltaic Grid-Connected System
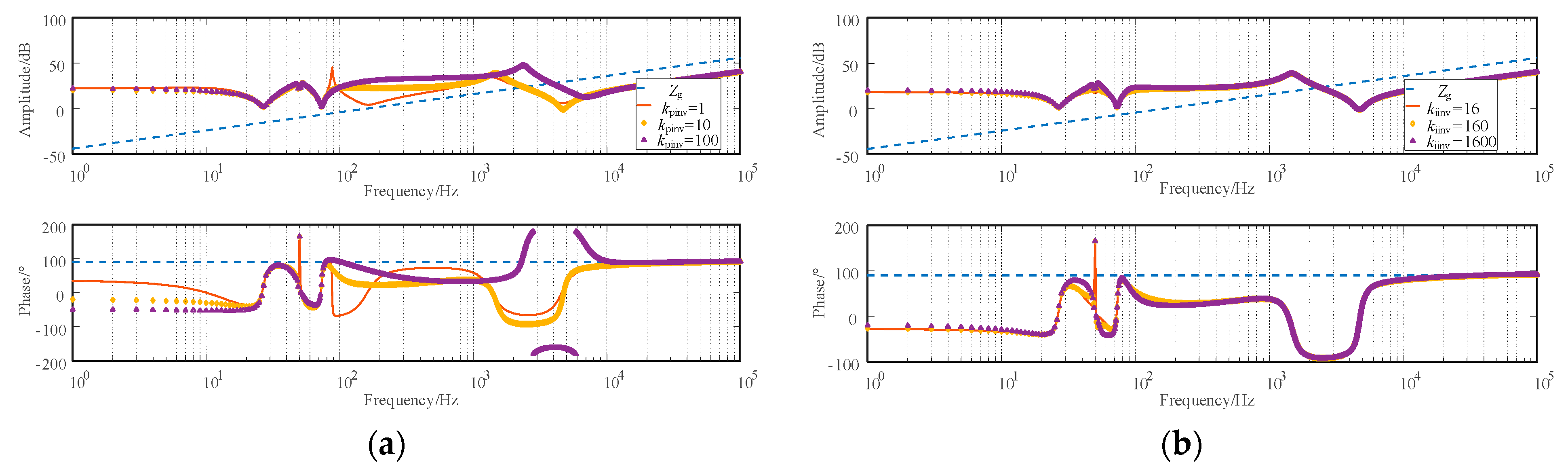
3.2.2. Analysis of the Influence of the Inner Loop Proportional Integral Coefficient Change in the Photovoltaic Grid-Connected System
- The parameters kpPLL_inv and kiPLL_inv of the phase locked loop (PLL) have a minor impact on the impedance characteristics of the photovoltaic grid-connected system, and they primarily affect the impedance characteristics around the fundamental frequency. kpPLL_inv mainly affects the impedance phase, while kiPLL_inv mainly affects the impedance magnitude. They do not impact the frequency of the intersection point between the impedance of the photovoltaic grid-connected system and the impedance magnitude of the power grid.
- The parameters kpinv and kiinv of the inner-loop current controller have a greater impact on the impedance characteristics of the photovoltaic grid-connected system than the parameters of the phase-locked loop. Among them, kpinv has the greatest impact on the impedance of the photovoltaic grid-connected system, and the impact band is broad, with the highest frequency of the impact band reaching 10 kHz. Within a certain range, as kpinv increases, the impedance phase of the photovoltaic grid-connected system in the low-frequency band (below 30 Hz) decreases, the frequency of the intersection point between the impedance of the photovoltaic grid-connected system and the grid impedance shifts backward, and the phase margin in the easily oscillating frequency band becomes smaller. kiinv affects the impedance characteristics of the photovoltaic grid-connected system below 200 Hz, mainly affecting the phase in the frequency band of 30 Hz–70 Hz, and the impact on the amplitude is somewhat smaller.
4. Active Damping Design of the Photovoltaic Grid-Connected System Based on Positive and Negative Sequence Impedance Models
4.1. Active Damping Design Based on Lead Correction and Capacitive Current Feedback
4.1.1. Additional Active Damping Method
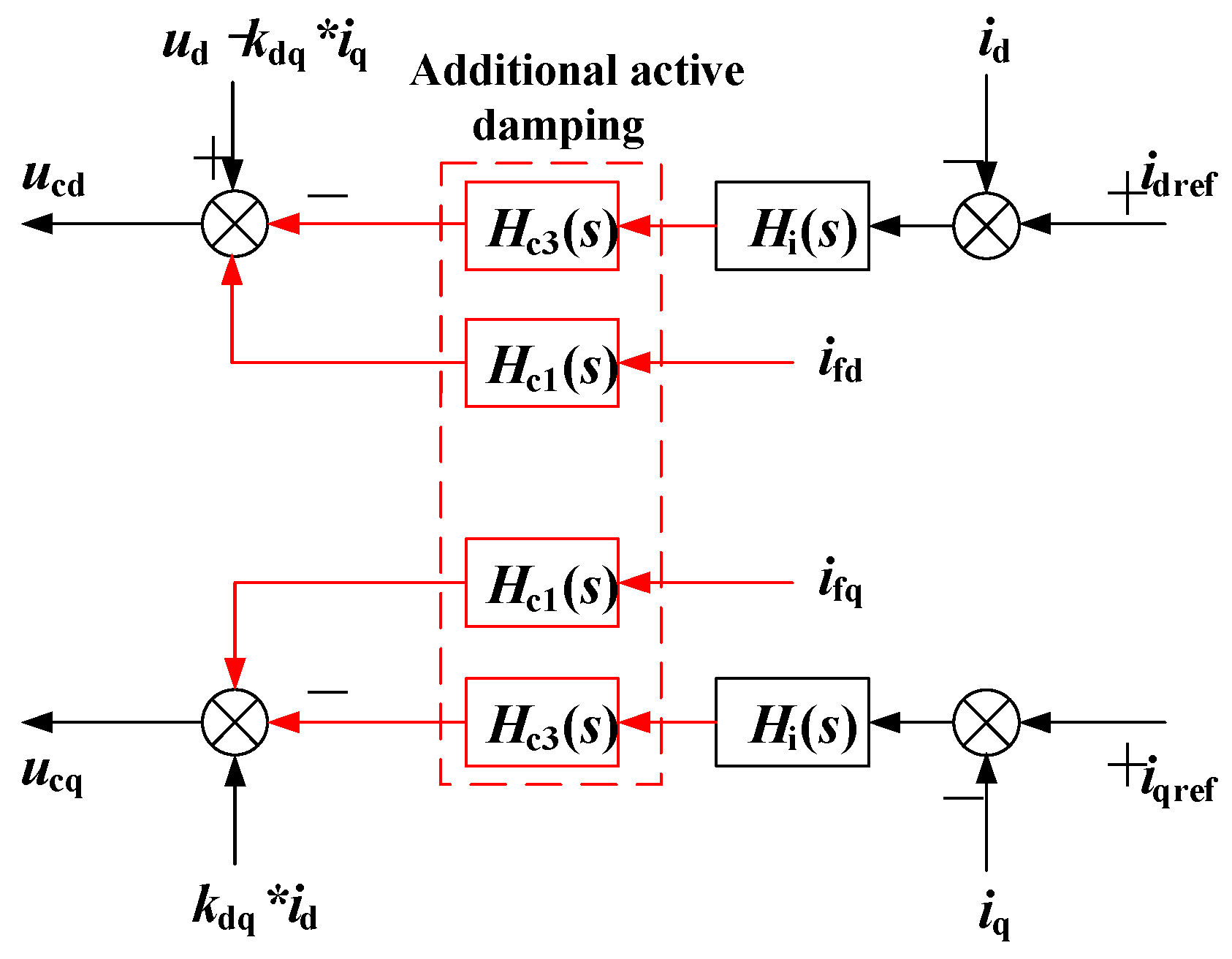
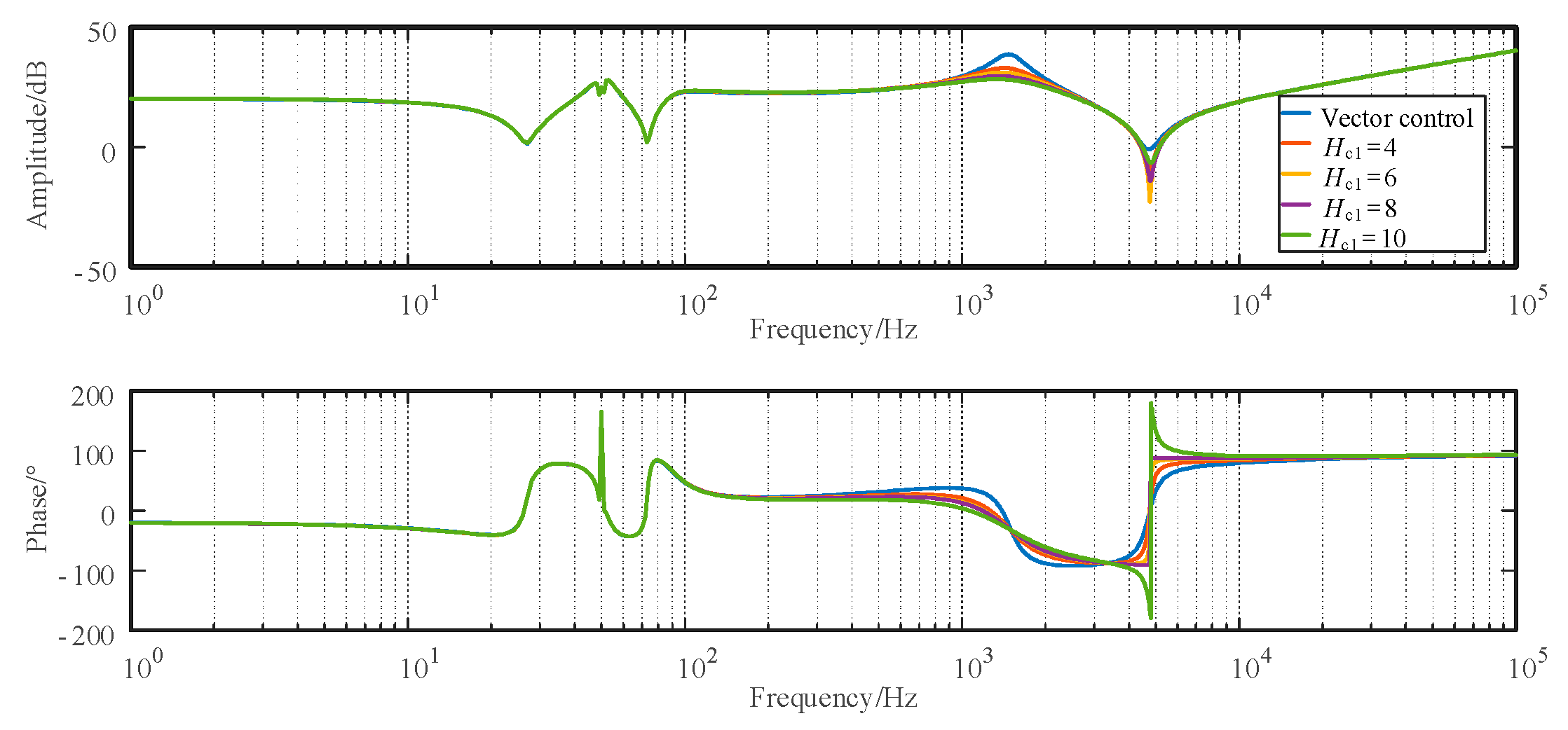
4.1.2. Parameter Tuning
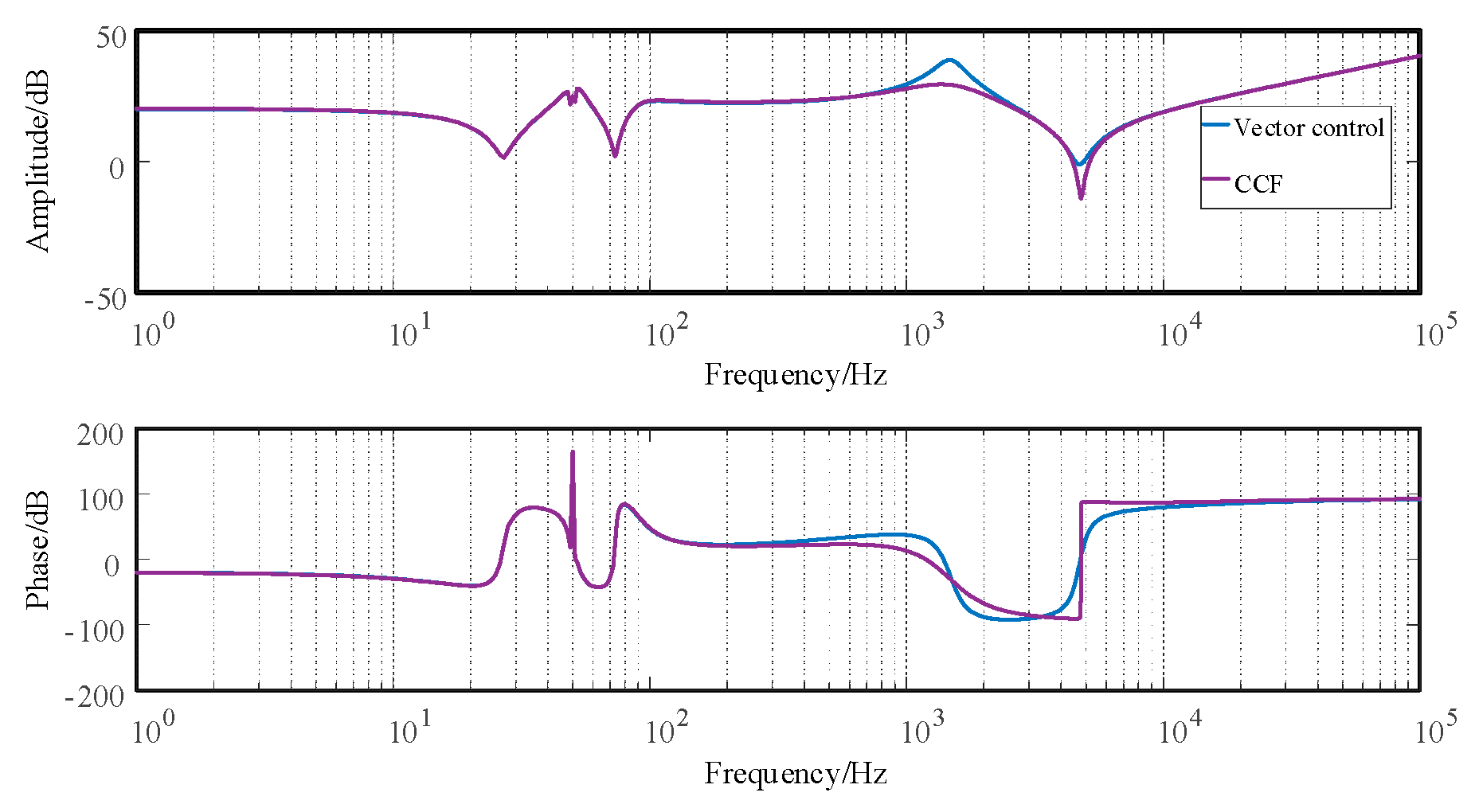
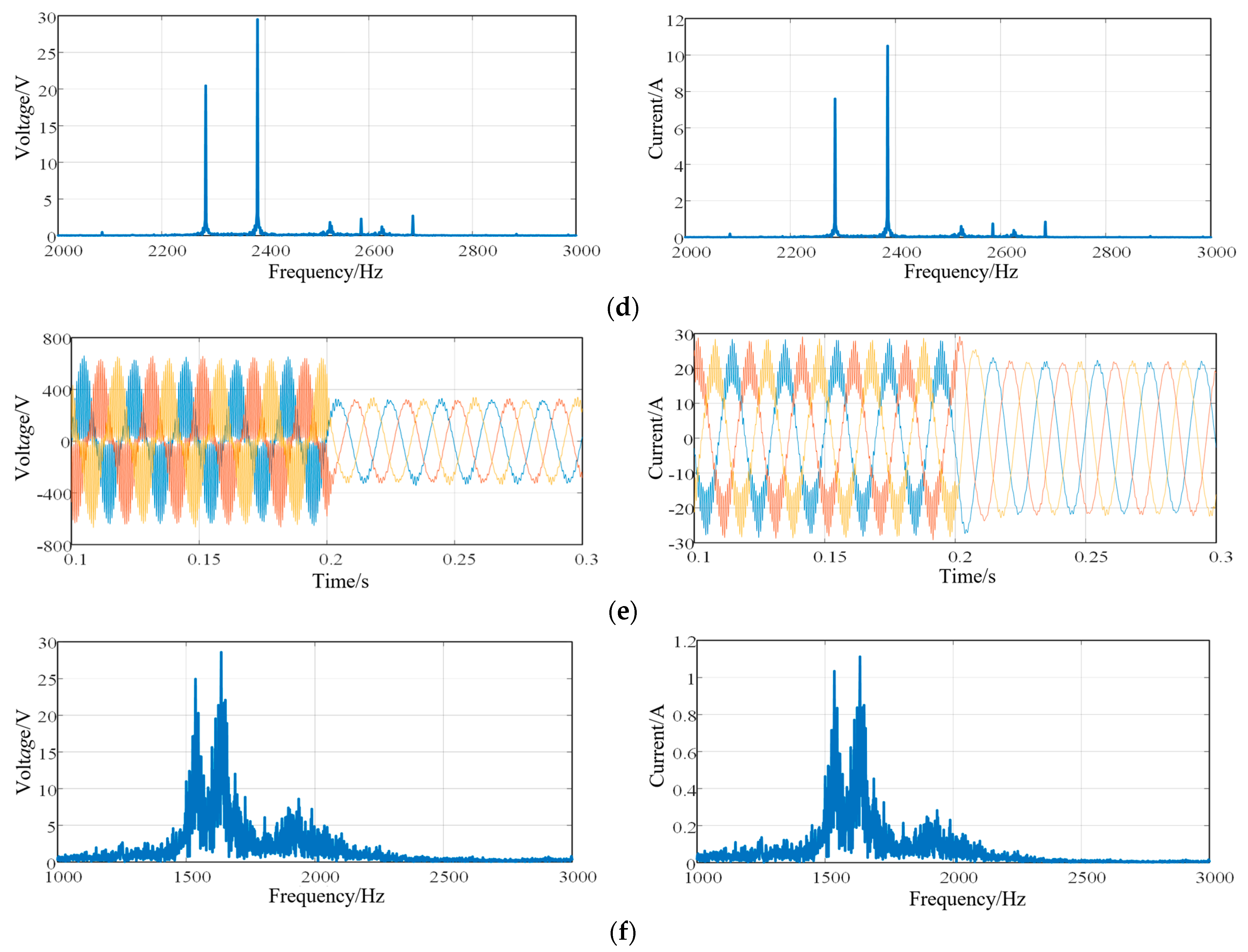
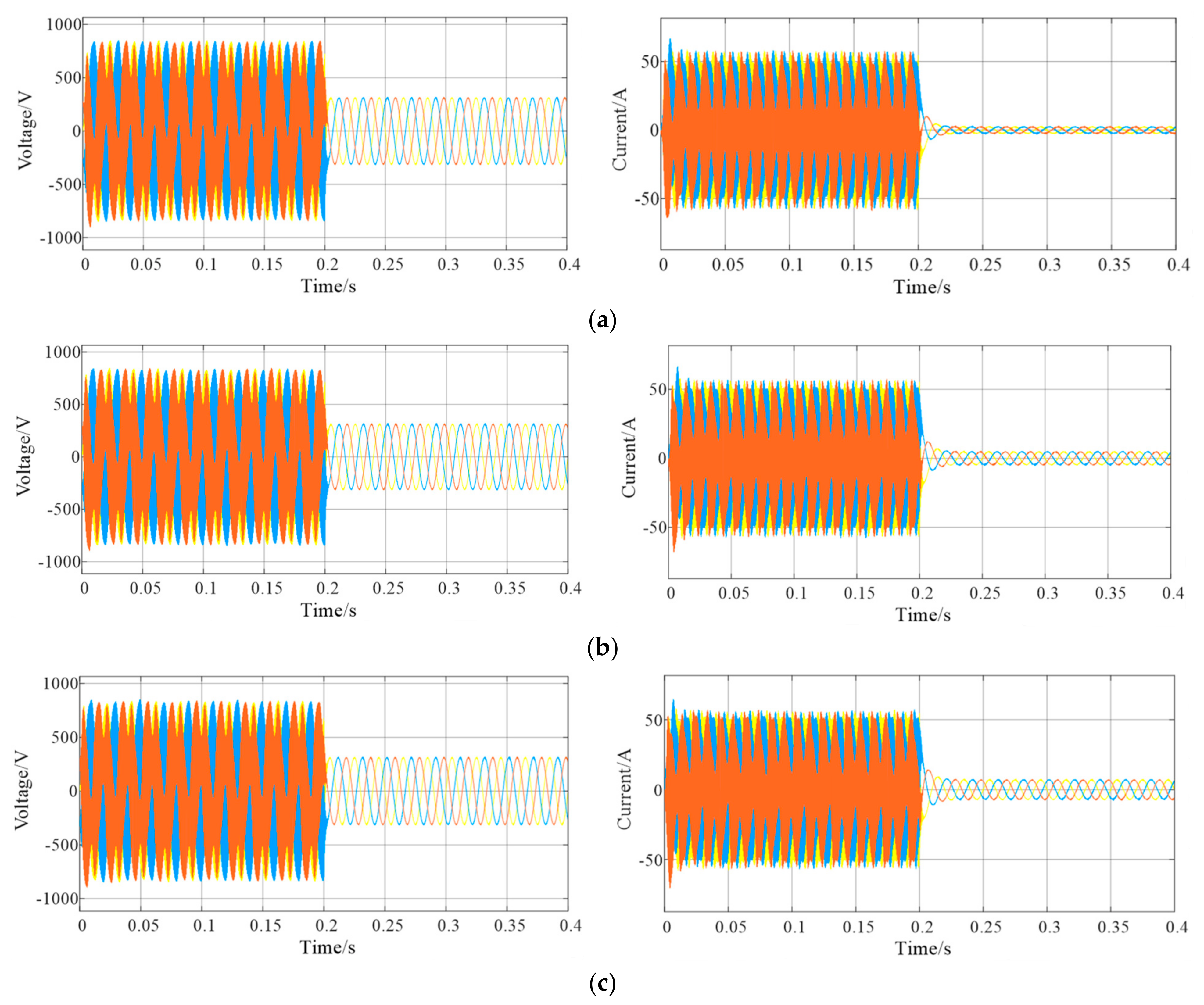
4.2. Simulation Verification of Active Damping Based on Lead Correction and Capacitive Current Feedback
5. Conclusions
- The proposed modular photovoltaic grid-connected system impedance modeling method greatly simplifies the secondary modeling process under active damping control. The mathematical model of sequence impedance derived based on the modular impedance modeling method, taking into account the coupling compensation term, matches well with the measured values obtained from actual simulations, which verifies the correctness of the established model and the effectiveness of the modular impedance modeling method.
- The photovoltaic grid-connected system exhibits an oscillatory frequency band. By analyzing the impedance characteristics of the photovoltaic grid-connected system under various parameters, it is observed that the inner-loop current controller’s proportional coefficient has the most significant impact on the system’s impedance characteristics. Moreover, using an impedance-based stability criterion, the stability of the photovoltaic grid-connected system under different parameters is assessed. This approach unveils the mechanism and characteristics of system harmonic resonance from the perspective of impedance stability.
- An active damping method utilizing lead correction and capacitive current feedback has been devised. This damping loop’s parameters are established using the impedance model of the photovoltaic power generation unit. In the frequency band prone to oscillations, an empirical contrast was drawn between active damping control and vector control. The experimental results reveal that the supplementary active damping control, without compromising its inherent dynamic properties, adeptly mitigates oscillations. This validates the efficacy and viability of the designed active damping control. In contrast to passive damping, active damping control merely introduces an extra control loop within the control segment, rendering it cost-effective and minimally complex. Furthermore, the active damping method presented in this paper enhances the robustness of the photovoltaic grid-connected system when compared to the conventional CCF approach. In the event of system oscillations, the proposed method offers an economical and efficacious remedy. Even in the absence of oscillations, this control can be incorporated as a preventive measure.
- The impedance model of the established photovoltaic grid-connected system is based on the premise of decoupling between positive and negative sequence impedance. However, in recent research, there may still be a coupling relationship between positive and negative sequence impedance. Therefore, there may be some errors between the calculated oscillation frequency and the actual oscillation frequency in the stability analysis of this article.
- Due to time and experimental constraints, the impedance model established in this article only considers the three-phase equilibrium condition. The actual system is more complex and may have three-phase imbalance, harmonic disturbance components, etc. Digital simulation verification is performed on the Matlab/Simulink simulation platform. In subsequent research, a semiphysical simulation platform will be built for physical experiment verification and comparative analysis.
- The active damping designed in this article only includes one feedback quantity, namely the capacitor current feedback. It is possible to further derive the effects of multiple feedback quantities and various feedback forms on the impedance characteristics of grid-connected inverters, and then design higher-performance and more economical active damping methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Haque, A.; Alshareef, A.; Khan, A.I.; Alam, M.M.; Kurukuru, V.S.B.; Irshad, K. Data Description Technique-Based Islanding Classification for Single-Phase Grid-Connected Photovoltaic System. Sensors 2020, 20, 3320. [Google Scholar] [CrossRef] [PubMed]
- Qaiyum, S.; Margala, M.; Kshirsagar, P.R.; Chakrabarti, P.; Irshad, K. Energy Performance Analysis of Photovoltaic Integrated with Microgrid Data Analysis Using Deep Learning Feature Selection and Classification Techniques. Sustainability 2023, 15, 11081. [Google Scholar] [CrossRef]
- Ebrahim, M.A.; Ward, S.A.; El-Gohary, M.F.; Mohamad, M.A.; Eid, M.M.; Alharbi, A.H.; Khafaga, D.S. AI-based voltage and power quality control of high-penetration grid-connected photovoltaic power plant. Front. Energy Res. 2023, 11, 1178521. [Google Scholar] [CrossRef]
- Ali, A.; Irshad, K.; Khan, M.F.; Hossain, M.M.; Al-Duais, I.N.A.; Malik, M.Z. Artificial Intelligence and Bio-Inspired Soft Computing-Based Maximum Power Plant Tracking for a Solar Photovoltaic System under Non-Uniform Solar Irradiance Shading Conditions—A Review. Sustainability 2021, 13, 10575. [Google Scholar] [CrossRef]
- Darwish, M.M.F.; Samy, A.; Abbas, A.A.; Mansour, D.-E.A.; Ward, S.A. Impact of On-grid Photovoltaic System on Thermal Performance of the Oil-filled Transformers. In Proceedings of the 2022 23rd International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 13–15 December 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Manef, B.; Azeddine, H.; Houda, B.A.S.; Mohamed, M. Modeling and Resonance Analysis of Parallel Grid-Connected Inverters with LCL Filters. In Proceedings of the 2018 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Algiers, Algeria, 29–31 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Hu, H.; Shi, Q.; He, Z.; He, J.; Gao, S. Potential Harmonic Resonance Impacts of PV Inverter Filters on Distribution Systems. IEEE Trans. Sustain. Energy 2015, 6, 151–161. [Google Scholar] [CrossRef]
- Xu, W.; Huang, Z.; Cui, Y.; Wang, H. Harmonic Resonance Mode Analysis. IEEE Trans. Power Deliv. 2005, 20, 1182–1190. [Google Scholar] [CrossRef]
- Teng, Y.; Zhang, X.; Fan, C.; Chen, X.; Zhang, R. Resonance Risk in Infirm-interconnected Grid Considering Photovoltaic Devices. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–9 November 2018; pp. 1004–1011. [Google Scholar] [CrossRef]
- Mahalakshmi, R.; Thampatty, K.S. Sub-Synchronous Resonance analysis on DFIG based windfarm. In Proceedings of the TENCON 2016—2016 IEEE Region 10 Conference, Singapore, 22–25 November 2016; pp. 930–935. [Google Scholar] [CrossRef]
- Kang, L.; Shi, L.; Ni, Y.; Yao, L.; Masoud, B. Small signal stability analysis with penetration of grid-connected wind farm of PMSG type. In Proceedings of the 2011 IEEE International Conference on Advanced Power System Automation and Protection (APAP), Beijing, China, 16–20 October 2011; pp. 147–151. [Google Scholar] [CrossRef]
- Yu, J.; He, T.; Wu, J.; Xu, J.; Wang, D.; Yu, Y. Study on Small Disturbance Stability of Photovoltaic Grid-Connected Power Generation System. In Proceedings of the 2023 5th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 23–26 March 2023; pp. 1429–1433. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Chen, Z.; Blaabjerg, F. State-space-based harmonic stability analysis for paralleled grid-connected inverters. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 24–27 October 2016; pp. 7040–7045. [Google Scholar] [CrossRef]
- Sun, J. Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Sun, Z.; Sun, Y.; Lin, J.; Xie, S.; Han, H.; Wu, Z. Impedance Modeling and Stability Analysis of Single-Phase LCL-type Grid-Connected VSC Based on Harmonic Linearization. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 2143–2148. [Google Scholar] [CrossRef]
- Lu, M.; Wang, X.; Blaabjerg, F.; Muyeen, S.; Al-Durra, A.; Leng, S. Grid-voltage-feedforward active damping for grid-connected inverter with LCL filter. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 25–29 February 2016; pp. 1941–1946. [Google Scholar] [CrossRef]
- Guo, W.; Mu, L. Control principles of micro-source inverters used in microgrid. Prot. Control Mod. Power Syst. 2016, 1, 5. [Google Scholar] [CrossRef]
- Yang, H.; Xia, D.; Zhang, X.; Xu, D. Impedance Modeling and Stability Analysis of Three-phase Grid-connected Inverter with LCL Filter in dq-frame. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ‘19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. P.1–P.10. [Google Scholar] [CrossRef]
- Wang, X.; Harnefors, L.; Blaabjerg, F. Unified Impedance Model of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 2017, 33, 1775–1787. [Google Scholar] [CrossRef]
- Ling, P.; Peng, Z.; Chao, G. An Impedance Reshaping Control Strategy to Enhance Adaptability to Grid for Grid-Connected Inverters. In Proceedings of the 2018 China International Conference on Electricity Distribution (CICED), Tianjin, China, 17–19 September 2018; pp. 12–18. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Bao, W.; Zhao, Y. Infinity-Norm of Impedance-Based Stability Criterion for Three-Phase AC Distributed Power Systems with Constant Power Loads. IEEE Trans. Power Electron. 2015, 30, 3030–3043. [Google Scholar] [CrossRef]
- Cespedes, M.; Sun, J. Impedance Modeling and Analysis of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 2014, 29, 1254–1261. [Google Scholar] [CrossRef]
- Pugliese, S.; Kwon, Y.; Liserre, M. Positive-Negative Sequence SRF-PLL Model for Accurate Stability Analysis in Grid-Tied Converters. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 3593–3600. [Google Scholar] [CrossRef]
- Li, S.; Lin, H. A Capacitor-Current-Feedback Positive Active Damping Control Strategy for LCL-Type Grid-Connected Inverter to Achieve High Robustness. IEEE Trans. Power Electron. 2022, 37, 6462–6474. [Google Scholar] [CrossRef]




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| DC side voltage Udc/V | 800 | line-side inductance L2/mH | 0.2 |
| effective value of grid line voltage/V | 380 | filter capacitor Cf/uF | 6.8 |
| output Active Power P/kW | 10 | damping resistor Rd/Ω | 1.7 |
| output reactive power Q/kVar | 0 | phase-locked loop kpPLL_inv | 1.72 |
| fundamental frequency f1/Hz | 50 | phase-locked loop kiPLL_inv | 492.2 |
| switching frequency fsw/kHz | 35 | Internal loop current controller kpinv | 10 |
| inverter side inductance L1/mH | 1.5 | Internal loop current controller kiinv | 1600 |
| Grid-Side Inductance | THD of Vector Control | THD of Damping Control | Oscillation Frequency |
|---|---|---|---|
| 0.5 mH | 15.4% | 4.8% | 3835 Hz 3935 Hz |
| 1 mH | 54.3% | 1.5% | 2283 Hz 2383 Hz |
| 6 mH | 73.6% | 4.7% | 1526 Hz 1626 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, T.; Huang, G.; Ouyang, X.; Zhang, W.; Wang, Y.; Ye, X.; Wang, Y.; Gao, S. Analysis and Suppression of Harmonic Resonance in Photovoltaic Grid-Connected Systems. Energies 2024, 17, 1218. https://doi.org/10.3390/en17051218
Zhu T, Huang G, Ouyang X, Zhang W, Wang Y, Ye X, Wang Y, Gao S. Analysis and Suppression of Harmonic Resonance in Photovoltaic Grid-Connected Systems. Energies. 2024; 17(5):1218. https://doi.org/10.3390/en17051218
Chicago/Turabian StyleZhu, Tong, Gechao Huang, Xuetong Ouyang, Weilin Zhang, Yanfeng Wang, Xi Ye, Yuhong Wang, and Shilin Gao. 2024. "Analysis and Suppression of Harmonic Resonance in Photovoltaic Grid-Connected Systems" Energies 17, no. 5: 1218. https://doi.org/10.3390/en17051218
APA StyleZhu, T., Huang, G., Ouyang, X., Zhang, W., Wang, Y., Ye, X., Wang, Y., & Gao, S. (2024). Analysis and Suppression of Harmonic Resonance in Photovoltaic Grid-Connected Systems. Energies, 17(5), 1218. https://doi.org/10.3390/en17051218






