Abstract
The transient characteristics of pressure in the condenser under fault conditions have a crucial impact on the safe operation of the entire nuclear power plant. In order to ascertain whether the condenser pressure of a HPR1000 nuclear power unit meets the requirements of the steam generator, this paper establishes a mathematical model of the condenser, along with the connected steam turbine bypass steam system and circulating water system, based on Apros. The accuracy of the simulation model is verified by comparing the coasting curve of the circulating water pump with the flow change curve under the pump-tripping condition in Apros. Under the initial CCR condition and the half-side operating condition of the condenser, simulation analyses were conducted for two transient sequences involving the loss of normal external power and the simultaneous tripping of two circulating water pumps. The corresponding changes of pressure in the condenser under the transient sequence were obtained. The study reveals that, under different initial conditions and transient sequences, the condenser pressure of the unit can meet the requirements of a 12 s steam discharge to the condenser before the internal pressure of the condenser reaches the “unavailable” set value when the turbine bypass system is under the fault condition. The research findings of this paper can provide reference data for the design, commissioning, and operation of subsequent HPR1000 nuclear power plants.
1. Introduction
In nuclear power plants, the condenser is the cold source of the secondary circuit system, and its equipment status has a great impact on the safe and stable operation of the entire nuclear power plant. Due to the complex working environment and high-intensity operating conditions, the condenser may malfunction and be damaged. When the condenser malfunctions, it may result in a decrease in the power output of the steam turbine or even lead to the halt and shutdown of the reactor. Therefore, studying the transient pressure characteristics of the condenser under different operating conditions is of great significance for the safe operation of units.
In the thermal design of condensers, empirical formulas are usually used for prediction. Komandur S. Sunder-Ra [1] predicted the performance under various operating conditions using the overall heat transfer coefficient formula of the condenser and proposed corresponding useful suggestions. In order to calculate the heat transfer more accurately, some researchers have adopted new methods. Patankar et al. [2] introduced the volumetric porosity model to calculate the heat transfer of the condenser, and they used the multi-node model to simplify the calculation of the shell-and-tube heat exchanger. In this model, they consider the factors, such as the tube bundle structure and baffles, as the resistance term and incorporate them into the condensation convection heat transfer model. Carlucci et al. [3] simulated the internal flow and heat transfer of the condenser, improved the existing model, and proposed measures to improve the vacuum condition of the condenser and minimize the vibration of the tube bundle. Botsch et al. [4] focused on the study of the dynamic process of shell-and-tube condensers and discussed the changes in their operation. Seungmin Oh et al. [5] conducted an experimental study on the heat transfer process inside a vertical tube bundle surface condenser and its characteristics under different operating conditions.
Wang et al. [6] developed a set of 3D numerical calculation programs for simulating the internal flow and heat transfer process of a condenser by using the porous medium assumption. Through extensive experimental verification, it has been confirmed that the program has high computational accuracy. Hou et al. [7,8] committed to optimizing the cold end performance of dual back pressure units in nuclear power plants. They constructed a calculation model for a dual back pressure unit that takes into account the pressure difference between high- and low-pressure steam chambers and analyzed in depth the impact of pressure on the small output increase of the unit. Guo [9] used the Adams multi-step simulation method to model and simulate the condenser of a nuclear power plant. In their research, they evaluated the impact of the temperature, flow rate of the circulating cooling water, and step changes in the steam turbine exhaust volume on the dynamic characteristics of the condenser operating parameters, providing a valuable reference for nuclear power condensers in variable operating conditions.
Apros is an add-on product of the Apros® (Advanced Process Simulation Environment) nuclear software Version 6.03 cooperatively developed by VTT (Technical Research Centre of Finland) and Fortum (Fortum Engineering Ltd. of Finland). It is used for the design and optimization of process systems and automation systems and the development of operating systems and training systems, as well as comprehensive dynamic analysis and accident analysis.
Silde et al. [10] provided a detailed validation of selected validation cases and demonstrated that Apros can be used for analyses of containment thermal-hydraulic behavior, including related aspects of engineering safety systems in various containment geometries. Xian et al. [11] developed the OTSG numerical model of ACP100 (Advance China Plant 100 MW, Modular Small Reactor developped in China) with Apros and gave the key parameters that influenced the OTSG’s operation during the whole startup process. Starkloff et al. [12] established the model of a large coal-fired power plant with minimal boundary conditions, with maximum relative errors of less than 5% regarding the mass flow rate, temperature, and pressure. Marton et al. [13] found that, although, in certain aspects, the Apros model showed acceptable behavior, on the other hand, considering turbine pressures and feedwater temperatures, the AUXB (Auxiliary boiler) power was not sufficient to maintain the desirable conditions during dwell, as postulated by Ebsilon Heat Balance. Al-Maliki et al. [14] made several improvements in the referenced parabolic trough power plant (PTPP) model (Andasol II) by Apros software. The findings revealed that the levelized energy cost of the optimized PTPP with storage energy was about 10.5% lower than that of the referenced PTPP.
Although there have been a large number of research achievements on condensers, direct research literature on the transient changes of condenser pressure when suddenly losing cooling water is relatively scarce. Patrick [15] conducted an in-depth study on the variation of the cooling water flow rate in a condenser after losing all the cooling water. Jiang and Ding [16] studied the pressure changes of a condenser under design conditions and summer conditions when all cooling water was lost. Wang and Zhou [17] constructed a mathematical model for transient heat transfer and pressure in a circulating cooling water system and condenser. Through numerical investigation, it was observed that, during a pump shutdown caused by a power outage, the cooling water flow rate exhibited a rapid decrease, reaching fluctuations close to zero, accompanied by the occurrence of a countercurrent phenomenon. The heat transfer coefficient of the condenser underwent three distinct stages: a sharp decrease, followed by an initial increase, subsequent decrease, and finally, a phase of relative constancy.
The HPR1000 nuclear power unit is a third-generation nuclear power technology independently developed and researched by China. It adopts the concept of combining active and passive safety systems in its design, and China has fully independent intellectual property rights. Cheng et al. [18], Sun et al. [19], and Lu et al. [20] researched the emergency passive residual heat removal system and steam generator secondary pH under the SGTR condition of HPR1000.
According to the results of the secondary circuit overpressure analysis, the HPR1000 series requires that the turbine bypass steam system can continue to discharge steam to the condenser for more than 12 s before the internal pressure reaches the “unavailable” set point under fault conditions. The existing literature has not yet studied the impact of steam discharge on the dynamic characteristics of the condenser pressure under condenser failure conditions. In order to determine whether the newly developed steam turbine generator unit equipped with the condenser can meet the requirements of steam discharge on the secondary side of the steam generator, this paper establishes a simulation model of the condenser in a certain nuclear power plant secondary circuit based on Apros software and conducts a simulation analysis on the pressure change law of the condenser under various transient conditions. The research in this article can provide reference data and basis documents for the design, commissioning, and operation of nuclear power plant units.
2. Numerical Model
2.1. Model Simplification Hypothesis
Based on the specific structure of the condenser and the characteristics of the problem to be studied, the following simplified assumptions were made:
- (1)
- Due to the low operating pressure of the condenser, the air inside the condenser is considered an ideal gas;
- (2)
- Besides the water in the hot well, the working fluid in the steam side of the condenser is in a saturated state;
- (3)
- The temperature of the steam and air mixture in the steam side of the condenser is equal to the saturation temperature at the corresponding pressure;
- (4)
- The velocity and mass flow of the condenser circulating cooling water are evenly distributed on the tube side;
- (5)
- The water temperature change rate of the circulating cooling water in the condenser is uniform;
- (6)
- The change in metal mass, specific heat capacity, and temperature of the condenser heat exchange tube are uniform;
- (7)
- The heat dissipation of the condenser is 0, and the amount of steam extracted from the vacuum equipment is 0.
2.2. Establishment of the Mathematical Model [21]
According to the structural characteristics of the condenser, the condenser model is divided into the shell side and the tube side when establishing a mathematical model. Among them, the shell side includes the entire steam/gas space and hot well water inside the condenser. The tube side includes the condenser cooling water heat exchange tube and its internal cooling water.
2.2.1. Condenser Shell-Side Mathematical Model
According to the different physical properties of the working fluid inside the condenser, the shell side of the condenser is divided into three areas: steam area, air area, and hot well area. In order to ensure that the model has a wide range of adaptability, comprehensive consideration was given to the mass flow rates of the steam, air, and condensate entering and exiting the condenser, as well as the possible physical changes that may occur on the shell side of the condenser.
- (1)
- Mathematical model of the steam zone
(1) Steam mass conservation equation
where
- is the steam storage capacity of the condenser, kg;
- is the exhaust steam mass of the steam turbine, kg/s;
- is the flash water added into the condenser, kg/s;
- is the dynamic evaporation amount of the hot well water surface, kg/s;
- is the dynamic condensation amount of the hot well water surface, kg/s;
- is the main amount of steam to condensate, kg/s.
(2) Calculation of the steam partial pressure
In the formula,
- is the steam partial pressure, MPa;
- is the amount of steam in the condenser. The model uses the total volume of the shell side minus the space occupied by the hot well water for the calculation, kg;
- is the gas constant of the steam, 461.5 kJ/(kg·K);
- is the average temperature of the steam, °C;
- is the volume of steam in the condenser, m3.
(3) Calculation of the average steam temperature
From the energy conservation equation, it can be written as
where
- is the enthalpy of steam storage in the condenser, kJ/kg;
- is the exhaust steam enthalpy of the steam turbine, kJ/kg;
- is the enthalpy of saturated water in the condenser, kJ/kg;
- is the enthalpy of saturated steam in the condenser, kJ/kg.
According to Equation (3) and the physical properties of water vapor, the average temperature of steam inside the condenser can be calculated.
- (2)
- Mathematical model of the air zone
(1) Calculation of the air partial pressure
In the formula,
- is the air partial pressure, MPa;
- is the amount of air in the condenser, kg;
- is the gas constant of air, 287.05 J/(kg·K);
- is the average temperature of the air, its value equal to the temperature of the steam in this paper, °C;
- is the volume of gas in the condenser, m3.
(2) Calculation of the air inventory in the condenser
The amount of air in the condenser can be calculated by the mass conservation equation.
In the formula,
- is the normal amount of air leaking into the condenser, kg/s;
- is the amount of air entering the condenser for the vacuum damage valve, kg/s;
- is the amount of air that the shaft seal leaks into the condenser, kg/s;
- is the mixture of steam and gas pumped out of a vacuum pump, kg/s;
- is the mass fraction of air in the condenser.
In the formula,
- is the total amount of air, kg/s;
- is the amount of steam entering the condenser, kg/s.
(3) Calculation of the absolute pressure of the condenser
After calculating the partial pressure of the steam and the partial pressure of the air , the absolute pressure of the condenser is calculated:
- (3)
- Mathematical model of the hot water well area
(1) Calculation of the hot water well quality
According to the mass conservation equation,
In the formula,
- is the hot water well quality, kg;
- is the drain water amount of the low-pressure heater, kg/s;
- is the drain water amount of the high-pressure heater, kg/s;
- is the leakage of the cooling water tube; it was taken as 0, kg/s;
- is the water output of the condenser through the condensate pump, kg/s.
(2) Calculation of the water level of the hot well
According to the structural characteristics, the hot well is regarded as a column with equal sections, and the calculation formula of the water level of the hot well is as follows:
In the formula,
- is the cross-sectional area of the condenser hot well, m2.
(3) Calculation of water enthalpy of the hot well
In the formula,
- is the heat dissipation from the hot well to the environment, kW;
- is the heat dissipation coefficient of the hot well to the environment;
- is the enthalpy of the saturated steam storage in the condenser, kJ/kg;
- is the enthalpy of the water output of the condenser through the condensate pump, kJ/kg.
By calculating the partial pressure of the steam and the enthalpy of the hot well water, the temperature of the hot well water can be calculated according to the properties.
2.2.2. Condenser Tube Side Mathematical Model
The condenser tube side includes the cooling water tube bundle and the cooling water inside the tube bundle. Because the submerged water level of the condenser is much higher than the normal water level and the idle time is very short, only the case that the hot well water is not submerged in the cooling tube bundle is considered when the model is established.
- (1)
- Calculation of the metal wall temperature of the cooling water tube
According to the heat transfer process of the condenser, it is divided into three links: steam condensate to the water, heat conduction of the cooling water tube, and convective heat absorption of the cooling water. According to the energy balance equation, the temperature change rate is
In the formula,
- is the steam condensation heat, kW;
- is the heat of the cooling water absorption, kW;
- is the cooling water tube metal quality, kg;
- is the specific volume of the cooling water tube metal, kJ/(kg·K).
- (2)
- Calculation of the cooling water outlet temperature
In the formula,
- is the heat of the cooling water absorption, kW;
- is the cooling water flow rate, kg/s;
- is the amount of water stored in the cooling water tube, kg;
- is the specific volume of the cooling water, kJ/(kg·K);
- is the temperature of the outlet cooling water, °C;
- is the temperature of the inlet cooling water, °C.
2.3. The Scope and Data of the Mathematical Model
The mathematical model of the condenser established in this paper is shown in Figure 1, which mainly includes the turbine bypass steam system, the condenser system, and the circulating water system. The main data of the condenser used are shown in Table 1.
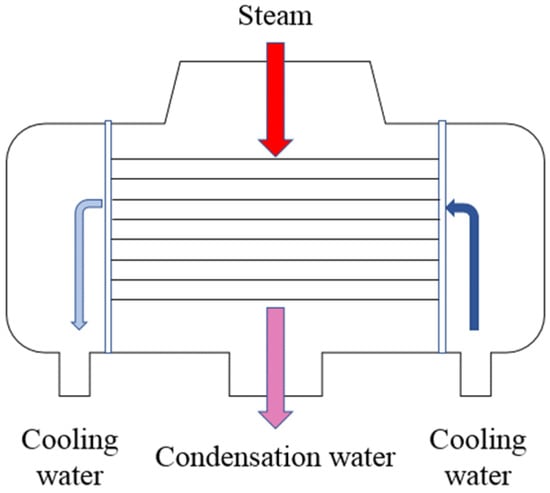
Figure 1.
Mathematical model diagram.

Table 1.
Main data of the condenser.
3. Verification of the Numerical Model
To validate the accuracy of the mathematical calculation model, the simulated circulating water flow response under the CCR (critical condition rate) condition and condenser half-side operation condition is compared with the circulating water pump idle curve provided by the manufacturer, and the specific data are shown in Figure 2. The black curve in the diagram is the condenser outlet flow change process curve provided by the circulating water pump manufacturer under the 100-year low tide level and the design flow condition, and the red curve is the circulating water flow response curve output by the corresponding working condition simulation calculation model. Through the comparison between the two, it can be seen that the flow change data of the circulating water pump are basically consistent, indicating that the validity of the established model is verified and can be used to analyze the pressure change of the condenser under fault conditions.
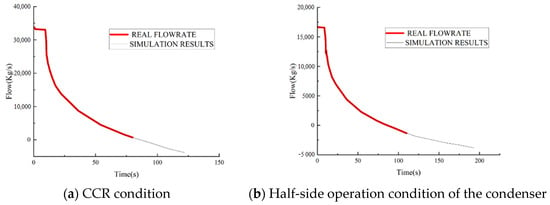
Figure 2.
Flow response curve of the circulating water pump.
4. Calculated Results and Analysis
4.1. Initial Conditions and Transient Sequence
In this paper, the simulation calculation under two initial conditions is considered, which are:
Condition 1: The unit is operated under a rated condition (conservatively considered, corresponding to the heat balance diagram of the CCR condition). The inlet and outlet temperatures of the cooling water are 35 °C and 42.138 °C, respectively, with the initial back pressure set at 11.8 kPa.
Condition 2: The unit is running on the half side of the condenser (corresponding to the heat balance diagram of a single condenser condition), the inlet and outlet temperatures of the cooling water are 26.5 °C and 36.82 °C, and the initial back pressure is 8.2 kPa.
Under the above conditions, the two transient sequences shown in Table 2 and Table 3 are considered, respectively. Transient sequence 1: the main transformer differential protection operates and loses normal off-site power; transient sequence 2: two circulating water pumps trip at the same time.

Table 2.
Transient sequence: unit state change sequence.

Table 3.
Transient sequence two: unit state change sequence.
Under the above initial states and transient sequences, except for the turbine bypass system continuing to discharge 85% of the main steam flow rate to the condenser, the turbine and generator, main feedwater pump, condensate pump, etc. of the unit have all been shut down.
4.2. Calculation of the Boundary Conditions and Assumptions
In order to ensure the credibility and conservatism of the simulation analysis and calculation, the calculation assumptions of this paper are as follows:
- (1)
- In the calculation process, all kinds of drains entering the condenser are considered to maintain the full power unchanged;
- (2)
- The remaining steam of the low pressure cylinder of the steam turbine is all discharged into the condenser;
- (3)
- The circulating water pump starts to stop at 0 s, considering the change of the circulating water pumps idle;
- (4)
- After the turbine tripping, the condensate pump is shut down without considering the idleness of the condensate pump, and water flow is instantaneously at 0;
- (5)
- After the turbine tripping, the vacuum pump is shut down without considering idle running;
- (6)
- The model needs to consider the influence of the steam side volume of the condenser on the vacuum;
- (7)
- Without considering the heat dissipation of the condenser shell due to the temperature rise, the metal heat storage inside the condenser should be considered;
- (8)
- According to the steam turbine bypass steam system, two sets of valves open at the same time calculation;
- (9)
- When the steam turbine bypass valve opens, the bypass steam flow reaches the maximum flow of the valve and maintains this until the end of the simulation;
- (10)
- According to the calculation assumptions (8) and (9), the pressure changes of the two condensers are consistent during the simulation process, and the model is only simulated for one.
4.3. Analysis of the Simulation Results under Different Transient Conditions
Figure 3 is the condenser pressure response curve after transient sequence 1 and transient sequence 2 under the initial state of working condition 1.
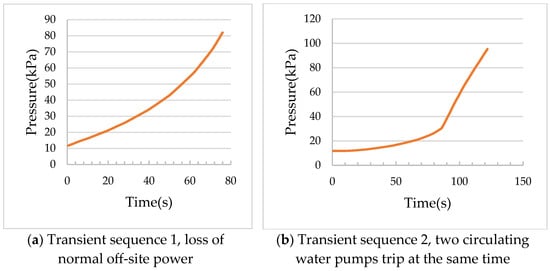
Figure 3.
Condenser pressure response curve transient under the initial state of working condition 1.
From the diagram, it can be seen that, under the initial state of the unit back pressure of 11.8 kPa, after experiencing transient sequence 1 (Figure 3a), the turbine generator set and the circulating water pumps, the main feed water pumps, and the condensate pumps tripped, and the condenser pressure increased rapidly. The time for the pressure from 11.8 kPa to 30 kPa is 34 s, and the time for the pressure from 11.8 kPa to 60 kPa is 63.9 s; the interval between the condenser pressure rising from 30 kPa to 60 kPa is 29.9 s—that is, the time from the condenser fault to the unusable signal triggering of the condenser is 29.9 s. After experiencing transient sequence 2 (Figure 3b), when two circulating water pumps trip at the same time, the turbine generator continues to operate at a rated power, and the main feed water pumps and condensate pumps do not trip, the vacuum deterioration rate of the condenser is relatively lower, mainly because the turbine generator set has not been shut down at this time, the main steam works through the turbine generator set, and the heat load of the condenser rises slowly. With the tripping of the turbine generator set, the pressure rise rate of the condenser is further accelerated. When the circulating water flows backward and the reverse flow gradually increases, the pressure rise rate of the condenser slows down. The time for the condenser pressure from 11.8 kPa to 30 kPa is 85.4 s, while the time for the pressure from 11.8 kPa to 60 kPa is 100.9 s, and the time interval from 30 kPa to 60 kPa is 15.5 s.
It can be seen that, under the back pressure of 8.2kPa and the initial state of the half side of the condenser, due to the shutdown of the circulating water pumps, the circulating water flow is reduced, and the bypass steam is discharged into the condenser. The pressure of the condenser rises rapidly first, and then, when the circulating water flows backward and the reverse flow increases gradually, the pressure rise rate slows down. The time for the pressure from 8.2 kPa to 30 kPa is 43.7 s, and the time for the pressure from 8.2 kPa to 60 kPa is 70.8 s. The interval between the condenser pressure rising from 30 kPa to 60 kPa is 27.1 s. After transient sequence 2 (Figure 3b), the condenser pressure rise rate is low before the tripping of the turbine generator set. When the condenser pressure reaches the shutdown value (condenser fault, 30 kPa), the pressure increases rapidly as the turbine bypass steam enters the condenser after the tripping of the turbine generator set. The time for the condenser pressure from 8.2 kPa to 30 kPa is 157.6 s, while the time for the pressure from 8.2 kPa to 60 kPa is 184.9 s, and the interval from 30 kPa to 60 kPa is 27.3 s.
Figure 4 is the condenser pressure response curve after transient sequence 1 and transient sequence 2 under the initial state of condition 2.
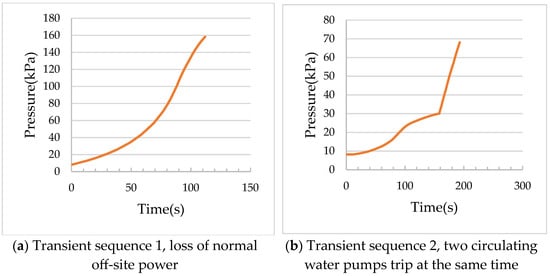
Figure 4.
Condenser pressure response curve transient under the initial state of working condition 2.
Under the two working conditions, a comparison of the pressure change data in the condenser after the unit undergoes different transient sequences is shown in Table 4.

Table 4.
Comparison of the pressure change data in the condenser after different transient sequences.
By comparison, when the transient sequence is the same, the time for the condenser pressure from 11.8 kPa to reach 30 kPa and 60 kPa in the initial state of condition 1 is shorter, and the time to reach the “unavailable” time is faster, mainly because the turbine exhaust steam flow rate is smaller (about 66%) and the pressure is lower in the initial state of condition 2. When the initial state is the same, the effect of losing normal off-site electricity on the condenser pressure is greater than that of two circulating water pumps tripping at the same time, and the time for the condenser pressure from initial value to 30 kPa and 60 kPa is shorter. Under the initial state of the above different working conditions, whether it is the loss of normal off-site electricity or the simultaneous tripping of two circulating water pumps, the time from the condenser failure (30 kPa) to the condenser unavailability (60 kPa) is greater than 12 s. Considering the establishment of the mathematical model and the determination of the boundary conditions, conservative assumptions have been made. It is reasonable to believe that the condenser of this project can meet the requirement that the turbine bypass steam system can continue to discharge steam to the condenser for 12 s before the internal pressure reaches the “unavailability” set value under the fault condition.
5. Conclusions
Based on Apros software, this study establishes the mathematical model of the condenser and the connected steam turbine bypass steam system and circulating water system of a HPR1000 nuclear power unit. By comparing the circulating water pump idle curve with the flow change curve under the pump jumping condition provided by the pump manufacturer, the accuracy of the mathematical model and the boundary condition hypothesis is verified. Aiming at the two initial states of the CCR condition and condenser half-side operation condition, the simulation analysis of two transient sequences of losing normal off-site electricity and two circulating water pumps tripping at the same time is carried out, and the variation law of the internal pressure of the condenser under the corresponding transient sequence is obtained. The analysis results show that, under the above different initial states and transient sequences, the condenser can meet the requirements of the condenser fault condition, and the steam turbine bypass steam system can still continue to discharge steam to the condenser for 12 s before its internal pressure reaches the “unavailable” set value. The research results of this paper provide design input conditions for the safety analysis of the unit and furnish valuable reference data for the design, commissioning, and operation of the subsequent HPR1000 nuclear power unit.
Author Contributions
Data curation, Q.Z.; Writing—original draft, J.Y.; Writing—review & editing, C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to company secrets.
Conflicts of Interest
Author Chuntian Lu and Jianjun Yang was employed by the company Hebei Branch, China Nuclear Power Engineering Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Sunder Raj, K.S. Deviations in predicted condenser performance for power plants using HEI correction factors: A case study. Eng. Gas Turbines Power 2008, 130, 023003. [Google Scholar] [CrossRef]
- Patankar, G.; Weibel, J.A.; Garimella, S.V. Patterning the condenser-side wick in ultra-thin vapor chamber heat spreaders to improve skin temperature uniformity of mobile devices. Int. J. Heat Mass Transf. 2016, 101, 927–936. [Google Scholar] [CrossRef]
- Ormiston, S.J.; Raithby, G.D.; Carlucci, L.N. Numerical modeling of power station steam condensers-Part 1: Convergence behavior of a finite-volume model. Numer. Heat Transf. 1995, 27, 81–102. [Google Scholar] [CrossRef]
- Botsch, T.W.; Stephan, K.; Alcock, J.L.; Webb, D.R. Modelling and simulation of the dynamic behavior of a shell-and-tube condenser. Int. J. Heat Mass Transf. 1997, 40, 4137–4149. [Google Scholar] [CrossRef]
- Oh, S.; Revankar, S.T. Experimental and theoretical investigation of film condensation with non-condensable gas. Int. J. Heat Mass Transf. 2006, 49, 2523–2534. [Google Scholar] [CrossRef]
- Wang, G.; Mao, X.; Hu, G.; Tian, Z.P. Development of A quasi-three-dimensional computer program for fluid flow fields and heat transfer performance of power plant condensers: PPOC3.0. Power Eng. 2001, 21, 1450–1454. [Google Scholar]
- Hou, P.; Tao, Z.; Hu, Y.; Qiao, L.; Li, Z.; Su, X. The turbine cold-end optimization of conventional island of inland AP1000 nuclear power plant. Turbine Technol. 2010, 52, 424–426. [Google Scholar]
- Hou, P.; Yan, H. A study of the turbine cold-end optimization method of conventional island double back pressure unit of inland nuclear power plant. J. Qingdao Univ. (Eng. Technol. Ed.) 2012, 27, 88–91. [Google Scholar]
- Guo, H. Simulation study on dynamic characteristics of condenser operating parameters of nuclear power steam turbine. China Meas. Test 2019, 45, 55–60. [Google Scholar]
- Silde, A.; Ylijoki, J.; Ahtinen, E. Containment model library of the Apros process simulation software: An overview of development and validation work. Prog. Nucl. Energy 2019, 116, 28–45. [Google Scholar] [CrossRef]
- Xian, L.; Yan, J.; Zhou, K.; Chen, G.; Dang, G.; Song, D. Analysis of startup process of small modular reactor with OTSGs. Nucl. Eng. Des. 2023, 415, 112669. [Google Scholar]
- Starkloff, R.; Alobaid, F.; Karner, K.; Epple, B.; Schmitz, M.; Boehm, F. Development and validation of a dynamic simulation model for a large coal-fired power plant. Appl. Therm. Eng. 2015, 91, 496–506. [Google Scholar] [CrossRef]
- Szogradi, M.; Norrman, S.; Bubelis, E. Dynamic modelling of the helium-cooled DEMO fusion power plant with an auxiliary boiler in Apros. Fusion Eng. Des. 2020, 160, 111970. [Google Scholar] [CrossRef]
- Al-Maliki WA, K.; Hadi, A.S.; Al-Khafaji, H.M.; Alobaid, F.; Epple, B. Novel feedwater preheating system for parabolic trough solar power plant. Energy Rep. 2022, 8, 10665–10687. [Google Scholar] [CrossRef]
- Patricks, R.P. Pressure Transient Analysis Circulating Cooling Water Pumps (CRF), LOT 24A; Weir Pumps Ltd.: Scotland, UK, 2006. [Google Scholar]
- Jiang, C.; Ding, J. Nuclear power station condenser unavailable calculation and analysis. Nucl. Power Eng. 2009, 30, 39–44. [Google Scholar]
- Wang, X.; Zhou, Z.; Song, Z.; Lu, Q.; Li, J. Transient characteristics of pressure variation in condensers of nuclear power station. J. Xi’an Jiaotong Univ. 2015, 49, 6–10. [Google Scholar]
- Cheng, H.; Wu, Y.; Song, D. HPR1000—Advanced pressurised water reactor with active and passive safety. Nucl. Future J. Inst. Nucl. Eng. Br. Nucl. Energy Soc. 2016, 12, 38–43. [Google Scholar]
- Sun, D.C.; Li, Y.; Xi, Z.; Zan, Y.F.; Li, P.Z.; Zhuo, W.B. Experimental evaluation of safety performance of emergency passive residual heat removal system in HPR1000. Nucl. Eng. Des. 2017, 318, 54–60. [Google Scholar] [CrossRef]
- Lu, C.; Le, Z.; Shen, Y.; Cai, W.; Yang, J.; Ji, W.; Zhang, Y. The prediction of steam generator secondary pH under SGTR condition of HPR1000. Prog. Nucl. Engergy 2021, 134, 103673. [Google Scholar] [CrossRef]
- Zhang, Z. Condenser in Large Scale Power Plant; China Machine Press: Beijing, China, 1993. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).