Residual Life Prediction of Low-Voltage Circuit Breaker Thermal Trip Based on the Wiener Process
Abstract
1. Introduction
2. Accelerated Degradation Test for Thermal Trip
2.1. Acceleration Modelling and Determination of Acceleration Stresses
2.2. Determination of Test Parameters
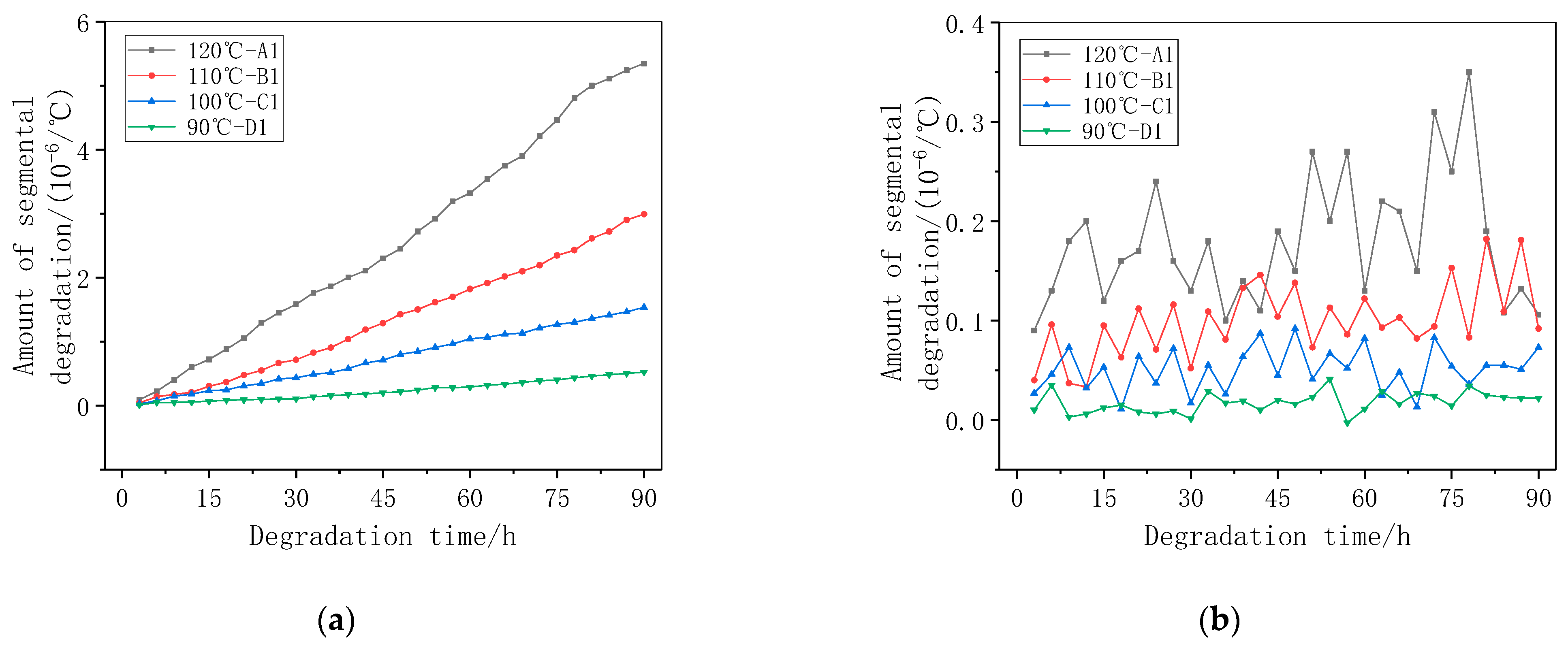
2.3. Accelerated Degradation Data Analysis
3. Residual Life Modelling Based on the Wiener Process
3.1. Wiener Degradation Model
3.2. Parameter Estimation
3.3. Remaining Life Probability Density Function and Reliability Function
4. Residual Life Prediction of Thermal Trips Based on the Wiener Process
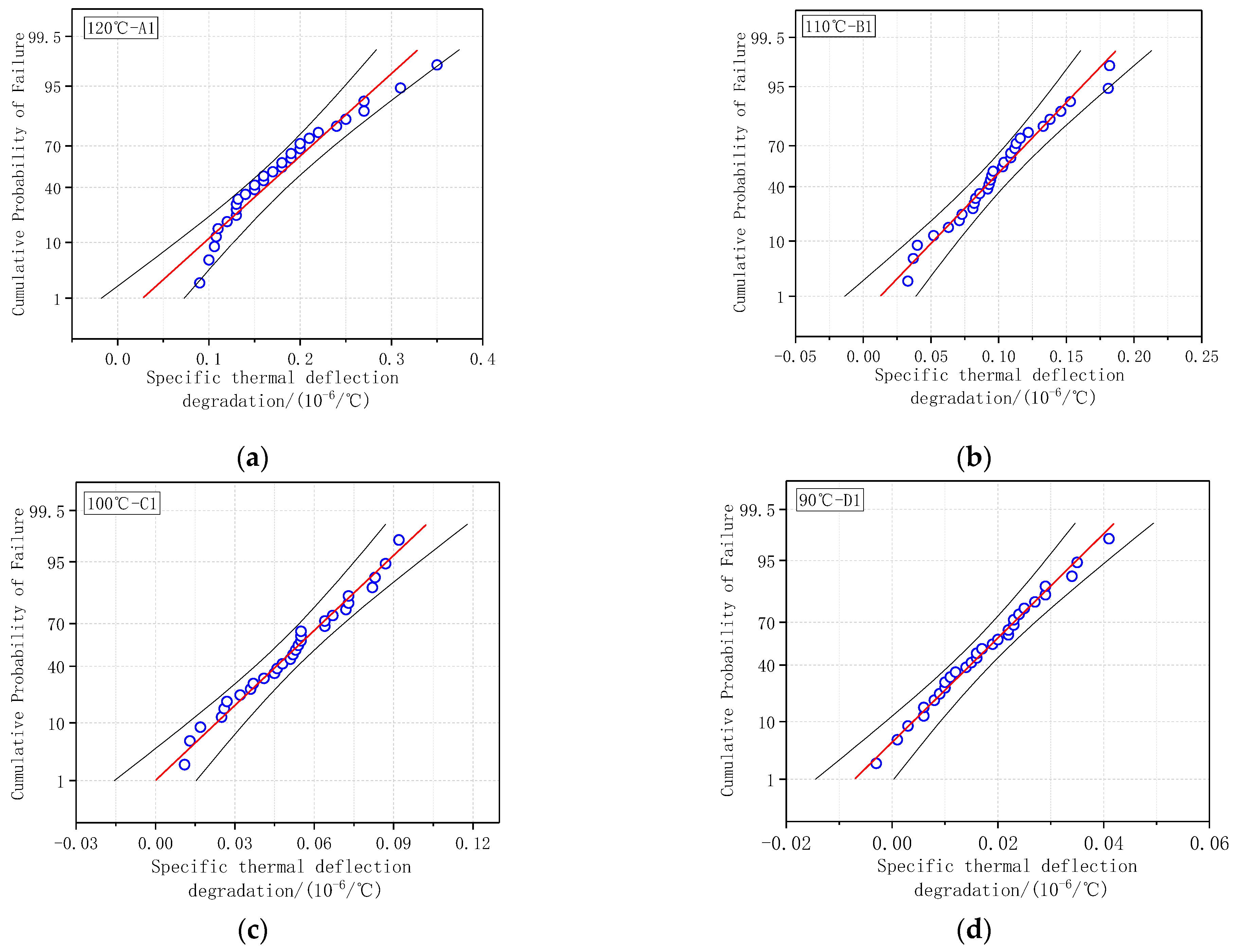
4.1. Test for Normal Distribution of specific thermal deflection Segmental Degradation Value
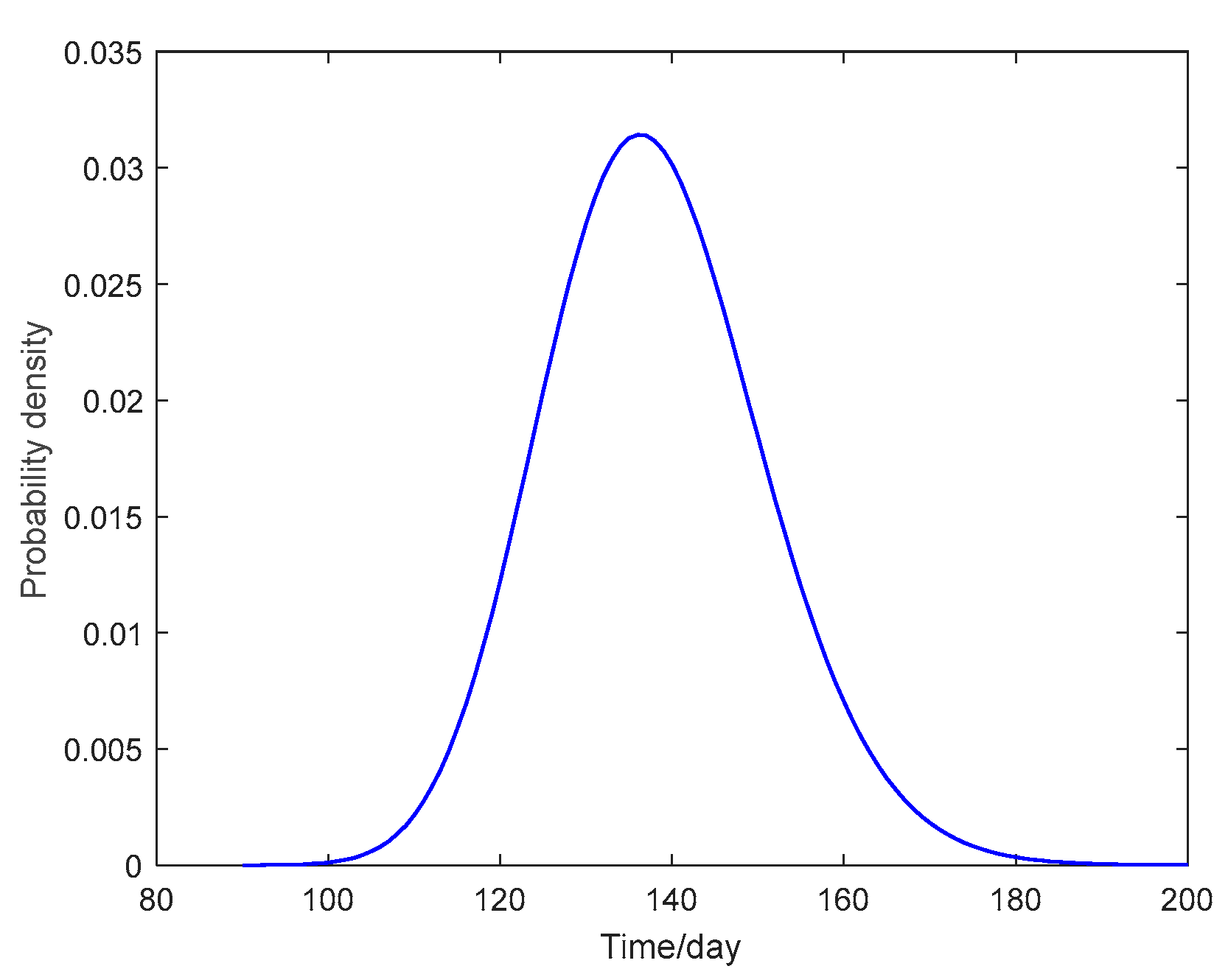
4.2. Residual Life Prediction of Thermal Trip Based on the Wiener Process
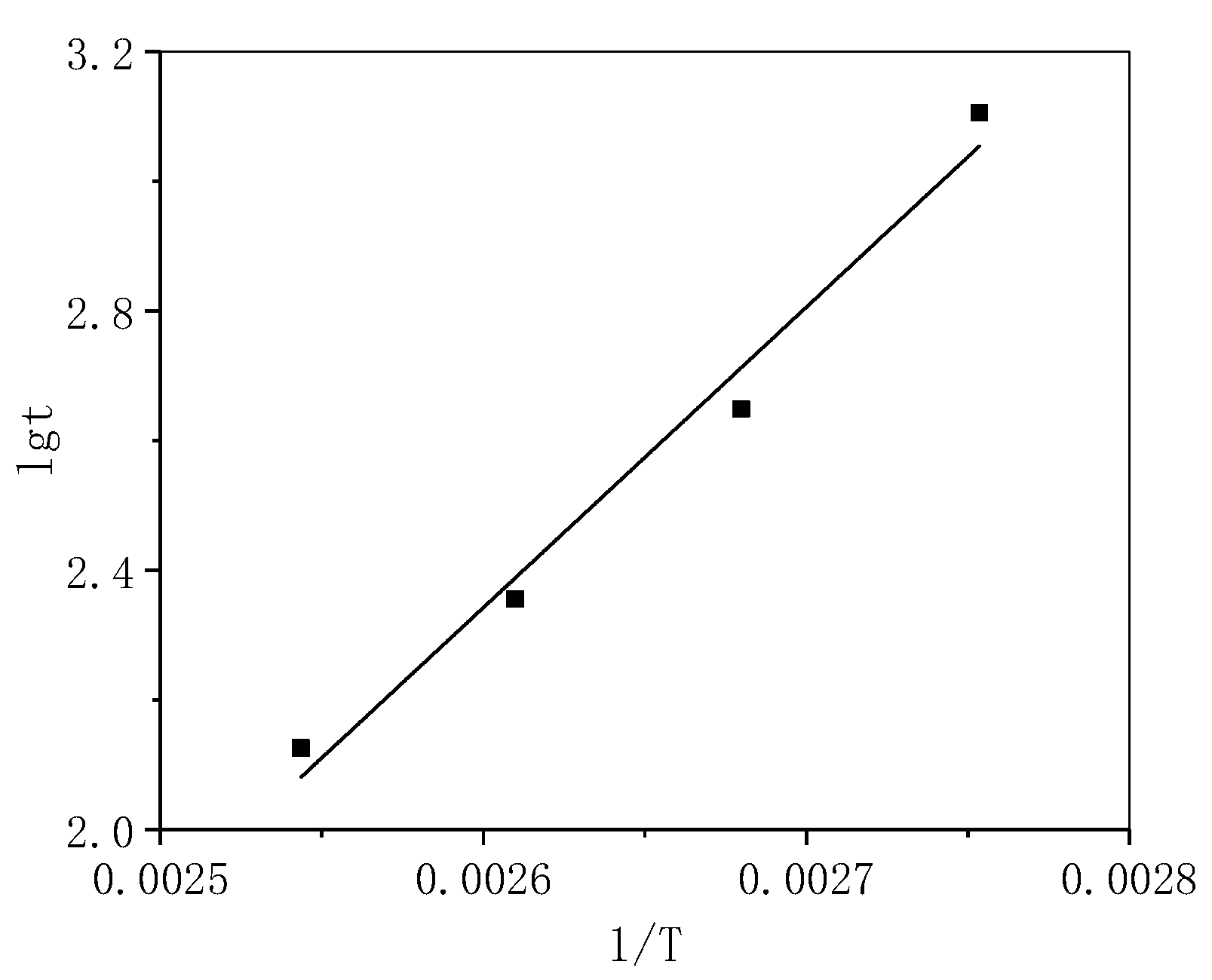
4.3. Normal Life Expectancy Projection
4.4. Comparison of Wiener Process and Grey-Model-Based Life Prediction
5. Conclusions
- (1)
- The performance degradation test scheme of a thermal trip is studied, and the constant-stress-accelerated degradation test with the Arrhenius equation as the accelerated model, temperature as the accelerated stress, and specific thermal deflection K as the degradation characteristic parameter is determined. The accelerated degradation test data were analysed to reveal the performance degradation law of the thermal trip.
- (2)
- A thermal trip performance degradation model based on the Wiener process is established, and the degradation data under accelerated stress are segmented, with a single cycle as the time segment, and according to the central limit theorem as well as the test chart of the normal distribution of segmented degradation, checking that the segmental degradation of the specific thermal deflection obeys a normal distribution, thus conforming to the Wiener process.
- (3)
- In this study, we used the method of probability statistics to derive its residual life probability density function and reliability function; used the method of great likelihood estimation to obtain the estimated values of μ and σ; established the residual life prediction model of thermal trips; predicted the pseudo-failure life of thermal trips at the initial moment of accelerating stress; and externally launched the service life of thermal trips of 6273 days in the normal situation through the Arrhenius accelerating model, utilising the least-squares method of linear regression analysis. The prediction results were also compared with the pseudo-failure life obtained from the grey model prediction, and it was found that the grey model prediction was large and the Wiener process prediction was more accurate.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yao, F.; Yao, Q.; Li, X. Research on the influence of thermal bimetal on overload protection characteristics of small circuit breakers. Wenzhou, Zhejiang, Reliability Research Society of Electrotechnical Products of China Electrotechnical Society. In Proceedings of the Fifth International Conference on Reliability and Electrical Contact of Electrotechnical Products, Wenzhou, China, 16 November 2014. [Google Scholar]
- Zhao, J.; Yan, H.; Jiang, M. Simulation tracking method for overload relay performance degradation. Electr. Appl. Energy Effic. Manag. Technol. 2018, 39–44+54. [Google Scholar]
- Cheng, S.; Liu, J.; Wu, X.; Yu, T.; Xiang, C.; Yuan, D. Residual life prediction of metallized film capacitors based on feature extraction and error compensation. Chin. J. Electr. Eng. 2022, 42, 2672–2681. [Google Scholar]
- You, Y.; Wang, J.; Shu, L.; Ni, K.; Zhou, X. An electrical life prediction method for AC contactors based on audio features. J. Electrotechnol. 2021, 36, 1986–1998. [Google Scholar]
- Chen, L.; Chen, J.; Wang, H.; Wei, H.; Pan, H. Remaining battery life prediction based on wavelet packet energy entropy. J. Electrotechnol. 2020, 35, 1827–1835. [Google Scholar]
- Liu, G.; Wang, Z.; Li, X.; Zhao, X.; Miao, J. Reliability assessment of electronic residual current operated circuit breakers based on improved Bootstrap-Bayes. J. Electrotechnol. 2022, 37, 4250–4258. [Google Scholar]
- Feng, H.; Wang, Y. Reliability analysis of performance degradation products based on support vector regression and Bayesian theory. J. Nanjing Univ. (Nat. Sci.) 2019, 55, 161–169. [Google Scholar]
- Zhang, Z.; Xu, X.; Yu, J. Study on life prediction of contactor in traction system of rolling stock based on accelerated life test. Railw. Roll. Stock. 2023, 43, 37–44. [Google Scholar]
- Li, K.; Gao, Z.; Wu, Y.; Zheng, S.; Li, J. Residual life prediction of AC contactors based on statistical regression and nonlinear Wiener process. J. Electrotechnol. 2019, 34, 4058–4070. [Google Scholar]
- Chen, L.; Wang, H.M.; Chen, J.; An, J.; Ji, B.; Lyu, Z.; Cao, W.; Pan, H. A novel remaining useful life prediction framework for lithium-ion battery using grey model and particle filtering. Int. J. Energy Res. 2020, 44, 7435–7449. [Google Scholar] [CrossRef]
- Li, K.; Li, X.; Zheng, S.; He, J.; Wu, Y. Residual electric life prediction of AC contactors based on BP neural network. J. Electrotechnol. 2017, 32, 120–127. [Google Scholar]
- Zhang, L.; Xita, A.; Tian, X.; Li, W. Multi-objective optimization design of accelerated degradation test based on Gamma process. J. Jilin Univ. (Eng. Ed.) 2022, 52, 361–367. [Google Scholar]
- BS EN 60947-2:2016; Low-Voltage Switchgear and Controlgear—Part 2: Circuit-breakers. International Electrotechnical Commission: Geneva, Switzerland, 2016.
- GB/T 14048.2-2020; Low-Voltage Switchgear and Controlgear—Part 2: Circuit-breakers. GB: Beijing, China, 2020.
- GB/T 2689.1-1981; General Rules for Constant Stress Life Test and Accelerated Life Test Method. National Technical Committee for Standardization of Low-Voltage Electrical Appliances: Shanghai, China, 1981.
- Liu, J.; Chen, A.; Yan, Y.; Zhang, M.; Qi, H. Reliability assessment method of electromagnetic contactors for high-speed trains. J. Electrotechnol. 2018, 33, 461–471. [Google Scholar]
- Li, J.; Huang, J.; Qiu, M.; Wang, Z.; Pang, X.; Dong, Y. Residual life prediction of rolling bearings based on generalized Wiener process. Comput. Integr. Manuf. Syst. 2022, 28, 1–17. [Google Scholar]
- Zhang, X.; Gockenbach, E.; Liu, Z.; Chen, H.; Yang, L. Reliability estimation of high voltage SF6 circuit breakers by statistical analysis on the basis of the field data. Electr. Power Syst. Res. 2013, 103, 105–113. [Google Scholar] [CrossRef]
- Lee ML, T.; Whitmore, G.A. Threshold regression for survival analysis: Modeling event times by a stochastic process reaching a boundary. Stat. Sci. 2006, 21, 501–513. [Google Scholar]
- Folks, J.L.; Chhikara, R.S. The Inverse Gaussian Distribution and Its Statistical Application—A Review. J. R. Stat. Soc. 1978, 40, 263–289. [Google Scholar] [CrossRef]
- Sawa, K.; Yoshida, K.; Watanabe, M.; Suzuki, K. Arc characteristics and electrode mass change of Ag-Ni contacts for electromagnetic contactors. In Proceedings of the 56th IEEE Holm Conference on Electrical Contacts, Charleston, SC, USA, 4–7 October 2010; pp. 1–6. [Google Scholar]
- Tang, S.; Guo, X.; Yu, C.; Zhou, Z.; Zhou, Z.; Zhang, B. Real time remaining useful life prediction based on nonlinear Wiener based degradation processes with measurement errors. J. Cent. South Univ. 2014, 12, 4509–4517. [Google Scholar] [CrossRef]
- Zhu, L.; Zuo, H.; Cai, J. Reliability prediction of civil aviation engine performance based on Wiener process. J. Aerosp. Dyn. 2013, 28, 1006–1012. [Google Scholar]




| Temperature/°C | Serial Number | Pseudo-Failure Life/Day | Temperature/°C | Serial Number | Pseudo-Failure Life/Day |
|---|---|---|---|---|---|
| 120 | A1 | 137 | 100 | C1 | 441 |
| A2 | 144 | C2 | 411 | ||
| A3 | 150 | C3 | 393 | ||
| A4 | 141 | C4 | 426 | ||
| A5 | 129 | C5 | 456 | ||
| 110 | B1 | 237 | 90 | D1 | 1350 |
| B2 | 249 | D2 | 1416 | ||
| B3 | 219 | D3 | 1410 | ||
| B4 | 213 | D4 | 1392 | ||
| B5 | 216 | D5 | 1425 |
| Temperature/°C | Statistic |
|---|---|
| 90 | 0.8757 |
| 100 | 0.9786 |
| 110 | 0.8714 |
| 120 | 0.9920 |
| Temperature/°C | μ/Day | σ/Day |
|---|---|---|
| 90 | 1398.6 | 29.73 |
| 100 | 425.4 | 24.68 |
| 110 | 226.8 | 15.53 |
| 120 | 139.8 | 7.85 |
| Parameters | a | b | r | RSS |
|---|---|---|---|---|
| Numerical value | −9.7012 | 4632.0903 | 0.98218 | 0.0098 |
| Temperature /°C | Wiener Pseudo-Failure Life/Day | Grey Pseudo-Failure Life/Day | Difference/Day |
|---|---|---|---|
| 90 | 1398.6 | 1555.1 | 156.5 |
| 100 | 425.4 | 542.4 | 117 |
| 110 | 226.8 | 279.4 | 52.6 |
| 120 | 139.8 | 161.8 | 22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, X.; Wang, L.; Zhang, Z.; Wang, D. Residual Life Prediction of Low-Voltage Circuit Breaker Thermal Trip Based on the Wiener Process. Energies 2024, 17, 1189. https://doi.org/10.3390/en17051189
Su X, Wang L, Zhang Z, Wang D. Residual Life Prediction of Low-Voltage Circuit Breaker Thermal Trip Based on the Wiener Process. Energies. 2024; 17(5):1189. https://doi.org/10.3390/en17051189
Chicago/Turabian StyleSu, Xiuping, Linlin Wang, Zhilin Zhang, and Dongyue Wang. 2024. "Residual Life Prediction of Low-Voltage Circuit Breaker Thermal Trip Based on the Wiener Process" Energies 17, no. 5: 1189. https://doi.org/10.3390/en17051189
APA StyleSu, X., Wang, L., Zhang, Z., & Wang, D. (2024). Residual Life Prediction of Low-Voltage Circuit Breaker Thermal Trip Based on the Wiener Process. Energies, 17(5), 1189. https://doi.org/10.3390/en17051189





