Abstract
Evaluating uncertainty in injection projections often requires numerous high-resolution geological realizations (GRs) which, although effective, are computationally demanding. This study proposes the use of representative geological realizations (RGRs) as an efficient approach to capture the uncertainty range of the full set while reducing computational costs. A predetermined number of RGRs is selected using an integrated unsupervised machine learning (UML) framework, which includes Euclidean distance measurement, multidimensional scaling (MDS), and a deterministic K-means (DK-means) clustering algorithm. In the context of the intricate 3D aquifer storage model, PUNQ-S3, these algorithms are utilized. The UML methodology selects five RGRs from a pool of 25 possibilities (20% of the total), taking into account the reservoir quality index (RQI) as a static parameter of the reservoir. To determine the credibility of these RGRs, their simulation results are scrutinized through the application of the Kolmogorov–Smirnov (KS) test, which analyzes the distribution of the output. In this assessment, 40 injection wells cover the entire reservoir alongside the full set. The end-point simulation results indicate that the structural, residual, and solubility trapping within the RGRs and full set follow the same distribution. Simulating five RGRs alongside the full set of 25 GRs over 200 years, involving 10 years of injection, reveals consistently similar trapping distribution patterns, with an average value of of 0.21 remaining lower than (0.66). Using this methodology, computational expenses related to scenario testing and development planning for storage reservoirs in the presence of geological uncertainties can be substantially reduced.
1. Introduction
The primary focus of carbon capture and storage (CCS) is the mitigation of human-induced emissions of [1]. This practical strategy entails the capture of from the atmosphere, its transport to an underground storage reservoir, and injection into deep formations, where it remains securely stored within the pore spaces of the rock [2]. Various geological formations, such as depleted oil and gas reservoirs and deep saline aquifers, have been identified as suitable sites for storage of at depths of several thousand meters [3,4,5]. The use of geological realizations (GRs) is common in the development and management of these storage reservoirs. GRs help to determine long-term trapping of , plume migration, and the potential for leakage [6,7,8]. However, due to the limited availability of geological data for each storage site, there is a notable level of uncertainty, affecting estimates of storage capacities, leakage risks, and the potential for groundwater contamination [1].
The evaluation and quantification of geological uncertainties have become increasingly crucial in industries dedicated to decarbonization [2,9,10]. The geological structure of a storage reservoir, coupled with variations in its petrophysical characteristics, constitutes the primary origin of geological uncertainty [11]. Traditional approaches to assessing geological uncertainty involve the generation of numerous potential GRs and the analysis of statistical metrics derived from ensemble objective functions [1]. To encompass the uncertainty space, Monte Carlo sampling is commonly employed to efficiently generate a large number of GRs [12]. However, the computational challenges associated with simulating numerous GRs pose a hurdle, leading to the exploration of methods to expedite this process. These methods can be categorized into two groups: data-driven approaches and physics-based simplifications [13].
Data-driven proxy models for uncertainty quantification rely on simplified fitting procedures, bypassing the flow simulation for injections and post-injection [14]. This enables the quick determination of many objective functions but may overlook fluid flow’s physical laws, potentially causing errors, especially in high-dimensional input-parameter spaces [15]. On the other hand, physics-based simplifications, such as low-fidelity realizations including up-scaled GRs or reduced ensembles, aim to simplify geological characteristics significantly. Although these methods provide simplicity in implementation, they may limit the representation of sub-grid heterogeneity impacts [14]. Representative geological realizations (RGRs) are a subset of reduced ensembles that aim to represent critical heterogeneity and injection phenomena, as long as the model’s fidelity is maintained. Their validity relies on the assumption that RGRs closely reflect the uncertainty of the full set. If this approximation fails, predictions about storage and migration may be inaccurate. Therefore, it is crucial to assess the representativeness of RGRs and explore optimal selection methods that maximize uncertainty representation. One of the RGR selection methods is the Unsupervised Machine Learning (UML) method [16].
Machine learning and deep learning have recently been explored in many fields to accelerate computationally heavy processes [17,18,19,20]. In this area, UML specifically stands out as a widely adopted method to select RGRs, as evidenced in several case studies [21,22,23,24]. UML is designed to uncover the underlying structures in unlabeled data, employing techniques such as dimensionality reduction and clustering [25,26]. Dimensionality reduction identifies crucial attributes for distinguishing data samples, while clustering groups similar samples. UML transforms realizations into a reduced-dimensional space and clusters them according to static and/or dynamic features [26]. For instance, UML is applied to discover similar realizations using 3D facies models [27], assess similarity based on generalized travel time (GTT) differences [28], and evaluate various properties for RGR selection [21,29]. In experiments with a 2D aquifer model, ref. [30] demonstrated that an effective UML framework for RGR selection involves utilizing Euclidean distance for dissimilarity, multidimensional scaling (MDS) for dimensionality reduction, and deterministic K-means (DK-means) for clustering realizations.
In our investigation, we try not only to select RGRs for a 3D synthetic aquifer storage model but also to delve into the efficacy of the optimal UML framework derived from the study by Mahjour and Faroughi [30]. Our objective is to explore the UML framework’s ability to maintain the inherent uncertainty found in the full set represented by the RGRs. To gauge the method’s performance, we conduct a series of statistical experiments, assessing the outcomes within the context of the PUNQ-S3 benchmark model [31]. This model, designed to mimic a folded geologic formation forming an anticline, serves as an excellent testing ground for examining the robustness and reliability of the UML-based RGR selection method under diverse geological scenarios. Through comprehensive analyses and assessments within this model, we aim to highlight the method’s strengths and limitations, offering insights into its practical applicability in capturing and preserving uncertainty within complex subsurface systems. This exploration is crucial for enhancing the efficiency and reliability of RGR selection processes in the context of storage initiatives.
2. Methodology
In this work, the RGR selection process is based on the optimal UML algorithm detailed by Mahjour and Faroughi [30], encompassing the measurement of the Euclidean distance, MDS, and the DK-means clustering. As shown in Figure 1, the workflow begins with the generation of numerous GRs while considering uncertainties. To evaluate the UML framework’s effectiveness, both the full and RGR sets undergo examination using CMG-GEM (Canada Modeling Group-Generalized Equation of State Model). Consequently, we compare the distributions of simulation outputs obtained from the RGRs with those originating from the full set.
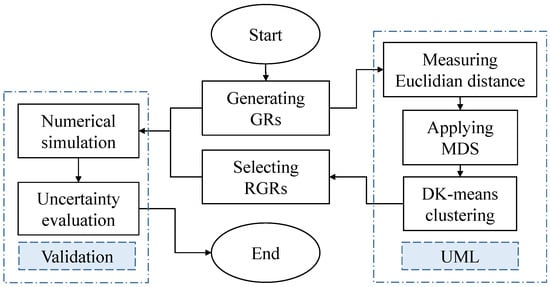
Figure 1.
RGR selection and validation workflow including (i) the selection of RGRs by measuring Euclidean distance, applying Multidimensional Scaling (MDS), and implementing Deterministic K-means (DK-means) clustering and (ii) the validation of the RGRs’ representativeness through the simulation of both the full and RGR sets using a numerical simulator.
2.1. Generate Multiple Geological Realizations (GRs)
In the initial phase, a set of GRs is generated to capture geological uncertainties. While there are various sampling techniques to create multiple GRs, this study specifically adopts Latin Hypercube Sampling (LHS). LHS serves as a probabilistic geostatistical approach tailored for uncertainty quantification, drawing from diverse data sources [32]. This method ensures comprehensive sampling across the entire parameter range, minimizing the number of simulations required while preserving the statistical integrity of the outcomes [33]. It is essential to emphasize that this particular step, while integral to the overall workflow, is not the primary focus of this study and operates independently of the technique used for scenario reduction. Following this initial stage, the main focus of the study is on the application of UML for the selection of RGRs.
2.2. Euclidean Distance Measurement between Realizations
Within the UML process, a crucial step involves constructing a matrix based on distance indicators, denoted as , calculated between each pair of realizations. This distance metric, , quantifies the similarity between realization ‘i’ and realization ‘j’ [34]. The selection of a specific reservoir attribute and an appropriate distance measurement method significantly impact the evaluation of these distance indicators [35]. Concerning geological distributions, multiple generated geological realizations may exhibit similarities at certain distances, resulting in comparable flow responses. The ability to distinguish these realizations enables the generation of simulation outputs based on a reduced subset of realizations, each representing diverse flow responses [24].
This study employs the Reservoir Quality Index () as a static reservoir attribute to measure the distance between pairs of realizations. finds widespread applications in various reservoir-related domains, including permeability estimation, stratigraphy, and reservoir modeling [36,37,38,39,40]. Porosity and permeability, integral petrophysical properties within the formulation, hold particular significance in the context of fluid flow modeling in heterogeneous porous media [41,42], especially in the modeling of storage and plume migration [43,44]. Studies by [16,24] have explored the effectiveness of in identifying realizations with similar flow behaviors, which yield promising results. The mathematical definition of is given by,
where K represents permeability in milli-darcy (), and is the porosity as a fraction. The constant serves as the conversion factor from permeability in to [45]. The is derived from the Kozeny–Carman equation, defined as,
where represents the shape factor, indicates tortuosity, and is the specific surface area per unit grain volume. Each grid cell within the GRs possesses spatial coordinates and a set of geological attributes, including porosity and permeability. To create maps, the value is computed for each grid cell. Subsequently, a distance indicator between these maps is measured using the Euclidean distance metric.
The measurement of the distance between two 3D samples, denoted as ‘X’ and ‘Y’, characterizes the degree of similarity between these samples [35]. In this study, we employ the Euclidean distance as the chosen measurement, given its widespread use and familiarity in similarity assessments [46]. After this step, we generate an ‘n × n’ distance matrix, D, based on the ‘n’ RQI models, which serve as input for the subsequent step.
2.3. Multidimensional Scaling (MDS)
MDS is used to represent the similarity measurements among objects as distances between points in a low-dimensional space, where each point corresponds to one object [47]. The fundamental concept behind MDS is to construct a map or configuration of points in a lower-dimensional space that accurately reflects the similarities between objects [48]. The outcomes of MDS are visualized by plotting the points in the k-dimensional space. As highlighted by Scheidt and Caers [35], using high-dimensional Euclidean spaces may not significantly enhance correlation, thereby suggesting that a 2D space () can be appropriate in such cases. Each point in this 2D space represents an individual realization, and the Euclidean distance between two points serves as the measure of similarity between these realizations.
2.4. Deterministic K-Means (DK-Means) Clustering
After the transformation of data from a high-dimensional initial space to a lower-dimensional one, clustering techniques are employed to categorize models into distinct clusters [23]. Realizations within the same cluster exhibit similarity to each other. This study employs DK-means for clustering similar realizations, representing a modification of the conventional K-means clustering algorithm [49]. The objective is to address K-means’ non-deterministic behavior resulting from its random choice of initial centroids. The DK-means algorithm incorporates a deterministic initialization approach by either exploring a range of potential centers through constrained bi-partitioning or implementing a novel systematic method to select initial centroids. The primary goal of DK-means is to enhance the reliability and consistency of clustering outcomes compared to the traditional K-means algorithm [50].
Upon grouping the realizations through clustering, a representative realization from each group is selected using centroid-based sampling. This method targets the model closest to the center of the cluster for selection [23]. To determine a representative, the Euclidean distance between a model and the center of its corresponding cluster is calculated, indicating the model’s closeness to that center. Determining the optimal number of RGRs poses a challenge, necessitating careful consideration of factors such as geological realization complexity, the number and types of uncertain parameters, desired accuracy levels, and available computational resources [16]. The chosen sample size aims to strike a balance between computational efficiency and comprehensive coverage of the entire uncertainty space.
2.5. Numerical Simulation and Uncertainty Evaluation
In this phase, we conduct a comparative analysis of simulation outputs from an injection plan (IP) for both RGRs and the full set to assess how well the RGRs capture the characteristics of the entire set. Initially, the simulation outputs for each set are processed using a commercial flow simulator. Throughout the simulation, numerical realizations are specified to define objectives over time. Focusing on trapping mechanisms, we explore the physics governing migration, resulting in three specific simulation outputs: (i) structural trapping, (ii) residual trapping, and (iii) solubility trapping, using CMG-GEM. Simulation outputs are employed to assess and compare uncertainty between the full set and the RGRs. The methodology for quantifying uncertainty plays a crucial role in evaluating the representativeness of the RGRs. In this study, we analyze the distribution of the simulation outputs at the end of the simulation process to provide insights for decision-making under uncertainty [14]. To compare the uncertainty ranges, we examine CDF curves [51] derived from the simulation results of the RGR set and the entire ensemble. The proximity of their uncertainty ranges is assessed by measuring the maximum vertical difference, denoted as , between the CDFs of the two datasets, and . This analysis is carried out using the Kolmogorov–Smirnov (KS) test [52]. The value is determined by,
Here, the number of realizations in the RGR set (m) and the whole set (n) is predetermined based on the budget and simulation time. If is lower than the critical , defined as,
Thus, if from the RGR and full-set samples is less than , we ensure that the RGR set adequately represents the full ensemble.
3. Model Description
3.1. Geometric Model
This study validates the effectiveness of the UML framework in selecting RGRs using the synthetic reservoir model PUNQ-S3. Specific details of the PUNQ-S3 model, adapted by Juanes et al. [31] to represent a storage aquifer, are documented by Floris et al. [53]. PUNQ-S3 consists of five layers of sand and shale, typical sedimentary phases commonly found in geological formations [54]. This configuration results in a grid layout of 19 × 28 × 5 grid blocks, totaling 1761 active blocks. The top formation is positioned at a depth of 2340 m with an average thickness of 15 m. Each grid’s length spans 180 m in the horizontal direction. The average horizontal permeability and porosity are 100 mD and 0.2, respectively. The initial pressure and the fixed temperature are set at 23,446 kPa and 32.2 °C, respectively. The rock compressibility is measured at kPa−1, and the water compressibility is kPa−1. Furthermore, the relative permeability curves, adapted from Juanes et al. [31], incorporate the Killough hysteresis model [55] for the non-wetting phase (). The relative permeability curves for and brine are shown in Figure 2. This study relies on Land’s trapping models [56] for the residual trapping mechanism. Hence, during the simulation process, computations for drainage and imbibition processes are conducted utilizing Land’s residual model. Residual water saturation is considered 0.31 for the simulation.
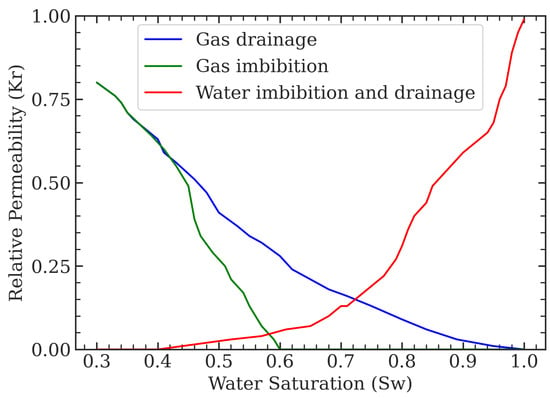
Figure 2.
Relative permeability curves used in the storage simulation (Killough’s model is used for hysteresis [55]).
3.2. Well Control Configurations
We implement an extensive injection plan (IP) specifically designed to elicit a comprehensive and varied response from the reservoir’s behavior, facilitating RGR selection. The IP includes forty vertical injection wells strategically positioned to cover the entire reservoir without restrictions in the injection system. The objective behind choosing this well configuration is to ensure unbiased coverage of the reservoir model and to address its inherent heterogeneity. Figure 3a,b shows the top view of the reference porosity map and the placement of these wells within the IP, respectively. Within IP, the surface gas rate (STG) is set at 10,000 m3/day, and the bottom hole pressure (BHP) is maintained at 44,500 kPa for each well. The wells are fully perforated from the top to the bottom of the reservoir.
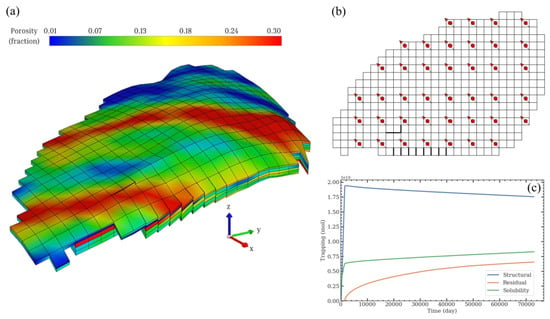
Figure 3.
Reference PUNQ-S3 model. Panel (a) shows the 3D porosity map. Panel (b) represents the well locations including forty wells, spanning the whole reservoir. Panel (c) shows the simulation outputs structural (i) trapping, (ii) residual trapping, and (iii) solubility trapping during 200 years with ten years of injection.
3.3. Reference Simulation Outputs
We delve into the physics underlying migration and extract three simulation outputs—(i) structural trapping, (ii) residual trapping, and (iii) solubility trapping—using CMG-GEM. In the solubility trapping simulation, we take into account the chemical interactions between the gaseous and aqueous phases [57]. However, mineral trapping is excluded from our study, as it predominantly occurs after 1000 years, whereas our simulation duration spans 200 years with 10 years of injection. The simulation output of the reference model is depicted in Figure 3c.
4. Results
We generated N = 25 realizations using LH sampling, considering diverse variations in porosity and permeability models to ensure comprehensive spatial sampling. The array of 25 porosity models (top views) is illustrated in Figure 4. Subsequently, we generated RQI models using porosity and permeability properties. The RQI for each grid cell was calculated to create the RQI map and determine the distances between pairwise GRs. In this study, we specifically chose five predetermined numbers of RGRs, amounting to 20% of the full set, using UML. This selection enables a reasonable reduction in both realizations and computational expenses while maintaining the full set’s uncertainty domain.
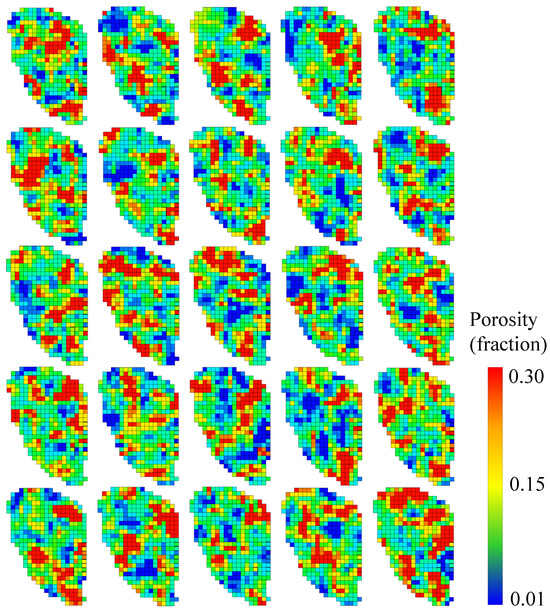
Figure 4.
Top views of the 25 3D porosity models generated through LH sampling, showing diverse variations in porosity and permeability.
Figure 5 displays a 2D map showing all the realizations obtained through the Euclidean/MDS/DK-means approach with five clusters. The MDS algorithm positions these realizations on a 2D map while preserving their distances based on Euclidean measurements in a distance matrix. Subsequently, the DK-means algorithm groups the realizations into multiple clusters. Using the centroid sampling method, one realization is selected as a representative of each cluster. The black points on the 2D map represent these five representative realizations. Upon visual examination, it is evident that the representative realizations are evenly distributed across all the models.
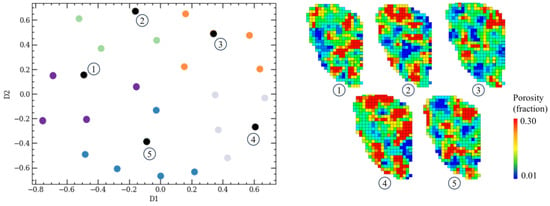
Figure 5.
A 2D map displaying all realizations generated through the Euclidean/MDS/DK-means framework employing five clusters. The X-axis corresponds to Dimension 1 (D1), and the Y-axis represents Dimension 2 (D2). Five RGRs, marked as black points, are selected through clustering and centroid-based sampling. These RGRs exhibit an even distribution across all models, effectively representing the full uncertain domain.
Next, we proceed with simulating the chosen five RGRs alongside the full set of 25 GRs to evaluate their simulation outputs over 200 years. This includes assessing trapping, residual trapping, and solubility trapping, taking into account the essential inputs for the simulation process. In Figure 6, we compared the CDFs based on the endpoint simulation results of both the RGRs and the entire set. The values for trapping, residual trapping, and solubility trapping are 0.20, 0.24, and 0.16, respectively. These values are lower than , 0.66. Additionally, we compute the total trapping, representing cumulative trapping at the endpoint simulation, generating CDF curves for both RGRs and the full set. The resulting value is 0.24, also lower than . Thus, the CDFs reveal that the simulation outputs from RGRs, selected through the Euclidean/MDS/DK-means framework, stem from the same distribution as the full set.
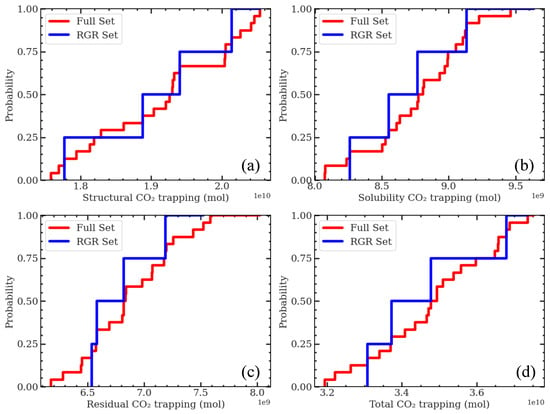
Figure 6.
Comparison of CDFs between RGRs and the full set for trapping mechanisms. The values for (a) structural, (b) residual, (c) solubility, and (d) total trapping are 0.20, 0.24, 0.16, and 0.24, respectively. The average is 0.21, which is lower than , 0.66, indicating a close similarity in the distribution patterns of trapping mechanisms between the RGRs and the entire set of 25 GRs.
Figure 7a displays the average trapping for different mechanisms from both the RGRs and the full set. The values obtained from the RGRs closely reflect those derived from the complete set of 25 GRs. The values obtained from the RGRs— for residual trapping, for structural trapping, for solubility trapping, and for total trapping—closely align with those derived from the complete set (, , , and , respectively). This alignment is evident across various trapping mechanisms, highlighting the effectiveness of the selected RGRs in representing the full set. The proximity in the averages indicates a consistent trend, emphasizing the reliability of the RGRs in simulating trapping mechanisms. Additionally, for visual validation, time series curves of the simulation outputs for both RGRs and the full set are depicted in Figure 7b–d. The figure clearly shows that the RGRs properly capture the entire uncertainty domain, confirming their ability to represent the full-set results.
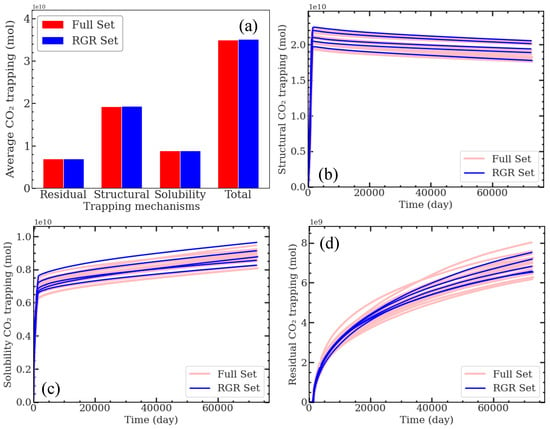
Figure 7.
Statistical analysis of trapping mechanisms between RGRs and the full set. Panel (a) compares the average of trapping mechanisms between RGRs and the full set. The average values obtained from the RGRs— for residual trapping, for structural trapping, for solubility trapping, and for total trapping—closely align with those derived from the full set (, , , and , respectively). Panels (b–d) show the time series curves of structural, residual, and solubility trapping, respectively, for both RGRs and the full set. The comparison validates the RGRs’ representation of the full-set results, confirming their reliability in simulating trapping mechanisms.
Furthermore, evaluating the UML framework involves a computational efficiency analysis to gauge its effectiveness. We compare the simulation time for the full set against the utilization of five RGRs chosen from Euclidean/MDS/DK means to quantify uncertainty. The results show a significant reduction in time, decreasing from approximately 16 min for the full set to only 3 min for the five RGRs, indicating an 80% time reduction for the simulation. While simulating all 25 GRs is not overly time-consuming at this stage, executing robust optimizations to maximize storage can be notably time-intensive with the full set. This highlights that the use of RGRs can significantly reduce the time required for storage reservoir development and management compared to employing the full set.
Our findings suggest that the UML framework, using static models for RGR selection without requiring forward numerical simulations, effectively identifies a smaller subset, capturing the uncertainty of the full set within a 3D model characterized by high heterogeneity. Subsequently, these selected RGRs can be employed for rapid scenario testing and development planning at storage locations under geological uncertainties. To enhance the efficacy and precision of these outcomes, we recommend further research and evaluation of the employed UML framework, including (i) implementing robust optimization on both the full set and RGRs, comparing results regarding storage maximization and computational costs, (ii) analyzing the optimal quantity of RGRs within the UML framework and assessing the trade-off between computational efficiency and accuracy, and (iii) investigating the spatial distribution and plume footprint of the plume across both the full set and the RGRs.
5. Conclusions
In this study, the efficacy of employing unsupervised machine learning (UML) to select representative geological realizations (RGRs) within a complex 3D aquifer storage model, PUNQ-S3 was investigated. To address the inherent geological uncertainty, a workflow generated 25 geological realizations (GRs) through Latin hypercube sampling (LHS) for uncertainty quantification. Subsequently, an integrated UML framework, including Euclidean distance measurement, multidimensional scaling (MDS), and deterministic K-means (DK-means) clustering, selected five RGRs (20% of the full set). The Kolmogorov–Smirnov (KS) test was used to evaluate the UML framework, comparing absolute distances () between the cumulative distribution functions (CDFs) of simulation outputs from the RGR sets and the full set. The findings demonstrated that the selected RGRs properly captured the uncertainty domain of the full set, evident through similar trapping distribution patterns, with an average value of 0.21, remaining lower than (0.66). Furthermore, the average trapping for different mechanisms from the RGRs was aligned with those derived from the full set of 25 GRs, highlighting the effectiveness of the selected RGRs in representing the full set. Computational time significantly decreased from around 16 min for the full set to only 3 min for the five RGRs, indicating an 80% reduction in simulation time. Extending verification to the synthetic reservoir model PUNQ-S3 showed the robustness of the UML-based RGR selection method, especially in scenarios with high heterogeneity. These results emphasized the potential of this approach for expediting scenario testing, decision-making, and development planning in storage locations faced with geological uncertainties.
Author Contributions
Conceptualization, S.K.M. and S.A.F.; methodology, S.K.M.; software, S.K.M.; validation, S.K.M. and S.A.F.; formal analysis, S.K.M.; investigation, J.H.B.; resources, S.K.M.; data curation, S.K.M. and J.H.B.; writing—original draft preparation, S.K.M.; writing—review and editing, S.K.M. and S.A.F.; visualization, S.K.M.; supervision, S.A.F.; project administration, S.A.F.; funding acquisition, S.A.F. All authors have read and agreed to the published version of the manuscript.
Funding
S.A.F. would like to acknowledge support by the Department of Energy’s Office of Fossil Energy and Carbon Management (DOE-FECM) (award no. DE-FE0032200).
Data Availability Statement
The data and materials used in this study are available upon request.
Conflicts of Interest
The authors declare that they have no known competing interests that could have appeared to influence the work reported in this paper.
Abbreviations
The following abbreviations are used in this manuscript:
| BHP | Bottom Hole Pressure |
| CCS | Carbon Capture and Storage |
| CDF | Cumulative Distribution Function |
| CMG-GEM | Canada Modeling Group-Generalized Equation of State Model |
| DK-means | Deterministic K-means |
| GR | Geological Realization |
| GTT | Generalized Travel Time |
| IP | Injection Plan |
| KS | Kolmogorov–Smirnov |
| LHS | Latin Hypercube Sampling |
| MDS | Multidimensional Scaling |
| RGR | Representative Geological Realization |
| RQI | Reservoir Quality Index |
| STG | Surface Gas Rate |
| UML | Unsupervised Machine Learning |
References
- Tadjer, A.; Bratvold, R.B. Managing Uncertainty in Geological CO2 Storage Using Bayesian Evidential Learning. Energies 2021, 14, 1557. [Google Scholar] [CrossRef]
- Wilkinson, M.; Polson, D. Uncertainty in regional estimates of capacity for carbon capture and storage. Solid Earth 2019, 10, 1707–1715. [Google Scholar] [CrossRef]
- Harp, D.R.; Stauffer, P.H.; O’Malley, D.; Jiao, Z.; Egenolf, E.P.; Miller, T.A.; Martinez, D.; Hunter, K.A.; Middleton, R.S.; Bielicki, J.M.; et al. Development of robust pressure management strategies for geologic CO2 sequestration. Int. J. Greenh. Gas Control 2017, 64, 43–59. [Google Scholar] [CrossRef]
- Jin, L.; Hawthorne, S.; Sorensen, J.; Pekot, L.; Kurz, B.; Smith, S.; Heebink, L.; Herdegen, V.; Bosshart, N.; Torres, J.; et al. Advancing CO2 enhanced oil recovery and storage in unconventional oil play—Experimental studies on Bakken shales. Appl. Energy 2017, 208, 171–183. [Google Scholar] [CrossRef]
- Nilsen, H.M.; Lie, K.A.; Andersen, O. Analysis of CO2 trapping capacities and long-term migration for geological formations in the Norwegian North Sea using MRST-co2lab. Comput. Geosci. 2015, 79, 15–26. [Google Scholar] [CrossRef]
- Diao, Y.; Zhu, G.; Li, X.; Bai, B.; Li, J.; Wang, Y.; Zhao, X.; Zhang, B. Characterizing CO2 plume migration in multi-layer reservoirs with strong heterogeneity and low permeability using time-lapse 2D VSP technology and numerical simulation. Int. J. Greenh. Gas Control. 2020, 92, 102880. [Google Scholar] [CrossRef]
- Langhi, L.; Strand, J.; Ricard, L. Flow modelling to quantify structural control on CO2 migration and containment, CCS South West Hub, Australia. Pet. Geosci. 2021, 27, petgeo2020-094. [Google Scholar] [CrossRef]
- Shepherd, A.; Martin, M.; Hastings, A. Uncertainty of modelled bioenergy with carbon capture and storage due to variability of input data. GCB Bioenergy 2021, 13, 691–707. [Google Scholar] [CrossRef]
- Jia, W.; McPherson, B.; Pan, F.; Dai, Z.; Xiao, T. Uncertainty quantification of CO2 storage using Bayesian model averaging and polynomial chaos expansion. Int. J. Greenh. Gas Control 2018, 71, 104–115. [Google Scholar] [CrossRef]
- Sun, W.; Durlofsky, L.J. Data-space approaches for uncertainty quantification of CO2 plume location in geological carbon storage. Adv. Water Resour. 2019, 123, 234–255. [Google Scholar] [CrossRef]
- Mahjour, S.K.; Faroughi, S.A. Risks and uncertainties in carbon capture, transport, and storage projects: A comprehensive review. Gas Sci. Eng. 2023, 119, 205117. [Google Scholar] [CrossRef]
- Bueno, J.F.; Drummond, R.D.; Vidal, A.C.; Sancevero, S.S. Constraining uncertainty in volumetric estimation: A case study from Namorado Field, Brazil. J. Pet. Sci. Eng. 2011, 77, 200–208. [Google Scholar] [CrossRef]
- Mahjour, S.K.; Santos, A.A.S.; Correia, M.G.; Schiozer, D.J. Scenario reduction methodologies under uncertainties for reservoir development purposes: Distance-based clustering and metaheuristic algorithm. J. Pet. Explor. Prod. Technol. 2021, 11, 3079–3102. [Google Scholar] [CrossRef]
- Schiozer, D.J.; dos Santos, A.A.d.S.; de Graça Santos, S.M.; von Hohendorff Filho, J.C. Model-based decision analysis applied to petroleum field development and management. Oil Gas Sci. Technol. Rev. D’Ifp Energies Nouv. 2019, 74, 46. [Google Scholar] [CrossRef]
- Trehan, S.; Carlberg, K.T.; Durlofsky, L.J. Error modeling for surrogates of dynamical systems using machine learning. Int. J. Numer. Methods Eng. 2017, 112, 1801–1827. [Google Scholar] [CrossRef]
- Mahjour, S.K.; da Silva, L.O.M.; Meira, L.A.A.; Coelho, G.P.; dos Santos, A.A.d.S.; Schiozer, D.J. Evaluation of unsupervised machine learning frameworks to select representative geological realizations for uncertainty quantification. J. Pet. Sci. Eng. 2022, 209, 109822. [Google Scholar] [CrossRef]
- Faroughi, S.A.; Soltanmohammadi, R.; Datta, P.; Mahjour, S.K.; Faroughi, S. Physics-informed neural networks with periodic activation functions for solute transport in heterogeneous porous media. Mathematics 2023, 12, 63. [Google Scholar] [CrossRef]
- Faroughi, S.A.; Pawar, N.M.; Fernandes, C.; Raissi, M.; Das, S.; Kalantari, N.K.; Mahjour, S.K. Physics-Guided, Physics-Informed, and Physics-Encoded Neural Networks and Operators in Scientific Computing: Fluid and Solid Mechanics. J. Comput. Inf. Sci. Eng. 2024, 24, 040802. [Google Scholar] [CrossRef]
- Datta, P.; Faroughi, S.A. A multihead LSTM technique for prognostic prediction of soil moisture. Geoderma 2023, 433, 116452. [Google Scholar] [CrossRef]
- Vaziri, P.; Sedaee, B. A machine learning-based approach to the multiobjective optimization of CO2 injection and water production during CCS in a saline aquifer based on field data. Energy Sci. Eng. 2023, 11, 1671–1687. [Google Scholar] [CrossRef]
- Shirangi, M.G.; Durlofsky, L.J. A general method to select representative models for decision making and optimization under uncertainty. Comput. Geosci. 2016, 96, 109–123. [Google Scholar] [CrossRef]
- Lee, K.; Jung, S.; Lee, T.; Choe, J. Use of clustered covariance and selective measurement data in ensemble smoother for three-dimensional reservoir characterization. J. Energy Resour. Technol. 2017, 139. [Google Scholar] [CrossRef]
- Mahjour, S.K.; Correia, M.G.; Santos, A.A.d.S.d.; Schiozer, D.J. Using an integrated multidimensional scaling and clustering method to reduce the number of scenarios based on flow-unit models under geological uncertainties. J. Energy Resour. Technol. 2020, 142, 063005. [Google Scholar] [CrossRef]
- Haddadpour, H.; Niri, M.E. Uncertainty assessment in reservoir performance prediction using a two-stage clustering approach: Proof of concept and field application. J. Pet. Sci. Eng. 2021, 204, 108765. [Google Scholar] [CrossRef]
- Hinton, G.; Sejnowski, T.J. Unsupervised Learning: Foundations of Neural Computation; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar] [CrossRef]
- Liu, Z.; Forouzanfar, F. Ensemble clustering for efficient robust optimization of naturally fractured reservoirs. Comput. Geosci. 2018, 22, 283–296. [Google Scholar] [CrossRef]
- Lee, K.; Jung, S.; Choe, J. Ensemble smoother with clustered covariance for 3D channelized reservoirs with geological uncertainty. J. Pet. Sci. Eng. 2016, 145, 423–435. [Google Scholar] [CrossRef]
- Park, J.; Jin, J.; Choe, J. Uncertainty quantification using streamline based inversion and distance based clustering. J. Energy Resour. Technol. 2016, 138, 012906. [Google Scholar] [CrossRef]
- Pinheiro, M.; Emery, X.; Miranda, T.; Lamas, L.; Espada, M. Modelling geotechnical heterogeneities using geostatistical simulation and finite differences analysis. Minerals 2018, 8, 52. [Google Scholar] [CrossRef]
- Mahjour, S.K.; Faroughi, S.A. Selecting representative geological realizations to model subsurface CO2 storage under uncertainty. Int. J. Greenh. Gas Control. 2023, 127, 103920. [Google Scholar] [CrossRef]
- Juanes, R.; Spiteri, E.; Orr Jr, F.; Blunt, M. Impact of relative permeability hysteresis on geological CO2 storage. Water Resour. Res. 2006, 42, 2005WR004806. [Google Scholar] [CrossRef]
- Pilger, G.; Costa, J.; Koppe, J. The benefits of Latin Hypercube Sampling in sequential simulation algorithms for geostatistical applications. Appl. Earth Sci. 2008, 117, 160–174. [Google Scholar] [CrossRef]
- Damblin, G.; Couplet, M.; Iooss, B. Numerical studies of space-filling designs: Optimization of Latin Hypercube Samples and subprojection properties. J. Simul. 2013, 7, 276–289. [Google Scholar] [CrossRef]
- Suzuki, S.; Caers, J.K. History matching with an uncertain geological scenario. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. [Google Scholar] [CrossRef]
- Scheidt, C.; Caers, J. Representing spatial uncertainty using distances and kernels. Math. Geosci. 2009, 41, 397–419. [Google Scholar] [CrossRef]
- Mahjour, S.K.; Al-Askari, M.K.G.; Masihi, M. Identification of flow units using methods of Testerman statistical zonation, flow zone index, and cluster analysis in Tabnaak gas field. J. Pet. Explor. Prod. Technol. 2016, 6, 577–592. [Google Scholar] [CrossRef]
- Shan, L.; Cao, L.; Guo, B. Identification of flow units using the joint of WT and LSSVM based on FZI in a heterogeneous carbonate reservoir. J. Pet. Sci. Eng. 2018, 161, 219–230. [Google Scholar] [CrossRef]
- Oliveira, G.; Santos, M.; Roque, W. Constrained clustering approaches to identify hydraulic flow units in petroleum reservoirs. J. Pet. Sci. Eng. 2020, 186, 106732. [Google Scholar] [CrossRef]
- Yu, P. Hydraulic unit classification of un-cored intervals/wells and its influence on the productivity performance. J. Pet. Sci. Eng. 2021, 197, 107980. [Google Scholar] [CrossRef]
- Belhouchet, H.; Benzagouta, M.; Dobbi, A.; Alquraishi, A.; Duplay, J. A new empirical model for enhancing well log permeability prediction, using nonlinear regression method: Case study from Hassi-Berkine oil field reservoir–Algeria. J. King Saud Univ. Eng. Sci. 2021, 33, 136–145. [Google Scholar] [CrossRef]
- Faroughi, S.A.; Faroughi, S.; McAdams, J. A prompt sequential method for subsurface flow modeling using the modified multi-scale finite volume and streamline methods. Int. J. Num. Anal. Model. 2013, 4, 129–150. [Google Scholar]
- Bordbar, A.; Faroughi, S.; Faroughi, S.A. A pseudo-TOF based streamline tracing for streamline simulation method in heterogeneous hydrocarbon reservoirs. Am. J. Eng. Res. 2018, 7, 23–31. [Google Scholar]
- Soong, Y.; Crandall, D.; Howard, B.H.; Haljasmaa, I.; Dalton, L.E.; Zhang, L.; Lin, R.; Dilmore, R.M.; Zhang, W.; Shi, F.; et al. Permeability and mineral composition evolution of primary seal and reservoir rocks in geologic carbon storage conditions. Environ. Eng. Sci. 2018, 35, 391–400. [Google Scholar] [CrossRef]
- Xu, R.; Li, R.; Ma, J.; He, D.; Jiang, P. Effect of mineral dissolution/precipitation and CO2 exsolution on CO2 transport in geological carbon storage. Accounts Chem. Res. 2017, 50, 2056–2066. [Google Scholar] [CrossRef]
- George, N.J.; Ekanem, A.M.; Ibanga, J.I.; Udosen, N.I. Hydrodynamic implications of aquifer quality index (AQI) and flow zone indicator (FZI) in groundwater abstraction: A case study of coastal hydro-lithofacies in South-eastern Nigeria. J. Coast. Conserv. 2017, 21, 759–776. [Google Scholar] [CrossRef]
- Ontañón, S. An overview of distance and similarity functions for structured data. Artif. Intell. Rev. 2020, 53, 5309–5351. [Google Scholar] [CrossRef]
- Fouedjio, F. Multidimensional Scaling. In Encyclopedia of Mathematical Geosciences; Springer: Cham, Switzerland, 2023; pp. 938–945. [Google Scholar] [CrossRef]
- Borg, I.; Groenen, P.J. Modern Multidimensional Scaling: Theory and Applications; Springer: New York, NY, USA, 2005. [Google Scholar] [CrossRef]
- Jothi, R.; Mohanty, S.K.; Ojha, A. DK-means: A deterministic k-means clustering algorithm for gene expression analysis. Pattern Anal. Appl. 2019, 22, 649–667. [Google Scholar] [CrossRef]
- Nidheesh, N.; Nazeer, K.A.; Ameer, P. An enhanced deterministic K-Means clustering algorithm for cancer subtype prediction from gene expression data. Comput. Biol. Med. 2017, 91, 213–221. [Google Scholar] [CrossRef] [PubMed]
- Xue, B.; Oldfield, C.J.; Dunker, A.K.; Uversky, V.N. CDF it all: Consensus prediction of intrinsically disordered proteins based on various cumulative distribution functions. FEBS Lett. 2009, 583, 1469–1474. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, C.J.; Davolio, A.; Schiozer, D.J. Evaluation of the Discrete Latin Hypercube with Geostatistical Realizations Sampling for History Matching Under Uncertainties for the Norne Benchmark Case. In Proceedings of the OTC Brasil, Rio de Janeiro, Brazil, 24–26 October 2017. [Google Scholar] [CrossRef]
- Floris, F.J.; Bush, M.; Cuypers, M.; Roggero, F.; Syversveen, A.R. Methods for quantifying the uncertainty of production forecasts: A comparative study. Pet. Geosci. 2001, 7, S87–S96. [Google Scholar] [CrossRef]
- Pan, B.; Liu, K.; Ren, B.; Zhang, M.; Ju, Y.; Gu, J.; Zhang, X.; Clarkson, C.R.; Edlmann, K.; Zhu, W.; et al. Impacts of relative permeability hysteresis, wettability, and injection/withdrawal schemes on underground hydrogen storage in saline aquifers. Fuel 2023, 333, 126516. [Google Scholar] [CrossRef]
- Killough, J. Reservoir simulation with history-dependent saturation functions. Soc. Pet. Eng. J. 1976, 16, 37–48. [Google Scholar] [CrossRef]
- Land, C.S. Calculation of imbibition relative permeability for two-and three-phase flow from rock properties. Soc. Pet. Eng. J. 1968, 8, 149–156. [Google Scholar] [CrossRef]
- Maalim, A.A.; Mahmud, H.B.; Seyyedi, M. Assessing roles of geochemical reactions on CO2 plume, injectivity and residual trapping. Energy Geosci. 2021, 2, 327–336. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).