Flow and Heat Transfer Characteristics of Superheater Tube of a Pulverized Coal-Fired Boiler Using Conjugate Heat Transfer Modeling
Abstract
1. Introduction
2. Modeling and Methodology
2.1. Physical Model
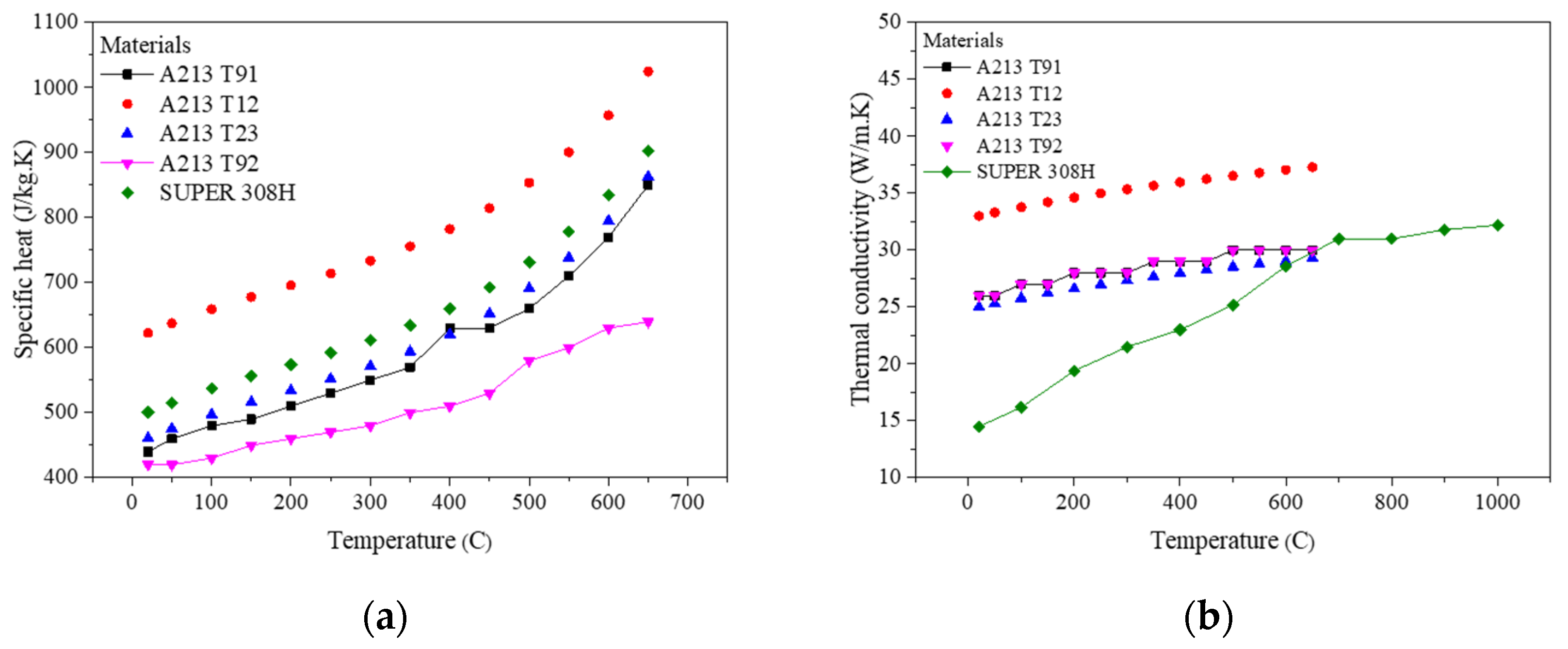
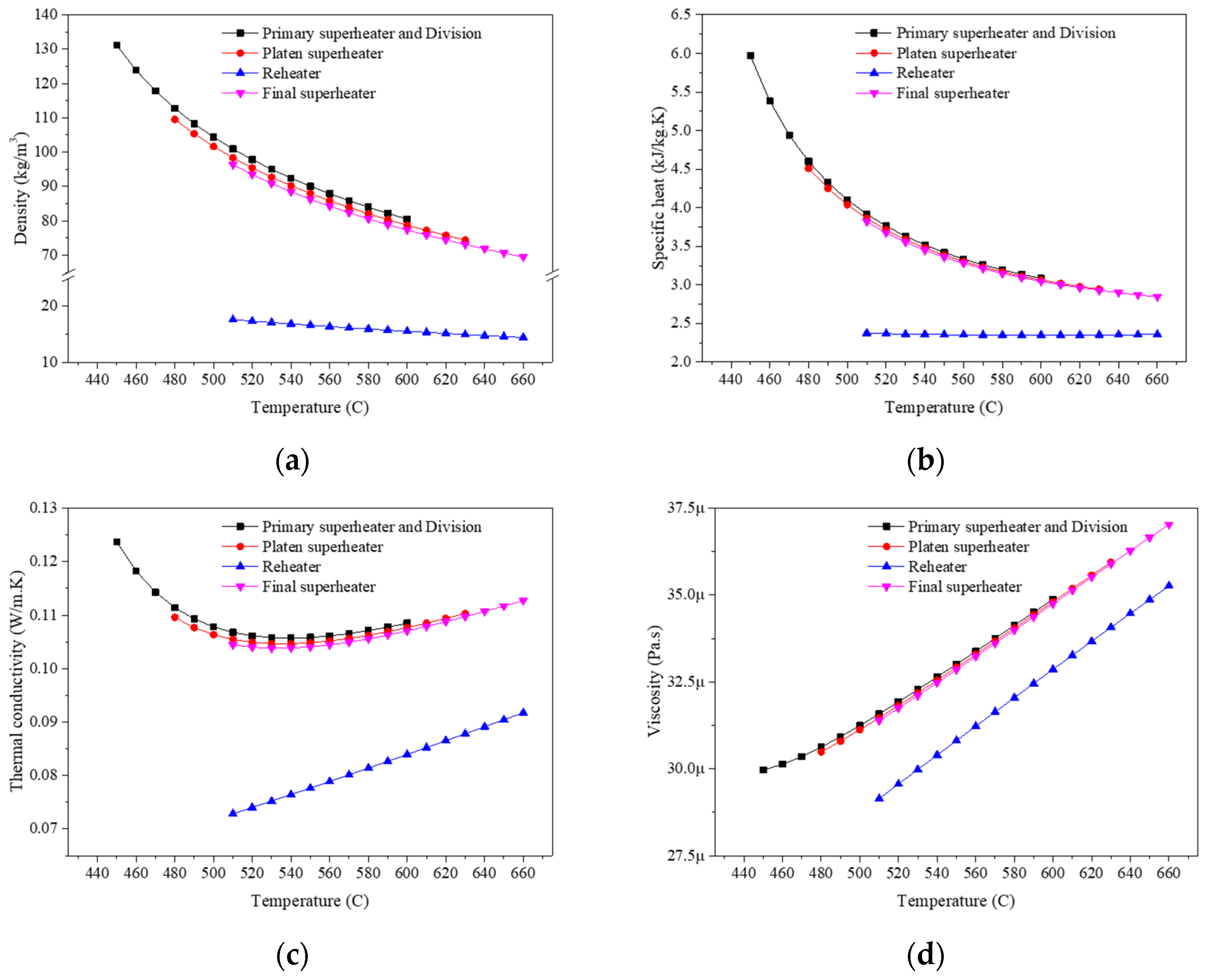
2.2. Thermophysical Properties
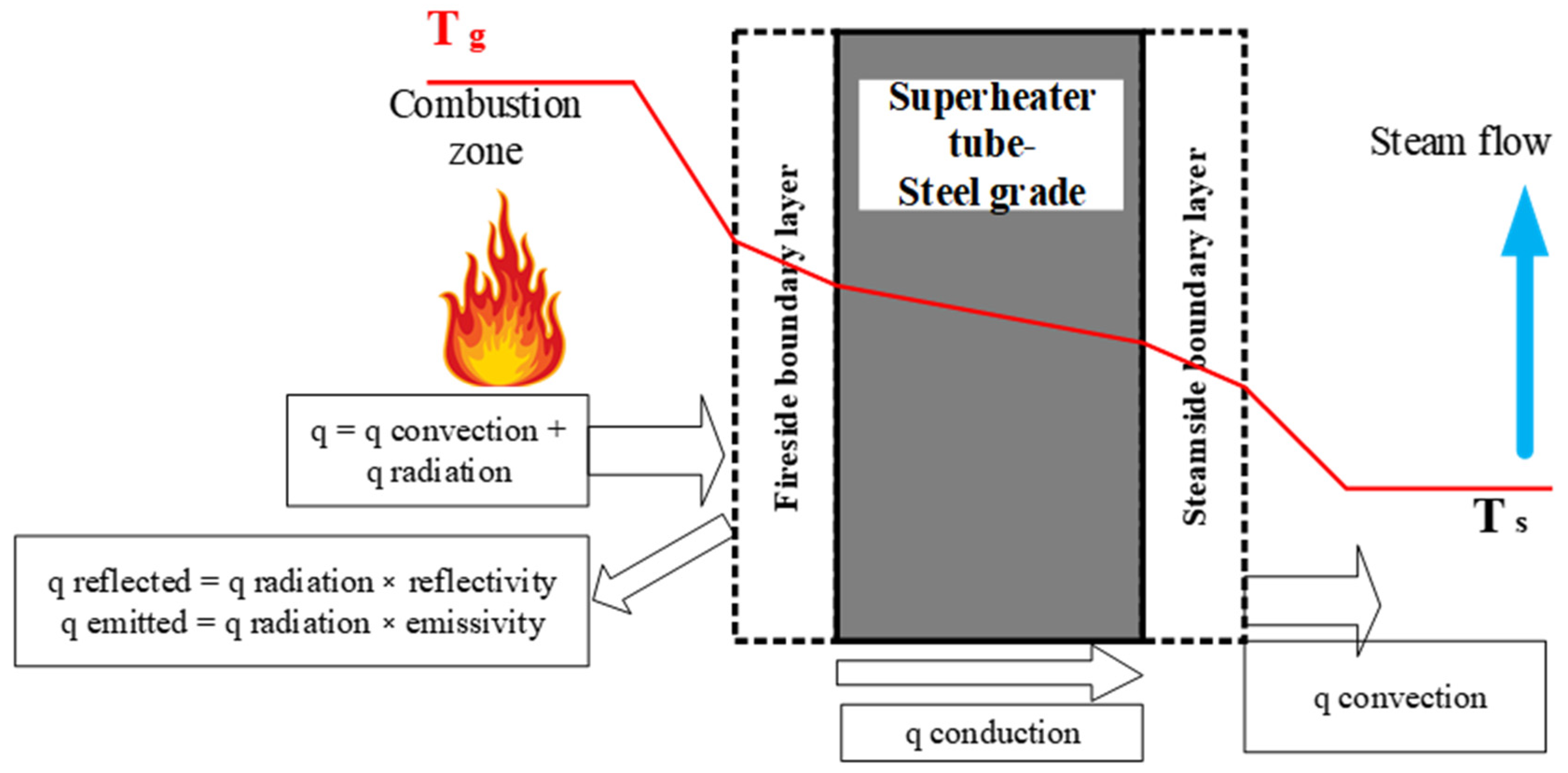
2.3. Mathematical Models
2.4. Simulation Conditions
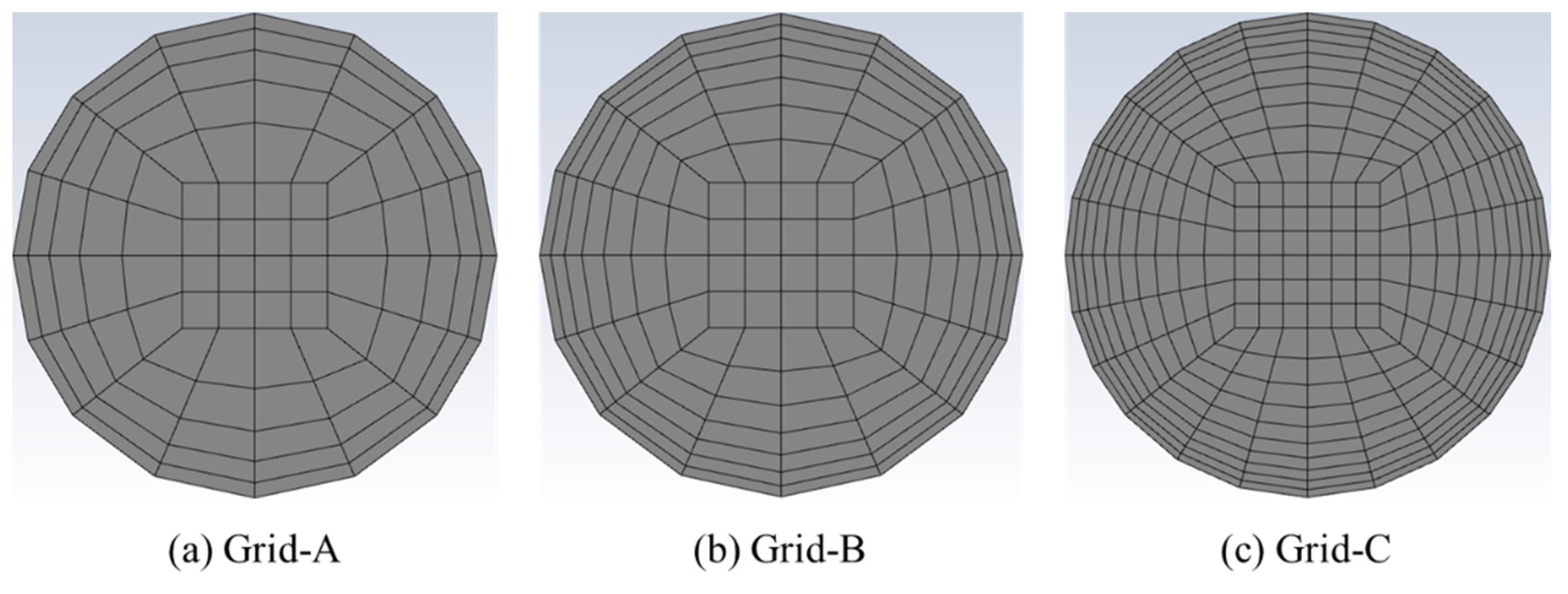
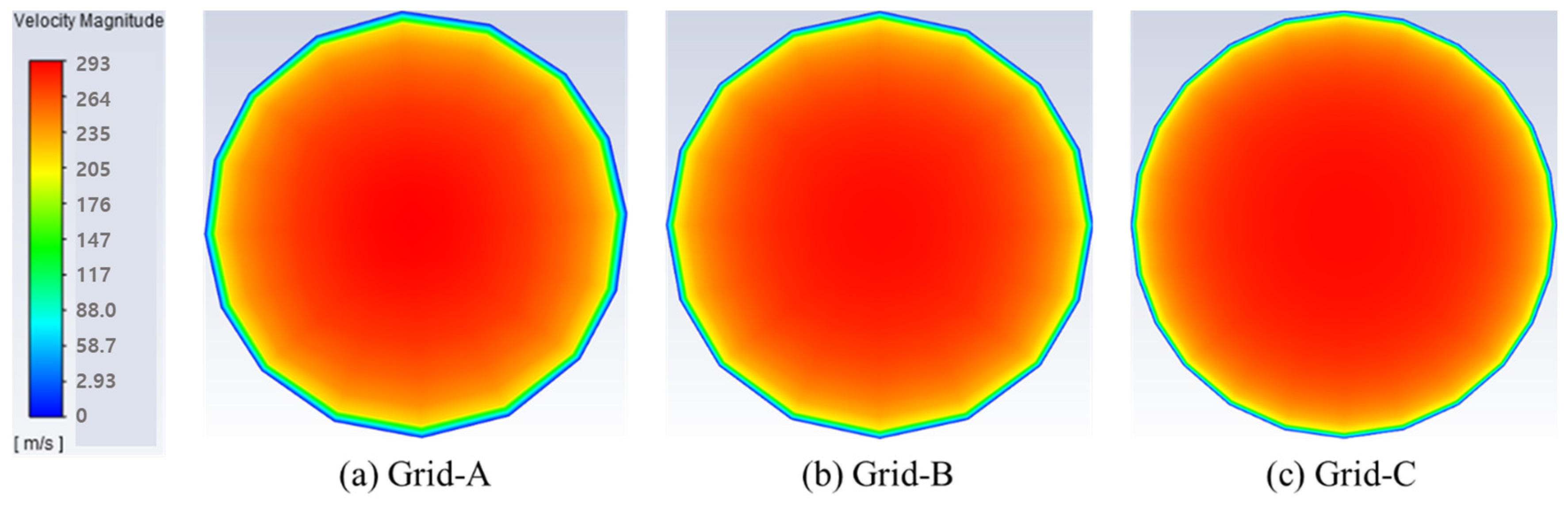
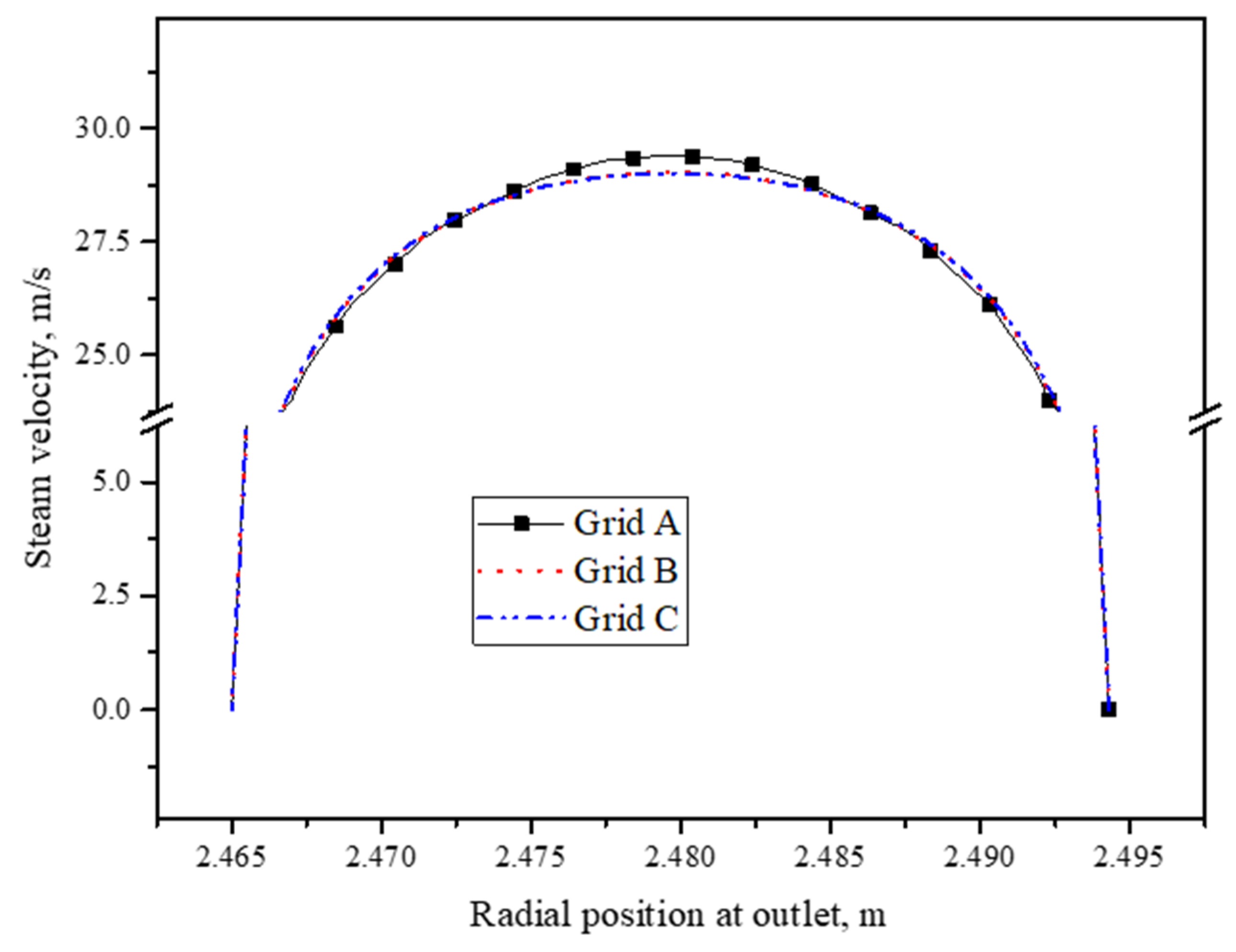
2.5. Grid Independence Study
3. Results and Discussion
3.1. Validation
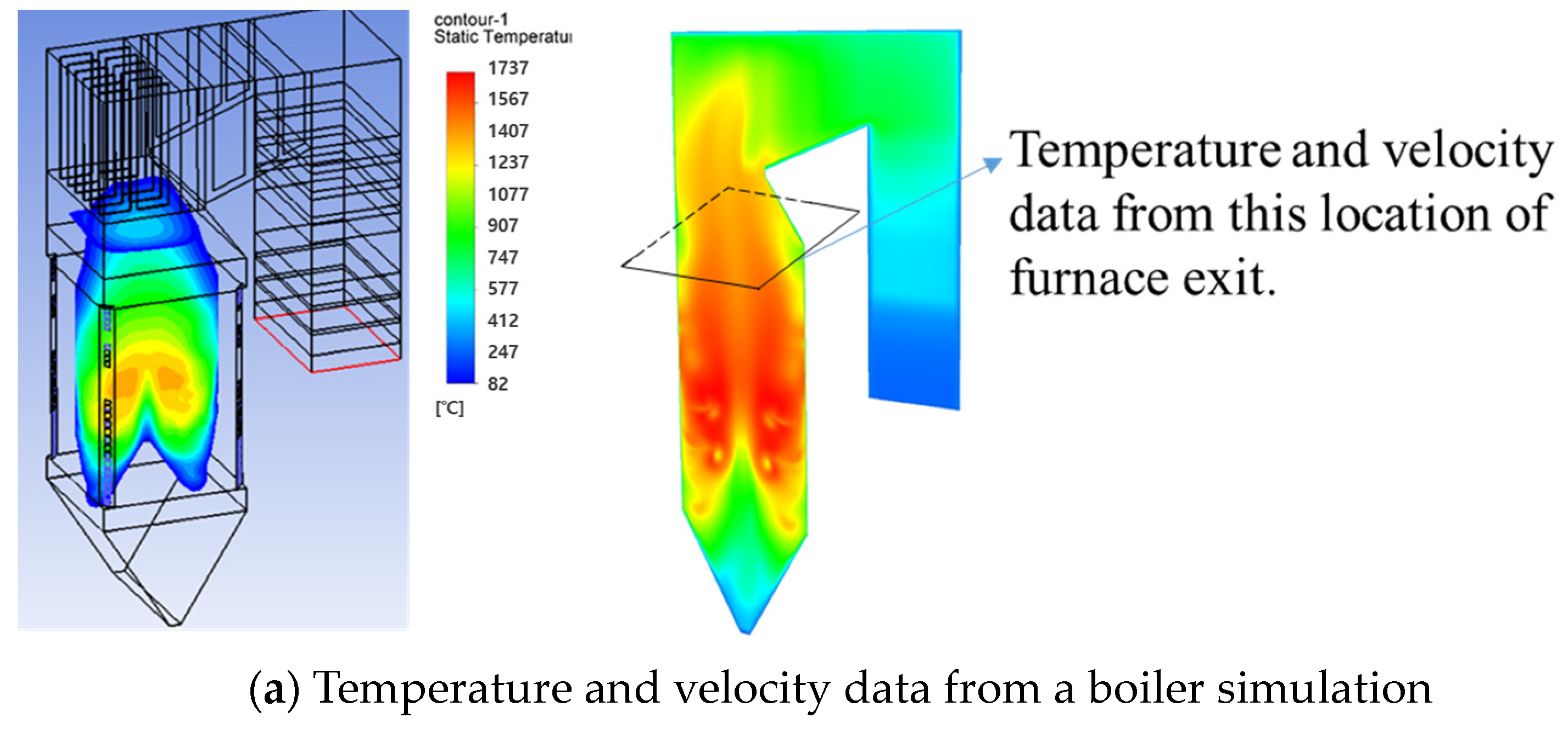
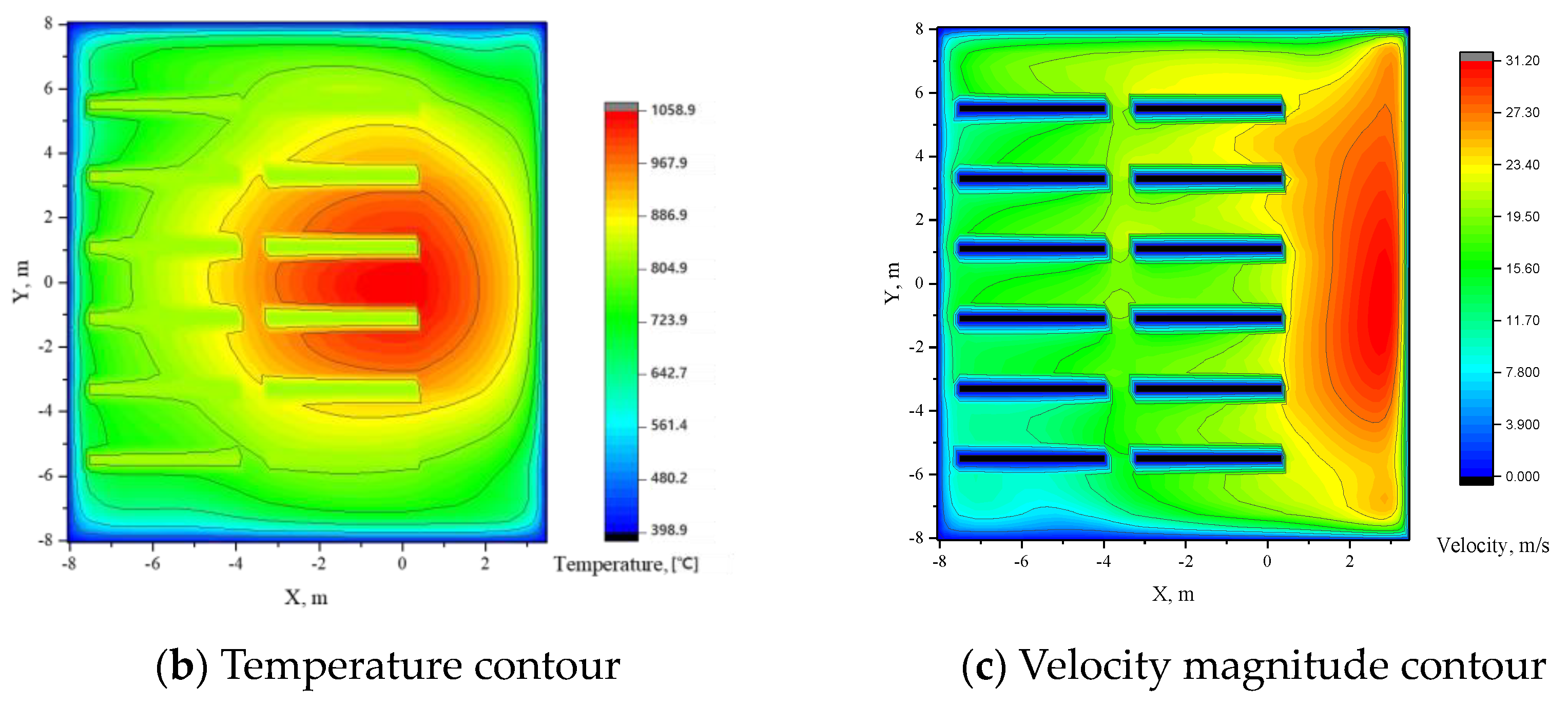
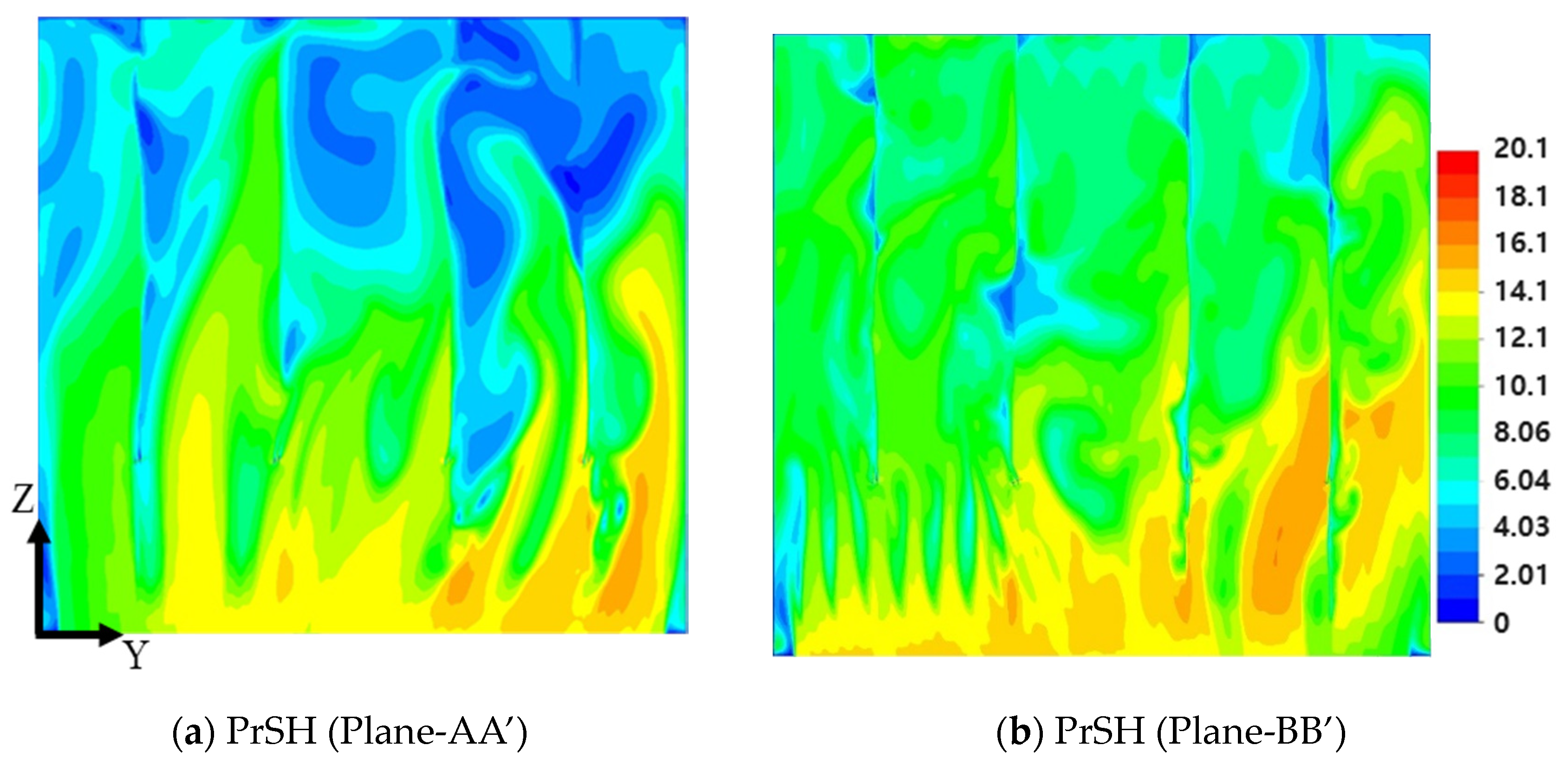
3.2. Hot Gas Flow Distribution in PrSH
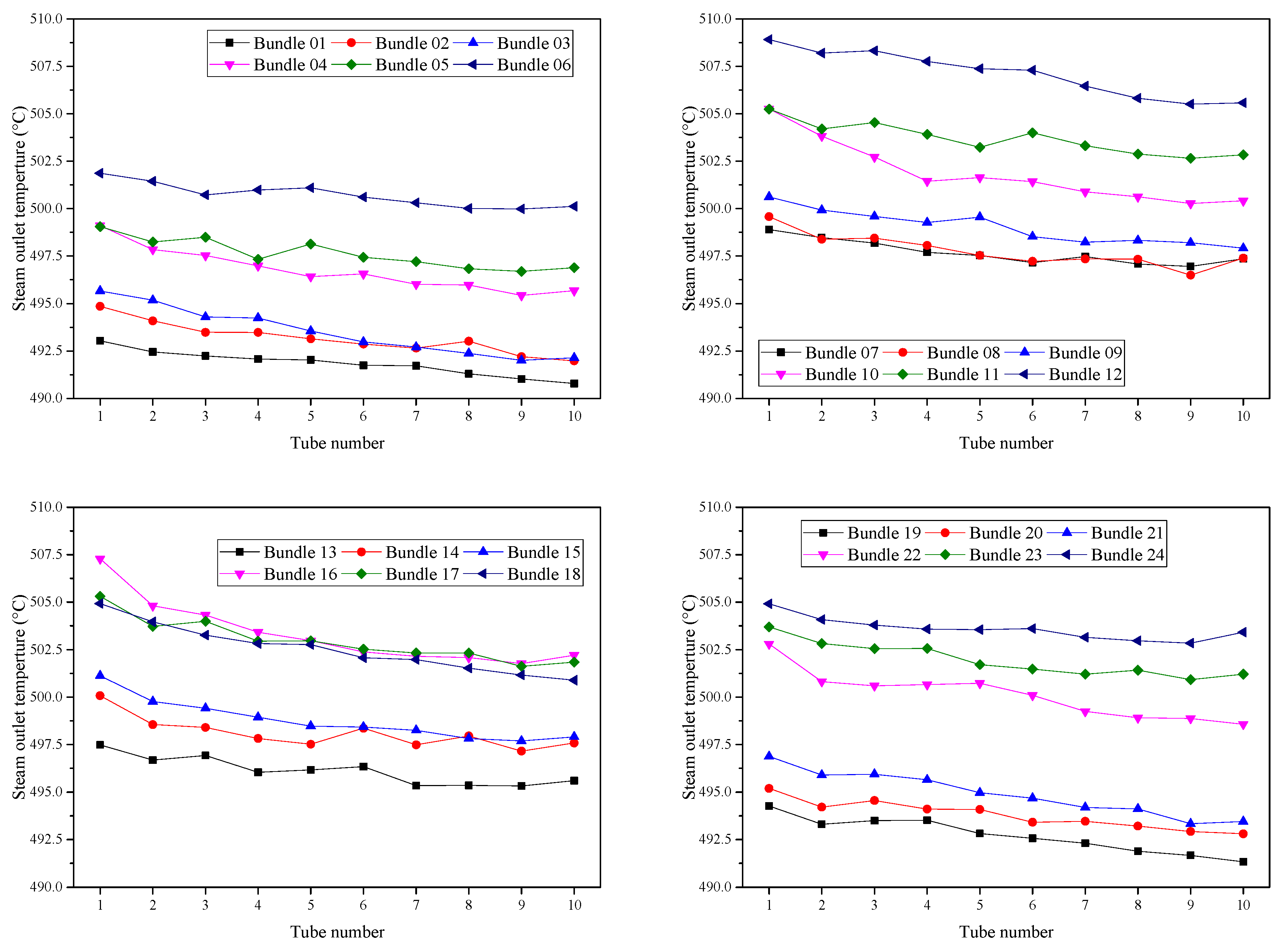
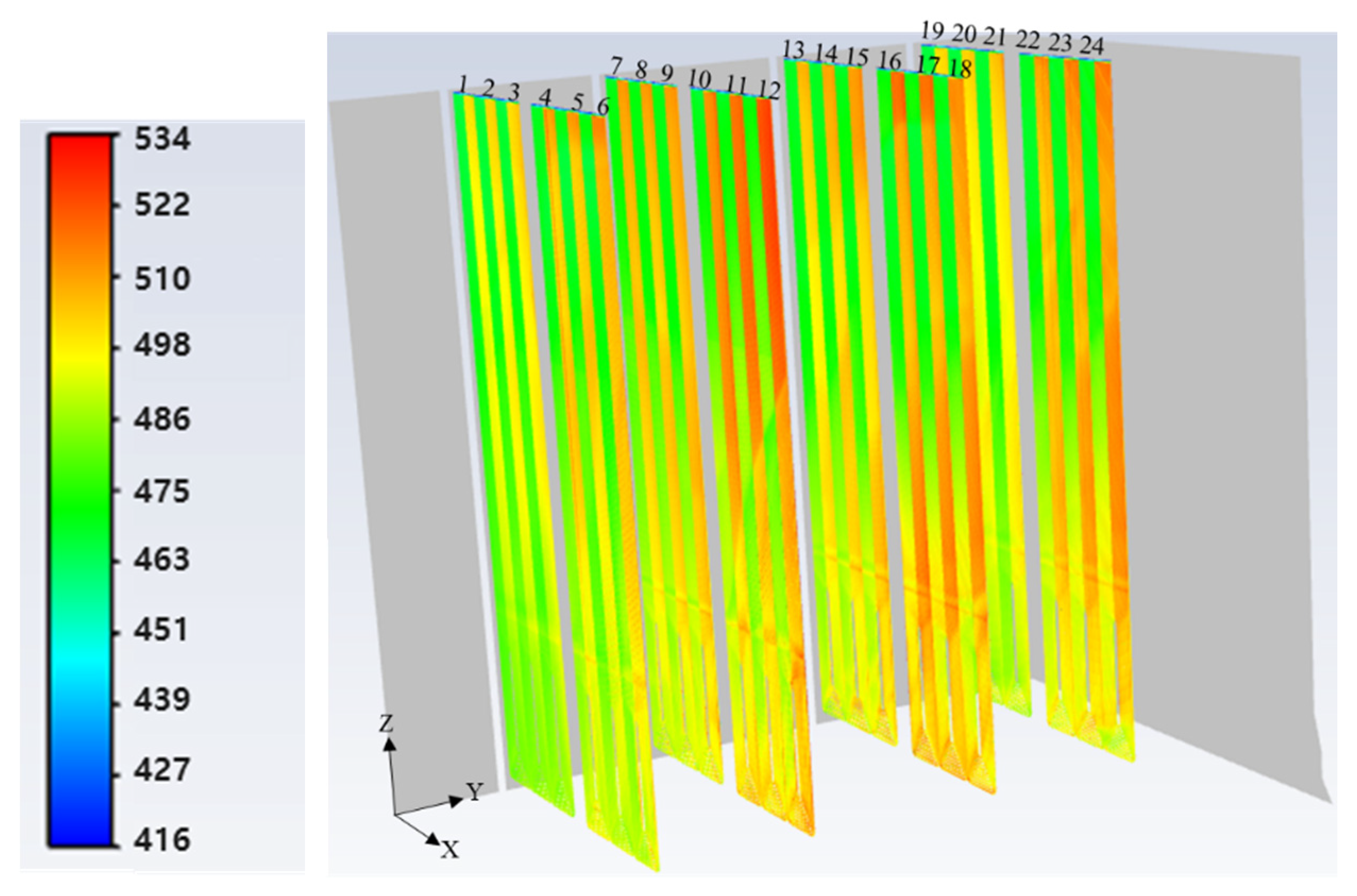
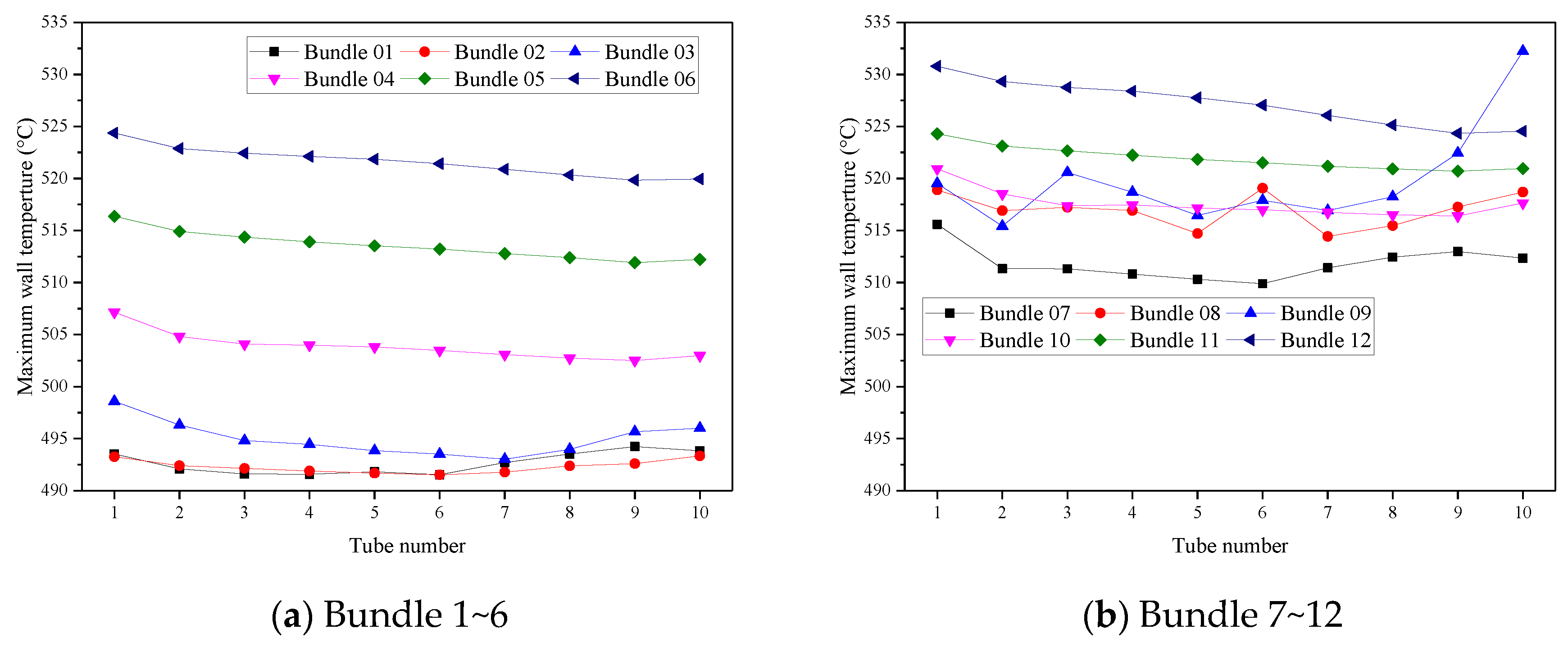
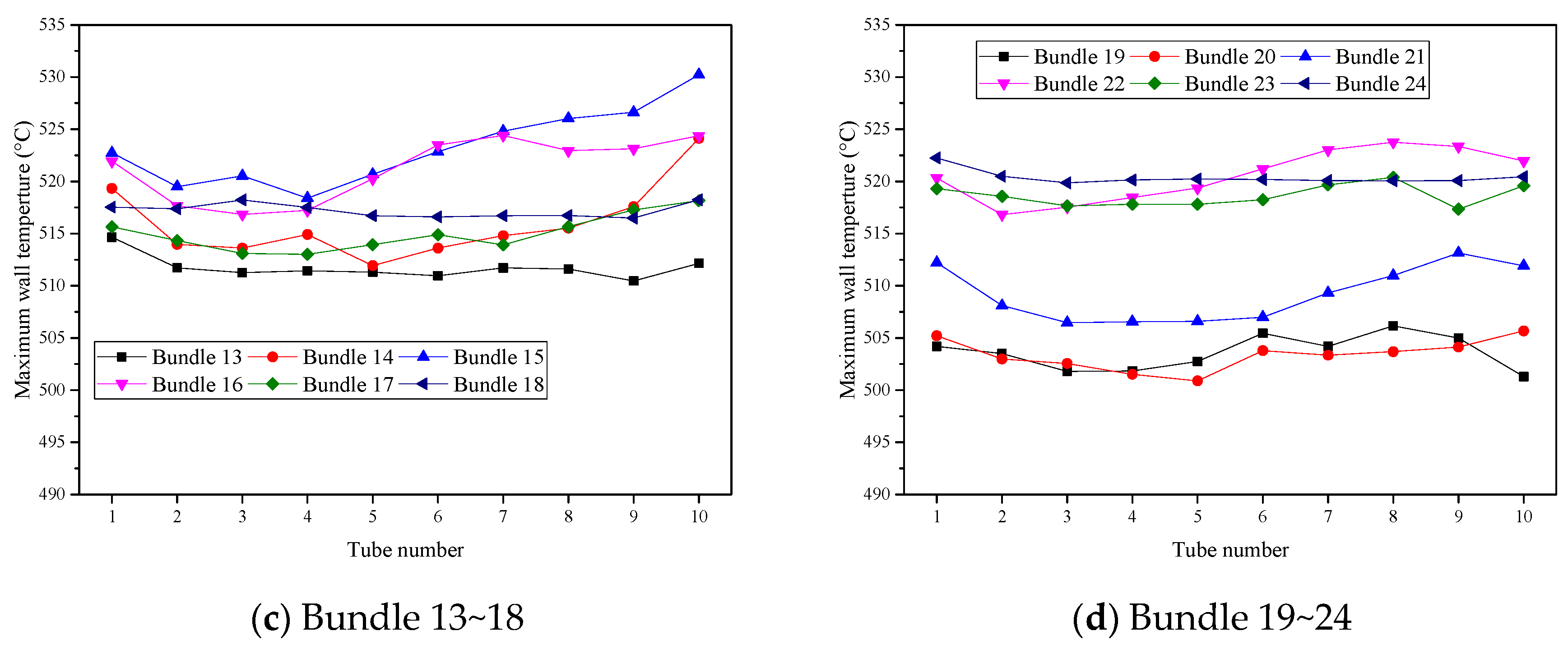
3.3. Wall Temperature and Steam Temperature of PrSH
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cai, Y.; Tay, K.; Zheng, Z.; Yang, W.; Wang, H.; Zeng, G.; Li, Z.; Siah, K.B.; Subbaiah, P. Modeling of ash formation and deposition processes in coal and biomass fired boilers: A comprehensive review. Appl. Energy 2018, 230, 1447–1544. [Google Scholar] [CrossRef]
- Sankar, G.; Kumar, D.S.; Balasubramanian, K.R. Computational modeling of pulverized coal fired boilers–A review on the current position. Fuel 2019, 236, 643–665. [Google Scholar] [CrossRef]
- Świeboda, T.; Krzyżyńska, R.; Bryszewska-Mazurek, A.; Mazurek, W.; Czapliński, T.; Przygoda, A. Advanced approach to modeling of pulverized coal boilers for SNCR process optimization-review and recommendations. Int. J. Thermofluids 2020, 7, 100051. [Google Scholar] [CrossRef]
- Modliński, N.; Szczepanek, K.; Nabagło, D.; Madejski, P.; Modliński, Z. Mathematical procedure for predicting tube metal temperature in the second stage reheater of the operating flexibly steam boiler. Appl. Therm. Eng. 2019, 146, 854–865. [Google Scholar] [CrossRef]
- Park, H.Y.; Faulkner, M.; Turrell, M.D.; Stopford, P.J.; Kang, D.S. Coupled fluid dynamics and whole plant simulation of coal combustion in a tangentially-fired boiler. Fuel 2010, 89, 2001–2010. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, Y.J.; Liao, M.R.; Wang, W.Z. Coupled modeling of combustion and hydrodynamics for a coal-fired supercritical boiler. Fuel 2019, 240, 49–56. [Google Scholar] [CrossRef]
- Schuhbauer, C.; Angerer, M.; Spliethoff, H.; Kluger, F.; Tschaffon, H. Coupled simulation of a tangentially hard coal fired 700 °C boiler. Fuel 2014, 122, 149–163. [Google Scholar] [CrossRef]
- Ranade, V.; Gupta, D. Computational Modeling of Pulverized Coal Fired Boilers, 1st ed.; Taylor & Francis: Boca Raton, FL, USA, 2015. [Google Scholar]
- Liu, Y.; Fan, W.; Li, Y. Numerical investigation of air-staged combustion emphasizing char gasification and gas temperature deviation in a large-scale, tangentially fired pulverized-coal boiler. Appl. Energy 2016, 177, 323–334. [Google Scholar] [CrossRef]
- Park, H.Y.; Baek, S.H.; Kim, Y.J.; Kim, T.H.; Kang, D.S.; Kim, D.W. Numerical and experimental investigations on the gas temperature deviation in a large scale, advanced low NOx, tangentially fired pulverized coal boiler. Fuel 2013, 104, 641–646. [Google Scholar] [CrossRef]
- Choi, C.R.; Kim, C.N. Numerical investigation on the flow, combustion and NOx emission characteristics in a 500 MWe tangentially fired pulverized-coal boiler. Fuel 2009, 88, 1720–1731. [Google Scholar] [CrossRef]
- Diez, L.I.; Cortes, C.; Pallares, J. Numerical investigation of NOx emissions from a tangentially-fired utility boiler under conventional and over fire air operation. Fuel 2008, 87, 1259–1269. [Google Scholar] [CrossRef]
- Viswanathan, R.; Bakker, W. Materials for ultrasupercritical coal power plants—Boiler materials: Part 1. J. Mater. Eng. Perform. 2001, 10, 81–95. [Google Scholar] [CrossRef]
- French, D. Metallurgical Failures in Fossil Fired Boilers; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Laubscher, R.; Rousseau, P. Coupled simulation and validation of a utility-scale pulverized coal-fired boiler radiant final-stage superheater. Therm. Sci. Eng. Prog. 2020, 18, 100512. [Google Scholar] [CrossRef]
- Modliński, N.; Madejski, P.; Janda, T.; Szczepanek, K.; Kordylewski, W. A validation of computational fluid dynamics temperature distribution prediction in a pulverized coal boiler with acoustic temperature measurement. Energy 2015, 92, 77–86. [Google Scholar] [CrossRef]
- Hottel, H.C.; Sarofim, A.F. Radiative Transfer; McGraw-Hill: New York, NY, USA, 1967. [Google Scholar]
- Smith, T.F.; Shen, Z.F.; Friedman, J.N. Evaluation of coefficients for the weighted sum of gray gases model. ASME J. Heat Transfer. 1982, 104, 602–608. [Google Scholar] [CrossRef]
- Laubscher, R.; Rousseau, P. CFD study of pulverized coal-fired boiler evaporator and radiant superheaters at varying loads. Appl. Therm. Eng. 2019, 160, 114057. [Google Scholar] [CrossRef]
- Vuthaluru, R.; Vuthaluru, H.B. Modelling of a wall fired furnace for different operating conditions using FLUENT. Fuel Process. Technol. 2006, 87, 633–639. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Y.; Yi, G.; Nie, L.; Che, D. Effects of air staging conditions on the combustion and NOx emission characteristics in a 600 MW wall fired utility boiler using lean coal. Energy Fuels 2013, 27, 5831–5840. [Google Scholar] [CrossRef]
- Taler, D.; Taler, J. Simplified analysis of radiation heat exchange in boiler superheaters. Heat Transf. Eng. 2009, 30, 661–669. [Google Scholar] [CrossRef]
- ANSYS, Inc. Fluent 2019 R3 Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2019. [Google Scholar]
- Gandhi, M.B.; Vuthaluru, R.; Vuthaluru, H.; French, D.; Shah, K. CFD based prediction of erosion rate in large scale wall-fired boiler. Appl. Therm. Eng. 2012, 42, 90–100. [Google Scholar] [CrossRef]
- Chen, K.; Liu, X.; Qin, Y. Numerical study on the influence of platen super-heater on combustion characteristics in a 600 MW tangentially fired pulverized-coal boiler. Therm. Sci. 2021, 25, 833–843. [Google Scholar] [CrossRef]
- Maakala, V.; Järvinen, M.; Vuorinen, V. Computational fluid dynamics modeling and experimental validation of heat transfer and fluid flow in the recovery boiler superheater region. Appl. Therm. Eng. 2018, 139, 222–238. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, C.; Liu, X. Heat transfer calculation methods in three-dimensional CFD model for pulverized coal-fired boilers. Appl. Therm. Eng. 2020, 166, 114633. [Google Scholar] [CrossRef]
- Graeser, P.; Schiemann, M. Investigations on the emissivity of burning coal char particles: Influence of particle temperature and composition of reaction atmosphere. Fuel 2020, 263, 116714. [Google Scholar] [CrossRef]
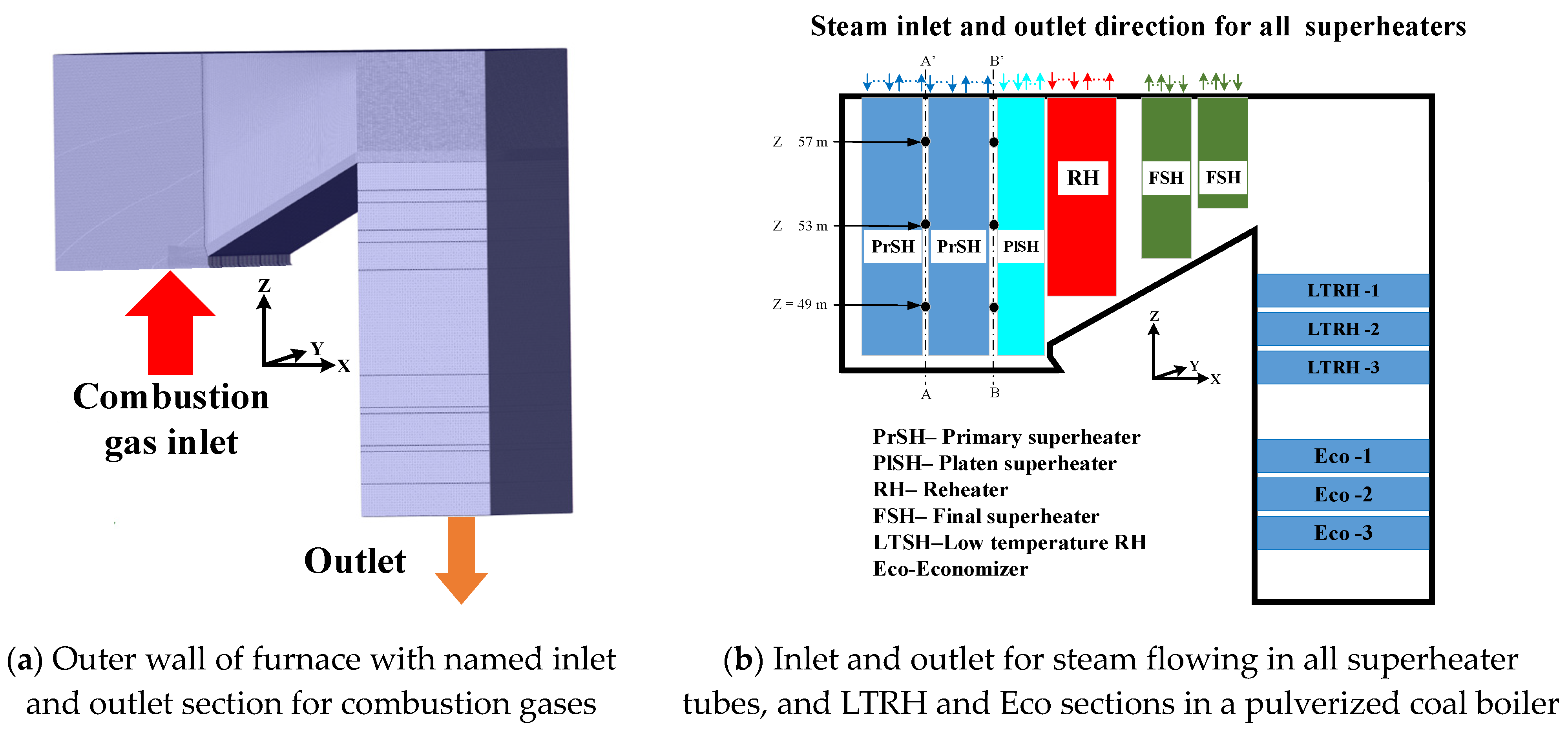
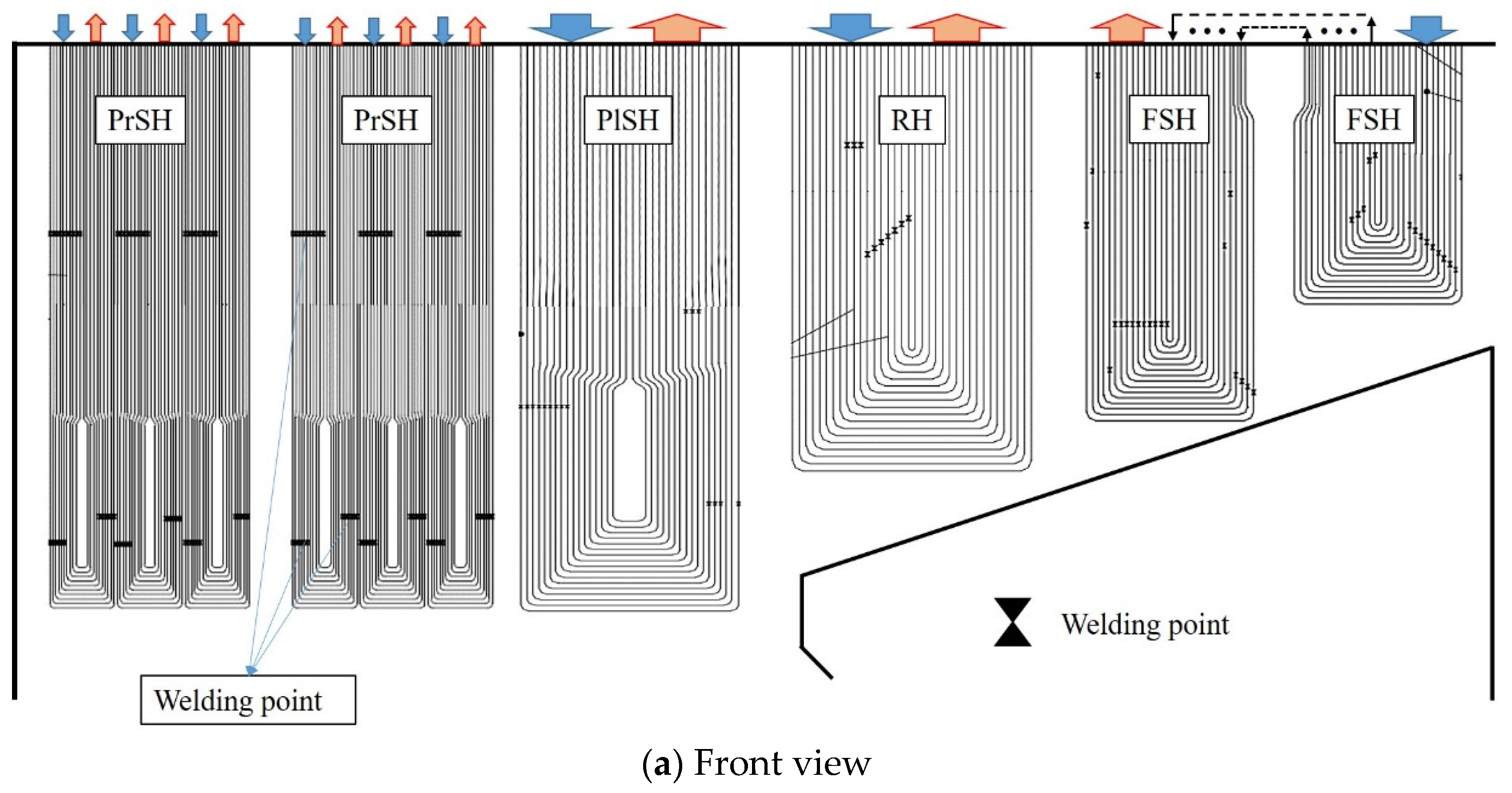
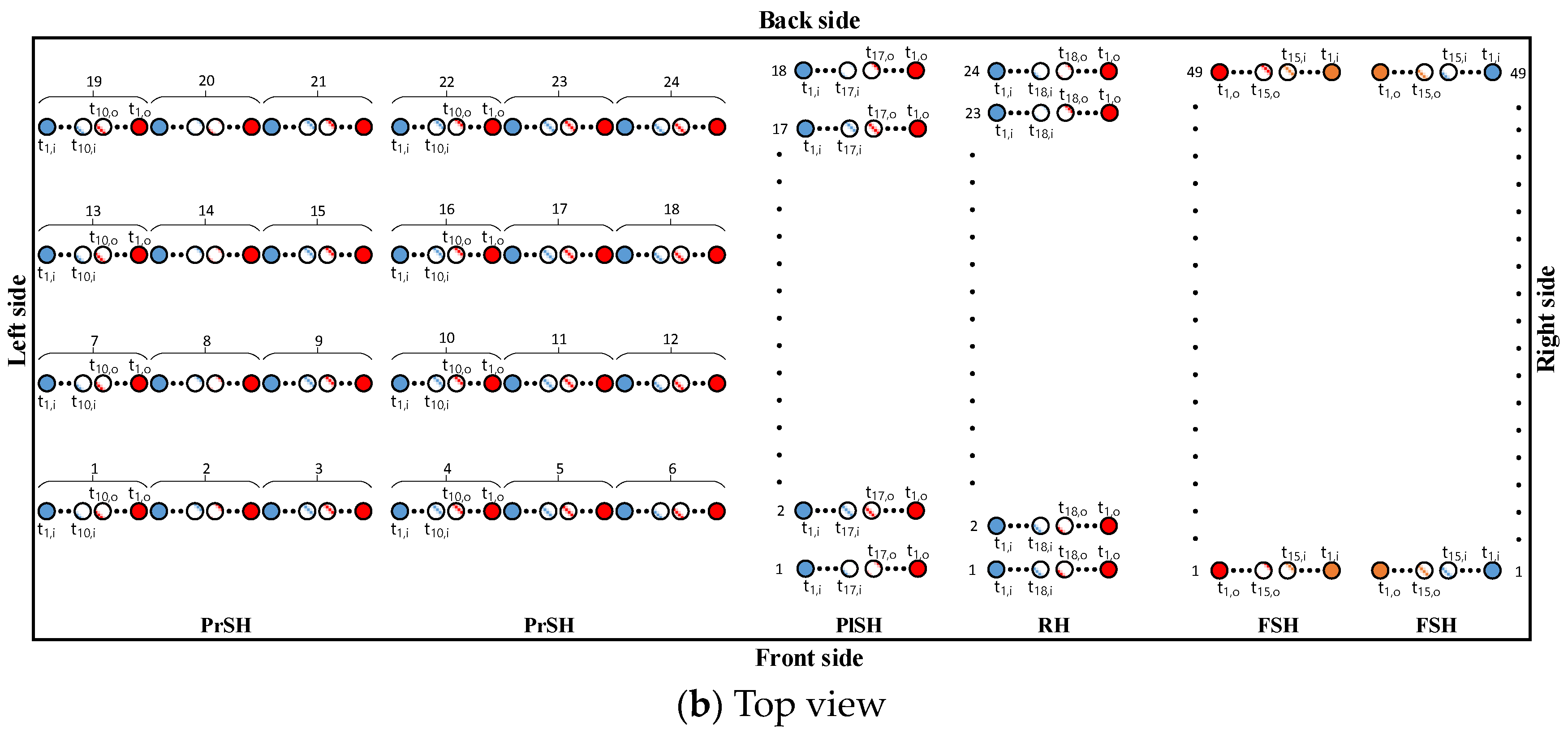




| Turbulence Model | Radiation Model | Emissivity | References | |
|---|---|---|---|---|
| Flue Gas | Wall | |||
| Realizable k-epsilon | Discrete ordinates | 0.9 in WSGGM | 0.85 | [15] |
| Realizable k-epsilon | Discrete ordinates | Not considered | 0.5, 0.7, 0.7 | [16] |
| Realizable k-epsilon | Discrete ordinates | 0.9 in WSGGM | - | [19] |
| Realizable k-epsilon | P-1 | Not considered | 0.8 | [20] |
| Standard k-epsilon | P-1 | WSGGM | 0.8 | [21] |
| Not mentioned | P-1, DTRM, DO | 0.2855, 0.1195, 0.295 | 0.8 | [22] |
| Standard k-epsilon | P-1 | WSGGM | Not mentioned | [24] |
| Superheater | Tube No. | Inlet to Outlet | ||||
|---|---|---|---|---|---|---|
| PrSH | Section-1 | Section-2 | Section-3 | Section-4 | ||
| Material type | 1~6 | A213-T12 | A213-T23 | A213-T91 | A213-T23 | |
| Length, m | 4.4 | 7.8 | 2.9 | 11.9 | ||
| Material type | 7~10 | A213-T12 | A213-T23 | - | - | |
| Length, m | 4.4 | 21.3 | - | - | ||
| PlSH | Material type | 1 | A213-T91 | SUPER304H | A213-T91 | |
| Length, m | 10.3 | 6.3 | 11.7 | |||
| Material type | 2~3 | A213-T23 | A213-T91 | |||
| Length, m | 10.3 | 17.8 | ||||
| Material type | 4~6 | A213-T23 | A213-T91 | A213-T23 | ||
| Length, m | 10.3 | 5.3 | 11.7 | |||
| Material type | 7~9 | A213-T23 | ||||
| Length, m | 26.5 | |||||
| Material type | 10~17 | A213-T23 | ||||
| Length, m | 25.5 | |||||
| RH | Material type | 1 | SUPER304H | |||
| Length, m | 23.3 | |||||
| Material type | 2 | SUPER304H | ||||
| Length, m | 23 | |||||
| Material type | 3~5 | SUPER304H | ||||
| Length, m | 21.8 | |||||
| Material type | 6~8 | A213-T92 | ||||
| Length, m | 21.4 | |||||
| Material type | 9 | A213-T23 | A213-T92 | |||
| Length, m | 2.5 | 17.6 | ||||
| Material type | 10~15 | A213-T23 | A213-T92 | |||
| Length, m | 4.6 | 14.5 | ||||
| FSH | Material type | 1~49 | A213-T91 | |||
| Length, m | 30~35 | |||||
| Superheater | Unit: mm | Tube No. | Inlet to Outlet | |||
|---|---|---|---|---|---|---|
| PrSH | Section-1 | Section-2 | Section-3 | Section-4 | ||
| Inner diameter | 1~6 | 35.3 | 36.8 | 36.8 | 36.8 | |
| Thickness | 7.75 | 7.0 | 7.0 | 7.0 | ||
| Inner diameter | 7~10 | 35.3 | 36.8 | - | - | |
| Thickness | 7.75 | 7.0 | - | - | ||
| PlSH | Inner diameter | 1 | 35 | 36.6 | 35 | |
| Thickness | 7.9 | 7.1 | 7.9 | - | ||
| Inner diameter | 2~3 | 35 | 35 | - | - | |
| Thickness | 7.9 | 7.9 | - | - | ||
| Inner diameter | 4~6 | 35.9 | 35 | 35 | - | |
| Thickness | 7.45 | 7.9 | 7.9 | - | ||
| Inner diameter | 7~9 | 35.9 | - | - | - | |
| Thickness | 7.45 | - | - | - | ||
| Inner diameter | 10~17 | 35.9 | - | - | - | |
| Thickness | 7.45 | - | - | - | ||
| RH | Inner diameter | 1 | 60.8 | - | - | - |
| Thickness | 4.6 | - | - | - | ||
| Inner diameter | 2~15 | 54.5 | - | - | - | |
| Thickness | 4.5 | - | - | - | ||
| FSH | Inner diameter | 1~49 | 29.3 | - | - | - |
| Thickness | 6.45 | - | - | - | ||
| Superheater | Steam Inlet | Steam Outlet | |
|---|---|---|---|
| P (atm) | T (℃) | (kg/s) | |
| PrSH | 276 | 459 | 1.8 |
| PlSH | 270 | 481 | 1.5 |
| RH | 60 | 517 | 0.9 |
| FSH | 266 | 514 | 0.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radhakrishnan, K.; Park, J.S. Flow and Heat Transfer Characteristics of Superheater Tube of a Pulverized Coal-Fired Boiler Using Conjugate Heat Transfer Modeling. Energies 2024, 17, 1161. https://doi.org/10.3390/en17051161
Radhakrishnan K, Park JS. Flow and Heat Transfer Characteristics of Superheater Tube of a Pulverized Coal-Fired Boiler Using Conjugate Heat Transfer Modeling. Energies. 2024; 17(5):1161. https://doi.org/10.3390/en17051161
Chicago/Turabian StyleRadhakrishnan, Kanmaniraja, and Jun Su Park. 2024. "Flow and Heat Transfer Characteristics of Superheater Tube of a Pulverized Coal-Fired Boiler Using Conjugate Heat Transfer Modeling" Energies 17, no. 5: 1161. https://doi.org/10.3390/en17051161
APA StyleRadhakrishnan, K., & Park, J. S. (2024). Flow and Heat Transfer Characteristics of Superheater Tube of a Pulverized Coal-Fired Boiler Using Conjugate Heat Transfer Modeling. Energies, 17(5), 1161. https://doi.org/10.3390/en17051161







