Research on Parameter Inversion of Coal Mining Subsidence Prediction Model Based on Improved Whale Optimization Algorithm

Abstract

Rapid coal mining results in a series of mining subsidence damages. Predicting surface movement and deformation accurately is essential to reducing mining damage. The accurate determination of parameters for a mining subsidence prediction model is crucial for accurately predicting mining subsidence. In this research, with the incorporation of the Sobol sequence and Lévy flight strategy, we propose an improved whale optimization algorithm (IWOA), thereby enhancing its global optimization capability and mitigating local optimization issues. Our simulation experiment results demonstrate that the IWOA achieved a root mean square error and relative error of less than 0.42 and 0.27%, respectively, indicating its superior accuracy compared to a basic algorithm. The IWOA inversion model also exhibits superior performance compared to a basic algorithm in mitigating gross error interference, Gaussian noise interference, and missing observation point interference. Additionally, it demonstrates enhanced global search capabilities. The IWOA was employed to perform parameter inversion for the working face 1414(1) in Guqiao Coal Mine. The root mean square error of the inversion results did not exceed 6.03, while the subsidence coefficient q, tangent of the main influence angle tanβ, horizontal movement coefficient b, and mining influence propagation angle θ were all below 0.32. The average value of the fitted root mean square error for the subsidence value’s fitted root mean square error and horizontal movement value’s fitted root mean square error of the IWOA was 91.51 mm, which satisfies the accuracy requirements for general engineering applications.

1. Introduction

The utilization of coal will remain predominant in China and unchanged in China’s economic development process for an extended period [1]. The rapid exploitation of coal will inevitably lead to deformation of overlying rock and settlement on the surface, resulting in a series of damages caused by mining subsidence. The accurate prediction of mining subsidence is crucial in mitigating the damage caused by coal mining, and obtaining high-precision parameters for prediction models is pivotal to achieving this goal. The study of the inversion method for mining subsidence prediction model parameters on the basis of measured surface data is therefore highly significant in accurately predicting mining subsidence and mitigating mining damage.

In the field of mining subsidence, the well-established and extensively utilized approach in China is the probability integral method (PIM), which is characterized by a multitude of parameters as well as a highly non-linear functional model. The traditional parameter inversion methods of this mining subsidence prediction model primarily consist of the linear approximation method [2], characteristic point method, and orthogonal experiment method [3]. However, these three algorithms possess certain drawbacks including a complex calculation process, low accuracy in parameter solving, and challenges in engineering applications. With the progressive advancement of intelligent optimization algorithms in recent years, numerous domestic scholars have developed parameter inversion models based on these intelligent optimization algorithms. The mode vector method was employed by Ge [4] to solve probability integral parameters, yielding results that are relatively accurate and reliable. The genetic algorithm inversion model was constructed by Zha et al. [5]. The inversion results obtained from this model exhibit high accuracy and robust anti-interference capability. The invasive weed optimization algorithm was employed by Yang et al. [6] to determine the parameters of the PIM, yielding parameter evaluation results that demonstrated enhanced accuracy, adaptability, and robustness. The wolf pack algorithm was incorporated by Li et al. [7] into the parameter inversion of PIM, resulting in inversion results that exhibit excellent robustness and meet the accuracy requirements for engineering applications. Teng et al. [8] developed a parameter inversion model on the basis of a shuffled frog leaping algorithm and demonstrated its effectiveness through simulation tests and engineering applications. The whale optimization algorithm (WOA) exhibits strong global search capabilities, superior performance, and simplicity in implementation, and it finds wide applications in facial recognition [9], feature selection [10], and various other fields. However, there are also shortcomings with a slow convergence speed, low solving accuracy, as well as a tendency to get trapped in local optima during later iterations.

In this study, an IWOA-based inversion model was constructed by improving the whale optimization algorithm using the Sobol sequence and the Lévy flight strategy. Additionally, a parameter inversion model based on IWOA was constructed. Simulation tests were devised to validate the reliability of the IWOA parameter inversion model, while also discussing its resistance against interference and global search capabilities. Finally, the model was implemented in engineering practice.

2. Probability Integral Method Predicted Model

Stochastic media theory considers the movement of rock particle media caused by mining subsidence as a random process obeying a statistic law [11]. Building upon this concept, Liu et al. developed the probability integral method (PIM), which represents the granular media movement law as a probability density function integral equation [12]. This approach has been widely adopted in mining subsidence prediction. As depicted in Figure 1 is its theoretical model.

The particle medium, assumed to have a uniform size and shape and be infinitesimally small as depicted in Figure 1a, exhibits a probabilistic behavior when the a₁ particle from the first layer is removed. Specifically, there is a 1/2 probability for particles a₂ and b₂ from the second layer to fill the void left by a₁, while particles a₃, b₃, and c₃ from the third layer have probabilities of 1/4, 2/4, and 1/4, respectively, to occupy the voids in the second layer. This process continues until an overall subsidence basin forms on the surface. The dynamics of granular media can be effectively described by a probability density function that tends towards a normal distribution in terms of its shape characteristics, as illustrated in Figure 1b.

While mining a tiny cell n(s, v), the subsidence value W(x, y) and the horizontal movement value U(x, y, φ) along the φ on the surface can be calculated, utilizing eight predicted parameters of the PIM: the mining influence propagation angle θ, tangent of main influence angle tanβ, horizontal movement coefficient b, subsidence coefficient q, upper inflection point offset S_u, lower inflection point offset S_d, and left and right inflection point offset S_l, S_r. The calculation formulas for these values are presented in Equations (1) and (3), respectively.

$$W\left(x,y\right)=W_{\max }{\displaystyle {\int }_0^{D_3}{\displaystyle {\int }_0^{D_1}\frac{{\left(\tan \beta \right)}^2}{H^2}{e}^{-\pi \frac{{\left(x-s\right)}^2+{\left(y-v\right)}^2}{r^2}}}}dvds=\frac{1}{W_{\max }}{W}^0\left(x\right)W^0\left(y\right)$$

(1)

$$\{\begin{array}{l}\begin{array}{l}\begin{array}{l}{W}^0\left(x\right)=\frac{W_{\max }}{2}\left\{\left[erf\left(\frac{\sqrt{\pi }\tan \beta }{H}x\right)+1\right]-\left[erf\left(\frac{\sqrt{\pi }\tan \beta }{H}\left(x-l_3\right)\right)+1\right]\right\}\hfill \\ W^0\left(y\right)=\frac{W_{\max }}{2}\left\{\left[erf\left(\frac{\sqrt{\pi }\tan {\beta }_1}{H_1}y\right)+1\right]-\left[erf\left(\frac{\sqrt{\pi }\tan {\beta }_2}{H_2}\left(y-l_1\right)\right)+1\right]\right\}\hfill \end{array}\hfill \end{array}\hfill \end{array}$$

(2)

$$U\left(x,y,\phi \right)=br\frac{\partial W\left(x,y\right)}{\partial \phi }=\frac{br}{W_{\max }}\left[\frac{\partial W^0\left(x\right)}{\partial x}{W}^0\left(y\right)\cos \phi +\frac{\partial W^0\left(y\right)}{\partial y}{W}^0\left(x\right)\sin \phi \right]$$

(3)

where the maximum surface subsidence value W_max = mqcosα, α represents the dip in the coal seam, m denotes the thickness, φ indicates the counterclockwise rotation angle of the X-axis to a specified position, and erf refers to the error function. The calculated lengths of the strike and inclination for the working face can be calculated as l₃ = D₃ – S_l – S_r and l₁ = (D₁ − S_u − S_d)sin(θ + α)/sinθ, respectively. Here, D₃ and D₁ represent the strike length and inclination length, respectively. The strike average mining depth, the mining depth of the lower boundary, and the mining depth of the upper boundary are denoted as H, H₁, and H₂, respectively. The main influence angle tangents of descending and ascending mountains are represented by tanβ₁ and tanβ₂, respectively.

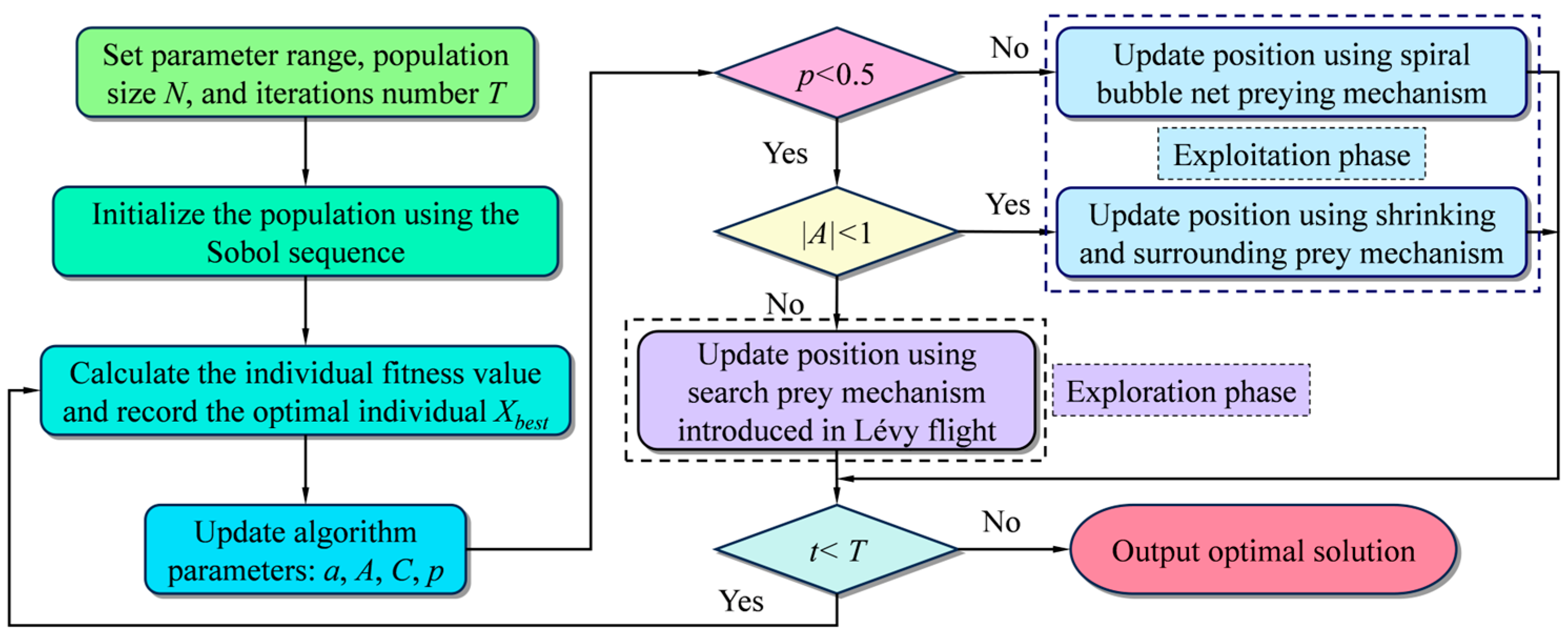
3. Parameter Inversion Model Based on IWOA

3.1. The Basic WOA

The basic whale optimization algorithm (WOA), proposed by Australian scholar Mirjalili S. and colleagues in 2016, emulates three mechanisms employed by humpback whales for prey encirclement: shrinking and encircling of prey, spiral bubble net hunting, and prey search [13]. The WOA assumes that the prey captured by the whale represents the optimal solution. In each iteration, the position update mechanism of each whale is determined by a random number p and a coefficient vector A [14].

3.1.1. Shrinking and Encircling of Prey

When |A| < 1, humpback whales are able to locate and encircle their prey [15]. As the optimal solution is uncertain within the search space, the target prey is assumed by the algorithm to be the solution with the optimal current adaptation value. Consequently, other whales will move towards this position with the behavior represented by Equation (4):

$$X\left(t+1\right)=X_{best}\left(t\right)-A\left|C{X}_{best}\left(t\right)-X\left(t\right)\right|$$

(4)

where X(t) represents the current whale position, X_best(t) represents the optimal individual position, T represents the current number of iterations, and A|CX_best(t) − X(t)| is the encircling step length of the current individual whale. The smaller A is, the smaller the swimming step length of the whale is. The coefficient vectors A and C are given by

$$A=2ar-a$$

(5)

$$C=2r$$

(6)

$$a=2-2\frac{t}{T}$$

(7)

where r is the random number in [0, 1] and T is the max iteration number.

3.1.2. Spiral Bubble Net Hunting

Humpback whales approach their prey along spirals and release a bubble net to ensnare their prey [16]. This behavior is emulated in the algorithm by narrowing down the search area as shown in Equation (8):

$$X\left(t+1\right)=X_{best}\left(t\right)+d{e}^{BL}cos\left(2pL\right)$$

(8)

$$d=\left|X_{best}\left(t\right)-X\left(t\right)\right|$$

(9)

where d expresses the distance between the target prey and the current individual whale, L is a randomly generated number between [−1, 1], and B is the constant coefficient that defines the shape of the helix.

3.1.3. Prey Search

Individual whales no longer update their positions according to the current optimal individual when |A| ≥ 1, but instead choose a random position. The mechanism can be expressed by Equation (10):

$$X\left(t+1\right)=X_{rand}-A\left|C{X}_{rand}-X\left(t\right)\right|$$

(10)

where X_rand(t) represents the stochastic selection of individual whales from the present population.

Humpback whales employ a spiral trajectory within a contracting circle to encircle their prey [17]. To simulate this coordinated behavior, we assume a 50% probability of selecting either a shrinking and encircling of prey mechanism or a spiral bubble net hunting mechanism for updating the position of a whale. This behavior can be represented by Equation (11):

$$X\left(t+1\right)=\{\begin{array}{l}{X}_{best}\left(t\right)-A\left|C{X}_{best}\left(t\right)-X\left(t\right)\right|,\hfill \\ X_{best}\left(t\right)+d{e}^{BL}\cos \left(2\pi L\right),\hfill \end{array}\begin{array}{c}if\begin{array}{c}\end{array}p<0.5\\ if\begin{array}{c}\end{array}p\ge 0.5\end{array}$$

(11)

3.2. Improvement Strategy

3.2.1. Sobol Sequence Initializes the Population

The distribution of initial solutions greatly affects an algorithm’s optimization accuracy and convergence speed, while the diverse and uniform ergodicity of a population distribution benefits the performance of the algorithm [18]. The basic WOA employs the Rand function to initialize the population, leading to an uneven distribution of whale population and significant randomness, which hampers the search for the global optimal location [19]. The Sobol sequence is employed for population initialization in order to mitigate the issue of blindness [20]. This approach ensures that the initial positions are more evenly distributed in the search space, thereby enhancing the diversity within the population. The two-dimensional random sequence distributions generated by the Sobol sequence and Rand function within the range of [0, 1] are depicted in Figure 2, under the condition that the population size is 1000. Upon comparison, it becomes evident that the population distribution obtained through the Sobol sequence exhibits a higher degree of regularity and uniformity, effectively covering the entire solution space.

3.2.2. Lévy Flight Strategy

In the exploration phase, a whale randomly selects a location within the current population as its target prey to update the locations of other individuals, thereby confining the algorithm to a limited search space and potentially trapping it in local optima. Lévy flight is a random walk process alternating between a short-distance search and long-distance walk, and its direction and step size are uncertain [21]. In the present research, the random step S generated by the Lévy flight strategy was incorporated into the prey seeking phase of the WOA, thereby enhancing its capacity for global exploration and preventing convergence to local optima. The mathematical representation of the Lévy flight strategy is as follows.

$$\mathrm{Levy}\left(S\right)\sim {\left|S\right|}^{-1-\beta },\begin{array}{l}\hfill \end{array}0<\beta \le 2$$

(12)

$$S=\frac{\mu }{{\left|\nu \right|}^{\frac{1}{\beta }}},\begin{array}{l}\hfill \end{array}\mu ~N\left(0,{\delta }_{\mu }^2\right),\begin{array}{l}\hfill \end{array}v~N(0,{\delta }_v^2)$$

(13)

$${\delta }_{\mu }={\left\{\frac{\mathsf{\Gamma }(\beta +1)\cdot \sin (\pi \beta /2)}{\beta \cdot 2^{\left(\beta -1\right)/2}\cdot \mathsf{\Gamma }\left[(\beta +1)/2\right]}\right\}}^{\frac{1}{\beta }}$$

(14)

where the value of β is set to 3/2, both μ and ν follow a normal distribution, the value of δ_ν is 1, and Γ is the gamma function.

The exploration phase position updates equation changes from Equation (10) to the following equation after the introduction of the Lévy flight strategy.

$$X\left(t+1\right)=X_{rand}-0.01\cdot \mathrm{sign}(\mathrm{rand}-0.5)\frac{\mu }{{\left|\nu \right|}^{\frac{1}{\beta }}}\cdot \left|X_{rand}-X\left(t\right)\right|$$

(15)

3.3. Parameter Inversion Model of the PIM

Combining the whale optimization algorithm with improved strategies and the PIM model, an inversion model for IWOA-based is constructed. The optimal solution is then searched for in accordance with the principle of minimizing the fitness function value. The parameters of this model are solved within the range ΔV = [Δq, Δtanβ, Δb, Δθ, ΔS_u, ΔS_d, ΔS_l, ΔS_r]. The central values of the parameters are V₀ = [q₀, tanβ₀, b₀, θ₀, S_u0, S_d0, S_l0, S_r0]. The constructed fitness function is shown in Equation (16).

$$F={\displaystyle \sum _{k=1}^M\left\{{\left[W_k\left(x,y\right)-W_k^0\left(x,y\right)\right]}^2+{\left[(U_k\left(x,y\right)-U_k^0\left(x,y\right)\right]}^2\right\}}$$

(16)

where W_k⁰(x, y) and W_k(x, y) represent the measured and predicted subsidence values at observation station k, respectively. Similarly, U_k⁰(x, y) and U_k(x, y) denote the measured and predicted horizontal movement values at observation station k. Additionally, M represents the total number of observation stations.

The parameter-solving procedure of the IWOA inversion model can be delineated as the following:

Step 1, Set the population size N = 100 and the number of iterations T = 300.

Step 2, Initialize the population using the Sobol sequence.

Step 3, Calculate the individual fitness value and record the current optimal individual X_best.

Step 4, Update algorithm parameters a, A, C, and p.

Step 5, When p < 0.5, if |A| < 1, the IWOA employs the shrinking and encircling of prey mechanism and utilizes Equation (4) to update the individual position. If |A| ≥ 1, the prey search mechanism with Lévy flight strategy is employed for global exploration, and the individual location is updated using Equation (15). When p ≥ 0.5, the spiral bubble net hunting mechanism is implemented, and the individual position is updated according to Equation (8).

Step 6, Verify if the iteration conditions are satisfied. If affirmative, output the global optimal solution; otherwise, proceed to Step 3 to continue executing the algorithm.

A flowchart depicting the IWOA inversion model is illustrated in Figure 3.

4. Simulation Experiment

To validate the accuracy of the inversion results obtained from the improved whale optimization algorithm, we designed a series of simulation experiments. The information regarding the simulated working face is the following: the average mining depth of the coal seam measured 400 m, with a mining thickness of 3.0 m and a coal seam dip of 5°. The strike length of the working face D₃ = 800 m, while the inclination length D₁ = 500 m. Additionally, the roof management technique employed involved a caving method.

Table 1. Parameters and fluctuation ranges of the simulated working face.

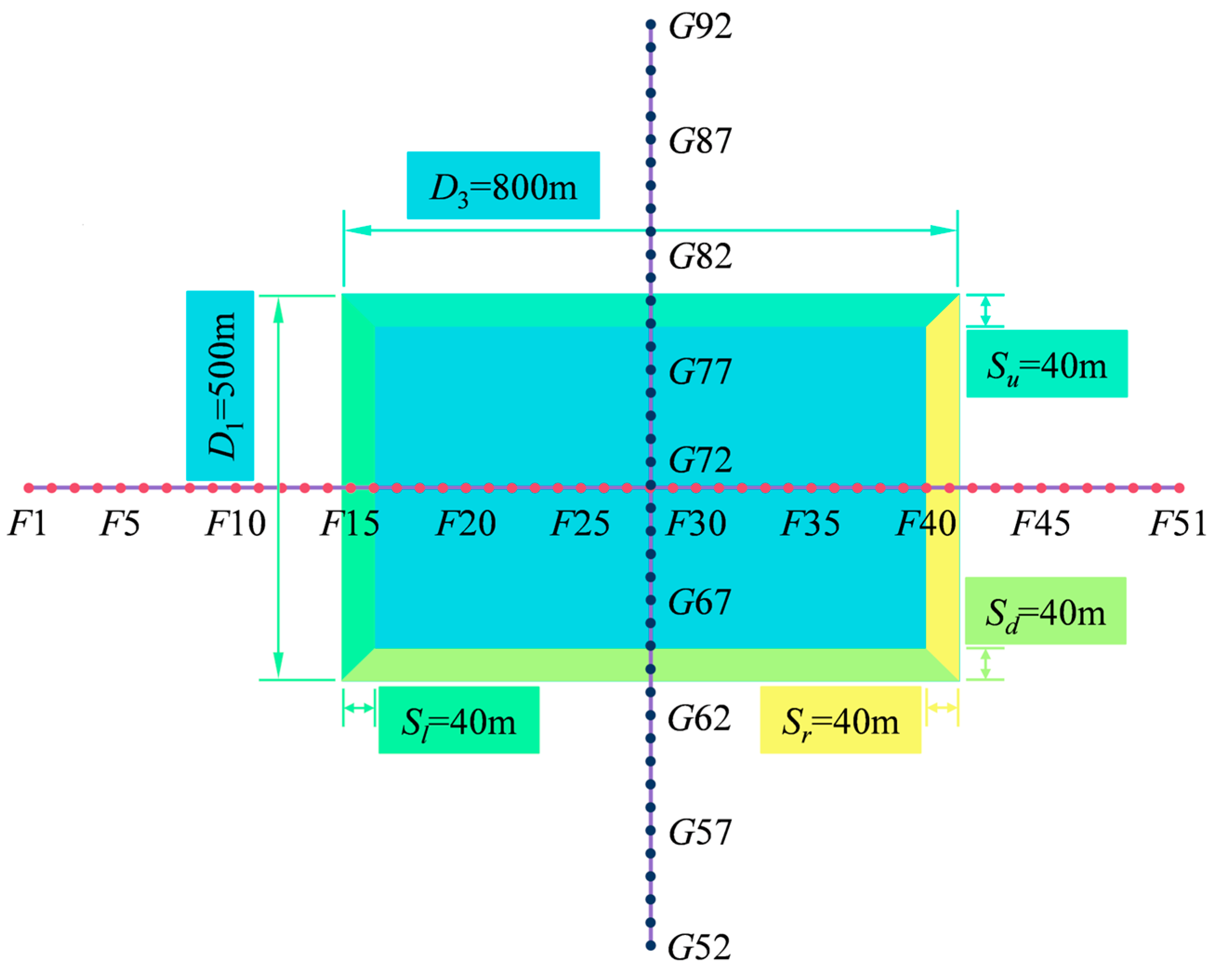
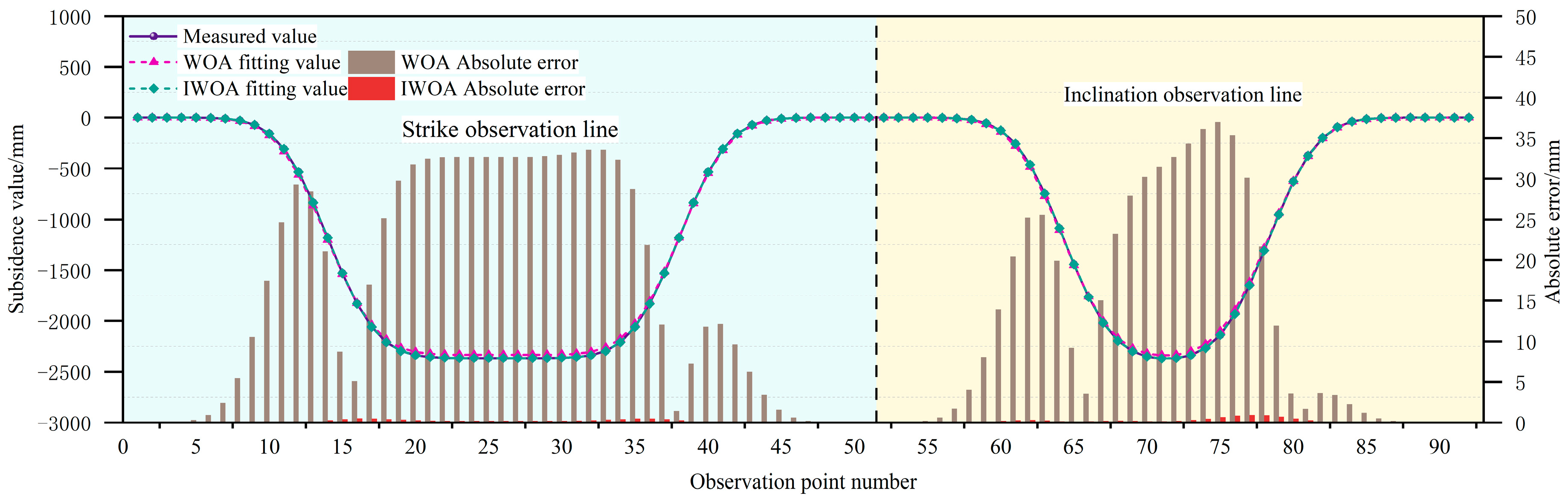
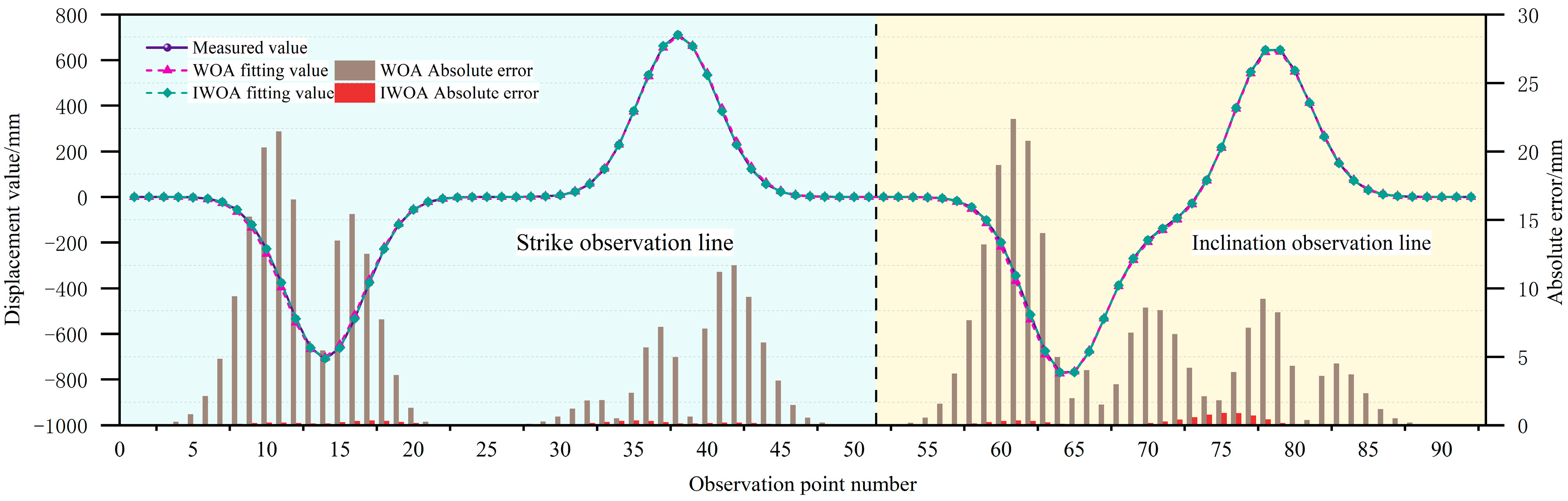
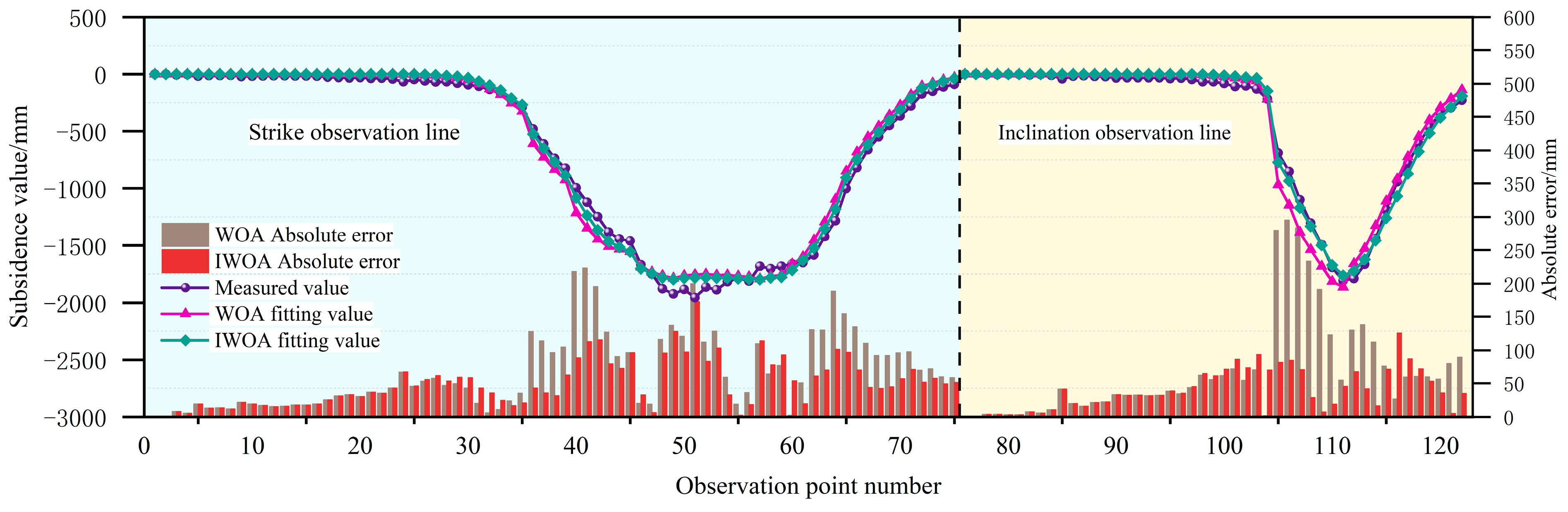
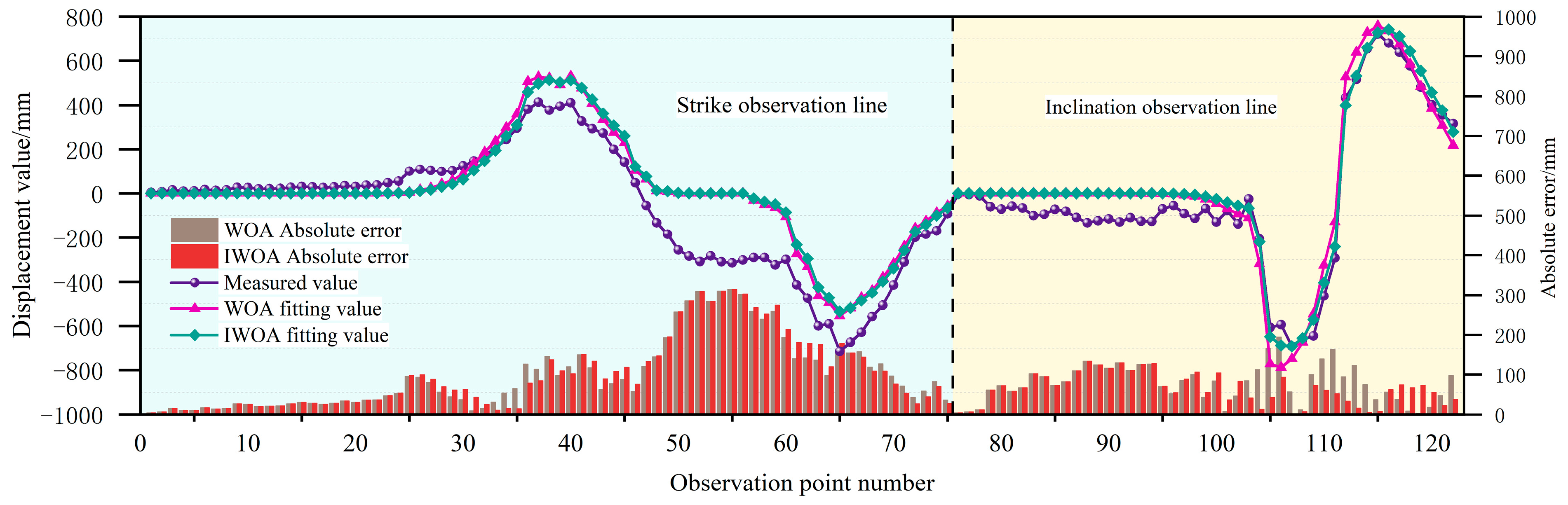
Parameter	q	tanβ	b	θ/°	Su/m	Sd/m	Sl/m	Sr/m
Design value	0.8	2.0	0.3	87	40	40	40	40
Range	[0.6~1.0]	[1.6~2.4]	[0.2~0.4]	[84~90]	[30~50]	[30~50]	[30~50]	[30~50]

presents both empirical values and fluctuation ranges for the parameters associated with the mining subsidence prediction model of the simulated working face. In the subsidence basin above the working face, 51 observation points (F1~F51) and 41 observation points (G52~G92) were arranged along the strike and inclination, respectively, with a spacing of 30 m between each observation point. The simulated working face layout is shown in Figure 4.

Simulation Experiment Results and Analysis

According to the design parameters of the mining subsidence prediction model, simulated values for subsidence and horizontal movement were generated. Based on this, both the basic WOA and the IWOA were employed to invert the PIM parameters for the simulated working face. To mitigate the impact of fortuitous errors on the parametric results, ten inversion tests were conducted under the same conditions. The inversion results are shown as

Table 2. Comparison of the inversion results from simulation experiments using the WOA and IWOA.

Parameter	Design Value	Average Value		RMSE	Relative Error/%
		WOA	IWOA	WOA	IWOA	WOA	IWOA
q	0.8	0.7898	0.8000	0.0138	0.0004	−1.2807	0.0035
tanβ	2.0	1.9706	2.0008	0.1758	0.0037	−1.4708	0.0400
b	0.3	0.3021	0.2999	0.0264	0.0006	0.7021	−0.0271
θ/°	87	86.7074	86.9943	0.9870	0.0267	−0.3363	−0.0065
Su/m	40	39.2454	40.0515	5.5328	0.2005	−1.8865	0.1288
Sd/m	40	38.4423	39.8955	5.3552	0.4123	−3.8943	−0.2612
Sl/m	40	36.7444	39.9850	4.6608	0.0864	−8.1391	−0.0376
Sr/m	40	38.7021	39.9852	6.2583	0.1630	−3.2449	−0.0371

.

The data in the table show that the IWOA exhibited smaller root mean square error (RMSE) and relative error in the parameter inversion results compared to the basic whale optimization algorithm. In terms of the RMSE, the basic whale optimization algorithm demonstrated a value below 6.26, while the improved whale optimization algorithm achieved a maximum value of 0.42, indicating enhanced inversion stability and more accurate results for the IWOA compared to the WOA. When compared with the design values, the WOA showed a relative error below 8.14%, whereas the IWOA exhibited a maximum relative error below 0.27%. With the exception of the inflection point offset, all other parameters in the IWOA inversion had a relative error less than 0.05%, resulting in more accurate inversion results than the WOA.

The subsidence value and horizontal movement value were predicted based on the aforementioned inversion results, in conjunction with the information of the working face. The fitting and comparison results with the measured values are presented in Figure 5 and Figure 6, respectively.

The above fitting graphs reveal that the predicted subsidence values of the WOA and IWOA exhibited a mean absolute error (MAE) of 14.68 mm and 0.19 mm, respectively, and a maximum absolute error of 36.96 mm and 0.95 mm, respectively, when compared to the simulated measured values. Additionally, their corresponding fitting RMSE were 19.99 mm and 0.29 mm, respectively. As for the horizontal movement value prediction, the MAE of the WOA and IWOA was found to be 4.79 mm and 0.14 mm, the maximum absolute error was 22.34 mm and 0.88 mm, and the fitting RMSE was 7.46 mm and 0.23 mm, respectively. It is evident that the IWOA demonstrated a higher level of accuracy in its prediction results compared to the WOA; it also exhibited superior fitting precision as evidenced by nearly perfect alignment between the predicted value curve and measured data curve.

5. Discussion

The above simulation experiments validate the robust stability and accurate results of the IWOA in solving parameters for the mining subsidence prediction model, meeting the general engineering requirements for accuracy. To investigate the parameter inversion performance of the IWOA, this study analyzed the performance from four perspectives: gross error interference, Gaussian noise interference, observation point missing interference, and different parameter ranges based on simulated working face data.

5.1. Anti-Gross Error Interference Experiment

When conducting field measurements at a ground movement observation station, an observer’s lack of attention or technical negligence, non-standard instrument operation procedures, and inherent limitations in instrument accuracy can lead to significant gross errors in their observation results [22]. These errors directly affect the parameter inversion results and the accuracy of mining subsidence prediction outcomes. To investigate the robustness of IWOA inversion mining subsidence prediction model parameters against gross error interference, simulated subsidence values were artificially increased by 0.1 W_max and 0.15 W_max at six points near both the maximum subsidence point and inflection point along the working face, respectively, as illustrated in Figure 7.

The ten inversion experiments were conducted using WOA and IWOA based on the measured data containing gross errors, and the corresponding results are presented in

Table 3. Comparison of gross error interference resistance experiment results between the WOA and IWOA.

Parameter	WOA				IWOA
	0.1 Wmax		0.15 Wmax		0.1 Wmax		0.15 Wmax
	Average Value	Relative Error/%	Average Value	Relative Error/%	Average Value	Relative Error/%	Average Value	Relative Error/%
q	0.8105	1.3114	0.8137	1.7088	0.8075	0.9345	0.8103	1.2913
tanβ	2.0110	0.5513	2.0052	0.2602	1.9778	−1.1076	1.9744	−1.2796
b	0.2935	−2.1742	0.2894	−3.5325	0.2953	−1.5647	0.2937	−2.0948
θ/°	86.9494	−0.0582	86.6635	−0.3867	86.9873	−0.0146	86.9612	−0.0446
Su/m	39.5275	−1.1812	38.8974	−2.7564	38.1947	−4.5133	37.1151	−7.2121
Sd/m	37.0992	−7.2519	36.5614	−8.5964	38.0041	−4.9898	36.7356	−8.1611
Sl/m	38.3102	−4.2246	38.4361	−3.9099	37.8268	−5.4330	36.2704	−9.3241
Sr/m	39.1182	−2.2044	38.7484	−3.1291	38.0919	−4.7701	36.9054	−7.7365

. After adding a gross error of 0.1 W_max, the RMSE for the WOA and IWOA inversion results was less than 6.75 and 0.88, respectively, with a relative error below 7.26% and 5.44%. The relative error for parameters q, tanβ, b, and θ in the WOA and IWOA inversion results was less than 2.18% and 1.57%, respectively. The average values of the fitted RMSE for the subsidence-fitted RMSE and horizontal movement-fitted RMSE of the WOA and IWOA were 16.12 mm and 13.20 mm, respectively. When a gross error of 0.15 W_max was introduced, the RMSE of the WOA and IWOA inversion results was below 6.80 and 1.19, respectively, with a relative error less than 8.60% and 9.32%, respectively. Although the relative error of the IWOA inversion results showed a slight increase, it still maintained a high accuracy. For parameters q, tanβ, b and θ, the relative error of the WOA and IWOA was below 3.54% and 2.10%, respectively. The average values of the fitted RMSE for the subsidence-fitted RMSE and horizontal movement-fitted RMSE of the WOA and IWOA were 21.03 mm and 20.31 mm, respectively. It can be observed that when solving mining subsidence prediction model parameters, the WOA with the improved strategy exhibits better resistance to gross errors compared to the basic WOA method and possesses a certain ability to withstand interference caused by gross errors.

5.2. Anti-Gaussian Noise Interference Experiment

In the process of actual measurement, fortuitous error is inevitable. To investigate the resistance of the IWOA against Gaussian noise interference in solving parameters for mining subsidence prediction models, random error following a normal distribution N(0,25) and N(0,100) was, respectively, introduced to the measured values. On this basis, ten parameter inversion experiments were conducted using the WOA and IWOA separately, and the results are shown as

Table 4. Comparison of anti-Gaussian noise interference experiment results between the WOA and IWOA.

Parameter	WOA				IWOA
	N(0,25)		N(0,100)		N(0,25)		N(0,100)
	Average Value	Relative Error/%	Average Value	Relative Error/%	Average Value	Relative Error/%	Average Value	Relative Error/%
q	0.7934	−0.8210	0.8107	1.3343	0.8004	0.0521	0.8093	1.1615
tanβ	1.9756	−1.2184	2.0934	4.6701	2.0057	0.2863	2.0161	0.8037
b	0.3096	3.2127	0.3036	1.1863	0.3009	0.2872	0.3021	0.7028
θ/°	86.6062	−0.4526	86.7436	−0.2947	86.9902	−0.0113	86.8347	−0.1900
Su/m	39.4309	−1.4228	40.9321	2.3302	39.9342	−0.1644	41.4598	3.6494
Sd/m	37.3908	−6.5230	38.7917	−3.0208	39.7481	−0.6298	41.0004	2.5010
Sl/m	36.7321	−8.1697	38.6135	−3.4663	39.4329	−1.4176	41.0847	2.7117
Sr/m	40.1607	0.4017	41.6880	4.2200	39.8610	−0.3474	40.3978	0.9945

.

After analyzing the data in the table, it can be observed that when random errors conforming to a normal distribution N(0,25) were introduced, the RMSE of the WOA and IWOA inversion results was found to be below 5.99 and 0.49, respectively, with a relative error below 8.17% and 1.42%, respectively. Regarding parameters q, tanβ, b, and θ, the relative error of the WOA and IWOA was less than 3.22% and 0.29%, correspondingly. The average values of the fitted RMSE for the subsidence-fitted RMSE and horizontal movement-fitted RMSE of the WOA and IWOA were 14.11 mm and 1.96 mm, respectively. After incorporating random error that followed a normal distribution N(0,100), the RMSE of the WOA and IWOA inversion results was found to be below 6.34 and 0.79, respectively, with a relative error below 4.68% and 3.64%, respectively. In terms of parameters q, tanβ, b, and θ, the relative error in the IWOA was less than 1.17%. The average values of the fitted RMSE for the subsidence-fitted RMSE and horizontal movement-fitted RMSE of the WOA and IWOA were 21.19 mm and 11.15 mm, respectively. The results demonstrate that the improved strategy enables the IWOA to exhibit superior resistance against Gaussian noise compared to the basic WOA. Despite a slight increase in relative error, the algorithm still maintains a high level of accuracy.

5.3. Anti-Missing Observation Point Interference Experiment

The actual measurement process of the field surface moving observation station is susceptible to various unfavorable factors, resulting in the damage or even loss of individual observation points. This leads to incomplete observation data, which significantly impacts the accuracy of parameter inversion results [23]. To investigate the anti-missing observation point interference performance in the process of the IWOA solving mining subsidence prediction model parameters, five and ten observation points near the maximum subsidence point, as well as all the inflection points and maximum subsidence points (referred to as key points here) were missing, respectively. On this basis, the IWOA was utilized to conduct three sets of comparative experiments, and the corresponding results are presented in

Table 5. Results of the IWOA’s anti-missing observation point interference experiment.

Parameter	Design Value	Missing 5 Points		Missing 10 Points		Missing Key Points
		Average Value	Relative Error/%	Average Value	Relative Error/%	Average Value	Relative Error/%
q	0.8	0.7999	−0.0092	0.7996	−0.0557	0.7998	−0.0278
tanβ	2.0	2.0006	0.0317	2.0030	0.1475	2.0019	0.0972
b	0.3	0.2997	−0.0847	0.3005	0.1617	0.3002	0.0724
θ/°	87	86.9931	−0.0079	86.9896	−0.0120	86.9933	−0.0077
Su/m	40	40.1022	0.2555	40.0749	0.1872	40.0828	0.2069
Sd/m	40	39.9852	−0.0371	39.8415	−0.3963	39.9485	−0.1287
Sl/m	40	39.8968	−0.2580	39.8458	−0.3855	39.9610	−0.0976
Sr/m	40	40.0010	0.0025	39.9250	−0.1874	40.0914	0.2284

.

After analyzing the data in Table 5, it is evident that the absence of data from the five and ten observation points near the maximum subsidence point led to a slight increase in both the RMSE and relative error of the IWOA. Specifically, the RMSE remained below 0.32 and 0.43, while the relative error stayed below 0.26% and 0.40%, respectively. This demonstrates that using the IWOA in solving mining subsidence prediction model parameters involved a certain level of resistance against interference caused by missing observation points. The RMSE was below 0.17, and the relative error was less than 0.23%, when both the maximum subsidence points and inflection points in the dip and strike directions were absent. This demonstrates that the IWOA can accurately determine PIM parameters even when observation point data are missing, enabling precise predictions of mining subsidence.

5.4. Global Search Performance

The range of parameters for mining subsidence prediction models is typically determined based on empirical formula in accordance with the geological and mining conditions of the mine. However, in cases where there are insufficient geological and mining data available, it becomes challenging to establish an appropriate parameter-solving range. This further complicates the optimization process [24]. The accuracy of the IWOA in solving mining subsidence prediction model parameters within different parameter ranges was investigated by setting three groups of fluctuation ranges as presented in

Table 6. Parameter ranges.

Parameter	Design Value	Rang 1	Rang 2	Rang 3
q	0.8	[0.7~0.9]	[0.6~1.0]	[0.5~1.1]
tanβ	2.0	[1.8~2.2]	[1.6~2.4]	[1.4~2.6]
b	0.3	[0.25~0.35]	[0.2~0.4]	[0.1~0.5]
θ/°	87	[85~89]	[84~90]	[80~90]
Su/m	40	[35~45]	[30~50]	[20~60]
Sd/m	40	[35~45]	[30~50]	[20~60]
Sl/m	40	[35~45]	[30~50]	[20~60]
Sr/m	40	[35~45]	[30~50]	[20~60]

. Ten parameter inversion experiments were conducted using the IWOA within each range, and the results are presented as

Table 7. IWOA inversion results in different parameter fluctuation ranges.

Parameter	Design Value	Rang 1		Rang 2		Rang 3
		Average Value	Relative Error/%	Average Value	Relative Error/%	Average Value	Relative Error/%
q	0.8	0.7998	−0.0224	0.8000	0.0035	0.7999	−0.0180
tanβ	2.0	2.0010	0.0492	2.0008	0.0400	2.0008	0.0408
b	0.3	0.3002	0.0583	0.2999	−0.0271	0.2998	−0.0747
θ/°	87	86.9995	−0.0006	86.9943	−0.0065	87.0108	0.0125
Su/m	40	39.9898	−0.0256	40.0515	0.1288	40.2229	0.5573
Sd/m	40	39.9955	−0.0113	39.8955	−0.2612	40.3886	0.9715
Sl/m	40	39.9486	−0.1284	39.9850	−0.0376	39.3002	−1.7494
Sr/m	40	39.9983	−0.0042	39.9852	−0.0371	39.9923	−0.0191

.

The data in Table 7 reveal that as the parameter range expands, there is a slightly increase in the relative error of the IWOA inversion results, leading to a decrease in inversion accuracy. The relative error for the first, second, and third ranges was below 0.13%, 0.27%, and 1.75%, while the corresponding RMSE was less than 0.15, 0.42, and 1.84, respectively. The average values of the fitted RMSE for the subsidence-fitted RMSE and horizontal movement-fitted RMSE of the IWOA were 0.19 mm, 0.26 mm, and 1.73 mm, respectively, under the specified parameter ranges. With the expansion of the parameter range, the relative error of the inversion results increased slightly, yet it still maintained a high level of precision that meets the accuracy requirements of general engineering. This demonstrates that the WOA with improved strategies exhibits robust global search performance and does not necessitate precise parameter ranges while solving mining subsidence prediction model parameters.

6. Engineering Applications

The parameter inversion of the PIM model was conducted on the 1414(1) face of Guqiao Coal Mine, located in Huainan City, Anhui province [25]. Its geological mining information is the following: its strike length is 2120 m, while its inclination length measures 251 m. The coal seam has an average mining depth of 735 m and a thickness of 3.0 m, while the dip is 5°. The observed line lengths for both the strike and inclination were, respectively, recorded as 3480 m and 1500 m. A total of six control points and 145 observation points were arranged, with adjacent points spaced at intervals of either 30 m or 60 m. The location of the mining area and the arrangement of the observation stations are illustrated in Figure 8.

Results and Analysis

The PIM parameters were inverted using the WOA and IWOA based on measured data from the 1414(1) working face. To ensure reliable inversion results, ten parameter inversions were conducted, with the results presented as

Table 8. Parameters inversion results of the 1414(1) working face.

Parameter	Range	Average Value		RMSE
		WOA	IWOA	WOA	IWO
q	[0.7~1.3]	1.034	0.966	0.086	0.033
tanβ	[1.5~2.5]	1.991	2.015	0.224	0.023
b	[0.05~0.45]	0.304	0.295	0.044	0.003
θ/°	[85~92]	89.213	91.179	0.626	0.313
Su/m	[−20~20]	1.572	−1.886	10.382	6.028
Sd/m	[−30~10]	−11.376	−18.860	9.852	5.070
Sl/m	[45~85]	70.370	57.146	13.519	4.848
Sr/m	[25~65]	43.089	60.970	9.883	4.851

.

As indicated in Table 8, the RMSE of the WOA was less than 13.52, while the RMSE of the IWOA was no more than 6.03. Furthermore, the RMSE of the IWOA inversion results was lower than that of the WOA. For parameters q, tanβ, b, and θ, the WOA and IWOA inversion results exhibited an RMSE below 0.63 and 0.32, respectively. This suggests that the parameter inversion results of the WOA with improved strategies are better than those of the basic WOA.

The parameter inversion results of the WOA and IWOA were utilized to predict the subsidence value and horizontal movement value, respectively. These predictions were then compared with the measured values, as shown in Figure 9 and Figure 10. The analysis revealed that for the WOA, the maximum absolute error was 295.01 mm, while for the IWOA, it was 172.91 mm; furthermore, their respective fitting RMSE was 79.53 mm and 55.50 mm. As for horizontal movement value prediction, the WOA exhibited a maximum absolute error of 314.77 mm compared to the measured value, whereas the IWOA had an error of 314.79 mm; correspondingly, their fitting RMSE was calculated as 124.62 mm and 127.52 mm accordingly. The average values of the fitted RMSE for the subsidence-fitted RMSE and horizontal movement-fitted RMSE of the WOA and IWOA were calculated to be 102.07 mm and 91.51 mm, respectively.

The above analysis demonstrates that in practical engineering applications, the IWOA exhibits superior accuracy in solving PIM parameters compared to the WOA. Moreover, the fitting accuracy between the predicted and measured values is higher with the IWOA, resulting in more precise predictions.

7. Conclusions

Based on the basic WOA, the Sobol sequence was incorporated to initialize the population and the Lévy flight strategy was employed to enhance the prey search mechanism. Simulation experiments were conducted to investigate the performance of the IWOA in parameter inversion for the PIM model. The results demonstrated that the RMSE of the IWOA inversion results was less than 0.42, with a relative error smaller than 0.27%, both values of which were lower than those obtained using the basic WOA. Moreover, all root mean square error values of q, tanβ, b, and θ were below 0.03, with a relative error less than 0.03%. The average values of the fitted RMSE for the subsidence-fitted RMSE and horizontal movement-fitted RMSE of the IWOA were calculated to be 0.23 mm, exhibiting almost complete consistency between fitting curves. The IWOA enables more accurate parameter inversion for mining subsidence prediction modeling and facilitates more precise mining subsidence predictions.

In this study, simulation experiments were conducted to analyze the parameter inversion performance of the IWOA from four perspectives: gross error interference, Gaussian noise interference, observation point missing interference, and different parameter ranges. The results demonstrated that, in comparison with the WOA model, the IWOA parameter inversion model exhibits superior performance in terms of global search performance, resistance against gross error interference, immunity to Gaussian noise interference, and resilience against missing observation point interference.

The IWOA was employed to solve the PIM parameters of the 1414(1) working face, located in Huainan City, Anhui province. The RMSE of the results obtained using the IWOA was consistently below 6.03, surpassing that achieved by the WOA. Moreover, the RMSE values of parameters q, tanβ, b, and θ were all below 0.32, indicating a higher level of accuracy in the inversion results. The average values of the fitted RMSE for the subsidence-fitted RMSE and horizontal movement-fitted RMSE of the IWOA were 91.51 mm, demonstrating an overall satisfactory fitting performance.