2. Analysis of Known Research Results
The results of numerous studies on heat transfer through single- and double-chamber windows are presented in previous works [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16]. Gan [
1] studied heat transfer through a double-glazed window. The corresponding heat transfer coefficients through windows and heat transfer resistances were determined. The thermal resistance of the glass unit obtained from the research results is consistent with the reference data. The influence of the width of the air gap between the glass surfaces on the heat transfer coefficient and the thermal resistance was determined. The two-dimensional problem of heat transfer through a double-glazed window connected to transparent photovoltaic elements was solved by Han et al. [
2]. The mechanisms of heat transfer by convection and radiation were studied. The influence of the Rayleigh number on the structure of the air flow, as well as the influence of low-emission coatings on the intensity of heat transfer through the window, has been determined. Based on the results of numerical modelling, the characteristics of free convection air flow in the gap between the glass and heat transfer through single-chamber, double-chamber, and three-chamber windows were studied by Arıcı et al. [
3]. The dependence of heat losses through windows on the number of chambers in a glass unit is shown, as well as the influence of low-emissivity coating on reducing heat losses through a window. The problem of heat transfer through single-chamber and double-chamber glass units is considered by Nia et al. [
4], taking into account the radiation of the gaseous medium in the chambers of windows. Its solution using a numerical method showed that at large values of the optical thickness of the gas layers, a multi-vortex flow structure is formed inside the chambers of the glass unit, which leads to a periodic distribution of heat flux on the surface of the window. The effect of the height of the window and the width of the gap between the glass layers in a glass unit on the nature of the flow of the gaseous medium and the intensity of heat transfer was studied by Ünalan and Özrahat [
5]. The gas flow inside the chambers can be either laminar or turbulent. The cases of air and argon gas media in chambers were considered. Numerical results showed that filling the gap between glass with argon instead of air leads to a decrease in heat flux through the window. It is also shown how the height of the window and the width of the gap between the glasses affect the structure of the gas flow and heat transfer in the glass unit. A second-order precise finite difference scheme was proposed by Coronel et al. [
6] to calculate heat transfer through a window. The scheme is constructed for a one-dimensional mathematical model of heat transfer through windows.
Previous works [
7,
8,
9] studied the influence of the angle of inclination of a translucent structure on the dynamics of gas flow in the gap between glass surfaces and heat transfer. The results of numerous studies on the flow of gas filling the gaps between glasses and the temperature regime of inclined window structures were considered by Toghroli et al. [
7]. When heat transfers, the effects of radiation from a gaseous medium are taken into account. The nature of streamlines, isotherms, and the distributions of the horizontal and vertical components of velocity in the cavity between glasses located at different angles of inclination was analyzed. The results showed that as the inclination angle increases, the velocity of the flow swirl decreases. The influence of the angle of inclination on the value of the overall heat transfer coefficient of the window was also shown. The effect of the angle of inclination of a window structure on heat transfer was also considered by Arıcı et al. [
8]. In addition to the effect of the angle
θ, varying from 0 to 90°, the dependence of heat transfer through uncoated glass units on the thickness of the air gap in the range from 6 to 18 mm, as well as on the number of chambers in the window, was also studied. The results of the numerical simulation were presented through the distribution of streamlines and isotherms. The results showed that the thickness of the air layer between the glass optimized for vertical windows can be considered for inclined windows, provided that the angle of inclination is greater than 45°. However, at smaller angles of inclination, the thickness of the air layer should be optimized by taking into account the magnitude of this angle.
Using numerical simulation, heat transfer and air flow in the gap between glass layers in a double-glazed window were studied by Basok et al. [
9]. It was shown that the cyclic regime of air flow in the form of ascending and descending boundary layers under certain conditions loses stability and the vortex regime changes. This transition depends on the width of the gap, the transverse temperature gradient, the angle of inclination, and the height of the window. The study made it possible to determine the critical values of the Rayleigh number at which the air flow regime in the inter-glass gap of the window changes. Based on the results of numerical modelling, the values of the heat transfer resistance of a double-glazed window were determined depending on the width of the gap between the glasses and the angle of inclination of the window.
Existing methods for numerically determining heat transfer coefficients through window structures were analyzed by Pavlenko and Sadko [
10]. Based on the results of the analysis, an assessment was made of the distributions of heat flux and temperature on glass surfaces. The precision of traditional approaches to determining heat loss through window structures was assessed. It was shown that the degree of unevenness of the heat flux density on the window surface can reach 60%, which in turn generates an error in heat transfer calculations under stationary conditions. In [
11], Aydın presented the results of solving the conjugate problem of heat transfer through a double-glazed window. To solve the problem, the finite difference method was used. Research was carried out to determine the optimal width of the air gap between two glasses for different climatic conditions. Ahmed et al. [
12] presented the results of numerical studies of heat transfer through innovative sliding windows. Window designs combine various approaches to increasing the energy efficiency of windows. Among them are the use of phase change material and the use of photovoltaic and vacuum glazing. These sliding windows are expected to generate electrical energy as well as provide effective thermal insulation. Shi et al. [
13] note that the modern approach to improving the thermal insulation characteristics of glass units involves a combination of vacuum glazing and the application of low-emission coatings to its surfaces. In this work, based on the results of numerical simulations and experimental studies, the influence of different positions of low-emission coatings in relation to vacuum glasses on the heat transfer characteristics of this system is analyzed. Aguilar et al. in [
14] presented the results of a numerical study of heat transfer through glass units. Options for three types of glass were considered: clear, absorbent, and reflective glass. Cases of warm and cold climates were analyzed. The glazing options that provided the highest energy savings in various climatic conditions were determined. In [
15], Etxeberria studied heat transfer through a window with glazing bars inside the gap between the two glazing panes. Research was carried out to determine the effect of these glazing bars on the air flow inside the gap and the overall heat transfer through the window. For comparison, numerical simulations were carried out for a model with glazing bars and a reference model without glazing bars. The comparison of the real model and the reference model showed that the glazing bars create recirculation inside the gap and a multicellular convective flow pattern that increases heat transfer through the window. Aguilar-Santana et al. [
16] reviewed the characteristics of various window technologies, covering the physical and optical properties of traditional windows and innovative window designs. In window technologies, one of the most important parameters is the heat transfer coefficient. The relationship between the physical and optical parameters of various types of windows and their heat transfer coefficient is discussed. It is noted that although some progress has been made in this area over the past decade, further research is needed to develop window technologies that not only have high insulating properties but can also generate energy.
From the analysis of the results given in the literature, it is found that the main attention in research is paid to the influence of the Rayleigh number, the width of the gap between the glasses, and the angle of inclination of the translucent structure on heat transfer through the windows. The influence of low-emissivity coatings on heat transfer resistance through windows is considered to a lesser extent. Importantly, new numerical and experimental results are of great interest.
3. Formulation of the Problem of Numerical Modelling and Calculation Procedure
To clarify the features of heat transfer through a double-chamber glass unit and physically substantiate measures to increase the heat transfer resistance of translucent enclosing structures, computational studies of this process are performed.
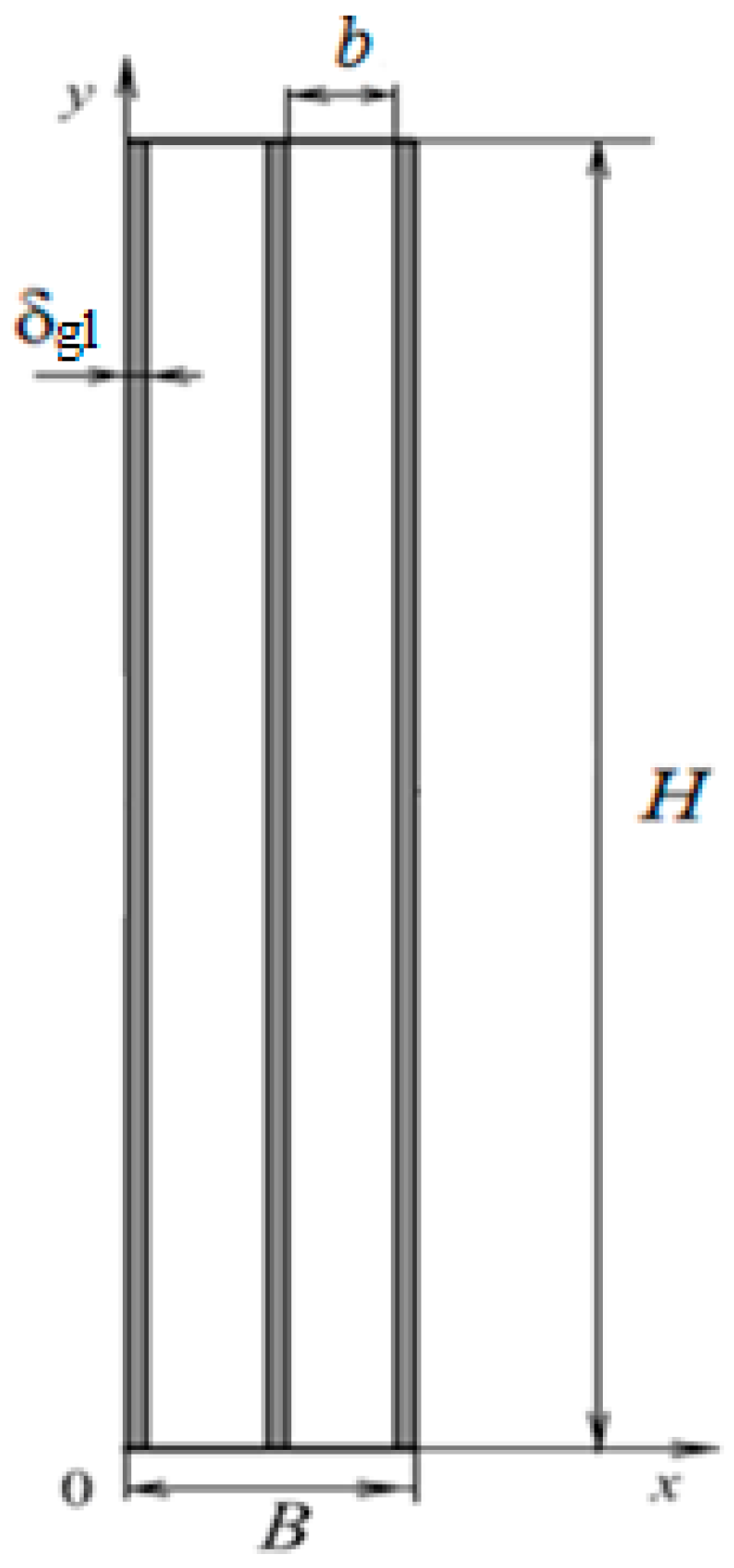
Numerical research is carried out in the computational domain, which is shown in
Figure 1. The figure shows a cross-section of a double-chamber glass unit with a vertical plane perpendicular to the glass surface. It is assumed that this plane passes through the middle of the glass unit, where the z-coordinate is considered equal to zero.
The geometric dimensions of the double-chamber glass unit are denoted as follows:
δgl—glass thickness;
B—the total thickness of the glass unit (0 ≤
x ≤ B);
b—the distance between the opposite surfaces of the glass in the double-chamber glass unit;
H—the height of the glass unit (0 ≤
y ≤ H);
L—width. It is assumed that −0.5
L ≤
z ≤ +0.5
L. Temperature, pressure, and flow velocities are assumed to be constant along the
z-coordinate and vary only along the
x- and
y-coordinates. The double-chamber window shown in
Figure 1 consists of external (
δgl ≤
x ≤
δgl +
b) and internal (2
δgl +
b ≤
x ≤ 2
δgl + 2
b) chambers. The chambers of the glass unit are filled with gas and separated by glass having a thickness of
δgl.
In a two-dimensional formulation of the heat transfer problem, the system of equations for dynamics and heat transfer has the following form:
- -
- -
Momentum transfer equation
- -
Energy equation for a gas medium:
where
x,
y—rectangular coordinates, (
x—horizontal;
y—vertical);
u,
v—horizontal and vertical projections of the velocity vector of the gas medium velocity vector;
p—pressure;
g—acceleration of gravity;
T—temperature;
—density of the gas medium;
—heat capacity of the gas;
μ(
T)—dynamic viscosity coefficient;
λg(
T)—gas thermal conductivity coefficient;
τ—time.
The equation of the state of an ideal gas is also added to the system of Equations (1)–(4).
Heat transfer in glass is described by the heat conduction equation:
where
—the heat capacity of the glass;
—the thermal conductivity coefficient of the glass;
—the density of the glass material.
Equations (1)–(6) are compiled in a coordinate system in which the horizontal 0X axis is directed from the outer surface of the glass unit (x = 0) towards the room, and the 0Y axis is directed vertically upward. The value y = 0 corresponds to the bottom edge of the glass unit. The thermophysical characteristics of glass are assumed to be unchanged, and the thermal conductivity and viscosity of the gaseous medium are considered to depend on temperature according to a linear law.
Boundary conditions on glass surfaces facing outward and toward the room are written in the form of boundary conditions of the first kind (Equations (7) and (8)) or the third kind (Equation (9)–(13)):
where
Tout—the temperature of the glass surface from the external environment and
Tin—the temperature of the glass surface on the side of the room.
where
Taout—the outside air temperature;
—heat transfer coefficient on the outer surface of the glass unit;
Tain—room air temperature;
—heat transfer coefficient on the inner surface of the glass unit. Thermal insulation conditions are accepted on the upper and lower surfaces of the glass unit:
Between the opposite surfaces of the glass in the glass unit chamber, heat is transferred by thermal conductivity, natural convection, and radiation. Based on this, the conjugate conditions on the internal surfaces of the glass are written as follows:
where
is the radiative heat flux density determined by the Stefan–Boltzmann law. Radiation flux
on the left inner surface of the outer chamber of a double-glazed window is calculated using the following formula:
where
,
—emissivities of the left and right surfaces of the glass unit chamber, respectively;
n1—the outer normal to the left inner surface of the chamber onto which this radiative flux falls;
n2—the outer normal to the opposite right inner surface of the chamber;
r—the length of the straight line connecting the point on the left surface of the glass unit with coordinates
y (0 ≤
y ≤
H),
x =
δgl;
z = 0, for which this boundary condition is written, with points on the right surface of the glass unit having coordinates
y′ (0 ≤
y′ ≤
H),
x = δ +
bgl;
z (−0.5
L z ≤ +0.5
L). The length of the segment
r is calculated using the following formula:
The cosines of the angles between this line segment
r and the normals to the surfaces
n1 and
n2 are defined as follows:
The expression for the radiative flux density
on the right inner surface of the outer chamber of a double-glazed window is written similarly:
Using a similar scheme, expressions are also compiled for the radiant heat flux densities on the left () and right () surfaces of the inner chamber of the glass unit. In contrast to the above expressions, the radiant heat flux density on the glass surfaces of the inner chamber of the glass unit will contain the values of emissivity of these surfaces, and , which may differ from the values and .
The system of Equations (1)–(6) with boundary conditions (7)–(13) is solved using the numerical method, described in the book by Patankar [
17]. To compile discrete analogues of differential equations that describe the movement of a gaseous medium and heat transfer through a double-glazed window, a spaced rectangular difference grid is used. The peculiarity of such a grid is that the nodes in which the components of the velocity vector are specified are located on opposite faces of the control volume, and the nodes associated with the mesh functions for temperature and density are located in the center of the control volume. In discrete transport equations, the ‘upstream’ scheme is used to approximate the first derivatives on the left sides of the difference equations. On the basis of the results of the numerical solution of the system of equations, the fields of velocity, pressure, and temperature in the glass and gas layers of the glass unit are determined. The numerical solution method is discussed in more detail in the works of Basok et al. [
18,
19].
The results of numerical studies presented in [
19] showed that central glass in a window with two chambers helps to reduce the convection heat transfer through a gaseous medium by reducing the velocity of free convection flows in the chambers. However, central glass has the greatest effect in reducing heat transfer by radiation. This glass acts as a thermal screen. It is also shown in [
19] that in both single-chamber and double-chamber windows with ordinary glass without low-emissivity coatings, the main part of the heat flux is transferred by radiation. Thus, for a single-chamber window, where the chambers are filled with air and the distance between the opposite glass surfaces is 24 mm, the radiation heat flux accounts for about 66% of the total heat flux. For a two-chamber window with a distance between the glass surfaces in the chambers of 10 mm, the radiation heat flux will usually be less than in a single-chamber window, but it will account for 59% of the total heat flux in the outer chamber and 62% in the inner chamber. Consequently, a well-known and effective way to reduce the total heat flux through a double-chamber window is to reduce its radiation component. For this purpose, low-emissivity coatings are applied to the internal surfaces of the glass unit chambers.
Analysis of the results of numerical studies. To clarify the issue of the influence of a low-emission coating on the characteristics of heat transfer through double-chamber windows, we carried out comparisons of these characteristics in cases where this coating was absent, as well as when it was present, on the internal surfaces of the glass unit chambers. The cases of one coating on the right surface of the inner chamber of a double-chamber window, as well as two coatings on the right surfaces of the inner and outer chambers, are considered. Numerical studies of the temperature regimes of double-chamber windows were carried out using the given mathematical model. We consider a double-chamber window with a height H = 1.08 m and a width L = 0.75 m. The glass has a thickness δgl = 4 mm. The distance between glasses is δ = 10 mm. The thermal conductivity coefficient of glass is λgl = 0.74 W/(m K). If the glass surfaces do not contain low-emission coatings, the emissivity of all glass surfaces is . If there is one coating, the emissivity of the right glass of the inner chamber is = 0.2. If the coating is located on both the surface of the right glass of the inner chamber and the surface of the right glass of the outer chamber, = 0.2 and = 0.2. The chambers of the glass unit are filled with air. Numerical studies are performed under boundary conditions of the third kind (8) on external surfaces. The indoor air temperature is Tain = 20.0 °C and the outdoor air temperature is Taout = −10.0 °C. The heat transfer coefficients on the outer and inner surfaces of the glass unit are αout = 23.0 W/(m2K); αin = 8.6 W/(m2K).
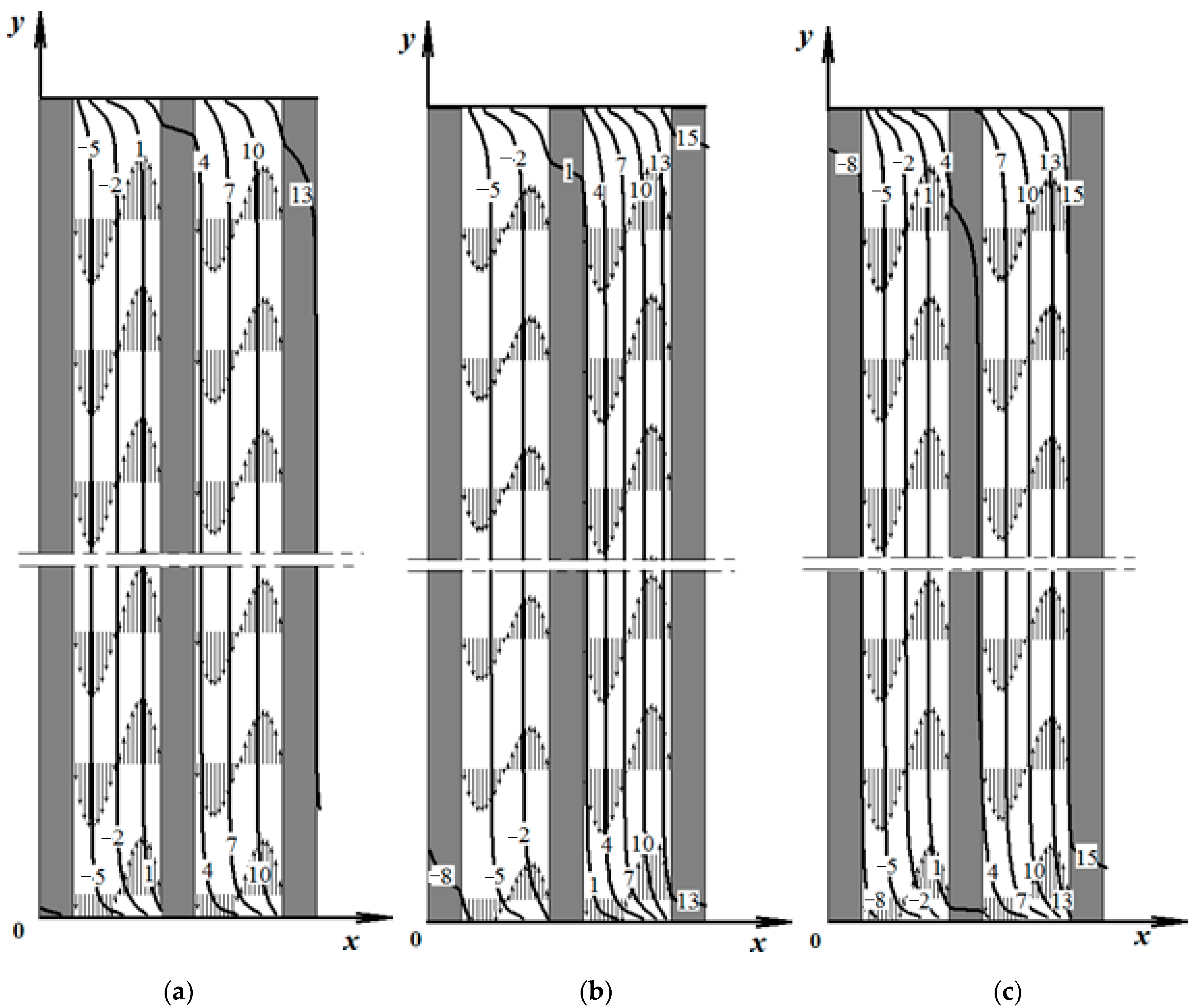
The velocity and temperature fields obtained as a result of solving the problem in the vertical sections of double-chamber windows for the three options under consideration are presented in
Figure 2. The distributions of vertical velocity in a gaseous medium and temperature along the thickness of double-chamber windows without coating and with coatings in their average horizontal sections for the three cases considered are shown in
Figure 3 and
Figure 4.
As can be seen from these figures, in both chambers of the double-chamber window, there is a circulation of free-convection air flow. For a window without coatings, the maximum vertical velocity in the outer chamber is
vmax = 0.022 m/s, and in the inner chamber it is
vmax = 0.0186 m/s (
Figure 3, curve 1). As a result of the small sizes of the indicated velocity values, convection in the layers between the glasses of a double-chamber window does not significantly affect heat transfer. Therefore, the temperature distribution over the thickness of the gas layer is close to linear (
Figure 4, curve 1), as is the case when heat transfer is carried out predominantly by thermal conductivity. A characteristic feature of this heat transfer mode is that the isotherms in the vertical section of a double-chamber window are almost parallel (
Figure 2a). A deviation from parallelism of isotherms is observed only in the upper and lower parts of the glass unit, where the flow of the gaseous medium unfolds, and the flow direction changes from upward to downward. According to the thickness of the glass, the temperature change is insignificant.
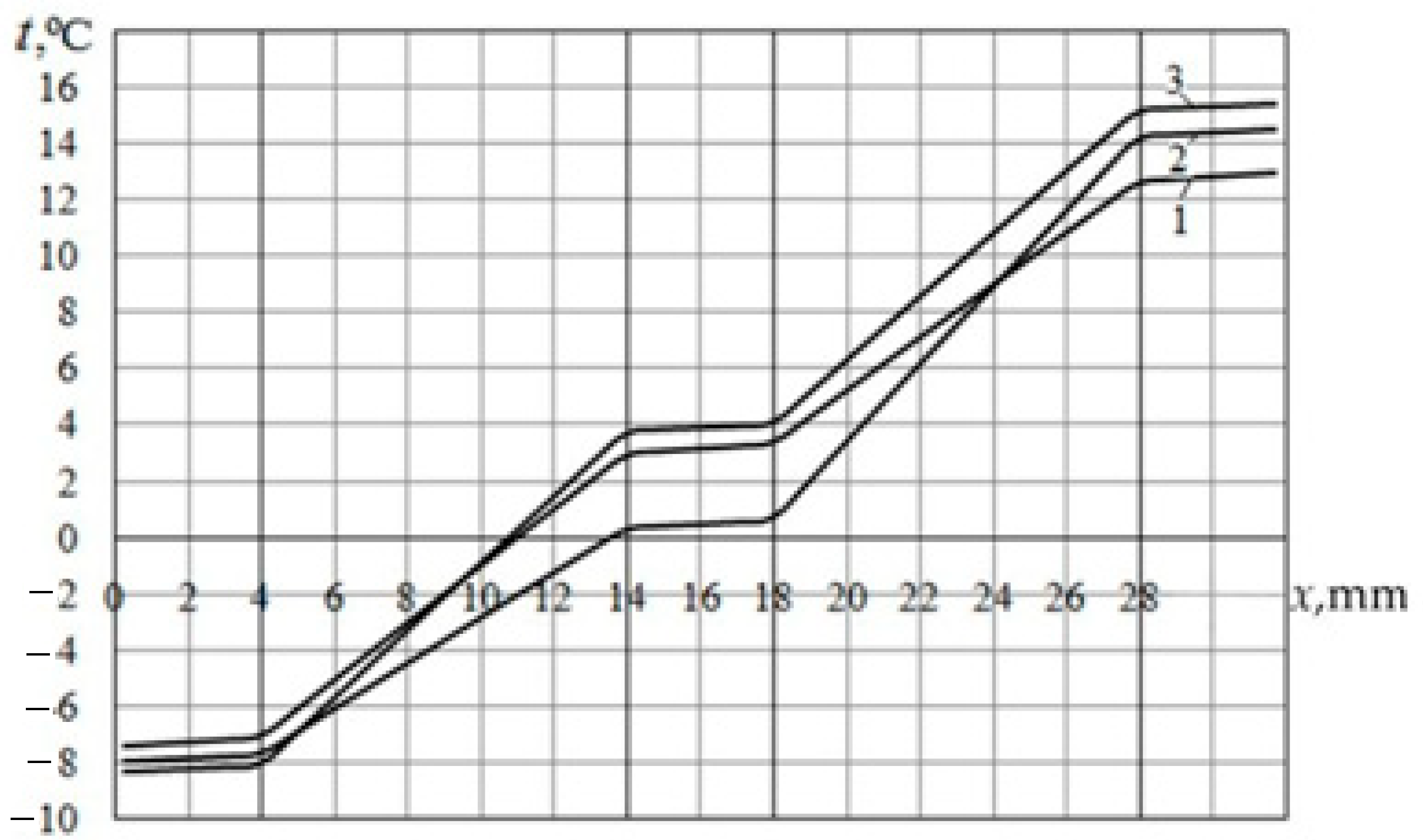
Figure 5 and
Figure 6 show the temperature distributions over the outer and inner surfaces of the glass units under study, as well as the distributions of heat flux densities on these surfaces. As can be seen in
Figure 5, the temperature distribution along the outer and inner surfaces of double-chamber windows in the middle parts is almost uniform. A deviation from the uniformity of the temperature distribution is observed in the upper and lower sections of the glass unit, which is associated with a change in the directions of movement of the air medium inside the chambers. For a double-chamber window without low-emission coatings, the average distribution temperature on the outer surface is
= −7.38 °C, and on the internal surface it is
= +13.0 °C. The average temperature difference is Δ
tc = 20.38 °C.
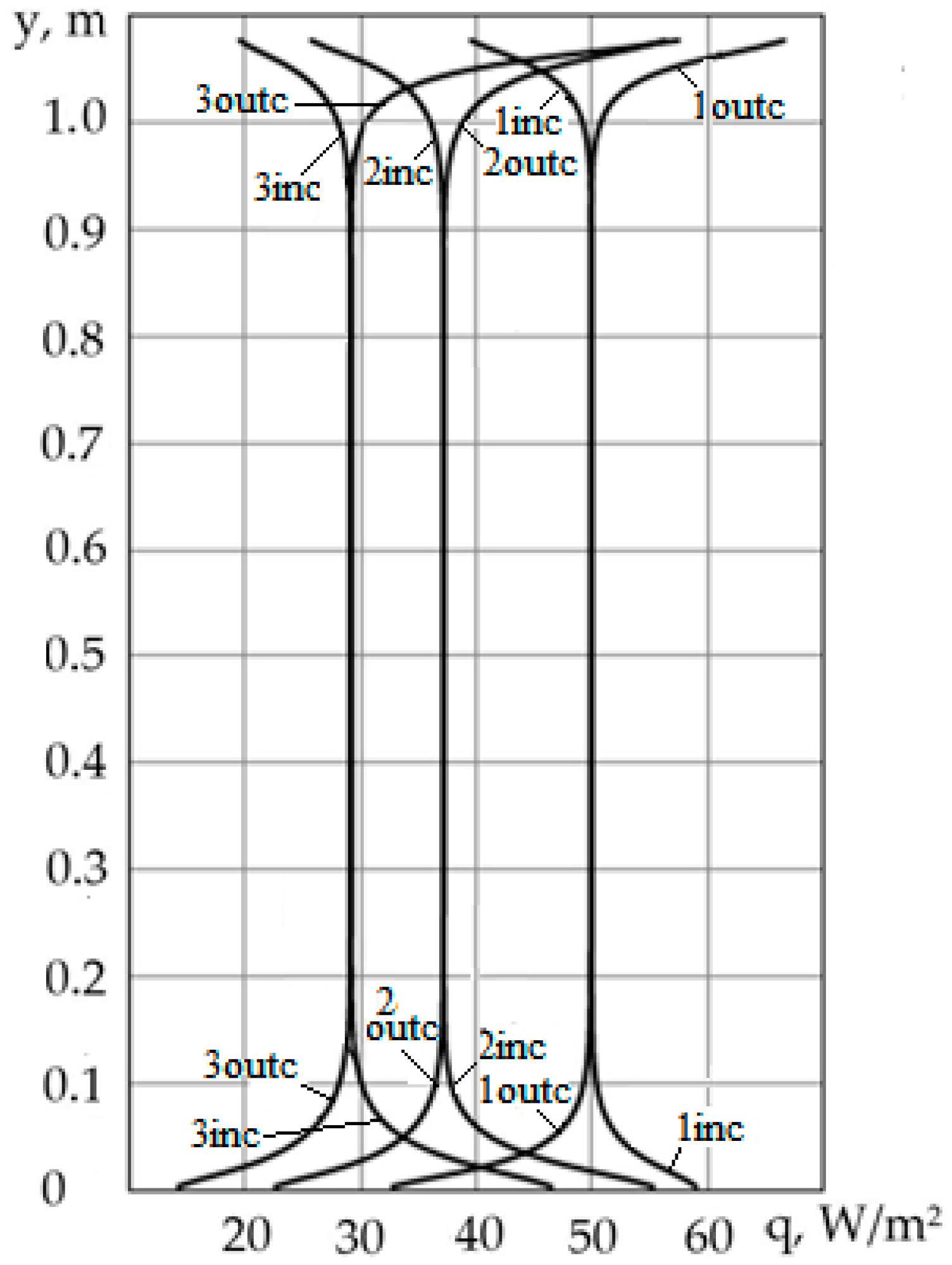
From
Figure 6, it can be seen that the heat flux densities on the inner and outer surfaces of the uncoated double-chamber glass unit practically coincide in the middle part of the double-chamber unit (curves 1 inner and 1 outer) and are approximately q = 60 W/m
2. Differences are observed in the upper and lower sections of these surfaces. The maximum values of the heat flux density on the outer surface of the double chamber unit (curve 1 outc) are observed in its upper part, and the maximum heat fluxes on the inner surface take place in its lower part (curve 1 inc). This feature of heat transfer through the double chamber window is explained by the presence of rising and falling flows of the gas medium inside the chambers. At the upper and lower ends of the double chamber unit, there are changes in the flow direction of the gas medium. As a result, near one surface, temperature gradients along the horizontal coordinate decrease, and near the opposite surface, they increase. In the middle part of the double chamber unit, the temperature gradients practically do not change along the thickness of the gas layer (
Figure 4, curve 1), and the temperature gradients along the vertical coordinate are practically zero (
Figure 2a). Therefore, the heat flux in the middle part of the double-chamber unit is the same on the outer and inner surfaces (
Figure 6, curves 1 outc and 1 inc).
In the case under consideration, the total heat flux through a double chamber window without coatings is Q = 48.6 W. In this case, the radiation component represents 58% of the total heat flux in the outer chamber (Qr = 28.3 W) and 60% in the inner chamber (Qr = 29.2 W).
An important characteristic of the thermal insulation capabilities of double chamber windows is the heat transfer resistance, calculated using the following formula:
From the analysis of the presented results, it follows that for a double-chamber window with the above geometry, in which the chambers contain air and the emissivity of the glass is ε = 0.89, the heat transfer resistance is equal to R ≈ 0.50 m2∙K/W.
For the case where a low emission coating is applied to the surface of the right glass of an internal chamber of double-chamber window, the temperature field (°C) and the direction of the velocity of the gaseous medium in the vertical section of a double-chamber window are shown in
Figure 2b. The distributions of vertical velocity in gas layers and temperature along the thickness of a double-chamber window with one coating are presented by curve 2 in
Figure 3 and
Figure 4.
Comparing the temperature distributions, which are represented by curves 1 and 2 in
Figure 4, it can be seen that in the case of a double-chamber window without coating on the glass, the temperature gradients in the inner and outer chambers differ insignificantly. At the same time, when applying a low-emissivity coating to the right glass of the inner chamber, the temperature gradient in the inner chamber becomes greater (
Figure 4, curve 2). One can also see the difference in the air velocity values in the glass unit chambers (
Figure 3). The maximum velocity value in a double-chamber window with one coating is observed not in the outer chamber, as in the case of a double-chamber window without coating, but, on the contrary, it was observed in the inner chamber. In the outer chamber, the maximum velocity is
vmax = 0.0176 m/s, and in the inner chamber,
vmax = 0.027 m/s. This is because the low-emissivity coating reduces the level of radiative heat transfer and increases the resistance to heat transfer through the inner chamber. As a result, the difference between the temperatures of opposite surfaces of the inner chamber of the double-chamber window increases, which helps to increase the rate of natural convection of air in this inner chamber.
For a double-chamber window with one coating, the average temperature on the outer glass is toutc = −7.94 °C and on the inner glass tinc = +14.5 °C. The average temperature difference is Δtc = 22.4 °C. The heat flux density in the middle part of the glass unit is approximately q = 47.3 W/m2. In the case under consideration, the total heat flux through a double-chamber window with one coating is reduced compared to the case without coating Q = 38.44 W (by 21%). The radiation component accounts for 57% of the total heat flux in the outer chamber (Qr = 21.91 W) and 27% in the inner chamber (Qr = 10.4 W), where a low-emission coating is applied. The heat transfer resistance of a double chamber window with a low-emission coating is R ≈ 0.632 m2∙K/W.
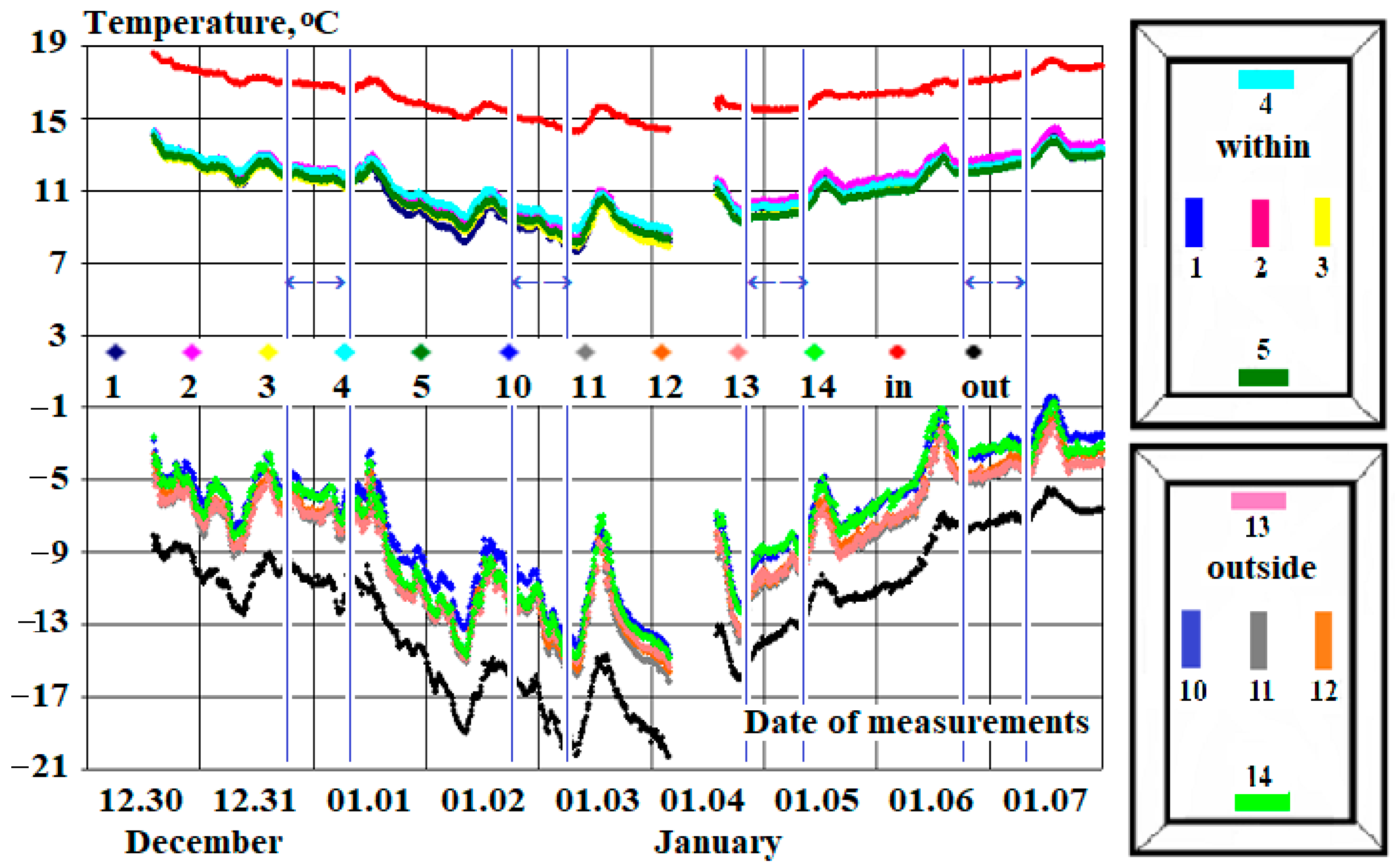
Experimental studies were carried out in the laboratory of energy-efficient windows of the IET of the National Academy of Sciences of Ukraine on the second floor of a typical three-story administrative building, and the location of the window was in the north orientation. For calculations, only the measurement data for the night-time period (from 20.00 to 05.00 in winter and from 12.00 to 15.00 in summer) were selected. During this period of time in winter, there was no solar radiation, and there were no personnel in the room. Moreover, the measured data of temperature, heat flux, and wind velocity were selected when they were almost constant within the limits of measurement errors during a certain time interval, i.e., an almost stationary mode was studied. The temperature was measured with platinum resistance sensors with a random error of 0.05 °C, and the heat flux density was measured by thermocouple sensors with a large number of junctions with an error of 0.3 W/m
2. The dimensions of the heat flux sensors (
Figure 7) are as follows: central no. 2 and no. 11 Ǿ = 100 mm, working zone Ǿ = 80 mm, peripheral—40 × 80 × 2.5 mm, working zone—30 × 70 mm. The periodicity of archiving measurements of each sensor is once every 10 min. The scheme of the location of the sensors on the inner surface of the first glass, related to the room, and on the outer surface of the third glass, connected to the environment, is shown on the right in
Figure 7. The sensors are located as follows: one is located in the geometric center of the double-chamber window, and the other four are located on all sides near the window profile, in the middle of each side of the window. The numbering of sensors is as follows: 1–5 for the inner surface of the double chamber unit (inside the room), and 10–14 for the outer surface of the double chamber unit on the facade of the building (environment). The final calculations used an array of heat flux values from central sensors 2 and 11 (both temperature and heat flux) for specially selected night periods (marked by gaps between vertical lines) from 20:00 on 31 December to 05:00 on 7 January. The values of heat fluxes for sensors 2 and 11 were close, and the arithmetic mean for the period of experimental data sampling (the interval between vertical lines) was chosen for thermal resistance calculations. On the afternoon of 4 January, temperature measurements were not carried out, as the current preventive inspection of the measuring block was taking place after the New Year holidays.
In the studied time range of December 30 to January 7, the ambient air temperature was quite low and decreased over five days from −9 to −20 °C. In the room, the temperature decreased from the standard 19 °C to a lowered 14.5 °C, which was associated with the thermal energy saving mode and, accordingly, the specified operation of the individual heating point. This decrease in temperature is explained by the fact that workers were absent on these dates because there were New Year holidays and weekends (2 and 3). The temperature difference between the room and the environment ranged from 28 to 34 °C; that is, it was significant and met the requirements of the State Technical Standard of Ukraine for conducting thermal measurements.
Figure 8A shows experimental data on the density of heat fluxes from ten sensors—five internal and five external, measured at the temperatures shown in
Figure 7. For resistance calculations, data from two central sensors were selected if their values coincided within the measurement error and only for the time range from 0.00 on 30 December to 24.00 on 7 January. Peripheral sensor data were used to understand the thermophysics of heat transfer effects. For example, fluctuations in heat flux are caused mainly by significant air velocity (up to 1.5 m/s) and, to a certain extent, temperature pulsations in the range of −3.0 ± 0.4 °C, as well as by changes in heat transfer coefficients from the air in the room to the double-chamber window and, especially, from the outer surface of the third glass into the environment. In the lower part of the window, temperatures are quite low; therefore, as shown by peripheral sensors 4 (blue dots) and especially 14 (light green dots), heat fluxes are the smallest. This is confirmed by thermal imaging using the “TESTO” thermal imager. Heat fluxes on one central horizontal of the window—q1, q2, q3 (inside the room) and q10, q11, q12 (outside) are close, although prone to significant fluctuations. As a typical example,
Figure 8B shows the data of the initial 200 measurements of the specific heat flux q by sensors no. 2 and no. 11 in the central part of the window in the period from 10:00 a.m. on December 30 to 11:50 p.m. on December 31. The average values were
q2 = 41 ± 5 W/m
2, and
q11 = 40 ± 6 W/m
2. The current values of
q11 are slightly smaller than the values of
q2, which means that in addition to the frontal heat losses to the environment, there is a heat flux in the end of the wall of the window opening of the wall structure.
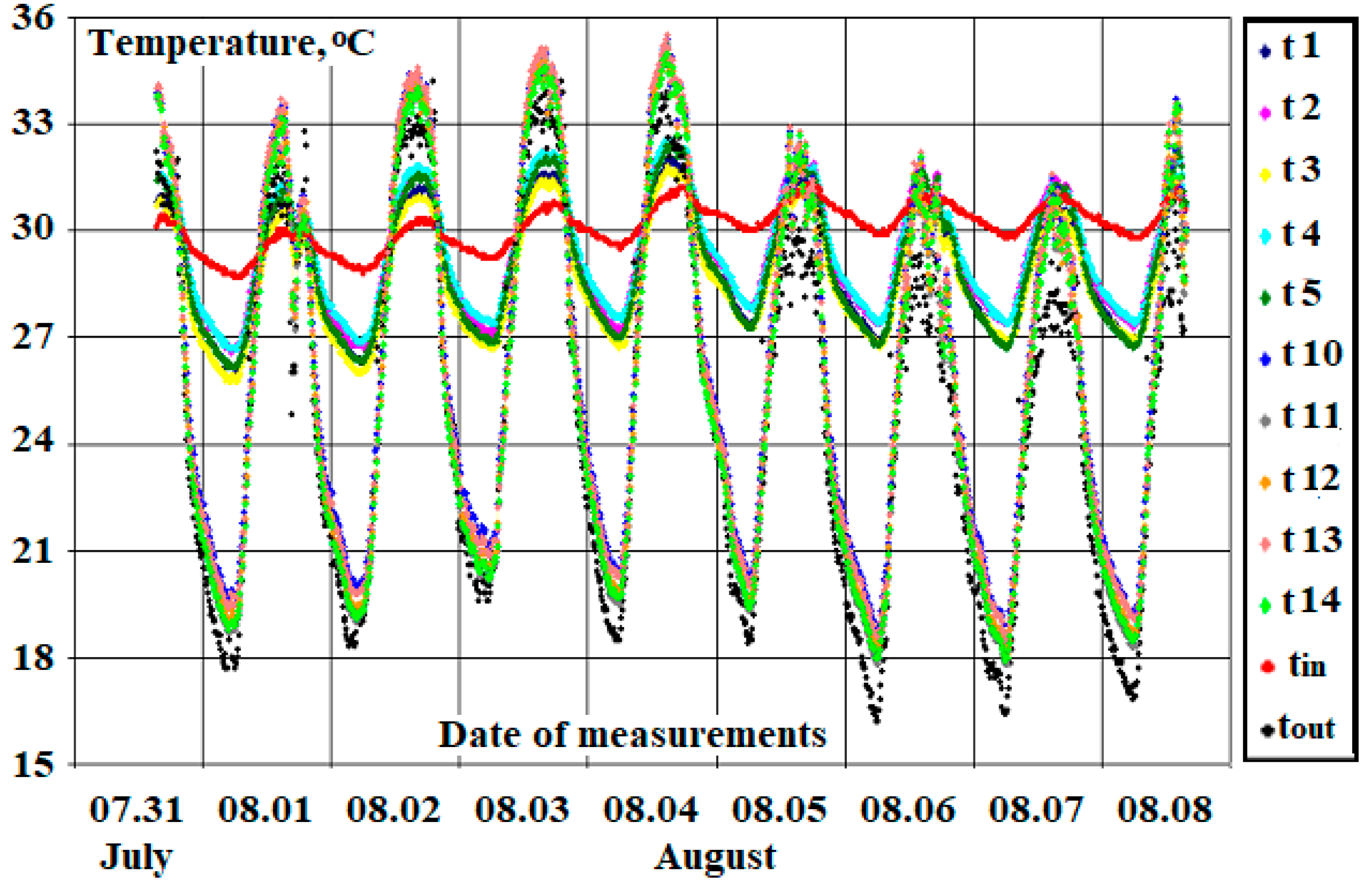
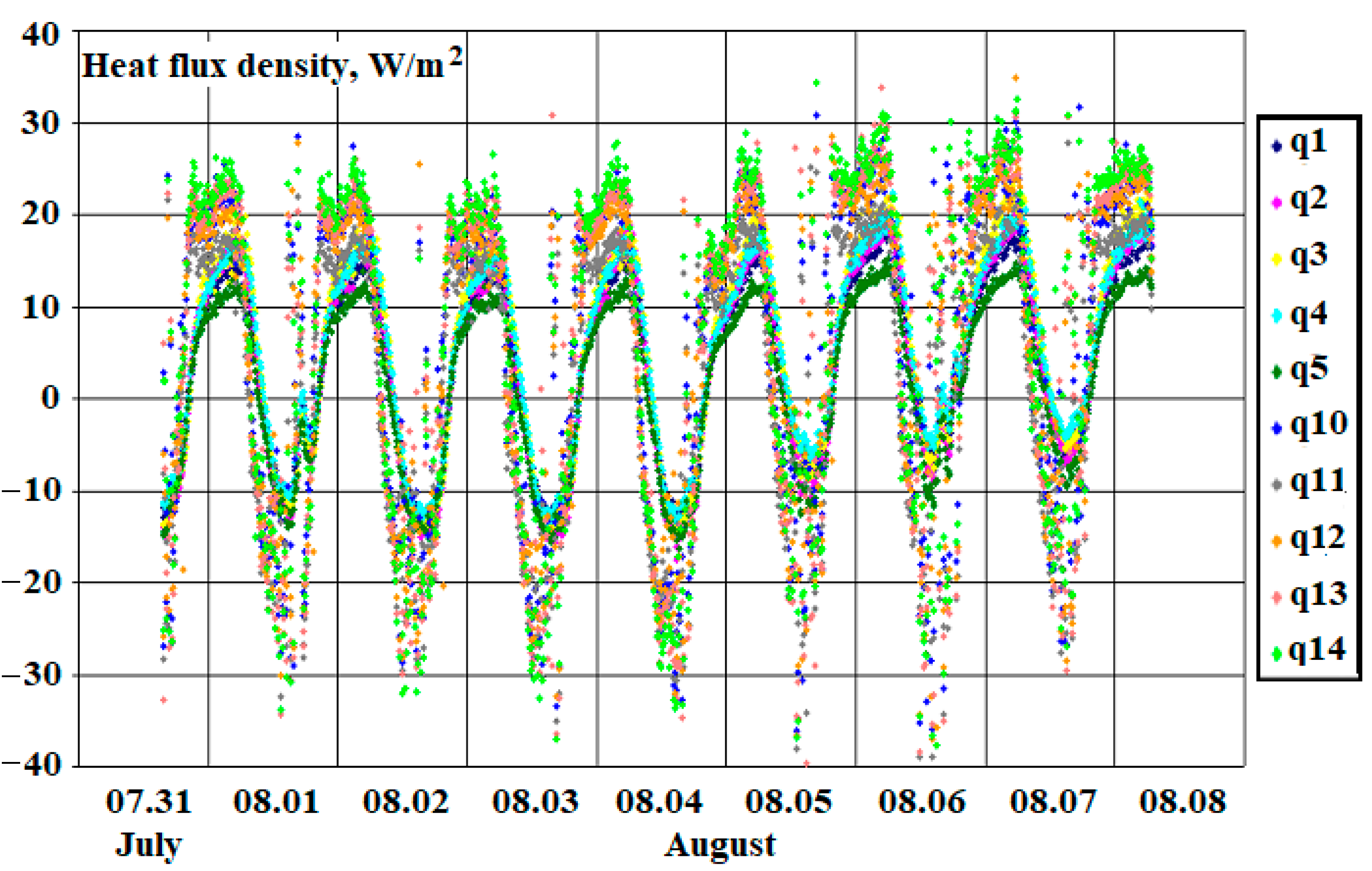
A similar set of measurements for this window was carried out in the summer during the period of the highest ambient temperatures and room air conditioning modes. These results are shown in
Figure 9 and
Figure 10.
From
Figure 10, it can be seen that during the day (somewhere from 10:00 a.m. to 8:00 p.m.) there is a reversal of the heat flux density with a maximum around 2:00 p.m. to 3:00 p.m. The nocturnal maximum of the heat flux is observed around 2.00–3.00 a.m., i.e., almost symmetrically in time to the daytime maximum.
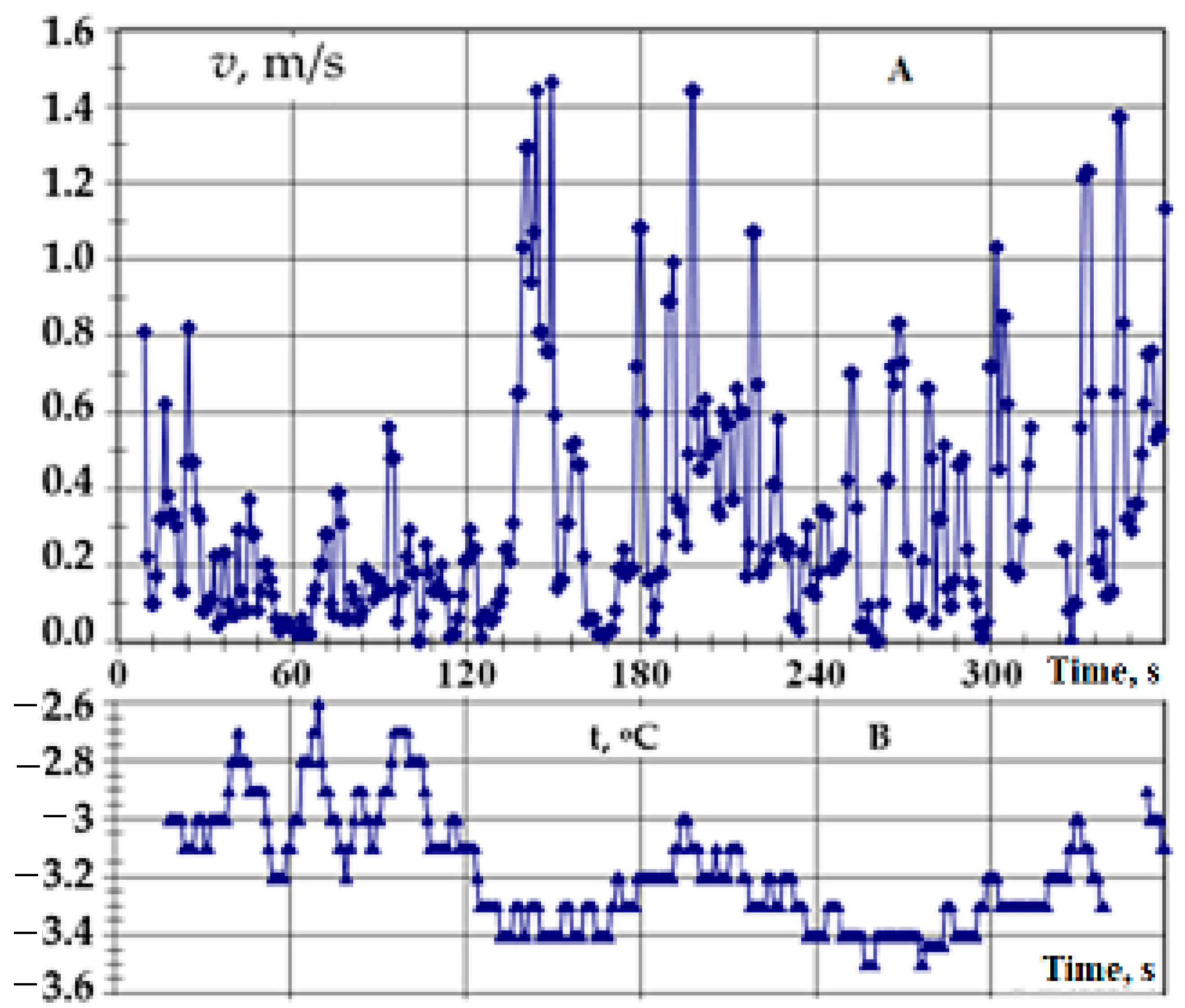
We emphasize that the pulsating chaotic fluctuations in heat flux (
Figure 8 and
Figure 10) are mainly caused by the pulsations of the velocity of air movement—these are wind currents outside the building and free convective air flows inside the room. This is confirmed in a certain way by the experimental data of
Figure 11 obtained for our north-facing building with a northwesterly wind direction. Heat flux pulsations outside have a larger amplitude than inside (
Figure 8B), because the average value of the environmental wind velocity and its pulsations (
Figure 11) have a larger amplitude and, therefore, have a stronger effect on the heat transfer coefficient.
The dependence of the heat transfer coefficient on the velocity and direction of the wind flow is quite complex because it is influenced by many physical factors, the accounting of which is burdened by complex experiments or complex and not always complete theoretical models. An analysis of 76 empirical models of heat transfer coefficients from the surfaces of enclosed structures into the environment was carried out by Mirsadegh et al. [
20] and Palyvos [
21]. As an example of a qualitative assessment of heat flux fluctuations, we will use the often-used McAdams dependence [
20] for the heat transfer coefficient
:
where for smooth surfaces (glass) at wind velocity less than 5 m/s,
m = 0.99 and
n = 0.21. For average velocity pulsations of 1.5/2 = 0.75 m/s (
Figure 11A), the growth (and therefore the heat flux) is up to 50%. The average value of all data in
Figure 8 corresponds to the range of 45 ± 20 W/m
2; that is, the difference is also almost half of the nominal value. Fluctuations in the temperature of ±0.4 °C with a normative temperature difference between the room and the environment of at least 20 °C affect the change in the heat flux only by 1.5%, that is, less significantly than fluctuations in the velocity of the outside air.
The experimental data in
Figure 8 with a relatively low heat flux value correspond to sensors located in the upper part of the glass unit near the window profile, where the temperature difference is the smallest. The average calculated value of thermal resistance according to stable and more accurate data for the central part of the glass unit was
Rc = 0.62 ± 0.02 m
2∙K/W.
Similar measurements were carried out for the summer period of the year (July–August). In this case, the heat flux was directed from the external environment into the air-conditioned (cooled) room, and the thermal resistance was
Rgl = 0.66 ± 0.03 m
2∙K/W. The experimental data obtained also confirmed the theoretical calculations. However, the experimentally obtained results of thermal resistance have a significant error, since the temperature difference between the room and the environment is less significant than in winter. For reference, in the Ukrainian State Technical Standard [
22], the standardized value of thermal resistance for the window under study is 0.64 m
2∙K/W [
19]. In our studies, the theoretically calculated thermal resistance was
Rgl = 0.63 m
2∙K/W. The results of experimental studies of thermal resistance for the winter period showed
Rgl = 0.62 m
2∙K/W; for the summer period,
Rgl = 0.66 m
2∙K/W. On the basis of the data obtained, we can conclude that the standard value of thermal resistance coincides with the obtained data from the research results within the error limits of their determination.
From numerical calculations, it follows that in the case of applying a coating to the right surface of both chambers of a window, the maximum velocity in the outer chamber is
vmax = 0.026 m/s, and in the inner chamber,
vmax = 0.022 m/s (
Figure 3, curve 3). That is, as in the case of the absence of a coating on the glass, in the outer chamber, the velocity of air movement is greater than in the inner chamber. But in absolute value, the velocity in the chambers in this case is slightly higher than in the case of no coverage. This is a consequence of higher temperature differences between the internal surfaces of the chambers than in the case of the absence of coatings (
Figure 4, curve 3;
Figure 5, curves 3 outc and 3 inc). There is also a greater difference between the temperatures of the internal and external surfaces of the glass unit Δ
tc = 23.7 °C. In this case,
toutc = –8.28 °C and
tinc = +15.4 °C.
The distribution of the heat flux density on the outer and inner surfaces of double-glazed double-chamber windows with two coatings is represented by curve
3 “outer” and curve 3 “inner” in
Figure 6. From the figure, it can be seen that the heat flux densities on the outer and inner surfaces of the glass unit in its middle part are almost the same and amount to
q = 39.3 W/m
2. The total heat flux through a window with two chambers is
Q = 32.0 W, which is 16.7% lower than in the case of one coating, and 34% lower than in the absence of low-emission coatings. The radiation component accounts for 26% of the total heat flux in the outer chamber (
Qr = 8.38 W) and 28% in the inner chamber (
Qr = 8.96 W). The heat transfer resistance of a double-chamber window with two low-emission coatings is
R ≈ 0.76 m
2∙K/W. The State Technical Standard of Ukraine [
23] recommends a value of
R = 0.74 m
2∙K/W, which is close to the theoretically calculated one.

 —data area that was used for the final calculation of the experimental heat transfer resistance of a double-chamber window 4M1-10-4M1-10-i4M1 (from the premises to the outside) with a size of 1080 × 750 mm.
—data area that was used for the final calculation of the experimental heat transfer resistance of a double-chamber window 4M1-10-4M1-10-i4M1 (from the premises to the outside) with a size of 1080 × 750 mm.
 —data area that was used for the final calculation of the experimental heat transfer resistance of a double-chamber window 4M1-10-4M1-10-i4M1 (from the premises to the outside) with a size of 1080 × 750 mm.
—data area that was used for the final calculation of the experimental heat transfer resistance of a double-chamber window 4M1-10-4M1-10-i4M1 (from the premises to the outside) with a size of 1080 × 750 mm.