Critical Inertia Calculation Method of Generators Using Energy Balance Condition in Power System
Abstract
1. Introduction
2. Critical Inertia in Power System Frequency Control
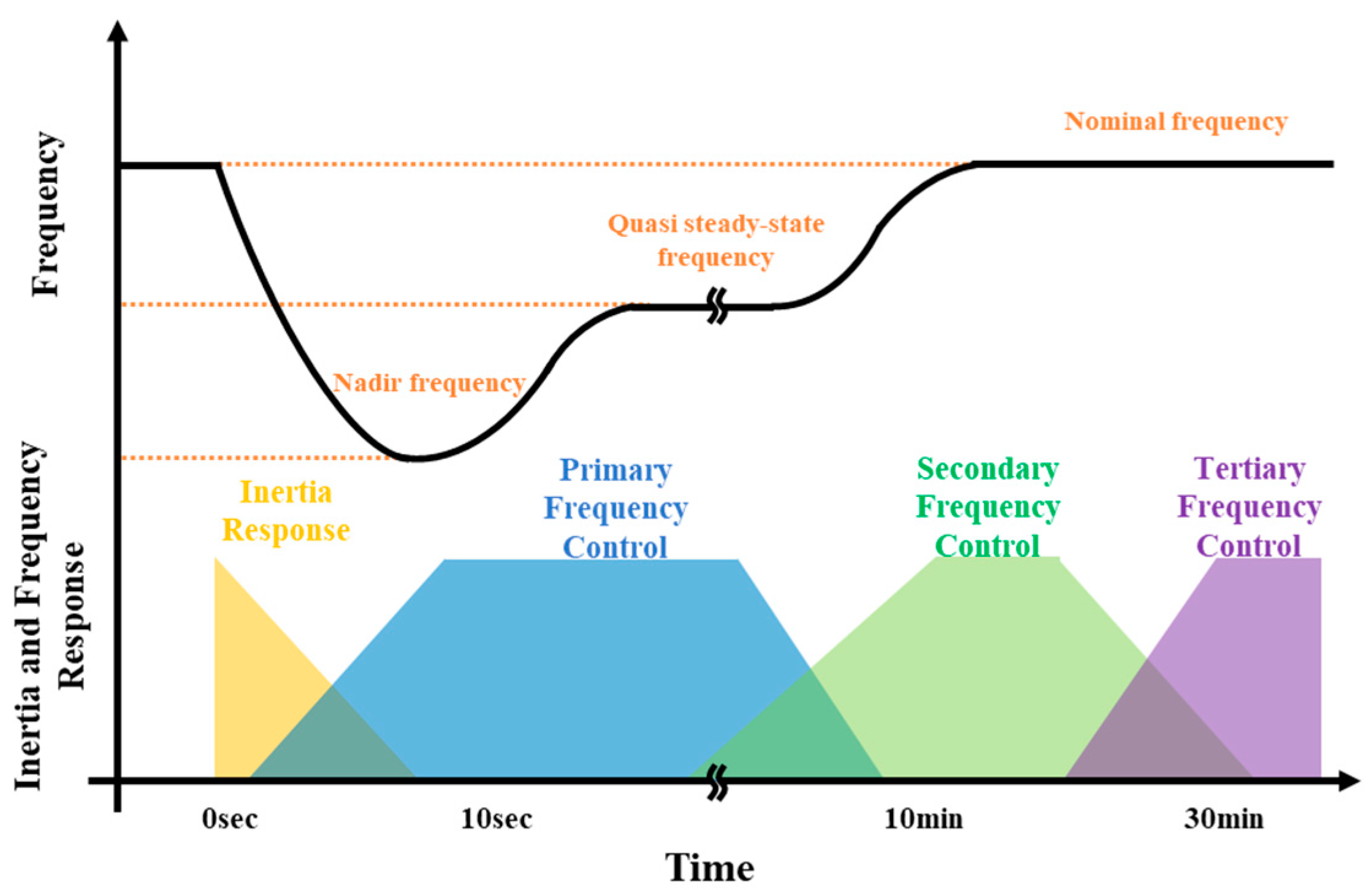
2.1. Inertia Response in Power System Frequency Control
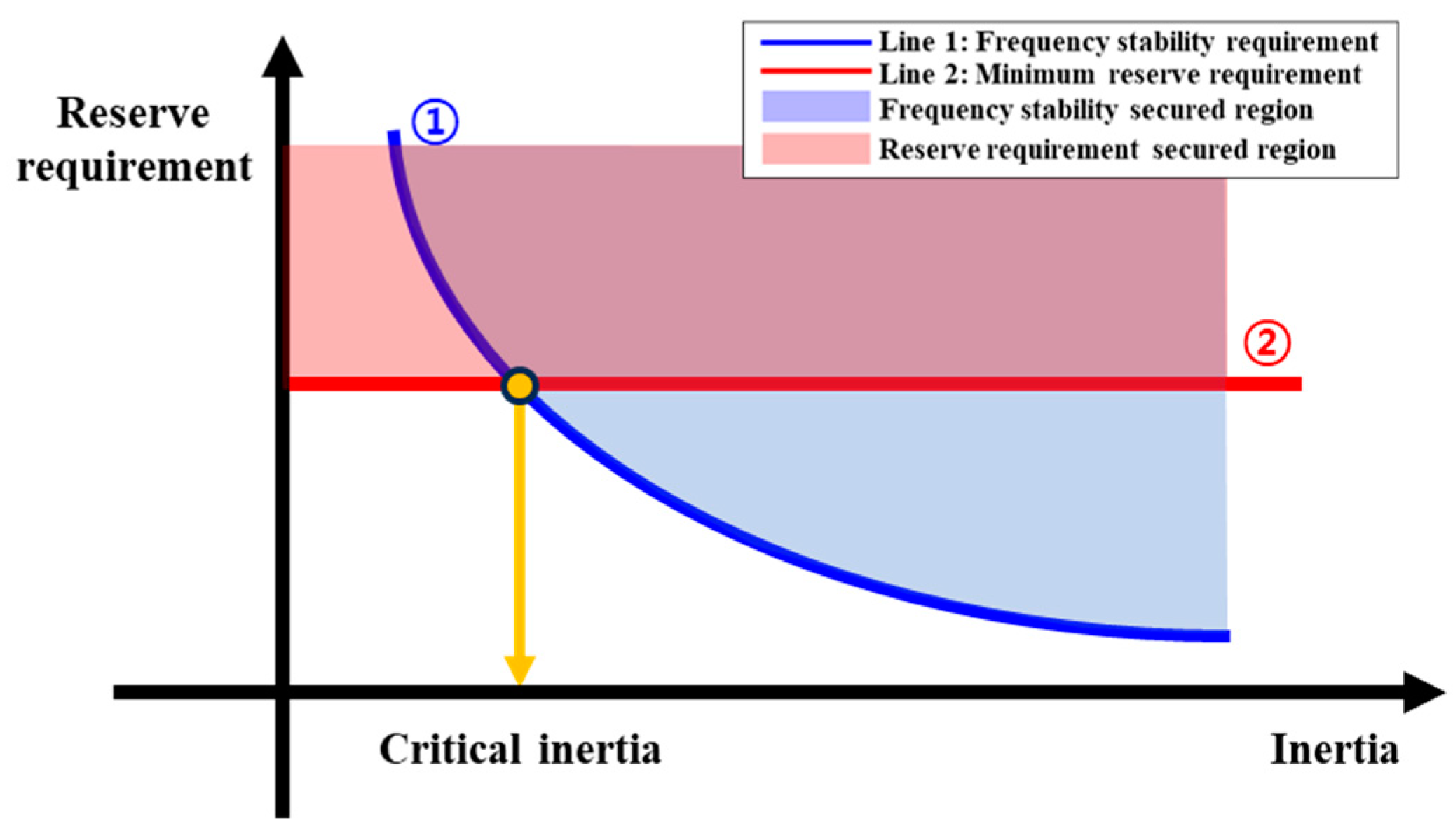
2.2. Definition and Importance of Critical Inertia
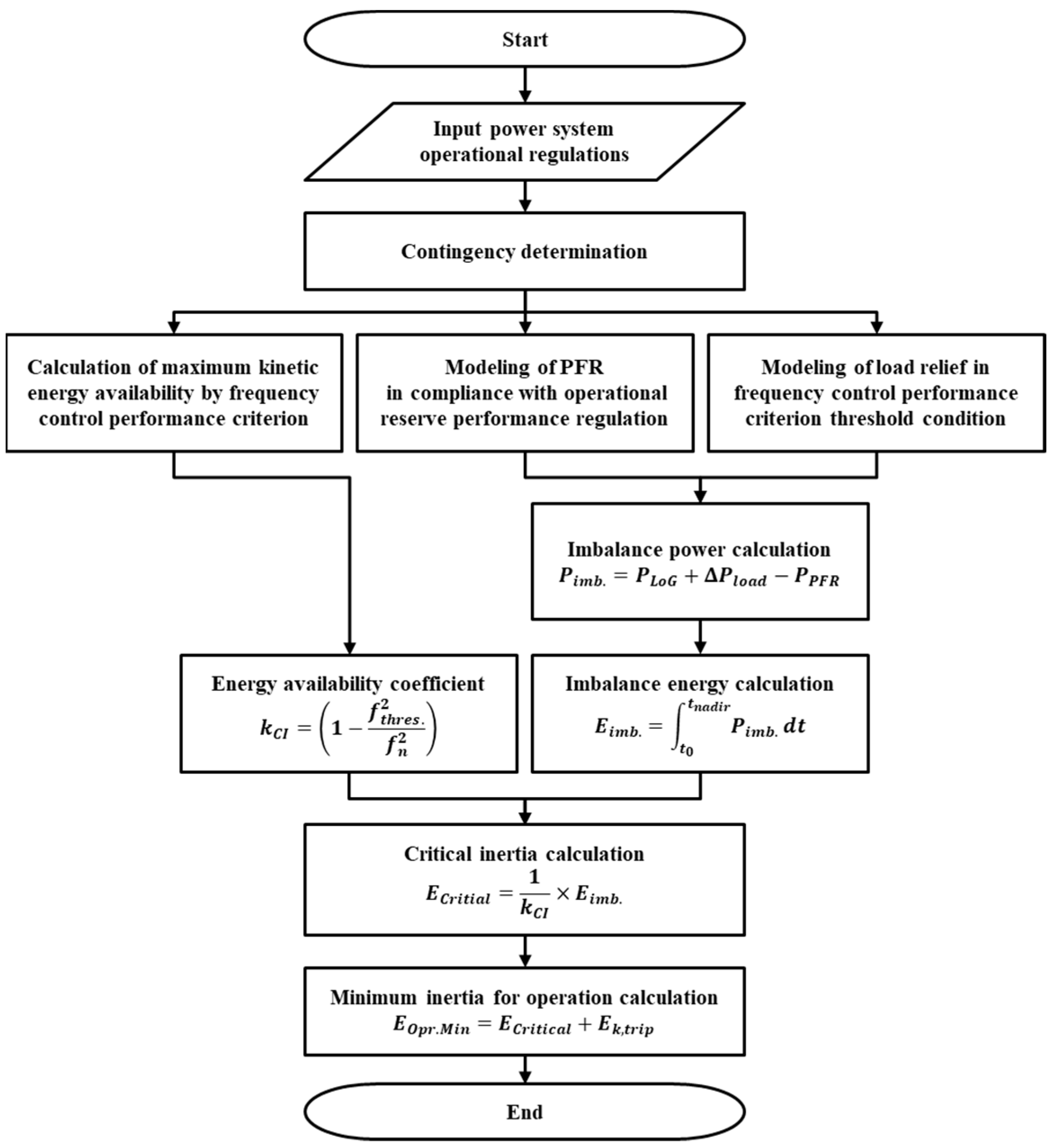
3. Proposed Critical Inertia Calculation Method
3.1. Reinterpretation of Critical Inertia Using Energy Balance Condition of Power Systems
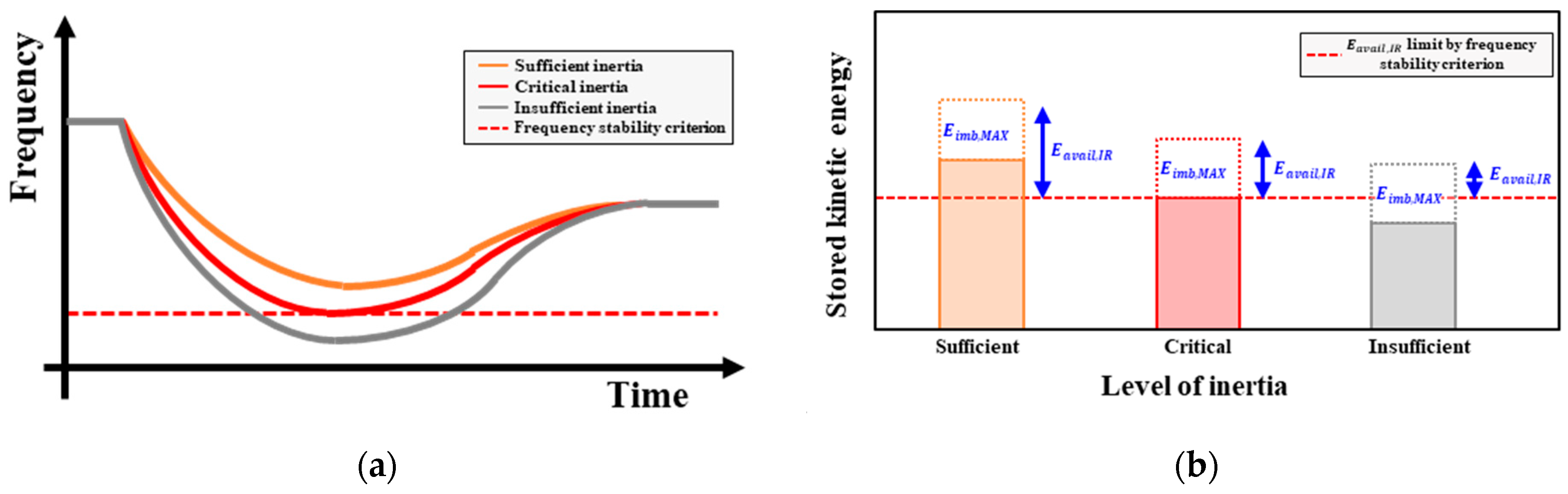
3.2. Kinetic Energy Availability under the Critical Condition of Frequency Stability
3.3. Imbalanced Energy Calculation
3.4. Calculation of Critical Inertia Using the Energy Balance Condition of the Power System
4. Case Study
4.1. Critical Inertia Calculation Using the Proposed Method
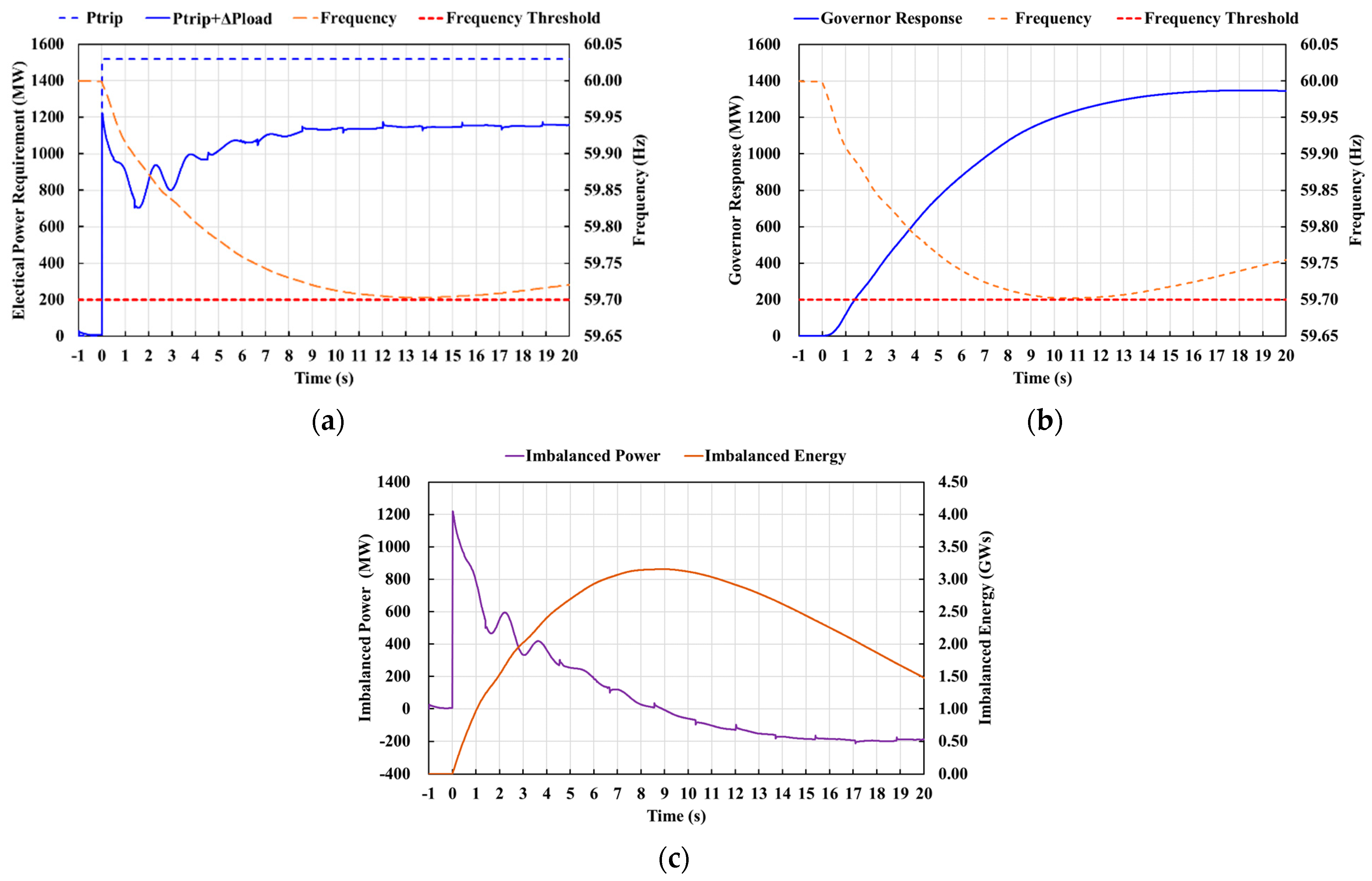
4.1.1. Calculation of Maximum Availability of Kinetic Energy
4.1.2. Imbalanced Energy in Power System Caused by LoG
4.1.3. Critical Inertia Calculation
4.2. Verification of Proposed Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ministry of Trade, Industry and Energy (MOTIE) (South Korea). Renewable Energy 3020 Plan, 2017. Available online: https://www.motie.go.kr/kor/article/ATCL3f49a5a8c/159996/view (accessed on 13 February 2024).
- Ministry of Trade, Industry and Energy (MOTIE) (South Korea). The 9th Basic Plan for Long-Term Electricity Supply and Demand (2020–2034), 2020. Available online: https://www.motie.go.kr/kor/article/ATCLf724eb567/210325/view (accessed on 13 February 2024).
- Joint with Related Ministries of South Korea. 2050 Carbon Neutral Scenario, 2021. Available online: https://www.2050cnc.go.kr/base/board/read?boardManagementNo=26&boardNo=101&menuLevel=2&menuNo=63 (accessed on 13 February 2024).
- European Network of Transmission System Operators for Electricity (ENTSO-E). Nordic Report Future System Inertia V2. 2018. Available online: https://docs.entsoe.eu/en/dataset/nordic-report-future-system-inertia/resource/6efce80b-2d87-48c0-b1fe-41b70f2e54e4 (accessed on 13 February 2024).
- Fernandez-Guillamon, A.; Gomez-Lazaro, E.; Muljadi, E.; Molina-Garcia, A. Power systems with high renewable energy sources: A review of inertia and frequency control strategies over time. Renew. Sustain. Energy Rev. 2019, 115, 109369. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory (NREL). Inertia and the Power Grid: A Guide Without the Spin. 2020. Available online: https://www.nrel.gov/news/program/2020/inertia-and-the-power-grid-a-guide-without-the-spin.html (accessed on 13 February 2024).
- Australian Energy Market Operator (AEMO). Renewable Integration Study Stage 1. 2020. Available online: https://aemo.com.au/energy-systems/major-publications/renewable-integration-study-ris (accessed on 13 February 2024).
- European Network of Transmission System Operators for Electricity (ENTSO-E). Requirement for Minimum Inertia in the Nordic Power System. 2021. Available online: https://en.energinet.dk/media/q1ulbrdk/requirement-for-minimum-inertia-in-the-nordic-power-system-2021.pdf (accessed on 13 February 2024).
- Ahmadyar, A.S.; Riaz, S.; Verbic, G.; Riesz, J.; Chapman, A. Assessment of Minimum Inertia Requirement for System Frequency Stability. In Proceedings of the 2016 IEEE International Conference on Power System Technology (Powercon), Wollongong, Australia, 28 September–1 October 2016. [Google Scholar] [CrossRef]
- Agathokleous, C.; Ehnberg, J. A Quantitative Study on the Requirement for Additional Inertia in the European Power System until 2050 and the Potential Role of Wind Power. Energies 2020, 13, 2309. [Google Scholar] [CrossRef]
- Mehigan, L.; Al Kez, D.; Collins, S.; Foley, A.; O’Gallachoir, B.; Deane, P. Renewables in the European power system and the impact on system rotational inertia. Energy 2020, 203, 117776. [Google Scholar] [CrossRef]
- Fernandez-Guillamon, A.; Gomez-Lazaro, E.; Molina-Garcia, A. Extensive frequency response and inertia analysis under high renewable energy source integration scenarios: Application to the European interconnected power system. IET Renew. Power Gen. 2020, 14, 2885–2896. [Google Scholar] [CrossRef]
- Electric Reliability Council of Texas (ERCOT). Inertia: Basic Concepts and Impacts on the ERCOT Grid. 2018. Available online: https://www.ercot.com/files/docs/2018/04/04/Inertia_Basic_Concepts_Impacts_On_ERCOT_v0.pdf (accessed on 13 February 2024).
- Australian Energy Market Operator (AEMO). Inertia Requirements Methodology Inertia Requirements & Shortfalls. 2018. Available online: https://www.aemo.com.au/-/media/files/electricity/nem/security_and_reliability/system-security-market-frameworks-review/2018/inertia_requirements_methodology_published.pdf (accessed on 13 February 2024).
- Lawrence Berkeley National Laboratory (LBNL). Use of Frequency Response Metrics to Assess the Planning and Operating Requirements for Reliable Integration of Variable Renewable Generation. 2010. Available online: https://www.ferc.gov/sites/default/files/2020-05/frequencyresponsemetrics-report.pdf (accessed on 13 February 2024).
- North American Electric Reliability Corporation (NERC). Fast Frequency Response Concepts and Bulk Power System Reliability Needs. 2020. Available online: https://www.nerc.com/comm/PC/InverterBased%20Resource%20Performance%20Task%20Force%20IRPT/Fast_Frequency_Response_Concepts_and_BPS_Reliability_Needs_White_Paper.pdf (accessed on 13 February 2024).
- Melbourne Energy Institute (MEI) University of Melbourne. Power System Security Assessment of the Future National Electricity Market. 2017. Available online: https://www.dcceew.gov.au/sites/default/files/documents/power-system-security-assessment-future-nem.pdf (accessed on 13 February 2024).
- Bian, Y.K.; Wyman-Pain, H.; Li, F.R.; Bhakar, R.; Mishra, S.; Padhy, N.P. Demand Side Contributions for System Inertia in the GB Power System. IEEE Trans. Power Syst. 2018, 33, 3521–3530. [Google Scholar] [CrossRef]
- Rezkalla, M.; Pertl, M.; Marinelli, M. Electric power system inertia: Requirements, challenges and solutions. Electr. Eng. 2018, 100, 2677–2693. [Google Scholar] [CrossRef]
- Prabha, K. Power System Stability and Control, 1st ed.; McGraw-Hill: New York, NY, USA, 1994; pp. 128–138. [Google Scholar]
- North American Electric Reliability Corporation (NERC). Frequency Response Standard Background Document. 2012. Available online: https://www.nerc.com/pa/Stand/Project%20200712%20Frequency%20Response%20DL/Bal-003-1-Background_Document-Clean-2013_FILING.pdf (accessed on 13 February 2024).
- Arif, A.; Wang, Z.Y.; Wang, J.H.; Mather, B.; Bashualdo, H.; Zhao, D.B. Load Modeling—A Review. IEEE Trans. Smart Grid 2018, 9, 5986–5999. [Google Scholar] [CrossRef]
- Ministry of Trade, Industry and Energy (MOTIE) (South Korea). Power System Reliability and Electricity Quality Maintenance Criterion, 2019. Available online: https://www.motie.go.kr/kor/article/ATCL0c554f816/64353/view (accessed on 13 February 2024).
- Korea Power Exchange (KPX). Korean Electricity Market Rule, 2021. Available online: https://new.kpx.or.kr/board.es?mid=a10205010000&bid=0030&act=view&list_no=71450 (accessed on 13 February 2024).

| Power System State | Frequency Control Performance Criteria |
|---|---|
| Steady state | (60 ± 0.2) Hz |
| Loss of the largest generator | Maintained at least 59.7 Hz Restored to 59.8 Hz within 1 min |
| Simultaneous loss of the two generators or SPS activation | Maintained at least 59.2 Hz Restored to 59.5 Hz within 1 min Restored to 59.8 Hz within 10 min |
| Power System State | Frequency Control Performance Threshold (Hz) | Nominal Frequency (Hz) | (%) |
|---|---|---|---|
| Steady state | 59.8 | 60 | 0.67 |
| Loss of the largest generator | 59.7 | 60 | 1.00 |
| Simultaneous loss of the two generators or SPS activation | 59.2 | 60 | 2.65 |
| Indices | Values |
|---|---|
| 0.01 | |
| 8.90 s | |
| 3.156 GWs | |
| 315.66 GWs | |
| 323.88 GWs |
| Load Level | Inertia (GWs) | Nadir Frequency (Hz) |
|---|---|---|
| 60% | 316.94 | 59.732 |
| 80% | 316.95 | 59.741 |
| 100% | 316.47 | 59.705 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.-Y.; Song, Y.H.; Kook, K.S. Critical Inertia Calculation Method of Generators Using Energy Balance Condition in Power System. Energies 2024, 17, 1097. https://doi.org/10.3390/en17051097
Yang J-Y, Song YH, Kook KS. Critical Inertia Calculation Method of Generators Using Energy Balance Condition in Power System. Energies. 2024; 17(5):1097. https://doi.org/10.3390/en17051097
Chicago/Turabian StyleYang, Jae-Young, Yu Hoon Song, and Kyung Soo Kook. 2024. "Critical Inertia Calculation Method of Generators Using Energy Balance Condition in Power System" Energies 17, no. 5: 1097. https://doi.org/10.3390/en17051097
APA StyleYang, J.-Y., Song, Y. H., & Kook, K. S. (2024). Critical Inertia Calculation Method of Generators Using Energy Balance Condition in Power System. Energies, 17(5), 1097. https://doi.org/10.3390/en17051097






