CFD Simulation Models and Diffusion Models for Predicting Carbon Dioxide Plumes following Tank and Pipeline Ruptures—Laboratory Test and a Real-World Case Study
Abstract
1. Introduction
2. Background on Dispersion Modeling and CFD
3. CFD Modeling of Plumes
3.1. Governing Equations
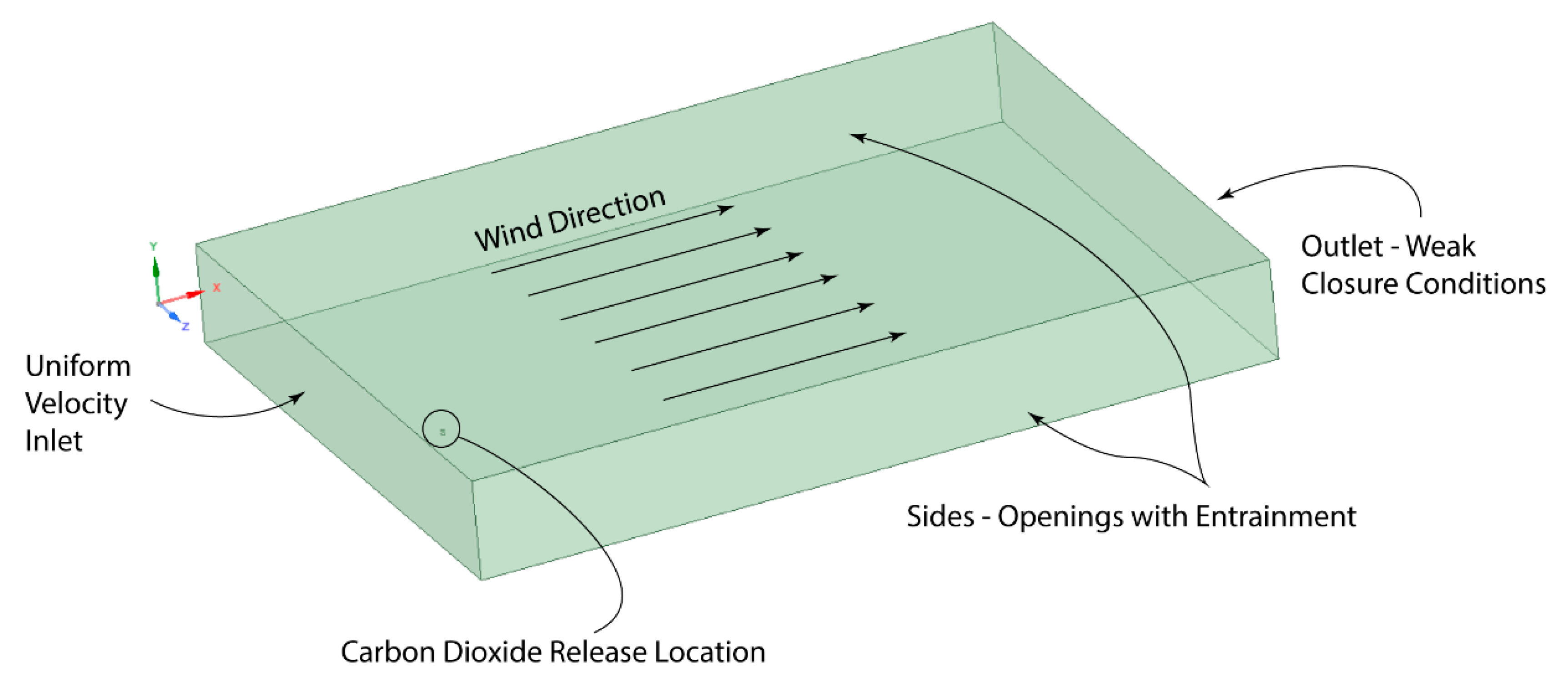
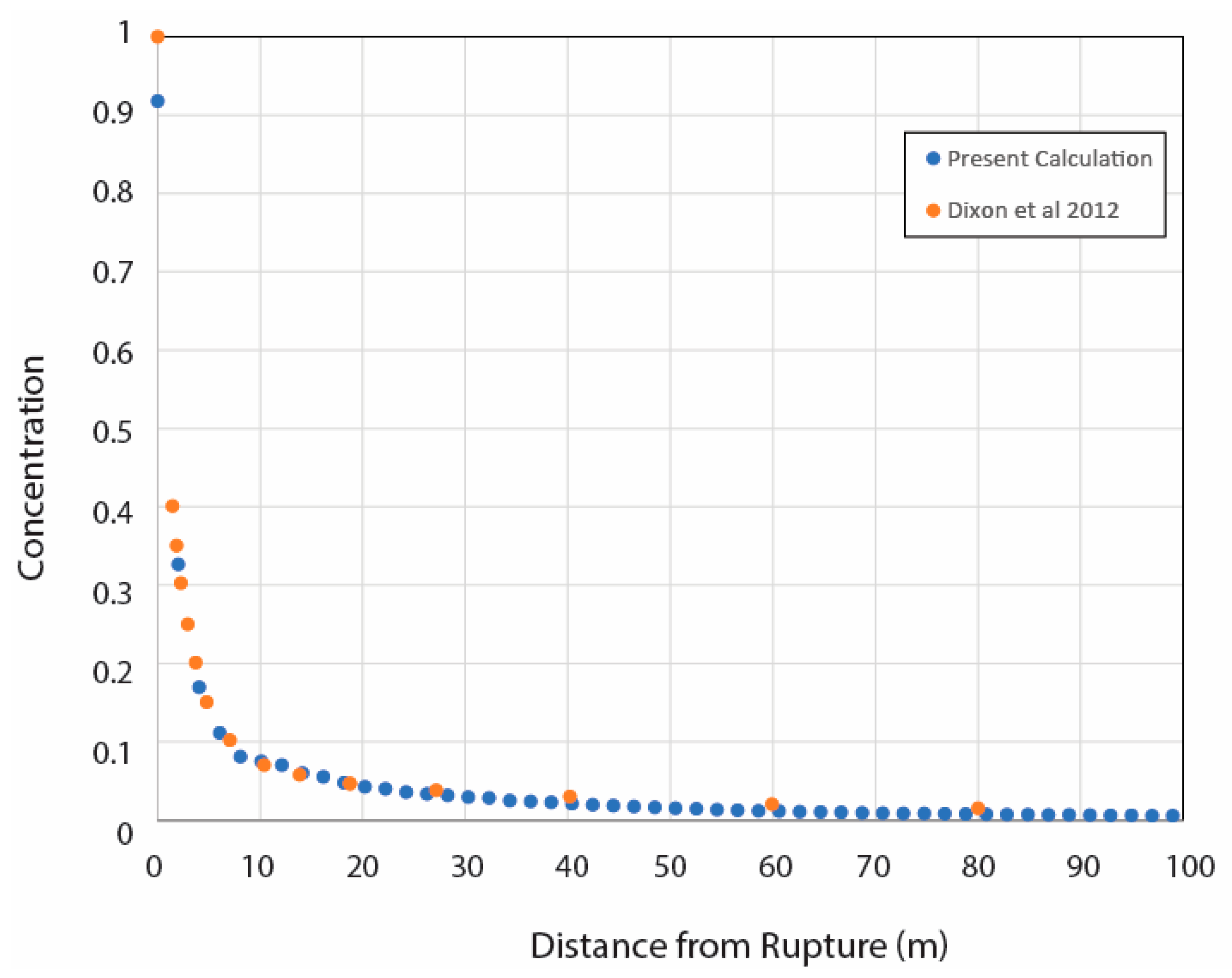
3.2. Validation
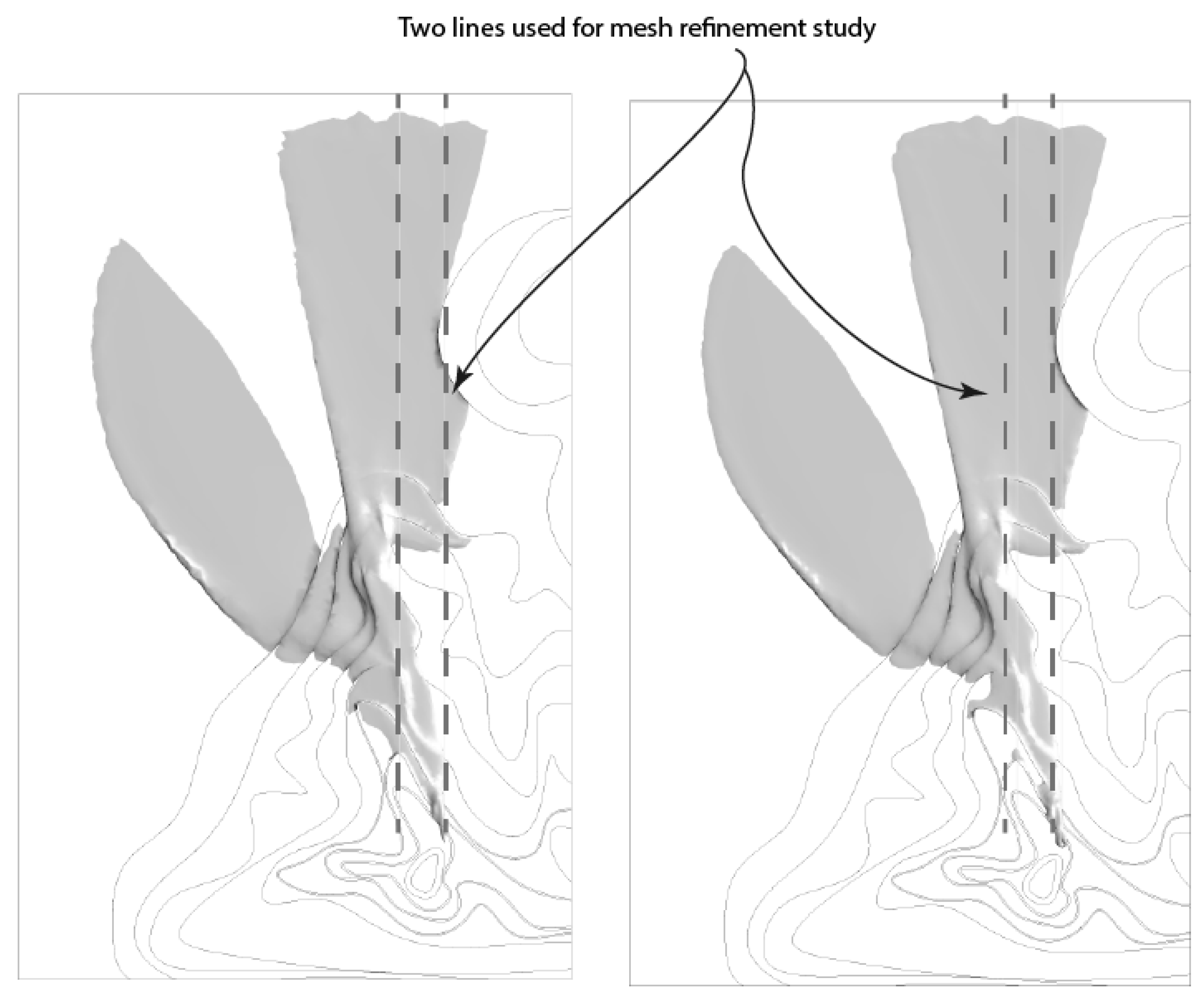
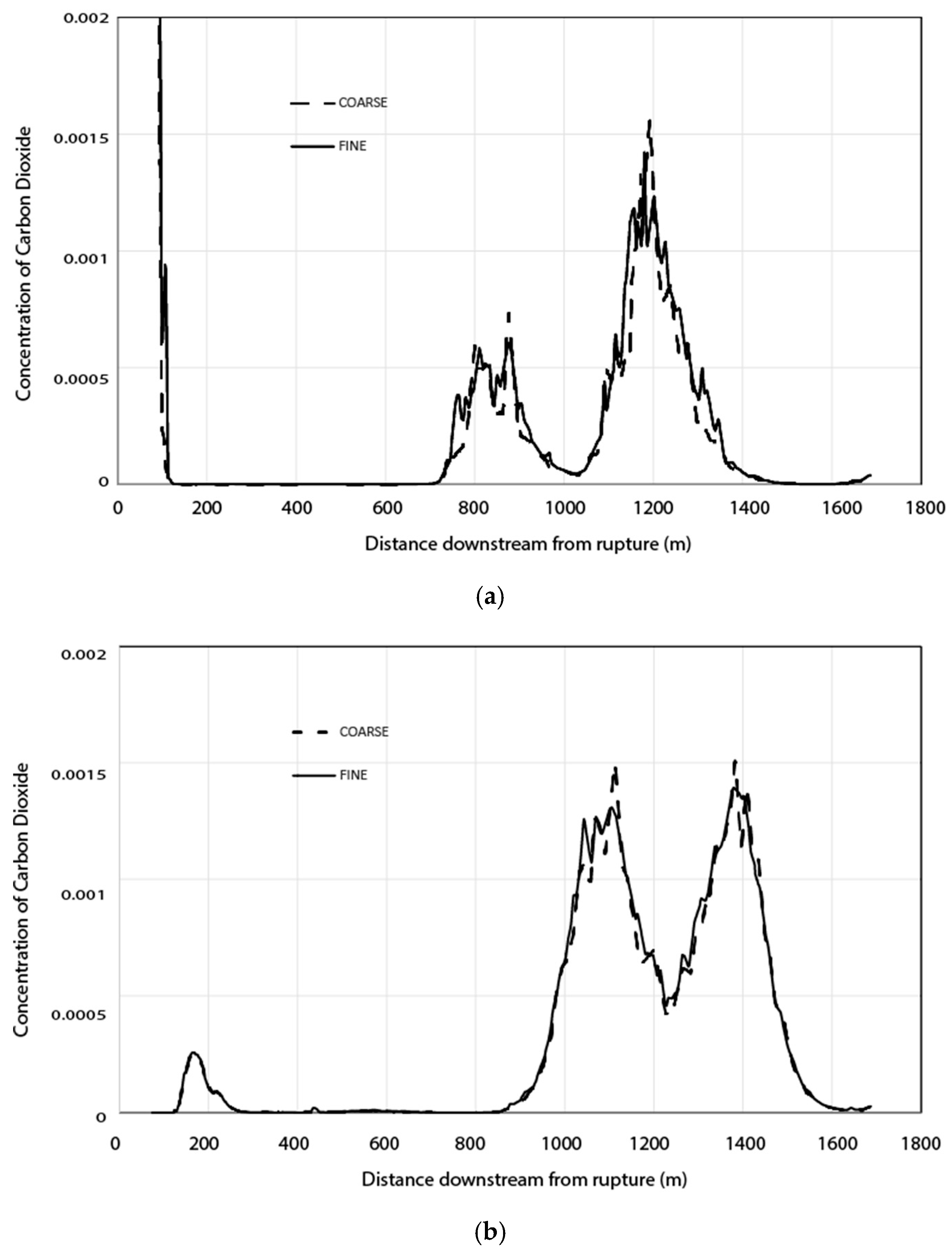
3.3. Real-World Model
3.4. Selection of CFD and Dispersion Models
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abraham, J.P.; Cheng, L.; Mann, M.E.; Trenberth, K.E.; von Schuckmann, K. The Ocean Response to Climate Change Guides Both Adaptation and Mitigation Efforts. Atmos. Ocean. Sci. Lett. 2022, 15, 100221. [Google Scholar] [CrossRef]
- Cheng, L.; Foster, G.; Hausfather, Z.; Trenberth, K.E.; Abraham, J.P. Improved Quantification of the Rate of Ocean Warming. J. Clim. 2022, 35, 4827–4840. [Google Scholar] [CrossRef]
- Cheng, L.; Abraham, J.; Trenberth, K.E.; Fasullo, J.; Boyer, T.; Mann, M.E.; Zhu, J.; Wang, F.; Locarnini, R.; Li, Y.; et al. Another Year of Record Heat for the Oceans. Adv. Atmos. Sci. 2023, 40, 963–974. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Abraham, J.; Trenberth, K.E.; Boyer, T.; Mann, M.E.; Zhu, J.; Wang, F.; Yu, F.; Locarnini, R.; Fasullo, J.; et al. New Record Ocean Temperatures and Related Climate Indicators in 2023. Adv. Atmos. Sci. 2024, in press. [Google Scholar] [CrossRef]
- Mazzoldi, A.; Hill, T.; Colls, J.J. A Consideration of the Jet-Mixing Effect when Modeling CO2 Emissions from High-Pressure CO2 Transportation Facilities. Energy Procedia 2009, 42, 1571–1578. [Google Scholar] [CrossRef][Green Version]
- Permentier, K.; Vercammen, S.; Soetaert, S.; Schellemans, C. Carbon Dioxide Poisoning: A Literature Review of an Often Forgotten Cause of Intoxication in the Emergency Department. Int. J. Emerg. Med. 2017, 10, 14. [Google Scholar] [CrossRef] [PubMed]
- Department of Health and Human Services; National Institute for Occupational Safe. NIOSH Pocket Guide to Chemical Hazards; DHSS (NIOSH) Publication no. 2005-149; Scholar’s Choice: London, UK, 2015. [Google Scholar]
- Woodward, J.L.; Cook, J.; Papadourakis, A. Modeling and Validation of a Dispersing Aerosol Jet. J. Hazard. Mater. 1995, 44, 185–207. [Google Scholar] [CrossRef]
- Woodward, J.L.; Papadourakis, A. Reassessment and reevaluation of rainout and drop zie correlation for an aerosol jet. J. Hazard. Mater. 1995, 44, 209–230. [Google Scholar] [CrossRef]
- Ermak, D. Users Manual for Slab: An Atmospheric Dispersion Model for Denser-than-Air Releases; Lawrence Livermore Laboratory: Livermore, CA, USA, June 1990. [Google Scholar]
- Colenbrander, G.W. A mathematical model for the transient behaviour of dense vapor clouds. In Proceedings of the 3rd International Symposium on Loss Prevention and Safety Promotion in the Process Industries, Basel, Switzerland, 15–18 September 1980. [Google Scholar]
- Havens, J. A Dispersion Model for Elevated Dense Gas Jet Chemical Releases, Vol. II: Users Guide; U.S. Environmental Protection Agency: Durham, NC, USA, 1988.
- Liu, X.; Godbole, A.; Lu, C.; Michal, G.; Venton, P. Optimization of Dispersion Parameters of Gaussian Plume Model for CO2 Dispersion. Environ. Sci. Pollut. Res 2015, 22, 18288–18299. [Google Scholar] [CrossRef]
- Witlox, H.; Holt, A. A Unified Model for Jet, Heavy, and Passive Dispersion Including Droplet Rainout and Re-evaporation. Center for Chemical Process Safety Conference. 1999. Available online: https://www.researchgate.net/profile/Henk-Witlox/publication/265566709_A_unified_model_for_jet_heavy_and_passive_dispersion_including_droplet_rainout_and_re-evaporation/links/54bcf5b50cf253b50e2d8830/A-unified-model-for-jet-heavy-and-passive-dispersion-including-droplet-rainout-and-re-evaporation.pdf (accessed on 1 February 2024).
- Witlox, H.; Harper, M.; Oke, A. Modeling of Discharge and Atmospheric Dispersion for Carbon Dioxide Release. J. Loss Prev. Process Ind. 2009, 22, 795–802. [Google Scholar] [CrossRef]
- Witlox, H.; Harper, M.; Oke, A. PHAST Validation of Discharge and Atmospheric Dispersion for Pressurized Carbon Dioxide Releases. In Proceedings of the Hazards XXIII Symposium Series 158, Southport, UK, 12–15 November 2012. [Google Scholar]
- Hill, T.A.; Fackrell, J.E.; Dubal, M.R.; Stiff, S.M. Understanding the Consequences of CO2 Leakage Downstream of the Capture Plant. Energy Procedia 2011, 4, 2230–2237. [Google Scholar] [CrossRef]
- Gant, S.E.; Kelsey, A.; McNally, K.; Witlox, H.; Bilio, M. Sensitivity Analysis of Dispersion Models for Jet Releases of Dense-Phase Carbon Dioxide. Chem. Eng. Trans. 2013, 31, 121–125. [Google Scholar]
- Gant, S.E.; Narasimhamurthy, V.D.; Skjold, T.; Jamois, D.; Proust, C. Evaluation of multi-Phase Atmospheric Dispersion Models for Application to Carbon Capture and Storage. J Loss Prev. Process Ind. 2014, 32, 286–298. [Google Scholar] [CrossRef]
- Liu, X.; Godbole, A.R.; Lu, C.; Michal, G. Investigation of Terrain Effects on the Consequence Distance of CO2 Released from High-Pressure Pipelines. Fac. Eng. Inf. Sci.–Pap. Part B 2017, 66, 995. [Google Scholar]
- Liu, X.; Godbole, A.; Lu, C.; Guillaume, M.; Linton, V. Consequence Modeling of CO2 Pipeline Failure. Energy Procedia. 2019, 159, 5109–5115. [Google Scholar] [CrossRef]
- Pontiggia, M.; Derudi, M.; Nusini, V.; Rota, R. Hazardous Gas Dispersion: A CFD model Accounting for Atmospheric Stability Classes. J. Hazard. Mater. 2009, 171, 739–747. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, K.J.; Lien, F.S.; Tee, E. Dense Gas Dispersion Modeling of CO2 Released from Carbon Capture and Storage Infrastructure into a Complex Environment. Int. J. Greenh. Gas Control 2013, 17, 127–139. [Google Scholar] [CrossRef]
- Wen, J.; Heidari, A.; Xu, B.; Jie, H. Dispersion of Carbon Dioxide from Vertical Vent and Horizontal Releases—A Numerical Study. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2013, 227, 125–139. [Google Scholar] [CrossRef]
- Xing, J.; Liu, Z.; Huang, P.; Zhou, Y.; Zhang, D.; Wang, F. Experimental and numerical study of the dispersion of carbon dioxide plume. J. Hazard. Mater. 2013, 256–257, 40–48. [Google Scholar] [CrossRef]
- Sklavounos, S.; Rigas, F. Validation of Turbulence Models in Heavy Gas Dispersion over Obstacles. J. Hazard. Mater. 2004, 108, 9–20. [Google Scholar] [CrossRef]
- Wang, H.; Zhanpang, Y.; Fan, M.; Bin, L.; Peng, H. Study on Dispersion of Carbon Dioxide over the Shrubbery Region. Front. Energy Res. 2021, 9, 695224. [Google Scholar]
- Wang, H.; Liu, B.; Liu, X.; Deng, J.; You, Z. Dispersion of Carbon Dioxide Released from Buried High-Pressure Pipeline Over Complex Terrain. Environ. Sci. Pollut. Res. Int. 2021, 28, 6635–6648. [Google Scholar] [CrossRef] [PubMed]
- Woolley, R.M.; Fairweather, M.; Wareing, C.J.; Falle, S.A.; Mahgerefteh, H.; Martynov, S.; Brown, S.; Narasimhamurthy, V.D.; Storvik, I.E.; Sælen, L.; et al. CO2PipeHaz: Quantitative Hazard Assessment for Next Generation CO2 Pipelines. In Proceedings of the 12th International Conference on Greenhouse Gas Technologies (GHGT-12), Austin, TX, USA, 5 October 2014. [Google Scholar]
- Godbole, A.; Liu, X.; Michael, G.; Davis, M.; Lu, C.; Armstrong, K.; Medina, C.H. Atmospheric Dispersion of CO2 Following Full-Scale Burst Tests. In Proceedings of the 14th International Convection on Greenhouse Gas Control Technologies (GHGT-14), Melbourne, Australia, 21–25 October 2018. [Google Scholar]
- Peterson, R.L. Effect of Homogeneous and Heterogeneous Surface Roughness on Heavier-than-Air-Gas Dispersion. J. Wind Eng. Ind. Aerodyn. 1990, 36, 643–652. [Google Scholar] [CrossRef]
- Hanna, S.R.; Chang, J.C. Use of the Kit Fox data to analyze dense gas dispersion modeling issues. Atmos. Environ. 2001, 35, 2231–2242. [Google Scholar] [CrossRef]
- Mack, A.; Spruijt, M.P.N. CFD Dispersion Investigation of CO2 Worst Case Scenarios Including Terrain and Release Effects. Energy Procedia 2014, 51, 363–372. [Google Scholar] [CrossRef]
- Mazzoldi, A.; Hill, T.; Colls, J. CFD and Gaussian Atmospheric dispersion models: A comparison for leak from Carbon Dioxide Transportation and Storage Facilities. Atmos. Environ. 2008, 42, 8046–8054. [Google Scholar] [CrossRef]
- Ahmad, M.; Lowesmith, B.; De Koeijer, G.; Nilsen, S.; Tonda, H.; Spinelli, C.; Cooper, R.; Clausen, S.; Mendes, R.; Florisson, O. COSHER Joint Industry Project: Large Scale Pipeline Rupture Tests to Study CO2 Release and Dispersion. Int. J. Greenh. Gas Control 2015, 37, 340–353. [Google Scholar] [CrossRef]
- Yan, X.; Guo, X.; Yu, J.; Chen, S.; Zhang, Y.; Mahgerefteh, H.; Martynov, S.; Brown, S. Flow and Characteristics and Dispersion Du ring the Vertical Anthropogenic Venting of Supercritical CO2 from an Industrial Scale Pipeline. Energy Procedia 2018, 154, 66–72. [Google Scholar] [CrossRef]
- Zhou, X.; Li, K.; Tu, R.; Xie, Q.; Jiang, X. A Modelling Study of the Multiphase Leakage Flow from Pressurized CO2 Pipeline. J. Hazard. Mater. 2016, 305, 286–294. [Google Scholar] [CrossRef]
- Vitali, M.; Zuliani, C.; Corvaro, F.; Marchetti, B.; Terenzi, A.; Tallone, F. Risks and Safety of CO2 Transport via Pipeline: A Review of Risk Analysis and Modeling Approaches for Accidental Releases. Energies 2021, 14, 4601. [Google Scholar] [CrossRef]
- Hanna, S.R.; Steinberg, K.W. Overview of Petroleum Environmental Research Forum (PERF) Dense Gas Dispersion Modeling. Atmos. Environ. 2001, 35, 2223–2229. [Google Scholar] [CrossRef]
- Hanna, S.R.; Strimaitis, D.G.; Chang, J.C. Hazard Response Modeling Uncertainty (A Quantitative Method) Vol. II—Evaluation of Commonly Used Hazardous Gas Dispersion Models; Report No. ESL-TR-01-29; Sigma Research Corporation: Westford, MA, USA, 1993. [Google Scholar]
- Pouyakian, M.; Ashouri, M.; Eidani, S.; Madvari, R.F.; Laal, F. A systematic review of Consequence Modeling Studies of the Process Accidents in Iran from 2006 to 2022. Heliyon 2023, 9, e13550. [Google Scholar] [CrossRef] [PubMed]
- Alivi, A.T.; Shahraki, F.; Sardashti Birjandi, M.R.; Khalilipour Langerudi, M.M. Consequence Moedling and Determining of Safe Distance in the Natural Gas Pressure Reduction Station Using PHAST Software (Case Study Borumi Station in Ahvax). Occup. Med. 2023, 15, 37–57. [Google Scholar]
- Ghasemi, M.; Givehchi, S.; Nasrabadi, M. Modeling the Outcome of Tank Explosion Using PHAST Software and Presentations of Emergency Operations Plan (Case Study: Ethylene Tank of Kavian Petrochemical Company). J. Fundam. Appl. Sci. 2016, 8, 2007–2021. [Google Scholar]
- Wang, B.; Chen, B.; Zhao, J. The Real-Time Estimation of Hazardous Gas Dispersion by the Integration of Gas Detectors, Neural Network and Gas Dispersion Models. J. Hazard. Mater. 2015, 300, 433–442. [Google Scholar] [CrossRef] [PubMed]
- Dai, Y.; Mak, C.M.; Ai, Z.; Hang, J. Evaluation of Computational and Physical Parameters Influencing CFD Simulations of Pollutant Dispersion in Building Arrays. Build. Environ. 2018, 137, 90–107. [Google Scholar] [CrossRef]
- Ai, Z.T.; Mak, C.M. Large-Eddy Simulation of Flow and Dispersion Around an Isolated Building: Analysis of Influencing Factors. Comput. Fluids 2015, 118, 89–100. [Google Scholar] [CrossRef]
- Abraham, J.P.; Plourde, B.D.; Vallez, L.J. Comprehensive Review and Study of Buoyant Air Flow Within Positive-Pressure Hospital Operating Rooms. Numer. Heat Transf. A 2018, 72, 1–20. [Google Scholar] [CrossRef]
- ANSYS. ANSYS-CFX Solver Theory; ANSYS, Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- Sparrow, E.M.; Abraham, J.P. A New Buoyancy Model Replacing the Standard Pseudo-Density Difference for Internal Natural Convection in Gases. Int. J. Heat Mass Transf. 2003, 46, 3583–3591. [Google Scholar] [CrossRef]
- Minkowycz, W.J.; Abraham, J.P.; Sparrow, E.M. Numerical Simulation of Laminar Breakdown and Subsequent Intermittent and Turbulent Flow in Parallel Plate Channels: Effects of Inlet Velocity Profile and Turbulence Intensity. Int. J. Heat Mass Transf. 2009, 52, 4040–4046. [Google Scholar] [CrossRef]
- Olsen, L.E.; Abraham, J.P.; Cheng, L.J.; Gorman, J.M.; Sparrow, E.M. Summary of Forced-Convection Fluid Flow and Heat Transfer for Square Cylinders of Different Aspect Ratios Ranging from the Cube to a Two-Dimensional Cylinder. Adv. Heat Transf. 2019, 51, 351–457. [Google Scholar]
- Abraham, J.P.; Bhattacharya, S.; Cheng, L.; Gorman, J.M. A Brief History of and Introduction to Computational Fluid Dynamics. In Computational Fluid Dynamics; Bhattacharya, S., Ed.; IntechOpen: London, UK, 2021. [Google Scholar]
- Gorman, J.; Bhattacharya, S.; Abraham, J.P.; Cheng, L. Turbulence Models Commonly used in CFD. In Computational Fluid Dynamics; Bhattacharya, S., Ed.; IntechOpen: London, UK, 2021. [Google Scholar]
- Menter, F. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Dixon, C.M.; Gant, S.E.; Obiorah, C.; Bilio, M. Validation of Dispersion Models for High Pressure Carbon Dioxide Releases. In Proceedings of the Hazards XXIII Symposium Series, Southport, UK, 12–15 November 2012; pp. 153–163. [Google Scholar]
- Liu, Y.; Ozbayoglu, E.M.; Upchurch, E.R.; Baldino, S. Computational Fluid Dynamics Simulations of Taylor Bubbles Rising in Vertical and Inclined Concentric Annuli. Int. J. Multiph. Flow 2023, 159, 104333. [Google Scholar] [CrossRef]
- Liu, Y.; Mitchell, T.; Upchurch, E.R.; Ozbayoglu, E.M.; Baldino, S. Investigation of Taylor Bubble Dynamics in Annula Conduits with Counter-Current Clow. Int. J. Multiph. Flow 2024, 170, 104626. [Google Scholar] [CrossRef]
- Ke, W.; Zeng, H.; Wang, Z.; Yu, H.; Liu, Y.; Zheng, D.; Zhu Jianjun, Z.; Zhu, H. A Numerical Study on Labyrinth Screw Pump (LSP) Performance Under Viscous Fluid Flow. Energies 2023, 16, 5997. [Google Scholar] [CrossRef]
- Brown Coal Innovation Australia Limited. Dispersion Modelling Techniques for Carbon Dioxide Pipelines in Australia; Document no. 20873-RP-001; Brown Coal Innovation Australia Limited: Melbourne, Australia, 2015; pp. 1–193.









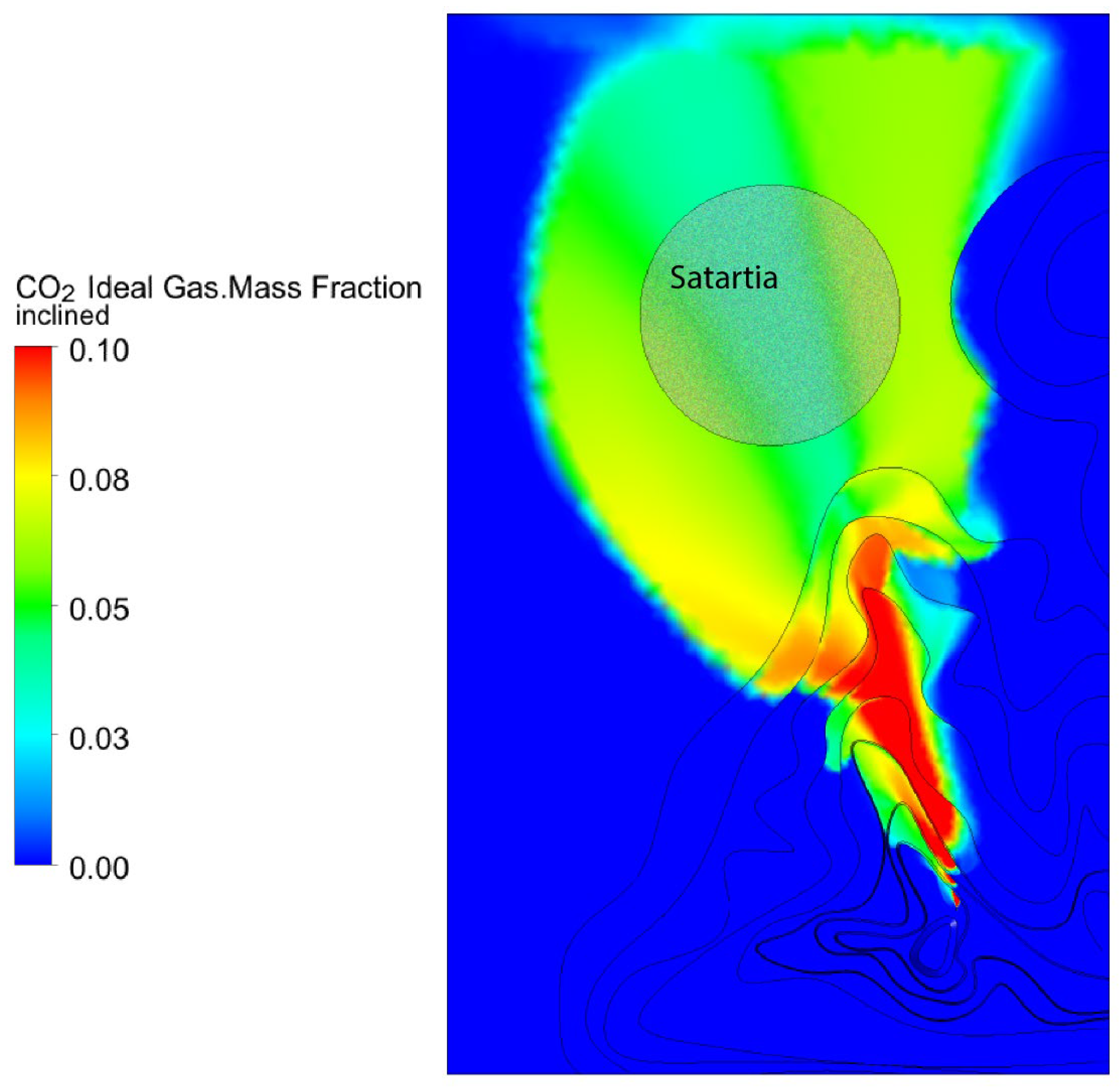
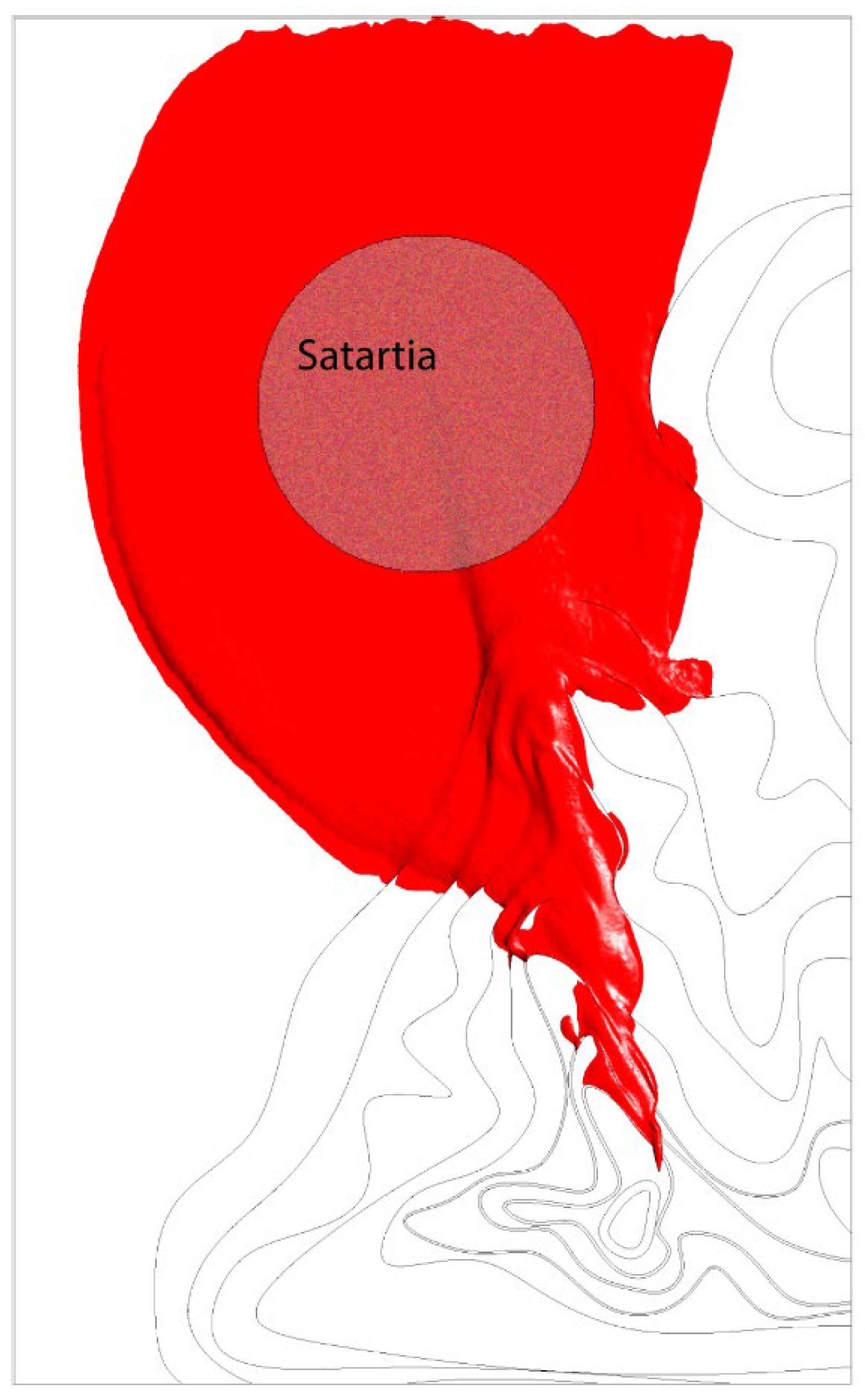


| Parameter | Test 9 | Test 11 |
|---|---|---|
| Storage pressure (atm) | 152 | 81 |
| Ambient temperature (°C) | 8.2 | 11.6 |
| Ambient pressure (atm) | 0.95 | 0.95 |
| Wind speed (m/s) | 4.04 | 5.99 |
| Discharge rate (kg/s) | 6.05 | 7.12 |
| Discharge temperature (°C) | −70 | −70 |
| Orifice diameter (mm) | 11.94 | 11.94 |
| Orifice opening area (mm2) | 112 | 112 |
| Case No. | Experimental (%) | CFD (%) | PHAST (%) |
|---|---|---|---|
| 9 | 1.9 | 2.1 | 1.3 |
| 11 | 3.4 | 2.3 | 1.9 |
| Parameter | Inputs |
|---|---|
| Pipe OD and ID (inches) | 24 and 23 |
| Pipeline pressure (psi) | 1336 |
| Ambient temperature (°C, °F) | 15.5 °C, 60 °F |
| Wind speed (m/s) | 2.25 |
| Discharge rates (kg/s) | 250 and 500 |
| Discharge temperature (°C, °F) | −56 °C, −70 °F |
| CO2 released (barrels) | 31,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abraham, J.; Cheng, L.; Gorman, J. CFD Simulation Models and Diffusion Models for Predicting Carbon Dioxide Plumes following Tank and Pipeline Ruptures—Laboratory Test and a Real-World Case Study. Energies 2024, 17, 1079. https://doi.org/10.3390/en17051079
Abraham J, Cheng L, Gorman J. CFD Simulation Models and Diffusion Models for Predicting Carbon Dioxide Plumes following Tank and Pipeline Ruptures—Laboratory Test and a Real-World Case Study. Energies. 2024; 17(5):1079. https://doi.org/10.3390/en17051079
Chicago/Turabian StyleAbraham, John, Lijing Cheng, and John Gorman. 2024. "CFD Simulation Models and Diffusion Models for Predicting Carbon Dioxide Plumes following Tank and Pipeline Ruptures—Laboratory Test and a Real-World Case Study" Energies 17, no. 5: 1079. https://doi.org/10.3390/en17051079
APA StyleAbraham, J., Cheng, L., & Gorman, J. (2024). CFD Simulation Models and Diffusion Models for Predicting Carbon Dioxide Plumes following Tank and Pipeline Ruptures—Laboratory Test and a Real-World Case Study. Energies, 17(5), 1079. https://doi.org/10.3390/en17051079







