Optimizing the Journey: Dynamic Charging Strategies for Battery Electric Trucks in Long-Haul Transport
Abstract
1. Introduction
1.1. Contribution
- Proposing an online algorithm for a dynamic charging strategy and corresponding framework for the operation simulation of BET:This paper proposes the first optimal online charging strategy considering real charging behavior and rest regulations. The proposed strategy can also handle real-world charging station behavior, such as occupation. We propose an open-source simulation framework for battery electric trucks, including vehicle, infrastructure, and operation simulation models, where we include the proposed strategy. This framework can be used for the simultaneous design of the BET and of the public charging infrastructure.
- Simulative case studies to outline recommendations of action for the efficient rollout of BET in long-haul applications:We use the proposed framework and charging strategy to first investigate the dependencies between truck and charging infrastructure properties. Second, we show which rollout of charging infrastructure is sufficient to ensure the operability of BET. For this, we use three case studies that address the following three research questions:
- (a)
- How do battery capacity and available charging power influence the operation time of BET in long-haul applications?
- (b)
- For today’s BET, which infrastructure properties of charger density and charging power should be applied?
- (c)
- How does real-world charging station behavior, such as occupation, change these fundamental requirements?
1.2. Article Organization
2. Method
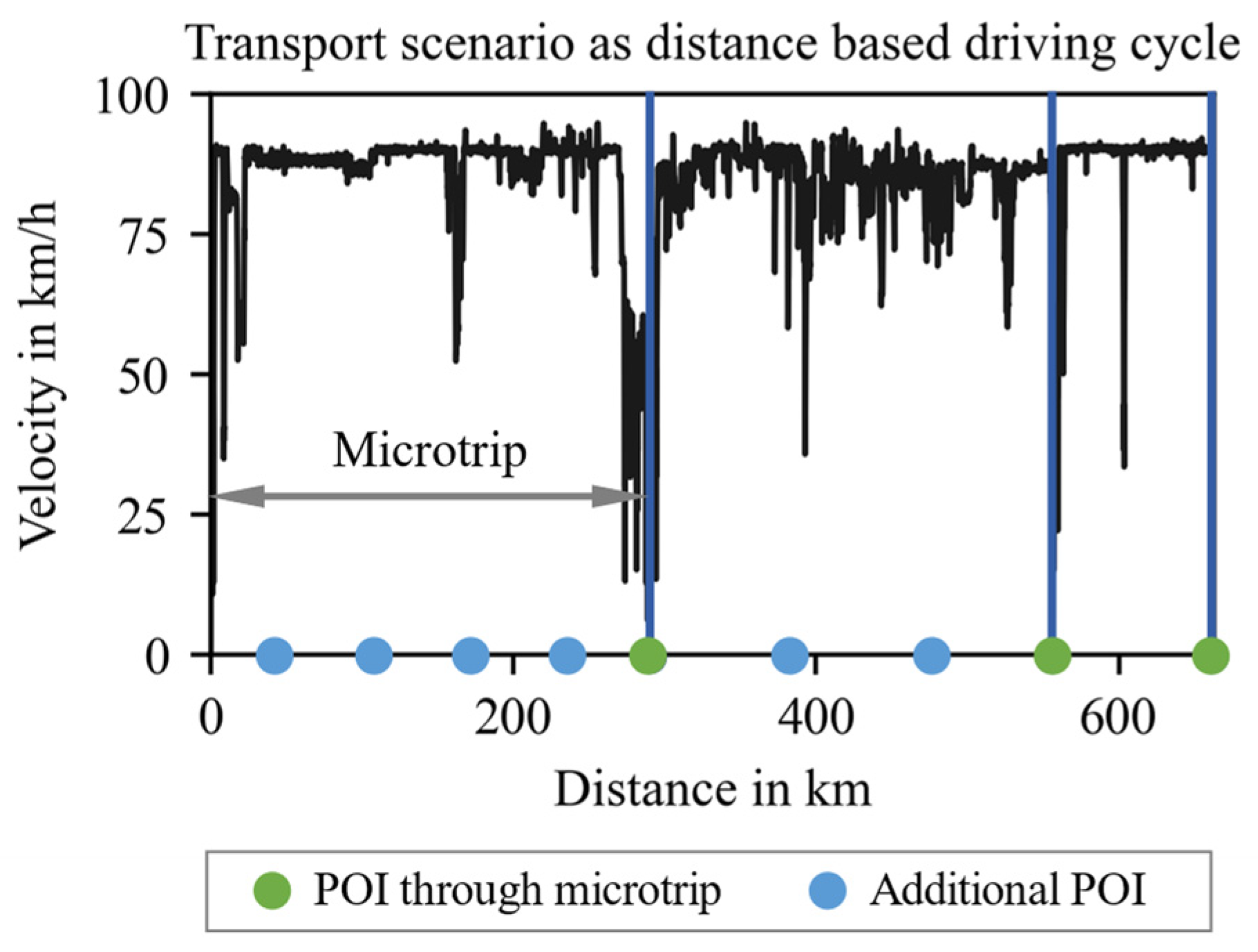
2.1. Problem Description
2.2. Mathematical Problem Formulation
2.3. Properties of the Considered Problem
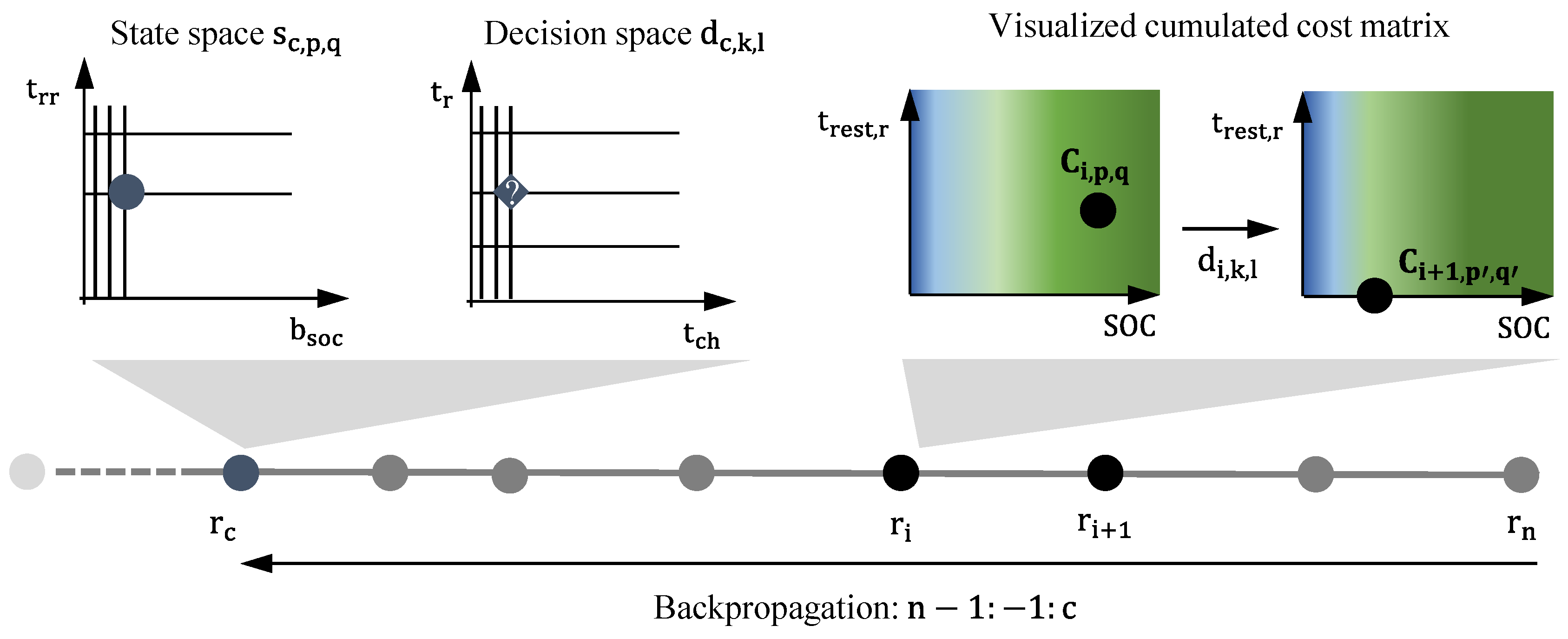
2.4. Solution Approach: Dynamic Programming
3. Simulation Framework and Parametrization
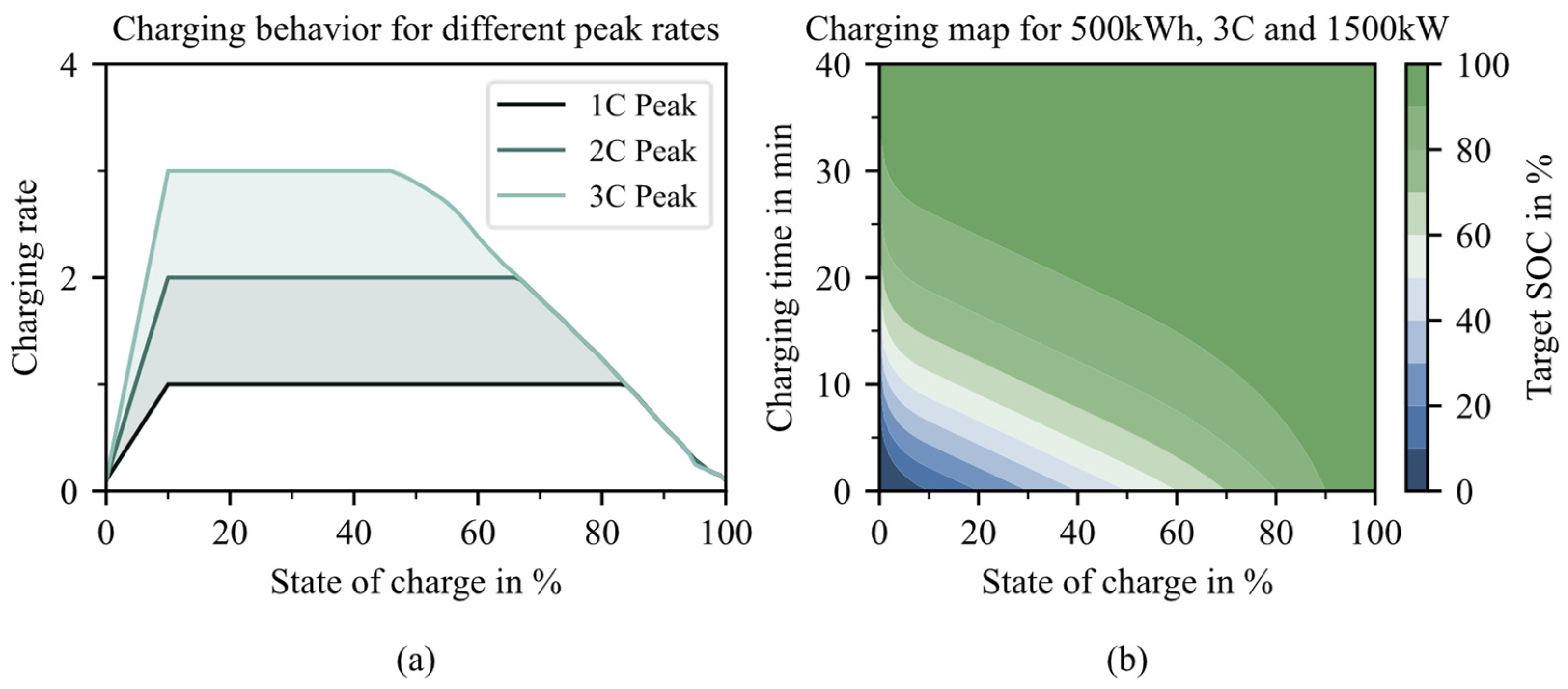
3.1. Model Parametrization
3.2. Strategy Parametrization
- (1)
- If the range is not sufficient for reaching the next POI, the minimum of full charging at the current POI and charging the amount of energy for reaching the destination is selected.
- (2)
- If the next POI can no longer be reached within the allowed driving time of 4.5 h, complete the full rest time, and charge the vehicle at the current POI.
4. Application in Different Scenarios
4.1. Idealized Static Conditions (CS 1)
4.2. Idealized Charging Network (CS 2)
4.2.1. Charging Network Properties
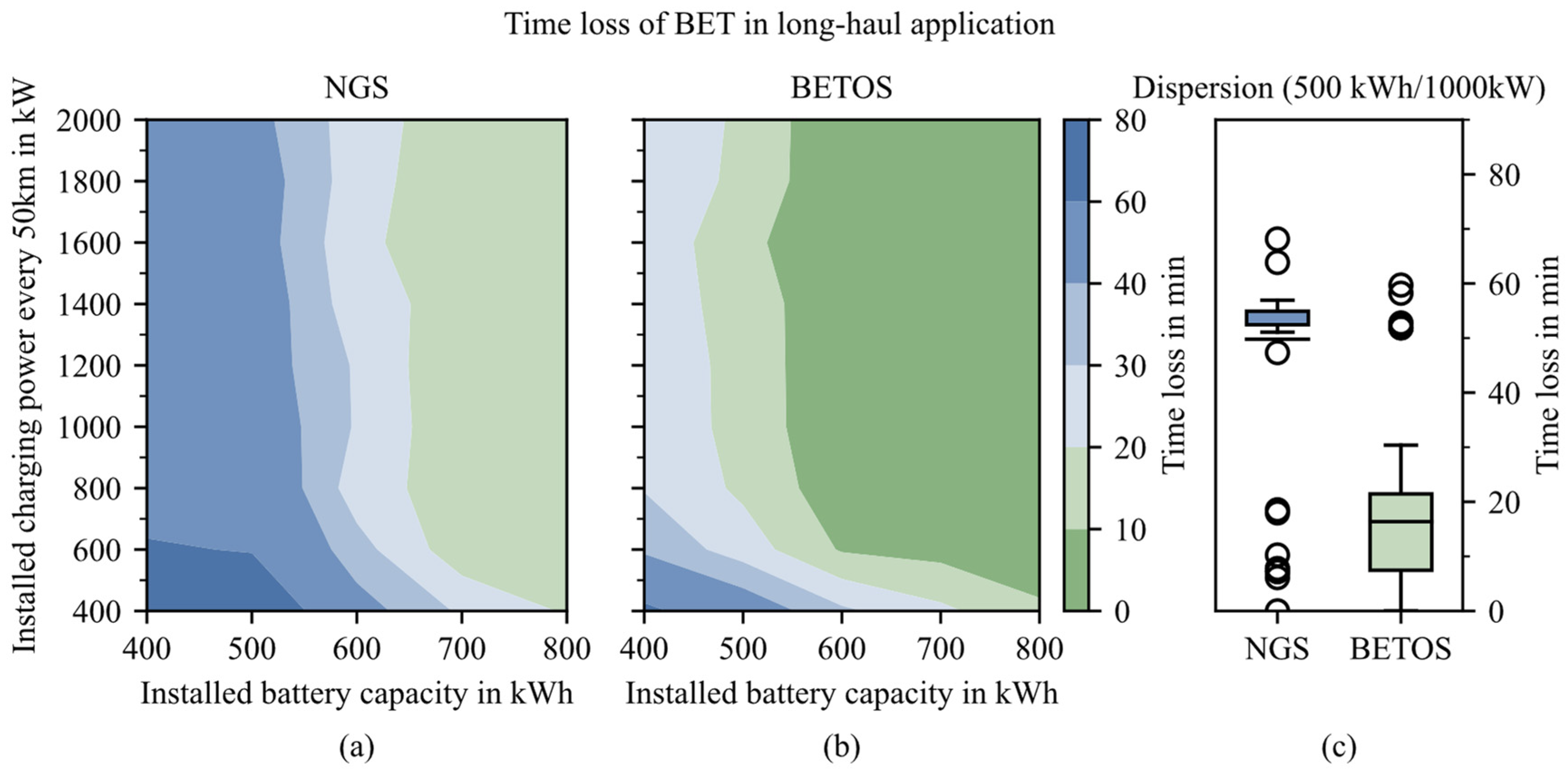
4.2.2. Results
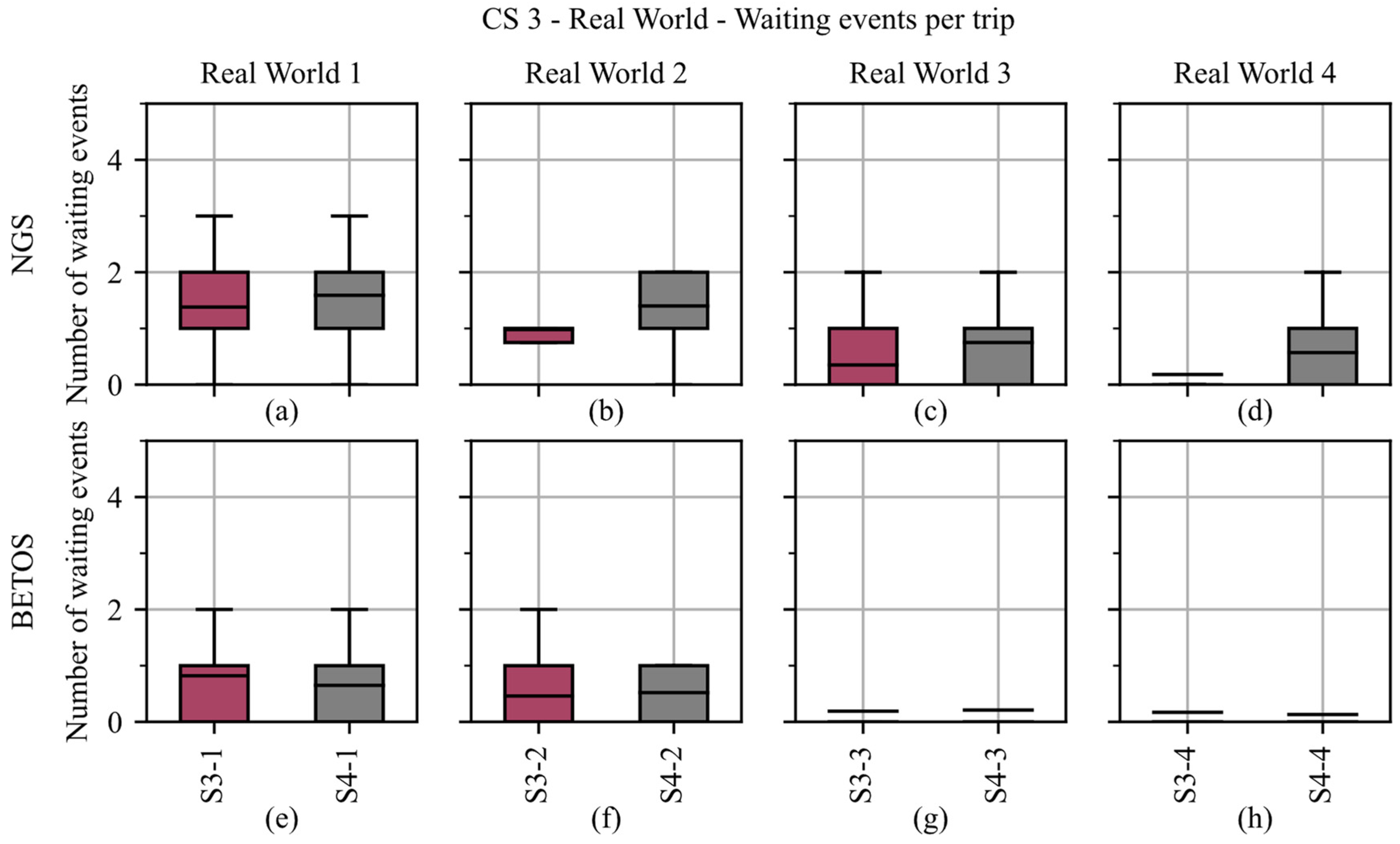
4.3. Real-World Charging Network Conditions (CS 3)
4.3.1. Charging Strategy Adaption for Uncertain Charging Station Availability
4.3.2. Charging Network Properties
4.3.3. Results
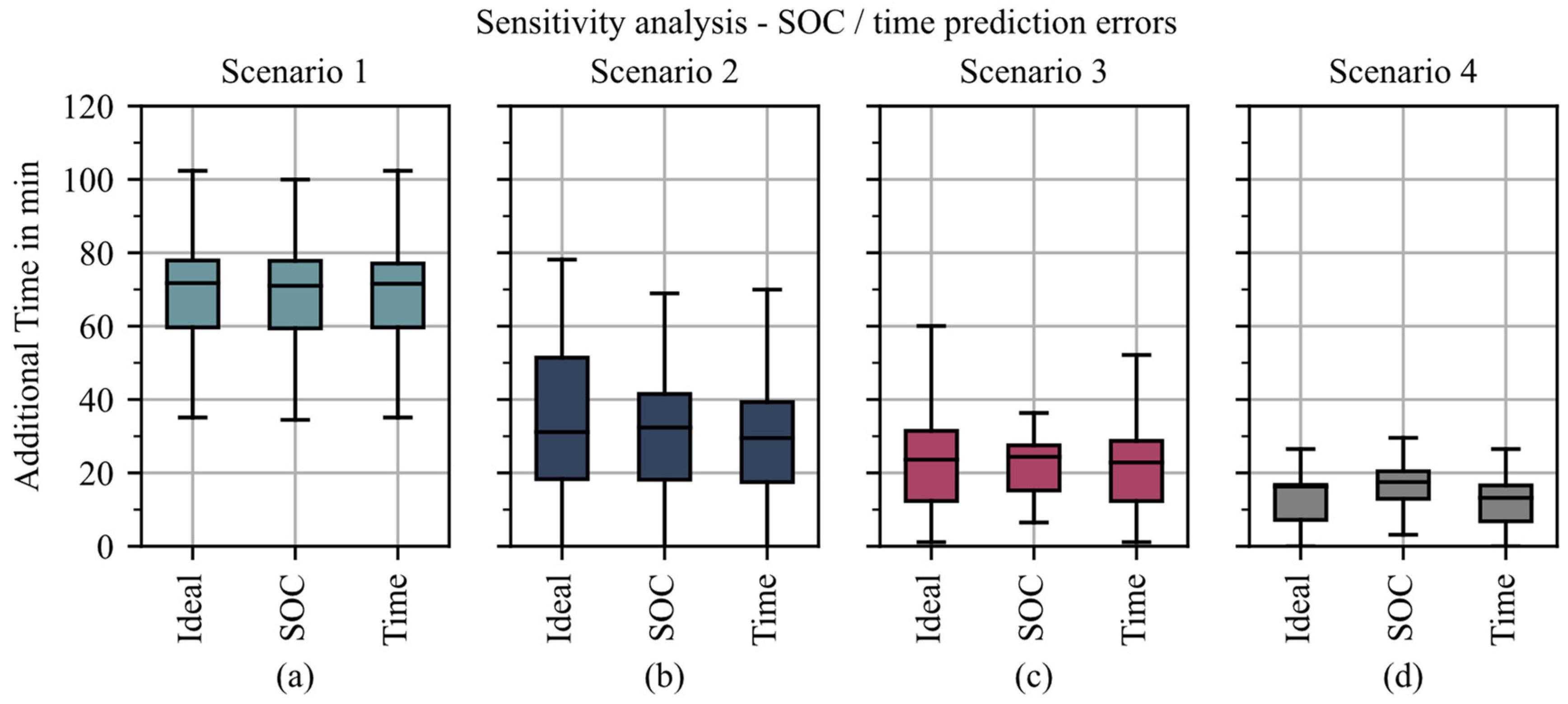
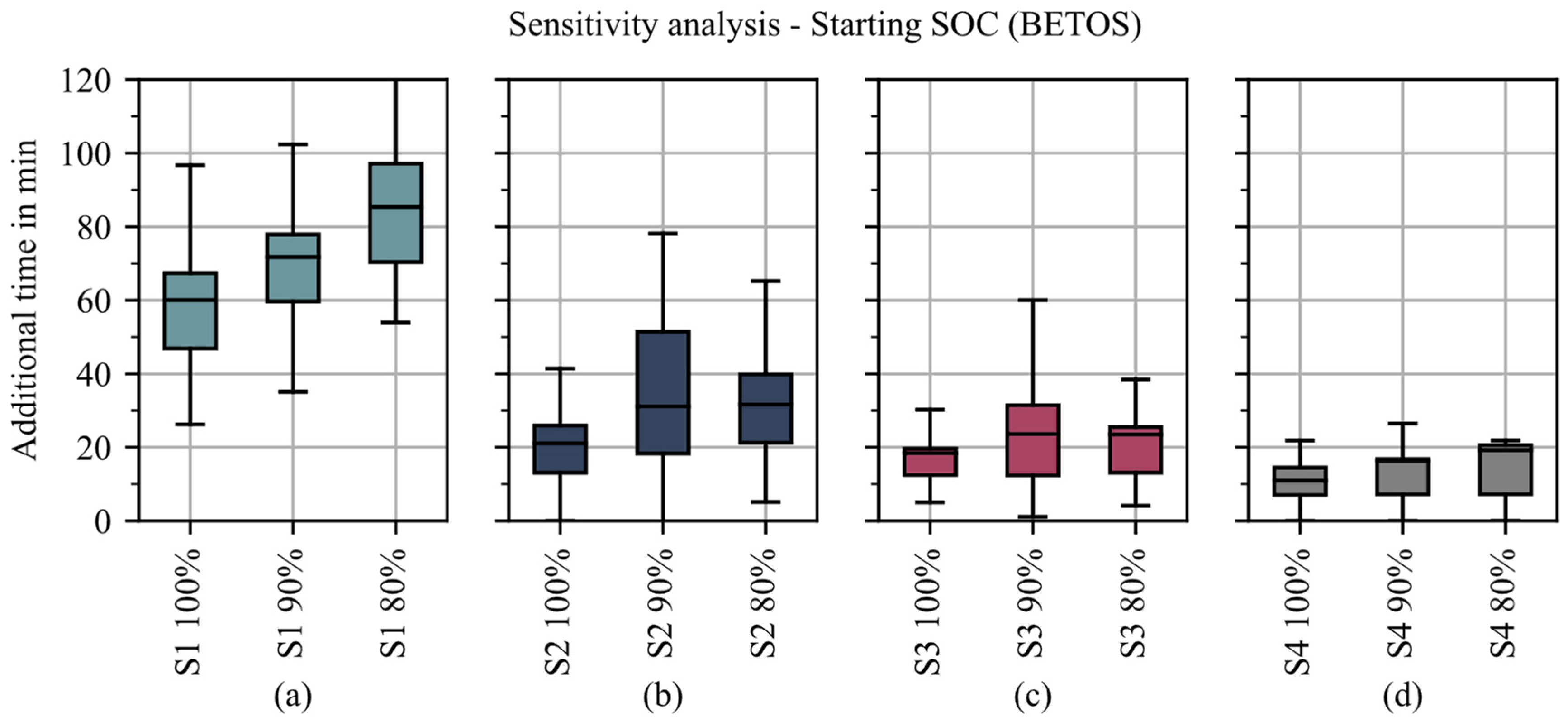
5. Sensitivity Analysis
5.1. Influence of Information Loss
5.2. Influence of Prediction Errors
5.3. Influence of Starting Conditions
6. Discussion
6.1. Algorithm
6.2. Simulation Studies and Results
6.3. Recommendations for Efficient Operation of Battery Electric Trucks in Long-Haul Application
7. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameter | Abbreviation | Value | Source |
|---|---|---|---|
| Drag coefficient | 0.55 | [15] | |
| Frontal area | [46] | ||
| Density air | - | ||
| Gravimetric acceleration | g | - | |
| Rolling resistance coefficient | 0.005 | [15] | |
| Dynamic tire radius | 0.4465 m | [47] | |
| Electric machine efficiency | 95% | [47] | |
| Maximum electric machine torque | 2018 Nm | [47] | |
| Auxiliary consumers | 4 kW | [48] | |
| Charging efficiency | 90% | [18] | |
| Minimal allowed state of charge | 15% | - | |
| SOC at start | 90% | - |
| Weight Parameter | Abbreviation | Value/Formular | Source |
|---|---|---|---|
| Trailer mass | 7500 kg | [3] | |
| Tractor without powertrain | 5400 kg | [49] | |
| Payload | 19.300 kg | [36] | |
| Density electric machine | 0.5 kg/kW | [50] | |
| Density gearbox | kg/Nm | [51] | |
| Density power electronics | 0.078 kg/kW | [50] | |
| Gravimetric density battery pack | 165 Wh/kg | [52] |
| Parameter | Abbreviation | Value/Formular | Source |
|---|---|---|---|
| Connection time | 6 min | [33] | |
| Waiting time in case of occupation | 15 min | - |
References
- European Commission. Directorate General for Mobility and Transport. EU Transport in Figures: Statistical Pocketbook 2022. LU: Publications Office, 2022. Available online: https://data.europa.eu/doi/10.2832/216553 (accessed on 2 June 2023).
- European Commission. Directorate General for Climate Action. Going Climate-Neutral by 2050: A Strategic Long Term Vision for a Prosperous, Modern, Competitive and Climate Neutral EU Economy. LU: Publications Office, 2019. Available online: https://data.europa.eu/doi/10.2834/02074 (accessed on 2 June 2023).
- e-Truck Studie 2023|Tankkarten und Services für Ihr Flottenmanagement|Tankkarte & Ladekarte—Flottenmanagement Services|Aral, Aral Card. Available online: https://www.aral.de/de/global/fleet_solutions/aral-flottenloesungen/e-Truck-Studie-2023.html (accessed on 2 June 2023).
- European Union. Directive (EU) 2022/2464 of the European Parliament and of the Council of 14 December 2022 Amending Regulation (EU) No 537/2014, Directive 2004/109/EC, Directive 2006/427EC and Directive 2013/34/EU, as Regards Corporate Sustainability Reporting; European Union: Brussels, Belgium, 2022. [Google Scholar]
- Huang, W.-D.; Zhang, Y.-H.P. Energy Efficiency Analysis: Biomass-to-Wheel Efficiency Related with Biofuels Production, Fuel Distribution, and Powertrain Systems. PLoS ONE 2011, 6, e22113. [Google Scholar] [CrossRef] [PubMed]
- Cunanan, C.; Tran, M.K.; Lee, Y.; Kwok, S.; Leung, V.; Fowler, M. A Review of Heavy-Duty Vehicle Powertrain Technologies: Diesel Engine Vehicles, Battery Electric Vehicles, and Hydrogen Fuel Cell Electric Vehicles. Clean Technol. 2021, 3, 474–489. [Google Scholar] [CrossRef]
- Volvo FH Electric. Available online: https://www.volvotrucks.de/de-de/trucks/trucks/volvo-fh/volvo-fh-electric.html (accessed on 7 December 2023).
- Showroom|Mercedes-Benz Trucks. Available online: https://eactros600.mercedes-benz-trucks.com/de/de/eactros-600/showroom.html (accessed on 7 December 2023).
- MAN Truck & Bus SE, Elektro-Lkw|MAN DE. Available online: https://www.man.eu/de/de/lkw/elektro-lkw/uebersicht.html (accessed on 7 December 2023).
- Lahmann, S. Aktivitäten zur Nutzfahrzeug Ladeinfrastruktur, Presented at the BMDV Fachkonferenz Klimafreundliche Nutzfahrzeuge, November 2022. Available online: https://www.now-gmbh.de/wp-content/uploads/2022/11/NFZ22_Aktivitaeten-zur-Nutzfahrzeug-Ladeinfrastruktur_Lahmann.pdf (accessed on 7 December 2023).
- Charging the Future of Road Transport, Milence. Available online: https://milence.com/ (accessed on 6 February 2024).
- Bp Pulse Builds Europe’s First Public Charging Corridor for Electric Trucks Along Major Logistics Route|News and Insights|Home, bp Global. Available online: https://www.bp.com/en/global/corporate/news-and-insights/press-releases/bp-pulse-build-europes-first-public-charging-corridor-for-electric-trucks-along-major-logistics-route.html (accessed on 6 February 2024).
- Plötz, P. Hydrogen technology is unlikely to play a major role in sustainable road transport. Nat. Electron. 2022, 5, 8–10. [Google Scholar] [CrossRef]
- Nykvist, B.; Olsson, O. The feasibility of heavy battery electric trucks. Joule 2021, 5, 901–913. [Google Scholar] [CrossRef]
- Link, S.; Plötz, P. Technical Feasibility of Heavy-Duty Battery-Electric Trucks for Urban and Regional Delivery in Germany—A Real-World Case Study. World Electr. Veh. J. 2022, 13, 161. [Google Scholar] [CrossRef]
- Wolff, S.; Seidenfus, M.; Brönner, M.; Lienkamp, M. Multi-disciplinary design optimization of life cycle eco-efficiency for heavy-duty vehicles using a genetic algorithm. J. Clean. Prod. 2021, 318, 128505. [Google Scholar] [CrossRef]
- Mareev, I.; Becker, J.; Sauer, D.U. Battery Dimensioning and Life Cycle Costs Analysis for a Heavy-Duty Truck Considering the Requirements of Long-Haul Transportation. Energies 2018, 11, 55. [Google Scholar] [CrossRef]
- Teichert, O.; Link, S.; Schneider, J.; Wolff, S.; Lienkamp, M. Techno-economic cell selection for battery-electric long-haul trucks. eTransportation 2023, 16, 100225. [Google Scholar] [CrossRef]
- Karlsson, J.; Grauers, A. Case Study of Cost-Effective Electrification of Long-Distance Line-Haul Trucks. Energies 2023, 16, 2793. [Google Scholar] [CrossRef]
- Schneider, J.; Teichert, O.; Zähringer, M.; Balke, G.; Lienkamp, M. The novel Megawatt Charging System standard: Impact on battery size and cell requirements for battery-electric long-haul trucks. eTransportation 2023, 17, 100253. [Google Scholar] [CrossRef]
- Depcik, C.; Gaire, A.; Gray, J.; Hall, Z.; Maharjan, A.; Pinto, D.; Prinsloo, A. Electrifying Long-Haul Freight—Part II: Assessment of the Battery Capacity. SAE Int. J. Commer. Veh. 2019, 12, 87–102. [Google Scholar] [CrossRef]
- Mauler, L.; Dahrendorf, L.; Duffner, F.; Winter, M.; Leker, J. Cost-effective technology choice in a decarbonized and diversified long-haul truck transportation sector: A U.S. case study. J. Energy Storage 2022, 46, 103891. [Google Scholar] [CrossRef]
- EU-Parlament, Verordnung (EG) Nr. 561/2006 des Europäischen Parlaments und des Rates vom 15. März 2006 zur Harmonisierung bestimmter Sozialvorschriften im Straßenverkehr und zur Änderung der Verordnungen (EWG) Nr. 3821/85 und (EG) Nr. 2135/98 des Rates sowie zur Aufhebung der Verordnung (EWG) Nr. 3820/85 des Rates. Available online: https://www.balm.bund.de/DE/Themen/RechtsentwicklungRechtsvorschriften/Rechtsvorschriften/Fahrpersonalrecht/fahrpersonalrecht_node.html (accessed on 19 April 2023).
- Speth, D.; Plötz, P.; Funke, S.; Vallarella, E. Public fast charging infrastructure for battery electric trucks—A model-based network for Germany. Environ. Res. Infrastruct. Sustain. 2022, 2, 025004. [Google Scholar] [CrossRef]
- Auer, J.; Link, S.; Plötz, P. Public Charging Locations for Battery Electric Trucks: A GIS-Based Statistical Analysis Using Real-world Truck Stop Data for Germany. 2023. Available online: https://publica.fraunhofer.de/handle/publica/439538 (accessed on 19 April 2023).
- Hecht, C.; Victor, K.; Zurmühlen, S.; Sauer, D.U. Electric vehicle route planning using real-world charging infrastructure in Germany. eTransportation 2021, 10, 100143. [Google Scholar] [CrossRef]
- Erdelić, T.; Carić, T. A Survey on the Electric Vehicle Routing Problem: Variants and Solution Approaches. J. Adv. Transp. 2019, 2019, e5075671. [Google Scholar] [CrossRef]
- Zähringer, M.; Wolff, S.; Schneider, J.; Balke, G.; Lienkamp, M. Time vs. Capacity—The Potential of Optimal Charging Stop Strategies for Battery Electric Trucks. Energies 2022, 15, 7137. [Google Scholar] [CrossRef]
- Sweda, T.M.; Dolinskaya, I.S.; Klabjan, D. Adaptive Routing and Recharging Policies for Electric Vehicles. Transp. Sci. 2017, 51, 1326–1348. [Google Scholar] [CrossRef]
- Guillet, M.; Hiermann, G.; Kröller, A.; Schiffer, M. Electric Vehicle Charging Station Search in Stochastic Environments. Transp. Sci. 2022, 56, 483–500. [Google Scholar] [CrossRef]
- Bai, T.; Li, Y.; Johansson, K.H.; Mårtensson, J. Rollout-Based Charging Strategy for Electric Trucks with Hours-of-Service Regulations. arXiv 2023, arXiv:2303.08895. [Google Scholar] [CrossRef]
- Balke, G.; Adenaw, L. Heavy commercial vehicles’ mobility: Dataset of trucks’ anonymized recorded driving and operation (DT-CARGO). Data Brief 2023, 48, 109246. [Google Scholar] [CrossRef]
- Cussigh, M.; Hamacher, T. Optimal Charging and Driving Strategies for Battery Electric Vehicles on Long Distance Trips: A Dynamic Programming Approach. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; IEEE Press: New York, NY, USA, 2019; pp. 2093–2098. [Google Scholar] [CrossRef]
- Huber, G.; Bogenberger, K. Long-Trip Optimization of Charging Strategies for Battery Electric Vehicles. Transp. Res. Rec. 2015, 2497, 45–53. [Google Scholar] [CrossRef]
- Wassiliadis, N.; Steinsträter, M.; Schreiber, M.; Rosner, P.; Nicoletti, L.; Schmid, F.; Ank, M.; Teichert, O.; Wildfeuer, L.; Schneider, J.; et al. Quantifying the state of the art of electric powertrains in battery electric vehicles: Range, efficiency, and lifetime from component to system level of the Volkswagen ID.3. eTransportation 2022, 12, 100167. [Google Scholar] [CrossRef]
- Fontaras, G.; Rexeis, M.; Dilara, P.; Hausberger, S.; Anagnostopoulos, K. The Development of a Simulation Tool for Monitoring Heavy-Duty Vehicle CO2 Emissions and Fuel Consumption in Europe; SAE Technical Paper 2013-24-0150; SAE International: Warrendale, PA, USA, 2013. [Google Scholar] [CrossRef]
- European Union. Verordnung (EU) 2018/858 Des Europäischen Parlamentes und Rates vom 30. Mai 2018 über die Genehmigung und die Marktüberwachung von Kraftfahrzeugen und Kraftfahrzeuganhängern sowie Systemen, Bauteilen und selbstständigen technischen Einheiten für diese Fahrzeuge, zur Änderung der Verordnung (EG) Nr. 715/2007 und (EG) 595/2009 und zur Aufhebung der Richtlinie 2007/46/EG.; European Union: Brussels, Belgium, 2018. [Google Scholar]
- Austin, T.; DiGenova, F.; Carlson, T.; Joy, R.; Gianolini, K.A. Characterization of Driving Patterns and Emissions from Light-Duty Vehicles in California. Final Report. November 1993. Available online: https://www.semanticscholar.org/paper/Characterization-of-driving-patterns-and-emissions-Austin-DiGenova/165fabafa081938fe77d9c432b4944ea867d16c0 (accessed on 26 May 2023).
- CharIN Whitepaper—Megawatt Charging System (MCS). 24 November 2022. Available online: https://www.charin.global/technology/mcs/ (accessed on 2 February 2024).
- European Parliament. Regulation (EU) 2023/1804 of the European Parliament and the Council of 13 September 2023 on the Deployment of Alternative Fuels Infrastructure, and Repealing Directive 2014/94/EU.; European Parliament: Strasbourg, France, 2023. [Google Scholar]
- Bundesregierung Deutschland. Masterplan Ladeinfrastruktur II der Bundesregierung; Bundesregierung Deutschland: Berlin, Germany, 2022. [Google Scholar]
- Bundesministerium für Digitales und Verkehr. Nebenbetriebe/Rastanlagen; Bundesministerium für Digitales und Verkehr: Berlin, Germany, 2021. [Google Scholar]
- European Electric Vehicle Charging Infrastructure Masterplan. ACEA—European Automobile Manufacturers’ Association. Available online: https://www.acea.auto/publication/european-electric-vehicle-charging-infrastructure-masterplan/ (accessed on 25 May 2023).
- Kahneman, D.; Tversky, A. Prospect Theory: An Analysis of Decision under Risk. Econometrica 1979, 47, 263. [Google Scholar] [CrossRef]
- BMDV—Verkehrsverflechtungsprognose 2030. Available online: https://bmdv.bund.de/Shared-Docs/DE/Arti-kel/G/verkehrsverflechtungsprognose-2030.html (accessed on 16 June 2023).
- Earl, T.; Mathieu, L.; Cornelis, S.; Kenny, S.; Ambel, C.C.; Nix, J.C. Analysis of Long Haul Battery Electric Trucks in EU Marketplace and Technology, Economic, Environmental, and Policy Perspectives. Available online: https://www.semanticscholar.org/paper/Analysis-of-long-haul-battery-electric-trucks-in-EU-EarlMathieu/21e0357feec21a0f6a4023b739e78855a81-40bfe (accessed on 19 April 2023).
- Wolff, S.; Kalt, S.; Bstieler, M.; Lienkamp, M. Influence of Powertrain Topology and Electric Machine Design on Efficiency of Battery Electric Trcuks—A Simulative Case-Study. Energies 2021, 14, 328. [Google Scholar] [CrossRef]
- MAN Truck & Bus SE, Internal Discussion on Powertrain Parameters. 2022.
- Verbruggen, F.J.R.; Rangarajan, V.; Hofman, T. Powertrain design optimization for a battery electric heavy-duty truck: 2019 American Control Conference (ACC 2019). In Proceedings of the 2019 American Control Conference, ACC 2019, Philadelphia, PA, USA, 10–12 July 2019; pp. 1488–1493. [Google Scholar] [CrossRef]
- Fries, M.; Wolff, S.; Horlbeck, L.; Kerler, M.; Lienkamp, M.; Burke, A.; Fulton, L. Optimization of hybrid electric drive system components in long-haul vehicles for the evaluation of customer requirements. In Proceedings of the 2017 IEEE 12th International Conference on Power Electronics and Drive Systems (PEDS), Honolulu, HI, USA, 12–15 December 2017; pp. 1–141. [Google Scholar] [CrossRef]
- Naunheimer, H.; Bertsche, B.; Ryborz, J.; Novak, W.; Fietkau, P. Fahrzeuggetriebe: Grundlagen, Auswahl, Auslegung und Konstruktion; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- König, A.; Nicoletti, L.; Schröder, D.; Wolff, S.; Waclaw, A.; Lienkamp, M. An Overview of Parameter and Cost for Battery Electric Vehicles. World Electr. Veh. J. 2021, 12, 21. [Google Scholar] [CrossRef]


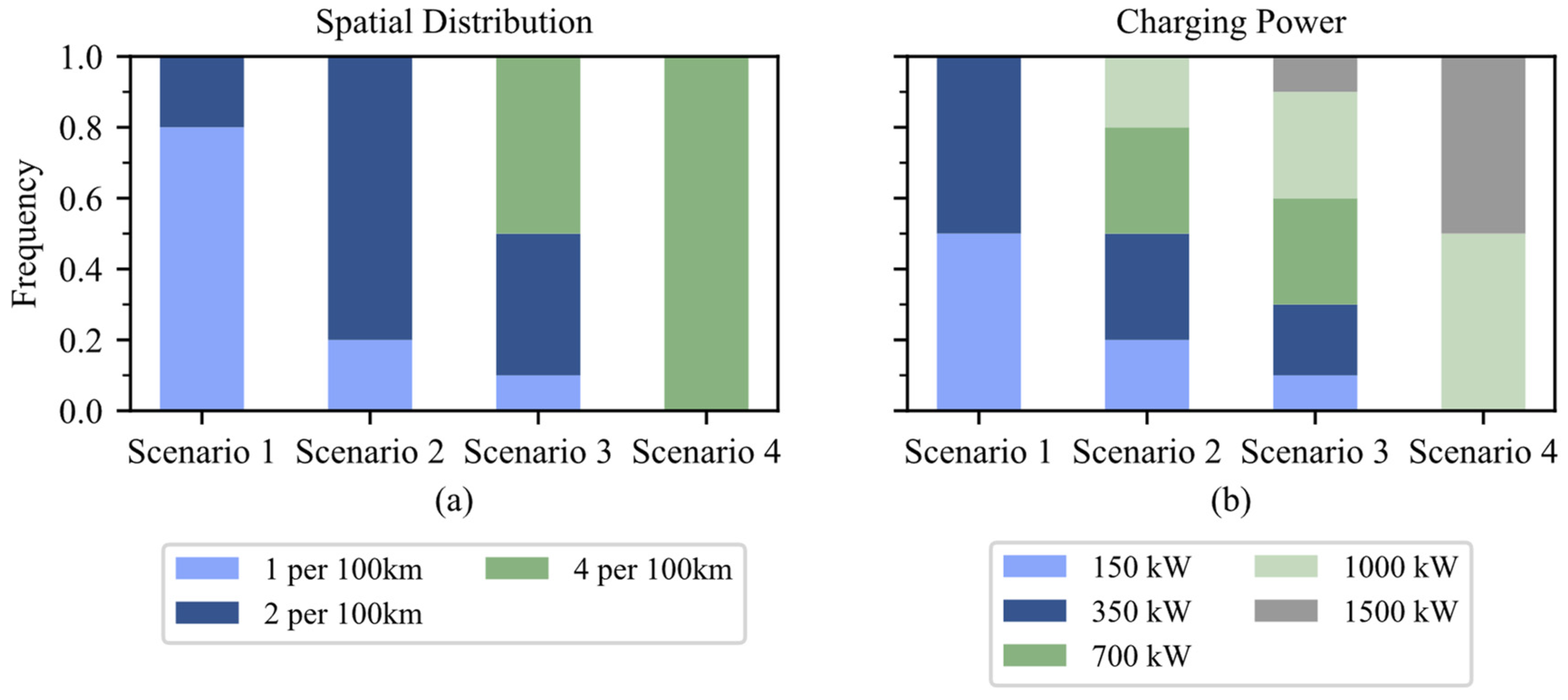
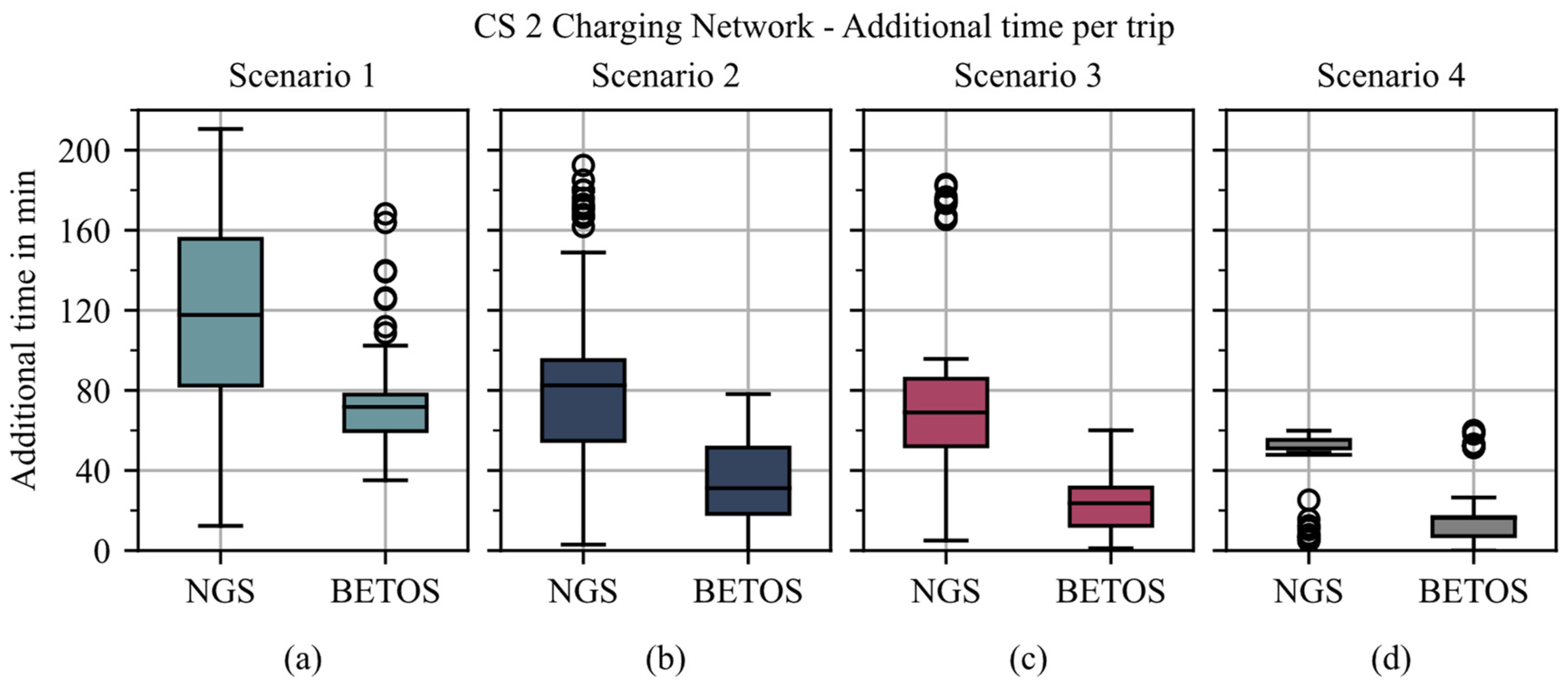
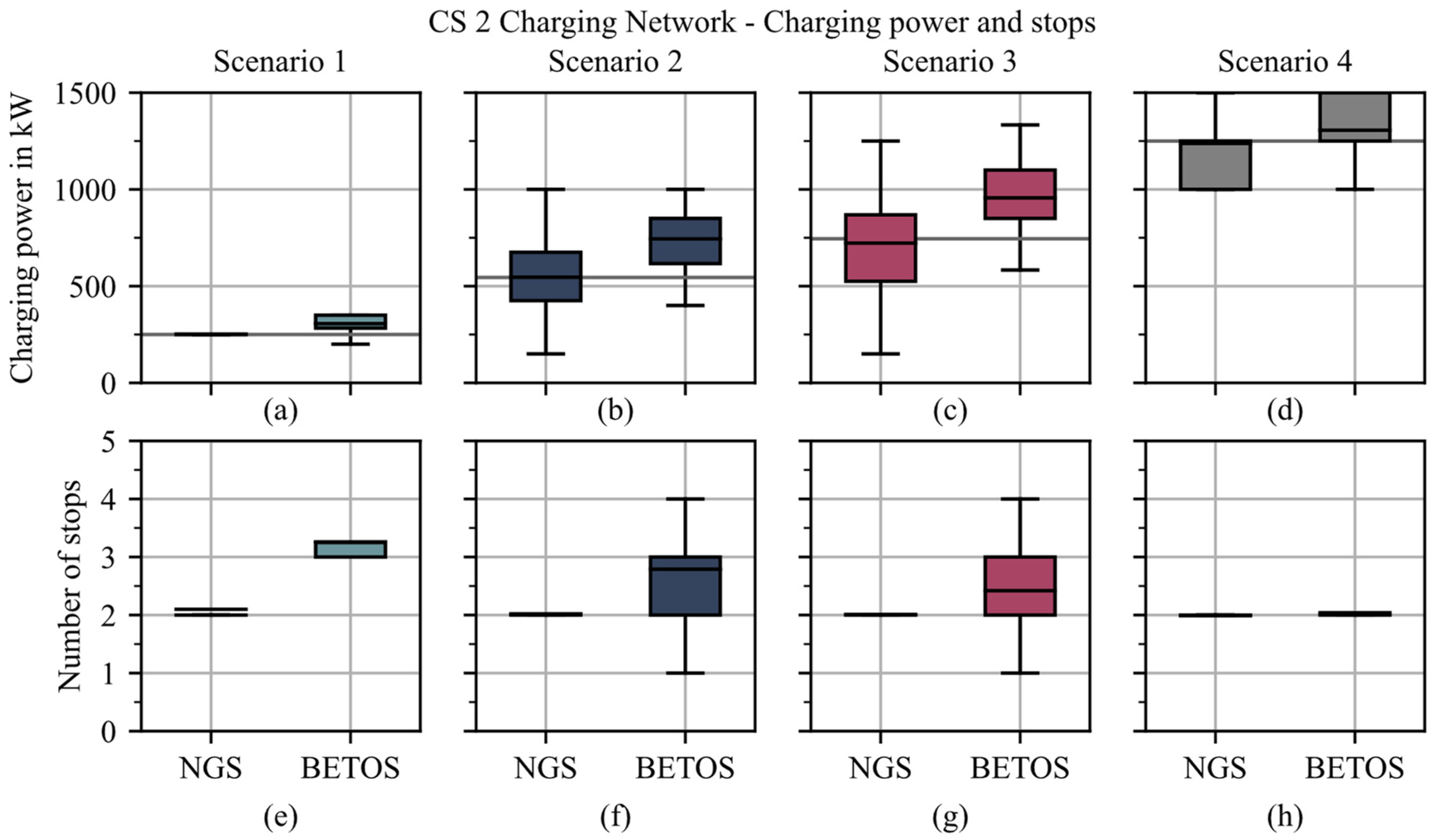
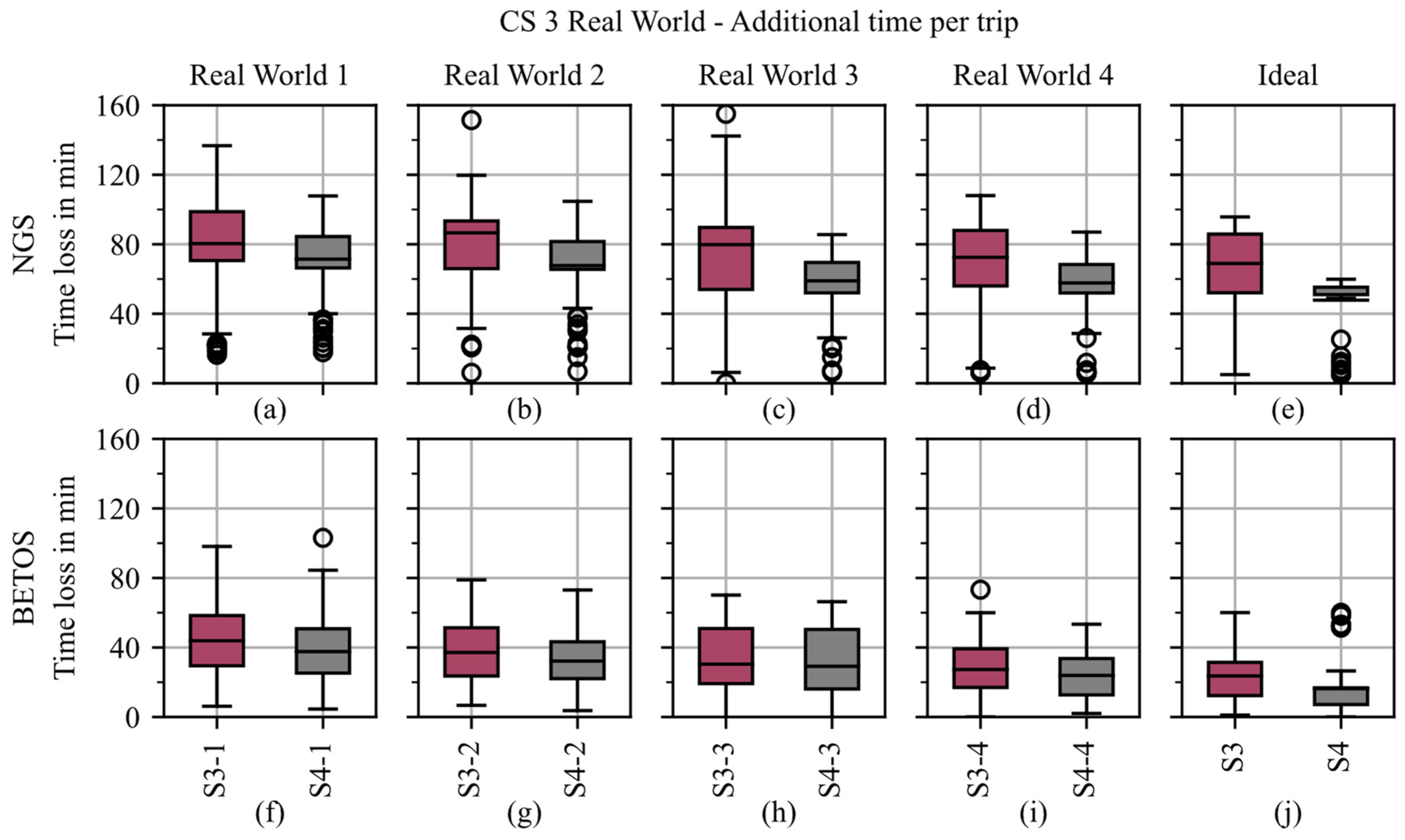

| Parameter | Value/Range |
|---|---|
| Starting SOC | 90% |
| DOD | 100–15% |
| Cost in DP Optimization | Time |
| SOC at destination | Min. 15% |
| Time to Connect/Pay | 6 min [33] |
| Battery Capacity | 500 kWh (varied in one case study) |
| Max. charging rate | 3 C |
| Tour length | 650–700 km |
| Payload | 19.3 t |
| Case Study (CS 1–3) | Distance between Two POI | Charging Power at POI | Availability of Charging Station |
|---|---|---|---|
| Idealized static conditions | constant | constant | permanent |
| Idealized charging network | distribution | distribution | permanent |
| Real-world charging network | distribution | distribution | probability with waiting time |
| Charging Power in kW | Availability Probability of POI | |||
|---|---|---|---|---|
| S 3/4-1 | S 3/4-2 | S 3/4-3 | S 3/4-4 | |
| 150 | 1.0 | 1.0 | 1.0 | 1.0 |
| 350 | 0.4 | 0.6 | 0.8 | 1.0 |
| 700 | 0.3 | 0.5 | 0.7 | 0.9 |
| 1000 | 0.2 | 0.4 | 0.7 | 0.8 |
| 1500 | 0.2 | 0.2 | 0.6 | 0.7 |
| Weighted Mean | 0.35/ 0.20 | 0.51/ 0.30 | 0.74/ 0.65 | 0.88/ 0.75 |
| Charging Power in kW | Availability Probability of POI | ||
|---|---|---|---|
| S4–5 | S4–6 | S4–7 | |
| 1000 | 1.0 | 1.0 | 1.0 |
| 1500 | 0.8 | 0.5 | 0.2 |
| Property | Error Interval | Description |
|---|---|---|
| Energy consumption | [−15, 0]% | Prediction of less energy consumption than needed. |
| Driving time | [−15, 0]% | Prediction of less time than needed. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zähringer, M.; Teichert, O.; Balke, G.; Schneider, J.; Lienkamp, M. Optimizing the Journey: Dynamic Charging Strategies for Battery Electric Trucks in Long-Haul Transport. Energies 2024, 17, 973. https://doi.org/10.3390/en17040973
Zähringer M, Teichert O, Balke G, Schneider J, Lienkamp M. Optimizing the Journey: Dynamic Charging Strategies for Battery Electric Trucks in Long-Haul Transport. Energies. 2024; 17(4):973. https://doi.org/10.3390/en17040973
Chicago/Turabian StyleZähringer, Maximilian, Olaf Teichert, Georg Balke, Jakob Schneider, and Markus Lienkamp. 2024. "Optimizing the Journey: Dynamic Charging Strategies for Battery Electric Trucks in Long-Haul Transport" Energies 17, no. 4: 973. https://doi.org/10.3390/en17040973
APA StyleZähringer, M., Teichert, O., Balke, G., Schneider, J., & Lienkamp, M. (2024). Optimizing the Journey: Dynamic Charging Strategies for Battery Electric Trucks in Long-Haul Transport. Energies, 17(4), 973. https://doi.org/10.3390/en17040973








