Abstract
The most general purpose of the current paper is to trace and discuss the history and state of the art of studies on vehicle motion (dynamics) in a transition curve above the critical velocity, with the aim of potentially increasing the circle of researchers involved in studying this issue and strengthening the will of the authors to continue their studies. This general goal is achieved in two ways: first, through a profiled literature analysis, showing the historical progress and current state of the research; and second, through reference to the history of stability studies as an example of selected studies’ development. In addition, this work has two more specific goals. Together, they consist of collecting the literature in a related field in one place and analyzing it on site to accomplish the review. Both specific goals are attained by dividing the literature into two corresponding parts. In the first part, the current issues of rail vehicle stability are analyzed and divided into four problems. The second part includes works that deal with the subject of the motion and dynamics of a rail vehicle on a transition curve section. Here, the works are divided into five groups and discussed. They are put in order from the closest to the furthest from this paper’s main subject; however, the last group includes the most recent references. In addition, information on the authors’ approach to the problem is provided, including the methods and models used, as well as example results. Based on the analysis of the literature and the state of the art, a summary of the analysis is presented at this paper’s end. It highlights the small number of works on the subject of interest, and based on the review of stability studies, it seeks to encourage present and potential authors to study this field and share their results with society.
1. Introduction
The general goal of this paper is to trace and discuss the history and state of the art of studies on vehicle motion (dynamics) in a transition curve (TC) above the critical velocity in order to strengthen the will of the authors to continue their studies and to increase the circle of researchers involved in studying this issue. This goal is achieved in two ways: first, through a profiled literature analysis, showing the historical progress and current state of the research; and second, through reference to the history of stability studies. This area of research is quite close to the problems covered in the current paper. Additionally, this paper offers an example of how a particular subject can develop over the years thanks to increasing interest and the increasing number of researchers studying it. Similarly to the case of stability studies, an increase in the number of researchers studying the dynamics of rail vehicles in a TC above the critical velocity could also rapidly speed up the gathering of new knowledge and improve comprehension of this complex issue. The undertaking of the task was motivated by papers [1,2] by K. Zboinski and the works of H. Tue and M. Hoffmann [3,4], including M. Hoffmann’s doctoral dissertation [5]. However, the purpose of all studies, the results of which are described in the aforementioned publications, was not unequivocally the dynamics or the motion of the vehicle in the transition curve (TC) above the nonlinear critical velocity vn. It should be noted that the research on motion in a TC cannot be unified with traditional research on stability solutions as this research concerns motion in a straight track (ST) and circular curve (CC). This is primarily due to the unsteady conditions of motion in a TC, represented by a monotonic change in the curve radius and track superelevation. The results in the abovementioned works that are interesting for the present authors were obtained as a kind of side effect of research with other objectives.
In addition to the main goal of this work, two specific goals can be distinguished. Jointly, they involve the collection of literature in a related field in one place and analyzing it on site. The corresponding literature review is performed by dividing the literature into two parts. These parts directly define the aforementioned two specific goals. The first part presents the literature dealing with stability issues. The number of publications in this area is really large. This is why the authors focus on the history of stability studies and contemporary topics. These topics are as follows: the use of bifurcation methods in a stability study; the application and determination of non-linear critical velocity as a certain contrast to linear critical velocity; the methods for studying and testing stability in a CC, including the bifurcation approach; and the study of chaotic solutions presented together with stable and unstable stationary and periodic solutions on bifurcation diagrams. The second part includes the works of most direct importance to the authors’ consideration. They deal with the subject of the motion and dynamics of a rail vehicle on a transition curve section. The publications here, and subsequently their discussions, are divided into five parts. The inclusion of a given publication in the particular group depends on how close it is to the main subject of this paper. The exception is the last group. Hence, we have publications in the following groups: publications closest to presenting the dynamical behavior of a vehicle in a TC at and above-critical velocity represented with lateral vehicle coordinates; publications in which analogous results were generated or could have been generated but are not presented; publications with analogous results but for the ST and CC cases only; publications close to the main subject with parameters variation, focusing on parameters being varied in the works of present authors; and finally, the most recent publications, without taking their proximity to this paper’s main subject into account. Based on our analysis of the literature and the state of the art, a summary is formulated at the end of this paper.
2. Rail Vehicle Motion Stability Tests
The study of the dynamics of rail vehicles is related to and involves research on the lateral stability of rail vehicles and their hunting motion. This statement is also true for studies on a curved track (i.e., on a circular curve (CC) and a transition curve (TC)). The connection takes place primarily through the concept of non-linear critical velocity vn, a key parameter in stability studies, and the simulation software that is used in stability analysis. However, it should be mentioned that the research on motion on a TC section is not the research on stability solutions as it is traditionally understood, which analyzes either stable stationary or stable periodic solutions. Such types of solutions simply cannot appear in a TC due to continuous changes in curve radius and superelevation.
The history of the development of the concept and research on the stability of rail vehicles and their hunting motion is presented in [6,7]. Further analysis is provided via a condensed extract based on the information contained in these publications.
The first documented research on the kinematics relating to the dynamics of rail vehicles dates back about 200 years. The beginning of these studies is considered to be the moment when the cylindrical profiles of wheels were replaced with conical ones, i.e., the beginning of the 19th century. The kinematic behavior related to these changes was described quite precisely by G. Stephenson (as quoted by A.H. Wickens in [6,7]). In Germany, the first to try to explain the behavior of the wheelset on the rail was F. Redtenbacher; he described it in the book Die Gesetze des Lokomotiv-Baues (in English, The Laws of Design of Locomotives). The main problem he dealt with was the behavior of a locomotive when negotiating curves [6,7]. He was probably the first German scientist to deal with the resonance phenomenon in rail vehicles. Then, in 1883, J. Klingel published Über den Lauf von Eisenbahnfahrzeugen auf Bahn gerader (in English, On the running of railway vehicles on straight track). He solved the problem dealt with by Stephenson in an analytical way. He derived the formula for the wavelength of lateral vibrations referred to as sinusoidal or hunting motion [6,7]. On the other hand, the question of whether limiting the wheel with the flange would make the motion stable remained unanswered. Ch. Boedecker was the first person who dealt with the stability of rail vehicles [6,7]. He dealt with kinematic relations in wheel–rail contact, taking Coulomb friction into account. He concluded that rail vehicles are always unstable and that the flanges ensure that the vehicle does not derail. At last, F.W. Carter was able to explain the hunting motion successfully. He aimed to make the processes described earlier by Boedecker concerning tangential contact under Coulomb’s law understandable. In his research in 1915, Carter applied the principle intuitively but correctly. However, it was not until 1926 that he substantiated a clear conclusion [6,7]. At the same time, H. Fromm dealt with similar problems. The results of his research were published in 1927. In 1928, Carter again began researching the foundations of the stability of locomotives [6,7]. In 1935, Y. Rocard issued two publications, one on his own and the second in collaboration with M. Julien, on the driving stability of locomotives [6,7]. In the second half of the 1940s, research into high-speed rail began in Japan. However, publications written in Japanese were unknown in Europe and America. In the 1950s, France took up the subject of high-speed rail. As a result of the hunting motion of a locomotive moving at velocity v = 331 km/h, the rail buckled along its considerable length. Soon after, a competition was announced to solve the problem of hunting motion. One of the winners was a Japanese researcher, T. Matsudaira, who published a paper on this problem as early as 1952. However, his publications from 1960 and 1965 deserve specific mention. Matsudaira designed a railway car bogie for the Tokaido high-speed railway, presented his research results on the stability of a rail vehicle with flexibly guided wheelsets, and described the differences between forced and self-exciting vibrations [6,7]. In 1958, K.L. Johnson’s works, which concerned the non-linear contact theory of an elastic spherical surface rolling on a flat surface, were published [6]. This theoretical research has also been confirmed by experimental research. In the 1960s, the Englishman A. H. Wickens and the German C.T. Müller carried out research on hunting motion. The results of the stability studies of linear systems can be found in works by Wickens [8,9,10,11]. Müller, in turn, wrote about the differences between forced and self-exciting vibrations occurring at high speeds [7]. These works resulted in the dissemination of the critical linear velocity, which took place later (e.g., [12,13]) and lasts until today (e.g., [14]). Around the same time, research on an initially linear and later also non-linear contact theory was led by J.J. Kalker [6]. He developed the CONTACT program [15], which takes account of non-elliptical contact areas, and the FASTSIM program [16] based on a simplified contact theory. The research on non-linear contact geometry was continued by K. Yokose, RJ Gostling, K. Knothe, NK Cooperrider, and N. Matsui [6]. In 1976, the MEDYNA program was developed in Germany based on the theory of one-wheel contact with one rail. In later years, the SIMPACK program was created, enabling research on driving comfort, stability, and the behavior of the vehicle in the arc. The 1970s and 1980s saw the further development of the high-speed rail that had already operated successfully in Japan, France, and Italy, as well as further research into stability and contact theory. In the 1980s, in many centers around the world, other programs for the automatic generation of equations of motion (automatic generation of equations of motion—AGEM), as well as for the simulation and analysis of the dynamics (stability) of rail vehicles, were created [17].
The theory of self-exciting vibrations and the bifurcation theory have an important place in this literature analysis. At some point, it was concluded that in order to investigate and understand hunting motion even more deeply, one should take account of the non-linear nature of the phenomena. The relationship between geometry and physics in contact mechanics is non-linear. Among of the first researchers to work with these non-linearities in mind were probably A.D. De Pater and P. Van Bommel [6]. Attempts were made to compare these non-linearities with stability analysis. One of the most promising attempts was the “quasi-linearization” technique introduced by N.K. Cooperrider, K. Hedrick, E.H. Law, and C.W. Malstrom [6]. The basic assumption here was that non-linear hunting motion is a periodic motion. In the same publication, there are self-exciting limit cycles and bifurcation diagrams. Among the first works on the bifurcation approach to stability studies were the works of C. Kass-Petersen and H. Tue [18,19] and of R. Gasch and D. Moelle [20,21]. In the works [20,21], the Fourier series described the non-linear motion, which resulted in a better approximation of the limit cycle. The results are presented in the form of limit cycles and bifurcation diagrams. In [22], Gasch and Moelle, along with W. Kik, presented the methods used to calculate the limit cycles in the dynamics of rail vehicles. The research found that the analysis of non-linear periodic limit cycles is insufficient to describe the behavior of wheelsets and bogies. First, it has not been proven that periodic vibrations always exist; and second, the possibility of chaotic behavior (solutions) has been demonstrated. The theories of self-exciting vibrations and bifurcations introduced the concept of non-linear critical velocity into stability analysis.
Examples of works not listed above, including those representing a modern approach to stability analysis, are [1,2,3,4,5,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70].
Currently, the attention of researchers dealing with the stability of rail vehicles is attracted primarily by the following four problems: the use of bifurcation methods in the stability study; application and determination of the non-linear critical velocity as a certain contrast to the critical linear velocity; methods and testing of stability in CC, including the bifurcation approach; study of chaotic solutions presented in bifurcation diagrams together with stable and unstable stationary and periodic solutions.
When listing the works that have addressed the first of the problems, it is worth paying specific attention to the work of R.R. Huilgol [30]; it is often overlooked and even forgotten, as evidenced by the history of stability described in [6,7]. The work [30] is the first to use the bifurcation approach to test rail vehicle stability. In this approach, the stability analysis results are presented in bifurcation diagrams, i.e., diagrams of the maximum lateral displacements of the wheelset(s) as a function of velocity. They typically contain both the areas of stable and unstable solutions. Other works that can be mentioned in this group are [2,3,4,5,25,27,28,29,31,44,46,47,48,49,50,54,55,56,57,60,62,64,65,66,67,69,70].
The second problem that nowadays attracts the attention of stability researchers is represented by the works in which the critical velocity of a rail vehicle is considered to be the so-called non-linear critical velocity vn but not linear velocity vc. From a practical point of view, this fact is of great importance because velocity vn may be less than velocity vc. This means the rail vehicle enters hunting motion earlier and sometimes much earlier than the velocity vc suggests. This may translate into an incorrect assessment of the safe motion of the vehicle. Examples of works in this group include [2,3,5,23,25,27,29,31,41,42,46,47,48,49,52,53,56,58,66,67,68]. Correct determination of the critical velocity value vn has become even more important due to the intensive development of high-speed railways worldwide. This development is discussed by K. Ebeling [71]; CW Yu, N. Menz, C. Hunter, YY Chen, and P. Farias [72]; J. Jiao, J. Harbin, and Y. Li [73]; S. Sone [74]; A. Purba, F. Nakamura, C. Niken, M. Jafri, and P. Pramoto [75]; and P. Zembri and E. Libourel [76], among others.
The third problem that attracts the attention of those researching the stability of rail vehicles, and which is currently being intensively studied, is the CC. The subjects of these works include both the methods of stability study in the CC and the testing of given objects. The initial works on this issue represent the authors’ struggle to break the stereotype that the hunting motion of a rail vehicle (periodic solutions) occurs only in ST, and that in the CC, the vehicle behavior (solutions) is stationary. It is worth mentioning that the first works that dealt with the problem of stability studies in the CC and offered some results were the works of K. Zboiński [1] and H. True and others [59]. Other works in this group include [2,3,5,24,27,37,38,39,40,41,42,43,45,60,65,67,68].
If looked at formally, the fourth problem concerning chaotic solutions could be omitted here. This is because in its theoretical, general examination, the analysis of the stability of stationary and periodic solutions, typically pertaining to rail vehicles, is only sometimes carried out. On the other hand, the works on stability and chaos related to rail vehicles are difficult to separate due to their similar methods of presenting the results in bifurcation plots. If a given object is subject to chaotic behavior, then the appropriate bifurcation diagram, if it is to be complete, must contain both areas of stable and unstable motion and areas of chaotic solutions. Examples of works in this group are [28,32,44,51,54,56,57,61,62,63,64,69,70].
The main essential achievements concerning rail vehicle stability and related problems are gathered chronologically in Table 1 to make the above literature analysis more readable. The exact or approximate dates of their appearance are included too.

Table 1.
Crucial achievements in studies of rail vehicle stability and related issues.
3. Motion of a Rail Vehicle in a Transition Curve above the Critical Velocity
The issues of the motion and dynamics of a rail vehicle on the TC section near the critical velocity vn are very rarely undertaken in both the domestic and the foreign literature. The authors, despite their efforts, are not able to find a larger number of literature items by other researchers who treat such issues directly. The only known works containing related results—which were not the direct aim of the research but obtained accidentally—are the publications of: K. Zboiński [1], H. True and M. Hoffmann [4,5], K. Wang and P. Liu [77], and M. Dusza [78]. In addition, the authors have not been able to find at least several publications the purpose of which would be the motion or dynamics of the vehicle along the TC above the critical velocity vn. The example publications are [79,80].
The five above-mentioned works contain the results of studies on the coordinates of lateral dynamics (lateral displacements y and/or yaw angles ψ (angles of rotation around the vertical axis)) of vehicle components (wheelsets, bogie frames, and vehicle body) at velocities higher than the critical velocity. The research in the five discussed publications was carried out for routes composed of at least the ST, the entrance TC, and the CC, or even more, i.e., the ST section, entrance TC, CC, exit TC, and ST section. In general, the results for the TC section were obtained as a result of stability studies in which stationary or periodic solutions were sought in the ST and CC. Also, the initial results by Zboiński in [1] were not the main subject of the research; they were obtained by accident while carrying out research with goals distinct from the main subject in the present paper. True and Hoffmann, in [4,5], tested a two-axle freight car on a transition curve. Wang and Liu, in their work [77], were considering a four-axle heavy-duty freight car composed of two bogies and a body. In the work of Dusza [78], the research subject was a four-axle passenger car consisting of two bogies and the body. Whereas Zboiński, in [1], was interested in two bogies and two two-axle freight wagons. In [4,5], the behavior on a TC is, to some extent, a logical continuation of the behavior occurring in the ST and CC, where vibrations occur. It shows the limit cycle in an ST. On the other hand, in curved sections, i.e., a TC and CC, a clear disturbance of regular behavior can be observed due to the dry friction and the non-smooth nature of the suspension description. What is interesting in [77] is the lack of vibrations in the ST and their appearance in the middle of the TC, as well as the continuation of these vibrations in the CC in the form of a limit cycle. In the work [78], the result for the TC appeared only as forced by the software used, which, due to limitations, does not allow for the simulation to be started in the CC. The simulation must start in the ST to obtain the result for the CC. To enter the CC, a vehicle model must pass through the TC. Here, the vibrations appear immediately at the beginning of the TC and continue in the CC in the form of a limit cycle. In [1], the author presented the results obtained for the TC as a logical transition from the ST to the CC, where there are limit cycles. In addition, three other more intriguing results were shown. One of them is the complete disappearance of vibrations in the TC with the simultaneous existence of limit cycles in the ST and CC (Figure 1). The second is the disappearance of vibrations existing in the ST and the TC after entering the CC but only for the front (attacking) wheelset. The third case is a shift of vibrations from one type of solution to another (different amplitude and frequency of vibrations) in the central part of the TC (Figure 2). The article [1] was published in 1998, and the results became the primary motivation for further research. These motivational results were utilized in [79]. A common feature of the results posted in [1,4,5,77,78] is the presence of only one result for each of the objects. These works did not intentionally change the system’s parameters or the motion conditions. The exceptions are [4,5], showing the results for two different velocities. However, the difference in both results is limited to the value of the vibration amplitude.
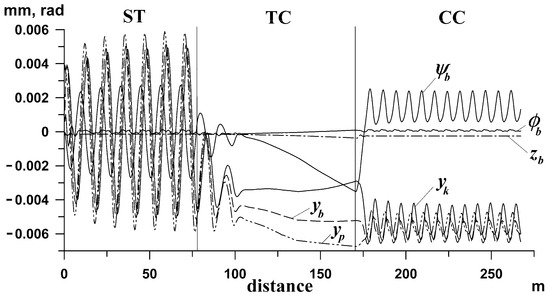
Figure 1.
Lateral and vertical displacement coordinates y and z, as well as yaw and roll angles ψ and ϕ for leading (index p) and rear (index k) wheelsets and bogie frame (index b) with the disappearance of vibrations in the TC [1]. (Reproduced from K. Zboiński. Dynamical investigation of railway vehicles on a curved track. European Journal of Mechanics-A/Solids, vol. 17, no. 6, pp. 1001–1020. Copyright © 1998, Elsevier Masson SAS).
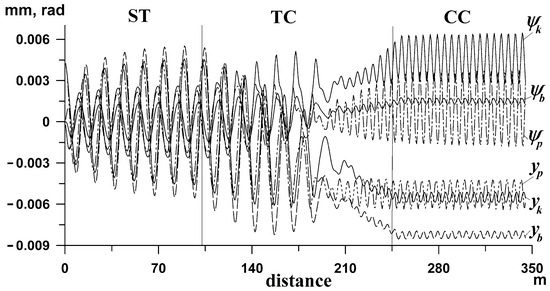
Figure 2.
Lateral displacement coordinates y and yaw angles ψ for leading (index p) and rear (index k) wheelsets and bogie frame (index b) with the switch from one type to another in the TC [1]. (Reproduced from K. Zboiński. Dynamical investigation of railway vehicles on a curved track. European Journal of Mechanics-A/Solids, vol. 17, no. 6, pp. 1001–1020. Copyright © 1998, Elsevier Masson SAS).
A group of works of some importance for vehicle motion in the TC above the critical velocity are those in which the results interesting to the present authors were actually generated but not published, or otherwise could potentially have been generated. The main reason why the results of the lateral dynamics coordinates above critical velocity vn are not shown is that such publications were interested in other coordinates or in the results obtained for a velocity below the critical one. Examples of such publications are [81,82,83,84,85,86,87,88,89,90]. J. Droździel and B. Sowiński, in [82], consider the dynamic behavior of a rail vehicle running along a TC of four types, below the critical velocity. They also consider the behavior of the vehicle moving after a passage through turnout. W.M. Zhai and K.Y. Wang, in [90], present examples of vibrations along the TC section but for low velocities. The topic of this article is the dynamics of a rail vehicle moving along circular sections with small radii (R < 500 m), which are found in the mountainous areas of China. In order to increase the train velocity and motion safety, they propose the strengthening of the already-worn wooden sleepers. The authors of this article compared the results of simulation studies with the results of experimental studies. J. Carballeira, L. Baeza, A. Rovira, and E. Garcia, in [81], show the results of lateral displacements and angles of rotation in a curved track for a railway vehicle using single-axle bogies with independently rotating wheels and a passive control system (steering). In the works of B. Kurzecek and M. Hecht [85] and O. Kondo and Y. Yamazaki [83], there are results for the TC but for a velocity below the critical one, and no coordinates of lateral dynamics are presented. T. Kuba and P. Lugner, in [84], show the results for the lateral displacements of the wheels with respect to the track centerline. The object is subject to variation here because the authors present the behavior of the trams with different types of bogies, including unconventional ones. In their diploma thesis [88], D. Prandi published the results of numerical simulations, among other kinds, for the TC but for a velocity below the critical one. This work aimed to compromise stability in an ST and good steering in a curved track, which is difficult in the case of a passive mechanical vehicle structure. In [89], R. Shaltout, C. Ulianov, and L. Baeza published the simulation results of lateral displacements and vehicle rotation angles in an ST, TC, and CC, albeit for low velocities. A. Lau and E. Kassa, in [86], report the results of the influence of modeling the wheel–rail contact on the dynamic behavior of the vehicle. The results of lateral dynamics for tight arcs (small curve radius) and several velocities are presented here. A. Matsumoto and Y. Michitsuji, in [87], present the results of simulation tests in a TC for a velocity below the critical velocity, but no results are illustrating lateral displacements. The vibrations that occur are probably due to the irregularities of the track.
In the literature, you can also find examples that present the results of the lateral dynamics of the vehicle above the critical velocity vn but on the ST and CC sections. The number of these works is incomparably greater than those relating to the same problem but on a TC. A significant number of these works deal with stability testing in the ST and CC, but only some directly present the courses of the coordinates of the lateral dynamics. Examples are the works by the group using the bifurcation approach and the group studying stability in the CC; these are [2,3,5,27,44,60,64,65,91]. In the research carried out by the authors, the TC is always between the ST and CC, i.e., most typically. Since a lot is already known about the vehicle’s behavior on sections with a fixed geometry (ST and CC), undertaking research on the transition section (TC with variable geometry) and expanding knowledge on this subject is, on the one hand, something obvious, and on the other, original and arouses natural interest.
It Is also worth mentioning the works on vehicles which aim to vary the parameters of their models. The number of such works is enormous. Here, only a small number of works will be indicated, i.e., those in which the variants of parameters coincide with the variations in the works by the present authors. The selected examples of such publications are [24,44,49,66,92,93,94,95,96,97]. G. Xu, A. Steindl, and H. Troger, in their work [66], vary the longitudinal damping of the bogie and discuss its influence on the subcritical or supercritical nature of bifurcation diagrams. M. Ahmadian and S. Yang in [92] and H.M. Sedighi and K.H. Shirazi in [96] investigate the influence of the lateral stiffness of the object and the lateral stiffness of the rail on the behavior of the model of a wheelset and a bogie, respectively. In addition, in [92], the influence of a torsional damper for rotation around the vertical axis (yaw motion) was investigated. The authors of these works determine bifurcation diagrams for variants of parameters and thus the values of the critical velocity vn. O. Froment, D. Aubry, and L. Castel investigate, in [95], the influence of lateral stiffness on non-linear critical velocity vn of the bogie model; whereas Y.C. Cheng, S.Y. Lee, and H.H. Chen investigate, in [24], the effect of longitudinal stiffness and lateral damping in the primary suspension, longitudinal and vertical stiffness, and longitudinal and vertical damping in the secondary suspension on the value of the critical velocity vn. Moreover, they do it depending on the type of model used. The differences between the models are their number of degrees of freedom and the wheel–rail contact model (linear and non-linear model). J. Warczek, R. Burdzik, and G. Peruń, in their work [97], vary the suspension damping (damper condition) and the relative velocity, and for their variants, they observe the acceleration of the vibrations of the car body frame. M. Dumitriu, in [94], examines the effect of the damping values of the primary and secondary suspension on the critical linear velocity vc and vehicle properties in the frequency domain. A. Chudzikiewicz and B. Sowiński, in [93], show the results of the dynamics of a tram model with a middle bogie with completely independently rotating wheels in the CC, taking into account the velocity v variants. G.W. Luo, Y.Q. Shi, X.F. Zhu, and S.S. Du [44] vary velocity, equivalent conicity, lateral stiffness, longitudinal suspension, and the coefficient of friction. They observe the influence of these variations on solutions over time, phase diagrams, and bifurcation diagrams. Moreover, M.A. Rezvani and A. Mazreah [49] show the test results in a CC while taking into account the influence of the curve radius and the friction coefficient on the value of the non-linear critical velocity vn.
The last works to discuss are the works from the last four years. They are represented with publications [98,99,100,101,102,103,104,105,106,107,108,109,110]. A survey of these works is undertaken to check if recently, some changes in the literature content are detectable compared to previous years. The only works where consideration of the presence of the TC is given are [106,110]. Luckily, a single publication was found where the dynamics of railway vehicles are studied on the TC at velocities higher than critical ones [106]. What can definitely be noticed is the ongoing interest in stability issues, albeit for the ST mainly [98,100,101,102,105,107]. In [98], the stability of passenger train bogie is studied on the ST, including non-linear critical velocity vn determination. Linear models of contact forces and geometry are applied. It is detected that the vertical stiffness in the primary suspension and the lateral damping in the secondary suspension strongly influence the vn value. The new element is the method used in the study, i.e., the root loci method, enabling the overcoming of the limitations of the linear models. In [107], the measurement system to detect and monitor hunting instability is described. It can predict the wheelset lateral displacement and yaw angle as well as the wheel/rail contact relationships. The system is verified through a comparison of the predicted results with the simulation and experimental results. Although not stated by the authors, it seems that the hunting motion on the ST and CC can be detected. In [108], new non-linear features are analyzed for the wheelset on the ST. The authors succeeded in showing with an analytical approach that the simultaneous existence of self-exciting vibrations and parametric vibrations is possible. They were also able to prove the correctness of this result experimentally using the apparatus with a roller rig. In [101], the authors studied the influence of modeling non-linear wheel–rail contact geometry, especially the flange profile, on the bifurcation character and values of stability features of a wheelset on an ST. They also considered the linear and non-linear terms of the wheelset’s rolling radius. Finally, they concluded that increasing the suspension stiffness should raise the running stability under wheel wear. In [100], two models of a wheelset were studied. One is a linear model with a constant value of equivalent conicity, while the other is non-linear due to a non-linear function of equivalent conicity based on measured profiles. Comparisons of the results from these models are made in order to explain the unfavorable unstable behavior of some Chinese high-speed trains. The bifurcation character of the non-linear model is analyzed while the influences of suspension longitudinal and lateral stiffnesses are considered. In [110], a heavy-haul railway vehicle–track system is studied on a CC and TC to find key the parameters for vehicle–track dynamical interactions represented with corresponding forces in a curved track. The authors found that the CC radius is the key parameter, and it should not be smaller than 800 m. The next important parameter is TC length, but it has some inflexion in its properties; so, its influence is strong for short TCs while almost negligible for long TCs. Superelevation as the parameter should prferably provide equilibriom or its deficiency nat bigger than 20 mm is recommended. Publication [99] treats the vibrations of a railway car in ST with two methods: the analytical method and the simulation method. All this is undertaken with the intention of reducing vibrations. The advantages of the simulation approach compared with the analytical approach are highlighted. In [105], the hunting motion of the unloaded freight car is studied, with some focus on non-linear critical velocity. Several methods of its determination are discussed. At the same time, different types of hunting were obtained in simulations thanks to a new idea concerning the initial conditions that excite them. In [103], a freight car with three-piece bogies is studied. The point of interest concerns the lateral frame forces exerted by bogies (vehicles) on the track. The cases of the ST and CC are considered. The authors analyze these forces for 30 different combinations of bolster suspension. The authors of [106] studied the car body hunting motion of an electric locomotive with experimental and simulation methods. They observed this phenomenon on the compound route ST, TC, CC, TC, and ST. Generally, the car body hunting phenomenon exists in the ST sections and disappears in the curved sections. The results for TCs are shown together with those for STs and CC; nevertheless, the authors omitted their discussion completely. The authors showed the results for the car body and the wheelset, and their behavior is analogous; i.e., the wheelset also undergoes hunting. So, the velocity is higher than the critical one. Some ideas of how to overcome hunting motion, with a focus on car body vibrations, are formulated and connected with suspension parameter variants. In [104], the gondola car with three-piece bogies is studied with analytical and experimental methods. The hunting phenomena of all vehicle model bodies are of interest. The frequencies of the bodies are compared in order to avoid resonance. The analysis is performed in the context of a permissible velocity increase with a simultaneous increase in the axle load. The calculations and measurement data were obtained for a few CC sections of the track. No results for the ST and TC are present. In [102], the method is elaborated to identify small-amplitude bogie hunting. These small vibrations are documented by the authors based on experiments and can also be seen in simulations. The obtained results provide theoretical support for monitoring hunting stability and real-time active control studies in high-speed trains. In [109], the wheelset and full vehicle models are considered in the context of wheelsets’ hunting motion. The main effort is to identify and study not only the fundamental hunting frequency but also the frequencies of higher orders. The hunting on the ST section is considered.
4. Information on Approach to the Problem by the Present Authors
In their studies so far, the authors started from the accidentally found intriguing results. Examples are shown in Figure 1 and Figure 2. Consequently, at the beginning, they continued their searches for wider groups of vehicles and conditions of motion, and this makes up the first group of studies and results. Next, the authors started to change the conditions of motion according to systematic, consequent research plans. These produced a lot of results. Some of them were interesting, while many were of lesser importance. This makes up the second group of studies and results. The third group of studies and results also underwent a systematic research process. Here, the suspension parameters of the studied objects (full vehicles and the bogies) were systematically variant under different conditions. Three groups of objects were and are actually studied. The first to be studied was a group of generic objects that included three bogies (freight, passenger, and universal ones), two two-axle freight cars (unladen and laden ones), and one four-axle passenger car supported on two bogies. Next were two existing but no-longer-produced vehicles. They were the four-axle gondola in the laden and unladen state and the passenger car with the full set of passengers. Presently, the authors intend to undertake studies of two four-axle freight cars; these are actually in production or there are plans for future production. The intention is to change the suspension parameters in these vehicles to improve their unfavorable non-linear features in the TC and their vicinity at velocities around critical value vn. In order to improve the readability of the above statements, Figure 3 presents them graphically. The two blocks at the bottom of the figure are still to be realised.

Figure 3.
Simulation studies as realized and planned by the present authors.
The already-published results [79,80] concern generic vehicles only. The considerable number of results for the existing-but-not-produced vehicles will make it possible to publish results for them in the near future. In [80], the results from the first group of studies were published; while in [79], those from the third group were published. Generally, all the results so far have revealed that all of the studied objects possess strongly non-linear features in the TC and its vicinity at velocities above critical ones. No object was found that does not exhibit such non-linear features. The two already-completed research projects concerning the main subject of the current paper treated generic and existing-but-no-longer produced vehicles, respectively.
The research method used by the present authors involves the simulation of objects’ motion with use of their dynamical models converted into numerical software, first of all resolving second-order differential equations. The simulations have collective, massive, but not individual character at the current stage. So, they are realized here according to extensive research plans but not the accidental trials. At the current stage, the suspension parameters in primary and secondary suspension are extensively variant, albeit at different conditions of motion.
While building the models, the authors use the approach developed by Zboinski [111,112] called the generalized method of modeling the dynamics of rail vehicles. There are many generalized elements in this approach. But there exists one which is crucial to consider here, which is the generalized treating of track sections of different shapes. In practice, it results in the same mathematical and subsequently the numerical models that serve as descriptions of vehicle dynamics in these sections (ST, TC, and CC). The most general shape is a three-dimensional curve representing the TC with any changes in curve radius and superelevation. The only condition is a description of the TC in the form of parametric equations. The CC and ST cases are the special cases of the three-dimensional TC, which are represented with two-dimensional and one-dimensional shapes, respectively. From the point of view of dynamics (mechanics), the approach uses the dynamics of relative motion. This means that vehicle dynamics are described in track-based moving coordinate systems (reference frames), with the longitudinal axis tangential to the track center line of any shape. In kinematics, this motion is referred to as transportation. The general form of the corresponding equations and their solutions is as follows [111,112]:
where fd is an operator that represents whichever formalism of equations building; fp is the operator of imaginary forces (inertia forces arising from, and depending on, the transportation); B′ denotes forces of inertia in motion relative to a moving coordinate system A′; Z denotes external forces; P denotes the imaginary forces (also called correction forces); v(t) and w(t) are functions of time representing velocities and accelerations of transportation, i.e., of A′ relative to absolute coordinate system A; and x and x· are solutions of the equations, namely, the coordinates and velocities, respectively. Switching from one track section to the other consists of changes to the v(t) and w(t); in the ST, they are constant, even often equal to zero, and the same holds for each ST section; in CC, they are of the same constant form but dependent on the curve radius R for the individual CCs; and in the case of the TC, the matter is most compilated due to its three-dimensional nature. The corresponding functions v(t) and w(t) represent the angular velocities and accelerations of the transportation. They are, of course, different for different TC shape types. The matter is precisely described in [111]. To conclude, all the inertia forces for motion in non-rectilinear track sections are taken into account without considerable simplifications and omissions.
fdB′ = fdZ+ fpP(v, w) ⇒ {x = x(t), x· = x·(t)},
The second important element of generalization in the authors’ approach is its validity for any formalism in the equations building (derivation). This feature is utilized by the authors in practice too. The authors make use of two formalisms: the Lagrange equation of type II and the Kanes equations adapted to the description of relative motion. Their forms, matching the general form of Equation (1), are shown and discussed in [111,112]. The use of a particular formalism is, in practice, interconnected with the numerical models. In the case of the models built by the authors individually for particular objects (two-axle ones, that is, bogies and freight cars), the first formalism was used. In the case of the use of the AGEM-type software to build the equations, the second formalism was used. It is implemented in the authors’ software, ULYSSES [111,112]. This was used to build numerical models of four-axle cars (passenger and freight cars).
Both types of software by the present authors have some further common elements. These are the ways of modeling the contact forces, contact geometry, and vertically and laterally flexible track, first of all. The non-linear tangential contact forces calculation is carried out with the FASTSIM program by J.J. Kalker. The non-linear contact geometry is represented in the models with real wheel and rail profiles, either not worn (nominal) or worn. The resulting contact parameters are calculated with the RSGEO program by ArgeCare (Calgary, AB, German). The whole-track–vehicle models use separate models of track flexibility, both laterally and vertically. They are described in [112]. To conclude, the approach and models used make it possible to use the same model for motion along a track section of any shape. Also, simulations on freely set compound routes with easy switches to particular changing sections are possible. The models are highly versatile, so except for the studies discussed in [79,80], they proved useful with respect to other subjects, e.g., those presented in [112], where a stability study is also included.
Example results of the authors’ studies so far are presented in Figure 4, Figure 5 and Figure 6. These are merged plots representing several courses in the single figures. Each course is a result of its individual simulation. Figure 4 and Figure 5 correspond with the stage of the authors’ studies as set out in the second block in Figure 3. Figure 6 refers to the third block in Figure 3. Nevertheless, it can also be treated as an introduction into the fifth and sixth blocks. Figure 4 and Figure 5 concern the same object, i.e., the laden two-axle freight car with its longitudinal and lateral stiffness changed, decreased, and increased, respectively, compared to the nominal values. Figure 4 represents the variation of vehicle velocity v to find and recognize the non-linear behaviors dependent on this parameter. Some untypical behavior can be observed. The stable stationary solutions in the ST for the whole v range exist, while stable periodic solutions in the CC (curve radius R = 600 m) appear starting from v = 28 m/s. This reveals a smaller critical velocity in the CC than in the ST. Usually, it is the opposite, especially for small and moderate R. Figure 5 represents the variation of the curve radius R to find and recognize the non-linear behaviors dependent on this parameter (velocity v = 45.3 m/s). Again, untypical non-linear behavior is shown in this figure. This reveals the smallest critical velocity for moderate R = 600 m (periodic solutions). Higher critical velocities exist for smaller R = 300 m and bigger R = 750, 1200, 2000, and 6000 m (stationary solutions). Typically, some monotonous relation is expected. Figure 6 concerns a four-axle passenger car and variation of the parameters in its secondary suspension. This is undertaken to find and recognize non-linear behaviors dependent on such parameters. The route, again, is the ST, TC, and CC at v = 35 m/s and R = 600 m. The untypical behavior is the dramatic increase in boogie lateral vibrations in the TC with an increase in secondary suspension lateral stiffness. The vibrations that are higher in the TC than in the ST and CC are truly untypical; usually, a mild and logical passage from the ST to the CC through the TC appears. Although such unfavorable behavior is shown for the increased lateral stiffness, one can imagine the opposite situation. Namely, the biggest vibration amplitudes in TC for the nominal suspension parameters and their improvement for the changed ones.

Figure 4.
Car body behavior of two-axle loaded freight car hsfv1 (generic) on compound route ST, TC, and CC, represented with lateral displacement yb for different velocities v = 20, 24, 25, 28, 45.3, and 49 m/s.
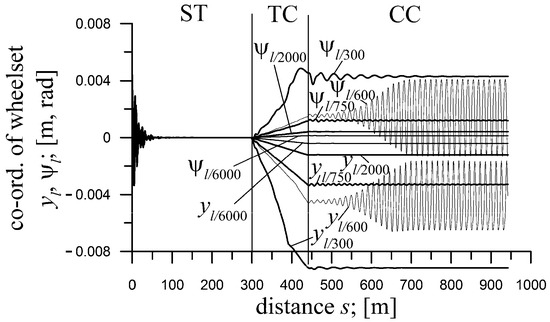
Figure 5.
Leading wheelset behavior of two-axle loaded freight car hsfv1 (generic) on compound route ST, TC, and CC, represented with lateral displacement yp and yaw angle ψp for different curve radii R = 300, 600, 750, 2000, and 6000 m.

Figure 6.
Rear bogie frame of four-axle passenger car MKIII (generic) on compound route ST, TC, and CC, represented with lateral displacement yb2 for different lateral stiffness kpzy in the secondary suspension (nominal value 1×, and increased by 10 times (10×)).
5. Conclusions
Analysis of the literature in the area of stability, both historic and contemporary, is useful in revealing how studies by individual researchers, intrigued, in this case, by the observed physical phenomenon of hunting motion and the use of a simple analytical approach, can develop. Develop finally to the state with dozens of researchers working on stability issues with the use of sophisticated theories implemented in advanced numerical tools for the needs of railways, including high-speed rail technology. So, starting from the purely kinematical considerations for an isolated wheelset with conical wheels, next inclusion of simple contact forces theory but still for a wheelset and conical wheels, then to achieve extension to linear dynamical models of wheelset still with conical wheels solved analytically with possibility to determine linear critical velocity vc. And further, this approach could be applied to the same simple wheelset models but with differential equations, solved numerically, as well as to numerical models with more degrees of freedom, i.e., those representing two-axle and four-axle bogies. At the same time, non-linear wheel–rail contact theories were included, and non-linear contact geometry representing real-wheel and rail profiles was also incorporated for the needs of more-and-more-accurate dynamical models. This state enabled us, first, to associate hunting motion with self-exciting vibrations; and second, to disclose the bifurcation characteristic of rail vehicle stability properties. As a consequence, the notion of non-linear critical velocity vn appeared different in physics—and, generally, in value—compared to linear velocity vc. Furthermore, the idea also appeared to relate differently to stability in CCs compared to the conservative approach. It took dozens of years for non-linear velocity vn and for the logic of studying stability in CCs to become accepted and beneficially applied by conservative practitioners and theoreticians. At the same time, commercial software has become available, based on AGEM, which is helpful in building numerical models of whole vehicles more easily. This directed methods of stability analysis and vn determination into numerical simulation methods. Nowadays, most of the interest concerning stability issues is still connected to the development and improvement of stability studies, including the determination of non-linear critical velocity values. The full-vehicle non-linear models are used in the simulation approach, and the models with linear elements or even linear wheelset models are used in analytical approaches. The trials with linear elements or models will hopefully increase the efficiency of the stability assessment because they are less time-consuming than full-vehicle models. The succesful, interesting example is [98]. Part of the works try to get into nonlinear phenomena even deeper than the typical bifurcation approach, what also includes chaotic features.
The literature review of works touching on the issue of railway vehicle dynamics in the TC at velocities above the non-linear critical value vn reveals that only a small number of the references cited concern it directly. Among the five groups of references connected with dynamics in the TC, only two include works show results in the TC above velocity vn represented with lateral dynamics coordinates. The number of works is indeed small. One can find seven works in the first group [1,4,5,77,78,79] and just one work in the fifth group [106]. Except for the works by the present authors [79,80], there are no other works in which the dynamics of vehicles in the TC constitute the main subject of study and where studying these dynamics involves intensive simulation experiments performed based on system parameters variation. This, of course, means that all the works in the second, third, and fourth groups, as well as the remaining works in the fifth group, are more-loosely related to the dynamics of rail vehicles in the TC. The review of the works in the fifth group, containing the works from the last four years, shows that the described situation has not changed over time.
Considering the methods, tools, and scope of the authors’ studies discussed in Section 4, it is worth saying that despite the clear benefits of the authors’ approach and simulation tools, these do not constitute the only possible approach. It should be clearly stated that many of the commercial packages for rail vehicle dynamics simulation possess the ability to simulate motion on compound routes (i.e., those composed of the ST, TC, and CC sections). A good example is [106], where the SIMPACK software was applied. Some of this software also possesses the ability to adopt different TC shape. The restrictions that some of them have do not seem to constitute an exclusionary limitation. This is because at this stage of the problem’s advancement, the main task is to find as many examples of non-linear behaviors in TCs and their vicinity as possible. Experiments with different TC shapes do not seem necessary to the undertaking of this primary task. The specific problem with the commercial simulation software is the so-called black box problem, i.e., that many of the assumptions adopted in the software and vehicle models are unknown to the user. This results in difficulties in comparing the results from different software tools because the reasons for the differences in the results cannot be reliably found. In this way, verifying the results is more complicated. On the other hand, this is not an exclusionary limitation at the current stage of the research. Building the researchers’ software is not unconditionally required, especially at the beginning of one’s studies. All these facts should encourage potential researchers to initiate an interest in the dynamics of rail vehicles in the TC above the critical velocity.
This literature analysis shows, univocally, that studies on rail vehicle dynamics in the TC at velocities above or close to vn are rarely undertaken. The combination of the complex issues of dynamics in the TC with the difficult stability issues seems to have discouraged researchers. On the other hand, the history of stability studies shows that progress is unstoppable. The example of stability studies confirms the well-known fact that quite often, quite a few researchers must participate in the studies in order to achieve a breakthrough in the paradigms of scientific and practitioner communities. Taking into account the fact that knowledge often spreads with difficulty in the beginning, new ideas will eventually become commonly accepted and beneficially applied. Even one of the coauthors of this paper can see that his earlier new ideas concerning the stability and non-linear critical velocity of railway vehicles in a CC were controversial at the beginning, but they became commonly studied and are now accepted all over the world. The authors feel that now is the time for the issue of rail vehicle dynamics in the TC around the critical velocity to be studied more frequently. Finally, it is through seeking to attain some common well-being, successfully applied for the benefit of science, technology, and society, that the authors are directly encouraged to continue with their own research.
Author Contributions
Conceptualization, K.Z. and M.G.-S.; Methodology, K.Z. and M.G.-S.; Investigation, K.Z. and M.G.-S.; Writing—original draft, Milena M.G.-S.; Writing—review & editing, K.Z.; Supervision, K.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were generated for the exclusive need of the current paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zboiński, K. Dynamical investigation of railway vehicles on a curved track. Eur. J. Mech. Part A Solids 1998, 17, 1001–1020. [Google Scholar] [CrossRef]
- Zboiński, K. Selected problems of non-linear (non-smooth) dynamics of rail vehicles in curved track. In Non-Smooth Problems in Vehicle System Dynamics; Thomsen, P.G., True, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 87–99. [Google Scholar] [CrossRef]
- Hoffmann, M. Dynamics of European Two-Axle Freight Wagons. Ph.D. Thesis, Technical University of Denmark, Informatics and Mathematical Modelling, Lyngby, Denmark, 2006; 159p. [Google Scholar]
- Hoffmann, M.; True, H. The dynamics of European two-axle railway freight wagons with UIC standard suspension. Veh. Syst. Dyn. 2008, 46 (Suppl. S1), 225–236. [Google Scholar] [CrossRef]
- Hoffmann, M.; True, H. The dynamics of two-axle freight wagons with UIC standard suspension. In Proceedings of the 10th VSDIA Conference on Vehicle System Dynamics, Identification and Anomalies, Budapest, Hungary, 6–8 November 2006; Zobory, I., Ed.; Budapest University of Technology and Economics: Budapest, Hungary, 2006; pp. 183–190, ISBN 978-963-420-968-3. [Google Scholar]
- Knothe, K.; Bohm, F. History of Stability of Railway and Road Vehicles. Veh. Syst. Dyn. 1999, 31, 283–323. [Google Scholar] [CrossRef]
- Knothe, K.; Stichel, S. Rail Vehicle Dynamics; Springer: Cham, Switzerland, 2017; 321p, ISBN 978-3-319-45374-3. [Google Scholar]
- Wickens, A.H. Static and Dynamic Stability of Unsymmetric Two-Axle Railway Vehicles Possessing Perfect Steering. Veh. Syst. Dyn. 1982, 11, 89–106. [Google Scholar] [CrossRef]
- Wickens, A.H. The dynamic stability of railway vehicle wheelsets and bogies having profiled wheels. Int. J. Solid Struct. 1965, 1, 319–341. [Google Scholar] [CrossRef]
- Wickens, A.H. The dynamics of railway vehicles on straight track: Fundamental consideration of lateral stability. Proc. IMechE Part F J. Rail Rapid Transit 1965, 180, 1–16. [Google Scholar] [CrossRef]
- Wickens, A.H. The dynamics stability of a simplified four-wheeled vehicle having profiled wheels. Int. J. Solid Struct. 1965, 1, 385–406. [Google Scholar] [CrossRef]
- Dukkipati, R.V. Modelling and simulation of the hunting of a three-piece railway truck on NCR curved track simulator. Veh. Syst. Dyn. 1994, 23 (Suppl. S1), 105–115. [Google Scholar] [CrossRef]
- Shen, Z. On principles and methods to reduce the wheel/rail forces for rail freight vehicles. Veh. Syst. Dyn. 1992, 20 (Suppl. S1), 584–595. [Google Scholar] [CrossRef]
- Liu, M. A Nonlinear Dynamic Model for Single-axle Wheelset with Profiled Wheels and Rails. In Proceedings of the International Conference of Control, Dynamic Systems, and Robotics, Ottawa, ON, Canada, 7–8 May 2014. Paper No. 60(1-8). [Google Scholar]
- Kalker, J.J. Simplified theory of rolling contact. Mech. Aeronaut. Eng. Shipbuild. 1873, 1, 1–10. [Google Scholar]
- Kalker, J.J. Three-Dimensional Elastic Bodies in Rolling Contact; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990; 314p, ISBN 978-0-7923-0712-9. [Google Scholar]
- Kortum, W.; Sharp, R.S.; De Pater, A.D. Application of Multibody Computer Codes to Vehicle System Dynamics—Progress Report to 12th IAVSD Symposium on a Workshop and Resulting Activities; Soc. for Eng. and Scientific Education Oberpfaffenhofen: Lyon, France, 1991. [Google Scholar]
- Kass-Petersen, C.; True, H. A bifurcation analysis of nonlinear oscillation in railway vehicles. Veh. Syst. Dyn. 1983, 12, 5–6. [Google Scholar] [CrossRef]
- Kass-Petersen, C.; True, H. A bifurcation analysis of nonlinear oscillations in railway vehicles. In Proceedings of the 8th IAVSD Symposium on Dynamics of Vehicles on Roads and Tracks, Cambridge, MA, USA, 15–19 August 1983; Hedrick, K., Ed.; Swets & Zeitlinger: Amsterdam, The Netherlands; Lisse, The Netherlands, 1984; pp. 655–665. [Google Scholar]
- Gasch, R.; Kik, W.; Moelle, D. Non-Linear Bogie Hunting. Veh. Syst. Dyn. 1981, 10, 145–148. [Google Scholar] [CrossRef]
- Gasch, R.; Moelle, D. Nonlinear bogie hunting. In Proceedings of the 7th IAVSD Symposium on Dynamics of Vehicles on Roads and Tracks, Cambridge, UK, 7–11 September 1981; Wickens, A.H., Ed.; Swets & Zeitlinger: Lisse, The Netherlands, 1982; pp. 455–467. [Google Scholar]
- Gasch, R.; Moelle, D.; Knothe, K. The effect of non-linearities on the limit-cycles of railway vehicles. In Proceedings of the 8th IAVSD Symposium on Dynamics of Vehicles on Roads and Tracks, Cambridge, MA, USA, 15–19 August 1983; Hedrick, K., Ed.; Swets & Zeitlinger: Amsterdam, The Netherlands; Lisse, The Netherlands, 1984; pp. 207–224. [Google Scholar]
- Aizpun, M.; Vinolas, J. Illustrating the implications of choices at the vehicle model building stage in simulation results. In The Dynamics of Vehicles on Roads and Tracks—Proceeding of the 24th IAVSD Symp; Rosenberger, M., Plochl, M., Six, K., Edelmann, J., Eds.; Taylor & Francis: London, UK, 2016; pp. 1033–1042. ISBN 978-1-138-02885-2. [Google Scholar]
- Cheng, Y.C.; Lee, S.Y.; Chen, H.H. Modelling and nonlinear hunting stability analysis of high-speed railway vehicle on curved tracks. J. Sound Vib. 2009, 324, 139–160. [Google Scholar] [CrossRef]
- Choi, Y.-S.; Shin, B.-S. Critical speed of high-speed trains considering wheel-rail contact. J. Mech. Sci. Technol. 2015, 29, 4593–4600. [Google Scholar] [CrossRef]
- Choromański, W.; Kisilowski, J.; Łopata, H. Investigation of technical stochastic stability of lateral vibrations of mathematical model of railway vehicle. Rozpr. Inż. 1985, 3, 219–234. [Google Scholar]
- Di Gialleonardo, E.; Bruni, S.; True, H. Analysis of the non-linear dynamics of a 2-axle freight wagon in curves. Veh. Syst. Dyn. 2014, 52, 125–141. [Google Scholar] [CrossRef]
- Gao, X.-J.; Li, Y.-H.; Yue, Y. The “resultant bifurcation diagram” method and its application to bifurcation behaviours of a symmetric railway bogie system. Nonlinear Dyn. 2012, 70, 363–380. [Google Scholar] [CrossRef]
- Goodall, R.M.; Iwnicki, S. Non-linear dynamic techniques v. equivalent conicity methods for rail vehicle stability assessment. In Proceedings of the 18th IAVSD Symposium on Dynamics of Vehicles on Roads and Tracks, Vehicle System Dynamics, Kanagawa, Japan, 24–30 August 2003; Abe, M., Ed.; Taylor & Francis: London, UK, 2004; Volume 41, pp. 791–799, ISBN 9026519729. [Google Scholar]
- Huilgol, R.R. Hopf-Friedrichs bifurcation and the hunting of a railway axle. Q. Appl. Math. 1978, 36, 85–94. [Google Scholar] [CrossRef]
- Iwnicki, S.; Stichel, S.; Orlova, A.; Hecht, M. Dynamics of railway freight vehicles. Veh. Syst. Dyn. 2015, 53, 995–1033. [Google Scholar] [CrossRef]
- Jensen, J.C.; True, H. On the new route to chaos in railway dynamics. Nonlinear Dyn. 1997, 13, 117–129. [Google Scholar] [CrossRef]
- Kardas-Cinal, E. Some Problems Related to Investigations of Wheelset Model Stability. In 2nd Polish-German Workshop; IPPT PAN: Warsaw, Poland, 1991; pp. 119–130. [Google Scholar]
- Kardas-Cinal, E.; Kisilowski, J. The influence of riding speed on vehicle track dynamics in the presence of track random irregularities. Mach. Dyn. Probl. 1995, 11, 55–67. [Google Scholar]
- Kisilowski, J.; Kardas-Cinal, E. On a certain method of examining stability of mathematical models of railway vehicle with disturbances occurring in real object. Veh. Syst. Dyn. 1994, 23 (Suppl. S1), 262–273. [Google Scholar] [CrossRef]
- Kisilowski, J.; Knothe, K. Advanced Railway Vehicle System Dynamics; WNT: Warszawa, Poland, 1991; 442p, ISBN 83-204-1348-6. [Google Scholar]
- Kumar, V.; Rastogi, V.; Pathak, P.M. Modelling and evaluation of the hunting behaviour of a high-speed railway vehicle on curved track. Proc. IMechE Part F J. Rail Rapid Transit 2018, 233, 220–236. [Google Scholar] [CrossRef]
- Lee, S.Y.; Cheng, Y.C. A new dynamic model of high-speed railway vehicle moving on curved tracks. ASME J. Vib. Acoust. 2008, 130, 011009. [Google Scholar] [CrossRef]
- Lee, S.Y.; Cheng, Y.C. Hunting stability analysis of a new dynamic model of high-speed railway vehicle moving on curved tracks. In Proceedings of the 15th IASTED International Conference on Applied Simulation and Modelling, Rhodes, Greece, 26–28 June 2006; pp. 8–14. [Google Scholar]
- Lee, S.Y.; Cheng, Y.C. Influence of the vertical and the roll motions of frames on the hunting stability of trucks moving on curved tracks. J. Sound Vib. 2006, 294, 441–453. [Google Scholar] [CrossRef]
- Lee, S.Y.; Cheng, Y.C. Nonlinear analysis on hunting stability for high-speed railway vehicle truck on curved tracks. ASME J. Vib. Acoust. 2005, 127, 324–332. [Google Scholar] [CrossRef]
- Lee, S.Y.; Cheng, Y.C. Nonlinear hunting stability analysis of high-speed railway vehicles on curved tracks. Int. J. Heavy Veh. Syst. 2003, 10, 344–361. [Google Scholar] [CrossRef]
- Lee, S.Y.; Cheng, Y.C.; Kuo, C.M. Non-linear modelling and analysis on the hunting stability of trucks moving on curved tracks. In Proceedings of the 14th IASTED International Conference on Applied Simulation and Modelling, Benalmadena, Spain, 15–17 June 2005; pp. 422–426. [Google Scholar]
- Luo, G.W.; Shi, Y.Q.; Zhu, X.F.; Du, S.S. Hunting patterns and bifurcation characteristics of a three-axle locomotive bogie system in the presence of the flange contact nonlinearity. Int. J. Mech. Sci. 2018, 136, 321–338. [Google Scholar] [CrossRef]
- Mazzola, L.; Alfi, S.; Bruni, S. Evaluation on the hunting behaviour of a railway vehicle in a curve. Proc. IMechE Part F J. Rail Rapid Transit 2015, 229, 530–541. [Google Scholar] [CrossRef]
- Park, J.-H.; Koh, H.-I.; Kim, N.-P. Parametric study of lateral stability for a railway vehicle. J. Mech. Sci. Technol. 2011, 25, 1657–1666. [Google Scholar] [CrossRef][Green Version]
- Polach, O. Characteristic parameters of nonlinear wheel/rail contact geometry. Veh. Syst. Dyn. 2010, 48 (Suppl. S1), 19–36. [Google Scholar] [CrossRef]
- Polach, O. On non-linear methods of bogie stability assessment using computer simulations. Proc. IMechE Part F J. Rail Rapid Transit 2006, 220, 13–27. [Google Scholar] [CrossRef]
- Rezvani, M.A.; Mazraeh, A. Dynamics and stability analysis of a freight wagon subjective to the railway track and wheelset operational conditions. Eur. J. Mech. A-Solids 2017, 61, 22–34. [Google Scholar] [CrossRef]
- Schupp, G. Computational bifurcation analysis of mechanical systems with applications to railway vehicles. In Proceedings of the 18th IAVSD Symposium on Dynamics of Vehicles on Roads and Tracks, Vehicle System Dynamics, Atsugi, Japan, 24–30 August 2003; Abe, M., Ed.; Taylor & Francis: London, UK, 2004; Volume 41, pp. 458–467, ISBN 9026519729. [Google Scholar]
- Stichel, S. Limit cycle behaviour and chaotic motions of two-axle freight wagons with friction damping. Multibody Syst. Dyn. 2002, 8, 243–255. [Google Scholar] [CrossRef]
- Toumi, M.; Chollet, H.; Yin, H. Effect of elasto-plasticity on the creep force characteristic and the railway vehicle stability. In The Dynamics of Vehicles on Roads and Tracks—Proceeding 24th IAVSD Symp; Rosenberger, M., Plochl, M., Six, K., Edelmann, J., Eds.; Taylor & Francis: London, UK, 2016; pp. 1015–1025. ISBN 978-1-138-02885-2. [Google Scholar]
- True, H. Does a critical speed for railroad vehicles exist? In Proceedings of the ASME/IEEE Joint Railroad Conference, Chicago, IL, USA, 22–24 March 1994; Hawthorne, K.L., Hill, R.J., Eds.; IEEE: Piscataway, NJ, USA, 1994; pp. 125–131. [Google Scholar] [CrossRef]
- True, H. Dynamics of a rolling wheelset. Appl. Mech. Rev. 1993, 46, 438–444. [Google Scholar] [CrossRef]
- True, H. Multiple attractors and critical parameters and how to find them numerically: The right, the wrong and the gambling way. Veh. Syst. Dyn. 2013, 51, 443–459. [Google Scholar] [CrossRef]
- True, H. On the theory of nonlinear dynamics and its applications in vehicle systems dynamics. Veh. Syst. Dyn. 1999, 31, 393–421. [Google Scholar] [CrossRef]
- True, H. Railway vehicle chaos and asymmetric hunting. Veh. Syst. Dyn. 1992, 20 (Suppl. S1), 625–637. [Google Scholar] [CrossRef]
- True, H. Recent advances in the fundamental understanding of railway vehicle dynamics. Int. J. Veh. Des. 2006, 40, 251–264. [Google Scholar] [CrossRef]
- True HBirkedal Nielsen, J. On the Dynamics of Steady Curving of Railway Vehicles. In Proceedings of the 6th Mini Conference on Vehicles System Dynamics, Identification and Anomalies, Budapest, Hungary, 9–11 November 1998; Zobory, I., Ed.; Technical University of Budapest: Budapest, Hungary, 1998; pp. 73–81, ISBN 9634206352. [Google Scholar]
- True, H.; Hansen, T.G.; Lundell, H. On the Quasi-Stationary Curving Dynamics of a Railroad Truck. In Proceedings of the 2005 ASME/IEEE Joint Rail Conference, Pueblo, CO, USA, 16–18 March 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 131–138. [Google Scholar] [CrossRef]
- True, H.; Jensen, J.C. Chaos and asymmetry in railway vehicle dynamics. Period. Polytech. Ser. Transp. Eng. 1994, 22, 55–68. [Google Scholar]
- True, H.; Jensen, J.C. Parameter study of hunting and chaos in railway vehicle dynamics. Veh. Syst. Dyn. 1994, 23 (Suppl. S1), 508–520. [Google Scholar] [CrossRef]
- True, H.; Jensen, J.C.; Slivsgaard, E. Non-linear Railway Dynamics and Chaos. In Proceedings of the 5th Mini Conference on Vehicles System Dynamics, Identification and Anomalies, Budapest, Hungary, 11–13 November 1996; Zobory, I., Ed.; Technical University of Budapest: Budapest, Hungary, 1996; pp. 51–60. [Google Scholar]
- True, H.; Trzepacz, L. The dynamics of railway freight wagon wheelset with dry friction damping in the suspension. Veh. Syst. Dyn. 2004, 41, 587–596. [Google Scholar]
- Uyulan, C.; Gokasan, M.; Bogosyan, S. Dynamic Investigation of the Hunting Motion of a Railway Bogie in a Curved Track via Bifurcation Analysis. Math. Probl. Eng. 2017, 2017, 8276245. [Google Scholar] [CrossRef]
- Xu, G.; Steindl, A.; Troger, H. Nonlinear stability analysis of a bogie of a low-platform wagon. Veh. Syst. Dyn. 1992, 20 (Suppl. S1), 653–665. [Google Scholar] [CrossRef]
- Zeng, J.; Wu, P. Stability analysis of high speed railway vehicles. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2004, 47, 464–470. [Google Scholar] [CrossRef]
- Zeng, J.; Wu, P. Stability of high-speed train. J. Traffic Transp. Eng. 2005, 5, 464–470. [Google Scholar]
- Zhang, T.; True, H.; Dai, H. The influence of the perturbation on wheel rotation speed on the stability of a railway bogie on steady curve sections of a track. Veh. Syst. Dyn. 2019, 57, 425–443. [Google Scholar] [CrossRef]
- Zhang, T.; True, H.; Dai, H. The lateral dynamics of a nonsmooth railway wheelset model. Int. J. Bifurc. Chaos 2018, 28, 1850095. [Google Scholar] [CrossRef]
- Ebeling, K. High-speed Railways in Germany. Jpn. Railw. Transp. Rev. 2005, 40, 36–45. [Google Scholar]
- Yu, C.W.; Menz, N.; Hunter, C.; Chen, Y.Y.; Farias, P. An analysis of the Chinese High-Speed Rail from the American perspective. In Proceedings of the 53rd Annual Transportation Research Forum, Tampa, FL, USA, 15–17 March 2012; p. 207119. [Google Scholar]
- Jiao, J.; Harbin, J.; Li, Y. Fast Tracks: A Comparison of High Speed Rail in China, Europe and the United States. J. Transp. Technol. 2013, 3, 57–62. [Google Scholar] [CrossRef]
- Sone, S. Comparison of the technologies of the Japanese Shinkansen and Chinese High-speed Railways. J. Zhejiang Univ. Sci. A 2015, 16, 769–780. [Google Scholar] [CrossRef]
- Purba, A.; Nakamura, F.; Niken, C.; Jafri, M.; Pratomo, P. A current review of high speed railways experiences in Asia and Europe. AIP Conf. Proc. 2017, 1903, 060004. [Google Scholar] [CrossRef]
- Zembri, P.; Libourel, E. Towards oversized high-speed rail systems? Some lessons from France and Spain. Transp. Res. Procedia 2017, 25, 368–385. [Google Scholar] [CrossRef]
- Wang, K.; Liu, P. Lateral stability Analysis of Heavy-Haul Vehicle on Curved Track Based on Wheel/Rail Coupled Dynamics. J. Transp. Technol. 2012, 2, 150–157. [Google Scholar] [CrossRef]
- Dusza, M. The study of track gauge influence on lateral stability of 4-axle rail vehicle model. Arch. Transp. 2014, 30, 7–20. [Google Scholar] [CrossRef]
- Zboiński, K.; Gołofit-Stawińska, M. The impact of primary suspension stiffness of 2-axle bogie of MKIII passenger car on its dynamical behaviour. Transp. Probl. 2018, 13, 135–146. [Google Scholar] [CrossRef]
- Zboinski, K.; Golofit-Stawinska, M. Investigation into nonlinear phenomena for various railway vehicles in transition curves at velocities close to critical one. Nonlinear Dyn. 2019, 98, 1555–1601. [Google Scholar] [CrossRef]
- Carballeira, J.; Baeza, L.; Rovira, A.; Garcia, E. Technical characteristics and dynamic modelling of Talgo trains. Veh. Syst. Dyn. 2008, 46 (Suppl. S1), 301–316. [Google Scholar] [CrossRef]
- Droździel, J.; Sowiński, B. Railway car dynamic response to track transition curve and single standard turnout. In Computers in Railways X. Computer System Design and Operation in the Railway and Other Transit Systems; Allen, J., Brebbia, C.A., Rumsey, A.F., Sciutto, G., Sone, S., Goodman, C.J., Eds.; WIT Transactions on The Built Environment; WIT Press: Billerica, MA, USA, 2006; Volume 88, pp. 849–858. [Google Scholar] [CrossRef]
- Kondo, O.; Yamazaki, Y. Simulation Technology for Railway Vehicle Dynamics; Nippon Steel & Sumitomo Metal Technical Report, Report No. 105; Nippon Steel & Sumitomo Metal: Tokyo, Japan, 2013. [Google Scholar]
- Kuba, T.; Lugner, P. Dynamic behaviour of tramways with different kinds of bogies. Veh. Syst. Dyn. 2012, 50, 277–289. [Google Scholar] [CrossRef]
- Kurzeck, B.; Hecht, M. Dynamic simulation of friction-induced vibrations in a light railway bogie while curving compared with measurement results. Veh. Syst. Dyn. 2010, 48 (Suppl. S1), 121–138. [Google Scholar] [CrossRef]
- Lau, A.; Kassa, E. Simulation of Vehicle-Track Interaction in Small Radius Curves and Switches and Crossings. In Proceedings of the Third International Conference on Railway Technology: Research, Development and Maintenance, Cagliari, Italy, 5–8 April 2016; Civil-Comp Press: Edinburgh, Scotland, 2016; p. 126. [Google Scholar] [CrossRef]
- Matsumoto, A.; Michitsuji, Y. Flange-Climb derailments of Freight Trains on Curved Tracks Due to Rolling. In Proceedings of the 10th International Conference on Railway Bogies and Running Gears, Budapest, Hungary, 12–15 September 2016; Scientific Society of Mechanical Engineers: New York, NY, USA, 2016; pp. 91–100. [Google Scholar]
- Prandi, D. Railway Bogie Stability Control From Secondary Yaw Actuators. Master’s Thesis, Politecnico di Milano, Scuola di Ingegneria Industriale e dell’Informazione, Milan, Italy, 2014; 64p. [Google Scholar]
- Shaltout, R.; Ulianov, C.; Baeza, L. Development of a Simulation Tool for the Dynamic Analysis of Railway Vehicle-Track Interaction. Transp. Probl. 2015, 10, 47–58. [Google Scholar] [CrossRef]
- Zhai, W.M.; Wang, K.Y. Lateral interactions of trains and tracks on small radius curves: Simulation and experiment. Veh. Syst. Dyn. 2006, 44 (Suppl. S1), 520–530. [Google Scholar] [CrossRef]
- Xia, F.; True, H. On the dynamics of the three-piece-freight truck. In Proceedings of the 2003 ASME/IEEE Joint Railroad Conference, Chicago, IL, USA, 24 April 2003; pp. 149–159. [Google Scholar] [CrossRef]
- Ahmadian, M.; Yang, S. Hopf bifurcation and hunting behavior in a rail wheelset with flange contact. Nonlinear Dyn. 1998, 15, 15–30. [Google Scholar] [CrossRef]
- Chudzikiewicz, A.; Sowiński, B. Modelling and simulation of trams bogies with fully independently rotating wheels. In The Dynamics of Vehicles on Roads and Tracs—Proceeding of the 24th IAVSD Symp; Rosenberger, M., Plochl, M., Six, K., Edelmann, J., Eds.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: London, UK, 2016; pp. 1427–1434. ISBN 978-1-138-02885-2. [Google Scholar]
- Dumitriu, M. Influence of the longitudinal and lateral suspension damping on the vibration behaviour in the railway vehicles. Arch. Mech. Eng. 2015, 62, 115–140. [Google Scholar] [CrossRef]
- Froment, O.; Aubry, D.; Castel, L. Analysis of the stability of nonlinear railways dynamics. In Computational Mechanics, New Trends and Applications; Idelsohn, S., Onate, E., Dvorkin, E., Eds.; CIMNE: Barcelona, Spain, 1998; pp. 1–9. [Google Scholar]
- Sedighi, H.M.; Shirazi, K.H. Bifurcation analysis in hunting dynamical behaviour in a railway bogie: Using novel exact equivalent functions for discontinuous nonlinearities. Sci. Iran. Trans. B Mech. Eng. 2012, 19, 1493–1501. [Google Scholar] [CrossRef]
- Warczek, J.; Burdzik, R.; Peruń, G. The method for identification of damping coefficient of the trucks suspension. Key Eng. Mater. 2014, 588, 281–289. [Google Scholar] [CrossRef]
- Bustos, A.; Tomas-Rodriguez, M.; Rubio, H.; Castejon, C. On the nonlinear hunting stability of a high-speed train boogie. Nonlinear Dyn. 2023, 111, 2059–2078. [Google Scholar] [CrossRef]
- Chernysheva, Y.; Gorskiy, A. Methods Proposed for Analysis of Vibrations of Railway Cars. In International Scientific SiberianTransport Forum TransSiberia—2021. TransSiberia 2021; Manakov, A., Edigarian, A., Eds.; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2022; Volume 402. [Google Scholar] [CrossRef]
- Ge, P.; Wie, X.; Liu, J.; Cao, H. Bifurcation of a modified railway wheelset model with nonlinear equivalent conicity and wheel–rail force. Nonlinear Dyn. 2020, 102, 79–100. [Google Scholar] [CrossRef]
- Guo, J.; Shi, H.; Luo, R.; Zeng, J. Bifurcation analysis of a railway wheelset with nonlinear wheel–rail contact. Nonlinear Dyn. 2021, 104, 989–1005. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, G.; Shi, H.; Zeng, J. Small amplitude bogie hunting identification method for high-speed trains based on machine learning. Veh. Syst. Dyn. 2023. [Google Scholar] [CrossRef]
- Pandey, M.; BBhattacharya, B. Effect of bolster suspension parameters of three-piece freight bogie on the lateral frame force. Int. J. Rail Transp. 2020, 8, 45–65. [Google Scholar] [CrossRef]
- Shvets, A.O. Dynamic interaction of a freight car body and a three-piece bogie during axle load increase. Veh. Syst. Dyn. 2022, 60, 3291–3313. [Google Scholar] [CrossRef]
- Skerman, D.; Colin Cole, C.; Spiryagin, M. Determining the critical speed for hunting of three-piece freight bogies: Practice versus simulation approaches. Veh. Syst. Dyn. 2022, 60, 3314–3335. [Google Scholar] [CrossRef]
- Sun, J.; Chi, M.; Jin, X.; Liang, S.; Wang, J.; Li, W. Experimental and numerical study on carbody hunting of electric locomotive induced by low wheel–rail contact conicity. Veh. Syst. Dyn. 2021, 59, 203–223. [Google Scholar] [CrossRef]
- Sun, J.; Meli, E.; Song, X.; Chi, M.; Jiao, W.; Jiang, Y. A novel measuring system for high-speed railway vehicles hunting monitoring able to predict wheelset motion and wheel/rail contact characteristics. Veh. Syst. Dyn. 2023, 61, 1621–1643. [Google Scholar] [CrossRef]
- Umemoto, J.; Yabuno, H. Parametric and self-excited oscillation produced in railway wheelset due to mass imbalance and large wheel tread angle. Nonlinear Dyn. 2023, 111, 4087–4106. [Google Scholar] [CrossRef]
- Wang, X.; Lu, Z.; Wen, J.; Wie, J.; Wang, Z. Kinematics modelling and numerical investigation on the hunting oscillation of wheel-rail nonlinear geometric contact system. Nonlinear Dyn. 2022, 107, 2075–2097. [Google Scholar] [CrossRef]
- Yang, C.; Huang, Y.; Li, F. Influence of Curve Geometric Parameters on Dynamic Interactions of Side-Frame Cross-Braced Bogie. In Proceedings of the ICRT 2021, Second International Conference on Rail Transportation, Chengdu, China, 5–6 July 2021. [Google Scholar]
- Zboinski, K. Modelling dynamics of certain class of discrete multi-body systems based on direct method of the dynamics of relative motion. Meccanica 2012, 47, 1527–1551. [Google Scholar] [CrossRef][Green Version]
- Zboinski, K. Modeling, Simulation, and Results of Their Use in Railway Vehicle Dynamics Studies. In Railway Research—Selected topics on Development, Safety and Technology; Zboinski, K., Ed.; InTech: Rijeka, Croatia, 2015; pp. 165–195. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).