Shear Behavior of Two-Dimensional Propped Rough Fractures
Abstract
1. Introduction
2. Materials and Methods
2.1. Specimen Preparation
2.2. Direct Shear Test (DST)
2.3. Analysis of Surface Damage
2.4. Dilatant Behavior Monitoring
3. Results
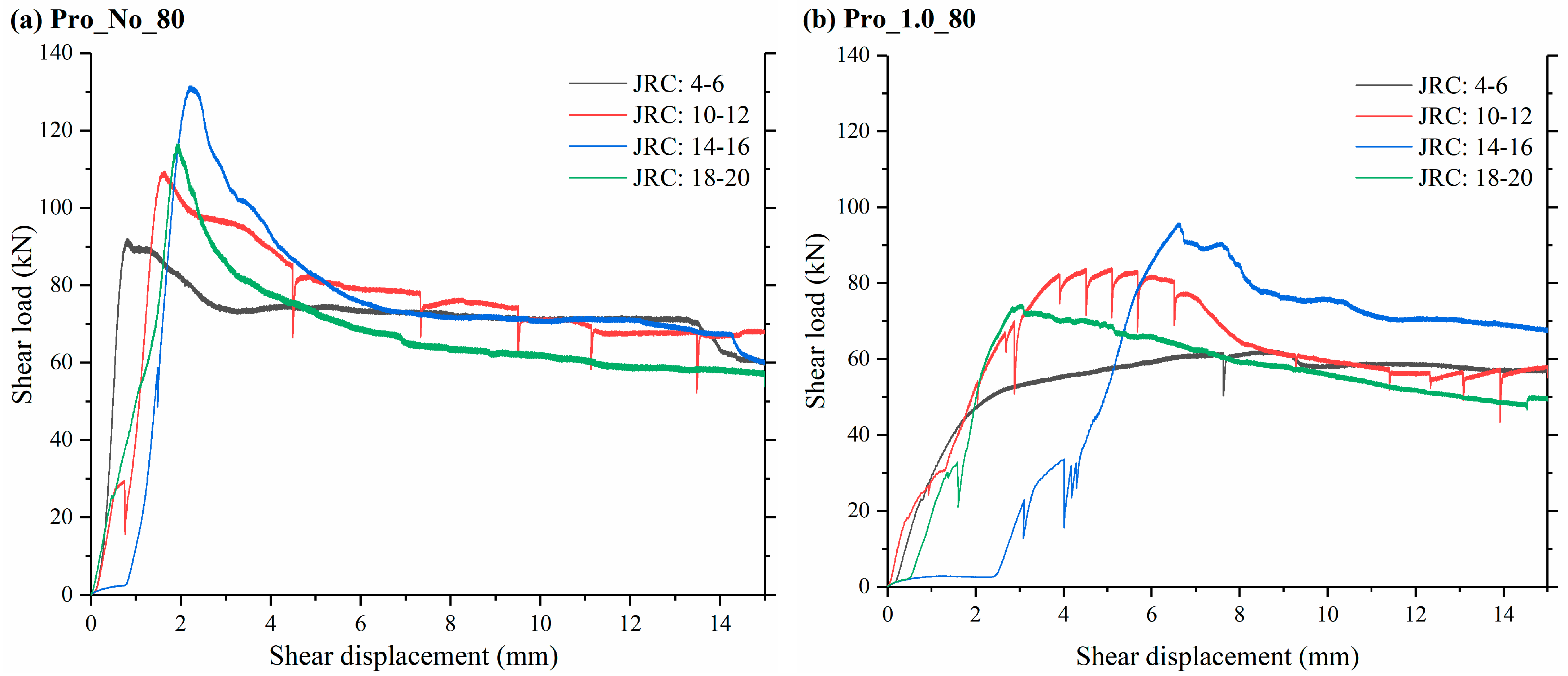
3.1. Load–Displacement Characteristics
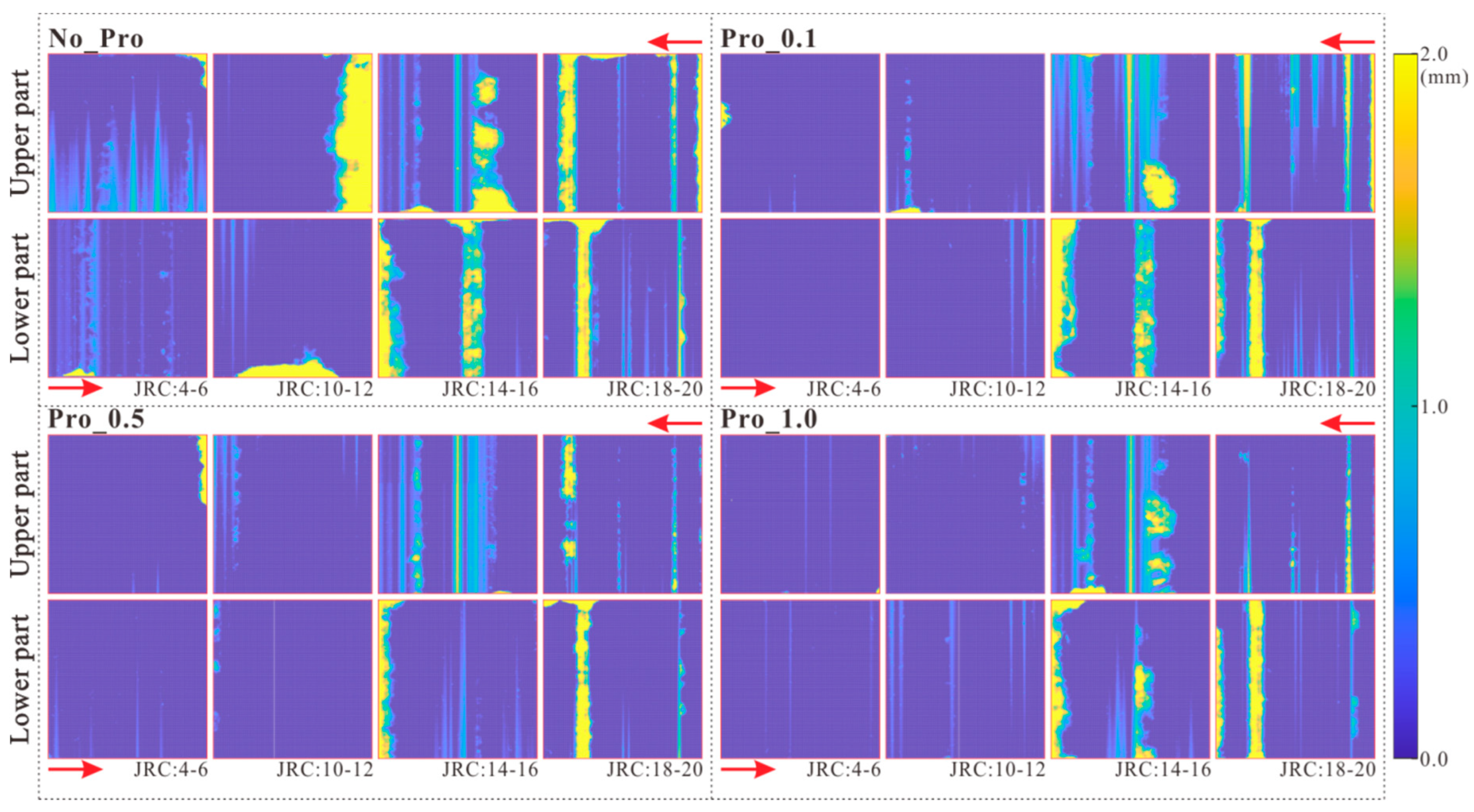
3.2. Surface Damage
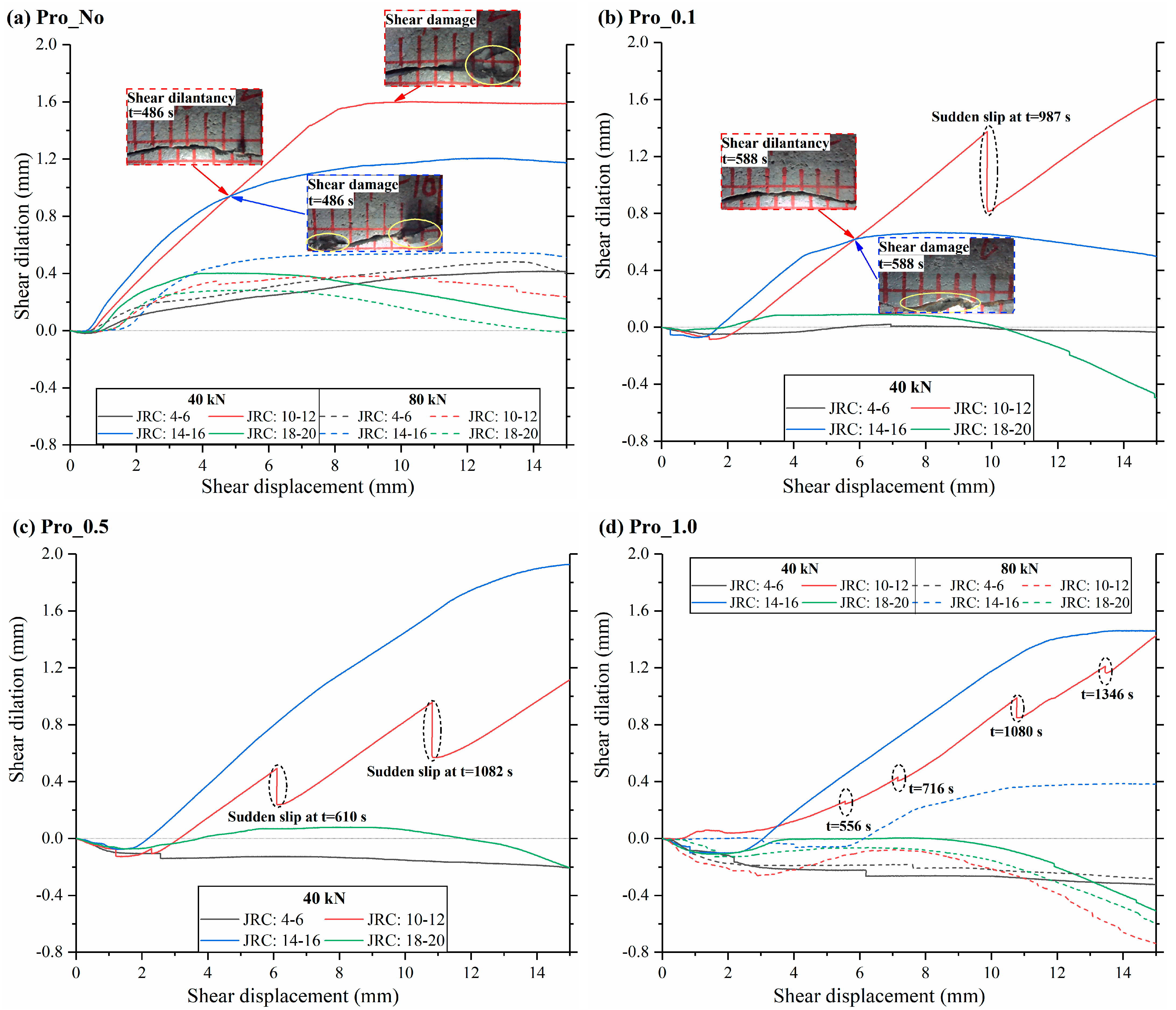
3.3. Shear Dilation Behavior
4. Discussion
4.1. Mechanical Behavior
4.2. Shear Dilatant Behavior
5. Conclusions
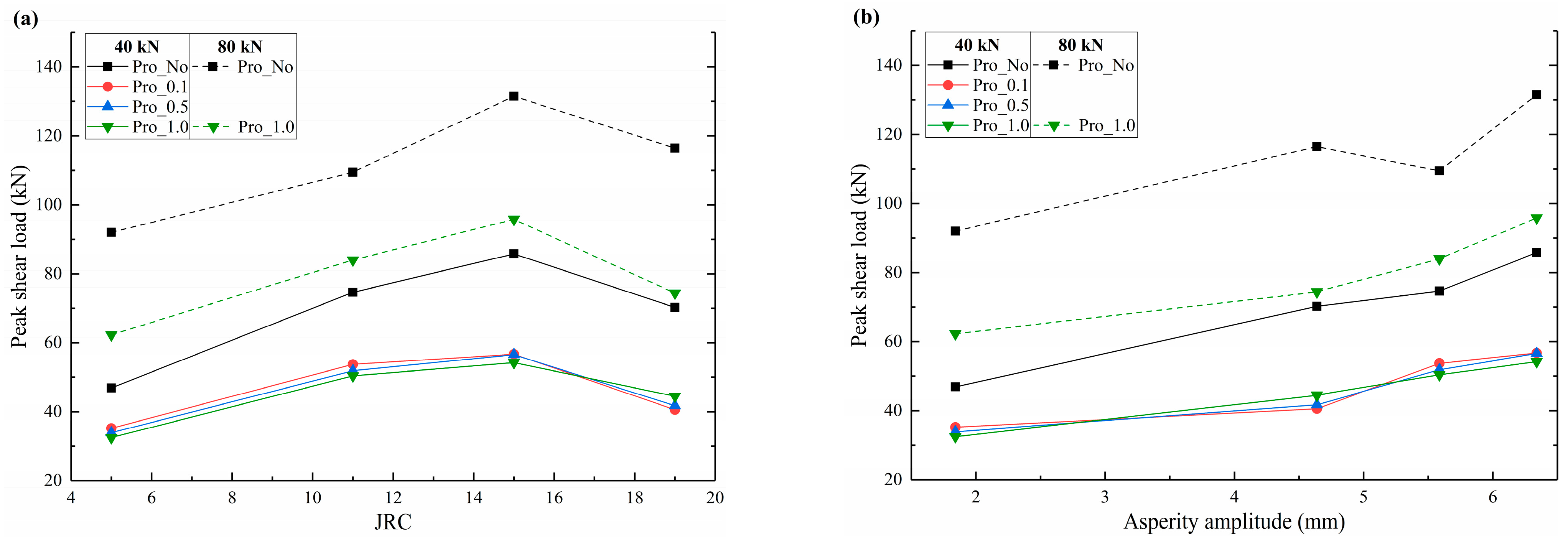
- The asperity amplitude plays a decisive role in the shear strength, and the peak shear strength is positively proportional to the asperity amplitude under the same propped conditions. The fracture with a JRC of 14–16 has the highest peak shear strength due to the highest asperity amplitude of 6.34 mm among all the specimens. The peak shear strength was reduced significantly by the deployment of proppants.
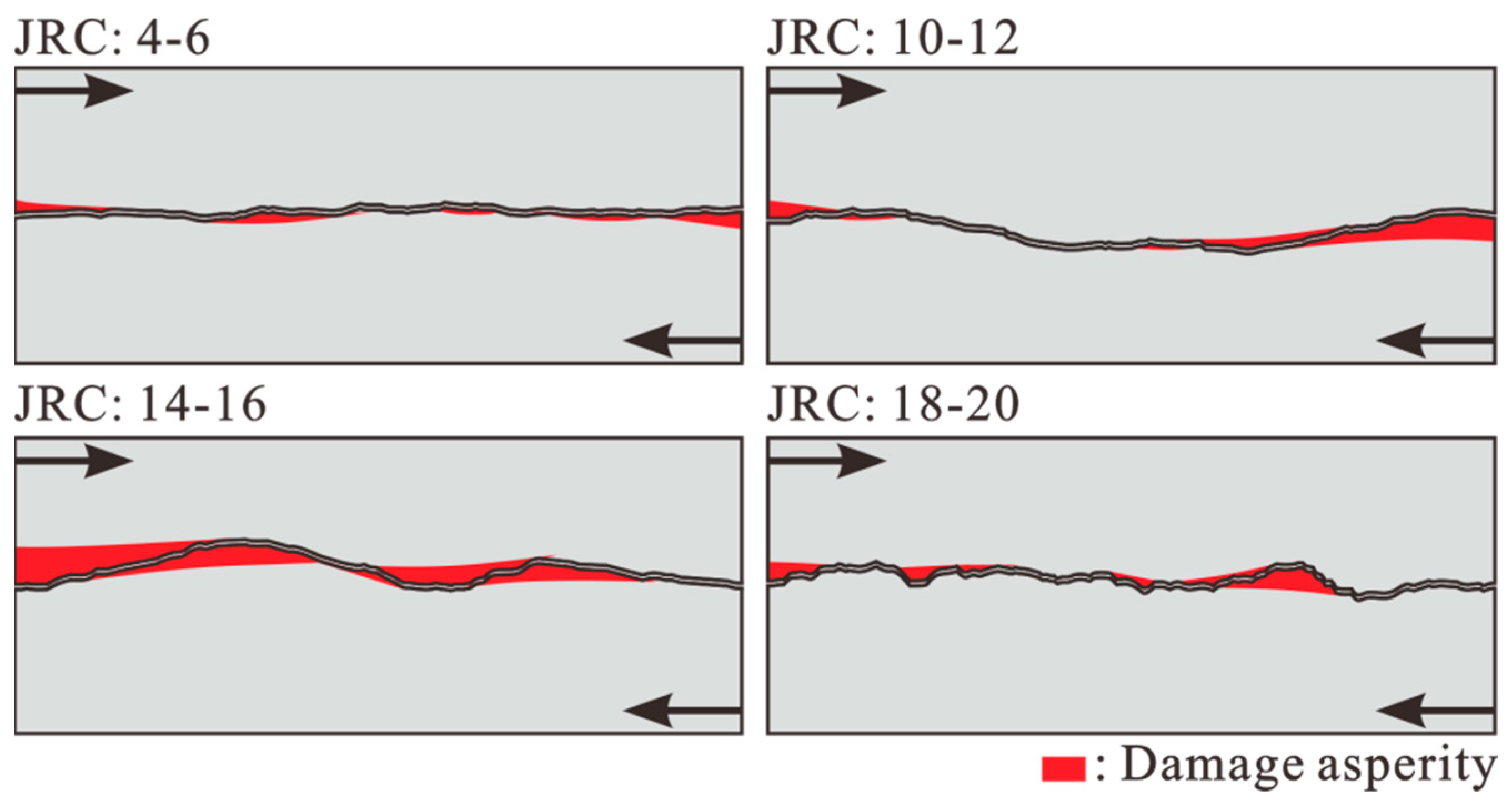
- Shear damage occurs in localized zones where the upper–lower surface asperity contacts. The damage zone was band-shaped, which became smaller when proppants were deployed. This is due to the proppants being concentrated at the gully of fracture, flattening the surface roughness and detaching the upper–lower asperity contact, which in turn reduces the asperity damage and decreases the peak shear strength.
- The highest shear dilatancy is determined at the fracture, with a roughness of JRC = 10–12 and JRC= 14–16. The shear dilatancy of a rough fracture was mainly attributed to the asperity amplitude due to the shear climbing effects. On the other hand, the shear damage of asperity induces frictional slip, which reduces the shear dialatancy. Moreover, the deployment of proppant weakens the shear dilatancy by flattening the fracture roughness, but it promotes the shear dilatancy by alleviating the shear damage. Thus, the proppant deployment has both negative and positive effects on stimulating the fracture shear dialatancy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ghassemi, A. A review of some rock mechanics issues in geothermal reservoir development. Geotech. Geol. Eng. 2012, 30, 647–664. [Google Scholar] [CrossRef]
- Ye, Z.; Ghassemi, A. Injection-induced shear slip and permeability enhancement in granite fractures. J. Geophys. Res. Solid Earth 2018, 123, 9009–9032. [Google Scholar] [CrossRef]
- Bijay, K.C.; Ghazanfari, E. Geothermal reservoir stimulation through hydro-shearing: An experimental study under conditions close to enhanced geothermal systems. Geothermics 2021, 96, 102200. [Google Scholar]
- Li, J.; Yuan, W.; Li, H.; Zou, C. Study on dynamic shear deformation behaviors and test methodology of sawtooth-shaped rock joints under impact load. Int. J. Rock Mech. Min. Sci. 2022, 158, 105210. [Google Scholar] [CrossRef]
- Ye, Z.; Ghassemi, A. Heterogeneous fracture slip and aseismic-seismic transition in a triaxial injection test. Geophys. Res. Lett. 2020, 47, e2020GL087739. [Google Scholar] [CrossRef]
- Vogler, D.; Amann, F.; Bayer, P.; Elsworth, D. Permeability evolution in natural fractures subject to cyclic loading and gouge formation. Rock Mech. Rock Eng. 2016, 49, 3463–3479. [Google Scholar] [CrossRef]
- Frash, L.P.; Carey, J.W.; Welch, N.J. EGS collab experiment 1 geomechanical and hydrological properties by triaxial direct shear. In Proceedings of the 44th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 11–13 February 2019. [Google Scholar]
- Nadimi, S.; Forbes, B.; Moore, J.; Ye, Z.; Ghassemi, A.; McLennan, J.D. Experimental evaluation of effect of hydro-shearing on fracture conductivity at the Utah FORGE site. In Proceedings of the 44th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 11–13 February 2019; pp. 11–13. [Google Scholar]
- Gong, Y.; Mehana, M.; El-Monier, I.; Viswanathan, H. Proppant placement in complex fracture geometries: A computational fluid dynamics study. J. Nat. Gas Sci. Eng. 2020, 79, 103295. [Google Scholar] [CrossRef]
- Aslannezhad, M.; Kalantariasl, A.; You, Z.; Iglauer, S.; Keshavarz, A. Micro-proppant placement in hydraulic and natural fracture stimulation in unconventional reservoirs: A review. Energy Rep. 2021, 7, 8997–9022. [Google Scholar] [CrossRef]
- Chen, T.; Fu, Y.; Feng, X.T.; Tan, Y.; Cui, G.; Elsworth, D.; Pan, Z. Gas permeability and fracture compressibility for proppant-supported shale fractures under high stress. J. Nat. Gas Sci. Eng. 2021, 95, 104157. [Google Scholar] [CrossRef]
- Tan, Y.; Pan, Z.; Liu, J.; Feng, X.T.; Connell, L.D. Laboratory study of proppant on shale fracture permeability and compressibility. Fuel 2018, 222, 83–97. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Y.; Zhou, F.; Liang, X. The influence of proppant breakage, embedding, and particle migration on fracture conductivity. J. Pet. Sci. Eng. 2020, 193, 107385. [Google Scholar] [CrossRef]
- Zhong, Y.; Kuru, E.; Zhang, H.; Kuang, J.; She, J. Effect of fracturing fluid/shale rock interaction on the rock physical and mechanical properties, the proppant embedment depth and the fracture conductivity. Rock Mech. Rock Eng. 2019, 52, 1011–1022. [Google Scholar] [CrossRef]
- Isah, A.; Hiba, M.; Al-Azani, K.; Aljawad, M.S.; Mahmoud, M. A comprehensive review of proppant transport in fractured reservoirs: Experimental, numerical, and field aspects. J. Nat. Gas Sci. Eng. 2021, 88, 103832. [Google Scholar] [CrossRef]
- Barboza, B.R.; Chen, B.; Li, C. A review on proppant transport modelling. J. Pet. Sci. Eng. 2021, 204, 108753. [Google Scholar] [CrossRef]
- Kou, M.; Liu, X.; Tang, S.; Wang, Y. Experimental study of the prepeak cyclic shear mechanical behaviors of artificial rock joints with multiscale asperities. Soil Dyn. Earthq. Eng. 2019, 120, 58–74. [Google Scholar] [CrossRef]
- Han, G.; Zhou, Y.; Liu, R.; Tang, Q.; Wang, X.; Song, L. Influence of surface roughness on shear behaviors of rock joints under constant normal load and stiffness boundary conditions. Nat. Hazards 2022, 112, 367–385. [Google Scholar] [CrossRef]
- Barton, N. Review of a new shear-strength criterion for rock joints. Eng. Geol. 1973, 7, 287–332. [Google Scholar] [CrossRef]
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Pakdaman, A.M.; Moosavi, M. Surface Roughness Assessment of Natural Rock Joints Based on an Unsupervised Pattern Recognition Technique Using 2D Profiles. Rud.-Geološko-Naft. Zb. 2023, 38, 185–198. [Google Scholar] [CrossRef]
- Barton, N.; Wang, C.; Yong, R. Advances in joint roughness coefficient (JRC) and its engineering applications. J. Rock Mech. Geotech. Eng. 2023, 15, 3352–3379. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, G.; Jiang, Y.; Wang, C.; Xu, F. Shear behaviours and roughness degeneration based on a quantified rock joint surface description. Int. J. Min. Sci. Technol. 2023, 33, 1301–1316. [Google Scholar] [CrossRef]
- Tang, Y.; Ranjith, P.G. An experimental and analytical study of the effects of shear displacement, fluid type, joint roughness, shear strength, friction angle and dilation angle on proppant embedment development in tight gas sandstone reservoirs. Int. J. Rock Mech. Min. Sci. 2018, 107, 94–109. [Google Scholar] [CrossRef]
- Liu, Q.; Tian, Y.; Liu, D.; Jiang, Y. Updates to JRC-JCS model for estimating the peak shear strength of rock joints based on quantified surface description. Eng. Geol. 2017, 228, 282–300. [Google Scholar] [CrossRef]
- Shen, H.; Liu, Y.; Li, H.; Wu, D.; Xia, X.; Liu, B.; Yu, C. Rate-Dependent Characteristics of Damage and Roughness Degradation of Three-Dimensional Artificial Joint Surfaces. Rock Mech. Rock Eng. 2022, 55, 2221–2237. [Google Scholar] [CrossRef]
- Barton, N.; Bandis, S.; Bakhtar, K. Strength, deformation and conductivity coupling of rock joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 121–140. [Google Scholar] [CrossRef]
- Hou, J.; Zhao, H.; Peng, W.; Zhao, M. A limit solution for predicting side resistance on rock-socketed piles. J. Eng. Mech. 2022, 148, 04021131. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, Q.; Elsworth, D.; Zhao, Q. Competing Effects of Proppant and Surface Roughness on the Frictional Stability of Propped Fractures. Rock Mech. Rock Eng. 2023, 56, 2923–2934. [Google Scholar] [CrossRef]
- Yang, K.; Hu, Q.; Zhao, H.; Zhao, M.; Zhou, S. Numerical study on the shear behavior of concrete-rock joints with similar triangular asperities. Comput. Geotech. 2023, 159, 105468. [Google Scholar] [CrossRef]
- Ban, L.; Qi, C.; Chen, H.; Yan, F.; Ji, C. A new criterion for peak shear strength of rock joints with a 3D roughness parameter. Rock Mech. Rock Eng. 2020, 53, 1755–1775. [Google Scholar] [CrossRef]
- Zhu, X.; Gao, M.; Si, G.; Zhang, C.; Moon, J.S.; Oh, J. An Improved Model for Evaluating the Hydraulic Behaviour of a Single Rock Joint Considering Contact Area Evolution During Shearing. Rock Mech. Rock Eng. 2023, 56, 8723–8743. [Google Scholar] [CrossRef]
- Olsson, R.; Barton, N. An improved model for hydromechanical coupling during shearing of rock joints. Int. J. Rock Mech. Min. Sci. 2001, 38, 317–329. [Google Scholar] [CrossRef]
- Grasselli, G. Manuel Rocha medal recipient shear strength of rock joints based on quantified surface description. Rock Mech. Rock Eng. 2006, 39, 295–314. [Google Scholar] [CrossRef]








| Proppant | Pro_No | Pro_0.1 | Pro_0.5 | Pro_1.0 | ||
|---|---|---|---|---|---|---|
| Vertical Load | 40 kN | 80 kN | 40 kN | 40 kN | 40 kN | 80 kN |
| JRC: 4–6 | No.1 | No.17 | No.5 | No.9 | No.13 | No.21 |
| JRC: 10–12 | No.2 | No.18 | No.6 | No.10 | No.14 | No.22 |
| JRC: 14–16 | No.3 | No.19 | No.7 | No.11 | No.15 | No.23 |
| JRC: 18–20 | No.4 | No.20 | No.8 | No.12 | No.16 | No.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Luo, J.; Wang, S.; Zhu, J.; Cui, D. Shear Behavior of Two-Dimensional Propped Rough Fractures. Energies 2024, 17, 956. https://doi.org/10.3390/en17040956
Zhang Q, Luo J, Wang S, Zhu J, Cui D. Shear Behavior of Two-Dimensional Propped Rough Fractures. Energies. 2024; 17(4):956. https://doi.org/10.3390/en17040956
Chicago/Turabian StyleZhang, Qi, Jin Luo, Sai Wang, Jinsong Zhu, and Deshan Cui. 2024. "Shear Behavior of Two-Dimensional Propped Rough Fractures" Energies 17, no. 4: 956. https://doi.org/10.3390/en17040956
APA StyleZhang, Q., Luo, J., Wang, S., Zhu, J., & Cui, D. (2024). Shear Behavior of Two-Dimensional Propped Rough Fractures. Energies, 17(4), 956. https://doi.org/10.3390/en17040956







