A Study on the Transient Response of Compressed Air Energy Storage in the Interaction between Gas Storage Chambers and Horseshoe-Shaped Tunnels in an Abandoned Coal Mine
Abstract
1. Introduction
2. Dynamics of Production Injection Cycle and Thermo-Solid Coupling Theory
3. Establishment and Verification of a Model for a Group of Compressed Air Energy Storage Chambers in Abandoned Coal Mines
4. Mechanical Response of Chamber Boundary during One Cycle
5. Overall Mechanical Responses of a Group of Chambers during One Cycle
6. Conclusions
- (1)
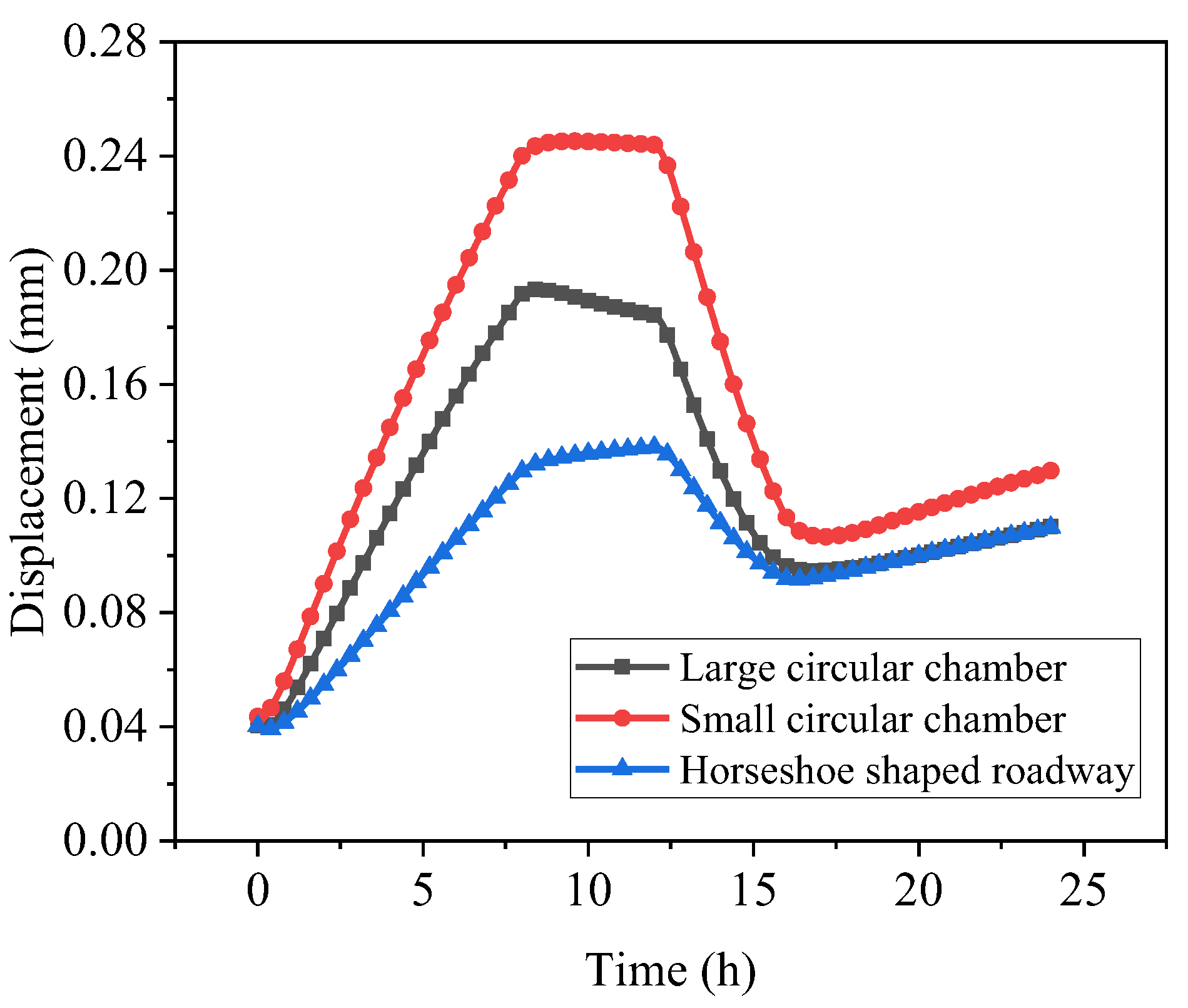
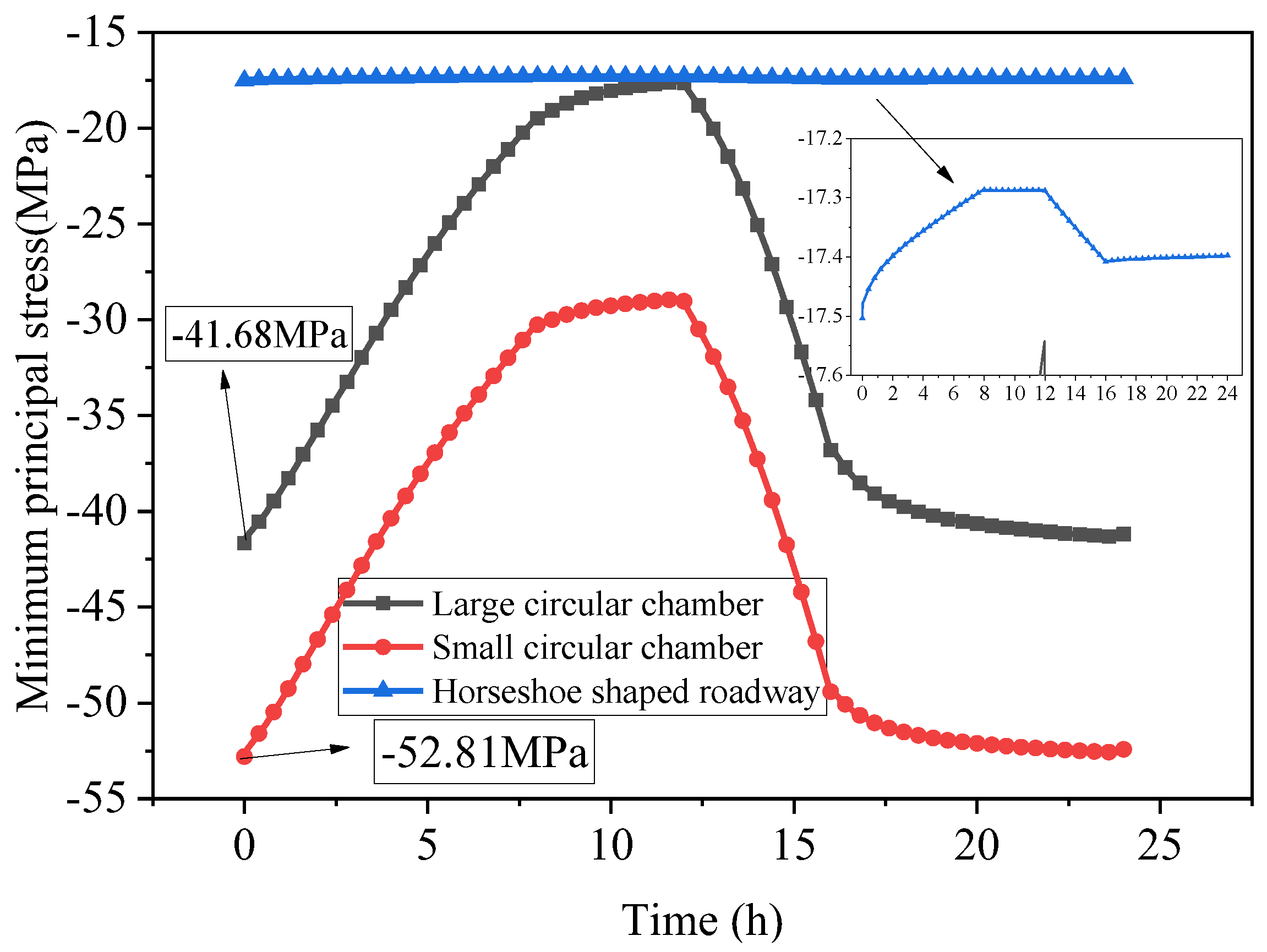
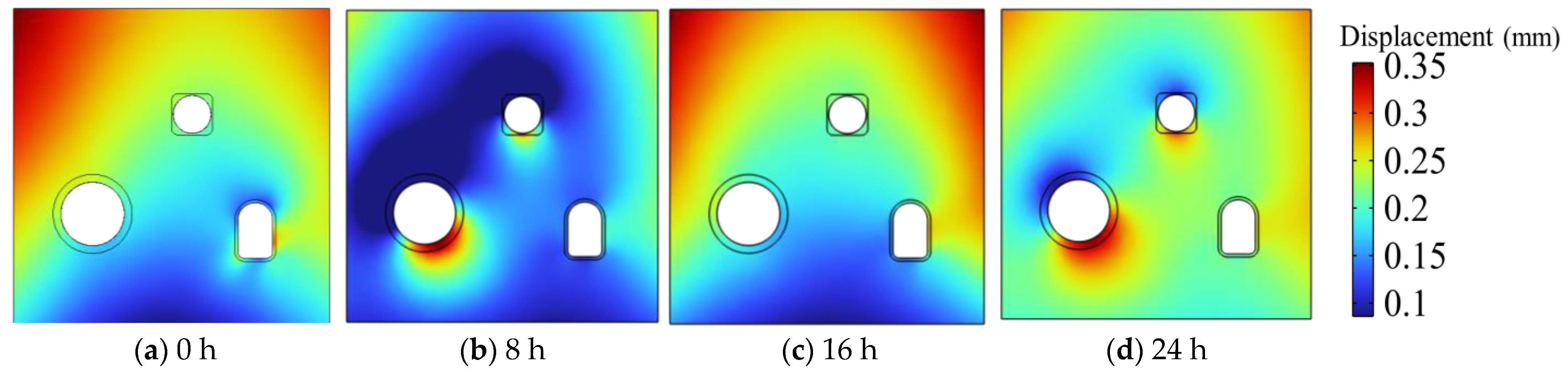
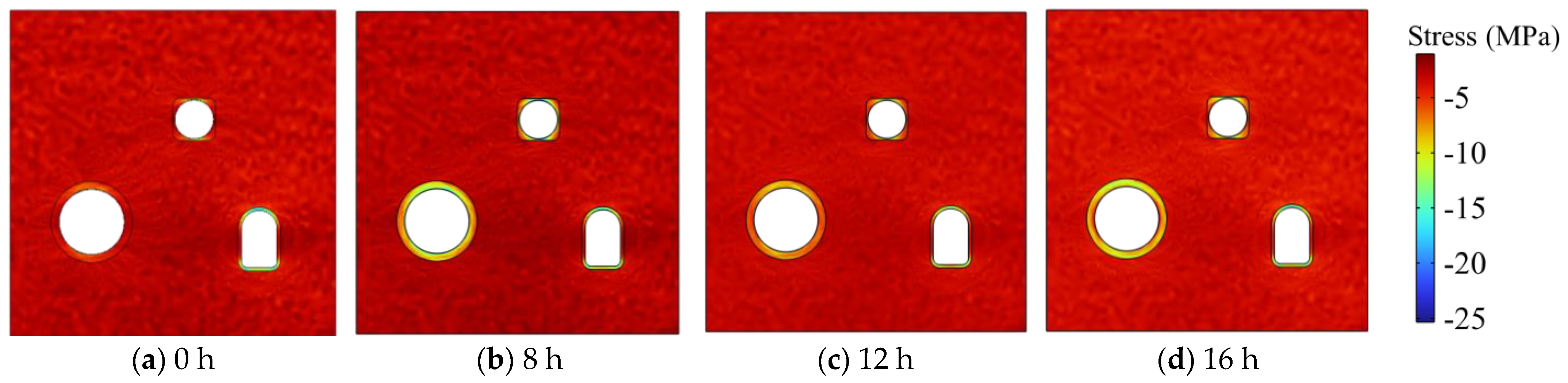
- The small circular chamber exhibited the most significant deformation, with an average displacement peak of 0.24 mm. This was followed by the large circular chamber and the horseshoe-shaped tunnel. The maximum displacement of the boundary between the small and large circular chambers peaked after inflation was completed. Peak displacements of the large and small circular chambers were concentrated at the chamber top, while the horseshoe-shaped roadway peaked after deflation was completed. This suggests a lag in displacement change for the horseshoe-shaped roadway.
- (2)
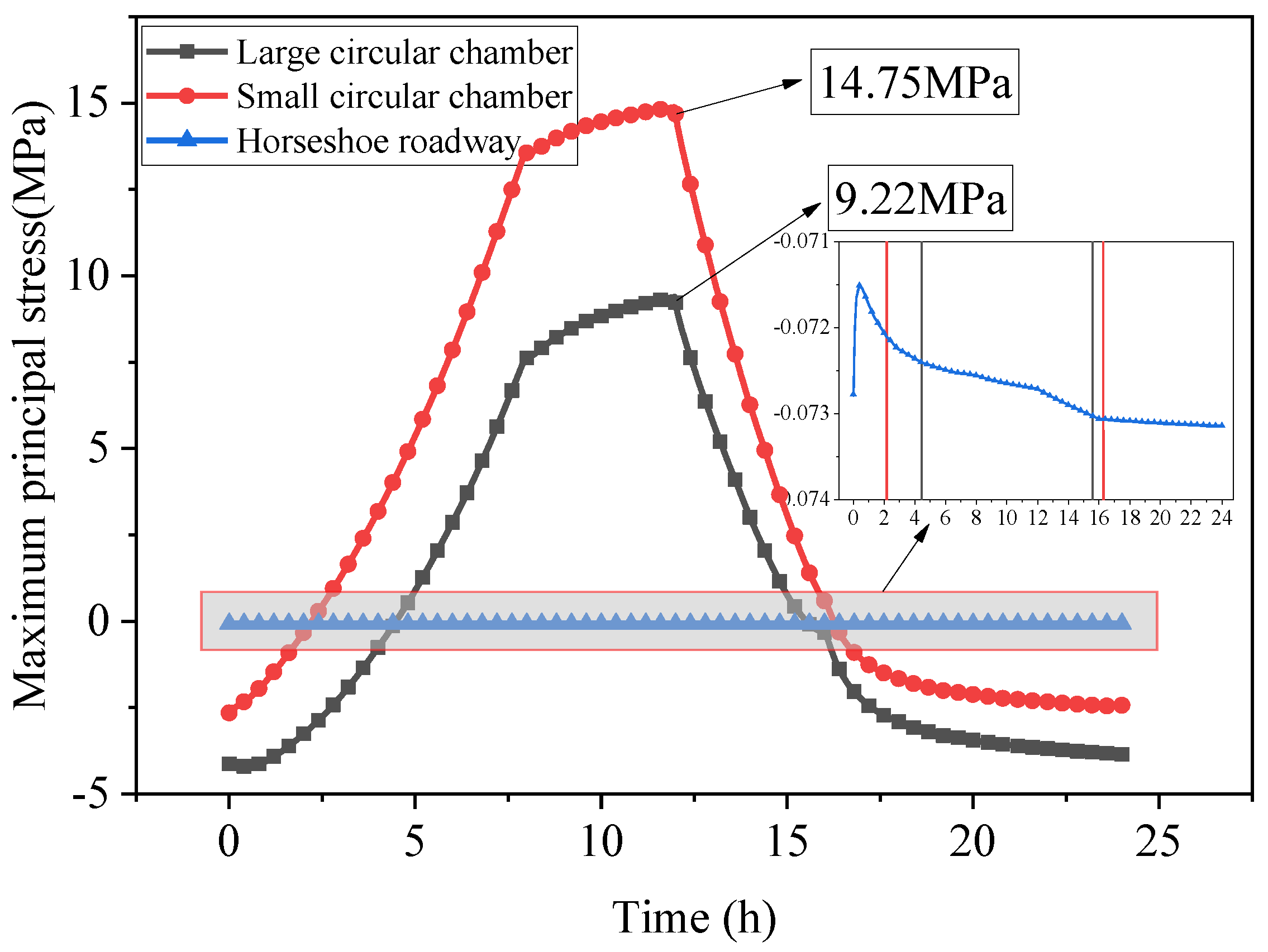
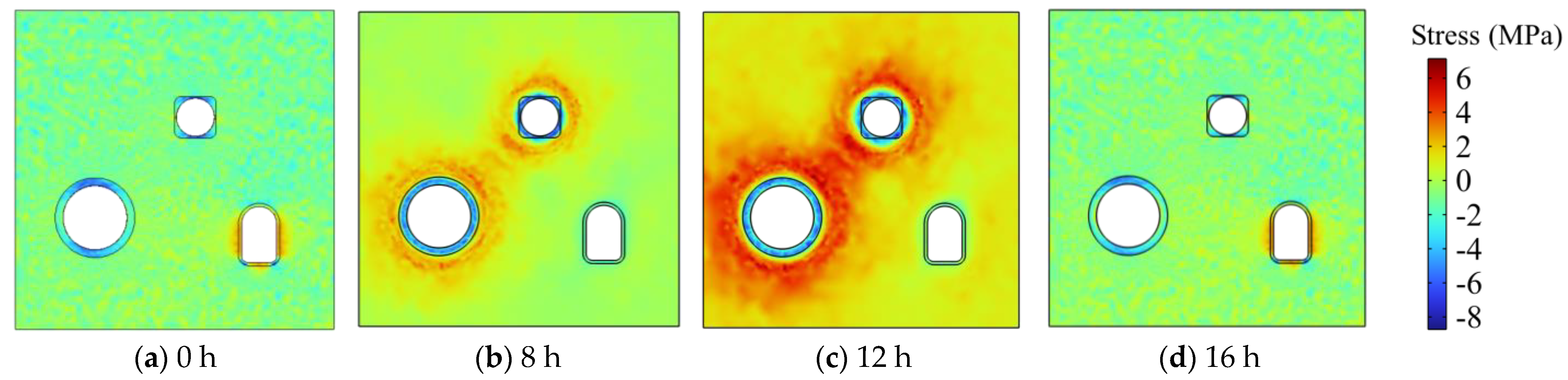
- The small circular chamber exhibited maximum tensile and compressive stresses. At the end of inflation and deflation, the maximum tensile stress primarily concentrated around the gas storage chamber. After deflation, the point of maximum tensile stress shifted to the left and right sides of the horseshoe-shaped tunnel.
- (3)
- The stress and displacement of the small circular chamber indicate that it is more prone to failure. Additionally, measures should be taken to reinforce the horseshoe-shaped roadway, particularly its left and right sides, to prevent damage caused by tensile stress during deflation. Reinforcement of the upper and lower sides is also necessary to prevent damage from compressive stress during deflation.
- (4)
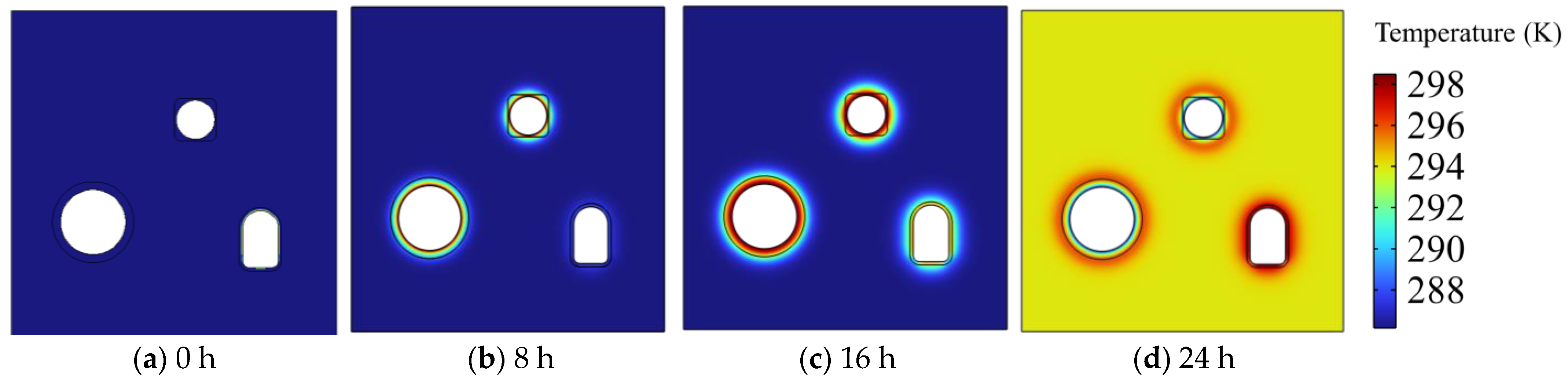
- The continuous charging and discharging of the two chambers of the gas storage tank in the energy storage cavern group results in continuous temperature changes throughout the entire cycle. Therefore, when considering multiple cycles, the influence of thermal stress should be taken into account. Additionally, the horseshoe-shaped roadway remains connected to external air, leading to temperature migration and changes. This study observed a similar temperature delay phenomenon during the calculations that is consistent with the understanding that temperature requires time to transfer when it changes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Li, J.; Wang, G.; Li, Z.; Yang, S.; Chong, W.T.; Xiang, X. A review on development of offshore wind energy conversion system. Int. J. Energy Res. 2020, 44, 9283–9297. [Google Scholar] [CrossRef]
- Wang, S.; Sun, L.; Iqbal, S. Green financing role on renewable energy dependence and energy transition in E7 economies. Renew. Energy 2022, 200, 1561–1572. [Google Scholar] [CrossRef]
- Yang, J.; Wang, J.; Hu, B. Numerical analysis of the impacts of multiscale fractures on geothermal reservoir capacity. J. Energy Eng. 2023, 149, 04023046. [Google Scholar] [CrossRef]
- Wu, X.; Cai, M.; Wu, X.; Zhang, K.; Yin, Z.; Zhu, Y. Impact of well placement and flow rate on production efficiency and stress field in the fractured geothermal reservoirs. Deep Undergr. Sci. Eng. 2023. [Google Scholar] [CrossRef]
- Ye, Z.; Wang, J.G.; Yang, J. A multi-objective optimization approach for a fault geothermal system based on response surface method. Geothermics 2024, 117, 102887. [Google Scholar] [CrossRef]
- Behabtu, H.A.; Vafaeipour, M.; Kebede, A.A.; Berecibar, M.; Van Mierlo, J.; Fante, K.A.; Messagie, M.; Coosemans, T. Smoothing intermittent output power in grid-connected doubly fed induction generator wind turbines with li-ion batteries. Energies 2023, 16, 7637. [Google Scholar] [CrossRef]
- Sun, R.; Wang, J. Effects of in situ stress and multiborehole cluster on hydraulic fracturing of shale gas reservoir from multiscale perspective. J. Energy Eng. 2024, 150, 04024002. [Google Scholar] [CrossRef]
- Li, P.; Wang, J.; Liang, W.; Sun, R. An analytical and numerical analysis for hydraulic fracture propagation through reservoir interface in coal-measure superimposed reservoirs. Sustainability 2023, 15, 4597. [Google Scholar] [CrossRef]
- Liang, W.; Wang, J.; Li, P.; Leung, C.; Goh, S.; Sang, S. New insight to interlayer interference during three-gas co-production based on a wellbore–reservoir coupling model. Nat. Resour. Res. 2023, 32, 2037–2052. [Google Scholar] [CrossRef]
- Liang, W.; Wang, J.G.; Leung, C.F.; Goh, S.; Li, P. Impact of crossflow and two-phase flow on gas production from stacked deposits. Energy Fuels 2023, 37, 8935–8948. [Google Scholar] [CrossRef]
- Martirosyan, A.V.; Ilyushin, Y.V. The Development of the Toxic and Flammable Gases Concentration Monitoring System for Coalmines. Energies 2022, 15, 8917. [Google Scholar] [CrossRef]
- Wang, J.; Wang, H.; Wang, X.; Yang, S.; Wu, H.; Leung, C.; Tian, J. A multiphysical-geochemical coupling model for caprock sealing efficiency in CO2 geosequestration. Deep Undergr. Sci. Eng. 2023, 2, 188–203. [Google Scholar] [CrossRef]
- Bekebrok, H.; Langnickel, H.; Pluta, A.; Zobel, M.; Dyck, A. Underground storage of green hydrogen—boundary conditions for compressor systems. Energies 2022, 15, 5972. [Google Scholar] [CrossRef]
- Vandeginste, V.; Ji, Y.; Buysschaert, F.; Anoyatis, G. Mineralogy, microstructures and geomechanics of rock salt for underground gas storage. Deep Undergr. Sci. Eng. 2023, 2, 129–147. [Google Scholar] [CrossRef]
- Qi, X.; Guo, P.; Guo, Y.; Liu, X.; Zhou, X. Understanding energy efficiency and its drivers: An empirical analysis of China’s 14 coal intensive industries. Energy 2020, 190, 116354. [Google Scholar] [CrossRef]
- Li, R.; Tang, B.J.; Yu, B.; Liao, H.; Zhang, C.; Wei, Y.M. Cost-optimal operation strategy for integrating large scale of renewable energy in China’s power system: From a multi-regional perspective. Appl. Energy 2022, 325, 119780. [Google Scholar] [CrossRef]
- Li, J.; Ho, M.S.; Xie, C.; Stern, N. China’s flexibility challenge in achieving carbon neutrality by 2060. Renew. Sustain. Energy Rev. 2022, 158, 112112. [Google Scholar] [CrossRef]
- Wu, D.; Wang, J.G.; Hu, B.W.; Yang, S.Q. A coupled thermo-hydro-mechanical model for evaluating air leakage from an unlined compressed air energy storage cavern. Renew. Energy 2020, 146, 907–920. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J.G. Stability analysis for compressed air energy storage cavern with initial excavation damage zone in an abandoned mining tunnel. J. Energy Storage 2022, 45, 103725. [Google Scholar] [CrossRef]
- Sun, R.; Wang, J.; Zhang, K.; Li, F.; Ding, X.; Guo, Q. Stress redistribution in a multilayer chamber for compressed air energy storage in abandoned coalmine: Elastic analytical insights and material choice. Energy Sci. Eng. 2023, 11, 4198–4223. [Google Scholar] [CrossRef]
- Polański, K. Influence of the variability of compressed air temperature on selected parameters of the deformation-stress state of the rock mass around a CAES salt cavern. Energies 2021, 14, 6197. [Google Scholar] [CrossRef]
- Xu, M.; Wang, X.; Wang, Z.; Zhao, P.; Dai, Y. Preliminary design and performance assessment of compressed supercritical carbon dioxide energy storage system. Appl. Therm. Eng. 2021, 183, 116153. [Google Scholar] [CrossRef]
- Rutqvist, J.; Kim, H.M.; Ryu, D.W.; Synn, J.H.; Song, W.K. Modeling of coupled thermodynamic and geomechanical performance of underground compressed air energy storage in lined rock caverns. Int. J. Rock Mech. Min. Sci. 2012, 52, 71–81. [Google Scholar] [CrossRef]
- Crotogino, F.; Mohmeyer, K.U.; Scharf, R. Huntorf CAES: More than 20 Years of Successful Operation. In Proceedings of the Solution Mining Research Institute (SMRI) Spring Meeting, Orlando, FL, USA, 15–18 April 2001; pp. 1–7. [Google Scholar]
- Olabi, A.G.; Wilberforce, T.; Ramadan, M.; Abdelkareem, M.A.; Alami, A.H. Compressed air energy storage systems: Components and operating parameters—A review. J. Energy Storage 2021, 34, 102000. [Google Scholar] [CrossRef]
- King, M.; Jain, A.; Bhakar, R.; Mathur, J.; Wang, J. Overview of current compressed air energy storage projects and analysis of the potential underground storage capacity in India and the UK. Renew. Sustain. Energy Rev. 2021, 139, 110705. [Google Scholar] [CrossRef]
- Stille, H.; Johansson, J.; Sturk, R. High pressure storage of gas in lined shallow rock caverns—Results from field tests. In Proceedings of the Rock Mechanics in Petroleum Engineering, Delft, The Netherlands, 29–31 August 1994. [Google Scholar]
- Chen, L.; Zheng, T.; Mei, S.; Xue, X.; Liu, B.; Lu, Q. Review and prospect of compressed air energy storage system. J. Mod. Power Syst. Clean Energy 2016, 4, 529–541. [Google Scholar] [CrossRef]
- Tong, Z.; Cheng, Z.; Tong, S. A review on the development of compressed air energy storage in China: Technical and economic challenges to commercialization. Renew. Sustain. Energy Rev. 2021, 135, 110178. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, S.W.; Xia, C.C.; Zhao, H.; Xue, X. Three-dimensional thermo-mechanical analysis of abandoned mine drifts for underground compressed air energy storage: A comparative study of two construction and plugging schemes. J. Energy Storage 2021, 39, 102696. [Google Scholar] [CrossRef]
- Li, J.; Wan, J.; Liu, H.; Jurado, M.J.; He, Y.; Yuan, G.; Xia, Y. Stability analysis of a typical salt cavern gas storage in the Jintan area of China. Energies 2022, 15, 4167. [Google Scholar] [CrossRef]
- Lyu, X.; Yang, K.; Fang, J. Utilization of resources in abandoned coal mines for carbon neutrality. Sci. Total Environ. 2022, 822, 153646. [Google Scholar] [CrossRef] [PubMed]
- Perazzelli, P.; Anagnostou, G. Design issues for compressed air energy storage in sealed underground cavities. J. Rock Mech. Geotech. Eng. 2016, 8, 314–328. [Google Scholar] [CrossRef]
- Xia, C.C.; Zhou, Y.; Zhou, S.W.; Zhang, P.; Wang, F. A simplified and unified analytical solution for temperature and pressure variations in compressed air energy storage caverns. Renew. Energy 2015, 74, 718–726. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, P.; Tang, D.; Zhao, H.; Li, Y. Experimental and numerical investigations of small-scale lined rock cavern at shallow depth for compressed air energy storage. Rock Mech. Rock Eng. 2020, 53, 2671–2683. [Google Scholar] [CrossRef]
- Wan, F.; Jiang, Z.; Tian, X.; Konietzky, H.; Xiao, Z. A thermo-hydro-mechanical damage model for lined rock cavern for compressed air energy storage. J. Energy Storage 2024, 78, 110186. [Google Scholar] [CrossRef]
- Damjanac, B.; Carranza-Torres, C.; Dexter, R. Technical review of the lined rock caverns (LRC) concept and design methodology steel liner response. Minnesota 2002, 32, 59–70. [Google Scholar]
- Kim, H.M.; Rutqvist, J.; Jeong, J.H.; Choi, B.H.; Ryu, D.W.; Song, W.K. Characterizing excavation damaged zone and stability of pressurized lined rock caverns for underground compressed air energy storage. Rock Mech. Rock Eng. 2012, 46, 1113–1124. [Google Scholar] [CrossRef]
- Mortazavi, A.; Molladavoodi, H. A numerical investigation of brittle rock damage model in deep underground openings. Eng. Fract. Mech. 2012, 90, 101–120. [Google Scholar] [CrossRef]
- Kushnir, R.; Dayan, A.; Ullmann, A. Temperature and pressure variations within compressed air energy storage caverns. Int. J. Heat Mass Transf. 2012, 55, 5616–5630. [Google Scholar] [CrossRef]
- Hu, B.W.; Wang, J.G.; Li, Z.Q.; Wang, H.M. Evolution of fractal dimensions and gas transport models during the gas recovery process from a gractured shale reservoir. Fractals 2019, 27, 1950129. [Google Scholar] [CrossRef]
- Martino, J.B.; Chandler, N.A. Excavation-induced damage studies at the underground research laboratory. Int. J. Rock Mech. Min. Sci. 2004, 41, 1413–1426. [Google Scholar] [CrossRef]
- Kim, H.M.; Rutqvist, J.; Ryu, D.W.; Choi, B.H.; Sunwoo, C.; Song, W.K. Exploring the concept of compressed air energy storage (CAES) in lined rock caverns at shallow depth: A modeling study of air tightness and energy balance. Appl. Energy 2012, 92, 653–667. [Google Scholar] [CrossRef]
- Wang, Z.H.; Yang, S.L.; Tang, Y.S. Mechanical behavior of different sedimentary rocks in the Brazilian test. Bull. Eng. Geol. Environ. 2020, 79, 5415–5432. [Google Scholar] [CrossRef]


| Position | Lithology and Changes | Rock Type | Stability |
|---|---|---|---|
| Roof | The direct roof is mainly composed of mudstone and sandy mudstone, with a thickness of 1.54–10.8 m and an average of 3.96 m. The thickness of sandstone is 5.99–22.1 m with an average of 12.9 m. | Mudstone | Unstable to moderately stable |
| Sandy mudstone | |||
| Floor | The direct bottom plate is limestone with a thickness of 0–2.45 m. The pseudo bottom is mudstone with a thickness of 0.1 m to 0.6 m. | Limestone | Moderately stable to sturdy |
| Parameters (Variables, Units) | Numerical Value | Parameter Source |
|---|---|---|
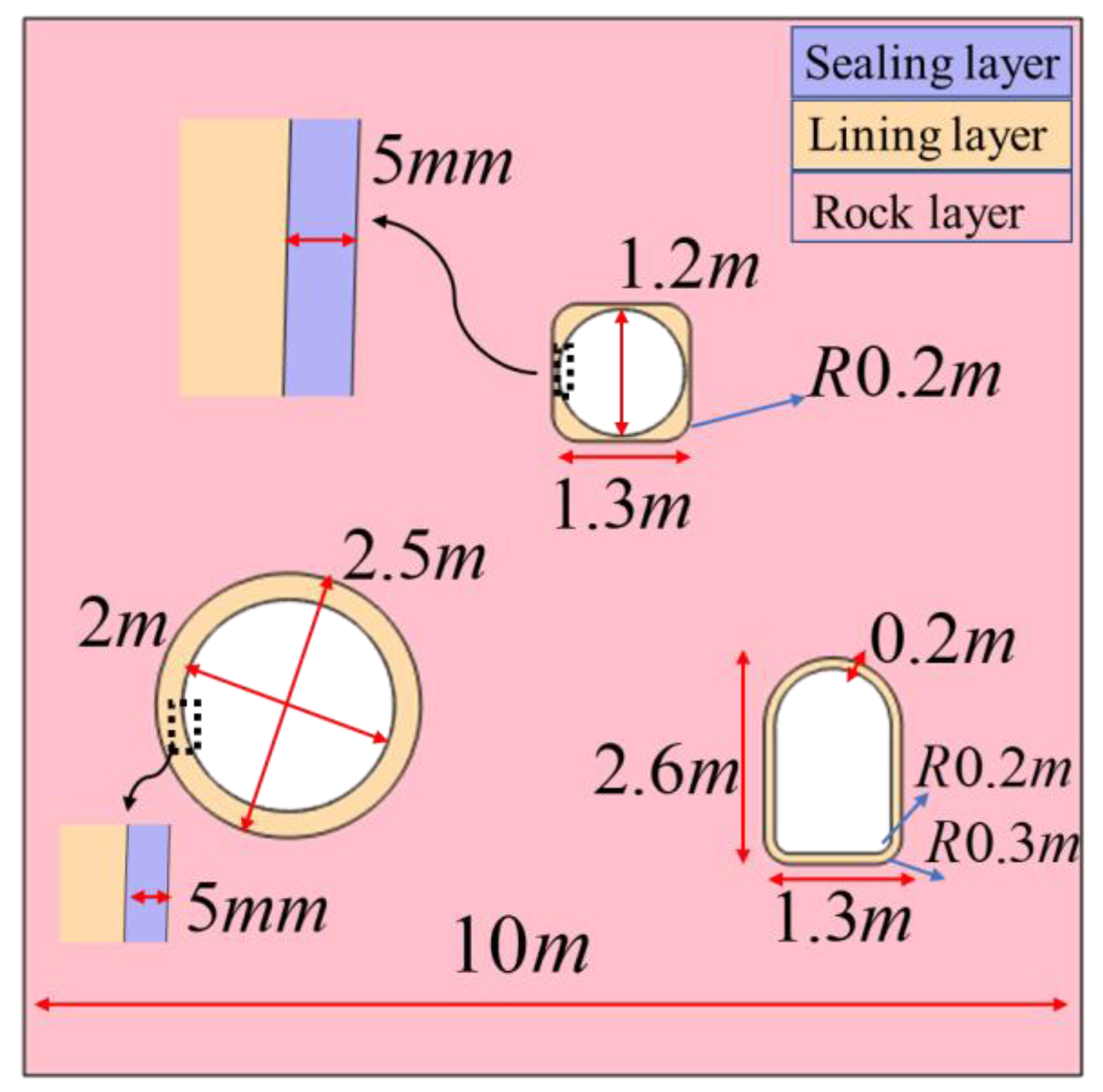
| Chamber radius, R1 (m) | 2.5 | Wu et al. [19] |
| Chamber length, H (m) | 5.093 × 103 | Wu et al. [19] |
| Surface area of the chamber, Ac (m2) | 8 × 104 | Wu et al. [19] |
| Chamber volume, V (m3) | 1 × 105 | Wu et al. [19] |
| Charge gas temperature, Ti (K) | 294.65 | Wu et al. [19] |
| Gas mass flow rate, mie (kg/s) | 100 | Wu et al. [19] |
| Heat exchange coefficient, hc (W/(m2·K)) | 30 | Wu et al. [19] |
| Initial pressure of the chamber, Pc0 (Pa) | 5 × 106 | Wu et al. [19] |
| Initial temperature of the chamber, T0 (K) | 286.15 | Wu et al. [19] |
| Initial permeability of rocks, k0 = kd0 (m2) | 1 × 10−17 | Martino et al. [43] |
| Initial porosity of rocks, ϕ0 = ϕd0 | 0.01 | Kim et al. [44] |
| Young’s modulus of rock, E = Ed (GPa) | 13.5 | Sun et al. [21] |
| Poisson’s ratio of rocks, ν | 0.3 | Kim et al. [44] |
| Rock density, ρs (kg/m3) | 2700 | Kim et al. [44] |
| Tensile strength of rocks, σt (MPa) | 13.4 | Wang et al. [45] |
| Rock thermal expansion coefficient, αT (1/K) | 1 × 10−5 | Kim et al. [44] |
| Rock thermal conductivity, βr (J/(m·s·K)) | 3 | Kim et al. [44] |
| Rock specific heat capacity, Cr (J/(kg·K)) | 0.9 × 103 | Kim et al. [44] |
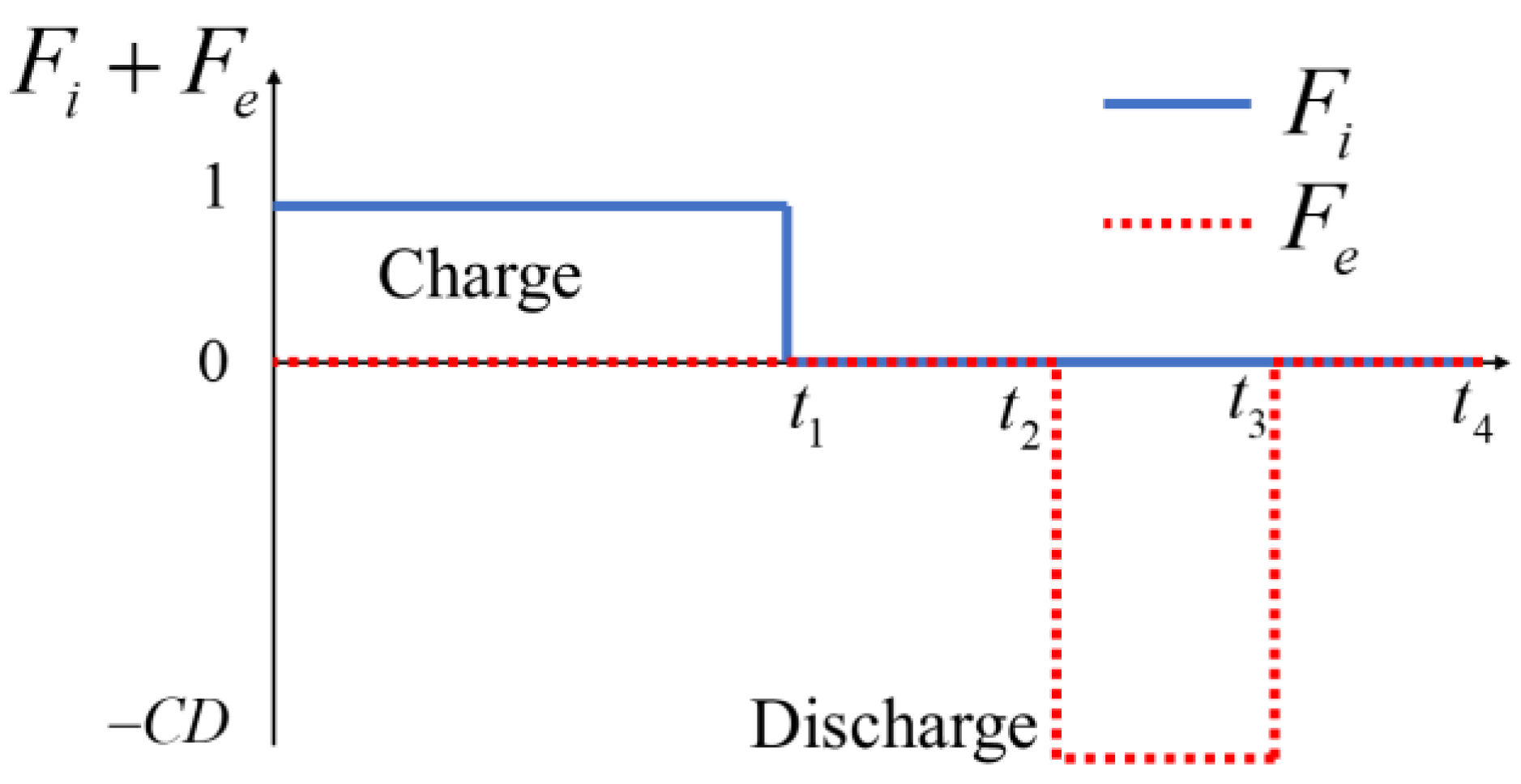
| Time point, t1 (h) | 8 | Kim et al. [44] |
| Time point, t2 (h) | 12 | Kim et al. [44] |
| Time point, t3 (h) | 16 | Kim et al. [44] |
| Time point, tp (h) | 24 | Kim et al. [44] |
| Sealing Layer | Lining Layer | Rock Layer | |
|---|---|---|---|
| E (GPa) | 210 | 35 | 13.7 |
| v | 0.27 | 0.25 | 0.24 |
| ρ (kg/m3) | 7800 | 2500 | 2000 |
| α (1/K) | 8 × 10−6 | 1.2 × 10−5 | 1.0 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Li, F.; Sun, R.; Zheng, J.; Li, X.; Shen, L.; Sun, Q.; Liu, Y.; Ji, Y.; Duan, Y. A Study on the Transient Response of Compressed Air Energy Storage in the Interaction between Gas Storage Chambers and Horseshoe-Shaped Tunnels in an Abandoned Coal Mine. Energies 2024, 17, 953. https://doi.org/10.3390/en17040953
Li F, Li F, Sun R, Zheng J, Li X, Shen L, Sun Q, Liu Y, Ji Y, Duan Y. A Study on the Transient Response of Compressed Air Energy Storage in the Interaction between Gas Storage Chambers and Horseshoe-Shaped Tunnels in an Abandoned Coal Mine. Energies. 2024; 17(4):953. https://doi.org/10.3390/en17040953
Chicago/Turabian StyleLi, Fuqing, Fufeng Li, Rui Sun, Jianjie Zheng, Xiaozhao Li, Lan Shen, Qiang Sun, Ying Liu, Yukun Ji, and Yinhang Duan. 2024. "A Study on the Transient Response of Compressed Air Energy Storage in the Interaction between Gas Storage Chambers and Horseshoe-Shaped Tunnels in an Abandoned Coal Mine" Energies 17, no. 4: 953. https://doi.org/10.3390/en17040953
APA StyleLi, F., Li, F., Sun, R., Zheng, J., Li, X., Shen, L., Sun, Q., Liu, Y., Ji, Y., & Duan, Y. (2024). A Study on the Transient Response of Compressed Air Energy Storage in the Interaction between Gas Storage Chambers and Horseshoe-Shaped Tunnels in an Abandoned Coal Mine. Energies, 17(4), 953. https://doi.org/10.3390/en17040953






