Study on the Thermal Field of a Hydro-Generator under the Effect of a Plateau Climate
Abstract
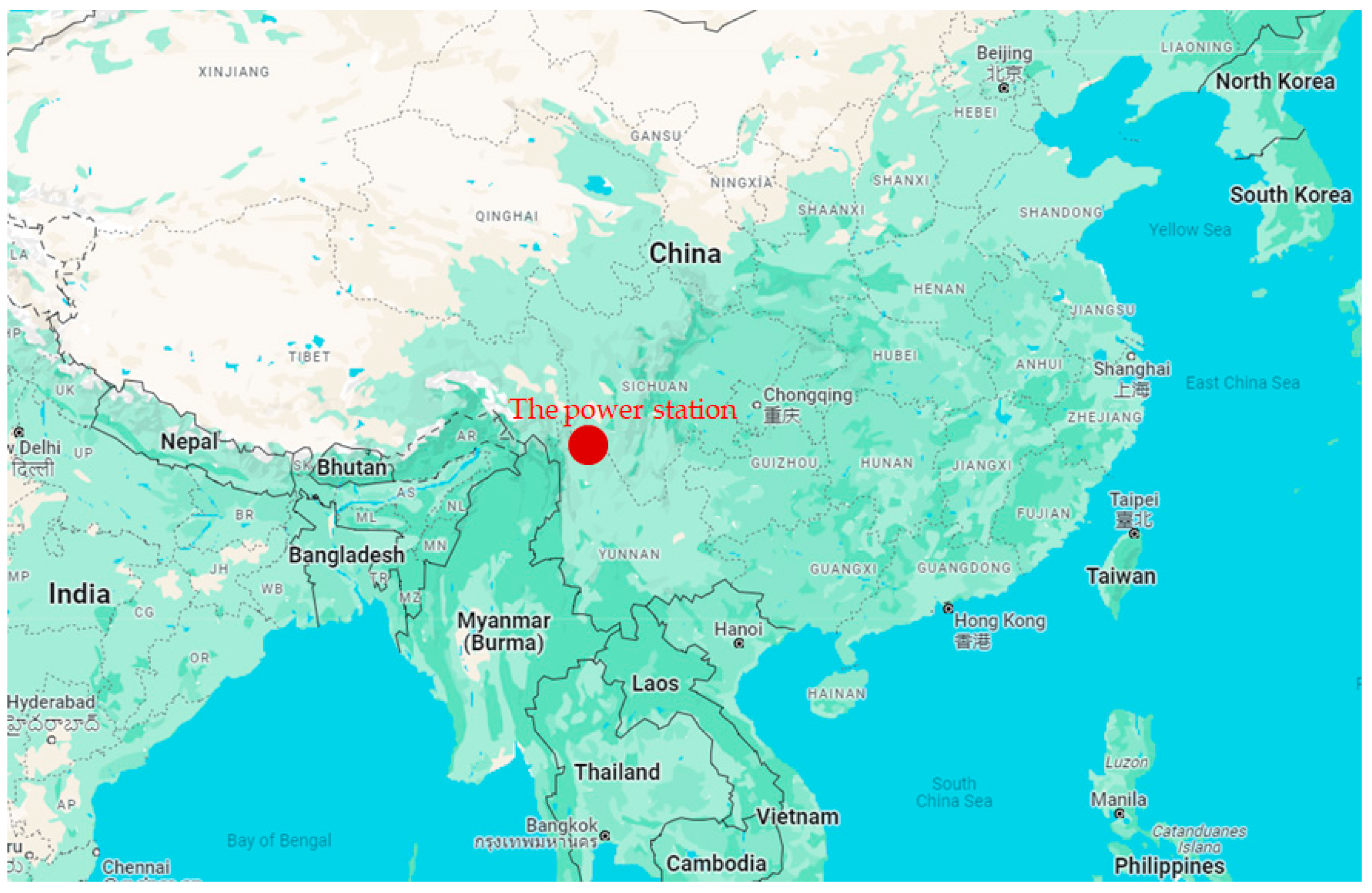
1. Introduction
2. Mathematical Model
2.1. Problem Statement
2.2. Mathematical Formulas
2.3. Boundary Conditions
2.4. Basic Assumptions
- (1)
- The fluid inside the hydro-generator has a large Reynolds number (Re > 2300) and its flow field is solved using a turbulent flow model [26];
- (2)
- Since the fluid flow velocity inside the turbine is much smaller than the speed of sound, the Mach number (Ma) is very small, Ma < 0.3, and the fluid is treated as an incompressible fluid [27];
- (3)
- (4)
- The thermal conductivity equation does not include a time term as only the steady-state of the fluid flow in the generator is studied, i.e., constant flow [26];
- (5)
- The losses in the tooth and yoke of the stator core are evenly distributed [29];
- (6)
- The air in the air gap is equated to a medium with only thermal conductivity efficacy, and the thermal conductivity is determined according to the results of the study by DANG D-D et al. [21].
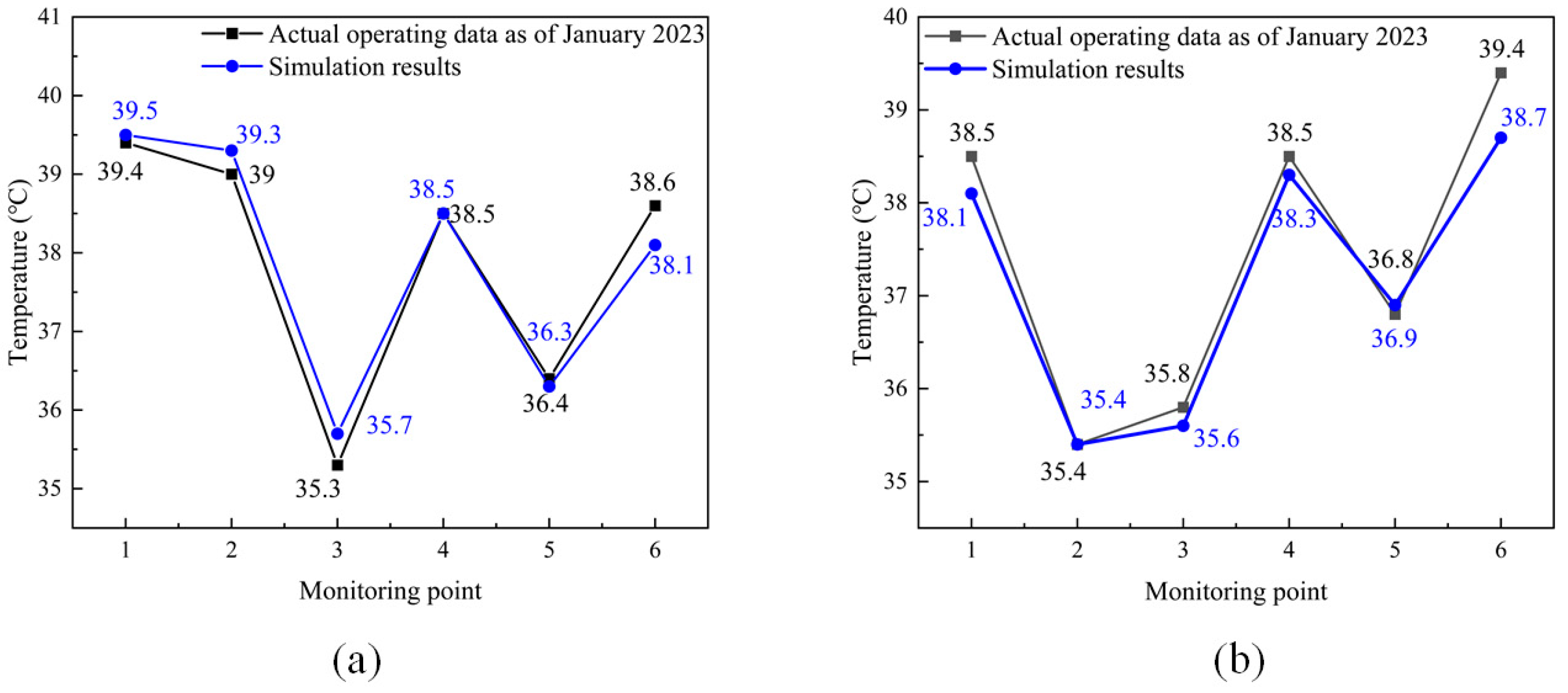
2.5. Numerical Validation
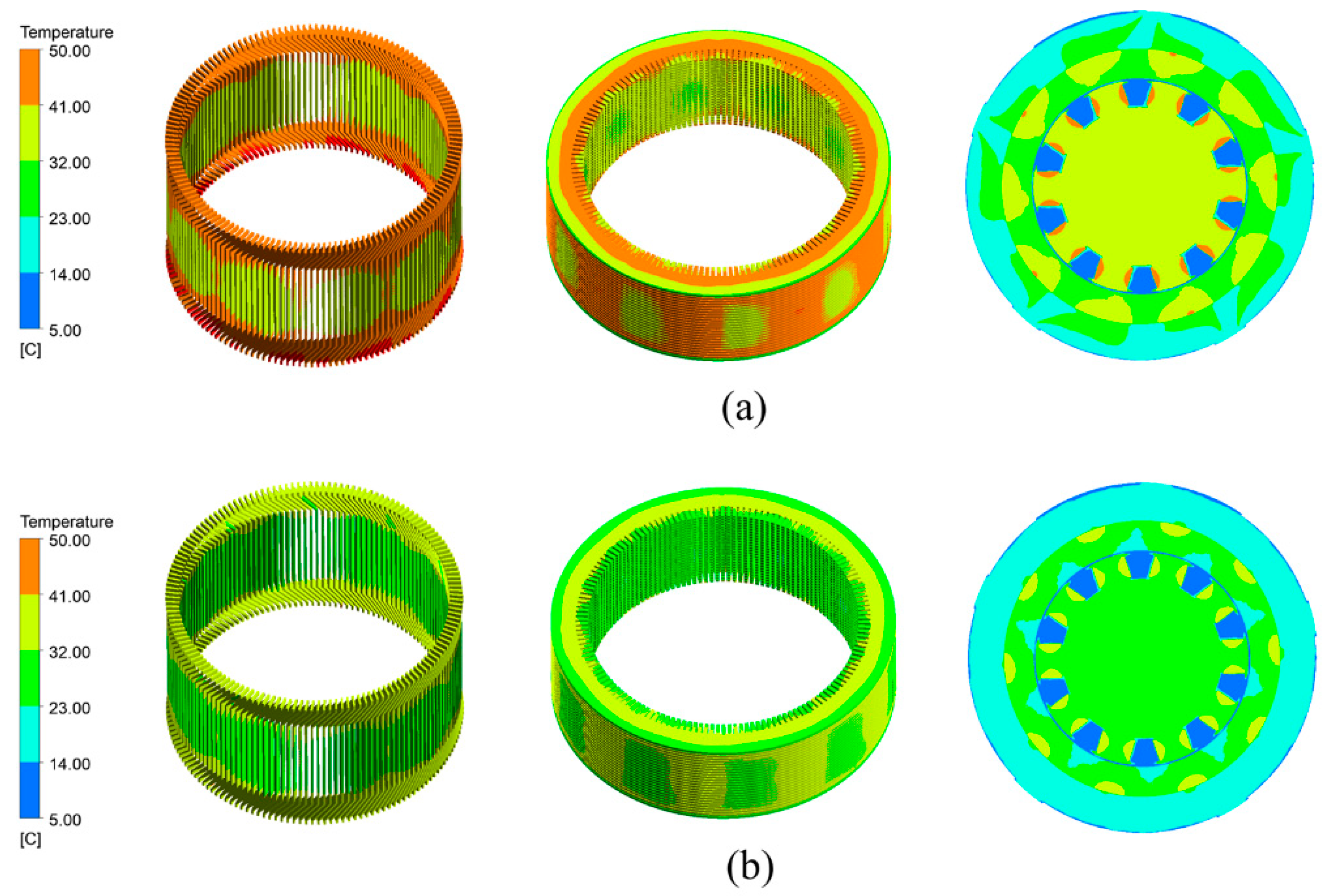
3. Discussion and Results
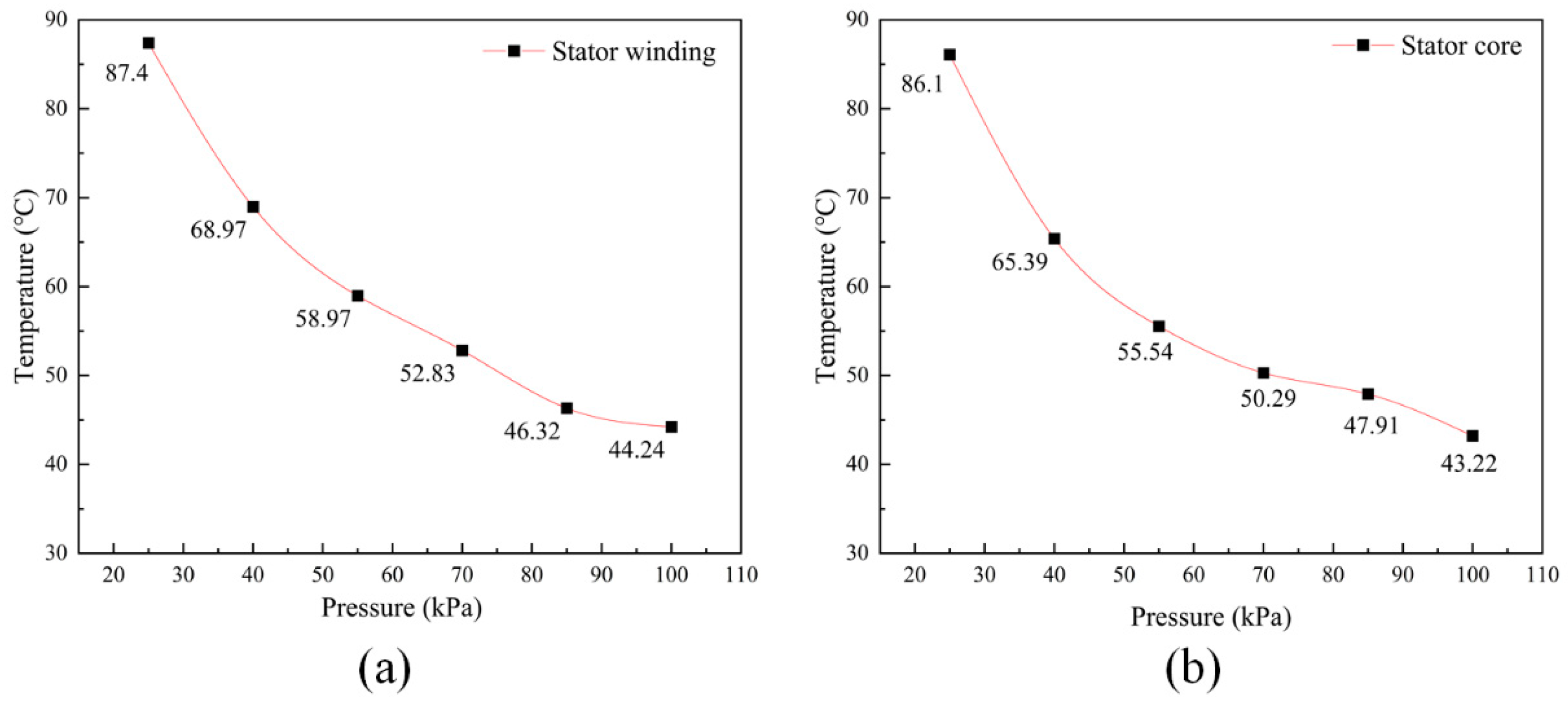
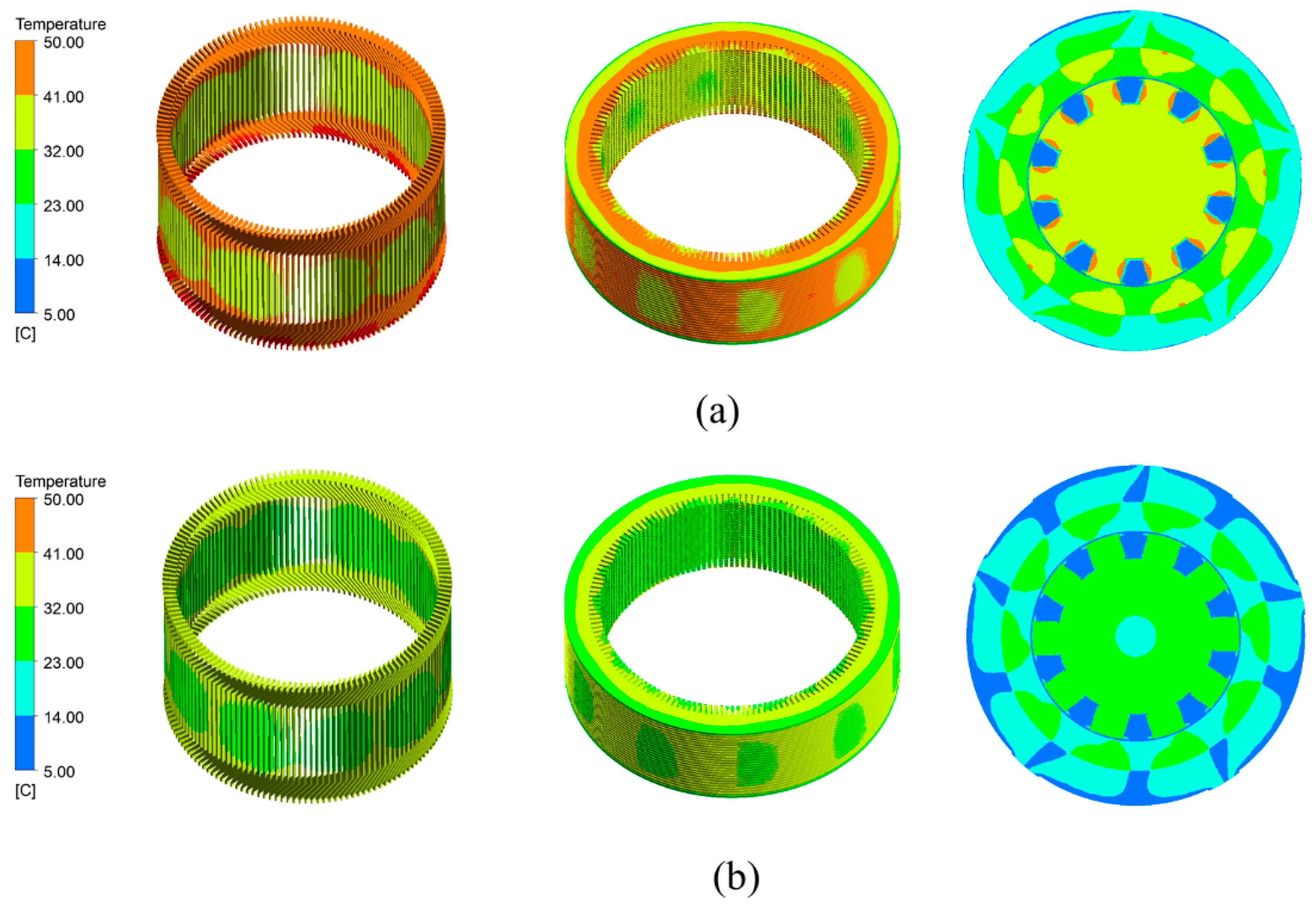
3.1. Temperature Distribution of Generators at Different Air Pressures
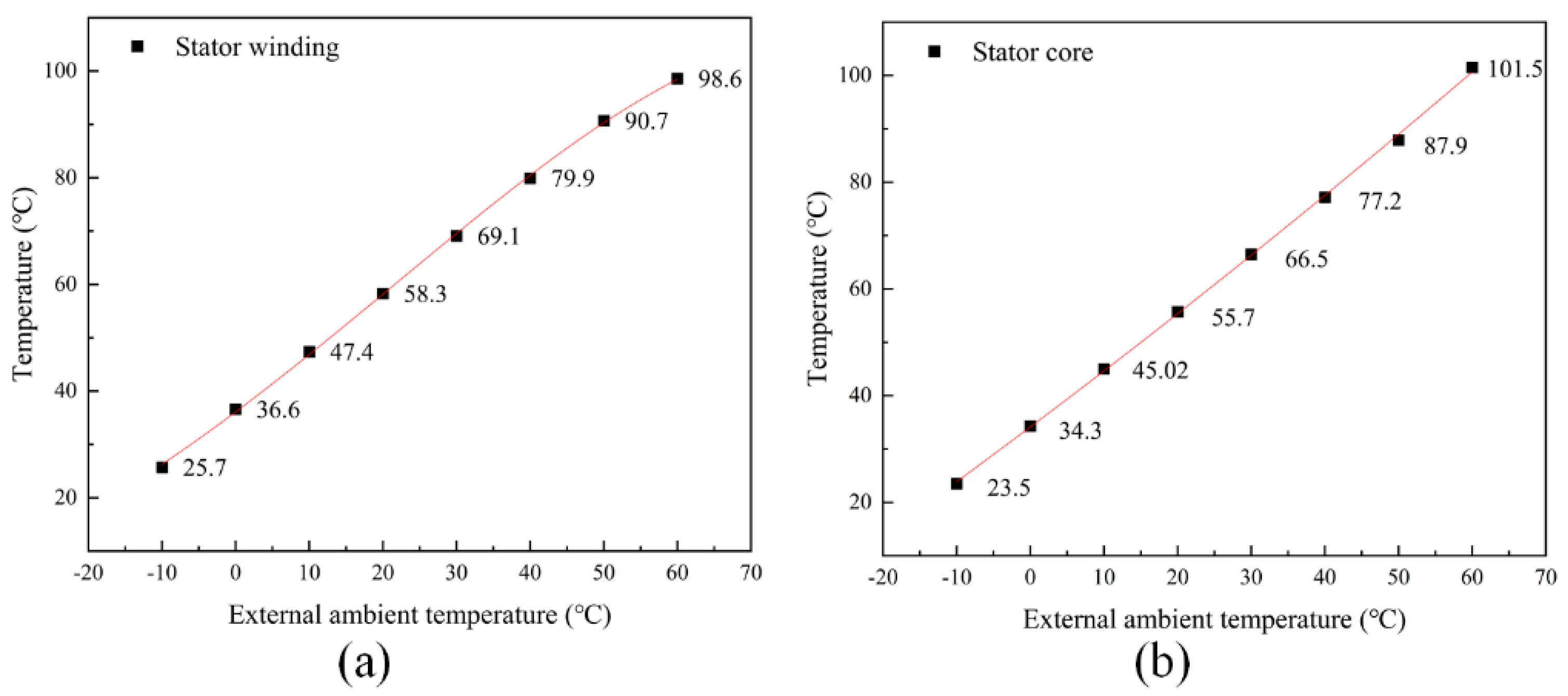
3.2. Temperature Distribution of Generators in Different Ambient Temperatures
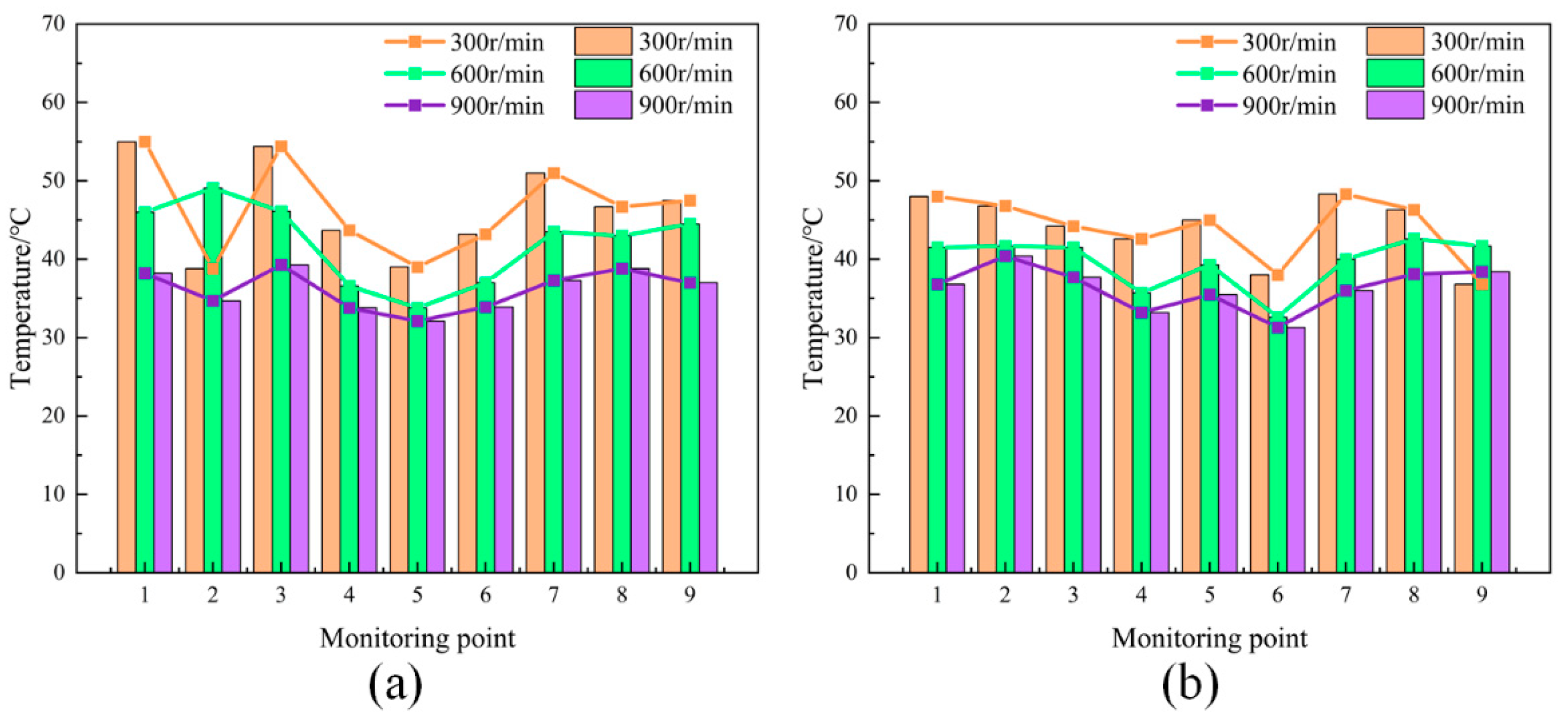
3.3. Temperature Distribution of the Generator at Different Speeds
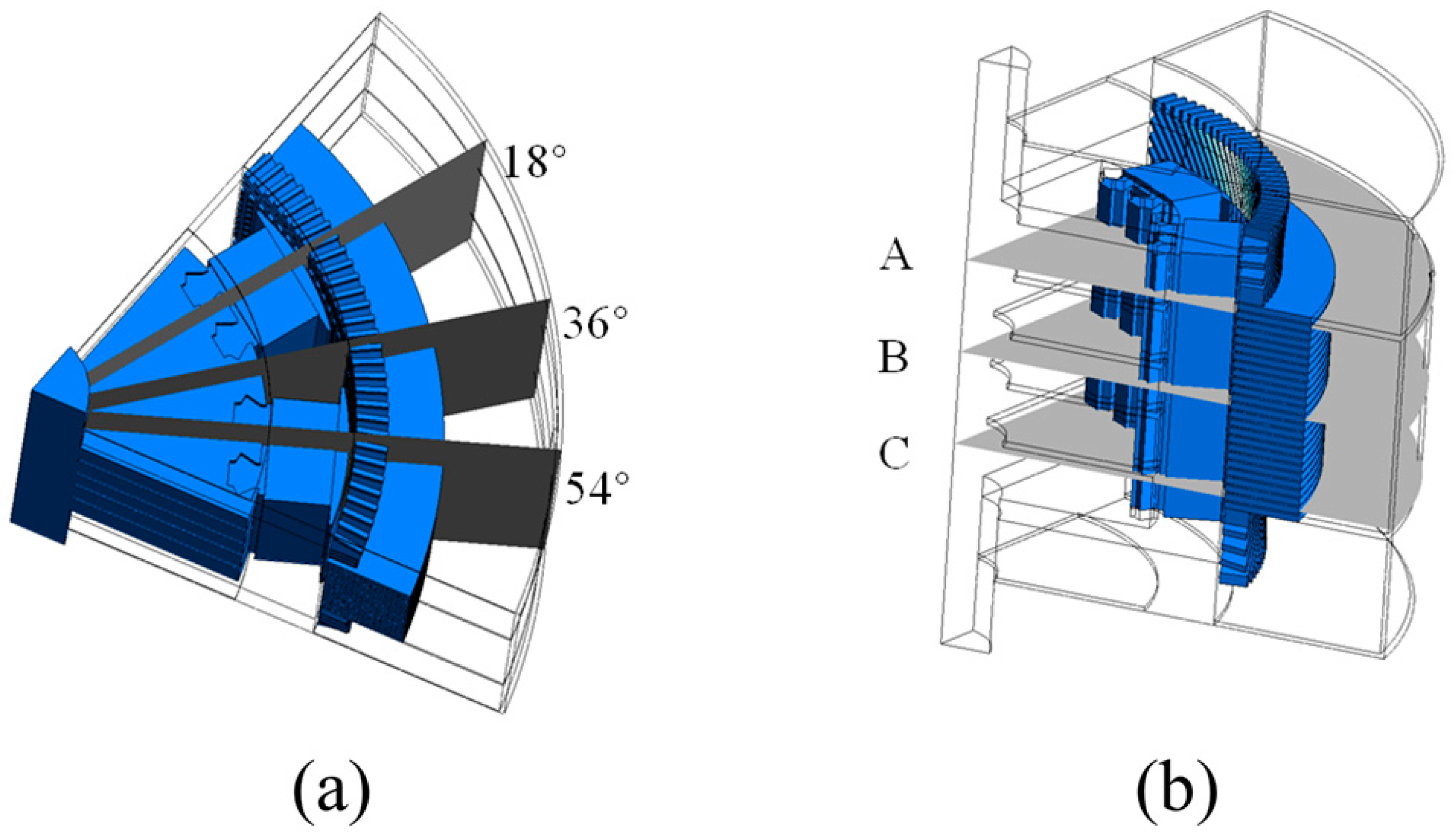
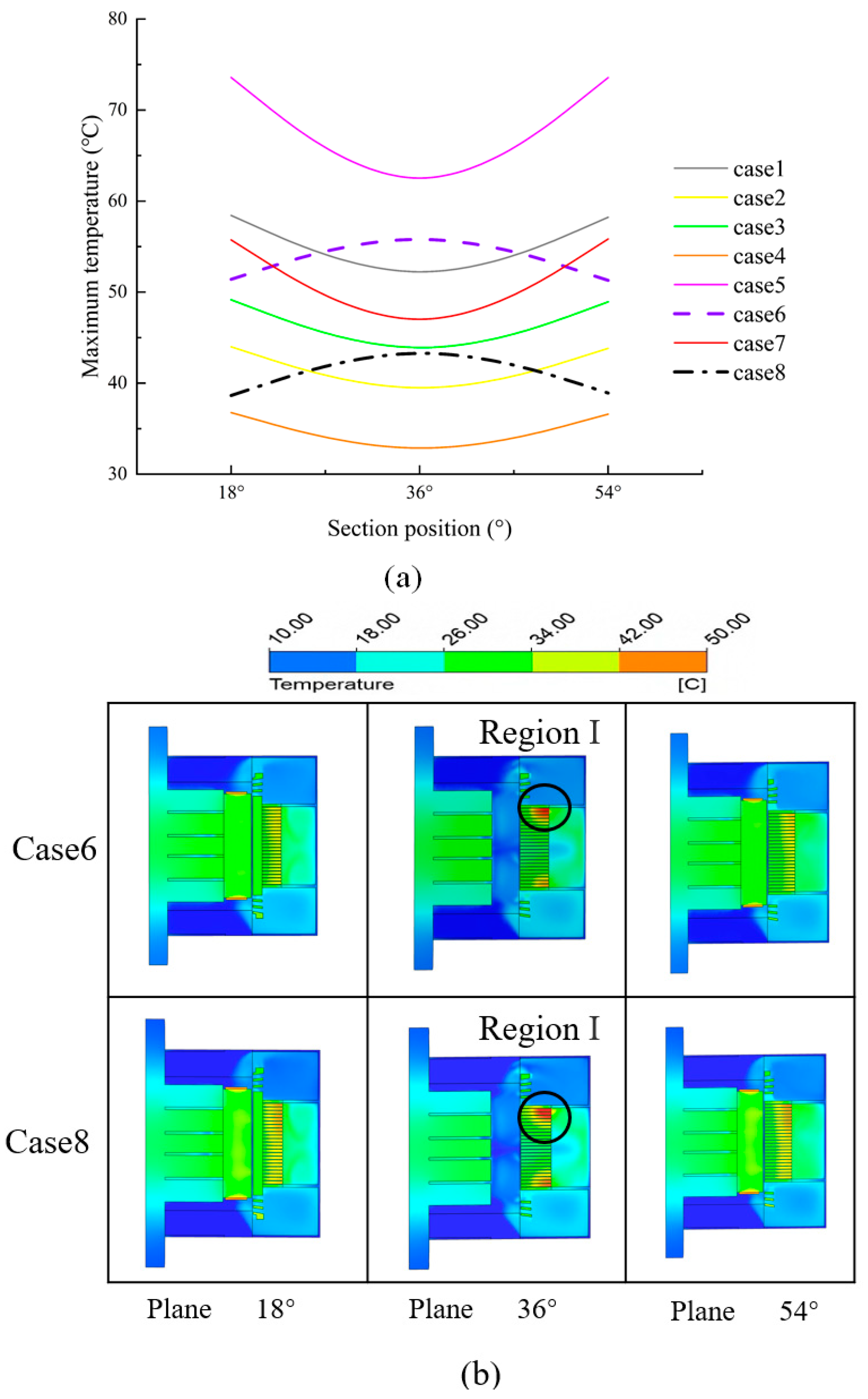
3.3.1. Vertical Section—High Speed
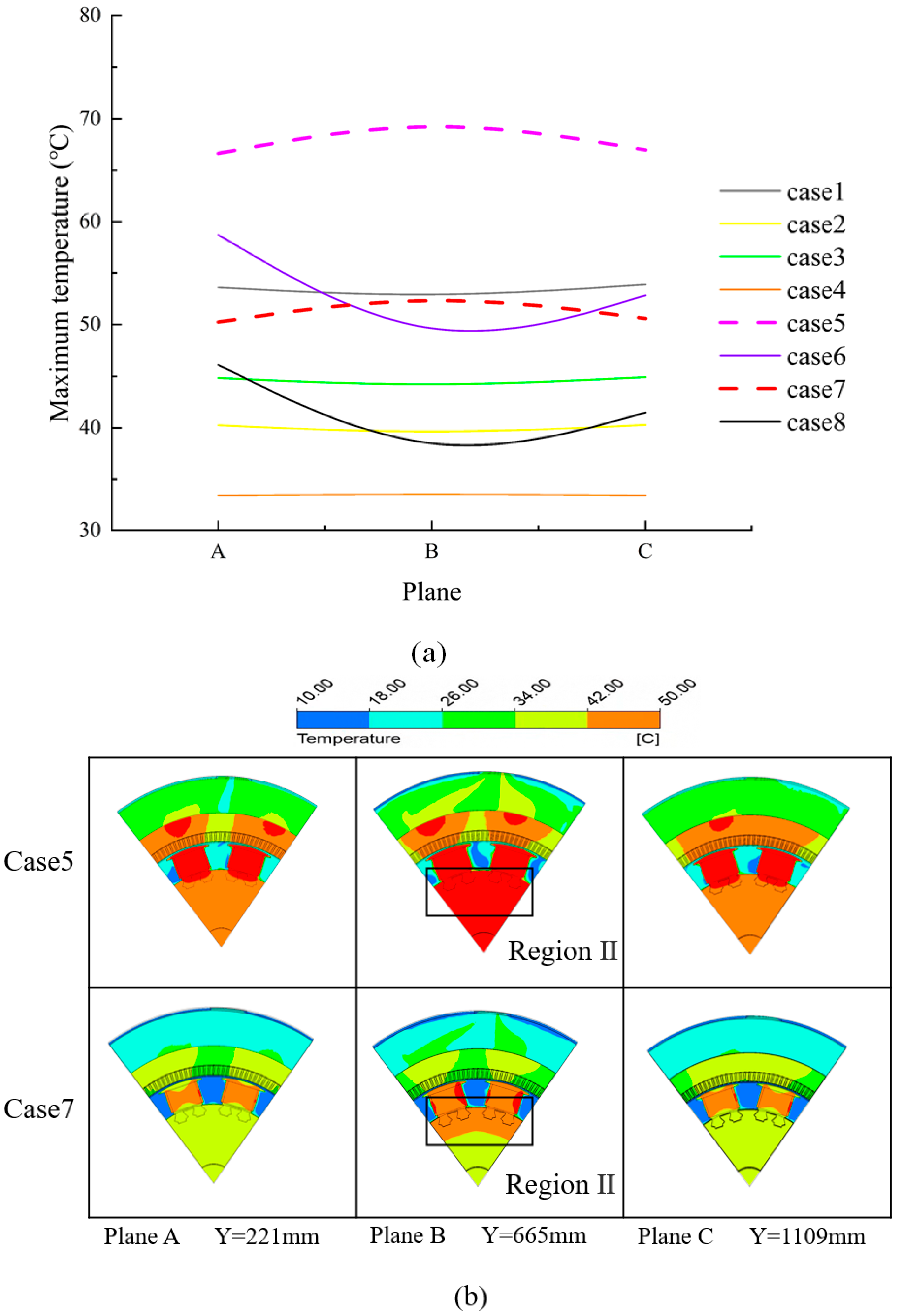
3.3.2. Horizontal Section—Low Speed
4. Conclusions
- The generator temperature decreases with increasing air pressure, and there is a negative correlation between the two. When the air pressure lies in the range of 25 kPa–85 kPa, the temperature change gradient of the stator structure is very large. The temperature difference gradually decreases with the increase in air pressure. In particular, when the air pressure is located at 55–85 kPa, the average temperature difference of the stator windings is 6.325 °C, and the average temperature difference of the stator core is 3.815 °C. The temperature gradient gradually slows down when the air pressure is above 85 kPa;
- The generator temperature increases linearly with increasing ambient temperature. An increase in external ambient temperature may be accompanied by an increase in load, resulting in more losses and heat generated by the generator. When the ambient temperature gradually increases from −10 °C to 60 °C, the temperature of the stator windings and stator core also gradually increases. Specifically, when the external ambient temperature increases by 10 °C, the generator temperature increases by 10 °C.
- The generator temperature decreases with increasing speed and the two are positively correlated. The temperature of the generator stator winding fluctuates greatly during below-the-rated-speed operation, with a difference of about 15 °C between the maximum and minimum temperatures. The temperature variations in both the vertical and the horizontal sections show an upward convex trend.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Torriano, F.; Lancial, N.; Lévesque, M.; Rolland, G.; Hudon, C.; Beaubert, F.; Morissette, J.-F.; Harmand, S. Heat transfer coefficient distribution on the pole face of a hydrogenerator scale model. Appl. Therm. Eng. 2014, 70, 153–162. [Google Scholar] [CrossRef]
- Wang, X.; Li, B.; Gerada, D.; Huang, K.; Stone, I.; Worrall, S.; Yan, Y. A critical review on thermal management technologies for motors in electric cars. Appl. Therm. Eng. 2022, 201, 117758. [Google Scholar] [CrossRef]
- Nogal, Ł.; Magdziarz, A.; Rasolomampionona, D.D.; Łukaszewski, P.; Sapuła, Ł.; Szreder, R. The laboratory Analysis of the thermal processes occurring in low-voltage asynchronous electric motors. Energies 2021, 14, 2056. [Google Scholar] [CrossRef]
- Chang, M.; Lai, B.; Wang, H.; Bai, J.; Mao, Z. Comprehensive efficiency analysis of air-cooled vs water-cooled electric motor for unmanned aerial vehicle. Appl. Therm. Eng. 2023, 225, 120226. [Google Scholar] [CrossRef]
- Ma, P.; Wang, G.; Duan, H.; Jiang, T.; Luo, Y. Investigation and application of thermal design of large-scale wind turbines based on CFD numerical simulation. J. Chin. Soc. Power Eng. 2023, 43, 568–574. [Google Scholar] [CrossRef]
- Wu, S.; Li, W.; An, Z.; Yu, S. Thermal analysis of variable-speed constant-voltage hybrid excited wind generators. Trans. China Electrotech. Soc. 2019, 34, 1857–1864. [Google Scholar] [CrossRef]
- Saleem, A.; Hyeon Park, M.; Ambreen, T.; Kim, S.C. Optimization of oil flow distribution inside the in-wheel motor assembly of electric vehicles for improved thermal performance. Appl. Therm. Eng. 2022, 201, 117753. [Google Scholar] [CrossRef]
- Venne, K.; Torriano, F.; Mydlarski, L.; Baliga, B. Validation of a numerical model for hot-spot detection on the surface of a rotor pole using a scale model of a hydroelectric generator. Appl. Therm. Eng. 2022, 215, 118967. [Google Scholar] [CrossRef]
- Su, Y.; Li, W.; Li, D.; Li, D.; Li, Y.; Liu, W. Influence of incident angle of hydrogen in the ventilation ducts on multi-physical fields of 1100 MW turbine-generator rotor. Int. J. Heat Mass Transf. 2019, 140, 852–861. [Google Scholar] [CrossRef]
- Zhao, Z.; Mei, T.; Li, J.; Liu, G. Ventilation structure design and heat transfer analysis of 3.3MW permanent magnet direct drive wind generators. Energy Rep. 2022, 8, 1280–1286. [Google Scholar] [CrossRef]
- Zhou, Y. Analysis and research on key technologies of high speed and large capacity horizontal hydro-generator. Manuf. Autom. 2022, 44, 137–141. [Google Scholar]
- Dang, D.-D.; Pham, X.-T.; Nguyen, C.-C. Thermal performance prediction in the air gap of a rotor-stator configuration: Effects of numerical models. J. Therm. Sci. 2020, 29, 206–218. [Google Scholar] [CrossRef]
- Yang, Y.; Xiao, Y.; Du, Z.; Feng, X. Data-driven varying state-space model based on thermal network for transient temperature field prediction of motorized spindles. Appl. Therm. Eng. 2023, 219, 119456. [Google Scholar] [CrossRef]
- Han, N.G.; Lee, H.L.; Kim, R.H.; Beom, T.Y.; Kim, Y.K.; Ha, T.W.; Lee, S.W.; Kim, D.K. Thermal analysis of the oil cooling motor according to the churning phenomenon. Appl. Therm. Eng. 2023, 220, 119791. [Google Scholar] [CrossRef]
- Liu, X.; Yu, H.; Shi, Z.; Xia, T.; Hu, M. Electromagnetic-fluid-thermal field calculation and analysis of a permanent magnet linear motor. Appl. Therm. Eng. 2018, 129, 802–811. [Google Scholar] [CrossRef]
- He, L.; Chen, H.; Wu, H.; Ge, S.; Shi, W.; Yan, X. Study on temperature rise characteristics of vehicle permanent magnet synchronous motors under peak working conditions considering boiling heat transfer. J. Xi’an Jiaotong Univ. 2022, 56, 138–146. [Google Scholar] [CrossRef]
- Li, W.; Li, D.; Li, J.; Zhang, X. Influence of rotor radial ventilation ducts number on temperature distribution of rotor excitation winding and fluid flow state between two poles of a fully air-cooled hydro-generator. IEEE Trans. Ind. Electron. 2017, 64, 3767–3775. [Google Scholar] [CrossRef]
- Han, J.; Ge, B.; Tao, D.; Zhao, H.; Xiao, F.; Li, W. Calculation and analysis of complex fluid flow and thermal fields in a fully air-cooled hydrogenerator. Int. J. Therm. Sci. 2017, 116, 278–286. [Google Scholar] [CrossRef]
- Tai, Y.; Liu, Z. Analysis on three-dimensional transient temperature field of induction motor. Proc. Chin. Soc. Electr. Eng. 2010, 30, 114–120. [Google Scholar] [CrossRef]
- He, J.; Bian, X.; Liang, Y. Design and Analysis for Stator Cooling Structure of Air Cooled Hydrogenerator. J. Xi’an Jiaotong Univ. 2019, 53, 111–119. [Google Scholar] [CrossRef]
- Dang, D.-D.; Pham, X.-T.; Labbe, P.; Torriano, F.; Morissette, J.-F.; Hudon, C. CFD analysis of turbulent convective heat transfer in a hydro-generator rotor-stator system. Appl. Therm. Eng. 2018, 130, 17–28. [Google Scholar] [CrossRef]
- Fang, X.; Wu, Y.; Wu, H. Calculation of Motor Temperature Field Based on Fluent. Electron. Sci. Technol. 2021, 34, 30–35. [Google Scholar] [CrossRef]
- Li, W.; Song, H.; Yang, F. Numerical of the tubular turbine hydroelectric generator ventilation system multi-field coupling. Electr. Mach. Control 2013, 17, 85–90. [Google Scholar] [CrossRef]
- Li, W.; Yuan, S.; Huo, F.; Zhang, Y. Calculation of temperature field of PM generator for wind turbine based on theory of fluid heat transfer. Electr. Mach. Control 2011, 15, 56–62. [Google Scholar] [CrossRef]
- Zhou, F.; Xiong, B.; Li, W.; Cheng, S.K. Numerical calculation of 3D stator fluid field for large electrical machine as well as influences on thermal field distribution. Proc. Chin. Soc. Electr. Eng. 2005, 25, 128–132. [Google Scholar] [CrossRef]
- Ding, S.; Sun, Z.; Jiang, N.; Deng, L.; Xie, Y. Numerical simulation of rheological properties inside large doubly-fed wind generator. Electr. Mach. Control 2011, 15, 28–34. [Google Scholar] [CrossRef]
- Gong, H.; Ge, B.; Tao, D.; Wang, L.; Li, Y. Research on coupling heat transfer of fluid and solid under rotating state of water-cooled permanent magnet synchronous motor for compressor. Proc. CSEE 2021, 41, 7830–7841. [Google Scholar] [CrossRef]
- Li, W.; Li, J.; Li, D. Influence of variable section Rotor ventilation ducts on temperature and fluid fields of a full air-cooled large hydro-generator rotor. Trans. China Electrotech. Soc. 2017, 32, 42–49. [Google Scholar] [CrossRef]
- He, J. Research on Modeling Method of Stator Fluid and Temperature Field and Cooling Structure of Hydro-Generator. Master’s Thesis, Harbin University of Science and Technology, Harbin, China, 2019. [Google Scholar]
- Zhang, S.; Li, W.; Li, J.; Wang, L.; Zhang, X. Research on flow rule and thermal dissipation between the rotor poles of a fully air-cooled hydrogenerator. IEEE Trans. Ind. Electron. 2015, 62, 3430–3437. [Google Scholar] [CrossRef]
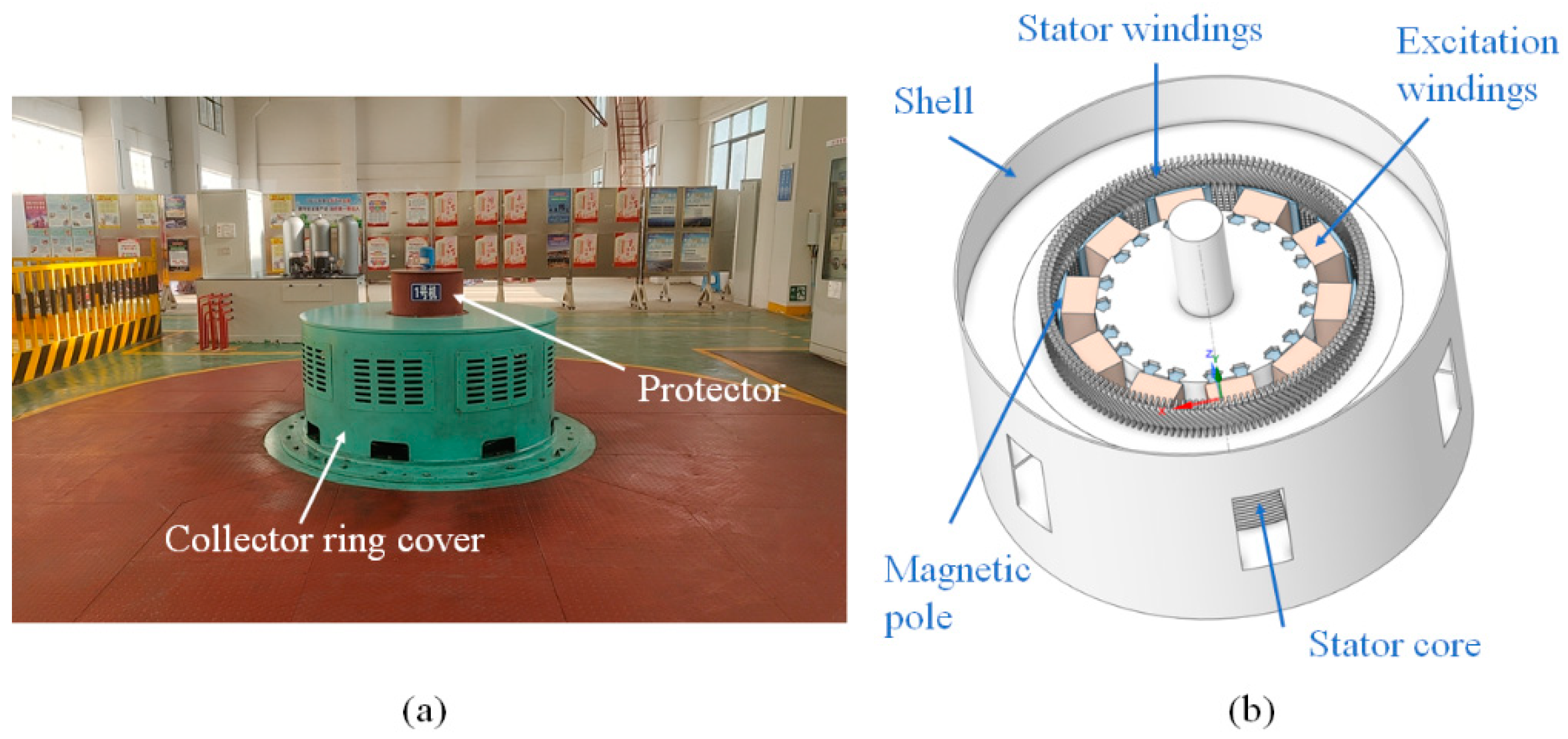
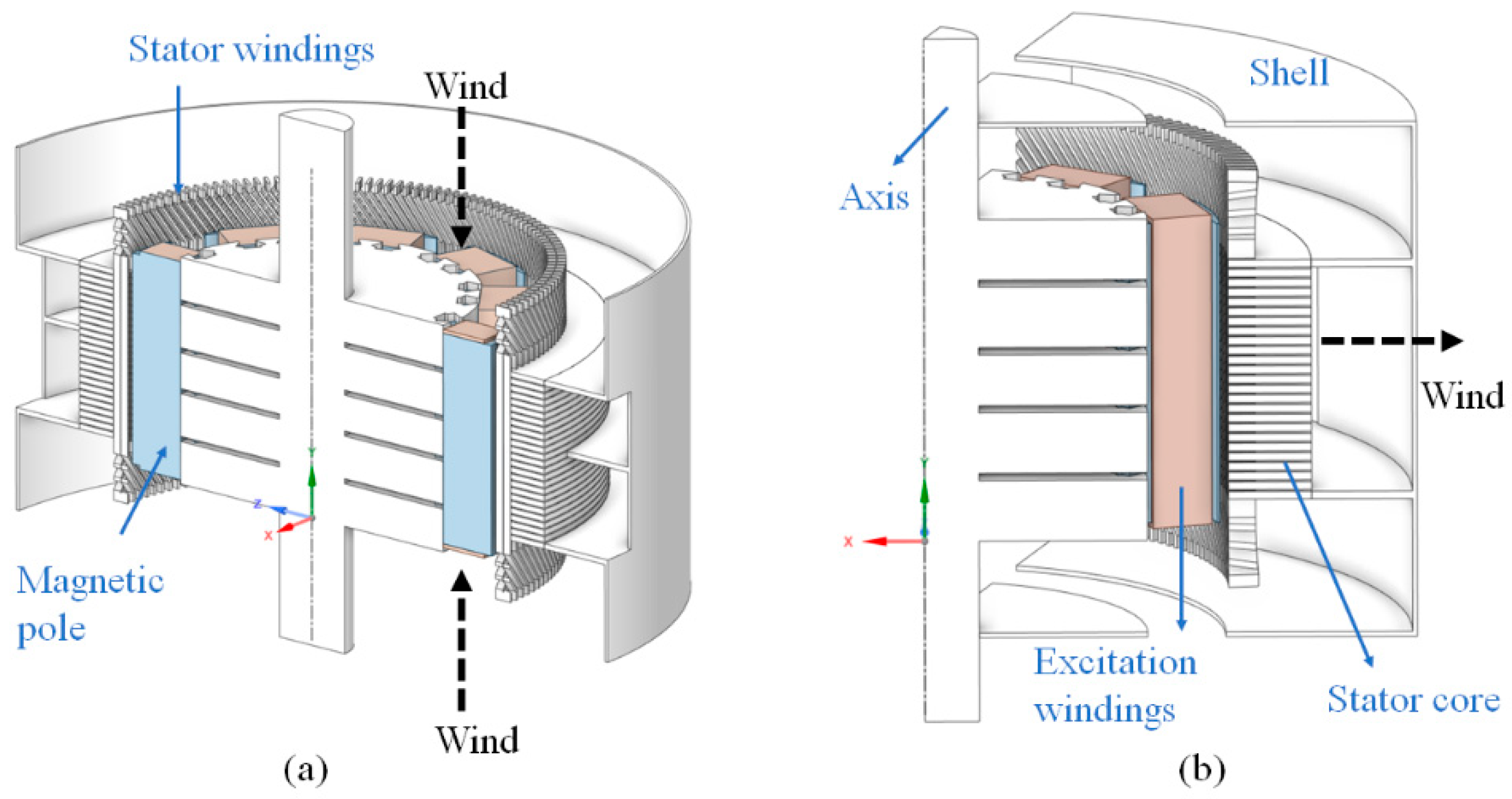
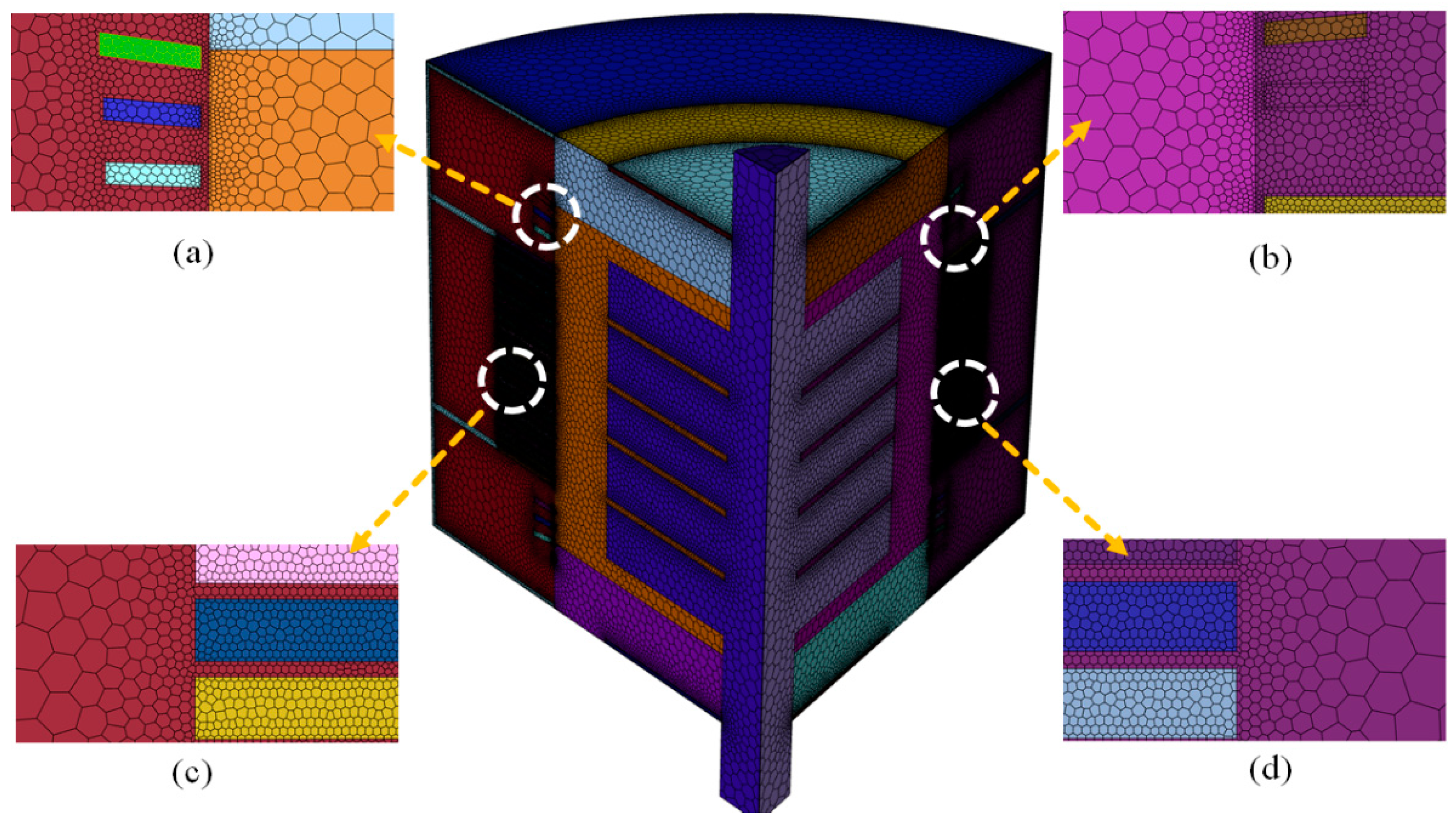

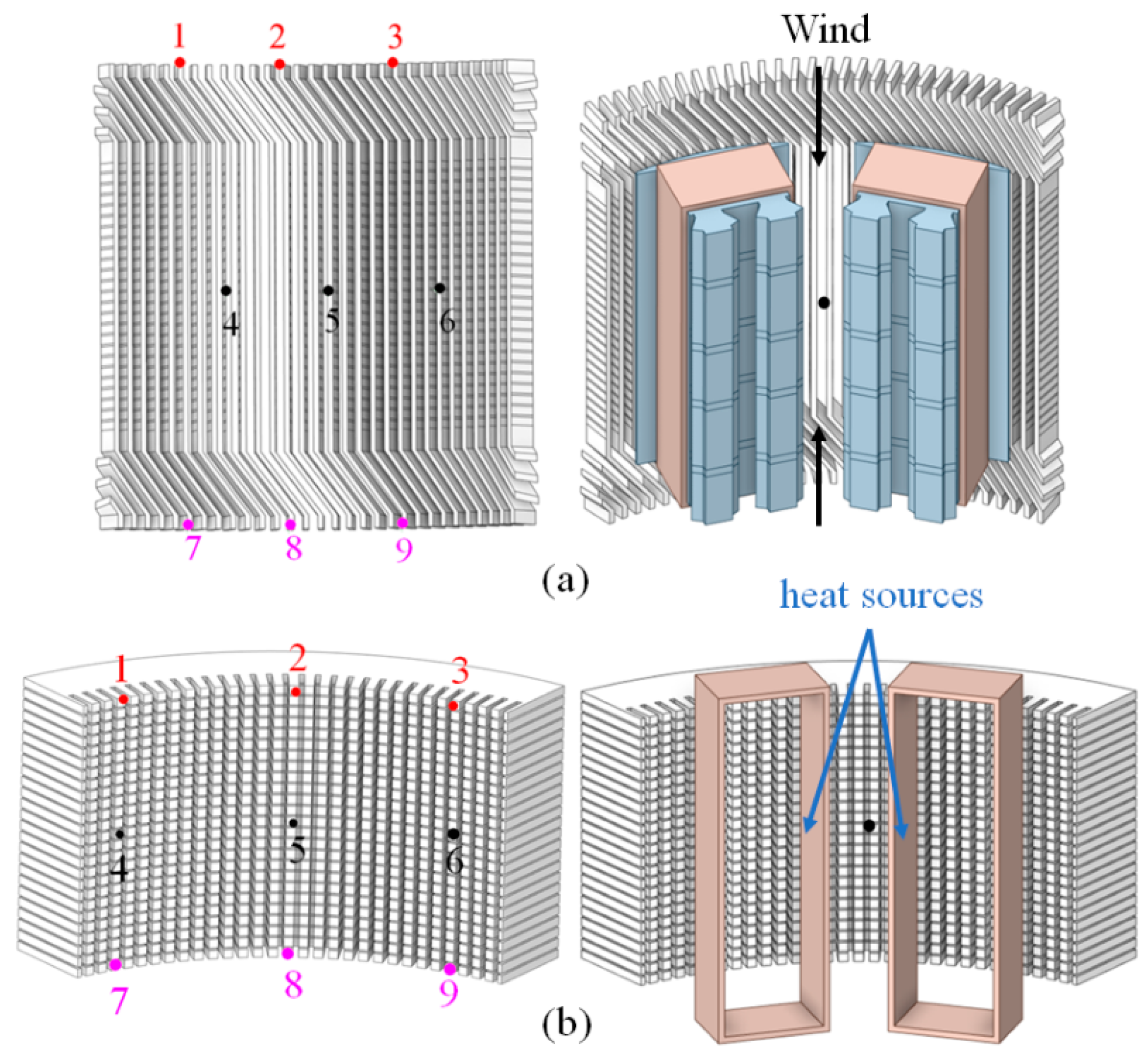




| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Rated power/kW | 20,000 | Rated speed/rpm | 600 |
| Rated voltage/kV | 10.5 | Rated current/A | 1293.8 |
| Stator outer diameter/mm | 3300 | Stator bore/mm | 2590 |
| Rotor outer diameter/mm | 2548 | Rotor inner diameter/mm | 1816 |
| Core length/mm | 990 | Number of generator poles | 10 |
| Case | Pressure | Ambient Temperature | Rotational Speed | Case | Pressure | Ambient Temperature | Rotational Speed |
|---|---|---|---|---|---|---|---|
| 1 | 70 kPa | 15 °C | 600 r/min | 11 | 55 kPa | 15 °C | 600 r/min |
| 2 | 70 kPa | 10 °C | 600 r/min | 12 | 85 kPa | 15 °C | 600 r/min |
| 3 | 100 kPa | 15 °C | 600 r/min | 13 | 70 kPa | −10 °C | 600 r/min |
| 4 | 100 kPa | 10 °C | 600 r/min | 14 | 70 kPa | 0 °C | 600 r/min |
| 5 | 70 kPa | 15 °C | 300 r/min | 15 | 70 kPa | 20 °C | 600 r/min |
| 6 | 70 kPa | 15 °C | 900 r/min | 16 | 70 kPa | 30 °C | 600 r/min |
| 7 | 70 kPa | 10 °C | 300 r/min | 17 | 70 kPa | 40 °C | 600 r/min |
| 8 | 70 kPa | 10 °C | 900 r/min | 18 | 70 kPa | 50 °C | 600 r/min |
| 9 | 25 kPa | 15 °C | 600 r/min | 19 | 70 kPa | 60 °C | 600 r/min |
| 10 | 40 kPa | 15 °C | 600 r/min |
| Operational Log of Temperature Values for Unit 1 of the Secondary Power Plant | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | H1/m | T1/°C | T2/°C | T3/°C | T4/°C | T5/°C | T6/°C | t1/°C | t2/°C | t3/°C | t4/°C | t5/°C | t6/°C | Tm/°C | P/MPa |
| 0:00 | 2582 | 50.6 | 50.5 | 43.7 | 48.2 | 45.3 | 48.7 | 48.2 | 43.3 | 44.2 | 49.1 | 45.7 | 49.8 | 35.4 | 5.88 |
| 1:00 | 2582 | 50.5 | 50.4 | 43.6 | 48.2 | 45.4 | 48.8 | 48.2 | 43.2 | 44.1 | 49.1 | 45.6 | 49.8 | 35.6 | 5.89 |
| 2:00 | 2582 | 50.5 | 50.4 | 43.5 | 48.1 | 45.3 | 48.7 | 48.1 | 43.2 | 44.1 | 49.1 | 45.6 | 49.8 | 35 | 6.1 |
| 3:00 | 2582 | 50.5 | 50.4 | 43.5 | 48.1 | 45.2 | 48.7 | 48.1 | 43.2 | 44 | 49.1 | 45.6 | 49.7 | 35 | 5.96 |
| 4:00 | 2582 | 50.5 | 50.4 | 43.5 | 48 | 45.2 | 48.6 | 48.1 | 43.1 | 44 | 49 | 45.5 | 49.7 | 34.8 | 5.83 |
| 5:00 | 2582 | 50.4 | 50.3 | 43.6 | 48 | 45.2 | 48.7 | 48 | 43.1 | 44 | 49 | 45.6 | 49.7 | 35.2 | 6.06 |
| 6:00 | 2582 | 50.4 | 50.3 | 43.5 | 48 | 45.1 | 48.7 | 48 | 43.1 | 43.9 | 48.9 | 45.5 | 49.6 | 35.2 | 5.94 |
| 7:00 | 2582 | 50.4 | 50.2 | 43.4 | 48 | 45.1 | 48.6 | 48 | 43.1 | 43.8 | 48.9 | 45.5 | 49.6 | 35.6 | 5.83 |
| 8:00 | 2582 | 50.4 | 50.3 | 43.5 | 48 | 45.2 | 48.7 | 48.1 | 43.1 | 43.8 | 48.9 | 45.5 | 49.6 | 35.8 | 6.05 |
| 9:00 | 2582 | 50.6 | 50.4 | 43.5 | 48.1 | 45.2 | 48.7 | 48.1 | 43.1 | 43.9 | 49.1 | 45.6 | 49.6 | 36.6 | 5.91 |
| 10:00 | 2582 | 50.5 | 50.3 | 43.5 | 48 | 45.2 | 48.6 | 48.1 | 43.1 | 43.8 | 49 | 45.5 | 49.6 | 36.4 | 6.1 |
| 11:00 | 2582 | 50.5 | 50.4 | 43.5 | 48 | 45.2 | 48.7 | 48.1 | 43.1 | 43.9 | 49 | 45.5 | 49.6 | 36.4 | 5.91 |
| 12:00 | 2582 | 50.5 | 50.4 | 43.5 | 48.1 | 45.3 | 48.7 | 48.1 | 43.1 | 43.9 | 49 | 45.6 | 49.6 | 35.3 | 6.17 |
| 13:00 | 2582 | 50.5 | 50.3 | 43.5 | 48.1 | 45.2 | 48.7 | 48.1 | 43.2 | 43.9 | 49 | 45.6 | 49.6 | 35.3 | 5.97 |
| 14:00 | 2582 | 50.6 | 50.4 | 43.5 | 48.2 | 45.3 | 48.8 | 48.2 | 43.2 | 44 | 49.1 | 45.6 | 49.7 | 35.5 | 5.82 |
| 15:00 | 2582 | 50.7 | 50.5 | 43.6 | 48.3 | 45.4 | 48.8 | 48.2 | 43.3 | 44 | 49.2 | 45.7 | 49.7 | 34.9 | 6.08 |
| 16:00 | 2582 | 50.7 | 50.6 | 43.7 | 48.3 | 45.4 | 48.9 | 48.3 | 43.2 | 44.1 | 49.3 | 45.7 | 49.8 | 34.3 | 5.96 |
| 17:00 | 2582 | 50.7 | 50.6 | 43.6 | 48.3 | 45.5 | 48.8 | 48.4 | 43.3 | 44.1 | 49.2 | 45.7 | 49.8 | 33.6 | 5.83 |
| 18:00 | 2582 | 50.8 | 50.5 | 43.7 | 48.3 | 45.4 | 48.9 | 48.3 | 43.3 | 44.1 | 49.2 | 45.7 | 49.8 | 34.6 | 6.02 |
| 19:00 | 2582 | 50.6 | 50.5 | 43.7 | 48.3 | 45.5 | 48.8 | 48.3 | 43.3 | 44.1 | 49.2 | 45.7 | 49.8 | 33.8 | 5.84 |
| 20:00 | 2582 | 50.7 | 50.5 | 43.7 | 48.2 | 45.5 | 48.9 | 48.3 | 43.3 | 44.1 | 49.2 | 45.7 | 49.8 | 33.8 | 6.08 |
| 21:00 | 2582 | 50.6 | 50.5 | 43.7 | 48.3 | 45.4 | 48.8 | 48.3 | 43.3 | 44.1 | 49.1 | 45.7 | 49.8 | 34.2 | 5.93 |
| 22:00 | 2582 | 50.6 | 50.5 | 43.7 | 48.2 | 45.4 | 48.9 | 48.3 | 43.2 | 44.1 | 49.2 | 45.7 | 49.9 | 34.6 | 6.15 |
| 23:00 | 2582 | 50.6 | 50.4 | 43.7 | 48.1 | 45.3 | 48.7 | 48.1 | 43.2 | 44 | 49.1 | 45.6 | 49.8 | 34.4 | 5.98 |
| max values | 2582 | 50.8 | 50.6 | 43.7 | 48.3 | 45.5 | 48.9 | 48.4 | 43.3 | 44.2 | 49.3 | 45.7 | 49.9 | 36.6 | 6.2 |
| Annotation | H1: pre-dam elevation T1–T6: the temperature of stator winding t1–t6: the temperature of stator core Tm: the temperature of main transformer No. 1 P: governor oil pressure | ||||||||||||||
| Operational Log of Temperature Values for Unit 1 of the Secondary Power Plant | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | H1/m | T1/°C | T2/°C | T3/°C | T4/°C | T5/°C | T6/°C | t1/°C | t2/°C | t3/°C | t4/°C | t5/°C | t6/°C | Tm/°C | P/MPa |
| 0:00 | 2581.3 | 38.5 | 38.1 | 34.7 | 37.8 | 35.8 | 37.8 | 37.8 | 34.9 | 35.4 | 37.6 | 36.2 | 38.6 | 52.2 | 5.95 |
| 1:00 | 2581.3 | 37.7 | 37.4 | 34.3 | 37.2 | 35.3 | 37.2 | 37.2 | 34.5 | 34.9 | 37 | 35.8 | 38.1 | 52.4 | 5.95 |
| 2:00 | 2581.3 | 37.6 | 37.3 | 34.1 | 37.1 | 35.2 | 37 | 37.1 | 34.4 | 34.8 | 36.9 | 35.6 | 37.9 | 52.2 | 5.81 |
| 3:00 | 2581.4 | 37.5 | 37.2 | 34.1 | 37 | 35.1 | 36.9 | 37 | 34.3 | 34.7 | 36.8 | 35.5 | 37.8 | 51.2 | 5.94 |
| 4:00 | 2581.4 | 37.5 | 37.2 | 34.1 | 37 | 35.1 | 36.9 | 37 | 34.3 | 34.7 | 36.8 | 35.5 | 37.8 | 50.6 | 6.01 |
| 5:00 | 2581.5 | 37.5 | 37.1 | 34 | 36.9 | 35 | 36.9 | 36.9 | 34.2 | 34.6 | 36.7 | 35.5 | 37.7 | 49.8 | 5.83 |
| 6:00 | 2581.5 | 37.4 | 37.1 | 34 | 36.9 | 35 | 36.9 | 36.9 | 34.2 | 34.6 | 36.7 | 35.5 | 37.8 | 50.0 | 5.94 |
| 7:00 | 2581.6 | 37.4 | 37 | 34 | 36.9 | 35 | 36.8 | 36.9 | 34.2 | 34.6 | 36.7 | 35.4 | 37.7 | 48.1 | 6.03 |
| 8:00 | 2581.6 | 37.4 | 37 | 33.9 | 36.9 | 35 | 36.8 | 36.8 | 34.1 | 34.5 | 36.6 | 35.4 | 37.6 | 50.1 | 5.84 |
| 9:00 | 2581.6 | 37.4 | 37 | 33.9 | 36.9 | 35 | 36.8 | 36.8 | 34.1 | 34.5 | 36.7 | 35.3 | 37.6 | 48.6 | 5.9 |
| 10:00 | 2581.7 | 37.3 | 36.9 | 33.8 | 36.7 | 34.9 | 36.6 | 36.7 | 34 | 34.4 | 36.6 | 35.3 | 37.5 | 50.5 | 6 |
| 11:00 | 2581.7 | 37.2 | 36.8 | 33.7 | 36.7 | 34.8 | 36.6 | 36.7 | 33.9 | 34.3 | 36.5 | 35.2 | 37.4 | 49.9 | 6.13 |
| 12:00 | 2581.8 | 36.8 | 36.5 | 33.5 | 36.4 | 34.5 | 36.2 | 36.3 | 33.7 | 34.1 | 36.1 | 34.9 | 37.1 | 51.9 | 5.94 |
| 13:00 | 2581.8 | 38.5 | 38.1 | 34.5 | 37.6 | 35.7 | 37.7 | 37.6 | 34.5 | 35.1 | 37.6 | 36 | 38.5 | 53.2 | 5.82 |
| 14:00 | 2581.8 | 39.2 | 38.8 | 35.1 | 38.3 | 36.2 | 38.4 | 38.3 | 35.2 | 35.6 | 38.2 | 36.5 | 39.2 | 55.9 | 6.05 |
| 15:00 | 2581.7 | 39.4 | 39 | 35.3 | 38.5 | 36.4 | 38.6 | 38.5 | 35.4 | 35.8 | 38.5 | 36.8 | 39.4 | 50.9 | 5.82 |
| 16:00 | 2581.7 | 38.4 | 38.1 | 34.8 | 37.7 | 35.8 | 37.7 | 37.8 | 35 | 35.4 | 37.6 | 36.3 | 38.6 | 42.9 | 5.89 |
| 17:00 | 2581.7 | 37.9 | 37.6 | 34.4 | 37.3 | 35.5 | 37.2 | 37.3 | 34.6 | 35 | 37 | 35.9 | 38.1 | 44.9 | 5.86 |
| 18:00 | 2581.8 | 37.6 | 37.3 | 34.2 | 37.1 | 35.2 | 37 | 37.1 | 34.4 | 34.8 | 36.9 | 35.6 | 37.8 | 50.8 | 6.06 |
| 19:00 | 2581.9 | 37.5 | 37.2 | 34.1 | 37 | 35.2 | 36.9 | 37 | 34.3 | 34.7 | 36.8 | 35.6 | 37.8 | 52.7 | 6.1 |
| 20:00 | 2581.9 | 37.4 | 37 | 34 | 36.9 | 35 | 36.7 | 36.9 | 34.2 | 34.6 | 36.7 | 35.4 | 37.6 | 52.2 | 6.01 |
| 21:00 | 2581.9 | 38.4 | 38 | 34.5 | 37.6 | 35.7 | 37.6 | 37.7 | 34.7 | 35.2 | 37.5 | 36.1 | 38.5 | 50.5 | 5.81 |
| 22:00 | 2581.9 | 38.8 | 38.4 | 34.8 | 38 | 35.9 | 38 | 38 | 34.9 | 35.4 | 37.9 | 36.3 | 38.8 | 49.2 | 5.98 |
| 23:00 | 2581.8 | 38.3 | 38 | 34.4 | 37.5 | 35.6 | 37.6 | 37.6 | 34.6 | 35.1 | 37.4 | 36 | 38.4 | 49.8 | 5.99 |
| max values | 2581.9 | 39.4 | 39 | 35.3 | 38.5 | 36.4 | 38.6 | 38.5 | 35.4 | 35.8 | 38.5 | 36.8 | 39.4 | 55.9 | 6.1 |
| Annotation | H1: pre-dam elevation T1–T6: the temperature of stator winding t1–t6: the temperature of stator core Tm: the temperature of main transformer No. 1 P: governor oil pressure | ||||||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, R.; Duan, J.; Zeng, Y.; Qian, J.; Dong, G.; Zhu, M.; Zhao, J. Study on the Thermal Field of a Hydro-Generator under the Effect of a Plateau Climate. Energies 2024, 17, 932. https://doi.org/10.3390/en17040932
Shan R, Duan J, Zeng Y, Qian J, Dong G, Zhu M, Zhao J. Study on the Thermal Field of a Hydro-Generator under the Effect of a Plateau Climate. Energies. 2024; 17(4):932. https://doi.org/10.3390/en17040932
Chicago/Turabian StyleShan, Rong, Juan Duan, Yun Zeng, Jing Qian, Guanghe Dong, Min Zhu, and Jigang Zhao. 2024. "Study on the Thermal Field of a Hydro-Generator under the Effect of a Plateau Climate" Energies 17, no. 4: 932. https://doi.org/10.3390/en17040932
APA StyleShan, R., Duan, J., Zeng, Y., Qian, J., Dong, G., Zhu, M., & Zhao, J. (2024). Study on the Thermal Field of a Hydro-Generator under the Effect of a Plateau Climate. Energies, 17(4), 932. https://doi.org/10.3390/en17040932







