Simulation Approaches and Validation Issues for Open-Cathode Fuel Cell Systems in Manned and Unmanned Aerial Vehicles
Abstract
1. Introduction
- -
- The review considers quasi-static and dynamic models of the whole fuel cell system and not only the stack;
- -
- The investigation addresses the complex phenomena taking place in an OCPEMFC and the recent approaches to control strategies;
- -
- The operation at variable altitudes and fast loads typical of UAV operation is specifically considered;
- -
- The review includes the recent hot topic of digital twins where semi-empirical models are an option together with data-driven approaches.
2. Open-Cathode PEM Fuel Cells
2.1. Performance and Efficiency Indexes
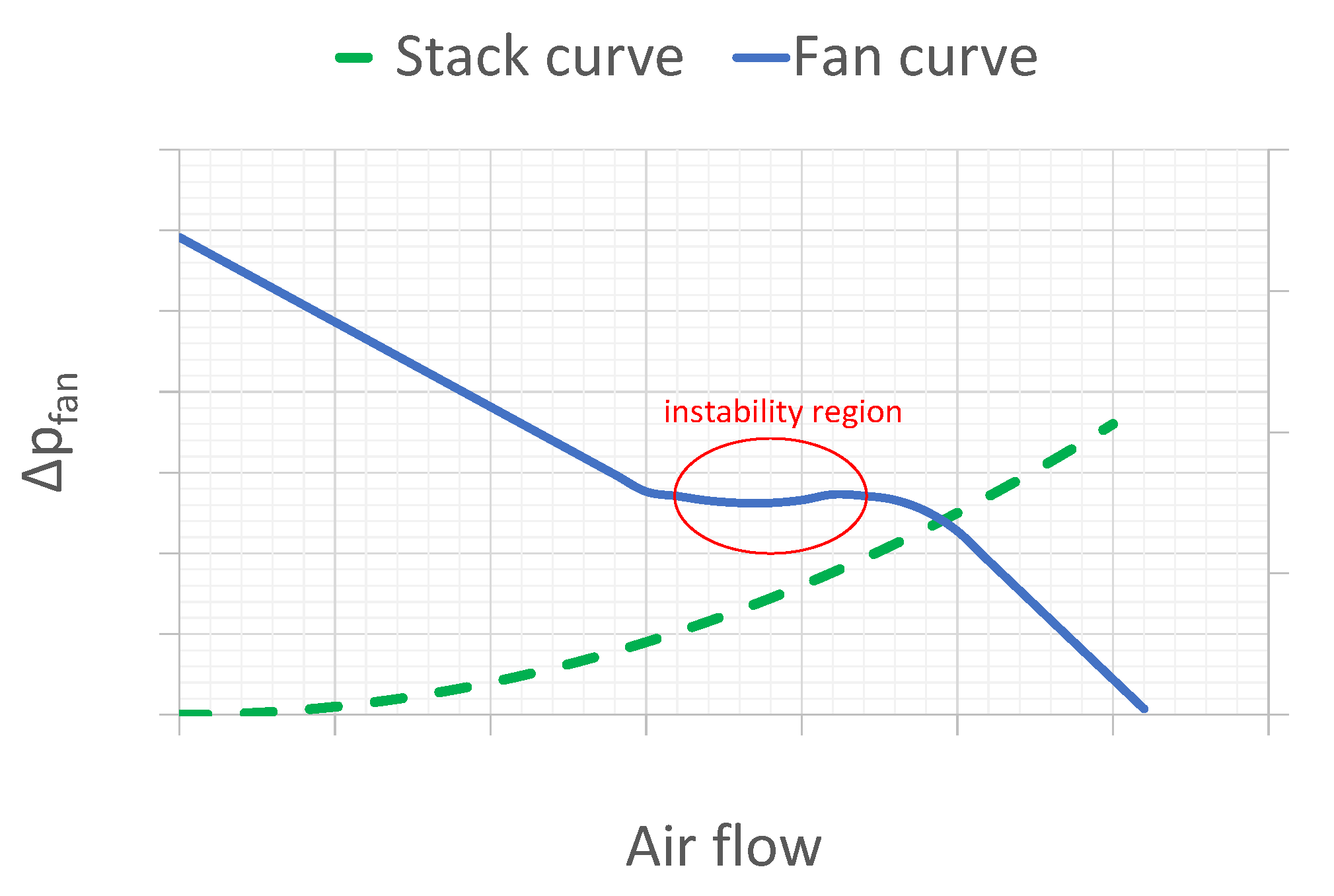
2.2. Fan Working Point and Speed Control
2.3. Testing Procedure and Facilities
- Overall performance (I–V curve, net power curve);
- Relative effect of the three main loss mechanisms;
- Mass transport proprieties;
- Parasitic losses;
- Structure of catalyst, electrodes and flows;
- Heat balance;
- Lifetime issues;
2.4. Transient Phenomena in an OCPEMFC
2.5. Control Methods
2.6. Effect of Altitude and Cold Start
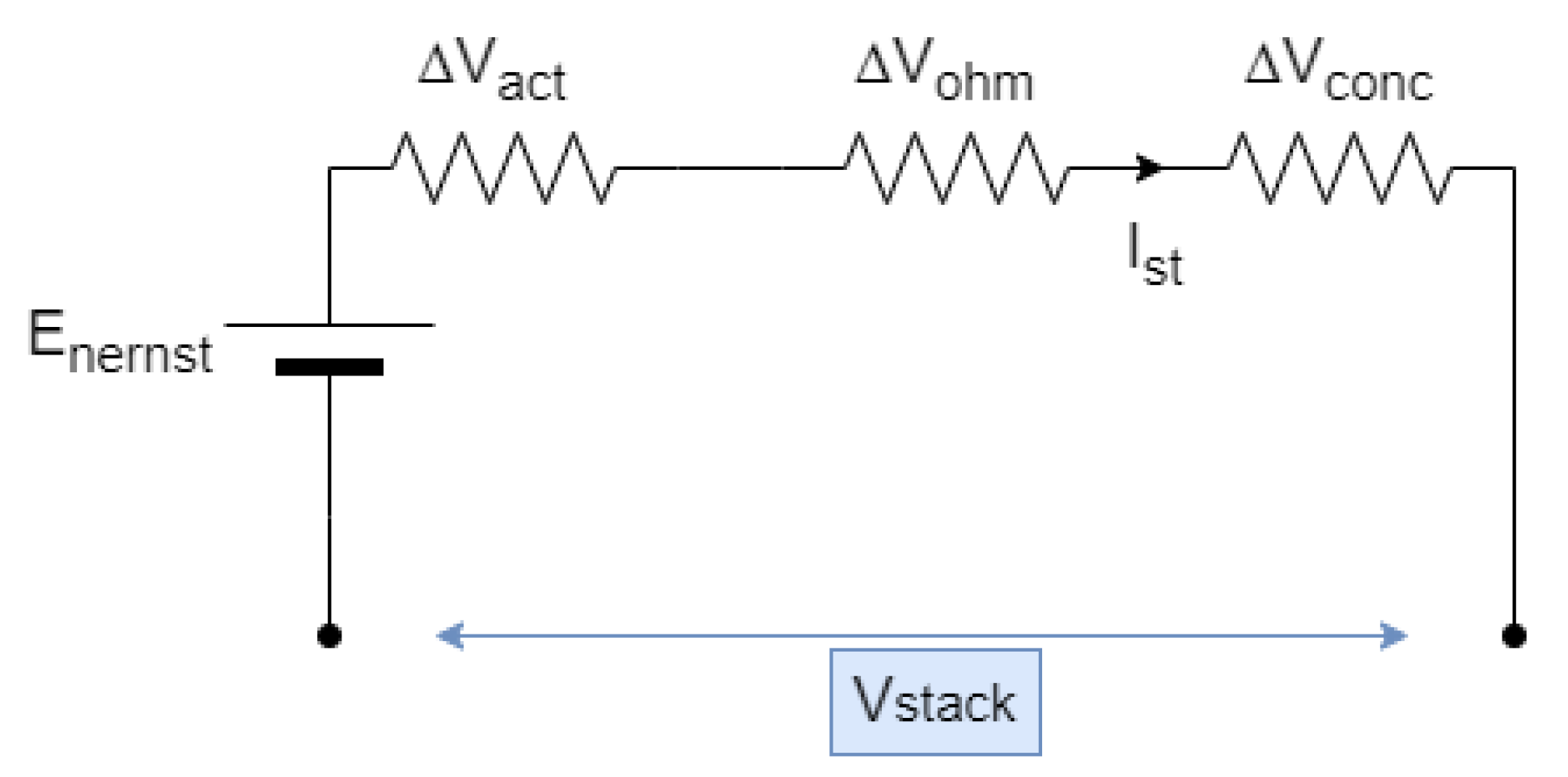
3. General Models for Fuel Cell Stack
3.1. Activation Losses
3.2. Ohmic Losses
3.3. Concentration Losses
3.4. Simplified Parametric Models
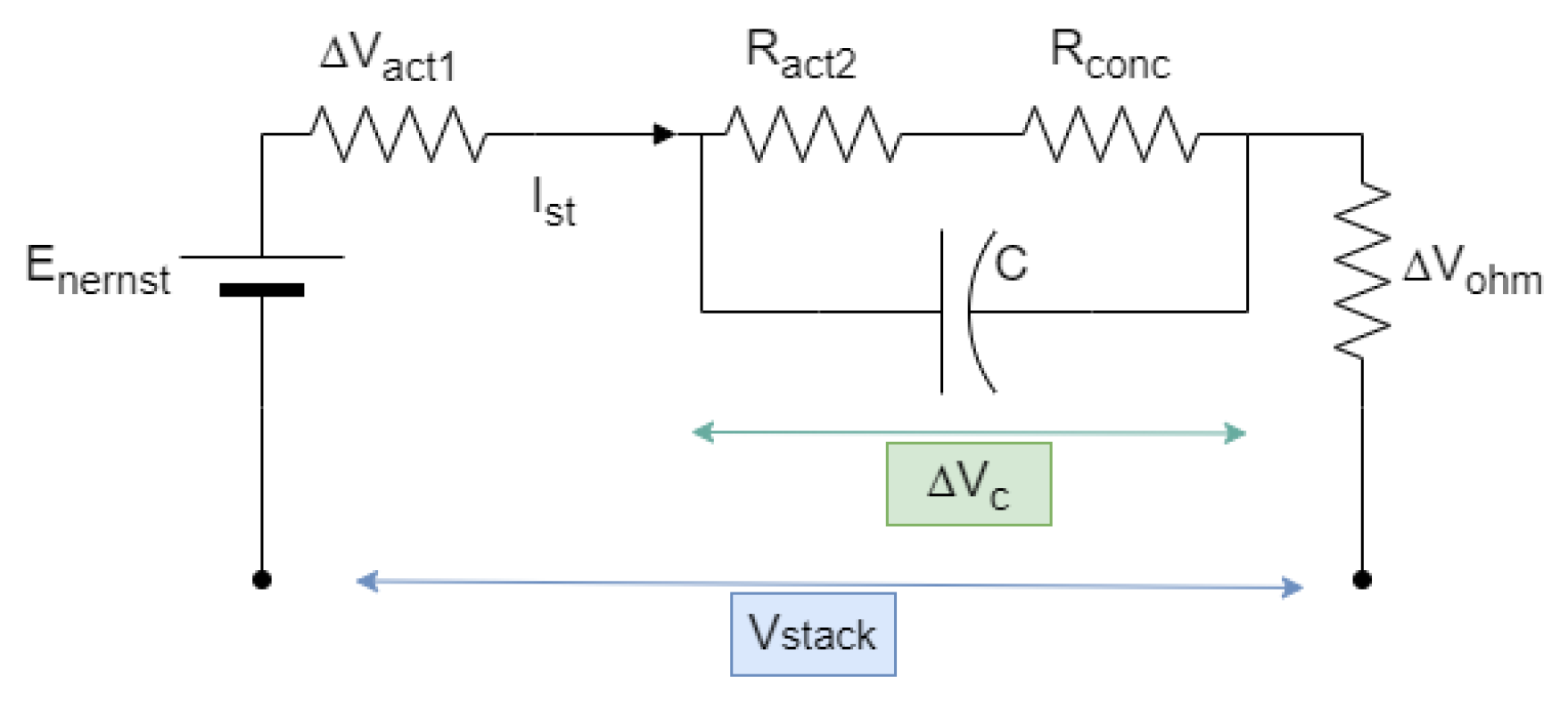
3.5. Double-Layer Capacitor Effect
4. Modeling the BOP of an Open-Cathode Fuel Cell
4.1. Flows of Reactants and Products
4.2. Cooling System
4.3. Comprehensive Dynamic Models
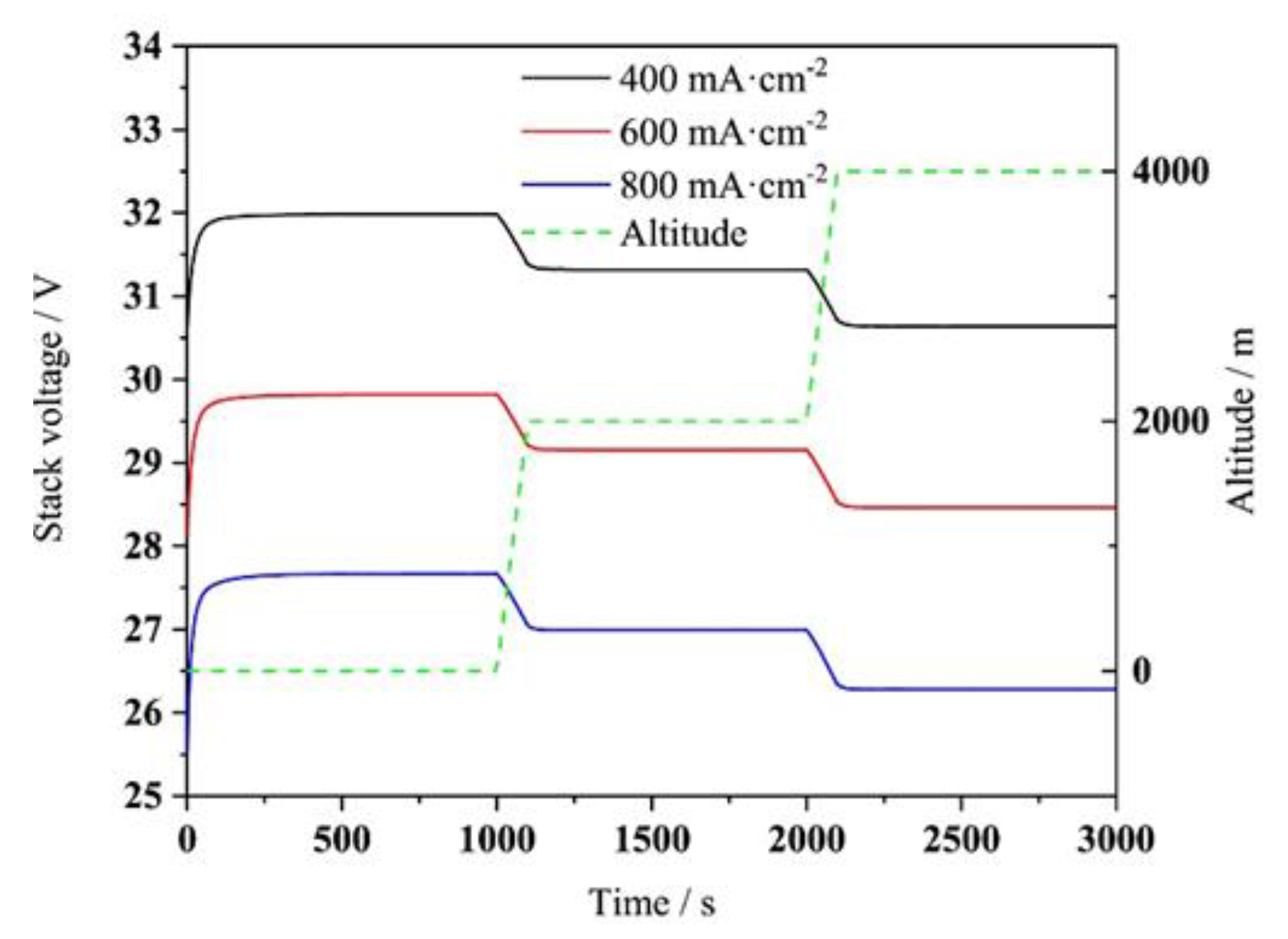
4.4. Effect of Altitude
5. Identification of the Best Simulation Approach
5.1. Uncertainties in the Specification of Fuel Cell Stacks
5.2. Uncertainties in the Operating Conditions
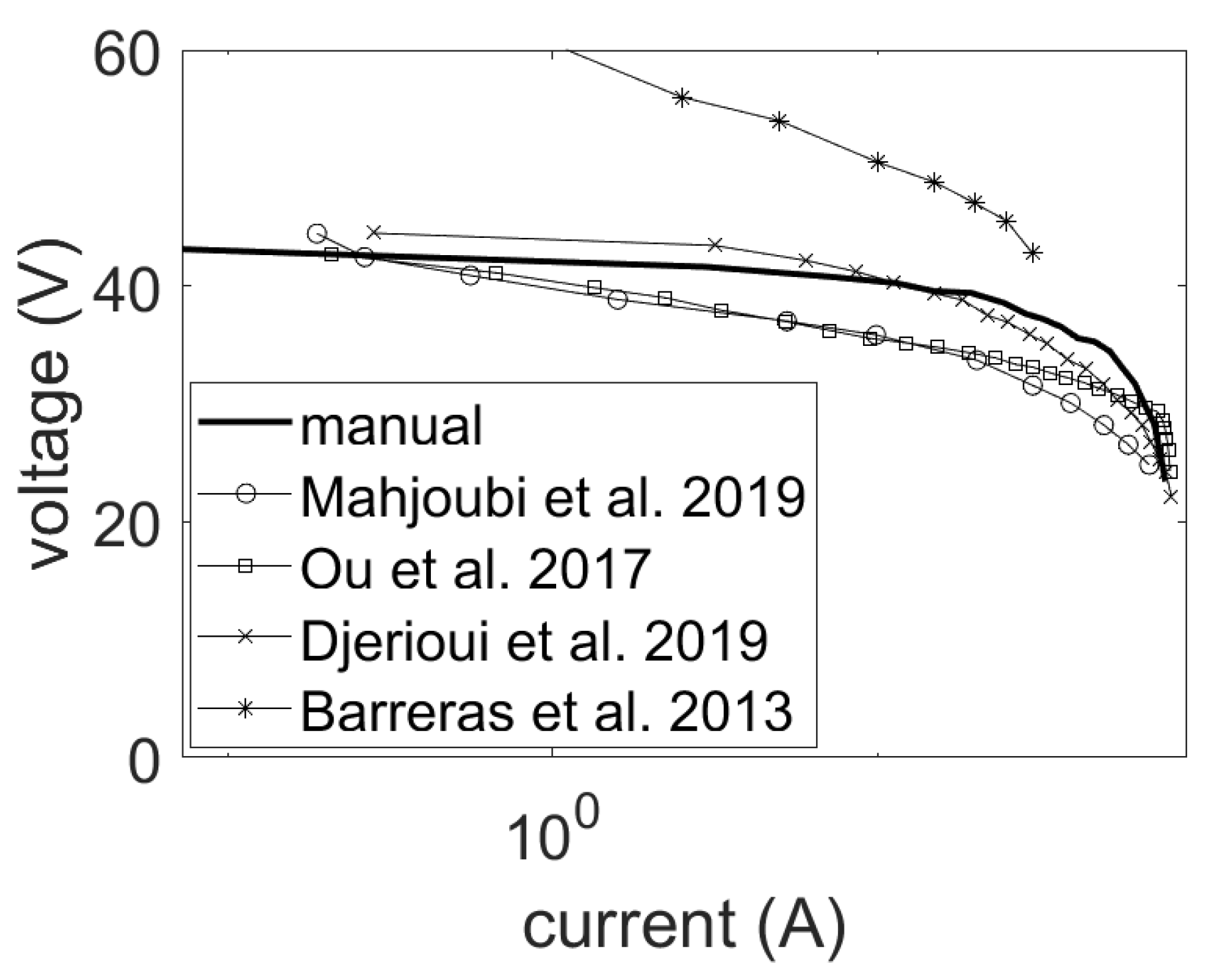
5.3. Uncertainties in the Values of the Empirical Parameter
5.4. From Dynamic Models to Digital Twins
- Monitor the deviation of the behavior of the single component from design conditions due to degradation and aging;
- Analyze the effect of flight speed and altitude and degradation on the voltage curve and in particular on the maximum current [110] of the fuel cell;
- Manage transient and cold-start operations;
- Predict the fan power and purging process on the performance of the system to optimize efficiency and power utilization [9] and, therefore, the range, in real time during the flight;
- Implement algorithms for energy management in hybrid electric configurations or route optimization in fleet analyses [118].
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, L.; Huangfu, Y.; Ma, R.; Xie, R.; Song, Z.; Zhao, D.; Yang, Y.; Wang, Y.; Xu, L. A Comprehensive Review on Fuel Cell UAV Key Technologies: Propulsion System, Management Strategy, and Design Procedure. IEEE Trans. Transp. Electrif. 2022, 8, 4118–4139. [Google Scholar] [CrossRef]
- Xiao, C.; Wang, B.; Zhao, D.; Wang, C. Comprehensive investigation on Lithium batteries for electric and hybrid-electric unmanned aerial vehicle applications. Therm. Sci. Eng. Prog. 2023, 38, 101677. [Google Scholar] [CrossRef]
- Zakhvatkin, L.; Schechter, A.; Avrahami, I. Water Recuperation from Hydrogen Fuel Cell during Aerial Mission. Energies 2022, 15, 6848. [Google Scholar] [CrossRef]
- O’Hayre, R.; Colella, W.; Cha, S.-W.; Prinz, F.B. Fuel Cell Fundamentals; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Larmine, J.; Dicks, A. Fuel Cell Systems Explained; Wiley: Hoboken, NJ, USA, 2003; ISBN 9780470848579. [Google Scholar]
- Barreras, F.; Lozano, A.; Barroso, J.; Roda, V.; Maza, M. Theoretical Model for the Optimal Design of an Air cooling System of Polymer Electrolyte Fuel cell. Application for a High-temperature PEMFC. Fuel Cells 2013, 13, 227–237. [Google Scholar] [CrossRef]
- Squadrito, G.; Maggio, G.; Passalacqua, E.; Lufrano, F.; Patti, A. An empirical equation for polymer electrolyte fuel cell (PEFC) behaviour. J. Appl. Electrochem. 1999, 29, 1449–1455. [Google Scholar] [CrossRef]
- Ishaku, J.; Lotfi, N.; Zomorodi, H.; Landers, R.G. Control-oriented modeling for open-cathode fuel cell systems. In Proceedings of the 2014 American Control Conference—ACC 2014, Portland, OR, USA, 4–6 June 2014; pp. 268–273. [Google Scholar]
- Nóbrega, P.H.A. A review of physics-based low-temperature proton-exchange membrane fuel cell models for system-level water and thermal management studies. J. Power Sources 2023, 558, 232585. [Google Scholar] [CrossRef]
- Wright, S.; Aaltonen, J. Fuel cells and novel thermal management advancements required for aviation. In Proceedings of the 33rd Congress of the International Council of the Aeronautical Sciences ICAS2022, Stockholm, Sweden, 4–9 September 2022; The International Council of the Aeronautical Sciences: Bonn, Germany, 2022. [Google Scholar]
- Nexa™ (310-0027) Power Module User’s Manual MAN5100078. Available online: http://faculty.stust.edu.tw/~wcchang/MAN5100078.pdf (accessed on 5 September 2023).
- Kim, T.; Kwon, S. Design and development of a fuel cell-powered small unmanned aircraft. Int. J. Hydrogen Energy 2012, 37, 615–622. [Google Scholar] [CrossRef]
- Pratt, J.W.; Brouwer, J.; Samuelsen, G.S. Performance of proton exchange membrane fuel cell at high-altitude conditions. J. Propuls. Power 2007, 23, 437–444. [Google Scholar] [CrossRef]
- Wang, Y.-X.; Chen, Q.; Zhang, J.; He, H. Real-time power optimization for an air-coolant proton exchange membrane fuel cell based on active temperature control. Energy 2021, 220, 119497. [Google Scholar] [CrossRef]
- Chen, F.; Yu, Y.; Gao, Y. Temperature Control for Proton Exchange Membrane Fuel Cell based on Current Constraint with Consideration of Limited Cooling Capacity. Fuel Cells 2017, 17, 662–670. [Google Scholar] [CrossRef]
- Tolj, I.; Penga, Ž.; Vukičević, D.; Barbir, F. Thermal management of edge-cooled 1 kW portable proton exchange membrane fuel cell stack. Appl. Energy 2020, 257, 114038. [Google Scholar] [CrossRef]
- Xing, S.; Zhao, C.; Zou, J.; Zaman, S.; Yu, Y.; Gong, H.; Wang, Y.; Chen, M.; Wang, M.; Lin, M.; et al. Recent advances in heat and water management of forced-convection open-cathode proton exchange membrane fuel cells. Renew. Sustain. Energy Rev. 2022, 165, 112558. [Google Scholar] [CrossRef]
- Zakhvatkin, L.; Schechter, A.; Buri, E.; Avrahami, I. Edge Cooling of a Fuel Cell during Aerial Missions by Ambient Air. Micromachines 2021, 12, 1432. [Google Scholar] [CrossRef] [PubMed]
- Rathke, P.; Thalau, O.; Kallo, J.; Schirmer, J.; Stephan, T. Long Distance Flight Testing with the Fuel Cell Powered Aircraft Antares DLR-H2. In Proceedings of the Deutscher Luft- und Raumfahrtkongress, Stuttgart, Germany, 10–12 September 2013; Deutsche Gesellschaft für Luft-und Raumfahrt-Lilienthal-Oberth eV.: Bonn, Germany, 2013. Document ID: 301219. [Google Scholar]
- Dudek, M.; Raźniak, A.; Rosół, M.; Siwek, T.; Dudek, P. Design, Development, and Performance of a 10 kW Polymer Exchange Membrane Fuel Cell Stack as Part of a Hybrid Power Source Designed to Supply a Motor Glider. Energies 2020, 13, 4393. [Google Scholar] [CrossRef]
- De Bernardinis, A.; Péra, M.C.; Garnier, J.; Hissel, D.; Coquery, G.; Kauffmann, J.M. Fuel cells multi-stack power architectures and experimental validation of 1 kW parallel twin stack PEFC generator based on high frequency magnetic coupling dedicated to on board power unit. Energy Convers. Manag. 2008, 49, 2367–2383. [Google Scholar] [CrossRef]
- Romeo, G.; Cestino, E.; Correa, G.; Borello, F. A fuel cell-based propulsion system for general aviation aircraft: The ENFI-CA-FC experience. SAE Int. J. Aerosp. 2011, 4, 724–737. [Google Scholar] [CrossRef]
- Geliev, A.; Varyukhin, A.; Zakharchenko, V.; Kiselev, I.; Zhuravlev, D. Conceptual Design of an Electric Propulsion System Based on Fuel Cells for an Ultralight Manned Aircraft. In Proceedings of the 2019 International Conference on Electrotechnical Complexes and Systems (ICOECS), Ufa, Russia, 21–25 October 2019; pp. 1–17. [Google Scholar]
- Donateo, T. Semi-Empirical Models for Stack and Balance of Plant in Closed-Cathode Fuel Cell Systems for Aviation. Energies 2023, 16, 7676. [Google Scholar] [CrossRef]
- Zhu, K.-Q.; Ding, Q.; Xu, J.-H.; Yang, C.; Zhang, J.; Zhang, Y.; Huang, T.-M.; Wan, Z.-M.; Wang, X.-D. Dynamic performance for a kW-grade air-cooled proton exchange membrane fuel cell stack. Int. J. Hydrogen Energy 2022, 47, 35398–35411. [Google Scholar] [CrossRef]
- Saadi, A.; Becherif, M.; Hissel, D.; Ramadan, H. Dynamic modeling and experimental analysis of PEMFCs: A comparative study. Int. J. Hydrogen Energy 2017, 42, 1544–1557. [Google Scholar] [CrossRef]
- Zeng, T.; Zhang, C.; Huang, Z.; Li, M.; Chan, S.H.; Li, Q.; Wu, X. Experimental investigation on the mechanism of variable fan speed control in Open cathode PEM fuel cell. Int. J. Hydrogen Energy 2019, 44, 24017–24027. [Google Scholar] [CrossRef]
- Wu, D.; Peng, C.; Yin, C.; Tang, H. Review of System Integration and Control of Proton Exchange Membrane Fuel Cells. Electrochem. Energy Rev. 2020, 3, 466–505. [Google Scholar] [CrossRef]
- Yang, C.-W.; Chen, Y.-S. A mathematical model to study the performance of a proton exchange membrane fuel cell in a dead-ended anode mode. Appl. Energy 2014, 130, 113–121. [Google Scholar] [CrossRef]
- Strahl, S.; Husar, A.; Puleston, P.; Riera, J. Performance Improvement by Temperature Control of an Open-Cathode PEM Fuel Cell System. Fuel Cells 2014, 14, 466–478. [Google Scholar] [CrossRef]
- Bradley, T.H.; Moffitt, B.A.; Mavris, D.N.; Parekh, D.E. Development and experimental characterization of a fuel cell powered aircraft. J. Power Sources 2007, 171, 793–801. [Google Scholar] [CrossRef]
- Lin, Y.-F.; Chen, Y.-S. Experimental study on the optimal purge duration of a proton exchange membrane fuel cell with a dead-ended anode. J. Power Sources 2017, 340, 176–182. [Google Scholar] [CrossRef]
- Zhao, D.; Xia, L.; Dang, H.; Wu, Z.; Li, H. Design and control of air supply system for PEMFC UAV based on dynamic decoupling strategy. Energy Convers. Manag. 2022, 253, 115159. [Google Scholar] [CrossRef]
- Peng, H.; Stefanopoulou, A.G. Simulation and analysis of transient fuel cell system performance-based on a dynamic reactant flow model. In Proceedings of the IMECE’02, ASME International Mechanical Engineering Congress & Exposition, New Orleans, LA, USA, 17–22 November 2002. [Google Scholar]
- Atkinson, R.W.; Hazard, M.W.; Rodgers, J.A.; Stroman, R.O.; Gould, B.D. An Open-Cathode Fuel Cell for Atmospheric Flight. J. Electrochem. Soc. 2017, 164, F46–F54. [Google Scholar] [CrossRef]
- Kandidayeni, M.; Macias, A.; Amamou, A.; Boulon, L.; Kelouwani, S.; Chaoui, H. Overview and benchmark analysis of fuel cell parameters estimation for energy management purposes. J. Power Sources 2018, 380, 92–104. [Google Scholar] [CrossRef]
- Sun, L.; Jin, Y.; You, F. Active disturbance rejection temperature control of open-cathode proton exchange membrane fuel cell. Appl. Energy 2020, 261, 114381. [Google Scholar] [CrossRef]
- Hu, M.; Zhao, R.; Pan, R.; Cao, G. Disclosure of the internal mechanism during activating a proton exchange membrane fuel cell based on the three-step activation method. Int. J. Hydrogen Energy 2021, 46, 3008–3021. [Google Scholar] [CrossRef]
- Zhan, Y.; Guo, Y.; Zhu, J.; Liang, B.; Yang, B. Comprehensive influences measurement and analysis of power converter low frequency current ripple on PEM fuel cell. Int. J. Hydrogen Energy 2019, 44, 31352–31359. [Google Scholar] [CrossRef]
- Tan, B.; Chen, H.; Quan, R.; Quan, S.; Zhou, Y. Study on data-driven PEMFC humidity mechanism soft-sensing model. J. Phys. Conf. Ser. 2019, 1423, 012043. [Google Scholar] [CrossRef]
- Guzzella, L.; Sciarretta, A. Vehicle Propulsion Systems, Introduction to Modeling and Optimization, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ren, P.; Pei, P.; Li, Y.; Wu, Z.; Chen, D.; Huang, S. Degradation mechanisms of proton exchange membrane fuel cell under typical automotive operating conditions. J. Prog. Energy Combust. Sci. 2020, 80, 100859. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M.; Shaw, S. Dynamic Models and Model Validation for PEM Fuel Cells Using Electrical Circuits. IEEE Trans. Energy Convers. 2005, 20, 442–451. [Google Scholar] [CrossRef]
- Restrepo, C.; Konjedic, T.; Garces, A.; Calvente, J.; Giral, R. Identification of a Proton-Exchange Membrane Fuel Cell’s Model Parameters by Means of an Evolution Strategy. IEEE Trans. Ind. Inform. 2015, 11, 548–559. [Google Scholar] [CrossRef]
- Boukoberine, M.N.; Zia, M.F.; Benbouzid, M.; Zhou, Z.; Donateo, T. Hybrid fuel cell powered drones energy management strategy improvement and hydrogen saving using real flight test data. Energy Convers. Manag. 2021, 236, 113987. [Google Scholar] [CrossRef]
- Boukoberine, M.N.; Donateo, T.; Benbouzid, M. Optimized energy management strategy for hybrid fuel cell powered drones in persistent missions using real flight test data. IEEE Trans. Energy Convers. 2022, 37, 2080–2091. [Google Scholar] [CrossRef]
- Ou, K.; Wang, Y.; Kim, Y. Performance Optimization for Open-cathode Fuel Cell Systems with Overheating Protection and Air Starvation Prevention. Fuel Cells 2017, 17, 299–307. [Google Scholar] [CrossRef]
- Lee, C.-H.; Yang, J.-T. Modeling the Ballard-Mark-5 proton exchange membrane fuel cell with power converters for applications in autonomous underwater vehicles. J. Power Sources 2011, 196, 3810–3823. [Google Scholar] [CrossRef]
- Vandana, G.A.; Panigrahi, B.K. Multi-dimensional digital twin of energy storage system for electrical vehicles: A brief review. Energy Storage Early View 2021, 3, e242. [Google Scholar] [CrossRef]
- Bhatti, G.; Mohan, H.; Singh, R. R Towards the future of smart electric vehicles: Digital twin technology. Renew. Sustain. Energy Rev. 2021, 141, 110801. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Duan, X.; Liu, S.; Liu, J.; Hu, S. Multi-objective energy management for Atkinson cycle engine and series hybrid electric vehicle based on evolutionary NSGA-II algorithm using digital twins. Energy Convers. Manag. 2021, 230, 113788. [Google Scholar] [CrossRef]
- Kamran, S.S.; Haleem, A.; Bahl, S.; Javaid, M.; Nandan, D.; Verma, A.S. Role of smart materials and digital twin (DT) for the adoption of electric vehicles in India. Mater. Today Proc. 2022, 52, 2295–2304. [Google Scholar] [CrossRef]
- Glaessgen, E.; Stargel, D. The digital twin paradigm for future NASA and U.S. Air DT9 Force vehicles. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012. [Google Scholar]
- Subin, K.; Jithesh, P.K. Experimental study on self-humidified operation in PEM fuel cells. Sustain. Energy Technol. Assess. 2018, 27, 17–22. [Google Scholar] [CrossRef]
- Abul-Hawa, A.A.; Ebaid, M.S.; Bhinder, F.S.; Calay, R.K. Control strategy for polymer electrolyte membrane fuel cell system. In Proceedings of the 2006 UKACC International Conference on Control, Glasgow, UK, 30 August–1 September 2006; p. 94. [Google Scholar]
- Le, P.-L.; Singh, B.; Chen, Y.-S.; Arpornwichanop, A. An experimental study for optimizing the energy efficiency of a proton exchange membrane fuel cell with an open-cathode. Int. J. Hydrogen Energy 2021, 46, 26507–26517. [Google Scholar] [CrossRef]
- Omran, A.; Lucchesi, A.; Smith, D.; Alaswad, A.; Amiri, A.; Wilberforce, T.; Sodré, J.R.; Olabi, A. Mathematical model of a proton-exchange membrane (PEM) fuel cell. Int. J. Thermofluids 2021, 11, 100110. [Google Scholar] [CrossRef]
- Choe, S.-Y.; Ahn, J.-W.; Lee, J.-G.; Baek, S.-H. Dynamic Simulator for a PEM Fuel Cell System with a PWM DC/DC Converter. IEEE Trans. Energy Convers. 2008, 23, 669–680. [Google Scholar] [CrossRef]
- Djerioui, A.; Houari, A.; Zeghlache, S.; Saim, A.; Benkhoris, M.F.; Meshabi, T.; Machmoum, M. Energy management strategy of Supercapacitor/Fuel Cell energy storage devices for vehicle applications. Int. J. Hydrogen Energy 2019, 44, 23416–23428. [Google Scholar] [CrossRef]
- Hoogendoorn, J. Fuel Cells and Battery Hybrid System Optimization. Master’s Thesis in Aerospace Engineering, DELFT University of Technology, Delft, The Netherlands, 2018. [Google Scholar]
- Chang, V.; Gallman, J. Altitude Testing of Fuel Cell Systems for Aircraft Applications. Power Systems Conference. J. Aerosp. 2004, 113, 1943–1957. [Google Scholar]
- Verstraete, D.; Lehmkuehler, K.; Gong, A.; Harvey, J.R.; Brian, G.; Palmer, J.L. Characterisation of a hybrid, fuel-cell-based propulsion system for small unmanned aircraft. J. Power Sources 2014, 250, 204–211. [Google Scholar] [CrossRef]
- Donateo, T.; Pacella, D.; Indiveri, G.; Ingrosso, F.; Damiani, A. Dynamic Modeling of a PEM Fuel Cell for a Low Consumption Prototype. SAE Tech. Pap. 2013, 2, 1–10. [Google Scholar] [CrossRef]
- Saleh, I.M.M.; Ali, R.; Zhang, H. Simplified mathematical model of proton exchange membrane fuel cell based on horizon fuel cell stack. J. Mod. Power Syst. Clean Energy 2016, 4, 668–679. [Google Scholar] [CrossRef]
- Sahel, I.M.M. Modeling, Simulation and Performance Evaluation: PEM Fuel Cells for High Altitude UAS. Ph.D. Thesis, Sheffield Hallam University, Sheffield, UK, 2015. [Google Scholar]
- Barelli, L.; Bidini, G.; Gallorini, F.; Ottaviano, A. Analysis of the operating conditions influence on PEM fuel cell performances by means of a novel semi-empirical model. Int. J. Hydrogen Energy 2011, 36, 10434–10442. [Google Scholar] [CrossRef]
- Fathy, A.; Abd Elaziz, M.; Alharbi, A.F. A novel approach based on hybrid vortex search algorithm and differential evolution for identifying the optimal parameters of PEM fuel cell. Renew. Energy 2020, 146, 1833–1845. [Google Scholar] [CrossRef]
- Qingshan, X.; Nianchun, W.; Ichiyanagi, K.; Yukita, K. PEM Fuel Cell modeling and parameter influences of performance evaluation. In Proceedings of the 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; pp. 2827–2832. [Google Scholar]
- Mohamed, W.W.; Kamil, M.H.M. Hydrogen preheating through waste heat recovery of an open-cathode PEM fuel cell leading to power output improvement. Energy Convers. Manag. 2016, 124, 543–555. [Google Scholar] [CrossRef]
- Musio, F.; Tacchi, F.; Omati, L.; Stampino, P.G.; Dotelli, G.; Limonta, S.; Brivio, D.; Grassini, P. PEMFC system simulation in MATLAB-Simulink® environment. Int. J. Hydrogen Energy 2011, 36, 8045–8052. [Google Scholar] [CrossRef]
- Barreras, F.; Lopez, A.M.; Lozano, A.; Barranco, J.E. Experimental study of the pressure drop in the cathode side of air-forced open-cathode proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2011, 36, 7612–7620. [Google Scholar] [CrossRef]
- Sasmito, A.P.; Birgersson, E.; Lum, K.W.; Mujumdar, A.S. Fan selection and stack design for open-cathode polymer electrolyte fuel cell stacks. Renew. Energy 2012, 37, 325–332. [Google Scholar] [CrossRef]
- Arredondo, A.; Roy, P.; Wofford, E. Implementing PWM fan speed control within a computer chassis power supply. In Proceedings of the Twentieth Annual IEEE Applied Power Electronics Conference and Exposition, APEC 2005, Austin, TX, USA, 6–10 March 2005. [Google Scholar]
- Wang, Y.-X.; Qin, F.-F.; Ou, K.; Kim, Y.-B. Temperature Control for a Polymer Electrolyte Membrane Fuel Cell by Using Fuzzy Rule. IEEE Trans. Energy Convers. 2016, 31, 667–675. [Google Scholar] [CrossRef]
- Barroso, J.; Renau, J.; Lozano, A.; Miralles, J.; Martín, J.; Sánchez, F.; Barreras, F. Experimental determination of the heat transfer coefficient for the optimal design of the cooling system of a PEM fuel cell placed inside the fuselage of an UAV. Appl. Therm. Eng. 2015, 89, 1–10. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.-Y. Dynamics of polymer electrolyte fuel cells undergoing load changes. Electrochim. Acta 2006, 51, 3924–3933. [Google Scholar] [CrossRef]
- Tahri, A.; El Fadil, H.; Belhaj, F.; Gaouzi, K.; Rachid, A.; Giri, F.; Chaoui, F. Management of fuel cell power and supercapacitor state-of-charge for electric vehicles. Electr. Power Syst. Res. 2019, 160, 89–98. [Google Scholar] [CrossRef]
- Ríos, G.M.; Becker, F.; Vorndran, A.; Gentner, C.; Ansar, S.A. Investigation of gas purging and cold storage impact on PEM fuel cell system performance for aeronautical applications. E3S Web Conf. 2022, 334, 06004. [Google Scholar] [CrossRef]
- Daud, W.; Rosli, R.; Majlan, E.; Hamid, S.; Mohamed, R.; Husaini, T. PEM fuel cell system control: A review. Renew. Energy 2017, 113, 620–638. [Google Scholar] [CrossRef]
- Mahjoubi, C.; Olivier, J.-C.; Skander-Mustapha, S.; Machmoum, M.; Slama-Belkhodja, I. An improved thermal control of open cathode proton exchange membrane fuel cell. 9th International Renewable Energy Congress (IREC). Int. J. Hydrogen Energy 2019, 44, 11332–11345. [Google Scholar] [CrossRef]
- Mirfarsi, S.H.; Parnian, M.J.; Rowshanzamir, S. Self-humidifying proton exchange membranes for fuel cell applications: Advances and challenges. Processes 2020, 8, 1069. [Google Scholar] [CrossRef]
- Kumar, S.S.; Cirrincione, M.; Lechappe, V.; Ram, K.R.; Mohammadi, A. A Simplified Control Oriented Model of an Open Cathode PEM Fuel Cell. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 2415–2420. [Google Scholar]
- Wang, Y.; Wang, C.Y. Transient analysis of polymer electrolyte fuel cells. Electrochim. Acta 2005, 50, 1307–1315. [Google Scholar] [CrossRef]
- López-Sabirón, A.M.; Barroso, J.; Roda, V.; Barranco, J.; Lozano, A.; Barreras, F. Design and development of the cooling system of a 2 kW nominal power open-cathode polymer electrolyte fuel cell stack. Int. J. Hydrogen Energy 2012, 37, 7289–7298. [Google Scholar] [CrossRef]
- Strahl, S.; Costa-Castello, R. Temperature control of open-cathode PEM fuel cells. IFAC PapersOnLine 2017, 50, 11088–11093. [Google Scholar] [CrossRef]
- Zhu, J.; Zou, J.; Li, X.; Peng, C. An adaptive sliding mode observer based near-optimum OER tracking control approach for PEMFC under dynamic operation condition. Int. J. Hydrogen Energy 2022, 47, 1157–1171. [Google Scholar] [CrossRef]
- Qi, Y.; Espinoza-Andaluz, M.; Thern, M.; Li, T.; Andersson, M. Dynamic modeling and controlling strategy of polymer electrolyte fuel cells. Int. J. Hydrogen Energy 2020, 45, 29718–29729. [Google Scholar] [CrossRef]
- Ou, K.; Yuan, W.-W.; Choi, M.; Yang, S.; Kim, Y.-B. Performance increase for an open-cathode PEM fuel cell with humidity and temperature control. Int. J. Hydrogen Energy 2017, 42, 29852–29862. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, P.; Li, X.; Jiang, B. Robust oxygen excess ratio control of PEMFC systems using adaptive dynamic programming. Energy Rep. 2022, 8, 2036–2044. [Google Scholar] [CrossRef]
- Zhang, B.; Lin, F.; Zhang, C.; Liao, R.; Wang, Y.-X. Design and implementation of model predictive control for an open-cathode fuel cell thermal management system. Renew. Energy 2020, 154, 1014–1024. [Google Scholar] [CrossRef]
- Li, X.; Qi, Y.; Li, S.; Tunestal, P.; Andersson, M. A multi-input and single-output voltage control for a polymer electrolyte fuel cell system using model predictive control method. Int. J. Energy Res. 2021, 45, 12854–12863. [Google Scholar] [CrossRef]
- Kandidayeni, M.; Macias, F.A.; Boulon, L.; Kelouwani, S. Efficiency Enhancement of an Open Cathode Fuel Cell Through a Systemic Management. IEEE Trans. Veh. Technol. 2019, 68, 11462–11472. [Google Scholar] [CrossRef]
- Çınar, H.; Kandemir, I.; Donateo, T. Current Technologies and Future Trends of Hydrogen Propulsion Systems in Hybrid Small Unmanned Aerial Vehicles. In Hydrogen Electrical Vehicles; Scrivener Publishing LLC: Beverly, MA, USA, 2023; pp. 75–109. [Google Scholar]
- Gong, C.; Xing, L.; Liang, C.; Tu, Z. Modeling and dynamic characteristic simulation of air-cooled proton exchange membrane fuel cell stack for unmanned aerial vehicle. Renew. Energy 2022, 188, 1094–1104. [Google Scholar] [CrossRef]
- Song, W.J.; Chen, H.; Guo, H.; Ye, F.; Li, J.R. Research progress of proton exchange membrane fuel cells utilizing in high altitude environments. Int. J. Hydrogen Energy 2022, 47, 24945–24962. [Google Scholar] [CrossRef]
- González-Espasandín, O.; Leo, T.J.; Raso, M.A.; Navarro, E. Direct methanol fuel cell (DMFC) and H2 proton exchange membrane fuel (PEMFC/H2) cell performance under atmospheric flight conditions of Unmanned Aerial Vehicles. Renew. Energy 2019, 130, 762–773. [Google Scholar] [CrossRef]
- Amphlett, J.C.; Baumert, R.M.; Harris, T.J.; Mann, R.F.; Peppley, B.A.; Roberge, P.R. Performance modeling of the Ballard Mark IV solid polymer electrolyte fuel cell: I. Mechanistic model development. J. Electrochem. Soc. 1995, 142, 1. [Google Scholar] [CrossRef]
- Corêa, J.M.; Farret, F.A.; Canha, L.N.; Simões, M.G. An Electrochemical-Based Fuel Cell Model Suitable for Electrical Engineering Automation Approach. IEEE Trans. Ind. Electron. 2004, 51, 1103–1111. [Google Scholar] [CrossRef]
- Mann, R.F.; Amphlett, J.C.; Hooper, M.A.I.; Jensen, H.M.; Peppley, B.A.; Roberge, P.R. Development and application of a generalised steady-state electrochemical model for a PEM fuel cell. J. Power Sources 2000, 86, 173–180. [Google Scholar] [CrossRef]
- El-Fergany, A.A. Electrical characterisation of proton exchange membrane fuel cells stack using grasshopper optimizer. IET Renew. Power Gener. 2017, 12, 9–17. [Google Scholar] [CrossRef]
- Lee, J.; Lalk, T.; Appleby, A. Modeling electrochemical performance in large scale proton exchange membrane fuel cell stacks. J. Power Sources 1998, 70, 258–268. [Google Scholar] [CrossRef]
- Dick, E. Dynamic Similitude. In Fundamentals of Turbomachines; Springer International Publishing: Cham, Switzerland, 2022; pp. 257–292. [Google Scholar]
- Li, Q.; Chen, W.; Wang, Y.; Liu, S.; Jia, J. Parameter identification for PEM fuel-cell mechanism model based on effective informed adaptive particle swarm optimization. IEEE Trans. Ind. Electron. 2010, 58, 2410–2419. [Google Scholar] [CrossRef]
- Lin, C.; Yan, X.; Wei, G.; Ke, C.; Shen, S.; Zhang, J. Optimization of configurations and cathode operating parameters on liquid-cooled proton exchange membrane fuel cell stacks by orthogonal method. Appl. Energy 2019, 253, 113496. [Google Scholar] [CrossRef]
- Al-Othman, A.K.; Ahmed, N.A.; Al-Fares, F.S.; AlSharidah, M.E. Parameter Identification of PEM Fuel Cell Using Quantum-Based Optimization Method. Arab. J. Sci. Eng. 2015, 40, 2619–2628. [Google Scholar] [CrossRef]
- Headley, H.; Yu, V.; Borduin, R.; Chen, D.; Li, W. Development and experimental validation of a physical-based PEM fuel cell model for cathode humidity control design. IEEE/ASME Trans. Mechatron. 2016, 21, 1775–1782. [Google Scholar] [CrossRef]
- Seleem, S.I.; Hasanien, H.M.; El-Fergany, A.A. Equilibrium optimizer for parameter extraction of a fuel cell dynamic model. Renew. Energy 2021, 169, 117–128. [Google Scholar] [CrossRef]
- Mitra, U.; Arya, A.; Gupta, S. A comprehensive and comparative review on parameter estimation methods for modelling proton exchange membrane fuel cell. Fuel 2023, 335, 127080. [Google Scholar] [CrossRef]
- Kandidayeni, M.; Macias, A.; Amamou, A.A.; Boulon, L.; Kelouwani, S. Comparative analysis of two online identification algorithms in a fuel cell system. Fuel Cells 2018, 18, 347–358. [Google Scholar] [CrossRef]
- Kandidayeni, M.; Chaoui, H.; Boulon, L.; Trovão, J.P.F. Adaptive parameter identification of a fuel cell system for health-conscious energy management applications. IEEE Trans. Intell. Transp. Syst. 2021, 23, 7963–7973. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, G.; Wang, H.; Xuan, J.; Jiao, K. Multi-physics-resolved digital twin of proton exchange membrane fuel cells with a data-driven surrogate model. Energy AI 2020, 1, 100004. [Google Scholar] [CrossRef]
- Meraghni, S.; Terrissa, L.S.; Yue, M.; Ma, J.; Jemei, S.; Zerhouni, N. A data-driven digital-twin prognostics method for proton exchange membrane fuel cell remaining useful life prediction. Int. J. Hydrogen Energy 2021, 46, 2555–2564. [Google Scholar] [CrossRef]
- Rassõlkin, A.; Vaimann, T.; Kallaste, A.; Kuts, V. Digital twin for propulsion drive of autonomous electric vehicle. In Proceedings of the 2019 IEEE 60th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 7–9 October 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Bartolucci, L.; Cennamo, E.; Cordiner, S.; Mulone, V.; Pasqualini, F.; Aimo Boot, F. Digital Twin of Fuel Cell Hybrid Electric Vehicle: A detailed modelling approach of the hydrogen powertrain and the auxiliary systems. E3S Web Conf. 2022, 334, 06003. [Google Scholar] [CrossRef]
- Bartolucci, L.; Cennamo, E.; Cordiner, S.; Mulone, V.; Pasqualini, F.; Boot, M.A. Digital twin of a hydrogen fuel cell hybrid electric vehicle: Effect of the control strategy on energy efficiency. Int. J. Hydrogen Energy 2023, 48, 20971–20985. [Google Scholar] [CrossRef]
- Bai, F.; Quan, H.B.; Yin, R.J.; Zhang, Z.; Jin, S.Q.; He, P.; Mu, Y.-T.; Gong, X.-M.; Tao, W.Q. Three-dimensional multi-field digital twin technology for proton exchange membrane fuel cells. Appl. Energy 2022, 324, 119763. [Google Scholar] [CrossRef]
- Yue, M.; Benaggoune, K.; Meng, J.; Diallo, D. Implementation of an early-stage fuel cell degradation prediction digital twin based on transfer learning. IEEE Trans. Transp. Electrif. 2022, 9, 3308–3318. [Google Scholar] [CrossRef]
- Kandidayeni, M.; Macias, A.; Boulon, L.; Trovão, J.P.F. Online modeling of a fuel cell system for an energy management strategy design. Energies 2020, 13, 3713. [Google Scholar] [CrossRef]
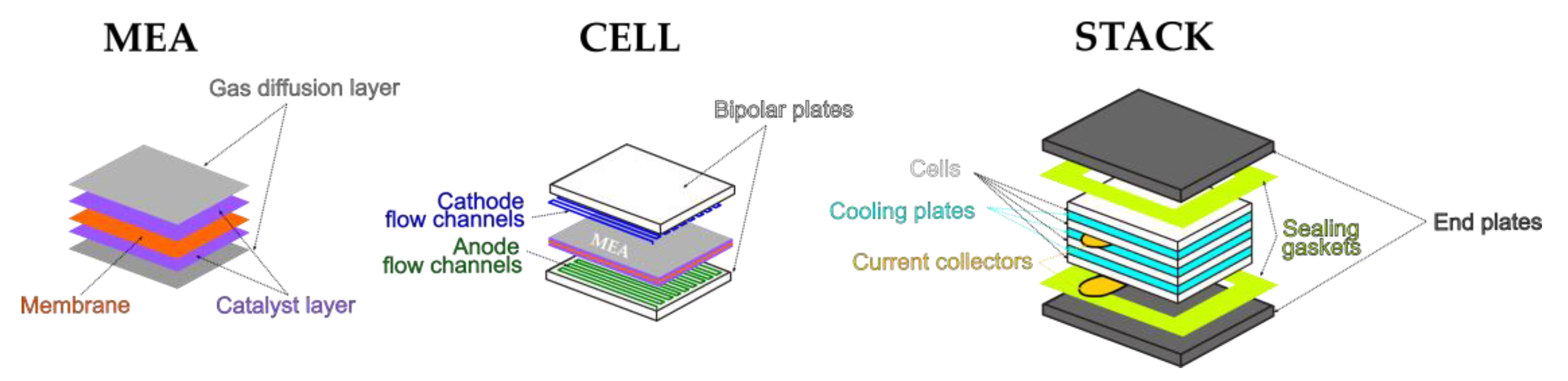
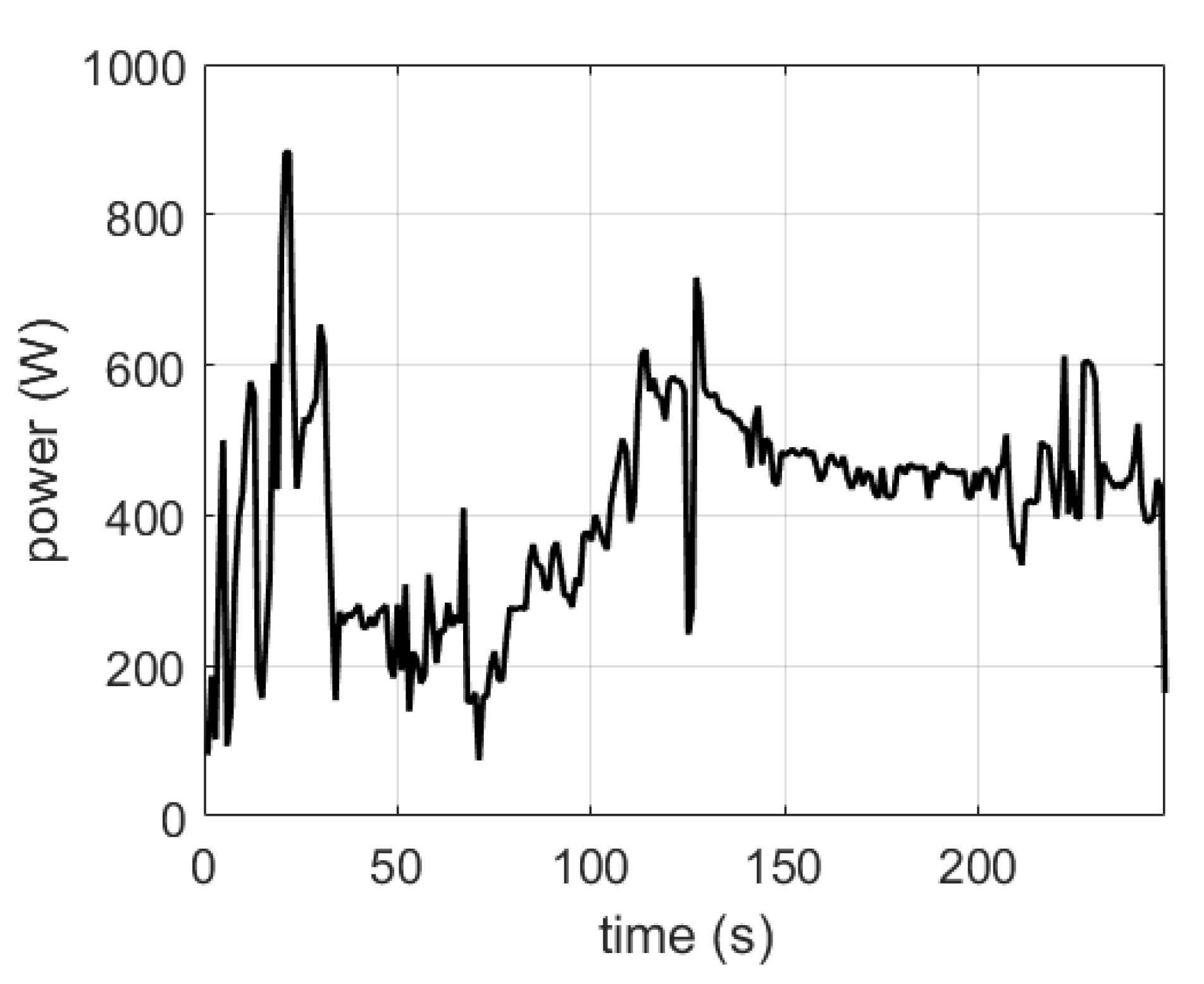
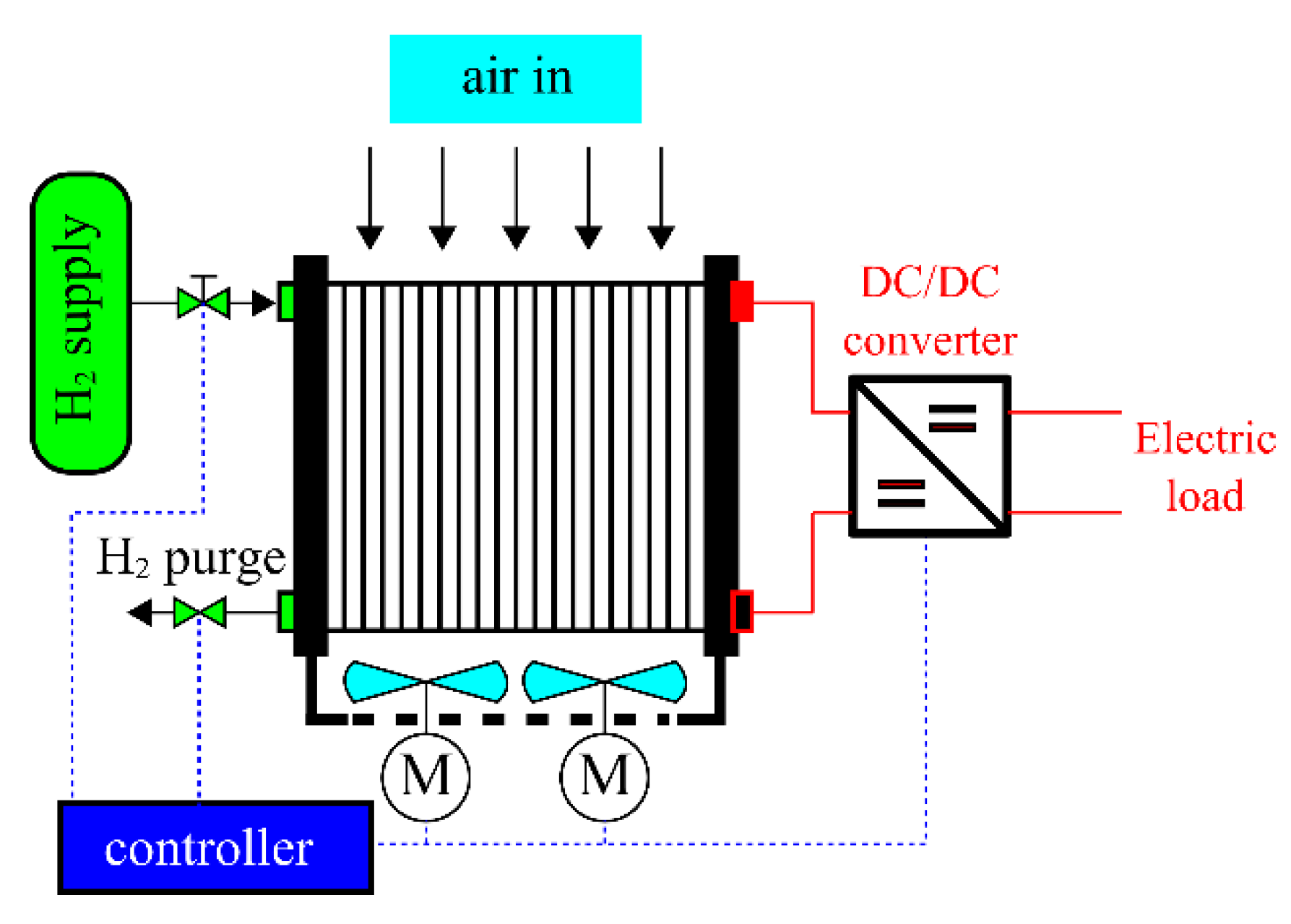
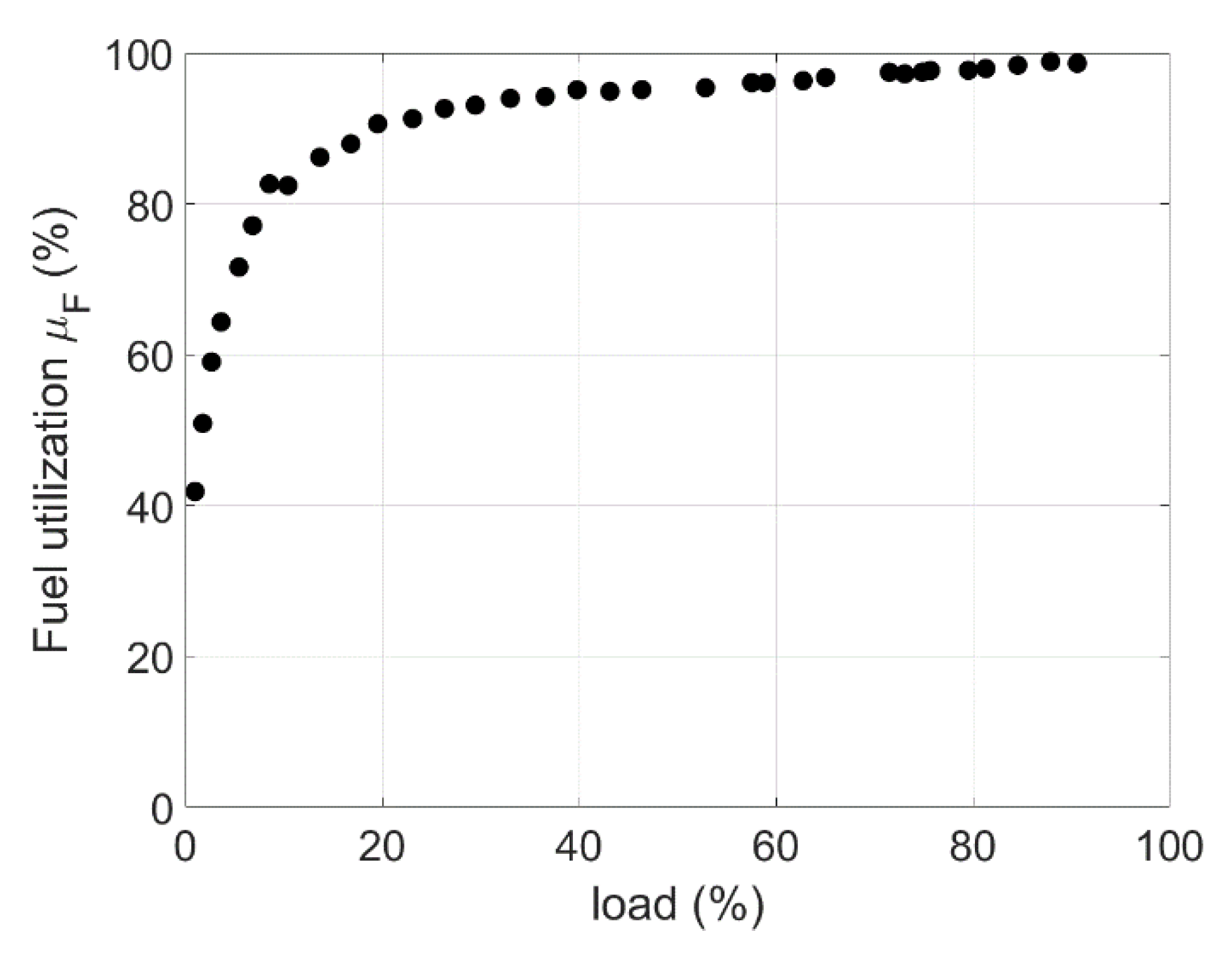



| Phenomenon | Scale of Time Constants | Source |
|---|---|---|
| Stack temperature | [55] | |
| Membrane hydration | [83] | |
| Fan speed | [30] | |
| Gas transport | [55] | |
| Double layer discharge | [83] |
| Stack Name | Ref. | ||||
|---|---|---|---|---|---|
| Horizon 2000 W | [69,88] | ||||
| Horizon 1000 W | −0.944 | 3.54 × 10−3 | [65] | ||
| Horizon 500 W | [57] | ||||
| 500 W | [92] | ||||
| Ballard Mark V FC 5 kW | From Equation (17) | [87] | |||
| Ballard Mark V FC 5 kW | 0.00312 | [98] | |||
| Ballard Mark IV FC | 0.00312 | [99] | |||
| Ballard Mark V FC | 0.00354 | [99] | |||
| NedStack PS6 (500 W) | −1.023071 | 3.4760 × 10−3 | 7.7883 × 10−5 | [91] | |
| NedStack PS6 (500 W) | −1.1997 | 3.4172 × 10−3 3.5505 × 10−3 | 3.66 × 10−5 4.614 × 10−5 | [100] | |
| Not declared | −0.944 | 3.54 × 10−3 | [55] | ||
| Unspecified 300 W stack | From Equation (17) | [94] |
| Component | Parameter | Ambient Temperature | Ambient Pressure | Relative Humidity |
|---|---|---|---|---|
| Stack | Nernst voltage | during transients, Equation (9) | Primary. Equation (9) | |
| Activation losses | during transients, Equation (16) Equation (15) | Primary through Equation (19) or secondary through Equation (26) | ||
| Ohmic losses | during transients Equation (21) | Secondary, not modeled | Equation (21) | |
| Concentration losses | during transients, Equation (23) | Equation (24) | ||
| Cooling system | Air flow rate and PWM duty cycle | Primary from thermal balance under static, Equation (43), or dynamic conditions, Equation (66), | Primary through air density, Equation (47) | (47) |
| Fan power | Primary through air density, Equation (64) or (65) | Primary through air density, Equation (64) or (65) | Secondary through air density, e Equation (64) or (65) | |
| Purging system | Hydrogen utilization | Negligible | Primary through Equation (33) or (34) | Negligible |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Donateo, T. Simulation Approaches and Validation Issues for Open-Cathode Fuel Cell Systems in Manned and Unmanned Aerial Vehicles. Energies 2024, 17, 900. https://doi.org/10.3390/en17040900
Donateo T. Simulation Approaches and Validation Issues for Open-Cathode Fuel Cell Systems in Manned and Unmanned Aerial Vehicles. Energies. 2024; 17(4):900. https://doi.org/10.3390/en17040900
Chicago/Turabian StyleDonateo, Teresa. 2024. "Simulation Approaches and Validation Issues for Open-Cathode Fuel Cell Systems in Manned and Unmanned Aerial Vehicles" Energies 17, no. 4: 900. https://doi.org/10.3390/en17040900
APA StyleDonateo, T. (2024). Simulation Approaches and Validation Issues for Open-Cathode Fuel Cell Systems in Manned and Unmanned Aerial Vehicles. Energies, 17(4), 900. https://doi.org/10.3390/en17040900






