A Grid-Connected Inverter with Grid-Voltage-Weighted Feedforward Control Based on the Quasi-Proportional Resonance Controller for Suppressing Grid Voltage Disturbances
Abstract
1. Introduction
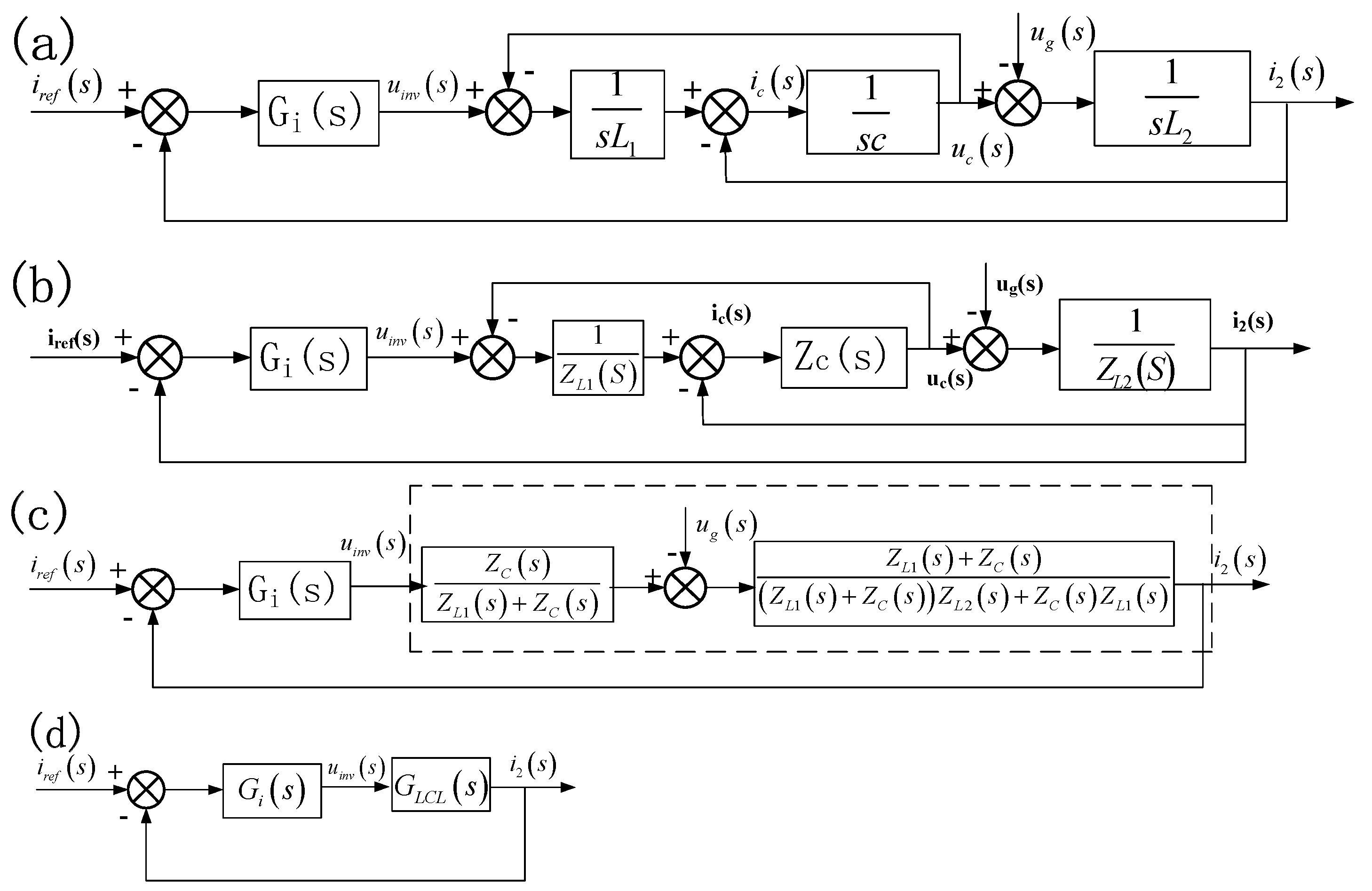
2. Control Strategy and Output Impedance of the LCL GCI
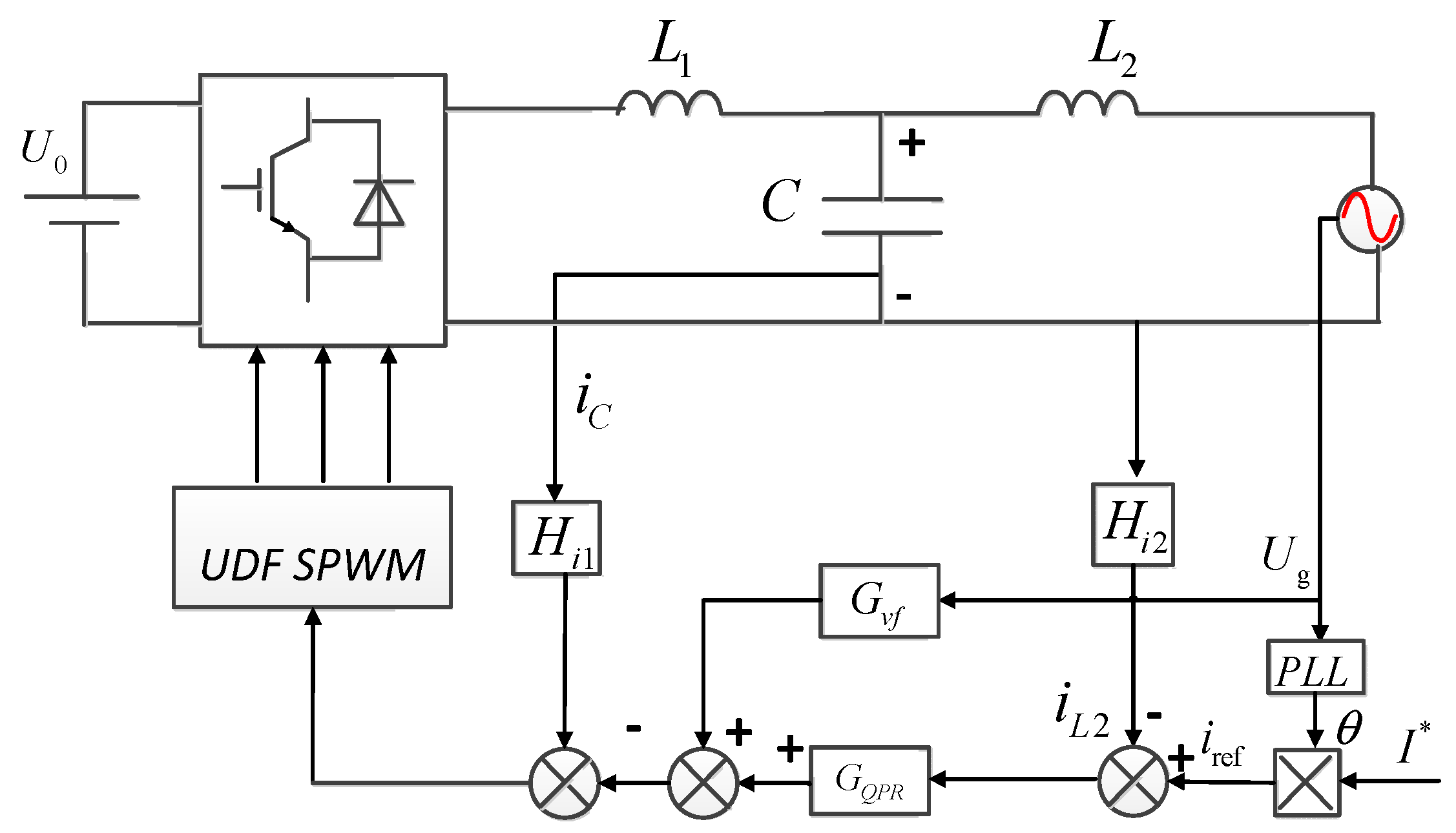
2.1. Unipolar Double-Frequency (UDF) SPWM
2.2. Stability Analysis of the LCL GCI
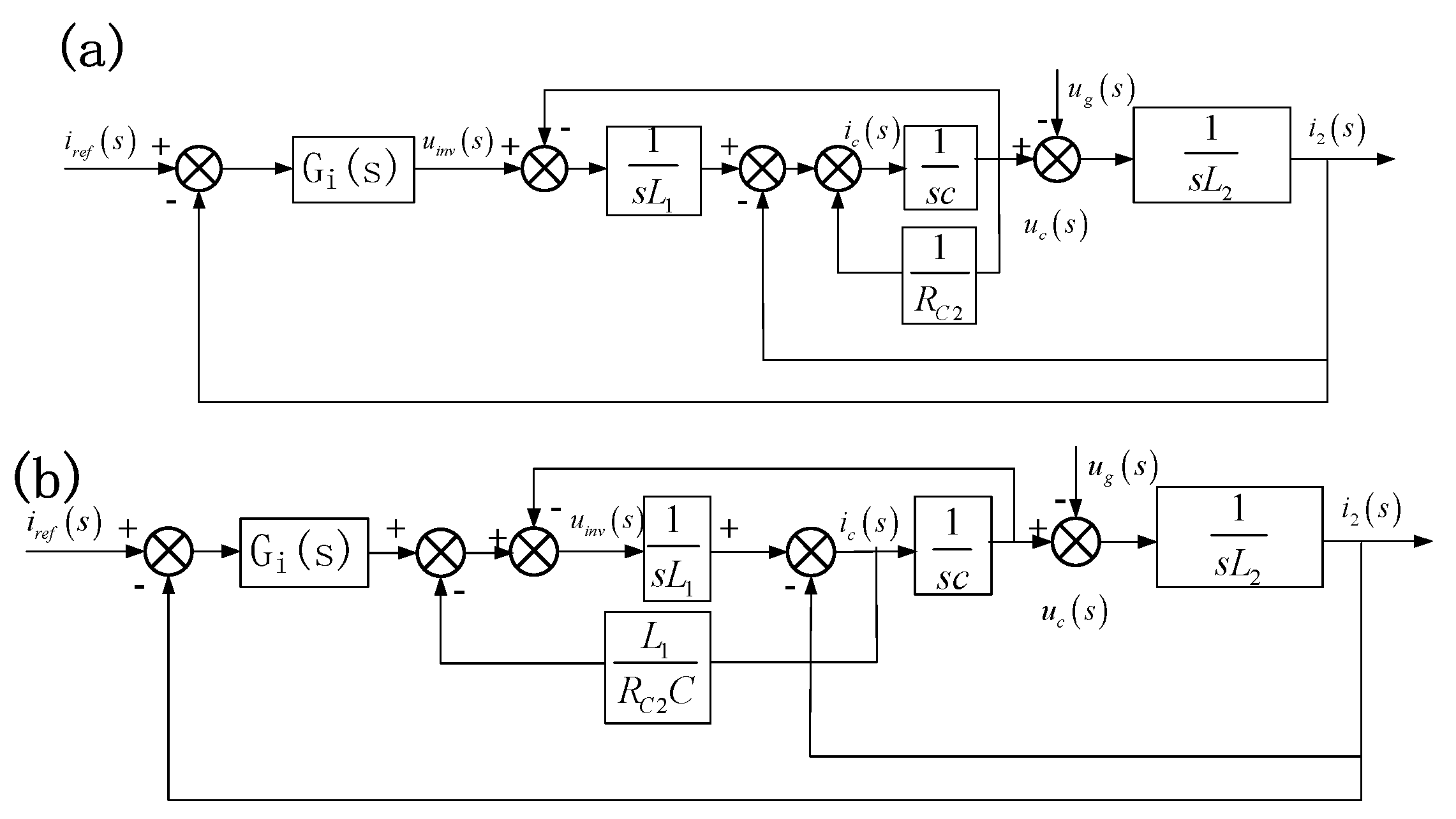
2.3. Active-Damped LCL GCI
2.4. Analysis of the Active-Damped LCL GCI
3. Proportional-Resonance Controller Based on a Voltage Weight Feedforward Scheme for LCL GCV
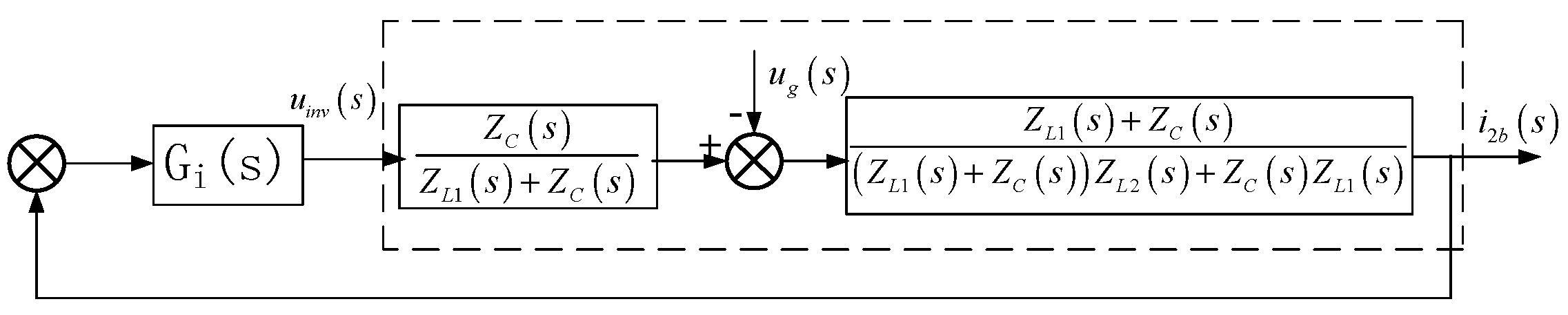
3.1. Analysis of the Influence of Power Grid Voltage on LCL Inverter
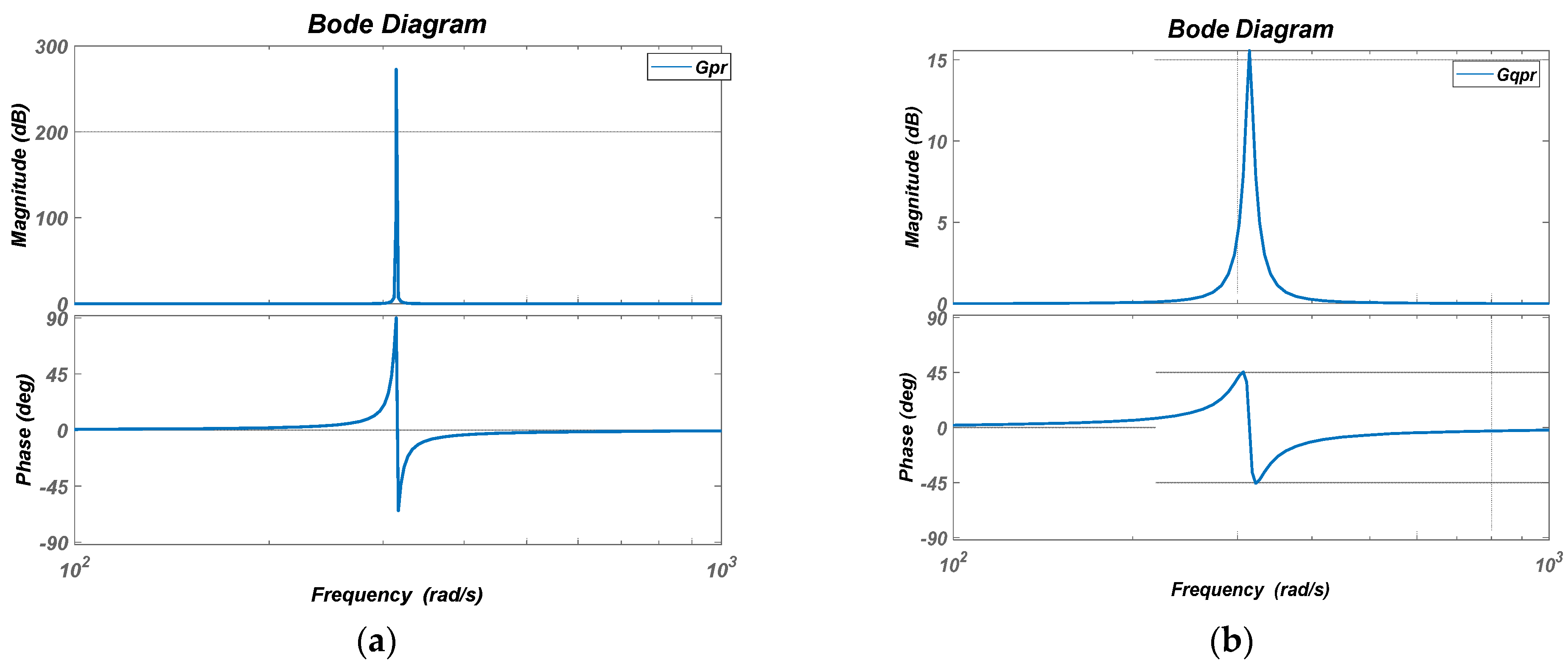
3.2. Proportional Resonance (PR) Controller
3.3. Grid-Voltage-Weighted Feedforward Scheme Based on the QPR
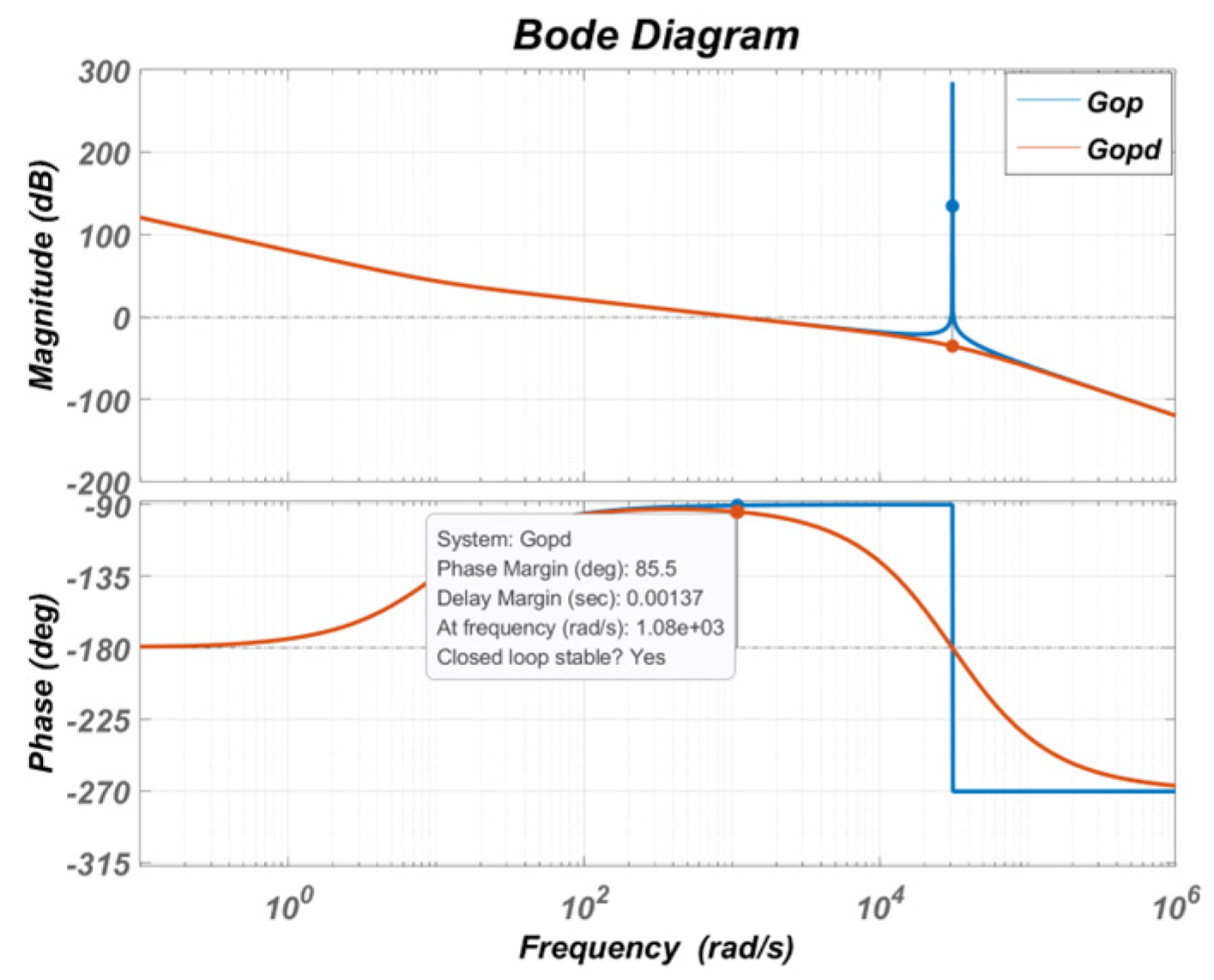
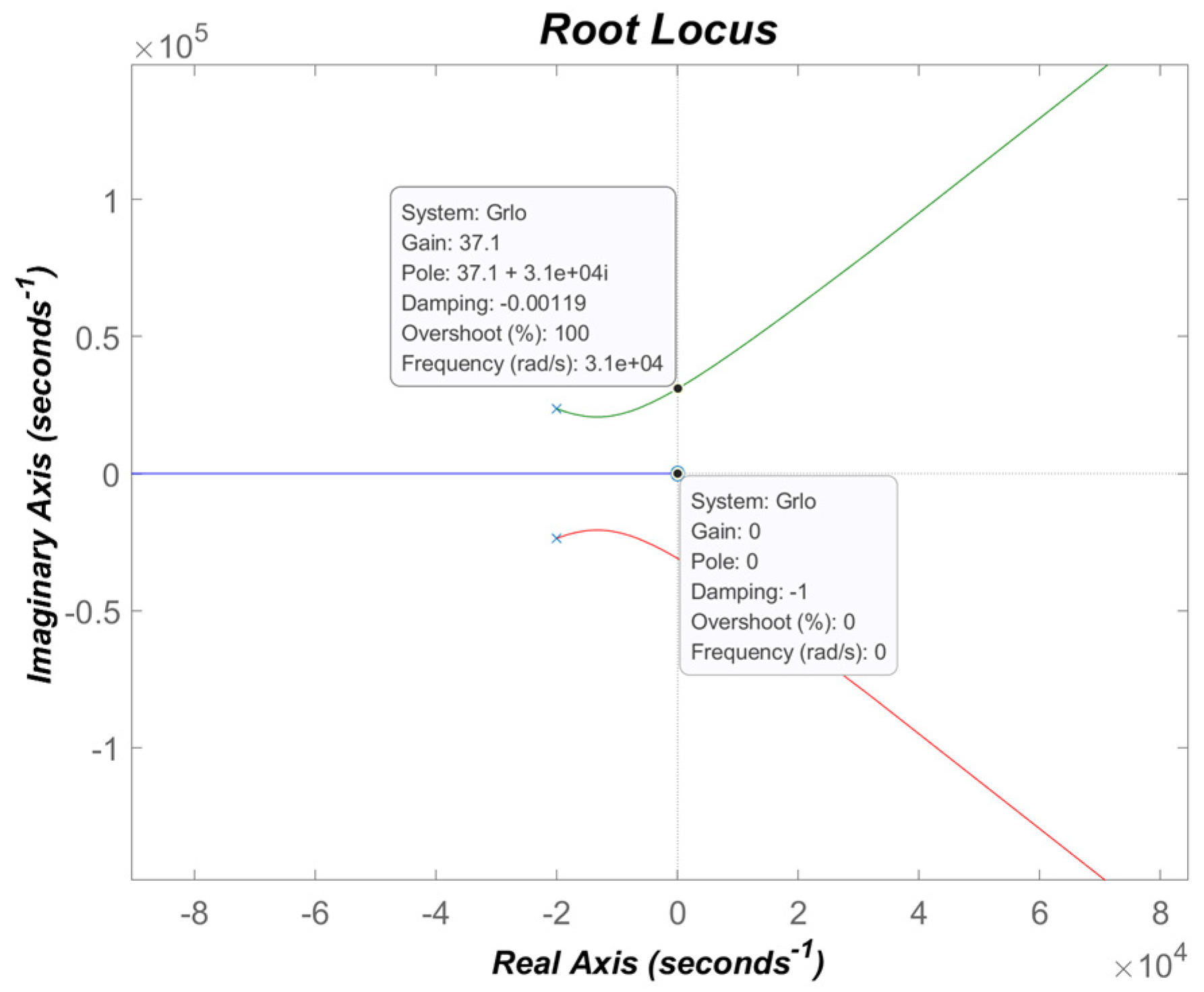
3.4. Stability Analysis of Voltage Full Feedforward in the QPR Controller
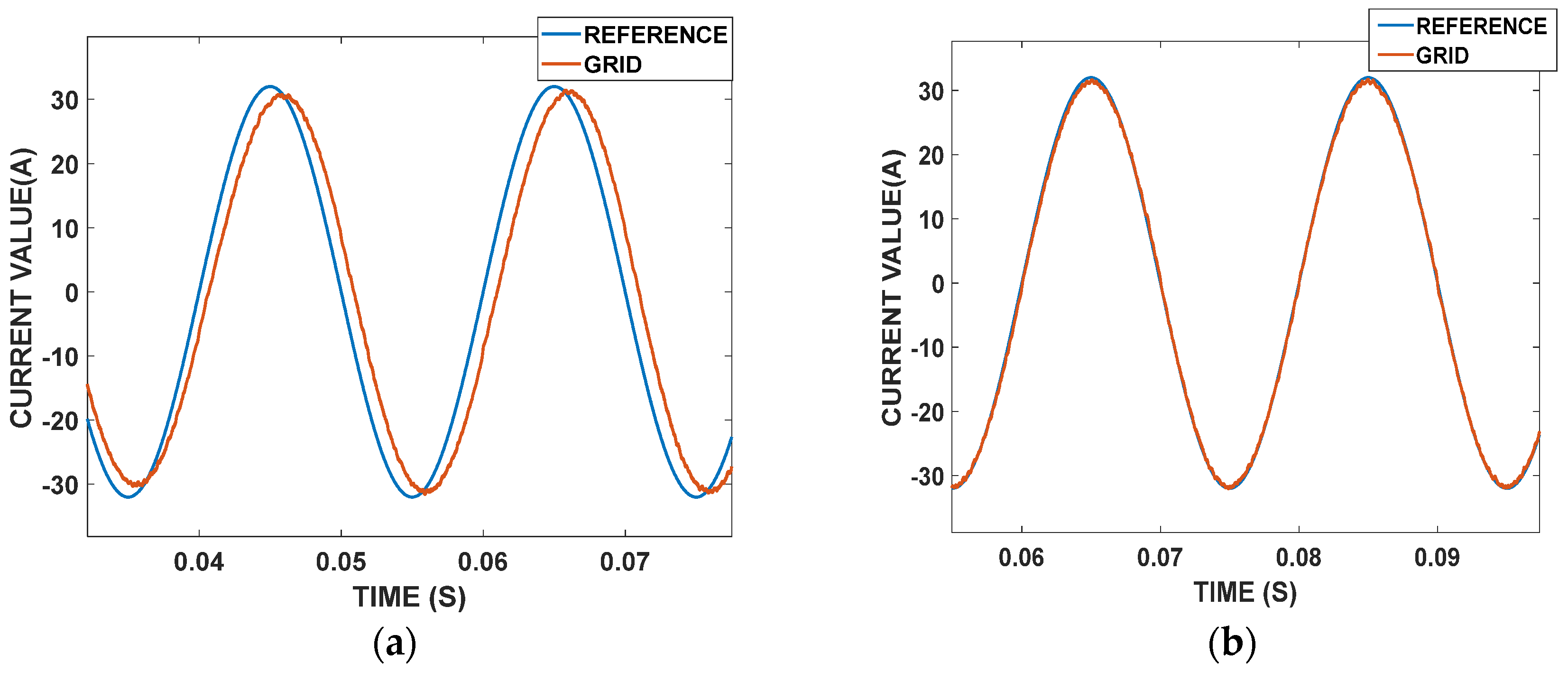
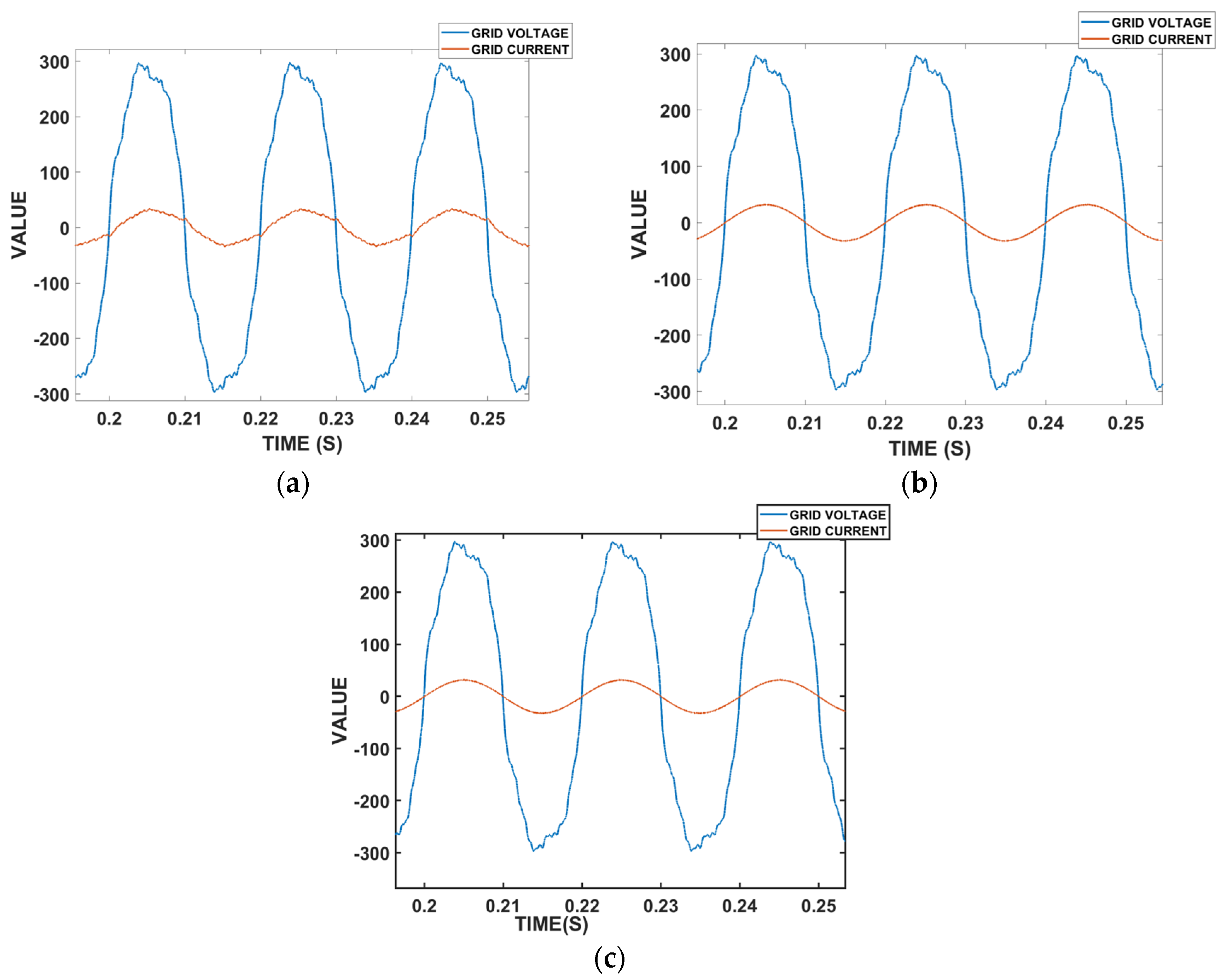
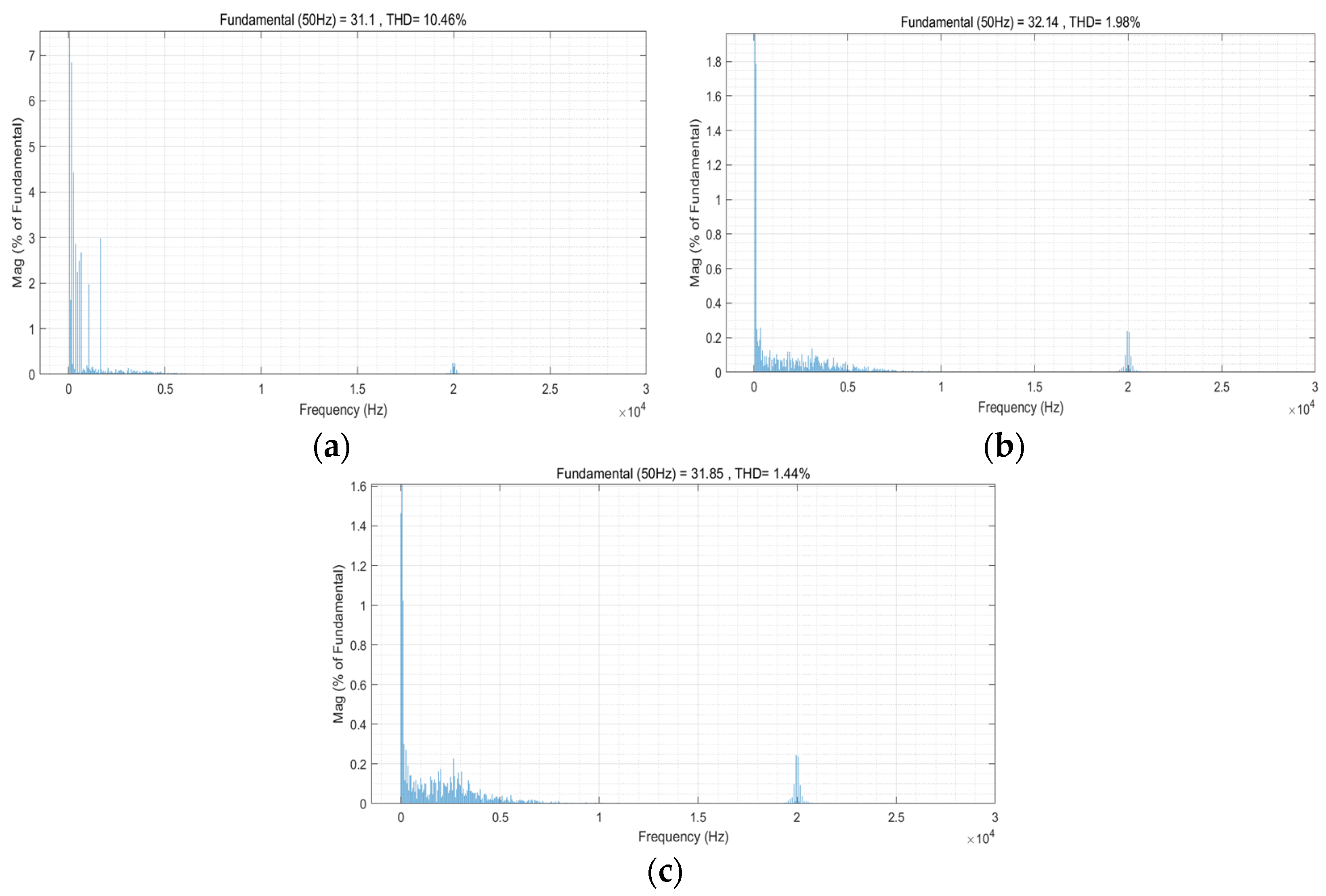
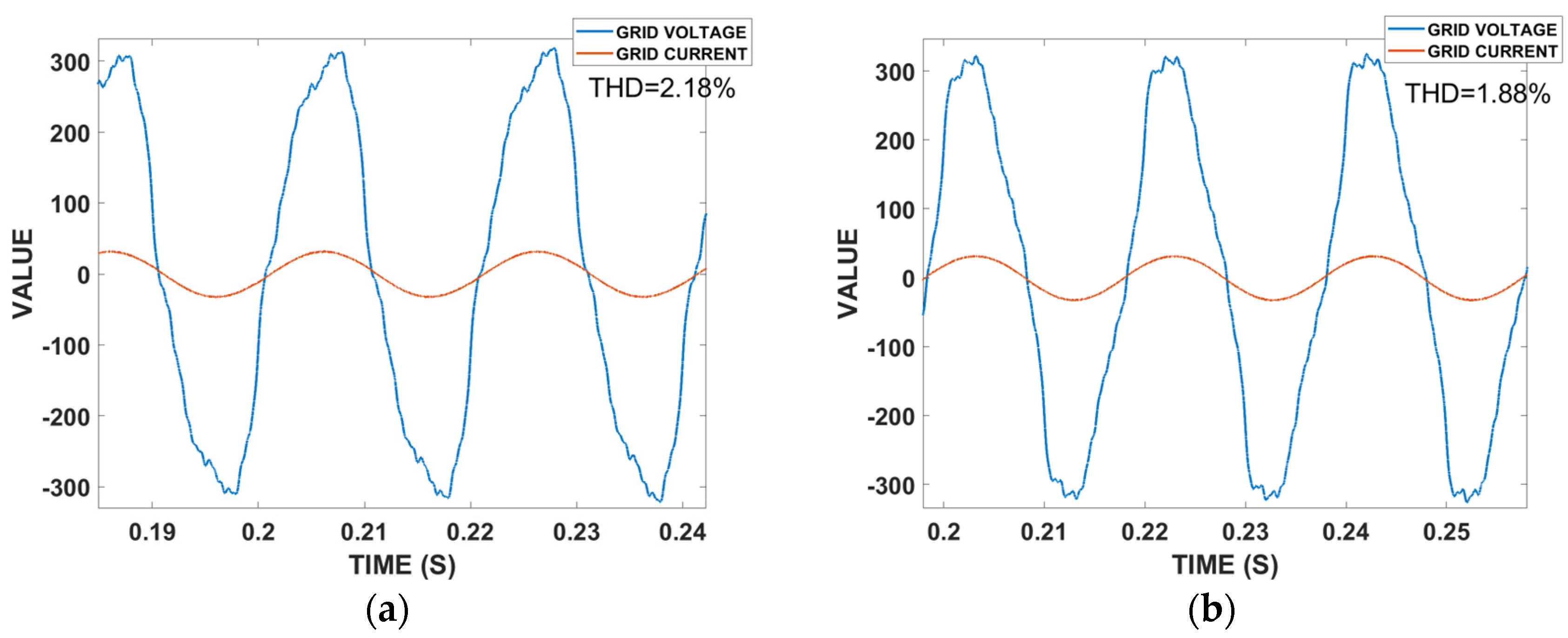
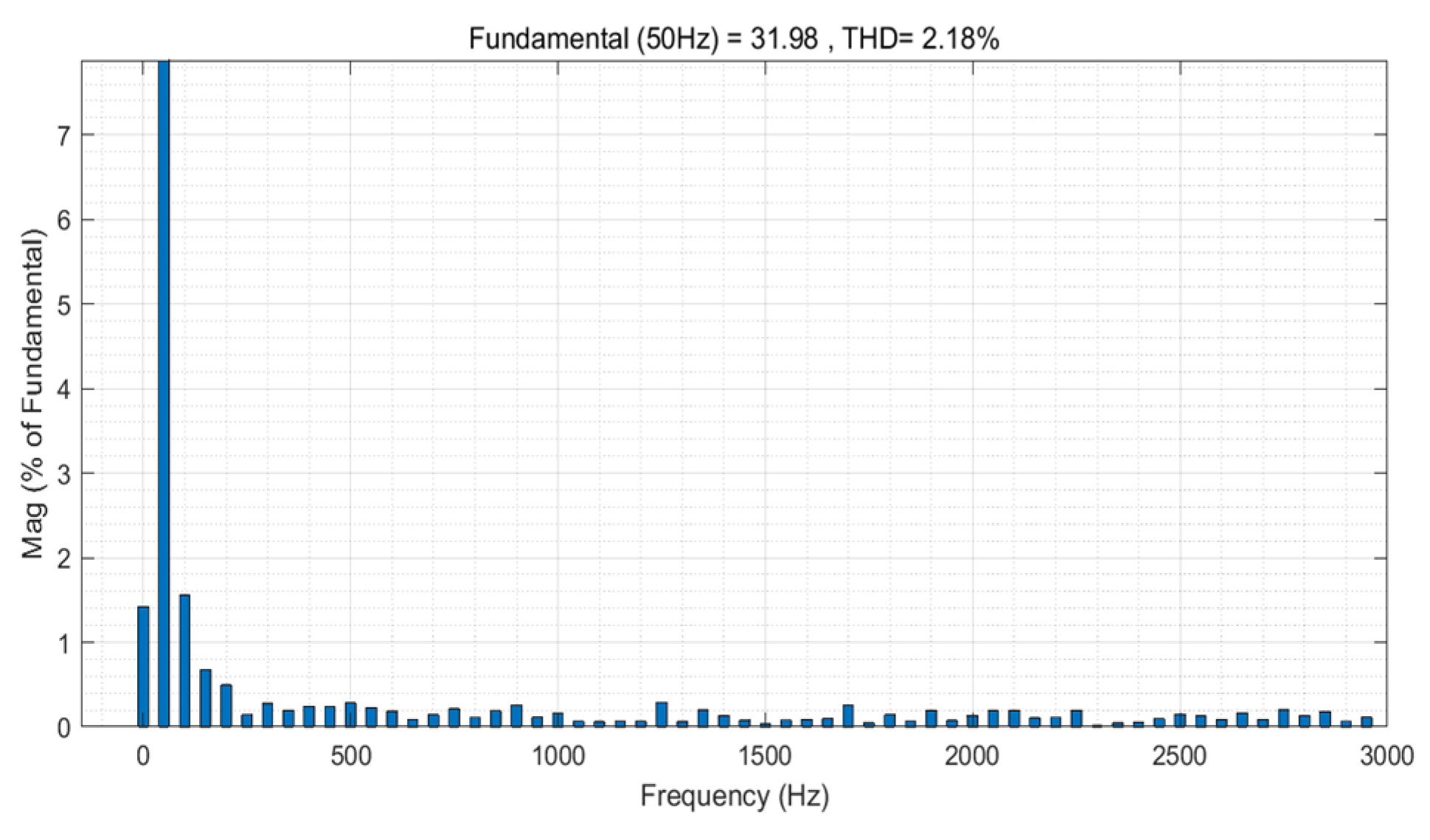
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Abbreviations
| Term | Meaning |
| GCI | Grid-Connected Inverter |
| QPR | Quasi-Proportional Resonance |
| GCC | Grid-Connected Current |
| THD | Total Harmonic Distortion |
| LCL filter | Line Reactor—Capacitor—Line Reactor filter |
| DPGS | The Distributed Power Generation System |
| PLL | Phase-Locked Loop |
| GCV | Grid-Connected Voltage |
| SPWM | Sine Pulse-Width Modulation |
| WACC | Weighted Average Current Control |
| LTP | Linear Time-Periodic |
| MPPT | Maximum Power Point Tracking |
| PI | Proportional Integral |
| PR | Proportional Resonance |
| UDF | Unipolar Double-Frequency |
| SOGI | Second-Order Generalized Integrator Phase |
| LC filter | Line Reactor—Capacitor filter |
| KVL | Kirchhoff’s Voltage Law |
| KCL | Kirchhoff’s Current Law |
References
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of Control and Grid Synchronization for Distributed Power Generation Systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Castilla, M.; Miret, J.; Matas, J.; Vicuna, L.G.; Guerrero, J.M. Control Design Guidelines for Single-Phase Grid-Connected Photovoltaic Inverters with Damped Resonant Harmonic Compensators. IEEE Trans. Ind. Electron. 2009, 56, 4492–4501. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values. IEEE Trans. Power Electron. 2006, 21, 263–272. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Multiple harmonics control for three-phase grid converter systems with the use of PI-RES current controller in a rotating frame. IEEE Trans. Power Electron. 2006, 21, 836–841. [Google Scholar] [CrossRef]
- Twining, E.; Holmes, D.G. Grid current regulation of a three-phase voltage source inverter with an LCL input filter. In Proceedings of the 2002 IEEE 33rd Annual IEEE Power Electronics Specialists Conference, Proceedings (Cat. No.02CH37289), Cairns, QLD, Australia, 23–27 June 2002; pp. 1189–1194. [Google Scholar]
- Walker, H.A.; Thye, S.R.; Simpson, B.; Lovaglia, M.J.; Willer, D.; Markovsky, B. Network exchange theory: Recent developments and new directions. Soc. Psychol. Q. 2000, 63, 324–337. [Google Scholar] [CrossRef]
- Charin, C.; Ishak, D.; Mohd Zainuri, M.A.A.; Ismail, B.; Alsuwian, T.; Alhawari, A.R.H. Modified Levy-based Particle Swarm Optimization (MLPSO) with Boost Converter for Local and Global Point Tracking. Energies 2022, 15, 7370. [Google Scholar] [CrossRef]
- Lin, X.; Wen, Y.; Yu, R.; Yu, J.; Wen, H. Improved Weak Grids Synchronization Unit for Passivity Enhancement of Grid-Connected Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 7084–7097. [Google Scholar] [CrossRef]
- Shao, B.; Xiao, Q.; Xiong, L.; Wang, L.; Yang, Y.; Chen, Z.; Blaabjerg, F.; Guerrero, J.M. Power coupling analysis and improved decoupling control for the VSC connected to a weak AC grid. Int. J. Electr. Power Energy Syst. 2023, 145, 108645. [Google Scholar] [CrossRef]
- Han, Y.; Yang, M.; Li, H.; Yang, P.; Xu, L.; Coelho, E.A.A.; Guerrero, J.M. Modeling and Stability Analysis of $LCL$ -Type Grid-Connected Inverters: A Comprehensive Overview. IEEE Access 2019, 7, 114975–115001. [Google Scholar] [CrossRef]
- Jayalath, S.; Hanif, M. Generalized LCL-Filter Design Algorithm for Grid-Connected Voltage-Source Inverter. IEEE Trans. Ind. Electron. 2017, 64, 1905–1915. [Google Scholar] [CrossRef]
- Liu, B.; Song, Z.; Yu, B.; Yang, G.; Liu, J. A Feedforward Control-Based Power Decoupling Strategy for Grid-Forming Grid-Connected Inverters. Energies 2024, 17, 424. [Google Scholar] [CrossRef]
- Xiao, P.; Corzine, K.A.; Venayagamoorthy, G.K. Multiple Reference Frame-Based Control of Three-Phase PWM Boost Rectifiers under Unbalanced and Distorted Input Conditions. IEEE Trans. Power Electron. 2008, 23, 2006–2017. [Google Scholar] [CrossRef]
- Zhou, S.; Zhou, G.; He, M.; Mao, S.; Zhao, H.; Liu, G. Stability Effect of Different Modulation Parameters in Voltage-Mode PWM Control for CCM Switching DC-DC Converter. IEEE Trans. Transp. Electrif. 2023, 1. [Google Scholar] [CrossRef]
- Guo, B.; Su, M.; Sun, Y.; Wang, H.; Liu, B.; Zhang, X.; Pou, J.; Yang, Y.; Davari, P. Optimization Design and Control of Single-Stage Single-Phase PV Inverters for MPPT Improvement. IEEE Trans. Power Electron. 2020, 35, 13000–13016. [Google Scholar] [CrossRef]
- Ramos, R.; Serrano, D.; Alou, P.; Oliver, J.Á.; Cobos, J.A. Control Design of a Single-Phase Inverter Operating with Multiple Modulation Strategies and Variable Switching Frequency. IEEE Trans. Power Electron. 2021, 36, 2407–2419. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Luo, A.; Li, M. A simple and robust method for designing a multi-loop controller for three-phase VSI with an LCL-filter under uncertain system parameters. Electr. Power Syst. Res. 2014, 117, 94–103. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W.; Bosnjak, D.; Harris, B. Investigation and Active Damping of Multiple Resonances in a Parallel-Inverter-Based Microgrid. IEEE Trans. Power Electron. 2013, 28, 234–246. [Google Scholar] [CrossRef]
- Parker, S.G.; McGrath, B.P.; Holmes, D.G. Regions of Active Damping Control for LCL Filters. IEEE Trans. Ind. Appl. 2014, 50, 424–432. [Google Scholar] [CrossRef]
- Xue, M.; Zhang, Y.; Kang, Y.; Yi, Y.; Li, S.; Liu, F. Full Feedforward of Grid Voltage for Discrete State Feedback Controlled Grid-Connected Inverter with LCL Filter. IEEE Trans. Power Electron. 2012, 27, 4234–4247. [Google Scholar] [CrossRef]
- Yang, D.; Ruan, X.; Wu, H. Impedance Shaping of the Grid-Connected Inverter with LCL Filter to Improve Its Adaptability to the Weak Grid Condition. IEEE Trans. Power Electron. 2014, 29, 5795–5805. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, D.; Liang, W.; Zhang, X. Current Reconstruction of Three-Phase Voltage Source Inverters Considering Current Ripple. IEEE Trans. Transp. Electrif. 2023, 9, 1416–1427. [Google Scholar] [CrossRef]
- Lin, X.; Liu, Y.; Yu, J.; Yu, R.; Zhang, J.; Wen, H. Stability analysis of Three-phase Grid-Connected inverter under the weak grids with asymmetrical grid impedance by LTP theory in time domain. Int. J. Electr. Power Energy Syst. 2022, 142, 108244. [Google Scholar] [CrossRef]
- He, N.; Xu, D.; Zhu, Y.; Zhang, J.; Shen, G.; Zhang, Y.; Ma, J.; Liu, C. Weighted Average Current Control in a Three-Phase Grid Inverter with an LCL Filter. IEEE Trans. Power Electron. 2013, 28, 2785–2797. [Google Scholar] [CrossRef]
- Zhou, S.; Sun, P.; Li, Q.; Lan, C.; Xu, Z. Resonance Suppression Strategy of the Multi-inverter Grid-connected System Based on Current Given Correction. In Proceedings of the 2022 Asian Conference on Frontiers of Power and Energy (ACFPE), Virtual, 21–23 October 2022; pp. 75–79. [Google Scholar]
- Poh Chiang, L.; Holmes, D.G.; Fukuta, Y.; Lipo, T.A. Reduced common-mode modulation strategies for cascaded multilevel inverters. IEEE Trans. Ind. Appl. 2003, 39, 1386–1395. [Google Scholar] [CrossRef]
- Xia, Y.; Roy, J.; Ayyanar, R. Optimal Variable Switching Frequency Scheme to Reduce Loss of Single-Phase Grid-Connected Inverter with Unipolar and Bipolar PWM. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1013–1026. [Google Scholar] [CrossRef]
- Lin, Z.; Ruan, X.; Wu, L.; Zhang, H.; Li, W. Multi resonant Component-Based Grid-Voltage-Weighted Feedforward Scheme for Grid-Connected Inverter to Suppress the Injected Grid Current Harmonics Under Weak Grid. IEEE Trans. Power Electron. 2020, 35, 9784–9793. [Google Scholar] [CrossRef]
- Gonçalves, D.; Farias, J.V.M.; Pereira, H.A.; Luiz, A.-S.A.; Stopa, M.M.; Cupertino, A.F. Design of Damping Strategies for LC Filter Applied in Medium Voltage Variable Speed Drive. Energies 2022, 15, 5644. [Google Scholar] [CrossRef]
- Saïd-Romdhane, M.B.; Naouar, M.W.; Slama-Belkhodja, I.; Monmasson, E. Robust Active Damping Methods for LCL Filter-Based Grid-Connected Converters. IEEE Trans. Power Electron. 2017, 32, 6739–6750. [Google Scholar] [CrossRef]
- Bennia, I.; Elbouchikhi, E.; Harrag, A.; Daili, Y.; Saim, A.; Bouzid, A.E.M.; Kanouni, B. Design, Modeling, and Validation of Grid-Forming Inverters for Frequency Synchronization and Restoration. Energies 2024, 17, 59. [Google Scholar] [CrossRef]
- Ruan, X.; Wang, X.; Pan, D.; Yang, D.; Li, W.; Bao, C. Control Techniques For LCL-Type Grid-Connected Inverters; Springer: Singapore, 2018. [Google Scholar]
- Chowdhury, V.R.; Singh, A.; Mather, B. Modified Virtual Oscillator based Operation of Grid Forming Converters with Single Voltage Sensor. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 934–938. [Google Scholar]
- Zhao, X.; Meng, L.; Xie, C.; Guerrero, J.M.; Wu, X.; Vasquez, J.C.; Savaghebi, M. A Voltage Feedback Based Harmonic Compensation Strategy for Current-Controlled Converters. IEEE Trans. Ind. Appl. 2018, 54, 2616–2627. [Google Scholar] [CrossRef]

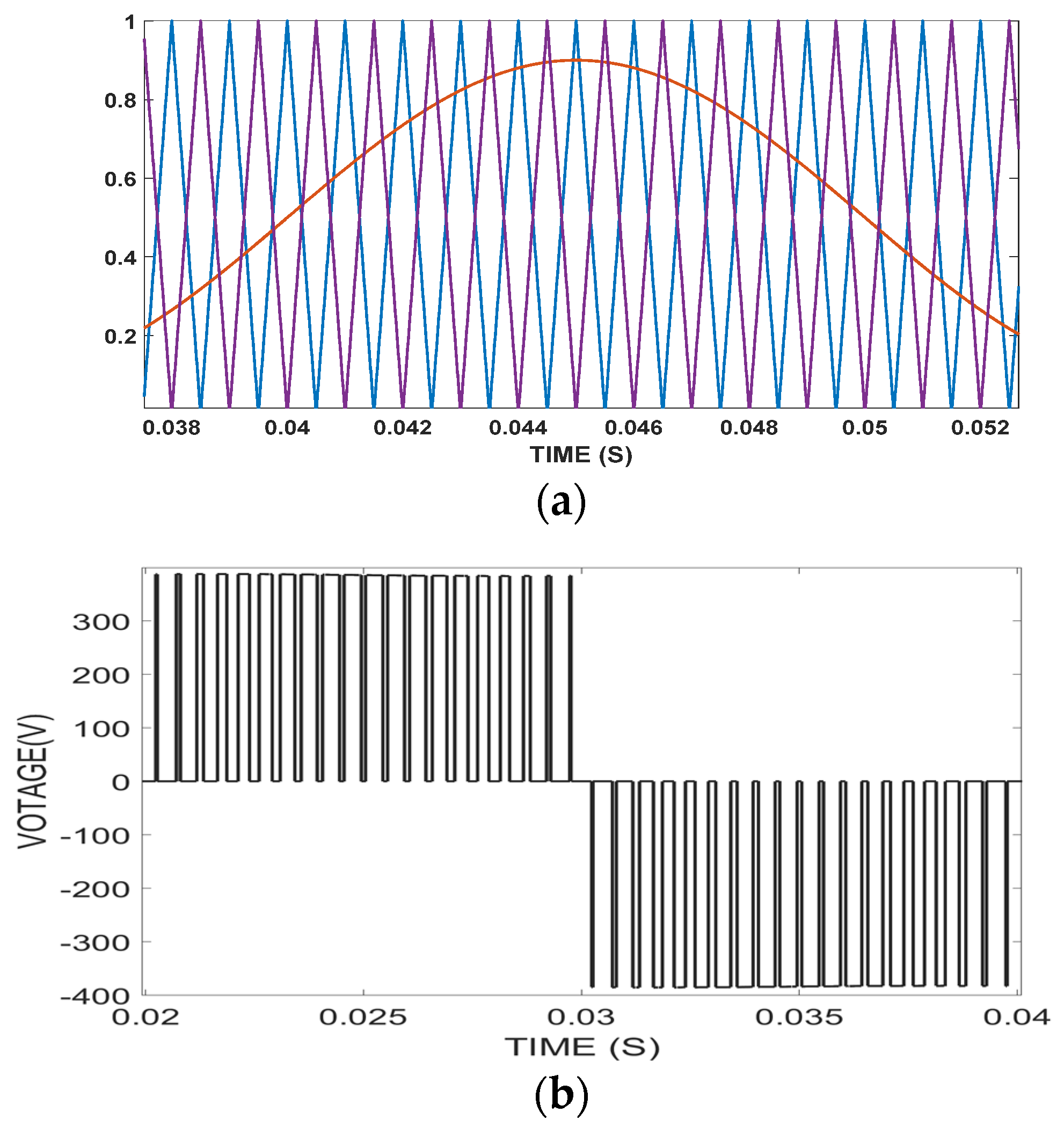
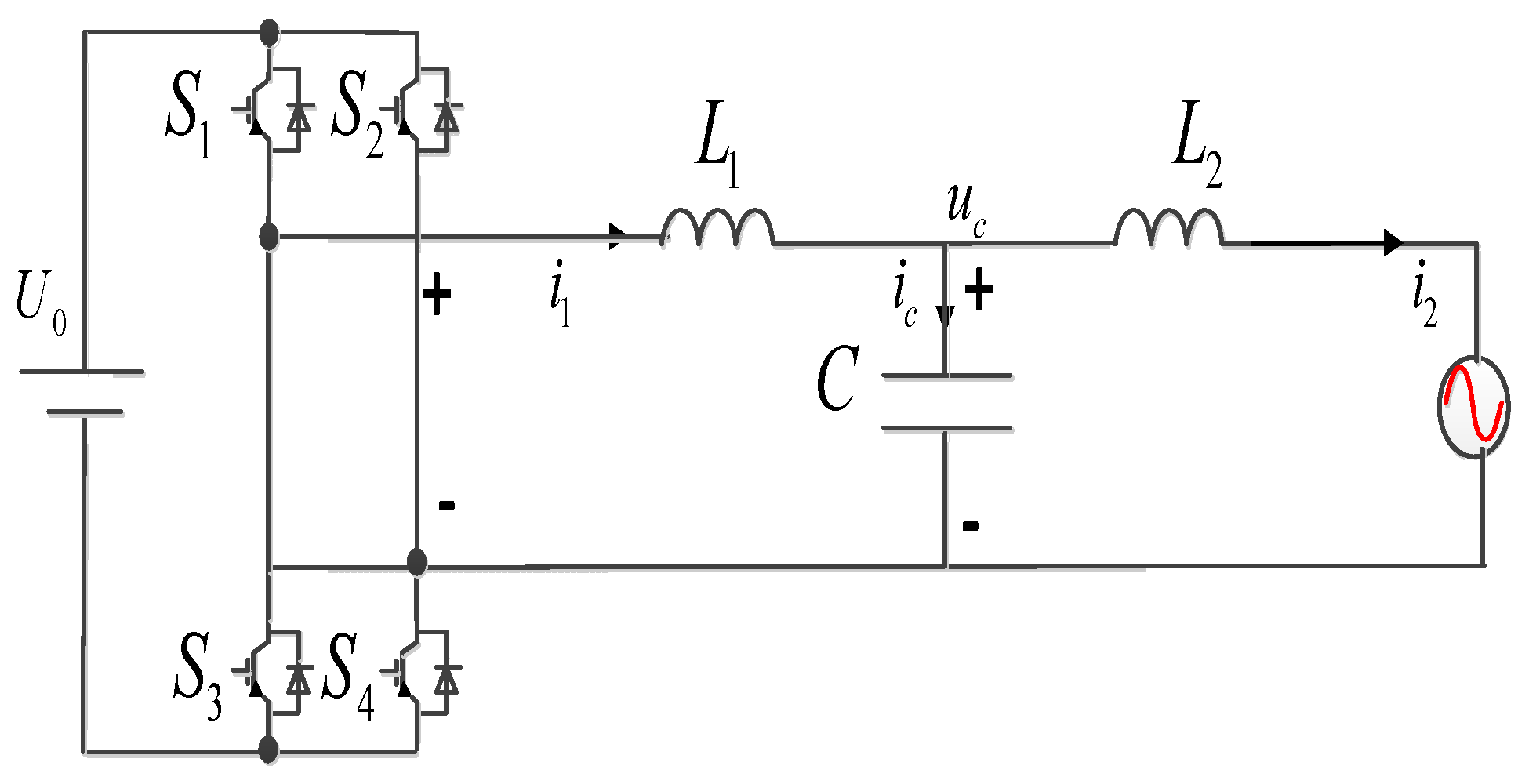
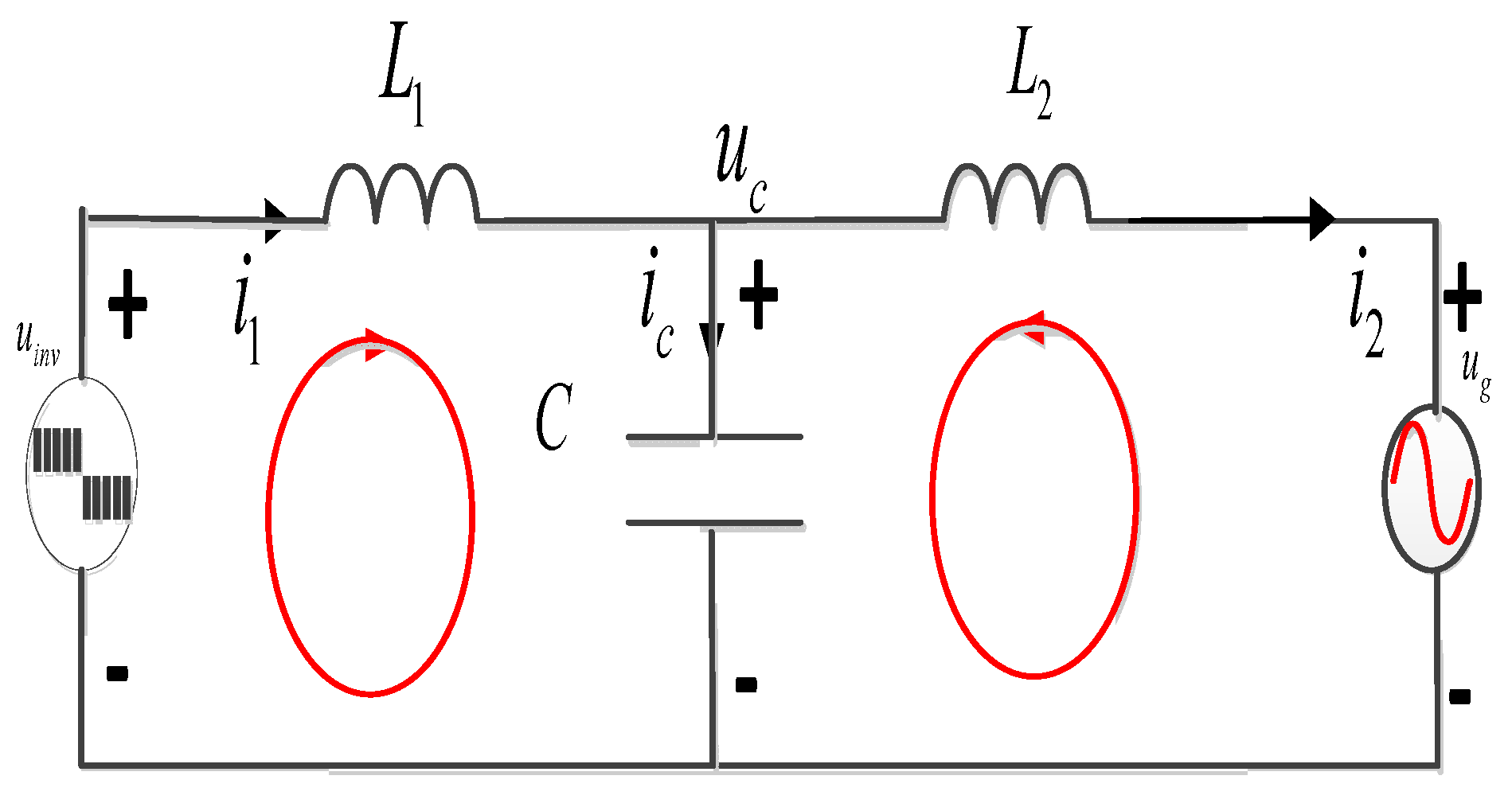
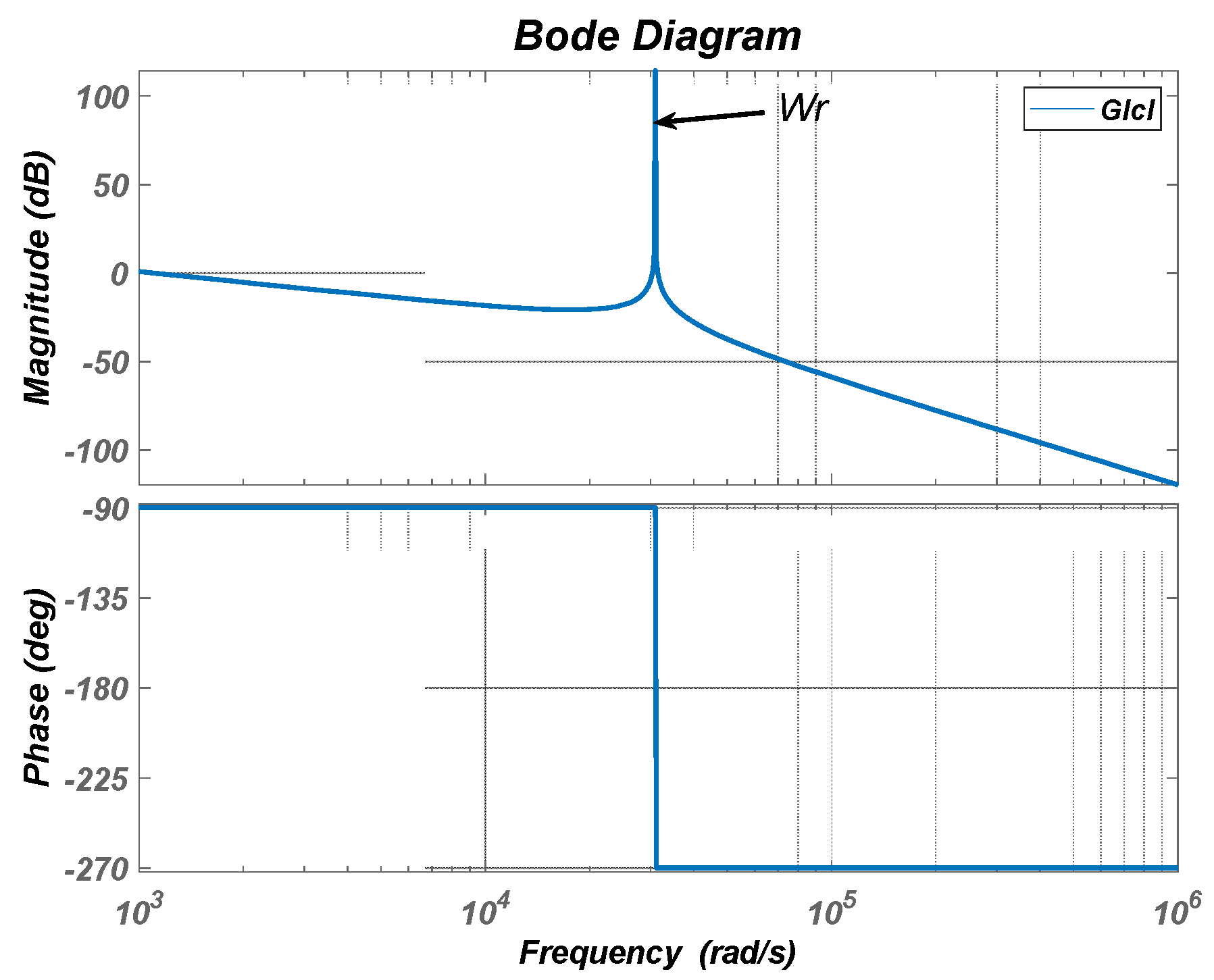



| Pa Parameters and Symbols | Values | Parameters and Symbols | Values |
|---|---|---|---|
| Input voltage | 400 V | Grid-side inductor | 0.00012 H |
| Grid voltage | 220 V | Carrier amplitude | 1 V |
| Fundamental frequency | 50 Hz | Carrier frequency | 10 kHz |
| Switching frequency | 20 kHz | Proportional coefficient of and Kp | 10 |
| Inverter-side inductor | 0.000 H | Integral coefficient of KR | 1000 |
| Filter capacitor C | 10 | Integral coefficient of KI | 1000 |
| Grid current sensor gain Hi1 | 1 | Sampling period | 50 |
| Feedback coefficient of capacitor-current Hi2 | 32 | Cutoff frequency | 5 |
| Harmonic orders | 3 | 5 | 7 | 13 | 21 | 33 |
| Amplitude ratio (%) | 33 | 21 | 13 | 7 | 5 | 3 |
| Relative phase (°) | 1 | 1 | 3 | 3 | 5 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhe, W.; Ishak, D.; Hamidi, M.N. A Grid-Connected Inverter with Grid-Voltage-Weighted Feedforward Control Based on the Quasi-Proportional Resonance Controller for Suppressing Grid Voltage Disturbances. Energies 2024, 17, 885. https://doi.org/10.3390/en17040885
Zhe W, Ishak D, Hamidi MN. A Grid-Connected Inverter with Grid-Voltage-Weighted Feedforward Control Based on the Quasi-Proportional Resonance Controller for Suppressing Grid Voltage Disturbances. Energies. 2024; 17(4):885. https://doi.org/10.3390/en17040885
Chicago/Turabian StyleZhe, Wang, Dahaman Ishak, and Muhammad Najwan Hamidi. 2024. "A Grid-Connected Inverter with Grid-Voltage-Weighted Feedforward Control Based on the Quasi-Proportional Resonance Controller for Suppressing Grid Voltage Disturbances" Energies 17, no. 4: 885. https://doi.org/10.3390/en17040885
APA StyleZhe, W., Ishak, D., & Hamidi, M. N. (2024). A Grid-Connected Inverter with Grid-Voltage-Weighted Feedforward Control Based on the Quasi-Proportional Resonance Controller for Suppressing Grid Voltage Disturbances. Energies, 17(4), 885. https://doi.org/10.3390/en17040885






