Multivariable Algorithm Using Signal-Processing Techniques to Identify Islanding Events in Utility Grid with Renewable Energy Penetration
Abstract
1. Introduction
1.1. Review of Literature
1.2. Research Gaps
1.3. Research Contributions
- An HIDM based on the hybrid combination of the ST, HT, and ALC is designed. This considers the processing of the current signals using the ST to compute the SIDF and CIDF. Currents are also processed using the HT and ALC to compute the HIDF and AIDF, respectively. The SIDF, CIDF, HIDF, AIDF, and IWF are multiplied to compute the HIDI. This HIDM combines the merits of the ST, HT, and ALC, which resulted in the following merits of the proposed HIDM:
- -
- The HIDM is effective at detecting islanding conditions and discriminating these events, fault events, and the operational conditions using the threshold HIDIT and HIDIFT
- -
- The HIDM is effective at detecting the islanding condition in the availability of the noise of 20 dB SNR.
- -
- The HIDM has a small non-detection zone.
- -
- The performance of the HIDM is not affected even with a 100% RE penetration level. However, the performance of the HIDM considering individual applications of either of the ST, HT, or ALC deteriorate when the RE penetration level increases above 50%.
- The HIDM was effectively tested on an IEEE-13 node network with a 50% and 100% contribution in the generation mix from RE plants (both solar and wind).
- The HIDM can effectively be used to identify the islanding conditions in a real-time distribution feeder of a practical utility grid.
- The performance of the HIDM is better relative to an IDM considering the DWT, an IDM using a combination of the slantlet transform and RPNN, an IDM using the wavelet transform multi-resolution (WT-MRA)-based image data, and an IDM based on the use of a Deep Neural Network (DNN).
1.4. Structure of the Paper
2. Test Utility Grid
3. Multi-Variable Hybrid Islanding Detection Method
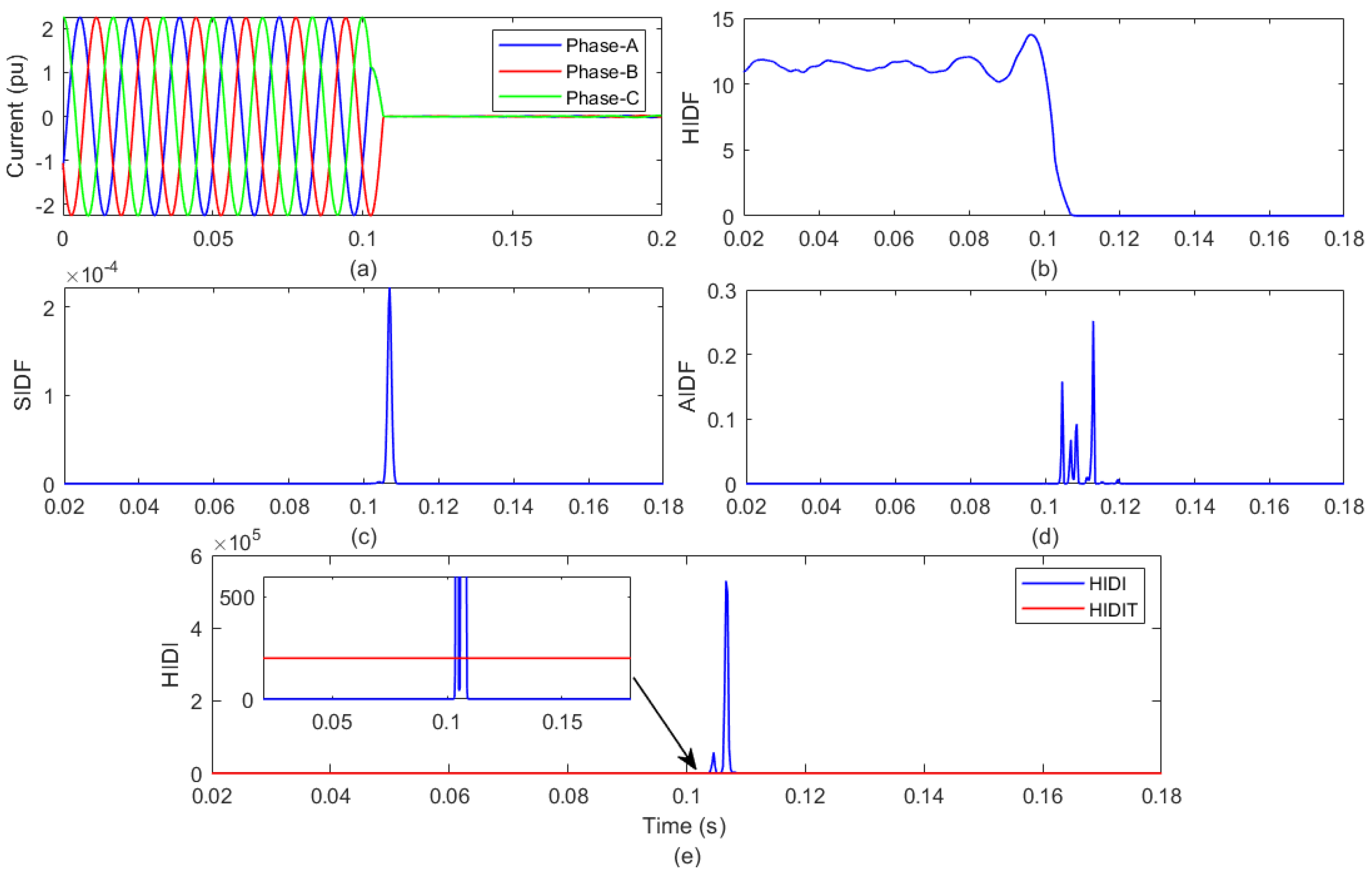
3.1. Hilbert Islanding-Detection Factor
3.2. Stockwell Islanding-Detection Factor
3.3. Co-Variance Islanding-Detection Factor
3.4. Alienation Islanding-Detection Factor
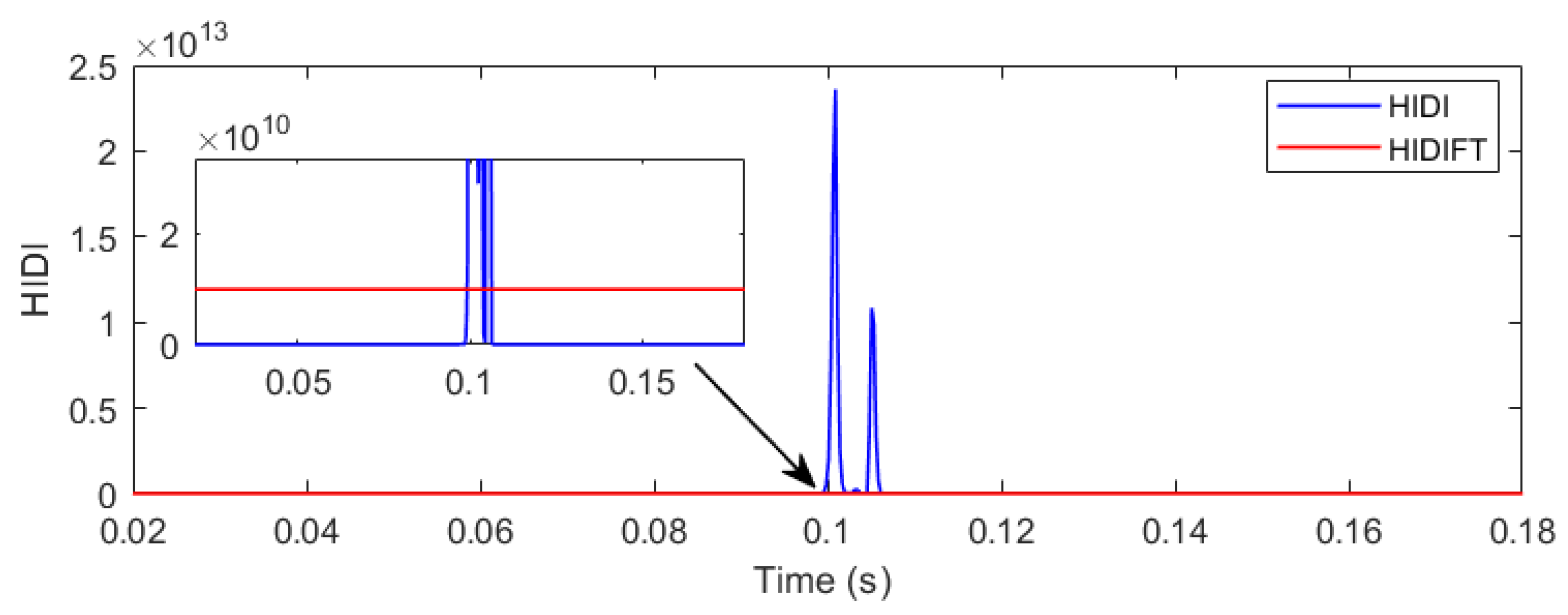
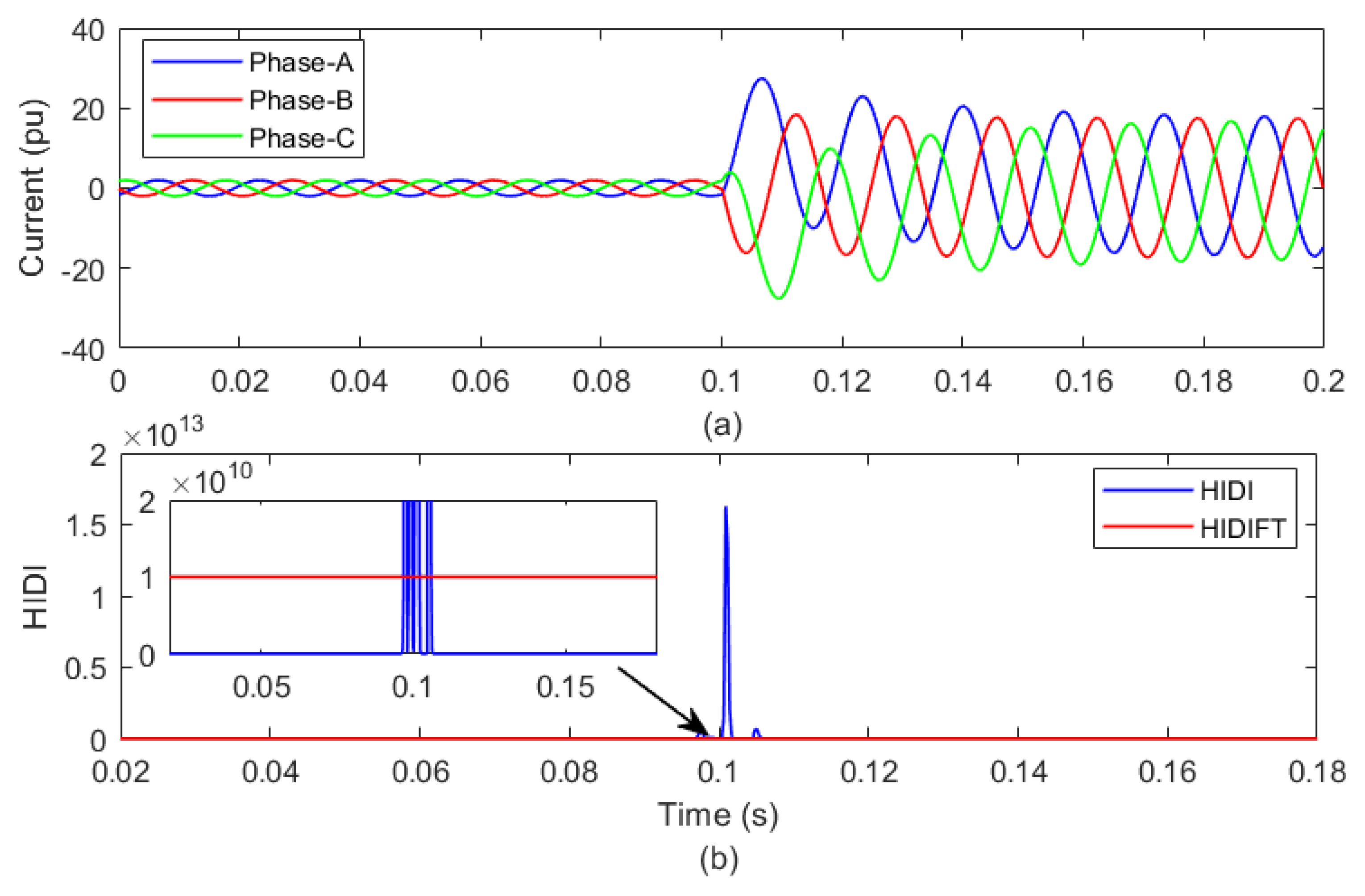
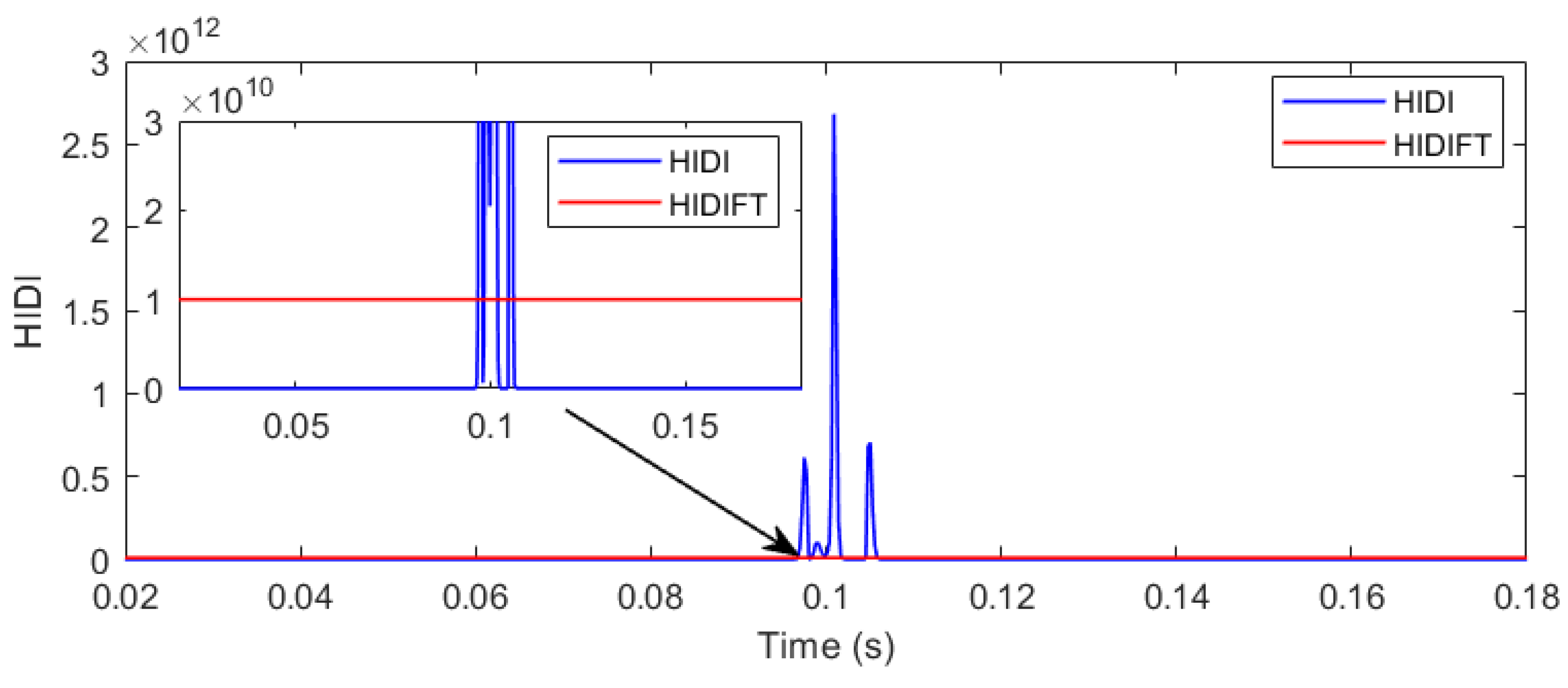
3.5. Hybrid Islanding-Detection Indicator
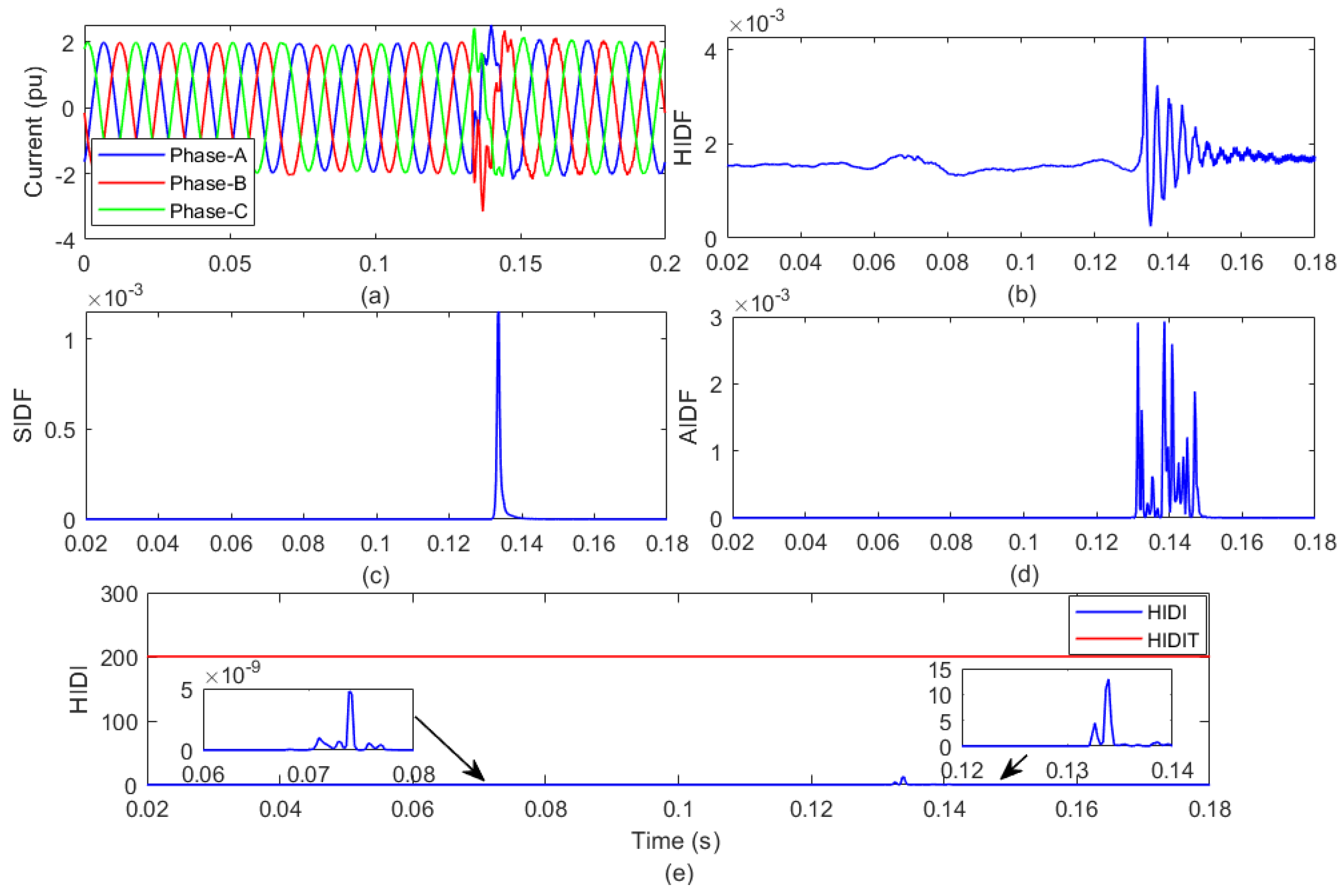
4. Detection of Islanding Events: Simulation Results and Discussion
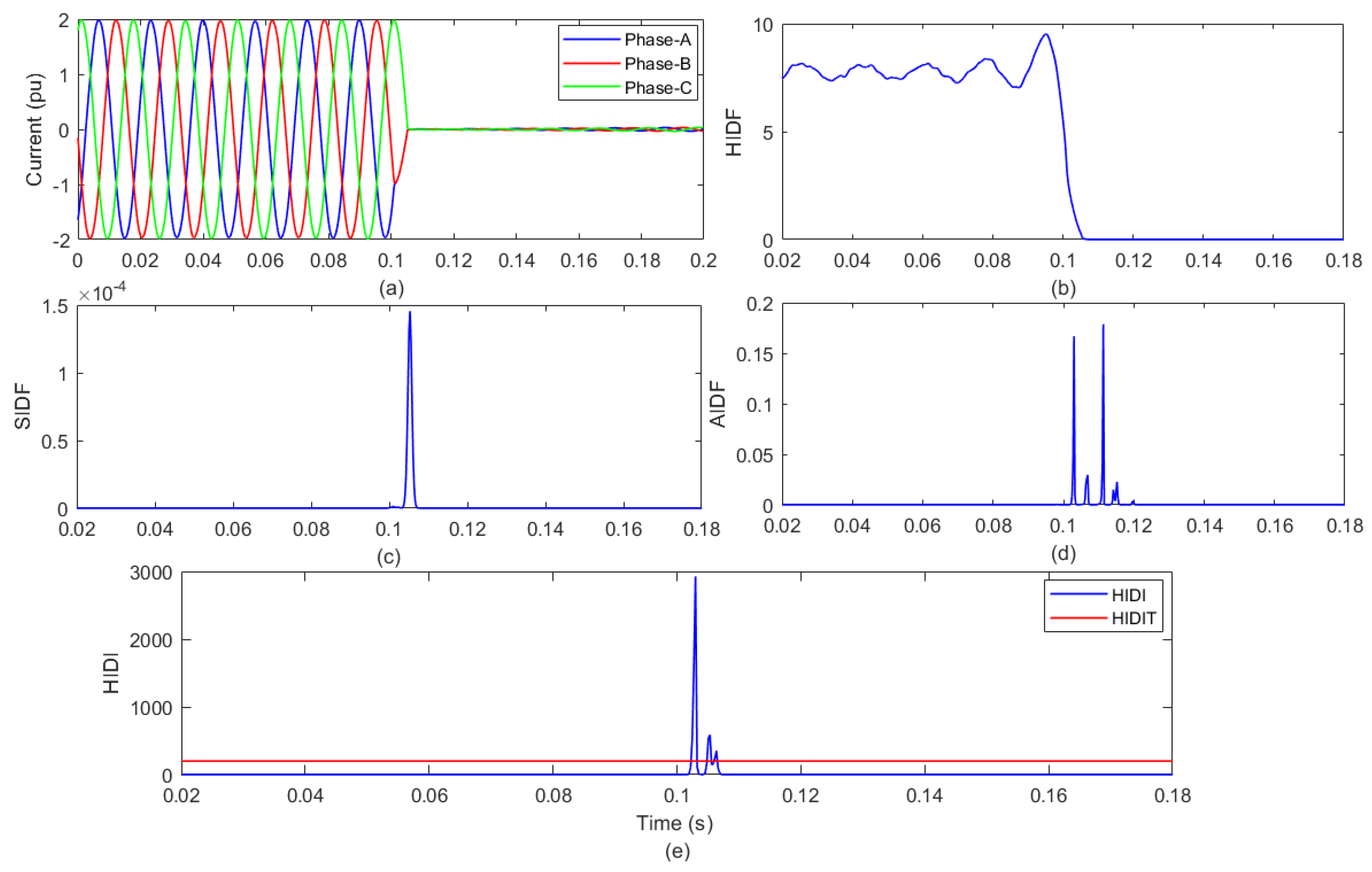
4.1. Detection of Islanding Event with Generation from WGP and SGP
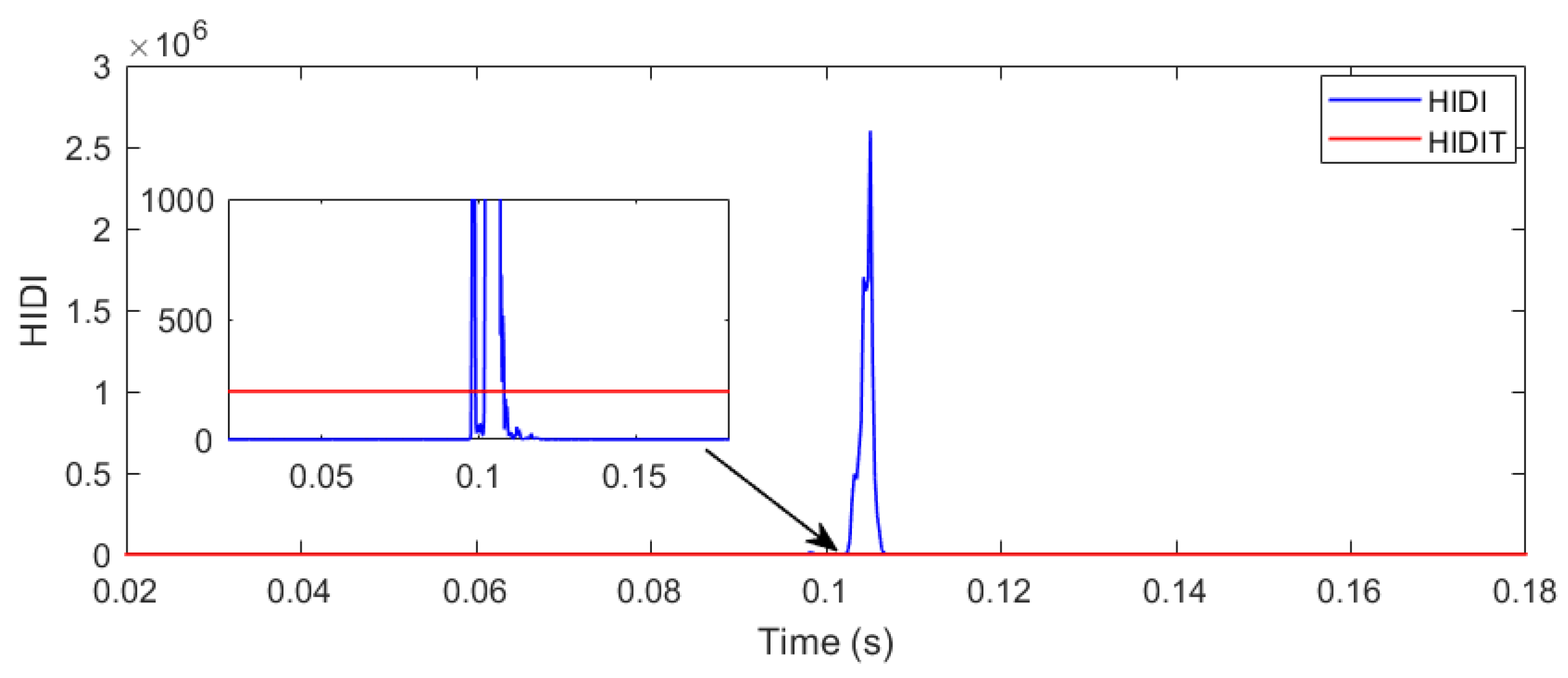
4.1.1. Testing of HIDM for Different Islanding Incidence Angles
4.1.2. Impact of Noise on HIDM Performance
4.1.3. Determination of NDZ of Islanding Event
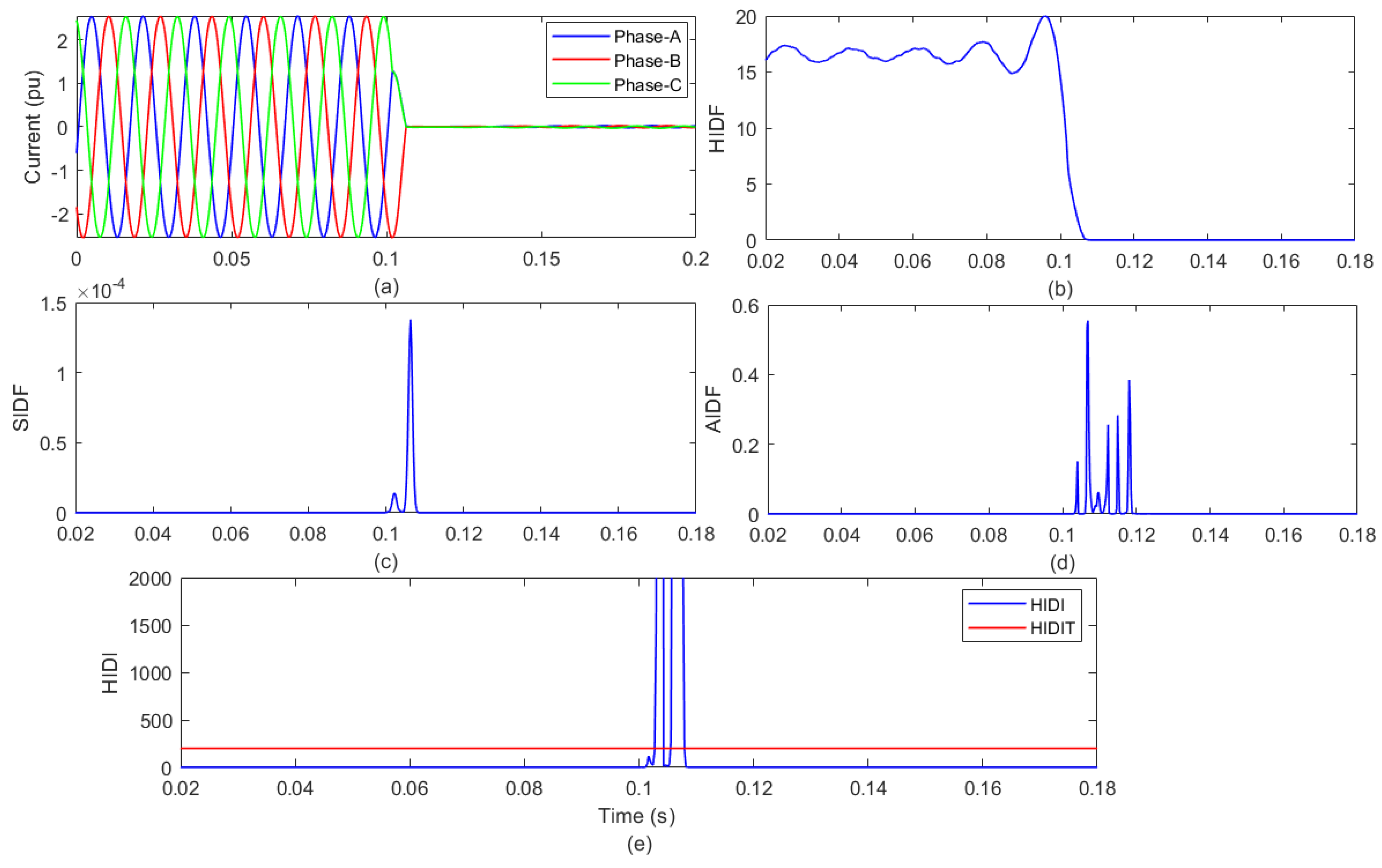
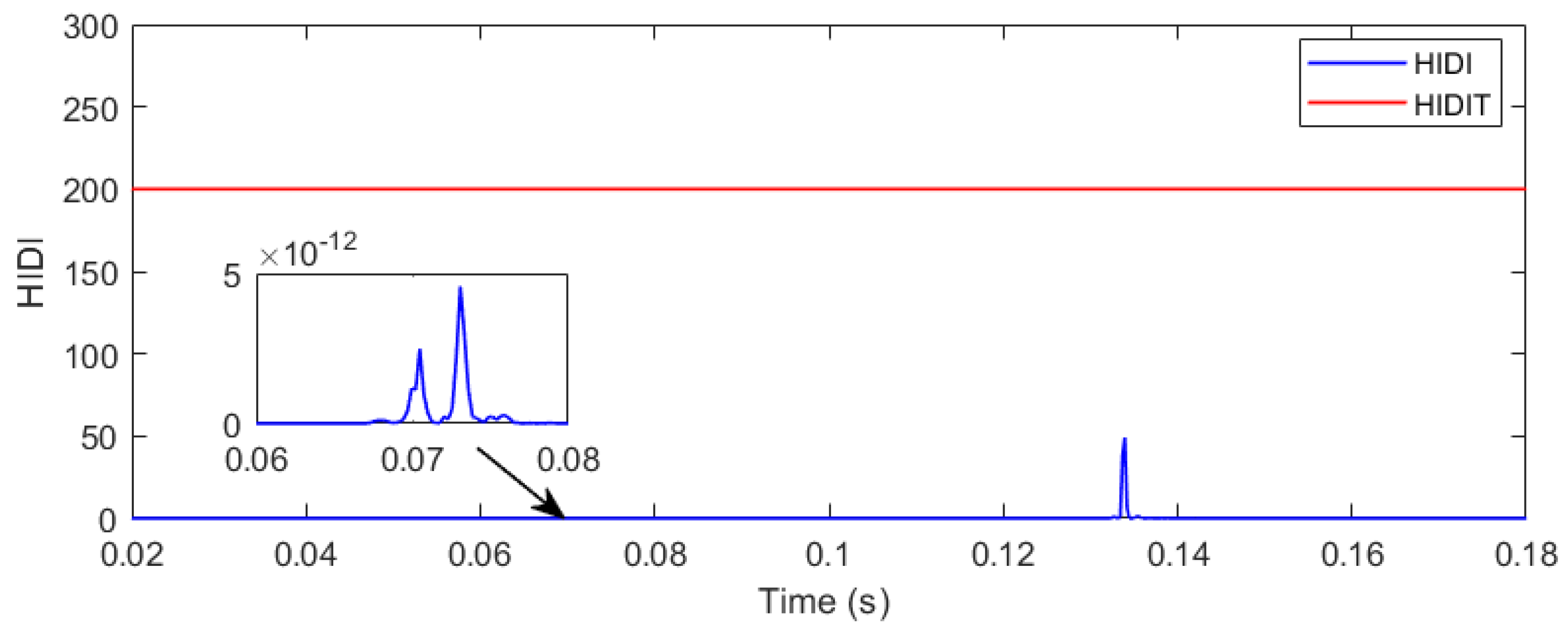
4.2. Detection of Islanding with SGP
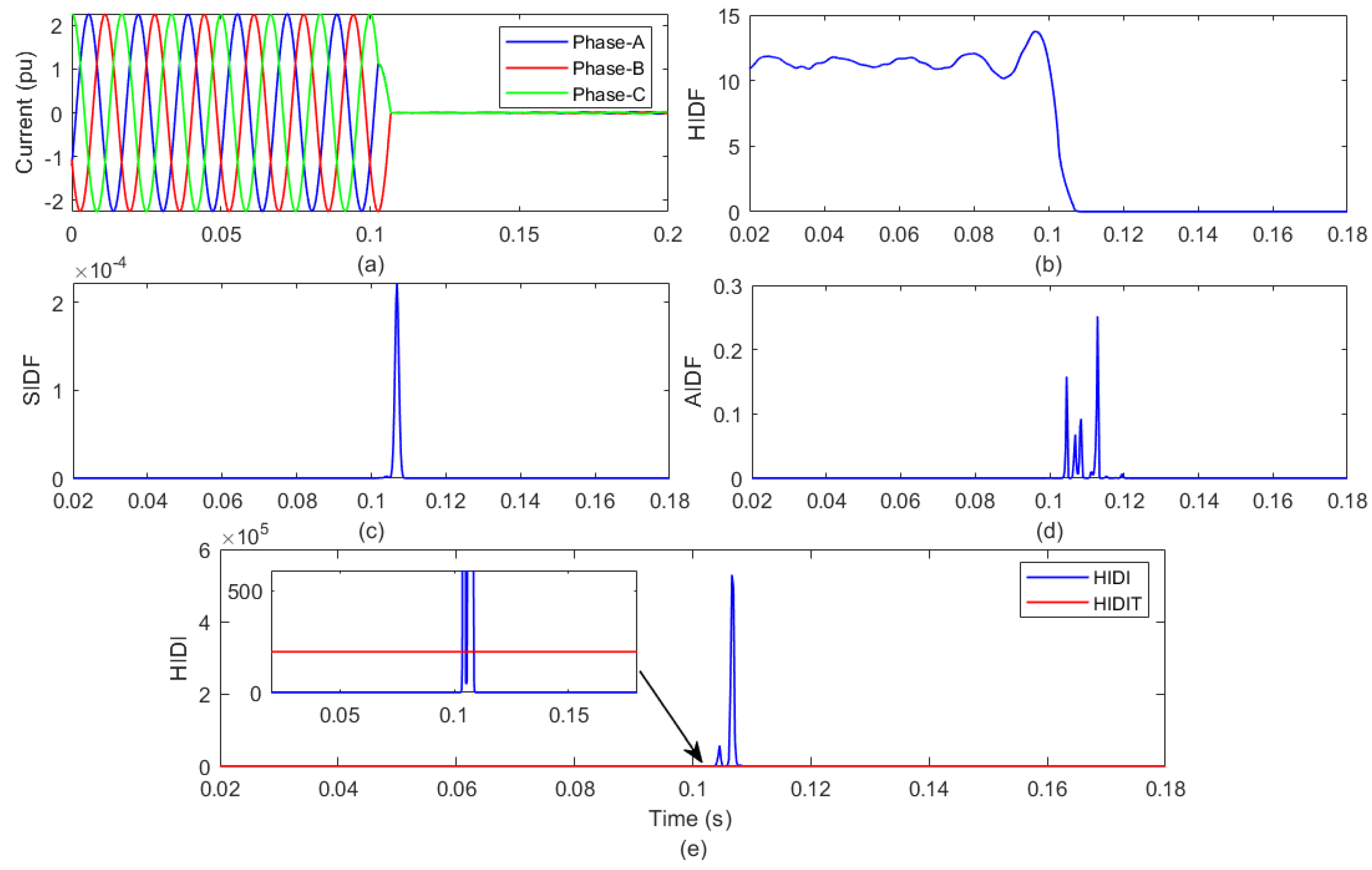
4.3. Detection of Islanding with WGP
4.4. High Penetration Level of RE (100%)
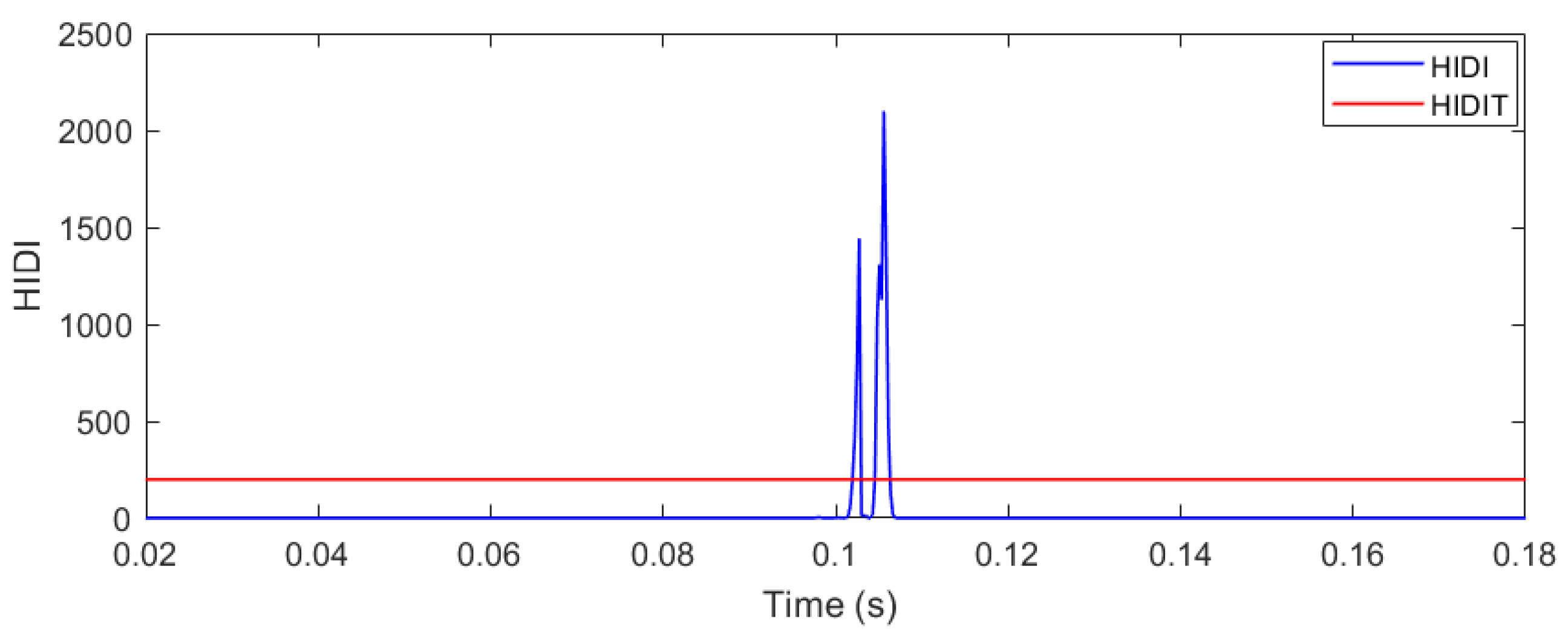
5. Testing of HIDM to Identify and Discriminate the Fault Events from Islanding Events: Simulation Results and Discussion
5.1. Phase to Ground Fault
5.2. Phase to Phase Fault
5.3. Two Phases to Ground Fault
5.4. Three-Phase Fault
5.5. Three Phases to Ground Fault
6. Testing of HIDM to Identify and Discriminate the Operational Events from Islanding Events: Simulation Results and Discussion
6.1. Feeder Operation
6.2. Capacitor Operation
6.3. Load Operation
7. Real-Time Validation of HIDM
8. Relative Performance of HIDM
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Alternating current |
| AIDF | Alienation islanding-detection factor |
| ALC | Alienation Coefficient |
| CIDF | Co-variance islanding-detection factor |
| CPU | Central processing unit |
| DC | Direct current |
| DF-T | Distribution feeder transformer |
| DFIG | Doubly fed induction generator |
| DG | Distributed generator |
| DNN | Deep Neural Network |
| DR | Disturbance recorder |
| DWT | Discrete wavelet transform |
| GSS | Grid sub-station |
| HIDF | Hilbert islanding-detection factor |
| HIDI | Hybrid islanding-detection indicator |
| HIDIFT | Hybrid islanding-detection indicator fault threshold |
| HIDIT | Hybrid islanding-detection indicator threshold |
| HIDM | Hybrid islanding-detection method |
| HT | Hilbert transform |
| IDM | Islanding-detection method |
| IEEE | Institute of Electrical and Electronics Engineering |
| IFS | Island formation switch |
| IWF | Islanding weight factor |
| LG | Phase to ground fault |
| LL | Phase to phase fault |
| LLG | Two phases to ground fault |
| LLL | Three-phase fault |
| LLLG | Three phases to ground fault |
| MATLAB | Matrix laboratory |
| NDZ | Non-detection zone |
| PMU | Phasor measurement unit |
| PCC | Point of common coupling |
| PQ | Power quality |
| PV | Photovoltaic |
| RE | Renewable energy |
| RPNN | Ridgelet probabilistic neural network |
| SGP | Solar generation plant |
| SGP-GT | Solar generation plant generator transformer |
| SIDF | Stockwell islanding-detection factor |
| SNR | Signal-to-noise ratio |
| ST | Stockwell transform |
| UG-T | Utility grid transformer |
| WGP | Wind generation plant |
| WGP-GT | Wind generation plant generator transformer |
| WT-MRA | Wavelet transform multi-resolution |
References
- Wei, W.; Shao, C.; Huang, H.; Zhuang, W. A novel formula for plastic hinge length of reinforced concrete columns in seismic regions. Struct. Infrastruct. Eng. 2022, 1–16. [Google Scholar] [CrossRef]
- Alhasnawi, B.N.; Jasim, B.H. A new energy management system of on-grid/off-grid using adaptive neuro-fuzzy inference system. J. Eng. Sci. Technol. 2020, 15, 3903–3919. [Google Scholar]
- Alhasnawi, B.N.; Jasim, B.H.; Rahman, Z.A.S.A.; Guerrero, J.M.; Esteban, M.D. A Novel Internet of Energy Based Optimal Multi-Agent Control Scheme for Microgrid including Renewable Energy Resources. Int. J. Environ. Res. Public Health 2021, 18, 8146. [Google Scholar] [CrossRef]
- Timbus, A.; Oudalov, A.; Ho, C.N. Islanding detection in smart grids. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 3631–3637. [Google Scholar] [CrossRef]
- Larik, N.A.; Tahir, M.F.; Elbarbary, Z.S.; Yousaf, M.Z.; Khan, M.A. A comprehensive literature review of conventional and modern islanding-detection methods. Energy Strategy Rev. 2022, 44, 101007. [Google Scholar] [CrossRef]
- Kumari, J.S.; Lenine, D.; Satish, A.; Kumar, T.S.; Kalaivani, C.; Kumar, M.D.; Swamy, G.K.; Suresh, Y.V.; Reddy, J.N.; Kumar, J.K.; et al. A model predictive Goertzel algorithm based active islanding detection for grid integrated photovoltaic systems. Microprocess. Microsystems 2022, 95, 104706. [Google Scholar] [CrossRef]
- Shukla, A.; Dutta, S.; Sadhu, P.K. An island detection approach by μ-PMU with reduced chances of cyber attack. Int. J. Electr. Power Energy Syst. 2021, 126, 106599. [Google Scholar] [CrossRef]
- Nale, R.; Biswal, M.; Kishor, N. A passive communication based islanding-detection technique for AC microgrid. Int. J. Electr. Power Energy Syst. 2022, 137, 107657. [Google Scholar] [CrossRef]
- Elshrief, Y.A.; Asham, A.D.; Bouallegue, B.; Ahmed, A.; Helmi, D.H.; Abozalam, B.A.; Abd-Elhaleem, S. An innovative hybrid method for islanding detection using fuzzy classifier for different circumstances including NDZ. J. Radiat. Res. Appl. Sci. 2022, 15, 129–142. [Google Scholar] [CrossRef]
- Alsabban, M.; Bertozzi, O.; Ahmed, S. Analysis and Verification of Islanding Detection Techniques for Grid-integrated PV Systems. In Proceedings of the 2023 IEEE PES Conference on Innovative Smart Grid Technologies—Middle East (ISGT Middle East), Abu Dhabi, United Arab Emirates, 12–15 March 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Shaik, A.G.; Mahela, O.P. Power quality assessment and event detection in hybrid power system. Electr. Power Syst. Res. 2018, 161, 26–44. [Google Scholar] [CrossRef]
- Kersting, W. Radial distribution test feeders. IEEE Trans. Power Syst. 1991, 6, 975–985. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Detection of power quality events associated with grid integration of 100kW solar PV plant. In Proceedings of the 2015 International Conference on Energy Economics and Environment (ICEEE), Greater Noida, India, 27–28 March 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Comprehensive overview of grid interfaced solar photovoltaic systems. Renew. Sustain. Energy Rev. 2017, 68, 316–332. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Comprehensive overview of grid interfaced wind energy generation systems. Renew. Sustain. Energy Rev. 2016, 57, 260–281. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Power Quality Detection in Distribution System with Wind Energy Penetration Using Discrete Wavelet Transform. In Proceedings of the 2015 Second International Conference on Advances in Computing and Communication Engineering, Dehradun, India, 1–2 May 2015; pp. 328–333. [Google Scholar] [CrossRef]
- Derviškadić, A.; Frigo, G.; Paolone, M. Beyond Phasors: Modeling of Power System Signals Using the Hilbert Transform. IEEE Trans. Power Syst. 2020, 35, 2971–2980. [Google Scholar] [CrossRef]
- Feldman, M. Hilbert transform in vibration analysis. Mech. Syst. Signal Process. 2011, 25, 735–802. [Google Scholar] [CrossRef]
- Arranz, R.; Ángel, P.; Rodríguez, A.; Muñoz, F. Fault location in Transmission System based on Transient Recovery Voltage using Stockwell transform and Artificial Neural Networks. Electr. Power Syst. Res. 2021, 201, 107569. [Google Scholar] [CrossRef]
- Rodríguez, A.; Aguado, J.; Martín, F.; López, J.; Muñoz, F.; Ruiz, J. Rule-based classification of power quality disturbances using S-transform. Electr. Power Syst. Res. 2012, 86, 113–121. [Google Scholar] [CrossRef]
- Ray, P.K.; Kishor, N.; Mohanty, S.R. Islanding and Power Quality Disturbance Detection in Grid-Connected Hybrid Power System Using Wavelet and S-Transform. IEEE Trans. Smart Grid 2012, 3, 1082–1094. [Google Scholar] [CrossRef]
- Rathore, B.; Shaik, A.G. Wavelet-Alienation based protection scheme for multi-terminal transmission line. Electr. Power Syst. Res. 2018, 161, 8–16. [Google Scholar] [CrossRef]
- Samet, H.; Hashemi, F.; Ghanbari, T. Minimum non detection zone for islanding detection using an optimal Artificial Neural Network algorithm based on PSO. Renew. Sustain. Energy Rev. 2015, 52, 1–18. [Google Scholar] [CrossRef]
- Sharma, R.; Singh, P. Islanding detection and control in grid based system using wavelet transform. In Proceedings of the 2012 IEEE Fifth Power India Conference, Murthal, India, 19–22 December 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Ahmadipour, M.; Hizam, H.; Othman, M.L.; Radzi, M.A.M.; Murthy, A.S. Islanding detection technique using Slantlet Transform and Ridgelet Probabilistic Neural Network in grid-connected photovoltaic system. Appl. Energy 2018, 231, 645–659. [Google Scholar] [CrossRef]
- Kong, X.; Xu, X.; Yan, Z.; Chen, S.; Yang, H.; Han, D. Deep learning hybrid method for islanding detection in distributed generation. Appl. Energy 2018, 210, 776–785. [Google Scholar] [CrossRef]
- Hussain, A.; Mirza, S.; Kim, C.H. Islanding detection and classification of non-islanding disturbance in multi-distributed generation power system using deep neural networks. Electr. Power Syst. Res. 2023, 224, 109807. [Google Scholar] [CrossRef]






| S. No. | Node Number | Load Detail |
|---|---|---|
| 1 | 634 | 400 kW and 290 kVAr |
| 2 | 645 | 170 kW and 125 kVAr |
| 3 | 646 | 230 kW and 132 kVAr |
| 4 | 652 | 128 kW and 86 kVAr |
| 5 | 671 | 1255 kW and 718 kVAr |
| 6 | 675 | 843 kW and 462 kVAr |
| 7 | 692 | 170 kW and 151 kVAr |
| 8 | 611 | 170 kW and 80 kVAr |
| 9 | 632–671 | 200 kW and 116 kVAr distributed load |
| S. No. | Transformer Symbol | MAV Rating | Voltage Ratio |
|---|---|---|---|
| 1 | UG-T | 10 MVA | 115 kV/4.16 kV |
| 2 | DF-T | 5 MVA | 4.16 kV/0.48 kV |
| 3 | WGP-GT | 5 MVA | 4.16 kV/0.575 kV |
| 4 | SGP-GT | 1 MVA | 4.16 kV/0.270 kV |
| S. No. | Islanding/Fault/Operational Event | Maximum HIDI |
|---|---|---|
| 1 | Islanding event with WGP and SGP generation | 2928.9 |
| 2 | Islanding event with generation from SGP | |
| 3 | Islanding event with generation from WGP | |
| 4 | Phase to ground fault | |
| 5 | Phase to phase fault | |
| 6 | Two phases to ground fault | |
| 7 | Three-phase fault | |
| 8 | Three phases to ground fault | |
| 9 | Feeder operation | 9.028 |
| 10 | Capacitor operation | 49.782 |
| 11 | Load operation |
| S. No. | Islanding/Fault/Operational Event | Computational Time (ms) |
|---|---|---|
| 1 | Islanding event with WGP and SGP generation | 0.278454 |
| 2 | Islanding event with generation from SGP | 1.650991 |
| 3 | Islanding event with generation from WGP | 0.443420 |
| 4 | Phase to ground fault | 1.320318 |
| 5 | Phase to phase fault | 1.631831 |
| 6 | Two phases to ground fault | 0.418473 |
| 7 | Three-phase fault | 1.397293 |
| 8 | Three phases to ground fault | 0.629446 |
| 9 | Feeder operation | 0.247305 |
| 10 | Capacitor operation | 0.282738 |
| 11 | Load operation | 0.344931 |
| S. No. | Islanding Incidence Angle | Peak Magnitude of HIDI |
|---|---|---|
| 1 | 2928.9 | |
| 2 | ||
| 3 | ||
| 4 | 64,472 | |
| 5 | 64,472 | |
| 6 | ||
| 7 |
| Voltage (pu) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| (kW) | 0.92 | 0.94 | 0.96 | 0.98 | 0.99 | 1.0 | 1.02 | 1.06 | 1.1 |
| 7 | ID | ID | ID | ID | ID | ID | ID | ID | ID |
| 6 | ID | ID | ID | ID | ID | ID | ID | ID | ID |
| 5 | ID | ID | ID | ID | ID | IND | ID | ID | ID |
| 4 | ID | ID | ID | ID | IND | IND | IND | ID | ID |
| 3 | ID | ID | ID | ID | IND | IND | IND | IND | ID |
| 2 | ID | ID | ID | IND | IND | IND | IND | IND | IND |
| 1 | ID | ID | ID | IND | IND | IND | IND | IND | IND |
| 0 | ID | ID | IND | IND | IND | IND | IND | IND | IND |
| −1 | ID | ID | ID | IND | IND | IND | IND | IND | IND |
| −2 | ID | ID | ID | ID | IND | IND | IND | IND | IND |
| −3 | ID | ID | ID | ID | IND | IND | IND | IND | ID |
| −4 | ID | ID | ID | ID | ID | IND | IND | ID | ID |
| −5 | ID | ID | ID | ID | ID | ID | ID | ID | ID |
| −6 | ID | ID | ID | ID | ID | ID | ID | ID | ID |
| −7 | ID | ID | ID | ID | ID | ID | ID | ID | ID |
| S. No. | Name of Parameter | Quantity of Parameter |
|---|---|---|
| 1 | Load | 9.28 MW |
| 2 | Rooftop solar plant | 0.9 MW |
| 3 | Solar PV plant | 3.40 MW |
| 4 | Wind power plant | 1.0 MW |
| S. No. | Reference | Technique | RE Penetration Level | Sampling Frequency | Computational Time | Noise Level for Performance of Algorithm Is Not Deteriorated | NDZ |
|---|---|---|---|---|---|---|---|
| 1 | [24] | DWT | 6.4 kHz | 2 s | 40 dB SNR | High | |
| 2 | [25] | Slantlet transform+RPNN | 19.8 kHz | 0.17 s | 25 dB SNR | High | |
| 3 | [26] | WT-MRA-based image data | 40% | 6.4 kHz | 0.18 s | 20 dB SNR | Moderate |
| 4 | [27] | DNN | 3.84 kHz | 2 s | 30 dB SNR | Not investigated | |
| 5 | Proposed HIDM | ST + HT + ALC | and | 3.84 kHz | t < 2 ms | 20 dB SNR | Moderate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Chen, A.; Liu, P.; Ren, W.; Zheng, C. Multivariable Algorithm Using Signal-Processing Techniques to Identify Islanding Events in Utility Grid with Renewable Energy Penetration. Energies 2024, 17, 877. https://doi.org/10.3390/en17040877
Li M, Chen A, Liu P, Ren W, Zheng C. Multivariable Algorithm Using Signal-Processing Techniques to Identify Islanding Events in Utility Grid with Renewable Energy Penetration. Energies. 2024; 17(4):877. https://doi.org/10.3390/en17040877
Chicago/Turabian StyleLi, Ming, Anqing Chen, Peixiong Liu, Wenbo Ren, and Chenghao Zheng. 2024. "Multivariable Algorithm Using Signal-Processing Techniques to Identify Islanding Events in Utility Grid with Renewable Energy Penetration" Energies 17, no. 4: 877. https://doi.org/10.3390/en17040877
APA StyleLi, M., Chen, A., Liu, P., Ren, W., & Zheng, C. (2024). Multivariable Algorithm Using Signal-Processing Techniques to Identify Islanding Events in Utility Grid with Renewable Energy Penetration. Energies, 17(4), 877. https://doi.org/10.3390/en17040877







