Abstract
The three-phase imbalance in low-voltage distribution networks (LVDNs) seriously threatens the security and stability of the power system. At present, a standard solution is automatic phase commutation, but this method has limitations because it does not address the branch imbalance and premature convergence or instability of the commutation algorithm. Therefore, this paper proposes a novel refined regulation commutation system, combined with a modified optimized commutation algorithm, and designs a model and simulation for feasibility verification. The refined regulatory model incorporates branch control units into the traditional commutation system. This effectively disperses the main controller’s functions to each branch and collaborates with intelligent fusion terminals for precise adjustment. The commutation algorithm designed in this paper, combined with the above model, adopts strategies such as symbol encoding, cubic chaotic mapping, and adaptive adjustment based on traditional genetic algorithms. In addition, in order to verify the effectiveness of the proposed method, this paper establishes a mathematical model with the minimum three-phase imbalance and commutation frequency as objectives and establishes a simulation model. The results of the simulation demonstrate that this method can successfully lower the three-phase imbalance of the low-voltage distribution network. It leads to a decrease of the main circuit’s three-phase load imbalance rate from 27% to 6% and reduces each branch line’s three-phase imbalance ratio to below 10%. After applying the method proposed in this paper, the main and branches circuit three-phase imbalance are both lower than the limit ratio of the LVDNs, which can improve the quality and safety of electricity consumption. Additionally, the results also prove that the commutation algorithm under this method has faster convergence speed, better application effect, and better stability, which has promotion and application value.
1. Introduction
The low-voltage distribution network is an important component of the power system and plays a crucial role in supplying power to end users. However, with the increase in power demand and variations in power load, the issue of three-phase imbalance in LVDNs is becoming increasingly prominent [1]. Uneven current distribution in the power grid, due to a three-phase imbalance, can cause equipment overload, damage, and low energy efficiency, all of which have a major negative impact on the dependability and quality of the power supply [2,3,4]. Therefore, it is of great theoretical and practical significance to solve the three-phase load imbalance problem in low-voltage distribution networks.
In China, the low-voltage feeders of LVDNs are usually three-phase, four-wire systems with two power supply modes: single-phase and three-phase [5]. At present, the main methods to solve the three-phase imbalance in LVDNs can be divided into manual phase adjustment, inter-phase reactive power compensation, and automatic phase commutation [6,7]. The method of manual phase sequence adjustment is to adjust the line load phase sequence manually regularly according to the monitoring data of the low-voltage side of the distribution transformer. This method cannot guarantee real-time and safety, and the workload is large [8]. Reactive power compensation refers to the parallel connection of capacitors between three phases to ensure a three-phase balance. This method can solve the three-phase imbalance to a certain extent, but it cannot fundamentally reduce line losses in the distribution area and has high maintenance costs [9]. The method of automatic phase commutation is based on an automatic commutation device (ACD). This device adjusts the phase sequence of some electrical loads through data collection and intelligent judgment. As a result, it fundamentally solves the problem of three-phase imbalance. This method can switch user load phases online, solve three-phase imbalance from the source, and improve power supply reliability [10,11].
At present, the method of automatic phase commutation often uses a one-multi-type commutation regulation system. In this system, a main controller monitors all intelligent commutation switches [12,13]. This method can indeed effectively balance the main circuit three-phase load of the low-voltage distribution network. However, since it is unable to monitor and adjust the current and voltage on each branch line, a serious three-phase imbalance still exists on the branch lines [6,14]. Moreover, with the continuous expansion of the power grid-scale and the continuous increase of load, the problem of three-phase load imbalance on branch lines also becomes more serious. Therefore, a more refined commutation regulation system should be designed, along with corresponding commutation algorithms with good convergence and stability.
The choice of optimization algorithm is key to reducing the degree of three-phase imbalance using ACDs [15]. Among them, artificial intelligence algorithms have significant advantages in data processing. These algorithms also have strong computational capabilities, enabling them to achieve ideal imbalance regulation through commutation. Artificial intelligence algorithms play an important role in various fields of application [16]. In terms of data processing, artificial intelligence algorithms can quickly and accurately analyze, extract, and understand a large amount of data. In terms of computing power, intelligence algorithms can utilize powerful computing resources for efficient calculations and improve the accuracy and efficiency of algorithms. In addition, artificial intelligence algorithms also have self-learning and adaptive capabilities. By continuously extracting patterns and patterns from data, artificial intelligence algorithms can self-learn and enhance their own abilities. These advantages enable intelligence algorithms to play an important role in various fields of application.
ACDs based on artificial intelligence algorithms are gradually receiving attention from researchers. For example, in [17], genetic algorithms were proposed to solve phase load balancing problems, optimize three-phase imbalance, and reduce terminal switch losses. In [18], the particle swarm optimization algorithm was employed to address the commutation scheme with optimization objectives of commutation frequency and three-phase imbalance. In [19], the optimal commutation scheme was solved using the modified Pigeon-Inspired Optimization. This approach demonstrated the advantages of introducing adaptive parameters and Cauchy perturbations in Pigeon-Inspired Optimization. In [20], the modified sparrow search algorithm was utilized to solve the multi-objective optimal model. The model aimed to minimize the commutation switch quantity and line loss cost, resulting in the derivation of an optimal commutation scheme. These methods have, to some extent, solved the three-phase imbalance on the main circuit, but the three-phase imbalance problem on the branch line still exists, and the optimization of commutation stability has not been taken into account.
Therefore, based on existing problems and references, this paper proposes a refined adjustment method with a modified genetic commutation algorithm to solve the problem of three-phase imbalance in LVDNs. This method aims to reduce the three-phase imbalance ratio on the main circuit and branch in LVDNs. It also focuses on optimizing the use of as few switch actions as possible during commutation. In addition, the commutation algorithm has good convergence and stability. This paper makes the following original contributions:
- (1)
- A new commutation regulation mode. This paper proposes a refined regulation model to solve the issue of three-phase imbalance on branches in LVDNs. Based on traditional commutation systems, this model adds branch control units to finely adjust the three-phase load.
- (2)
- A new commutation algorithm. To improve the commutation effect and stability, and minimize the number of commutation actions, this paper proposes a new commutation algorithm. This algorithm adopts strategies such as symbol encoding, cubic chaotic mapping, and adaptive adjustments based on a genetic algorithm to optimize algorithm performance.
- (3)
- Simulation examples in combination with (1) and (2). To verify the effectiveness of the proposed method, this paper establishes a mathematical model with the objectives of minimizing three-phase imbalance and commutation frequency. Additionally, a simulation model is created using the data of LVDNs as an example.
2. Analysis and Modeling of Three-Phase Imbalanced System Commutation Considering Refined Regulation
2.1. Refined Regulation Commutation System
The automatic phase commutation method is one of the standard methods to solve the three-phase imbalance problem in LVDNs, with advantages such as low cost, simple, and safe use. This method does not alter the existing structure of the power grid’s distribution network. It achieves an even distribution of unbalanced loads to each phase through automatic phase-shifting, resulting in a reduction of the three-phase imbalance ratio. With the continuous rise of branch loads in distribution networks and the increasing demand for electricity, researching more scientific and efficient intelligent commutation systems is the key content of automatic phase commutation methods [21,22,23]. Traditional commutation systems often adopt a one-multi-type regulation mode, where one master controller monitors all commutation switches, as shown in Figure 1. A △/Y-connected transformer is used as an example.
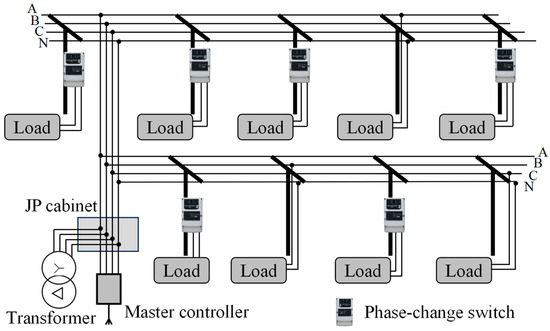
Figure 1.
Traditional commutation mode diagram of LVDNs.
In traditional commutation systems, the master controller is usually installed at the low-voltage outlet line on the secondary side of the distribution transformer to collect real-time three-phase data and calculate three-phase imbalance. When the three-phase imbalance is too large, the commutation scheme is calculated according to the commutation algorithm and sent to the switches for commutation operation through wireless. Assuming there are three branches in a traditional system, where all loads on the first branch are in phase A, all loads on the second branch are in phase B, and all loads on the third branch are in phase C. Obviously, in this situation, the main circuit is in a completely three-phase balance state, but each branch is in a serious three-phase imbalance state. Therefore, the traditional commutation mode cannot solve the three-phase imbalance problem on each branch. In order to solve the three-phase imbalance problem of the main circuit and each branch in the LVDNs, this paper proposes a refined commutation mode, as shown in Figure 2.
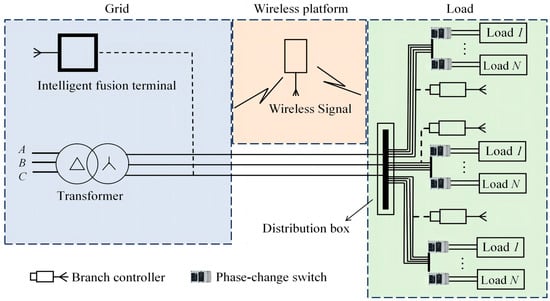
Figure 2.
Three-phase balance commutation system under refined regulation mode.
The refined regulation of the commutation system involves overlaying the host functions in a traditional mode onto the unit monitoring points of each branch. This enables real-time monitoring and regulation of the load on each branch by the respective units. Then, using communication technology, the current data is uploaded to the intelligent terminal equipment on the distribution transformer side. The terminal calculates the imbalance degree based on the current situation of each branch line. Then, an improved genetic algorithm is used to optimize the commutation strategy and determine the optimal commutation switch action plan. It is then issued to the intelligent commutation switch to complete live commutation.
This method can effectively regulate the three-phase load imbalance in each branch line, which avoids the shortcomings of the traditional centralized adjustment mode. The key to the commutation system in the refined commutation mode is the commutation control terminal of the branch unit detection node. The intelligent commutation terminal is installed on the bus of each branch, and it needs to detect the total current and voltage of this branch in real-time to determine whether the branch has three-phase imbalance problems. When a three-phase imbalance problem is detected, the terminal generates a control signal based on the load current of the commutation switch collected by the terminal. The commutation switch is then driven to complete the commutation operation, enabling the intelligent management of the three-phase imbalance. Among them, the commutation switching device in the new mode still adopts the seamless commutation technology with an equal voltage of 0 milliseconds, which can switch the single-phase load’s uninterrupted power supply between the three phases. Finally, the collected load current and fault signals need to be uploaded to the cloud server to achieve remote detection and control of the commutation system, ensuring the safe and stable operation of the system. Therefore, optimizing the quality of the commutation algorithm is one of the decisive factors for intelligent commutation, and it is also the key to refining the commutation effect of the commutation system. This paper establishes a mathematical model for branch line commutation, which is used for subsequent commutation algorithm improvement.
2.2. Mathematical Model of Branch Commutation
Whether the three-phase imbalance in the distribution area can be reduced and whether the number of commutation switch actions can be minimized are two important criteria for judging the effectiveness of the phase sequence adjustment methods. In addition, considering the voltage imbalance and various indicators at the point of common coupling as a comprehensive indicator will be more comprehensive. However, considering the efficiency and stability of the commutation algorithm, this section takes the minimum three-phase imbalance and the minimum number of switch actions as the objective functions. On this basis, constraints such as commutation switch phase sequence were established, and a branch commutation mathematical model was established for the commutation algorithm model.
Three-phase imbalance generally refers to the phenomenon of three-phase load imbalance in the power system, and the degree of imbalance exceeds a certain range. The measurement of three-phase imbalance serves as an indicator for this phenomenon, yet, a universally standardized calculation method for the three-phase imbalance is currently lacking across different fields worldwide. In practical engineering, the calculation method for current unbalance is widely used and provides more accurate results [24]. Therefore, this paper calculates the three-phase current unbalance based on the distribution network operation and maintenance regulations:
where iavg = (iA + iB + iC)/3 represents the average current of the three phases, and iA, iB, and iC represent the currents of phases A, B, and C, respectively.
Assuming there are N ACDs in the substation area, the objective function for minimizing the three-phase unbalance is shown as, as derived from Equation (1):
Each time a commutation command is issued, a commutation switch operation is performed, and excessive switch operations can shorten the lifespan of the switch. Therefore, it is critical to reduce how often the ACD switch actions occur. This solves practical issues like cost reductions in addition to guaranteeing the long-term use of commutation switches. The current phase sequence of a specific ACD in the substation area can be represented as:
During the optimization process, the switch state matrix has only three possible states, representing the connection to phases A, B, and C, respectively. The phase sequence states of each ACD in the substation area can be represented as Mx:
By multiplying the phase sequence states of each ACD with the user-side currents, the sum of currents for each phase can be obtained:
After commutation, the phase sequence states of each ACD will change, denoted as M′. A change in phase sequence for an ACD is represented as 1, while no change is represented as 0:
The total number of commutation actions for all phasing devices can be expressed as:
The function for minimizing the number of commutation operations for all phasing devices can be expressed as:
To simplify the use of the optimization commutation algorithm, weights are assigned to δ1 and δ2, resulting in the final objective function expression for the three-phase load imbalance commutation model established in this paper:
3. Optimization Commutation Algorithm Based on Cubic Adaptive Modified Genetic
In order to achieve comprehensive optimization of three-phase imbalance in LVDNs, it is essential to develop an intelligent optimization algorithm. This algorithm will provide effective strategies for the commutation system to ensure optimal results. Genetic algorithm has relatively loose requirements for functions during the operation process, and there are no certain rules to constrain the algorithm. When encountering nonlinear problems, compared to other algorithms, this algorithm has obvious advantages in dealing with nonlinear problems. With the highlighting of this advantage, this algorithm becomes effortless in dealing with practical problems and often appears in production optimization problems [25,26,27]. Therefore, this paper focuses on solving the function optimization problem with the three-phase imbalance and commutation frequency as the objectives. It utilizes the modified genetic algorithm (MGA) as the main commutation strategy. The proposed algorithm modifies the TGA, mainly using symbol encoding to represent commutation. The algorithm incorporates cubic chaotic mapping and stochastic universal selection to mitigate the risk of local optima. It also utilizes adaptive adjustment and species invasion interference to expedite the optimization process.
3.1. Encoding Method
In genetic algorithms, the encoding method directly affects the operation of genetic operators such as crossover and mutation operators, which largely determines the efficiency of genetic evolution [28]. Therefore, the encoding method should not only meet the needs of practical problems but also consider algorithm performance. In the context of this paper, the executing devices for automatic phase commutation are commutation switches, which can switch between phases A, B, and C, defined as:
Matrix encoding is commonly employed in classical genetic algorithms. However, the high dimensionality of the matrix leads to long gene lengths, potentially hampering convergence speed and decreasing algorithm efficiency [29]. Therefore, this paper chooses symbol encoding in terms of the encoding method. Symbol encoding refers to the collection of gene values in a chromosome encoding string taken from a symbol set with no numerical meaning but only code meaning. This method offers the advantages of simple mutation and the freedom from accuracy limitations. It facilitates the integration of specialized problem-solving knowledge and the incorporation of relevant approximation algorithms. In the automatic optimization commutation problem of this paper, the symbol codes corresponding to the three phases are shown in Table 1.

Table 1.
The phase sequence encoding of the optimized commutation process.
3.2. Modified Algorithm Process
The traditional genetic algorithm (TGA), also known as a simple genetic algorithm, is a heuristic optimization algorithm that simulates biological evolution. The basic process of this algorithm involves determining the encoding method and fitness calculation method. An initial population is generated and subsequent iterations involve steps such as selection, crossover, and mutation until a convergence condition is reached. The traditional algorithm flowchart is shown in Figure 3.
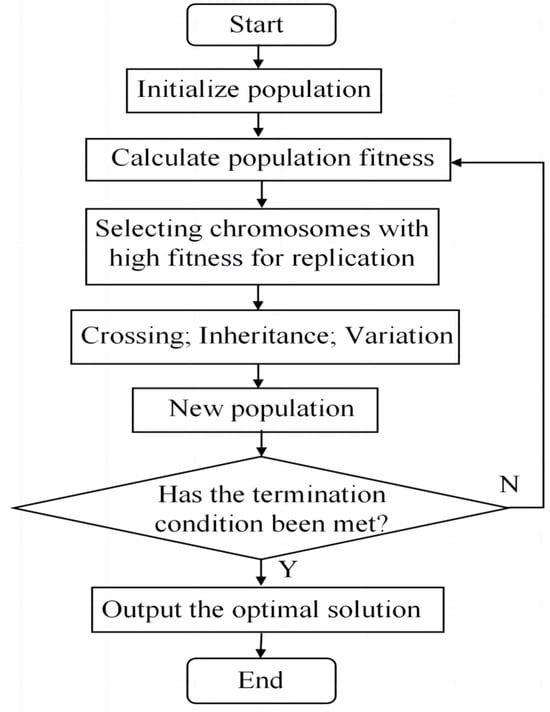
Figure 3.
Flow chart of the traditional genetic algorithm.
The TGA possesses a straightforward genetic evolution process, straightforward operation, and significant application value. Nonetheless, in the context of practical problem solving, the TGA exhibits sluggish convergence speed and susceptibility to being trapped in local optima. Additionally, mutation may also lead to individuals who do not satisfy the constraint conditions [30]. In order to solve the above problems, this paper has made improvements and proposed the MGA: cubic adaptive genetic algorithm (CAGA), as shown in Figure 4.
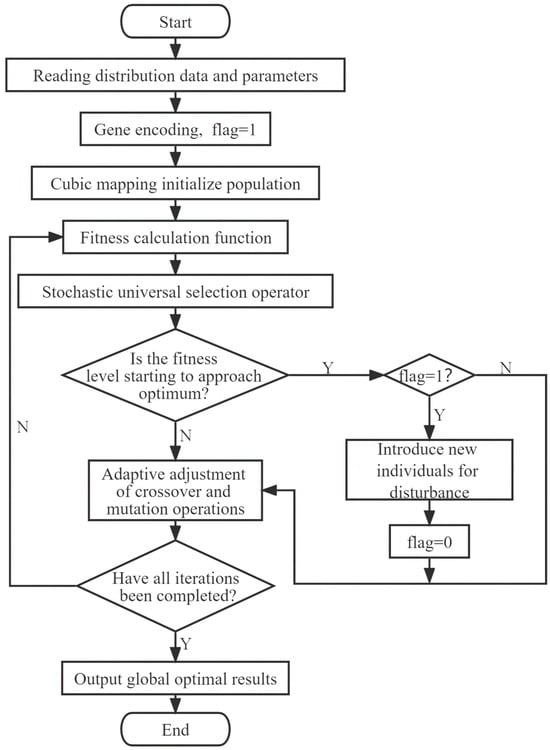
Figure 4.
Flow chart of the modified genetic algorithm.
The individual genes in the population of TGA are generated randomly. This leads to uncertainty in population initialization and increases the risk of entering a local optimal state. To form an initial population with uniformity and diversity, MGA uses a cubic chaotic mapping function to initialize the population. The mathematical expression of the cubic chaotic map used in this paper is shown in Equation (11):
where Zk represents the current input value, Zk+1 represents the next value, and ρ is a constant.
After initializing the population through the cubic chaotic mapping function, the population is encoded according to the encoding method in Table 1 to form the initial population. Then, use the objective function established in Section 2.2 as the fitness function of the genetic algorithm for the next step of operation.
During the iteration process, due to the calculation of fitness for each generation of population individuals, the fitness matrix is constantly updated [31,32]. To obtain the optimal commutation sequence, MGA adopts a stochastic universal selection method to select excellent individuals as parents. Then, a dynamic probability strategy is adopted to meet the iterative requirements of crossover and mutation. In genetic algorithms, the crossover and mutation operations synergistically compete and cooperate, allowing the algorithm to achieve a balance between global and local search capabilities. However, in the TGA, the probabilities of crossover and mutation are constant and cannot meet the changing needs of the population during the genetic process. To solve this problem, this paper proposes modified formulas for crossover and mutation probabilities, as shown in Equations (12) and (13):
where Pc and Pm represent the probabilities of crossover and mutation, respectively, fmax and fmin represent the maximum and minimum fitness values of the current generation, favg represents the average fitness value of the current generation, f represents the fitness value of an individual in the current generation, and C represents a constant.
Moreover, to ensure that the algorithm does not fall into local optima, a disturbance called species invasion is introduced. When the fitness stabilizes, a fixed individual is randomly generated and added to the current population to break out of the current optimal solution and continue searching for the global optimum. In addition, MGA adopts an adaptive adjustment strategy to further adjust the proportion of outstanding individuals in the parents. In the early stages of algorithm operation, the population needs to constantly approach excellent individuals. MGA retains a small number of outstanding individuals from the current generation. The excellent offspring obtained through selection, crossover, and mutation are then used as the initial population for the next generation. As the algorithm iterates, the number of outstanding individuals increases, resulting in an increased proportion of retained parents. This effectively accelerates the optimization process of the algorithm. The Equation is as follows:
where c1, c2, c3 and c4 are constants; g represents the current population genetic algebra; and gmax represents the total algebra of population genetics.
Through continuous iterative calculation, the fitness value and switch state are continuously updated until the iteration process is completed. The output of the optimal commutation switch state, commutation frequency, and current imbalance value are sent to the optimal commutation command based on the switch state under the global extreme value. Finally, combined with the optimized commutation algorithm proposed in this paper, the refined commutation mode is shown in Figure 5.
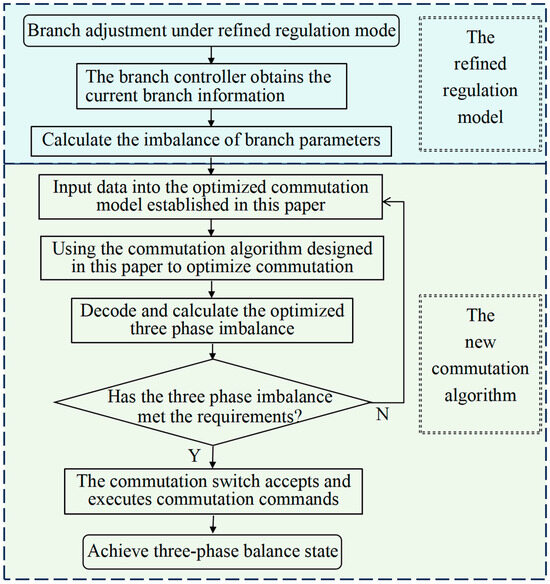
Figure 5.
Proposed optimized commutation process.
4. Refined Commutation Case of LVDNs Based on Modified Genetic Algorithm
4.1. Case Data and Analysis
The distribution network structure of the LVDNs is generally a three-phase, four-wire system, and the commutation execution household wiring is generally a single-phase, two-wire system. Taking a certain distribution station area as an example, there are four branches connected to a transformer. Each branch has a varying number of commutation switches. Assuming that each branch has 30 users, and each branch is fixed with 10 commutation switches. The topology structure of this distribution substation is shown in Figure 6.
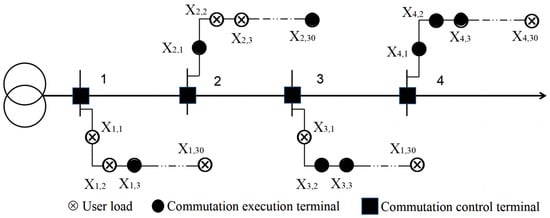
Figure 6.
Topology of the distribution substation.
The execution end of the commutation device works in conjunction with the monitoring and control end of each branch. Each branch adjusts the current on the branch line by manipulating the commutation switches to achieve three-phase load balancing. The installation positions of commutation switches, the current value, and the imbalance of each branch in the distribution station area are shown in Table 2.

Table 2.
Installation position of commutation switches, current value, and imbalance value for each branch line.
According to Equation (1), the three-phase load imbalance of each branch in the substation is calculated as follows: 35%, 12%, 23%, and 38%. The main circuit three-phase load imbalance of the substation is as high as 27%. At this time, both the branch lines and the main circuit of the case substation have high three-phase load imbalances, which will affect the safety and economic benefits of the substation operation. The following section will use optimization algorithms to solve the three-phase load imbalance problem in the case substation.
4.2. Comparison of Optimization Commutation Algorithms
The use of a TGA to solve the three-phase load imbalance problem in the substation has drawbacks such as poor convergence, high instability of calculation results, etc. Therefore, this section conducted comparative experiments on the traditional commutation algorithm and the proposed commutation algorithm. These algorithms were used to individually solve the three-phase load imbalance problem in the branch-independent commutation station area.
The algorithm experiment is based on MATLAB R2021a, with a population size of 100, and the number of iterations set to 50. The comprehensive objective function is shown in Equation (9), where the value ω1 is 0.95 and the value ω2 is 0.05, and the reciprocal is used to represent the minimum value of the comprehensive objective function. We conducted algorithm comparison experiments using the classic genetic algorithm before the improvement and the CAGA modified in this paper. The comparison results of the comprehensive objective function evolution curves for each branch are shown in Figure 7.
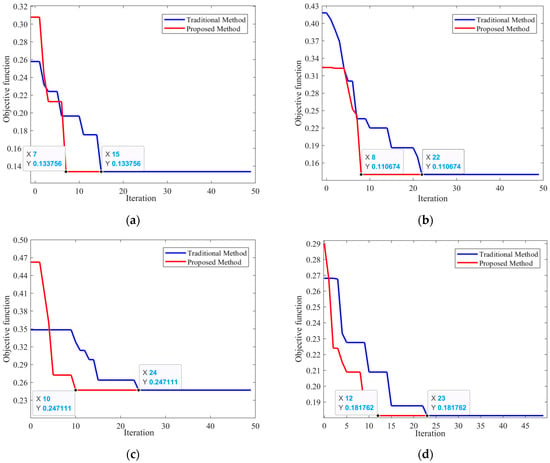
Figure 7.
Comparison of optimized commutation effects for each branch using traditional and proposed methods. (a) Branch 1; (b) branch 2; (c) branch 3; and (d) branch 4.
The figure shows the comparison of algorithm improvement effects under different branches. In this embodiment, the genetic algorithm demonstrates a good optimization effect for the four branches in the station area. Although the final convergence values are consistent, the number of iterations when the improved algorithm reaches the optimal value is significantly smaller than the traditional algorithm. For example, the proposed method converges in the eighth generation in the optimization commutation of branch 2. In comparison, the traditional method converges in the 22nd generation. The efficiency of the modified iteration curve is significantly improved. Therefore, compared with traditional methods, the method proposed in this paper has a better imbalance resolution effect and the advantages of faster convergence speed and higher iteration efficiency.
To further demonstrate the stability of this algorithm in optimizing commutation problems, this paper further conducted algorithm stability verification experiments. Taking 20 populations in branch 1 as an example, compare the optimal imbalance and imbalance under the optimal fitness of each population, as well as the minimum number of commutations for each population and the number of commutations under the optimal fitness, to achieve a stability evaluation. The comparison results of the imbalance before and after the application of the modified algorithm for optimizing commutation are shown in Figure 8.
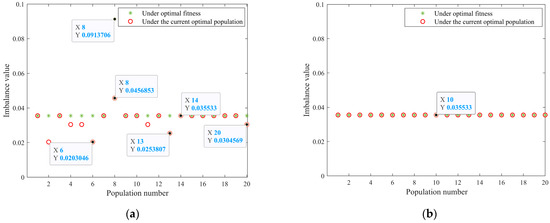
Figure 8.
Stability comparison of commutation algorithms based on imbalance before and after improvement. (a) Traditional method; (b) proposed method.
From the figure, the distribution of imbalance results under traditional methods is chaotic and there are many deviations, resulting in poor stability of algorithm operations. Among them, the marked black dots represent partial deviation points. The proposed method demonstrates a high coincidence rate of two imbalances and a concentrated distribution of results. This indicates its good robustness and effectiveness in reducing three-phase imbalances. As shown in Figure 9, the comparison results of the number of commutations before and after the application of the modified algorithm for optimizing commutation are presented.
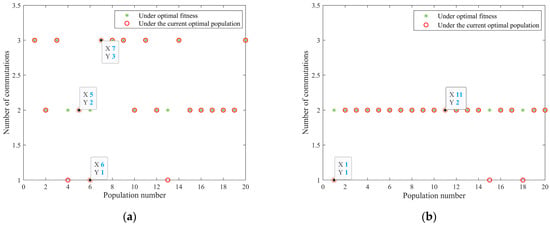
Figure 9.
Comparison of the stability of the number of commutation actions between traditional and proposed methods. (a) Traditional method; (b) proposed method.
As shown in the figure, the distribution of results under traditional methods is too discrete, resulting in poor commutation effect and poor stability of the results. The two results obtained by applying the proposed method have a relatively concentrated distribution, high coincidence rate, and good robustness. Among them, the marked black dots represent partial deviation points. In summary, the CAGA designed in this paper is significantly superior to the TGA in solving the problem of optimal commutation. This algorithm can effectively reduce the imbalance of three-phase load and has both stability and convergence.
4.3. Main and Branch Circuit Commutation Results of LVDNs
The method designed in this paper is applied to optimize the commutation of each branch in the case substation. The comparative results of the commutation effects for each branch and the main circuit are shown in Table 3.

Table 3.
Comparative table of optimization commutation effects for different algorithms.
From Table 3, the main circuit three-phase imbalance of the substation area has decreased from 27% before governance to 6%. The imbalance of branch 1 has decreased from 35% before governance to 4%. The imbalance of branch 2 has decreased from 12% to 1%. The imbalance of branch 3 has decreased from 23% to 10%. The imbalance of branch 4 has decreased from 38% to 9%. This not only solves the three-phase imbalance of each branch but also reduces the number of commutation switches. MATLAB R2021a/Simulink is employed to facilitate the simulation and comparative analysis of the three-phase currents in the substation, both before and after the optimization commutation process. The parameters are set as follows: power supply voltage of 5 kV, transformer of 5 kV/220 V, total length of 10 km (total resistance of 2 Ω, reactance of 2 Ω), three-phase loads of 100 kW each, and neutral line resistance of 2 Ω. The comparative results of the three-phase currents before and after optimization commutation in the substation are shown in Figure 10.
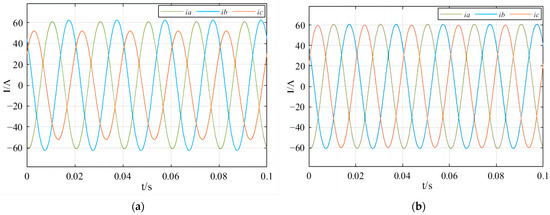
Figure 10.
Comparative waveform of three-phase currents before and after optimization commutation. (a) Without the method proposed in this paper; (b) with the method proposed in this paper.
From the figure, it can be intuitively observed that the amplitude difference of the three-phase current before optimizing commutation is significant. At this time, the phase difference is not 120 degrees, and the amplitude of the current on the neutral line is also large. This will lead to significant line power consumption on the neutral line, seriously affecting the operational efficiency of the substation area. In contrast, after optimizing the commutation, the amplitude of the three-phase current is basically the same, with a phase difference of about 120 degrees. The current on the neutral line is close to zero, indicating that the three-phase current in the power system is balanced during normal operation. Currently, the distribution station area forms a relatively balanced power system. Therefore, the method proposed in this paper can effectively solve the three-phase imbalance of the main circuit, and the three-phase imbalance problem on each branch line has also been effectively solved.
5. Conclusions
This paper proposes a novel refined regulation method with faster convergence speed and better stability to solve the problem of branch three-phase load imbalance in low-voltage distribution networks. In the proposed refined regulation model, the three-phase imbalance on the branches is fully considered, and the branch control unit is added, which performs tuning in conjunction with intelligent fusion terminals. In the proposed algorithm, symbol encoding is used to represent the phase of commutation, and cubic chaotic mapping and stochastic universal selection are used to avoid local optima, and adaptive adjustment and species invasion disturbance are used to accelerate the optimization process. To test the practical application effect of the proposed algorithm, an example model was established based on the branch topology structure and branch commutation data of a certain distribution station area. In simulation, the comprehensive objective functions were set as the minimum three-phase imbalance and the minimum number of commutation actions. This method was then compared with TGA-based methods. The simulation results show that the proposed method has faster convergence speed and better stability. After independent branch commutation based on the proposed method, the three-phase load imbalance of each branch is reduced to below 10%, and the three-phase load imbalance of the main circuit is reduced from 27% to 6%. Therefore, after applying the proposed method, the main circuit three-phase imbalance in the distribution area and each branch line has been effectively solved, proving that this method has high practical value and development prospects. In future work, consideration can be given to line loss, commutation time, transient state of the circuit, etc., in order to further study the three-phase imbalance problem in LVDNs.
Author Contributions
Project administration, methodology, software, D.L.; conceptualization, investigation, data curation, Z.L. and T.W.; data curation, Z.X.; writing—original draft preparation, project supervision, T.H. and A.D.; writing—review and editing, Z.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the State Grid Beijing Electric Power Company under Grant 520204230002.
Data Availability Statement
Data available in a publicly accessible repository.
Conflicts of Interest
Dazhao Liu, Zhe Liu, Ti Wang, Zhiguang Xie were employed by the State Grid Beijing Electric Power Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LVDNs | Low-voltage distribution network |
| ACDs | Automatic commutation devices |
| MGA | Modified genetic algorithm |
| TGA | Traditional genetic algorithm |
| CAGA | Cubic adaptive genetic algorithm |
References
- Xiao, M.; Wang, S.; Ullah, Z. D-pmu and 5g-network-based coordination control method for three-phase imbalance mitigation units in the lvdn. Energies 2021, 14, 2754. [Google Scholar] [CrossRef]
- Ma, K.; Fang, L.; Kong, W. Review of distribution network phase unbalance: Scale, causes, consequences, solutions, and future research directions. CSEE J. Power Energy Syst. 2020, 6, 479–488. [Google Scholar]
- Yan, S.; Tan, S.-C.; Lee, C.-K.; Chaudhuri, B.; Hui, S.Y.R. Electric springs for reducing power imbalance in three-phase power systems. IEEE Trans. Power Electron. 2015, 30, 3601–3609. [Google Scholar] [CrossRef]
- Heidari-Akhijahani, A.; Safdarian, A.; Lehtonen, M. Unbalance mitigation by optimal placement of static transfer switches in low voltage distribution feeders. IET Gener. Transm. Distrib. 2020, 14, 4612–4621. [Google Scholar] [CrossRef]
- Bao, G.; Ke, S. Load transfer device for solving a three-phase unbalance problem under a low-voltage distribution network. Energies 2019, 12, 2842. [Google Scholar] [CrossRef]
- Zeraati, M.; Golshan, M.E.H.; Guerrero, J.M. Voltage quality improvement in low voltage distribution networks using reactive power capability of single-phase PV inverters. IEEE Trans. Smart Grid 2018, 10, 5057–5065. [Google Scholar] [CrossRef]
- Pati, U.; Mistry, K.D. Management of three-phase electrical loads using phase balancing optimization technique to reduce voltage imbalance in distribution networks. Electr. Eng. 2023, 14, 3997–4010. [Google Scholar] [CrossRef]
- Wang, Y.; Chu, Z.; Chen, G.; Zhang, T.; Ma, Y.; Chen, C.; Lin, Z. A robust control strategy for the automatic load commutation device considering uncertainties of source and load. Appl. Sci. 2023, 13, 7390. [Google Scholar] [CrossRef]
- Wang, X.; Dai, K.; Chen, X.; Zhang, X.; Wu, Q.; Dai, Z. Reactive power compensation and imbalance suppression by star-connected buck-type D-CAP. Energies 2019, 12, 1914. [Google Scholar] [CrossRef]
- Fang, L.; Ma, K.; Zhang, X. A statistical approach to guide phase swapping for data-scarce low voltage networks. IEEE Trans. Power Syst. 2020, 35, 751–765. [Google Scholar] [CrossRef]
- Ferreira, P.D.F.; Carvalho, P.M.S.; Ferreira, L.A.F.M.; Ilic, M.D. Distributed energy resources integration challenges in low-voltage networks: Voltage control limitations and risk of cascading. IEEE Trans. Sustain. Energy 2013, 4, 82–88. [Google Scholar] [CrossRef]
- Liu, S.; Jin, R.; Qiu, H.; Cui, X.; Lin, Z.; Lian, Z.; Lin, Z.; Wen, F.; Ding, Y.; Wang, Q.; et al. Practical method for mitigating three-phase unbalance based on data-driven user phase identification. IEEE Trans. Power Syst. 2020, 35, 1653–1656. [Google Scholar] [CrossRef]
- Wang, X.; Ji, Y.; Wang, J.; Zhao, Y.; Ye, P.; Qi, L.; Yang, S.; Liu, S. Research on reconfiguration of distribution network considering three-phase unbalance. Wirel. Commun. Mob. Comput. 2022, 2022, 9906100. [Google Scholar] [CrossRef]
- Li, W.; Li, M.; Zhang, N.; Zhou, X.; Zhou, J.; Song, G. Optimizing allocation of distributed electric heating for large-scale access distribution considering the influence of power quality. Energies 2022, 15, 3587. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, F.; Gu, L.; Yin, H.; Zhang, L.; Gao, C. Evaluation index and evaluation method of three-phase imbalance treatment effect based on commutation. IEEE Access 2022, 10, 101913–101921. [Google Scholar] [CrossRef]
- Ahmed, I.; Jeon, G.; Piccialli, F. From artificial intelligence to explainable artificial intelligence in industry 4.0: A survey on what, how, and where. IEEE Trans. Ind. Inform. 2022, 18, 5031–5042. [Google Scholar] [CrossRef]
- Han, P.; Pan, W.; Zhang, N.; Wu, H.; Qiu, R.; Zhang, Z. Optimization method for artificial phase sequence based on load forecasting and non-dominated sorting genetic algorithm. Dianll Xltong Zidonghua/Autom. Electr. Power Syst. 2020, 44, 71–78. [Google Scholar]
- Zhang, J.; Hao, S. Treatment of three-phase imbalance based on commutation switch. Electr. Autom. 2021, 43, 98–100+104. [Google Scholar]
- Hu, M.-Y.; Zhang, H.-F.; Miao, S.-P.; Yang, F.; Qu, Z.M. Phase sequence adjustment method for three-phase load imbalance in station area based on improved pigeon-inspired optimization. China Electr. Power 2022, 55, 121–128. [Google Scholar]
- Wang, J.-Y.; Wu, Z. Research on three-phase unbalanced load management based on improved sparrow search algorithm. Jilin Electr. Power 2022, 50, 19–24. [Google Scholar]
- Rocha, N.; de Oliveira, Í.A.; de Menezes, C.E.C.; Jacobina, C.B.; Dias, J.A.A. Single-phase to three-phase converters with two parallel single-phase rectifiers and reduced switch count. IEEE Trans. Power Electron. 2016, 31, 3704–3716. [Google Scholar] [CrossRef]
- Coppo, M.; Bignucolo, F.; Turri, R. Generalized transformer modelling for power flow calculation in multi-phase unbalanced networks. IET Gener. Transm. Distrib. 2017, 11, 3843–3852. [Google Scholar] [CrossRef]
- Borges, P.R.O.; Ramos, J.E.; Carvalho, C.A.T.; Pires, V.A.; Carsoso, G.; Ramos, D.B.; de Morais, A.P. Repowering rural single-phase distribution network: A non-conventional proposal using two overhead wires and the ground as the third phase. Electr. Power Syst. Res. 2017, 150, 105–117. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, X.; Zhu, L.; Yang, S.; Sun, Y. Research on three-phase unbalanced commutation strategy based on the spotted hyena optimizer algorithm. Complexity 2022, 2022, 2092421. [Google Scholar] [CrossRef]
- Vasconcelos, J.A.; Ramirez, J.A.; Takahashi, R.H.C.; Saldanha, R.R. Improvements in genetic algorithms. IEEE Trans. Magn. 2001, 37, 3414–3417. [Google Scholar] [CrossRef]
- Wen, S.; Rios, A.; Ge, Y.; Itti, L. Beneficial perturbation network for designing general adaptive artificial intelligence systems. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3778–3791. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Vairam, S.; Selladurai, V. Permutation genetic algorithm based encoding method for parallel machine scheduling and balancing. Appl. Mech. Mater. 2014, 573, 368–373. [Google Scholar]
- Zhang, Y.; Liu, M. An improved genetic algorithm encoded by adaptive degressive ary number. Soft Comput. 2018, 22, 6861–6875. [Google Scholar] [CrossRef]
- Jiacheng, L.; Lei, L. A hybrid genetic algorithm based on information entropy and game theory. IEEE Access 2020, 8, 36602–36611. [Google Scholar] [CrossRef]
- Wang, C.; Liu, X.; Hu, H.; Han, Y.; Yao, M. Energy-efficient and load-balanced clustering routing protocol for wireless sensor networks using a chaotic genetic algorithm. IEEE Access 2020, 8, 158082–158096. [Google Scholar] [CrossRef]
- Shrestha, A.; Mahmood, A. Improving genetic algorithm with fine-tuned crossover and scaled architecture. J. Math. 2016, 2016, 4015845. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).