Abstract
The supercritical carbon dioxide (S-CO2) Brayton cycle efficiency increases as the compressor inlet condition approaches the critical point. However, the thermodynamic properties of CO2 vary dramatically near the critical point, and phase change is most likely to happen. Both cavitation and condensation bring about significant adverse effects on the performance of compressors. In this paper, the quantitative effects of nonequilibrium condensation and cavitation on the performance of an S-CO2 centrifugal compressor with different inlet-relative entropy values are investigated. The properties of CO2 were provided by the real-gas property table, and the nonequilibrium phase-change model was adopted. The numerical simulation method with the nonequilibrium phase-change model was validated in the Lettieri nozzle and Sandia compressor. Furthermore, simulations were carried out in a two-stage centrifugal compressor under conditions of various inlet-relative entropy values. The type of nonequilibrium phase change can be distinguished by inlet-relative entropy. Cavitation makes the choke mass flow rate decrease due to the drop in the speed of sound. Condensation mainly occurs on the leading edge of the main blade at a large mass flow rate, but cavitation occurs on the splitter. The condensation is more evenly distributed on the main blade, but the cavitation is mainly centered on the leading edge.
1. Introduction
With the growing problem of energy scarcity and the increase in people’s awareness of environmental protection, society has been placing a great emphasis on an efficient and environmentally friendly power cycle. Various countries are now developing clean and renewable energy, reducing greenhouse gas and harmful gas emissions, optimizing current energy systems and improving cycle efficiency.
The Brayton cycle of supercritical carbon dioxide (S-CO2) is an attractive power generation technology that offers potential advantages in terms of cycle efficiency [1,2]. As a working fluid, CO2 has good stability and abundant storage. In a supercritical state, CO2 has large specific heat capacity, large compressibility, large density, low viscosity and other qualities that can significantly reduce the compression work and then improve the cycle efficiency [3]. The closer the inlet condition is to the critical point, the greater the system performance is [4,5,6]. However, when the compressor inlet condition approaches the critical point, the thermophysical properties of CO2 will change dramatically, deviate significantly from the ideal gas and show a strong real-gas effect [7,8]. On the other hand, the critical point is the end of the saturation line. When the inlet condition of a compressor approaches the critical point, cavitation and condensation may be triggered in the impeller blade channel due to the local flow acceleration [9]. In Figure 1, the processes of phase change are illustrated on a pressure–temperature diagram. The working fluid expands isentropically from the supercritical region (point A) to the gas region and then reaches the saturation line (point B). The phase change manifests as condensation, where the droplets are generated in a gas environment. Condensation does not occur immediately when the saturation line is reached but continues to expand isentropically in the form of gas. The working fluid enters a metastable state until it arrives at the Wilson line (point D), where the spontaneous nucleation process will be triggered [10,11]. Finally, the fluid will return to equilibrium (point E). If condensation is equilibrium, the fluid will condense along the saturation line (from point B to point C). Cavitation process starts in supercritical conditions (A’), which are closer to the liquid phase. The fluid also expands isentropically, passes through the liquid region and reaches the saturation line (point B’). The fluid has low compressibility, which results in a small temperature drop and a large pressure drop. The fluid continues to expand to point D’ and then cavitation occurs. The phase change usually occurs on the suction side. Condensation and cavitation do not occur at the same time. Condensation occurs in the gas environment, and cavitation occurs in the liquid environment. Condensation droplets on the impeller blade may further deteriorate the performance of the compressor or cause erosion [11,12,13,14]. Cavitation can generate large amounts of bubbles, and bubbles occupy most of the channel, resulting in blockage [15,16,17]. Also, it is possible for the temperature and pressure of S-CO2 fluid to decrease below the critical point and pass through the saturation line, causing the phase change under the compressor’s start–stop and off-design settings. Few experiments have been conducted on the flow and phase change of S-CO2 compressors. The studies of Sandia National Laboratories have shown that an S-CO2 compressor can work stably no matter what phase the inlet condition is in [18,19,20]. Noall [21] believed that a compressor could achieve a long-term stable operation with a two-phase inlet condition, which is limited to a low rotational speed. The preceding investigations are concerned with the overall performance of a compressor and do not provide a clear picture of the specific internal flow characteristic of an S-CO2 compressor. It is still difficult to measure the internal flow through experiments due to the small size of the impeller. Although some studies state that the phase change has little effect on a compressor’s performance, most studies consider a potential two-phase operation as a high risk and do not recommend it for a high-reliability system [22]. Therefore, it is necessary to investigate the quantitative effect of the near-critical nonequilibrium phase change on the performance of a S-CO2 centrifugal compressor and provide theoretical guidance for the design and operation strategy for S-CO2 compressors.
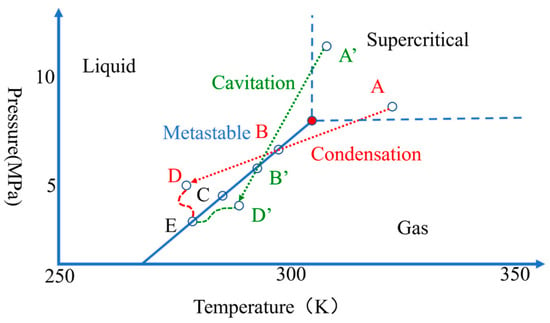
Figure 1.
Nonequilibrium phase change and metastable state.
2. Numerical Investigation
2.1. CO2 Condensation in Lettieri Nozzle
2.1.1. Condensation Model
The multiphase model is set to a mixture model, and the Lee Model is chosen as the condensation model. The slip effect can be neglected due to the fast expansion rate. The liquid–vapor mass transfer is governed by the vapor transport equation [23]:
where represents the vapor phase, is the volume fraction of the vapor, is the vapor density, is the vapor-phase velocity and are the rates of mass transfer due to evaporation and condensation, respectively. The units of the rates of mass transfer are kg/s/m3.
The mass transfer can be described as follows:
where is the saturation temperature and and are the Lee model coefficients.
In the saturation conditions, temperature and pressure can be expressed by the Clausius–Clapeyron equation:
where is the latent heat.
When the temperature and pressure are close to the saturation line, the Equation (4) can be simplified as:
The evaporation–condensation flux, based on the kinetic theory for a flat interface, can be expressed by Hertz Knudsen equations:
where has units of kg/s/m2, is the accommodation coefficient, is the molecular mass and is the universal gas constant. In the process of condensation, is the ratio between the condensation rate in the experiment and the maximum theoretical condensation rate.
Using the above equation in the Hertz Knudsen equations:
Assume all bubbles have the same diameter. The interfacial area density can be expressed as:
where is the bubble diameter, and the phase source term can be:
From the above equation, the Lee model coefficient is defined as:
where represent the inverse of the relaxation time of evaporation and condensation, respectively, which can control the rate of evaporation and condensation. For different kinds of numerical simulation, the Lee model coefficient should be different. The Fluent Theory guide suggests to set the coefficient as 1000 [23].
2.1.2. Simulation in Lettieri Nozzle
The internal flow of the S-CO2 centrifugal compressor is approximately the isentropic flow with local expansion processes. Therefore, numerical simulations under various, different near-critical conditions can be carried out in a relatively simple geometric model, which is the Laval nozzle. The simulations are to test the reliability of the nonequilibrium phase-change model and the corresponding two-phase-flow simulation method. The characteristics of the nonequilibrium phase-change flow field have been analyzed, and the results have been compared to the experimental data of Lettieri [10]. The experimental test apparatus consists of a blowdown test rig filled with high-pressure CO2. The exhaust gas flows through the Laval nozzle. The nozzle length is 91.3 mm, the throat area is 20 mm2, the height of the throat is 3.09 mm, and the distance from the throat to the exit is 61.3 mm. The inlet-to-throat and outlet-to-throat area ratios are 4.1 and 1.3, respectively. The grid independence analysis is carried out with three kinds of mesh sizes. The inlet conditions are set as 7.4 MPa and 310 K. The pressure distribution along the axial center of the nozzle is shown in Figure 2. It is evident that the distribution of pressure has no significant difference between 1,176,277 cells and 2,293,147 cells. Therefore, the mesh size is set as 1,176,277 cells, as shown in Figure 3.
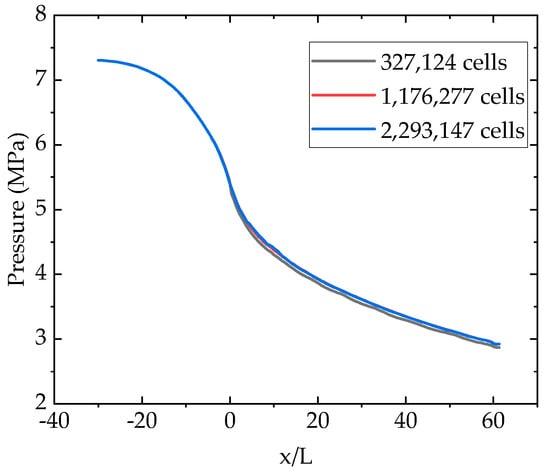
Figure 2.
Pressure distribution along the axial center of the nozzle with different mesh sizes.

Figure 3.
Grid of Lettieri nozzle.
In the numerical procedure, Fluent was used as the numerical solver of the mesh model to solve the governing equations and the addition nonequilibrium phase-change model. A 3D steady-state simulation was carried out in Fluent. Two turbulence equations of the SST model were applied to calculate the turbulence characteristics of the flow. The coupled algorithm was utilized for the coupling of the pressure-velocity field, and second-order upwind discretization was used for the continuity, momentum and energy equation. The boundary conditions were set as adiabatic, no-slip and smooth wall. The inlet and outlet boundary conditions were set as pressure boundary conditions. The turbulent intensities at the inlet and outlet were set at 5%. The inlet hydraulic diameter was set as 17.16 mm, and the outlet hydraulic diameter was set as 9.89 mm. The inlet vapor volume fraction was set to 1. When the relative residuals of energy and other dependent variables were less than 1 × 10−6, respectively, and the mass flow rate between the inlet and outlet was less than 1 × 10−4, the numerical program could be considered to converge. The inlet conditions are shown in Table 1, which is the same as in the Lettieri experiment [24]. Due to the strong real-gas effect near the critical point, the real-gas properties table (RGP table) was used in the simulation. The thermophysical properties of CO2 are provided in the form of a table, which is a function of the temperature and pressure. These properties come from the Nation Institute for Standards and Technology (NIST) database, using the Span and Wagner equation of state (S-W EOS). The RGP table can save calculation time with a certain accuracy. The real-gas properties table bounds vary from 220 K, 0.1 MPa, to 400 K, 30 MPa. There are 500 temperature, pressure and saturation points in the table.

Table 1.
Inlet conditions of nozzle.
The nozzle with different Lee model coefficient values was simulated under an inlet condition with a relative entropy of 1.18. The pressure profile in the nozzle for various Lee model coefficient values is illustrated in Figure 4. In Figure 4, P0 is the inlet pressure, L is the length of the nozzle, and P is the pressure at the centerline. When the Lee model coefficient is 10 or 0.1, the effect on the flow field is almost insignificant, and the pressure profile is the same as the profile without phase change. If the coefficient is 1 × 106, the effect on the flow field is too strong. The pressure deviates from the experimental data, and the flow will approach equilibrium soon. When the working fluid passes through the saturation line, condensation occurs immediately, behaving as equilibrium condensation. Finally, the coefficient of 1 × 104 is adopted in this paper. The pressure profile with this coefficient matches the experiment data very well, which manifests as nonequilibrium condensation. Nonequilibrium condensation is a delayed condensing phenomenon affected by flow velocity. The fluid will not condense on the saturation line due to the short timescale of condensation to expansion until it reaches the Wilson line with a certain value of subcooling.
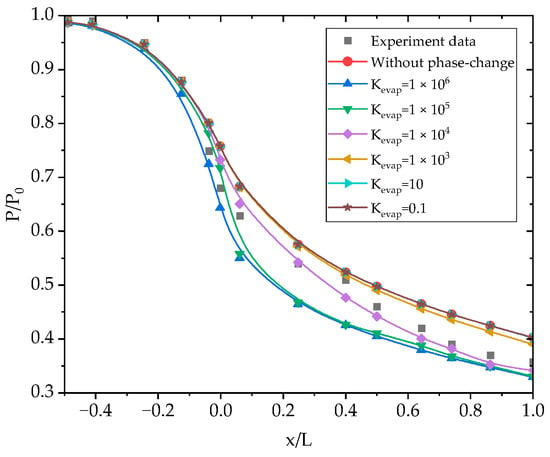
Figure 4.
Pressure profile in the nozzle for various Lee model coefficient values.
As the high-pressure CO2 fluid expands and accelerates in the throat, the fluid speeds up into supersonic flow with a decrease in temperature and pressure. When the fluid enters the liquid region, condensation occurs. The comparison of the condensation onset between the experiment results and numerical simulations is shown in Figure 5. Figure 5a shows the results of the Lettieri experiment. The white region is the condensation place of CO2, the black region is the non-condensation region, and the red line indicates the throat. Figure 5b shows the contour of the predicted liquid CO2 volume fraction by Brinckman [25]. When the relaxation time coefficient in the Lee model approaches infinity, the fluid-phase transition rate also approaches infinity. Condensation will occur as long as the fluid passes through the saturation line, which can be regarded as an equilibrium phase-change model. Figure 5c is the contour of the liquid CO2 volume fraction with a smaller relaxation time coefficient, which is the outcome of a nonequilibrium condensation simulation. Figure 5d is the contour of the liquid CO2 volume fraction with a bigger relaxation time coefficient, which is the result of an equilibrium condensation simulation. The numerical simulation can better predict the trend of condensation onset under various inlet pressures. In addition, due to the high precision of the real-gas property table and the nonequilibrium condensation model, the prediction results in this paper are more accurate than those of Brinckman. The RGP table contains subcritical and supercritical thermophysical properties and fully considers the thermophysical properties of the two-phase region. The supercritical thermophysical properties can be read directly from the table and have sufficient resolution near the critical point. For the properties of the metastable region, the thermophysical properties will be interpolated. Secondly, the simulation considers the nonequilibrium condensation model. When the fluid passes through the saturation line, condensation will not occur immediately, but it will take a certain amount of relaxation time. As the picture indicates, the condensation onset will move to the inlet with the increase in inlet-relative entropy. The throat has a small area, and the density will change drastically. The difficulty of convergences will also increase, and the prediction of case 5 deviates slightly more from the experimental data. Comparing Figure 5c and Figure 5d, the condensation onset of the equilibrium condensation model is closer to the inlet, and the volume fraction of liquid CO2 is larger.
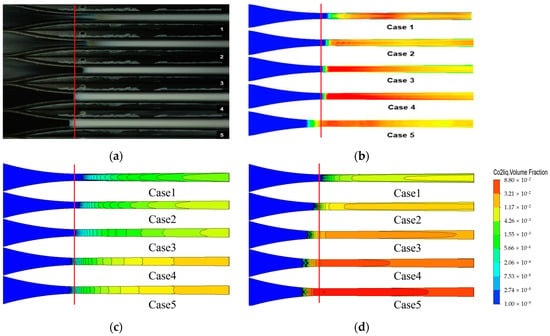
Figure 5.
Comparisons of condensation onset: (a) Lettieri experiment; (b) Brinckman numerical simulation; (c) the numerical simulation in this paper (nonequilibrium condensation model); and (d) the numerical simulation in this paper (equilibrium condensation model).
The comparison of pressure and temperature profiles between the nonequilibrium condensation model and the equilibrium condensation model in case 3 is shown in Figure 6. The temperature and pressure are 294.97 K and 5.96 MPa, respectively, which are measured at the condensation onset of the equilibrium condensation model. The saturation pressure at 294.97 K is 5.97 MPa, which is slightly higher. Considering how the RGP table works, the temperature and pressure are estimated by interpolation, and there will be some errors. Therefore, this point can be regarded as saturated. However, the temperature and pressure are 286.47 K and 5.31 MPa, respectively, in the nonequilibrium condensation model. The pressure is much lower than the saturation pressure of 286.74 K, which means this point is far from the saturation line. As a result, the CO2 fluid will not condense immediately after passing through the saturation line but will continue to expand isentropically as a gas below the critical point before condensation occurs.
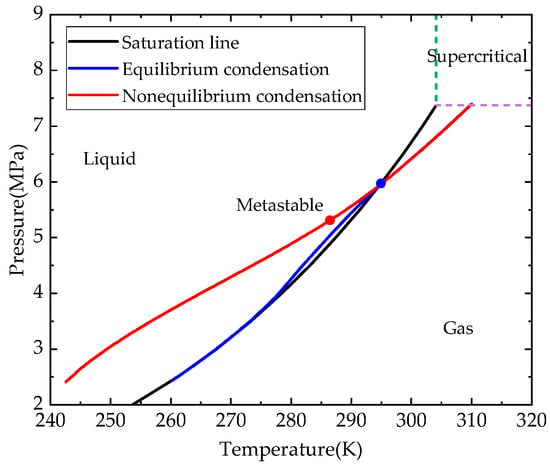
Figure 6.
Comparison of pressure and temperature profile.
A quantitative comparison of condensation onset is described in Figure 7. The relative entropy is the ratio of the inlet entropy to the critical entropy. The numerical calculation prediction findings are closer to the throat than the experimental data, and the curve distribution variations follow a similar pattern. The flow field of the nozzle becomes unstable when modeling nonequilibrium phase-change condensation. However, the condensation onset is dictated by thermodynamic conditions, so it can be considered practically unchanged.
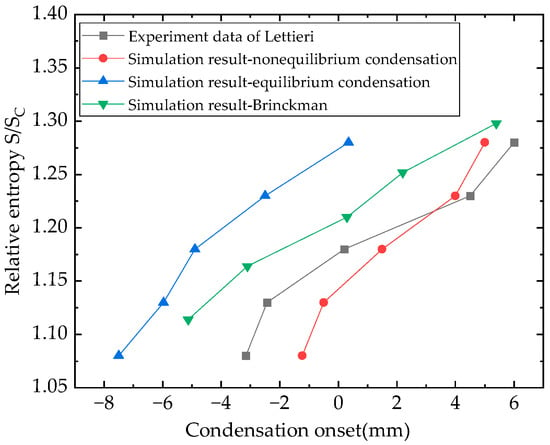
Figure 7.
Quantitative comparison of condensation onset.
The Wilson line is plotted using the data from Figure 7. Figure 8 shows the comparison between the Wilson line calculated by Fluent and the experimental test data. T is the temperature at condensation onset, and Tc is the critical temperature. The Wilson line can be regarded as a kind of material property of condensing vapor substance [11], which is affected by the expansion rate. Bigger expansion rates cause the Wilson line to shift towards greater subcooling. The Wilson line is used to assess the subcooling of nonequilibrium condensation. These two lines exhibit a similar trend, and the simulation prediction is closer to the throat. As the inlet entropy approaches the critical point, the difference between them decreases because condensation occurs faster at this point. The nonequilibrium condensation phenomenon is more drastic with increasing inlet entropy, and the condensation shows noticeable hysteresis. The degree of subcooling before condensation is underestimated by the Fluent numerical simulation. In comparison to the Lettieri experimental results, the nonequilibrium phase-change model and the associated two-phase-flow simulation method employed above are reliable and can be applied to the subsequent compressor research.
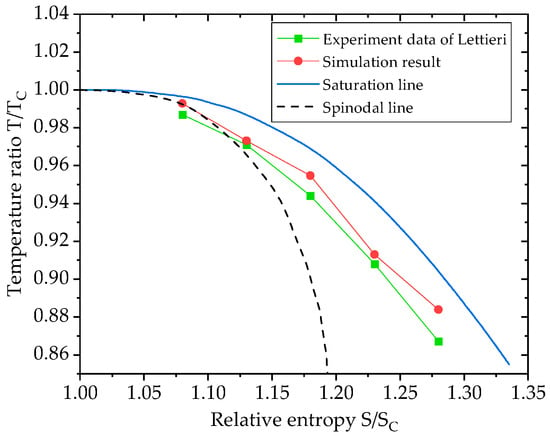
Figure 8.
Wilson line computed from Fluent compared with test data from the experiment.
2.2. Verification of Sandia Compressor Simulation
Sandia Laboratory previously conducted the S-CO2 centrifugal compressor experiment and published more comprehensive geometric parameters and experimental data [20]. This section mainly focuses on this compressor and carries out numerical simulations. The two-dimensional and three-dimensional models of the compressor have been reconstructed according to the geometry parameters released by Sandia Laboratory. The design inlet’s total pressure is 7.678 MPa, the total temperature is 305.3 K, the mass flow rate is 3.53 kg/s, the rotation speed is 75 krpm, the pressure ratio is 1.818, and the efficiency is 66.38%. Because the operating temperature and pressure range of the Sandia compressor are identical to those of the Lettieri nozzle experiment, the same real-gas property table can be employed. The geometry parameters of the compressor impeller are shown in Table 2. Figure 9 depicts the reconstructed Sandia compressor impeller. The inlet width of the vaneless diffuser is the same as the outlet width. In order to have the same pressure ratio as the vaned diffuser, the radius of the vanless diffuser is larger. The vanless diffuser outlet radius is 31.5 mm, and the ratio of the outlet radius to the inlet radius is 1.7.

Table 2.
Geometry parameters of Sandia main compressor impeller.

Figure 9.
Geometry of Sandia impeller: Reconstructed impeller mesh.
Due to the difficulty of modeling the S-CO2 centrifugal compressor, the drastic change in thermophysical properties and various inlet conditions make it difficult to simulate and compare all the experimental data. Additionally, the experimental data at a speed of 50 krpm is more comprehensive than the publicly available data. Therefore, the simulation shaft speed was set to 50 krpm. The same numerical solver was adopted. Two turbulence equations of the SST model were applied, and a coupled algorithm was utilized for the coupling of the pressure-velocity field. The inlet boundary condition was set at 305.3 K and 7.687 MPa. The outlet was set as a mass flow outlet. Since there are no significant strong temperature gradients in the flow field, the assumption of adiabatic walls was used. No-slip boundary conditions were taken into account on the walls, and a constant rotation speed was applied to the hub and impeller.
The comparisons between the experimental data and the results from computational fluid dynamics (CFD) simulations are shown in Figure 10. The trends of the pressure ratio and the efficiency of the numerical simulation are close to the experiment data. The pressure ratio is the ratio of the inlet’s total pressure to the outlet’s total pressure. With the increase in the mass flow rate, the pressure ratio of the compressor gradually decreases, while the efficiency initially increases before decreasing. The maximum error could result from the volute, which is not taken into account during the simulation, and only some parameters of the compressor are provided in the Sandia report. There may be differences between the simulated impeller geometry and the prototype impeller. The aforementioned reasons contribute to a slight deviation from the experimental results.
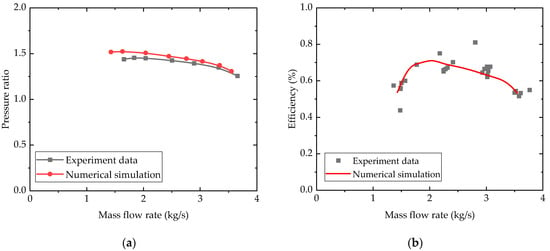
Figure 10.
Comparisons of performance curve simulated to experiment data: (a) pressure ratio and (b) efficiency.
The contour of the liquid CO2 volume fraction at 0.5 span is presented in Figure 11. The mass flow rate is 2.543 kg/s. The low-pressure and low-temperature regions are found at the leading-edge suction sides of blades. The regions result from the flow acceleration around the suction side of the blade’s leading edge, which is caused by the geometrical curvature. Due to the short passage before the impeller inlet, only a small amount of energy can be added to the fluid converted from the mechanical energy of the blades, which is insufficient to compensate for the internal energy decline caused by flow acceleration. If the speed of the CO2 working fluid is very high, the impeller does not have enough time to work on the fluid. The S-CO2 may slip into a two-phase region, where condensation might take place in those regions. The condensation place is marked out in Figure 10, and the maximum CO2 liquid volume fraction is 2.91 × 10−5. As the working fluid continues to flow through the passage, the impeller interacts with the fluid, leading to an increase in temperature and pressure beyond the critical point, resulting in the disappearance of condensation.
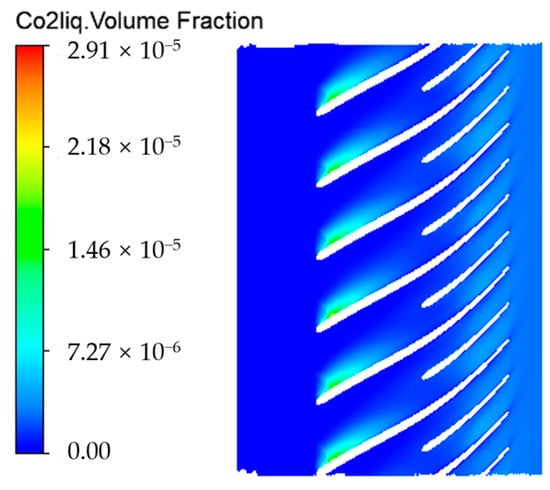
Figure 11.
Liquid CO2 volume fraction contour at 50% span.
The aforementioned findings demonstrate that simulating an S-CO2 compressor can effectively utilize the condensation model and two-phase-flow simulation methods. This method will be applied in the next section to investigate the quantitative impact of the phase change on the compressor’s aerodynamic performance at various inlet conditions.
3. Main Compressor Simulation
3.1. Geometry of Main Compressor
Simulations of a two-stage centrifugal compressor for an 8 MWt S-CO2 power cycle test rig were carried out in this section. The design parameters of the main compressor are shown in Table 3. The two-dimensional and three-dimensional diagrams of centrifugal impellers are shown in Figure 12. The first stage of the main compressor has seven main blades and seven splitters, the return channel has fifteen blades, and the second stage has eight main blades and eight splitters. The splitters can reduce the choke at the impeller. In order to obtain a wide operation range, a vanless diffuser was used.

Table 3.
Design parameters of the main compressor.
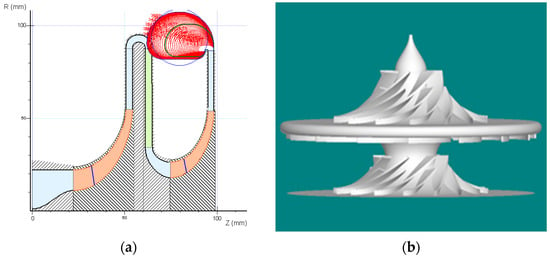
Figure 12.
Design diagram of centrifugal impeller: (a) 2D and (b) 3D.
3.2. Numerical Simulation for Different Inlet Conditions
The same numerical solver and settings are used for the numerical calculation of this compressor. The fluid domains of the first and second stages are defined as rotating domains with the same rotational speed. The fluid domain of the return channel is defined as a static domain.
The overall aerodynamic performance of the compressor at its design point is assessed in Figure 13 in terms of the pressure ratio and efficiency. The relative mass flow rate is the ratio of the compressor mass flow rate to the design mass flow rate. The design speed N is 25 krpm, and the performance of the compressor at five speeds was calculated. In the simulations, the back pressure was adjusted to alter the compressor mass flow rate. At low rotation speeds and mass flow rates, the pressure ratio is relatively small, and the stable operation range will be narrower. The pressure ratio from the simulations demonstrates a nearly linear dependence on the mass flow rate. As the rotation speed increases, the pressure ratio also increases. However, stability issues in the simulations arise when dealing with a large mass flow rate, resulting in a rapid decline in efficiency. The primary inefficiency in the numerical simulation presented in this paper stems from the omission of the volute’s influence on the compressor.
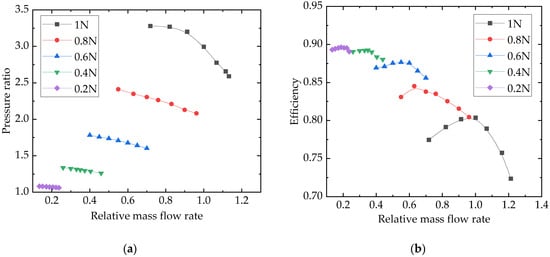
Figure 13.
Main compressor performance curve: (a) pressure ratio and (b) efficiency.
This section concentrates on the specific internal flow field of the compressor at various inlet conditions. In terms of the compressor inlet temperature, it is much easier to fluctuate than pressure. Assuming that the isothermal lines are at 305.15 K, 306.16 K and 307.15 K, 11 exemplary inlet conditions are taken into consideration, where the relative entropy varies from 0.897 to 1.133. The detailed information is shown in Table 4, and the inlet points are plotted in the Temperature-Relative entropy diagram in Figure 14. The solid black line is the saturation line. The green points represent cavitation inlet conditions, and the red points represent condensation inlet conditions.

Table 4.
Inlet conditions of the main compressor.
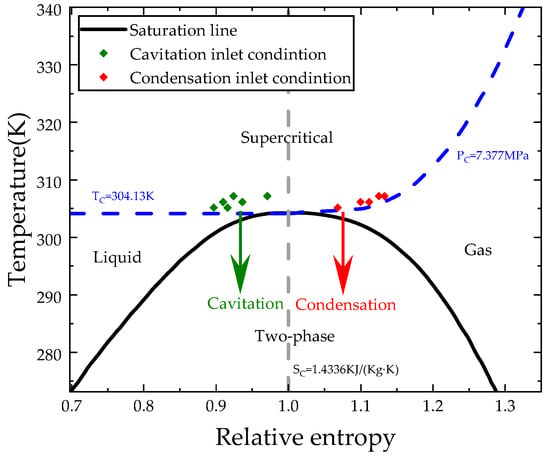
Figure 14.
Relative entropy–temperature state diagram of CO2.
As we all know, the intake of a compressor features nearly isentropic suction phenomena. If the relative entropy is smaller than one, the S-CO2 fluid behaves like a liquid. The working fluid will first pass through the liquid region and then penetrate within the two-phase region; moreover, the phase change occurs as cavitation. The compressor has a large pressure ratio and a small temperature rise, reflecting the characteristics of a pump. The small temperature rise is consistent with the fact that compressibility in liquid states is low. If the relative entropy is greater than the critical point, the working fluid will pass through the gas region rather than the liquid region and then arrive at the two-phase region. The S-CO2 fluid behaves like a gas. In this situation, the phase change occurs as condensation. The temperature rise is large due to the compressibility of the fluid—the low density of the fluid results in a significantly low dimensional pressure rise in the compressor. In case 5 and case 9 inlet conditions, Figure 15 compares the performance curves of the compressor with and without phase changes. Cavitation has little effect on the pressure ratio of the compressor, but it does affect the compressor’s choke mass flow rate. Cavitation reduces the choke mass flow rate of the compressor, but condensation makes the compressor pressure ratio increase slightly.
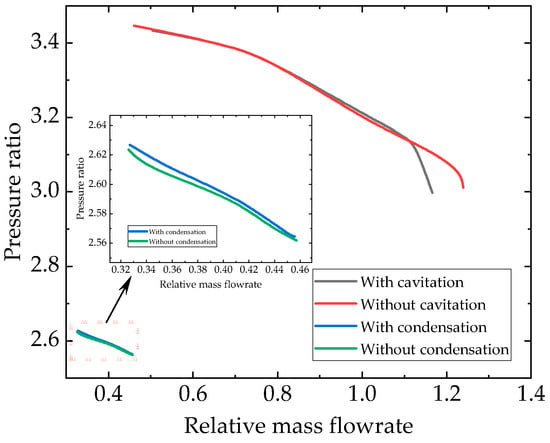
Figure 15.
Comparison of compressor pressure ratio curve.
Performance curves for the various relative entropy inlet conditions are illustrated in Figure 16. If the inlet-relative entropy is smaller than one, the surge mass flow rate remains nearly the same, but the choking-limit mass flow rate decreases as the relative entropy increases due to the drop in the speed of sound. The simulation indicates that at high mass flow rates, the flow may transition into transonic flow, as shown in Figure 17. Figure 17 depicts the contours of the compressor for large mass flow rates, which include density, local sound of speed and relative Mach numbers. A sharp decline in pressure takes place, leading to a sudden drop in density and the speed of sound, and then the relative Mach number will rise, which may cause the blockage to come into being earlier. If the relative entropy is greater than one, the stable operation mass flow rate becomes smaller since the density decreases with the relative entropy.
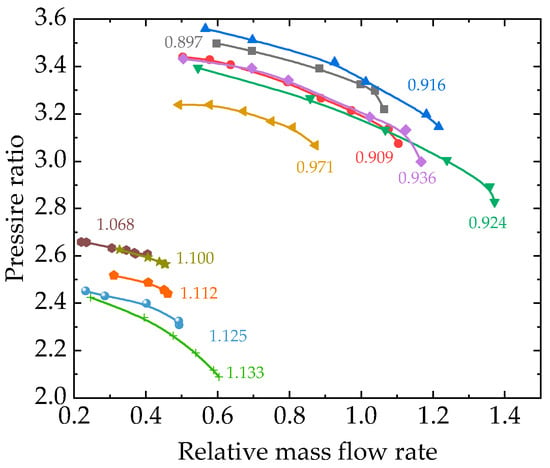
Figure 16.
Performance curve for various inlet conditions.
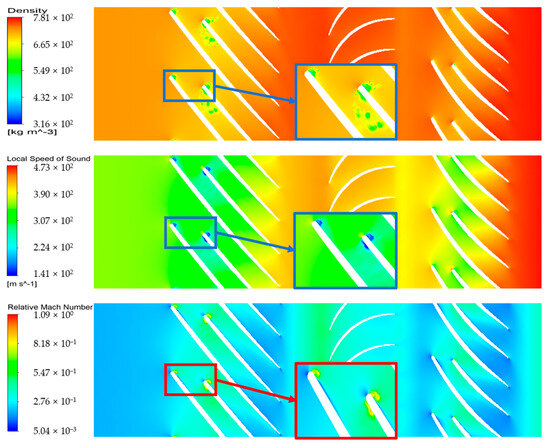
Figure 17.
Contours of the compressor at 90% span for large mass flow rate.
The volume fraction contours for various relative entropy and mass flow rates are compared in Figure 18. Each row represents the same inlet condition. From left to right, the mass flow rate increases gradually. The phase change becomes drastic with an increase in the mass flow rate. When the relative entropy approaches one, the phase change will also become drastic. Now, consider cases of cavitation. As the mass flow rate increases, the suction on the pressure side will suddenly increase, and the front loading will also increase. A well-defined low-density and low-speed sound region is found in both the main blade and splitter. What is more, cavitation becomes more severe, and a wide range of two-phase regions come into being at the leading edge of the splitter. At this time, the cavitation is more severe at the leading edge of the splitter than that in the main blade. As this region grows, the two-phase region will become wide enough to cover the channel, resulting in blockage. The same phenomenon will happen with an increase in the relative entropy of the inlet. In cases of condensation, the severity of condensation increases with the higher mass flow rate. However, condensation primarily occurs on the leading edge of the main blade at a large mass flow rate rather than on the splitter blade, which differs from cavitation. The condensation is more evenly distributed on the main blade, while the cavitation is mostly centered on the leading edge.

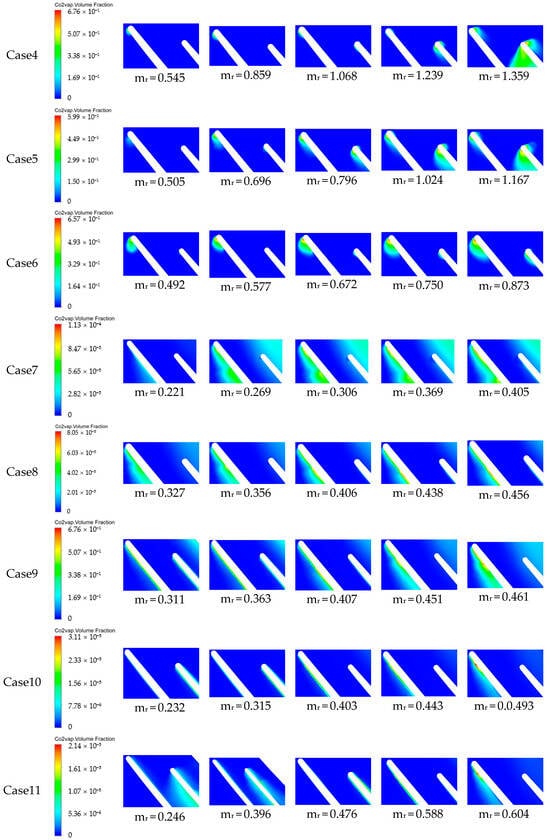
Figure 18.
Comparison of volume fraction contours at 90% span.
Two realistic thermodynamic states are simulated, both of which have the same relative entropy. These two conditions represent the high temperature (313.15 K) and low temperature (306.15 K), respectively. Figure 19 illustrates the contours of the temperature, pressure, vapor volume fraction of CO2, and density on the blade-to-blade surface at a 90% span for case 4 and case 5. The pressure of the CO2 working fluid progressively increases along the flow passage throughout the first stage, and the total pressure at the exit of the first stage is roughly 1.95 times greater than the inlet pressure. After that, the fluid will go through the return channel with a little bit of pressure drop and then go through the second stage with a pressure rise. The temperature trend is similar to the pressure trend. On the whole, the temperature rises along the flow passage. However, there will be a localized low-temperature and low-pressure region on the leading edge of the blade. This phenomenon occurs in both the first and second stages due to the acceleration at the leading edge of the blade. There are three main reasons causing the acceleration, namely, the incidence, loading on the front suction side and choke of the leading edge. After the pressure and temperature rise in the first stage, the inlet temperature and pressure are very high. Therefore, the low-temperature and low-pressure region of the second stage is far away from the critical point, so the phase change will not occur in the second stage. A local low-temperature and low-pressure region also developed at the tail of the blade as a result of the fluid mixing on the pressure side and suction side of the main blade tail. Due to the nonequilibrium phase-change effect, cavitation does not occur at the leading edge of the blade, even if the local low-temperature and low-pressure region in case 4 is below the critical point. A well-defined region of low density is observed at the leading edges and trailing edges of the blade in case 5, which can indicate the occurrence of cavitation.
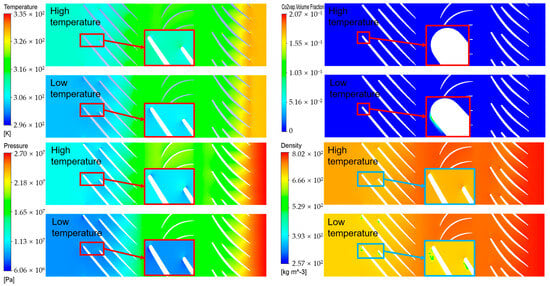
Figure 19.
Contours of the compressor at 90% span for different temperatures.
4. Conclusions
In this paper, a series of simulations of an S-CO2 centrifugal compressor operating under various inlet conditions are conducted. The phase change involves cavitation and condensation, which occur at the leading edge of the blades. This study investigates the quantitative effect of the nonequilibrium phase change on the performance of an S-CO2 centrifugal compressor. Here are the conclusions as follows:
(1) The real-gas properties table includes the supercritical and subcritical thermophysical properties of CO2, with a thorough consideration of the properties in the two-phase region. The metastable properties are calculated by inverse interpolation. The nonequilibrium condensation model and the related multiphase flow simulation method are validated using test data in the Lettieri nozzle. The onset of condensation and the Wilson line are well predicted using the nonequilibrium condensation model in combination with the RGP table. As the inlet-relative entropy approaches one, the onset of condensation becomes closer to the inlet, and the condensation becomes more drastic and rapid. The performance curve of Sandia is in good agreement with the experimental data. The condensation at the leading edge of the blades is well predicted.
(2) The phase change is significant in the compressor, and the inlet-relative entropy can distinguish the type of phase change. If the inlet-relative entropy is smaller than one, the S-CO2 behaves like a liquid. The phase change occurs as cavitation on the leading edge of the blade. The choking-limit mass flow rate decreases with the increase in relative entropy due to the drop in the speed of sound. As the mass flow rate increases, cavitation becomes more severe, resulting in a wider range of cavitation regions in the splitter. However, condensation primarily occurs on the leading edge of the main blade at a large mass flow rate. When this two-phase region grows wide enough to cover the channel, the choke will soon happen. The stable operation range may be significantly reduced. If the inlet-relative entropy is greater than one, the S-CO2 behaves like a gas. The phase change occurs as condensation. The stable operation range will shift to the small mass flow due to the lower density. The condensation is more evenly distributed on the main blade, but the cavitation is mostly concentrated on the leading edge.
The compressor aerodynamic losses caused by the phase change (condensation or cavitation) under different inlet conditions need further study.
Author Contributions
Conceptualization, Y.T.; methodology, W.X. and Y.T.; software, W.X.; validation, P.J. and B.W.; formal analysis, P.J.; investigation, B.W.; resources, W.X.; data curation, W.X.; writing—original draft preparation, W.X.; writing—review and editing, P.J.; visualization, W.X.; supervision, Y.T.; project administration, X.X.; funding acquisition, X.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation of China (No.52006216) and the CAS Project for Young Scientists in Basic Research (No. YSBR-043).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Pt | total pressure |
| Tt | total temperature |
| S | entropy |
| Pc | pressure of CO2 critical point |
| Tc | temperature of CO2 critical point |
| Sc | entropy of CO2 critical point |
| P0 | inlet pressure of nozzle |
| L | total length of nozzle |
| N | shaft speed |
| mr | relative mass flow rate |
| CFD | computational fluid dynamics |
| RGP | real gas properties |
References
- Cho, J.; Shin, H.; Cho, J.; Kang, Y.S.; Ra, H.S.; Roh, C.; Lee, B.; Lee, G.; Kim, B.; Baik, Y.J. Preliminary experimental study of a supercritical CO2 power cycle test loop with a high-speed turbo-generator using R134a under similarity conditions. Front. Energy 2017, 11, 452–460. [Google Scholar] [CrossRef]
- Cheng, W.L.; Huang, W.X.; Nian, Y.L. Global parameter optimization and criterion formula of supercritical carbon dioxide Brayton cycle with recompression. Energy Convers. Manag. 2017, 150, 669–677. [Google Scholar] [CrossRef]
- Feher, E.G. The supercritical thermodynamic power cycle. Energy Convers. 1968, 8, 85–90. [Google Scholar] [CrossRef]
- Dostal, V.; Driscoll, M.J.; Hejzlar, P. A Supercritical Carbon Dioxide Cycle for Next Generation Nuclear Reactors. 2004. Available online: https://web.mit.edu/22.33/www/dostal.pdf (accessed on 29 December 2023).
- Poerner, M.; Musgrove, G.; Beck, G. Liquid CO2 Formation, Impact, and Mitigation at the Inlet to a Supercritical CO2 Compressor. In Proceedings of the ASME Turbo Expo: Turbine Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016; pp. 351–360. [Google Scholar]
- Liu, C.; Zhang, L. Research Progress of Supercritical Carbon Dioxide Centrifugal Compressor. Therm. Power Gener. 2021, 50, 34–42. [Google Scholar]
- Baltadjiev, N.D.; Lettieri, C.; Spakovszky, Z.S. An Investigation of Real Gas Effects in Supercritical CO2 Centrifugal Compressors. J. Turbomach. Trans. ASME 2015, 137, 13. [Google Scholar] [CrossRef]
- Pei, J.; Zhao, Y.; Zhao, M.; Liu, G.; Yang, Q.; Li, L. Effects of leading edge profiles on flow behavior and performance of supercritical CO2 centrifugal compressor. Int. J. Mech. Sci. 2022, 229, 107520. [Google Scholar] [CrossRef]
- Rinaldi, E.; Pecnik, R.; Colonna, P. Computational Fluid Dynamic Simulation of a Supercritical CO2 Compressor Performance Map. J. Eng. Gas. Turbines Power-Trans. ASME 2015, 137, 7. [Google Scholar] [CrossRef]
- Lettieri, C.; Spakovszky, Z.; Paxson, D.; Bryanston-Cross, P. Characterization of non-equilibrium condensation of supercritical carbon dioxide in a de Laval nozzle. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Gyarmathy, G. Nucleation of steam in high-pressure nozzle experiments. Proc. Inst. Mech. Eng. Part A-J. Power Energy 2005, 219, 511–521. [Google Scholar] [CrossRef]
- Shao, W.Y.; Yang, J.G.; Wang, X.F.; Ma, Z.Y. A real gas-based throughflow method for the analysis of SCO2 centrifugal compressors. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2020, 234, 1943–1958. [Google Scholar] [CrossRef]
- Melissa Poerner, P.E. Understanding Wet Gas in A Supercritical Carbon Dioxide Cycle. In Proceedings of the 5th International Symposium—Supercritical CO2 Power Cycles, San Antonio, TX, USA, 28–31 March 2016. [Google Scholar]
- Furusawa, T.; Miyazawa, H.; Moriguchi, S.; Yamamoto, S. NUMERICAL METHOD for SIMULATING HIGH PRESSURE CO2 FLOWS with NONEQUILIBRIUM CONDENSATION. In Proceedings of the ASME Turbo Expo: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Anderson, M.R. Atypical Fluid Behavior on the Liquid Side of the Saturation Line of CO2 with Implications for Compressor Design. In Proceedings of the 6th International Supercritical CO2 Power Cycles Symposium, Pittsburgh, PA, USA, 27–29 March 2018. [Google Scholar]
- Persico, G.; Gaetani, P.; Romei, A.; Toni, L.; Bellobuono, E.F.; Valente, R. Implications of phase change on the aerodynamics of centrifugal compressors for supercritical carbon dioxide applications. In Proceedings of the ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition, Virtual, 21–25 September 2020; International Gas Turbine Institute: Houston, TX, USA. [Google Scholar]
- Hosangadi, A.; Liu, Z.S.; Weathers, T.; Ahuja, V.; Busby, J. Modeling Multiphase Effects in CO2 Compressors at Subcritical Inlet Conditions. J. Eng. Gas. Turbines Power-Trans. ASME 2019, 141, 13. [Google Scholar] [CrossRef]
- Conboy, T.M.; Wright, S.A. Experimental Investigation of the S-CO2 Condensing Cycle; Sandia National Lab.: Albuquerque, NM, USA, 2011. [Google Scholar]
- Wright, S.; Conboy, T.; Radel, R.; Rochau, G. Modeling and Experimental Results for Condensing Supercritical CO2 Power Cycles; Office of Scientific and Technical Information (OSTI): Oak Ridge, TN, USA, 2011.
- Wright, S.; Radel, R.; Vernon, M.; Pickard, P.; Rochau, G. Operation and Analysis of a Supercritical CO2 Brayton Cycle; Office of Scientific and Technical Information (OSTI): Oak Ridge, TN, USA, 2010.
- Noall, J.S.; Nichols, B.; Pasch, J.J. Achievable Efficiency and Stability of Supercritical CO2 Compression Systems. 2014. Available online: https://sco2symposium.com/papers2014/turbomachinery/51PPT-Noall.pdf (accessed on 29 December 2023).
- Allison, T.C.; McClung, A. Limiting Inlet Conditions for Phase Change Avoidance in Supercritical CO2 Compressors. In Proceedings of the ASME Turbo Expo: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
- Ansys Inc. Ansys Fluent Theory Guide; Ansys Inc.: Canonsburg, PA, USA, 2022. [Google Scholar]
- Lettieri, C.; Yang, D.; Spakovszky, Z. An Investigation of Condensation Effects in Supercritical Carbon Dioxide Compressors. J. Eng. Gas. Turbines Power-Trans. ASME 2015, 137, 8. [Google Scholar] [CrossRef]
- Brinckman, K.W.; Hosangadi, A.; Liu, Z.S.; Weathers, T. NUMERICAL SIMULATION of NON-EQUILIBRIUM CONDENSATION in SUPERCRITICAL CO2 COMPRESSORS. In Proceedings of the ASME Turbo Expo: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).