Optimization of Blades and Impellers for Electric Vehicle Centrifugal Pumps via Numerical Analysis
Abstract
1. Introduction
1.1. Research Background
1.2. Literature Review
1.3. Motivation and Novelty
2. Computational Models and Verification
2.1. Water Pump Geometry
2.2. Numerical Analysis
2.2.1. Governing Equation
2.2.2. Turbulent Model
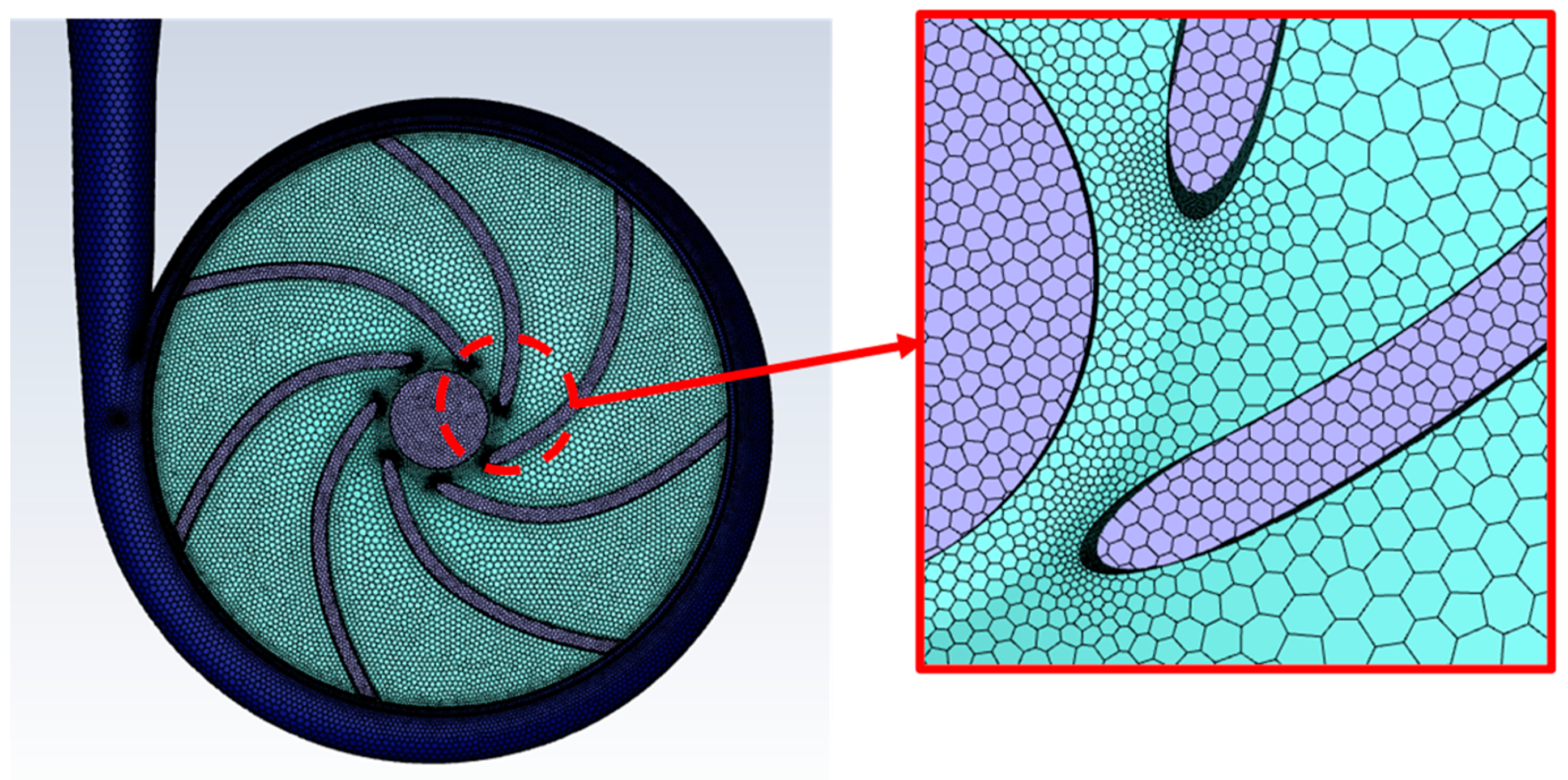
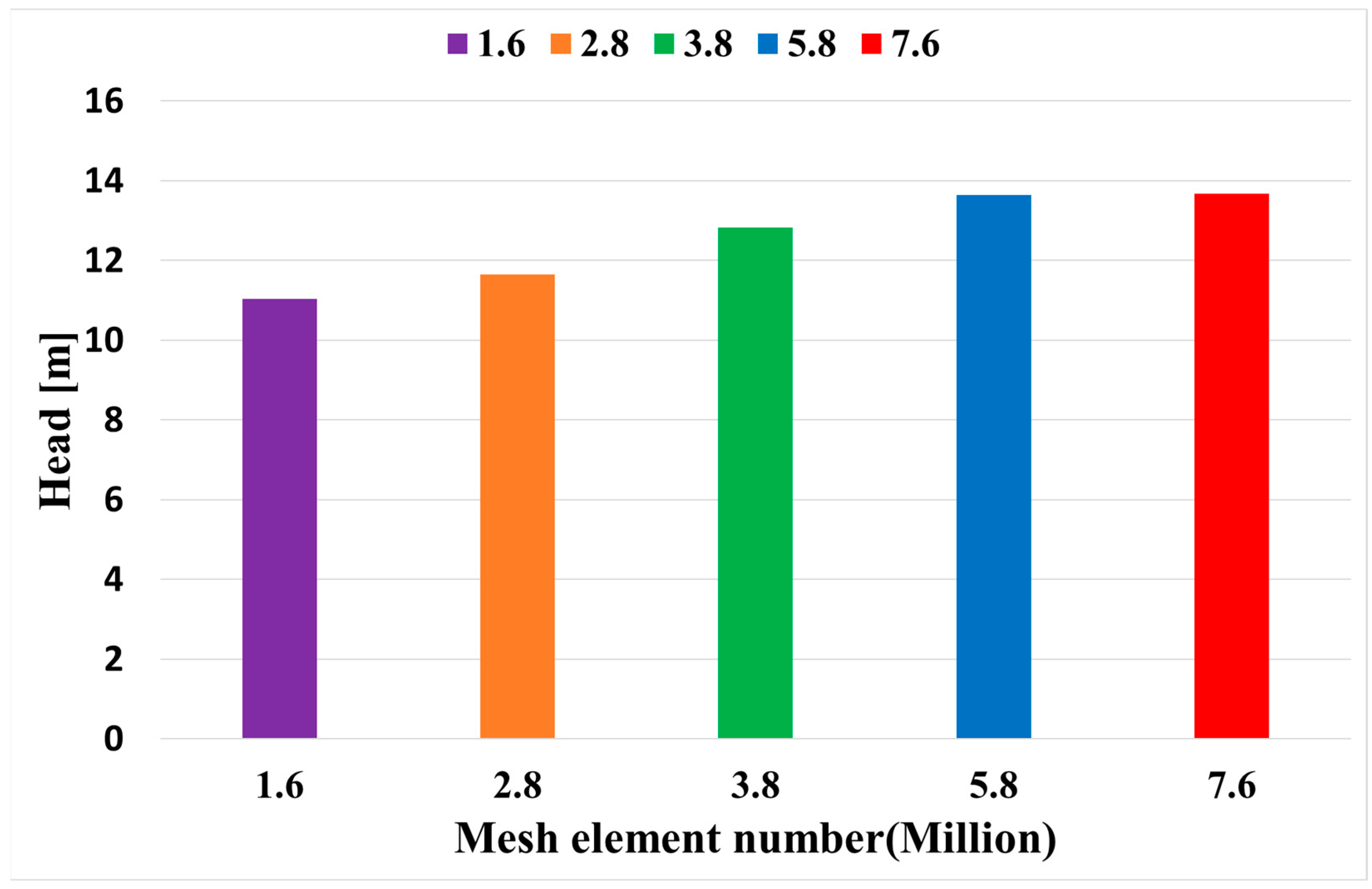
2.3. Grid Generation and Dependency Verification
2.4. Boundary Conditions
3. Results and Discussion
3.1. Experiment and Simulation Validation
- The part that drives the impeller rotation;
- Cooling passage;
- Control device to regulate impeller rotation speed and coolant temperature;
- Control unit to measure pressure and flow at the pump inlet and outlet.
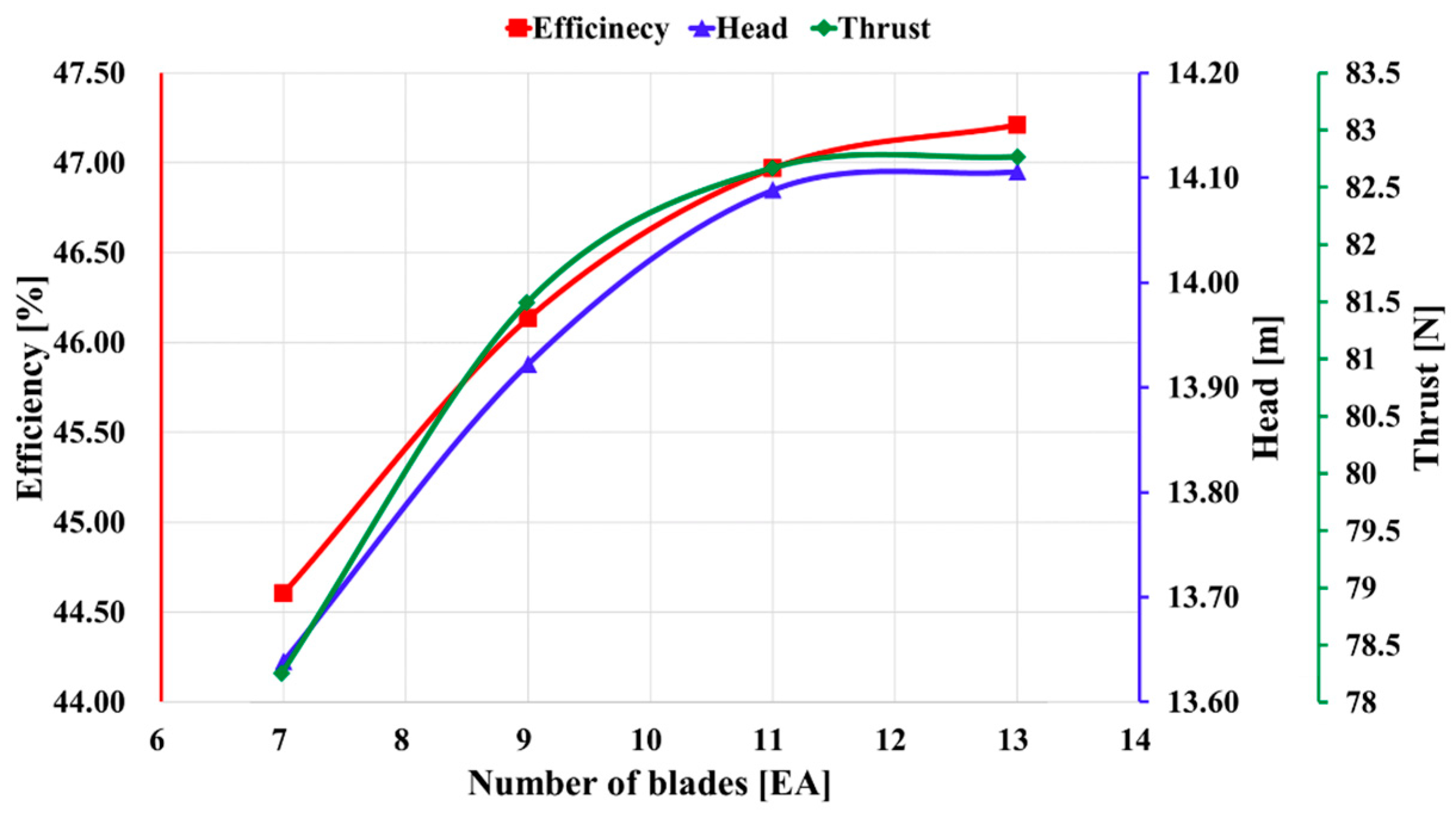
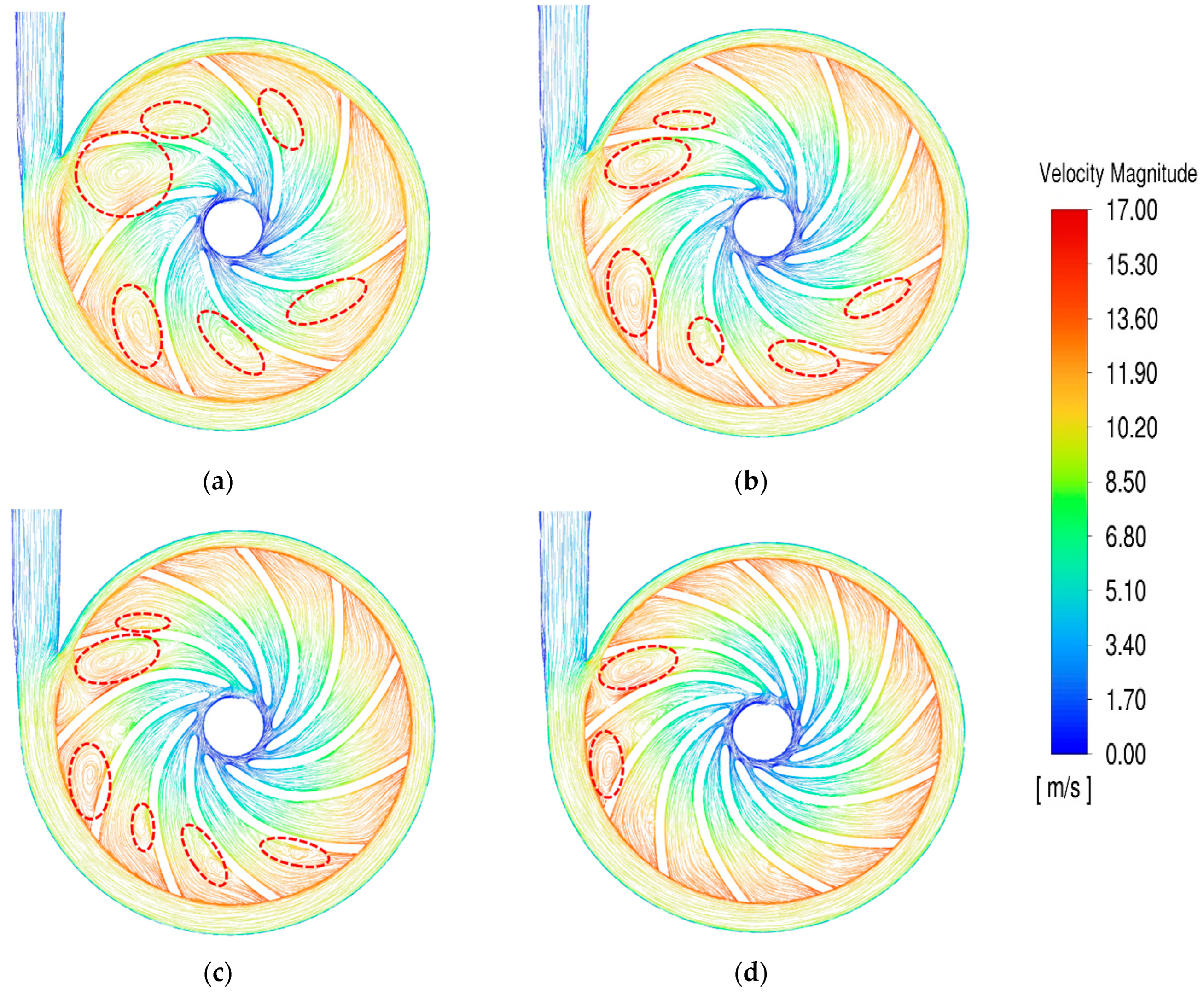
3.2. Impact of Blade Number on Water Pump
3.3. Effect of Water Pump Cavitation
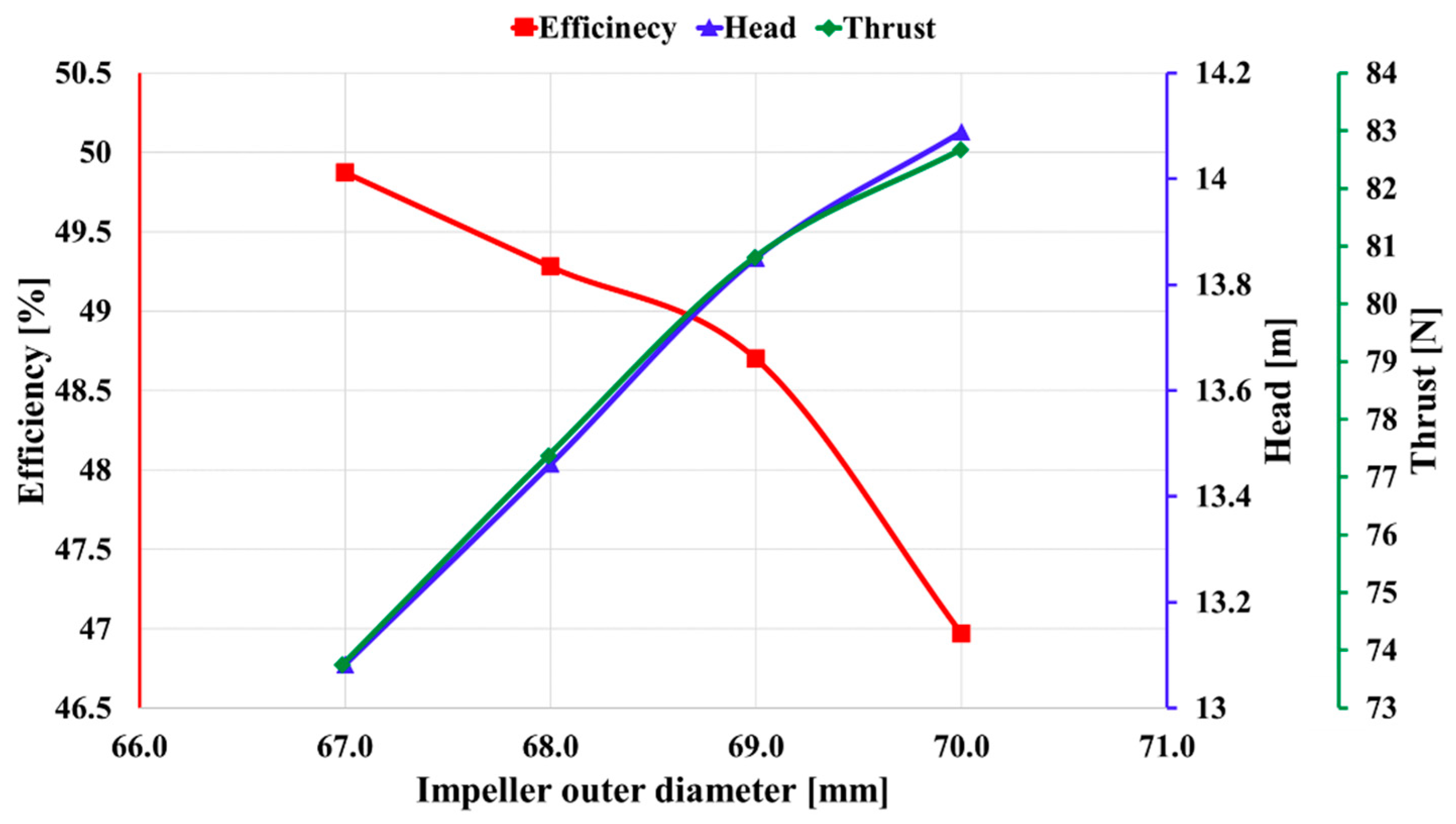
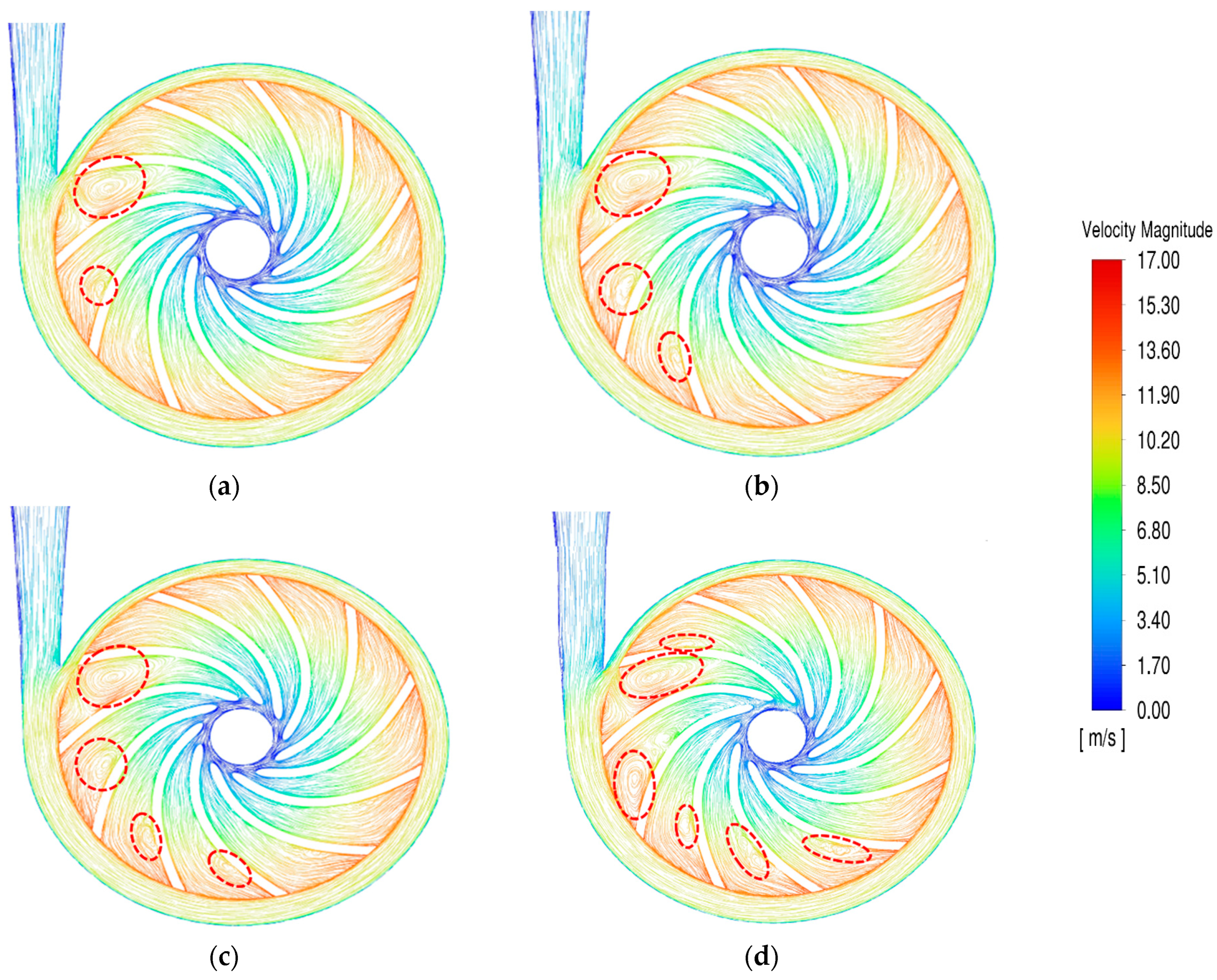
3.4. Impact of Impeller Outer Diameter on Water Pump
4. Conclusions
- As the number of blades increases, both efficiency and positive thrust tend to increase. In particular, when the number of blades increases from 11 to 13, efficiency increases of 5.8%, 3.4%, and 5.7% are observed, respectively. However, when the number of blades is 13, cavitation occurs, which can adversely affect the durability of the pump. For this reason, it was concluded the optimal state is reached when the number of blades is 11.
- When the number of blades is fixed at 11, efficiency tends to decrease and performance increases with an increase in the outer diameter of the impeller. However, since an electric vehicle water pump must consider both efficiency and performance, the optimal state is attained with an impeller outer diameter of 68~69 mm, where efficiency and performance are balanced.
- Therefore, based on a comprehensive analysis, it can be concluded that number of blades of 11 and impeller outer diameter of 68–69 mm determine the optimal condition for the pump.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rogelj, J.; Den Elzen, M.; Höhne, N.; Fransen, T.; Fekete, H.; Winkler, H.; Schaeffer, R.; Sha, F.; Riahi, K.; Meinshausen, M. Paris Agreement climate proposals need a boost to keep warming well below 2 °C. Nature 2016, 534, 631–639. [Google Scholar] [CrossRef] [PubMed]
- Quadrelli, R.; Peterson, S. The energy–climate challenge: Recent trends in CO2 emissions from fuel combustion. Energy Policy 2007, 35, 5938–5952. [Google Scholar] [CrossRef]
- Teske, S.; Bratzel, S.; Tellermann, R.; Stephan, B.; Vargas, M. Net Zero: The remaining global market volume for internal combustion engines in light-duty vehicles under a 1.5 °C carbon budget trajectory. Energies 2022, 15, 8037. [Google Scholar] [CrossRef]
- Kumar, L.; Jain, S. Electric propulsion system for electric vehicular technology: A review. Renew. Sustain. Energy Rev. 2014, 29, 924–940. [Google Scholar] [CrossRef]
- Mathieu, R.; Briat, O.; Gyan, P.; Vinassa, J.-M. Comparison of the impact of fast charging on the cycle life of three lithium-ion cells under several parameters of charge protocol and temperatures. Appl. Energy 2021, 283, 116344. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, W.; Li, H.; Wan, W.; Zhang, W.; Zhuo, W.; Liu, Q. Heat transfer characteristics and low-temperature performance of a lithium-ion battery with an inner cooling/heating structure. Appl. Therm. Eng. 2023, 219, 119352. [Google Scholar] [CrossRef]
- Wang, H.; Tao, T.; Xu, J.; Mei, X.; Liu, X.; Gou, P. Cooling capacity of a novel modular liquid-cooled battery thermal management system for cylindrical lithium ion batteries. Appl. Therm. Eng. 2020, 178, 115591. [Google Scholar] [CrossRef]
- Mistruzzi, E. Investigation of Engine Coolant Loop Flow Modelling from a System Simulation Perspective. Master’s Dissertation, University of Windsor, Windsor, ON, Canada, 2019. [Google Scholar]
- Park, S.-J. Simulation of hybrid and electric vehicle thermal management system. Mag. Soc. Air-Cond. Refrig. Eng. Korea 2013, 42, 48–57. [Google Scholar]
- Fernández Oro, J.M.; Barrio Perotti, R.; Galdo Vega, M.; González, J. Effect of the radial gap size on the deterministic flow in a centrifugal pump due to impeller-tongue interactions. Energy 2023, 278, 127820. [Google Scholar] [CrossRef]
- Wu, C.; Pu, K.; Shi, P.; Wu, P.; Huang, B.; Wu, D. Blade redesign based on secondary flow suppression to improve the dynamic performance of a centrifugal pump. J. Sound Vib. 2023, 554, 117689. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Liu, Z.; Hong, Y. Understanding of energy conversion and losses in a centrifugal pump impeller. Energy 2023, 263, 125787. [Google Scholar] [CrossRef]
- Arun Shankar, V.K.; Umashankar, S.; Paramasivam, S.; Hanigovszki, N. A comprehensive review on energy efficiency enhancement initiatives in centrifugal pumping system. Appl. Energy 2016, 181, 495–513. [Google Scholar] [CrossRef]
- Capurso, T.; Bergamini, L.; Torresi, M. A new generation of centrifugal pumps for high conversion efficiency. Energy Convers. Manag. 2022, 256, 115341. [Google Scholar] [CrossRef]
- Kim, N.H. Analysis of flow characteristic in centrifugal pump. kfma 2019, 22, 56–61. [Google Scholar] [CrossRef]
- Ramadhan Al-Obaidi, A. Effects of different turbulence models on three-dimensional unsteady cavitating flows in the centrifugal pump and performance prediction. Int. J. Nonlinear Sci. Numer. Simul. 2019, 20, 487–509. [Google Scholar] [CrossRef]
- Sun, S.-K.; Zhao, B.; Jia, X.-H.; Peng, X.-Y. Three-dimensional numerical simulation and experimental validation of flows in working chambers and inlet/outlet pockets of roots pump. Vacuum 2017, 137, 195–204. [Google Scholar] [CrossRef]
- Medvitz, R.B.; Kunz, R.F.; Boger, D.A.; Lindau, J.W.; Yocum, A.M.; Pauley, L.L. Performance analysis of cavitating flow in centrifugal pumps using multiphase CFD. J. Fluids Eng. 2002, 124, 377–383. [Google Scholar] [CrossRef]
- Hornsby, C. CFD—Driving pump design forward. World Pumps 2002, 431, 18–22. [Google Scholar] [CrossRef]
- Cao, S.; Peng, G.; Yu, Z. Hydrodynamic design of rotodynamic pump impeller for multiphase pumping by combined approach of inverse design and CFD analysis. J. Fluids Eng. 2005, 127, 330–338. [Google Scholar] [CrossRef]
- Tan, L.; Zhu, B.; Cao, S.; Bing, H.; Wang, Y. Influence of Blade Wrap Angle on Centrifugal Pump Performance by Numerical and Experimental Study. Chin. J. Mech. Eng. 2014, 27, 171–177. [Google Scholar] [CrossRef]
- Xu, Z.; Kong, F.; Tang, L.; Liu, M.; Wang, J.; Qiu, N. Effect of blade thickness on internal flow and performance of a plastic centrifugal pump. Machines 2022, 10, 61. [Google Scholar] [CrossRef]
- Peng, G.; Chen, Q.; Zhou, L.; Pan, B.; Zhu, Y. Effect of blade outlet angle on the flow field and preventing overload in a centrifugal pump. Micromachines 2020, 11, 811. [Google Scholar] [CrossRef] [PubMed]
- Abo Elyamin, G.R.H.; Bassily, M.A.; Khalil, K.Y.; Gomaa, M.S. Effect of impeller blades number on the performance of a centrifugal pump. Alex. Eng. J. 2019, 58, 39–48. [Google Scholar] [CrossRef]
- Houlin, L. Effects of blade number on characteristics of centrifugal pumps. Chin. J. Mech. Eng. 2010, 23, 742. [Google Scholar]
- Jafarzadeh, B.; Hajari, A.; Alishahi, M.M.; Akbari, M.H. The flow simulation of a low-specific-speed high-speed centrifugal pump. Appl. Math. Modell. 2011, 35, 242–249. [Google Scholar] [CrossRef]
- Shojaeefard, M.H.; Tahani, M.; Ehghaghi, M.B.; Fallahian, M.A.; Beglari, M. Numerical study of the effects of some geometric characteristics of a centrifugal pump impeller that pumps a viscous fluid. Comput. Fluids 2012, 60, 61–70. [Google Scholar] [CrossRef]
- Kaewnai, S.; Chamaoot, M.; Wongwises, S. Predicting performance of radial flow type impeller of centrifugal pump using CFD. J. Mech. Sci. Technol. 2009, 23, 1620–1627. [Google Scholar] [CrossRef]
- Jeanty, F.; De Andrade, J.; Asuaje, M.; Kenyery, F.; Vásquez, A.; Aguillón, O.; Tremante, A. Numerical simulation of cavitation phenomena in a centrifugal pump. In Proceedings of the ASME 2009 Fluids Engineering Division Summer Meeting, B & C., Vail, CO, USA, 2–6 August 2009; ASME: New York, NY, USA, 2009; Volume 1, pp. 331–338. [Google Scholar] [CrossRef]


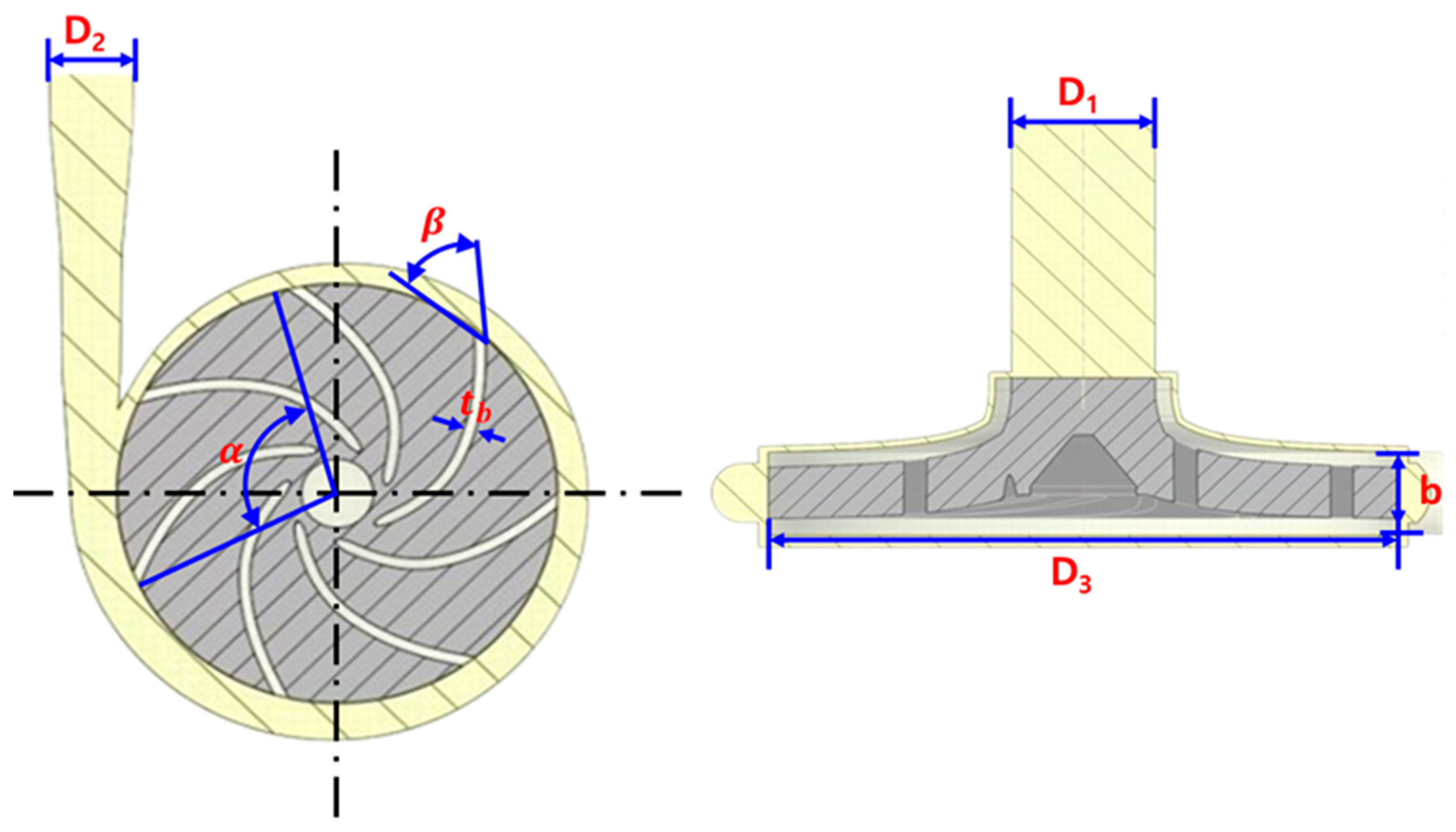




| Parameters | Symbols | Values | Units |
|---|---|---|---|
| Blade outlet angle | 45 | ° | |
| Blade wrap angle | 123 | ° | |
| Blade thickness | 1.8 | mm | |
| Blade number | 7 | EA | |
| Impeller inlet diameter | 16 | mm | |
| Impeller outlet diameter | 13.6 | mm | |
| Impeller outer diameter | 70 | mm | |
| Impeller height | b | 6 | mm |
| Properties | Values | Units |
|---|---|---|
| Coolant | Water: Ethylene Glycol = 1:1 | - |
| Coolant Temperature | 65 | °C |
| Coolant density | 1045.03 | |
| Coolant viscosity | 0.00136981 |
| Boundary Conditions | Values | Units |
|---|---|---|
| Inlet pressure | 0 | kPa |
| Outlet Mass flow | 0.2438403333 | |
| Rotation velocity | 3800 | RPM |
| Conditions | Values | Units |
|---|---|---|
| Coolant | Water: Ethylene Glycol = 1:1 | - |
| Coolant Temperature | 65 | °C |
| System Pressure | 140 | kPa |
| Motor Voltage | 12 | V |
| Rotational speed | 3800 | RPM |
| Experiment (Q) | ) | Simulation (Q) | |
|---|---|---|---|
| 5 | 134.8 | 5 | 135.28 |
| 10 | 137.5 | 10 | 137.51 |
| 14.3 | 140.3 | 14 | 139.65 |
| 15.3 | 140.1 | 15 | 139.91 |
| 20.5 | 138.7 | 20 | 140.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, H.; Hyun, D.; Lee, H.; Son, S.; Han, J. Optimization of Blades and Impellers for Electric Vehicle Centrifugal Pumps via Numerical Analysis. Energies 2024, 17, 853. https://doi.org/10.3390/en17040853
Jeon H, Hyun D, Lee H, Son S, Han J. Optimization of Blades and Impellers for Electric Vehicle Centrifugal Pumps via Numerical Analysis. Energies. 2024; 17(4):853. https://doi.org/10.3390/en17040853
Chicago/Turabian StyleJeon, Hyeonchang, Daeil Hyun, Hyuntae Lee, Seongjin Son, and Jaeyoung Han. 2024. "Optimization of Blades and Impellers for Electric Vehicle Centrifugal Pumps via Numerical Analysis" Energies 17, no. 4: 853. https://doi.org/10.3390/en17040853
APA StyleJeon, H., Hyun, D., Lee, H., Son, S., & Han, J. (2024). Optimization of Blades and Impellers for Electric Vehicle Centrifugal Pumps via Numerical Analysis. Energies, 17(4), 853. https://doi.org/10.3390/en17040853







