Multi-Fracture Propagation Considering Perforation Erosion with Respect to Multi-Stage Fracturing in Shale Reservoirs
Abstract
1. Introduction
2. Numerical Model
2.1. Rock Deformation and Fluid Flow
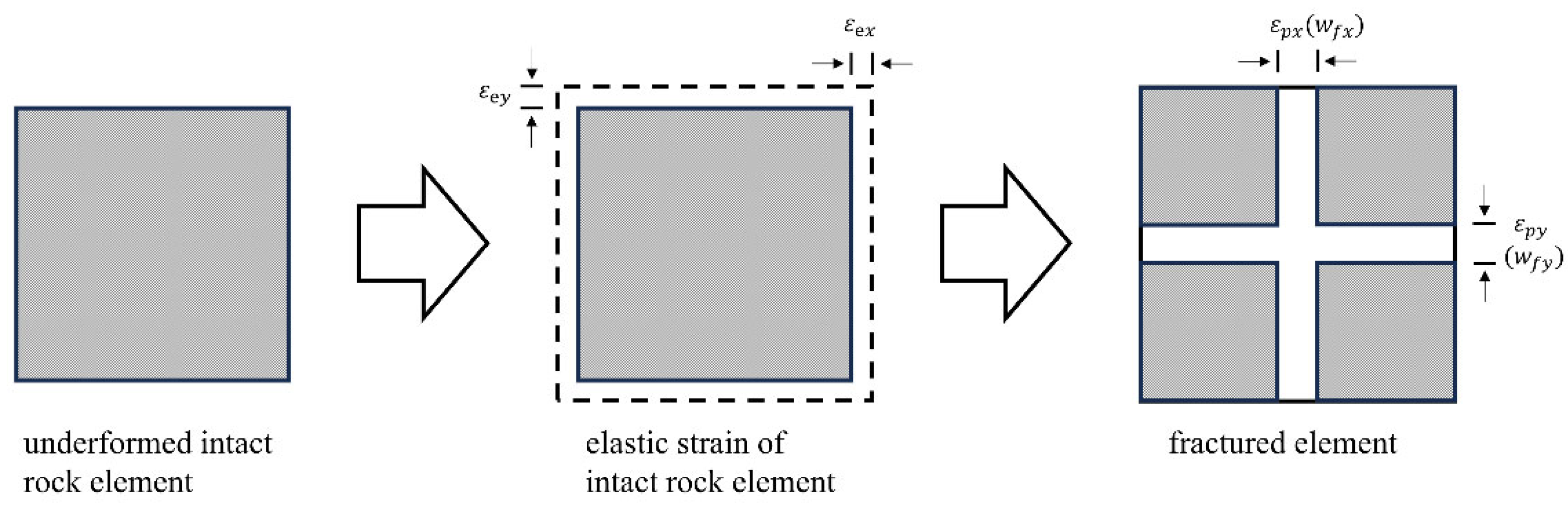
2.2. Fracture Propagation
2.3. Fluid Flow within the Wellbore
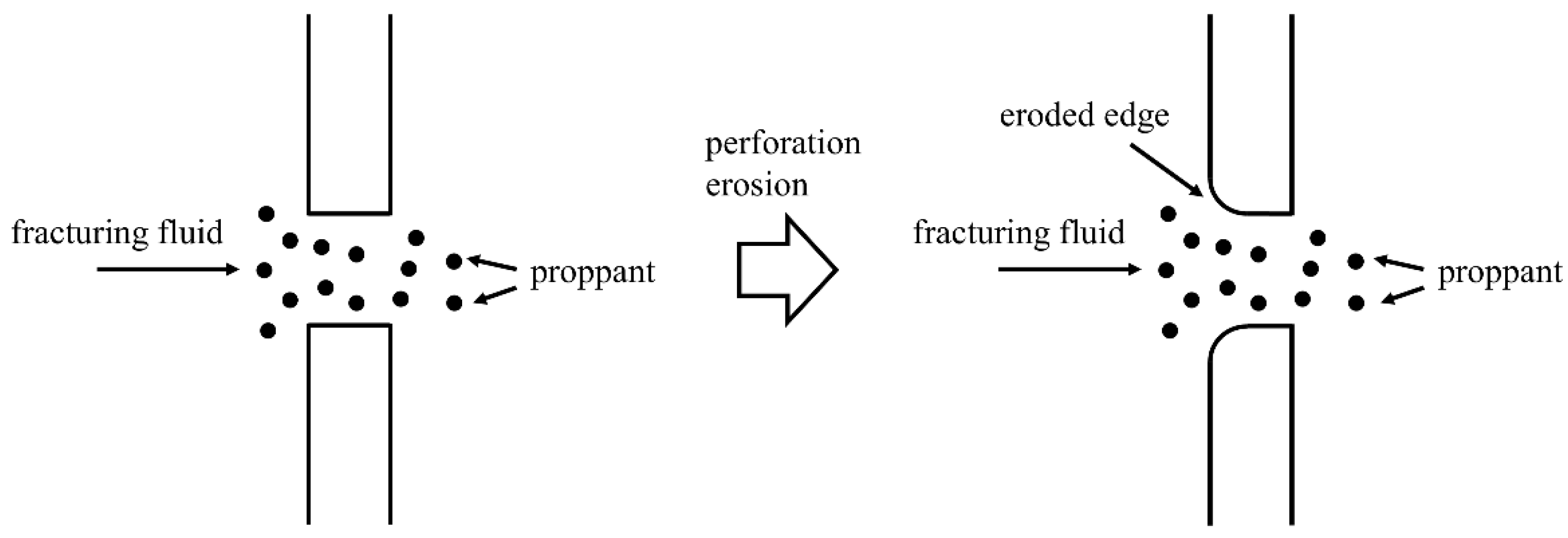
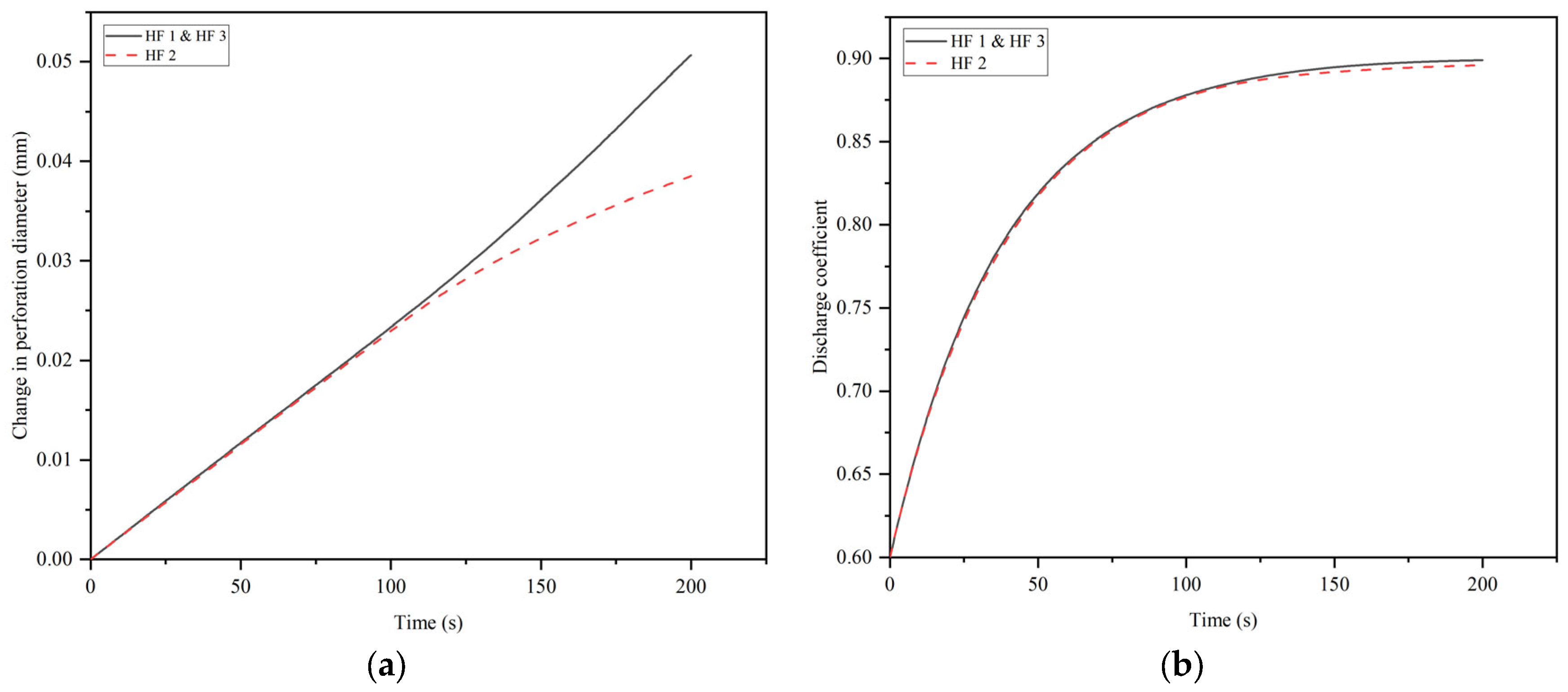
2.4. Perforation Erosion
3. Model Verification and Model Establishment
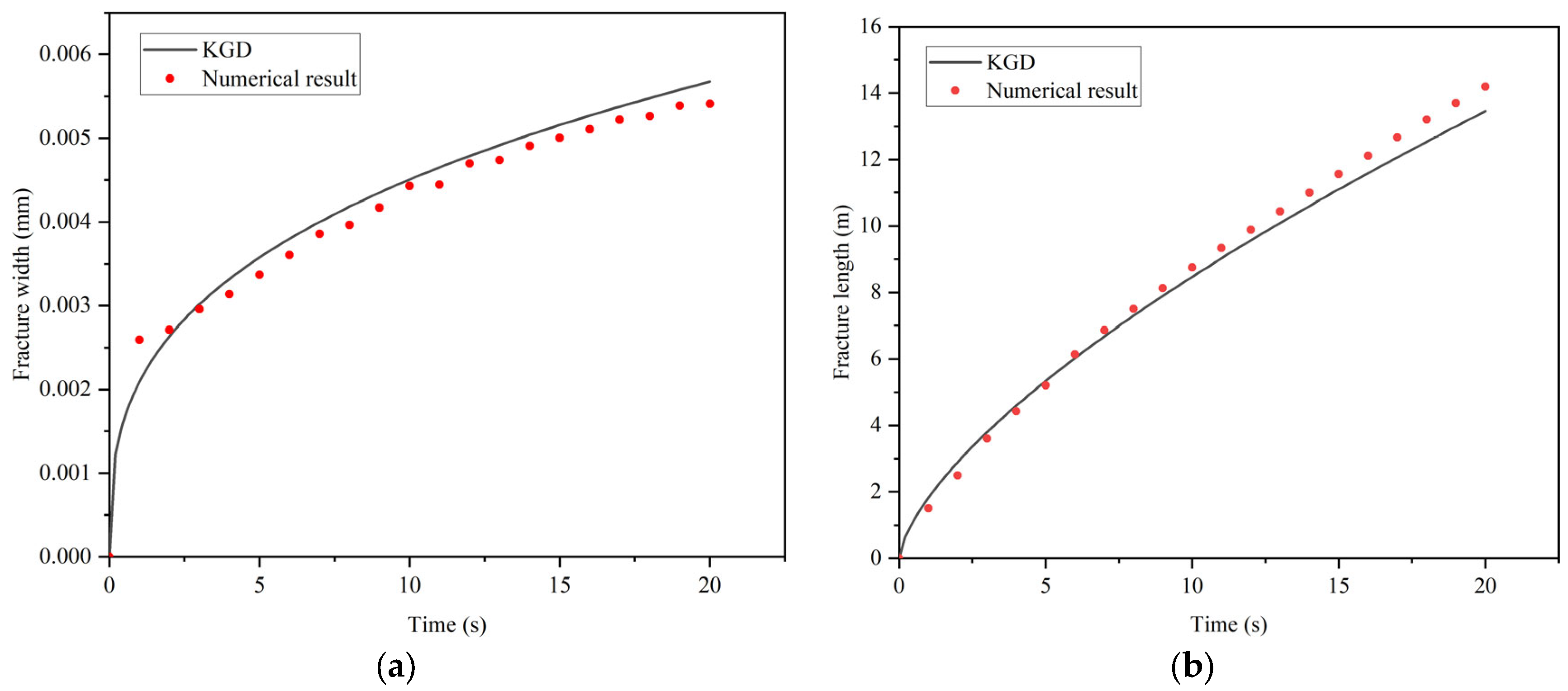
3.1. Comparison with the Classical KGD Model
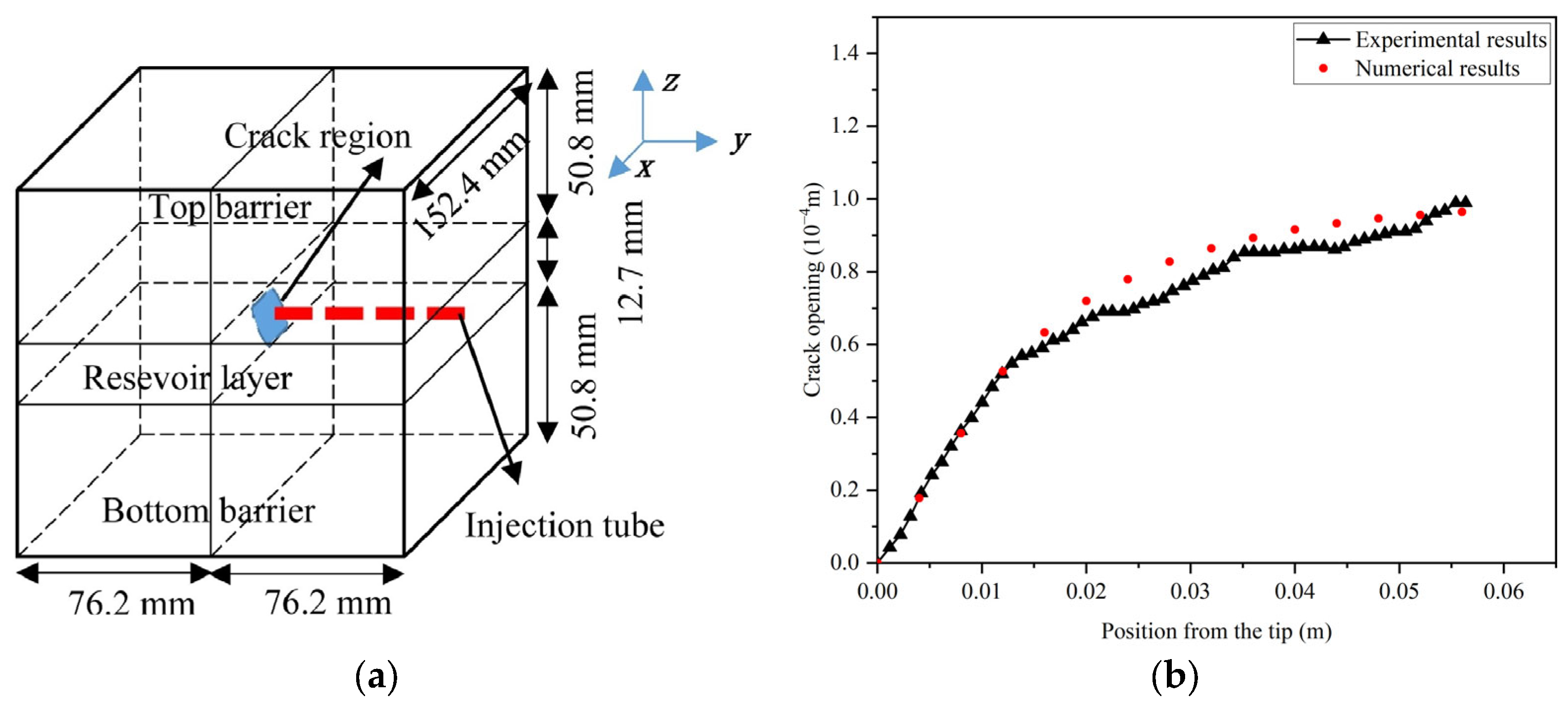
3.2. Comparison with a Lab-Scale Experiment
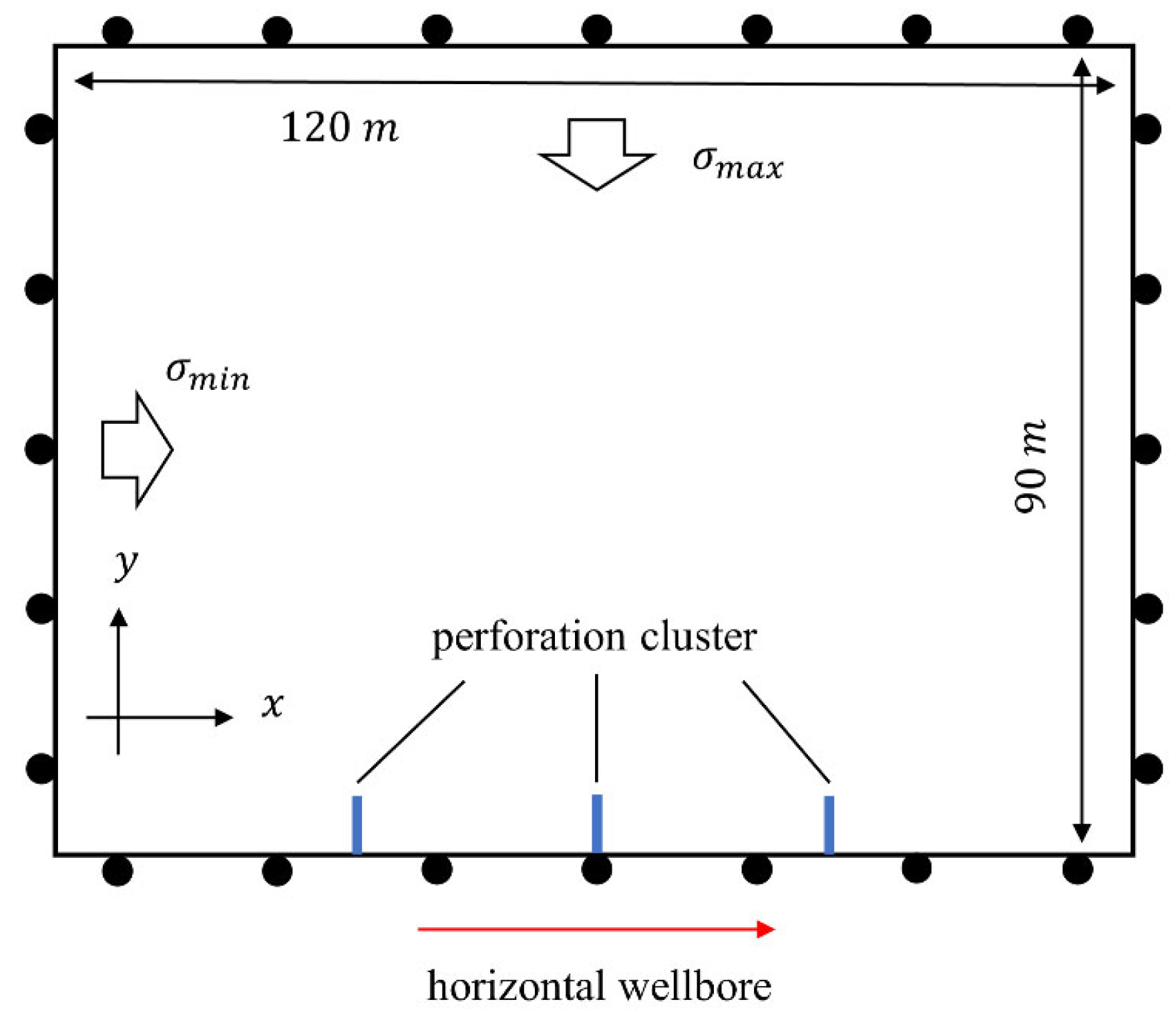
3.3. Model Establishment
4. Results and Discussion
4.1. The Impact of Perforation Erosion on Multi-Fracture Propagation
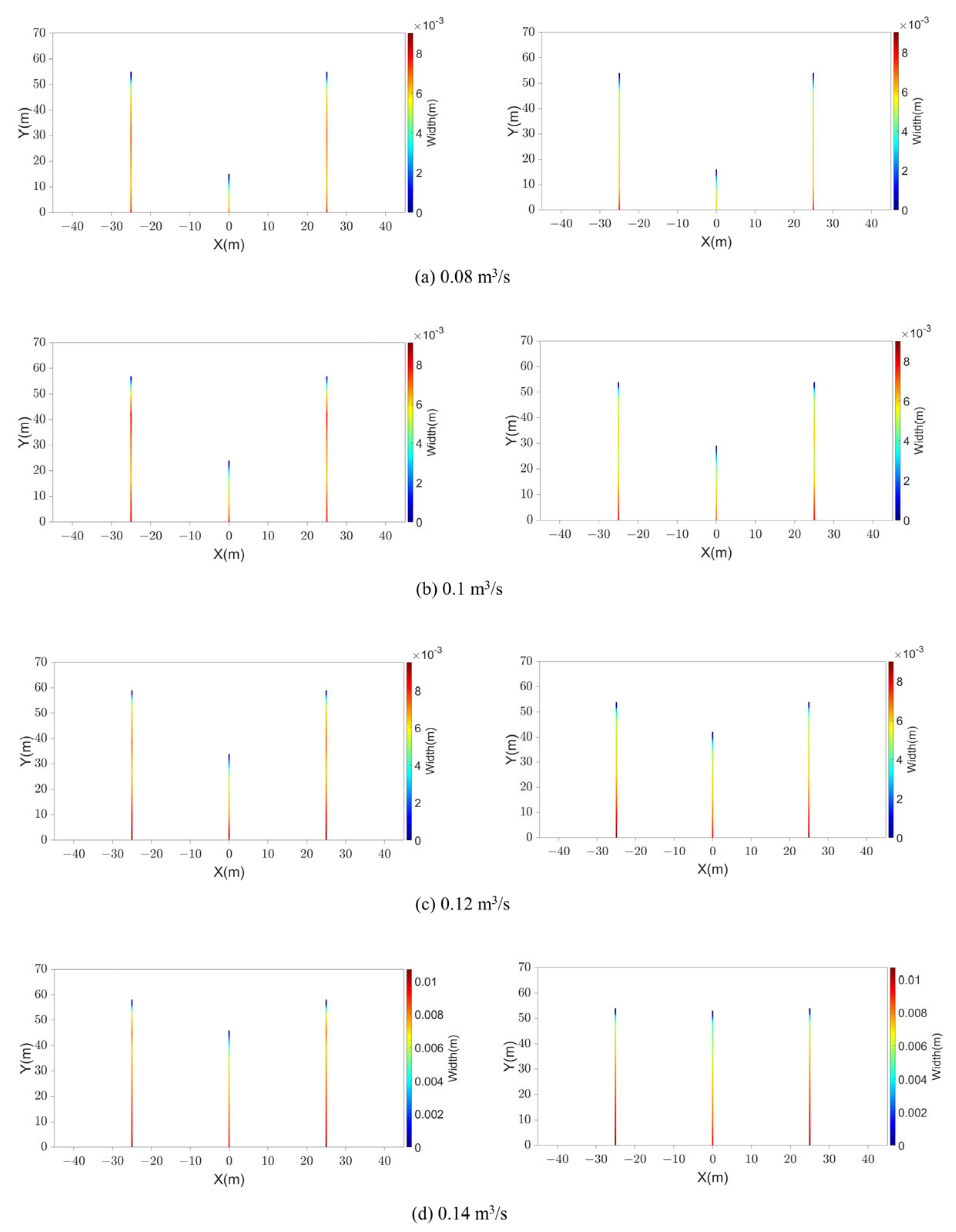
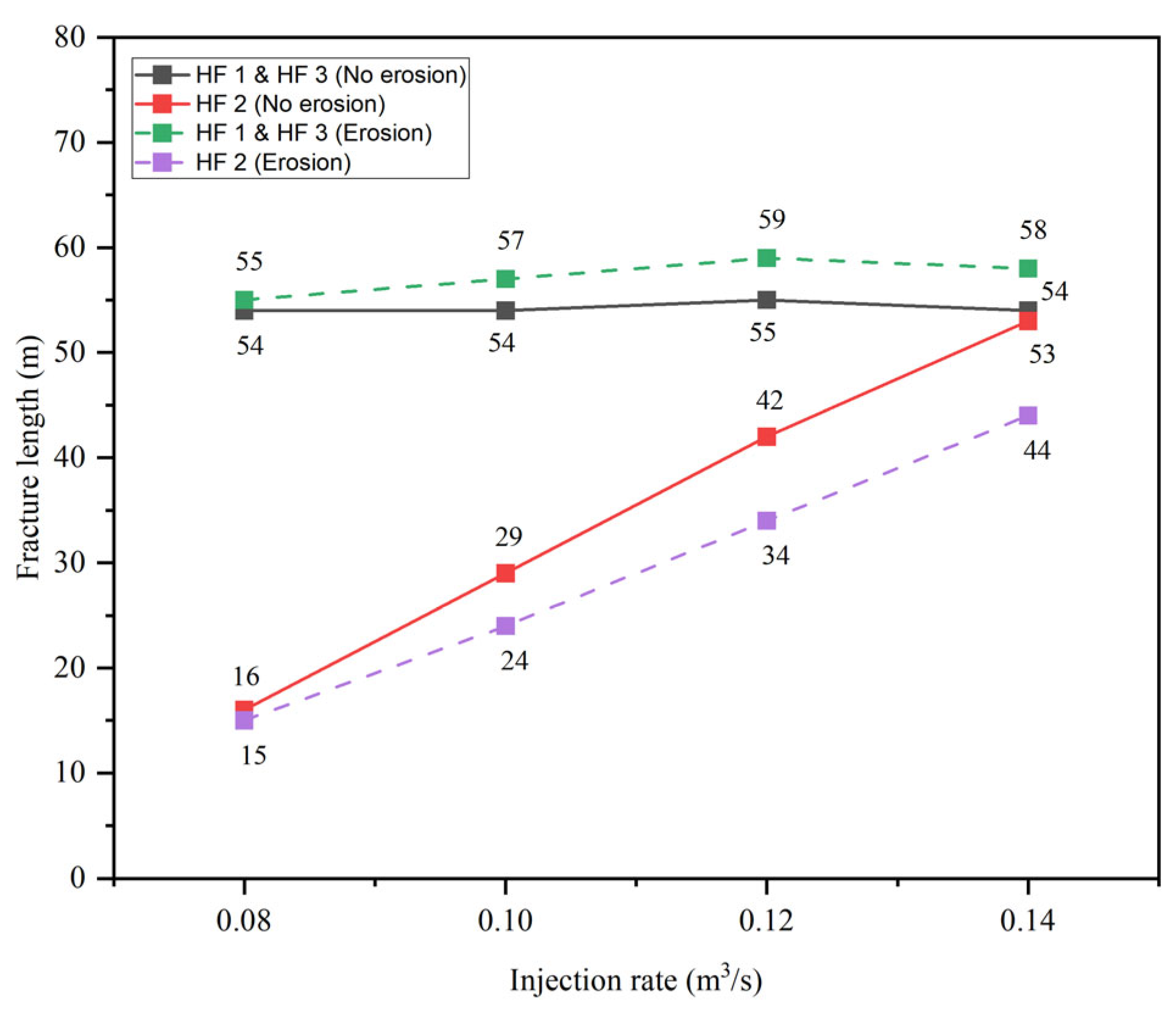
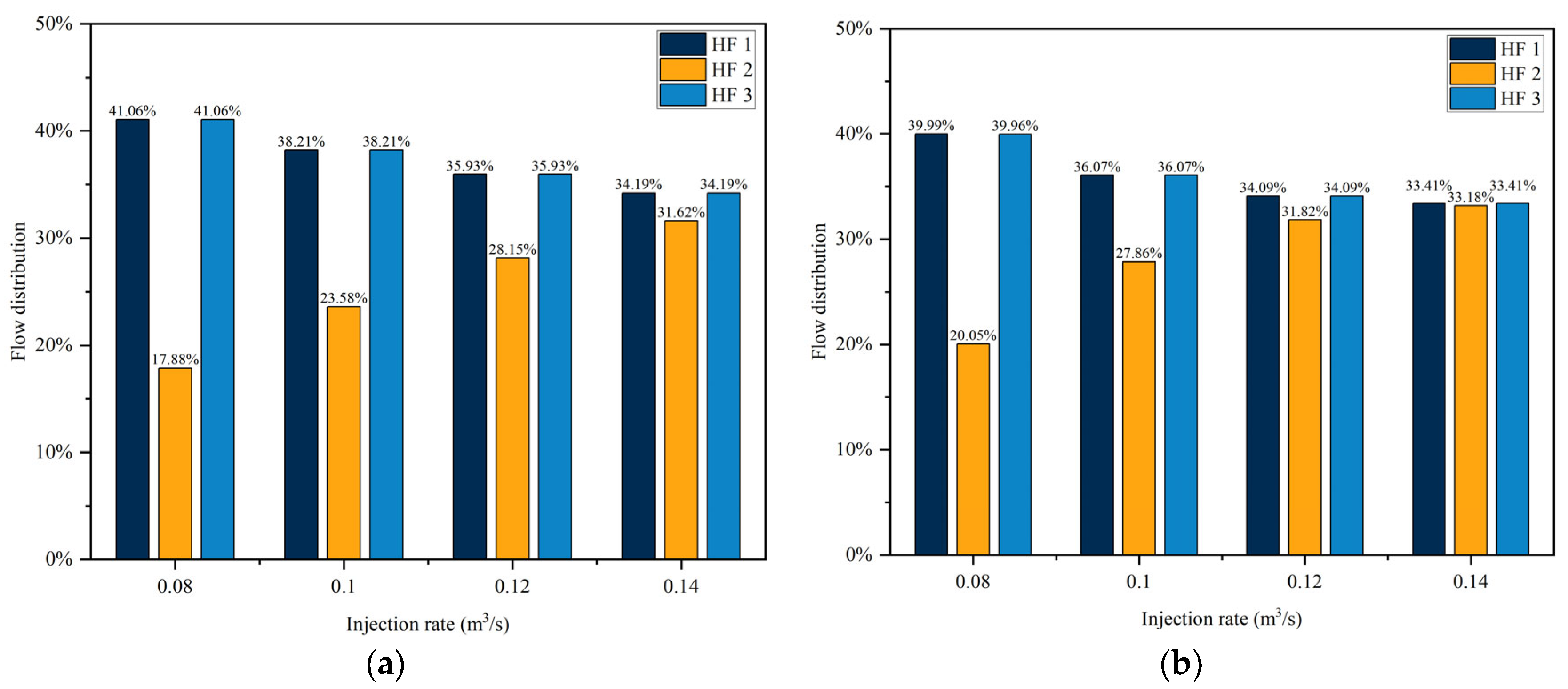
4.2. The Effects of the Injection Rate
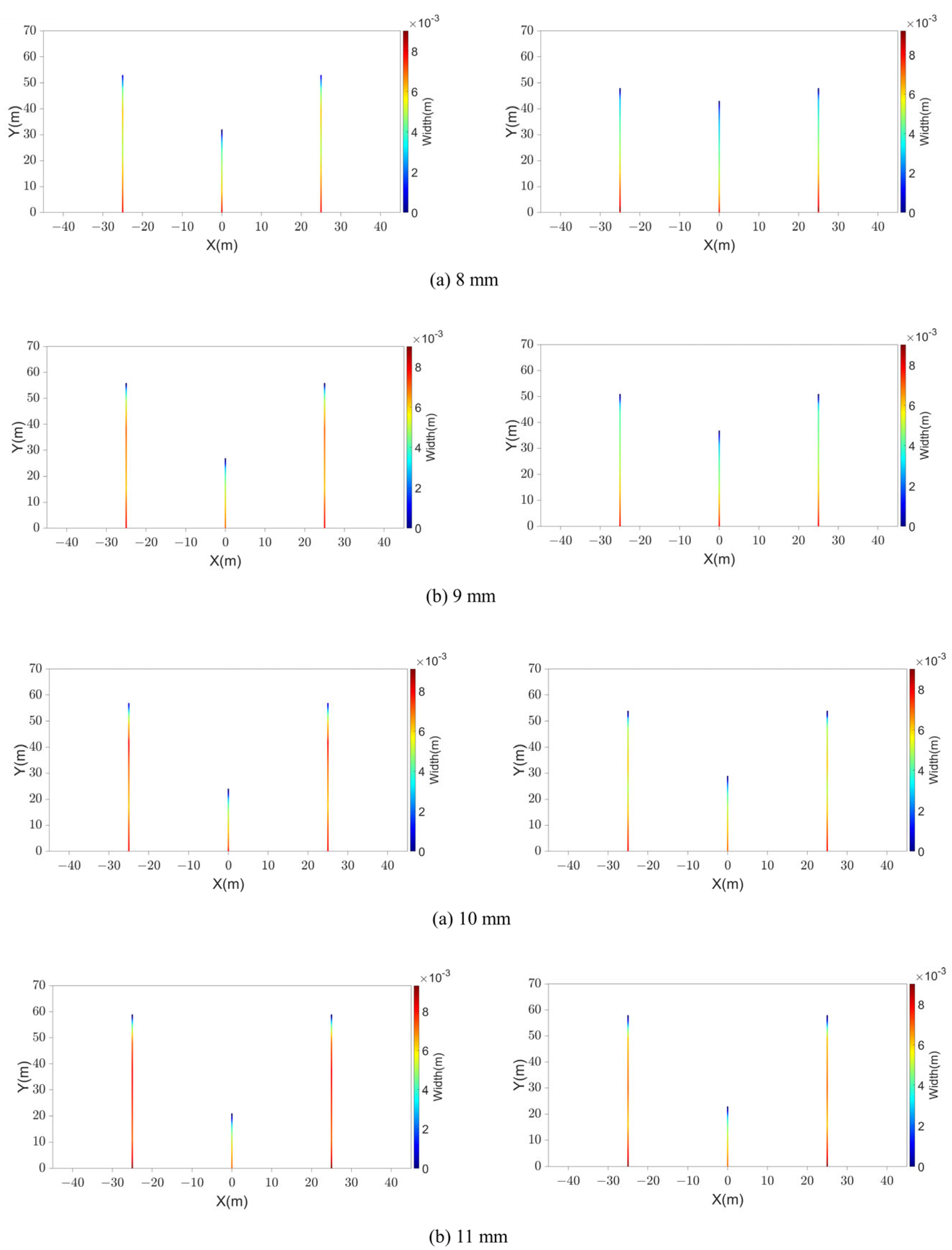
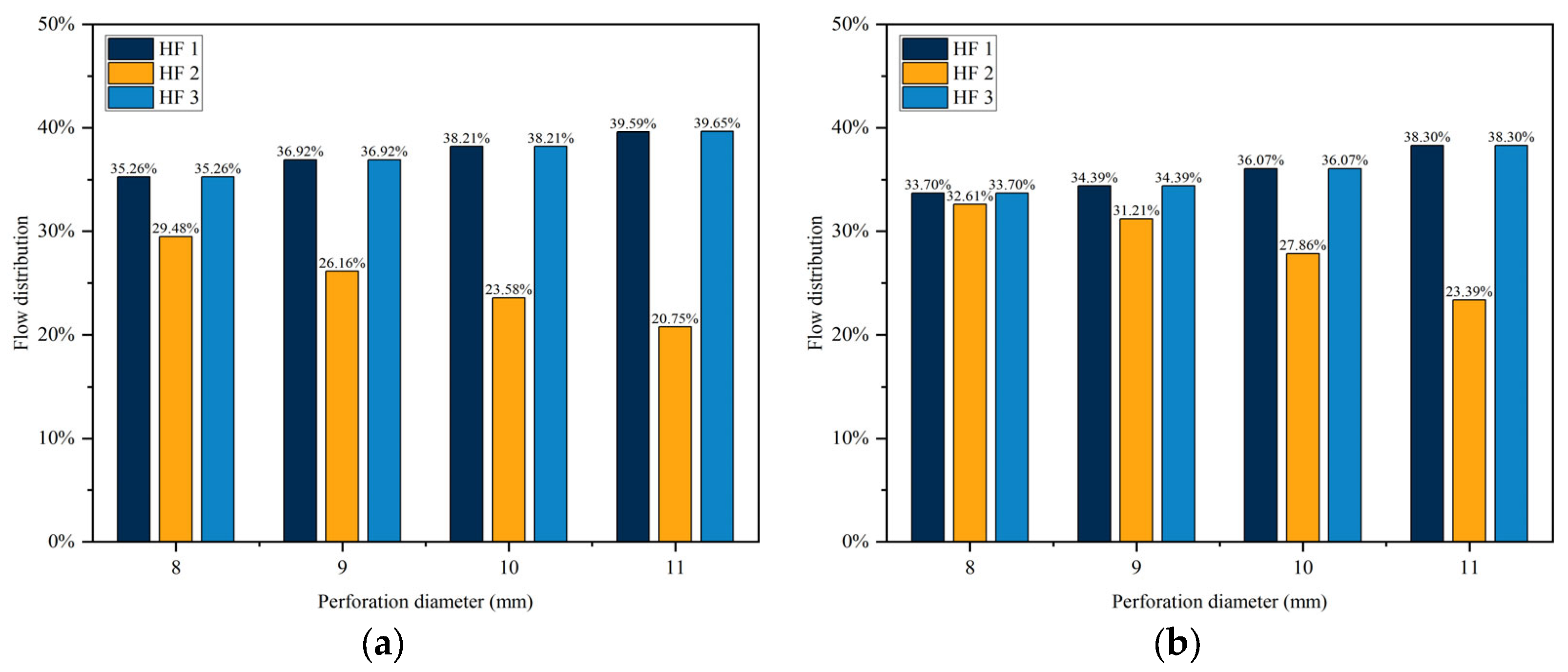
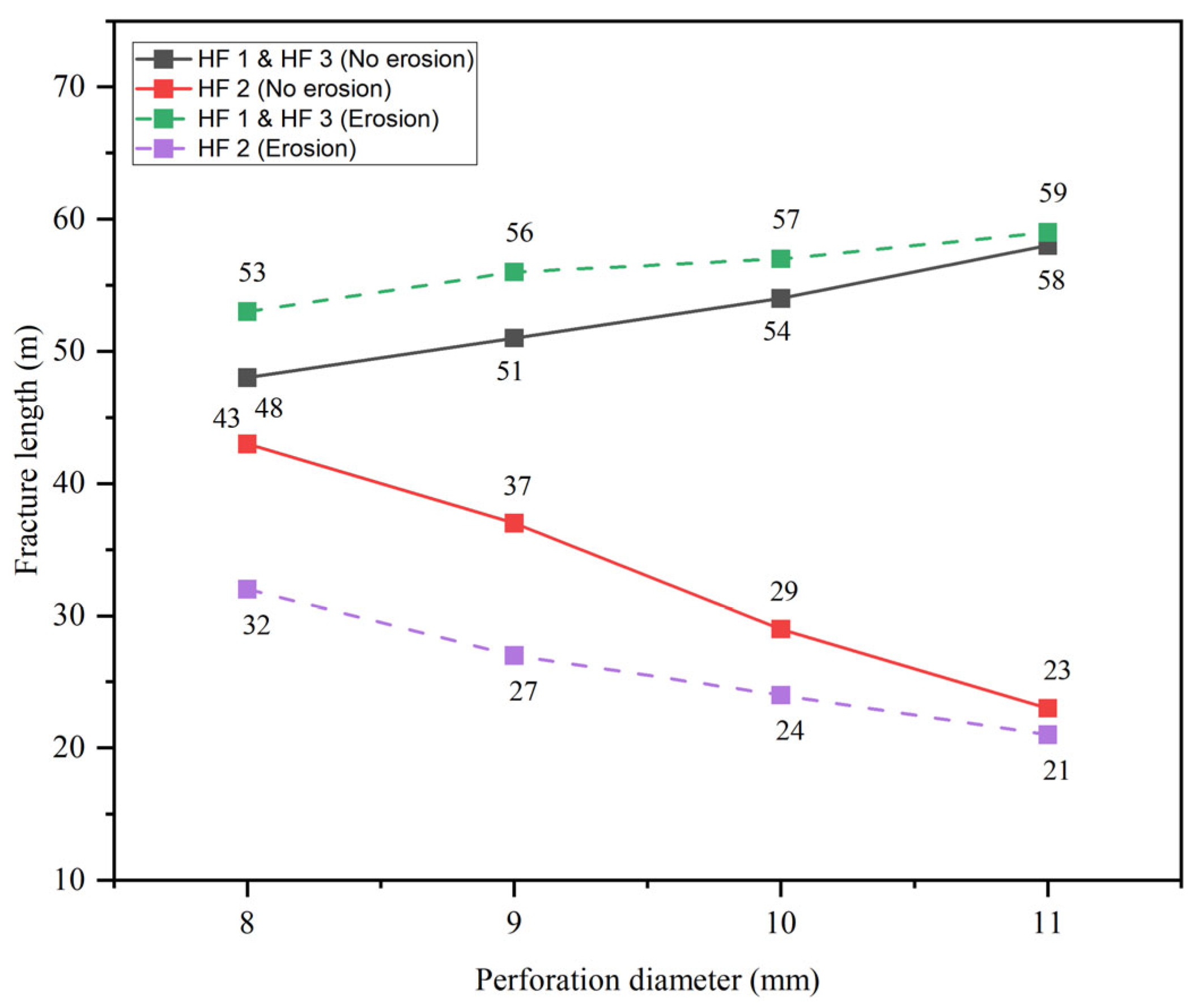
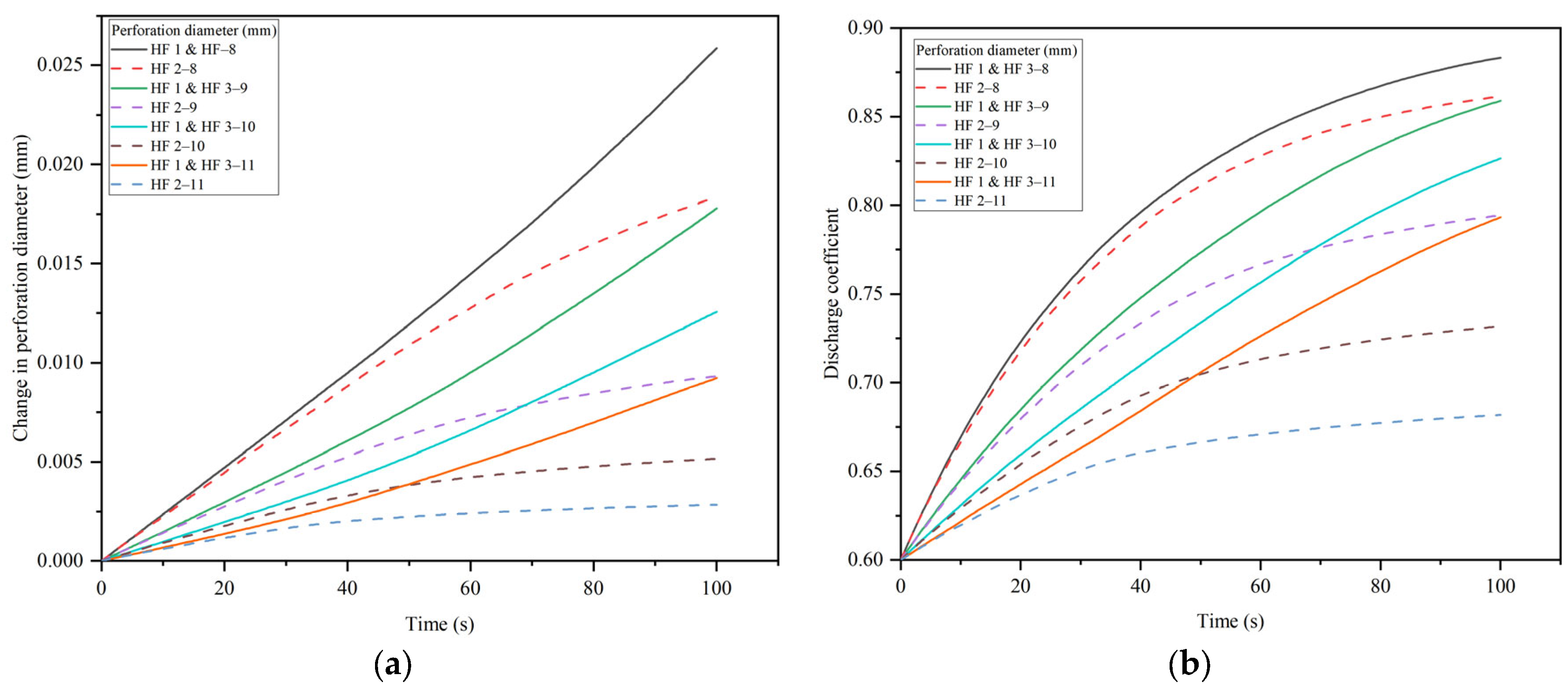
4.3. The Effects of the Perforation Diameter
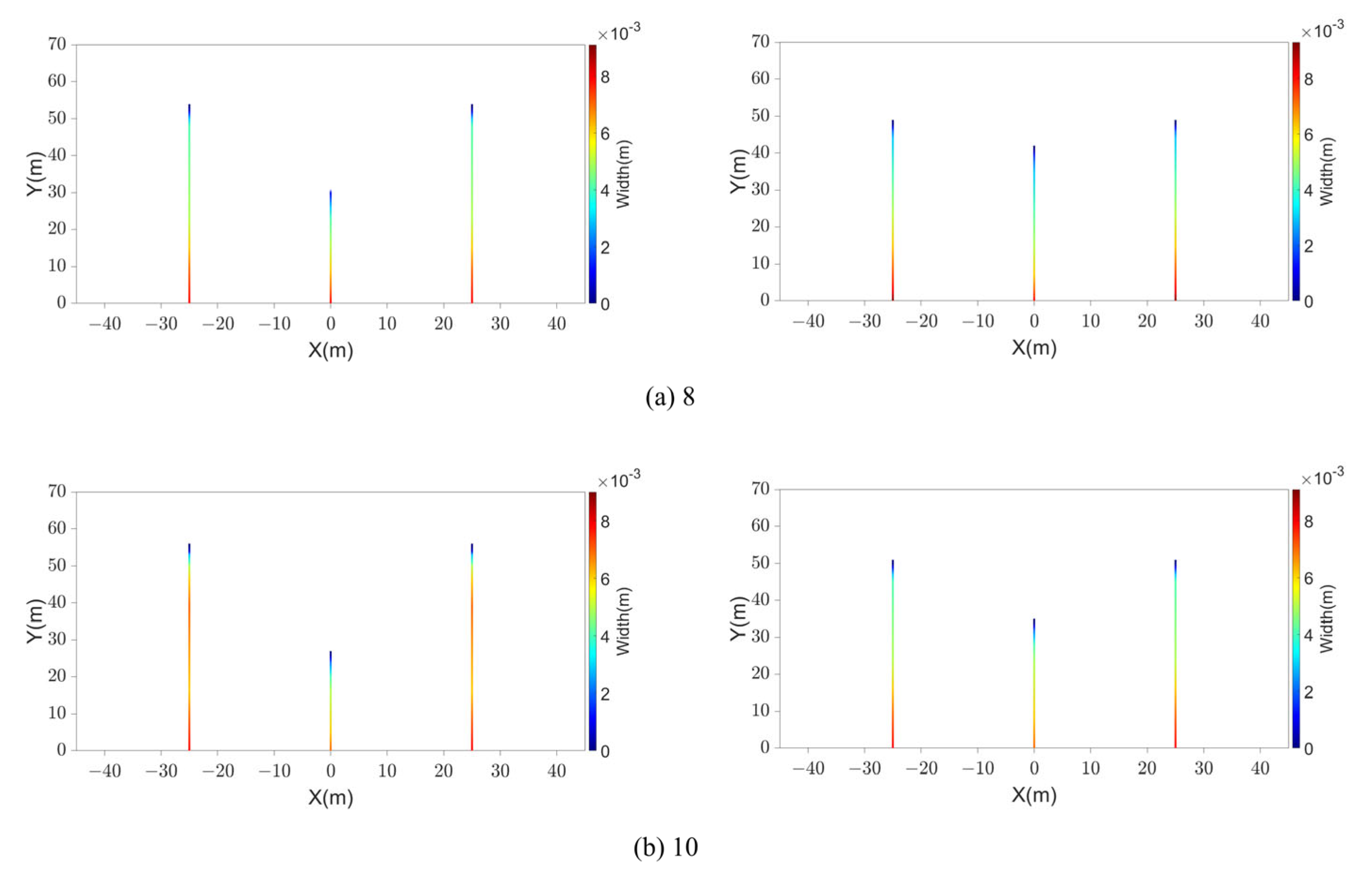
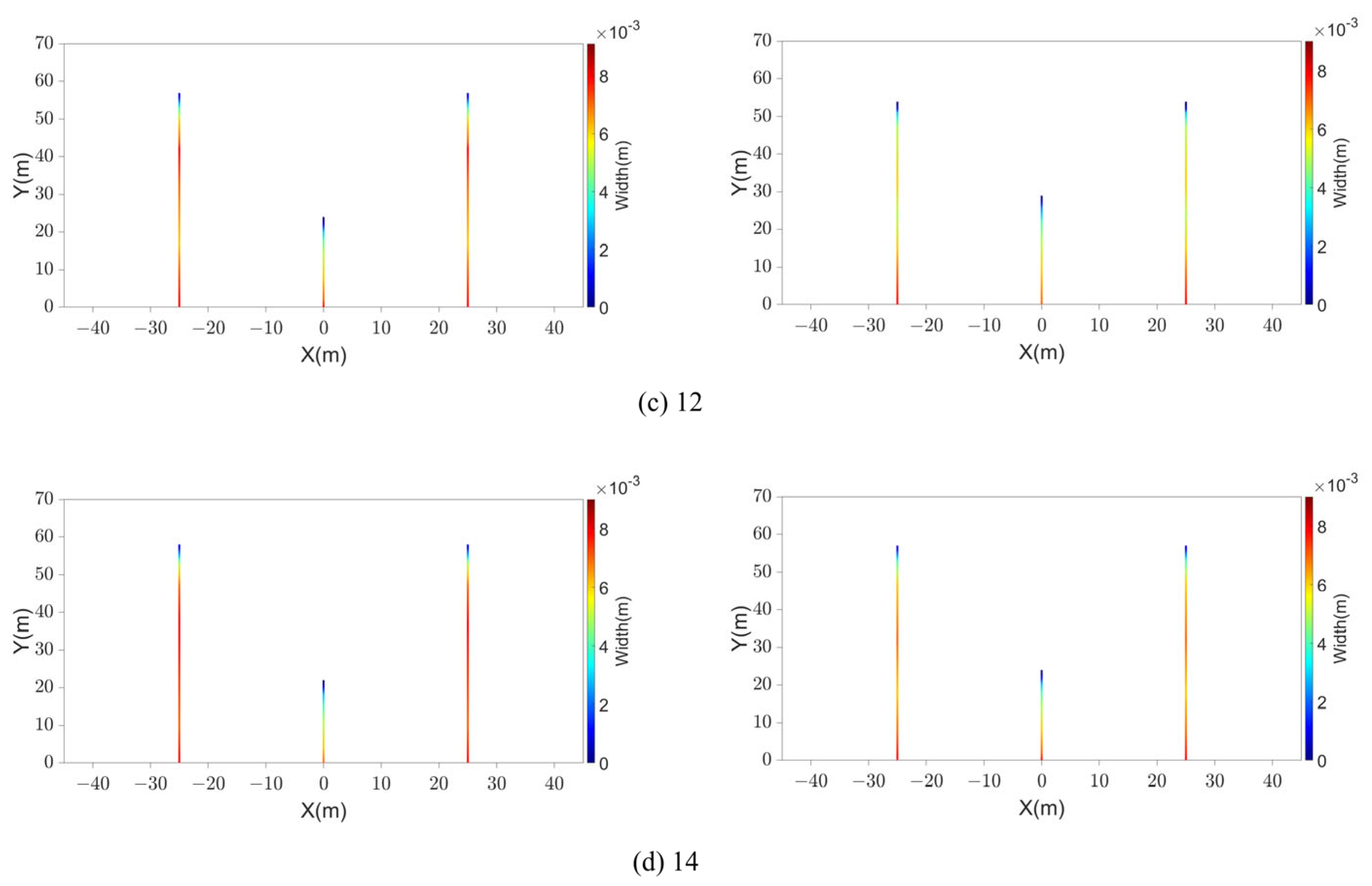
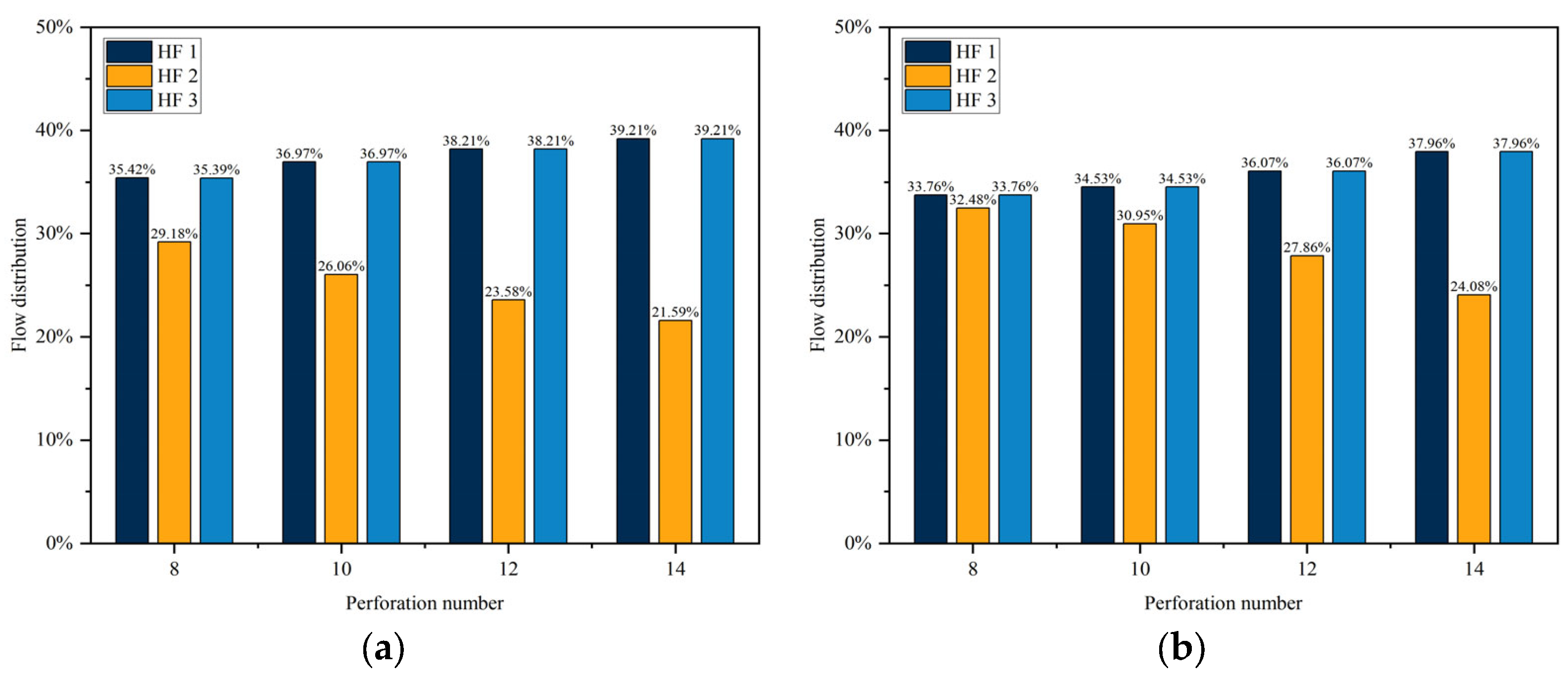
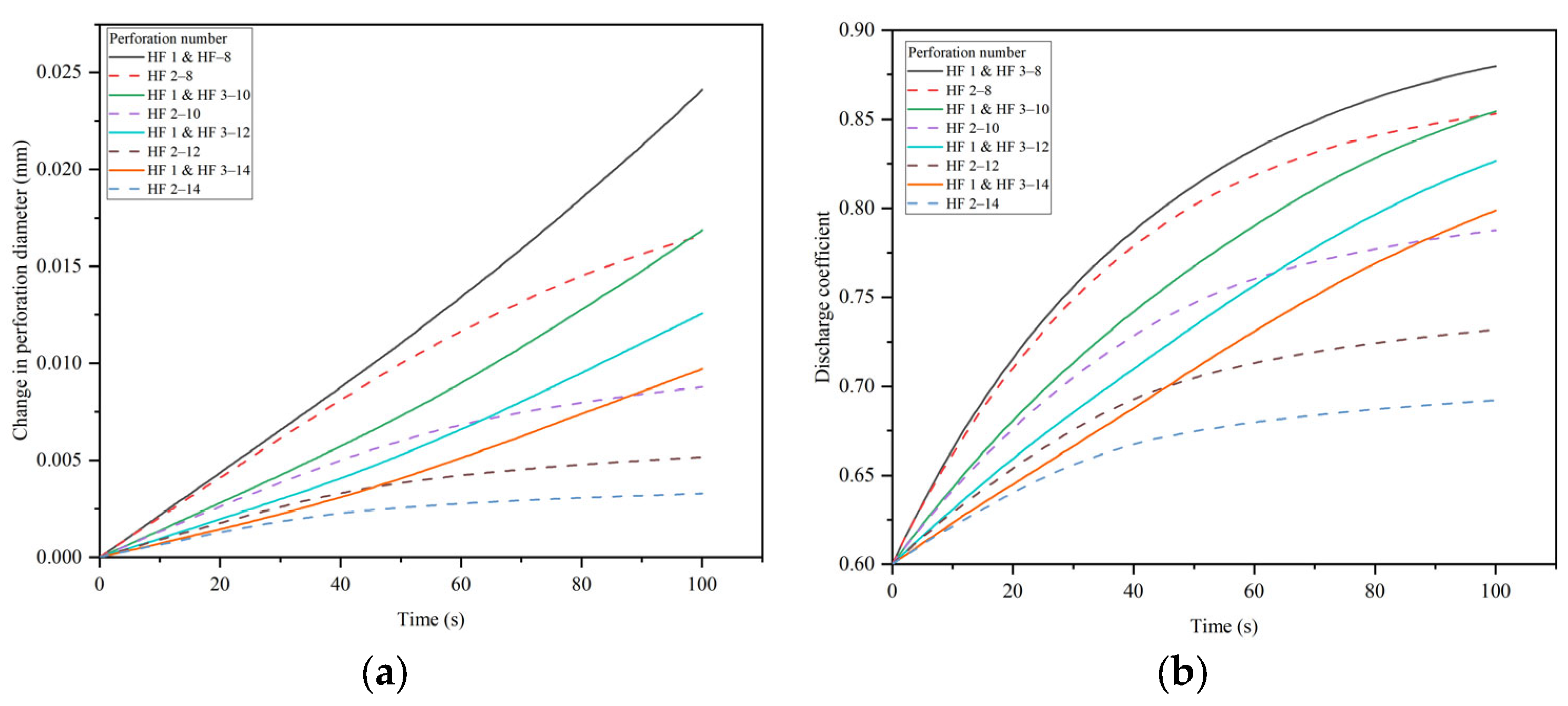
4.4. The Effects of the Perforation Number
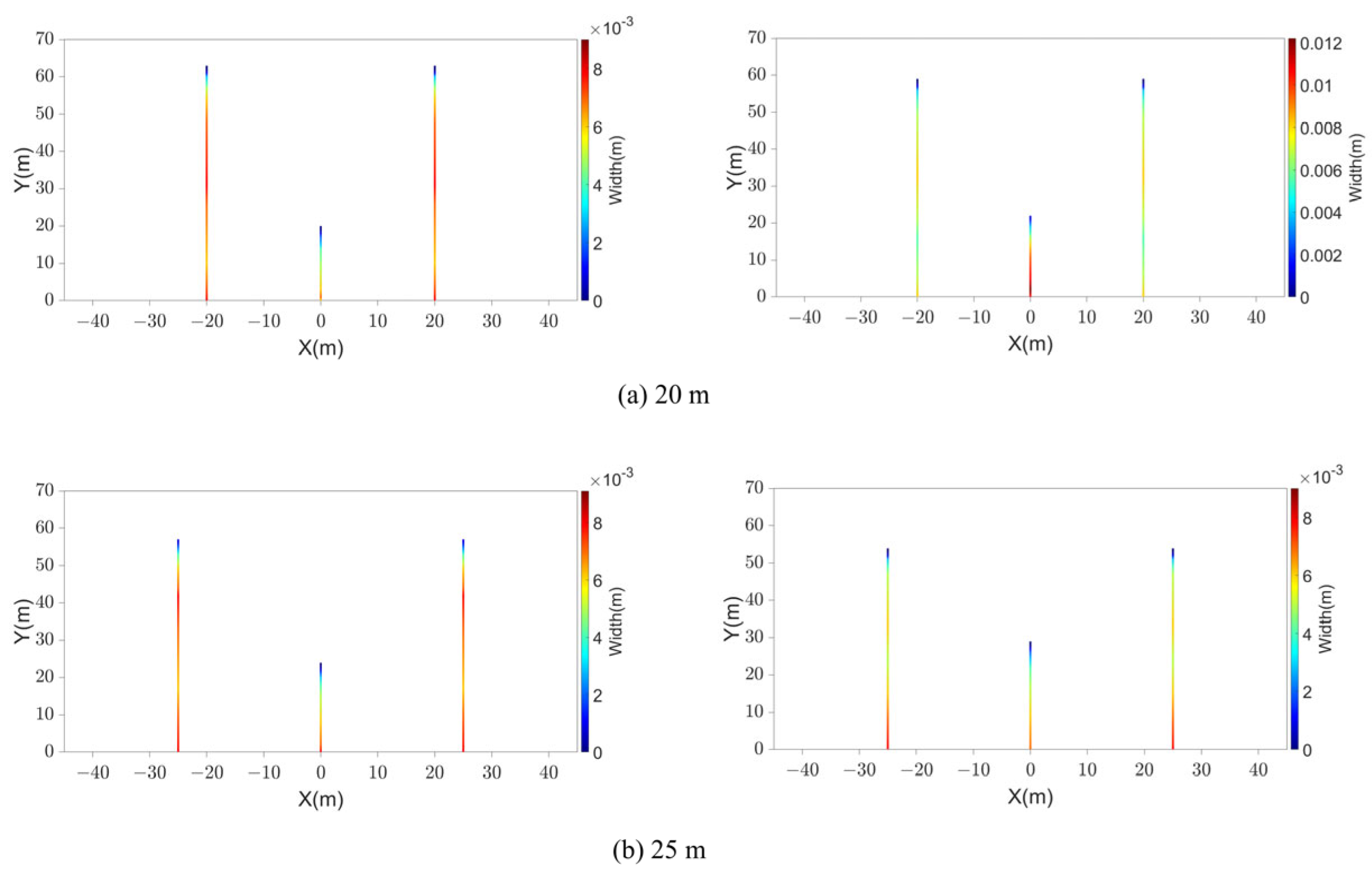
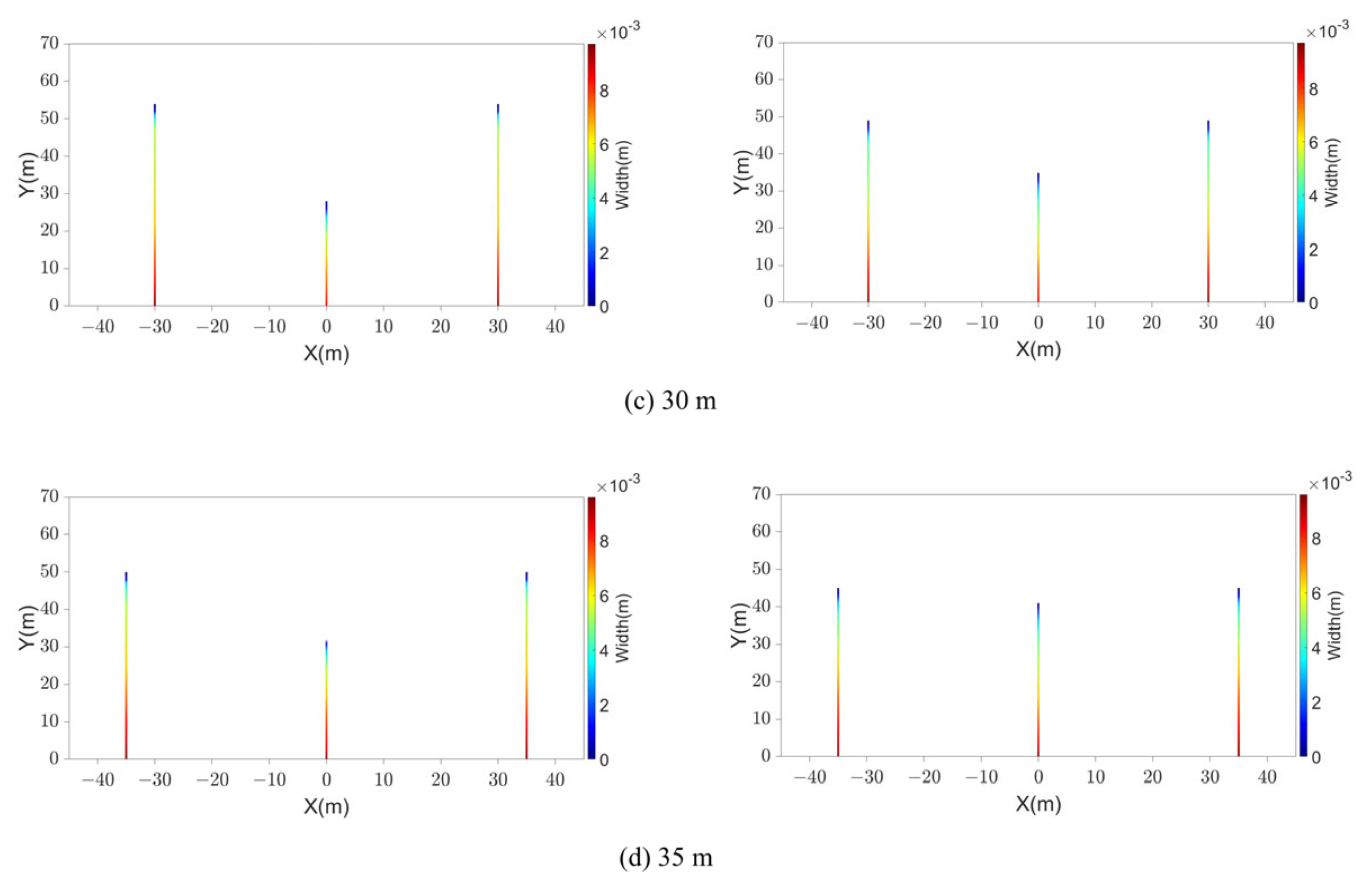
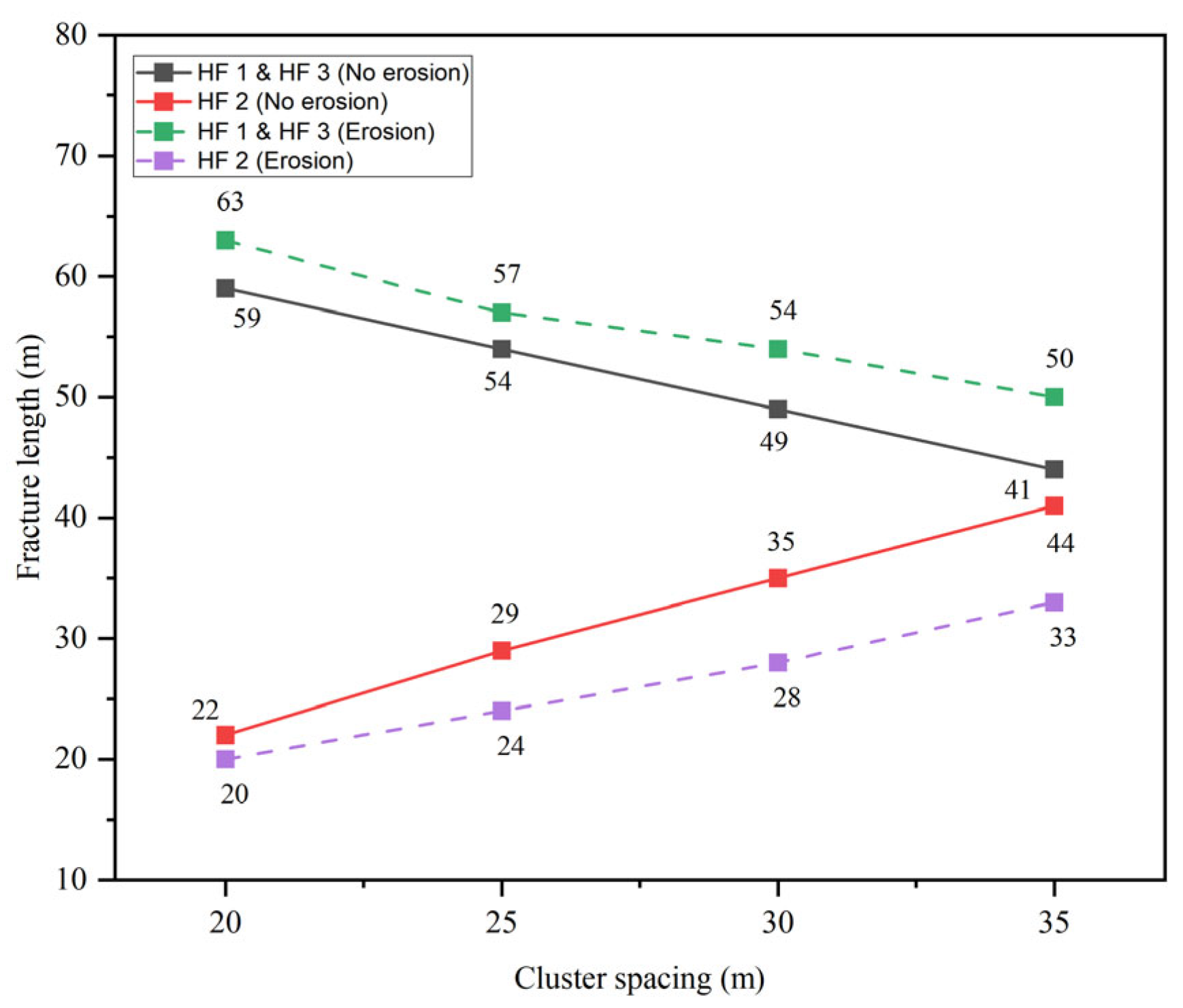
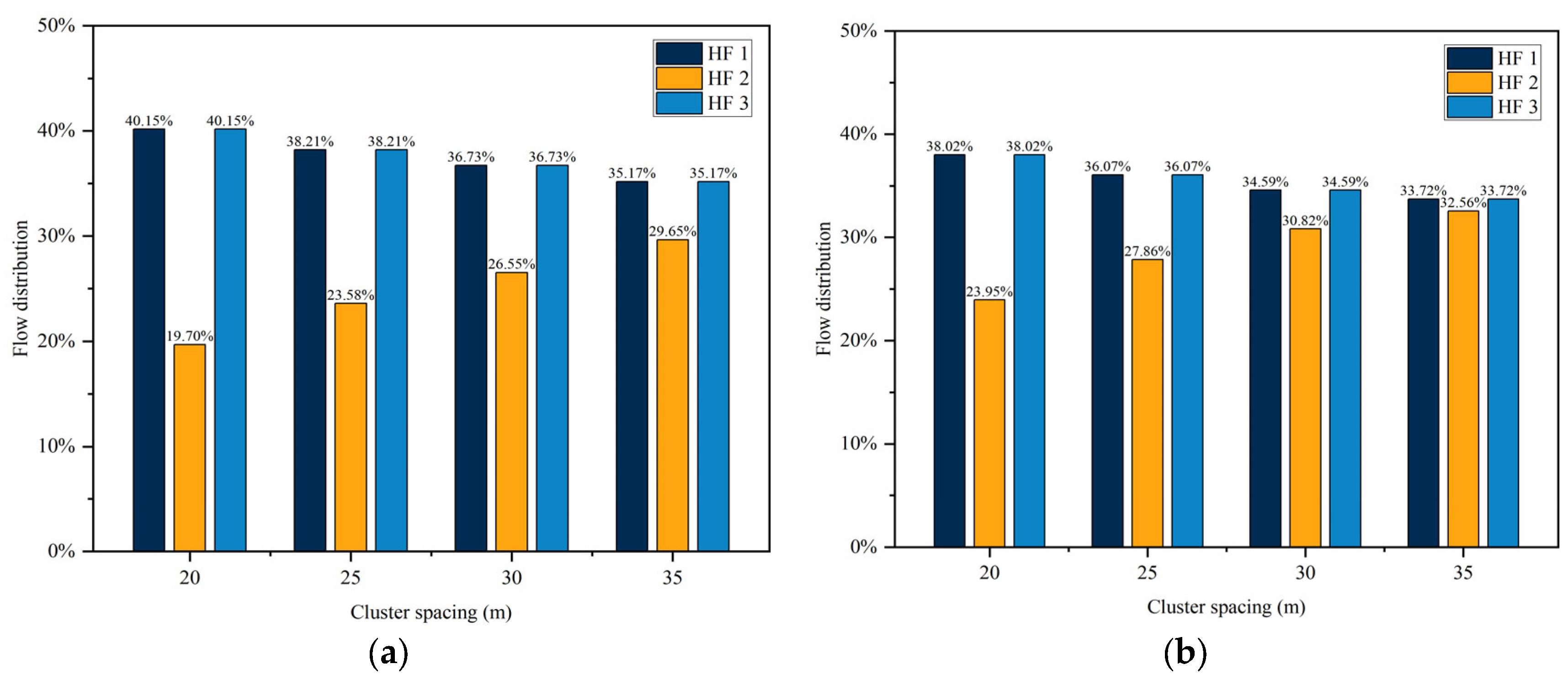
4.5. The Effects of Cluster Spacing
5. Conclusions
- Perforation erosion increases the discharge coefficient and perforation diameter, which results in a reduction in the perforation friction and aggravates uneven fracture propagation.
- For a certain volume of fracturing fluid, although the injection time is longer at a lower injection rate, the effects of erosion on multi-fracture propagation are more severe at a high injection rate. Nevertheless, an increasing injection rate is still beneficial for promoting uniform fracture propagation, and a higher injection rate is recommended.
- When the perforation number and perforation diameter decrease, the erosion of the perforations is aggravated, which leads to a sharp decrease in the perforation friction and aggravates the effects of erosion on the multi-fracture propagation. To overcome the effect of perforation erosion, a smaller perforation diameter and perforation number are recommended to ensure the initial perforation friction is much higher than the perforation friction after perforation erosion.
- The cluster spacing has less effect on perforation erosion. And stress shadow can diminish the effects of erosion on multi-fracture propagation, which indicates that the effects of erosion on multi-fracture propagation are enhanced as the cluster spacing is increased. Nevertheless, increasing the cluster spacing is still conducive to promoting uniform fracture propagation, and larger cluster spacing can be considered to promote uniform fracture propagation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, J.; Luo, D.; Feng, L. A review of the technical and economic evaluation techniques for shale gas development. Appl. Energy 2015, 148, 49–65. [Google Scholar] [CrossRef]
- U.S. EIA. Technically Recoverable Shale Oil and Shale Gas Resources: An Assessment of 137 Shale Formation: 41 Countries outside the United States; U.S. EIA: Washington, DC, USA, 2013.
- Niu, W.; Lu, J.; Sun, Y.; Liu, H.; Cao, X.; Zhan, H.; Zhang, J. A review of the application of data-driven technology in shale gas production evaluation. Energy Rep. 2023, 10, 213–227. [Google Scholar] [CrossRef]
- Li, H. Coordinated development of shale gas benefit exploitation and ecological environmental conservation in China: A mini review. Front. Ecol. Evol. 2023, 11. [Google Scholar] [CrossRef]
- Liu, J.; Bai, X.; Elsworth, D. Evolution of pore systems in low-maturity oil shales during thermal upgrading—Quantified by dynamic SEM and machine learning. Pet. Sci. 2023, in press. [Google Scholar] [CrossRef]
- Xu, Y.; Lun, Z.; Pan, Z.; Wang, H.; Zhou, X.; Zhao, C.; Zhang, D. Occurrence space and state of shale oil: A review. J. Pet. Sci. Eng. 2022, 211, 110183. [Google Scholar] [CrossRef]
- Tang, H.; Winterfeld, P.H.; Wu, Y.-S.; Huang, Z.-q.; Di, Y.; Pan, Z.; Zhang, J. Integrated simulation of multi-stage hydraulic fracturing in unconventional reservoirs. J. Nat. Gas Sci. Eng. 2016, 36, 875–892. [Google Scholar] [CrossRef]
- Sobhaniaragh, B.; Mansur, W.J.; Peters, F.C. Three-dimensional investigation of multiple stage hydraulic fracturing in unconventional reservoirs. J. Pet. Sci. Eng. 2016, 146, 1063–1078. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, J.; Hu, Y.; Zhang, S.; Huang, T.; Liu, X. Numerical simulation of multistage fracturing optimization and application in coalbed methane horizontal wells. Eng. Fract. Mech. 2020, 223, 106738. [Google Scholar] [CrossRef]
- Modeland, N.; Buller, D.; Chong, K.K. Statistical Analysis of the Effect of Completion Methodology on Production in the Haynesville Shale. In Proceedings of the North American Unconventional Gas Conference and Exhibition, The Woodlands, TX, USA, 12–16 June 2011; p. SPE-144120-MS. [Google Scholar]
- Cheng, Y. Impacts of the Number of Perforation Clusters and Cluster Spacing on Production Performance of Horizontal Shale-Gas Wells. SPE Reserv. Eval. Eng. 2012, 15, 31–40. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, Y.; Wang, X.; Wang, T.; Zhang, S. Volume fracturing technology of unconventional reservoirs: Connotation, design optimization and implementation. Pet. Explor. Dev. 2012, 39, 377–384. [Google Scholar] [CrossRef]
- Miller, C.; Waters, G.; Rylander, E. Evaluation of Production Log Data from Horizontal Wells Drilled in Organic Shales. In Proceedings of the North American Unconventional Gas Conference and Exhibition, The Woodlands, TX, USA, 12–16 June 2011. [Google Scholar]
- Ugueto, C.G.A.; Huckabee, P.T.; Molenaar, M.M.; Wyker, B.; Somanchi, K. Perforation Cluster Efficiency of Cemented Plug and Perf Limited Entry Completions; Insights from Fiber Optics Diagnostics. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 9–11 February 2016. [Google Scholar]
- Rainbolt, M.F.; Esco, J. Frac Hit Induced Production Losses: Evaluating Root Causes, Damage Location, Possible Prevention Methods and Success of Remediation Treatments, Part II. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Muscat, Oman, 16–18 October 2018; p. D021S006R004. [Google Scholar]
- Li, Y.; Deng, J.; Liu, W.; Yan, W.; Feng, Y.; Cao, W.; Wang, P.; Hou, Y. Numerical simulation of limited-entry multi-cluster fracturing in horizontal well. J. Pet. Sci. Eng. 2017, 152, 443–455. [Google Scholar] [CrossRef]
- Zeng, Q.; Liu, Z.; Wang, T.; Gao, Y.; Zhuang, Z. Fully coupled simulation of multiple hydraulic fractures to propagate simultaneously from a perforated horizontal wellbore. Comput. Mech. 2018, 61, 137–155. [Google Scholar] [CrossRef]
- Zheng, P.; Xia, Y.; Yao, T.; Jiang, X.; Xiao, P.; He, Z.; Zhou, D. Formation mechanisms of hydraulic fracture network based on fracture interaction. Energy 2022, 243, 123057. [Google Scholar] [CrossRef]
- ElGibaly, A.; Abdalla Osman, M. Perforation friction modeling in limited entry fracturing using artificial neural network. Egypt. J. Pet. 2019, 28, 297–305. [Google Scholar] [CrossRef]
- Zhou, T.; Chen, M.; Zhang, S.; Li, Y.; Li, F.; Zhang, C. Simulation of fracture propagation and optimization of ball-sealer in-stage diversion under the effect of heterogeneous stress field. Nat. Gas Ind. B 2020, 7, 523–532. [Google Scholar] [CrossRef]
- Lim, P.; Goddard, P.; Sink, J.; Abou-Sayed, I. Hydraulic Fracturing: A Marcellus Case Study of an Engineered Staging Completion Based on Rock Properties. In Proceedings of the SPE/CSUR Unconventional Resources Conference—Canada, Calgary, AB, Canada, 30 September–2 October 2014; p. D011S003R006. [Google Scholar]
- Wu, K.; Olson, J.; Balhoff, M.T.; Yu, W. Numerical Analysis for Promoting Uniform Development of Simultaneous Multiple-Fracture Propagation in Horizontal Wells. SPE Prod. Oper. 2016, 32, 41–50. [Google Scholar]
- Peirce, A.P.P.; Bunger, A.P.P. Interference Fracturing: Nonuniform Distributions of Perforation Clusters That Promote Simultaneous Growth of Multiple Hydraulic Fractures. SPE J. 2014, 20, 384–395. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, S.; Ma, X.; Zhou, T.; Zou, Y. A semi-analytical model for predicting fluid partitioning among multiple hydraulic fractures from a horizontal well. J. Pet. Sci. Eng. 2018, 171, 1041–1051. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, X.; Tang, M.; Du, X.; Xu, C.; Tang, J.; Damjanac, B. Numerical Investigation on Hydraulic Fracturing of Extreme Limited Entry Perforating in Plug-and-Perforation Completion of Shale Oil Reservoir in Changqing Oilfield, China. Rock Mech. Rock Eng. 2021, 54, 2925–2941. [Google Scholar] [CrossRef]
- Li, M.; Lv, W.; Liu, J.; Sun, Z.; Zhou, F.; Wang, B. Effect of perforation friction on 3D In-stage multiple fracture propagation: A numerical study. Eng. Fract. Mech. 2022, 267, 108415. [Google Scholar] [CrossRef]
- Lecampion, B.; Desroches, J.; Weng, X.; Burghardt, J.; Brown, J.E.E. Can We Engineer Better Multistage Horizontal Completions? Evidence of the Importance of Near-wellbore Fracture Geometry from Theory, Lab and Field Experiments. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 3–5 February 2015; p. D021S003R001. [Google Scholar]
- Somanchi, K.; O’Brien, C.; Huckabee, P.; Ugueto, G. Insights and Observations into Limited Entry Perforation Dynamics from Fiber-Optic Diagnostics. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, San Antonio, TX, USA, 1–3 August 2016; p. URTEC-2458389-MS. [Google Scholar]
- Roberts, G.; Whittaker, J.; McDonald, J.; Paxson, T. Proppant Distribution Observations from 20,000+ Perforation Erosion Measurements. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 4–6 February 2020; p. D011S002R002. [Google Scholar]
- Crump, J.B.; Conway, M.W. Effects of Perforation-Entry Friction on Bottomhole Treating Analysis. J. Pet. Technol. 1988, 40, 1041–1048. [Google Scholar] [CrossRef]
- Roberts, G.; Lilly, T.B.; Tymons, T.R. Improved Well Stimulation through the Application of Downhole Video Analytics. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 23–25 January 2018; p. D011S001R005. [Google Scholar]
- Cramer, D.; Friehauf, K.; Roberts, G.; Whittaker, J. Integrating Distributed Acoustic Sensing, Treatment-Pressure Analysis, and Video-Based Perforation Imaging to Evaluate Limited-Entry-Treatment Effectiveness. SPE Prod. Oper. 2020, 35, 0730–0755. [Google Scholar] [CrossRef]
- Guo, J.; Zhao, X.; Zhu, H.; Zhang, X.; Pan, R. Numerical simulation of interaction of hydraulic fracture and natural fracture based on the cohesive zone finite element method. J. Nat. Gas Sci. Eng. 2015, 25, 180–188. [Google Scholar] [CrossRef]
- Zhao, P.; Xie, L.; Ge, Q.; Zhang, Y.; Liu, J.; He, B. Numerical study of the effect of natural fractures on shale hydraulic fracturing based on the continuum approach. J. Pet. Sci. Eng. 2020, 189, 107038. [Google Scholar] [CrossRef]
- Dong, Y.; Tian, W.; Li, P.; Zeng, B.; Lu, D. Numerical investigation of complex hydraulic fracture network in naturally fractured reservoirs based on the XFEM. J. Nat. Gas Sci. Eng. 2021, 96, 104272. [Google Scholar] [CrossRef]
- Li, Z.-Q.; Li, X.-L.; Yu, J.-B.; Cao, W.-D.; Liu, Z.-F.; Wang, M.; Liu, Z.-F.; Wang, X.-H. Influence of existing natural fractures and beddings on the formation of fracture network during hydraulic fracturing based on the extended finite element method. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 6, 58. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Oh, B.H. Crack band theory for fracture of concrete. Matériaux Et Constr. 1983, 16, 155–177. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Shiomi, T. Dynamic behaviour of saturated porous media; The generalized Biot formulation and its numerical solution. Int. J. Numer. Anal. Methods Geomech. 1984, 8, 71–96. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Zhang, D. A fully coupled thermo-hydro-mechanical, three-dimensional model for hydraulic stimulation treatments. J. Nat. Gas Sci. Eng. 2016, 34, 64–84. [Google Scholar] [CrossRef]
- Zhou, L.; Hou, M.Z. A new numerical 3D-model for simulation of hydraulic fracturing in consideration of hydro-mechanical coupling effects. Int. J. Rock Mech. Min. Sci. 2013, 60, 370–380. [Google Scholar] [CrossRef]
- Roostaei, M.; Taghipoor, S.; Nouri, A.; Fattahpour, V.; Chan, D. Smeared modeling of hydraulic fracture using partially coupled reservoir and geomechanics simulators. Int. J. Rock Mech. Min. Sci. 2019, 113, 99–111. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, J.; Li, Y.; Yan, W.; Zhang, X. Numerical Simulation of Simultaneous Hydraulic Fracture Growth within a Rock Layer: Implications for Stimulation of Low-Permeability Reservoirs. J. Geophys. Res.-Solid Earth 2019, 124, 13227–13249. [Google Scholar] [CrossRef]
- Lecampion, B.; Desroches, J. Simultaneous initiation and growth of multiple radial hydraulic fractures from a horizontal wellbore. J. Mech. Phys. Solids 2015, 82, 235–258. [Google Scholar] [CrossRef]
- Long, G.; Liu, S.; Xu, G.; Wong, S.-W. Modeling of Perforation Erosion for Hydraulic Fracturing Applications. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015; p. D021S015R008. [Google Scholar]
- Valko, P.P.; Economides, M.J. Hydraulic Fracture Mechanics; Wiley: Chichester, UK, 1995. [Google Scholar]
- Xing, P.; Yoshioka, K.; Adachi, J.; El-Fayoumi, A.; Bunger, A.P. Laboratory measurement of tip and global behavior for zero-toughness hydraulic fractures with circular and blade-shaped (PKN) geometry. J. Mech. Phys. Solids 2017, 104, 172–186. [Google Scholar] [CrossRef]
- Harris, P.C.; Pippin, P.M. High-Rate Foam Fracturing: Fluid Friction and Perforation Erosion. SPE Prod. Facil. 2000, 15, 27–32. [Google Scholar] [CrossRef]
- Shin, D.H.; Sharma, M.M. Factors Controlling the Simultaneous Propagation of Multiple Competing Fractures in a Horizontal Well. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2014; p. SPE-168599-MS. [Google Scholar]
- Yang, C.-X.; Yi, L.-P.; Yang, Z.-Z.; Li, X.-G. Numerical investigation of the fracture network morphology in multi-cluster hydraulic fracturing of horizontal wells: A DDM-FVM study. J. Pet. Sci. Eng. 2022, 215, 110723. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Young’s modulus | 20 GPa |
| Poisson’s ratio | 0.2 |
| Tensile strength | 6 MPa |
| Injection rate | |
| Viscosity | 70 cP |
| Pay thickness | 1 m |
| Minimum horizontal stress | 7 MPa |
| Parameter | Value |
|---|---|
| Young’s modulus | 0.1 GPa |
| Poisson’s ratio | 0.48 |
| Injection rate | 8 mL/min |
| Viscosity | 300 cP |
| Minimum horizontal stress | 0.31 MPa |
| Parameter | Value |
|---|---|
| Young’s modulus | 15 GPa |
| Poisson’s ratio | 0.2 |
| Density | 2400 |
| Tensile strength | 6 MPa |
| Biot coefficient | 0.7 |
| Injection rate | |
| Viscosity | 1 cP |
| Maximum horizontal stress | 71 MPa |
| Minimum horizontal stress | 63 MPa |
| Perforation diameter | 10 mm |
| Perforation number | 12 |
| Cluster spacing | 25 m |
| Initial discharge coefficient | 0.6 |
| Maximum discharge coefficient | 0.9 |
| Sand concentration | 720 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, L.; Xie, L.; He, B.; Zhang, Y. Multi-Fracture Propagation Considering Perforation Erosion with Respect to Multi-Stage Fracturing in Shale Reservoirs. Energies 2024, 17, 828. https://doi.org/10.3390/en17040828
Tan L, Xie L, He B, Zhang Y. Multi-Fracture Propagation Considering Perforation Erosion with Respect to Multi-Stage Fracturing in Shale Reservoirs. Energies. 2024; 17(4):828. https://doi.org/10.3390/en17040828
Chicago/Turabian StyleTan, Lin, Lingzhi Xie, Bo He, and Yao Zhang. 2024. "Multi-Fracture Propagation Considering Perforation Erosion with Respect to Multi-Stage Fracturing in Shale Reservoirs" Energies 17, no. 4: 828. https://doi.org/10.3390/en17040828
APA StyleTan, L., Xie, L., He, B., & Zhang, Y. (2024). Multi-Fracture Propagation Considering Perforation Erosion with Respect to Multi-Stage Fracturing in Shale Reservoirs. Energies, 17(4), 828. https://doi.org/10.3390/en17040828





