Similarity Coefficient Generation Using Adjoint-Based Sensitivity and Uncertainty Method and Stochastic Sampling Method
Abstract
1. Introduction
2. Similarity Coefficient Generation
2.1. Similarity Coefficient Generation with the Adjoint-Based S/U Method
2.2. Similarity Coefficient Generation with the S.S. Method
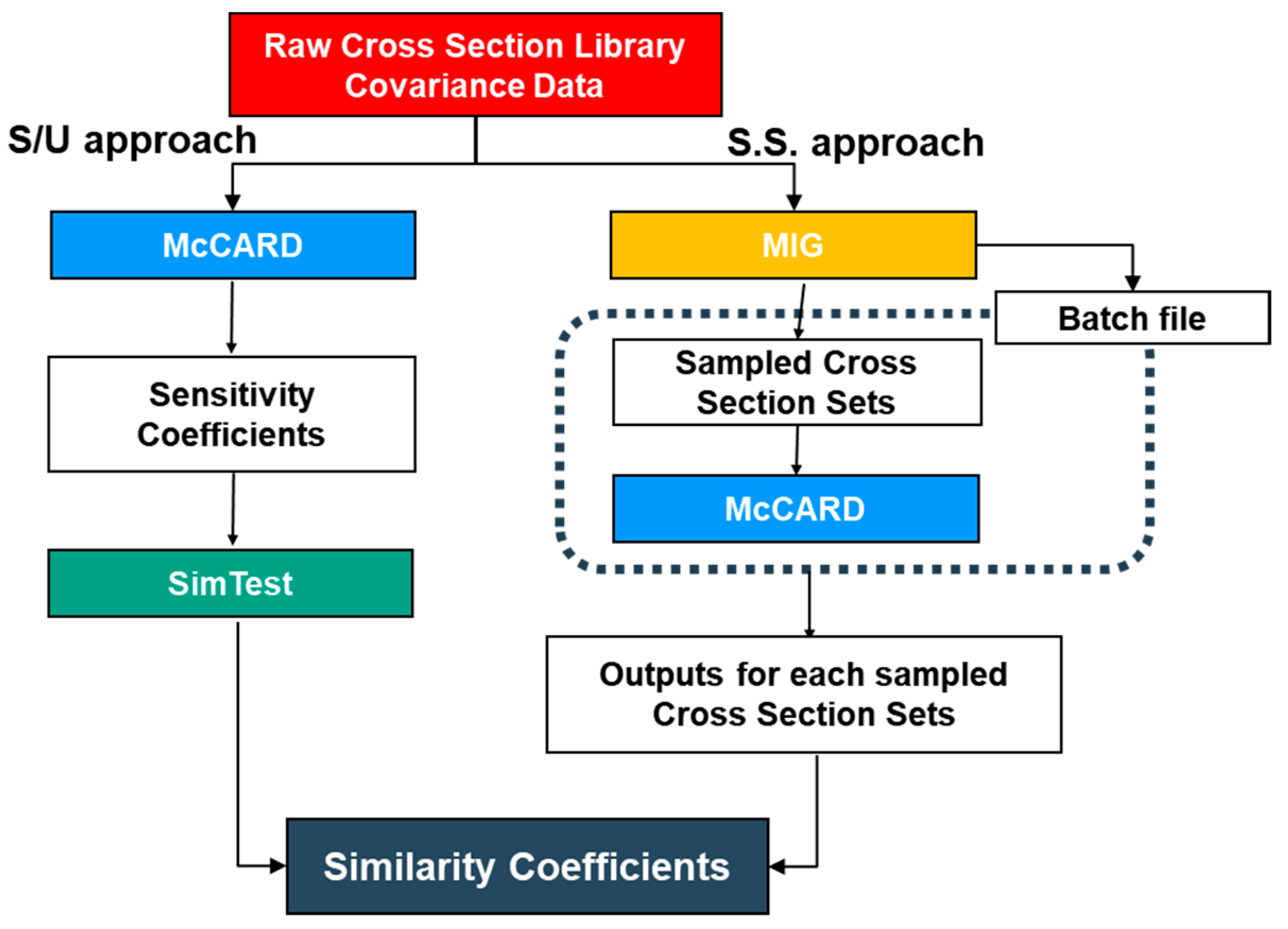
2.3. McCARD/MIG Similarity Coefficient Generation Code System
3. Similarity Tests among Various Systems
3.1. Similarity Test for SMART SMR System
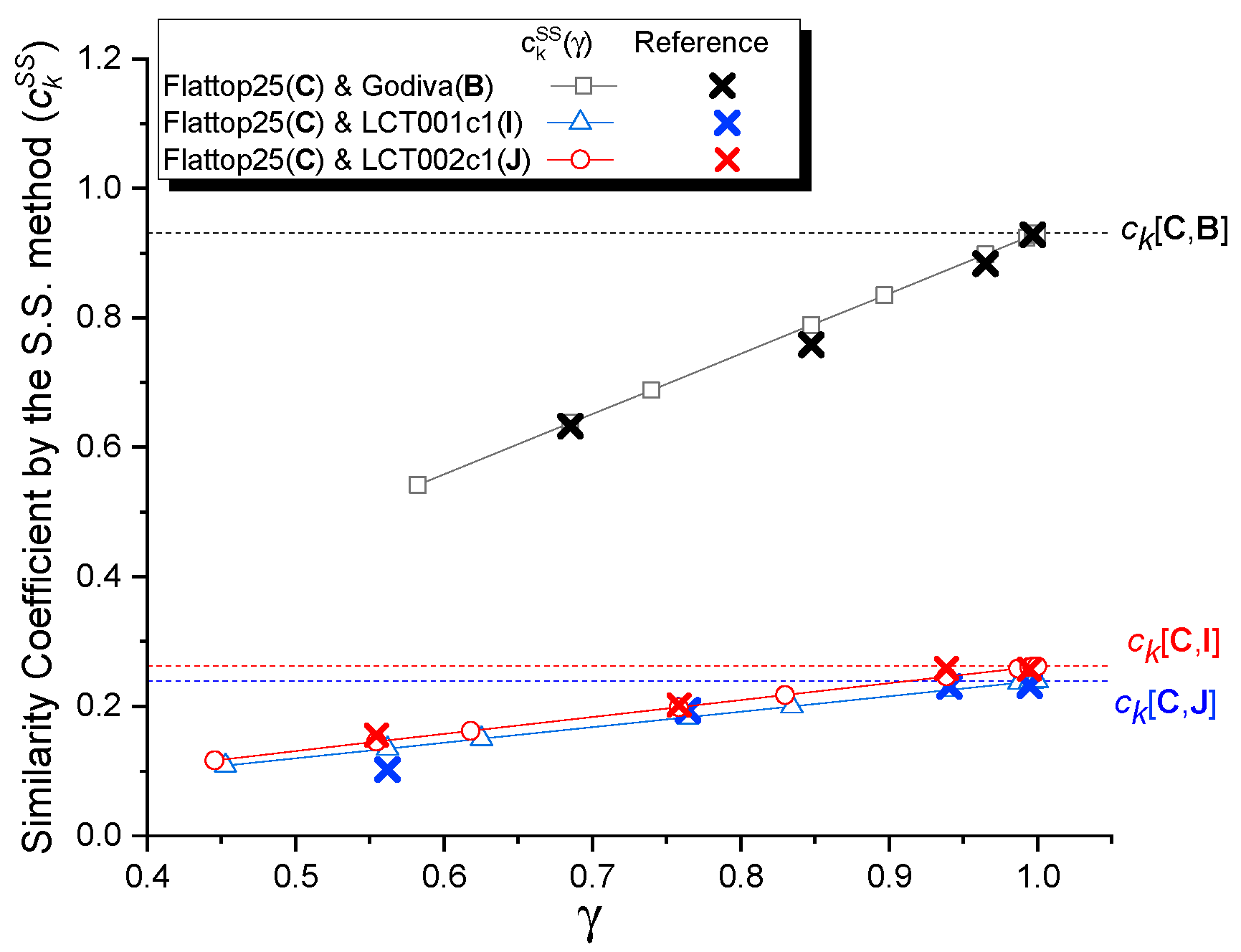
3.2. Impact on the S.S. Method-Based Similarity Coefficients from MC Statistical Uncertainties
3.3. Sensitivity of Similarity Coefficients due to Covariance Data
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CE | Critical experiment |
| ENDF | Evaluated nuclear data file |
| HEU | High-enriched uranium |
| ICSBEP | International Criticality Safety Benchmark Problem |
| JEFF | Joint Evaluated Fission and Fusion |
| JENDL | Japanese Evaluated Nuclear Data Library |
| LANL | Los Alamos National Laboratory |
| LEU | Low-enriched uranium |
| MC | Monte Carlo |
| McCARD | Monte Carlo Code for Advanced Reactor Design |
| MCNP | Monte Carlo N-Particle Transport |
| MIG | McCARD Input Generator |
| NCS | Nuclear criticality safety |
| NRC | Nuclear Regulatory Commission |
| SCALE | Standardized Computer Analysis for Licensing Evaluation |
| SMR | Small modular reactor |
| SMART | System-Integrated Modular Advanced Reactor |
| S.S. | Stochastic sampling |
| S/U | Sensitivity and uncertainty |
| TSUNAMI | Tools for Sensitivity and Uncertainty Analysis Methodology Implementation |
| USL | Upper subcritical limit |
References
- Dean, J.C.; Tayloe, R.W. Guide for Validation of Nuclear Criticality Safety Calculational Methodology; Division of Fuel Cycle Safety and Safeguards, Office of Nuclear Material Safety and Safeguards, US Nuclear Regulatory Commission: Washington, DC, USA, 2001.
- Broadhead, B.L.; Rearden, B.T.; Hopper, C.M.; Wagschal, J.J.; Parks, C.V. Sensitivity and Uncertainty-Based Criticality Safety Validation Techniques. Nucl. Sci. Eng. 2004, 146, 340–366. [Google Scholar] [CrossRef]
- Perfetti, C.M.; Rearden, B.T. Estimating Code Biases for Criticality Safety Applications with Few Relevant Benchmarks. Nucl. Sci. Eng. 2019, 193, 1090–1128. [Google Scholar] [CrossRef]
- Forrest, B.B.; Evan, R.M.; Louise, A.J. User Manual for Whisper-1.1; LA-UR-17-20567; Los Alamos National Laboratory: Los Alamos, NM, USA, 2017.
- Huang, D.; Mertyurek, U.; Abdel-Khalik, H. Verification of the sensitivity and uncertainty-based criticality safety validation techniques: ORNL’s SCALE case study. Nucl. Eng. Des. 2020, 361, 110571. [Google Scholar] [CrossRef]
- Shim, H.-J.; Han, B.-S.; Jung, J.-S.; Park, H.-J.; Kim, C.-H. McCARD: An Monte Carlo Code for Advanced Reactor Design and Analysis. Nucl. Eng. Technol. 2012, 44, 161–176. [Google Scholar] [CrossRef]
- Park, H.J. McCARD/MIG Stochastic Sampling Calculations for Nuclear Cross Section Sensitivity and Uncertainty Analysis. Nucl. Eng. Technol. 2022, 54, 4272–4279. [Google Scholar] [CrossRef]
- Park, H.J.; Cho, J.Y. Establishment of DeCART/MIG stochastic sampling code system and Application to UAM and BEAVRS benchmarks. Nucl. Eng. Technol. 2023, 55, 1563–1570. [Google Scholar] [CrossRef]
- International Handbook of Evaluated Criticality Safety Benchmark Experiments; OECD Nuclear Energy Agency Report NEA/NSC/COD(95)03; OECD Nuclear Energy Agency: Paris, France, 1998.
- Lee, K.H.; Park, S.Y.; Lee, C.C.; Cho, J.Y.; Song, J.S.; Zee, S.Q.; Kim, K.Y. The Nuclear Design Report for SMART Standard Design Cycle 1; KAERI/TR-4522/2012; Korea Atomic Energy Research Institute: Daejeon, Republic of Korea, 2012. [Google Scholar]
- Chadwick, M.; Herman, M.; Obložinský, P.; Dunn, M.; Danon, Y.; Kahler, A.; Smith, D.; Pritychenko, B.; Arbanas, G.; Arcilla, R.; et al. ENDF/B-VII.1 Nuclear Data for Science and Technology: Cross Sections, Covariances, Fission Product Yields and Decay Data. Nucl. Data Sheets 2011, 112, 2887–2996. [Google Scholar] [CrossRef]
- Brown, D.A.; Chadwick, M.B.; Capote, R.; Kahler, A.C.; Trkov, A.; Herman, M.W.; Sonzogni, A.A.; Danon, Y.; Carlson, A.D.; Dunn, M.; et al. ENDF/B-VIII.0: The 8th Major Release of the Nuclear Reaction Data Library with CIELO-project Cross Sections, New Standards and Thermal Scattering Data. Nucl. Data Sheets 2018, 148, 1–142. [Google Scholar] [CrossRef]
- Iwamoto, O.; Iwamoto, N.; Kunieda, S.; Minato, F.; Nakayama, S.; Abe, Y.; Tsubakihara, K.; Okumura, S.; Ishizuka, C.; Yoshida, T.; et al. Japanese evaluated nuclear data library version 5: JENDL-5. J. Nucl. Sci. Technol. 2023, 1, 1–60. [Google Scholar] [CrossRef]
- Plompen, A.J.M.; Cabellos, O.; Jean, C.D.S.; Fleming, M.; Algora, A.; Angelone, M.; Archier, P.; Bauge, E.; Bersillon, O.; Blokhin, A.; et al. The Joint Evaluated Fission and Fusion Nuclear Data Library, JEFF-3.3. Eur. Phys. J. A 2020, 56, 181. [Google Scholar] [CrossRef]
- Pearson, K. Notes on Regression and Inheritance in the Case of Two Parents. Proc. R. Soc. Lond. 1895, 58, 240. [Google Scholar]
- Park, H.J.; Shim, H.J.; Kim, C.H. Uncertainty Propagation in Monte Carlo Depletion Analysis. Nucl. Sci. Eng. 2011, 167, 196–208. [Google Scholar] [CrossRef]
- Wu, Q.; Peng, X.; Xu, F.; Shi, G.; Yu, Y.; Li, Q.; Wang, K. Generalized sensitivity analysis of responses to nuclear data in 2-D/1-D transport code KYADJ. Prog. Nucl. Energy. 2019, 113, 128–134. [Google Scholar] [CrossRef]
- Kim, M.H. Final Safety Analysis Report for AGN-201K; Kyung Hee University: Yongin, Republic of Korea, 2021. [Google Scholar]
- Justification for Minimum Margin of Subcriticality for Safety; FCSS ISG-10, Rev. 0; U.S. Nuclear Regulatory Commission, Office of Nuclear Material Safety and Safeguards, Division of Fuel Cycle Safety and Safeguards: Washington, DC, USA, 2006.
- Scale: A Comprehensive Modeling and Simulation Suite for Nuclear Safety Analysis and Design; ORNL/TM-2005/39, Version 6.1; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2011.
| ID | Short Name | Benchmark ID | Ref No. | Spectrum | 235U Enrichments (w/o) | Pin Pitch (cm) | Pellet Radius (cm) |
|---|---|---|---|---|---|---|---|
| A | SMART | [10] | Thermal | 2.82/4.88 | 1.26 | 0.4096 | |
| B | GODIVA | HEU-MET-FAST-001 | [9] | Fast | 94.0 | - | - |
| C | FLATTOP25 | HEU-MET-FAST-028 | Fast | 93.2 | - | - | |
| D | HMF-002c2 | HEU-MET-FAST-002 case2 | Fast | 97.6 | - | - | |
| E | HMF-004 | HEU-MET-FAST-004 | Fast | 97.7 | - | - | |
| F | HMF-018 | HEU-MET-FAST-018 | Fast | 90.0 | - | - | |
| G | HMF-027 | HEU-MET-FAST-027 | Fast | 90.0 | - | - | |
| H | HMF-032 | HEU-MET-FAST-032 | Fast | 93.5 | - | - | |
| I | LCT-001c1 | LEU-COMP-THERM-001 case1 | Thermal | 2.35 | 2.032 | 0.635 | |
| J | LCT-002c1 | LEU-COMP-THERM-002 case1 | Thermal | 4.31 | 2.54 | 0.6325 | |
| K | LCT-003c1 | LEU-COMP-THERM-003 case1 | Thermal | 2.35 | 1.684 | 0.5588 | |
| L | LCT-004c1 | LEU-COMP-THERM-004 case1 | Thermal | 4.31 | 1.892 | 0.6325 | |
| M | LCT-005c1 | LEU-COMP-THERM-005 case1 | Thermal | 4.31 | 2.398 | 0.6325 | |
| N | LCT-006c1 | LEU-COMP-THERM-006 case1 | Thermal | 1.5 | 1.849 | 0.625 | |
| O | LCT-010c9 | LEU-COMP-THERM-010 case9 | Thermal | 4.31 | 2.54 | 0.6325 | |
| P | LCT-017c13 | LEU-COMP-THERM-017case13 | Thermal | 2.35 | 2.032 | 0.5588 | |
| Q | LMT-007c1 | LEU-MET-THERM-007 case1 | Thermal | 4.95 | 1.30 | 0.38645 | |
| R | LMT-007c2 | LEU-MET-THERM-007 case2 | Thermal | 4.95 | 1.53 | 0.38645 | |
| S | ORNL1 | HEU-SOL-THERM-013 case1 | Thermal | 93.2 | - | - | |
| T | ORNL2 | HEU-SOL-THERM-013 case2 | Thermal | 93.2 | - | - | |
| U | ORNL3 | HEU-SOL-THERM-013 case3 | Thermal | 93.2 | - | - | |
| V | ORNL4 | HEU-SOL-THERM-013 case4 | Thermal | 93.2 | - | - | |
| W | ORNL10 | HEU-SOL-THERM-032 | Thermal | 93.2 | - | - | |
| X | AGN-201K | [18] | Thermal | 19.5 | - | - | |
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1.00 * | 0.32 | 0.34 | 0.32 | 0.40 | 0.34 | 0.33 | 0.32 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.98 | 0.99 | 0.99 | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 | 0.99 |
| B | 0.32 | 1.00 | 0.95 | 0.99 | 0.97 | 0.96 | 0.97 | 0.99 | 0.20 | 0.22 | 0.23 | 0.28 | 0.24 | 0.25 | 0.22 | 0.20 | 0.34 | 0.28 | 0.17 | 0.17 | 0.18 | 0.18 | 0.17 | 0.19 |
| C | 0.34 | 0.95 | 1.00 | 0.95 | 0.98 | 0.99 | 0.99 | 0.96 | 0.22 | 0.24 | 0.24 | 0.30 | 0.26 | 0.26 | 0.24 | 0.22 | 0.35 | 0.30 | 0.19 | 0.20 | 0.20 | 0.20 | 0.19 | 0.21 |
| D | 0.32 | 0.99 | 0.95 | 1.00 | 0.97 | 0.96 | 0.97 | 0.99 | 0.20 | 0.22 | 0.23 | 0.28 | 0.24 | 0.25 | 0.22 | 0.20 | 0.34 | 0.28 | 0.17 | 0.18 | 0.18 | 0.18 | 0.17 | 0.19 |
| E | 0.40 | 0.97 | 0.98 | 0.97 | 1.00 | 0.98 | 0.99 | 0.98 | 0.28 | 0.30 | 0.31 | 0.37 | 0.32 | 0.33 | 0.31 | 0.28 | 0.42 | 0.36 | 0.26 | 0.26 | 0.26 | 0.26 | 0.25 | 0.27 |
| F | 0.34 | 0.96 | 0.99 | 0.96 | 0.98 | 1.00 | 0.99 | 0.97 | 0.22 | 0.24 | 0.24 | 0.30 | 0.26 | 0.26 | 0.24 | 0.22 | 0.35 | 0.30 | 0.19 | 0.19 | 0.20 | 0.20 | 0.19 | 0.21 |
| G | 0.33 | 0.97 | 0.99 | 0.97 | 0.99 | 0.99 | 1.00 | 0.98 | 0.22 | 0.23 | 0.24 | 0.30 | 0.25 | 0.26 | 0.24 | 0.22 | 0.35 | 0.30 | 0.19 | 0.19 | 0.19 | 0.19 | 0.18 | 0.20 |
| H | 0.32 | 0.99 | 0.96 | 0.99 | 0.98 | 0.97 | 0.98 | 1.00 | 0.20 | 0.22 | 0.23 | 0.29 | 0.24 | 0.25 | 0.22 | 0.20 | 0.34 | 0.28 | 0.17 | 0.18 | 0.18 | 0.18 | 0.17 | 0.19 |
| I | 0.98 | 0.20 | 0.22 | 0.20 | 0.28 | 0.22 | 0.22 | 0.20 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| J | 0.98 | 0.22 | 0.24 | 0.22 | 0.30 | 0.24 | 0.23 | 0.22 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| K | 0.99 | 0.23 | 0.24 | 0.23 | 0.31 | 0.24 | 0.24 | 0.23 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| L | 0.99 | 0.28 | 0.30 | 0.28 | 0.37 | 0.30 | 0.30 | 0.29 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.99 |
| M | 0.99 | 0.24 | 0.26 | 0.24 | 0.32 | 0.26 | 0.25 | 0.24 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 |
| N | 0.99 | 0.25 | 0.26 | 0.25 | 0.33 | 0.26 | 0.26 | 0.25 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 |
| O | 0.98 | 0.22 | 0.24 | 0.22 | 0.31 | 0.24 | 0.24 | 0.22 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| P | 0.98 | 0.20 | 0.22 | 0.20 | 0.28 | 0.22 | 0.22 | 0.20 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| Q | 0.99 | 0.34 | 0.35 | 0.34 | 0.42 | 0.35 | 0.35 | 0.34 | 0.98 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 0.98 | 0.98 | 1.00 | 0.99 | 0.97 | 0.97 | 0.97 | 0.97 | 0.96 | 0.98 |
| R | 0.99 | 0.28 | 0.30 | 0.28 | 0.36 | 0.30 | 0.30 | 0.28 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.99 |
| S | 0.97 | 0.17 | 0.19 | 0.17 | 0.26 | 0.19 | 0.19 | 0.17 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.97 | 0.98 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| T | 0.97 | 0.17 | 0.20 | 0.18 | 0.26 | 0.19 | 0.19 | 0.18 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.97 | 0.98 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 |
| U | 0.97 | 0.18 | 0.20 | 0.18 | 0.26 | 0.20 | 0.19 | 0.18 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.97 | 0.98 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 |
| V | 0.97 | 0.18 | 0.20 | 0.18 | 0.26 | 0.20 | 0.19 | 0.18 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.97 | 0.98 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 |
| W | 0.97 | 0.17 | 0.19 | 0.17 | 0.25 | 0.19 | 0.18 | 0.17 | 0.99 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.99 | 0.99 | 0.96 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 |
| X | 0.99 | 0.19 | 0.21 | 0.19 | 0.27 | 0.21 | 0.20 | 0.19 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 |
| S.S. | Godiva (B *) | Flattop25 (C) | LCT001c1 (I) | LCT002c1 (J) | ORNL1 (S) | ORNL2 (T) |
|---|---|---|---|---|---|---|
| Adjoint S/U | ||||||
| Godiva (B) | 1.00 | 0.94 ± 0.01 ** | 0.19 ± 0.06 | 0.22 ± 0.06 | 0.20 ± 0.06 | 0.20 ± 0.06 |
| 0.95 | 0.20 | 0.22 | 0.17 | 0.18 | ||
| Flattop25 (C) | 0.94 ± 0.01 | 1.00 | 0.21 ± 0.06 | 0.24 ± 0.07 | 0.16 ± 0.07 | 0.17 ± 0.07 |
| 0.95 | 0.22 | 0.24 | 0.19 | 0.20 | ||
| LCT001c1 (I) | 0.19 ± 0.06 | 0.21 ± 0.06 | 1.00 | 0.99 ± 0.01 | 0.88 ± 0.01 | 0.88 ± 0.01 |
| 0.20 | 0.22 | 0.99 | 0.99 | 0.99 | ||
| LCT002c1 (J) | 0.22 ± 0.06 | 0.26 ± 0.08 | 0.99 ± 0.01 | 1.00 | 0.91 ± 0.02 | 0.91 ± 0.02 |
| 0.22 | 0.24 | 0.99 | 0.99 | 0.99 | ||
| ORNL1 (S) | 0.20 ± 0.06 | 0.26 ± 0.08 | 0.88 ± 0.01 | 0.91 ± 0.01 | 1.00 | 0.99 ± 0.01 |
| 0.17 | 0.19 | 0.99 | 0.99 | 0.99 | ||
| ORNL2 (T) | 0.20 ± 0.06 | 0.26 ± 0.08 | 0.88 ± 0.01 | 0.91 ± 0.01 | 0.99 ± 0.01 | 1.00 |
| 0.18 | 0.20 | 0.99 | 0.99 | 0.99 |
| Uncertainties of keff (pcm) | |||||
|---|---|---|---|---|---|
| Critical Experiment (ID *) | Godiva (B) | Flattop25 (C) | LCT001c1 (I) | LCT002c1 (J) | |
| 1266 | 1108 | 770 | 750 | ||
| 10,000 × 100 ** | 60 | 65 | 66 | 75 | |
| 10,000 × 10 | 225 | 233 | 225 | 262 | |
| 10,000 × 5 | 378 | 447 | 408 | 453 | |
| 1000 × 10 | 632 | 701 | 725 | 822 | |
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1.00 * | 0.59 | 0.57 | 0.58 | 0.70 | 0.57 | 0.59 | 0.60 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.97 | 0.97 | 0.97 | 0.97 | 0.96 | 0.98 |
| B | 0.59 | 1.00 | 0.95 | 0.99 | 0.97 | 0.96 | 0.97 | 0.99 | 0.54 | 0.53 | 0.55 | 0.54 | 0.53 | 0.54 | 0.53 | 0.55 | 0.55 | 0.53 | 0.56 | 0.56 | 0.56 | 0.56 | 0.57 | 0.54 |
| C | 0.57 | 0.95 | 1.00 | 0.95 | 0.97 | 0.99 | 0.99 | 0.96 | 0.54 | 0.51 | 0.54 | 0.51 | 0.51 | 0.53 | 0.52 | 0.55 | 0.51 | 0.50 | 0.58 | 0.58 | 0.58 | 0.58 | 0.60 | 0.54 |
| D | 0.58 | 0.99 | 0.95 | 1.00 | 0.97 | 0.95 | 0.97 | 0.99 | 0.54 | 0.52 | 0.54 | 0.54 | 0.52 | 0.54 | 0.53 | 0.54 | 0.55 | 0.53 | 0.55 | 0.55 | 0.55 | 0.55 | 0.56 | 0.53 |
| E | 0.70 | 0.97 | 0.97 | 0.97 | 1.00 | 0.97 | 0.98 | 0.98 | 0.67 | 0.64 | 0.66 | 0.64 | 0.63 | 0.65 | 0.65 | 0.67 | 0.64 | 0.63 | 0.71 | 0.71 | 0.71 | 0.71 | 0.72 | 0.67 |
| F | 0.57 | 0.96 | 0.99 | 0.95 | 0.97 | 1.00 | 0.99 | 0.97 | 0.54 | 0.51 | 0.54 | 0.51 | 0.51 | 0.53 | 0.52 | 0.55 | 0.52 | 0.50 | 0.58 | 0.58 | 0.58 | 0.58 | 0.60 | 0.54 |
| G | 0.59 | 0.97 | 0.99 | 0.97 | 0.98 | 0.99 | 1.00 | 0.98 | 0.56 | 0.53 | 0.55 | 0.53 | 0.52 | 0.54 | 0.54 | 0.56 | 0.53 | 0.52 | 0.60 | 0.60 | 0.60 | 0.60 | 0.61 | 0.56 |
| H | 0.60 | 0.99 | 0.96 | 0.99 | 0.98 | 0.97 | 0.98 | 1.00 | 0.55 | 0.53 | 0.56 | 0.55 | 0.53 | 0.55 | 0.54 | 0.56 | 0.56 | 0.54 | 0.58 | 0.58 | 0.58 | 0.58 | 0.59 | 0.55 |
| I | 0.98 | 0.54 | 0.54 | 0.54 | 0.67 | 0.54 | 0.56 | 0.55 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 |
| J | 0.99 | 0.53 | 0.51 | 0.52 | 0.64 | 0.51 | 0.53 | 0.53 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.98 | 0.97 | 0.99 |
| K | 0.99 | 0.55 | 0.54 | 0.54 | 0.66 | 0.54 | 0.55 | 0.56 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.99 |
| L | 0.99 | 0.54 | 0.51 | 0.54 | 0.64 | 0.51 | 0.53 | 0.55 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.97 | 0.97 | 0.97 | 0.97 | 0.96 | 0.98 |
| M | 0.99 | 0.53 | 0.51 | 0.52 | 0.63 | 0.51 | 0.52 | 0.53 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.97 | 0.97 | 0.98 | 0.98 | 0.97 | 0.99 |
| N | 0.99 | 0.54 | 0.53 | 0.54 | 0.65 | 0.53 | 0.54 | 0.55 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.98 | 0.97 | 0.99 |
| O | 0.99 | 0.53 | 0.52 | 0.53 | 0.65 | 0.52 | 0.54 | 0.54 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.98 | 0.97 | 0.99 |
| P | 0.98 | 0.55 | 0.55 | 0.54 | 0.67 | 0.55 | 0.56 | 0.56 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 |
| Q | 0.99 | 0.55 | 0.51 | 0.55 | 0.64 | 0.52 | 0.53 | 0.56 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 1.00 | 0.99 | 0.96 | 0.96 | 0.96 | 0.96 | 0.95 | 0.98 |
| R | 0.99 | 0.53 | 0.50 | 0.53 | 0.63 | 0.50 | 0.52 | 0.54 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.97 | 0.97 | 0.97 | 0.97 | 0.96 | 0.98 |
| S | 0.97 | 0.56 | 0.58 | 0.55 | 0.71 | 0.58 | 0.60 | 0.58 | 0.99 | 0.98 | 0.98 | 0.97 | 0.97 | 0.98 | 0.98 | 0.99 | 0.96 | 0.97 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| T | 0.97 | 0.56 | 0.58 | 0.55 | 0.71 | 0.58 | 0.60 | 0.58 | 0.99 | 0.98 | 0.98 | 0.97 | 0.97 | 0.98 | 0.98 | 0.99 | 0.96 | 0.97 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 |
| U | 0.97 | 0.56 | 0.58 | 0.55 | 0.71 | 0.58 | 0.60 | 0.58 | 0.99 | 0.98 | 0.98 | 0.97 | 0.98 | 0.98 | 0.98 | 0.99 | 0.96 | 0.97 | 0.99 | 0.99 | 1.00 | 1.00 | 0.99 | 0.99 |
| V | 0.97 | 0.56 | 0.58 | 0.55 | 0.71 | 0.58 | 0.60 | 0.58 | 0.99 | 0.98 | 0.98 | 0.97 | 0.98 | 0.98 | 0.98 | 0.99 | 0.96 | 0.97 | 0.99 | 0.99 | 1.00 | 1.00 | 0.99 | 0.99 |
| W | 0.96 | 0.57 | 0.60 | 0.56 | 0.72 | 0.60 | 0.61 | 0.59 | 0.98 | 0.97 | 0.98 | 0.96 | 0.97 | 0.97 | 0.97 | 0.98 | 0.95 | 0.96 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.98 |
| X | 0.98 | 0.54 | 0.54 | 0.53 | 0.67 | 0.54 | 0.56 | 0.55 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 1.00 |
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1.00 * | 0.11 | 0.03 | 0.11 | 0.09 | 0.03 | 0.03 | 0.10 | 0.92 | 0.90 | 0.91 | 0.81 | 0.85 | 0.89 | 0.91 | 0.94 | 0.73 | 0.77 | 0.83 | 0.83 | 0.83 | 0.83 | 0.82 | 0.89 |
| B | 0.11 | 1.00 | 0.44 | 0.99 | 0.39 | 0.46 | 0.49 | 0.91 | −0.08 | −0.10 | −0.10 | −0.17 | −0.15 | −0.12 | −0.09 | −0.06 | −0.20 | −0.18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.01 |
| C | 0.03 | 0.44 | 1.00 | 0.41 | 0.95 | 0.99 | 0.99 | 0.57 | 0.02 | 0.03 | 0.03 | 0.05 | 0.03 | 0.03 | 0.03 | 0.02 | 0.06 | 0.06 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| D | 0.11 | 0.99 | 0.41 | 1.00 | 0.36 | 0.43 | 0.46 | 0.86 | −0.10 | −0.13 | −0.13 | −0.22 | −0.19 | −0.15 | −0.11 | −0.08 | −0.26 | −0.24 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.02 |
| E | 0.09 | 0.39 | 0.95 | 0.36 | 1.00 | 0.94 | 0.95 | 0.51 | 0.08 | 0.09 | 0.08 | 0.09 | 0.09 | 0.08 | 0.09 | 0.08 | 0.09 | 0.10 | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | 0.08 |
| F | 0.03 | 0.46 | 0.99 | 0.43 | 0.94 | 1.00 | 0.99 | 0.59 | 0.02 | 0.03 | 0.03 | 0.05 | 0.04 | 0.04 | 0.03 | 0.02 | 0.07 | 0.07 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 |
| G | 0.03 | 0.49 | 0.99 | 0.46 | 0.95 | 0.99 | 1.00 | 0.62 | 0.02 | 0.03 | 0.03 | 0.05 | 0.04 | 0.04 | 0.03 | 0.02 | 0.07 | 0.07 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| H | 0.10 | 0.91 | 0.57 | 0.86 | 0.51 | 0.59 | 0.62 | 1.00 | 0.01 | 0.01 | 0.02 | 0.02 | 0.01 | 0.02 | 0.00 | 0.01 | 0.04 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| I | 0.92 | −0.08 | 0.02 | −0.10 | 0.08 | 0.02 | 0.02 | 0.01 | 1.00 | 0.98 | 0.98 | 0.94 | 0.97 | 0.97 | 0.98 | 0.99 | 0.88 | 0.91 | 0.86 | 0.87 | 0.87 | 0.87 | 0.86 | 0.92 |
| J | 0.90 | −0.10 | 0.03 | −0.13 | 0.09 | 0.03 | 0.03 | 0.01 | 0.98 | 1.00 | 0.97 | 0.96 | 0.98 | 0.97 | 0.99 | 0.97 | 0.91 | 0.95 | 0.87 | 0.87 | 0.87 | 0.87 | 0.86 | 0.93 |
| K | 0.91 | −0.10 | 0.03 | −0.13 | 0.08 | 0.03 | 0.03 | 0.02 | 0.98 | 0.97 | 1.00 | 0.96 | 0.97 | 0.99 | 0.97 | 0.98 | 0.92 | 0.94 | 0.79 | 0.79 | 0.79 | 0.79 | 0.78 | 0.86 |
| L | 0.81 | −0.17 | 0.05 | −0.22 | 0.09 | 0.05 | 0.05 | 0.02 | 0.94 | 0.96 | 0.96 | 1.00 | 0.99 | 0.98 | 0.94 | 0.92 | 0.98 | 0.99 | 0.73 | 0.73 | 0.73 | 0.73 | 0.71 | 0.81 |
| M | 0.85 | −0.15 | 0.03 | −0.19 | 0.09 | 0.04 | 0.04 | 0.01 | 0.97 | 0.98 | 0.97 | 0.99 | 1.00 | 0.98 | 0.97 | 0.95 | 0.96 | 0.98 | 0.81 | 0.81 | 0.81 | 0.81 | 0.80 | 0.88 |
| N | 0.89 | −0.12 | 0.03 | −0.15 | 0.08 | 0.04 | 0.04 | 0.02 | 0.97 | 0.97 | 0.99 | 0.98 | 0.98 | 1.00 | 0.96 | 0.96 | 0.94 | 0.96 | 0.76 | 0.76 | 0.76 | 0.76 | 0.75 | 0.84 |
| O | 0.91 | −0.09 | 0.03 | −0.11 | 0.09 | 0.03 | 0.03 | 0.00 | 0.98 | 0.99 | 0.97 | 0.94 | 0.97 | 0.96 | 1.00 | 0.98 | 0.89 | 0.93 | 0.89 | 0.89 | 0.89 | 0.89 | 0.88 | 0.94 |
| P | 0.94 | −0.06 | 0.02 | −0.08 | 0.08 | 0.02 | 0.02 | 0.01 | 0.99 | 0.97 | 0.98 | 0.92 | 0.95 | 0.96 | 0.98 | 1.00 | 0.85 | 0.89 | 0.88 | 0.88 | 0.88 | 0.88 | 0.87 | 0.93 |
| Q | 0.73 | −0.20 | 0.06 | −0.26 | 0.09 | 0.07 | 0.07 | 0.04 | 0.88 | 0.91 | 0.92 | 0.98 | 0.96 | 0.94 | 0.89 | 0.85 | 1.00 | 0.99 | 0.64 | 0.64 | 0.64 | 0.64 | 0.63 | 0.72 |
| R | 0.77 | −0.18 | 0.06 | −0.24 | 0.10 | 0.07 | 0.07 | 0.04 | 0.91 | 0.95 | 0.94 | 0.99 | 0.98 | 0.96 | 0.93 | 0.89 | 0.99 | 1.00 | 0.71 | 0.71 | 0.71 | 0.71 | 0.70 | 0.79 |
| S | 0.83 | 0.00 | 0.00 | 0.00 | 0.07 | 0.00 | 0.00 | 0.00 | 0.86 | 0.87 | 0.79 | 0.73 | 0.81 | 0.76 | 0.89 | 0.88 | 0.64 | 0.71 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 |
| T | 0.83 | 0.00 | 0.00 | 0.00 | 0.07 | 0.00 | 0.00 | 0.00 | 0.87 | 0.87 | 0.79 | 0.73 | 0.81 | 0.76 | 0.89 | 0.88 | 0.64 | 0.71 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.98 |
| U | 0.83 | 0.00 | 0.00 | 0.00 | 0.07 | 0.00 | 0.00 | 0.00 | 0.87 | 0.87 | 0.79 | 0.73 | 0.81 | 0.76 | 0.89 | 0.88 | 0.64 | 0.71 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.98 |
| V | 0.83 | 0.00 | 0.00 | 0.00 | 0.07 | 0.00 | 0.00 | 0.00 | 0.87 | 0.87 | 0.79 | 0.73 | 0.81 | 0.76 | 0.89 | 0.88 | 0.64 | 0.71 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.98 |
| W | 0.82 | 0.00 | 0.00 | 0.00 | 0.07 | 0.00 | 0.00 | 0.00 | 0.86 | 0.86 | 0.78 | 0.71 | 0.80 | 0.75 | 0.88 | 0.87 | 0.63 | 0.70 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.97 |
| X | 0.89 | −0.01 | 0.00 | −0.02 | 0.08 | 0.01 | 0.00 | 0.00 | 0.92 | 0.93 | 0.86 | 0.81 | 0.88 | 0.84 | 0.94 | 0.93 | 0.72 | 0.79 | 0.98 | 0.98 | 0.98 | 0.98 | 0.97 | 1.00 |
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1.00 * | 0.44 | 0.36 | 0.44 | 0.49 | 0.36 | 0.38 | 0.43 | 0.96 | 0.96 | 0.97 | 0.95 | 0.96 | 0.96 | 0.96 | 0.96 | 0.93 | 0.94 | 0.88 | 0.88 | 0.89 | 0.89 | 0.87 | 0.92 |
| B | 0.44 | 1.00 | 0.86 | 0.99 | 0.86 | 0.88 | 0.89 | 0.98 | 0.42 | 0.44 | 0.45 | 0.50 | 0.45 | 0.48 | 0.43 | 0.40 | 0.53 | 0.50 | 0.30 | 0.30 | 0.30 | 0.30 | 0.29 | 0.32 |
| C | 0.36 | 0.86 | 1.00 | 0.87 | 0.96 | 0.99 | 0.99 | 0.83 | 0.34 | 0.35 | 0.34 | 0.36 | 0.35 | 0.34 | 0.36 | 0.34 | 0.36 | 0.36 | 0.33 | 0.33 | 0.33 | 0.33 | 0.32 | 0.34 |
| D | 0.44 | 0.99 | 0.87 | 1.00 | 0.88 | 0.89 | 0.90 | 0.96 | 0.40 | 0.42 | 0.44 | 0.47 | 0.43 | 0.46 | 0.41 | 0.39 | 0.50 | 0.47 | 0.30 | 0.30 | 0.30 | 0.30 | 0.30 | 0.32 |
| E | 0.49 | 0.86 | 0.96 | 0.88 | 1.00 | 0.96 | 0.97 | 0.83 | 0.45 | 0.47 | 0.45 | 0.47 | 0.47 | 0.45 | 0.48 | 0.45 | 0.46 | 0.46 | 0.45 | 0.45 | 0.45 | 0.45 | 0.44 | 0.47 |
| F | 0.36 | 0.88 | 0.99 | 0.89 | 0.96 | 1.00 | 0.99 | 0.85 | 0.34 | 0.36 | 0.35 | 0.37 | 0.36 | 0.35 | 0.36 | 0.34 | 0.38 | 0.37 | 0.32 | 0.32 | 0.32 | 0.33 | 0.32 | 0.34 |
| G | 0.38 | 0.89 | 0.99 | 0.90 | 0.97 | 0.99 | 1.00 | 0.86 | 0.36 | 0.37 | 0.36 | 0.38 | 0.37 | 0.36 | 0.37 | 0.35 | 0.39 | 0.38 | 0.34 | 0.34 | 0.34 | 0.34 | 0.33 | 0.35 |
| H | 0.43 | 0.98 | 0.83 | 0.96 | 0.83 | 0.85 | 0.86 | 1.00 | 0.43 | 0.46 | 0.47 | 0.52 | 0.47 | 0.50 | 0.44 | 0.41 | 0.57 | 0.54 | 0.29 | 0.29 | 0.29 | 0.29 | 0.29 | 0.32 |
| I | 0.96 | 0.42 | 0.34 | 0.40 | 0.45 | 0.34 | 0.36 | 0.43 | 1.00 | 0.99 | 0.99 | 0.97 | 0.98 | 0.98 | 0.99 | 0.99 | 0.94 | 0.96 | 0.93 | 0.93 | 0.93 | 0.93 | 0.92 | 0.95 |
| J | 0.96 | 0.44 | 0.35 | 0.42 | 0.47 | 0.36 | 0.37 | 0.46 | 0.99 | 1.00 | 0.98 | 0.98 | 0.99 | 0.98 | 0.99 | 0.98 | 0.96 | 0.98 | 0.92 | 0.92 | 0.92 | 0.92 | 0.91 | 0.95 |
| K | 0.97 | 0.45 | 0.34 | 0.44 | 0.45 | 0.35 | 0.36 | 0.47 | 0.99 | 0.98 | 1.00 | 0.98 | 0.99 | 0.99 | 0.98 | 0.98 | 0.96 | 0.98 | 0.88 | 0.88 | 0.89 | 0.89 | 0.87 | 0.92 |
| L | 0.95 | 0.50 | 0.36 | 0.47 | 0.47 | 0.37 | 0.38 | 0.52 | 0.97 | 0.98 | 0.98 | 1.00 | 0.99 | 0.99 | 0.97 | 0.96 | 0.99 | 0.99 | 0.85 | 0.85 | 0.85 | 0.85 | 0.83 | 0.89 |
| M | 0.96 | 0.45 | 0.35 | 0.43 | 0.47 | 0.36 | 0.37 | 0.47 | 0.98 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.98 | 0.97 | 0.98 | 0.90 | 0.90 | 0.90 | 0.90 | 0.89 | 0.94 |
| N | 0.96 | 0.48 | 0.34 | 0.46 | 0.45 | 0.35 | 0.36 | 0.50 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 1.00 | 0.98 | 0.97 | 0.98 | 0.98 | 0.86 | 0.86 | 0.86 | 0.86 | 0.85 | 0.90 |
| O | 0.96 | 0.43 | 0.36 | 0.41 | 0.48 | 0.36 | 0.37 | 0.44 | 0.99 | 0.99 | 0.98 | 0.97 | 0.99 | 0.98 | 1.00 | 0.99 | 0.95 | 0.97 | 0.93 | 0.93 | 0.93 | 0.93 | 0.92 | 0.96 |
| P | 0.96 | 0.40 | 0.34 | 0.39 | 0.45 | 0.34 | 0.35 | 0.41 | 0.99 | 0.98 | 0.98 | 0.96 | 0.98 | 0.97 | 0.99 | 1.00 | 0.93 | 0.95 | 0.94 | 0.94 | 0.94 | 0.94 | 0.93 | 0.96 |
| Q | 0.93 | 0.53 | 0.36 | 0.50 | 0.46 | 0.38 | 0.39 | 0.57 | 0.94 | 0.96 | 0.96 | 0.99 | 0.97 | 0.98 | 0.95 | 0.93 | 1.00 | 0.99 | 0.80 | 0.80 | 0.80 | 0.80 | 0.78 | 0.84 |
| R | 0.94 | 0.50 | 0.36 | 0.47 | 0.46 | 0.37 | 0.38 | 0.54 | 0.96 | 0.98 | 0.98 | 0.99 | 0.98 | 0.98 | 0.97 | 0.95 | 0.99 | 1.00 | 0.84 | 0.84 | 0.84 | 0.84 | 0.83 | 0.88 |
| S | 0.88 | 0.30 | 0.33 | 0.30 | 0.45 | 0.32 | 0.34 | 0.29 | 0.93 | 0.92 | 0.88 | 0.85 | 0.90 | 0.86 | 0.93 | 0.94 | 0.80 | 0.84 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| T | 0.88 | 0.30 | 0.33 | 0.30 | 0.45 | 0.32 | 0.34 | 0.29 | 0.93 | 0.92 | 0.88 | 0.85 | 0.90 | 0.86 | 0.93 | 0.94 | 0.80 | 0.84 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 |
| U | 0.89 | 0.30 | 0.33 | 0.30 | 0.45 | 0.32 | 0.34 | 0.29 | 0.93 | 0.92 | 0.89 | 0.85 | 0.90 | 0.86 | 0.93 | 0.94 | 0.80 | 0.84 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 |
| V | 0.89 | 0.30 | 0.33 | 0.30 | 0.45 | 0.33 | 0.34 | 0.29 | 0.93 | 0.92 | 0.89 | 0.85 | 0.90 | 0.86 | 0.93 | 0.94 | 0.80 | 0.84 | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 |
| W | 0.87 | 0.29 | 0.32 | 0.30 | 0.44 | 0.32 | 0.33 | 0.29 | 0.92 | 0.91 | 0.87 | 0.83 | 0.89 | 0.85 | 0.92 | 0.93 | 0.78 | 0.83 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 0.98 |
| X | 0.92 | 0.32 | 0.34 | 0.32 | 0.47 | 0.34 | 0.35 | 0.32 | 0.95 | 0.95 | 0.92 | 0.89 | 0.94 | 0.90 | 0.96 | 0.96 | 0.84 | 0.88 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 1.00 |
| Covariance | A | B | C | E | I | J | K | L | M | Q | R | W | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ENDF/B-VII.1 | A | 1.00 | 0.33 | 0.34 | 0.41 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.97 | 0.99 |
| ENDF/B-VIII.0 | 1.00 | 0.60 | 0.57 | 0.70 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.97 | 0.99 | |
| JENDL-5.0 | 1.00 | 0.11 | 0.03 | 0.10 | 0.93 | 0.90 | 0.92 | 0.82 | 0.85 | 0.74 | 0.78 | 0.83 | 0.89 | |
| JEFF-3.3 | 1.00 | 0.45 | 0.37 | 0.49 | 0.96 | 0.96 | 0.97 | 0.96 | 0.96 | 0.94 | 0.94 | 0.88 | 0.93 | |
| SCALE 6.1 | 1.00 | 0.23 | 0.19 | 0.23 | 0.85 | 0.74 | 0.82 | 0.68 | 0.71 | 0.58 | 0.57 | 0.75 | 0.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, H.J.; Park, J.W. Similarity Coefficient Generation Using Adjoint-Based Sensitivity and Uncertainty Method and Stochastic Sampling Method. Energies 2024, 17, 827. https://doi.org/10.3390/en17040827
Park HJ, Park JW. Similarity Coefficient Generation Using Adjoint-Based Sensitivity and Uncertainty Method and Stochastic Sampling Method. Energies. 2024; 17(4):827. https://doi.org/10.3390/en17040827
Chicago/Turabian StylePark, Ho Jin, and Jeong Woo Park. 2024. "Similarity Coefficient Generation Using Adjoint-Based Sensitivity and Uncertainty Method and Stochastic Sampling Method" Energies 17, no. 4: 827. https://doi.org/10.3390/en17040827
APA StylePark, H. J., & Park, J. W. (2024). Similarity Coefficient Generation Using Adjoint-Based Sensitivity and Uncertainty Method and Stochastic Sampling Method. Energies, 17(4), 827. https://doi.org/10.3390/en17040827






