Abstract
With the rapid advancement of battery technology, the energy density and power density of lithium-ion batteries (LIBs) as a key component of electric vehicles have been increasing. However, accidents triggered by the thermal runaway of LIBs have been occurring frequently. Therefore, to address this issue, it is imperative to investigate the TR characteristics of the battery under various conditions. This study investigates the TR characteristics of ternary pouch LIBs induced by surface heating, using techniques such as voltage and temperature acquisition, as well as video imaging. The experimental results are analyzed to elucidate the venting and combustion characteristics of the cells. Furthermore, in order to provide a more comprehensive elucidation of the TR behavior of the battery, a corresponding 3D model for surface-induced TR was constructed. The simulation results of this model are in good agreement with the experimental results and effectively capture the TR characteristics of the cells under surface heating. Finally, the simulation results showed that the cells are more prone to venting from the side due to the lower melting point of the polypropylene (PP) adhesive used for cell sealing. The use of high-temperature-resistant sealing adhesives is crucial in preventing uncontrolled lateral venting of the cells.
1. Introduction
To address the energy crisis and the greenhouse gas effect, global transportation is gradually transitioning towards electrification of vehicles. As a result, the traditional car, an essential mode of transportation, is being replaced by EVs. With the rapid popularization of EVs and the continuous improvement of power battery energy density, fire incidents in EVs are becoming increasingly common. These incidents not only endanger the safety of EV users, but also significantly impede the development of EVs. The main cause of these accidents is the TR of the power battery. To address power battery TR, it is essential to gain a deep understanding of its underlying mechanisms. TR is primarily caused by mechanical abuse, electrical abuse, and thermal abuse. Mechanical abuse can alter the internal structure of the battery, leading to separator rupture and causing internal short-circuit (ISC), ultimately resulting in TR of the battery [1,2,3]. Electrical abuse can lead to a series of adverse effects, such as the growth of Cu dendrites inside batteries, ultimately resulting in TR [4,5,6,7]. Generally, both mechanical and electrical abuses can lead to thermal abuse of the battery. Thermal abuse causes an abnormal increase in battery temperature [8,9]. When the temperature of the battery reaches a certain value, a series of exothermic side reactions inside the battery are triggered. The occurrence of the exothermic side reactions will further increase the temperature of the battery, ultimately resulting in TR [10,11,12]. In most cases, the TR process involves combustion and explosion, which has drawn significant attention from the industry. In recent years, numerous scholars have investigated the TR properties of LIBs through experimental and modeling approaches. Tang et al. [13] categorized the TR of the battery into five main stages based on characteristic temperatures observed during the TR process: start of self-heating, venting of flammable gases, volatilization of electrolyte, melt of separator, and massive ISC. They also developed a TR model incorporating five side reactions (SEI decomposition, anode-electrolyte reaction, separator melt, cathode decomposition, and electrolyte decomposition) to predict the TR behavior of the battery. Zhao et al. [14] also established a TR model incorporating five subsidiary reactions, albeit without considering the melting of the diaphragm, but instead focusing on adhesive reactions. Feng et al. [15], drawing from hundreds of accelerating rate calorimeter (ARC) experimental data, identified three characteristic temperatures (T1, T2, and T3) associated with the TR process. T1 signifies the onset of self-heating in the battery, serving as a measure of the battery’s thermal stability; a higher T1 indicates greater thermal stability. T2 represents the triggering temperature of the battery TR, signifying the critical point where temperature escalation becomes pronounced. T3 corresponds to the maximum temperature reached by the battery during the TR process, reflecting the total heat released during TR. Wang et al. [16] conducted a study on the combustion behavior of lithium iron phosphate (LFP) batteries using external radiant heating. They observed that the battery undergoes several stages once its temperature reaches 126.7 °C: venting of flammable gases, ignition, first flaming stage, stable combustion stage, second and third flaming stages, ultimate stable combustion stage, and extinguishment. While they performed a detailed analysis of the combustion behavior, they did not establish a corresponding model. Jin et al. [17] investigated the impact of heating power and heating area on the TR of batteries. They observed a positive correlation between higher heating power and increased peak temperatures during the TR process. Furthermore, they noted that, under constant heating power, a smaller heating area was associated with a shorter time to trigger TR. Additionally, the researchers developed a corresponding TR model and provided a quantitative description of the TR mechanism based on model simulations. Feng et al. [18] introduced a graphical approach encompassing all critical physical and chemical processes occurring during battery TR to elucidate the underlying mechanisms. They experimentally validated the effectiveness of this method using two battery samples. This graphical approach provides an intuitive means to explain the underlying mechanisms during battery TR processes.
Scholars have delineated the TR of batteries into several principal stages based on characteristic temperatures or behaviors exhibited by the batteries during the TR process in order to explain the phenomenon of TR in batteries. However, numerous studies have overlooked the TR characteristics of batteries under actual operating conditions. Under such conditions, batteries are subjected to a certain pre-tension force. The application of this force results in inadequate expansion space for the batteries, leading to higher internal pressures when the batteries undergo expansion during TR due to the limited expansion space available. As the internal pressure within the batteries increases, so does the temperature, with the resulting consequence being the premature venting or ignition of the batteries. Furthermore, under actual conditions, if a single battery within a battery pack undergoes TR, the surrounding batteries will be subject to the elevated temperatures emanating from it, creating a scenario akin to surface heating. Hence, it is imperative to study the thermal runaway characteristics induced by surface heating of the battery under actual operating conditions. In this investigation, the TR characteristics of ternary pouch LIBs were explored under realistic grouping conditions, using surface-induced heating. Initially, the entire thermal runaway process was documented through voltage and temperature acquisition, as well as video imaging techniques, followed by an analysis of the battery’s combustion and temperature characteristics. A corresponding 3D surface-induced TR model was then established and validated for accuracy using experimental data. Ultimately, the simulation results were employed to explain the combustion jetting behavior of the battery.
2. Experiment
2.1. Fixture Design
In order to secure the battery during the TR process caused by surface heating, a special battery fixture was developed. As shown in Figure 1, the battery splints are 15 mm stainless steel, positioned with M16 studs, and locked with double M16 nuts both above and below. On the one hand, this design aims to simulate the thermal response of the battery in a real-world scenario (with limited space for expansion, close to other batteries), and on the other hand, to prevent the thermocouple and heating sheet from falling off because of the battery eruption or bulge during the experiment.
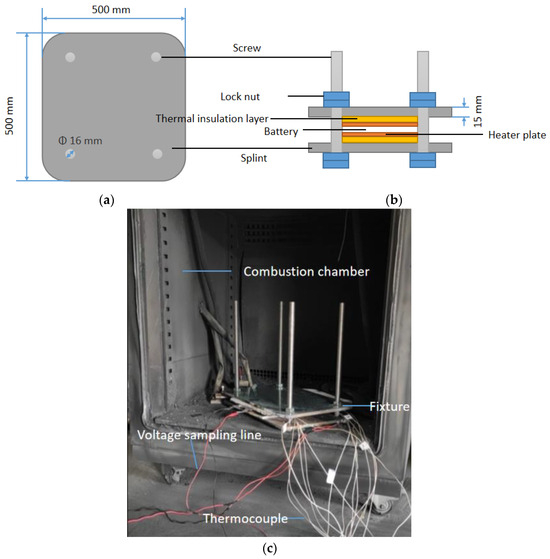
Figure 1.
Fixture design. (a) Top view of the battery fixture, (b) side view of the battery fixture, and (c) the fixture diagram.
2.2. Experimental Setup
The battery parameters for testing are shown in Table 1. Prior to the experiment, the battery is fully charged to 100% SOC. The thermocouple arrangement, as depicted in Figure 2, involves placing thermocouples No. 1–3 on the front surface of the battery and thermocouples No. 4–6 on the back surface of the battery to collect surface temperature data during the experiment. The red point No. 7 serves as the monitoring point for the simulated central temperature inside the battery, while red points No. 8 and No. 9, respectively, serve as the temperature monitoring points for the left side and top center of the battery. For the convenience of subsequent observation and analysis, the positive electrode side of the battery is defined as end A, the negative electrode side as end B, the tab side as end C, and the bottom of the battery as end D, as shown in Figure 2. Subsequently, the battery is placed in the fixture, with a layer of the asbestos board added to both the top and bottom of the battery as a heat-insulating layer. Then, the upper clamp plate is placed and secured with double nuts. Finally, the fixture is placed in a combustion chamber and the TR is triggered by activating heater plate 1 and heater plate 2. The heating power is set to 50 W, and the sampling frequency of temperature and voltage is set to 1 Hz. When the temperature of the battery reaches 170 °C (the onset temperature of TR), the battery is considered to have entered the TR state, at which point the heater plates stop heating.

Table 1.
Battery parameters.
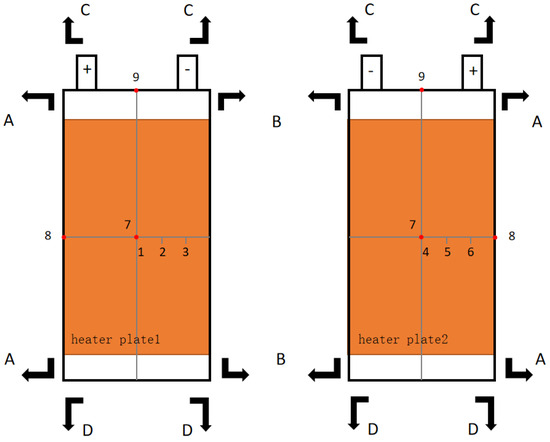
Figure 2.
Heater plate and thermocouple layout.
2.3. Experimental Results and Analysis
2.3.1. Combustion Behavior
The combustion behavior of the fully charged battery was recorded by video imaging, voltage monitoring, and temperature monitoring. Figure 3 shows the evolution of the TR process. The relationship between temperature and voltage vs. time ((T-V)-t) in the TR process is shown in Figure 4.

Figure 3.
Bilateral heating induces TR combustion behavior. (a) Start 00of the experiment. (b) End A is emitting smoke. (c) Smoke is emanating from end B. (d) Sparks are emanating from end B. (e) Flames are jetting from end B. (f) Jet emanates from end C. (g) Sparks are emanating from end A. (h) Combustion occurring at end C. (i) The emission of flames from end A. (j) Intense combustion occurs at end C. (k) The flame at end B reaches its maximum intensity. (l) The flame is extinguished.
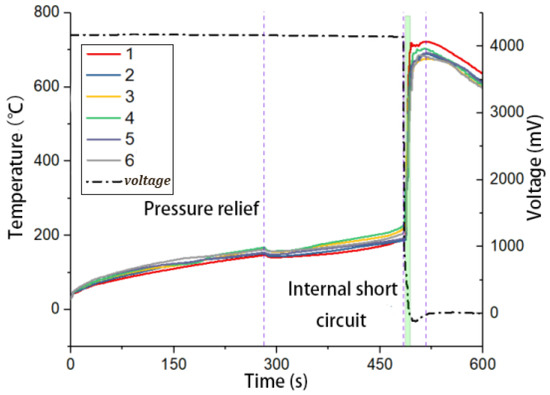
Figure 4.
Temperature and voltage curve in the process of TR induced by bilateral heating.
Figure 3a shows the initial state of the battery before the test started. At 281.051 s (Figure 3b), white smoke was released from end A of the battery. At this time, the increase in internal pressure caused the edge of the aluminum-plastic film shell of the battery to break, resulting in battery pressure relief. Subsequently, at 287.505 s (Figure 3c), the white smoke began to release from end B. During this process, the white smoke slowly wafted out and sank, which is because the mixture produced at this moment was denser than the air. At 485.011 s, a spark sputtering erupted from the crevasse at end B (Figure 3d), followed by a deflagration at 485.075 s (Figure 3e), resulting in a jet-shaped flame. The combustible gas at end D was then ignited, producing a flame that was immediately extinguished (Figure 3f). As a result of combustion, the gas produced inside the battery expanded violently, and almost simultaneously, end C (electrode side) broke and erupted, emitting a large amount of white smoke, while the leaked smoke at end A changed from a slight leak to a jet like emission (Figure 3g). At 486.651 s, deflagration occurred at end C, and the flame showed a tendency to gradually intensify (Figure 3h). At 487.346 s, combustible gas at end A erupted and was ignited by a spark, resulting in a jet-like flame emission. (Figure 3i). At 487.617 s, end C displayed a jet eruption and combustion with the highest intensity, and then showed a weakening trend (Figure 3j). At 490.922 s, the flame at end B reached its peak intensity. The bending of the flame shown in Figure 3k was caused by the obstruction of the side wall of the combustion chamber. The combustion continued for the rest of the time, but gradually weakened, and extinguished at 527.080 s (Figure 3l).
For this pouch battery, the aluminum-plastic film package was damaged at a relatively low temperature, and mild pressure relief began at 285.051 s, lasting for nearly 200 s before the spark jet erupted from end B. There was only a 0.064s interval from the occurrence of spark splashing at end B to the deflagration of combustible gas. The time interval from the occurrence of spark sputtering at end A to the deflagration at end A was 1.073 s. The duration from the occurrence of spark sputtering at end B to the complete extinguishment of the flame was 42.069 s. TR was a violent and short process, with its complex combustion mainly concentrated between 485 and 490 s. This interval is marked by green color blocks in Figure 4. The experimental battery experienced a total of three jet spouts. The pressure relief jet went through the process of A-B-C, the spark sputtering sequence was B-A, and the combustion went through the process of B-C-A-D. No obvious spark sputtering behavior was observed at end C.
2.3.2. Temperature and Voltage Characteristics
Figure 4 shows the (T-V)-t curve during the TR process. When the battery was heated by the heater plate, the heat was transferred from the surface to the inside of the battery, causing a chemical reaction in the material inside the battery, and eventually causing TR. The temperature data measured by the thermocouple attached to the battery surface showed a good temperature consistency during the heating stage. At 281 s, the battery temperature plummeted, which was caused by the damage of the battery aluminum-plastic film sealing edge, leading to pressure relief and heat dissipation (Figure 3b); white smoke was emitted from end A of the battery. The highest temperature recorded at this moment was at No. 3 (163.5 °C), while the lowest temperature appeared at No. 1 (146.7 °C), resulting in a temperature difference of 16.8 °C, with an average of 157.5 °C for the six thermocouples. The temperature difference during this stage was due to heat transfer caused by surface heating. The voltage dropped drastically, caused by massive ISC at 483 s, reaching its minimum value within 9 s. At this time, the highest temperature was recorded at thermocouple No. 4 (226.3 °C), while the lowest temperature was recorded by thermocouple No. 2 (186.4 °C), resulting in a temperature difference of 39.9 °C, with an average temperature of 203.1 °C for the six thermocouples. There was a time difference of 6 s from the occurrence of massive ISC to the inflection point of temperature. At 517 s, the temperature reached its peak, with No. 1 recording a temperature of 722.2 °C and No. 3 recording a temperature of 674.8 °C. The temperature difference was 47.4 °C, and the average temperature was 693.5 °C.
The experimental data and phenomena showed that the TR triggered by the surface heat source of the battery is similar to the adiabatic TR process [13]. As the temperature increases, the decomposition of the SEI on the negative electrode surface occurs, and a large amount of flammable and explosive gas is generated by the reaction between the negative electrode and the electrolyte, causing an increase in the internal pressure of the battery [14]. When the aluminum-plastic envelope cannot withstand the increased internal pressure of the battery, the battery will vent. The results showed that the venting temperature of the aluminum-plastic film battery was relatively low. The weakness of the battery casing lies in the sealing edge of the aluminum-plastic film, where venting occurs at the edge of the battery. The cell depressurizes in a relatively mild and stable manner. As the temperature continues to rise, the electrolyte will evaporate and overflow through the breach [13]. During the test, the erupting flammable and explosive gases served as the fuel, the oxygen provided by the external environment served as the oxidizer, and the splashing sparks served as the ignition source. The ignition of the battery followed the process of gas leakage, spark splashing, and flame jetting. The time interval from spark splashing to deflagration varied from 0.064 s to 2.306 s.
With the increase in temperature, the side reaction was intensified, and the whole combustion process lasted about 40 s. The pouch cell lacked a dedicated venting channel, leading to uncertainty during the venting process. There was a strong correlation between eruption and spark splashing, with eruptions often occurring after spark splashing. The pouch cell’s structure provided ample space for internal expansion, and the relatively low venting temperature may have partially slowed down the occurrence of TR. However, the disorderliness of eruptive combustion poses challenges for the design of TR protection.
3. Analysis of TR Model Triggered by Surface Heating
In this section, a 3D TR model for LIBs under surface heating triggering conditions is established based on the reaction kinetics parameters obtained from Ref. [13].
3.1. Thermal Model
The temperature of the battery can be calculated using Equation (1).
T0 represents the initial temperature of the battery. The control equation is as depicted in Equation (2),
where Q represents the heat generation rate, M denotes the mass of the battery, and Cp signifies the specific heat capacity of the battery. As depicted in Equation (3), Q is further composed of the side reaction heat generation rate Qchem, the electrical energy release rate QE, and the heat transfer rate, denoted as Φht [13,14,19].
3.1.1. Side Reaction
The heat generation rate Qchem from side reactions can be calculated using Equation (4) [20,21,22],
where QSEI represents the heat generation rate of SEI decomposition, Qanode denotes the heat generation rate of the anode reacting with the electrolyte, Qseparator stands for the heat generation rate of the separator melting, Qelectrolyte signifies the heat generation rate of the electrolyte oxidation, and Qcathode indicates the heat generation rate of the cathode decomposition.
The various side reactions mentioned above can all be described using the Arrhenius equation as shown in Equation (5), where Ax represents the frequency factor, Ea,x denotes the activation energy, R is the ideal gas constant, gx(t) is the correction term of reaction, and Tonset,x is the reaction onset temperature. The values of the above parameters are depicted in Table 2. The heat generation rate of the side reactions can be calculated using Equation (6), where X can represent the SEI, anode, electrolyte, cathode, separator, and so on [23,24].

Table 2.
The values of parameters for each reaction.
SEI decomposition: The heat generation rate QSEI of the SEI decomposition reaction is calculated using Equation (7), and dcSEI(t)/dt can be obtained from Equation (8), where the calculation method of cSEI in Equation (8) is shown as Equation (9), and cSEI,0 represents the initial value of cSEI.
Anode reaction with electrolyte: The calculation formula for the heat generation rate Qanode of the anode reaction with the electrolyte is given by Equation (10).
The melt of the separator: The calculation of the heat generation rate for the separator melting reaction is shown in Equation (11). It is important to note that the melting of the diaphragm is an endothermic process and thus, its heat generation rate is negative.
Cathode decomposition: Considering that NCM will undergo a phase transition during the TR process, the heat generation rate of the cathode decomposition reaction is calculated using Equations (14) and (15).
Electrolyte decomposition: The heat generation rate Qelectrolyte of the electrolyte decomposition reaction is calculated using Equation (18).
3.1.2. Electrical Energy Release
ΔEele denotes the total electrical energy released during a massive ISC, Δt represents the occurrence time of the massive ISC, and Qele signifies the total electrical energy release rate of the short circuit. Vbat stands for the volume of the battery, while cele denotes the normalized concentration of the released electrical energy, with an initial value of 1 and a final value of 0 and dcele/dt set as a constant of 12 s−1. According to Ref. [13], it is known that the duration of the massive ISC is 10 s, and the released electrical energy amounts to 19,440 J [25,26].
3.1.3. The Rate of Heat Transfer
In order to simplify the model, the battery is considered as a homogeneous entity in this study, with the homogenization treatment of the battery material’s density ρ, specific heat capacity Cp, and thermal conductivity λ. The equation for energy conservation within the battery is expressed as follows [13]:
where ∆E represents the battery’s internal energy change rate, Qgen represents the battery heat generation power, and Φht represents the heat transfer power [27,28].
Cp represents the specific heat capacity of the battery, ρ represents the density of the battery, dT/dt stands for temperature rise rate, Qchem represents the unit volume heat production power of the side reaction inside the battery, Qele is the ISC energy release rate, and λ represents the thermal conductivity of the battery in each direction [29,30].
3.2. The Simplification and Configuration of the Model
The surface heating-induced TR model is simulated using the COMSOL Multiphysics 5.5 software.
Based on experimental analysis, the model makes the following assumptions and simplifications:
- The battery is simplified as a homogeneous body.
- The thermal physical properties inside the battery do not change with temperature.
- The model does not consider the influence of active substances and smoke ejection on battery temperature during TR processes.
- The insulating surfaces wrapped with asbestos on the top and bottom of the battery are considered to have no heat exchange.
The physical parameters of the battery required for modeling are as indicated in Table 3.

Table 3.
The physical parameters of the battery.
The battery is simplified as a regular cuboid, and a structured mesh is used to divide the battery into grid cells. The boundary settings are shown in Figure 5, with the blue areas representing the heating surfaces, divided into heating surface 1 (top) and heating surface 2 (bottom), with a heating power of 50 W. Ends A, B, C, and D are the heat exchange surfaces for convective heat transfer with the surrounding air, while the top and bottom surfaces are set as adiabatic surfaces. An average convective heat transfer coefficient of 7 W/(m2 K) was adopted from Refs. [14,22].

Figure 5.
Grid division of the heating-induced TR model.
3.3. Analysis of the Simulation Results
The comparison between the simulated and experimental temperature curves at positions 1, 3, 4, and 6 is shown in Figure 6a–d. The simulation results indicate an inflection point at around 170 °C, primarily due to the heater plate reaching the final temperature of 170 °C, and the subsequent temperature rise was caused by exothermic reactions. On the other hand, the measured curve exhibited an inflection point near 280 °C, mainly attributed to the venting and ejection phenomenon during the test, which removed some of the heat. Before the temperature surge, the simulation data aligned closely with the experimental data. The maximum temperature difference occurred at position 1, with an error of 30 °C, while the errors at the other temperature measurement points were within 15 °C for both the model and the measurements. Discrepancies between simulation and measurement occurred near the peak temperature, with the maximum temperature errors detailed in the Table 4 below:
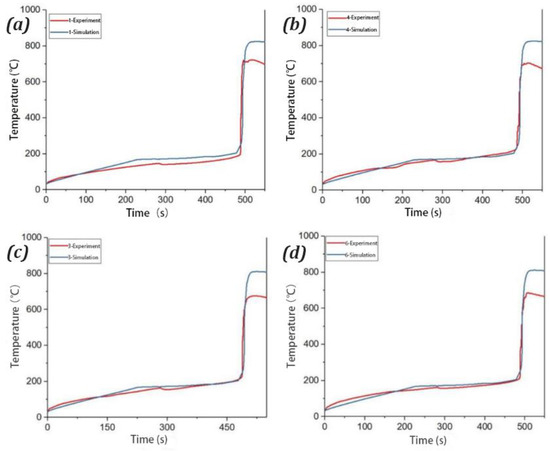
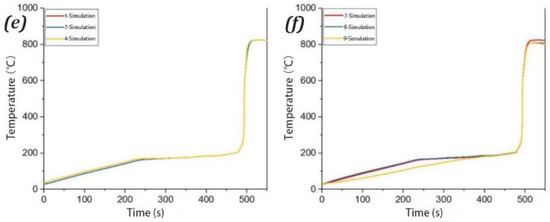
Figure 6.
Comparison of simulation and experimental results for TR caused by surface heating. (a) Comparison of experiment and simulation at point No. 1. (b) Comparison of experiment and simulation at point No. 4. (c) Comparison of experiment and simulation at point No. 3. (d) Comparison of experiment and simulation at point No. 6. (e) Comparison of simulation results at points No. 1, 7, and 4. (f) Comparison of simulation results at points No. 7, 8, and 9.

Table 4.
The maximum temperature error between the experiment and the simulation.
The results show that the simulation of the four points aligns well with the experimental data in terms of the time of the maximum temperature, with a maximum error of 16 s (at No. 6) and a minimum of 1 s (at No. 3), while the temperature error ranges between 102.1–135.9 °C. Combined with the combustion characteristics analysis in Section 2.3.1, it was found that the three severe jet combustions of the battery occurred after 485 s, coinciding with the temperature inflection point. The severe jet combustion caused serious mass and heat losses of the sample, indicating a mismatch between the temperature rise and the heat generation rate of the battery. This phenomenon is currently difficult to express with the model and affects the accuracy of the simulation.
Figure 6 compares the simulated temperature curves for measurement points No. 1, 4, and 7, representing the temperature rise curves at the center of the top surface, the center of the battery, and the center of the bottom surface, respectively. Due to the thinness of the battery, it exhibits good temperature uniformity. However, there was a certain lag in the temperature at the center of the battery, which is slightly slower than the heating surfaces. During the heating process, there was an 8.6 °C temperature lag between the center and the heating surfaces, and the temperatures tended to converge after the heating stopped. Figure 6f presents the simulation results for the center temperature of the battery (No. 7), the center of end B (No. 8), and the center of end C (No. 9). The simulation results show that the center temperature of end B is higher than that at battery center before the temperature inflection point at 485 s. Meanwhile, because the top end of the battery was located away from the heating surface, the temperature at end C was much lower than that of the battery center and the center point of end B. The highest temperature occurred at the battery center, reaching 824.3 °C, followed by 807.8 °C at the center point of end B and 807.7 °C at the center point of end C.
The 3D model results in Figure 7 depict the TR triggered by surface heating in the battery within the first 500 s, describing the process of temperature diffusion within the battery. The battery is divided into 5 sections along the major surface direction, showing that there is little temperature difference across the thickness direction of the battery. As shown in Figure 7a–g, heat accumulation was observed at the edges of the battery (end A and end B) within the first 400 s, with the center point having the highest temperature point in the battery (No. 8). At 281 s, the temperature at No. 8 reached 171.2 °C, which is the melting temperature of the polypropylene (PP) adhesive used in the pouch battery sealing process. The high temperature combined with the internal pressure of the battery, collectively damaged the battery seal and caused venting. This effectively explains the occurrence of smoke emission from end A at 281.051 s (Figure 3b), followed by smoke emission from end B at 287.505 s (Figure 3c). At 500 s (Figure 7j), the battery heated up, with the temperature exceeding 700 °C.
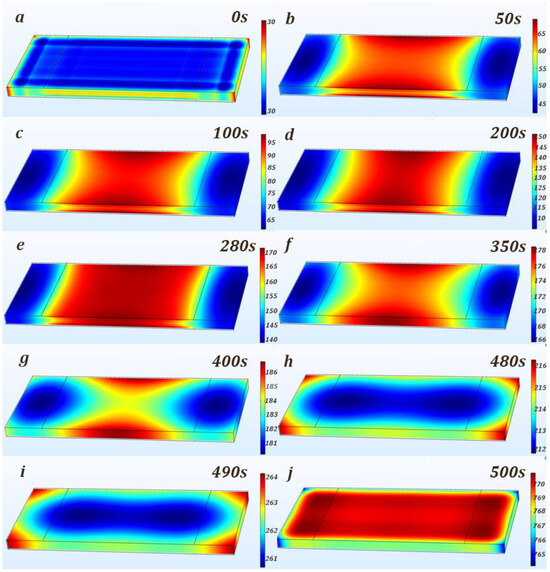
Figure 7.
3D simulation results of TR in batteries induced by surface heating. (a–j) The simulated temperature distribution at timepoints 0 s, 50 s, 100 s, 200 s, 280 s, 350 s, 400 s, 480 s, 490 s, and 500 s.
The concentration changes of various reactants during the TR process are shown in Figure 8. It is evident that before the inflection point at 480 s, the temperature rise was mainly caused by the decomposition of the SEI and electrolyte, which generate heat over a long reaction time. The decomposition of the SEI continued from 77 s to 291 s, while the electrolyte decomposition reaction lasted from 163 s to 494 s. At 480 s, the concentration of reactants at the negative and positive electrodes decreased rapidly, and the two phase transitions of the positive electrode occurred within a short time interval. This rapid reaction intensified the heat generation in the battery. The combination of this rapid reaction and the Joule heat from the separator rupture causing an ISC led to the rapid rise in battery temperature from 192.8 °C (at 486 s) to 719.1 °C (at 495 s).
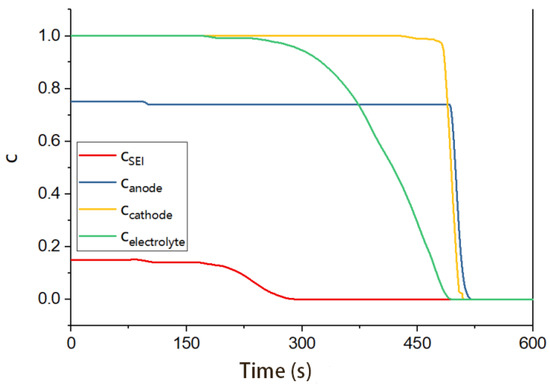
Figure 8.
Changes in reactant concentrations.
4. Conclusions
This study focused on the TR induced by surface heating in a 17.5 Ah ternary pouch battery. It provides a comprehensive record and analysis of the TR characteristics through methods such as video observation, temperature measurement, and voltage measurement. Furthermore, a surface heating-induced TR model was established based on the adiabatic TR model. The experimental and simulation results were used to elucidate the combustion behavior of the battery.
The experimental results indicate that the battery tends to vent from both lateral sides, due to the lower melting point of the PP adhesive sealing the pouch battery. The venting lasted for approximately 200 s until sparks were ejected from one end of the battery, whereupon that end burst into flames immediately. The combustion of the battery was caused by the ignition of the flammable gas and air mixture by ejected sparks. If sparks splash during the venting process, the combustible gas on that side will combust within a short time. In this experiment, there were a total of three instances of flame ejection, all following the sequence of venting, spark splashing, and flame ejection; yet, the ejections appeared to be disordered.
The simulation results of the established 3D surface heating-induced TR model are in good agreement with the experimental findings. Prior to the occurrence of massive ISC, the temperature deviation at all locations, except for point one, was below 15 °C, with a discrepancy of 30 °C. Additionally, a simulation of the battery temperature field revealed that under the given heating conditions, the highest temperature of the battery appeared at the center of ends A and B within the first 400 s. At the moment of battery venting (around t = 280.051 s), the simulation results showed that the temperatures at the center of ends A and B had already reached 170 °C, which is the melting point of the PP adhesive used for heat sealing the aluminum-plastic film battery shell. The continuous gas generation inside the battery, combined with the melting failure of the heat-sealing adhesive, caused the failure of the A and B end seals, explaining the tendency of the battery to vent from the sides. Prior to 480 s, the temperature rise of the battery was primarily attributed to the decomposition of the SEI and the electrolyte, although the resulting temperature rise rate was relatively slow. The rapid decrease in the concentration of the positive and negative electrode active materials occurred at around 480 s, combined with ISC, leading to a drastic rise in the battery temperature. This explains the intense jetting combustion of the battery within the rapid temperature increase interval at 480 s observed in the experiment. Based on the simulated changes in reactant concentrations, it is apparent that the battery experiences a rapid increase in temperature during the thermal runaway, which is incited by the decomposition of the positive and negative electrodes and massive ISC. The heat generated from the decomposition of SEI and electrolyte further elevates the battery’s temperature to levels that trigger the decomposition of the positive and negative electrodes and extensive internal short circuits. The established model effectively predicted the temperature and voltage characteristics of the battery, providing a valuable reference for engineers in designing battery systems.
Author Contributions
Writing—original draft, Z.W. and H.H.; Writing—review & editing, X.T.; Project administration, Y.Z. and H.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (NSFC, Grant No. 5217525).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal runaway mechanism of lithium ion battery for electric vehicles: A review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Spielbauer, M.; Berg, P.; Ringat, M.; Bohlen, O.; Jossen, A. Experimental study of the impedance behavior of 18650 lithium-ion battery cells under deforming mechanical abuse. J. Energy Storage 2019, 26, 101039. [Google Scholar] [CrossRef]
- Yiding, L.; Wenwei, W.; Cheng, L.; Xiaoguang, Y.; Fenghao, Z. Multi-physics safety model based on structure damage for lithium-ion battery under mechanical abuse. J. Clean. Prod. 2020, 277, 124094. [Google Scholar] [CrossRef]
- Wu, H.; Chen, S.; Hong, Y.; Xu, C.; Zheng, Y.; Jin, C.; Chen, K.; He, Y.; Feng, X.; Wei, X.; et al. Thermal safety boundary of lithium-ion battery at different state of charge. J. Energy Chem. 2024, 91, 59–72. [Google Scholar] [CrossRef]
- Lin, C.-K.; Ren, Y.; Amine, K.; Qin, Y.; Chen, Z. In situ high-energy X-ray diffraction to study overcharge abuse of 18650-size lithium-ion battery. J. Power Sources 2013, 230, 32–37. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, X.; Meng, N.; Yu, Z.; Yang, H. Study of thermal runaway and the combustion behavior of lithium-ion batteries overcharged with high current rates. Thermochim. Acta 2022, 715, 179276. [Google Scholar] [CrossRef]
- Guo, R.; Lu, L.; Ouyang, M.; Feng, X. Mechanism of the entire overdischarge process and overdischarge-induced internal short circuit in lithium-ion batteries. Sci. Rep. 2016, 6, 30248. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Wei, X.; Chen, S.; Zhu, J.; Han, G.; Tang, X.; Hua, W.; Dai, H.; Ye, J. Comprehensive Investigation of a Slight Overcharge on Degradation and Thermal Runaway Behavior of Lithium-Ion Batteries. ACS Appl. Mater. Interfaces 2021, 13, 35054–35068. [Google Scholar] [CrossRef] [PubMed]
- Ren, D.; Feng, X.; Liu, L.; Hsu, H.; Lu, L.; Wang, L.; He, X.; Ouyang, M. Investigating the relationship between internal short circuit and thermal runaway of lithium-ion batteries under thermal abuse condition. Energy Storage Mater. 2021, 34, 563–573. [Google Scholar] [CrossRef]
- Shelkea, A.V.; Buston, J.E.H.; Gill, J.; Howard, D.; Williams, R.C.E.; Read, E.; Abaza, A.; Cooper, B.; Richards, P.; Wen, J.X. Combined numerical and experimental studies of 21,700 lithium-ion battery thermal runaway induced by different thermal abuse. Int. J. Heat Mass Transf. 2022, 194, 123099. [Google Scholar] [CrossRef]
- Zhou, H.; Parmananda, M.; Crompton, K.R.; Hladky, M.P.; Dann, M.A.; Ostanek, J.K.; Mukherjee, P.P. Effect of electrode crosstalk on heat release in lithium-ion batteries under thermal abuse scenarios. Energy Storage Mater. 2022, 44, 326–341. [Google Scholar] [CrossRef]
- Liu, L.; Lin, C.; Fan, B.; Wang, F.; Lao, L.; Yang, P. A new method to determine the heating power of ternary cylindrical lithium ion batteries with highly repeatable thermal runaway test characteristics. J. Power Sources 2020, 472, 228503. [Google Scholar] [CrossRef]
- Tang, X.; Wei, X.; Zhang, H.; Li, D.; Zhang, G.; Wang, X.; Zhu, J.; Dai, H. Experimental and modeling analysis of thermal runaway for LiNi0.5Mn0.3Co0.2O2/graphite pouch cell under adiabatic condition. Int. J. Energy Res. 2021, 45, 10667–10681. [Google Scholar] [CrossRef]
- Lei, Z.; Maotao, Z.; Xiaoming, X.; Junkui, G. Thermal runaway characteristics on NCM lithium-ion batteries triggered by local heating under different heat dissipation conditions. Appl. Therm. Eng. 2019, 159, 113847. [Google Scholar] [CrossRef]
- Feng, X.; Zheng, S.; Ren, D.; He, X.; Wang, L.; Cui, H.; Liu, X.; Jin, C.; Zhang, F.; Xu, C.; et al. Investigating the thermal runaway mechanisms of lithium-ion batteries based on thermal analysis database. Appl. Energy 2019, 246, 53–64. [Google Scholar] [CrossRef]
- Wang, Q.; Huang, P.; Ping, P.; Du, Y.; Li, K.; Sun, J. Combustion behavior of lithium iron phosphate battery induced by external heat radiation. J. Loss Prev. Process Ind. 2017, 49, 961–969. [Google Scholar] [CrossRef]
- Jin, C.; Sun, Y.; Wang, H.; Lai, X.; Wang, S.; Chen, S.; Rui, X.; Zheng, Y.; Feng, X.; Wang, H.; et al. Model and experiments to investigate thermal runaway characterization of lithium-ion batteries induced by external heating method. J. Power Sources 2021, 504, 230065. [Google Scholar] [CrossRef]
- Feng, X.; Zheng, S.; He, X.; Wang, L.; Wang, Y.; Ren, D.; Ouyang, M. Time Sequence Map for Interpreting the Thermal Runaway Mechanism of Lithium-Ion Batteries with LiNixCoyMnzO2 Cathode. Front. Energy Res. 2018, 6, 126. [Google Scholar] [CrossRef]
- Xu, X.; Sun, X.; Zhao, L.; Li, R.; Tang, W. Research on thermal runaway characteristics of NCM lithium-ion battery under thermal-electrical coupling abuse. Ionics 2022, 28, 5449–5467. [Google Scholar] [CrossRef]
- Liu, X.; Ren, D.; Hsu, H.; Feng, X.; Xu, G.-L.; Zhuang, M.; Gao, H.; Lu, L.; Han, X.; Chu, Z.; et al. Thermal Runaway of Lithium-Ion Batteries without Internal Short Circuit. Joule 2018, 2, 2047–2064. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, T.; Wang, Q. Experimental study on the influence of different heating methods on thermal runaway of lithium-ion battery. J. Energy Storage 2021, 42, 103063. [Google Scholar] [CrossRef]
- Kim, G.-H.; Pesaran, A.; Spotnitz, R. A three-dimensional thermal abuse model for lithium-ion cells. J. Power Sources 2007, 170, 476–489. [Google Scholar] [CrossRef]
- Nyman, A.; Behm, M.; Lindbergh, G. Electrochemical characterisation and modelling of the mass transport phenomena in LiPF6–EC–EMC electrolyte. Electrochim. Acta 2008, 53, 6356–6365. [Google Scholar] [CrossRef]
- Zavalis, T.G.; Behm, M.; Lindbergh, G. Investigation of Short-Circuit Scenarios in a Lithium-Ion Battery Cell. J. Electrochem. Soc. 2012, 159, A848–A859. [Google Scholar] [CrossRef]
- Feng, X.; Lu, L.; Ouyang, M.; Li, J.; He, X. A 3D thermal runaway propagation model for a large format lithium ion battery module. Energy 2016, 115, 194–208. [Google Scholar] [CrossRef]
- Zhang, C.; Santhanagopalan, S.; Sprague, M.A.; Pesaran, A.A. Coupled mechanical-electrical-thermal modeling for short-circuit prediction in a lithium-ion cell under mechanical abuse. J. Power Sources 2015, 290, 102–113. [Google Scholar] [CrossRef]
- Yin, H.; Ma, S.; Li, H.; Wen, G.; Santhanagopalan, S.; Zhang, C. Modeling strategy for progressive failure prediction in lithium-ion batteries under mechanical abuse. eTransportation 2021, 7, 100098. [Google Scholar] [CrossRef]
- Guo, G.; Long, B.; Cheng, B.; Zhou, S.; Xu, P.; Cao, B. Three-dimensional thermal finite element modeling of lithium-ion battery in thermal abuse application. J. Power Sources 2010, 195, 2393–2398. [Google Scholar] [CrossRef]
- Gümüşsu, E.; Ekici, Ö.; Köksal, M. 3-D CFD modeling and experimental testing of thermal behavior of a Li-Ion battery. Appl. Therm. Eng. 2017, 120, 484–495. [Google Scholar] [CrossRef]
- Li, K.; Xu, C.; Wang, H.; Jin, C.; Rui, X.; Chen, S.; Feng, X.; Fan, L.; Ouyang, M. Investigation for the effect of side plates on thermal runaway propagation characteristics in battery modules. Appl. Therm. Eng. 2022, 201, 117774. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).