Optimal Allocation Stochastic Model of Distributed Generation Considering Demand Response
Abstract
1. Introduction
- (1)
- The price-based DR is adopted in the DG allocation, where the detailed functions of DR (such as increasing the accommodation rate of wind power and solar power and reducing the total cost) are analyzed.
- (2)
- The uncertainty of wind power and solar power is addressed by the stochastic optimization method, where multiple scenarios of wind and solar power are generated by the k-means method.
2. Uncertainty Handling
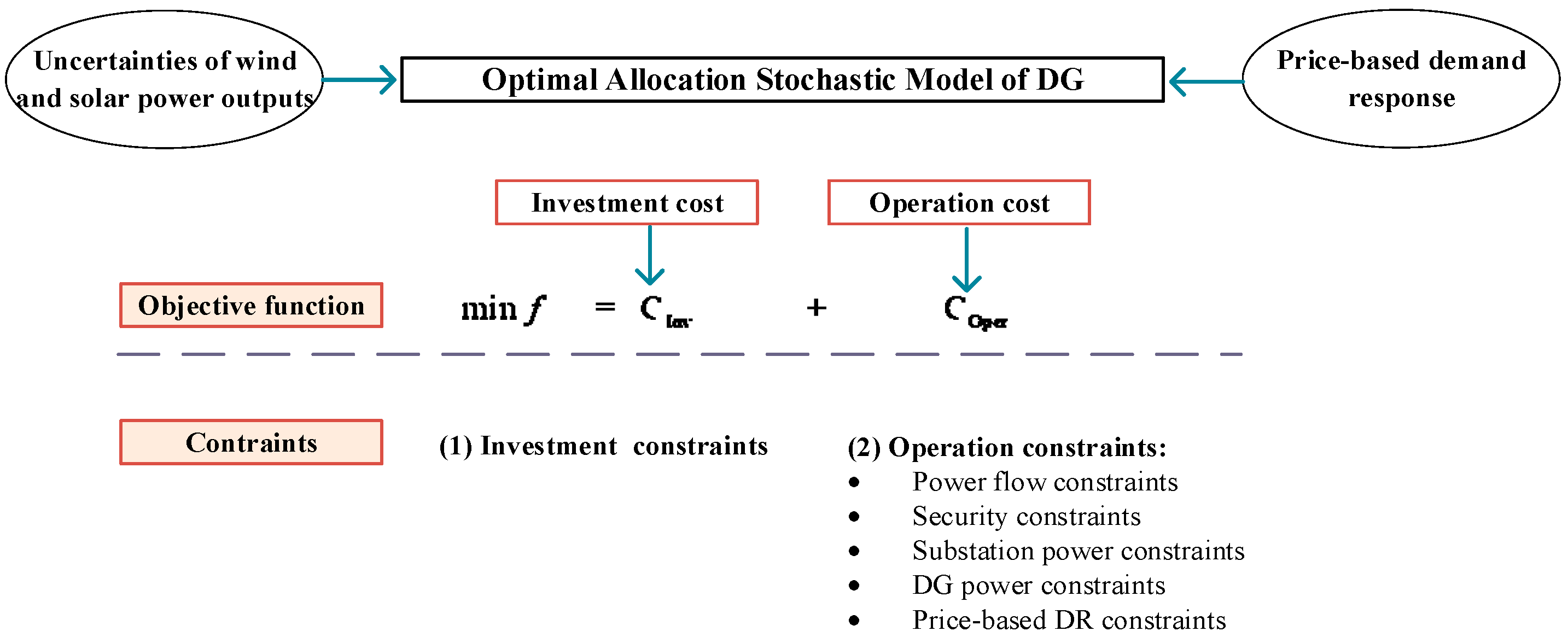
3. Optimal Allocation Model for DG
3.1. Objective Function
3.2. Constraints
3.2.1. Investment Constraints
3.2.2. Operation Constraints
- (a)
- Power flow constraints.
- (b)
- Security constraints.
- (c)
- Substation power constraints.
- (d)
- DG power constraints.
- (e)
- Price-based DR constraints.
4. Problem Reformulation
4.1. Reformulation of the Net Annual Profit
4.2. Reformulation of the Power Flow Model
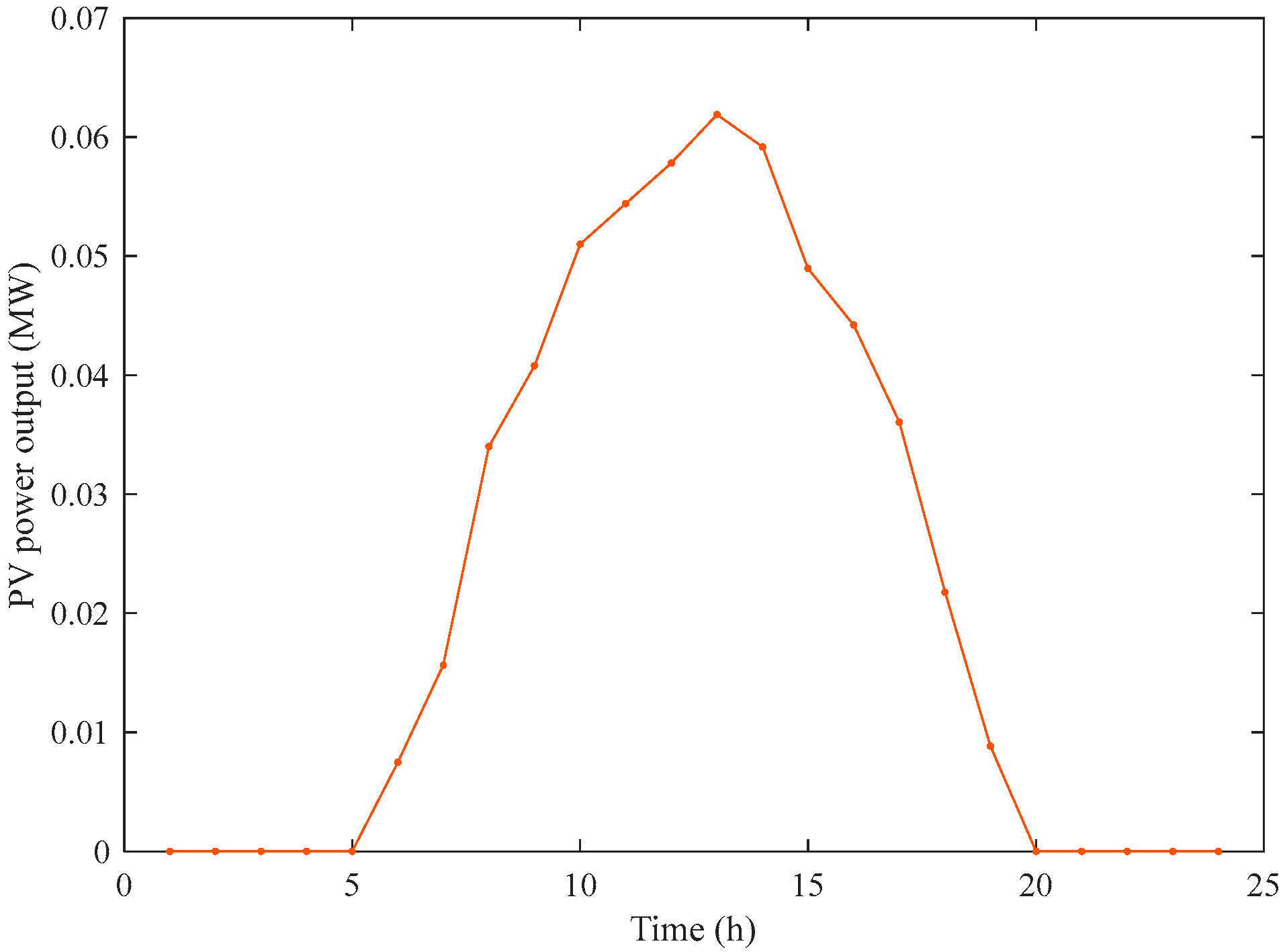
5. Case Studies
5.1. Impact of DR on Planning Results
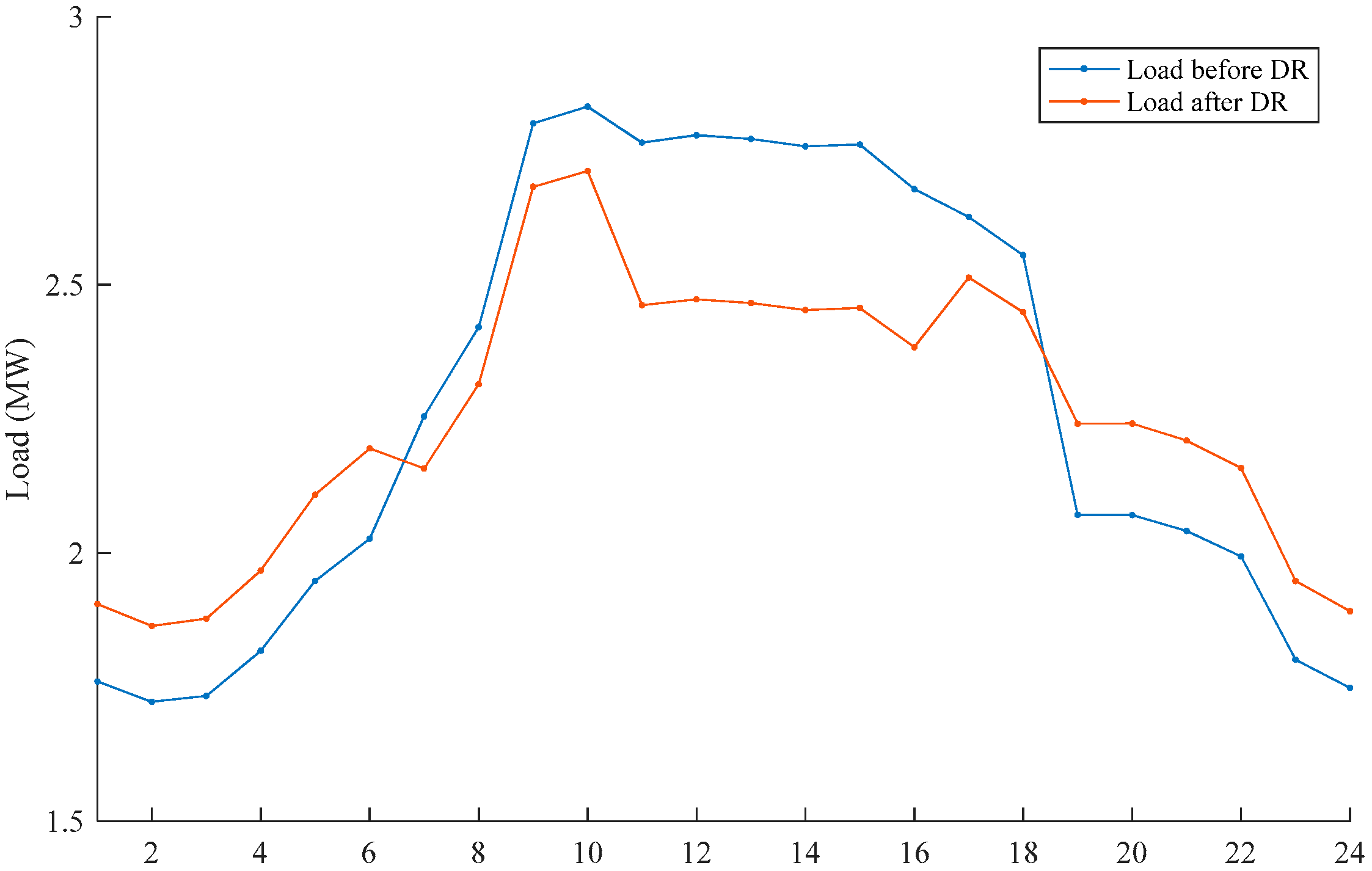
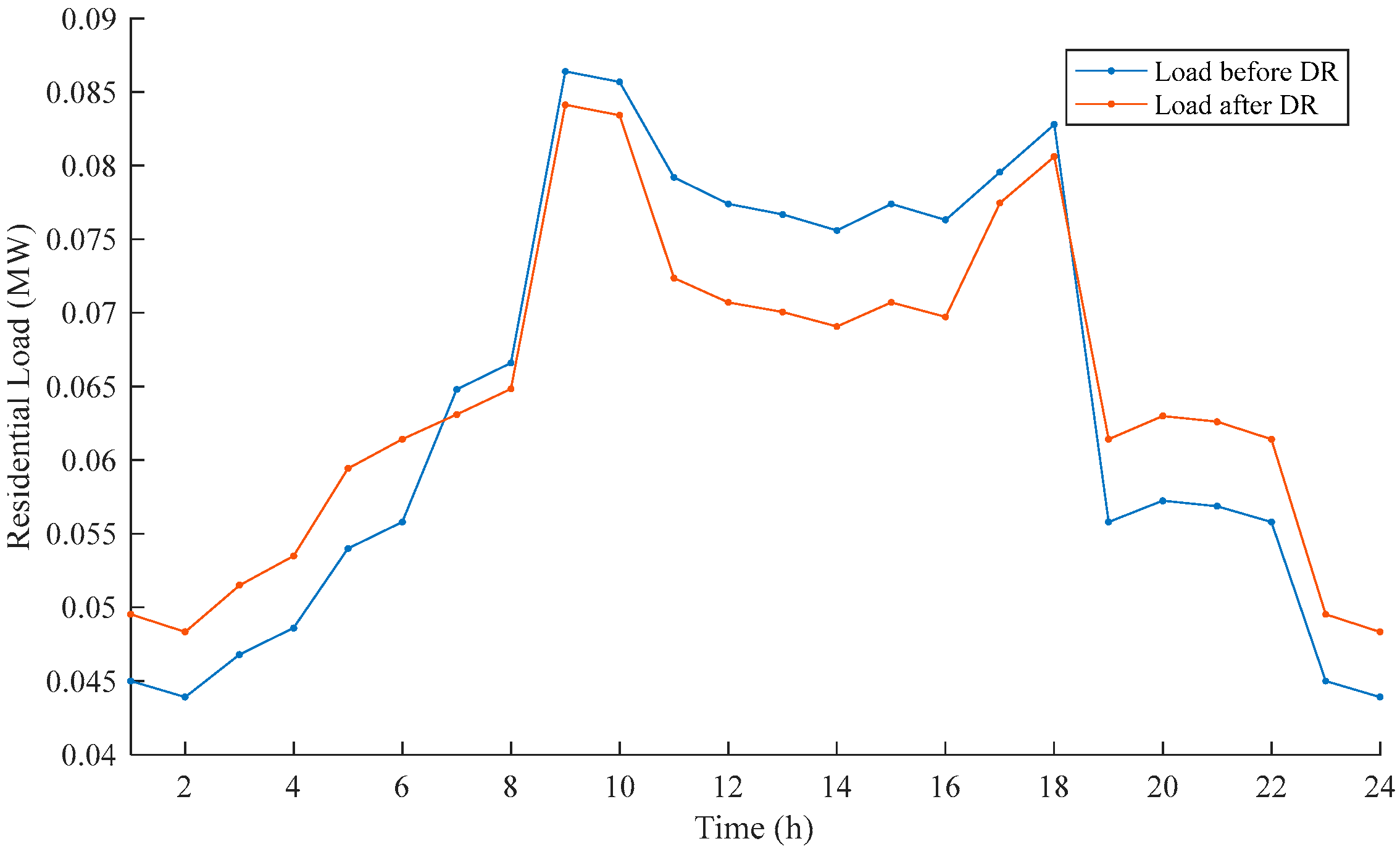
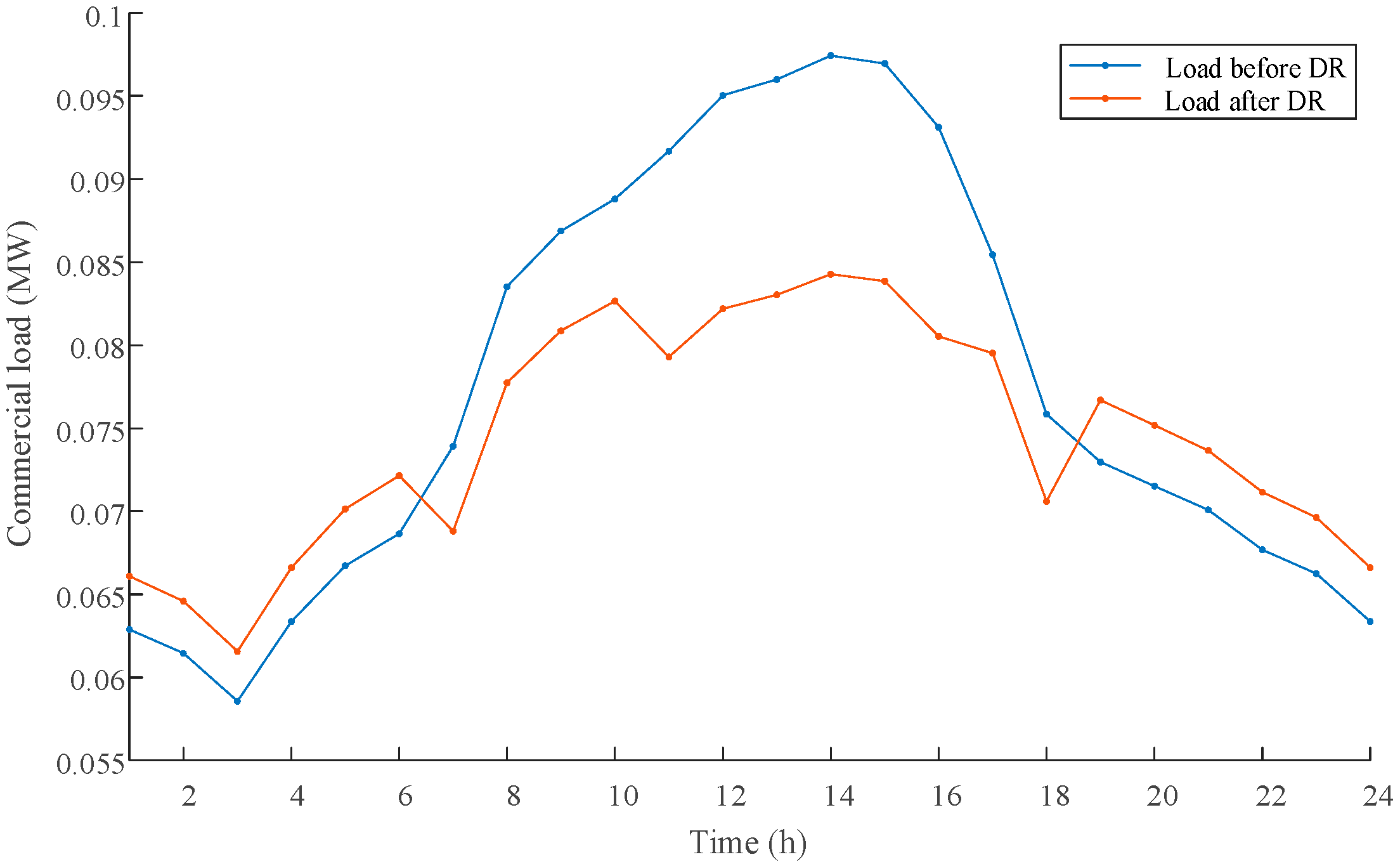
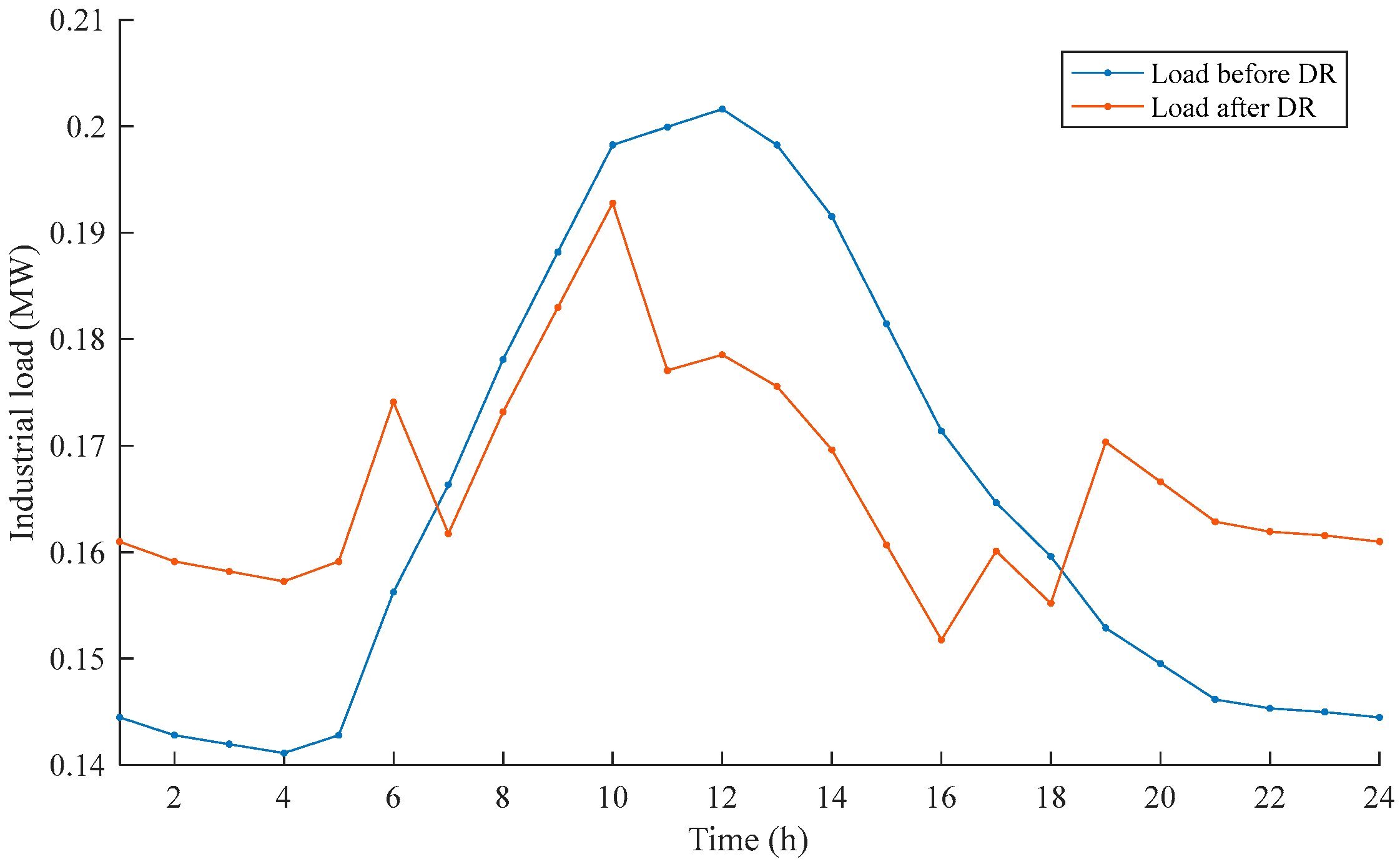
5.2. Impact of DR on Load Curves
5.3. Impact of DR Capacity Limit on Planning Results
6. Conclusions
- (1)
- DR can improve the allocation of DG by improving the renewable energy accommodation ability of a distribution network. Meanwhile, DR can also increase the profits of the power company and significantly reduce the annual total cost of the power company when planning distributed generations in the distribution network. The network flow of the system can be improved and network losses reduced. However, the system may experience a loss of load as a result.
- (2)
- DR shows a significant effect on peak shaving and valley filling. Compared with the planning results without DR, DR can significantly adjust the system load curve and user electricity consumption habits. Different types of users have different sensitivities to electricity prices, resulting in varying degrees of participation in demand response. Residential users have the smallest sensitivity to electricity prices while industrial users are the most sensitive to electricity prices.
- (3)
- The DR response capacity limit has a significant impact on optimization results. The larger the upper limit of DR response capacity is, the higher the system’s accommodation of renewable energy is. However, an increase in the upper limit of the DR response capacity may cause more severe system load loss and even generate new peak loads. The probability of encountering security threats in the system may increase, which affects the safe and stable operation of the system. Therefore, it is necessary to reasonably consider DR response capacity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| DG | Distributed generation. |
| DR | Demand response. |
| MTG | Micro-turbine generation. |
| PV | Photovoltaic generation. |
| RO | Robust optimization. |
| SO | Stochastic optimization. |
| WTG | Wind-turbine generation. |
| Indices | |
| i, j, k | Index of buses. |
| ij, ki | Index of lines. |
| s | Index of scenarios. |
| t, t′ | Index of time slots. |
| Sets | |
| // //// | Bus set of WTG/PV/MTG/system node/load/substation/lines. |
| Parameters | |
| Own elasticity or cross elasticity. | |
| Price before demand response. | |
| / | The upper/lower limits of price. |
| / | Price to transmission/power losses. |
| / | Price to load loss/MTG generation power. |
| // | Capital cost of WTG/PV/MTG. |
| / | Price of WTG power curtailment/PV power curtailment. |
| The upper limit of current. | |
| lki/lij | Length of line ki/ij. |
| Number of total scenarios. | |
| // | The maximal installation number of WTG/PV/MTG. |
| Probability value of each scenario. | |
| Active load before demand response. | |
| / | The upper limits of active/reactive power injected by the substation. |
| / | The upper/lower limits of active load after demand response. |
| / | The upper/lower limits of active power of MTG. |
| / | Forecast power of WTG/PV in typical scenarios. |
| r | Discount rate |
| Rij, Rki/Xij, Xki | Resistance/reactance of line ij/ki. |
| / | The upper/lower limits of voltage. |
| The lifespan of DG. | |
| Variables | |
| Price after demand response. | |
| / | Current of line ki/ij. |
| / | Active/reactive load after demand response. |
| Power losses through line ij. | |
| / | Active/reactive power of PV. |
| / | Active/reactive power of MTG. |
| , /, | Active/reactive power of line ij/ki. |
| / | Active/reactive power injected by the substation. |
| / | Active/reactive power of WTG. |
| Integer variables; numbers of some elements (WTG, PV and MTG) | |
| / | Voltage at node i/j. |
| , /, | Auxiliary variables; square of branch current branch and bus voltage. |
References
- Salama, H.S.; Magdy, G.; Bakeer, A.; Vokony, I. Adaptive coordination control strategy of renewable energy sources, hydrogen production unit, and fuel cell for frequency regulation of a hybrid distributed power system. Prot. Control Mod. Power Syst. 2022, 7, 34. [Google Scholar] [CrossRef]
- Uma, U.U.; Nmadu, D.; Ugwuanyi, N.; Ogah, O.E.; Eli-Chukwu, N.; Eheduru, M.; Ekwue, A. Adaptive overcurrent protection scheme coordination in presence of distributed generation using radial basis neural network. Prot. Control Mod. Power Syst. 2023, 8, 1–19. [Google Scholar] [CrossRef]
- Shu, H.; Li, W.; Wang, G.; Han, Y.; Li, J.; Tang, Y. Online Collaborative Estimation Technology for SOC and SOH of Frequency Regulation of a Lead-Carbon Battery in a Power System with a High Proportion of Renewable Energy. Prot. Control Mod. Power Syst. 2024, 9, 52–64. [Google Scholar] [CrossRef]
- Zhang, D.; Shafiullah, G.M.; Das, C.K.; Wong, K.W. A systematic review of optimal planning and deployment of distributed generation and energy storage systems in power networks. J. Energy Storage 2022, 56, 105937. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, G.; Li, K.; Li, B.; Chi, H.; Yao, Y.; Fan, Z. Reactive power optimization of a distribution network with high-penetration of wind and solar renewable energy and electric vehicles. Prot. Control Mod. Power Syst. 2022, 7, 51. [Google Scholar] [CrossRef]
- He, Q.; Lin, Z.; Chen, H.; Dai, X.; Li, Y.; Zeng, X. Bi-level optimization based two-stage market clearing model considering guaranteed accommodation of renewable energy generation. Prot. Control Mod. Power Syst. 2022, 7, 30. [Google Scholar] [CrossRef]
- Fathabad, A.M.; Cheng, J.; Pan, K.; Qiu, F. Data-driven planning for renewable distributed generation integration. IEEE Trans. Power Syst. 2020, 35, 4357–4368. [Google Scholar] [CrossRef]
- Kumar, S.; Manjrekar, V.; Singh, V.; Lad, B.K. Integrated yet distributed operations planning approach: A next generation manufacturing planning system. J. Manuf. Syst. 2020, 54, 103–122. [Google Scholar] [CrossRef]
- Ali, Z.M.; Diaaeldin, I.M.; El-Rafei, A.; Hasanien, H.M.; Aleem, S.H.A.; Abdelaziz, A.Y. A novel distributed generation planning algorithm via graphically-based network reconfiguration and soft open points placement using Archimedes optimization algorithm. Ain Shams Eng. J. 2021, 12, 1923–1941. [Google Scholar] [CrossRef]
- Rigo-Mariani, R.; Vai, V. An iterative linear distflow for dynamic optimization in distributed generation planning studies. Int. J. Electr. Power Energy Syst. 2022, 138, 107936. [Google Scholar] [CrossRef]
- Bai, W.; Zhang, W.; Allmendinger, R.; Enyekwe, I.; Lee, K.Y. A Comparative Study of Optimal PV Allocation in a Distribution Network Using Evolutionary Algorithms. Energies 2024, 17, 511. [Google Scholar] [CrossRef]
- Prakash, R. Optimal Distributed Generation Planning Considering Economic and Operational Aspects. Electr. Power Compon. Syst. 2023, 1–16. [Google Scholar] [CrossRef]
- Ding, X.; Xu, J.; Sun, Y.; Liao, S.; Zheng, J. A demand side controller of electrolytic aluminum industrial microgrids considering wind power fluctuations. Prot. Control Mod. Power Syst. 2022, 7, 49. [Google Scholar] [CrossRef]
- Fan, D.; Zhang, S.; Huang, H.; Zhou, L.; Wang, Y.; Xiao, X. Three-stage day-ahead scheduling strategy for regional thermostatically controlled load aggregators. Prot. Control Mod. Power Syst. 2023, 8, 19. [Google Scholar] [CrossRef]
- Gao, H.; Wang, R.; He, S.; Wang, Z.; Liu, J. Bi-level Stackelberg game-based distribution system expansion planning model considering long-term renewable energy contracts. Prot. Control Mod. Power Syst. 2023, 8, 62. [Google Scholar] [CrossRef]
- Koutsoukis, N.C.; Georgilakis, P.S. A multistage distribution network planning method considering distributed generation active management and demand response. IET Renew. Power Gener. 2022, 16, 65–76. [Google Scholar] [CrossRef]
- Dang, C.; Wang, X.; Shao, C.; Wang, X. Distributed generation planning for diversified participants in demand response to promote renewable energy integration. J. Mod. Power Syst. Clean Energy 2019, 7, 1559–1572. [Google Scholar] [CrossRef]
- Melgar-Dominguez, O.D.; Pourakbari-Kasmaei, M.; Lehtonen, M.; Mantovani, J.R.S. An economic-environmental asset planning in electric distribution networks considering carbon emission trading and demand response. Electr. Power Syst. Res. 2020, 181, 106202. [Google Scholar] [CrossRef]
- Xu, W.; Zhou, D.; Huang, X.; Lou, B.; Liu, D. Optimal allocation of power supply systems in industrial parks considering multi-energy complementarity and demand response. Appl. Energy 2020, 275, 115407. [Google Scholar] [CrossRef]
- He, S.; Gao, H.; Tian, H.; Wang, L.; Liu, Y.; Liu, J. A two-stage robust optimal allocation model of distributed generation considering capacity curve and real-time price based demand response. J. Mod. Power Syst. Clean Energy 2020, 9, 114–127. [Google Scholar] [CrossRef]
- Fu, X. Statistical machine learning model for capacitor planning considering uncertainties in photovoltaic power. Prot. Control Mod. Power Syst. 2022, 7, 5. [Google Scholar] [CrossRef]
- Fu, X.; Wu, X.; Zhang, C.; Fan, S.; Liu, N. Planning of distributed renewable energy systems under uncertainty based on statistical machine learning. Prot. Control Mod. Power Syst. 2022, 7, 41. [Google Scholar] [CrossRef]
- Xiao, D.; Chen, H.; Cai, W.; Wei, C.; Zhao, Z. Integrated risk measurement and control for stochastic energy trading of a wind storage system in electricity markets. Prot. Control Mod. Power Syst. 2023, 8, 1–11. [Google Scholar] [CrossRef]
- Wang, J.; Xie, N.; Huang, C.; Wang, Y. Two-stage stochastic-robust model for the self-scheduling problem of an aggregator participating in energy and reserve markets. Prot. Control Mod. Power Syst. 2023, 8, 1–20. [Google Scholar] [CrossRef]
- Roy, T.K.; Ghosh, S.K.; Saha, S. Robust backstepping global integral terminal sliding mode controller to enhance dynamic stability of hybrid AC/DC microgrids. Prot. Control Mod. Power Syst. 2023, 8, 8. [Google Scholar] [CrossRef]
- Yin, M.; Li, K.; Yu, J. A data-driven approach for microgrid distributed generation planning under uncertainties. Appl. Energy 2022, 309, 118429. [Google Scholar] [CrossRef]
- Jin, W.; Zhang, S.; Li, J. Robust planning of distributed generators in active distribution network considering network reconfiguration. Appl. Sci. 2023, 13, 7747. [Google Scholar] [CrossRef]
- Bazrafshan, M.; Yalamanchili, L.; Gatsis, N.; Gomez, J. Stochastic planning of distributed PV generation. Energies 2019, 12, 459. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. Coordinated investment planning of distributed multi-type stochastic generation and battery storage in active distribution networks. IEEE Trans. Sustain. Energy 2018, 10, 1813–1822. [Google Scholar] [CrossRef]
- Sunderland, K.; Woolmington, T.; Blackledge, J.; Conlon, M. Small wind turbines in turbulent (urban) environments: A consideration of normal and Weibull distributions for power prediction. J. Wind Eng. Ind. Aerodyn. 2013, 121, 70–81. [Google Scholar] [CrossRef]
- Lei, K.; Chang, J.; Wang, X.; Guo, A.; Wang, Y.; Ren, C. Peak shaving and short-term economic operation of hydro-wind-PV hybrid system considering the uncertainty of wind and PV power. Renew. Energy 2023, 215, 118903. [Google Scholar] [CrossRef]




| Node Type | Period | Peak Period | Flat Period | Valley Period |
|---|---|---|---|---|
| Residential | Peak period | −0.150 | 0.080 | 0.070 |
| Flat period | 0.080 | −0.140 | 0.050 | |
| Valley period | 0.070 | 0.050 | −0.120 | |
| Commercial | Peak period | −0.180 | 0.070 | 0.050 |
| Flat period | 0.070 | −0.170 | 0.030 | |
| Valley period | 0.050 | 0.030 | −0.160 | |
| Industrial | Peak period | −0.180 | 0.100 | 0.080 |
| Flat period | 0.100 | −0.180 | 0.060 | |
| Valley period | 0.080 | 0.060 | −0.160 |
| Parameters | Value |
|---|---|
| The lifetime of DG (year) | 20 |
| The discount rate | 0.08 |
| The losses price (USD/MWh) | 500 |
| The generation price of MTG (USD/MWh) | 85 |
| The price of wind power curtailed (USD/MWh) | 120 |
| The price of PV power curtailed (USD/MWh) | 80 |
| The price of loss of load (USD/MWh) | 130 |
| Results | Case 1 | Case 2 | |
|---|---|---|---|
| DG | WTG | 9 at bus 3; 4 at bus 17; 1 at bus 21 | 10 at bus 3; 5 at bus 17; 2 at bus 21 |
| PV | 3 at bus 16; 0 at bus 19; 8 at bus 30; 6 at bus 31 | 4 at bus 16; 0 at bus 19; 9 at bus 30; 7 at bus 31 | |
| MTG | 0 at bus 2; 1 at bus 10 | 0 at bus 2; 1 at bus 10 | |
| Cost (USD × 106) | Total cost | 6.6600 | 5.4946 |
| Network loss cost | 0.5865 | 0.5088 | |
| Penalty costs of wind power | 0.2642 | 0.2742 | |
| Penalty costs of solar power | 0.0991 | 0.1089 | |
| DR cost | 0 | −1.1615 | |
| Cost of energy not supplied | 0 | 0.0158 | |
| Results | Percentage of the DR Capacity Limit Accounting for the Predicted Load (%) | ||||||
|---|---|---|---|---|---|---|---|
| 5 | 15 | 25 | |||||
| Planning scheme | MTG | 2(0) | 10(1) | 2(0) | 10(1) | 2(0) | 10(1) |
| PV | 16(3) | 19(0) | 16(4) | 19(0) | 16(5) | 19(2) | |
| 30(8) | 31(6) | 30(9) | 31(7) | 30(8) | 31(7) | ||
| WTG | 3(10) | 17(5) | 3(10) | 17(5) | 3(10) | 17(4) | |
| 21(3) | 21(2) | 21(2) | |||||
| Cost (USD × 106) | Total cost | 5.6399 | 5.4946 | 5.4554 | |||
| Network loss cost | 0.5427 | 0.5088 | 0.4803 | ||||
| Penalty costs of wind power | 0.3139 | 0.2742 | 0.2393 | ||||
| Penalty costs of solar power | 0.1097 | 0.1089 | 0.1012 | ||||
| DR cost | −0.7586 | −1.1615 | −1.1924 | ||||
| Cost of energy not supplied | 0.0314 | 0.0158 | 0.0309 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, S.; Liu, J. Optimal Allocation Stochastic Model of Distributed Generation Considering Demand Response. Energies 2024, 17, 795. https://doi.org/10.3390/en17040795
He S, Liu J. Optimal Allocation Stochastic Model of Distributed Generation Considering Demand Response. Energies. 2024; 17(4):795. https://doi.org/10.3390/en17040795
Chicago/Turabian StyleHe, Shuaijia, and Junyong Liu. 2024. "Optimal Allocation Stochastic Model of Distributed Generation Considering Demand Response" Energies 17, no. 4: 795. https://doi.org/10.3390/en17040795
APA StyleHe, S., & Liu, J. (2024). Optimal Allocation Stochastic Model of Distributed Generation Considering Demand Response. Energies, 17(4), 795. https://doi.org/10.3390/en17040795






